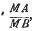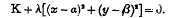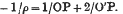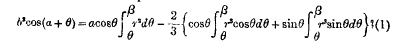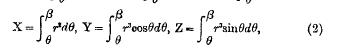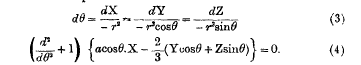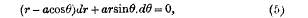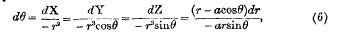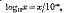Office-Bearers
Office-Bearers
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 1
-
- Article
-
- You have access
- Export citation
Research Article
Solutions of Euclid's Problems, with a rule and one fixed aperture of the compasses, by the Italian geometers of the sixteenth century
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 2-22
-
- Article
-
- You have access
- Export citation
Composition de Mathématiques Élémentaires proposée au Concours d' Agrégation de 1886
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 23-28
-
- Article
-
- You have access
- Export citation
The Equilateral and the Equiangular Polygon
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 28-38
-
- Article
-
- You have access
- Export citation
On Certain Inverse Roulette Problems
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 38-50
-
- Article
-
- You have access
- Export citation
Other
Trigonometrical Mnemonics
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 50
-
- Article
-
- You have access
- Export citation
Research Article
Proof of a Geometrical Theorem
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 51
-
- Article
-
- You have access
- Export citation
On Vortices
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 52-59
-
- Article
-
- You have access
- Export citation
Other
A Trigonometrical Note
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 61
-
- Article
-
- You have access
- Export citation
Research Article
A Theorem in Algebra
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 59-61
-
- Article
-
- You have access
- Export citation
Historical Notes on a Geometrical Theorem and its Developments. [18th century.]
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 62-78
-
- Article
-
- You have access
- Export citation
Geometrical Notes
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 78-83
-
- Article
-
- You have access
- Export citation
On the value of Δn0m/nm, when m and n are very large
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 83-84
-
- Article
-
- You have access
- Export citation
Sur les cordes communes à une conique et à un cercle de rayon nul: Application à la théorie géométrique des foyers dans les coniques
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 84-92
-
- Article
-
- You have access
- Export citation
Note on the Kinematics of a Quadrilateral
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 92-93
-
- Article
-
- You have access
- Export citation
Other
Some Correspondence between Robert Simson, Professor of Mathematics in the University of Glasgow, and Matthew Stewart, Professor of Mathematics in the University of Edinburgh
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 94
-
- Article
-
- You have access
- Export citation
Research Article
An Experiment in the Teaching of Geometry
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 94-97
-
- Article
-
- You have access
- Export citation
Note on Milner's Lamp
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 97-98
-
- Article
-
- You have access
- Export citation
On a Differential Equation and the Construction of Milner's Lamp
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 99-101
-
- Article
-
- You have access
- Export citation
An Exercise on Logarithmic Tables
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 101-102
-
- Article
-
- You have access
- Export citation