Most read
This page lists the top ten most read articles for this journal based on the number of full text views and downloads recorded on Cambridge Core over the last 90 days. This list is updated on a daily basis.
Contents
Irrational-slope versions of thompson's groups T and V
- Part of:
-
- Published online by Cambridge University Press:
- 11 February 2022, pp. 244-262
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Schur-Cohn theorem for matrix polynomials
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 337-366
-
- Article
-
- You have access
- Export citation
Homotopy of the exceptional Lie group G2
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 145-169
-
- Article
-
- You have access
- Export citation
The six trisectors of each of the angles of a triangle
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 119-131
-
- Article
-
- You have access
- Export citation
Bessel-integral functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 276-285
-
- Article
-
- You have access
- Export citation
A Matrix Form of Taylor's Theorem
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 33-54
-
- Article
-
- You have access
- Export citation
w. G. Cochran, Sampling Techniques (John Wiley & Sons, 2nd edition, 1963), ix+413 pp., 72s.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 342-343
-
- Article
-
- You have access
- Export citation
Mean Value Theorems for Vector Valued Functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 197-209
-
- Article
-
- You have access
- Export citation
Dehn surgeries on some classical links
- Part of:
-
- Published online by Cambridge University Press:
- 19 January 2011, pp. 33-45
-
- Article
-
- You have access
- Export citation
History of the Nine-point Circle
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 19-57
-
- Article
-
- You have access
- Export citation
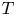
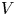
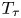
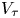
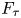
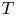
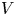
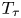
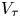
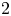
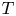
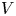
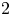
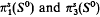 respectively.)
respectively.)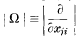 , where
, where 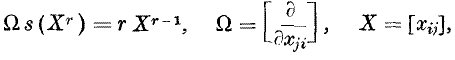

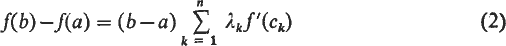
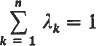 .
.