Compact hypersurfaces in a unit sphere
Published online by Cambridge University Press: 12 July 2007
Abstract
We study curvature structures of compact hypersurfaces in the unit sphere Sn+1(1) with two distinct principal curvatures. First of all, we prove that the Riemannian product 
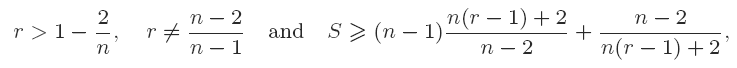 where n(n − 1)r is the scalar curvature of hypersurfaces and c2 = (n − 2)/nr. This generalized the result of Cheng, where the scalar curvature is constant is assumed. Secondly, we prove that the Riemannian product
where n(n − 1)r is the scalar curvature of hypersurfaces and c2 = (n − 2)/nr. This generalized the result of Cheng, where the scalar curvature is constant is assumed. Secondly, we prove that the Riemannian product 
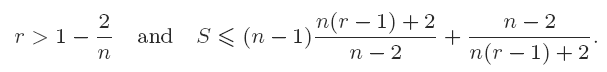 This gives a partial answer for the problem proposed by Cheng.
This gives a partial answer for the problem proposed by Cheng.
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 135 , Issue 6 , December 2005 , pp. 1129 - 1137
- Copyright
- Copyright © Royal Society of Edinburgh 2005
- 5
- Cited by

