Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lacey, A. A.
1986.
Global blow-up of a nonlinear heat equation.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 104,
Issue. 1-2,
p.
161.
Friedman, Avner
and
Lacey, Andrew A.
1987.
The Blow-Up Time for Solutions of Nonlinear Heat Equations with Small Diffusion.
SIAM Journal on Mathematical Analysis,
Vol. 18,
Issue. 3,
p.
711.
Bebernes, J.
and
Troy, W.
1987.
Existence for the modified Kassoy problem.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 106,
Issue. 1-2,
p.
131.
Bebernes, J.
and
Troy, W.
1987.
Nonexistence for the Kassoy Problem.
SIAM Journal on Mathematical Analysis,
Vol. 18,
Issue. 4,
p.
1157.
Berger, Marsha
and
Kohn, Robert V.
1988.
A rescaling algorithm for the numerical calculation of blowing‐up solutions.
Communications on Pure and Applied Mathematics,
Vol. 41,
Issue. 6,
p.
841.
Friedman, Avner
1988.
Nonlinear Diffusion Equations and Their Equilibrium States I.
Vol. 12,
Issue. ,
p.
301.
Chipot, M.
and
Weissler, F. B.
1989.
Some Blowup Results for a Nonlinear Parabolic Equation with a Gradient Term.
SIAM Journal on Mathematical Analysis,
Vol. 20,
Issue. 4,
p.
886.
Stuart, A. M.
and
Floater, M. S.
1990.
On the computation of blow-up.
European Journal of Applied Mathematics,
Vol. 1,
Issue. 1,
p.
47.
Herrero, M. A.
and
Vel�zquez, J. J. L.
1990.
Asymptotic properties of a semilinear heat equation with strong absorption and small diffusion.
Mathematische Annalen,
Vol. 288,
Issue. 1,
p.
675.
Floater, M. S.
1991.
Blow-up at the boundary for degenerate semilinear parabolic equations.
Archive for Rational Mechanics and Analysis,
Vol. 114,
Issue. 1,
p.
57.
Hu, Bei
1992.
A nonlinear nonlocal parabolic equation for channel flow.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 18,
Issue. 10,
p.
973.
Velázquez, J. J. L.
1992.
Higher Dimensional Blow Up for Semilinear Parabolic Equations.
Communications in Partial Differential Equations,
Vol. 17,
Issue. 9-10,
p.
1567.
Herrero, M. A.
and
Velázquez, J. J. L.
1992.
Blow–Up Profiles in One–Dimensional. Semilinear Parabolic Problems.
Communications in Partial Differential Equations,
Vol. 17,
Issue. 1-2,
p.
205.
Velázquez, J. J. L.
1993.
Classification of singularities for blowing up solutions in higher dimensions.
Transactions of the American Mathematical Society,
Vol. 338,
Issue. 1,
p.
441.
Herrero, M.A.
and
Velázquez, J.J.L.
1993.
Blow-up behaviour of one-dimensional semilinear parabolic equations.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 10,
Issue. 2,
p.
131.
King, J.R.
1994.
Asymptotic results for nonlinear outdiffusion.
European Journal of Applied Mathematics,
Vol. 5,
Issue. 3,
p.
359.
Chan, C. Y.
and
Kong, P. C.
1997.
Channel flow of a viscous fluid in the boundary layer.
Quarterly of Applied Mathematics,
Vol. 55,
Issue. 1,
p.
51.
Budd, C. J.
Galaktionov, V. A.
and
Chen, Jianping
1998.
Focusing blow-up for quasilinear parabolic equations.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 128,
Issue. 5,
p.
965.
Giga, Yoshikazu
and
Umeda, Noriaki
2006.
On blow-up at space infinity for semilinear heat equations.
Journal of Mathematical Analysis and Applications,
Vol. 316,
Issue. 2,
p.
538.
Ma, Zhongtai
and
Wen, Guochun
2007.
Iterative approximation of solutions for semilinear parabolic equations system.
Journal of Computational and Applied Mathematics,
Vol. 209,
Issue. 2,
p.
167.
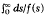 is finite, are known to exhibit the phenomenon of blow-up, i.e. for sufficiently large S, u becomes infinite after a finite time t*. We consider one-dimensional problems in the semi-infinite region x>0 and find the time to blow-up (t*). Also, the limiting behaviour of u as t→t*- and x→∞ is determined; in particular, it is seen that u blows up at infinity, i.e. for any given finite x, u is bounded as t→t*. The results are extended to problems with convection.
is finite, are known to exhibit the phenomenon of blow-up, i.e. for sufficiently large S, u becomes infinite after a finite time t*. We consider one-dimensional problems in the semi-infinite region x>0 and find the time to blow-up (t*). Also, the limiting behaviour of u as t→t*- and x→∞ is determined; in particular, it is seen that u blows up at infinity, i.e. for any given finite x, u is bounded as t→t*. The results are extended to problems with convection.

