1 INTRODUCTION
The Planck mass, mP = √ℏc/G, is a fundamental quantity of stellar astrophysics. The Chandrasekhar mass to order unity is mC = m 3 p /m 2 p , where mp is the proton mass. The maximum mass of a star is approximately the Chandrasekhar mass multiplied by the square of the ratio of radiation pressure to gas pressure (Eddington Reference Eddington1917). The minimum mass of a black hole is within order unity of the Planck mass. Variation of Newton’s constant affects supernova cosmology via change in the Planck mass over cosmic time and was first considered by Gaztañaga et al. (Reference Gaztañaga2002). At that time there were 42 SNe available; there are now 581 (Suzuki et al. Reference Suzuki2012).
Uzan (Reference Uzan2003), Narimani, Moss, & Scott (Reference Narimani2012), and Moss, Nariamni, & Scott (Reference Moss2010) advise that constraining the constancy of dimensional quantities is perilous. Preferred quantities are, for example, the ‘gravitational fine structure constant’, αg≡Gm 2 p/ℏc. The lunar laser ranging experiment initiated by NASA’s Apollo mission is an αg experiment, monitoring the specific potential energy of the Earth-Moon system Gm 2 p/ct, where t is the time of flight of Earth launched photons. Measuring the luminosity distance of galaxies, DL , from type Ia supernovae is an αg experiment, as D 2 L ∝mC /mp , assuming a fixed fraction, f, of mC is turned into energy and stellar luminosities are calibrated by hydrogen burning stars. Specifically, to within a numerical constant of order unity, mC /mp = α−3/2 g.
Speculation about varying G began with Dirac (Reference Dirac1937), who noted that the ratio of the electrostatic and gravitational forces between an electron and a proton was of the same order as the number of times an electron orbits a proton in the age of the Universe. He conjectured that αg might decay as the inverse of cosmic time. This 20th century gravity problem (which is sometimes tackled anthropically) has been totally eclipsed in the last decade by the cosmological constant problem (Solà Reference Solà2013). The contribution to the vacuum energy density of fluctuations in the gravitational field is larger than is observationally allowed by some 120 orders of magnitude. Instead, the vacuum energy density is of the same order of magnitude as the present mass density of the Universe. Although ongoing type Ia supernova observations indicate that the equation of state of Einstein’s General Relativity is the best fit, this gross cosmological constant problem provides no comfort for constant G orthodoxy.
Garcia-Berro et al. (Reference Garcia-Berro2007) review astronomical measurements and constraints on the variability of fundamental constants generally. Garcia-Berro et al. (Reference Garcia-Berro2006) fit a polynomial G(z) = Go
(1 − 0.01z + 0.3z
2 − 0.17z
3) to the SNIa data, suggestive of a G larger in the past. Verbiest et al. (Reference Verbiest2008) measure orbital period rates of pulsars and set a limit of
![]() $|\dot{G}/G| = 23 \times 10^{-12} yr^{-1}$
. From white dwarf cooling, Garcia-Berro et al. (Reference Garcia-Berro2011) derive an upper bound
$|\dot{G}/G| = 23 \times 10^{-12} yr^{-1}$
. From white dwarf cooling, Garcia-Berro et al. (Reference Garcia-Berro2011) derive an upper bound
![]() $\dot{G}/G = -1.8 \times 10^{-12}\ yr^{-1}$
and Corsico et al. (Reference Corsico2013) find a white dwarf pulsation limit of
$\dot{G}/G = -1.8 \times 10^{-12}\ yr^{-1}$
and Corsico et al. (Reference Corsico2013) find a white dwarf pulsation limit of
![]() $\dot{G}/G = -1.3 \times 10^{-10} yr^{-1}$
. Tomaschitz (Reference Tomaschitz2010) considers a gravitational constant scaling linearly with the Hubble parameter, and fits the SNIa Hubble diagram and AGN source counts, concluding that further observational constraints are required.
$\dot{G}/G = -1.3 \times 10^{-10} yr^{-1}$
. Tomaschitz (Reference Tomaschitz2010) considers a gravitational constant scaling linearly with the Hubble parameter, and fits the SNIa Hubble diagram and AGN source counts, concluding that further observational constraints are required.
Furthermore, the luminosity of degenerate carbon core supernovae is proportional to the mass of carbon burned to 56Ni. The precise mechanism, which powers a type Ia supernova explosion, is a matter of lively debate, and we do not know yet whether a detonation or a deflagration occurs. What is clear is the close correlation between the mass of nickel synthesised in the outburst and the luminosity. This is discussed in quantitative experiments by Gaztañaga et al. (Reference Gaztañaga2002). The type SNIa standard candle is thought to result from a high degree of regulation of this quantity, such as would be provided by approach to a physical limit, the Chandrasekhar mass. However, one may conjecture that the fraction of mC , which is turned into energy, may also vary with z. Like variation of G with z, this is also an issue for constraints on the equation of state of the Universe arising from supernova measurements.
2 VARYING G
There are two constraints on varying G, that which has been established from the lunar distance since 1969 (current epoch in Table 1) and astrophysical constraints acting over cosmic time, such as the ages of the oldest stars. According to the theories of G variation reviewed by Faulkner (Reference Faulkner1976), G may have been larger in the past and may be considered to follow a t
−1 decline to the current epoch. Williams and Dickey (Reference Williams and Dickey2002) placed a 1σ limit of
![]() $\dot{G}/G$
= 1.1 × 10−12 per year in recent time. If G exceeded the present value by –3 >
$\dot{G}/G$
= 1.1 × 10−12 per year in recent time. If G exceeded the present value by –3 >
![]() $\dot{G}/G$
> + 7.3 × 10−11 per year 13.7 Gyrs ago, and we assume the supernova luminosity scales with the Chandrasekhar mass, we obtain Figure 1. This includes variation of the density term in the Friedmann equation, i.e. Ω
m
(t) with two cases (1) Ω
m
(t) + ΩΛ(t) = 1 to retain flatness and (2) the dark energy density ΩΛ = 0.73 with Ω
k
= 1 − Ω
m
(t) − ΩΛ(t). We characterise type (2) models by the value of the curvature, Ω
k
, at z = 0.5. We adopt the WMAP9 limits on curvature (Hinshaw et al. Reference Hinshaw2013), –0.0065 <Ω
k
< 0.0012.
$\dot{G}/G$
> + 7.3 × 10−11 per year 13.7 Gyrs ago, and we assume the supernova luminosity scales with the Chandrasekhar mass, we obtain Figure 1. This includes variation of the density term in the Friedmann equation, i.e. Ω
m
(t) with two cases (1) Ω
m
(t) + ΩΛ(t) = 1 to retain flatness and (2) the dark energy density ΩΛ = 0.73 with Ω
k
= 1 − Ω
m
(t) − ΩΛ(t). We characterise type (2) models by the value of the curvature, Ω
k
, at z = 0.5. We adopt the WMAP9 limits on curvature (Hinshaw et al. Reference Hinshaw2013), –0.0065 <Ω
k
< 0.0012.
Table 1. Constraints on the rate of variation of the gravitational constant.

Notes : the uncertainties are 1σ unless otherwise noted.
1: (Muller & Biskupek Reference Muller and Biskupek2007); 2: (Copi, Davis, & Krauss Reference Copi, Davis and Krauss2004); 3: (Kaspi et al. Reference Kaspi, Taylor and Ryba1994); 4: (Li et al. Reference Li2013).
5: (Guenther, Krauss & Demarque Reference Guenther, Krauss and Demarque1998); 6: (Thorsett Reference Thorsett1996); 7: (Verbiest et al. Reference Verbiest2008).

Figure 1. Luminosity distance versus redshift. The lower plot shows residuals from the standard model. The solid symbols are supernovae. The standard model is the dashed curve. The solid line and the red dotted line are the G varied expectations, the former with non-zero curvature. The most distant SNIa is at 9 billion light years in the standard cosmology with H 0 = 73.8 ± 2.4 km/s/Mpc, given by Riess et al. (Reference Riess2012).
2.1 The supernova Ia constraint
The current supernova data (Suzuki et al. Reference Suzuki2012) are shown in Figure 1. If we assume ΛCDM cosmology with w = –1, current SNIa data constrain G stability to
![]() $\dot{G}/G$
= (–3,+7.3) × 10−11 per year. This constraint is obtained if we adopt the standard model of cosmology as a prior. We now (1) reexpress this as a constraint on
$\dot{G}/G$
= (–3,+7.3) × 10−11 per year. This constraint is obtained if we adopt the standard model of cosmology as a prior. We now (1) reexpress this as a constraint on
![]() $\dot{\alpha _{\rm g}}/\alpha _{\rm g}$
, and (2) invert the argument to constrain w, given laboratory limits on G variation.
$\dot{\alpha _{\rm g}}/\alpha _{\rm g}$
, and (2) invert the argument to constrain w, given laboratory limits on G variation.
(1) To determine the upper limit on
![]() $\dot{\alpha _{\rm g}}/\alpha _{\rm g}$
, we calculate χ2 to compare the data with the prediction, marginalising over H0, and show this in Figure 2. The contours of χ2 are oriented close to vertical, resulting in clear limits on G variation. This constraint, our main result, –3 <1011
$\dot{\alpha _{\rm g}}/\alpha _{\rm g}$
, we calculate χ2 to compare the data with the prediction, marginalising over H0, and show this in Figure 2. The contours of χ2 are oriented close to vertical, resulting in clear limits on G variation. This constraint, our main result, –3 <1011
![]() $\dot{G}/G$
< 7.3 per year, may be expected to strengthen towards parity with the laboratory, in the era of dark energy experiments such as LSST; see Weinberg et al. (Reference Weinberg2013). An equivalent dimensionless limit is –0.5
$\dot{G}/G$
< 7.3 per year, may be expected to strengthen towards parity with the laboratory, in the era of dark energy experiments such as LSST; see Weinberg et al. (Reference Weinberg2013). An equivalent dimensionless limit is –0.5
![]() $< \dot{G}/(GH_0) <$
1, where 1/H
0 is the age of the Universe.
$< \dot{G}/(GH_0) <$
1, where 1/H
0 is the age of the Universe.

Figure 2. A vertical central valley of parameter space is permitted by these χ2 contours. The first contour on either side of zero is χ2 per degree of freedom = 1.2 with a spacing between triplet contours of 0.2. Positive values of
![]() $\dot{\alpha _{\rm g}}$
have the sense of G larger in the past. With the WMAP9 limits on curvature (Hinshaw et al. Reference Hinshaw2013) shown by the vertical error bar this implies a SNIa cosmology constraint on G stability in the standard cosmology of (–3, + 7.3) × 10−11 per year, evaluated at χ2 = 2.
$\dot{\alpha _{\rm g}}$
have the sense of G larger in the past. With the WMAP9 limits on curvature (Hinshaw et al. Reference Hinshaw2013) shown by the vertical error bar this implies a SNIa cosmology constraint on G stability in the standard cosmology of (–3, + 7.3) × 10−11 per year, evaluated at χ2 = 2.
(2) This constraint is obtained if we adopt the standard model of cosmology as a prior. However, these SNIa data are conventionally used as a measurement of ΩΛ. There is therefore a degeneracy between this and
![]() $\dot{G}$
addressed by the same data. We can quantify the degeneracy using the generalisation of the Friedmann equation as a polynomial by Mould (Reference Mould2011). Mould showed that if, such a polynomial is adopted to fit Figure 1,
$\dot{G}$
addressed by the same data. We can quantify the degeneracy using the generalisation of the Friedmann equation as a polynomial by Mould (Reference Mould2011). Mould showed that if, such a polynomial is adopted to fit Figure 1,
relationships (degeneracies) between the Ω
n
coefficients result from the limited available constraints (SNIa, CMB). If the SNIa data are used to constrain the equation of state of the Universe with w ≈ –1, there is therefore a degeneracy between w and
![]() $\dot{G}$
addressed by the same data. For z ~ 1 and zero curvature, δw≈2δΩ
m
from Equations (3) and (11) of Mould (Reference Mould2011). For G stability to two parts in 1012 per year, δαg/αg = 0.0137 at z = 1, which corresponds to δw≈ 0.03. The current experimental uncertainty in w (Rapetti et al. Reference Rapetti2013) is 0.07. Both quantities therefore need to be constrained jointly. On the other hand, if one is prepared to adopt the lunar laser ranging results as a prior on dark energy experiments valid over all of cosmic time, the effect of variable G is constrained so that δw < 0.02 (95% confidence). This is not a negligible contribution to the w error budget, and it should not be ignored (cf. Mortonson et al. Reference Mortonson2014).
$\dot{G}$
addressed by the same data. For z ~ 1 and zero curvature, δw≈2δΩ
m
from Equations (3) and (11) of Mould (Reference Mould2011). For G stability to two parts in 1012 per year, δαg/αg = 0.0137 at z = 1, which corresponds to δw≈ 0.03. The current experimental uncertainty in w (Rapetti et al. Reference Rapetti2013) is 0.07. Both quantities therefore need to be constrained jointly. On the other hand, if one is prepared to adopt the lunar laser ranging results as a prior on dark energy experiments valid over all of cosmic time, the effect of variable G is constrained so that δw < 0.02 (95% confidence). This is not a negligible contribution to the w error budget, and it should not be ignored (cf. Mortonson et al. Reference Mortonson2014).
Finally, the coupling of DL , f, and mC is direct. Analytically, 2δDL /DL = δf/f = –1.5δG/G = δmC /mC . Our limit on δαg/αg is thus degenerate with an equivalent limit on δf/f.
2.2 Other parameterisations
Pragmatically, the key result here devolves from an assumed t −1 variation of αg. Its basis is historical and traces back to Dirac’s (Reference Dirac1937) large numbers hypothesis and the steady state Universe, neither of which have any real traction today. Other parameterisations are possible and even natural, such as 1+z scaling. One form is αg = α0 + α′z. In this case we obtain –0.02 <α′/α0< 0.04.
If G ~ 1+z, the Ω3 coefficient in Equation (1) is promoted to Ω4; that is, it becomes an anti-radiation pressure term. Assuming Ω1 = 0, the resulting degeneracies can be expressed (Mould Reference Mould2011)
where
Any G variation that scales as 1+z is traded off against ΩΛ, according to (from Table 2) δΩΛ = δΩ0 = 301.5δΩ4, when SNIa and CMB anisotropy data measure cosmological parameters simultaneously. A universe with just conventional dark energy and ‘radiation’ like this has an age in units of 1/H0 obtained by integrating Equation (1) with a −1 = 1 + z.
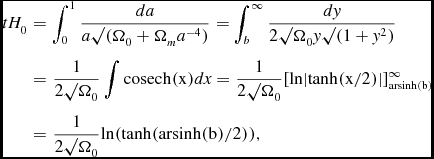 \begin{eqnarray}
tH_0 &=& \int _0^1 \frac{da}{a\surd (\Omega _0+\Omega _m a^{-4})} = \int _b^\infty \frac{dy}{2\surd \Omega _0 y\surd (1+y^2)}\nonumber\\
&=& \frac{1}{2\surd \Omega _0}\int {\rm cosech(x)} dx = \frac{1}{2\surd \Omega _0}[\rm {ln}|\rm {tanh}(x/2)|]_{arsinh(b)}^\infty\nonumber\\
&=& \frac{1}{2\surd \Omega _0}\rm {ln} (\rm {tanh (arsinh}(b)/2)),
\end{equation}
\begin{eqnarray}
tH_0 &=& \int _0^1 \frac{da}{a\surd (\Omega _0+\Omega _m a^{-4})} = \int _b^\infty \frac{dy}{2\surd \Omega _0 y\surd (1+y^2)}\nonumber\\
&=& \frac{1}{2\surd \Omega _0}\int {\rm cosech(x)} dx = \frac{1}{2\surd \Omega _0}[\rm {ln}|\rm {tanh}(x/2)|]_{arsinh(b)}^\infty\nonumber\\
&=& \frac{1}{2\surd \Omega _0}\rm {ln} (\rm {tanh (arsinh}(b)/2)),
\end{equation}
and
Table 2. Equation of state components.

The fn coefficients have been evaluated at Ω3 = 0.27.
For Ω M = 0.27, x = 0.575 at z = 0 and the age is 0.745. This is a second contradiction with the standard model of cosmology, as Planck finds an age approximately one in these units (Ade et al. Reference Ade2013, Efstathiou Reference Efstathiou2013). A further contradiction with the age of the globular clusters is mildly ameliorated by higher central temperatures of stars (GM mp /kR, where M, R are the stellar mass and radius) during the epoch of re-ionisation, when they were formed, and the extraordinary temperature sensitivity of the CN cycle of fusion, but for most of the low mass stars’ lifetime core temperatures are close to normal and ages are only mildly affected (Vandenberg Reference Vandenberg1977).
How severe a constraint on G ~ 1+z is this? Error analysis gives terms in δΩ M /Ω M , δΩΛ/ΩΛandδH 0/H 0. The first and last of these are of order a few percent and the second is smaller. This parameterisation can therefore be rejected with 99% confidence. G ~(1 + z)1/n would be less unacceptable for large n, but is not a natural parameterisation.
3 SUMMARY
Our conclusions from this work are as follows.
-
1. The validity of the SNIa standard candle depends on the stability of G and the stability of f, the fraction of the Chandrasekhar mass turned into energy. We have considered the former in this paper and derived a constraint on the gravitational fine structure constant which can be compared with other combined astrophysical-cosmological constraints. But this is inextricably degenerate with possible evolution of f due to changes over cosmic time of SNIa progenitor astrophysics. With this caveat, we set a SNIa cosmology constraint on G stability in the standard cosmology of (–3, + 7.3) × 10−11 per year.
-
2. This limit is two orders of magnitude weaker than that from lunar laser ranging. But that is a current epoch result and complements, but does not replace, a constraint that spans cosmic time.
-
3. The limit is also two orders of magnitude weaker than that arising from the great sensitivity to density of Big Bang nucleosynthesis. The SNIa standard candle, however, has the distinct advantage of covering the last 1010 years of cosmic time, rather than the first 20 minutes.
-
4. Our result is an update of Gaztañaga et al. (Reference Gaztañaga2002), who found
 $\dot{G}/G <$
12 × 10−12
h
70 /yr for ΩΛ = 0.8, Ω
M
= 0.2. This is a 1σ limit, like ours, and directly comparable since h
70≈ 1. The order of magnitude more supernovae now available have allowed us to relax their flat Universe assumption, but has also relaxed their limit on
$\dot{G}/G <$
12 × 10−12
h
70 /yr for ΩΛ = 0.8, Ω
M
= 0.2. This is a 1σ limit, like ours, and directly comparable since h
70≈ 1. The order of magnitude more supernovae now available have allowed us to relax their flat Universe assumption, but has also relaxed their limit on
 $\dot{G}$
.
$\dot{G}$
. -
5. Caution would dictate that experiments to measure the equation of state of the Universe carry the caveat that f and G stability is assumed. For the latter, lunar laser ranging is available as a prior and limits δw to 0.02, but the former has not been quantified and demands further understanding of the SNIa mechanism.
-
6. A parameterisation G ~ 1+z is interesting on theoretical grounds related to the unity of forces. However, with such an equation of state the expansion age of the Universe is too short. That parameterisation can therefore be rejected with 99% confidence.
ACKNOWLEDGEMENTS
The authors are grateful to Chris Blake and Michael Murphy for helpful advice and to an anonymous referee for emphasising the issue of the quantum of 56Ni. CAASTRO is the ARC’s Centre of Excellence for All-Sky Astrophysics, funded by grant CE11001020.