According to the Priority View, benefiting individuals matters more the worse off these individuals are.Footnote 1 The most influential version of the view is known as Prioritarianism. It is probably best understood as a variation of utilitarianism, because (except for giving priority to the worse off) Prioritarianism has the same aggregative structure as utilitarianism. According to utilitarianism, the value of a final outcome (an outcome without any risk or uncertainty) is the sum total of well-being in that outcome. Let I(x) be the set of individuals in outcome x, and let v i(x) be the well-being of individual i in outcome x. Then, according to utilitarianism, the value of a final outcome x is
Prioritarianism values final outcomes in almost the same way. The difference is that well-being levels aren't added up directly; they are first transformed by a strictly increasing, strictly concave function in order to give more weight to the worse off. Let f be this transformation function. Then the value of a final outcome x according to Prioritarianism can be calculated as follows:Footnote 2
This prioritarian formula, like the utilitarian one, assumes a total rather than average approach. But, since we will only be concerned with fixed populations, the differences between average and total versions of Prioritarianism won't matter for our discussion.
While the above formula tells us how to value final outcomes, it doesn't tell us how to value risky prospects – that is, prospects from which two or more final outcomes may result with some positive probability, depending on chance.
There are two main ways of extending Prioritarianism so that it applies to choices between risky prospects: the ex-post approach and the ex-ante approach.Footnote 3 To state these approaches, let S be a partition of states of nature, let p(s) be the probability of state s, and let o[x, s] be the final outcome of prospect x in state s. Then we can state the ex-post approach as follows:Footnote 4
Ex-Post Prioritarianism
A prospect x is choice-worthy if and only if there is no available prospect y such that V EPP(y) > V EPP(x),
where
And we can state the ex-ante approach as follows:Footnote 5
Ex-Ante Prioritarianism
A prospect x is choice-worthy if and only if there is no available prospect y such that V EAP(y) > V EAP(x),
where
The difference between these approaches lies in where we apply the transformation function f that gives priority to the worse off. The ex-post approach adjusts for priority directly on the individuals’ well-being levels in the final outcomes, and then it calculates the expectation of this transformed value. But the ex-ante approach first calculates individuals’ expectations of well-being, and then it adjusts for priority on these expectations of untransformed well-being levels.
A well-known problem for Ex-Post Prioritarianism is that it violates the Weak Ex-Ante Pareto Principle:Footnote 6
The Weak Ex-Ante Pareto Principle
If each individual has a higher expectation of well-being in prospect x than in prospect y, then y is not choice-worthy if x available.Footnote 7
Ex-Ante Prioritarianism, on the other hand, satisfies the Weak Ex-Ante Pareto Principle. This might seem like a significant advantage for Ex-Ante Prioritarianism over Ex-Post Prioritarianism. Nevertheless, in this article, I will argue that the former suffers from much the same problem as the latter: Ex-Ante Prioritarianism violates a sequential version of the Weak Ex-Ante Pareto Principle.Footnote 8
These violations are potentially a more pressing problem for Ex-Ante Prioritarianism than for Ex-Post Prioritarianism, because Ex-Post Prioritarianism (unlike Ex-Ante Prioritarianism) favours an ex-post perspective in general.Footnote 9
1 Ex-Post Prioritarianism
Ex-Post Prioritarianism violates the Weak Ex-Ante Pareto Principle no matter which strictly increasing, strictly concave function f we choose as the transformation function. To see this, note first that, since f is strictly concave, there must be some positive constants δ and ε such that f(1) − f(1 − δ) > f(1 + δ + ε) − f(1). This is so, because the smaller benefit of δ units of well-being when it's added at the lower level of well-being, 1 − δ, matters more than the greater benefit of δ + ε units of well-being matters when it's added at the higher level of well-being, 1. This need not be so if ε is sufficiently great, but it will be so if ε is sufficiently small.
Now, consider
Case One
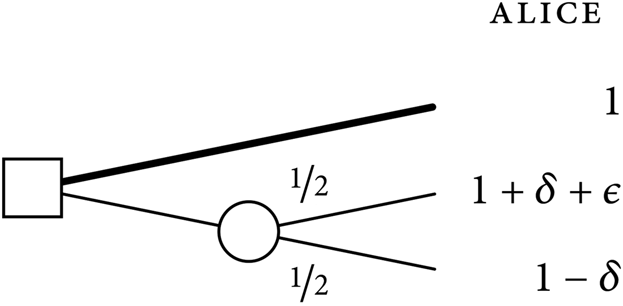
Here, the square represents a choice node, where we have a choice between going up or going down. If we go up, Alice gets a well-being of 1. If we go down, we reach a chance node, represented by the circle, where there is a one-in-two probability that chance goes up and a one-in-two probability that chance goes down. If chance goes up, Alice gets a well-being of 1 + δ + ε. And, if chance goes down, she gets a well-being of 1 − δ.
Let Up be the prospect of going up at the choice node, and let Down be the prospect of going down at the choice node. Given that f(1) − f(1 − δ) > f(1 + δ + ε) − f(1), we find that V EPP(Up) = f(1) > V EPP(Down) = (1/2)f(1 + δ + ε) + (1/2)f(1 − δ). Accordingly, Ex-Post Prioritarianism prescribes going up in Case One – that is, it entails that Up is the only choice-worthy prospect. (This prescribed option is marked by the thicker line.) Alice's expectation of well-being if we go up is 1. And her expectation of well-being if we go down is (1/2)(1 + δ + ε) + (1/2)(1 − δ) = 1 + ε/2. Hence Alice's expectation of well-being is higher if we go down than if we go up.
Individual expectations at the initial node of Case One

Therefore, since Ex-Post Prioritarianism prescribes going up, it violates the Weak Ex-Ante Pareto Principle.
2 Ex-Ante Prioritarianism
Ex-Ante Prioritarianism satisfies the Weak Ex-Ante Pareto Principle.Footnote 10 Nonetheless, I will show that Ex-Ante Prioritarianism still violates a sequential version of this principle. This sequential version concerns plans rather than individual choices.
Let a plan at a node be a specification of what to choose at each choice node that can be reached from that node while following the specification. Let us say that one follows a plan at node n if and only if, for each choice node n′ that can be reached from n while choosing in accordance with the plan, one would choose in accordance with that plan if one were to face n′. Let us say that one intentionally follows a plan at node n if and only if one follows the plan at n and, for all nodes n′ such that n′ can be reached from n by following the plan, if one were to face n′, one would either form or have formed at n′ an intention to choose in accordance with the plan at every choice node that can be reached from n′ and can be reached from n by following the plan.Footnote 11 (In other words, the difference between following a plan and intentionally following a plan is that the latter requires that you, at each step of the plan, intend to follow the rest of the plan.) Let us say that a plan is feasible at a node n if and only if the plan can be intentionally followed at n.Footnote 12 Finally, let us say that a plan is choice-worthy at a node if and only if, at each choice node that can be reached from that node, only choice-worthy options are specified to be chosen on the plan.
Then, according to
The Weak Sequential Ex-Ante Pareto Principle
If each individual has a higher expectation of well-being in prospect x than in prospect y, then a plan is not choice-worthy if its prospect is y and there is a feasible plan whose prospect is x.
This principle (unlike the Weak Ex-Ante Pareto Principle) is sequential, because it assesses plans rather than individual choices. Note that, while plans can consist of sequences of choices, they can also consist of a single choice (in case there are no further choice nodes that can be reached after the first choice).
Ex-Ante Prioritarianism violates the Weak Sequential Ex-Ante Pareto Principle no matter which strictly increasing, strictly concave function f we choose as the transformation function. As before, note that there must be some positive constants δ and ε such that f(1) − f(1 − δ) > f(1 + δ + ε) − f(1), since f is strictly concave. And consider
Case Two
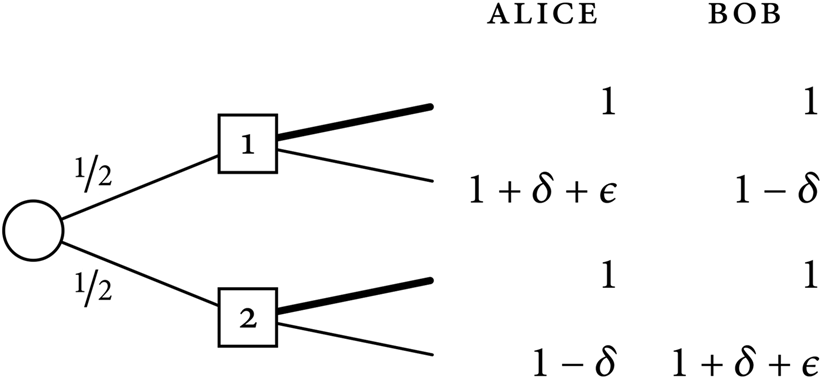
Let Up in 1 be the prospect of going up at node 1, let Down in 1 be the prospect of going down at node 1, let Up in 2 be the prospect of going up at node 2, and let Down in 2 be the prospect of going down at node 2. Since f(1) − f(1 − δ) > f(1 + δ + ε) − f(1), we see that V EAP(Up in 1) = f(1) + f(1) > V EAP(Down in 1) = f(1 + δ + ε) + f(1 − δ) and that V EAP(Up in 2) = f(1) + f(1) > V EAP(Down in 2) = f(1 − δ) + f(1 + δ + ε). Accordingly, at each choice node, Ex-Ante Prioritarianism prescribes going up. (The prescribed options are marked by the thicker lines.)
Let the Up-Up Plan be the plan of going up at node 1 and going up at node 2. Ex-Ante Prioritarianism prescribes the Up-Up Plan in the sense that following Ex-Ante Prioritarianism requires following the Up-Up Plan. Let the Down-Down Plan be the opposite plan, that is, the plan of going down at node 1 and going down at node 2. In addition to the Down-Down Plan and the Up-Up Plan, let the Up-Down Plan be the plan of going up at node 1 and down at node 2 and let the Down-Up Plan be the plan of going down at node 1 and up at node 2. We suppose that these four plans are feasible at the initial node. Now, compare Alice's and Bob's expectations of well-being at the initial node from each plan:
Individual expectations at the initial node of Case Two

At the initial node, everyone gets a higher expectation of well-being from the Down-Down Plan than from the Up-Up Plan. Therefore, since Ex-Ante Prioritarianism prescribes the Up-Up Plan, it violates the Weak Sequential Ex-Ante Pareto Principle.
Since the choices in Case Two are decisions under certainty and also terminal choices (they're not followed by any further choices), this result holds not only for Ex-Ante Prioritarianism but also for any form of Prioritarianism which satisfies decision-tree separability (that is, the condition that options are classified as choice-worthy as if the sub-tree of the decision tree that starts with current node were the whole decision tree).Footnote 13
It may be objected that following the Up-Up Plan needn't violate the Weak Sequential Ex-Ante Pareto Principle, since the sequence of choices leading to A might not be feasible in the relevant sense at the initial node. The idea is that the Down-Down Plan isn't securable at the initial node, because, at that node, you can't make your future self comply with the plan to execute that sequence of choices.Footnote 14 But the mere fact that you wouldn't act in accordance with the Down-Down Plan at future nodes is not sufficient to make that plan infeasible in the relevant sense at the initial node, because that fact is due to your choice function – which is the very thing we are trying to assess.Footnote 15
It may next be objected that you can't form the intention to follow a plan that you know you won't follow. And, if you can't form an intention to follow a plan, then it's infeasible. Therefore, since you know that you won't follow the Down-Down Plan, that plan is infeasible. But the initial premise of this objection is implausible. While it may be irrational to form an intention to do something you know you won't do, it seems that you may still be able to (irrationally) form the intention.
3 Resolute Ex-Ante Prioritarianism
As we have seen, any form of Prioritarianism violates the Weak Sequential Ex-Ante Pareto Principle if it conforms to decision-tree separability. But we can avoid violations of the Weak Sequential Ex-Ante Pareto Principle if we violate this kind of separability and adopt a resolute approach to sequential choice.
It should be noted, however, that giving up decision-tree separability is a significant departure from consequentialism. Because, without this kind of separability, the choice-worthiness of an option in a situation no longer supervenes on the consequences of the feasible options in that situation.Footnote 16
Consider the following resolute variation of Ex-Ante Prioritarianism, which evaluates plans relative to a certain privileged node:Footnote 17
Resolute Ex-Ante Prioritarianism
An option is choice-worthy if and only if choosing it is in accordance with a feasible plan that has a prospect x such that there is no feasible plan that has a prospect y such that, with expectations calculated relative to the privileged node, V EAP(y) > V EAP(x).
Note that the privileged node need not be a choice node. The privileged node may just as well be a chance node as a choice node.
If the initial node of Case Two is the privileged node, then Resolute Ex-Ante Prioritarianism avoids violating the Weak Sequential Ex-Ante Pareto Principle in that case. To see this, consider the feasible plans at the initial node of Case Two. If the initial node is the privileged node, then Resolute Ex-Ante Prioritarianism evaluates plans at all nodes by their V EAP value calculated relative to the initial node:
VEAP value of plans at the initial node of Case Two

Let Up-Up be the prospect of following the Up-Up Plan at the initial node, let Up-Down be the prospect of following the Up-Down Plan at the initial node, let Down-Up be the prospect of following the Down-Up Plan at the initial node, and let Down-Down be the prospect of following the Down-Down Plan at the initial node. Since f is strictly concave, we find that f(1 + ε/2) − f(1 − δ/2) > f(1 + δ/2 + ε/2) − f(1 + ε/2). Therefore, V EAP(Down-Down) is greater than each of V EAP(Down-Up) and V EAP(Up-Down). And, since f is strictly increasing, we find that V EAP(Down-Down) is greater than V EAP(Up-Up). Accordingly, Resolute Ex-Ante Prioritarianism prescribes that we follow the Down-Down Plan.
A first general problem with Resolute Ex-Ante Prioritarianism is that the choice of a privileged node seems arbitrary.Footnote 18 Suppose that we face the choice at node 1. Why would any specific node in the past, such as the initial chance node, have any special ethical significance? The fact that a certain node is the first node in the decision tree is just an arbitrary feature of how we have chosen to model the situation. We could have represented the situation with a larger decision tree that went back further into the past so that the current initial node would have been one of the later nodes.
One, potentially compelling, suggestion is that, for each agent, the privileged node is the first choice that agent ever faced – or, alternatively, the privileged node is the first point in the agent's life at which the agent considers (or is capable of considering) how the future might unfold and what choices the agent might be presented with later. This yields the following proposal:
Agent-Relative Resolute Ex-Ante Prioritarianism
An option is choice-worthy if and only if choosing it is in accordance with a feasible plan that has a prospect x such that there is no feasible plan that has a prospect y such that, with expectations calculated relative to the agent's first choice node, V EAP(y) > V EAP(x).
But this proposal does not avoid violations of the Weak Sequential Ex-Ante Pareto Principle. To see this, consider Case Two. Suppose that Alice is the agent at node 1 and that it would be her first choice node. And suppose that Bob is the agent at node 2 and that it would be his first choice node.Footnote 19 Then, given Agent-Relative Resolute Ex-Ante Prioritarianism, Alice would make the choice at node 1 based on evaluations of the options calculated at that node; and Bob would make the choice at node 2 based on evaluations of the options calculated at that node. Accordingly, Agent-Relative Resolute Ex-Ante Prioritarianism prescribes that Alice goes up at node 1 and that Bob goes up at node 2, just like standard Ex-Ante Prioritarianism. Therefore, Agent-Relative Resolute Ex-Ante Prioritarianism prescribes that Alice and Bob jointly implement the Up-Up Plan. But, as we saw earlier, the Up-Up Plan gives everyone a worse expectation than the Down-Down Plan.
To get around this problem, we could let the privileged node be the earliest possible node, that is, the node at the beginning of time. This yields the following proposal:
Universally Resolute Ex-Ante Prioritarianism
An option is choice-worthy if and only if choosing it is in accordance with a feasible plan that has a prospect x such that there is no feasible plan that has a prospect y such that, with expectations calculated relative to the beginning of time, V EAP(y) > V EAP(x).
This proposal avoids the earlier problem for Agent-Relative Resolute Ex-Ante Prioritarianism, since a single privileged node is used for all evaluations at all choice nodes for all agents.
But there's another worry about Universally Resolute Ex-Ante Prioritarianism, namely, that it is unclear whether everyone had a well-defined expectation of well-being at the beginning of time. In order to have an expectation at a certain point in time, one must have a level of well-being in every potential outcome that has some positive probability at that point. Some of us weren't alive at the beginning of time, and history could have gone differently so that we would never have a life. And, if so, we did not have a well-defined expectation of well-being at the beginning of time unless we have a level of well-being in the potential outcomes where we never ever have a life.Footnote 20 Yet it's doubtful whether one could have a level of well-being without having a life.Footnote 21 So it's doubtful whether we can evaluate prospects where there is some positive probability that some individuals will exist and also some positive probability that they will not exist.Footnote 22 And, consequently, it is doubtful whether we can apply Universally Resolute Ex-Ante Prioritarianism.
A second general problem for Resolute Ex-Ante Prioritarianism is that this version of Prioritarianism need not give the worse off the amount of priority that is reflected in the concavity of the transformation function. Suppose, as before, that the initial node in Case Two is the privileged node and that we face the choice at node 1. We then find that Resolute Ex-Ante Prioritarianism prescribes going down. But, if we go down at node 1, we favour benefiting Alice, who would otherwise get a well-being of 1, over benefiting Bob, who gets a well-being of 1 − δ, even though these alternative benefits could be arbitrarily similar in size.Footnote 23 Therefore, it seems that Resolute Ex-Ante Prioritarianism conflicts with the underlying idea behind Prioritarianism, namely, the Priority View: that benefiting individuals matters more the worse off these individuals are.Footnote 24
It may be objected that Resolute Ex-Ante Prioritarianism can still conform to the Priority View as long as the latter is only applied to the expectations of plans considered from the privileged initial node. The trouble with this response is that there seems to be no compelling reason to attach any normative significance, at either of the choice nodes in Case Two, to expectations calculated from the perspective of the initial node, which is now in the past. At the choice nodes, we already know how the chance event of the chance node resolved. So it would be strange to still attach any normative significance to expectations calculated without knowledge of how that event resolved. Likewise, the part of the decision tree that would have been reached if the chance event had resolved the other way should no longer be relevant. What should matter is what you can affect with the last remaining choice between going up or down at one of the choice nodes. And, applied to the outcomes of these options, the Priority View implies that the outcome of going up is better than the outcome of going down, since the gain for the worse off matters more than the greater loss for the better off if we go up rather than down. Since this evaluation of outcomes should capture everything that matters, one should go up at each of the choice nodes if one accepts the Priority View.Footnote 25 Nevertheless, Resolute Ex-Ante Prioritarianism prescribes that one goes down.
(Could this objection to the normative significance of expectations calculated from some earlier node also be levelled against the normative significance of the Weak Sequential Ex-Ante Pareto Principle? It couldn't. While you shouldn't attach any significance to expectations calculated from the perspective of earlier nodes, those expectations should still be significant at those earlier nodes. At the initial node in Case Two, it is a significant problem if you follow a moral theory that will tell you to choose in a way that lowers everyone's expectation of well-being. This problem, raised at the initial node, does not attach any significance to expectations calculated from the perspective of earlier nodes.)
Finally, note that the problem is not that the choices prescribed by Resolute Ex-Ante Prioritarianism could turn out ex post to benefit the better off rather than the worse off (this is true but unproblematic). The problem is that Resolute Ex-Ante Prioritarianism requires, for some choices, that we knowingly choose not to give priority to the worse off. So the prescriptions of this theory don't seem to match the intuitive verdicts that motivate the Priority View in some cases where no uncertainty is involved – cases where we might have thought that Ex-Ante and Ex-Post Prioritarianism would agree.
4 Conclusion
We have seen that Ex-Post Prioritarianism violates the Weak Ex-Ante Pareto Principle and that Ex-Ante Prioritarianism faces much the same problem: Ex-Ante Prioritarianism violates the Weak Sequential Ex-Ante Pareto Principle. There seems to be no good reason to accept the Weak Ex-Ante Pareto Principle but not the Weak Sequential Ex-Ante Pareto Principle. (While Resolute Ex-Ante Prioritarianism may avoid this sequential problem, it faces other problems, as we have seen.) Hence the standard argument in favour of Ex-Ante Prioritarianism over Ex-Post Prioritarianism does not work. So it's a general problem for Prioritarianism that, in some cases, everyone would get a lower expectation of well-being if these theories were followed.Footnote 26


