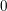1 Introduction and main theorems
Consider an algebraic stack
![]() $X$
which is smooth over a field
$X$
which is smooth over a field
![]() $k$
. If
$k$
. If
![]() $X$
has finite inertia, then there is a canonical map
$X$
has finite inertia, then there is a canonical map
 $X\rightarrow X_{\text{cs}}$
to a coarse (moduli) space. The algebraic space
$X\rightarrow X_{\text{cs}}$
to a coarse (moduli) space. The algebraic space
![]() $X_{\text{cs}}$
will, however, in general not be smooth. Given a morphism
$X_{\text{cs}}$
will, however, in general not be smooth. Given a morphism
 $f:X^{\prime }\rightarrow X$
of stacks with finite inertia, we get an induced map
$f:X^{\prime }\rightarrow X$
of stacks with finite inertia, we get an induced map
 $f_{\text{cs}}:X_{\text{cs}}^{\prime }\rightarrow X_{\text{cs}}$
. If
$f_{\text{cs}}:X_{\text{cs}}^{\prime }\rightarrow X_{\text{cs}}$
. If
![]() $f$
is proper and birational, we call
$f$
is proper and birational, we call
![]() $f$
a stacky modification. Our goal is to find nice choices of
$f$
a stacky modification. Our goal is to find nice choices of
![]() $f$
and
$f$
and
![]() $X^{\prime }$
such that the map
$X^{\prime }$
such that the map
![]() $f_{\text{cs}}$
becomes a desingularisation.
$f_{\text{cs}}$
becomes a desingularisation.
The stacky modifications we will work with are usual blow-ups with smooth centres and root stacks, where we take roots of smooth divisors. Such modifications will collectively be referred to as stacky blow-ups with smooth centres, and sequences of such stacky blow-ups will be referred to as smooth stacky blow-up sequences (see Definition 2.2).
It is useful to think of the process described above as a process to remove stackiness from a smooth stack. The method described in this paper will produce a roof-shaped diagram

where
![]() $\unicode[STIX]{x1D70B}$
is the coarse map. The map
$\unicode[STIX]{x1D70B}$
is the coarse map. The map
![]() $f$
is a composition of a sequence of stacky blow-ups and
$f$
is a composition of a sequence of stacky blow-ups and
![]() $\unicode[STIX]{x1D70B}$
is a root stack if we start with an orbifold
$\unicode[STIX]{x1D70B}$
is a root stack if we start with an orbifold
![]() $X$
and a composition of a gerbe and a root stack otherwise. We will use the term destackification (see Definition 2.3) for a process producing such a roof.
$X$
and a composition of a gerbe and a root stack otherwise. We will use the term destackification (see Definition 2.3) for a process producing such a roof.
In this paper, we will focus on the case when
![]() $X$
has diagonalisable stabilisers. This allows us to attack the problem with toric methods. The combinatorial nature of toric methods makes them quite insensitive to assumptions on the base we are working over. Hence, we will assume that the base is an arbitrary scheme rather than a field. In fact, we could just as easily work over an arbitrary algebraic stack if we used the appropriate relative versions of concepts such as coarse space and stabilisers, but we will not work in this generality.
$X$
has diagonalisable stabilisers. This allows us to attack the problem with toric methods. The combinatorial nature of toric methods makes them quite insensitive to assumptions on the base we are working over. Hence, we will assume that the base is an arbitrary scheme rather than a field. In fact, we could just as easily work over an arbitrary algebraic stack if we used the appropriate relative versions of concepts such as coarse space and stabilisers, but we will not work in this generality.
Just as in the classical method for desingularisation by Hironaka [Reference HironakaHir64a, Reference HironakaHir64b], divisors with simple normal crossings will play an important role in the algorithms used in this paper. Typically, the divisors will be exceptional divisors for the various blow-ups during the destackification process. Furthermore, the centre of each stacky blow-up will have normal crossings with the given simple normal crossings divisor. As in Hironaka’s method, it will be crucial to keep track of the order in which the divisors have been created in order to achieve functoriality. The main object that we will work with will therefore be a pair
![]() $(X,\boldsymbol{E})$
, where
$(X,\boldsymbol{E})$
, where
![]() $X$
is a tame, smooth stack and
$X$
is a tame, smooth stack and
![]() $\boldsymbol{E}$
an ordered set of smooth divisors on
$\boldsymbol{E}$
an ordered set of smooth divisors on
![]() $X$
which have simple normal crossings. For brevity, we will call such a pair a standard pair (see Definition 2.1 for technical details). The elements of
$X$
which have simple normal crossings. For brevity, we will call such a pair a standard pair (see Definition 2.1 for technical details). The elements of
![]() $\boldsymbol{E}$
will be called the components of
$\boldsymbol{E}$
will be called the components of
![]() $\boldsymbol{E}$
.
$\boldsymbol{E}$
.
The first step in the destackification process is to create enough components of the divisor
![]() $\boldsymbol{E}$
to be able to attack the problem with toric methods. We do this by making the pair
$\boldsymbol{E}$
to be able to attack the problem with toric methods. We do this by making the pair
![]() $(X,\boldsymbol{E})$
divisorial (see Definition 7.13). The reader should be warned that the term divisorial in this context is used in a non-standard way. If
$(X,\boldsymbol{E})$
divisorial (see Definition 7.13). The reader should be warned that the term divisorial in this context is used in a non-standard way. If
![]() $X$
is an orbifold, the pair
$X$
is an orbifold, the pair
![]() $(X,\boldsymbol{E})$
is divisorial precisely when the stacky locus is contained in the divisor
$(X,\boldsymbol{E})$
is divisorial precisely when the stacky locus is contained in the divisor
![]() $\boldsymbol{E}$
. An alternative description is that
$\boldsymbol{E}$
. An alternative description is that
![]() $(X,\boldsymbol{E})$
is divisorial when the
$(X,\boldsymbol{E})$
is divisorial when the
![]() $\mathbb{G}_{\text{m}}^{n}$
-torsor associated to the divisor
$\mathbb{G}_{\text{m}}^{n}$
-torsor associated to the divisor
![]() $\boldsymbol{E}$
is an algebraic space (see Remark 7.14).
$\boldsymbol{E}$
is an algebraic space (see Remark 7.14).
Theorem 1.1 (Functorial divisorialification).
Let
 $(X,\boldsymbol{E})/S$
be a standard pair, as defined in Definition 2.1. If
$(X,\boldsymbol{E})/S$
be a standard pair, as defined in Definition 2.1. If
![]() $X$
has diagonalisable stabilisers, then there exists a smooth, ordinary blow-up sequence
$X$
has diagonalisable stabilisers, then there exists a smooth, ordinary blow-up sequence
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}:(X_{n},\boldsymbol{E}_{n})\rightarrow \cdots \rightarrow (X_{0},\boldsymbol{E}_{0})=(X,\boldsymbol{E})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}:(X_{n},\boldsymbol{E}_{n})\rightarrow \cdots \rightarrow (X_{0},\boldsymbol{E}_{0})=(X,\boldsymbol{E})\end{eqnarray}$$
such that the pair
 $(X_{n},\boldsymbol{E}_{n})$
is divisorial. The construction is functorial (see Definition 2.6) with respect to arbitrary base change
$(X_{n},\boldsymbol{E}_{n})$
is divisorial. The construction is functorial (see Definition 2.6) with respect to arbitrary base change
 $S^{\prime }\rightarrow S$
and with respect to gerbes and smooth, stabiliser-preserving morphisms
$S^{\prime }\rightarrow S$
and with respect to gerbes and smooth, stabiliser-preserving morphisms
 $X^{\prime }\rightarrow X$
.
$X^{\prime }\rightarrow X$
.
In [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73], a combinatorial method for desingularising toroidal varieties is described. Toroidal varieties naturally occur as coarse spaces of toroidal stacks (see Definition 7.4) and the methods in [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73] could quite easily be adapted to handle destackification of toroidal stacks. However, it seems non-trivial to obtain a toroidal structure on a smooth stack with diagonalisable stabilisers if not given one from the start. Note that toroidality is a much stronger property than the divisoriality described above and, whereas divisorialification may be reached via the naivest possible method using just usual blow-ups (see Algorithm C), toroidalification requires the whole arsenal of stacky blow-ups. In fact, it seems like the easiest way to obtain a toroidal structure is to simultaneously achieve destackification.
The method described in this paper makes use of two different invariants associated to each point of the stack. The independency index (see Definition 7.1) measures how far the stack is from being destackified at the point and the toroidal index (see Definition 7.4) measures how far the stack is from being toroidal. The destackification process alternates between reducing the toroidal index and the independency index in a controlled way. A complication is that the locus where the toroidal index is maximal is not smooth in general, and therefore cannot be blown up. Instead, other invariants must be used to single out suitable substacks for modification. The result of the process is summarised in the following theorem, which is the main theorem of the article.
Theorem 1.2 (Functorial destackification).
Let
 $(X,\boldsymbol{E})/S$
be a standard pair, as defined in Definition 2.1, over a quasi-compact scheme
$(X,\boldsymbol{E})/S$
be a standard pair, as defined in Definition 2.1, over a quasi-compact scheme
![]() $S$
. If
$S$
. If
![]() $X$
has diagonalisable stabilisers, then there exists a smooth, stacky blow-up sequence
$X$
has diagonalisable stabilisers, then there exists a smooth, stacky blow-up sequence
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}:(X_{m},\boldsymbol{E}_{m})\rightarrow \cdots \rightarrow (X_{0},\boldsymbol{E}_{0})=(X,\boldsymbol{E}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}:(X_{m},\boldsymbol{E}_{m})\rightarrow \cdots \rightarrow (X_{0},\boldsymbol{E}_{0})=(X,\boldsymbol{E}),\end{eqnarray}$$
which is a destackification as in Definition 2.3. In particular, the coarse space of
![]() $X_{m}$
is smooth, and the coarse map can be factored as a gerbe followed by a root stack. The construction is functorial (see Definition 2.6) with respect to arbitrary base change
$X_{m}$
is smooth, and the coarse map can be factored as a gerbe followed by a root stack. The construction is functorial (see Definition 2.6) with respect to arbitrary base change
 $S^{\prime }\rightarrow S$
and with respect to gerbes and smooth, stabiliser-preserving morphisms
$S^{\prime }\rightarrow S$
and with respect to gerbes and smooth, stabiliser-preserving morphisms
 $X^{\prime }\rightarrow X$
.
$X^{\prime }\rightarrow X$
.
The functorial properties of the algorithm have the pleasant side effect that they guarantee that the locus
![]() $U$
of the stack
$U$
of the stack
![]() $X$
which only has generic stackiness will not be modified by the algorithm. More precisely, each of the stacky blow-ups in the blow-up sequence will have centres lying above the complement
$X$
which only has generic stackiness will not be modified by the algorithm. More precisely, each of the stacky blow-ups in the blow-up sequence will have centres lying above the complement
![]() $X\setminus U$
. In particular, the algorithm will not modify the locus where
$X\setminus U$
. In particular, the algorithm will not modify the locus where
![]() $X$
is an algebraic space.
$X$
is an algebraic space.
Applications
To illustrate how the destackification theorem may be applied, we will study three corollaries. The proofs given here will be sketchy, since a more detailed account will appear later in a joint paper with David Rydh.
The destackification algorithm is useful even if one is not primarily interested in stacks. Let
![]() $X$
be a variety over a field
$X$
be a variety over a field
![]() $k$
whose singular points are all simplicial, toric singularities. By this we mean that each point
$k$
whose singular points are all simplicial, toric singularities. By this we mean that each point
![]() $\unicode[STIX]{x1D709}\in X$
has an étale neighbourhood
$\unicode[STIX]{x1D709}\in X$
has an étale neighbourhood
 $X^{\prime }\rightarrow X$
with
$X^{\prime }\rightarrow X$
with
 $X^{\prime }=U/\unicode[STIX]{x1D6E5}$
for some smooth variety
$X^{\prime }=U/\unicode[STIX]{x1D6E5}$
for some smooth variety
![]() $U$
and finite diagonalisable group
$U$
and finite diagonalisable group
![]() $\unicode[STIX]{x1D6E5}$
. In this situation, there exists a canonical stack
$\unicode[STIX]{x1D6E5}$
. In this situation, there exists a canonical stack
![]() $X_{\text{can}}$
which is smooth and has
$X_{\text{can}}$
which is smooth and has
![]() $X$
as coarse space [Reference VistoliVis89, Reference SatrianoSat12]. By applying the functorial destackification algorithm on
$X$
as coarse space [Reference VistoliVis89, Reference SatrianoSat12]. By applying the functorial destackification algorithm on
![]() $X_{\text{can}}$
, we obtain a functorial desingularisation algorithm.
$X_{\text{can}}$
, we obtain a functorial desingularisation algorithm.
Corollary 1.3 (Functorial desingularisation of simplicial toric singularities).
Let
![]() $X$
be an algebraic space of finite type over an arbitrary field
$X$
be an algebraic space of finite type over an arbitrary field
![]() $k$
. Assume that
$k$
. Assume that
![]() $X$
has simplicial toric singularities only. Then there exists a sequence
$X$
has simplicial toric singularities only. Then there exists a sequence
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}:X_{m}\rightarrow \cdots \rightarrow X_{0}=X\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}:X_{m}\rightarrow \cdots \rightarrow X_{0}=X\end{eqnarray}$$
of proper birational modifications such that
![]() $X_{m}$
is smooth. The construction is functorial with respect to change of base field and with respect to smooth morphisms
$X_{m}$
is smooth. The construction is functorial with respect to change of base field and with respect to smooth morphisms
 $X^{\prime }\rightarrow X$
.
$X^{\prime }\rightarrow X$
.
Note that no toroidal structure is needed. This makes the corollary more general than the toroidal methods described in [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73]. On the other hand, the methods described in this article are somewhat less explicit. It recently came to the author’s knowledge that a similar result was obtained in the recent preprint [Reference BuonerbaBuo15].
At first sight, the assumption in Theorem 1.2 that the stack
![]() $X$
has diagonalisable stabilisers seems to be quite restrictive. But at least if we work over a field of characteristic 0, this can be overcome. By first using functorial embedded desingularisation on the stacky locus of
$X$
has diagonalisable stabilisers seems to be quite restrictive. But at least if we work over a field of characteristic 0, this can be overcome. By first using functorial embedded desingularisation on the stacky locus of
![]() $X$
with the Bierstone–Milman variant of Hironaka’s method [Reference Bierstone and MilmanBM97], we reduce to the case where the stacky locus is contained in a simple normal crossings divisor. But this implies that the stabilisers are in fact diagonalisable [Reference Reichstein and YoussinRY00, Theorem 4.1], so we are in a situation where we can apply Theorem 1.2.
$X$
with the Bierstone–Milman variant of Hironaka’s method [Reference Bierstone and MilmanBM97], we reduce to the case where the stacky locus is contained in a simple normal crossings divisor. But this implies that the stabilisers are in fact diagonalisable [Reference Reichstein and YoussinRY00, Theorem 4.1], so we are in a situation where we can apply Theorem 1.2.
Corollary 1.4 (Functorial destackification of Deligne–Mumford stacks in characteristic 0).
Let
![]() $X$
be a Deligne–Mumford stack which is smooth and of finite type over a field of characteristic
$X$
be a Deligne–Mumford stack which is smooth and of finite type over a field of characteristic
![]() $0$
. Also assume that
$0$
. Also assume that
![]() $X$
has finite inertia. Then there exists a smooth stacky blow-up sequence
$X$
has finite inertia. Then there exists a smooth stacky blow-up sequence
![]() $\unicode[STIX]{x1D6F1}$
, as in the functorial destackification theorem, such that
$\unicode[STIX]{x1D6F1}$
, as in the functorial destackification theorem, such that
 $(X_{m},\boldsymbol{E}_{m})$
has the same properties as mentioned in that theorem.
$(X_{m},\boldsymbol{E}_{m})$
has the same properties as mentioned in that theorem.
Finally, destackification can be used to obtain a stacky version of the weak factorisation theorem by Włodarczyk [Reference WłodarczykWło00] for Deligne–Mumford stacks in characteristic 0. The corollary is obtained by applying Włodarczyk’s result on the algebraic space obtained after destackifying using Corollary 1.4.
Corollary 1.5 (Weak factorisation of orbifolds in characteristic 0).
Consider a proper birational map
 $f:X{\dashrightarrow}Y$
of orbifolds over a field of characteristic
$f:X{\dashrightarrow}Y$
of orbifolds over a field of characteristic
![]() $0$
. Then there exists a factorisation of
$0$
. Then there exists a factorisation of
![]() $f$
in stacky blow-ups and blow-downs which is an isomorphism over the non-stacky locus where
$f$
in stacky blow-ups and blow-downs which is an isomorphism over the non-stacky locus where
![]() $f$
is an isomorphism.
$f$
is an isomorphism.
Outline of the paper
Section 2 collects some preliminaries on algebraic stacks and clarifies the terminology used in this paper. We will also make precise definitions of certain terms, such as functoriality and blow-up sequence, used in the main theorems. In § 3, we will review some basic facts about toric stacks. These will be used in § 4, where we describe two algorithms, Algorithms A and B, which prove the destackification theorems in the toric case. The algorithms are based on the classical toric desingularisation algorithm, but have an additional twist in order to make the process functorial.
From § 5 and onwards, we leave the realm of toric stacks and work with more general smooth stacks with finite diagonalisable stabilisers. First we show that any such stack is locally toric, which allows us to work with local homogeneous coordinates. Then, in § 6, we introduce an invariant, which we call the conormal representation. This invariant captures the local structure of a stack near each point. In characteristic 0, we could have worked with the canonical action of the stabiliser on the tangent space at each point, but, in positive characteristic, the tangent space is not well behaved. Instead, we work with the conormal bundle of the residual gerbe. We will also study a framework for constructing special purpose invariants, called conormal invariants, based on the conormal representation. Simple, well-known examples of such invariants are the order of the stabiliser and the multiplicity of the toric singularity of the corresponding point in the coarse space.
In § 7, we give an outline of the general destackification algorithms and introduce all conormal invariants used by these algorithms. Finally, in § 8, we go through the actual destackification algorithms and prove their correctness.
The paper also includes three appendices, collecting results of more general interest. In Appendix A, we prove a structure theorem for smooth, tame stacks in the spirit of the general structure theorem given in [Reference Abramovich, Olsson and VistoliAOV08]. We will also simplify parts of the proof of the general structure theorem given in [Reference Abramovich, Olsson and VistoliAOV08]. In Appendix B, we compute the cotangent complex of a basic toric stack and, in Appendix C, we give an alternative interpretation of the conormal representation in terms of the cotangent complex.
2 Stacky blow-up sequences and functoriality
2.1 Preliminaries and basic terminology
The cyclic (abstract) group of order
![]() $n$
will be denoted by
$n$
will be denoted by
![]() $C_{n}$
.
$C_{n}$
.
We will use the definitions of algebraic stack and algebraic space used in the Stacks project [Sta17]. By a sheaf, we mean a sheaf on the site of schemes with coverings given by faithfully flat morphisms which are locally of finite presentation, i.e., the fppf topology. By a stack, we mean a stack in groupoids over the same site. An atlas for a stack
![]() $X$
is a 1-morphism
$X$
is a 1-morphism
 $f:U\rightarrow X$
, where
$f:U\rightarrow X$
, where
![]() $U$
and
$U$
and
![]() $f$
are representable by algebraic spaces and
$f$
are representable by algebraic spaces and
![]() $f$
is faithfully flat and locally of finite presentation. If the morphism
$f$
is faithfully flat and locally of finite presentation. If the morphism
![]() $f$
is smooth, we call it a smooth atlas. A stack is algebraic if it admits an atlas, and it is a theorem that every algebraic stack admits a smooth atlas.
$f$
is smooth, we call it a smooth atlas. A stack is algebraic if it admits an atlas, and it is a theorem that every algebraic stack admits a smooth atlas.
Let
![]() $X$
be an algebraic stack. A morphism
$X$
be an algebraic stack. A morphism
 $\unicode[STIX]{x1D70B}:X\rightarrow X_{\text{cs}}$
is called a coarse space if it is initial among morphisms to algebraic spaces and the induced map
$\unicode[STIX]{x1D70B}:X\rightarrow X_{\text{cs}}$
is called a coarse space if it is initial among morphisms to algebraic spaces and the induced map
 $|\unicode[STIX]{x1D70B}|:|X|\rightarrow |X_{\text{cs}}|$
between topological spaces is a homeomorphism. Usually, this is called a coarse moduli space, but we drop the word moduli since we are discussing algebraic stacks without having any specific moduli problem in mind. Due to a classical theorem by Keel and Mori [Reference Keel and MoriKM97] with generalisations by Rydh [Reference RydhRyd13], an algebraic stack
$|\unicode[STIX]{x1D70B}|:|X|\rightarrow |X_{\text{cs}}|$
between topological spaces is a homeomorphism. Usually, this is called a coarse moduli space, but we drop the word moduli since we are discussing algebraic stacks without having any specific moduli problem in mind. Due to a classical theorem by Keel and Mori [Reference Keel and MoriKM97] with generalisations by Rydh [Reference RydhRyd13], an algebraic stack
![]() $X$
has a coarse space if its inertia stack is finite over
$X$
has a coarse space if its inertia stack is finite over
![]() $X$
.
$X$
.
Let
![]() $X$
be an algebraic stack which is quasi-separated and locally of finite presentation over a base scheme
$X$
be an algebraic stack which is quasi-separated and locally of finite presentation over a base scheme
![]() $S$
. Following Abramovich et al. [Reference Abramovich, Olsson and VistoliAOV08], we say that
$S$
. Following Abramovich et al. [Reference Abramovich, Olsson and VistoliAOV08], we say that
![]() $X$
is tame if it has finite inertia and linearly reductive stabilisers. This property is reviewed in Appendix A. We will be particularly interested in the case when
$X$
is tame if it has finite inertia and linearly reductive stabilisers. This property is reviewed in Appendix A. We will be particularly interested in the case when
![]() $X$
has diagonalisable stabilisers. We will use the term orbifold, in the relative sense, for a tame stack
$X$
has diagonalisable stabilisers. We will use the term orbifold, in the relative sense, for a tame stack
![]() $X\rightarrow S$
which is smooth over the base scheme, and which has fibrewise generically trivial stabilisers.
$X\rightarrow S$
which is smooth over the base scheme, and which has fibrewise generically trivial stabilisers.
We recall the definition of a simple normal crossings divisor on a regular scheme
![]() $X$
. Let
$X$
. Let
 $E=E^{1}+\cdots +E^{r}$
be an effective Cartier divisor on
$E=E^{1}+\cdots +E^{r}$
be an effective Cartier divisor on
![]() $X$
. Given a point
$X$
. Given a point
![]() $\unicode[STIX]{x1D709}\in X$
, we consider the stalk
$\unicode[STIX]{x1D709}\in X$
, we consider the stalk
![]() ${\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
with maximal ideal
${\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
with maximal ideal
![]() $\mathfrak{m}_{\unicode[STIX]{x1D709}}$
. Each divisor
$\mathfrak{m}_{\unicode[STIX]{x1D709}}$
. Each divisor
![]() $E^{i}$
defines a regular element
$E^{i}$
defines a regular element
 $f_{\unicode[STIX]{x1D709}}^{i}\in {\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
which is well defined up to multiplication by a unit. We say that
$f_{\unicode[STIX]{x1D709}}^{i}\in {\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
which is well defined up to multiplication by a unit. We say that
![]() $E$
is a simple normal crossings divisor if it can be written as a sum
$E$
is a simple normal crossings divisor if it can be written as a sum
 $E=E^{1}+\cdots +E^{r}$
of Cartier divisors such that at each point
$E=E^{1}+\cdots +E^{r}$
of Cartier divisors such that at each point
![]() $\unicode[STIX]{x1D709}\in X$
, the subsequence of regular parameters
$\unicode[STIX]{x1D709}\in X$
, the subsequence of regular parameters
![]() $f_{\unicode[STIX]{x1D709}}^{i}$
satisfying
$f_{\unicode[STIX]{x1D709}}^{i}$
satisfying
 $f_{\unicode[STIX]{x1D709}}^{i}\in \mathfrak{m}_{\unicode[STIX]{x1D709}}$
extends to a regular system of parameters
$f_{\unicode[STIX]{x1D709}}^{i}\in \mathfrak{m}_{\unicode[STIX]{x1D709}}$
extends to a regular system of parameters
 $(t_{\unicode[STIX]{x1D709}}^{1},\ldots ,t_{\unicode[STIX]{x1D709}}^{n})$
. A closed subscheme
$(t_{\unicode[STIX]{x1D709}}^{1},\ldots ,t_{\unicode[STIX]{x1D709}}^{n})$
. A closed subscheme
![]() $Z$
of
$Z$
of
![]() $X$
is said to have simple normal crossings with
$X$
is said to have simple normal crossings with
![]() $E$
if at each point
$E$
if at each point
![]() $\unicode[STIX]{x1D709}\in X$
, the system
$\unicode[STIX]{x1D709}\in X$
, the system
 $(t_{\unicode[STIX]{x1D709}}^{1},\ldots ,t_{\unicode[STIX]{x1D709}}^{n})$
described above can be chosen such that the ideal corresponding to
$(t_{\unicode[STIX]{x1D709}}^{1},\ldots ,t_{\unicode[STIX]{x1D709}}^{n})$
described above can be chosen such that the ideal corresponding to
![]() $Z$
in
$Z$
in
![]() ${\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
is generated by a subsequence of
${\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
is generated by a subsequence of
 $(t_{\unicode[STIX]{x1D709}}^{1},\ldots ,t_{\unicode[STIX]{x1D709}}^{n})$
.
$(t_{\unicode[STIX]{x1D709}}^{1},\ldots ,t_{\unicode[STIX]{x1D709}}^{n})$
.
The definitions above generalise directly to stacks. Let
![]() $X$
be a regular algebraic stack with a smooth atlas
$X$
be a regular algebraic stack with a smooth atlas
 $\unicode[STIX]{x1D70B}:U\rightarrow X$
. An effective Cartier divisor
$\unicode[STIX]{x1D70B}:U\rightarrow X$
. An effective Cartier divisor
![]() $E$
is a simple normal crossings divisor if
$E$
is a simple normal crossings divisor if
![]() $E$
can be written as a sum
$E$
can be written as a sum
 $E^{1}+\cdots +E^{r}$
of regular divisors and the pull-back
$E^{1}+\cdots +E^{r}$
of regular divisors and the pull-back
![]() $E_{U}$
to
$E_{U}$
to
![]() $U$
is a simple normal crossings divisor. Similarly, a closed substack
$U$
is a simple normal crossings divisor. Similarly, a closed substack
![]() $Z$
has simple normal crossings with
$Z$
has simple normal crossings with
![]() $E$
if the same holds for
$E$
if the same holds for
![]() $Z_{U}$
with respect to
$Z_{U}$
with respect to
![]() $E_{U}$
.
$E_{U}$
.
We will also consider the relative version of the definitions above. Let
![]() $X\rightarrow S$
be a smooth stack over a scheme and let
$X\rightarrow S$
be a smooth stack over a scheme and let
 $E=E^{1}+\cdots +E^{r}$
be an effective Cartier divisor on
$E=E^{1}+\cdots +E^{r}$
be an effective Cartier divisor on
![]() $X$
, with each
$X$
, with each
![]() $E^{i}$
smooth over
$E^{i}$
smooth over
![]() $S$
. Note that
$S$
. Note that
![]() $E$
is a relative effective Cartier divisor in the sense of [Reference Dieudonné and GrothendieckEGAIV, § 21.15]. We say that
$E$
is a relative effective Cartier divisor in the sense of [Reference Dieudonné and GrothendieckEGAIV, § 21.15]. We say that
![]() $E$
is a (relative) simple normal crossings divisor if
$E$
is a (relative) simple normal crossings divisor if
![]() $E_{\unicode[STIX]{x1D709}}$
is a simple normal crossings divisor on the fibre
$E_{\unicode[STIX]{x1D709}}$
is a simple normal crossings divisor on the fibre
![]() $X_{\unicode[STIX]{x1D709}}$
for each geometric point
$X_{\unicode[STIX]{x1D709}}$
for each geometric point
 $\unicode[STIX]{x1D709}:\text{Spec}\,\bar{k}\rightarrow S$
. Similarly, we define what is meant for a substack
$\unicode[STIX]{x1D709}:\text{Spec}\,\bar{k}\rightarrow S$
. Similarly, we define what is meant for a substack
![]() $Z\subset X$
which is smooth over
$Z\subset X$
which is smooth over
![]() $S$
to have simple normal crossings with
$S$
to have simple normal crossings with
![]() $E$
.
$E$
.
Definition 2.1. Let
![]() $S$
be a scheme and consider a pair
$S$
be a scheme and consider a pair
 $(X,\boldsymbol{E})/S$
, where:
$(X,\boldsymbol{E})/S$
, where:
-
(i)
 $X$
is a tame algebraic stack which is smooth and of finite presentation over
$X$
is a tame algebraic stack which is smooth and of finite presentation over
 $S$
;
$S$
; -
(ii)
 $\boldsymbol{E}=(E^{1},\ldots ,E^{r})$
is an ordered set of distinct, effective Cartier divisors on
$\boldsymbol{E}=(E^{1},\ldots ,E^{r})$
is an ordered set of distinct, effective Cartier divisors on
 $X$
, called the components of
$X$
, called the components of
 $\boldsymbol{E}$
. Each component
$\boldsymbol{E}$
. Each component
 $E^{i}$
is required to be smooth over
$E^{i}$
is required to be smooth over
 $S$
and their sum
$S$
and their sum
 $E=\sum E^{i}$
is required to be a simple normal crossings divisor.
$E=\sum E^{i}$
is required to be a simple normal crossings divisor.
We call such a pair
 $(X,\boldsymbol{E})/S$
a standard pair.
$(X,\boldsymbol{E})/S$
a standard pair.
Note that the term component in this context does not refer to connected component; the components of
![]() $\boldsymbol{E}$
, as in the definition above, may well be empty or disconnected.
$\boldsymbol{E}$
, as in the definition above, may well be empty or disconnected.
When referring to the ordering of the components of an ordered simple normal crossings divisor, we will use an age metaphor. The components of such a divisor form a sequence
 $E^{1}\!,\ldots ,E^{r}\!$
. The indices may be thought of as birth dates of the components, and we say that
$E^{1}\!,\ldots ,E^{r}\!$
. The indices may be thought of as birth dates of the components, and we say that
![]() $E^{i}$
is older than
$E^{i}$
is older than
![]() $E^{j}$
, and that
$E^{j}$
, and that
![]() $E^{j}$
is younger than
$E^{j}$
is younger than
![]() $E^{i}$
, provided that
$E^{i}$
, provided that
![]() $i<j$
.
$i<j$
.
2.2 Stacky blow-up sequences
Let
![]() $S$
be a scheme and let
$S$
be a scheme and let
 $(X,\boldsymbol{E})/S$
be a standard pair. By a smooth blow-up of
$(X,\boldsymbol{E})/S$
be a standard pair. By a smooth blow-up of
 $(X,\boldsymbol{E})/S$
, we mean a blow-up
$(X,\boldsymbol{E})/S$
, we mean a blow-up
 $\unicode[STIX]{x1D70B}:\text{Bl}_{Z}X\rightarrow X$
in a centre
$\unicode[STIX]{x1D70B}:\text{Bl}_{Z}X\rightarrow X$
in a centre
![]() $Z$
which is smooth over
$Z$
which is smooth over
![]() $S$
and has simple normal crossings with
$S$
and has simple normal crossings with
![]() $E$
. The transform of
$E$
. The transform of
 $(X,\boldsymbol{E})/S$
along
$(X,\boldsymbol{E})/S$
along
![]() $\unicode[STIX]{x1D70B}$
is the pair
$\unicode[STIX]{x1D70B}$
is the pair
 $(\text{Bl}_{Z}X,\boldsymbol{E}^{\prime })$
, where
$(\text{Bl}_{Z}X,\boldsymbol{E}^{\prime })$
, where
![]() $\boldsymbol{E}^{\prime }$
denotes the ordered set of the strict transforms of the components of
$\boldsymbol{E}^{\prime }$
denotes the ordered set of the strict transforms of the components of
![]() $\boldsymbol{E}$
followed by the exceptional divisor. In other words, the ordering of the components
$\boldsymbol{E}$
followed by the exceptional divisor. In other words, the ordering of the components
![]() $\boldsymbol{E}^{\prime }$
is the one induced by the ordering on
$\boldsymbol{E}^{\prime }$
is the one induced by the ordering on
![]() $\boldsymbol{E}$
with the exceptional divisor added as the youngest divisor.
$\boldsymbol{E}$
with the exceptional divisor added as the youngest divisor.
The root construction of a stack in an effective Cartier divisor is thoroughly described in for instance [Reference Abramovich, Graber and VistoliAGV08, Reference CadmanCad07] and [Reference Fantechi, Mann and NironiFMN10, § 1.3.b]. Let
 $(X,\boldsymbol{E})/S$
be a standard pair. We will only consider root stacks with roots taken of components of
$(X,\boldsymbol{E})/S$
be a standard pair. We will only consider root stacks with roots taken of components of
![]() $\boldsymbol{E}$
. Such a root stack will be called a smooth root stack. If
$\boldsymbol{E}$
. Such a root stack will be called a smooth root stack. If
![]() $E^{i}\in \boldsymbol{E}$
, we use the notation
$E^{i}\in \boldsymbol{E}$
, we use the notation
 $X_{d^{-1}E^{i}}\rightarrow X$
for the
$X_{d^{-1}E^{i}}\rightarrow X$
for the
![]() $d$
th root of
$d$
th root of
![]() $E^{i}$
. If
$E^{i}$
. If
![]() $\boldsymbol{d}$
is a sequence of positive integers indexed by the elements of
$\boldsymbol{d}$
is a sequence of positive integers indexed by the elements of
![]() $\boldsymbol{E}$
, then
$\boldsymbol{E}$
, then
 $X_{\boldsymbol{d}^{-1}\boldsymbol{E}}\rightarrow X$
denotes the fibre product of the stacks
$X_{\boldsymbol{d}^{-1}\boldsymbol{E}}\rightarrow X$
denotes the fibre product of the stacks
![]() $X_{d_{i}^{-1}E^{i}}$
over
$X_{d_{i}^{-1}E^{i}}$
over
![]() $X$
for all
$X$
for all
![]() $E^{i}\in \boldsymbol{E}$
with
$E^{i}\in \boldsymbol{E}$
with
![]() $d_{i}$
as corresponding element in
$d_{i}$
as corresponding element in
![]() $\boldsymbol{d}$
. The sum of the components of
$\boldsymbol{d}$
. The sum of the components of
![]() $\boldsymbol{E}$
for which the corresponding index in
$\boldsymbol{E}$
for which the corresponding index in
![]() $\boldsymbol{d}$
is larger than one is called the centre of the root stack. If
$\boldsymbol{d}$
is larger than one is called the centre of the root stack. If
![]() $\boldsymbol{E}^{\prime }$
is a subsequence of
$\boldsymbol{E}^{\prime }$
is a subsequence of
![]() $\boldsymbol{E}$
and
$\boldsymbol{E}$
and
![]() $\boldsymbol{d}$
is a sequence of positive integers indexed by
$\boldsymbol{d}$
is a sequence of positive integers indexed by
![]() $\boldsymbol{E}^{\prime }$
, then we sometimes use the notation
$\boldsymbol{E}^{\prime }$
, then we sometimes use the notation
 $X_{\boldsymbol{d}^{-1}\boldsymbol{E}^{\prime }}\rightarrow X$
for the root stack obtained by extending
$X_{\boldsymbol{d}^{-1}\boldsymbol{E}^{\prime }}\rightarrow X$
for the root stack obtained by extending
![]() $\boldsymbol{d}$
to
$\boldsymbol{d}$
to
![]() $\boldsymbol{E}$
by ones. The transform of a pair
$\boldsymbol{E}$
by ones. The transform of a pair
 $(X,\boldsymbol{E})/S$
along a smooth root stack
$(X,\boldsymbol{E})/S$
along a smooth root stack
 $\unicode[STIX]{x1D70B}:X_{\boldsymbol{d}^{-1}\boldsymbol{E}}\rightarrow X$
is the pair
$\unicode[STIX]{x1D70B}:X_{\boldsymbol{d}^{-1}\boldsymbol{E}}\rightarrow X$
is the pair
 $(X_{\boldsymbol{d}^{-1}\boldsymbol{E}},\unicode[STIX]{x1D70B}^{-1}\boldsymbol{E})$
. Here
$(X_{\boldsymbol{d}^{-1}\boldsymbol{E}},\unicode[STIX]{x1D70B}^{-1}\boldsymbol{E})$
. Here
![]() $\unicode[STIX]{x1D70B}^{-1}\boldsymbol{E}$
denotes the sequence
$\unicode[STIX]{x1D70B}^{-1}\boldsymbol{E}$
denotes the sequence
 $(d_{i}^{-1}\unicode[STIX]{x1D70B}^{\ast }E^{i})$
of roots of the components
$(d_{i}^{-1}\unicode[STIX]{x1D70B}^{\ast }E^{i})$
of roots of the components
![]() $E^{i}$
of
$E^{i}$
of
![]() $\boldsymbol{E}$
.
$\boldsymbol{E}$
.
A smooth stacky blow-up is either a smooth root stack or a smooth blow-up. Note that the transform of a standard pair along a smooth stacky blow-up is again a standard pair.
Definition 2.2. Let
 $(X_{0},\boldsymbol{E}_{0})/S$
be a standard pair. A smooth, stacky blow-up sequence of
$(X_{0},\boldsymbol{E}_{0})/S$
be a standard pair. A smooth, stacky blow-up sequence of
 $(X_{0},\boldsymbol{E}_{0})/S$
of length
$(X_{0},\boldsymbol{E}_{0})/S$
of length
![]() $n$
is a sequence
$n$
is a sequence
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}:(X_{n},\boldsymbol{E}_{n})\stackrel{\unicode[STIX]{x1D70B}_{n}}{\longrightarrow }\cdots \stackrel{\unicode[STIX]{x1D70B}_{1}}{\longrightarrow }(X_{0},\boldsymbol{E}_{0}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}:(X_{n},\boldsymbol{E}_{n})\stackrel{\unicode[STIX]{x1D70B}_{n}}{\longrightarrow }\cdots \stackrel{\unicode[STIX]{x1D70B}_{1}}{\longrightarrow }(X_{0},\boldsymbol{E}_{0}),\end{eqnarray}$$
where each
![]() $\unicode[STIX]{x1D70B}_{i}$
, for
$\unicode[STIX]{x1D70B}_{i}$
, for
 $1\leqslant i\leqslant n$
, is a smooth stacky blow-up in a centre
$1\leqslant i\leqslant n$
, is a smooth stacky blow-up in a centre
![]() $Z_{i-1}$
and each
$Z_{i-1}$
and each
 $(X_{i},\boldsymbol{E}_{i})$
is the transform of
$(X_{i},\boldsymbol{E}_{i})$
is the transform of
 $(X_{i-1},\boldsymbol{E}_{i-1})$
along
$(X_{i-1},\boldsymbol{E}_{i-1})$
along
![]() $\unicode[STIX]{x1D70B}_{i}$
. The centres
$\unicode[STIX]{x1D70B}_{i}$
. The centres
![]() $Z_{i}$
for
$Z_{i}$
for
 $0\leqslant i\leqslant n-1$
, although suppressed from the notation, are considered part of the structure. We require each
$0\leqslant i\leqslant n-1$
, although suppressed from the notation, are considered part of the structure. We require each
![]() $Z_{i}$
to have positive codimension in
$Z_{i}$
to have positive codimension in
![]() $X_{i}$
at each of its points. If all stacky blow-ups are in fact usual blow-ups, we call
$X_{i}$
at each of its points. If all stacky blow-ups are in fact usual blow-ups, we call
![]() $\unicode[STIX]{x1D6F1}$
a smooth, ordinary blow-up sequence.
$\unicode[STIX]{x1D6F1}$
a smooth, ordinary blow-up sequence.
Since all blow-up sequences we consider in this article will be smooth, stacky blow-up sequences, we will usually drop the modifiers smooth and stacky and just say blow-up sequence.
Definition 2.3. Let
 $(X_{0},\boldsymbol{E}_{0})/S$
be a standard pair and let
$(X_{0},\boldsymbol{E}_{0})/S$
be a standard pair and let
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}:(Y,\boldsymbol{F})=(X_{n},\boldsymbol{E}_{n})\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{n}}\cdots \xrightarrow[{}]{\unicode[STIX]{x1D70B}_{1}}(X_{0},\boldsymbol{E}_{0})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}:(Y,\boldsymbol{F})=(X_{n},\boldsymbol{E}_{n})\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{n}}\cdots \xrightarrow[{}]{\unicode[STIX]{x1D70B}_{1}}(X_{0},\boldsymbol{E}_{0})\end{eqnarray}$$
be a smooth, stacky blow-up sequence on
 $(X_{0},\boldsymbol{E}_{0})/S$
. Let
$(X_{0},\boldsymbol{E}_{0})/S$
. Let
 $\unicode[STIX]{x1D70B}:Y\rightarrow Y_{\text{cs}}$
be the coarse space. We call
$\unicode[STIX]{x1D70B}:Y\rightarrow Y_{\text{cs}}$
be the coarse space. We call
![]() $\unicode[STIX]{x1D6F1}$
a destackification if the following conditions hold.
$\unicode[STIX]{x1D6F1}$
a destackification if the following conditions hold.
-
(i) The space
 $Y_{\text{cs}}$
is smooth over
$Y_{\text{cs}}$
is smooth over
 $S$
.
$S$
. -
(ii) Each component of
 $\boldsymbol{F}_{\text{cs}}=(F_{\text{cs}}^{i}\mid F^{i}\in \boldsymbol{F})$
is smooth and
$\boldsymbol{F}_{\text{cs}}=(F_{\text{cs}}^{i}\mid F^{i}\in \boldsymbol{F})$
is smooth and
 $\sum _{i}F^{i}$
has simple normal crossings.
$\sum _{i}F^{i}$
has simple normal crossings. -
(iii) The divisor
 $\boldsymbol{F}$
is a
$\boldsymbol{F}$
is a
 $\boldsymbol{d}$
th root of the pull-back
$\boldsymbol{d}$
th root of the pull-back
 $\unicode[STIX]{x1D70B}^{\ast }\boldsymbol{F}_{\text{cs}}$
for some sequence
$\unicode[STIX]{x1D70B}^{\ast }\boldsymbol{F}_{\text{cs}}$
for some sequence
 $\boldsymbol{d}$
of positive integers indexed by the components of
$\boldsymbol{d}$
of positive integers indexed by the components of
 $\boldsymbol{F}$
.
$\boldsymbol{F}$
. -
(iv) The canonical factorisation
 $Y\rightarrow (Y_{\text{cs}})_{\boldsymbol{d}^{-1}\boldsymbol{F}_{\text{cs}}}\rightarrow Y_{\text{cs}}$
through the root stack makes
$Y\rightarrow (Y_{\text{cs}})_{\boldsymbol{d}^{-1}\boldsymbol{F}_{\text{cs}}}\rightarrow Y_{\text{cs}}$
through the root stack makes
 $Y$
a gerbe over
$Y$
a gerbe over
 $(Y_{\text{cs}})_{\boldsymbol{d}^{-1}\boldsymbol{F}_{\text{cs}}}$
. In particular, if
$(Y_{\text{cs}})_{\boldsymbol{d}^{-1}\boldsymbol{F}_{\text{cs}}}$
. In particular, if
 $X_{0}$
is an orbifold, then
$X_{0}$
is an orbifold, then
 $Y\rightarrow (Y_{\text{cs}})_{\boldsymbol{d}^{-1}\boldsymbol{F}_{\text{cs}}}$
is an isomorphism.
$Y\rightarrow (Y_{\text{cs}})_{\boldsymbol{d}^{-1}\boldsymbol{F}_{\text{cs}}}$
is an isomorphism.
The conditions (i) and (ii) can be summarised by saying that the pair
 $(Y_{\text{cs}},\boldsymbol{F}_{\text{cs}})/S$
is a standard pair.
$(Y_{\text{cs}},\boldsymbol{F}_{\text{cs}})/S$
is a standard pair.
A stacky blow-up is said to be empty if the centre is empty. Although the algorithms used in the constructions mentioned in the main theorems will never produce blow-up sequences containing empty blow-ups, such may occur after pulling back blow-up sequences along morphisms which are not surjective. We will consider such pull-backs when discussing functoriality below. We regard two blow-up sequences
![]() $\unicode[STIX]{x1D6F1}$
and
$\unicode[STIX]{x1D6F1}$
and
![]() $\unicode[STIX]{x1D6F1}^{\prime }$
to be equivalent if, after pruning them from empty blow-ups, they fit into a 2-commutative ladder
$\unicode[STIX]{x1D6F1}^{\prime }$
to be equivalent if, after pruning them from empty blow-ups, they fit into a 2-commutative ladder

such that the vertical morphisms are isomorphisms preserving the centres.
2.3 Gerbes
Given a stack
![]() $X$
, we denote by
$X$
, we denote by
 $X\rightarrow X_{\text{sh}}$
the canonical morphism to the coarse sheaf. This is, by definition, a morphism which is initial among morphisms to sheaves in the fppf topology. An algebraic stack
$X\rightarrow X_{\text{sh}}$
the canonical morphism to the coarse sheaf. This is, by definition, a morphism which is initial among morphisms to sheaves in the fppf topology. An algebraic stack
![]() $X$
is called a gerbe if its associated coarse sheaf is an algebraic space. In this case, the morphism
$X$
is called a gerbe if its associated coarse sheaf is an algebraic space. In this case, the morphism
 $\unicode[STIX]{x1D70B}:X\rightarrow X_{\text{sh}}$
is called the structure morphism of the gerbe. There is also a relative notion of gerbe. A morphism
$\unicode[STIX]{x1D70B}:X\rightarrow X_{\text{sh}}$
is called the structure morphism of the gerbe. There is also a relative notion of gerbe. A morphism
 $\unicode[STIX]{x1D70B}:X\rightarrow Y$
of algebraic stacks is called a gerbe if the base change
$\unicode[STIX]{x1D70B}:X\rightarrow Y$
of algebraic stacks is called a gerbe if the base change
 $X^{\prime }\rightarrow Y^{\prime }$
of
$X^{\prime }\rightarrow Y^{\prime }$
of
![]() $\unicode[STIX]{x1D70B}$
along any morphism
$\unicode[STIX]{x1D70B}$
along any morphism
 $Y^{\prime }\rightarrow Y$
, with
$Y^{\prime }\rightarrow Y$
, with
![]() $Y^{\prime }$
an algebraic space, is the structure morphism of a gerbe in the sense described above.
$Y^{\prime }$
an algebraic space, is the structure morphism of a gerbe in the sense described above.
This definition is standard and coincides with the one given in, for instance, the Stacks project [Sta17]. It is related to the definition given by Giraud [Reference GiraudGir71, Definition 2.1.1] in the following way. A stack
![]() $Y$
has a canonical structure of a site induced by the fppf topology on the site of schemes. A morphism
$Y$
has a canonical structure of a site induced by the fppf topology on the site of schemes. A morphism
 $\unicode[STIX]{x1D70B}:X\rightarrow Y$
of algebraic stacks is a gerbe in our sense if and only if
$\unicode[STIX]{x1D70B}:X\rightarrow Y$
of algebraic stacks is a gerbe in our sense if and only if
![]() $X$
is a gerbe in the sense of Giraud when viewed as a stack in groupoids over the site
$X$
is a gerbe in the sense of Giraud when viewed as a stack in groupoids over the site
![]() $Y$
.
$Y$
.
Note that in the context of algebraic stacks, the terminology for gerbes sometimes conflicts with algebrogeometric notions. For instance, the structure morphism
 $\unicode[STIX]{x1D70B}:X\rightarrow Y$
of a gerbe in our sense is always smooth (see Proposition A.2). In particular, the morphism
$\unicode[STIX]{x1D70B}:X\rightarrow Y$
of a gerbe in our sense is always smooth (see Proposition A.2). In particular, the morphism
![]() $\unicode[STIX]{x1D70B}$
always admits a section étale locally on
$\unicode[STIX]{x1D70B}$
always admits a section étale locally on
![]() $Y$
. This does, however, not imply that
$Y$
. This does, however, not imply that
![]() $X$
is a gerbe as a stack in groupoids over
$X$
is a gerbe as a stack in groupoids over
![]() $Y$
considered as a site endowed with the smooth or étale topology. This is a potential source of confusion as it makes terms such as smooth gerbe ambiguous. In this article, we try to avoid the confusion by consistently working with the fppf topology.
$Y$
considered as a site endowed with the smooth or étale topology. This is a potential source of confusion as it makes terms such as smooth gerbe ambiguous. In this article, we try to avoid the confusion by consistently working with the fppf topology.
2.4 Stabiliser-preserving maps
We recall the definition and some basic facts about stabiliser-preserving 1-morphisms of stacks. Let
 $f:X\rightarrow Y$
be a 1-morphism of stacks. Given a generalised point
$f:X\rightarrow Y$
be a 1-morphism of stacks. Given a generalised point
 $\unicode[STIX]{x1D709}:T\rightarrow X$
, where
$\unicode[STIX]{x1D709}:T\rightarrow X$
, where
![]() $T$
is a scheme, we get an induced map of stabilisers
$T$
is a scheme, we get an induced map of stabilisers
 $\text{Stab}_{\unicode[STIX]{x1D709}}X\rightarrow \text{Stab}_{f\circ \unicode[STIX]{x1D709}}Y$
over
$\text{Stab}_{\unicode[STIX]{x1D709}}X\rightarrow \text{Stab}_{f\circ \unicode[STIX]{x1D709}}Y$
over
![]() $T$
. The map
$T$
. The map
![]() $f$
also induces a pair of 2-commutative diagrams
$f$
also induces a pair of 2-commutative diagrams

Here
 $I_{X}\rightarrow X$
denotes the inertia stack of
$I_{X}\rightarrow X$
denotes the inertia stack of
![]() $X$
, and the map
$X$
, and the map
 $X\rightarrow X_{\text{sh}}$
is the coarse sheaf of
$X\rightarrow X_{\text{sh}}$
is the coarse sheaf of
![]() $X$
(as defined in the previous section).
$X$
(as defined in the previous section).
Definition 2.4. The 1-morphism
 $f:X\rightarrow Y$
is called stabiliser-preserving if any of the following conditions, which are easily seen to be equivalent, hold.
$f:X\rightarrow Y$
is called stabiliser-preserving if any of the following conditions, which are easily seen to be equivalent, hold.
-
(i) The map
 $\text{Stab}_{\unicode[STIX]{x1D709}}X\rightarrow \text{Stab}_{f\circ \unicode[STIX]{x1D709}}Y$
is an isomorphism for any generalised point
$\text{Stab}_{\unicode[STIX]{x1D709}}X\rightarrow \text{Stab}_{f\circ \unicode[STIX]{x1D709}}Y$
is an isomorphism for any generalised point
 $\unicode[STIX]{x1D709}$
.
$\unicode[STIX]{x1D709}$
. -
(ii) The left 2-commutative square above is 2-cartesian.
-
(iii) The right 2-commutative square above is 2-cartesian.
If the first condition holds for all geometric points, we say that
![]() $f$
is point-wise stabiliser-preserving.
$f$
is point-wise stabiliser-preserving.
In particular, monomorphisms between stacks are stabiliser-preserving. Note that the notions of stabiliser-preserving and point-wise stabiliser-preserving maps are distinct. Both properties are preserved under composition and arbitrary base change. They are also local on the base in the fppf topology.
Example 2.5. Let
![]() $k$
be a field and let
$k$
be a field and let
 $X=\text{Spec}\,k[\unicode[STIX]{x1D700}]$
be the spectrum of the dual numbers over
$X=\text{Spec}\,k[\unicode[STIX]{x1D700}]$
be the spectrum of the dual numbers over
![]() $k$
. Furthermore, let the group
$k$
. Furthermore, let the group
![]() $\unicode[STIX]{x1D707}_{2}$
act on
$\unicode[STIX]{x1D707}_{2}$
act on
![]() $X$
by giving
$X$
by giving
![]() $\unicode[STIX]{x1D700}$
degree 1. Then we get a map
$\unicode[STIX]{x1D700}$
degree 1. Then we get a map
 $[X/\unicode[STIX]{x1D707}_{2}]\rightarrow \text{B}\unicode[STIX]{x1D707}_{2}$
from the quotient stack to the classifying stack of
$[X/\unicode[STIX]{x1D707}_{2}]\rightarrow \text{B}\unicode[STIX]{x1D707}_{2}$
from the quotient stack to the classifying stack of
![]() $\unicode[STIX]{x1D707}_{2}$
, which is point-wise stabiliser-preserving, but not stabiliser-preserving.
$\unicode[STIX]{x1D707}_{2}$
, which is point-wise stabiliser-preserving, but not stabiliser-preserving.
A useful fact is that if
 $f:X\rightarrow Y$
is an étale map between algebraic stacks with finite inertia, then the locus where
$f:X\rightarrow Y$
is an étale map between algebraic stacks with finite inertia, then the locus where
![]() $f$
is point-wise stabiliser-preserving is open in
$f$
is point-wise stabiliser-preserving is open in
![]() $X$
, and
$X$
, and
![]() $f$
is stabiliser-preserving over this locus [Reference RydhRyd11, Proposition 6.5]. In fact, if the stacks are tame, the corresponding fact for smooth morphisms is also true, but we will not use this here.
$f$
is stabiliser-preserving over this locus [Reference RydhRyd11, Proposition 6.5]. In fact, if the stacks are tame, the corresponding fact for smooth morphisms is also true, but we will not use this here.
2.5 Functoriality
We consider two basic situations when a smooth stacky blow-up sequence can be transferred from one standard pair to another. Fix a standard pair
 $(X,\boldsymbol{E})/S$
.
$(X,\boldsymbol{E})/S$
.
The first situation is when we change base scheme. Given a morphism
 $S^{\prime }\rightarrow S$
, we can form the pull-backs
$S^{\prime }\rightarrow S$
, we can form the pull-backs
 $X_{S^{\prime }}=X\times _{S}S^{\prime }$
and
$X_{S^{\prime }}=X\times _{S}S^{\prime }$
and
 $\boldsymbol{E}_{S^{\prime }}=\boldsymbol{E}\times _{S}S^{\prime }$
. Then the pair
$\boldsymbol{E}_{S^{\prime }}=\boldsymbol{E}\times _{S}S^{\prime }$
. Then the pair
 $(X_{S^{\prime }},\boldsymbol{E}_{S^{\prime }})/S^{\prime }$
is also standard, and any smooth stacky blow-up sequence on
$(X_{S^{\prime }},\boldsymbol{E}_{S^{\prime }})/S^{\prime }$
is also standard, and any smooth stacky blow-up sequence on
 $(X,\boldsymbol{E})/S$
pulls back to a smooth stacky blow-up sequence on
$(X,\boldsymbol{E})/S$
pulls back to a smooth stacky blow-up sequence on
 $(X_{S^{\prime }},\boldsymbol{E}_{S^{\prime }})/S^{\prime }$
.
$(X_{S^{\prime }},\boldsymbol{E}_{S^{\prime }})/S^{\prime }$
.
The second situation is when we have a morphism of stacks
 $X^{\prime }\rightarrow X$
which is smooth. Then we can form the pull-back
$X^{\prime }\rightarrow X$
which is smooth. Then we can form the pull-back
 $\boldsymbol{E}^{\prime }=\boldsymbol{E}\times _{X}X^{\prime }$
, and we get a standard pair
$\boldsymbol{E}^{\prime }=\boldsymbol{E}\times _{X}X^{\prime }$
, and we get a standard pair
 $(X^{\prime },\boldsymbol{E}^{\prime })/S$
. Again, any smooth stacky blow-up sequence on
$(X^{\prime },\boldsymbol{E}^{\prime })/S$
. Again, any smooth stacky blow-up sequence on
 $(X,\boldsymbol{E})/S$
pulls back to a smooth stacky blow-up sequence on
$(X,\boldsymbol{E})/S$
pulls back to a smooth stacky blow-up sequence on
 $(X^{\prime },\boldsymbol{E}^{\prime })/S$
.
$(X^{\prime },\boldsymbol{E}^{\prime })/S$
.
Definition 2.6. Let
 $(X,\boldsymbol{E})/S$
be a standard pair. We say that a construction of a blow-up sequence is functorial with respect to base change
$(X,\boldsymbol{E})/S$
be a standard pair. We say that a construction of a blow-up sequence is functorial with respect to base change
 $S^{\prime }\rightarrow S$
if the blow-up sequence obtained by applying the construction to
$S^{\prime }\rightarrow S$
if the blow-up sequence obtained by applying the construction to
 $(X_{S^{\prime }},\boldsymbol{E}_{S^{\prime }})/S^{\prime }$
is equivalent (see § 2.2) to the pull-back of the blow-up sequence obtained by applying the construction to
$(X_{S^{\prime }},\boldsymbol{E}_{S^{\prime }})/S^{\prime }$
is equivalent (see § 2.2) to the pull-back of the blow-up sequence obtained by applying the construction to
 $(X,\boldsymbol{E})/S$
as described in the first situation above.
$(X,\boldsymbol{E})/S$
as described in the first situation above.
We say that a construction of a blow-up sequence is functorial with respect to a morphism
 $X^{\prime }\rightarrow X$
if the blow-up sequence obtained by applying the construction to
$X^{\prime }\rightarrow X$
if the blow-up sequence obtained by applying the construction to
 $(X^{\prime },\boldsymbol{E}^{\prime })/S$
is equivalent to the pull-back of the blow-up sequence obtained by applying the construction to
$(X^{\prime },\boldsymbol{E}^{\prime })/S$
is equivalent to the pull-back of the blow-up sequence obtained by applying the construction to
 $(X,\boldsymbol{E})/S$
as described in the second situation above. In order for this to make sense, the morphism
$(X,\boldsymbol{E})/S$
as described in the second situation above. In order for this to make sense, the morphism
 $X^{\prime }\rightarrow X$
must be smooth.
$X^{\prime }\rightarrow X$
must be smooth.
The constructions in the main theorems are functorial with respect to arbitrary base change
![]() $S^{\prime }\rightarrow S$
and with respect to morphisms
$S^{\prime }\rightarrow S$
and with respect to morphisms
 $X^{\prime }\rightarrow X$
which are either gerbes or smooth and stabiliser-preserving. It is, however, not reasonable to expect the construction to be functorial with respect to any smooth morphism. Indeed, if
$X^{\prime }\rightarrow X$
which are either gerbes or smooth and stabiliser-preserving. It is, however, not reasonable to expect the construction to be functorial with respect to any smooth morphism. Indeed, if
 $X^{\prime }\rightarrow X$
is a smooth atlas, any reasonable destackification of
$X^{\prime }\rightarrow X$
is a smooth atlas, any reasonable destackification of
![]() $X^{\prime }$
must be trivial, whereas a destackification of
$X^{\prime }$
must be trivial, whereas a destackification of
![]() $X$
cannot be trivial in general.
$X$
cannot be trivial in general.
2.6 Distinguished structure
We do not want our algorithms to modify the locus lying over the smooth locus of the coarse space of the original stack. This poses a problem when it comes to root stacks, since they always modify the entire divisor of which the root is taken. Thus, we would like to keep track of divisors which we are allowed to root. We do this by marking certain divisors as distinguished.
Definition 2.7. Let
 $(X,\boldsymbol{E})/S$
be a standard pair, and let
$(X,\boldsymbol{E})/S$
be a standard pair, and let
![]() $\boldsymbol{D}\subset \boldsymbol{E}$
be a subset such that all divisors in
$\boldsymbol{D}\subset \boldsymbol{E}$
be a subset such that all divisors in
![]() $\boldsymbol{D}$
are younger than the divisors in the complement
$\boldsymbol{D}$
are younger than the divisors in the complement
![]() $\boldsymbol{E}\setminus \boldsymbol{D}$
. We say that
$\boldsymbol{E}\setminus \boldsymbol{D}$
. We say that
 $(X,\boldsymbol{E},\boldsymbol{D})/S$
is a standard pair with distinguished structure, and call the components of
$(X,\boldsymbol{E},\boldsymbol{D})/S$
is a standard pair with distinguished structure, and call the components of
![]() $\boldsymbol{E}$
lying in
$\boldsymbol{E}$
lying in
![]() $\boldsymbol{D}$
distinguished. A smooth stacky blow-up of
$\boldsymbol{D}$
distinguished. A smooth stacky blow-up of
 $(X,\boldsymbol{E},\boldsymbol{D})/S$
is simply a smooth stacky blow-up of the underlying standard pair
$(X,\boldsymbol{E},\boldsymbol{D})/S$
is simply a smooth stacky blow-up of the underlying standard pair
 $(X,\boldsymbol{E})/S$
. Such a blow-up is called admissible if its centre is contained in the support of the divisors in
$(X,\boldsymbol{E})/S$
. Such a blow-up is called admissible if its centre is contained in the support of the divisors in
![]() $\boldsymbol{D}$
.
$\boldsymbol{D}$
.
The transform
 $(X^{\prime },\boldsymbol{E}^{\prime })/S$
of an admissible stacky blow-up of a standard pair with distinguished structure
$(X^{\prime },\boldsymbol{E}^{\prime })/S$
of an admissible stacky blow-up of a standard pair with distinguished structure
 $(X,\boldsymbol{E},\boldsymbol{D})/S$
again has a distinguished structure
$(X,\boldsymbol{E},\boldsymbol{D})/S$
again has a distinguished structure
 $\boldsymbol{D}^{\prime }\subset \boldsymbol{E}^{\prime }$
. It consists of the strict transforms of all distinguished divisors along with the exceptional divisor.
$\boldsymbol{D}^{\prime }\subset \boldsymbol{E}^{\prime }$
. It consists of the strict transforms of all distinguished divisors along with the exceptional divisor.
3 Smooth toric stacks
The theory of toric stacks has been treated by several authors. We mention a few. Borisov et al. [Reference Borisov, Chen and SmithBCS05] gave a basic definition of smooth toric Deligne–Mumford stacks via the Cox construction. Iwanari gave a moduli interpretation of toric stacks using logarithmic geometry [Reference IwanariIwa09b]. He also gave a structure theorem, characterising toric orbifolds over a field of characteristic
![]() $0$
in terms of stacks with torus actions [Reference IwanariIwa09a]. A similar result was obtained independently by Fantechi et al. [Reference Fantechi, Mann and NironiFMN10], using a bottom-up construction. Geraschenko and Satriano [Reference Geraschenko and SatrianoGS15a, Reference Geraschenko and SatrianoGS15b] extended the theory to non-smooth stacks and stacks with positive-dimensional stabilisers and unified the theory with other notions of toric stacks.
$0$
in terms of stacks with torus actions [Reference IwanariIwa09a]. A similar result was obtained independently by Fantechi et al. [Reference Fantechi, Mann and NironiFMN10], using a bottom-up construction. Geraschenko and Satriano [Reference Geraschenko and SatrianoGS15a, Reference Geraschenko and SatrianoGS15b] extended the theory to non-smooth stacks and stacks with positive-dimensional stabilisers and unified the theory with other notions of toric stacks.
In this section, we summarise some basic results from the theory of toric stacks. Since there are several different suggestions on what a toric stack should be in the literature, we give the following comparison.
-
(i) For the definition of toric stack, we follow [Reference Borisov, Chen and SmithBCS05]. The same definition is used in [Reference IwanariIwa09b], [Reference IwanariIwa09a] and [Reference Fantechi, Mann and NironiFMN10]. In the language of [Reference Geraschenko and SatrianoGS15a, Reference Geraschenko and SatrianoGS15b], this is equivalent to a non-strict, smooth, separated toric stack.
-
(ii) We use the term toric orbifold for a toric stack which is also an orbifold. That is, a toric stack with trivial generic stabilisers.
-
(iii) For the definition of a stacky fan, we basically follow [Reference Borisov, Chen and SmithBCS05, § 3]. However, since we only need to consider stacky fans which give rise to toric orbifolds, we only consider such fans. We call such fans orbifold fans.
-
(iv) We work with toric stacks over an arbitrary base scheme
 $S$
. Some of the references restrict the discussion to the situation when
$S$
. Some of the references restrict the discussion to the situation when
 $S$
is a field, but at least for our needs considering general
$S$
is a field, but at least for our needs considering general
 $S$
comes with no extra complications.
$S$
comes with no extra complications. -
(v) Note that this definition of stacky fan used here is essentially different to the one given in [Reference Geraschenko and SatrianoGS15a, Definition 2.4]. The definition given in [Reference Geraschenko and SatrianoGS15a, Definition 2.4] is less suitable for our needs, since it makes the relation between the fan and the coarse space of the toric stack less explicit.
Whenever it applies, we try to follow the notation and terminology for classical toric varieties from [Reference Cox, Little and SchenckCLS11] as closely as possible.
3.1 Basic toric stacks
First we introduce basic toric stacks. They play a similar role in the theory of toric stacks as affine toric varieties in the theory of toric varieties. Toric stacks in general are obtained by gluing basic toric stacks together along toric morphisms in the Zariski topology. Note that the term basic toric stack is non-standard.
Fix a scheme
![]() $S$
. Consider a finitely generated abelian group
$S$
. Consider a finitely generated abelian group
![]() $A$
and an
$A$
and an
![]() $A$
-graded quasi-coherent sheaf of
$A$
-graded quasi-coherent sheaf of
![]() ${\mathcal{O}}_{S}$
-algebras
${\mathcal{O}}_{S}$
-algebras
![]() ${\mathcal{R}}$
. The
${\mathcal{R}}$
. The
![]() $A$
-grading on
$A$
-grading on
![]() ${\mathcal{R}}$
corresponds to an action of the Cartier dual
${\mathcal{R}}$
corresponds to an action of the Cartier dual
![]() $A^{\vee }$
(over
$A^{\vee }$
(over
![]() $S$
) on the relative spectrum
$S$
) on the relative spectrum
 $\text{Spec}_{{\mathcal{O}}_{S}}{\mathcal{R}}$
. We get an algebraic stack associated to the pair
$\text{Spec}_{{\mathcal{O}}_{S}}{\mathcal{R}}$
. We get an algebraic stack associated to the pair
![]() $({\mathcal{R}},A)$
by taking the stack quotient
$({\mathcal{R}},A)$
by taking the stack quotient
 $[\text{Spec}_{{\mathcal{O}}_{S}}{\mathcal{R}}/A^{\vee }]$
.
$[\text{Spec}_{{\mathcal{O}}_{S}}{\mathcal{R}}/A^{\vee }]$
.
Let
![]() $({\mathcal{R}}^{\prime },A^{\prime })$
be another pair as above. A graded homomorphism
$({\mathcal{R}}^{\prime },A^{\prime })$
be another pair as above. A graded homomorphism
 $(f,\unicode[STIX]{x1D711}):({\mathcal{R}},A)\rightarrow ({\mathcal{R}}^{\prime },A^{\prime })$
is a pair where
$(f,\unicode[STIX]{x1D711}):({\mathcal{R}},A)\rightarrow ({\mathcal{R}}^{\prime },A^{\prime })$
is a pair where
 $\unicode[STIX]{x1D711}:A\rightarrow A^{\prime }$
is a group homomorphism and
$\unicode[STIX]{x1D711}:A\rightarrow A^{\prime }$
is a group homomorphism and
 $f:{\mathcal{R}}\rightarrow {\mathcal{R}}^{\prime }$
a morphism of sheaves of
$f:{\mathcal{R}}\rightarrow {\mathcal{R}}^{\prime }$
a morphism of sheaves of
![]() ${\mathcal{O}}_{S}$
-algebras. The morphism
${\mathcal{O}}_{S}$
-algebras. The morphism
![]() $f$
is required to take homogeneous sections of degree
$f$
is required to take homogeneous sections of degree
![]() $a\in A$
to homogeneous sections of degree
$a\in A$
to homogeneous sections of degree
![]() $\unicode[STIX]{x1D711}(a)$
. Such a graded homomorphism induces a morphism
$\unicode[STIX]{x1D711}(a)$
. Such a graded homomorphism induces a morphism
 $[\text{Spec}_{{\mathcal{O}}_{S}}{\mathcal{R}}^{\prime }/{A^{\prime }}^{\vee }]\rightarrow [\text{Spec}_{{\mathcal{O}}_{S}}{\mathcal{R}}/A^{\vee }]$
of quotient stacks.
$[\text{Spec}_{{\mathcal{O}}_{S}}{\mathcal{R}}^{\prime }/{A^{\prime }}^{\vee }]\rightarrow [\text{Spec}_{{\mathcal{O}}_{S}}{\mathcal{R}}/A^{\vee }]$
of quotient stacks.
Definition 3.1. An algebraic stack
![]() $X$
associated to a pair
$X$
associated to a pair
![]() $({\mathcal{R}},A)$
, as described above, is called a basic toric stack provided that the following conditions hold.
$({\mathcal{R}},A)$
, as described above, is called a basic toric stack provided that the following conditions hold.
-
(a) The sheaf of rings
 ${\mathcal{R}}$
is of the form
${\mathcal{R}}$
is of the form
 ${\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}][x_{s+1}^{-1},\ldots ,x_{r}^{-1}]$
for some
${\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}][x_{s+1}^{-1},\ldots ,x_{r}^{-1}]$
for some
 $r$
and
$r$
and
 $s$
such that
$s$
such that
 $0\leqslant s\leqslant r$
.
$0\leqslant s\leqslant r$
. -
(b) Each coordinate function
 $x_{i}$
, with
$x_{i}$
, with
 $1\leqslant i\leqslant r$
, is homogeneous of degree
$1\leqslant i\leqslant r$
, is homogeneous of degree
 $a_{i}\in A$
.
$a_{i}\in A$
. -
(c) The quotient group
 $A/\langle a_{s+1},\ldots ,a_{r}\rangle$
is finite.
$A/\langle a_{s+1},\ldots ,a_{r}\rangle$
is finite.
The triple
 $({\mathcal{R}},A,\boldsymbol{a})$
, where
$({\mathcal{R}},A,\boldsymbol{a})$
, where
 $\boldsymbol{a}=(a_{1},\ldots ,a_{r})$
, is called a homogeneous coordinate ring for
$\boldsymbol{a}=(a_{1},\ldots ,a_{r})$
, is called a homogeneous coordinate ring for
![]() $X$
. The closed substacks of the form
$X$
. The closed substacks of the form
 $E^{i}=V(x_{i})$
, for
$E^{i}=V(x_{i})$
, for
 $1\leqslant i\leqslant s$
, are called the toric divisors of
$1\leqslant i\leqslant s$
, are called the toric divisors of
![]() $X$
. A morphism of basic toric stacks is called toric provided that it comes from a morphism
$X$
. A morphism of basic toric stacks is called toric provided that it comes from a morphism
 $({\mathcal{R}},A)\rightarrow ({\mathcal{R}}^{\prime },A^{\prime })$
such that the underlying
$({\mathcal{R}},A)\rightarrow ({\mathcal{R}}^{\prime },A^{\prime })$
such that the underlying
![]() ${\mathcal{O}}_{S}$
-algebra homomorphism
${\mathcal{O}}_{S}$
-algebra homomorphism
 ${\mathcal{R}}\rightarrow {\mathcal{R}}^{\prime }$
takes monomials to monomials. A basic toric stack admitting a homogeneous coordinate ring with
${\mathcal{R}}\rightarrow {\mathcal{R}}^{\prime }$
takes monomials to monomials. A basic toric stack admitting a homogeneous coordinate ring with
![]() $s=r$
is said to be without torus factors.
$s=r$
is said to be without torus factors.
It should be noted that the homogeneous coordinate ring does not determine the isomorphism class of the basic toric stack uniquely.
Proposition 3.2. Let
![]() $X$
be a basic toric stack with homogeneous coordinate ring
$X$
be a basic toric stack with homogeneous coordinate ring
 $({\mathcal{R}},A,\boldsymbol{a})$
with
$({\mathcal{R}},A,\boldsymbol{a})$
with
 $$\begin{eqnarray}{\mathcal{R}}={\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}][x_{s+1}^{-1},\ldots ,x_{r}^{-1}].\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{R}}={\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}][x_{s+1}^{-1},\ldots ,x_{r}^{-1}].\end{eqnarray}$$
Let
![]() $K$
be the subgroup
$K$
be the subgroup
 $\langle a_{s+1},\ldots ,a_{r}\rangle$
and define
$\langle a_{s+1},\ldots ,a_{r}\rangle$
and define
![]() $r^{\prime }$
as
$r^{\prime }$
as
![]() $r$
minus the rank of
$r$
minus the rank of
![]() $K$
. Consider the
$K$
. Consider the
![]() $A/K$
-graded sheaf of
$A/K$
-graded sheaf of
![]() ${\mathcal{O}}_{S}$
-algebras
${\mathcal{O}}_{S}$
-algebras
 $$\begin{eqnarray}{\mathcal{R}}^{\prime }={\mathcal{O}}_{S}[x_{1},\ldots ,x_{r^{\prime }}][x_{s+1}^{-1},\ldots ,x_{r^{\prime }}^{-1}]\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{R}}^{\prime }={\mathcal{O}}_{S}[x_{1},\ldots ,x_{r^{\prime }}][x_{s+1}^{-1},\ldots ,x_{r^{\prime }}^{-1}]\end{eqnarray}$$
with the grading given by the weight vector
 $\overline{\boldsymbol{a}}=(\overline{a}_{1},\ldots ,\overline{a}_{r^{\prime }})$
, where
$\overline{\boldsymbol{a}}=(\overline{a}_{1},\ldots ,\overline{a}_{r^{\prime }})$
, where
![]() $\overline{a}_{i}$
denotes the image of
$\overline{a}_{i}$
denotes the image of
![]() $a_{i}$
in
$a_{i}$
in
![]() $A/K$
. Then the basic toric stack associated to the triple
$A/K$
. Then the basic toric stack associated to the triple
 $({\mathcal{R}}^{\prime },A/K,\overline{\boldsymbol{a}})$
is isomorphic to
$({\mathcal{R}}^{\prime },A/K,\overline{\boldsymbol{a}})$
is isomorphic to
![]() $X$
.
$X$
.
Proof. The proposition is trivial if all of the weights
 $a_{s+1},\ldots ,a_{r}$
are zero. Hence, we assume that one of these weights, which we without loss of generality may assume is
$a_{s+1},\ldots ,a_{r}$
are zero. Hence, we assume that one of these weights, which we without loss of generality may assume is
![]() $a_{r}$
, is non-zero. By induction, it is enough to prove that the stack
$a_{r}$
, is non-zero. By induction, it is enough to prove that the stack
![]() $X$
is isomorphic to the stack associated to
$X$
is isomorphic to the stack associated to
 $({\mathcal{R}}^{\prime },A/K,\overline{\boldsymbol{a}})$
with
$({\mathcal{R}}^{\prime },A/K,\overline{\boldsymbol{a}})$
with
 $K=\langle a_{r}\rangle$
and
$K=\langle a_{r}\rangle$
and
![]() ${\mathcal{R}}^{\prime }$
,
${\mathcal{R}}^{\prime }$
,
![]() $r^{\prime }$
and
$r^{\prime }$
and
![]() $\overline{\boldsymbol{a}}$
being as in the statement of the proposition.
$\overline{\boldsymbol{a}}$
being as in the statement of the proposition.
Assume that
![]() $a_{r}$
has infinite order. Then it is straightforward to verify that the graded homomorphism
$a_{r}$
has infinite order. Then it is straightforward to verify that the graded homomorphism
 ${\mathcal{R}}\rightarrow {\mathcal{R}}^{\prime }$
defined by
${\mathcal{R}}\rightarrow {\mathcal{R}}^{\prime }$
defined by
 $$\begin{eqnarray}x_{i}\mapsto \left\{\begin{array}{@{}ll@{}}1 & \text{if }i=r,\\ x_{i} & \text{otherwise}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}x_{i}\mapsto \left\{\begin{array}{@{}ll@{}}1 & \text{if }i=r,\\ x_{i} & \text{otherwise}\end{array}\right.\end{eqnarray}$$
induces an isomorphism of stacks.
Now assume that
![]() $a_{r}$
has finite order
$a_{r}$
has finite order
![]() $m$
. By a simple group theoretical argument, we may find an element
$m$
. By a simple group theoretical argument, we may find an element
![]() $a_{r}^{\prime }\in A$
such that
$a_{r}^{\prime }\in A$
such that
 $a_{r}=na_{r}^{\prime }$
for some positive integer
$a_{r}=na_{r}^{\prime }$
for some positive integer
![]() $n$
and
$n$
and
![]() $A$
splits as
$A$
splits as
 $A_{0}\oplus \langle a_{r}^{\prime }\rangle$
. Consider the surjective homomorphism
$A_{0}\oplus \langle a_{r}^{\prime }\rangle$
. Consider the surjective homomorphism
 $A^{\prime }=A_{0}\oplus \mathbb{Z}\rightarrow A$
taking
$A^{\prime }=A_{0}\oplus \mathbb{Z}\rightarrow A$
taking
![]() $(a,1)$
to
$(a,1)$
to
![]() $a+a_{r}^{\prime }$
. We endow the sheaf of rings
$a+a_{r}^{\prime }$
. We endow the sheaf of rings
 ${\mathcal{R}}[t,t^{-1}]$
with an
${\mathcal{R}}[t,t^{-1}]$
with an
![]() $A$
-grading, with
$A$
-grading, with
 $|x_{r}|=(1,n)$
,
$|x_{r}|=(1,n)$
,
 $|t|=(1,nm)$
and
$|t|=(1,nm)$
and
![]() $|x_{i}|$
are arbitrary lifts of
$|x_{i}|$
are arbitrary lifts of
![]() $a_{i}$
to
$a_{i}$
to
![]() $A^{\prime }$
for
$A^{\prime }$
for
 $i\in \{1,\ldots ,r-1\}$
. Then the graded ring homomorphism
$i\in \{1,\ldots ,r-1\}$
. Then the graded ring homomorphism
 $({\mathcal{R}}[t,t^{-1}],A^{\prime })\rightarrow ({\mathcal{R}},A)$
taking
$({\mathcal{R}}[t,t^{-1}],A^{\prime })\rightarrow ({\mathcal{R}},A)$
taking
![]() $x_{i}$
to
$x_{i}$
to
![]() $x_{i}$
for
$x_{i}$
for
 $i=1,\ldots ,r$
and
$i=1,\ldots ,r$
and
![]() $t$
to
$t$
to
![]() $1$
induces an isomorphism of stacks, since the order of
$1$
induces an isomorphism of stacks, since the order of
![]() $|t|$
is infinite. But the graded homomorphism
$|t|$
is infinite. But the graded homomorphism
 $({\mathcal{R}}[t,t^{-1}],A^{\prime })\rightarrow ({\mathcal{R}}^{\prime },A/K)$
taking
$({\mathcal{R}}[t,t^{-1}],A^{\prime })\rightarrow ({\mathcal{R}}^{\prime },A/K)$
taking
![]() $x_{i}$
to
$x_{i}$
to
![]() $x_{i}$
for
$x_{i}$
for
 $i=1,\ldots ,r-1$
,
$i=1,\ldots ,r-1$
,
![]() $x_{r}$
to 1 and
$x_{r}$
to 1 and
![]() $t$
to
$t$
to
![]() $x_{r}$
also induces an isomorphism, since also
$x_{r}$
also induces an isomorphism, since also
![]() $|x_{r}|$
has infinite order in
$|x_{r}|$
has infinite order in
 $({\mathcal{R}}[t,t^{-1}],A^{\prime })$
. This concludes the proof.◻
$({\mathcal{R}}[t,t^{-1}],A^{\prime })$
. This concludes the proof.◻
Remark 3.3. Let
![]() $X$
be an algebraic stack associated to a homogeneous coordinate ring
$X$
be an algebraic stack associated to a homogeneous coordinate ring
![]() $({\mathcal{R}},A)$
satisfying (a) and (b) from Definition 3.1, but not necessarily (c). Then
$({\mathcal{R}},A)$
satisfying (a) and (b) from Definition 3.1, but not necessarily (c). Then
![]() $X$
has finite stabilisers if and only if also (c) is satisfied. This follows easily from Proposition 3.2, which holds also if condition (c) is omitted.
$X$
has finite stabilisers if and only if also (c) is satisfied. This follows easily from Proposition 3.2, which holds also if condition (c) is omitted.
Remark 3.4. Another consequence of Proposition 3.2 is that we always may choose homogeneous coordinates for our basic toric stacks such that the weights of the invertible coordinate functions are zero. This shows that a basic toric stack always is a product of a basic toric stack without torus factors and a torus.
Remark 3.5. From Proposition 3.2, it is also easy to determine when a basic toric stack is an orbifold. Let
 $({\mathcal{R}},A,\boldsymbol{a}=(a_{1},\ldots ,a_{r}))$
be homogeneous coordinates for a basic toric stack
$({\mathcal{R}},A,\boldsymbol{a}=(a_{1},\ldots ,a_{r}))$
be homogeneous coordinates for a basic toric stack
![]() $X$
and let
$X$
and let
![]() $E$
be the support of the toric divisors in
$E$
be the support of the toric divisors in
![]() $X$
. Let
$X$
. Let
![]() $A_{\text{rig}}$
be the subgroup of
$A_{\text{rig}}$
be the subgroup of
![]() $A$
generated by the weights
$A$
generated by the weights
 $a_{1},\ldots ,a_{r}$
. Then
$a_{1},\ldots ,a_{r}$
. Then
![]() $X\setminus E$
is a product of a torus and the classifying stack
$X\setminus E$
is a product of a torus and the classifying stack
 $\text{B}(A/A_{\text{rig}})^{\vee }$
. In particular, the basic toric stack
$\text{B}(A/A_{\text{rig}})^{\vee }$
. In particular, the basic toric stack
![]() $X$
is an orbifold if and only if the weights
$X$
is an orbifold if and only if the weights
 $a_{1},\ldots ,a_{r}$
generate
$a_{1},\ldots ,a_{r}$
generate
![]() $A$
.
$A$
.
Note that there is a canonical graded homomorphism
 $({\mathcal{R}},A_{\text{rig}},\boldsymbol{a})\rightarrow ({\mathcal{R}},A,\boldsymbol{a})$
induced by the inclusion
$({\mathcal{R}},A_{\text{rig}},\boldsymbol{a})\rightarrow ({\mathcal{R}},A,\boldsymbol{a})$
induced by the inclusion
 $A_{\text{rig}}{\hookrightarrow}A$
. This corresponds to the rigidification
$A_{\text{rig}}{\hookrightarrow}A$
. This corresponds to the rigidification
 $\unicode[STIX]{x1D70C}:X\rightarrow X_{\text{rig}}$
of
$\unicode[STIX]{x1D70C}:X\rightarrow X_{\text{rig}}$
of
![]() $X$
(cf. [Reference Abramovich, Olsson and VistoliAOV08, Appendix A]). Here
$X$
(cf. [Reference Abramovich, Olsson and VistoliAOV08, Appendix A]). Here
![]() $\unicode[STIX]{x1D70C}$
is a gerbe banded by
$\unicode[STIX]{x1D70C}$
is a gerbe banded by
 $(A/A_{\text{rig}})^{\vee }$
and
$(A/A_{\text{rig}})^{\vee }$
and
![]() $X_{\text{rig}}$
is a basic toric orbifold.
$X_{\text{rig}}$
is a basic toric orbifold.
Remark 3.6. Let
![]() $X$
be a basic toric stack with homogeneous coordinates
$X$
be a basic toric stack with homogeneous coordinates
 $({\mathcal{R}},A,\boldsymbol{a})$
, and let
$({\mathcal{R}},A,\boldsymbol{a})$
, and let
 $({\mathcal{R}}_{0},0,\mathbf{0})$
denote the weight-zero part of
$({\mathcal{R}}_{0},0,\mathbf{0})$
denote the weight-zero part of
![]() ${\mathcal{R}}$
together with the trivial grading by the trivial group. We have an obvious graded homomorphism
${\mathcal{R}}$
together with the trivial grading by the trivial group. We have an obvious graded homomorphism
 $({\mathcal{R}}_{0},0,\mathbf{0})\rightarrow ({\mathcal{R}},A,\boldsymbol{a})$
induced by inclusion. This corresponds to the coarse space
$({\mathcal{R}}_{0},0,\mathbf{0})\rightarrow ({\mathcal{R}},A,\boldsymbol{a})$
induced by inclusion. This corresponds to the coarse space
 $\unicode[STIX]{x1D70B}:X\rightarrow X_{\text{cs}}$
of
$\unicode[STIX]{x1D70B}:X\rightarrow X_{\text{cs}}$
of
![]() $X$
. Note that according to our convention that toric stacks be smooth, the space
$X$
. Note that according to our convention that toric stacks be smooth, the space
![]() $X_{\text{cs}}$
is not a toric stack in general. It is, however, an affine toric variety (over
$X_{\text{cs}}$
is not a toric stack in general. It is, however, an affine toric variety (over
![]() $S$
).
$S$
).
Remark 3.7. If we order the coordinate functions, then the set
![]() $\boldsymbol{E}$
of toric divisors on a basic toric stack
$\boldsymbol{E}$
of toric divisors on a basic toric stack
![]() $X$
inherits an ordering, and we get a standard pair
$X$
inherits an ordering, and we get a standard pair
![]() $(X,\boldsymbol{E})$
. Indeed, this kind of standard pair is prototypical and, in § 5, we will see that any standard pair with diagonalisable stabilisers is locally a basic toric stack.
$(X,\boldsymbol{E})$
. Indeed, this kind of standard pair is prototypical and, in § 5, we will see that any standard pair with diagonalisable stabilisers is locally a basic toric stack.
3.2 Toric orbifolds
As with toric varieties, the gluing together of basic toric stacks can be described combinatorially. We review the parts of the theory we need in this article, restricting the discussion to toric orbifolds with no torus factors.
Let
![]() $N$
be a lattice of rank
$N$
be a lattice of rank
![]() $n$
, and consider it as a subset of the vector space
$n$
, and consider it as a subset of the vector space
 $N_{\mathbb{R}}:=N\otimes _{\mathbb{Z}}\mathbb{R}$
. By a cone
$N_{\mathbb{R}}:=N\otimes _{\mathbb{Z}}\mathbb{R}$
. By a cone
![]() $\unicode[STIX]{x1D70E}$
in
$\unicode[STIX]{x1D70E}$
in
![]() $N_{\mathbb{R}}$
, we will always mean a polyhedral, rational and strictly convex cone. We write
$N_{\mathbb{R}}$
, we will always mean a polyhedral, rational and strictly convex cone. We write
![]() $\unicode[STIX]{x1D70F}\preccurlyeq \unicode[STIX]{x1D70E}$
if
$\unicode[STIX]{x1D70F}\preccurlyeq \unicode[STIX]{x1D70E}$
if
![]() $\unicode[STIX]{x1D70F}$
is a face of
$\unicode[STIX]{x1D70F}$
is a face of
![]() $\unicode[STIX]{x1D70E}$
. By
$\unicode[STIX]{x1D70E}$
. By
![]() $\unicode[STIX]{x1D70E}(1)$
, we mean the set of one-dimensional faces, also called the extremal rays, of
$\unicode[STIX]{x1D70E}(1)$
, we mean the set of one-dimensional faces, also called the extremal rays, of
![]() $\unicode[STIX]{x1D70E}$
. Recall that
$\unicode[STIX]{x1D70E}$
. Recall that
![]() $\unicode[STIX]{x1D70E}$
is called simplicial if the cardinality of
$\unicode[STIX]{x1D70E}$
is called simplicial if the cardinality of
![]() $\unicode[STIX]{x1D70E}(1)$
equals the dimension of the subspace of
$\unicode[STIX]{x1D70E}(1)$
equals the dimension of the subspace of
![]() $N_{\mathbb{R}}$
spanned by
$N_{\mathbb{R}}$
spanned by
![]() $\unicode[STIX]{x1D70E}(1)$
.
$\unicode[STIX]{x1D70E}(1)$
.
Given a fan
![]() $\unicode[STIX]{x1D6F4}$
in
$\unicode[STIX]{x1D6F4}$
in
![]() $N_{\mathbb{R}}$
, we denote the set of rays, that is, the set of one-dimensional cones, in
$N_{\mathbb{R}}$
, we denote the set of rays, that is, the set of one-dimensional cones, in
![]() $\unicode[STIX]{x1D6F4}$
by
$\unicode[STIX]{x1D6F4}$
by
![]() $\unicode[STIX]{x1D6F4}(1)$
. A fan is simplicial if all its cones are. We will frequently consider the free abelian group
$\unicode[STIX]{x1D6F4}(1)$
. A fan is simplicial if all its cones are. We will frequently consider the free abelian group
![]() $\mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)}$
on the set of rays in a fan
$\mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)}$
on the set of rays in a fan
![]() $\unicode[STIX]{x1D6F4}$
. An element
$\unicode[STIX]{x1D6F4}$
. An element
 $c_{1}\unicode[STIX]{x1D70C}_{1}+\cdots +c_{r}\unicode[STIX]{x1D70C}_{r}\in \mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)}$
, with
$c_{1}\unicode[STIX]{x1D70C}_{1}+\cdots +c_{r}\unicode[STIX]{x1D70C}_{r}\in \mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)}$
, with
![]() $c_{i}\in \mathbb{Z}$
and
$c_{i}\in \mathbb{Z}$
and
 $\unicode[STIX]{x1D70C}_{i}\in \unicode[STIX]{x1D6F4}(1)$
, is called effective if all coefficients
$\unicode[STIX]{x1D70C}_{i}\in \unicode[STIX]{x1D6F4}(1)$
, is called effective if all coefficients
![]() $c_{i}$
are greater than or equal to zero.
$c_{i}$
are greater than or equal to zero.
Definition 3.8. An orbifold fan is a triple
 $\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
, where
$\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
, where
![]() $N$
is a finitely generated free abelian group,
$N$
is a finitely generated free abelian group,
![]() $\unicode[STIX]{x1D6F4}$
is a simplicial fan in
$\unicode[STIX]{x1D6F4}$
is a simplicial fan in
![]() $N_{\mathbb{R}}$
such that
$N_{\mathbb{R}}$
such that
![]() $|\unicode[STIX]{x1D6F4}|$
spans
$|\unicode[STIX]{x1D6F4}|$
spans
![]() $N_{\mathbb{R}}$
and
$N_{\mathbb{R}}$
and
 $\unicode[STIX]{x1D6FD}:\mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)}\rightarrow N$
is a group homomorphism taking each generator
$\unicode[STIX]{x1D6FD}:\mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)}\rightarrow N$
is a group homomorphism taking each generator
 $\unicode[STIX]{x1D70C}\in \mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)}$
to a non-zero lattice point on the ray
$\unicode[STIX]{x1D70C}\in \mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)}$
to a non-zero lattice point on the ray
![]() $\unicode[STIX]{x1D70C}$
.
$\unicode[STIX]{x1D70C}$
.
Given an orbifold fan
 $\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
, we construct a toric orbifold via the Cox construction. Denote the dual
$\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
, we construct a toric orbifold via the Cox construction. Denote the dual
 $\text{Hom}_{\mathbb{Z}}(N,\mathbb{Z})$
by
$\text{Hom}_{\mathbb{Z}}(N,\mathbb{Z})$
by
![]() $M$
. Then the Cartier dual of
$M$
. Then the Cartier dual of
![]() $M$
over
$M$
over
![]() $S$
is an
$S$
is an
![]() $n$
-dimensional torus, which we denote by
$n$
-dimensional torus, which we denote by
![]() $T_{N}$
. Its cocharacter and character groups may be canonically identified with
$T_{N}$
. Its cocharacter and character groups may be canonically identified with
![]() $N$
and
$N$
and
![]() $M$
, respectively. The morphism
$M$
, respectively. The morphism
![]() $\unicode[STIX]{x1D6FD}$
induces a homomorphism of algebraic groups
$\unicode[STIX]{x1D6FD}$
induces a homomorphism of algebraic groups
 $T_{\mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)}}\rightarrow T_{N}$
, which fits into an exact sequence
$T_{\mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)}}\rightarrow T_{N}$
, which fits into an exact sequence
 $$\begin{eqnarray}1\rightarrow \unicode[STIX]{x1D6E5}(\boldsymbol{\unicode[STIX]{x1D6F4}})\rightarrow T_{\mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)}}\rightarrow T_{N}\rightarrow 1,\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow \unicode[STIX]{x1D6E5}(\boldsymbol{\unicode[STIX]{x1D6F4}})\rightarrow T_{\mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)}}\rightarrow T_{N}\rightarrow 1,\end{eqnarray}$$
where the exactness at the term
![]() $T_{N}$
is ensured by the fact that
$T_{N}$
is ensured by the fact that
![]() $|\unicode[STIX]{x1D6F4}|$
spans
$|\unicode[STIX]{x1D6F4}|$
spans
![]() $N_{\mathbb{R}}$
. Now consider the lattice
$N_{\mathbb{R}}$
. Now consider the lattice
![]() $\mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)}$
and the corresponding space
$\mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)}$
and the corresponding space
![]() $\mathbb{R}^{\unicode[STIX]{x1D6F4}(1)}$
. Given a cone
$\mathbb{R}^{\unicode[STIX]{x1D6F4}(1)}$
. Given a cone
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
, we have a corresponding cone
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
, we have a corresponding cone
![]() $\widetilde{\unicode[STIX]{x1D70E}}$
in
$\widetilde{\unicode[STIX]{x1D70E}}$
in
![]() $\mathbb{R}^{\unicode[STIX]{x1D6F4}(1)}$
spanned by the rays
$\mathbb{R}^{\unicode[STIX]{x1D6F4}(1)}$
spanned by the rays
 $\unicode[STIX]{x1D70C}\in \unicode[STIX]{x1D70E}(1)$
viewed as generators in
$\unicode[STIX]{x1D70C}\in \unicode[STIX]{x1D70E}(1)$
viewed as generators in
![]() $\mathbb{R}^{\unicode[STIX]{x1D6F4}(1)}$
. Collectively, the cones
$\mathbb{R}^{\unicode[STIX]{x1D6F4}(1)}$
. Collectively, the cones
![]() $\widetilde{\unicode[STIX]{x1D70E}}$
, for
$\widetilde{\unicode[STIX]{x1D70E}}$
, for
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
, form a fan
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
, form a fan
![]() $\widetilde{\unicode[STIX]{x1D6F4}}$
in
$\widetilde{\unicode[STIX]{x1D6F4}}$
in
![]() $\mathbb{R}^{\unicode[STIX]{x1D6F4}(1)}$
. Denote the corresponding toric variety, or rather family of toric varieties over
$\mathbb{R}^{\unicode[STIX]{x1D6F4}(1)}$
. Denote the corresponding toric variety, or rather family of toric varieties over
![]() $S$
, by
$S$
, by
![]() $X_{\widetilde{\unicode[STIX]{x1D6F4}}}$
.
$X_{\widetilde{\unicode[STIX]{x1D6F4}}}$
.
We give an explicit description of the family
![]() $X_{\widetilde{\unicode[STIX]{x1D6F4}}}$
of varieties. The total coordinate ring associated to
$X_{\widetilde{\unicode[STIX]{x1D6F4}}}$
of varieties. The total coordinate ring associated to
![]() $\unicode[STIX]{x1D6F4}$
is the sheaf of rings
$\unicode[STIX]{x1D6F4}$
is the sheaf of rings
 ${\mathcal{R}}={\mathcal{O}}_{S}[x_{\unicode[STIX]{x1D70C}}\mid \unicode[STIX]{x1D70C}\in \unicode[STIX]{x1D6F4}(1)]$
. The irrelevant ideal is the ideal sheaf
${\mathcal{R}}={\mathcal{O}}_{S}[x_{\unicode[STIX]{x1D70C}}\mid \unicode[STIX]{x1D70C}\in \unicode[STIX]{x1D6F4}(1)]$
. The irrelevant ideal is the ideal sheaf
 $$\begin{eqnarray}B(\unicode[STIX]{x1D6F4})=\langle x^{\hat{\unicode[STIX]{x1D70E}}}\mid \unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}\rangle ,\end{eqnarray}$$
$$\begin{eqnarray}B(\unicode[STIX]{x1D6F4})=\langle x^{\hat{\unicode[STIX]{x1D70E}}}\mid \unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}\rangle ,\end{eqnarray}$$
where
![]() $x^{\hat{\unicode[STIX]{x1D70E}}}$
denotes the product of all elements
$x^{\hat{\unicode[STIX]{x1D70E}}}$
denotes the product of all elements
![]() $x_{\unicode[STIX]{x1D70C}}$
with
$x_{\unicode[STIX]{x1D70C}}$
with
 $\unicode[STIX]{x1D70C}\not \in \unicode[STIX]{x1D70E}(1)$
. Let
$\unicode[STIX]{x1D70C}\not \in \unicode[STIX]{x1D70E}(1)$
. Let
 $\mathbb{A}_{S}^{\unicode[STIX]{x1D6F4}(1)}=\text{Spec}_{{\mathcal{O}}_{S}}{\mathcal{R}}$
be the relative spectrum and
$\mathbb{A}_{S}^{\unicode[STIX]{x1D6F4}(1)}=\text{Spec}_{{\mathcal{O}}_{S}}{\mathcal{R}}$
be the relative spectrum and
![]() $Z(\unicode[STIX]{x1D6F4})$
be the closed subscheme associated to the irrelevant ideal
$Z(\unicode[STIX]{x1D6F4})$
be the closed subscheme associated to the irrelevant ideal
![]() $B(\unicode[STIX]{x1D6F4})$
. The scheme
$B(\unicode[STIX]{x1D6F4})$
. The scheme
![]() $X_{\widetilde{\unicode[STIX]{x1D6F4}}}$
is simply
$X_{\widetilde{\unicode[STIX]{x1D6F4}}}$
is simply
 $\mathbb{A}_{S}^{\unicode[STIX]{x1D6F4}(1)}\setminus Z(\unicode[STIX]{x1D6F4})$
. Note that the torus
$\mathbb{A}_{S}^{\unicode[STIX]{x1D6F4}(1)}\setminus Z(\unicode[STIX]{x1D6F4})$
. Note that the torus
![]() $T_{\mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)}}$
is embedded in
$T_{\mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)}}$
is embedded in
![]() $X_{\widetilde{\unicode[STIX]{x1D6F4}}}$
in a natural way, and the action of
$X_{\widetilde{\unicode[STIX]{x1D6F4}}}$
in a natural way, and the action of
![]() $\unicode[STIX]{x1D6E5}(\boldsymbol{\unicode[STIX]{x1D6F4}})$
on
$\unicode[STIX]{x1D6E5}(\boldsymbol{\unicode[STIX]{x1D6F4}})$
on
![]() $T_{\mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)}}$
extends to
$T_{\mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)}}$
extends to
![]() $X_{\widetilde{\unicode[STIX]{x1D6F4}}}$
.
$X_{\widetilde{\unicode[STIX]{x1D6F4}}}$
.
Definition 3.9 (The Cox construction).
Let
 $\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
be an orbifold fan, and consider the group
$\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
be an orbifold fan, and consider the group
![]() $\unicode[STIX]{x1D6E5}(\boldsymbol{\unicode[STIX]{x1D6F4}})$
acting on the scheme
$\unicode[STIX]{x1D6E5}(\boldsymbol{\unicode[STIX]{x1D6F4}})$
acting on the scheme
![]() $X_{\widetilde{\unicode[STIX]{x1D6F4}}}$
over the base scheme
$X_{\widetilde{\unicode[STIX]{x1D6F4}}}$
over the base scheme
![]() $S$
as defined above. The toric orbifold
$S$
as defined above. The toric orbifold
![]() $X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}$
associated to
$X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}$
associated to
![]() $\boldsymbol{\unicode[STIX]{x1D6F4}}$
is defined as the stack quotient
$\boldsymbol{\unicode[STIX]{x1D6F4}}$
is defined as the stack quotient
 $[X_{\widetilde{\unicode[STIX]{x1D6F4}}}/\unicode[STIX]{x1D6E5}(\boldsymbol{\unicode[STIX]{x1D6F4}})]$
.
$[X_{\widetilde{\unicode[STIX]{x1D6F4}}}/\unicode[STIX]{x1D6E5}(\boldsymbol{\unicode[STIX]{x1D6F4}})]$
.
Just like in the case with usual toric varieties, there is an order-reversing correspondence between cones in
 $\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
and orbit closures in
$\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
and orbit closures in
![]() $X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}$
. Given a cone
$X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}$
. Given a cone
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
, we have a closed variety
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
, we have a closed variety
 $V(\langle x_{\unicode[STIX]{x1D70C}},\unicode[STIX]{x1D70C}\in \unicode[STIX]{x1D70E}(1)\rangle )$
in
$V(\langle x_{\unicode[STIX]{x1D70C}},\unicode[STIX]{x1D70C}\in \unicode[STIX]{x1D70E}(1)\rangle )$
in
![]() $X_{\widetilde{\unicode[STIX]{x1D6F4}}}$
. Since this closed variety is
$X_{\widetilde{\unicode[STIX]{x1D6F4}}}$
. Since this closed variety is
![]() $\unicode[STIX]{x1D6E5}(\boldsymbol{\unicode[STIX]{x1D6F4}})$
-invariant, it descends to a closed substack
$\unicode[STIX]{x1D6E5}(\boldsymbol{\unicode[STIX]{x1D6F4}})$
-invariant, it descends to a closed substack
![]() $V(\unicode[STIX]{x1D70E})$
of
$V(\unicode[STIX]{x1D70E})$
of
![]() $X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}$
. In the particular case when we have a ray
$X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}$
. In the particular case when we have a ray
 $\unicode[STIX]{x1D70C}\in \unicode[STIX]{x1D6F4}(1)$
, the substack
$\unicode[STIX]{x1D70C}\in \unicode[STIX]{x1D6F4}(1)$
, the substack
 $V(\unicode[STIX]{x1D70C})\subset X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}$
is a prime divisor, and we denote it by
$V(\unicode[STIX]{x1D70C})\subset X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}$
is a prime divisor, and we denote it by
![]() $D_{\unicode[STIX]{x1D70C}}$
. The divisor
$D_{\unicode[STIX]{x1D70C}}$
. The divisor
![]() $D_{\unicode[STIX]{x1D70C}}$
is a smooth Cartier divisor. More generally, if
$D_{\unicode[STIX]{x1D70C}}$
is a smooth Cartier divisor. More generally, if
 $\unicode[STIX]{x1D713}=c_{1}\unicode[STIX]{x1D70C}_{1}+\cdots +c_{r}\unicode[STIX]{x1D70C}_{r}$
is an element of
$\unicode[STIX]{x1D713}=c_{1}\unicode[STIX]{x1D70C}_{1}+\cdots +c_{r}\unicode[STIX]{x1D70C}_{r}$
is an element of
![]() $\mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)}$
, we let
$\mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)}$
, we let
![]() $D_{\unicode[STIX]{x1D713}}$
denote the divisor
$D_{\unicode[STIX]{x1D713}}$
denote the divisor
 $c_{1}D_{\unicode[STIX]{x1D70C}_{1}}+\cdots +c_{r}D_{\unicode[STIX]{x1D70C}_{r}}$
. Such a divisor is called a toric divisor, and is a simple normal crossings divisor.
$c_{1}D_{\unicode[STIX]{x1D70C}_{1}}+\cdots +c_{r}D_{\unicode[STIX]{x1D70C}_{r}}$
. Such a divisor is called a toric divisor, and is a simple normal crossings divisor.
3.3 Morphisms of toric orbifolds
Next we describe morphisms of orbifold fans and toric orbifolds. Our definition is different from, but equivalent to, the one given by Iwanari in [Reference IwanariIwa09a].
Recall that a morphism of fans
 $f:(N,\unicode[STIX]{x1D6F4})\rightarrow (N^{\prime },\unicode[STIX]{x1D6F4}^{\prime })$
is a group homomorphism
$f:(N,\unicode[STIX]{x1D6F4})\rightarrow (N^{\prime },\unicode[STIX]{x1D6F4}^{\prime })$
is a group homomorphism
 $f:N\rightarrow N^{\prime }$
such that the induced map
$f:N\rightarrow N^{\prime }$
such that the induced map
 $f_{\mathbb{R}}=f\otimes _{\mathbb{Z}}\mathbb{R}$
maps each cone
$f_{\mathbb{R}}=f\otimes _{\mathbb{Z}}\mathbb{R}$
maps each cone
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
into a cone
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
into a cone
![]() $\unicode[STIX]{x1D70E}^{\prime }\in \unicode[STIX]{x1D6F4}^{\prime }$
. This extends to orbifold fans as follows.
$\unicode[STIX]{x1D70E}^{\prime }\in \unicode[STIX]{x1D6F4}^{\prime }$
. This extends to orbifold fans as follows.
Definition 3.10. Consider the orbifold fans
 $\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
and
$\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
and
 $\boldsymbol{\unicode[STIX]{x1D6F4}}^{\prime }=(N^{\prime },\unicode[STIX]{x1D6F4}^{\prime },\unicode[STIX]{x1D6FD}^{\prime })$
. A morphism
$\boldsymbol{\unicode[STIX]{x1D6F4}}^{\prime }=(N^{\prime },\unicode[STIX]{x1D6F4}^{\prime },\unicode[STIX]{x1D6FD}^{\prime })$
. A morphism
 $\boldsymbol{\unicode[STIX]{x1D6F4}}\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}^{\prime }$
of orbifold fans is a pair
$\boldsymbol{\unicode[STIX]{x1D6F4}}\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}^{\prime }$
of orbifold fans is a pair
![]() $(f,\hat{f})$
of group homomorphisms fitting into a commutative square
$(f,\hat{f})$
of group homomorphisms fitting into a commutative square

such that both
 $f:(N,\unicode[STIX]{x1D6F4})\rightarrow (N^{\prime },\unicode[STIX]{x1D6F4}^{\prime })$
and
$f:(N,\unicode[STIX]{x1D6F4})\rightarrow (N^{\prime },\unicode[STIX]{x1D6F4}^{\prime })$
and
 $\hat{f}:(\mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)},\widetilde{\unicode[STIX]{x1D6F4}})\rightarrow (\mathbb{Z}^{\unicode[STIX]{x1D6F4}^{\prime }(1)},\widetilde{\unicode[STIX]{x1D6F4}}^{\prime })$
are morphisms of fans. Since
$\hat{f}:(\mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)},\widetilde{\unicode[STIX]{x1D6F4}})\rightarrow (\mathbb{Z}^{\unicode[STIX]{x1D6F4}^{\prime }(1)},\widetilde{\unicode[STIX]{x1D6F4}}^{\prime })$
are morphisms of fans. Since
![]() $\hat{f}$
is uniquely determined by
$\hat{f}$
is uniquely determined by
![]() $f$
, we often omit
$f$
, we often omit
![]() $\hat{f}$
from the notation, and simply say that
$\hat{f}$
from the notation, and simply say that
 $f:\boldsymbol{\unicode[STIX]{x1D6F4}}\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}^{\prime }$
is a morphism of orbifold fans.
$f:\boldsymbol{\unicode[STIX]{x1D6F4}}\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}^{\prime }$
is a morphism of orbifold fans.
It is easy to see that a morphism
 $f:\boldsymbol{\unicode[STIX]{x1D6F4}}\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}^{\prime }$
of orbifold fans induces a corresponding equivariant morphism of pairs
$f:\boldsymbol{\unicode[STIX]{x1D6F4}}\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}^{\prime }$
of orbifold fans induces a corresponding equivariant morphism of pairs
 $(X_{\widetilde{\unicode[STIX]{x1D6F4}}},\unicode[STIX]{x1D6E5}(\boldsymbol{\unicode[STIX]{x1D6F4}}))\rightarrow (X_{\widetilde{\unicode[STIX]{x1D6F4}}^{\prime }},\unicode[STIX]{x1D6E5}(\boldsymbol{\unicode[STIX]{x1D6F4}}^{\prime }))$
, which, in turn, induces a 1-morphism
$(X_{\widetilde{\unicode[STIX]{x1D6F4}}},\unicode[STIX]{x1D6E5}(\boldsymbol{\unicode[STIX]{x1D6F4}}))\rightarrow (X_{\widetilde{\unicode[STIX]{x1D6F4}}^{\prime }},\unicode[STIX]{x1D6E5}(\boldsymbol{\unicode[STIX]{x1D6F4}}^{\prime }))$
, which, in turn, induces a 1-morphism
 $X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}\rightarrow X_{\boldsymbol{\unicode[STIX]{x1D6F4}}^{\prime }}$
of toric orbifolds. This gives a functor from the category of orbifold fans to the category of orbifolds over a base scheme
$X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}\rightarrow X_{\boldsymbol{\unicode[STIX]{x1D6F4}}^{\prime }}$
of toric orbifolds. This gives a functor from the category of orbifold fans to the category of orbifolds over a base scheme
![]() $S$
, and we call its essential image the category of toric orbifolds (without torus factors).
$S$
, and we call its essential image the category of toric orbifolds (without torus factors).
The simplest example of a toric morphism is that of toric open immersions, which correspond to subfans of stacky fans. Let
 $\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
be an orbifold fan. A subfan
$\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
be an orbifold fan. A subfan
![]() $\boldsymbol{\unicode[STIX]{x1D6F4}}^{\prime }\subset \boldsymbol{\unicode[STIX]{x1D6F4}}$
is a triple
$\boldsymbol{\unicode[STIX]{x1D6F4}}^{\prime }\subset \boldsymbol{\unicode[STIX]{x1D6F4}}$
is a triple
 $\boldsymbol{\unicode[STIX]{x1D6F4}}^{\prime }=(N,\unicode[STIX]{x1D6F4}^{\prime },\unicode[STIX]{x1D6FD}^{\prime })$
, where
$\boldsymbol{\unicode[STIX]{x1D6F4}}^{\prime }=(N,\unicode[STIX]{x1D6F4}^{\prime },\unicode[STIX]{x1D6FD}^{\prime })$
, where
![]() $\unicode[STIX]{x1D6F4}^{\prime }\subset \unicode[STIX]{x1D6F4}$
is a subset, which is a fan in its own right, and
$\unicode[STIX]{x1D6F4}^{\prime }\subset \unicode[STIX]{x1D6F4}$
is a subset, which is a fan in its own right, and
![]() $\unicode[STIX]{x1D6FD}^{\prime }$
is the restriction of
$\unicode[STIX]{x1D6FD}^{\prime }$
is the restriction of
![]() $\unicode[STIX]{x1D6FD}$
to
$\unicode[STIX]{x1D6FD}$
to
![]() $\mathbb{Z}^{\unicode[STIX]{x1D6F4}^{\prime }(1)}$
. The canonical map
$\mathbb{Z}^{\unicode[STIX]{x1D6F4}^{\prime }(1)}$
. The canonical map
 $\boldsymbol{\unicode[STIX]{x1D6F4}}^{\prime }\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}$
, which is the identity on
$\boldsymbol{\unicode[STIX]{x1D6F4}}^{\prime }\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}$
, which is the identity on
![]() $N$
, corresponds to an open immersion
$N$
, corresponds to an open immersion
 $X_{\boldsymbol{\unicode[STIX]{x1D6F4}}^{\prime }}\rightarrow X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}$
. We say that
$X_{\boldsymbol{\unicode[STIX]{x1D6F4}}^{\prime }}\rightarrow X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}$
. We say that
![]() $X_{\boldsymbol{\unicode[STIX]{x1D6F4}}^{\prime }}$
is a toric open substack of
$X_{\boldsymbol{\unicode[STIX]{x1D6F4}}^{\prime }}$
is a toric open substack of
![]() $X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}$
. The toric substacks corresponding to orbifold fans with a single maximal cone
$X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}$
. The toric substacks corresponding to orbifold fans with a single maximal cone
![]() $\unicode[STIX]{x1D70E}\in \boldsymbol{\unicode[STIX]{x1D6F4}}$
are of particular importance. We denote the corresponding substack, which is a basic toric orbifold, by
$\unicode[STIX]{x1D70E}\in \boldsymbol{\unicode[STIX]{x1D6F4}}$
are of particular importance. We denote the corresponding substack, which is a basic toric orbifold, by
![]() $U_{\unicode[STIX]{x1D70E}}$
.
$U_{\unicode[STIX]{x1D70E}}$
.
Remark 3.11. Let
 $\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
be an orbifold fan. Then the coarse space of the toric orbifold
$\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
be an orbifold fan. Then the coarse space of the toric orbifold
![]() $X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}$
coincides with the toric variety
$X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}$
coincides with the toric variety
![]() $X_{\unicode[STIX]{x1D6F4}}$
associated to the fan
$X_{\unicode[STIX]{x1D6F4}}$
associated to the fan
![]() $\unicode[STIX]{x1D6F4}$
. The association
$\unicode[STIX]{x1D6F4}$
. The association
 $(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})\mapsto (N,\unicode[STIX]{x1D6F4})$
extends to a functor from the category of orbifold fans to the category of usual fans, and this functor corresponds to the functor taking a toric orbifold to its coarse space.
$(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})\mapsto (N,\unicode[STIX]{x1D6F4})$
extends to a functor from the category of orbifold fans to the category of usual fans, and this functor corresponds to the functor taking a toric orbifold to its coarse space.
Remark 3.12. Let
![]() $\unicode[STIX]{x1D6F4}$
be a simplicial fan on a lattice
$\unicode[STIX]{x1D6F4}$
be a simplicial fan on a lattice
![]() $N$
. Then there is a canonical function
$N$
. Then there is a canonical function
 $\unicode[STIX]{x1D6FD}_{\text{can}}:\mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)}\rightarrow N$
taking
$\unicode[STIX]{x1D6FD}_{\text{can}}:\mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)}\rightarrow N$
taking
 $\unicode[STIX]{x1D70C}\in \unicode[STIX]{x1D6F4}(1)$
to the non-zero lattice point
$\unicode[STIX]{x1D70C}\in \unicode[STIX]{x1D6F4}(1)$
to the non-zero lattice point
![]() $u_{\unicode[STIX]{x1D70C}}$
on
$u_{\unicode[STIX]{x1D70C}}$
on
![]() $\unicode[STIX]{x1D70C}$
which is closest to the origin. The orbifold
$\unicode[STIX]{x1D70C}$
which is closest to the origin. The orbifold
![]() $X_{\text{can}}$
associated to the orbifold fan
$X_{\text{can}}$
associated to the orbifold fan
 $(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD}_{\text{can}})$
is the canonical stack of the toric variety
$(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD}_{\text{can}})$
is the canonical stack of the toric variety
 $X=X_{\unicode[STIX]{x1D6F4}}$
. Similarly as in the previous remark, the association
$X=X_{\unicode[STIX]{x1D6F4}}$
. Similarly as in the previous remark, the association
 $(N,\unicode[STIX]{x1D6F4})\mapsto (N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD}_{\text{can}})$
extends to a functor.
$(N,\unicode[STIX]{x1D6F4})\mapsto (N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD}_{\text{can}})$
extends to a functor.
3.4 Toric stacky blow-ups
For smooth toric varieties, blow-ups at orbit closures correspond to star subdivisions. This generalises to toric orbifolds (see [Reference Edidin and MoreEM12]). We recall the definition here.
Definition 3.13. Let
 $\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
be an orbifold fan. Let
$\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
be an orbifold fan. Let
![]() $\unicode[STIX]{x1D70E}$
be a cone in
$\unicode[STIX]{x1D70E}$
be a cone in
![]() $\unicode[STIX]{x1D6F4}$
and let
$\unicode[STIX]{x1D6F4}$
and let
 $v=\sum _{\unicode[STIX]{x1D70C}\in \unicode[STIX]{x1D70E}(1)}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D70C})$
. Denote the ray generated by
$v=\sum _{\unicode[STIX]{x1D70C}\in \unicode[STIX]{x1D70E}(1)}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D70C})$
. Denote the ray generated by
![]() $v$
by
$v$
by
![]() $\unicode[STIX]{x1D70C}_{0}$
. We define the star subdivision of the orbifold fan
$\unicode[STIX]{x1D70C}_{0}$
. We define the star subdivision of the orbifold fan
![]() $\boldsymbol{\unicode[STIX]{x1D6F4}}$
along
$\boldsymbol{\unicode[STIX]{x1D6F4}}$
along
![]() $\unicode[STIX]{x1D70E}$
as
$\unicode[STIX]{x1D70E}$
as
 $\boldsymbol{\unicode[STIX]{x1D6F4}}^{\ast }(\unicode[STIX]{x1D70E})=(N,\unicode[STIX]{x1D6F4}^{\ast }(v),\unicode[STIX]{x1D6FD}^{\prime })$
. Here
$\boldsymbol{\unicode[STIX]{x1D6F4}}^{\ast }(\unicode[STIX]{x1D70E})=(N,\unicode[STIX]{x1D6F4}^{\ast }(v),\unicode[STIX]{x1D6FD}^{\prime })$
. Here
![]() $\unicode[STIX]{x1D6F4}^{\ast }(v)$
denotes the subdivision of the fan
$\unicode[STIX]{x1D6F4}^{\ast }(v)$
denotes the subdivision of the fan
![]() $\unicode[STIX]{x1D6F4}$
obtained by adding the ray
$\unicode[STIX]{x1D6F4}$
obtained by adding the ray
![]() $\unicode[STIX]{x1D70C}_{0}$
and subdividing each cone containing it, as described in [Reference Cox, Little and SchenckCLS11, § 11.1]. The function
$\unicode[STIX]{x1D70C}_{0}$
and subdividing each cone containing it, as described in [Reference Cox, Little and SchenckCLS11, § 11.1]. The function
![]() $\unicode[STIX]{x1D6FD}^{\prime }$
is the extension of
$\unicode[STIX]{x1D6FD}^{\prime }$
is the extension of
![]() $\unicode[STIX]{x1D6FD}$
to
$\unicode[STIX]{x1D6FD}$
to
![]() $\mathbb{Z}^{\unicode[STIX]{x1D6F4}^{\ast }(v)}$
taking the ray
$\mathbb{Z}^{\unicode[STIX]{x1D6F4}^{\ast }(v)}$
taking the ray
![]() $\unicode[STIX]{x1D70C}_{0}$
to
$\unicode[STIX]{x1D70C}_{0}$
to
![]() $v$
. There is a canonical map
$v$
. There is a canonical map
 $\boldsymbol{\unicode[STIX]{x1D6F4}}^{\ast }(\unicode[STIX]{x1D70E})\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}$
, which is the identity on
$\boldsymbol{\unicode[STIX]{x1D6F4}}^{\ast }(\unicode[STIX]{x1D70E})\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}$
, which is the identity on
![]() $N$
. The ray
$N$
. The ray
![]() $\unicode[STIX]{x1D70C}_{0}$
is called the exceptional ray of the star subdivision.
$\unicode[STIX]{x1D70C}_{0}$
is called the exceptional ray of the star subdivision.
If
![]() $X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}$
is the toric orbifold corresponding to the orbifold fan
$X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}$
is the toric orbifold corresponding to the orbifold fan
![]() $\boldsymbol{\unicode[STIX]{x1D6F4}}$
, and
$\boldsymbol{\unicode[STIX]{x1D6F4}}$
, and
![]() $\unicode[STIX]{x1D70E}$
is a cone in
$\unicode[STIX]{x1D70E}$
is a cone in
![]() $\boldsymbol{\unicode[STIX]{x1D6F4}}$
, then the map
$\boldsymbol{\unicode[STIX]{x1D6F4}}$
, then the map
 $X_{\boldsymbol{\unicode[STIX]{x1D6F4}}^{\ast }(\unicode[STIX]{x1D70E})}\rightarrow X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}$
corresponding to the star subdivision is the blow-up of
$X_{\boldsymbol{\unicode[STIX]{x1D6F4}}^{\ast }(\unicode[STIX]{x1D70E})}\rightarrow X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}$
corresponding to the star subdivision is the blow-up of
![]() $X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}$
with centre
$X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}$
with centre
![]() $V(\unicode[STIX]{x1D70E})$
. The divisor
$V(\unicode[STIX]{x1D70E})$
. The divisor
![]() $D_{\unicode[STIX]{x1D70C}_{0}}$
on
$D_{\unicode[STIX]{x1D70C}_{0}}$
on
![]() $X_{\boldsymbol{\unicode[STIX]{x1D6F4}}^{\ast }(\unicode[STIX]{x1D70E})}$
corresponding to the exceptional ray
$X_{\boldsymbol{\unicode[STIX]{x1D6F4}}^{\ast }(\unicode[STIX]{x1D70E})}$
corresponding to the exceptional ray
![]() $\unicode[STIX]{x1D70C}_{0}$
is the exceptional divisor of the blow-up.
$\unicode[STIX]{x1D70C}_{0}$
is the exceptional divisor of the blow-up.
Definition 3.14. Let
 $\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
be an orbifold fan and
$\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
be an orbifold fan and
 $\boldsymbol{\unicode[STIX]{x1D70C}}=\{\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{r}\}\subset \unicode[STIX]{x1D6F4}(1)$
a set of rays. For each
$\boldsymbol{\unicode[STIX]{x1D70C}}=\{\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{r}\}\subset \unicode[STIX]{x1D6F4}(1)$
a set of rays. For each
![]() $\unicode[STIX]{x1D70C}_{i}\in \boldsymbol{\unicode[STIX]{x1D70C}}$
, we assign a weight
$\unicode[STIX]{x1D70C}_{i}\in \boldsymbol{\unicode[STIX]{x1D70C}}$
, we assign a weight
![]() $d_{i}$
, which is a positive integer. Denote the function taking each ray to its weight by
$d_{i}$
, which is a positive integer. Denote the function taking each ray to its weight by
![]() $\boldsymbol{d}$
. Consider the group homomorphism
$\boldsymbol{d}$
. Consider the group homomorphism
 $\unicode[STIX]{x1D6FD}^{\prime }:\mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)}\rightarrow N$
defined by
$\unicode[STIX]{x1D6FD}^{\prime }:\mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)}\rightarrow N$
defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D6FD}^{\prime }(\unicode[STIX]{x1D70C})=\left\{\begin{array}{@{}ll@{}}\boldsymbol{d}(\unicode[STIX]{x1D70C})\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D70C}) & \text{if }\unicode[STIX]{x1D70C}\in \boldsymbol{\unicode[STIX]{x1D70C}},\\ \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D70C}) & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}^{\prime }(\unicode[STIX]{x1D70C})=\left\{\begin{array}{@{}ll@{}}\boldsymbol{d}(\unicode[STIX]{x1D70C})\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D70C}) & \text{if }\unicode[STIX]{x1D70C}\in \boldsymbol{\unicode[STIX]{x1D70C}},\\ \unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D70C}) & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
We denote the orbifold fan given by the triple
 $(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD}^{\prime })$
by
$(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD}^{\prime })$
by
![]() $\boldsymbol{\unicode[STIX]{x1D6F4}}_{\boldsymbol{d}^{-1}\boldsymbol{\unicode[STIX]{x1D70C}}}$
. The natural morphism
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{\boldsymbol{d}^{-1}\boldsymbol{\unicode[STIX]{x1D70C}}}$
. The natural morphism
 $\boldsymbol{\unicode[STIX]{x1D6F4}}_{\boldsymbol{d}^{-1}\boldsymbol{\unicode[STIX]{x1D70C}}}\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}$
of orbifold fans, which is the identity map on the underlying group
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{\boldsymbol{d}^{-1}\boldsymbol{\unicode[STIX]{x1D70C}}}\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}$
of orbifold fans, which is the identity map on the underlying group
![]() $N$
, is called the root construction of
$N$
, is called the root construction of
![]() $\boldsymbol{\unicode[STIX]{x1D6F4}}$
with respect to the rays in
$\boldsymbol{\unicode[STIX]{x1D6F4}}$
with respect to the rays in
![]() $\boldsymbol{\unicode[STIX]{x1D70C}}$
with weights
$\boldsymbol{\unicode[STIX]{x1D70C}}$
with weights
![]() $\boldsymbol{d}$
.
$\boldsymbol{d}$
.
The terminology in the definition above is, of course, motivated by its relation to the root stack of the corresponding toric stacks. Using the same notation as in the definition above, we let
 $\unicode[STIX]{x1D70B}:X^{\prime }\rightarrow X$
be the morphism of toric orbifolds associated to the root fan
$\unicode[STIX]{x1D70B}:X^{\prime }\rightarrow X$
be the morphism of toric orbifolds associated to the root fan
 $\boldsymbol{\unicode[STIX]{x1D6F4}}_{\boldsymbol{d}^{-1}\boldsymbol{\unicode[STIX]{x1D70C}}}\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}$
. On both
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{\boldsymbol{d}^{-1}\boldsymbol{\unicode[STIX]{x1D70C}}}\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}$
. On both
![]() $X$
and
$X$
and
![]() $X^{\prime }$
we have toric divisors corresponding to the rays
$X^{\prime }$
we have toric divisors corresponding to the rays
 $\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{r}$
. Denote the sets of such divisors by
$\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{r}$
. Denote the sets of such divisors by
 $\boldsymbol{D}=\{D_{1},\ldots ,D_{r}\}$
and
$\boldsymbol{D}=\{D_{1},\ldots ,D_{r}\}$
and
 $\boldsymbol{D}^{\prime }=\{D_{1}^{\prime },\ldots ,D_{r}^{\prime }\}$
, respectively. Then each divisor
$\boldsymbol{D}^{\prime }=\{D_{1}^{\prime },\ldots ,D_{r}^{\prime }\}$
, respectively. Then each divisor
![]() $D_{i}^{\prime }$
is a
$D_{i}^{\prime }$
is a
![]() $d_{i}$
th root of
$d_{i}$
th root of
![]() $\unicode[STIX]{x1D70B}^{\ast }D_{i}$
, and this structure identifies
$\unicode[STIX]{x1D70B}^{\ast }D_{i}$
, and this structure identifies
 $X^{\prime }\rightarrow X$
with the root stack
$X^{\prime }\rightarrow X$
with the root stack
 $X_{\boldsymbol{d}^{-1}\boldsymbol{D}}\rightarrow X$
, where we consider
$X_{\boldsymbol{d}^{-1}\boldsymbol{D}}\rightarrow X$
, where we consider
![]() $\boldsymbol{d}$
as a function on
$\boldsymbol{d}$
as a function on
![]() $\boldsymbol{D}$
in the obvious way.
$\boldsymbol{D}$
in the obvious way.
In terms of homogeneous coordinates, the root stack of a basic toric stack has the following description. Let
![]() $X$
be a basic toric stack with homogeneous coordinates
$X$
be a basic toric stack with homogeneous coordinates
 $({\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}],A,\boldsymbol{a})$
. Assume that
$({\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}],A,\boldsymbol{a})$
. Assume that
![]() $\boldsymbol{D}$
is a set of toric divisors corresponding to the coordinates
$\boldsymbol{D}$
is a set of toric divisors corresponding to the coordinates
 $x_{1},\ldots ,x_{s}$
for some
$x_{1},\ldots ,x_{s}$
for some
![]() $s\leqslant r$
. Denote the generators of the group
$s\leqslant r$
. Denote the generators of the group
![]() $\mathbb{Z}^{s}$
by
$\mathbb{Z}^{s}$
by
 $e_{1},\ldots ,e_{s}$
and define the group
$e_{1},\ldots ,e_{s}$
and define the group
 $$\begin{eqnarray}A_{\boldsymbol{d}^{-1}\boldsymbol{a}}=A\oplus \mathbb{Z}^{s}/\langle d_{1}e_{1}-a_{1},\ldots ,d_{s}e_{s}-a_{s}\rangle ,\end{eqnarray}$$
$$\begin{eqnarray}A_{\boldsymbol{d}^{-1}\boldsymbol{a}}=A\oplus \mathbb{Z}^{s}/\langle d_{1}e_{1}-a_{1},\ldots ,d_{s}e_{s}-a_{s}\rangle ,\end{eqnarray}$$
which we think of as the group obtained from
![]() $A$
by formally adjoining the roots
$A$
by formally adjoining the roots
 $e_{i}=a_{i}/d_{i}$
. Also, let
$e_{i}=a_{i}/d_{i}$
. Also, let
 $\boldsymbol{a}^{\prime }=(e_{1},\ldots ,e_{s},a_{s+1},\ldots ,a_{r})$
. Then the homogeneous coordinates of
$\boldsymbol{a}^{\prime }=(e_{1},\ldots ,e_{s},a_{s+1},\ldots ,a_{r})$
. Then the homogeneous coordinates of
![]() $X_{\boldsymbol{d}^{-1}\boldsymbol{D}}$
are given by
$X_{\boldsymbol{d}^{-1}\boldsymbol{D}}$
are given by
 $$\begin{eqnarray}({\mathcal{O}}_{S}[x_{1}^{1/d_{1}},\ldots ,x_{s}^{1/d_{s}},x_{s+1},\ldots ,x_{r}],A_{\boldsymbol{d}^{-1}\boldsymbol{a}},\boldsymbol{a}^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}({\mathcal{O}}_{S}[x_{1}^{1/d_{1}},\ldots ,x_{s}^{1/d_{s}},x_{s+1},\ldots ,x_{r}],A_{\boldsymbol{d}^{-1}\boldsymbol{a}},\boldsymbol{a}^{\prime })\end{eqnarray}$$
and the map
 $X_{\boldsymbol{d}^{-1}\boldsymbol{D}}\rightarrow X$
corresponds to the map of graded rings taking
$X_{\boldsymbol{d}^{-1}\boldsymbol{D}}\rightarrow X$
corresponds to the map of graded rings taking
![]() $x_{i}$
to
$x_{i}$
to
 $x_{i}=(x_{i}^{1/d_{i}})^{d_{i}}$
.
$x_{i}=(x_{i}^{1/d_{i}})^{d_{i}}$
.
Remark 3.15. Any toric stack
 $X=X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}$
can be built up from the corresponding toric variety
$X=X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}$
can be built up from the corresponding toric variety
 $X_{\text{cs}}=X_{\unicode[STIX]{x1D6F4}}$
as follows. There are canonical morphisms
$X_{\text{cs}}=X_{\unicode[STIX]{x1D6F4}}$
as follows. There are canonical morphisms
 $$\begin{eqnarray}X\rightarrow X_{\text{rig}}\rightarrow X_{\text{can}}\rightarrow X_{\text{cs}},\end{eqnarray}$$
$$\begin{eqnarray}X\rightarrow X_{\text{rig}}\rightarrow X_{\text{can}}\rightarrow X_{\text{cs}},\end{eqnarray}$$
where the first is a gerbe (the rigidification of
![]() $X$
), the second is a root stack and the third is the canonical stack associated to
$X$
), the second is a root stack and the third is the canonical stack associated to
![]() $X_{\unicode[STIX]{x1D6F4}}$
. We describe this in terms of basic toric stacks. Let
$X_{\unicode[STIX]{x1D6F4}}$
. We describe this in terms of basic toric stacks. Let
![]() $X$
be a basic toric stack with homogeneous coordinates
$X$
be a basic toric stack with homogeneous coordinates
 $({\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}],A,(a_{1},\ldots ,a_{r}))$
. Then its rigidification
$({\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}],A,(a_{1},\ldots ,a_{r}))$
. Then its rigidification
![]() $X_{\text{rig}}$
is a basic toric orbifold with homogeneous coordinates
$X_{\text{rig}}$
is a basic toric orbifold with homogeneous coordinates
 $({\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}],A_{\text{rig}},(a_{1},\ldots ,a_{r}))$
, with
$({\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}],A_{\text{rig}},(a_{1},\ldots ,a_{r}))$
, with
 $A_{\text{rig}}=\langle a_{1},\ldots ,a_{r}\rangle$
(see Remark 3.5).
$A_{\text{rig}}=\langle a_{1},\ldots ,a_{r}\rangle$
(see Remark 3.5).
For each
 $i=1,\ldots ,r$
, we define
$i=1,\ldots ,r$
, we define
 $A_{i}=A_{\text{rig}}/\langle a_{1},\ldots ,\widehat{a}_{i},\ldots ,a_{r}\rangle$
, where
$A_{i}=A_{\text{rig}}/\langle a_{1},\ldots ,\widehat{a}_{i},\ldots ,a_{r}\rangle$
, where
![]() $\widehat{a}_{i}$
indicates that the element
$\widehat{a}_{i}$
indicates that the element
![]() $a_{i}$
is omitted. Then we have an exact sequence
$a_{i}$
is omitted. Then we have an exact sequence
 $$\begin{eqnarray}0\rightarrow A_{\text{can}}\rightarrow A_{\text{rig}}\xrightarrow[{}]{\unicode[STIX]{x1D711}}A_{1}\times \cdots \times A_{r}\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow A_{\text{can}}\rightarrow A_{\text{rig}}\xrightarrow[{}]{\unicode[STIX]{x1D711}}A_{1}\times \cdots \times A_{r}\rightarrow 0,\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D711}$
is the morphism induced by the canonical projections
$\unicode[STIX]{x1D711}$
is the morphism induced by the canonical projections
 $A\rightarrow A_{i}$
. Denote the order of
$A\rightarrow A_{i}$
. Denote the order of
![]() $A_{i}$
by
$A_{i}$
by
![]() $d_{i}$
, and note that
$d_{i}$
, and note that
 $a_{i}^{d_{i}}\in A_{\text{can}}$
for each
$a_{i}^{d_{i}}\in A_{\text{can}}$
for each
 $i=1,\ldots ,r$
. Furthermore, we have a graded homomorphism
$i=1,\ldots ,r$
. Furthermore, we have a graded homomorphism
 $$\begin{eqnarray}({\mathcal{O}}_{S}[x_{1}^{d_{1}},\ldots ,x_{r}^{d_{1}}],A_{\text{can}},(a_{1}^{d_{1}},\ldots ,a_{r}^{d_{r}}))\rightarrow ({\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}],A_{\text{rig}},(a_{1},\ldots ,a_{r}))\end{eqnarray}$$
$$\begin{eqnarray}({\mathcal{O}}_{S}[x_{1}^{d_{1}},\ldots ,x_{r}^{d_{1}}],A_{\text{can}},(a_{1}^{d_{1}},\ldots ,a_{r}^{d_{r}}))\rightarrow ({\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}],A_{\text{rig}},(a_{1},\ldots ,a_{r}))\end{eqnarray}$$
given by obvious inclusion of sheaves of
![]() ${\mathcal{O}}_{S}$
-algebras. It is straightforward to verify that this corresponds to a
${\mathcal{O}}_{S}$
-algebras. It is straightforward to verify that this corresponds to a
![]() $\boldsymbol{d}$
th root stack in the toric divisors, where
$\boldsymbol{d}$
th root stack in the toric divisors, where
 $\boldsymbol{d}=(d_{1},\ldots ,d_{r})$
, and that the corresponding morphism
$\boldsymbol{d}=(d_{1},\ldots ,d_{r})$
, and that the corresponding morphism
 $X_{\text{rig}}\rightarrow X_{\text{can}}$
of basic toric orbifolds is the canonical morphism to the canonical stack.
$X_{\text{rig}}\rightarrow X_{\text{can}}$
of basic toric orbifolds is the canonical morphism to the canonical stack.
3.5 Multiplicity, independency and smoothness
The toric destackification algorithm, which is described in the next section, is based on the well-known toric desingularisation algorithm described in for instance [Reference Cox, Little and SchenckCLS11, § 11]. In particular, the multiplicity of a cone plays an important role. Here we will briefly recall the main properties of multiplicities. We will also introduce the related concept of independency of toric divisors.
As usual, we let
 $\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
be an orbifold fan and
$\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
be an orbifold fan and
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
a cone. Let
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
a cone. Let
 $\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{r}$
be the rays in
$\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{r}$
be the rays in
![]() $\unicode[STIX]{x1D70E}(1)$
, and let
$\unicode[STIX]{x1D70E}(1)$
, and let
![]() $u_{i}$
be the non-zero lattice point on the ray
$u_{i}$
be the non-zero lattice point on the ray
![]() $\unicode[STIX]{x1D70C}_{i}$
which is closest to the origin. We associate the parallelotope
$\unicode[STIX]{x1D70C}_{i}$
which is closest to the origin. We associate the parallelotope
 $$\begin{eqnarray}P_{\unicode[STIX]{x1D70E}}=\biggl\{\mathop{\sum }_{i=1}^{r}\unicode[STIX]{x1D706}_{i}u_{i}\biggm\vert0\leqslant \unicode[STIX]{x1D706}_{i}<1\biggr\}\end{eqnarray}$$
$$\begin{eqnarray}P_{\unicode[STIX]{x1D70E}}=\biggl\{\mathop{\sum }_{i=1}^{r}\unicode[STIX]{x1D706}_{i}u_{i}\biggm\vert0\leqslant \unicode[STIX]{x1D706}_{i}<1\biggr\}\end{eqnarray}$$
to the cone
![]() $\unicode[STIX]{x1D70E}$
. Then the number of lattice points in
$\unicode[STIX]{x1D70E}$
. Then the number of lattice points in
![]() $P_{\unicode[STIX]{x1D70E}}$
is called the multiplicity of
$P_{\unicode[STIX]{x1D70E}}$
is called the multiplicity of
![]() $\unicode[STIX]{x1D70E}$
and is denoted by
$\unicode[STIX]{x1D70E}$
and is denoted by
 $\text{mult}\,(\unicode[STIX]{x1D70E})$
. The multiplicity satisfies the basic property
$\text{mult}\,(\unicode[STIX]{x1D70E})$
. The multiplicity satisfies the basic property
 $\text{mult}\,(\unicode[STIX]{x1D70F})|\text{mult}\,(\unicode[STIX]{x1D70E})$
if
$\text{mult}\,(\unicode[STIX]{x1D70F})|\text{mult}\,(\unicode[STIX]{x1D70E})$
if
![]() $\unicode[STIX]{x1D70F}\preccurlyeq \unicode[STIX]{x1D70E}$
. It should be noted that the stacky structure
$\unicode[STIX]{x1D70F}\preccurlyeq \unicode[STIX]{x1D70E}$
. It should be noted that the stacky structure
![]() $\unicode[STIX]{x1D6FD}$
plays no part in the definition of multiplicity. In particular, the multiplicity of a cone is preserved by the root construction. A cone
$\unicode[STIX]{x1D6FD}$
plays no part in the definition of multiplicity. In particular, the multiplicity of a cone is preserved by the root construction. A cone
![]() $\unicode[STIX]{x1D70E}$
is called smooth provided that the multiplicity
$\unicode[STIX]{x1D70E}$
is called smooth provided that the multiplicity
 $\text{mult}\,(\unicode[STIX]{x1D70E})$
equals one. An orbifold fan is smooth provided that all its cones are smooth.
$\text{mult}\,(\unicode[STIX]{x1D70E})$
equals one. An orbifold fan is smooth provided that all its cones are smooth.
The multiplicity
 $\text{mult}\,(\unicode[STIX]{x1D709})$
at a point
$\text{mult}\,(\unicode[STIX]{x1D709})$
at a point
![]() $\unicode[STIX]{x1D709}\in X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}$
in the toric orbifold is defined as the multiplicity of the cone spanned by the rays corresponding to the toric divisors passing through
$\unicode[STIX]{x1D709}\in X_{\boldsymbol{\unicode[STIX]{x1D6F4}}}$
in the toric orbifold is defined as the multiplicity of the cone spanned by the rays corresponding to the toric divisors passing through
![]() $\unicode[STIX]{x1D709}$
. The multiplicity is one at
$\unicode[STIX]{x1D709}$
. The multiplicity is one at
![]() $\unicode[STIX]{x1D709}$
if and only if the corresponding point in the coarse space
$\unicode[STIX]{x1D709}$
if and only if the corresponding point in the coarse space
![]() $X_{\unicode[STIX]{x1D6F4}}$
is smooth over the base. In particular, the coarse space is smooth if and only if the orbifold fan is smooth.
$X_{\unicode[STIX]{x1D6F4}}$
is smooth over the base. In particular, the coarse space is smooth if and only if the orbifold fan is smooth.
The following proposition describes how to read off the multiplicity from the homogeneous coordinates of a basic toric orbifold.
Proposition 3.16. Let
![]() $X$
be a basic toric orbifold with homogeneous coordinates
$X$
be a basic toric orbifold with homogeneous coordinates
 $$\begin{eqnarray}({\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}],A,\boldsymbol{a})\end{eqnarray}$$
$$\begin{eqnarray}({\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}],A,\boldsymbol{a})\end{eqnarray}$$
and let
 $(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
be an orbifold fan defining
$(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
be an orbifold fan defining
![]() $X$
. Let
$X$
. Let
![]() $\unicode[STIX]{x1D70E}$
be the (unique) maximal cone in
$\unicode[STIX]{x1D70E}$
be the (unique) maximal cone in
![]() $\unicode[STIX]{x1D6F4}$
. Then
$\unicode[STIX]{x1D6F4}$
. Then
 $\text{mult}\,(\unicode[STIX]{x1D70E})=|A_{\text{can}}|$
, where
$\text{mult}\,(\unicode[STIX]{x1D70E})=|A_{\text{can}}|$
, where
![]() $A_{\text{can}}$
is defined as in Remark 3.15.
$A_{\text{can}}$
is defined as in Remark 3.15.
Proof. Let
 $u_{1},\ldots ,u_{r}$
be the non-zero lattice points closest to the origin on the rays
$u_{1},\ldots ,u_{r}$
be the non-zero lattice points closest to the origin on the rays
 $\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{r}\in \unicode[STIX]{x1D6F4}(1)$
. Let
$\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{r}\in \unicode[STIX]{x1D6F4}(1)$
. Let
 $(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD}_{\text{can}})$
be the orbifold fan describing the canonical stack. Then
$(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD}_{\text{can}})$
be the orbifold fan describing the canonical stack. Then
 $\unicode[STIX]{x1D6FD}_{\text{can}}(\unicode[STIX]{x1D70C}_{i})=u_{i}$
. By [Reference Cox, Little and SchenckCLS11, (11.1.5)], the multiplicity of
$\unicode[STIX]{x1D6FD}_{\text{can}}(\unicode[STIX]{x1D70C}_{i})=u_{i}$
. By [Reference Cox, Little and SchenckCLS11, (11.1.5)], the multiplicity of
![]() $\unicode[STIX]{x1D70E}$
is given by the index
$\unicode[STIX]{x1D70E}$
is given by the index
 $[N:\mathbb{Z}u_{1}+\cdots +\mathbb{Z}u_{r}]$
. Hence, the result follows from the exact sequence
$[N:\mathbb{Z}u_{1}+\cdots +\mathbb{Z}u_{r}]$
. Hence, the result follows from the exact sequence
 $$\begin{eqnarray}0\rightarrow M\xrightarrow[{}]{\unicode[STIX]{x1D6FD}_{\text{can}}^{\prime }}\text{Hom}_{\mathbb{ Z}}(\mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)},\mathbb{Z})\rightarrow A_{\text{can}}\rightarrow 0,\quad \unicode[STIX]{x1D6FD}_{\text{can}}^{\prime }=\text{Hom}_{\mathbb{ Z}}(\unicode[STIX]{x1D6FD}_{\text{can}},\mathbb{Z})\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow M\xrightarrow[{}]{\unicode[STIX]{x1D6FD}_{\text{can}}^{\prime }}\text{Hom}_{\mathbb{ Z}}(\mathbb{Z}^{\unicode[STIX]{x1D6F4}(1)},\mathbb{Z})\rightarrow A_{\text{can}}\rightarrow 0,\quad \unicode[STIX]{x1D6FD}_{\text{can}}^{\prime }=\text{Hom}_{\mathbb{ Z}}(\unicode[STIX]{x1D6FD}_{\text{can}},\mathbb{Z})\end{eqnarray}$$
from the Cox construction for the canonical stack
![]() $X_{\text{can}}$
.◻
$X_{\text{can}}$
.◻
Singularities on toric varieties only occur at the intersections of the toric divisors. Generally singularities get worse at points where more divisors intersect in the sense that the multiplicity grows. We introduce the concept of independency to capture the idea of nice divisors which do not make singularities worse.
Definition 3.17. Let
 $\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
be an orbifold fan,
$\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
be an orbifold fan,
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
a cone and
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
a cone and
 $\unicode[STIX]{x1D70C}\in \unicode[STIX]{x1D70E}(1)$
a ray. We say that
$\unicode[STIX]{x1D70C}\in \unicode[STIX]{x1D70E}(1)$
a ray. We say that
![]() $\unicode[STIX]{x1D70C}$
is independent at
$\unicode[STIX]{x1D70C}$
is independent at
![]() $\unicode[STIX]{x1D70E}$
if
$\unicode[STIX]{x1D70E}$
if
 $\text{mult}\,\unicode[STIX]{x1D70F}=\text{mult}\,\unicode[STIX]{x1D70E}$
, where
$\text{mult}\,\unicode[STIX]{x1D70F}=\text{mult}\,\unicode[STIX]{x1D70E}$
, where
![]() $\unicode[STIX]{x1D70F}$
is the face of
$\unicode[STIX]{x1D70F}$
is the face of
![]() $\unicode[STIX]{x1D70E}$
spanned by the rays
$\unicode[STIX]{x1D70E}$
spanned by the rays
![]() $\unicode[STIX]{x1D70E}(1)\setminus \unicode[STIX]{x1D70C}$
. A ray
$\unicode[STIX]{x1D70E}(1)\setminus \unicode[STIX]{x1D70C}$
. A ray
![]() $\unicode[STIX]{x1D70C}$
is independent if it is independent at all cones
$\unicode[STIX]{x1D70C}$
is independent if it is independent at all cones
![]() $\unicode[STIX]{x1D70E}$
containing
$\unicode[STIX]{x1D70E}$
containing
![]() $\unicode[STIX]{x1D70C}$
.
$\unicode[STIX]{x1D70C}$
.
Proposition 3.18. Let
 $\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
be an orbifold fan and let
$\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
be an orbifold fan and let
![]() $\unicode[STIX]{x1D70E}$
be a cone in
$\unicode[STIX]{x1D70E}$
be a cone in
![]() $\unicode[STIX]{x1D6F4}$
. Then
$\unicode[STIX]{x1D6F4}$
. Then
![]() $\unicode[STIX]{x1D70E}$
is smooth if and only if all rays in
$\unicode[STIX]{x1D70E}$
is smooth if and only if all rays in
![]() $\unicode[STIX]{x1D70E}(1)$
are independent at
$\unicode[STIX]{x1D70E}(1)$
are independent at
![]() $\unicode[STIX]{x1D70E}$
. In particular, the fan
$\unicode[STIX]{x1D70E}$
. In particular, the fan
![]() $\boldsymbol{\unicode[STIX]{x1D6F4}}$
is smooth if and only if all rays in
$\boldsymbol{\unicode[STIX]{x1D6F4}}$
is smooth if and only if all rays in
![]() $\boldsymbol{\unicode[STIX]{x1D6F4}}(1)$
are independent.
$\boldsymbol{\unicode[STIX]{x1D6F4}}(1)$
are independent.
Proof. Let
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
. Assume that
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6F4}$
. Assume that
![]() $\unicode[STIX]{x1D70E}$
is smooth. Then
$\unicode[STIX]{x1D70E}$
is smooth. Then
 $\text{mult}\,\unicode[STIX]{x1D70E}^{\prime }=\text{mult}\,\unicode[STIX]{x1D70E}=1$
for any facet
$\text{mult}\,\unicode[STIX]{x1D70E}^{\prime }=\text{mult}\,\unicode[STIX]{x1D70E}=1$
for any facet
![]() $\unicode[STIX]{x1D70E}^{\prime }\prec \unicode[STIX]{x1D70E}$
. In particular, any ray in
$\unicode[STIX]{x1D70E}^{\prime }\prec \unicode[STIX]{x1D70E}$
. In particular, any ray in
![]() $\unicode[STIX]{x1D70E}(1)$
is independent at
$\unicode[STIX]{x1D70E}(1)$
is independent at
![]() $\unicode[STIX]{x1D70E}$
.
$\unicode[STIX]{x1D70E}$
.
Conversely, assume that all rays in
![]() $\unicode[STIX]{x1D70E}(1)$
are independent at
$\unicode[STIX]{x1D70E}(1)$
are independent at
![]() $\unicode[STIX]{x1D70E}$
. Denote the rays in
$\unicode[STIX]{x1D70E}$
. Denote the rays in
![]() $\unicode[STIX]{x1D70E}(1)$
by
$\unicode[STIX]{x1D70E}(1)$
by
 $\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{r}$
and let
$\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{r}$
and let
![]() $u_{i}$
denote the non-zero lattice points closest to the origin at
$u_{i}$
denote the non-zero lattice points closest to the origin at
![]() $\unicode[STIX]{x1D70C}_{i}$
for each
$\unicode[STIX]{x1D70C}_{i}$
for each
 $i=1,\ldots ,r$
. Assume that
$i=1,\ldots ,r$
. Assume that
 $P=\unicode[STIX]{x1D706}_{1}u_{1}+\cdots +\unicode[STIX]{x1D706}_{r}u_{r}$
is a lattice point in the parallelotope
$P=\unicode[STIX]{x1D706}_{1}u_{1}+\cdots +\unicode[STIX]{x1D706}_{r}u_{r}$
is a lattice point in the parallelotope
![]() $P_{\unicode[STIX]{x1D70E}}$
. By the assumption that all rays are independent, we have
$P_{\unicode[STIX]{x1D70E}}$
. By the assumption that all rays are independent, we have
 $\text{mult}\,\unicode[STIX]{x1D70F}=\text{mult}\,\unicode[STIX]{x1D70E}$
for each facet
$\text{mult}\,\unicode[STIX]{x1D70F}=\text{mult}\,\unicode[STIX]{x1D70E}$
for each facet
![]() $\unicode[STIX]{x1D70F}$
of
$\unicode[STIX]{x1D70F}$
of
![]() $\unicode[STIX]{x1D70E}$
. In particular, the point
$\unicode[STIX]{x1D70E}$
. In particular, the point
![]() $P$
is contained in
$P$
is contained in
![]() $P_{\unicode[STIX]{x1D70F}}$
for each
$P_{\unicode[STIX]{x1D70F}}$
for each
![]() $\unicode[STIX]{x1D70F}$
. Since the lattice points
$\unicode[STIX]{x1D70F}$
. Since the lattice points
 $u_{1},\ldots ,u_{r}$
are linearly independent in
$u_{1},\ldots ,u_{r}$
are linearly independent in
![]() $N_{\mathbb{R}}$
, this forces each
$N_{\mathbb{R}}$
, this forces each
![]() $\unicode[STIX]{x1D706}_{i}=0$
. Hence, the only lattice point in
$\unicode[STIX]{x1D706}_{i}=0$
. Hence, the only lattice point in
![]() $P_{\unicode[STIX]{x1D70E}}$
is the origin, that is,
$P_{\unicode[STIX]{x1D70E}}$
is the origin, that is,
 $\text{mult}\,\unicode[STIX]{x1D70E}=1$
.◻
$\text{mult}\,\unicode[STIX]{x1D70E}=1$
.◻
Proposition 3.19. Let
![]() $X$
be a basic toric orbifold with homogeneous coordinates
$X$
be a basic toric orbifold with homogeneous coordinates
 $$\begin{eqnarray}({\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}],A,(a_{1},\ldots ,a_{r}))\end{eqnarray}$$
$$\begin{eqnarray}({\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}],A,(a_{1},\ldots ,a_{r}))\end{eqnarray}$$
and let
 $(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
be an orbifold fan defining
$(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
be an orbifold fan defining
![]() $X$
. Denote the rays of
$X$
. Denote the rays of
![]() $\unicode[STIX]{x1D6F4}$
by
$\unicode[STIX]{x1D6F4}$
by
 $\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{r}$
and let
$\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{r}$
and let
![]() $\unicode[STIX]{x1D70E}$
denote the (unique) maximal cone of
$\unicode[STIX]{x1D70E}$
denote the (unique) maximal cone of
![]() $\unicode[STIX]{x1D6F4}$
. Then
$\unicode[STIX]{x1D6F4}$
. Then
![]() $\unicode[STIX]{x1D70C}_{i}$
is independent at
$\unicode[STIX]{x1D70C}_{i}$
is independent at
![]() $\unicode[STIX]{x1D70E}$
if and only if the intersection
$\unicode[STIX]{x1D70E}$
if and only if the intersection
 $\langle a_{1},\ldots ,\widehat{a}_{i},\ldots ,a_{r}\rangle \cap \langle a_{i}\rangle$
is trivial.
$\langle a_{1},\ldots ,\widehat{a}_{i},\ldots ,a_{r}\rangle \cap \langle a_{i}\rangle$
is trivial.
Proof. We assume, without loss of generality, that
![]() $i=r$
. Let
$i=r$
. Let
![]() $\unicode[STIX]{x1D70F}$
be the cone spanned by the rays
$\unicode[STIX]{x1D70F}$
be the cone spanned by the rays
 $\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{r-1}$
. By Proposition 3.16, the open substack
$\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{r-1}$
. By Proposition 3.16, the open substack
 $U_{\unicode[STIX]{x1D70F}}\subset U_{\unicode[STIX]{x1D70E}}=X$
has homogeneous coordinates
$U_{\unicode[STIX]{x1D70F}}\subset U_{\unicode[STIX]{x1D70E}}=X$
has homogeneous coordinates
 $$\begin{eqnarray}({\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}][x_{r}^{-1}],A^{\prime },(\bar{a}_{1},\ldots ,\bar{a}_{r})),\end{eqnarray}$$
$$\begin{eqnarray}({\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}][x_{r}^{-1}],A^{\prime },(\bar{a}_{1},\ldots ,\bar{a}_{r})),\end{eqnarray}$$
where
 $A^{\prime }=A/\langle a_{r}\rangle$
. Define
$A^{\prime }=A/\langle a_{r}\rangle$
. Define
![]() $A_{\text{can}}$
and
$A_{\text{can}}$
and
![]() $A_{i}$
as in Remark 3.15, and similarly for
$A_{i}$
as in Remark 3.15, and similarly for
![]() $A_{\text{can}}^{\prime }$
and
$A_{\text{can}}^{\prime }$
and
![]() $A_{i}^{\prime }$
. Since the morphism
$A_{i}^{\prime }$
. Since the morphism
 $\langle a_{r}\rangle \rightarrow A_{r}$
is surjective, the snake lemma gives us the diagram
$\langle a_{r}\rangle \rightarrow A_{r}$
is surjective, the snake lemma gives us the diagram

with exact rows and columns. By Proposition 3.16, we have
 $\text{mult}\,(\unicode[STIX]{x1D70E})=|A_{\text{can}}|$
and
$\text{mult}\,(\unicode[STIX]{x1D70E})=|A_{\text{can}}|$
and
 $\text{mult}\,(\unicode[STIX]{x1D70F})=|A_{\text{can}}^{\prime }|$
. Thus, it follows from Definition 3.17 and the diagram above that the ray
$\text{mult}\,(\unicode[STIX]{x1D70F})=|A_{\text{can}}^{\prime }|$
. Thus, it follows from Definition 3.17 and the diagram above that the ray
![]() $\unicode[STIX]{x1D70C}_{r}$
is independent at
$\unicode[STIX]{x1D70C}_{r}$
is independent at
![]() $\unicode[STIX]{x1D70E}$
if and only if
$\unicode[STIX]{x1D70E}$
if and only if
![]() $K$
vanishes. This is obviously equivalent to the condition stated in the proposition.◻
$K$
vanishes. This is obviously equivalent to the condition stated in the proposition.◻
4 Toric destackification
In this section, we give an algorithm for functorial destackification (Definition 2.3) of toric orbifolds. Recall that for an orbifold, a destackification is roughly given by a sequence of smooth stacky blow-ups (see § 2.2) such that the modified orbifold becomes a root stack over its coarse space. For a toric orbifold this translates to the combinatorial problem of subdividing an orbifold fan (Definition 3.8) using star subdivisions at cones (Definition 3.13) and roots of rays (Definition 3.14), such that the resulting fan becomes smooth (see § 3.5). If we do not care about functoriality, this can be achieved by using an algorithm which is very similar to the classical algorithm for resolving singularities of a simplicial toric variety (see [Reference Cox, Little and SchenckCLS11, § 11]). We illustrate the procedure by giving an example.
Example 4.1. Consider the orbifold fan given in Figure 4.1(a). The maximal cone
 $\unicode[STIX]{x1D70E}=\text{Cone}\,(\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2})$
has multiplicity 5. To obtain a subdivision of the fan into cones with lower multiplicity, we subdivide
$\unicode[STIX]{x1D70E}=\text{Cone}\,(\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2})$
has multiplicity 5. To obtain a subdivision of the fan into cones with lower multiplicity, we subdivide
![]() $\unicode[STIX]{x1D70E}$
at a ray passing through a non-zero lattice point in the parallelotope
$\unicode[STIX]{x1D70E}$
at a ray passing through a non-zero lattice point in the parallelotope
![]() $P_{\unicode[STIX]{x1D70E}}$
. This can be achieved by first taking the third root at the ray
$P_{\unicode[STIX]{x1D70E}}$
. This can be achieved by first taking the third root at the ray
![]() $\unicode[STIX]{x1D70C}_{1}$
and then taking the star subdivision at
$\unicode[STIX]{x1D70C}_{1}$
and then taking the star subdivision at
![]() $\unicode[STIX]{x1D70E}$
, which yields the fan in Figure 4.1(b). Note that the exceptional ray
$\unicode[STIX]{x1D70E}$
, which yields the fan in Figure 4.1(b). Note that the exceptional ray
![]() $\unicode[STIX]{x1D70C}_{3}$
passes through the lattice point
$\unicode[STIX]{x1D70C}_{3}$
passes through the lattice point
![]() $(1,1)$
, which indeed lies in
$(1,1)$
, which indeed lies in
![]() $P_{\unicode[STIX]{x1D70E}}$
. The situation has improved, since the new maximal cones have multiplicities
$P_{\unicode[STIX]{x1D70E}}$
. The situation has improved, since the new maximal cones have multiplicities
![]() $1$
and
$1$
and
![]() $3$
, respectively. To complete the destackification, we take the second root of
$3$
, respectively. To complete the destackification, we take the second root of
![]() $\unicode[STIX]{x1D70C}_{2}$
followed by a star subdivision at
$\unicode[STIX]{x1D70C}_{2}$
followed by a star subdivision at
 $\text{Cone}\,(\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D70C}_{3})$
, which yields a smooth orbifold fan. The last steps are not shown in the figure.
$\text{Cone}\,(\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D70C}_{3})$
, which yields a smooth orbifold fan. The last steps are not shown in the figure.
The problem with the naive algorithm outlined in Example 4.1 is that it is not functorial (Definition 2.6) with respect to toric open immersions, as illustrated in the next example. In particular, this means that it will be hard to use it as a building block for a global destackification algorithm which works for stacks which are only locally toric.
Example 4.2. The toric suborbifolds
![]() $U_{\unicode[STIX]{x1D70C}_{1}}$
and
$U_{\unicode[STIX]{x1D70C}_{1}}$
and
![]() $U_{\unicode[STIX]{x1D70C}_{2}}$
of the toric orbifold associated to the orbifold fan given in Figure 4.1(a) are isomorphic. Yet, corresponding suborbifolds in Figure 4.1(b) are non-isomorphic since we have stackiness along the divisor corresponding to
$U_{\unicode[STIX]{x1D70C}_{2}}$
of the toric orbifold associated to the orbifold fan given in Figure 4.1(a) are isomorphic. Yet, corresponding suborbifolds in Figure 4.1(b) are non-isomorphic since we have stackiness along the divisor corresponding to
![]() $\unicode[STIX]{x1D70C}_{1}$
, but not along the divisor corresponding to
$\unicode[STIX]{x1D70C}_{1}$
, but not along the divisor corresponding to
![]() $\unicode[STIX]{x1D70C}_{2}$
. This shows that destackification described in Example 4.1 cannot be obtained from running a destackification algorithm which is functorial with respect to toric open immersions. In fact, both the orbifolds
$\unicode[STIX]{x1D70C}_{2}$
. This shows that destackification described in Example 4.1 cannot be obtained from running a destackification algorithm which is functorial with respect to toric open immersions. In fact, both the orbifolds
![]() $U_{\unicode[STIX]{x1D70C}_{1}}$
and
$U_{\unicode[STIX]{x1D70C}_{1}}$
and
![]() $U_{\unicode[STIX]{x1D70C}_{2}}$
are smooth toric varieties and any sensible destackification algorithm should leave such varieties unmodified.
$U_{\unicode[STIX]{x1D70C}_{2}}$
are smooth toric varieties and any sensible destackification algorithm should leave such varieties unmodified.
The problem illustrated in Example 4.2 is really intrinsic to the root construction; taking a root modifies the stack along a whole divisor, even at points lying over smooth points of the coarse space. On the other hand, it is in general not possible to destackify by just using star subdivisions at cones, as shown by the following example (cf. [Reference KollárKol07, Claim 2.29.2]).
Example 4.3. Let us, for simplicity, assume that we are working over a field
![]() $k$
. Then the basic toric orbifold associated to the orbifold fan in Figure 4.1 has homogeneous coordinate ring
$k$
. Then the basic toric orbifold associated to the orbifold fan in Figure 4.1 has homogeneous coordinate ring
 $(k[x_{1},x_{2}],C_{5},(1,3))$
. Blowing up the origin yields two charts with homogeneous coordinate rings
$(k[x_{1},x_{2}],C_{5},(1,3))$
. Blowing up the origin yields two charts with homogeneous coordinate rings
 $(k[x_{1},x_{2}/x_{1}],C_{5},(1,2))$
and
$(k[x_{1},x_{2}/x_{1}],C_{5},(1,2))$
and
 $(k[x_{1}/x_{2},x_{2}],C_{5},(3,3))$
, respectively. But the first chart is isomorphic to the toric orbifold we started with since the weight vector
$(k[x_{1}/x_{2},x_{2}],C_{5},(3,3))$
, respectively. But the first chart is isomorphic to the toric orbifold we started with since the weight vector
![]() $(1,3)$
can be obtained from
$(1,3)$
can be obtained from
![]() $(1,2)$
by multiplying with the unit 3 and swapping the coordinates. Thus, no improvement towards destackification has been achieved.
$(1,2)$
by multiplying with the unit 3 and swapping the coordinates. Thus, no improvement towards destackification has been achieved.
Our solution to the problem is to admit only stacky blow-ups in centres lying over the original problematic locus. In particular, this means that the first stacky blow-up must be an ordinary blow-up.
Example 4.4. We describe how the toric stack given by the orbifold fan in Figure 4.1(a) can be destackified using only stacky blow-ups with loci lying over the original problematic locus. Instead of taking the third root of
![]() $\unicode[STIX]{x1D70C}_{1}$
and subdividing as in Figure 4.1(a), we take three subsequent subdivisions at the cones
$\unicode[STIX]{x1D70C}_{1}$
and subdividing as in Figure 4.1(a), we take three subsequent subdivisions at the cones
 $\text{Cone}\,(\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2})$
,
$\text{Cone}\,(\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2})$
,
 $\text{Cone}\,(\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D6FF}_{1})$
and
$\text{Cone}\,(\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D6FF}_{1})$
and
 $\text{Cone}\,(\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D6FF}_{2})$
with
$\text{Cone}\,(\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D6FF}_{2})$
with
![]() $\unicode[STIX]{x1D6FF}_{1}$
,
$\unicode[STIX]{x1D6FF}_{1}$
,
![]() $\unicode[STIX]{x1D6FF}_{1}$
and
$\unicode[STIX]{x1D6FF}_{1}$
and
![]() $\unicode[STIX]{x1D6FF}_{3}$
denoting the exceptional rays of each subdivision. The resulting fan is pictured in Figure 4.1(c). Note that
$\unicode[STIX]{x1D6FF}_{3}$
denoting the exceptional rays of each subdivision. The resulting fan is pictured in Figure 4.1(c). Note that
 $\text{Cone}\,(\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D6FF}_{3})$
is identical to
$\text{Cone}\,(\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D6FF}_{3})$
is identical to
 $\text{Cone}\,(\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{3})$
from Figure 4.1(b). In particular, it has multiplicity 1. The other cones of Figure 4.1(c) have multiplicities 1, 5 and 5 respectively when enumerated from left to right. The cone
$\text{Cone}\,(\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{3})$
from Figure 4.1(b). In particular, it has multiplicity 1. The other cones of Figure 4.1(c) have multiplicities 1, 5 and 5 respectively when enumerated from left to right. The cone
 $\text{Cone}\,(\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D70C}_{2})$
can be destackified by a single star subdivision (this is not shown in the figure). But, as was shown in Example 4.3, the cone
$\text{Cone}\,(\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D70C}_{2})$
can be destackified by a single star subdivision (this is not shown in the figure). But, as was shown in Example 4.3, the cone
 $\text{Cone}\,(\unicode[STIX]{x1D6FF}_{2},\unicode[STIX]{x1D6FF}_{1})$
is isomorphic to
$\text{Cone}\,(\unicode[STIX]{x1D6FF}_{2},\unicode[STIX]{x1D6FF}_{1})$
is isomorphic to
 $\text{Cone}\,(\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2})$
in Figure 4.1(a) which we started with. Hence, it may seem that no progress has been made. However, since both the rays
$\text{Cone}\,(\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2})$
in Figure 4.1(a) which we started with. Hence, it may seem that no progress has been made. However, since both the rays
![]() $\unicode[STIX]{x1D6FF}_{1}$
and
$\unicode[STIX]{x1D6FF}_{1}$
and
![]() $\unicode[STIX]{x1D6FF}_{2}$
correspond to divisors lying over the original problematic locus, we may now root them. This allows us to complete the destackification by proceeding as in Example 4.1 with the rays
$\unicode[STIX]{x1D6FF}_{2}$
correspond to divisors lying over the original problematic locus, we may now root them. This allows us to complete the destackification by proceeding as in Example 4.1 with the rays
![]() $\unicode[STIX]{x1D6FF}_{2}$
and
$\unicode[STIX]{x1D6FF}_{2}$
and
![]() $\unicode[STIX]{x1D6FF}_{1}$
taking the roles of
$\unicode[STIX]{x1D6FF}_{1}$
taking the roles of
![]() $\unicode[STIX]{x1D70C}_{1}$
and
$\unicode[STIX]{x1D70C}_{1}$
and
![]() $\unicode[STIX]{x1D70C}_{2}$
, respectively (this is not shown in the figure).
$\unicode[STIX]{x1D70C}_{2}$
, respectively (this is not shown in the figure).
Note that the philosophy behind this solution is similar to the one behind classical strong desingularisation algorithms. We relax the functoriality requirement and do not demand the process to be functorial with respect to open immersions after each stacky blow-up. This requires us to somehow keep track of the history of the destackification process. We do this by adding additional structure to our toric orbifolds.
Firstly, we will assume that the rays of the orbifold fan are ordered. Note that the ordering of the rays also induces a total ordering on the set of cones. This is induced by the lexicographic ordering of the power set of the set of rays. The ordering of the rays ensures that the pair
![]() $(X,\boldsymbol{E})$
, where
$(X,\boldsymbol{E})$
, where
![]() $X$
is the toric stack and
$X$
is the toric stack and
![]() $\boldsymbol{E}$
is the set of toric divisors, is a standard pair in the sense of Definition 2.1. When taking roots and star subdivisions of cones, we use similar conventions regarding the ordering of the rays of the new stacky fans as was described in § 2.2.
$\boldsymbol{E}$
is the set of toric divisors, is a standard pair in the sense of Definition 2.1. When taking roots and star subdivisions of cones, we use similar conventions regarding the ordering of the rays of the new stacky fans as was described in § 2.2.
Secondly, we make use of a distinguished structure (Definition 2.7) on our toric orbifold. Combinatorially, the distinguished structure corresponds to a subset of the set of rays in the orbifold fan. As we will see, these rays represent divisors which lie over the original problematic locus.
Roughly, Algorithm B, which is the main toric destackification algorithm, works as follows. At each iteration of the main loop one problematic cone is identified. This cone is subdivided with a single star subdivision and the exceptional ray is marked as distinguished. The resulting cones are then improved by invoking Algorithm A, which performs a sequence of admissible stacky blow-ups (Definition 2.7). Combinatorially, admissible stacky blow-ups correspond to roots of distinguished rays and star subdivisions of cones containing at least one distinguished ray. Note that the admissible stacky blow-ups precisely correspond to stacky blow-ups in centres lying over the problematic cone identified in the first step of the iteration.
Example 4.5. In principle, the destackification described in Example 4.4 corresponds to a single iteration of Algorithm B. The first blow-up creates the exceptional ray
![]() $\unicode[STIX]{x1D6FF}_{1}$
, which is marked as distinguished. Since the exceptional ray of each admissible star subdivision is distinguished, all subsequent star subdivisions and roots described in the example are distinguished.
$\unicode[STIX]{x1D6FF}_{1}$
, which is marked as distinguished. Since the exceptional ray of each admissible star subdivision is distinguished, all subsequent star subdivisions and roots described in the example are distinguished.
Note that the actual output of Algorithm B will be slightly different (and considerably harder to draw) than that described in Example 4.4. The output depends on the somewhat arbitrary choice of ordering made in Step A2.
In Example 4.4, we could make all cones smooth via admissible stacky blow-ups after a single initial blow-up creating a distinguished exceptional ray. This is always possible for two-dimensional cones, but not for cones of higher dimension. Instead we focus on making all distinguished rays independent (Definition 3.17). Since independent rays do not contribute to the multiplicity of the cone, this effectively reduces the problem of destackifying the cone to the problem of destackifying a cone of lower dimension.
Algorithm A (Partial toric destackification).
The input of the algorithm is an orbifold fan
![]() $\boldsymbol{\unicode[STIX]{x1D6F4}}_{0}$
with an ordered set of rays having a distinguished structure. The output is a sequence
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{0}$
with an ordered set of rays having a distinguished structure. The output is a sequence
 $$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D6F4}}_{n}\rightarrow \cdots \rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}_{0}\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D6F4}}_{n}\rightarrow \cdots \rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}_{0}\end{eqnarray}$$
of admissible stacky blow-ups, with the property that all distinguished rays of
![]() $\boldsymbol{\unicode[STIX]{x1D6F4}}_{n}$
are independent. The construction is functorial with respect to isomorphisms
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{n}$
are independent. The construction is functorial with respect to isomorphisms
 $\boldsymbol{\unicode[STIX]{x1D6F4}}_{0}^{\prime }\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}_{0}$
of stacky fans preserving the ordering and the distinguished structure. We use the notation
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{0}^{\prime }\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}_{0}$
of stacky fans preserving the ordering and the distinguished structure. We use the notation
 $\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}=(N,\unicode[STIX]{x1D6F4}_{i},\unicode[STIX]{x1D6FD}_{i})$
in the description of the algorithm.
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}=(N,\unicode[STIX]{x1D6F4}_{i},\unicode[STIX]{x1D6FD}_{i})$
in the description of the algorithm.
- A0.
-
[Initialise.] Set
 $i=0$
.
$i=0$
. - A1.
-
[Choose a cone.] Let
 ${\mathcal{S}}$
be the set of cones
${\mathcal{S}}$
be the set of cones
 $\unicode[STIX]{x1D70E}\in \boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
such that
$\unicode[STIX]{x1D70E}\in \boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
such that
 $\unicode[STIX]{x1D70E}(1)$
contains a distinguished divisor and such that the relative interior of the parallelotope
$\unicode[STIX]{x1D70E}(1)$
contains a distinguished divisor and such that the relative interior of the parallelotope
 $P_{\unicode[STIX]{x1D70E}}$
contains a lattice point. Order the cones
$P_{\unicode[STIX]{x1D70E}}$
contains a lattice point. Order the cones
 $\unicode[STIX]{x1D70E}\in {\mathcal{S}}$
first by number of non-distinguished rays in
$\unicode[STIX]{x1D70E}\in {\mathcal{S}}$
first by number of non-distinguished rays in
 $\unicode[STIX]{x1D70E}(1)$
, then by multiplicity and finally by the ordering induced by the ordering on
$\unicode[STIX]{x1D70E}(1)$
, then by multiplicity and finally by the ordering induced by the ordering on
 $\unicode[STIX]{x1D6F4}_{i}(1)$
. If
$\unicode[STIX]{x1D6F4}_{i}(1)$
. If
 ${\mathcal{S}}$
is empty, the algorithm terminates. Otherwise let
${\mathcal{S}}$
is empty, the algorithm terminates. Otherwise let
 $\unicode[STIX]{x1D70E}_{i}$
be the largest element of
$\unicode[STIX]{x1D70E}_{i}$
be the largest element of
 ${\mathcal{S}}$
with respect to the ordering described above.
${\mathcal{S}}$
with respect to the ordering described above. - A2.
-
[Choose a formal sum of rays.] Let
 ${\mathcal{P}}$
be the set of formal sums
${\mathcal{P}}$
be the set of formal sums
 $\unicode[STIX]{x1D713}\in \mathbb{Z}^{\unicode[STIX]{x1D70E}_{i}(1)}$
such that the ray
$\unicode[STIX]{x1D713}\in \mathbb{Z}^{\unicode[STIX]{x1D70E}_{i}(1)}$
such that the ray
 $\mathbb{R}_{{\geqslant}0}\unicode[STIX]{x1D6FD}_{i}(\unicode[STIX]{x1D713})$
passes through a lattice point in the relative interior of the parallelotope
$\mathbb{R}_{{\geqslant}0}\unicode[STIX]{x1D6FD}_{i}(\unicode[STIX]{x1D713})$
passes through a lattice point in the relative interior of the parallelotope
 $P_{\unicode[STIX]{x1D70E}_{i}}$
. This set is non-empty by our choice of
$P_{\unicode[STIX]{x1D70E}_{i}}$
. This set is non-empty by our choice of
 $\unicode[STIX]{x1D70E}_{i}$
in the previous step. Let
$\unicode[STIX]{x1D70E}_{i}$
in the previous step. Let
 $\unicode[STIX]{x1D713}_{i}$
be the smallest element of
$\unicode[STIX]{x1D713}_{i}$
be the smallest element of
 ${\mathcal{P}}$
with respect to the lexicographic ordering of
${\mathcal{P}}$
with respect to the lexicographic ordering of
 $\mathbb{Z}^{\unicode[STIX]{x1D70E}_{i}(1)}$
induced by the ordering of
$\mathbb{Z}^{\unicode[STIX]{x1D70E}_{i}(1)}$
induced by the ordering of
 $\unicode[STIX]{x1D6F4}_{i}(1)$
.
$\unicode[STIX]{x1D6F4}_{i}(1)$
. - A3.
-
[Root distinguished rays.] Assume that
 $\unicode[STIX]{x1D713}_{i}=d_{1}\unicode[STIX]{x1D70C}_{1}+\cdots +d_{s}\unicode[STIX]{x1D70C}_{s}+c_{1}\unicode[STIX]{x1D6FF}_{1}+\cdots +c_{r}\unicode[STIX]{x1D6FF}_{r}$
, with
$\unicode[STIX]{x1D713}_{i}=d_{1}\unicode[STIX]{x1D70C}_{1}+\cdots +d_{s}\unicode[STIX]{x1D70C}_{s}+c_{1}\unicode[STIX]{x1D6FF}_{1}+\cdots +c_{r}\unicode[STIX]{x1D6FF}_{r}$
, with
 $\unicode[STIX]{x1D70C}_{j}$
and
$\unicode[STIX]{x1D70C}_{j}$
and
 $\unicode[STIX]{x1D6FF}_{j}$
being distinct non-distinguished and distinguished rays, respectively. Let
$\unicode[STIX]{x1D6FF}_{j}$
being distinct non-distinguished and distinguished rays, respectively. Let
 $\boldsymbol{\unicode[STIX]{x1D6F4}}_{i+1}\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
be the root construction
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{i+1}\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
be the root construction
 $(\boldsymbol{\unicode[STIX]{x1D6F4}}_{i})_{c_{1}^{-1}\unicode[STIX]{x1D6FF}_{1},\ldots ,c_{r}^{-1}\unicode[STIX]{x1D6FF}_{r}}\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
and
$(\boldsymbol{\unicode[STIX]{x1D6F4}}_{i})_{c_{1}^{-1}\unicode[STIX]{x1D6FF}_{1},\ldots ,c_{r}^{-1}\unicode[STIX]{x1D6FF}_{r}}\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
and
 $\unicode[STIX]{x1D713}_{i+1}=d_{1}\unicode[STIX]{x1D70C}_{1}+\cdots +d_{s}\unicode[STIX]{x1D70C}_{s}+\unicode[STIX]{x1D6FF}_{1}+\cdots +\unicode[STIX]{x1D6FF}_{r}$
. Increment
$\unicode[STIX]{x1D713}_{i+1}=d_{1}\unicode[STIX]{x1D70C}_{1}+\cdots +d_{s}\unicode[STIX]{x1D70C}_{s}+\unicode[STIX]{x1D6FF}_{1}+\cdots +\unicode[STIX]{x1D6FF}_{r}$
. Increment
 $i$
by one. Note that after this step all distinguished rays in the support of
$i$
by one. Note that after this step all distinguished rays in the support of
 $\unicode[STIX]{x1D713}_{i}$
have coefficient one. Also, the transformation rule asserts that
$\unicode[STIX]{x1D713}_{i}$
have coefficient one. Also, the transformation rule asserts that
 $\unicode[STIX]{x1D6FD}_{i}(\unicode[STIX]{x1D713}_{i})=\unicode[STIX]{x1D6FD}_{i-1}(\unicode[STIX]{x1D713}_{i-1})$
.
$\unicode[STIX]{x1D6FD}_{i}(\unicode[STIX]{x1D713}_{i})=\unicode[STIX]{x1D6FD}_{i-1}(\unicode[STIX]{x1D713}_{i-1})$
. - A4.
-
[Perform a stacky star subdivision.] Let
 $\unicode[STIX]{x1D70E}_{i}$
be the cone generated by the support of
$\unicode[STIX]{x1D70E}_{i}$
be the cone generated by the support of
 $\unicode[STIX]{x1D713}_{i}$
. Let
$\unicode[STIX]{x1D713}_{i}$
. Let
 $\boldsymbol{\unicode[STIX]{x1D6F4}}_{i+1}\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
be the stacky star subdivision
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{i+1}\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
be the stacky star subdivision
 $\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}(\unicode[STIX]{x1D70E}_{i})\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
and denote the exceptional ray by
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}(\unicode[STIX]{x1D70E}_{i})\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
and denote the exceptional ray by
 $\unicode[STIX]{x1D700}_{i+1}$
. Furthermore, let
$\unicode[STIX]{x1D700}_{i+1}$
. Furthermore, let
 $\unicode[STIX]{x1D713}_{i+1}=\unicode[STIX]{x1D713}_{i}-\sum _{\unicode[STIX]{x1D70C}\in \unicode[STIX]{x1D70E}_{i}(1)}\unicode[STIX]{x1D70C}+\unicode[STIX]{x1D700}_{i+1}$
and then increment
$\unicode[STIX]{x1D713}_{i+1}=\unicode[STIX]{x1D713}_{i}-\sum _{\unicode[STIX]{x1D70C}\in \unicode[STIX]{x1D70E}_{i}(1)}\unicode[STIX]{x1D70C}+\unicode[STIX]{x1D700}_{i+1}$
and then increment
 $i$
by 1. Note that after this step the support of
$i$
by 1. Note that after this step the support of
 $\unicode[STIX]{x1D713}_{i}$
contains just one distinguished ray
$\unicode[STIX]{x1D713}_{i}$
contains just one distinguished ray
 $\unicode[STIX]{x1D700}_{i}$
, which occurs with coefficient one. Also, the transformation rule asserts that
$\unicode[STIX]{x1D700}_{i}$
, which occurs with coefficient one. Also, the transformation rule asserts that
 $\unicode[STIX]{x1D6FD}_{i}(\unicode[STIX]{x1D713}_{i})=\unicode[STIX]{x1D6FD}_{i-1}(\unicode[STIX]{x1D713}_{i-1})$
.
$\unicode[STIX]{x1D6FD}_{i}(\unicode[STIX]{x1D713}_{i})=\unicode[STIX]{x1D6FD}_{i-1}(\unicode[STIX]{x1D713}_{i-1})$
. - A5.
-
[Iterate inner loop.] While the support of
 $\unicode[STIX]{x1D713}_{i}$
contains more than one ray, repeat from Step A4.
$\unicode[STIX]{x1D713}_{i}$
contains more than one ray, repeat from Step A4. - A6.
-
[Iterate main loop.] Repeat from Step A1.
Proof of correctness of Algorithm A.
Functoriality is clear, since all choices in the algorithm depend only on properties preserved by isomorphisms.
If
![]() $\unicode[STIX]{x1D70E}$
is a cone containing a distinguished, non-independent ray
$\unicode[STIX]{x1D70E}$
is a cone containing a distinguished, non-independent ray
![]() $\unicode[STIX]{x1D6FF}$
, then there is a face
$\unicode[STIX]{x1D6FF}$
, then there is a face
![]() $\unicode[STIX]{x1D70E}^{\prime }$
of
$\unicode[STIX]{x1D70E}^{\prime }$
of
![]() $\unicode[STIX]{x1D70E}$
containing
$\unicode[STIX]{x1D70E}$
containing
![]() $\unicode[STIX]{x1D6FF}$
with
$\unicode[STIX]{x1D6FF}$
with
![]() $P_{\unicode[STIX]{x1D70E}^{\prime }}$
containing a lattice point in its relative interior. Hence, the algorithm does not halt prematurely.
$P_{\unicode[STIX]{x1D70E}^{\prime }}$
containing a lattice point in its relative interior. Hence, the algorithm does not halt prematurely.
It remains to prove that the algorithm halts. For notational convenience, we assume, without loss of generality, that
![]() $i=0$
at the beginning of an iteration of the main loop and
$i=0$
at the beginning of an iteration of the main loop and
![]() $i=n$
when the iteration ends.
$i=n$
when the iteration ends.
Denote the cone generated by the support of
![]() $\unicode[STIX]{x1D713}_{0}$
by
$\unicode[STIX]{x1D713}_{0}$
by
![]() $\unicode[STIX]{x1D70E}_{0}$
, and let
$\unicode[STIX]{x1D70E}_{0}$
, and let
![]() $\unicode[STIX]{x1D70F}_{0}$
be any cone in
$\unicode[STIX]{x1D70F}_{0}$
be any cone in
![]() $\boldsymbol{\unicode[STIX]{x1D6F4}}_{0}$
of maximal dimension containing
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{0}$
of maximal dimension containing
![]() $\unicode[STIX]{x1D70E}_{0}$
. Using the notation in Step A3, we have
$\unicode[STIX]{x1D70E}_{0}$
. Using the notation in Step A3, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{0}=\text{Cone}\,(\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{s},\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{r},\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{t})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{0}=\text{Cone}\,(\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{s},\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{r},\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{t})\end{eqnarray}$$
for some rays
 $\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{t}$
. By maximality of
$\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{t}$
. By maximality of
![]() $\unicode[STIX]{x1D70E}_{0}$
with respect to the ordering defined in Step A1, we have
$\unicode[STIX]{x1D70E}_{0}$
with respect to the ordering defined in Step A1, we have
 $\text{mult}\,(\unicode[STIX]{x1D70F}_{0})=\text{mult}\,(\unicode[STIX]{x1D70E}_{0})$
. Define
$\text{mult}\,(\unicode[STIX]{x1D70F}_{0})=\text{mult}\,(\unicode[STIX]{x1D70E}_{0})$
. Define
![]() $\unicode[STIX]{x1D70F}_{i+1}$
recursively as any choice of cone of maximal dimension in the subdivision of
$\unicode[STIX]{x1D70F}_{i+1}$
recursively as any choice of cone of maximal dimension in the subdivision of
![]() $\unicode[STIX]{x1D70F}_{i}$
such that
$\unicode[STIX]{x1D70F}_{i}$
such that
![]() $\unicode[STIX]{x1D70F}_{i+1}$
has the same number of non-distinguished rays as
$\unicode[STIX]{x1D70F}_{i+1}$
has the same number of non-distinguished rays as
![]() $\unicode[STIX]{x1D70F}_{i}$
. For
$\unicode[STIX]{x1D70F}_{i}$
. For
![]() $i\geqslant 2$
, we have
$i\geqslant 2$
, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{i}=\text{Cone}\,(\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{s},\unicode[STIX]{x1D6FF}_{1},\ldots ,\widehat{\unicode[STIX]{x1D6FF}}_{k},\ldots ,\unicode[STIX]{x1D6FF}_{r},\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{t},\unicode[STIX]{x1D700}_{i}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{i}=\text{Cone}\,(\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{s},\unicode[STIX]{x1D6FF}_{1},\ldots ,\widehat{\unicode[STIX]{x1D6FF}}_{k},\ldots ,\unicode[STIX]{x1D6FF}_{r},\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{t},\unicode[STIX]{x1D700}_{i}),\end{eqnarray}$$
where
![]() $\widehat{\unicode[STIX]{x1D6FF}}_{k}$
indicates that the ray
$\widehat{\unicode[STIX]{x1D6FF}}_{k}$
indicates that the ray
![]() $\unicode[STIX]{x1D6FF}_{k}$
should be omitted from the list for some
$\unicode[STIX]{x1D6FF}_{k}$
should be omitted from the list for some
![]() $k$
with
$k$
with
 $1\leqslant k\leqslant r$
.
$1\leqslant k\leqslant r$
.
The transformation rule for the elements
![]() $\unicode[STIX]{x1D713}_{i}$
asserts that
$\unicode[STIX]{x1D713}_{i}$
asserts that
 $\unicode[STIX]{x1D6FD}_{i+1}(\unicode[STIX]{x1D713}_{i+1})=\unicode[STIX]{x1D6FD}_{i}(\unicode[STIX]{x1D713}_{i})$
throughout a whole iteration of the main loop. In particular, we have
$\unicode[STIX]{x1D6FD}_{i+1}(\unicode[STIX]{x1D713}_{i+1})=\unicode[STIX]{x1D6FD}_{i}(\unicode[STIX]{x1D713}_{i})$
throughout a whole iteration of the main loop. In particular, we have
 $\unicode[STIX]{x1D6FD}_{n}(\unicode[STIX]{x1D713}_{n})=\unicode[STIX]{x1D6FD}_{n}(\unicode[STIX]{x1D700}_{n})=\unicode[STIX]{x1D6FD}_{0}(\unicode[STIX]{x1D713}_{0})$
. But the ray through
$\unicode[STIX]{x1D6FD}_{n}(\unicode[STIX]{x1D713}_{n})=\unicode[STIX]{x1D6FD}_{n}(\unicode[STIX]{x1D700}_{n})=\unicode[STIX]{x1D6FD}_{0}(\unicode[STIX]{x1D713}_{0})$
. But the ray through
![]() $\unicode[STIX]{x1D6FD}_{0}(\unicode[STIX]{x1D713}_{0})$
passes through a lattice point in
$\unicode[STIX]{x1D6FD}_{0}(\unicode[STIX]{x1D713}_{0})$
passes through a lattice point in
 $P_{\unicode[STIX]{x1D70E}_{0}}\subset P_{\unicode[STIX]{x1D70F}_{0}}$
by choice of
$P_{\unicode[STIX]{x1D70E}_{0}}\subset P_{\unicode[STIX]{x1D70F}_{0}}$
by choice of
![]() $\unicode[STIX]{x1D713}_{0}$
. For the same reason as for the traditional algorithm for toric varieties, it follows that the multiplicity of
$\unicode[STIX]{x1D713}_{0}$
. For the same reason as for the traditional algorithm for toric varieties, it follows that the multiplicity of
![]() $\unicode[STIX]{x1D70F}_{n}$
is strictly smaller than
$\unicode[STIX]{x1D70F}_{n}$
is strictly smaller than
![]() $\text{mult}\,\unicode[STIX]{x1D70F}_{0}$
. Since any cone produced in the iteration of the main loop is either a face of
$\text{mult}\,\unicode[STIX]{x1D70F}_{0}$
. Since any cone produced in the iteration of the main loop is either a face of
![]() $\unicode[STIX]{x1D70F}_{n}$
for some choice of sequence
$\unicode[STIX]{x1D70F}_{n}$
for some choice of sequence
 $\unicode[STIX]{x1D70F}_{0},\ldots ,\unicode[STIX]{x1D70F}_{n}$
or has fewer non-distinguished rays, it follows that all new cones are smaller than
$\unicode[STIX]{x1D70F}_{0},\ldots ,\unicode[STIX]{x1D70F}_{n}$
or has fewer non-distinguished rays, it follows that all new cones are smaller than
![]() $\unicode[STIX]{x1D70E}_{0}$
with respect to the ordering defined in Step A2. Since
$\unicode[STIX]{x1D70E}_{0}$
with respect to the ordering defined in Step A2. Since
![]() $\unicode[STIX]{x1D70E}_{0}$
has been removed, this process cannot continue indefinitely, and the algorithm eventually stops.◻
$\unicode[STIX]{x1D70E}_{0}$
has been removed, this process cannot continue indefinitely, and the algorithm eventually stops.◻
The inner workings of Algorithm A are best understood by considering some examples.
Example 4.6. We given an explicit example of the formal sum
![]() $\unicode[STIX]{x1D713}_{i}$
associated to a cone
$\unicode[STIX]{x1D713}_{i}$
associated to a cone
![]() $\unicode[STIX]{x1D70E}_{i}$
as described in A2. For notational convenience, we assume that
$\unicode[STIX]{x1D70E}_{i}$
as described in A2. For notational convenience, we assume that
![]() $i=0$
. Assume that
$i=0$
. Assume that
![]() $\unicode[STIX]{x1D70E}_{0}$
is a cone spanned by the three rays
$\unicode[STIX]{x1D70E}_{0}$
is a cone spanned by the three rays
 $\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D70C}_{3}$
and that the marked lattice points on the rays are given by
$\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D70C}_{3}$
and that the marked lattice points on the rays are given by
 $$\begin{eqnarray}\unicode[STIX]{x1D6FD}_{0}(\unicode[STIX]{x1D70C}_{1})=(6,3,3),\quad \unicode[STIX]{x1D6FD}_{0}(\unicode[STIX]{x1D70C}_{2})=(0,2,1),\quad \unicode[STIX]{x1D6FD}_{0}(\unicode[STIX]{x1D70C}_{3})=(0,0,1).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}_{0}(\unicode[STIX]{x1D70C}_{1})=(6,3,3),\quad \unicode[STIX]{x1D6FD}_{0}(\unicode[STIX]{x1D70C}_{2})=(0,2,1),\quad \unicode[STIX]{x1D6FD}_{0}(\unicode[STIX]{x1D70C}_{3})=(0,0,1).\end{eqnarray}$$
Then the non-zero lattice points on the rays in
![]() $\unicode[STIX]{x1D70E}_{0}(1)$
closest to the origin are given by
$\unicode[STIX]{x1D70E}_{0}(1)$
closest to the origin are given by
 $$\begin{eqnarray}u_{1}=(2,1,1),\quad u_{2}=(0,2,1),\quad u_{3}=(0,0,1)\end{eqnarray}$$
$$\begin{eqnarray}u_{1}=(2,1,1),\quad u_{2}=(0,2,1),\quad u_{3}=(0,0,1)\end{eqnarray}$$
and we see that the multiplicity of
![]() $\unicode[STIX]{x1D70E}_{0}$
equals
$\unicode[STIX]{x1D70E}_{0}$
equals
 $|\!\det (u_{1},u_{2},u_{3})|=4$
. Hence, the parallelotope
$|\!\det (u_{1},u_{2},u_{3})|=4$
. Hence, the parallelotope
![]() $P_{\unicode[STIX]{x1D70E}_{0}}$
contains three non-trivial lattice points. It is easily verified that these are given by
$P_{\unicode[STIX]{x1D70E}_{0}}$
contains three non-trivial lattice points. It is easily verified that these are given by
 $$\begin{eqnarray}v_{1}=(1,2,2),\quad v_{2}=(0,1,1),\quad v_{3}=(1,1,1).\end{eqnarray}$$
$$\begin{eqnarray}v_{1}=(1,2,2),\quad v_{2}=(0,1,1),\quad v_{3}=(1,1,1).\end{eqnarray}$$
Note that only
![]() $v_{1}$
and
$v_{1}$
and
![]() $v_{3}$
lie in the relative interior of
$v_{3}$
lie in the relative interior of
![]() $P_{\unicode[STIX]{x1D70E}_{0}}$
. These points can also be expressed as
$P_{\unicode[STIX]{x1D70E}_{0}}$
. These points can also be expressed as
 $$\begin{eqnarray}v_{1}={\textstyle \frac{1}{12}}\unicode[STIX]{x1D6FD}_{0}(2\unicode[STIX]{x1D70C}_{1}+9\unicode[STIX]{x1D70C}_{2}+9\unicode[STIX]{x1D70C}_{3}),\quad v_{3}={\textstyle \frac{1}{12}}\unicode[STIX]{x1D6FD}_{0}(2\unicode[STIX]{x1D70C}_{1}+3\unicode[STIX]{x1D70C}_{2}+3\unicode[STIX]{x1D70C}_{3}).\end{eqnarray}$$
$$\begin{eqnarray}v_{1}={\textstyle \frac{1}{12}}\unicode[STIX]{x1D6FD}_{0}(2\unicode[STIX]{x1D70C}_{1}+9\unicode[STIX]{x1D70C}_{2}+9\unicode[STIX]{x1D70C}_{3}),\quad v_{3}={\textstyle \frac{1}{12}}\unicode[STIX]{x1D6FD}_{0}(2\unicode[STIX]{x1D70C}_{1}+3\unicode[STIX]{x1D70C}_{2}+3\unicode[STIX]{x1D70C}_{3}).\end{eqnarray}$$
Hence,
 $\unicode[STIX]{x1D713}_{0}=2\unicode[STIX]{x1D70C}_{1}+3\unicode[STIX]{x1D70C}_{2}+3\unicode[STIX]{x1D70C}_{3}$
since this expression is smaller than
$\unicode[STIX]{x1D713}_{0}=2\unicode[STIX]{x1D70C}_{1}+3\unicode[STIX]{x1D70C}_{2}+3\unicode[STIX]{x1D70C}_{3}$
since this expression is smaller than
 $2\unicode[STIX]{x1D70C}_{1}+9\unicode[STIX]{x1D70C}_{2}+9\unicode[STIX]{x1D70C}_{3}$
lexicographically.
$2\unicode[STIX]{x1D70C}_{1}+9\unicode[STIX]{x1D70C}_{2}+9\unicode[STIX]{x1D70C}_{3}$
lexicographically.

Figure 4.2. Examples of the subdivision procedure from Algorithm A in the three different cases described in Example 4.7. In each case only the intersection of the respective fan with the plane through the points
 $\unicode[STIX]{x1D6FD}_{0}(\unicode[STIX]{x1D70E}_{0}(1))$
is shown, and the resulting intersection is affinely transformed such that the cone
$\unicode[STIX]{x1D6FD}_{0}(\unicode[STIX]{x1D70E}_{0}(1))$
is shown, and the resulting intersection is affinely transformed such that the cone
![]() $\unicode[STIX]{x1D70E}_{0}$
is pictured as an equilateral triangle. The maximal cones which are guaranteed to have lower multiplicity than
$\unicode[STIX]{x1D70E}_{0}$
is pictured as an equilateral triangle. The maximal cones which are guaranteed to have lower multiplicity than
![]() $\unicode[STIX]{x1D70E}_{0}$
are shaded and the distinguished rays are marked by black dots.
$\unicode[STIX]{x1D70E}_{0}$
are shaded and the distinguished rays are marked by black dots.
Example 4.7. We continue the previous example by tracing what happens when executing the Steps A3 through A5 of Algorithm A. The results depend on which rays in
![]() $\unicode[STIX]{x1D70E}_{0}$
are distinguished, and we consider three different cases. In the first case all rays are distinguished and we let
$\unicode[STIX]{x1D70E}_{0}$
are distinguished, and we consider three different cases. In the first case all rays are distinguished and we let
 $\unicode[STIX]{x1D6FF}_{1}=\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D6FF}_{2}=\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D6FF}_{3}=\unicode[STIX]{x1D70C}_{3}$
. In the second case the rays
$\unicode[STIX]{x1D6FF}_{1}=\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D6FF}_{2}=\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D6FF}_{3}=\unicode[STIX]{x1D70C}_{3}$
. In the second case the rays
 $\unicode[STIX]{x1D6FF}_{1}=\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D6FF}_{2}=\unicode[STIX]{x1D70C}_{3}$
are distinguished. In the third case only the ray
$\unicode[STIX]{x1D6FF}_{1}=\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D6FF}_{2}=\unicode[STIX]{x1D70C}_{3}$
are distinguished. In the third case only the ray
![]() $\unicode[STIX]{x1D6FF}_{1}=\unicode[STIX]{x1D70C}_{3}$
is distinguished. Table 4.1 shows how the formal sum
$\unicode[STIX]{x1D6FF}_{1}=\unicode[STIX]{x1D70C}_{3}$
is distinguished. Table 4.1 shows how the formal sum
![]() $\unicode[STIX]{x1D713}_{i}$
changes with
$\unicode[STIX]{x1D713}_{i}$
changes with
![]() $i$
.
$i$
.
Table 4.1. The formal sum
![]() $\unicode[STIX]{x1D713}_{i}$
for the three examples described in Example 4.7.
$\unicode[STIX]{x1D713}_{i}$
for the three examples described in Example 4.7.

The resulting fans are illustrated in Figure 4.2. The key things to note about these fans are the following.
-
(i) Since the lattice point
 $\unicode[STIX]{x1D6FD}_{i}(\unicode[STIX]{x1D713}_{i})$
is independent of
$\unicode[STIX]{x1D6FD}_{i}(\unicode[STIX]{x1D713}_{i})$
is independent of
 $i$
during the execution of the Steps A3 through A5, the ray
$i$
during the execution of the Steps A3 through A5, the ray
 $\unicode[STIX]{x1D700}:=\unicode[STIX]{x1D700}_{i}$
is the same in all three cases when the inner loop terminates. Note also that
$\unicode[STIX]{x1D700}:=\unicode[STIX]{x1D700}_{i}$
is the same in all three cases when the inner loop terminates. Note also that
 $\unicode[STIX]{x1D700}$
passes through
$\unicode[STIX]{x1D700}$
passes through
 $v_{3}$
, which lies in the parallelotope
$v_{3}$
, which lies in the parallelotope
 $P_{\unicode[STIX]{x1D70E}_{0}}$
as explained in Example 4.6. Hence, any cone containing
$P_{\unicode[STIX]{x1D70E}_{0}}$
as explained in Example 4.6. Hence, any cone containing
 $\unicode[STIX]{x1D700}$
and two of the rays in
$\unicode[STIX]{x1D700}$
and two of the rays in
 $\unicode[STIX]{x1D70E}_{0}(1)$
must have strictly lower multiplicity than
$\unicode[STIX]{x1D70E}_{0}(1)$
must have strictly lower multiplicity than
 $\unicode[STIX]{x1D70E}_{0}$
. These cones are shaded in Figure 4.2.
$\unicode[STIX]{x1D70E}_{0}$
. These cones are shaded in Figure 4.2. -
(ii) For the other maximal cones in the subdivision we have no control over the multiplicity, which might well be higher than what we started with. However, each of these cones has fewer non-distinguished rays. The distinguished rays are marked by black dots in Figure 4.2.
This shows that all maximal cones in the subdivision are smaller than the cone
![]() $\unicode[STIX]{x1D70E}_{0}$
with respect to the ordering introduced in Step A1. Hence, we do get an improvement towards destackification.
$\unicode[STIX]{x1D70E}_{0}$
with respect to the ordering introduced in Step A1. Hence, we do get an improvement towards destackification.
We conclude the section by describing the functorial toric destackification algorithm. We leave the (easy) proof of correctness to the reader, since the algorithm is a special case of the more general Algorithm E.
Algorithm B (Functorial toric destackification).
The input of the algorithm is an orbifold fan
![]() $\boldsymbol{\unicode[STIX]{x1D6F4}}_{0}$
together with a total ordering on the set
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{0}$
together with a total ordering on the set
![]() $\boldsymbol{\unicode[STIX]{x1D6F4}}_{0}(1)$
of rays. The output is a sequence
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{0}(1)$
of rays. The output is a sequence
 $$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D6F4}}_{n}\rightarrow \cdots \rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}_{0}\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D6F4}}_{n}\rightarrow \cdots \rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}_{0}\end{eqnarray}$$
of stacky modifications such that all rays in
![]() $\boldsymbol{\unicode[STIX]{x1D6F4}}_{n}(1)$
are independent. In particular, all cones in
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{n}(1)$
are independent. In particular, all cones in
![]() $\boldsymbol{\unicode[STIX]{x1D6F4}}_{n}$
are smooth. The construction is functorial in the obvious sense with respect to isomorphisms
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{n}$
are smooth. The construction is functorial in the obvious sense with respect to isomorphisms
 $\boldsymbol{\unicode[STIX]{x1D6F4}}_{0}^{\prime }\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}_{0}$
preserving the ordering of the rays and subfans
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{0}^{\prime }\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}_{0}$
preserving the ordering of the rays and subfans
 $\boldsymbol{\unicode[STIX]{x1D6F4}}_{0}^{\prime \prime }\subseteq \boldsymbol{\unicode[STIX]{x1D6F4}}_{0}$
.
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{0}^{\prime \prime }\subseteq \boldsymbol{\unicode[STIX]{x1D6F4}}_{0}$
.
- B0.
-
[Initialise.] Set
 $i=0$
.
$i=0$
. - B1.
-
[Choose a cone.] Consider the set
 ${\mathcal{S}}$
of cones
${\mathcal{S}}$
of cones
 $\unicode[STIX]{x1D70E}$
in
$\unicode[STIX]{x1D70E}$
in
 $\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
with the property that none of the rays in
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
with the property that none of the rays in
 $\unicode[STIX]{x1D70E}(1)$
are independent at
$\unicode[STIX]{x1D70E}(1)$
are independent at
 $\unicode[STIX]{x1D70E}$
. If this set is empty, then all rays in
$\unicode[STIX]{x1D70E}$
. If this set is empty, then all rays in
 $\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
are independent and the algorithm terminates. Choose a cone
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
are independent and the algorithm terminates. Choose a cone
 $\unicode[STIX]{x1D70E}\in {\mathcal{S}}$
of maximal dimension. If several such cones exist, choose the largest one with respect to the natural ordering on the cones in
$\unicode[STIX]{x1D70E}\in {\mathcal{S}}$
of maximal dimension. If several such cones exist, choose the largest one with respect to the natural ordering on the cones in
 $\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
.
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
. - B2.
-
[Create distinguished ray.] Let
 $\boldsymbol{\unicode[STIX]{x1D6F4}}_{i+1}\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
be the star subdivision of
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{i+1}\rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
be the star subdivision of
 $\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
in
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
in
 $\unicode[STIX]{x1D70E}$
. Give
$\unicode[STIX]{x1D70E}$
. Give
 $\boldsymbol{\unicode[STIX]{x1D6F4}}_{i+1}$
a distinguished structure by letting the exceptional ray from the subdivision be the only distinguished ray. Increment
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{i+1}$
a distinguished structure by letting the exceptional ray from the subdivision be the only distinguished ray. Increment
 $i$
by one.
$i$
by one. - B3.
-
[Resolve the cone.] Invoke Algorithm A and append the output to the sequence. Increment
 $i$
by the length of this output.
$i$
by the length of this output. - B4.
-
[Iterate.] Forget the distinguished structure, and iterate from Step B1.
5 Local homogeneous coordinates
In § 3, we introduced basic toric stacks. Here we will show that every smooth tame stack with diagonalisable stabilisers is locally of this form in a certain sense. This will allow us to use local homogeneous coordinates even for non-toric stacks, which in turn will allow us to generalise the toric destackification algorithm. We start by making a precise definition of what we mean by a stack being locally toric.
Definition 5.1. Let
![]() $X$
be an algebraic stack which is smooth over a scheme
$X$
be an algebraic stack which is smooth over a scheme
![]() $S$
, and let
$S$
, and let
![]() $\unicode[STIX]{x1D709}\in X$
be a point. By a toric chart of
$\unicode[STIX]{x1D709}\in X$
be a point. By a toric chart of
![]() $X$
over
$X$
over
![]() $S$
at
$S$
at
![]() $\unicode[STIX]{x1D709}$
, we mean a diagram
$\unicode[STIX]{x1D709}$
, we mean a diagram

of algebraic stacks over
![]() $S$
, together with a point
$S$
, together with a point
![]() $\unicode[STIX]{x1D709}^{\prime }\in X^{\prime }$
. The data are required to satisfy the following properties.
$\unicode[STIX]{x1D709}^{\prime }\in X^{\prime }$
. The data are required to satisfy the following properties.
-
(i) The stack
 $X^{\prime \prime }$
is a basic toric stack over
$X^{\prime \prime }$
is a basic toric stack over
 $S$
.
$S$
. -
(ii) The point
 $\unicode[STIX]{x1D709}^{\prime }$
maps to
$\unicode[STIX]{x1D709}^{\prime }$
maps to
 $\unicode[STIX]{x1D709}$
in
$\unicode[STIX]{x1D709}$
in
 $X$
and to a point
$X$
and to a point
 $\unicode[STIX]{x1D709}^{\prime \prime }\in X^{\prime \prime }$
lying in the intersection of the prime toric divisors of
$\unicode[STIX]{x1D709}^{\prime \prime }\in X^{\prime \prime }$
lying in the intersection of the prime toric divisors of
 $X^{\prime \prime }$
.
$X^{\prime \prime }$
. -
(iii) The maps
 $f$
and
$f$
and
 $g$
are étale and stabiliser-preserving.
$g$
are étale and stabiliser-preserving.
A homogeneous coordinate ring of
![]() $X^{\prime \prime }$
is called a local homogeneous coordinate ring at
$X^{\prime \prime }$
is called a local homogeneous coordinate ring at
![]() $\unicode[STIX]{x1D709}$
. Assume that
$\unicode[STIX]{x1D709}$
. Assume that
![]() $E$
is a simple normal crossings divisor on
$E$
is a simple normal crossings divisor on
![]() $X$
and that
$X$
and that
![]() $Z$
is a closed substack of
$Z$
is a closed substack of
![]() $X$
having simple normal crossings with
$X$
having simple normal crossings with
![]() $E$
. Then we say that
$E$
. Then we say that
![]() $E$
and
$E$
and
![]() $Z$
are compatible with the toric chart if the pull-back of
$Z$
are compatible with the toric chart if the pull-back of
![]() $E$
to
$E$
to
![]() $X^{\prime }$
coincides with the pull-back of a toric divisor on
$X^{\prime }$
coincides with the pull-back of a toric divisor on
![]() $X^{\prime \prime }$
, and the pull-back of
$X^{\prime \prime }$
, and the pull-back of
![]() $Z$
to
$Z$
to
![]() $X^{\prime }$
coincides with the pull-back of an intersection of prime toric divisors on
$X^{\prime }$
coincides with the pull-back of an intersection of prime toric divisors on
![]() $X^{\prime \prime }$
.
$X^{\prime \prime }$
.
To prove that a smooth tame stack with diagonalisable stabilisers has a toric chart at every point, we need a version of the structure theorem for tame algebraic stacks which takes smoothness into account. We give such a theorem in Appendix A. We will also need the following lemma.
Lemma 5.2. Let
 $X=\text{Spec}\,A$
be an affine scheme over an affine base scheme
$X=\text{Spec}\,A$
be an affine scheme over an affine base scheme
![]() $S$
, and let
$S$
, and let
![]() $G$
be a finite, linearly reductive, locally free group scheme over
$G$
be a finite, linearly reductive, locally free group scheme over
![]() $S$
acting on
$S$
acting on
![]() $X$
. Let
$X$
. Let
![]() $\unicode[STIX]{x1D709}\in X$
be a point, and let
$\unicode[STIX]{x1D709}\in X$
be a point, and let
![]() $D(f)$
be a distinguished open subscheme of
$D(f)$
be a distinguished open subscheme of
![]() $X$
containing the orbit of
$X$
containing the orbit of
![]() $\unicode[STIX]{x1D709}$
. Then there is a refinement
$\unicode[STIX]{x1D709}$
. Then there is a refinement
 $\unicode[STIX]{x1D709}\in D(g)\subset D(f)$
such that
$\unicode[STIX]{x1D709}\in D(g)\subset D(f)$
such that
![]() $g$
is an invariant section which is a multiple of
$g$
is an invariant section which is a multiple of
![]() $f$
.
$f$
.
Proof. Let
 $\unicode[STIX]{x1D70B}:X\rightarrow X/G=\text{Spec}\,A_{0}$
be the coarse quotient, where
$\unicode[STIX]{x1D70B}:X\rightarrow X/G=\text{Spec}\,A_{0}$
be the coarse quotient, where
![]() $A_{0}\subset A$
is the ring of invariant sections. The map
$A_{0}\subset A$
is the ring of invariant sections. The map
![]() $\unicode[STIX]{x1D70B}$
is integral and therefore closed. The set
$\unicode[STIX]{x1D70B}$
is integral and therefore closed. The set
 $\unicode[STIX]{x1D70B}(V(f))$
does not contain
$\unicode[STIX]{x1D70B}(V(f))$
does not contain
![]() $\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709})$
, by the assumption that the orbit of
$\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709})$
, by the assumption that the orbit of
![]() $\unicode[STIX]{x1D709}$
is contained in
$\unicode[STIX]{x1D709}$
is contained in
![]() $D(f)$
. Let
$D(f)$
. Let
![]() $D(h)$
, with
$D(h)$
, with
![]() $h\in A_{0}$
, be a distinguished open neighbourhood of
$h\in A_{0}$
, be a distinguished open neighbourhood of
![]() $\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709})$
in the complement of
$\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709})$
in the complement of
 $\unicode[STIX]{x1D70B}(V(f))$
in
$\unicode[STIX]{x1D70B}(V(f))$
in
![]() $X/G$
. This pulls back to an open subset, also denoted by
$X/G$
. This pulls back to an open subset, also denoted by
![]() $D(h)$
, satisfying
$D(h)$
, satisfying
 $\unicode[STIX]{x1D709}\in D(h)\subset D(f)$
. The condition
$\unicode[STIX]{x1D709}\in D(h)\subset D(f)$
. The condition
 $D(h)\subset D(f)$
implies that
$D(h)\subset D(f)$
implies that
 $\text{rad}\,(h)\subset \text{rad}\,(f)$
. Hence, there is a power
$\text{rad}\,(h)\subset \text{rad}\,(f)$
. Hence, there is a power
![]() $g=h^{n}$
of
$g=h^{n}$
of
![]() $h$
which is a multiple of
$h$
which is a multiple of
![]() $f$
.◻
$f$
.◻
Now we are ready for the main result of this section.
Proposition 5.3. Let
![]() $X$
be an algebraic stack with finite inertia and diagonalisable geometric stabilisers. Assume that
$X$
be an algebraic stack with finite inertia and diagonalisable geometric stabilisers. Assume that
![]() $X$
is smooth and quasi-separated over a scheme
$X$
is smooth and quasi-separated over a scheme
![]() $S$
. Then
$S$
. Then
![]() $X$
admits toric charts over
$X$
admits toric charts over
![]() $S$
at each of its points. Furthermore, if
$S$
at each of its points. Furthermore, if
![]() $E$
is a simple normal crossings divisor on
$E$
is a simple normal crossings divisor on
![]() $X$
, and
$X$
, and
![]() $Z$
is a closed substack of
$Z$
is a closed substack of
![]() $X$
having simple normal crossings with
$X$
having simple normal crossings with
![]() $E$
, then the toric charts may be chosen such that they are compatible with
$E$
, then the toric charts may be chosen such that they are compatible with
![]() $E$
and
$E$
and
![]() $Z$
.
$Z$
.
Proof. The question is local on
![]() $X$
with respect to stabiliser-preserving étale morphisms. Thus, by Propositions A.8 and A.9, we may assume that
$X$
with respect to stabiliser-preserving étale morphisms. Thus, by Propositions A.8 and A.9, we may assume that
![]() $X$
is of the form
$X$
is of the form
![]() $[U/\unicode[STIX]{x1D6E5}]$
, where
$[U/\unicode[STIX]{x1D6E5}]$
, where
![]() $U$
is an affine scheme which is smooth over
$U$
is an affine scheme which is smooth over
![]() $S$
and
$S$
and
![]() $\unicode[STIX]{x1D6E5}$
is a diagonalisable group acting on
$\unicode[STIX]{x1D6E5}$
is a diagonalisable group acting on
![]() $U$
. Furthermore, we may assume that
$U$
. Furthermore, we may assume that
![]() $\unicode[STIX]{x1D709}$
lifts to a point
$\unicode[STIX]{x1D709}$
lifts to a point
![]() $\unicode[STIX]{x1D709}^{\prime }\in U$
which is fixed under the
$\unicode[STIX]{x1D709}^{\prime }\in U$
which is fixed under the
![]() $\unicode[STIX]{x1D6E5}$
-action.
$\unicode[STIX]{x1D6E5}$
-action.
The
![]() $\unicode[STIX]{x1D6E5}$
-action corresponds to a grading on
$\unicode[STIX]{x1D6E5}$
-action corresponds to a grading on
![]() ${\mathcal{O}}_{U}$
by the character group
${\mathcal{O}}_{U}$
by the character group
![]() $\unicode[STIX]{x1D6E5}^{\vee }$
, which is a finite abelian group. Choose homogeneous global sections
$\unicode[STIX]{x1D6E5}^{\vee }$
, which is a finite abelian group. Choose homogeneous global sections
 $f_{1},\ldots ,f_{n}$
of
$f_{1},\ldots ,f_{n}$
of
![]() ${\mathcal{O}}_{U}$
such that the differentials
${\mathcal{O}}_{U}$
such that the differentials
 $df_{1},\ldots ,df_{n}$
form a basis of
$df_{1},\ldots ,df_{n}$
form a basis of
 $\unicode[STIX]{x1D6FA}_{U/S}\otimes _{{\mathcal{O}}_{U}}\unicode[STIX]{x1D705}(\unicode[STIX]{x1D709}^{\prime })$
. Consider the map
$\unicode[STIX]{x1D6FA}_{U/S}\otimes _{{\mathcal{O}}_{U}}\unicode[STIX]{x1D705}(\unicode[STIX]{x1D709}^{\prime })$
. Consider the map
 ${\mathcal{O}}_{S}[x_{1},\ldots ,x_{n}]\rightarrow {\mathcal{O}}_{U}$
taking
${\mathcal{O}}_{S}[x_{1},\ldots ,x_{n}]\rightarrow {\mathcal{O}}_{U}$
taking
![]() $x_{i}$
to
$x_{i}$
to
![]() $f_{i}$
. We give the polynomial ring a
$f_{i}$
. We give the polynomial ring a
![]() $\unicode[STIX]{x1D6E5}^{\vee }$
-graded structure, by letting
$\unicode[STIX]{x1D6E5}^{\vee }$
-graded structure, by letting
![]() $x_{i}$
have the same degree as
$x_{i}$
have the same degree as
![]() $f_{i}$
. This gives an equivariant map
$f_{i}$
. This gives an equivariant map
 $\widehat{g}:U\rightarrow \mathbb{A}_{S}^{n}$
over
$\widehat{g}:U\rightarrow \mathbb{A}_{S}^{n}$
over
![]() $S$
. By construction, the canonical map
$S$
. By construction, the canonical map
 $$\begin{eqnarray}\unicode[STIX]{x1D6FA}_{\mathbb{A}_{S}^{n}/S}\otimes _{{\mathcal{O}}_{S}[x_{1},\ldots ,x_{n}]}\unicode[STIX]{x1D705}(\unicode[STIX]{x1D709}^{\prime })\rightarrow \unicode[STIX]{x1D6FA}_{U/S}\otimes _{{\mathcal{O}}_{U}}\unicode[STIX]{x1D705}(\unicode[STIX]{x1D709}^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FA}_{\mathbb{A}_{S}^{n}/S}\otimes _{{\mathcal{O}}_{S}[x_{1},\ldots ,x_{n}]}\unicode[STIX]{x1D705}(\unicode[STIX]{x1D709}^{\prime })\rightarrow \unicode[STIX]{x1D6FA}_{U/S}\otimes _{{\mathcal{O}}_{U}}\unicode[STIX]{x1D705}(\unicode[STIX]{x1D709}^{\prime })\end{eqnarray}$$
is an isomorphism. Since
![]() $U$
is smooth over
$U$
is smooth over
![]() $S$
, it follows that
$S$
, it follows that
![]() $\widehat{g}$
is étale at
$\widehat{g}$
is étale at
![]() $\unicode[STIX]{x1D709}^{\prime }$
by [Reference Dieudonné and GrothendieckEGAIV, Corollary 17.11.2]. Denote the corresponding map
$\unicode[STIX]{x1D709}^{\prime }$
by [Reference Dieudonné and GrothendieckEGAIV, Corollary 17.11.2]. Denote the corresponding map
 $[U/\unicode[STIX]{x1D6E5}]\rightarrow [\mathbb{A}_{S}^{n}/\unicode[STIX]{x1D6E5}]$
of stacks by
$[U/\unicode[STIX]{x1D6E5}]\rightarrow [\mathbb{A}_{S}^{n}/\unicode[STIX]{x1D6E5}]$
of stacks by
![]() $g$
. The map
$g$
. The map
![]() $g$
is representable, so the stabiliser of
$g$
is representable, so the stabiliser of
![]() $\unicode[STIX]{x1D709}$
injects into the stabiliser of
$\unicode[STIX]{x1D709}$
injects into the stabiliser of
![]() $g(\unicode[STIX]{x1D709})$
. Since
$g(\unicode[STIX]{x1D709})$
. Since
![]() $\unicode[STIX]{x1D709}^{\prime }$
is fixed by the action of
$\unicode[STIX]{x1D709}^{\prime }$
is fixed by the action of
![]() $\unicode[STIX]{x1D6E5}$
, the stabiliser at
$\unicode[STIX]{x1D6E5}$
, the stabiliser at
![]() $\unicode[STIX]{x1D709}$
is
$\unicode[STIX]{x1D709}$
is
![]() $\unicode[STIX]{x1D6E5}$
, so the map of stabilisers must be an isomorphism. Since the locus where
$\unicode[STIX]{x1D6E5}$
, so the map of stabilisers must be an isomorphism. Since the locus where
![]() $f$
is étale and stabiliser-preserving is open [Reference RydhRyd13, Proposition 6.5], we may as well assume that
$f$
is étale and stabiliser-preserving is open [Reference RydhRyd13, Proposition 6.5], we may as well assume that
 $[U/\unicode[STIX]{x1D6E5}]\rightarrow [\mathbb{A}_{S}^{n}/\unicode[STIX]{x1D6E5}]$
is étale and stabiliser-preserving, after shrinking
$[U/\unicode[STIX]{x1D6E5}]\rightarrow [\mathbb{A}_{S}^{n}/\unicode[STIX]{x1D6E5}]$
is étale and stabiliser-preserving, after shrinking
![]() $U$
invariantly by using Lemma 5.2 if necessary. Finally, we simply remove the prime toric divisors from
$U$
invariantly by using Lemma 5.2 if necessary. Finally, we simply remove the prime toric divisors from
![]() $[\mathbb{A}_{S}^{n}/\unicode[STIX]{x1D6E5}]$
which do not contain
$[\mathbb{A}_{S}^{n}/\unicode[STIX]{x1D6E5}]$
which do not contain
![]() $g(\unicode[STIX]{x1D709})$
.
$g(\unicode[STIX]{x1D709})$
.
Now we turn to the statement about the simple normal crossings divisors. Let
 $E_{1},\ldots ,E_{r}$
be the components of
$E_{1},\ldots ,E_{r}$
be the components of
![]() $E$
passing through
$E$
passing through
![]() $\unicode[STIX]{x1D709}$
. They correspond to locally principal homogeneous ideals
$\unicode[STIX]{x1D709}$
. They correspond to locally principal homogeneous ideals
![]() $I_{i}$
in
$I_{i}$
in
![]() ${\mathcal{O}}_{U}$
. Also, denote the homogeneous ideal corresponding to
${\mathcal{O}}_{U}$
. Also, denote the homogeneous ideal corresponding to
![]() $Z$
by
$Z$
by
![]() $I$
. Next we choose our sections
$I$
. Next we choose our sections
 $f_{1},\ldots ,f_{n}$
one by one in a way such that the differentials
$f_{1},\ldots ,f_{n}$
one by one in a way such that the differentials
![]() $df_{i}$
remain linearly independent in
$df_{i}$
remain linearly independent in
 $\unicode[STIX]{x1D6FA}_{U/S}\otimes _{{\mathcal{O}}_{U}}\unicode[STIX]{x1D705}(\unicode[STIX]{x1D709}^{\prime })$
. First we pick homogeneous
$\unicode[STIX]{x1D6FA}_{U/S}\otimes _{{\mathcal{O}}_{U}}\unicode[STIX]{x1D705}(\unicode[STIX]{x1D709}^{\prime })$
. First we pick homogeneous
![]() $f_{i}$
from
$f_{i}$
from
![]() $I_{i}$
for
$I_{i}$
for
 $1\leqslant i\leqslant r$
. Then we pick homogeneous
$1\leqslant i\leqslant r$
. Then we pick homogeneous
 $f_{r+1},\ldots ,f_{s}$
from
$f_{r+1},\ldots ,f_{s}$
from
![]() $I$
with
$I$
with
![]() $s$
as large as possible. Finally, we pick the remaining homogeneous sections from
$s$
as large as possible. Finally, we pick the remaining homogeneous sections from
![]() ${\mathcal{O}}_{U}$
. By the normal crossings assumption, we get compatibility in a neighbourhood of
${\mathcal{O}}_{U}$
. By the normal crossings assumption, we get compatibility in a neighbourhood of
![]() $\unicode[STIX]{x1D709}^{\prime }$
, which we may assume is
$\unicode[STIX]{x1D709}^{\prime }$
, which we may assume is
![]() $\unicode[STIX]{x1D6E5}$
-invariant by Lemma 5.2.◻
$\unicode[STIX]{x1D6E5}$
-invariant by Lemma 5.2.◻
6 Conormal invariants
In the last section, we established that any standard pair
![]() $(X,\boldsymbol{E})$
with diagonalisable stabilisers locally looks like a basic toric stack. This basic toric stack is described by a set of combinatorial parameters, which we will call the toric type. In principle, the toric type captures the information of the stacky fan describing the basic toric stack together with how the rays in this stacky fan correspond to the components of
$(X,\boldsymbol{E})$
with diagonalisable stabilisers locally looks like a basic toric stack. This basic toric stack is described by a set of combinatorial parameters, which we will call the toric type. In principle, the toric type captures the information of the stacky fan describing the basic toric stack together with how the rays in this stacky fan correspond to the components of
![]() $\boldsymbol{E}$
. As we will see, the toric type at a given point can be recovered in a coordinate-free manner.
$\boldsymbol{E}$
. As we will see, the toric type at a given point can be recovered in a coordinate-free manner.
In the destackification algorithms, several different invariants are used in order to determine appropriate loci to blow up. In this section, we develop a common framework for studying a class of invariants, which we will call conormal invariants. By definition, the value of a conormal invariant at a given point depends only on the toric type. Given a standard pair
![]() $(X,\boldsymbol{E})$
, a conormal invariant induces an upper semi-continuous function on the underlying topological space
$(X,\boldsymbol{E})$
, a conormal invariant induces an upper semi-continuous function on the underlying topological space
![]() $|X|$
taking values in some ordered set. Since we usually want to blow up the locus where the function obtains its maximum, we need to assert that this locus is smooth. We also need to assert invariance under base change and compositions with smooth, stabiliser-preserving morphisms and rigidifications in order to get the right functorial properties. We will establish simple combinatorial criteria for conormal invariants to satisfy these properties.
$|X|$
taking values in some ordered set. Since we usually want to blow up the locus where the function obtains its maximum, we need to assert that this locus is smooth. We also need to assert invariance under base change and compositions with smooth, stabiliser-preserving morphisms and rigidifications in order to get the right functorial properties. We will establish simple combinatorial criteria for conormal invariants to satisfy these properties.
Let
![]() $(X,\boldsymbol{E})$
be a standard pair over a scheme
$(X,\boldsymbol{E})$
be a standard pair over a scheme
![]() $S$
, and assume that
$S$
, and assume that
![]() $X$
has diagonalisable stabilisers. The stabiliser at a geometric point
$X$
has diagonalisable stabilisers. The stabiliser at a geometric point
 $\unicode[STIX]{x1D709}:\text{Spec}\,\bar{k}\rightarrow X$
will be denoted
$\unicode[STIX]{x1D709}:\text{Spec}\,\bar{k}\rightarrow X$
will be denoted
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
. Denote the pull-back of
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
. Denote the pull-back of
![]() $X$
along the composition
$X$
along the composition
 $\text{Spec}\,\bar{k}\rightarrow X\rightarrow S$
by
$\text{Spec}\,\bar{k}\rightarrow X\rightarrow S$
by
![]() $X_{\bar{k}}$
. Then the morphism
$X_{\bar{k}}$
. Then the morphism
![]() $\unicode[STIX]{x1D709}$
factors as
$\unicode[STIX]{x1D709}$
factors as
 $$\begin{eqnarray}\text{Spec}\,\bar{k}\rightarrow \text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}{\hookrightarrow}X_{\bar{k}}\rightarrow X.\end{eqnarray}$$
$$\begin{eqnarray}\text{Spec}\,\bar{k}\rightarrow \text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}{\hookrightarrow}X_{\bar{k}}\rightarrow X.\end{eqnarray}$$
The map
 $\text{Spec}\,\bar{k}\rightarrow X_{\bar{k}}$
is a section of the natural projection. By Lemma A.10, this implies that the canonical monomorphism
$\text{Spec}\,\bar{k}\rightarrow X_{\bar{k}}$
is a section of the natural projection. By Lemma A.10, this implies that the canonical monomorphism
 $\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}{\hookrightarrow}X_{\bar{k}}$
is a closed immersion. The invariants which we are interested in will be derived form the conormal bundle
$\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}{\hookrightarrow}X_{\bar{k}}$
is a closed immersion. The invariants which we are interested in will be derived form the conormal bundle
 ${\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}$
.
${\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}$
.
Let
![]() $A(\unicode[STIX]{x1D709})$
denote the character group of
$A(\unicode[STIX]{x1D709})$
denote the character group of
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
. Since
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
. Since
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
is assumed to be diagonalisable, the category of coherent
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
is assumed to be diagonalisable, the category of coherent
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}}$
-modules is simply equivalent to the category of
${\mathcal{O}}_{\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}}$
-modules is simply equivalent to the category of
![]() $A(\unicode[STIX]{x1D709})$
-graded
$A(\unicode[STIX]{x1D709})$
-graded
![]() $\bar{k}$
-vector spaces. In particular, the sheaf
$\bar{k}$
-vector spaces. In particular, the sheaf
 ${\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}$
splits into rank-1 locally free subsheaves. In general, this splitting is non-canonical, but each divisor in the set
${\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}$
splits into rank-1 locally free subsheaves. In general, this splitting is non-canonical, but each divisor in the set
![]() $\boldsymbol{E}$
passing through the point
$\boldsymbol{E}$
passing through the point
![]() $\unicode[STIX]{x1D709}$
canonically determines a rank-1 subbundle of
$\unicode[STIX]{x1D709}$
canonically determines a rank-1 subbundle of
 ${\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}$
.
${\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}$
.
Proposition 6.1. Let
![]() $(X,\boldsymbol{E})$
be a standard pair over a scheme
$(X,\boldsymbol{E})$
be a standard pair over a scheme
![]() $S$
and assume that
$S$
and assume that
![]() $X$
has diagonalisable stabilisers. Given a geometric point
$X$
has diagonalisable stabilisers. Given a geometric point
 $\unicode[STIX]{x1D709}:\text{Spec}\,\bar{k}\rightarrow X$
, we let
$\unicode[STIX]{x1D709}:\text{Spec}\,\bar{k}\rightarrow X$
, we let
 $E^{1},\ldots ,E^{s}$
be the components of
$E^{1},\ldots ,E^{s}$
be the components of
![]() $\boldsymbol{E}$
passing through
$\boldsymbol{E}$
passing through
![]() $\unicode[STIX]{x1D709}$
. Let
$\unicode[STIX]{x1D709}$
. Let
 $g_{i}:\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}{\hookrightarrow}E_{\bar{k}}^{i}$
denote the canonical morphism to the fibre of the component
$g_{i}:\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}{\hookrightarrow}E_{\bar{k}}^{i}$
denote the canonical morphism to the fibre of the component
![]() $E^{i}$
. Then the conormal bundle
$E^{i}$
. Then the conormal bundle
 ${\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}$
splits as a direct sum
${\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}$
splits as a direct sum
 $$\begin{eqnarray}\displaystyle {\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}=g_{1}^{\ast }{\mathcal{N}}_{E_{\bar{k}}^{1}/X_{\bar{k}}}\oplus \cdots \oplus g_{s}^{\ast }{\mathcal{N}}_{E_{\bar{k}}^{s}/X_{\bar{k}}}\oplus {\mathcal{N}}_{\text{res}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}=g_{1}^{\ast }{\mathcal{N}}_{E_{\bar{k}}^{1}/X_{\bar{k}}}\oplus \cdots \oplus g_{s}^{\ast }{\mathcal{N}}_{E_{\bar{k}}^{s}/X_{\bar{k}}}\oplus {\mathcal{N}}_{\text{res}}, & & \displaystyle\end{eqnarray}$$
where each summand
 $g_{i}^{\ast }{\mathcal{N}}_{E_{\bar{k}}^{i}/X_{\bar{k}}}V_{i}$
has rank
$g_{i}^{\ast }{\mathcal{N}}_{E_{\bar{k}}^{i}/X_{\bar{k}}}V_{i}$
has rank
![]() $1$
.
$1$
.
Proof. By passing to the fibre, we may, without loss of generality, assume that
 $S=\text{Spec}\,\bar{k}$
. Let
$S=\text{Spec}\,\bar{k}$
. Let
 $Z_{0}=X$
and define
$Z_{0}=X$
and define
![]() $Z_{i}$
recursively by means of the cartesian diagrams
$Z_{i}$
recursively by means of the cartesian diagrams

Since we assume that the divisors
![]() $E^{i}$
intersect transversally, each
$E^{i}$
intersect transversally, each
![]() $Z_{i}$
is smooth and we have canonical isomorphisms
$Z_{i}$
is smooth and we have canonical isomorphisms
 ${\mathcal{N}}_{Z_{i}/Z_{i-1}}\simeq h_{i}^{\ast }{\mathcal{N}}_{E^{i}/X}$
by [Reference Dieudonné and GrothendieckEGAIV, Proposition 17.13.2]. Now consider the increasing filtration
${\mathcal{N}}_{Z_{i}/Z_{i-1}}\simeq h_{i}^{\ast }{\mathcal{N}}_{E^{i}/X}$
by [Reference Dieudonné and GrothendieckEGAIV, Proposition 17.13.2]. Now consider the increasing filtration
 $$\begin{eqnarray}\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}{\hookrightarrow}Z_{s}{\hookrightarrow}\cdots {\hookrightarrow}Z_{0}=X\end{eqnarray}$$
$$\begin{eqnarray}\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}{\hookrightarrow}Z_{s}{\hookrightarrow}\cdots {\hookrightarrow}Z_{0}=X\end{eqnarray}$$
of closed immersions between stacks which are smooth over
![]() $S$
. We denote the various compositions by
$S$
. We denote the various compositions by
 $f_{i}:\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}\rightarrow Z_{i}$
. By [Reference Dieudonné and GrothendieckEGAIV, Proposition 16.9.13], we have short exact sequences
$f_{i}:\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}\rightarrow Z_{i}$
. By [Reference Dieudonné and GrothendieckEGAIV, Proposition 16.9.13], we have short exact sequences
 $$\begin{eqnarray}0\rightarrow f_{i}^{\ast }{\mathcal{N}}_{Z_{i}/Z_{i-1}}\rightarrow {\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/Z_{i-1}}\rightarrow {\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/Z_{i}}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow f_{i}^{\ast }{\mathcal{N}}_{Z_{i}/Z_{i-1}}\rightarrow {\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/Z_{i-1}}\rightarrow {\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/Z_{i}}\rightarrow 0\end{eqnarray}$$
for each
 $i\in \{1,\ldots ,s\}$
. Since the group
$i\in \{1,\ldots ,s\}$
. Since the group
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
is linearly reductive, these sequences split, and we get a decomposition
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
is linearly reductive, these sequences split, and we get a decomposition
 $$\begin{eqnarray}{\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X}=f_{1}^{\ast }{\mathcal{N}}_{Z_{1}/Z_{0}}\oplus \cdots \oplus f_{r}^{\ast }{\mathcal{N}}_{Z_{s}/Z_{s-1}}\oplus {\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/Z_{s}}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X}=f_{1}^{\ast }{\mathcal{N}}_{Z_{1}/Z_{0}}\oplus \cdots \oplus f_{r}^{\ast }{\mathcal{N}}_{Z_{s}/Z_{s-1}}\oplus {\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/Z_{s}}.\end{eqnarray}$$
But the maps
![]() $g_{i}$
factors through
$g_{i}$
factors through
![]() $h_{i}$
, which implies that we get canonical isomorphisms
$h_{i}$
, which implies that we get canonical isomorphisms
 $g_{i}^{\ast }{\mathcal{N}}_{E^{i}/X}\simeq f_{i}^{\ast }{\mathcal{N}}_{Z_{i}/Z_{i-1}}$
. We therefore get the desired decomposition by letting
$g_{i}^{\ast }{\mathcal{N}}_{E^{i}/X}\simeq f_{i}^{\ast }{\mathcal{N}}_{Z_{i}/Z_{i-1}}$
. We therefore get the desired decomposition by letting
 ${\mathcal{N}}_{\text{res}}={\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/Z_{s}}$
. Since the substacks
${\mathcal{N}}_{\text{res}}={\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/Z_{s}}$
. Since the substacks
![]() $E^{i}$
are effective Cartier divisors, the bundles
$E^{i}$
are effective Cartier divisors, the bundles
![]() ${\mathcal{N}}_{E^{i}/X}$
are locally free of rank 1.◻
${\mathcal{N}}_{E^{i}/X}$
are locally free of rank 1.◻
For the purpose of constructing the invariants needed in the destackification algorithm, we only need some combinatorial information extracted from the conormal representation. The next step is to give a precise description of this information.
Given a finite set
![]() $\boldsymbol{E}$
, we denote its associated pointed set by
$\boldsymbol{E}$
, we denote its associated pointed set by
![]() $\boldsymbol{E}_{+}$
. That is, the pointed set
$\boldsymbol{E}_{+}$
. That is, the pointed set
![]() $\boldsymbol{E}_{+}$
is the disjoint union of
$\boldsymbol{E}_{+}$
is the disjoint union of
![]() $\boldsymbol{E}$
with the singleton set
$\boldsymbol{E}$
with the singleton set
![]() $\{\ast \}$
, with
$\{\ast \}$
, with
![]() $\ast$
regarded as the distinguished point in
$\ast$
regarded as the distinguished point in
![]() $\boldsymbol{E}_{+}$
.
$\boldsymbol{E}_{+}$
.
Consider the class of pairs
![]() $(A,\boldsymbol{v})$
, where
$(A,\boldsymbol{v})$
, where
![]() $A$
is a finite abelian group and
$A$
is a finite abelian group and
![]() $\boldsymbol{v}$
is an unordered sequence of pairs
$\boldsymbol{v}$
is an unordered sequence of pairs
 $v_{i}=(a_{i},e_{i})\in A\times \boldsymbol{E}_{+}$
such that each element of
$v_{i}=(a_{i},e_{i})\in A\times \boldsymbol{E}_{+}$
such that each element of
![]() $\boldsymbol{E}$
occurs at most once in the sequence
$\boldsymbol{E}$
occurs at most once in the sequence
 $e_{1},\ldots ,e_{r}$
. Such a pair
$e_{1},\ldots ,e_{r}$
. Such a pair
![]() $(A,\boldsymbol{v})$
is considered equivalent to another pair
$(A,\boldsymbol{v})$
is considered equivalent to another pair
![]() $(A^{\prime },\boldsymbol{v}^{\prime })$
provided that there exists a group isomorphism
$(A^{\prime },\boldsymbol{v}^{\prime })$
provided that there exists a group isomorphism
 $\unicode[STIX]{x1D711}:A\rightarrow A^{\prime }$
such that
$\unicode[STIX]{x1D711}:A\rightarrow A^{\prime }$
such that
 $\boldsymbol{v}^{\prime }=((\unicode[STIX]{x1D711}(a_{1}),e_{1}),\ldots ,(\unicode[STIX]{x1D711}(a_{r}),e_{r}))$
for some suitable ordering of the elements in the sequence
$\boldsymbol{v}^{\prime }=((\unicode[STIX]{x1D711}(a_{1}),e_{1}),\ldots ,(\unicode[STIX]{x1D711}(a_{r}),e_{r}))$
for some suitable ordering of the elements in the sequence
![]() $\boldsymbol{v}^{\prime }$
.
$\boldsymbol{v}^{\prime }$
.
Definition 6.2. The set
![]() $U(\boldsymbol{E})$
of toric types parametrised by a finite set
$U(\boldsymbol{E})$
of toric types parametrised by a finite set
![]() $\boldsymbol{E}$
is defined as the set of equivalence classes of pairs
$\boldsymbol{E}$
is defined as the set of equivalence classes of pairs
![]() $(A,\boldsymbol{v})$
with
$(A,\boldsymbol{v})$
with
![]() $A$
a finite abelian group and
$A$
a finite abelian group and
![]() $\boldsymbol{v}$
an unordered sequence of elements
$\boldsymbol{v}$
an unordered sequence of elements
 $v_{i}=(a_{i},e_{i})\in A\times \boldsymbol{E}_{+}$
as described above. The element
$v_{i}=(a_{i},e_{i})\in A\times \boldsymbol{E}_{+}$
as described above. The element
![]() $a_{i}$
is called the weight of
$a_{i}$
is called the weight of
![]() $v_{i}$
. If
$v_{i}$
. If
![]() $e_{i}\in \boldsymbol{E}$
, we say that
$e_{i}\in \boldsymbol{E}$
, we say that
![]() $v_{i}$
is marked by
$v_{i}$
is marked by
![]() $e_{i}$
. Otherwise, we say that
$e_{i}$
. Otherwise, we say that
![]() $v_{i}$
is unmarked.
$v_{i}$
is unmarked.
The conormal representation lets us associate a toric type to each point of a standard pair
![]() $(X,\boldsymbol{E})$
.
$(X,\boldsymbol{E})$
.
Definition 6.3. Let
![]() $(X,\boldsymbol{E})$
be a standard pair and let
$(X,\boldsymbol{E})$
be a standard pair and let
![]() $\unicode[STIX]{x1D709}\in X$
be a point in
$\unicode[STIX]{x1D709}\in X$
be a point in
![]() $X$
. Let
$X$
. Let
 ${\mathcal{N}}_{1}\oplus \cdots \oplus {\mathcal{N}}_{r}$
be a splitting of the conormal bundle
${\mathcal{N}}_{1}\oplus \cdots \oplus {\mathcal{N}}_{r}$
be a splitting of the conormal bundle
 ${\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}$
into locally free sheaves of rank 1. Denote the character group of the stabiliser at
${\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}$
into locally free sheaves of rank 1. Denote the character group of the stabiliser at
![]() $\unicode[STIX]{x1D709}$
by
$\unicode[STIX]{x1D709}$
by
![]() $A$
and let
$A$
and let
![]() $a_{i}$
be the character corresponding to
$a_{i}$
be the character corresponding to
![]() ${\mathcal{N}}_{i}$
.
${\mathcal{N}}_{i}$
.
We assume that the splitting is compatible with the splitting given in (6.1) in the sense that
 ${\mathcal{N}}_{i}=g_{i}^{\ast }{\mathcal{N}}_{E_{\bar{k}}^{i}/X_{\bar{k}}}$
for
${\mathcal{N}}_{i}=g_{i}^{\ast }{\mathcal{N}}_{E_{\bar{k}}^{i}/X_{\bar{k}}}$
for
 $1\leqslant i\leqslant s$
using the notation and the indexing from Proposition 6.1. Let
$1\leqslant i\leqslant s$
using the notation and the indexing from Proposition 6.1. Let
 $$\begin{eqnarray}v_{i}=\left\{\begin{array}{@{}ll@{}}(a_{i},E^{i}) & \text{if }1\leqslant i\leqslant s,\\ (a_{i},\ast ) & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}v_{i}=\left\{\begin{array}{@{}ll@{}}(a_{i},E^{i}) & \text{if }1\leqslant i\leqslant s,\\ (a_{i},\ast ) & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
We define the toric type of
![]() $(X,\boldsymbol{E})$
at
$(X,\boldsymbol{E})$
at
![]() $\unicode[STIX]{x1D709}$
as the element in
$\unicode[STIX]{x1D709}$
as the element in
![]() $U(\boldsymbol{E})$
represented by
$U(\boldsymbol{E})$
represented by
 $(A,(v_{1},\ldots ,v_{r}))$
in
$(A,(v_{1},\ldots ,v_{r}))$
in
![]() $U(\boldsymbol{E})$
.
$U(\boldsymbol{E})$
.
Remark 6.4. Note that the unordered sequence
 $a_{1},\ldots ,a_{r}$
referred to in Definition 6.3 depends only on the class
$a_{1},\ldots ,a_{r}$
referred to in Definition 6.3 depends only on the class
 $[{\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}]$
of the conormal bundle in the Grothendieck group
$[{\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}]$
of the conormal bundle in the Grothendieck group
 $\text{K}_{0}(\text{Coh}\,(\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}))$
. Alternatively, one could instead consider the class of the derived pull-back of the cotangent complex to the Grothendieck group of the triangulated category of perfect complexes on
$\text{K}_{0}(\text{Coh}\,(\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}))$
. Alternatively, one could instead consider the class of the derived pull-back of the cotangent complex to the Grothendieck group of the triangulated category of perfect complexes on
![]() $\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
. This is proved in Appendix C.
$\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
. This is proved in Appendix C.
Next we investigate how the toric type varies over a basic toric stack.
Proposition 6.5. Let
![]() $S$
be a scheme and let
$S$
be a scheme and let
![]() $X$
be a basic toric stack with homogeneous coordinate ring
$X$
be a basic toric stack with homogeneous coordinate ring
 $({\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}],A,\boldsymbol{a})$
. Assume that
$({\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}],A,\boldsymbol{a})$
. Assume that
 $1\leqslant s\leqslant r$
, and let
$1\leqslant s\leqslant r$
, and let
 $\boldsymbol{E}=(E^{1},\ldots ,E^{s})$
with
$\boldsymbol{E}=(E^{1},\ldots ,E^{s})$
with
 $E^{i}=V(x_{i})$
. We consider the standard pair
$E^{i}=V(x_{i})$
. We consider the standard pair
 $(X,\boldsymbol{E})/S$
.
$(X,\boldsymbol{E})/S$
.
Let
![]() $\unicode[STIX]{x1D709}$
be an arbitrary point in
$\unicode[STIX]{x1D709}$
be an arbitrary point in
![]() $X$
. Then we have a surjection
$X$
. Then we have a surjection
 $\unicode[STIX]{x1D711}:A\rightarrow A(\unicode[STIX]{x1D709})$
to the character group of the stabiliser at a geometric point representing
$\unicode[STIX]{x1D711}:A\rightarrow A(\unicode[STIX]{x1D709})$
to the character group of the stabiliser at a geometric point representing
![]() $\unicode[STIX]{x1D709}$
. The kernel of
$\unicode[STIX]{x1D709}$
. The kernel of
![]() $\unicode[STIX]{x1D711}$
is generated by the elements
$\unicode[STIX]{x1D711}$
is generated by the elements
![]() $a_{i}$
such that
$a_{i}$
such that
 $\unicode[STIX]{x1D709}\not \in V(x_{i})$
. The toric type at
$\unicode[STIX]{x1D709}\not \in V(x_{i})$
. The toric type at
![]() $\unicode[STIX]{x1D709}$
is given by
$\unicode[STIX]{x1D709}$
is given by
 $$\begin{eqnarray}(A(\unicode[STIX]{x1D709}),(v_{1},\ldots ,v_{r})),\quad v_{i}=(\unicode[STIX]{x1D711}(a_{i}),e_{i}),\end{eqnarray}$$
$$\begin{eqnarray}(A(\unicode[STIX]{x1D709}),(v_{1},\ldots ,v_{r})),\quad v_{i}=(\unicode[STIX]{x1D711}(a_{i}),e_{i}),\end{eqnarray}$$
where
![]() $e_{i}=E^{i}$
if
$e_{i}=E^{i}$
if
![]() $i\leqslant s$
and the divisor
$i\leqslant s$
and the divisor
![]() $E^{i}$
passes through
$E^{i}$
passes through
![]() $\unicode[STIX]{x1D709}$
and
$\unicode[STIX]{x1D709}$
and
![]() $\ast$
otherwise.
$\ast$
otherwise.
Proof. Since the field
![]() $\bar{k}$
is algebraically closed, the map
$\bar{k}$
is algebraically closed, the map
![]() $\unicode[STIX]{x1D709}$
factors through
$\unicode[STIX]{x1D709}$
factors through
 $\text{Spec}_{{\mathcal{O}}_{S}}{\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}]$
. Let
$\text{Spec}_{{\mathcal{O}}_{S}}{\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}]$
. Let
![]() $\unicode[STIX]{x1D6FC}_{i}$
be the image of
$\unicode[STIX]{x1D6FC}_{i}$
be the image of
![]() $x_{i}$
through the corresponding map
$x_{i}$
through the corresponding map
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}({\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}])\rightarrow \bar{k}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}({\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}])\rightarrow \bar{k}.\end{eqnarray}$$
Then we have
![]() $\unicode[STIX]{x1D6FC}_{i}=0$
precisely when
$\unicode[STIX]{x1D6FC}_{i}=0$
precisely when
![]() $\unicode[STIX]{x1D709}$
passes through
$\unicode[STIX]{x1D709}$
passes through
![]() $V(x_{i})$
.
$V(x_{i})$
.
Consider the atlas
 $\widetilde{X}_{\bar{k}}=\text{Spec}\,\bar{k}[x_{1},\ldots ,x_{r}]$
of
$\widetilde{X}_{\bar{k}}=\text{Spec}\,\bar{k}[x_{1},\ldots ,x_{r}]$
of
![]() $X_{\bar{k}}$
. The closed immersion
$X_{\bar{k}}$
. The closed immersion
 $\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}{\hookrightarrow}X_{\bar{k}}$
corresponds to the slice of the action groupoid at the closed subscheme
$\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}{\hookrightarrow}X_{\bar{k}}$
corresponds to the slice of the action groupoid at the closed subscheme
 $V(I)\subset \widetilde{X}_{\bar{k}}$
defined by the ideal
$V(I)\subset \widetilde{X}_{\bar{k}}$
defined by the ideal
 $I=(x_{1}-\unicode[STIX]{x1D6FC}_{1},\ldots ,x_{r}-\unicode[STIX]{x1D6FC}_{r})$
. In other words, we have the cartesian diagram
$I=(x_{1}-\unicode[STIX]{x1D6FC}_{1},\ldots ,x_{r}-\unicode[STIX]{x1D6FC}_{r})$
. In other words, we have the cartesian diagram

The map
![]() $g$
corresponds to the
$g$
corresponds to the
![]() $\bar{k}$
-algebra map
$\bar{k}$
-algebra map
 $\bar{k}[x_{1},\ldots ,x_{r},y_{1},\ldots ,y_{r}]\rightarrow \bar{k}$
taking
$\bar{k}[x_{1},\ldots ,x_{r},y_{1},\ldots ,y_{r}]\rightarrow \bar{k}$
taking
![]() $x_{i}$
and
$x_{i}$
and
![]() $y_{i}$
to
$y_{i}$
to
![]() $\unicode[STIX]{x1D6FC}_{i}$
, and the map
$\unicode[STIX]{x1D6FC}_{i}$
, and the map
![]() $f$
corresponds to the
$f$
corresponds to the
![]() $\bar{k}$
-algebra map
$\bar{k}$
-algebra map
 $$\begin{eqnarray}\bar{k}[x_{1},\ldots ,x_{r},y_{1},\ldots ,y_{r}]\rightarrow \bar{k}[x_{1},\ldots ,x_{r}][A]\end{eqnarray}$$
$$\begin{eqnarray}\bar{k}[x_{1},\ldots ,x_{r},y_{1},\ldots ,y_{r}]\rightarrow \bar{k}[x_{1},\ldots ,x_{r}][A]\end{eqnarray}$$
taking
![]() $x_{i}$
to
$x_{i}$
to
![]() $x_{i}$
and
$x_{i}$
and
![]() $y_{i}$
to
$y_{i}$
to
![]() $a_{i}x_{i}$
. It follows that the map
$a_{i}x_{i}$
. It follows that the map
![]() $g^{\prime }$
corresponds to
$g^{\prime }$
corresponds to
 $$\begin{eqnarray}\bar{k}[x_{1},\ldots ,x_{r}][A]\rightarrow \bar{k}[A]/(\unicode[STIX]{x1D6FC}_{i}-a_{i}\unicode[STIX]{x1D6FC}_{i})\end{eqnarray}$$
$$\begin{eqnarray}\bar{k}[x_{1},\ldots ,x_{r}][A]\rightarrow \bar{k}[A]/(\unicode[STIX]{x1D6FC}_{i}-a_{i}\unicode[STIX]{x1D6FC}_{i})\end{eqnarray}$$
taking
![]() $x_{i}$
to
$x_{i}$
to
![]() $\unicode[STIX]{x1D6FC}_{i}$
, where
$\unicode[STIX]{x1D6FC}_{i}$
, where
![]() $i$
ranges from
$i$
ranges from
![]() $1$
to
$1$
to
![]() $r$
. Since the relation
$r$
. Since the relation
 $\unicode[STIX]{x1D6FC}_{i}=a_{i}\unicode[STIX]{x1D6FC}_{i}$
is trivial if
$\unicode[STIX]{x1D6FC}_{i}=a_{i}\unicode[STIX]{x1D6FC}_{i}$
is trivial if
![]() $\unicode[STIX]{x1D6FC}_{i}=0$
and equivalent to
$\unicode[STIX]{x1D6FC}_{i}=0$
and equivalent to
![]() $a_{i}=1$
otherwise, the right-hand side is the group algebra
$a_{i}=1$
otherwise, the right-hand side is the group algebra
![]() $\bar{k}[A(\unicode[STIX]{x1D709})]$
in the statement of the proposition. The conormal representation is the
$\bar{k}[A(\unicode[STIX]{x1D709})]$
in the statement of the proposition. The conormal representation is the
![]() $\bar{k}$
-vector space
$\bar{k}$
-vector space
![]() $I/I^{2}$
, which has the elements
$I/I^{2}$
, which has the elements
 $u_{i}=(x_{i}-\unicode[STIX]{x1D6FC}_{i})+I^{2}$
for
$u_{i}=(x_{i}-\unicode[STIX]{x1D6FC}_{i})+I^{2}$
for
 $i\in \{1,\ldots ,r\}$
as basis. Since
$i\in \{1,\ldots ,r\}$
as basis. Since
![]() $u_{i}$
has weight
$u_{i}$
has weight
![]() $\unicode[STIX]{x1D711}(a_{i})$
and corresponds to the divisor
$\unicode[STIX]{x1D711}(a_{i})$
and corresponds to the divisor
![]() $V(x_{i})$
precisely when
$V(x_{i})$
precisely when
![]() $\unicode[STIX]{x1D6FC}_{i}=0$
, the result follows.◻
$\unicode[STIX]{x1D6FC}_{i}=0$
, the result follows.◻
Table 6.1. The table shows how the conormal representation varies over the strata defined by the toric divisors of the basic toric stack in Example 6.6. The stratum
 $\bigcap _{s_{i}=1}V(x_{i})\setminus \bigcup _{s_{i}=0}V(x_{i})$
corresponds to the row labelled by the binary word
$\bigcap _{s_{i}=1}V(x_{i})\setminus \bigcup _{s_{i}=0}V(x_{i})$
corresponds to the row labelled by the binary word
![]() $s_{1}s_{2}s_{3}$
.
$s_{1}s_{2}s_{3}$
.

Example 6.6. Let
![]() $k$
be a field and
$k$
be a field and
![]() $(X,\boldsymbol{E})$
the standard pair with
$(X,\boldsymbol{E})$
the standard pair with
![]() $X$
being the basic toric stack with homogeneous coordinates
$X$
being the basic toric stack with homogeneous coordinates
 $(k[x_{1},x_{2},x_{3}],C_{2}\times C_{2},((1,0),(0,1),(1,1)))$
and
$(k[x_{1},x_{2},x_{3}],C_{2}\times C_{2},((1,0),(0,1),(1,1)))$
and
![]() $\boldsymbol{E}$
being the sequence
$\boldsymbol{E}$
being the sequence
 $(E^{1},E^{2})$
with
$(E^{1},E^{2})$
with
 $E^{i}=V(x_{i})$
for
$E^{i}=V(x_{i})$
for
![]() $i=1,2$
. Table 6.1 shows how the toric type varies over the strata defined by the toric divisors. Note that the toric types in the rows 1 through 7 are distinct whereas the toric type in row 8 is identical to the toric type in row 7.
$i=1,2$
. Table 6.1 shows how the toric type varies over the strata defined by the toric divisors. Note that the toric types in the rows 1 through 7 are distinct whereas the toric type in row 8 is identical to the toric type in row 7.
Motivated by Proposition 6.5, we introduce a partial ordering on the set
![]() $U(\boldsymbol{E})$
for each finite set
$U(\boldsymbol{E})$
for each finite set
![]() $\boldsymbol{E}$
. Let
$\boldsymbol{E}$
. Let
![]() $X$
be a basic toric stack and let
$X$
be a basic toric stack and let
![]() $\boldsymbol{E}$
be a sequence of toric divisors on
$\boldsymbol{E}$
be a sequence of toric divisors on
![]() $X$
. By design, the ordering on
$X$
. By design, the ordering on
![]() $U(\boldsymbol{E})$
makes the function taking a point in
$U(\boldsymbol{E})$
makes the function taking a point in
![]() $X$
to the toric type at that point upper semi-continuous.
$X$
to the toric type at that point upper semi-continuous.
Definition 6.7. Let
 $\unicode[STIX]{x1D6FC}\in U(\boldsymbol{E})$
be a toric type represented by the triple
$\unicode[STIX]{x1D6FC}\in U(\boldsymbol{E})$
be a toric type represented by the triple
![]() $(A,\boldsymbol{v})$
with
$(A,\boldsymbol{v})$
with
 $\boldsymbol{v}=(v_{1},\ldots ,v_{r})$
and
$\boldsymbol{v}=(v_{1},\ldots ,v_{r})$
and
 $v_{i}=(a_{i},e_{i})$
. Given
$v_{i}=(a_{i},e_{i})$
. Given
 $\unicode[STIX]{x1D6FC}^{\prime }\in U(\boldsymbol{E})$
, we write
$\unicode[STIX]{x1D6FC}^{\prime }\in U(\boldsymbol{E})$
, we write
![]() $\unicode[STIX]{x1D6FC}\geqslant \unicode[STIX]{x1D6FC}^{\prime }$
if there exists a subset
$\unicode[STIX]{x1D6FC}\geqslant \unicode[STIX]{x1D6FC}^{\prime }$
if there exists a subset
 $J\subset \{1,\ldots ,r\}$
such that
$J\subset \{1,\ldots ,r\}$
such that
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
is represented by
$\unicode[STIX]{x1D6FC}^{\prime }$
is represented by
 $(A^{\prime },(v_{1}^{\prime },\ldots ,v_{r}^{\prime }))$
with
$(A^{\prime },(v_{1}^{\prime },\ldots ,v_{r}^{\prime }))$
with
 $A^{\prime }=A/\langle a_{i}\rangle _{i\in J}$
and
$A^{\prime }=A/\langle a_{i}\rangle _{i\in J}$
and
 $$\begin{eqnarray}v_{i}^{\prime }=\left\{\begin{array}{@{}ll@{}}(\overline{a}_{i},e_{i}) & \text{if }i\not \in J,\\ (0,\ast ) & \text{if }i\in J,\\ \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}v_{i}^{\prime }=\left\{\begin{array}{@{}ll@{}}(\overline{a}_{i},e_{i}) & \text{if }i\not \in J,\\ (0,\ast ) & \text{if }i\in J,\\ \end{array}\right.\end{eqnarray}$$
where
![]() $\overline{a}_{i}$
denotes the image of
$\overline{a}_{i}$
denotes the image of
![]() $a_{i}$
through the canonical morphism
$a_{i}$
through the canonical morphism
 $A\rightarrow A^{\prime }$
.
$A\rightarrow A^{\prime }$
.
We are now ready define what we mean by a conormal invariant.
Definition 6.8. A conormal invariant
![]() $\unicode[STIX]{x1D704}$
is a rule which to each finite totally ordered set
$\unicode[STIX]{x1D704}$
is a rule which to each finite totally ordered set
![]() $\boldsymbol{E}$
associates an order-preserving function
$\boldsymbol{E}$
associates an order-preserving function
 $\unicode[STIX]{x1D704}_{\boldsymbol{E}}:U(\boldsymbol{E})\rightarrow W(\boldsymbol{E})$
to a partially ordered set
$\unicode[STIX]{x1D704}_{\boldsymbol{E}}:U(\boldsymbol{E})\rightarrow W(\boldsymbol{E})$
to a partially ordered set
![]() $W(\boldsymbol{E})$
and, to each injective order-preserving function
$W(\boldsymbol{E})$
and, to each injective order-preserving function
 $f:\boldsymbol{E}\rightarrow \boldsymbol{E}^{\prime }$
associates an order-preserving function
$f:\boldsymbol{E}\rightarrow \boldsymbol{E}^{\prime }$
associates an order-preserving function
 $W(f):W(\boldsymbol{E})\rightarrow W(\boldsymbol{E}^{\prime })$
such that the diagram
$W(f):W(\boldsymbol{E})\rightarrow W(\boldsymbol{E}^{\prime })$
such that the diagram

commutes.
For each standard pair
![]() $(X,\boldsymbol{E})$
, we get a function
$(X,\boldsymbol{E})$
, we get a function
 $\unicode[STIX]{x1D704}_{(X,\boldsymbol{E})}:|X|\rightarrow W(\boldsymbol{E})$
taking a point
$\unicode[STIX]{x1D704}_{(X,\boldsymbol{E})}:|X|\rightarrow W(\boldsymbol{E})$
taking a point
![]() $\unicode[STIX]{x1D709}\in X$
to
$\unicode[STIX]{x1D709}\in X$
to
![]() $\unicode[STIX]{x1D704}_{\boldsymbol{E}}(\unicode[STIX]{x1D6FC})$
, where
$\unicode[STIX]{x1D704}_{\boldsymbol{E}}(\unicode[STIX]{x1D6FC})$
, where
![]() $\unicode[STIX]{x1D6FC}$
is the toric type at
$\unicode[STIX]{x1D6FC}$
is the toric type at
![]() $\unicode[STIX]{x1D709}$
. We call the function
$\unicode[STIX]{x1D709}$
. We call the function
![]() $\unicode[STIX]{x1D704}_{\boldsymbol{E}}(\unicode[STIX]{x1D6FC})$
the realisation of the conormal invariant for the standard pair
$\unicode[STIX]{x1D704}_{\boldsymbol{E}}(\unicode[STIX]{x1D6FC})$
the realisation of the conormal invariant for the standard pair
![]() $(X,\boldsymbol{E})$
.
$(X,\boldsymbol{E})$
.
Remark 6.9. Note that a conormal invariant is simply a natural transformation
 $U\rightarrow W$
between functors from the category of finite totally ordered sets and injective order-preserving functions to the category of partially ordered sets.
$U\rightarrow W$
between functors from the category of finite totally ordered sets and injective order-preserving functions to the category of partially ordered sets.
For most of the conormal invariants actually used by the destackification algorithm, the partially ordered set
![]() $W(\boldsymbol{E})$
will simply be the set
$W(\boldsymbol{E})$
will simply be the set
![]() $\mathbb{N}$
of natural numbers with its standard ordering.
$\mathbb{N}$
of natural numbers with its standard ordering.
Example 6.10. Let
 $(X,\boldsymbol{E})/S$
be a standard pair and let
$(X,\boldsymbol{E})/S$
be a standard pair and let
![]() $\unicode[STIX]{x1D709}\in X$
be a point with toric type
$\unicode[STIX]{x1D709}\in X$
be a point with toric type
![]() $(A,\boldsymbol{v})$
. The following example illustrates that several well-known invariants can be thought of as realisations of conormal invariants
$(A,\boldsymbol{v})$
. The following example illustrates that several well-known invariants can be thought of as realisations of conormal invariants
![]() $U\rightarrow \mathbb{N}$
, where we regard
$U\rightarrow \mathbb{N}$
, where we regard
![]() $\mathbb{N}$
as the constant functor.
$\mathbb{N}$
as the constant functor.
-
(i) The relative dimension of
 $X$
over
$X$
over
 $S$
at
$S$
at
 $\unicode[STIX]{x1D709}$
is the length of the sequence
$\unicode[STIX]{x1D709}$
is the length of the sequence
 $\boldsymbol{v}$
.
$\boldsymbol{v}$
. -
(ii) The order of the stabiliser at
 $\unicode[STIX]{x1D709}$
is the order of
$\unicode[STIX]{x1D709}$
is the order of
 $A$
.
$A$
. -
(iii) The multiplicity at
 $\unicode[STIX]{x1D709}$
is the order of
$\unicode[STIX]{x1D709}$
is the order of
 $A_{\text{can}}$
, with
$A_{\text{can}}$
, with
 $A_{\text{can}}$
defined by the exact sequence in Remark 3.15.
$A_{\text{can}}$
defined by the exact sequence in Remark 3.15.
Example 6.11. For the conormal invariants given in Example 6.10, the ordered set
![]() $\boldsymbol{E}$
played no part. Here we give some examples where
$\boldsymbol{E}$
played no part. Here we give some examples where
![]() $\boldsymbol{E}$
does play a part.
$\boldsymbol{E}$
does play a part.
-
(i) The identity natural transformation
 $U\rightarrow U$
can be regarded as the universal conormal invariant. Its realisation for the standard pair
$U\rightarrow U$
can be regarded as the universal conormal invariant. Its realisation for the standard pair
 $(X,\boldsymbol{E})$
evaluated at a point
$(X,\boldsymbol{E})$
evaluated at a point
 $\unicode[STIX]{x1D709}$
is simply the toric type at
$\unicode[STIX]{x1D709}$
is simply the toric type at
 $\unicode[STIX]{x1D709}$
.
$\unicode[STIX]{x1D709}$
. -
(ii) Let
 $2^{\boldsymbol{E}}$
denote the power set of
$2^{\boldsymbol{E}}$
denote the power set of
 $\boldsymbol{E}$
endowed with the lexicographical ordering induced by the ordering on
$\boldsymbol{E}$
endowed with the lexicographical ordering induced by the ordering on
 $\boldsymbol{E}$
. Consider the conormal representation given by the natural transformation
$\boldsymbol{E}$
. Consider the conormal representation given by the natural transformation
 $U(\boldsymbol{E})\rightarrow 2^{\boldsymbol{E}}$
which takes
$U(\boldsymbol{E})\rightarrow 2^{\boldsymbol{E}}$
which takes
 $(A,\boldsymbol{v})$
to the set of elements in
$(A,\boldsymbol{v})$
to the set of elements in
 $\boldsymbol{E}$
marking some element in
$\boldsymbol{E}$
marking some element in
 $\boldsymbol{v}$
. Its realisation for the standard pair
$\boldsymbol{v}$
. Its realisation for the standard pair
 $(X,\boldsymbol{E})$
evaluated at a point
$(X,\boldsymbol{E})$
evaluated at a point
 $\unicode[STIX]{x1D709}$
is the set of components of
$\unicode[STIX]{x1D709}$
is the set of components of
 $\boldsymbol{E}$
passing through
$\boldsymbol{E}$
passing through
 $\unicode[STIX]{x1D709}$
.
$\unicode[STIX]{x1D709}$
.
Example 6.12. Let
 $\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{n}$
be conormal invariants taking values in the totally ordered sets
$\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{n}$
be conormal invariants taking values in the totally ordered sets
 $W_{1},\ldots ,W_{n}$
. Then we can form its lexicographical composition
$W_{1},\ldots ,W_{n}$
. Then we can form its lexicographical composition
 $\unicode[STIX]{x1D704}_{1}\times \cdots \times \unicode[STIX]{x1D704}_{n}$
taking values in the product set
$\unicode[STIX]{x1D704}_{1}\times \cdots \times \unicode[STIX]{x1D704}_{n}$
taking values in the product set
 $W_{1}\times \cdots \times W_{n}$
endowed with the lexicographical ordering.
$W_{1}\times \cdots \times W_{n}$
endowed with the lexicographical ordering.
Next we the investigate the functorial properties of conormal invariants. Let
 $(X,\boldsymbol{E})/S$
be a standard pair and
$(X,\boldsymbol{E})/S$
be a standard pair and
 $\unicode[STIX]{x1D704}:U\rightarrow W$
a conormal invariant. As described in §2.5, we a get new standard pair
$\unicode[STIX]{x1D704}:U\rightarrow W$
a conormal invariant. As described in §2.5, we a get new standard pair
 $(X_{S^{\prime }},\boldsymbol{E}_{S^{\prime }})/S^{\prime }$
given any base change
$(X_{S^{\prime }},\boldsymbol{E}_{S^{\prime }})/S^{\prime }$
given any base change
 $S^{\prime }\rightarrow S$
. Note that we have a naturally defined one-to-one correspondence between the ordered sets
$S^{\prime }\rightarrow S$
. Note that we have a naturally defined one-to-one correspondence between the ordered sets
![]() $\boldsymbol{E}$
and the base change
$\boldsymbol{E}$
and the base change
![]() $\boldsymbol{E}_{S^{\prime }}$
induced by pull-back. Hence, we get a diagram
$\boldsymbol{E}_{S^{\prime }}$
induced by pull-back. Hence, we get a diagram

Similarly, given a smooth morphism
 $f:X^{\prime }\rightarrow X$
, we get a standard pair
$f:X^{\prime }\rightarrow X$
, we get a standard pair
 $(X^{\prime },\boldsymbol{E}^{\prime })/S$
and a naturally defined order-preserving function
$(X^{\prime },\boldsymbol{E}^{\prime })/S$
and a naturally defined order-preserving function
 $\boldsymbol{E}^{\prime }\rightarrow \boldsymbol{E}$
. This function is injective, but not necessarily surjective since we allow ourselves to omit empty divisors from
$\boldsymbol{E}^{\prime }\rightarrow \boldsymbol{E}$
. This function is injective, but not necessarily surjective since we allow ourselves to omit empty divisors from
![]() $\boldsymbol{E}^{\prime }$
. This gives us a diagram
$\boldsymbol{E}^{\prime }$
. This gives us a diagram

We want to establish conditions when the two diagrams above commute.
Definition 6.13. We define the following two properties which a conormal invariant
 $\unicode[STIX]{x1D704}:U\rightarrow W$
may have.
$\unicode[STIX]{x1D704}:U\rightarrow W$
may have.
-
(P1) For any finite ordered set
 $\boldsymbol{E}$
and any
$\boldsymbol{E}$
and any
 $(A,\boldsymbol{v})\in U(\boldsymbol{E})$
, we have
$(A,\boldsymbol{v})\in U(\boldsymbol{E})$
, we have
 $\unicode[STIX]{x1D704}(A,\boldsymbol{v})=\unicode[STIX]{x1D704}(A,\boldsymbol{v}^{\prime })$
, where
$\unicode[STIX]{x1D704}(A,\boldsymbol{v})=\unicode[STIX]{x1D704}(A,\boldsymbol{v}^{\prime })$
, where
 $\boldsymbol{v}^{\prime }$
is the subsequence of
$\boldsymbol{v}^{\prime }$
is the subsequence of
 $\boldsymbol{v}$
consisting of the elements distinct from the trivial element
$\boldsymbol{v}$
consisting of the elements distinct from the trivial element
 $(0,\ast )\in A\times \boldsymbol{E}_{+}$
.
$(0,\ast )\in A\times \boldsymbol{E}_{+}$
. -
(P2) For any finite ordered set
 $\boldsymbol{E}$
and any
$\boldsymbol{E}$
and any
 $(A,\boldsymbol{v})\in U(\boldsymbol{E})$
, we have
$(A,\boldsymbol{v})\in U(\boldsymbol{E})$
, we have
 $\unicode[STIX]{x1D704}(A,\boldsymbol{v})=\unicode[STIX]{x1D704}(A_{\text{rig}},\boldsymbol{v})$
, where
$\unicode[STIX]{x1D704}(A,\boldsymbol{v})=\unicode[STIX]{x1D704}(A_{\text{rig}},\boldsymbol{v})$
, where
 $A_{\text{rig}}$
is the subgroup of
$A_{\text{rig}}$
is the subgroup of
 $A$
generated by the weights of
$A$
generated by the weights of
 $\boldsymbol{v}$
. That is, the subgroup
$\boldsymbol{v}$
. That is, the subgroup
 $A_{\text{rig}}=\langle a_{1},\ldots ,a_{r}\rangle$
if
$A_{\text{rig}}=\langle a_{1},\ldots ,a_{r}\rangle$
if
 $\boldsymbol{v}=((a_{1},e_{1}),\ldots ,(a_{r},e_{r}))$
.
$\boldsymbol{v}=((a_{1},e_{1}),\ldots ,(a_{r},e_{r}))$
.
Proposition 6.14. Let
 $\unicode[STIX]{x1D704}:U\rightarrow W$
be a conormal invariant and let
$\unicode[STIX]{x1D704}:U\rightarrow W$
be a conormal invariant and let
 $(X,\boldsymbol{E})/S$
be a standard pair with diagonalisable stabilisers. Consider the
$(X,\boldsymbol{E})/S$
be a standard pair with diagonalisable stabilisers. Consider the
![]() $2$
-commutative diagrams
$2$
-commutative diagrams

where
![]() $f$
is smooth and the square is
$f$
is smooth and the square is
![]() $2$
-cartesian. Let
$2$
-cartesian. Let
![]() $\boldsymbol{F}$
be the pull-back of
$\boldsymbol{F}$
be the pull-back of
![]() $\boldsymbol{E}$
along
$\boldsymbol{E}$
along
![]() $f$
and let
$f$
and let
![]() $\boldsymbol{E}^{\prime }$
be the pull-back of
$\boldsymbol{E}^{\prime }$
be the pull-back of
![]() $\boldsymbol{E}$
along
$\boldsymbol{E}$
along
![]() $g$
. Then
$g$
. Then
 $\unicode[STIX]{x1D704}_{(X^{\prime },\boldsymbol{E}^{\prime })/S^{\prime }}=\unicode[STIX]{x1D704}_{(X,\boldsymbol{E})/S}\circ |g|$
. Furthermore, we have the equality
$\unicode[STIX]{x1D704}_{(X^{\prime },\boldsymbol{E}^{\prime })/S^{\prime }}=\unicode[STIX]{x1D704}_{(X,\boldsymbol{E})/S}\circ |g|$
. Furthermore, we have the equality
 $\unicode[STIX]{x1D704}_{(Y,\boldsymbol{F})/S}=\unicode[STIX]{x1D704}_{(X,\boldsymbol{E})/S}\circ |f|$
under any of the following circumstances.
$\unicode[STIX]{x1D704}_{(Y,\boldsymbol{F})/S}=\unicode[STIX]{x1D704}_{(X,\boldsymbol{E})/S}\circ |f|$
under any of the following circumstances.
-
(i) The morphism
 $f$
is étale and stabiliser-preserving.
$f$
is étale and stabiliser-preserving. -
(ii) The morphism
 $f$
is smooth and stabiliser-preserving and
$f$
is smooth and stabiliser-preserving and
 $\unicode[STIX]{x1D704}$
satisfies property (P1).
$\unicode[STIX]{x1D704}$
satisfies property (P1). -
(iii) The morphism
 $f$
is a gerbe and
$f$
is a gerbe and
 $\unicode[STIX]{x1D704}$
satisfies property (P2).
$\unicode[STIX]{x1D704}$
satisfies property (P2).
Proof. Let
 $\unicode[STIX]{x1D709}^{\prime }:\text{Spec}\,\bar{k}\rightarrow X^{\prime }$
be a geometric point. Since we have a canonical isomorphism between
$\unicode[STIX]{x1D709}^{\prime }:\text{Spec}\,\bar{k}\rightarrow X^{\prime }$
be a geometric point. Since we have a canonical isomorphism between
 $X^{\prime }\times _{S}\text{Spec}\,\bar{k}$
and
$X^{\prime }\times _{S}\text{Spec}\,\bar{k}$
and
 $X\times _{S}\text{Spec}\,\bar{k}$
, functoriality with respect to base change follows immediately.
$X\times _{S}\text{Spec}\,\bar{k}$
, functoriality with respect to base change follows immediately.
We explore the other functoriality properties by examining the first diagram. Let
 $\unicode[STIX]{x1D709}:\text{Spec}\,\bar{k}\rightarrow Y$
be a geometric point. By the previous paragraph, we may, without loss of generality, assume that
$\unicode[STIX]{x1D709}:\text{Spec}\,\bar{k}\rightarrow Y$
be a geometric point. By the previous paragraph, we may, without loss of generality, assume that
 $S=\text{Spec}\,\bar{k}$
. Denote the toric type at
$S=\text{Spec}\,\bar{k}$
. Denote the toric type at
![]() $\unicode[STIX]{x1D709}$
, as defined in Definition 6.3, by
$\unicode[STIX]{x1D709}$
, as defined in Definition 6.3, by
 $$\begin{eqnarray}(A,(v_{1},\ldots ,v_{r})),\quad v_{i}=(a_{i},e_{i}).\end{eqnarray}$$
$$\begin{eqnarray}(A,(v_{1},\ldots ,v_{r})),\quad v_{i}=(a_{i},e_{i}).\end{eqnarray}$$
We may assume that
 $v_{1},\ldots ,v_{s}$
are marked by the components
$v_{1},\ldots ,v_{s}$
are marked by the components
 $E^{1},\ldots ,E^{s}$
of
$E^{1},\ldots ,E^{s}$
of
![]() $\boldsymbol{E}$
and that
$\boldsymbol{E}$
and that
![]() $v_{i}$
is unmarked for
$v_{i}$
is unmarked for
![]() $i>s$
. Similarly, we denote the toric type at
$i>s$
. Similarly, we denote the toric type at
![]() $f\circ \unicode[STIX]{x1D709}$
by
$f\circ \unicode[STIX]{x1D709}$
by
 $$\begin{eqnarray}(A^{\prime },(v_{1}^{\prime },\ldots ,v_{r^{\prime }}^{\prime })),\quad v_{i}^{\prime }=(a_{i}^{\prime },e_{i}^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}(A^{\prime },(v_{1}^{\prime },\ldots ,v_{r^{\prime }}^{\prime })),\quad v_{i}^{\prime }=(a_{i}^{\prime },e_{i}^{\prime })\end{eqnarray}$$
and assume that
 $v_{1}^{\prime },\ldots ,v_{s}^{\prime }$
are marked by the components
$v_{1}^{\prime },\ldots ,v_{s}^{\prime }$
are marked by the components
 $F^{1},\ldots ,F^{s}$
, where
$F^{1},\ldots ,F^{s}$
, where
![]() $F^{i}$
denotes the pull-back of
$F^{i}$
denotes the pull-back of
![]() $E^{i}$
. The elements
$E^{i}$
. The elements
![]() $v_{i}^{\prime }$
for
$v_{i}^{\prime }$
for
![]() $i>s$
are unmarked. We have 2-commutative diagrams
$i>s$
are unmarked. We have 2-commutative diagrams

where the rightmost square is 2-cartesian and
![]() $i$
ranges from 1 to
$i$
ranges from 1 to
![]() $s$
.
$s$
.
First assume that the morphism
![]() $f$
is stabiliser-preserving. Then we can identify
$f$
is stabiliser-preserving. Then we can identify
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
with
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
with
![]() $\unicode[STIX]{x1D6E5}_{f\circ \unicode[STIX]{x1D709}}$
and assume that
$\unicode[STIX]{x1D6E5}_{f\circ \unicode[STIX]{x1D709}}$
and assume that
![]() $a$
is the identity map. In particular, the character groups
$a$
is the identity map. In particular, the character groups
![]() $A$
and
$A$
and
![]() $A^{\prime }$
are equal. Since conormal bundles commute with flat base change, we get
$A^{\prime }$
are equal. Since conormal bundles commute with flat base change, we get
 $$\begin{eqnarray}h_{i}^{\ast }{\mathcal{N}}_{E^{i}/X}\cong g_{i}^{\ast }f_{i}^{\ast }{\mathcal{N}}_{E^{i}/X}\cong g_{i}^{\ast }{\mathcal{N}}_{F^{i}/Y}\end{eqnarray}$$
$$\begin{eqnarray}h_{i}^{\ast }{\mathcal{N}}_{E^{i}/X}\cong g_{i}^{\ast }f_{i}^{\ast }{\mathcal{N}}_{E^{i}/X}\cong g_{i}^{\ast }{\mathcal{N}}_{F^{i}/Y}\end{eqnarray}$$
from the right-hand diagram. It follows that
![]() $a_{i}=a_{i}^{\prime }$
for
$a_{i}=a_{i}^{\prime }$
for
 $1\leqslant i\leqslant s$
.
$1\leqslant i\leqslant s$
.
We introduce the shorthand notation
![]() $\widetilde{Y}$
for the fibre product
$\widetilde{Y}$
for the fibre product
 $\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}\times _{X}Y$
and denote the canonical projections to
$\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}\times _{X}Y$
and denote the canonical projections to
![]() $\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
and
$\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
and
![]() $Y$
by
$Y$
by
![]() $p$
and
$p$
and
![]() $q$
, respectively. Note that
$q$
, respectively. Note that
![]() $p$
is smooth and
$p$
is smooth and
![]() $q$
is a regular immersion. Consider the sequence
$q$
is a regular immersion. Consider the sequence
 $\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}\xrightarrow[{}]{\unicode[STIX]{x1D70E}}\widetilde{Y}\xrightarrow[{}]{q}Y$
of morphisms, where
$\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}\xrightarrow[{}]{\unicode[STIX]{x1D70E}}\widetilde{Y}\xrightarrow[{}]{q}Y$
of morphisms, where
![]() $\unicode[STIX]{x1D70E}$
is the canonical morphism induced by
$\unicode[STIX]{x1D70E}$
is the canonical morphism induced by
![]() $b$
. Since
$b$
. Since
![]() $\unicode[STIX]{x1D70E}$
is a regular immersion, being a section of
$\unicode[STIX]{x1D70E}$
is a regular immersion, being a section of
![]() $p$
, we get an exact sequence
$p$
, we get an exact sequence
 $$\begin{eqnarray}\displaystyle 0\rightarrow \unicode[STIX]{x1D70E}^{\ast }{\mathcal{N}}_{\widetilde{Y}/Y}\rightarrow {\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/Y}\rightarrow {\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/\widetilde{Y}}\rightarrow 0 & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow \unicode[STIX]{x1D70E}^{\ast }{\mathcal{N}}_{\widetilde{Y}/Y}\rightarrow {\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/Y}\rightarrow {\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/\widetilde{Y}}\rightarrow 0 & & \displaystyle\end{eqnarray}$$
by [Reference Dieudonné and GrothendieckEGAIV, Proposition 16.9.3]. The bundle
![]() ${\mathcal{N}}_{\widetilde{Y}/Y}$
is the pull-back of
${\mathcal{N}}_{\widetilde{Y}/Y}$
is the pull-back of
 ${\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X}$
along the projection
${\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X}$
along the projection
![]() $p$
. Since
$p$
. Since
![]() $\unicode[STIX]{x1D70E}$
is a section of
$\unicode[STIX]{x1D70E}$
is a section of
![]() $p$
, this allows us identify the first term in (6.5) with
$p$
, this allows us identify the first term in (6.5) with
 ${\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X}$
. Consider the 2-commutative square
${\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X}$
. Consider the 2-commutative square

induced by passing to coarse spaces. Since
![]() $p$
is stabiliser-preserving and
$p$
is stabiliser-preserving and
![]() $\unicode[STIX]{x1D70B}$
is a gerbe, this square is 2-cartesian. It follows that the conormal bundle
$\unicode[STIX]{x1D70B}$
is a gerbe, this square is 2-cartesian. It follows that the conormal bundle
 ${\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/\widetilde{Y}}$
associated to the section
${\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/\widetilde{Y}}$
associated to the section
![]() $\unicode[STIX]{x1D70E}$
is isomorphic to the pull-back
$\unicode[STIX]{x1D70E}$
is isomorphic to the pull-back
 $\unicode[STIX]{x1D70B}^{\ast }{\mathcal{N}}_{S/\widetilde{Y}_{\text{cs}}}$
of the conormal bundle
$\unicode[STIX]{x1D70B}^{\ast }{\mathcal{N}}_{S/\widetilde{Y}_{\text{cs}}}$
of the conormal bundle
![]() ${\mathcal{N}}_{S/\widetilde{Y}_{\text{cs}}}$
associated to
${\mathcal{N}}_{S/\widetilde{Y}_{\text{cs}}}$
associated to
![]() $\unicode[STIX]{x1D70E}_{\text{cs}}$
. Hence, the sequence (6.5) can be rewritten as
$\unicode[STIX]{x1D70E}_{\text{cs}}$
. Hence, the sequence (6.5) can be rewritten as
 $$\begin{eqnarray}0\rightarrow {\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X}\rightarrow {\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/Y}\rightarrow \unicode[STIX]{x1D70B}^{\ast }{\mathcal{N}}_{S/\widetilde{Y}_{\text{cs}}}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X}\rightarrow {\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/Y}\rightarrow \unicode[STIX]{x1D70B}^{\ast }{\mathcal{N}}_{S/\widetilde{Y}_{\text{cs}}}\rightarrow 0.\end{eqnarray}$$
Since the bundle
 $\unicode[STIX]{x1D70B}^{\ast }{\mathcal{N}}_{S/\widetilde{Y}_{\text{cs}}}$
is defined over the base field
$\unicode[STIX]{x1D70B}^{\ast }{\mathcal{N}}_{S/\widetilde{Y}_{\text{cs}}}$
is defined over the base field
![]() $S$
, it must correspond to the trivial character. It follows that we can choose the indexing of the toric types such that
$S$
, it must correspond to the trivial character. It follows that we can choose the indexing of the toric types such that
![]() $a_{i}=a_{i}^{\prime }$
whenever
$a_{i}=a_{i}^{\prime }$
whenever
 $1\leqslant i\leqslant r$
and
$1\leqslant i\leqslant r$
and
![]() $a_{i}^{\prime }=0$
whenever
$a_{i}^{\prime }=0$
whenever
![]() $i>r$
. In particular, this implies (ii). Furthermore, the difference
$i>r$
. In particular, this implies (ii). Furthermore, the difference
![]() $r^{\prime }-r$
is easily seen to be equal to the relative dimension of
$r^{\prime }-r$
is easily seen to be equal to the relative dimension of
![]() $f$
, which implies (i).
$f$
, which implies (i).
Next we instead assume that
![]() $f$
is a gerbe. In this case we have
$f$
is a gerbe. In this case we have
![]() $r^{\prime }=r$
since the relative dimensions of
$r^{\prime }=r$
since the relative dimensions of
![]() $X$
and
$X$
and
![]() $Y$
over
$Y$
over
![]() $S$
are equal. Furthermore, all squares in the diagram (6.4) are 2-cartesian. We have a surjective group homomorphism
$S$
are equal. Furthermore, all squares in the diagram (6.4) are 2-cartesian. We have a surjective group homomorphism
 $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}\rightarrow \unicode[STIX]{x1D6E5}_{f\circ \unicode[STIX]{x1D709}}$
, which allows us to identify
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}\rightarrow \unicode[STIX]{x1D6E5}_{f\circ \unicode[STIX]{x1D709}}$
, which allows us to identify
![]() $A$
with a subgroup of
$A$
with a subgroup of
![]() $A^{\prime }$
. Since conormal bundles commute with flat base change, we get
$A^{\prime }$
. Since conormal bundles commute with flat base change, we get
 $$\begin{eqnarray}{\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/Y}=a^{\ast }{\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{f\circ \unicode[STIX]{x1D709}}/X}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/Y}=a^{\ast }{\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{f\circ \unicode[STIX]{x1D709}}/X}.\end{eqnarray}$$
The pull-back functor
 $a^{\ast }:\text{Coh}\,(\text{B}\unicode[STIX]{x1D6E5}_{f\circ \unicode[STIX]{x1D709}})\rightarrow \text{Coh}\,(\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}})$
corresponds to the obvious functor from the category of
$a^{\ast }:\text{Coh}\,(\text{B}\unicode[STIX]{x1D6E5}_{f\circ \unicode[STIX]{x1D709}})\rightarrow \text{Coh}\,(\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}})$
corresponds to the obvious functor from the category of
![]() $A$
-graded vector spaces to the category of
$A$
-graded vector spaces to the category of
![]() $A^{\prime }$
-graded vector spaces, which preserves the grading. This implies that
$A^{\prime }$
-graded vector spaces, which preserves the grading. This implies that
![]() $a_{i}^{\prime }=a_{i}$
for
$a_{i}^{\prime }=a_{i}$
for
 $1\leqslant i\leqslant r$
for a suitable indexing of the toric types. A similar argument applied to the right-hand diagram in (6.4) shows that we also have
$1\leqslant i\leqslant r$
for a suitable indexing of the toric types. A similar argument applied to the right-hand diagram in (6.4) shows that we also have
![]() $e_{i}^{\prime }=e_{i}$
, which proves (iii).◻
$e_{i}^{\prime }=e_{i}$
, which proves (iii).◻
As a direct consequence of Proposition 6.14, it follows that realisations of conormal invariants are upper semi-continuous.
Proposition 6.15. Let
 $\unicode[STIX]{x1D704}:U\rightarrow W$
be a conormal invariant and let
$\unicode[STIX]{x1D704}:U\rightarrow W$
be a conormal invariant and let
![]() $(X,\boldsymbol{E})$
be a standard pair with diagonalisable stabilisers. Then the realisation
$(X,\boldsymbol{E})$
be a standard pair with diagonalisable stabilisers. Then the realisation
 $\unicode[STIX]{x1D704}_{(X,\boldsymbol{E})/S}$
is an upper semi-continuous function. In particular, the locus where
$\unicode[STIX]{x1D704}_{(X,\boldsymbol{E})/S}$
is an upper semi-continuous function. In particular, the locus where
 $\unicode[STIX]{x1D704}_{(X,\boldsymbol{E})/S}$
obtains a maximum is a closed subset of
$\unicode[STIX]{x1D704}_{(X,\boldsymbol{E})/S}$
obtains a maximum is a closed subset of
![]() $|X|$
.
$|X|$
.
Proof. Since the property of being semi-continuous is preserved under post composition by order-preserving functions, it is enough to verify semi-continuity for the toric type. Furthermore, it is enough to verify that the locus
![]() $Z\subset X$
where the toric type is maximal is closed. If
$Z\subset X$
where the toric type is maximal is closed. If
![]() $X$
is a basic toric stack and
$X$
is a basic toric stack and
![]() $\boldsymbol{E}$
a subset of the toric divisors, this is clear from the computation of toric types for basic toric stacks given in Proposition 6.5 and the construction of the order relation in Definition 6.7. In general, we may choose a toric chart
$\boldsymbol{E}$
a subset of the toric divisors, this is clear from the computation of toric types for basic toric stacks given in Proposition 6.5 and the construction of the order relation in Definition 6.7. In general, we may choose a toric chart

as in Definition 5.1, at any point
![]() $\unicode[STIX]{x1D709}\in X$
by Proposition 5.3. Since the property of
$\unicode[STIX]{x1D709}\in X$
by Proposition 5.3. Since the property of
![]() $Z$
being closed can be verified locally on
$Z$
being closed can be verified locally on
![]() $X$
, we may assume that
$X$
, we may assume that
![]() $f$
is surjective. Let
$f$
is surjective. Let
![]() $Z^{\prime }$
and
$Z^{\prime }$
and
![]() $Z^{\prime \prime }$
denote the loci where the toric type is maximal in
$Z^{\prime \prime }$
denote the loci where the toric type is maximal in
![]() $X^{\prime }$
and
$X^{\prime }$
and
![]() $X^{\prime \prime }$
, respectively. Since both
$X^{\prime \prime }$
, respectively. Since both
![]() $f$
and
$f$
and
![]() $g$
are étale and stabiliser-preserving, we have
$g$
are étale and stabiliser-preserving, we have
 $Z^{\prime }=f^{-1}(Z)=g^{-1}(Z^{\prime \prime })$
by Proposition 6.14(i). Since
$Z^{\prime }=f^{-1}(Z)=g^{-1}(Z^{\prime \prime })$
by Proposition 6.14(i). Since
![]() $X^{\prime \prime }$
is a basic toric stack, the locus
$X^{\prime \prime }$
is a basic toric stack, the locus
![]() $Z^{\prime \prime }$
is closed. Hence,
$Z^{\prime \prime }$
is closed. Hence,
![]() $Z^{\prime }$
is closed by continuity of
$Z^{\prime }$
is closed by continuity of
![]() $g$
. Since
$g$
. Since
![]() $f$
is submersive, it follows that also
$f$
is submersive, it follows that also
![]() $Z$
is closed, which concludes the proof.◻
$Z$
is closed, which concludes the proof.◻
In the destackification algorithm we need to blow up
![]() $X$
in a locus which is maximal with respect to some conormal invariant. Since we only want blow-ups with smooth centres, we need a criterion to ensure that the maximal locus has a structure of a smooth substack. If the base
$X$
in a locus which is maximal with respect to some conormal invariant. Since we only want blow-ups with smooth centres, we need a criterion to ensure that the maximal locus has a structure of a smooth substack. If the base
![]() $S$
is reduced, it is obvious that there can be at most one such structure, but in the general case this is not so clear. Fortunately, there exists a simple combinatorial condition, which is easy to verify in practice, which ensures both of these properties.
$S$
is reduced, it is obvious that there can be at most one such structure, but in the general case this is not so clear. Fortunately, there exists a simple combinatorial condition, which is easy to verify in practice, which ensures both of these properties.
Definition 6.16. Let
 $\unicode[STIX]{x1D704}:U\rightarrow W$
be a conormal invariant. We say that
$\unicode[STIX]{x1D704}:U\rightarrow W$
be a conormal invariant. We say that
![]() $\unicode[STIX]{x1D704}$
is smooth provided that for each finite ordered set
$\unicode[STIX]{x1D704}$
is smooth provided that for each finite ordered set
![]() $\boldsymbol{E}$
and each triple
$\boldsymbol{E}$
and each triple
 $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC}^{\prime },\unicode[STIX]{x1D6FC}^{\prime \prime }\in U(\boldsymbol{E})$
such that
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC}^{\prime },\unicode[STIX]{x1D6FC}^{\prime \prime }\in U(\boldsymbol{E})$
such that
![]() $\unicode[STIX]{x1D6FC}\geqslant \unicode[STIX]{x1D6FC}^{\prime }$
and
$\unicode[STIX]{x1D6FC}\geqslant \unicode[STIX]{x1D6FC}^{\prime }$
and
![]() $\unicode[STIX]{x1D6FC}\geqslant \unicode[STIX]{x1D6FC}^{\prime \prime }$
, the condition
$\unicode[STIX]{x1D6FC}\geqslant \unicode[STIX]{x1D6FC}^{\prime \prime }$
, the condition
 $\unicode[STIX]{x1D704}(\unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D704}(\unicode[STIX]{x1D6FC}^{\prime })=\unicode[STIX]{x1D704}(\unicode[STIX]{x1D6FC}^{\prime \prime })$
implies that
$\unicode[STIX]{x1D704}(\unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D704}(\unicode[STIX]{x1D6FC}^{\prime })=\unicode[STIX]{x1D704}(\unicode[STIX]{x1D6FC}^{\prime \prime })$
implies that
 $\unicode[STIX]{x1D704}(\unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D704}(\unicode[STIX]{x1D6FC}^{\prime }\wedge \unicode[STIX]{x1D6FC}^{\prime \prime })$
.
$\unicode[STIX]{x1D704}(\unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D704}(\unicode[STIX]{x1D6FC}^{\prime }\wedge \unicode[STIX]{x1D6FC}^{\prime \prime })$
.
This definition has a rather combinatorial flavour. To get a feeling for what it means geometrically, it is useful to note that the order relation
![]() ${\geqslant}$
on the set
${\geqslant}$
on the set
![]() $U(\boldsymbol{E})$
corresponds to generalisation in the following sense: if
$U(\boldsymbol{E})$
corresponds to generalisation in the following sense: if
![]() $(X,\boldsymbol{E})$
is a standard pair and
$(X,\boldsymbol{E})$
is a standard pair and
 $Z_{\unicode[STIX]{x1D6FC}}\subseteq X$
denotes the locus with toric type
$Z_{\unicode[STIX]{x1D6FC}}\subseteq X$
denotes the locus with toric type
 $\unicode[STIX]{x1D6FC}\in U(\boldsymbol{E})$
, then
$\unicode[STIX]{x1D6FC}\in U(\boldsymbol{E})$
, then
![]() $\unicode[STIX]{x1D6FC}^{\prime }\leqslant \unicode[STIX]{x1D6FC}$
implies that
$\unicode[STIX]{x1D6FC}^{\prime }\leqslant \unicode[STIX]{x1D6FC}$
implies that
![]() $Z_{\unicode[STIX]{x1D6FC}}$
lies in the closure of
$Z_{\unicode[STIX]{x1D6FC}}$
lies in the closure of
![]() $Z_{\unicode[STIX]{x1D6FC}}^{\prime }$
. Thus, Definition 6.16 has the following interpretation: let
$Z_{\unicode[STIX]{x1D6FC}}^{\prime }$
. Thus, Definition 6.16 has the following interpretation: let
![]() $(X,\boldsymbol{E})$
be a standard pair and consider a smooth conormal invariant
$(X,\boldsymbol{E})$
be a standard pair and consider a smooth conormal invariant
![]() $\unicode[STIX]{x1D704}$
. Assume that
$\unicode[STIX]{x1D704}$
. Assume that
![]() $\unicode[STIX]{x1D709}\in X$
is a point where (the realisation of)
$\unicode[STIX]{x1D709}\in X$
is a point where (the realisation of)
![]() $\unicode[STIX]{x1D704}$
assumes it maximum. If the invariant
$\unicode[STIX]{x1D704}$
assumes it maximum. If the invariant
![]() $\unicode[STIX]{x1D704}$
remains constant when we generalise in two different directions separately, then it must remain constant if we generalise in both these directions at the same time.
$\unicode[STIX]{x1D704}$
remains constant when we generalise in two different directions separately, then it must remain constant if we generalise in both these directions at the same time.
Example 6.17. All the conormal invariants given in Examples 6.10 and 6.11 are smooth, but since we are not going to use this fact, its proof is left to the reader.
Example 6.18. To understand the condition in Definition 6.16, it is useful to study a situation where it is not satisfied. Let
![]() $\unicode[STIX]{x1D70F}$
be the conormal invariant which takes a toric type represented by
$\unicode[STIX]{x1D70F}$
be the conormal invariant which takes a toric type represented by
![]() $(A,\boldsymbol{v})$
to the number of elements
$(A,\boldsymbol{v})$
to the number of elements
 $v_{i}=(a_{i},e_{i})$
in the sequence
$v_{i}=(a_{i},e_{i})$
in the sequence
![]() $\boldsymbol{v}$
satisfying
$\boldsymbol{v}$
satisfying
![]() $a_{i}\neq 0$
and
$a_{i}\neq 0$
and
![]() $e_{i}=\ast$
. Consider the case where
$e_{i}=\ast$
. Consider the case where
 $\boldsymbol{E}=(E^{1},E^{2})$
and the toric type
$\boldsymbol{E}=(E^{1},E^{2})$
and the toric type
![]() $\unicode[STIX]{x1D6FC}$
is represented by
$\unicode[STIX]{x1D6FC}$
is represented by
![]() $(A,\boldsymbol{v})$
, where
$(A,\boldsymbol{v})$
, where
 $A=C_{2}\times C_{2}$
and
$A=C_{2}\times C_{2}$
and
![]() $\boldsymbol{v}$
has three elements
$\boldsymbol{v}$
has three elements
 $v_{i}=(a_{i},e_{i})$
with
$v_{i}=(a_{i},e_{i})$
with
 $$\begin{eqnarray}a_{1}=(1,0),\quad a_{2}=(0,1),\quad a_{3}=(1,1),\quad e_{1}=E^{1},\quad e_{2}=E^{2},\quad e_{3}=\ast .\end{eqnarray}$$
$$\begin{eqnarray}a_{1}=(1,0),\quad a_{2}=(0,1),\quad a_{3}=(1,1),\quad e_{1}=E^{1},\quad e_{2}=E^{2},\quad e_{3}=\ast .\end{eqnarray}$$
Then
 $\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FC})=1$
. The basic toric stack over the field
$\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FC})=1$
. The basic toric stack over the field
![]() $k$
associated to this toric type has homogeneous coordinate ring
$k$
associated to this toric type has homogeneous coordinate ring
 $(k[x_{1},x_{2},x_{3}],A,(a_{1},a_{2},a_{3}))$
with
$(k[x_{1},x_{2},x_{3}],A,(a_{1},a_{2},a_{3}))$
with
 $E^{1}=V(x_{1})$
and
$E^{1}=V(x_{1})$
and
 $E^{2}=V(x_{2})$
. One verifies that the invariant
$E^{2}=V(x_{2})$
. One verifies that the invariant
![]() $\unicode[STIX]{x1D70F}$
assumes the value 1 at the locus
$\unicode[STIX]{x1D70F}$
assumes the value 1 at the locus
 $(V(x_{1})\cup V(x_{2}))\cap V(x_{3})$
and 0 outside this locus. In other words, if we start in the origin, the invariant
$(V(x_{1})\cup V(x_{2}))\cap V(x_{3})$
and 0 outside this locus. In other words, if we start in the origin, the invariant
![]() $\unicode[STIX]{x1D70F}$
remains constant if we generalise in the
$\unicode[STIX]{x1D70F}$
remains constant if we generalise in the
![]() $x_{1}$
or the
$x_{1}$
or the
![]() $x_{2}$
directions separately, but not if we generalise in both these directions at the same time. In particular, the locus where
$x_{2}$
directions separately, but not if we generalise in both these directions at the same time. In particular, the locus where
![]() $\unicode[STIX]{x1D70F}$
assumes its maximum is not smooth.
$\unicode[STIX]{x1D70F}$
assumes its maximum is not smooth.
As a side remark, the conormal invariant
![]() $\unicode[STIX]{x1D70F}$
actually plays a role in the destackification algorithm and will be introduced as the toroidal index in Definition 7.4 in the next section.
$\unicode[STIX]{x1D70F}$
actually plays a role in the destackification algorithm and will be introduced as the toroidal index in Definition 7.4 in the next section.
Proposition 6.19. Let
 $(X,\boldsymbol{E})/S$
be a standard pair with diagonalisable stabilisers and let
$(X,\boldsymbol{E})/S$
be a standard pair with diagonalisable stabilisers and let
 $\unicode[STIX]{x1D704}:U\rightarrow W$
be a smooth conormal invariant. Let
$\unicode[STIX]{x1D704}:U\rightarrow W$
be a smooth conormal invariant. Let
![]() $m$
be a maximal value for
$m$
be a maximal value for
 $\unicode[STIX]{x1D704}_{(X,\boldsymbol{E})/S}$
. Then the locus where
$\unicode[STIX]{x1D704}_{(X,\boldsymbol{E})/S}$
. Then the locus where
 $\unicode[STIX]{x1D704}_{(X,\boldsymbol{E})/S}$
obtains
$\unicode[STIX]{x1D704}_{(X,\boldsymbol{E})/S}$
obtains
![]() $m$
has a unique structure of a smooth substack of
$m$
has a unique structure of a smooth substack of
![]() $X$
having normal crossings with
$X$
having normal crossings with
![]() $\boldsymbol{E}$
.
$\boldsymbol{E}$
.
Proof. The question is local on the base, so we may assume that
 $S=\text{Spec}\,R$
is affine. By a standard limit argument, we may also assume that
$S=\text{Spec}\,R$
is affine. By a standard limit argument, we may also assume that
![]() $R$
is noetherian.
$R$
is noetherian.
We start by investigating the situation locally. Let
![]() $X$
be a basic toric stack with homogeneous coordinates
$X$
be a basic toric stack with homogeneous coordinates
 $$\begin{eqnarray}(R[x_{1},\ldots ,x_{r}],A,(a_{1},\ldots ,a_{r}))\end{eqnarray}$$
$$\begin{eqnarray}(R[x_{1},\ldots ,x_{r}],A,(a_{1},\ldots ,a_{r}))\end{eqnarray}$$
and let
 $\boldsymbol{E}=(E^{1},\ldots ,E^{s})$
, with
$\boldsymbol{E}=(E^{1},\ldots ,E^{s})$
, with
 $E^{i}=V(x_{i})$
for some
$E^{i}=V(x_{i})$
for some
![]() $s\leqslant r$
.
$s\leqslant r$
.
Now let
 $\unicode[STIX]{x1D6FC}=(A,\boldsymbol{v})$
be the toric type at the origin, and let
$\unicode[STIX]{x1D6FC}=(A,\boldsymbol{v})$
be the toric type at the origin, and let
 $\unicode[STIX]{x1D6FD}=(A^{\prime },\boldsymbol{v}^{\prime })$
be the greatest lower bound of the set
$\unicode[STIX]{x1D6FD}=(A^{\prime },\boldsymbol{v}^{\prime })$
be the greatest lower bound of the set
 $\{\unicode[STIX]{x1D6FC}^{\prime }\mid \unicode[STIX]{x1D6FC}\geqslant \unicode[STIX]{x1D6FC}^{\prime },\unicode[STIX]{x1D704}(\unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D704}(\unicode[STIX]{x1D6FC}^{\prime })\}$
. Such an element exists since the set is finite, and it is contained in the set by the smoothness hypothesis for
$\{\unicode[STIX]{x1D6FC}^{\prime }\mid \unicode[STIX]{x1D6FC}\geqslant \unicode[STIX]{x1D6FC}^{\prime },\unicode[STIX]{x1D704}(\unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D704}(\unicode[STIX]{x1D6FC}^{\prime })\}$
. Such an element exists since the set is finite, and it is contained in the set by the smoothness hypothesis for
![]() $\unicode[STIX]{x1D704}$
. Let
$\unicode[STIX]{x1D704}$
. Let
 $J\subseteq \{1,\ldots ,r\}$
be the maximal subset defining the relation
$J\subseteq \{1,\ldots ,r\}$
be the maximal subset defining the relation
![]() $\unicode[STIX]{x1D6FD}\leqslant \unicode[STIX]{x1D6FC}$
as in Definition 6.7, and let
$\unicode[STIX]{x1D6FD}\leqslant \unicode[STIX]{x1D6FC}$
as in Definition 6.7, and let
![]() $K$
be the kernel of the canonical group homomorphism
$K$
be the kernel of the canonical group homomorphism
 $A\rightarrow A^{\prime }$
. Furthermore, define
$A\rightarrow A^{\prime }$
. Furthermore, define
 $O=\{1,\ldots ,s\}\setminus J$
and
$O=\{1,\ldots ,s\}\setminus J$
and
 $P=\{s+1,\ldots ,r\}\setminus J$
. From the explicit description of the toric type for a basic toric stack given in Proposition 6.5, it is easy to see that the maximal locus for
$P=\{s+1,\ldots ,r\}\setminus J$
. From the explicit description of the toric type for a basic toric stack given in Proposition 6.5, it is easy to see that the maximal locus for
 $\unicode[STIX]{x1D704}_{(X,\boldsymbol{E})/S}$
is
$\unicode[STIX]{x1D704}_{(X,\boldsymbol{E})/S}$
is
 $Z=V(x_{i}\mid i\in O\cup P)$
. In particular, the substack
$Z=V(x_{i}\mid i\in O\cup P)$
. In particular, the substack
![]() $Z$
is smooth. The locus
$Z$
is smooth. The locus
 $F=V(x_{i}\mid i\in O)$
is the intersection of the divisors
$F=V(x_{i}\mid i\in O)$
is the intersection of the divisors
![]() $E^{i}$
containing
$E^{i}$
containing
![]() $Z$
.
$Z$
.
If
![]() $S$
is reduced, the substack
$S$
is reduced, the substack
![]() $Z\subset X$
is clearly the only substack structure on the underlying space
$Z\subset X$
is clearly the only substack structure on the underlying space
![]() $|Z|$
of the required form. If
$|Z|$
of the required form. If
![]() $S$
is non-reduced, we can, by the noetherian hypothesis, factor the map
$S$
is non-reduced, we can, by the noetherian hypothesis, factor the map
 $S_{\text{red}}{\hookrightarrow}S$
into a finite sequence of nilpotent thickenings defined by square zero ideals. It is enough to show that the substack structure of
$S_{\text{red}}{\hookrightarrow}S$
into a finite sequence of nilpotent thickenings defined by square zero ideals. It is enough to show that the substack structure of
![]() $Z_{\text{red}}$
lifts uniquely at each step. This reduces the situation to the following deformation problem:
$Z_{\text{red}}$
lifts uniquely at each step. This reduces the situation to the following deformation problem:

where the map
 $S_{0}\rightarrow S$
is a nilpotent thickening defined by a square zero ideal
$S_{0}\rightarrow S$
is a nilpotent thickening defined by a square zero ideal
![]() $N$
. We want to show that the stack
$N$
. We want to show that the stack
![]() $Z$
, together with the dashed arrows, is essentially the only stack fitting into the diagram, in a way such that the leftmost square becomes cartesian and the stack becomes smooth over
$Z$
, together with the dashed arrows, is essentially the only stack fitting into the diagram, in a way such that the leftmost square becomes cartesian and the stack becomes smooth over
![]() $S$
. Note that, since we require
$S$
. Note that, since we require
![]() $Z$
to have normal crossings with
$Z$
to have normal crossings with
![]() $\boldsymbol{E}$
, we deform
$\boldsymbol{E}$
, we deform
![]() $Z$
inside
$Z$
inside
![]() $F$
and not inside
$F$
and not inside
![]() $X$
. Let
$X$
. Let
![]() $I$
be the ideal
$I$
be the ideal
 $\langle x_{i}\mid i\in P\rangle$
in the homogeneous coordinate ring of
$\langle x_{i}\mid i\in P\rangle$
in the homogeneous coordinate ring of
![]() $F_{0}$
and let
$F_{0}$
and let
![]() ${\mathcal{I}}$
be the corresponding ideal in
${\mathcal{I}}$
be the corresponding ideal in
![]() ${\mathcal{O}}_{F_{0}}$
. Let
${\mathcal{O}}_{F_{0}}$
. Let
![]() ${\mathcal{M}}$
be the sheaf of
${\mathcal{M}}$
be the sheaf of
![]() ${\mathcal{O}}_{Z_{0}}$
-modules
${\mathcal{O}}_{Z_{0}}$
-modules
 ${\mathcal{H}}om_{{\mathcal{O}}_{Z_{0}}}({\mathcal{I}}/{\mathcal{I}}^{2},N\otimes {\mathcal{O}}_{Z_{0}})$
. Then the set of objects completing the diagram is a torsor under the group
${\mathcal{H}}om_{{\mathcal{O}}_{Z_{0}}}({\mathcal{I}}/{\mathcal{I}}^{2},N\otimes {\mathcal{O}}_{Z_{0}})$
. Then the set of objects completing the diagram is a torsor under the group
 $\text{H}^{0}(Z_{0},{\mathcal{M}})$
. The sheaf
$\text{H}^{0}(Z_{0},{\mathcal{M}})$
. The sheaf
![]() ${\mathcal{M}}$
corresponds to the graded
${\mathcal{M}}$
corresponds to the graded
![]() $R^{\prime }$
-module
$R^{\prime }$
-module
 $$\begin{eqnarray}M^{\bullet }=\text{Hom}_{R^{\prime }}^{\bullet }(I/I^{2},N\otimes R^{\prime }),\end{eqnarray}$$
$$\begin{eqnarray}M^{\bullet }=\text{Hom}_{R^{\prime }}^{\bullet }(I/I^{2},N\otimes R^{\prime }),\end{eqnarray}$$
where
![]() $R^{\prime }$
is the
$R^{\prime }$
is the
![]() $A$
-graded ring
$A$
-graded ring
 $R[x_{1},\ldots ,x_{s}]/\langle x_{i}\mid i\in O\cup P\rangle$
. The global sections functor factors through the pushforward functor
$R[x_{1},\ldots ,x_{s}]/\langle x_{i}\mid i\in O\cup P\rangle$
. The global sections functor factors through the pushforward functor
![]() $\unicode[STIX]{x1D70B}_{\ast }$
, where
$\unicode[STIX]{x1D70B}_{\ast }$
, where
 $\unicode[STIX]{x1D70B}:Z_{0}\rightarrow (Z_{0})_{\text{cs}}$
is the map to the coarse space, and
$\unicode[STIX]{x1D70B}:Z_{0}\rightarrow (Z_{0})_{\text{cs}}$
is the map to the coarse space, and
![]() $\unicode[STIX]{x1D70B}_{\ast }{\mathcal{M}}$
is simply the degree-zero part of
$\unicode[STIX]{x1D70B}_{\ast }{\mathcal{M}}$
is simply the degree-zero part of
![]() $M^{\bullet }$
, viewed as an
$M^{\bullet }$
, viewed as an
![]() $(R^{\prime })^{0}$
-module. But the homogeneous elements of
$(R^{\prime })^{0}$
-module. But the homogeneous elements of
![]() $R^{\prime }$
have degrees in
$R^{\prime }$
have degrees in
![]() $K$
, whereas
$K$
, whereas
![]() $I$
is generated by homogeneous elements with degrees not in
$I$
is generated by homogeneous elements with degrees not in
![]() $K$
. It follows that the degree-zero part of
$K$
. It follows that the degree-zero part of
![]() $M^{\bullet }$
is the zero module, which shows that the lift of
$M^{\bullet }$
is the zero module, which shows that the lift of
![]() $Z_{0}$
is unique.
$Z_{0}$
is unique.
Now let
 $X^{\prime }\rightarrow X$
be an étale stabiliser-preserving map. Denote the pull-backs of
$X^{\prime }\rightarrow X$
be an étale stabiliser-preserving map. Denote the pull-backs of
![]() $Z_{0}$
and
$Z_{0}$
and
![]() $Z$
by
$Z$
by
![]() $Z_{0}^{\prime }$
and
$Z_{0}^{\prime }$
and
![]() $Z^{\prime }$
, respectively. The natural map
$Z^{\prime }$
, respectively. The natural map
 $Z_{0}^{\prime }\rightarrow Z_{0}$
is also étale and stabiliser-preserving. By flatness, the sheaf
$Z_{0}^{\prime }\rightarrow Z_{0}$
is also étale and stabiliser-preserving. By flatness, the sheaf
![]() ${\mathcal{M}}$
pulls back to the sheaf
${\mathcal{M}}$
pulls back to the sheaf
 ${\mathcal{M}}^{\prime }={\mathcal{H}}om_{{\mathcal{O}}_{Z_{0}^{\prime }}}({\mathcal{I}}^{\prime }/({\mathcal{I}}^{\prime })^{2},N\otimes {\mathcal{O}}_{Z_{0}^{\prime }})$
, where
${\mathcal{M}}^{\prime }={\mathcal{H}}om_{{\mathcal{O}}_{Z_{0}^{\prime }}}({\mathcal{I}}^{\prime }/({\mathcal{I}}^{\prime })^{2},N\otimes {\mathcal{O}}_{Z_{0}^{\prime }})$
, where
![]() ${\mathcal{I}}^{\prime }$
is the ideal sheaf defining
${\mathcal{I}}^{\prime }$
is the ideal sheaf defining
![]() $Z_{0}^{\prime }$
in
$Z_{0}^{\prime }$
in
![]() $X_{0}$
. The square
$X_{0}$
. The square

formed by the maps to the coarse spaces is cartesian and the horizontal maps are étale. Hence, also
 $\text{H}^{0}(Z_{0}^{\prime },{\mathcal{M}}^{\prime })=0$
, and we get unicity for the closed substack
$\text{H}^{0}(Z_{0}^{\prime },{\mathcal{M}}^{\prime })=0$
, and we get unicity for the closed substack
 $Z^{\prime }\subset X^{\prime }$
. A general stack
$Z^{\prime }\subset X^{\prime }$
. A general stack
 $(X^{\prime \prime },E^{\prime \prime })$
satisfying the standard hypothesis can be covered by stacks as
$(X^{\prime \prime },E^{\prime \prime })$
satisfying the standard hypothesis can be covered by stacks as
![]() $X^{\prime }$
above. The unicity of
$X^{\prime }$
above. The unicity of
 $Z^{\prime }\subset X^{\prime }$
asserts that the stack structure descends to a closed substack
$Z^{\prime }\subset X^{\prime }$
asserts that the stack structure descends to a closed substack
![]() $Z^{\prime \prime }$
of
$Z^{\prime \prime }$
of
![]() $X^{\prime \prime }$
, as desired.◻
$X^{\prime \prime }$
, as desired.◻
7 Outline of the algorithms
In this section, we outline the destackification algorithms. We also introduce the various conormal invariants used by the algorithms and describe how they are used. All invariants we define, except the divisorial type, take values among the natural numbers.
Definition 7.1 (Independency index).
Let
 $\unicode[STIX]{x1D6FC}=(A,\boldsymbol{v})$
be a toric type with
$\unicode[STIX]{x1D6FC}=(A,\boldsymbol{v})$
be a toric type with
 $\boldsymbol{v}=(v_{1},\ldots ,v_{r})$
and
$\boldsymbol{v}=(v_{1},\ldots ,v_{r})$
and
 $v_{j}=(a_{j},e_{j})$
. An element
$v_{j}=(a_{j},e_{j})$
. An element
![]() $v_{j}$
of the sequence
$v_{j}$
of the sequence
![]() $\boldsymbol{v}$
is called independent if the intersection
$\boldsymbol{v}$
is called independent if the intersection
 $$\begin{eqnarray}\displaystyle \langle a_{j}\rangle \cap \langle a_{1},\ldots ,\widehat{a}_{j},\ldots ,a_{r}\rangle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle a_{j}\rangle \cap \langle a_{1},\ldots ,\widehat{a}_{j},\ldots ,a_{r}\rangle & & \displaystyle\end{eqnarray}$$
is the trivial subgroup. The independency index of
![]() $\unicode[STIX]{x1D6FC}$
is the number of elements in the sequence
$\unicode[STIX]{x1D6FC}$
is the number of elements in the sequence
![]() $\boldsymbol{v}$
which are not independent.
$\boldsymbol{v}$
which are not independent.
The following definition is a direct generalisation of the concept of independency for toric divisors on toric stacks (see Definition 3.17).
Definition 7.2. Let
 $(X,\boldsymbol{E})/S$
be a standard pair with diagonalisable stabilisers. Let
$(X,\boldsymbol{E})/S$
be a standard pair with diagonalisable stabilisers. Let
![]() $\unicode[STIX]{x1D709}$
be a point in
$\unicode[STIX]{x1D709}$
be a point in
![]() $X$
and
$X$
and
![]() $E$
a component of
$E$
a component of
![]() $\boldsymbol{E}$
passing through
$\boldsymbol{E}$
passing through
![]() $\unicode[STIX]{x1D709}$
. Assume that the toric type at
$\unicode[STIX]{x1D709}$
. Assume that the toric type at
![]() $\unicode[STIX]{x1D709}$
is
$\unicode[STIX]{x1D709}$
is
![]() $(A,\boldsymbol{v})$
. Then
$(A,\boldsymbol{v})$
. Then
![]() $E$
is said to be independent at
$E$
is said to be independent at
![]() $\unicode[STIX]{x1D709}$
provided that the element in
$\unicode[STIX]{x1D709}$
provided that the element in
![]() $\boldsymbol{v}$
marked by
$\boldsymbol{v}$
marked by
![]() $E$
is independent in the sense of Definition 7.1. The component
$E$
is independent in the sense of Definition 7.1. The component
![]() $E$
is said to be independent if it is independent at each of its points.
$E$
is said to be independent if it is independent at each of its points.
The independency index measures how far the coarse space
![]() $X_{\text{cs}}$
is from being smooth. In particular, the invariant vanishes at a point
$X_{\text{cs}}$
is from being smooth. In particular, the invariant vanishes at a point
![]() $\unicode[STIX]{x1D709}\in |X|$
precisely when
$\unicode[STIX]{x1D709}\in |X|$
precisely when
![]() $X_{\text{cs}}$
is smooth at the corresponding point. This easily follows from Propositions 3.18 and 3.19 by using local homogeneous coordinates as described in §5. Thus, one of the main objectives of the destackification process is to make this invariant vanish.
$X_{\text{cs}}$
is smooth at the corresponding point. This easily follows from Propositions 3.18 and 3.19 by using local homogeneous coordinates as described in §5. Thus, one of the main objectives of the destackification process is to make this invariant vanish.
Table 7.1. The table shows some conormal invariants computed for various toric types. The columns marked by
![]() $\unicode[STIX]{x1D704}$
,
$\unicode[STIX]{x1D704}$
,
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $\unicode[STIX]{x1D6FF}$
contain the independency index, the toroidal index and the divisorial index, respectively. The column marked by
$\unicode[STIX]{x1D6FF}$
contain the independency index, the toroidal index and the divisorial index, respectively. The column marked by
![]() $\unicode[STIX]{x1D6FF}_{i}$
, for
$\unicode[STIX]{x1D6FF}_{i}$
, for
 $i\in \{1,2,3,4\}$
, contains the
$i\in \{1,2,3,4\}$
, contains the
![]() $E^{i}$
-divisorial index.
$E^{i}$
-divisorial index.

Example 7.3. Table 7.1 gives several examples where the various conormal invariants introduced in this section are computed. An example where the independency index does not vanish is given in row 3. Here
![]() $v_{1}$
and
$v_{1}$
and
![]() $v_{4}$
are independent whereas
$v_{4}$
are independent whereas
![]() $v_{2}$
and
$v_{2}$
and
![]() $v_{3}$
are not. Hence, the independency index is 2.
$v_{3}$
are not. Hence, the independency index is 2.
Although the independency index is a smooth conormal invariant, in the sense of Definition 6.16, it is not fruitful to just repeatedly blow up the locus where the invariant assumes its maximum, as was demonstrated in Example 4.3. Instead we would like to use the combinatorial approach described in Algorithm A. This requires that we have enough globally defined divisors to work with. We introduce a conormal invariant that quantifies this.
Definition 7.4 (Toroidal index).
Let
 $\unicode[STIX]{x1D6FC}=(A,\boldsymbol{v})$
be a toric type with
$\unicode[STIX]{x1D6FC}=(A,\boldsymbol{v})$
be a toric type with
 $\boldsymbol{v}=(v_{1},\ldots ,v_{r})$
and
$\boldsymbol{v}=(v_{1},\ldots ,v_{r})$
and
 $v_{i}=(a_{i},e_{i})$
. The toroidal index of
$v_{i}=(a_{i},e_{i})$
. The toroidal index of
![]() $\unicode[STIX]{x1D6FC}$
is the number of elements in the sequence
$\unicode[STIX]{x1D6FC}$
is the number of elements in the sequence
![]() $\boldsymbol{v}$
which are unmarked and have non-trivial weight. That is, the number of elements
$\boldsymbol{v}$
which are unmarked and have non-trivial weight. That is, the number of elements
![]() $v_{i}$
of the form
$v_{i}$
of the form
 $v_{i}=(a_{i},\ast )$
with
$v_{i}=(a_{i},\ast )$
with
![]() $a_{i}\neq 0$
. If the toroidal index is zero at a point
$a_{i}\neq 0$
. If the toroidal index is zero at a point
![]() $\unicode[STIX]{x1D709}\in X$
, we say that
$\unicode[STIX]{x1D709}\in X$
, we say that
 $(X,\boldsymbol{E})/S$
is toroidal at
$(X,\boldsymbol{E})/S$
is toroidal at
![]() $\unicode[STIX]{x1D709}$
. The standard pair
$\unicode[STIX]{x1D709}$
. The standard pair
 $(X,\boldsymbol{E})/S$
is toroidal if it is toroidal at each of its points.
$(X,\boldsymbol{E})/S$
is toroidal if it is toroidal at each of its points.
Remark 7.5. This definition of toroidal stack is closely related to the classical definition of toroidal variety given in [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73]. By using local homogeneous coordinates, it is easy to see that a stack is toroidal at a point
![]() $\unicode[STIX]{x1D709}$
precisely when it has a toric chart at
$\unicode[STIX]{x1D709}$
precisely when it has a toric chart at
![]() $\unicode[STIX]{x1D709}$
, which is compatible with
$\unicode[STIX]{x1D709}$
, which is compatible with
![]() $\boldsymbol{E}$
in the sense of Definition 5.1, such that
$\boldsymbol{E}$
in the sense of Definition 5.1, such that
![]() $\boldsymbol{E}(\unicode[STIX]{x1D709})$
is in one-to-one correspondence with the toric divisors of the chart. If
$\boldsymbol{E}(\unicode[STIX]{x1D709})$
is in one-to-one correspondence with the toric divisors of the chart. If
![]() $S$
is the spectrum of a field, this implies that the pair
$S$
is the spectrum of a field, this implies that the pair
 $(X_{\text{cs}},U_{\text{cs}})$
is a toroidal variety in the sense of [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73], where
$(X_{\text{cs}},U_{\text{cs}})$
is a toroidal variety in the sense of [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73], where
![]() $U_{\text{cs}}$
is the coarse space of the complement of the support of
$U_{\text{cs}}$
is the coarse space of the complement of the support of
![]() $\boldsymbol{E}$
. More generally, if
$\boldsymbol{E}$
. More generally, if
![]() $S$
is a scheme, then
$S$
is a scheme, then
 $(X_{\text{cs}},U_{\text{cs}})/S$
is a flat family of toroidal varieties. It should be noted that since we assume that our toric stacks are simplicial, not every toroidal variety can be constructed in this way.
$(X_{\text{cs}},U_{\text{cs}})/S$
is a flat family of toroidal varieties. It should be noted that since we assume that our toric stacks are simplicial, not every toroidal variety can be constructed in this way.
Let
![]() $(X,\boldsymbol{E})$
be a standard pair. The following example illustrates that in order to obtain a destackification in the sense of Definition 2.3, it is necessary to bring both the independency index and the toroidal index to zero. That this is also sufficient, at least if the components of
$(X,\boldsymbol{E})$
be a standard pair. The following example illustrates that in order to obtain a destackification in the sense of Definition 2.3, it is necessary to bring both the independency index and the toroidal index to zero. That this is also sufficient, at least if the components of
![]() $\boldsymbol{E}$
are connected, will be proved in Proposition 8.7.
$\boldsymbol{E}$
are connected, will be proved in Proposition 8.7.
Example 7.6. Let
![]() $C$
be a nodal cubic in the projective plane
$C$
be a nodal cubic in the projective plane
![]() $\mathbb{P}_{k}^{2}$
, where
$\mathbb{P}_{k}^{2}$
, where
![]() $k$
is a field, and denote the node by
$k$
is a field, and denote the node by
![]() $P\in \mathbb{P}_{k}^{2}$
. By using the construction from [Reference Matsuki and OlssonMO05, Theorem 4.1], which is a generalisation of the root construction, it is possible to construct a stack
$P\in \mathbb{P}_{k}^{2}$
. By using the construction from [Reference Matsuki and OlssonMO05, Theorem 4.1], which is a generalisation of the root construction, it is possible to construct a stack
![]() $X$
with coarse space
$X$
with coarse space
![]() $\mathbb{P}^{2}$
such that the stabiliser over the smooth locus of
$\mathbb{P}^{2}$
such that the stabiliser over the smooth locus of
![]() $C$
is
$C$
is
![]() $\unicode[STIX]{x1D707}_{3}$
. Although the coarse space of
$\unicode[STIX]{x1D707}_{3}$
. Although the coarse space of
![]() $X$
is smooth, the standard pair
$X$
is smooth, the standard pair
![]() $(X,\emptyset )$
is not toroidal. The toric type at the point lying over the node of
$(X,\emptyset )$
is not toroidal. The toric type at the point lying over the node of
![]() $C$
will be as in row 2 of Table 7.1. Note that although
$C$
will be as in row 2 of Table 7.1. Note that although
![]() $X$
is a root stack over its coarse space over an étale neighbourhood of
$X$
is a root stack over its coarse space over an étale neighbourhood of
![]() $P$
, it is not possible to describe
$P$
, it is not possible to describe
![]() $X$
as a root stack of
$X$
as a root stack of
![]() $X_{\text{cs}}$
in any simple normal crossings divisor.
$X_{\text{cs}}$
in any simple normal crossings divisor.
Since the toric destackification process is essentially a global approach, some care must be taken when destackifying stacks which are not toric, but only toroidal. This is illustrated by the following example.
Example 7.7. Consider a two-dimensional toroidal stack
![]() $(X,\boldsymbol{E})$
, where
$(X,\boldsymbol{E})$
, where
![]() $\boldsymbol{E}$
has two components
$\boldsymbol{E}$
has two components
![]() $E^{1}$
and
$E^{1}$
and
![]() $E^{2}$
that intersect at two points
$E^{2}$
that intersect at two points
![]() $P$
and
$P$
and
![]() $Q$
.
$Q$
.

Assume that the independency index is 2 at
![]() $P$
and
$P$
and
![]() $Q$
. Clearly, we must blow up both
$Q$
. Clearly, we must blow up both
![]() $P$
and
$P$
and
![]() $Q$
during the destackification process, but not necessarily at the same time. Locally, at each of the points
$Q$
during the destackification process, but not necessarily at the same time. Locally, at each of the points
![]() $P$
and
$P$
and
![]() $Q$
, the stack
$Q$
, the stack
![]() $X$
is isomorphic to toric stacks, but these stacks need not be isomorphic to each other. Thus, it might be necessary to apply different combinatorial recipes to destackify the points. Even if they are isomorphic, the components
$X$
is isomorphic to toric stacks, but these stacks need not be isomorphic to each other. Thus, it might be necessary to apply different combinatorial recipes to destackify the points. Even if they are isomorphic, the components
![]() $E^{1}$
and
$E^{1}$
and
![]() $E^{2}$
may play different roles, so the order of the components are important.
$E^{2}$
may play different roles, so the order of the components are important.
The example shows that we need an invariant which captures the combinatorial recipe for destackification. In principle, we use the stacky cone describing the toric stack to which
![]() $X$
is locally isomorphic at the point in question. We shall, however, use a more algebraic description.
$X$
is locally isomorphic at the point in question. We shall, however, use a more algebraic description.
Definition 7.8 (Divisorial type).
Let
![]() $\boldsymbol{E}$
be a finite set. The set
$\boldsymbol{E}$
be a finite set. The set
![]() $T(\boldsymbol{E})$
of divisorial types parametrised by
$T(\boldsymbol{E})$
of divisorial types parametrised by
![]() $\boldsymbol{E}$
is the subset of the set
$\boldsymbol{E}$
is the subset of the set
![]() $U(\boldsymbol{E})$
of toric types consisting of elements represented by pairs
$U(\boldsymbol{E})$
of toric types consisting of elements represented by pairs
![]() $(A,\boldsymbol{v})$
such that:
$(A,\boldsymbol{v})$
such that:
-
(i) all elements in
 $\boldsymbol{v}$
are marked by some divisor in
$\boldsymbol{v}$
are marked by some divisor in
 $\boldsymbol{E}$
;
$\boldsymbol{E}$
; -
(ii) no element in
 $\boldsymbol{v}$
is independent in the sense of Definition 7.1;
$\boldsymbol{v}$
is independent in the sense of Definition 7.1; -
(iii) the group
 $A$
is generated by the weights of the elements of
$A$
is generated by the weights of the elements of
 $\boldsymbol{v}$
.
$\boldsymbol{v}$
.
Given a toric type
![]() $(A,\boldsymbol{v})$
, its associated divisorial type is the pair
$(A,\boldsymbol{v})$
, its associated divisorial type is the pair
![]() $(A^{\prime },\boldsymbol{v}^{\prime })$
, where
$(A^{\prime },\boldsymbol{v}^{\prime })$
, where
![]() $\boldsymbol{v}^{\prime }$
is the subsequence of
$\boldsymbol{v}^{\prime }$
is the subsequence of
![]() $\boldsymbol{v}$
of elements which are marked and not independent and
$\boldsymbol{v}$
of elements which are marked and not independent and
![]() $A^{\prime }$
is the subgroup generated by the weights of
$A^{\prime }$
is the subgroup generated by the weights of
![]() $\boldsymbol{v}^{\prime }$
.
$\boldsymbol{v}^{\prime }$
.
Example 7.9. The divisorial type associated to the toric type in row 4 in Table 7.1 is
 $(C_{6}\times C_{2},(a_{1},E_{1}),(a_{2},E_{2}))$
, with
$(C_{6}\times C_{2},(a_{1},E_{1}),(a_{2},E_{2}))$
, with
 $a_{1}=(1,0)$
and
$a_{1}=(1,0)$
and
 $a_{2}=(5,1)$
. Note that this is the same as the divisorial type for the toric type in row 5. Indeed, since
$a_{2}=(5,1)$
. Note that this is the same as the divisorial type for the toric type in row 5. Indeed, since
![]() $v_{3}$
is independent, it is omitted from the divisorial type and the subgroup of
$v_{3}$
is independent, it is omitted from the divisorial type and the subgroup of
 $C_{6}\times C_{6}$
generated by
$C_{6}\times C_{6}$
generated by
![]() $(1,0)$
and
$(1,0)$
and
![]() $(5,3)$
is isomorphic to
$(5,3)$
is isomorphic to
 $C_{6}\times C_{2}$
with
$C_{6}\times C_{2}$
with
![]() $(1,0)$
and
$(1,0)$
and
![]() $(5,3)$
in
$(5,3)$
in
 $C_{6}\times C_{6}$
corresponding to
$C_{6}\times C_{6}$
corresponding to
![]() $(1,0)$
and
$(1,0)$
and
![]() $(5,1)$
in
$(5,1)$
in
 $C_{6}\times C_{2}$
under this isomorphism. The divisorial type for row 6 is given by
$C_{6}\times C_{2}$
under this isomorphism. The divisorial type for row 6 is given by
 $(C_{6}\times C_{2},(a_{1},E_{1}),(a_{2},E_{2}))$
, with
$(C_{6}\times C_{2},(a_{1},E_{1}),(a_{2},E_{2}))$
, with
 $a_{1}=(1,0)$
and
$a_{1}=(1,0)$
and
 $a_{2}=(1,1)$
. Although the set of divisors and the isomorphism class of the group are the same as for row 4, this divisorial type is different since there is no automorphism of
$a_{2}=(1,1)$
. Although the set of divisors and the isomorphism class of the group are the same as for row 4, this divisorial type is different since there is no automorphism of
 $C_{6}\times C_{2}$
taking the pair
$C_{6}\times C_{2}$
taking the pair
![]() $(1,0)$
,
$(1,0)$
,
![]() $(5,1)$
to the pair
$(5,1)$
to the pair
![]() $(1,0)$
,
$(1,0)$
,
![]() $(1,1)$
.
$(1,1)$
.
The set
![]() $T(\boldsymbol{E})$
of divisorial types parametrised by
$T(\boldsymbol{E})$
of divisorial types parametrised by
![]() $\boldsymbol{E}$
inherits a partial ordering from the partial ordering on
$\boldsymbol{E}$
inherits a partial ordering from the partial ordering on
![]() $U(\boldsymbol{E})$
. We refine this partial ordering to a total ordering. First we give an alternative description of the set
$U(\boldsymbol{E})$
. We refine this partial ordering to a total ordering. First we give an alternative description of the set
![]() $T(\boldsymbol{E})$
. Let
$T(\boldsymbol{E})$
. Let
![]() $(A,\boldsymbol{v})$
be a divisorial type with
$(A,\boldsymbol{v})$
be a divisorial type with
 $\boldsymbol{v}=v_{1},\ldots ,v_{r}$
and
$\boldsymbol{v}=v_{1},\ldots ,v_{r}$
and
 $v_{i}=(a_{i},e_{i})$
. By Definition 7.8(i), each element
$v_{i}=(a_{i},e_{i})$
. By Definition 7.8(i), each element
![]() $e_{i}$
is an element
$e_{i}$
is an element
![]() $E^{i}$
of
$E^{i}$
of
![]() $\boldsymbol{E}$
and we may assume that indexing is chosen such that
$\boldsymbol{E}$
and we may assume that indexing is chosen such that
 $e_{1},\ldots ,e_{r}$
is decreasing. The sequence
$e_{1},\ldots ,e_{r}$
is decreasing. The sequence
 $a_{1},\ldots ,a_{r}$
of weights defines a group homomorphism
$a_{1},\ldots ,a_{r}$
of weights defines a group homomorphism
 $\unicode[STIX]{x1D711}:\mathbb{Z}^{r}\rightarrow A$
. By Definition 7.8(ii), this is surjective and therefore fits into an exact sequence
$\unicode[STIX]{x1D711}:\mathbb{Z}^{r}\rightarrow A$
. By Definition 7.8(ii), this is surjective and therefore fits into an exact sequence
 $$\begin{eqnarray}\displaystyle 0\rightarrow K\xrightarrow[{}]{f}\mathbb{Z}^{r}\xrightarrow[{}]{\unicode[STIX]{x1D711}}A\rightarrow 0 & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\rightarrow K\xrightarrow[{}]{f}\mathbb{Z}^{r}\xrightarrow[{}]{\unicode[STIX]{x1D711}}A\rightarrow 0 & & \displaystyle\end{eqnarray}$$
with
![]() $K$
being free of rank
$K$
being free of rank
![]() $r$
since
$r$
since
![]() $A$
is finite. Note that the divisorial type
$A$
is finite. Note that the divisorial type
![]() $(A,\boldsymbol{v})$
is uniquely determined by the subsequence
$(A,\boldsymbol{v})$
is uniquely determined by the subsequence
 $(E^{1},\ldots ,E^{s})$
of
$(E^{1},\ldots ,E^{s})$
of
![]() $\boldsymbol{E}$
together with
$\boldsymbol{E}$
together with
![]() $f$
up to composition by an automorphism of
$f$
up to composition by an automorphism of
![]() $K$
. By choosing a basis of
$K$
. By choosing a basis of
![]() $K$
, we may view
$K$
, we may view
![]() $f$
as a non-singular
$f$
as a non-singular
![]() $r$
-by-
$r$
-by-
![]() $r$
matrix with integer entries and the automorphisms of
$r$
matrix with integer entries and the automorphisms of
![]() $K$
as elements in the unimodular group
$K$
as elements in the unimodular group
![]() $\text{GL}_{r}(\mathbb{Z})$
. A coset in
$\text{GL}_{r}(\mathbb{Z})$
. A coset in
 $\text{Mat}_{r\times r}(\mathbb{Z})/\text{GL}_{r}(\mathbb{Z})$
has a unique representative on Hermite normal form (see [Reference CohenCoh93, § 2.4.2]). Recall that a non-singular matrix
$\text{Mat}_{r\times r}(\mathbb{Z})/\text{GL}_{r}(\mathbb{Z})$
has a unique representative on Hermite normal form (see [Reference CohenCoh93, § 2.4.2]). Recall that a non-singular matrix
 $H=(a_{ij})$
is on Hermite normal form if it is upper triangular, with
$H=(a_{ij})$
is on Hermite normal form if it is upper triangular, with
![]() $a_{ii}>0$
for all
$a_{ii}>0$
for all
![]() $i$
, and
$i$
, and
 $a_{ii}>a_{ij}\geqslant 0$
for
$a_{ii}>a_{ij}\geqslant 0$
for
![]() $j>i$
. This allows us to uniquely associate a pair
$j>i$
. This allows us to uniquely associate a pair
![]() $(\boldsymbol{E}^{\prime },H)$
to each element of
$(\boldsymbol{E}^{\prime },H)$
to each element of
![]() $T(\boldsymbol{E})$
, where
$T(\boldsymbol{E})$
, where
![]() $\boldsymbol{E}^{\prime }$
is a subsequence of
$\boldsymbol{E}^{\prime }$
is a subsequence of
![]() $\boldsymbol{E}$
of some length
$\boldsymbol{E}$
of some length
![]() $r$
and
$r$
and
![]() $H$
is a non-singular
$H$
is a non-singular
![]() $r$
-by-
$r$
-by-
![]() $r$
matrix with integer entries on Hermite normal form. We order such pairs first lexicographically on
$r$
matrix with integer entries on Hermite normal form. We order such pairs first lexicographically on
![]() $\boldsymbol{E}^{\prime }$
and then lexicographically on the entries of
$\boldsymbol{E}^{\prime }$
and then lexicographically on the entries of
![]() $H$
. Here the entries are ordered first by rows, with high row numbers being more significant, and then by columns, with low column numbers being more significant. We illustrate the ordering by an example.
$H$
. Here the entries are ordered first by rows, with high row numbers being more significant, and then by columns, with low column numbers being more significant. We illustrate the ordering by an example.
Example 7.10. The Hermite normal forms of the matrices, as discussed above, associated to the examples in the rows 4, 5 and 6 in Table 7.1 are computed to
 $$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}6 & 2\\ 0 & 2\end{array}\right),\quad \left(\begin{array}{@{}cc@{}}6 & 2\\ 0 & 2\end{array}\right),\quad \left(\begin{array}{@{}cc@{}}6 & 4\\ 0 & 2\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}6 & 2\\ 0 & 2\end{array}\right),\quad \left(\begin{array}{@{}cc@{}}6 & 2\\ 0 & 2\end{array}\right),\quad \left(\begin{array}{@{}cc@{}}6 & 4\\ 0 & 2\end{array}\right),\end{eqnarray}$$
respectively. In particular, the divisorial type of the example in row 6 is larger than the divisorial type for the others.
It is easy to see that this ordering is a refinement of the partial ordering inherited by
![]() $U(\boldsymbol{E})$
and that taking the associated divisorial type of an arbitrary toric type gives a conormal invariant
$U(\boldsymbol{E})$
and that taking the associated divisorial type of an arbitrary toric type gives a conormal invariant
![]() $U\rightarrow E$
.
$U\rightarrow E$
.
Remark 7.11. To any divisorial type
![]() $(A,\boldsymbol{v})$
, we get an associated orbifold fan
$(A,\boldsymbol{v})$
, we get an associated orbifold fan
 $\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
with a unique maximal cone such that the rays in
$\boldsymbol{\unicode[STIX]{x1D6F4}}=(N,\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D6FD})$
with a unique maximal cone such that the rays in
![]() $\unicode[STIX]{x1D6F4}(1)$
are labelled by the markings on the elements of
$\unicode[STIX]{x1D6F4}(1)$
are labelled by the markings on the elements of
![]() $\boldsymbol{v}$
. Indeed, consider the exact sequence 7.2. Define
$\boldsymbol{v}$
. Indeed, consider the exact sequence 7.2. Define
![]() $N$
as the dual
$N$
as the dual
 $\text{Hom}_{\mathbb{Z}}(K,\mathbb{Z})$
of
$\text{Hom}_{\mathbb{Z}}(K,\mathbb{Z})$
of
![]() $K$
and
$K$
and
![]() $\unicode[STIX]{x1D6FD}$
as the dual
$\unicode[STIX]{x1D6FD}$
as the dual
 $\text{Hom}_{\mathbb{Z}}(f,\mathbb{Z})$
of
$\text{Hom}_{\mathbb{Z}}(f,\mathbb{Z})$
of
![]() $f$
. The cones of
$f$
. The cones of
![]() $\unicode[STIX]{x1D6F4}$
are the cones spanned by all subsets of
$\unicode[STIX]{x1D6F4}$
are the cones spanned by all subsets of
 $\{\unicode[STIX]{x1D6FD}(u_{1}),\ldots ,\unicode[STIX]{x1D6FD}(u_{s})\}$
, where
$\{\unicode[STIX]{x1D6FD}(u_{1}),\ldots ,\unicode[STIX]{x1D6FD}(u_{s})\}$
, where
![]() $u_{i}$
denotes the dual of the standard basis of
$u_{i}$
denotes the dual of the standard basis of
![]() $\mathbb{Z}^{s}$
.
$\mathbb{Z}^{s}$
.

Figure 7.1. The stacky fans associated to the divisorial types associated to the toric types in rows 4 and 5 (left-hand picture) and row 6 (right-hand picture) of Table 7.1.
Example 7.12. The stacky fans associated to the divisorial types described in Example 7.10 are pictured in Figure 7.1. Running Algorithm B on the orbifold fan in the left-hand picture yields a destackification in three steps (this is illustrated in Figure 8.3). The corresponding destackification for the orbifold fan in the right-hand picture terminates after a single blow-up. This illustrates that different combinatorial recipes may be needed for different divisorial types.
The techniques described so far are enough to solve the destackification problem in the toroidal case. The procedure is described by Algorithm E in the next section if we omit Step E5. If we do not have a toroidal structure when we start, we need to create one. One problem is that the toroidal index is not a smooth conormal invariant, as was demonstrated in Example 6.18. Instead of using the toroidal index directly, we introduce a coarser invariant, the divisorial index, which may be thought of as a smoothed version of the toroidal index.
Definition 7.13 (Divisorial index).
Let
 $\unicode[STIX]{x1D6FC}=(A,\boldsymbol{v})$
be a toric type and let
$\unicode[STIX]{x1D6FC}=(A,\boldsymbol{v})$
be a toric type and let
 $A_{\text{div}}\subseteq A$
be the subgroup generated by the weights of the elements of
$A_{\text{div}}\subseteq A$
be the subgroup generated by the weights of the elements of
![]() $\boldsymbol{v}$
which are marked by some divisor. The divisorial index of
$\boldsymbol{v}$
which are marked by some divisor. The divisorial index of
![]() $\unicode[STIX]{x1D6FC}$
is the number of elements
$\unicode[STIX]{x1D6FC}$
is the number of elements
![]() $v_{i}$
in the sequence
$v_{i}$
in the sequence
![]() $\boldsymbol{v}$
with weights
$\boldsymbol{v}$
with weights
![]() $a_{i}$
satisfying
$a_{i}$
satisfying
 $a_{i}\not \in A_{\text{div}}$
. If the divisorial index is zero at
$a_{i}\not \in A_{\text{div}}$
. If the divisorial index is zero at
![]() $\unicode[STIX]{x1D709}$
, we say that the standard pair
$\unicode[STIX]{x1D709}$
, we say that the standard pair
 $(X,\boldsymbol{E})/S$
is divisorial at
$(X,\boldsymbol{E})/S$
is divisorial at
![]() $\unicode[STIX]{x1D709}$
. Furthermore, we say that the pair
$\unicode[STIX]{x1D709}$
. Furthermore, we say that the pair
 $(X,\boldsymbol{E})/S$
is divisorial if it is divisorial at each of its points.
$(X,\boldsymbol{E})/S$
is divisorial if it is divisorial at each of its points.
Remark 7.14. Geometrically, the property for a stack of being divisorial can be understood as follows: each of the components
![]() $E^{i}$
of
$E^{i}$
of
![]() $\boldsymbol{E}$
gives rise to a
$\boldsymbol{E}$
gives rise to a
![]() $\mathbb{G}_{\text{m}}$
-torsor
$\mathbb{G}_{\text{m}}$
-torsor
![]() $F^{i}$
, and the fibre product
$F^{i}$
, and the fibre product
 $F=F^{1}\times _{X}\cdots \times _{X}F^{m}$
is a
$F=F^{1}\times _{X}\cdots \times _{X}F^{m}$
is a
![]() $\mathbb{G}_{\text{m}}^{r}$
-torsor. If
$\mathbb{G}_{\text{m}}^{r}$
-torsor. If
![]() $X$
is an orbifold, the pair
$X$
is an orbifold, the pair
![]() $(X,\boldsymbol{E})$
is divisorial precisely when
$(X,\boldsymbol{E})$
is divisorial precisely when
![]() $F$
is an algebraic space. This is equivalent to the stacky locus being contained in the divisor
$F$
is an algebraic space. This is equivalent to the stacky locus being contained in the divisor
![]() $\boldsymbol{E}$
. In general, the pair
$\boldsymbol{E}$
. In general, the pair
![]() $(X,\boldsymbol{E})$
is divisorial precisely when
$(X,\boldsymbol{E})$
is divisorial precisely when
![]() $F$
is a gerbe.
$F$
is a gerbe.
Classically, a scheme is called divisorial [Reference IllusieSGA6, Definition 2.2.5] if it has an ample family of line bundles. This is equivalent to the scheme having a
![]() $\mathbb{G}_{m}^{n}$
-torsor, for some
$\mathbb{G}_{m}^{n}$
-torsor, for some
![]() $n$
, whose total space is quasi-affine (see [Reference HausenHau02, Theorem 1] for varieties and [Reference GrossGro13, Corollary 5.5] for the generalisation to stacks). Hence, our notion of divisorial stack is related, but not equivalent, to the classical definition.
$n$
, whose total space is quasi-affine (see [Reference HausenHau02, Theorem 1] for varieties and [Reference GrossGro13, Corollary 5.5] for the generalisation to stacks). Hence, our notion of divisorial stack is related, but not equivalent, to the classical definition.
The process of modifying
![]() $X$
such that it becomes divisorial is straightforward, and described in Algorithm C. But to modify a divisorial stack such that it becomes toroidal is trickier. It turns out that, in general, this is not possible by just using ordinary blow-ups; root stacks are needed. It seems that the easiest approach is to interleave the process of reducing the toroidal index with the process of reducing the independency index. Simply put, we just ignore the fact that
$X$
such that it becomes divisorial is straightforward, and described in Algorithm C. But to modify a divisorial stack such that it becomes toroidal is trickier. It turns out that, in general, this is not possible by just using ordinary blow-ups; root stacks are needed. It seems that the easiest approach is to interleave the process of reducing the toroidal index with the process of reducing the independency index. Simply put, we just ignore the fact that
![]() $(X,\boldsymbol{E})$
is not toroidal, and use exactly the same algorithm as in the toroidal case. The distinguished divisors we create will, in general, not be independent in this case, but they will have the weaker property of being divisorially independent.
$(X,\boldsymbol{E})$
is not toroidal, and use exactly the same algorithm as in the toroidal case. The distinguished divisors we create will, in general, not be independent in this case, but they will have the weaker property of being divisorially independent.
Definition 7.15. We assume that
 $(X,\boldsymbol{E})/S$
is divisorial. Let
$(X,\boldsymbol{E})/S$
is divisorial. Let
![]() $\unicode[STIX]{x1D709}\in X$
be a point and let
$\unicode[STIX]{x1D709}\in X$
be a point and let
![]() $E$
be a component of
$E$
be a component of
![]() $\boldsymbol{E}$
passing through
$\boldsymbol{E}$
passing through
![]() $\unicode[STIX]{x1D709}$
. Assume that the toric type at
$\unicode[STIX]{x1D709}$
. Assume that the toric type at
![]() $\unicode[STIX]{x1D709}$
is
$\unicode[STIX]{x1D709}$
is
![]() $(A,\boldsymbol{v})$
with
$(A,\boldsymbol{v})$
with
 $\boldsymbol{v}=(v_{1},\ldots ,v_{r})$
and
$\boldsymbol{v}=(v_{1},\ldots ,v_{r})$
and
 $v_{i}=(a_{i},e_{i})$
. Choose the indexing such that
$v_{i}=(a_{i},e_{i})$
. Choose the indexing such that
![]() $v_{1}$
is marked by
$v_{1}$
is marked by
![]() $E$
and
$E$
and
 $v_{2},\ldots ,v_{s}$
are the other marked elements of
$v_{2},\ldots ,v_{s}$
are the other marked elements of
![]() $\boldsymbol{v}$
. We say that
$\boldsymbol{v}$
. We say that
![]() $E$
is divisorially independent at
$E$
is divisorially independent at
![]() $\unicode[STIX]{x1D709}$
provided that the intersection
$\unicode[STIX]{x1D709}$
provided that the intersection
 $\langle a_{1}\rangle \cap \langle a_{2},\ldots ,a_{s}\rangle$
is the trivial subgroup. A component of
$\langle a_{1}\rangle \cap \langle a_{2},\ldots ,a_{s}\rangle$
is the trivial subgroup. A component of
![]() $\boldsymbol{E}$
not passing through
$\boldsymbol{E}$
not passing through
![]() $\unicode[STIX]{x1D709}$
is considered divisorially independent at
$\unicode[STIX]{x1D709}$
is considered divisorially independent at
![]() $\unicode[STIX]{x1D709}$
by default.
$\unicode[STIX]{x1D709}$
by default.
Note that the property for a component of
![]() $\boldsymbol{E}$
of being independent at a point
$\boldsymbol{E}$
of being independent at a point
![]() $\unicode[STIX]{x1D709}\in X$
does not depend on the other components of
$\unicode[STIX]{x1D709}\in X$
does not depend on the other components of
![]() $\boldsymbol{E}$
, whereas the property of being divisorially independent does.
$\boldsymbol{E}$
, whereas the property of being divisorially independent does.
This reduces the problem to modifying
![]() $(X,\boldsymbol{E})$
such that the divisorially independent divisors become independent. This is achieved by Algorithm D. Or, rather, the algorithm ensures that either the divisor becomes independent or the toroidal index drops. In either case we get an improvement, which allows us to solve the problem by repeating the procedure.
$(X,\boldsymbol{E})$
such that the divisorially independent divisors become independent. This is achieved by Algorithm D. Or, rather, the algorithm ensures that either the divisor becomes independent or the toroidal index drops. In either case we get an improvement, which allows us to solve the problem by repeating the procedure.
The main invariant used by Algorithm D is slightly more subtle than the others.
Definition 7.16 (
 $E$
-divisorial index).
$E$
-divisorial index).
Let
 $\unicode[STIX]{x1D6FC}=(A,\boldsymbol{v})\in U(\boldsymbol{E})$
be a toric type with divisorial index zero, with
$\unicode[STIX]{x1D6FC}=(A,\boldsymbol{v})\in U(\boldsymbol{E})$
be a toric type with divisorial index zero, with
 $\boldsymbol{v}=(v_{1},\ldots ,v_{r})$
and
$\boldsymbol{v}=(v_{1},\ldots ,v_{r})$
and
 $v_{i}=(a_{i},e_{i})$
. Fix a component
$v_{i}=(a_{i},e_{i})$
. Fix a component
![]() $E$
of
$E$
of
![]() $\boldsymbol{E}$
. If none of the elements of
$\boldsymbol{E}$
. If none of the elements of
![]() $\boldsymbol{v}$
are marked by
$\boldsymbol{v}$
are marked by
![]() $E$
, then the
$E$
, then the
![]() $E$
-divisorial index of
$E$
-divisorial index of
![]() $\unicode[STIX]{x1D6FC}$
is defined to be zero. Otherwise, we choose the indexing such that
$\unicode[STIX]{x1D6FC}$
is defined to be zero. Otherwise, we choose the indexing such that
![]() $e_{1}=E$
and consider the groups
$e_{1}=E$
and consider the groups
 $$\begin{eqnarray}A_{\text{div}}=\langle a_{i}\mid e_{i}\neq \ast \rangle ,\quad A_{\text{div}}^{1}=\langle a_{i}\mid e_{i}\neq \ast \text{and }i\neq 1\rangle .\end{eqnarray}$$
$$\begin{eqnarray}A_{\text{div}}=\langle a_{i}\mid e_{i}\neq \ast \rangle ,\quad A_{\text{div}}^{1}=\langle a_{i}\mid e_{i}\neq \ast \text{and }i\neq 1\rangle .\end{eqnarray}$$
Then the subquotient
 $A^{E}=A_{\text{div}}/A_{\text{div}}^{1}$
of
$A^{E}=A_{\text{div}}/A_{\text{div}}^{1}$
of
![]() $A$
is cyclic and generated by the canonical image
$A$
is cyclic and generated by the canonical image
![]() $\bar{a}_{1}$
of
$\bar{a}_{1}$
of
![]() $a_{1}$
in
$a_{1}$
in
![]() $A^{E}$
. Since the divisorial index is assumed to be zero, each weight
$A^{E}$
. Since the divisorial index is assumed to be zero, each weight
![]() $a_{i}$
for any element has a canonical image
$a_{i}$
for any element has a canonical image
![]() $\overline{a}_{i}$
in
$\overline{a}_{i}$
in
![]() $A^{E}$
. Let
$A^{E}$
. Let
![]() $c_{i}$
be the smallest non-negative number such that
$c_{i}$
be the smallest non-negative number such that
 $\overline{a}_{i}=c_{i}\overline{a}_{1}$
. The
$\overline{a}_{i}=c_{i}\overline{a}_{1}$
. The
![]() $E$
-divisorial index is defined as the sum
$E$
-divisorial index is defined as the sum
 $$\begin{eqnarray}c=\mathop{\sum }_{e_{j}=\ast }c_{j}.\end{eqnarray}$$
$$\begin{eqnarray}c=\mathop{\sum }_{e_{j}=\ast }c_{j}.\end{eqnarray}$$
Example 7.17. Consider the toric type in row 7 in Table 7.1. Using the notation from Definition 7.16, we have
 $A^{E^{1}}\cong C_{3}$
. Choose the isomorphism such that the image of
$A^{E^{1}}\cong C_{3}$
. Choose the isomorphism such that the image of
![]() $a_{1}$
is 1 in
$a_{1}$
is 1 in
![]() $C_{3}$
. Then the images of
$C_{3}$
. Then the images of
![]() $a_{3}$
and
$a_{3}$
and
![]() $a_{4}$
are 1 and 2, respectively. Hence, the
$a_{4}$
are 1 and 2, respectively. Hence, the
![]() $E^{1}$
-divisorial index is 3.
$E^{1}$
-divisorial index is 3.
The
![]() $E$
-divisorial index measures how far a divisorially independent divisor
$E$
-divisorial index measures how far a divisorially independent divisor
![]() $E$
is from being actually independent. More precisely, the following is true: let
$E$
is from being actually independent. More precisely, the following is true: let
![]() $(X,\boldsymbol{E})$
be a standard pair and let
$(X,\boldsymbol{E})$
be a standard pair and let
![]() $E^{i}$
be a component of
$E^{i}$
be a component of
![]() $\boldsymbol{E}$
. Choose a point
$\boldsymbol{E}$
. Choose a point
![]() $\unicode[STIX]{x1D709}\in E^{i}$
, where
$\unicode[STIX]{x1D709}\in E^{i}$
, where
![]() $(X,\boldsymbol{E})$
is divisorial and
$(X,\boldsymbol{E})$
is divisorial and
![]() $E^{i}$
divisorially independent. Then
$E^{i}$
divisorially independent. Then
![]() $E^{i}$
is independent at
$E^{i}$
is independent at
![]() $\unicode[STIX]{x1D709}$
if and only if the
$\unicode[STIX]{x1D709}$
if and only if the
![]() $E^{i}$
-divisorial index vanishes at
$E^{i}$
-divisorial index vanishes at
![]() $\unicode[STIX]{x1D709}$
.
$\unicode[STIX]{x1D709}$
.
We conclude the section by summarising the properties of the conormal invariants introduced here.
Proposition 7.18. All of the following conormal invariants satisfy the properties (P1) and (P2) defined in § 6:
-
(a) independency index;
-
(b) toroidal index;
-
(c) divisorial type;
-
(d) divisorial index;
-
(e)
 $E$
-divisorial index for any component
$E$
-divisorial index for any component
 $E\in \boldsymbol{E}$
.
$E\in \boldsymbol{E}$
.
Of these, the invariants (a), (d) and (e) are smooth. The invariants (b) and (c) are not smooth, but they are locally constant on the locus where the independency index obtains its maximum.
Proof. Let
 $(A,\boldsymbol{v})\in U(\boldsymbol{E})$
be a toric type with
$(A,\boldsymbol{v})\in U(\boldsymbol{E})$
be a toric type with
 $\boldsymbol{v}=(v_{1},\ldots ,v_{r})$
and
$\boldsymbol{v}=(v_{1},\ldots ,v_{r})$
and
 $v_{j}=(a_{j},e_{j})$
. We choose the indexing and integers
$v_{j}=(a_{j},e_{j})$
. We choose the indexing and integers
![]() $s,t$
such that
$s,t$
such that
![]() $e_{j}=\ast$
precisely when
$e_{j}=\ast$
precisely when
![]() $j>s$
and
$j>s$
and
 $v_{j}=(0,\ast )$
precisely when
$v_{j}=(0,\ast )$
precisely when
![]() $j>t$
. We denote the subgroup generated by
$j>t$
. We denote the subgroup generated by
 $a_{1},\ldots ,a_{r}$
by
$a_{1},\ldots ,a_{r}$
by
![]() $A_{\text{rig}}$
.
$A_{\text{rig}}$
.
Let
![]() $\unicode[STIX]{x1D704}$
be one of the conormal invariants in (a)–(e). To see that the conditions (P1) and (P2) are satisfied for
$\unicode[STIX]{x1D704}$
be one of the conormal invariants in (a)–(e). To see that the conditions (P1) and (P2) are satisfied for
![]() $\unicode[STIX]{x1D704}$
, we need to verify that
$\unicode[STIX]{x1D704}$
, we need to verify that
 $\unicode[STIX]{x1D704}(A,\boldsymbol{v})=\unicode[STIX]{x1D704}(A_{\text{rig}},(v_{1},\ldots ,v_{s}))$
. For the independency index this is clear since the definition only involves
$\unicode[STIX]{x1D704}(A,\boldsymbol{v})=\unicode[STIX]{x1D704}(A_{\text{rig}},(v_{1},\ldots ,v_{s}))$
. For the independency index this is clear since the definition only involves
![]() $A_{\text{rig}}$
and the sequence
$A_{\text{rig}}$
and the sequence
 $a_{1},\ldots ,a_{r}$
and since the condition (7.1) is trivially verified whenever
$a_{1},\ldots ,a_{r}$
and since the condition (7.1) is trivially verified whenever
![]() $a_{j}=0$
. The conditions are equally easy to verify for the other invariants and we leave the details to the reader.
$a_{j}=0$
. The conditions are equally easy to verify for the other invariants and we leave the details to the reader.
Now consider a toric type
![]() $(A^{\prime },\boldsymbol{v}^{\prime })$
which is dominated by
$(A^{\prime },\boldsymbol{v}^{\prime })$
which is dominated by
![]() $(A,\boldsymbol{v})$
and use the notation
$(A,\boldsymbol{v})$
and use the notation
 $\boldsymbol{v}^{\prime }=(v_{1}^{\prime },\ldots ,v_{r}^{\prime })$
and
$\boldsymbol{v}^{\prime }=(v_{1}^{\prime },\ldots ,v_{r}^{\prime })$
and
 $v_{j}^{\prime }=(a_{j}^{\prime },e_{j}^{\prime })$
. By definition, we obtain
$v_{j}^{\prime }=(a_{j}^{\prime },e_{j}^{\prime })$
. By definition, we obtain
![]() $(A^{\prime },\boldsymbol{v}^{\prime })$
by choosing a subset
$(A^{\prime },\boldsymbol{v}^{\prime })$
by choosing a subset
 $J\subset \{1,\ldots ,r\}$
and letting
$J\subset \{1,\ldots ,r\}$
and letting
 $$\begin{eqnarray}A^{\prime }=A/\langle a_{j}\mid j\in J\rangle ,\quad a_{j}^{\prime }=\bar{a}_{j},\quad e_{j}^{\prime }=\left\{\begin{array}{@{}ll@{}}\ast & \text{if }j\in J,\\ e_{j} & \text{otherwise,}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}A^{\prime }=A/\langle a_{j}\mid j\in J\rangle ,\quad a_{j}^{\prime }=\bar{a}_{j},\quad e_{j}^{\prime }=\left\{\begin{array}{@{}ll@{}}\ast & \text{if }j\in J,\\ e_{j} & \text{otherwise,}\end{array}\right.\end{eqnarray}$$
where
![]() $\bar{a}_{j}$
denotes the canonical image of
$\bar{a}_{j}$
denotes the canonical image of
![]() $a_{j}$
in
$a_{j}$
in
![]() $A^{\prime }$
. Let
$A^{\prime }$
. Let
![]() $\unicode[STIX]{x1D704}$
denote one of the conormal invariants in (a), (d) or (e). In each case we state the precise condition on
$\unicode[STIX]{x1D704}$
denote one of the conormal invariants in (a), (d) or (e). In each case we state the precise condition on
![]() $J$
under which we have
$J$
under which we have
 $\unicode[STIX]{x1D704}(A,\boldsymbol{v})=\unicode[STIX]{x1D704}(A^{\prime },\boldsymbol{v}^{\prime })$
:
$\unicode[STIX]{x1D704}(A,\boldsymbol{v})=\unicode[STIX]{x1D704}(A^{\prime },\boldsymbol{v}^{\prime })$
:
- (a)
-
 $\langle a_{j}\rangle \cap \langle a_{1},\ldots ,\hat{a}_{j},\ldots ,a_{r}\rangle =0$
for each
$\langle a_{j}\rangle \cap \langle a_{1},\ldots ,\hat{a}_{j},\ldots ,a_{r}\rangle =0$
for each
 $j\in J$
;
$j\in J$
; - (d)
-
 $a_{j}\in A_{\text{div}}=\langle a_{1},\ldots ,a_{s}\rangle$
for each
$a_{j}\in A_{\text{div}}=\langle a_{1},\ldots ,a_{s}\rangle$
for each
 $j\in J$
;
$j\in J$
; - (e)
-
 $a_{j}\in \langle a_{1},\ldots ,\widehat{a}_{k},\ldots ,a_{s}\rangle$
for each
$a_{j}\in \langle a_{1},\ldots ,\widehat{a}_{k},\ldots ,a_{s}\rangle$
for each
 $j\in J$
, where
$j\in J$
, where
 $k$
corresponds to the given divisor.
$k$
corresponds to the given divisor.
From these characterisations, it is clear that the smoothness condition of Definition 6.16 is satisfied for all three invariants.
The last statement follows from the fact that the independency index must drop if either the toroidal index or the divisorial type drops. ◻
8 The destackification algorithm
In this section, we give the full details of the destackification algorithms outlined in the previous section. We fix some notation which will be used throughout the section.
Let
 $(X_{0},\boldsymbol{E}_{0})/S$
be a standard pair with diagonalisable stabilisers over a quasi-compact scheme
$(X_{0},\boldsymbol{E}_{0})/S$
be a standard pair with diagonalisable stabilisers over a quasi-compact scheme
![]() $S$
. We wish to construct a smooth, stacky blow-up sequence
$S$
. We wish to construct a smooth, stacky blow-up sequence
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}:(X_{n},\boldsymbol{E}_{n})\rightarrow \cdots \rightarrow (X_{0},\boldsymbol{E}_{0}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}:(X_{n},\boldsymbol{E}_{n})\rightarrow \cdots \rightarrow (X_{0},\boldsymbol{E}_{0}).\end{eqnarray}$$
Each stacky blow-up
 $\unicode[STIX]{x1D70B}_{i}:(X_{i+1},\boldsymbol{E}_{i+1})\rightarrow (X_{i},\boldsymbol{E}_{i})$
in the sequence will have a centre
$\unicode[STIX]{x1D70B}_{i}:(X_{i+1},\boldsymbol{E}_{i+1})\rightarrow (X_{i},\boldsymbol{E}_{i})$
in the sequence will have a centre
![]() $Z_{i}$
which is determined by some smooth conormal invariant
$Z_{i}$
which is determined by some smooth conormal invariant
![]() $\unicode[STIX]{x1D704}$
as described in Proposition 6.19. Different invariants
$\unicode[STIX]{x1D704}$
as described in Proposition 6.19. Different invariants
![]() $\unicode[STIX]{x1D704}$
will be used at different stages of the algorithm.
$\unicode[STIX]{x1D704}$
will be used at different stages of the algorithm.
Let
![]() $\unicode[STIX]{x1D709}_{i}\in X_{i}$
be a point, which we assume lies in
$\unicode[STIX]{x1D709}_{i}\in X_{i}$
be a point, which we assume lies in
![]() $Z_{i}$
. Typically, we wish to investigate how the value of some conormal invariant
$Z_{i}$
. Typically, we wish to investigate how the value of some conormal invariant
![]() $\unicode[STIX]{x1D704}$
under consideration at a lift
$\unicode[STIX]{x1D704}$
under consideration at a lift
![]() $\unicode[STIX]{x1D709}_{i+1}$
of
$\unicode[STIX]{x1D709}_{i+1}$
of
![]() $\unicode[STIX]{x1D709}_{i}$
to
$\unicode[STIX]{x1D709}_{i}$
to
![]() $X_{i+1}$
relates to the value of
$X_{i+1}$
relates to the value of
![]() $\unicode[STIX]{x1D704}$
at
$\unicode[STIX]{x1D704}$
at
![]() $\unicode[STIX]{x1D709}_{i}$
. Assume that the toric type of
$\unicode[STIX]{x1D709}_{i}$
. Assume that the toric type of
![]() $X_{i}$
at
$X_{i}$
at
![]() $\unicode[STIX]{x1D709}_{i}$
is
$\unicode[STIX]{x1D709}_{i}$
is
![]() $(A,\boldsymbol{v})$
, where
$(A,\boldsymbol{v})$
, where
 $\boldsymbol{v}=(v_{1},\ldots ,v_{r})$
and
$\boldsymbol{v}=(v_{1},\ldots ,v_{r})$
and
 $v_{j}=(a_{j},e_{j})$
. It is convenient to work with local homogeneous coordinates, which we may do in light of the locally toric description of standard pairs given in Proposition 5.3 together with the functoriality properties of conormal invariants described in Proposition 6.14. Hence, we may just as well assume that
$v_{j}=(a_{j},e_{j})$
. It is convenient to work with local homogeneous coordinates, which we may do in light of the locally toric description of standard pairs given in Proposition 5.3 together with the functoriality properties of conormal invariants described in Proposition 6.14. Hence, we may just as well assume that
![]() $X_{i}$
is a basic toric stack with homogeneous coordinates
$X_{i}$
is a basic toric stack with homogeneous coordinates
 $$\begin{eqnarray}\displaystyle ({\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}],A,(a_{1},\ldots ,a_{r})) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle ({\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}],A,(a_{1},\ldots ,a_{r})) & & \displaystyle\end{eqnarray}$$
and that
![]() $\unicode[STIX]{x1D709}_{i}$
lies in the locus where the toric type is maximal, which is
$\unicode[STIX]{x1D709}_{i}$
lies in the locus where the toric type is maximal, which is
 $V(x_{j}\mid a_{j}\neq 0\text{ or }e_{i}\neq \ast )$
. The substack
$V(x_{j}\mid a_{j}\neq 0\text{ or }e_{i}\neq \ast )$
. The substack
![]() $Z_{i}$
is of the form
$Z_{i}$
is of the form
 $$\begin{eqnarray}\displaystyle Z_{i}=V(x_{j}\mid j\in J),\quad J\subseteq \{1,\ldots ,r\}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Z_{i}=V(x_{j}\mid j\in J),\quad J\subseteq \{1,\ldots ,r\}, & & \displaystyle\end{eqnarray}$$
where the subset
![]() $J$
depends on the toric type
$J$
depends on the toric type
![]() $(A,\boldsymbol{v})$
as well as the conormal invariant
$(A,\boldsymbol{v})$
as well as the conormal invariant
![]() $\unicode[STIX]{x1D704}$
under consideration. The blow-up
$\unicode[STIX]{x1D704}$
under consideration. The blow-up
![]() $X_{i+1}$
is covered by
$X_{i+1}$
is covered by
![]() $|J|$
coordinate patches indexed by
$|J|$
coordinate patches indexed by
![]() $p\in J$
. The coordinates for these patches are
$p\in J$
. The coordinates for these patches are
 $$\begin{eqnarray}\displaystyle ({\mathcal{O}}_{S}[\widetilde{x}_{1},\ldots ,\widetilde{x}_{r}],\widetilde{A},(\widetilde{a}_{1},\ldots ,\widetilde{a}_{r})) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle ({\mathcal{O}}_{S}[\widetilde{x}_{1},\ldots ,\widetilde{x}_{r}],\widetilde{A},(\widetilde{a}_{1},\ldots ,\widetilde{a}_{r})) & & \displaystyle\end{eqnarray}$$
with
 $$\begin{eqnarray}\displaystyle \widetilde{A}=A,\quad \widetilde{x}_{j}=\left\{\begin{array}{@{}ll@{}}x_{j}/x_{p} & \text{if }j\in J\setminus \{p\},\\ x_{j} & \text{otherwise, }\end{array}\right.\quad \widetilde{a}_{j}=\left\{\begin{array}{@{}ll@{}}a_{j}-a_{p} & \text{if }j\in J\setminus \{p\},\\ a_{j} & \text{otherwise.}\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{A}=A,\quad \widetilde{x}_{j}=\left\{\begin{array}{@{}ll@{}}x_{j}/x_{p} & \text{if }j\in J\setminus \{p\},\\ x_{j} & \text{otherwise, }\end{array}\right.\quad \widetilde{a}_{j}=\left\{\begin{array}{@{}ll@{}}a_{j}-a_{p} & \text{if }j\in J\setminus \{p\},\\ a_{j} & \text{otherwise.}\end{array}\right. & & \displaystyle\end{eqnarray}$$
In these coordinates
![]() $V(\widetilde{x}_{j})$
is the strict transform of
$V(\widetilde{x}_{j})$
is the strict transform of
![]() $V(x_{j})$
if
$V(x_{j})$
if
![]() $j\neq p$
and
$j\neq p$
and
![]() $V(\widetilde{x}_{p})$
is the exceptional divisor, which we denote by
$V(\widetilde{x}_{p})$
is the exceptional divisor, which we denote by
![]() $F$
. We see that the toric type at the patch is bounded above by
$F$
. We see that the toric type at the patch is bounded above by
![]() $(\widetilde{A},\widetilde{\boldsymbol{v}})$
, with
$(\widetilde{A},\widetilde{\boldsymbol{v}})$
, with
 $\widetilde{\boldsymbol{v}}=(\widetilde{v}_{j})$
and
$\widetilde{\boldsymbol{v}}=(\widetilde{v}_{j})$
and
 $\widetilde{v}_{j}=(\widetilde{a}_{j},\widetilde{e}_{j})$
, where
$\widetilde{v}_{j}=(\widetilde{a}_{j},\widetilde{e}_{j})$
, where
![]() $\widetilde{e}_{j}$
is given by
$\widetilde{e}_{j}$
is given by
 $$\begin{eqnarray}\displaystyle \widetilde{e}_{j}=\left\{\begin{array}{@{}ll@{}}F & \text{if }j=p,\\ \unicode[STIX]{x1D70B}_{i}^{-1}(e_{j}) & \text{if }e_{j}\in \boldsymbol{E}_{i}\text{ and }j\neq p,\\ \ast & \text{otherwise.}\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{e}_{j}=\left\{\begin{array}{@{}ll@{}}F & \text{if }j=p,\\ \unicode[STIX]{x1D70B}_{i}^{-1}(e_{j}) & \text{if }e_{j}\in \boldsymbol{E}_{i}\text{ and }j\neq p,\\ \ast & \text{otherwise.}\end{array}\right. & & \displaystyle\end{eqnarray}$$
Algorithm C (Divisorialification).
The input of the algorithm is a standard pair
![]() $(X,\boldsymbol{E})$
over a quasi-compact scheme
$(X,\boldsymbol{E})$
over a quasi-compact scheme
![]() $S$
, with
$S$
, with
![]() $X$
having diagonalisable stabilisers. The output of the algorithm is a smooth, ordinary blow-up sequence
$X$
having diagonalisable stabilisers. The output of the algorithm is a smooth, ordinary blow-up sequence
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}:(X_{n},\boldsymbol{E}_{n})\rightarrow \cdots \rightarrow (X_{0},\boldsymbol{E}_{0})=(X,\boldsymbol{E})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}:(X_{n},\boldsymbol{E}_{n})\rightarrow \cdots \rightarrow (X_{0},\boldsymbol{E}_{0})=(X,\boldsymbol{E})\end{eqnarray}$$
such that
 $(X_{n},\boldsymbol{E}_{n})/S$
is divisorial. The construction is functorial (see Definition 2.6) with respect to arbitrary base change
$(X_{n},\boldsymbol{E}_{n})/S$
is divisorial. The construction is functorial (see Definition 2.6) with respect to arbitrary base change
![]() $S^{\prime }\rightarrow S$
and with respect to morphisms
$S^{\prime }\rightarrow S$
and with respect to morphisms
 $X^{\prime }\rightarrow X$
which are either gerbes or smooth and stabiliser-preserving.
$X^{\prime }\rightarrow X$
which are either gerbes or smooth and stabiliser-preserving.
- C0.
-
[Initialise.] Set
 $i=0$
.
$i=0$
. - C1.
-
[Finished?] Let
 $Z_{i}$
be the locus in
$Z_{i}$
be the locus in
 $X_{i}$
where the divisorial index of the standard pair
$X_{i}$
where the divisorial index of the standard pair
 $(X_{i},\boldsymbol{E}_{i})$
is maximal. If
$(X_{i},\boldsymbol{E}_{i})$
is maximal. If
 $Z_{i}=X_{i}$
, then the algorithm terminates.
$Z_{i}=X_{i}$
, then the algorithm terminates. - C2.
-
[Blow up.] Let
 $\unicode[STIX]{x1D70B}_{i}:(X_{i+1},\boldsymbol{E}_{i+1})\rightarrow (X_{i},\boldsymbol{E}_{i})$
be the blow-up of
$\unicode[STIX]{x1D70B}_{i}:(X_{i+1},\boldsymbol{E}_{i+1})\rightarrow (X_{i},\boldsymbol{E}_{i})$
be the blow-up of
 $X_{i}$
in
$X_{i}$
in
 $Z_{i}$
.
$Z_{i}$
. - C3.
-
[Iterate.] Increment
 $i$
by 1 and iterate from Step C1.
$i$
by 1 and iterate from Step C1.
Proof of correctness of Algorithm C.
We will show that the maximum of the divisorial index decreases strictly after each iteration of the algorithm. This cannot continue forever, so the algorithm eventually halts. Since the divisorial index vanishes generically, it must vanish identically when the algorithm halts, which proves that
 $(X_{n},\boldsymbol{E}_{n})$
is indeed divisorial. The functoriality properties follow directly from the corresponding functoriality properties of conormal invariants described in Proposition 6.14.
$(X_{n},\boldsymbol{E}_{n})$
is indeed divisorial. The functoriality properties follow directly from the corresponding functoriality properties of conormal invariants described in Proposition 6.14.
Assume that we are in Step C2 and fix a point
![]() $\unicode[STIX]{x1D709}_{i}\in Z_{i}$
with toric type
$\unicode[STIX]{x1D709}_{i}\in Z_{i}$
with toric type
![]() $(A,\boldsymbol{v})$
. We use the notation from the introduction of the section. To verify that the divisorial index decreases, we may work locally and without loss of generality assume that
$(A,\boldsymbol{v})$
. We use the notation from the introduction of the section. To verify that the divisorial index decreases, we may work locally and without loss of generality assume that
![]() $X_{i}$
is a basic toric stack with homogeneous coordinates as in (8.1). Let
$X_{i}$
is a basic toric stack with homogeneous coordinates as in (8.1). Let
 $A_{\text{div}}\subset A$
be the subgroup of
$A_{\text{div}}\subset A$
be the subgroup of
![]() $A$
generated by the weights
$A$
generated by the weights
![]() $a_{j}$
such that
$a_{j}$
such that
![]() $e_{j}\neq \ast$
. Recall from Definition 7.13 that the divisorial index is the number of indices
$e_{j}\neq \ast$
. Recall from Definition 7.13 that the divisorial index is the number of indices
 $j\in \{1,\ldots ,r\}$
such that
$j\in \{1,\ldots ,r\}$
such that
 $a_{j}\not \in A_{\text{div}}$
. It follows that the set
$a_{j}\not \in A_{\text{div}}$
. It follows that the set
![]() $J$
, as defined in (8.2), corresponding to the divisorial index is simply
$J$
, as defined in (8.2), corresponding to the divisorial index is simply
 $J=\{j\mid a_{j}\not \in A_{\text{div}}\}$
.
$J=\{j\mid a_{j}\not \in A_{\text{div}}\}$
.
Now consider the coordinate patch of
![]() $X_{i+1}$
corresponding to
$X_{i+1}$
corresponding to
![]() $p\in J$
, with coordinates as in (8.3). From (8.4) and (8.5), we see that the subgroup
$p\in J$
, with coordinates as in (8.3). From (8.4) and (8.5), we see that the subgroup
 $\widetilde{A}_{\text{div}}\subseteq A$
generated by the weights
$\widetilde{A}_{\text{div}}\subseteq A$
generated by the weights
![]() $\widetilde{a}_{j}$
for which
$\widetilde{a}_{j}$
for which
![]() $\widetilde{e}_{j}\neq \ast$
is generated by
$\widetilde{e}_{j}\neq \ast$
is generated by
![]() $A_{\text{div}}$
and
$A_{\text{div}}$
and
![]() $a_{p}$
. It follows that
$a_{p}$
. It follows that
 $\widetilde{a}_{j}\not \in \widetilde{A}_{\text{div}}$
implies that
$\widetilde{a}_{j}\not \in \widetilde{A}_{\text{div}}$
implies that
 $a_{j}\not \in A_{\text{div}}$
. Moreover, we have
$a_{j}\not \in A_{\text{div}}$
. Moreover, we have
 $\widetilde{a}_{p}\in \widetilde{A}_{\text{div}}$
whereas
$\widetilde{a}_{p}\in \widetilde{A}_{\text{div}}$
whereas
 $a_{p}\not \in A_{\text{div}}$
. Hence, the divisorial index at each point in
$a_{p}\not \in A_{\text{div}}$
. Hence, the divisorial index at each point in
 $(X_{i+1},\boldsymbol{E}_{i+1})$
is strictly smaller that the divisorial index at
$(X_{i+1},\boldsymbol{E}_{i+1})$
is strictly smaller that the divisorial index at
![]() $\unicode[STIX]{x1D709}_{i}$
, which concludes the proof.◻
$\unicode[STIX]{x1D709}_{i}$
, which concludes the proof.◻

Figure 8.1. The blow-up tree produced by Algorithm C for the input described in Example 8.1. The first three columns correspond to the three blow-ups performed by the algorithm and, at each blow-up, the coordinate patches marked by
![]() $\bullet$
are replaced by one or more patches. These columns are labelled by the exceptional divisor of the corresponding blow-up. The indices
$\bullet$
are replaced by one or more patches. These columns are labelled by the exceptional divisor of the corresponding blow-up. The indices
![]() $j$
in the set
$j$
in the set
![]() $J$
, as defined in (8.2), are indicated by underlining the corresponding weight
$J$
, as defined in (8.2), are indicated by underlining the corresponding weight
![]() $a_{j}$
. The column marked by
$a_{j}$
. The column marked by
![]() $\unicode[STIX]{x1D6FF}$
contains the divisorial index.
$\unicode[STIX]{x1D6FF}$
contains the divisorial index.
Example 8.1. Let
![]() $k$
be a field and consider the basic toric stack
$k$
be a field and consider the basic toric stack
![]() $(X,\boldsymbol{E})$
with homogeneous coordinates
$(X,\boldsymbol{E})$
with homogeneous coordinates
 $(k[x_{1},x_{2},x_{3}],C_{6},(4,2,3))$
and
$(k[x_{1},x_{2},x_{3}],C_{6},(4,2,3))$
and
![]() $\boldsymbol{E}=\emptyset$
. The blow-up tree generated by Algorithm C with this input is described in Figure 8.1. The algorithm terminates after three iterations. Note that the third blow-up does not modify the underlying stack. However, it is non-trivial in the sense that it modifies the ordered set of divisors.
$\boldsymbol{E}=\emptyset$
. The blow-up tree generated by Algorithm C with this input is described in Figure 8.1. The algorithm terminates after three iterations. Note that the third blow-up does not modify the underlying stack. However, it is non-trivial in the sense that it modifies the ordered set of divisors.
The following example illustrates that divisorialification can be non-trivial even if the stack we start with has a smooth coarse space.
Example 8.2. Consider the standard pair
![]() $(X,\emptyset )$
described in 7.6. The divisorialification algorithm will first blow up the point lying over the node of
$(X,\emptyset )$
described in 7.6. The divisorialification algorithm will first blow up the point lying over the node of
![]() $C$
, which has divisorial index 2. Note that the strict transform
$C$
, which has divisorial index 2. Note that the strict transform
![]() $\widetilde{C}$
of the divisor
$\widetilde{C}$
of the divisor
![]() $C$
is smooth. The divisorial index vanishes away from
$C$
is smooth. The divisorial index vanishes away from
![]() $\widetilde{C}$
and is one at each point of
$\widetilde{C}$
and is one at each point of
![]() $\widetilde{C}$
. Hence, the algorithm terminates after blowing up
$\widetilde{C}$
. Hence, the algorithm terminates after blowing up
![]() $\widetilde{C}$
in the second iteration. In this particular case, we actually even get a destackification of
$\widetilde{C}$
in the second iteration. In this particular case, we actually even get a destackification of
![]() $(X,\emptyset )$
.
$(X,\emptyset )$
.
Recall the definition of a distinguished structure on a standard pair from Definition 2.7.
Algorithm D (Divisorialification along distinguished divisors).
The input of the algorithm is a divisorial stack with distinguished structure
 $(X,\boldsymbol{E},\boldsymbol{D})$
over a quasi-compact base scheme
$(X,\boldsymbol{E},\boldsymbol{D})$
over a quasi-compact base scheme
![]() $S$
. The output of the algorithm is a smooth, ordinary blow-up sequence
$S$
. The output of the algorithm is a smooth, ordinary blow-up sequence
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}:(X_{n},\boldsymbol{E}_{n},\boldsymbol{D}_{n})\rightarrow \cdots \rightarrow (X_{0},\boldsymbol{E}_{0},\boldsymbol{D}_{0})=(X,\boldsymbol{E},\boldsymbol{D}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}:(X_{n},\boldsymbol{E}_{n},\boldsymbol{D}_{n})\rightarrow \cdots \rightarrow (X_{0},\boldsymbol{E}_{0},\boldsymbol{D}_{0})=(X,\boldsymbol{E},\boldsymbol{D}),\end{eqnarray}$$
with each blow-up being admissible (see Definition 2.7). The resulting triple
 $(X_{n},\boldsymbol{E}_{n},\boldsymbol{D}_{n})$
has the property that for each component
$(X_{n},\boldsymbol{E}_{n},\boldsymbol{D}_{n})$
has the property that for each component
![]() $D$
of
$D$
of
![]() $\boldsymbol{D}_{n}$
, the
$\boldsymbol{D}_{n}$
, the
![]() $D$
-divisorial index, in the sense of Definition 7.16, vanishes. Furthermore, each of the centres
$D$
-divisorial index, in the sense of Definition 7.16, vanishes. Furthermore, each of the centres
![]() $Z_{i}$
in the blow-up sequence is contained in exactly one of the components of
$Z_{i}$
in the blow-up sequence is contained in exactly one of the components of
![]() $\boldsymbol{D}_{i}$
and transversal to all other components of
$\boldsymbol{D}_{i}$
and transversal to all other components of
![]() $\boldsymbol{E}_{i}$
. The construction is functorial (see Definition 2.6) with respect to arbitrary base change
$\boldsymbol{E}_{i}$
. The construction is functorial (see Definition 2.6) with respect to arbitrary base change
![]() $S^{\prime }\rightarrow S$
and with respect to morphisms
$S^{\prime }\rightarrow S$
and with respect to morphisms
 $X^{\prime }\rightarrow X$
which are either gerbes or smooth and stabiliser-preserving.
$X^{\prime }\rightarrow X$
which are either gerbes or smooth and stabiliser-preserving.
- D0.
-
[Initialise.] Let
 $i=0$
.
$i=0$
. - D1.
-
[Finished?] Let
 $D_{i}^{\prime }$
denote the oldest component of
$D_{i}^{\prime }$
denote the oldest component of
 $\boldsymbol{D}_{i}$
for which the
$\boldsymbol{D}_{i}$
for which the
 $D_{i}^{\prime }$
-divisorial index does not vanish identically. If no such component exists, the algorithm terminates. Otherwise, we let
$D_{i}^{\prime }$
-divisorial index does not vanish identically. If no such component exists, the algorithm terminates. Otherwise, we let
 $Z_{i}$
be the smooth substack of
$Z_{i}$
be the smooth substack of
 $X_{i}$
where the
$X_{i}$
where the
 $D_{i}^{\prime }$
-divisorial index assumes its maximal value.
$D_{i}^{\prime }$
-divisorial index assumes its maximal value. - D2.
-
[Blow up maximal locus.] Let
 $\unicode[STIX]{x1D70B}_{i}:(X_{i+1},\boldsymbol{E}_{i+1},\boldsymbol{D}_{i+1})\rightarrow (X_{i},\boldsymbol{E}_{i},\boldsymbol{D}_{i})$
be the blow-up of
$\unicode[STIX]{x1D70B}_{i}:(X_{i+1},\boldsymbol{E}_{i+1},\boldsymbol{D}_{i+1})\rightarrow (X_{i},\boldsymbol{E}_{i},\boldsymbol{D}_{i})$
be the blow-up of
 $X_{i}$
in
$X_{i}$
in
 $Z_{i}$
.
$Z_{i}$
. - D3.
-
[Iterate.] Increment
 $i$
by one and iterate from Step D1.
$i$
by one and iterate from Step D1.
Proof of correctness of Algorithm D.
Assume that we are in iteration
![]() $i$
. Let
$i$
. Let
![]() $\unicode[STIX]{x1D709}_{i}\in Z_{i}$
be a point in the centre of the blow-up, and let
$\unicode[STIX]{x1D709}_{i}\in Z_{i}$
be a point in the centre of the blow-up, and let
![]() $\unicode[STIX]{x1D709}_{i+1}$
be an arbitrary lifting of
$\unicode[STIX]{x1D709}_{i+1}$
be an arbitrary lifting of
![]() $\unicode[STIX]{x1D709}_{i}$
to the exceptional locus. We will prove the following three statements.
$\unicode[STIX]{x1D709}_{i}$
to the exceptional locus. We will prove the following three statements.
-
(i) The
 $\widetilde{D}$
-divisorial index at
$\widetilde{D}$
-divisorial index at
 $\unicode[STIX]{x1D709}_{i+1}$
for the strict transform
$\unicode[STIX]{x1D709}_{i+1}$
for the strict transform
 $\widetilde{D}$
of any component
$\widetilde{D}$
of any component
 $D$
of
$D$
of
 $\boldsymbol{D}_{i}$
is not larger than the
$\boldsymbol{D}_{i}$
is not larger than the
 $D$
-divisorial index at
$D$
-divisorial index at
 $\unicode[STIX]{x1D709}_{i}$
.
$\unicode[STIX]{x1D709}_{i}$
. -
(ii) In the case where the component in the previous statement is
 $D_{i}^{\prime }$
, the index is strictly smaller.
$D_{i}^{\prime }$
, the index is strictly smaller. -
(iii) The
 $F$
-divisorial index at
$F$
-divisorial index at
 $\unicode[STIX]{x1D709}_{i+1}$
, where
$\unicode[STIX]{x1D709}_{i+1}$
, where
 $F$
is the exceptional divisor of the blow-up, is strictly smaller than the
$F$
is the exceptional divisor of the blow-up, is strictly smaller than the
 $D_{i}^{\prime }$
-divisorial index at
$D_{i}^{\prime }$
-divisorial index at
 $\unicode[STIX]{x1D709}_{i}$
.
$\unicode[STIX]{x1D709}_{i}$
.
Together these statements prove that the algorithm terminates with the right exit condition. Indeed, let
![]() $N$
be the maximum of the
$N$
be the maximum of the
![]() $D$
-divisorial index where
$D$
-divisorial index where
![]() $D$
ranges through the components of
$D$
ranges through the components of
![]() $\boldsymbol{D}_{0}$
. At each iteration
$\boldsymbol{D}_{0}$
. At each iteration
![]() $i$
, let
$i$
, let
![]() $w_{j}$
be the number of components
$w_{j}$
be the number of components
![]() $D$
of
$D$
of
![]() $\boldsymbol{D}_{i}$
such that the maximum of the
$\boldsymbol{D}_{i}$
such that the maximum of the
![]() $D$
-divisorial index is
$D$
-divisorial index is
![]() $j$
. Then the
$j$
. Then the
![]() $N$
-tuple
$N$
-tuple
 $(w_{N},w_{N-1},\ldots ,w_{1})$
decreases strictly in lexicographical ordering with each iteration of the algorithm.
$(w_{N},w_{N-1},\ldots ,w_{1})$
decreases strictly in lexicographical ordering with each iteration of the algorithm.
We use the notation from the introduction of the section. To verify the statements above, we may work locally and assume that
![]() $X_{i}$
is a basic toric stack with homogeneous coordinates as in (8.1). We choose the indexing such that the divisor
$X_{i}$
is a basic toric stack with homogeneous coordinates as in (8.1). We choose the indexing such that the divisor
![]() $D_{i}^{\prime }$
as defined in Step D1 is
$D_{i}^{\prime }$
as defined in Step D1 is
![]() $V(x_{1})$
. For each
$V(x_{1})$
. For each
 $k\in \{1,\ldots ,r\}$
, we define the subgroup
$k\in \{1,\ldots ,r\}$
, we define the subgroup
 $$\begin{eqnarray}A_{\text{div}}^{k}=\langle a_{j}\mid j\neq k,e_{j}\neq \ast \rangle\end{eqnarray}$$
$$\begin{eqnarray}A_{\text{div}}^{k}=\langle a_{j}\mid j\neq k,e_{j}\neq \ast \rangle\end{eqnarray}$$
and, for each
 $j\in \{1,\ldots ,r\}$
, we define
$j\in \{1,\ldots ,r\}$
, we define
![]() $c_{j}^{k}$
as the smallest natural numbers such that
$c_{j}^{k}$
as the smallest natural numbers such that
 $a_{j}\equiv c_{j}^{k}a_{k}\text{ mod}~A_{\text{div}}^{k}$
. Recall from Definition 7.16 that if
$a_{j}\equiv c_{j}^{k}a_{k}\text{ mod}~A_{\text{div}}^{k}$
. Recall from Definition 7.16 that if
![]() $V(x_{k})$
corresponds to a component
$V(x_{k})$
corresponds to a component
![]() $E$
of
$E$
of
![]() $\boldsymbol{E}$
, the
$\boldsymbol{E}$
, the
![]() $E$
-divisorial index is given by
$E$
-divisorial index is given by
![]() $\sum c_{j}^{k}$
, where the sum is taken over the indices
$\sum c_{j}^{k}$
, where the sum is taken over the indices
![]() $j$
such that
$j$
such that
![]() $e_{j}=\ast$
.
$e_{j}=\ast$
.
The set
![]() $J$
, defined as in (8.2), with respect to the
$J$
, defined as in (8.2), with respect to the
![]() $D^{\prime }$
-divisorial index is the set of indices
$D^{\prime }$
-divisorial index is the set of indices
![]() $j$
such that
$j$
such that
![]() $c_{j}^{1}\neq 0$
. Fix
$c_{j}^{1}\neq 0$
. Fix
![]() $p\in J$
and consider the corresponding patch of
$p\in J$
and consider the corresponding patch of
![]() $X_{i+1}$
with homogeneous coordinates as in (8.3). We define
$X_{i+1}$
with homogeneous coordinates as in (8.3). We define
![]() $\widetilde{A}_{\text{div}}^{k}$
and
$\widetilde{A}_{\text{div}}^{k}$
and
![]() $\widetilde{c}_{j}^{k}$
similarly as above.
$\widetilde{c}_{j}^{k}$
similarly as above.
Now assume that
![]() $V(x_{k})$
corresponds to a component
$V(x_{k})$
corresponds to a component
![]() $D$
of the distinguished divisor
$D$
of the distinguished divisor
![]() $\boldsymbol{D}_{i}$
. When computing the
$\boldsymbol{D}_{i}$
. When computing the
![]() $\unicode[STIX]{x1D70B}_{i}^{-1}(D)$
-divisorial index, we may assume that
$\unicode[STIX]{x1D70B}_{i}^{-1}(D)$
-divisorial index, we may assume that
![]() $k\neq p$
. Then
$k\neq p$
. Then
 $\widetilde{A}_{\text{div}}^{k}=A_{\text{div}}^{k}+\langle a_{p}\rangle$
. It follows that for any
$\widetilde{A}_{\text{div}}^{k}=A_{\text{div}}^{k}+\langle a_{p}\rangle$
. It follows that for any
![]() $j$
such that
$j$
such that
 $1\leqslant j\leqslant r$
, we have
$1\leqslant j\leqslant r$
, we have
 $$\begin{eqnarray}\widetilde{a}_{j}\equiv c_{j}^{k}a_{k}\quad \text{mod}~\widetilde{A}_{\text{div}}^{k},\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{a}_{j}\equiv c_{j}^{k}a_{k}\quad \text{mod}~\widetilde{A}_{\text{div}}^{k},\end{eqnarray}$$
so
![]() $\widetilde{c}_{j}^{k}\leqslant c_{j}^{k}$
. By taking the sum over all
$\widetilde{c}_{j}^{k}\leqslant c_{j}^{k}$
. By taking the sum over all
![]() $j$
such that
$j$
such that
![]() $\widetilde{e}_{j}=\ast$
, we see that the
$\widetilde{e}_{j}=\ast$
, we see that the
![]() $\unicode[STIX]{x1D70B}_{i}^{-1}(D)$
-divisorial index is bounded above by the
$\unicode[STIX]{x1D70B}_{i}^{-1}(D)$
-divisorial index is bounded above by the
![]() $D$
-divisorial index, which proves the first statement. In the particular case when
$D$
-divisorial index, which proves the first statement. In the particular case when
![]() $k=1$
, one verifies that
$k=1$
, one verifies that
![]() $\widetilde{c}_{p}^{1}=0$
, whereas
$\widetilde{c}_{p}^{1}=0$
, whereas
![]() $c_{p}^{1}\neq 0$
, which proves the second statement.
$c_{p}^{1}\neq 0$
, which proves the second statement.
Finally, we investigate the
![]() $F$
-divisorial index where
$F$
-divisorial index where
![]() $F$
is the exceptional divisor, which is given by
$F$
is the exceptional divisor, which is given by
![]() $V(y_{p})$
. We have
$V(y_{p})$
. We have
 $\widetilde{A}_{\text{div}}^{p}=A_{\text{div}}^{1}+\langle a_{1}-a_{p}\rangle$
, so
$\widetilde{A}_{\text{div}}^{p}=A_{\text{div}}^{1}+\langle a_{1}-a_{p}\rangle$
, so
 $\widetilde{a}_{p}\equiv a_{p}\equiv a_{1}~~\text{mod}~\widetilde{A}_{\text{div}}^{p}$
. For
$\widetilde{a}_{p}\equiv a_{p}\equiv a_{1}~~\text{mod}~\widetilde{A}_{\text{div}}^{p}$
. For
![]() $j\in J$
, we get
$j\in J$
, we get
 $$\begin{eqnarray}\widetilde{a}_{j}\equiv a_{j}-a_{p}\equiv (c_{j}^{1}-1)\widetilde{a}_{p}\quad \text{mod}~\widetilde{A}_{\text{div}}^{p},\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{a}_{j}\equiv a_{j}-a_{p}\equiv (c_{j}^{1}-1)\widetilde{a}_{p}\quad \text{mod}~\widetilde{A}_{\text{div}}^{p},\end{eqnarray}$$
which proves that
![]() $\widetilde{c}_{j}^{p}<c_{j}^{1}$
, and the third statement follows.◻
$\widetilde{c}_{j}^{p}<c_{j}^{1}$
, and the third statement follows.◻
Example 8.3. Let
![]() $k$
be a field. Figure 8.2 illustrates the blow-up tree produced by Algorithm D when applied to the standard pair
$k$
be a field. Figure 8.2 illustrates the blow-up tree produced by Algorithm D when applied to the standard pair
 $(X,\boldsymbol{E},\boldsymbol{D})$
with distinguished structure
$(X,\boldsymbol{E},\boldsymbol{D})$
with distinguished structure
![]() $\boldsymbol{D}$
defined as follows: the stack
$\boldsymbol{D}$
defined as follows: the stack
![]() $X$
is the basic toric stack with homogeneous coordinates
$X$
is the basic toric stack with homogeneous coordinates
 $(k[x_{1},\ldots ,x_{4}],(C_{3})^{2},\boldsymbol{a})$
, where
$(k[x_{1},\ldots ,x_{4}],(C_{3})^{2},\boldsymbol{a})$
, where
 $\boldsymbol{a}=((0,1),(1,0),(1,1),(2,1))$
. We let
$\boldsymbol{a}=((0,1),(1,0),(1,1),(2,1))$
. We let
 $E^{1}=V(x_{1})$
and
$E^{1}=V(x_{1})$
and
 $D^{1}=V(x_{2})$
. The ordered sets
$D^{1}=V(x_{2})$
. The ordered sets
![]() $\boldsymbol{E}$
and
$\boldsymbol{E}$
and
![]() $\boldsymbol{D}$
are defined as
$\boldsymbol{D}$
are defined as
 $(E^{1},D^{1})$
and
$(E^{1},D^{1})$
and
![]() $(D^{1})$
, respectively.
$(D^{1})$
, respectively.
Lemma 8.4. Let
 $(X,\boldsymbol{E},\boldsymbol{D})$
be a divisorial stack with distinguished structure over a quasi-compact scheme
$(X,\boldsymbol{E},\boldsymbol{D})$
be a divisorial stack with distinguished structure over a quasi-compact scheme
![]() $S$
, and let
$S$
, and let
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}:(X_{n},\boldsymbol{E}_{n},\boldsymbol{D}_{n})\rightarrow \cdots \rightarrow (X_{0},\boldsymbol{E}_{0},\boldsymbol{D}_{0})=(X,\boldsymbol{E},\boldsymbol{D})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}:(X_{n},\boldsymbol{E}_{n},\boldsymbol{D}_{n})\rightarrow \cdots \rightarrow (X_{0},\boldsymbol{E}_{0},\boldsymbol{D}_{0})=(X,\boldsymbol{E},\boldsymbol{D})\end{eqnarray}$$
be the output of Algorithm D applied to
 $(X,\boldsymbol{E},\boldsymbol{D})$
. Let
$(X,\boldsymbol{E},\boldsymbol{D})$
. Let
 $\unicode[STIX]{x1D709}_{0}\in X_{0}$
be a point at which all distinguished divisors are divisorially independent in the sense of Definition 7.15. For each
$\unicode[STIX]{x1D709}_{0}\in X_{0}$
be a point at which all distinguished divisors are divisorially independent in the sense of Definition 7.15. For each
![]() $i$
such that
$i$
such that
 $0<i\leqslant n$
, let
$0<i\leqslant n$
, let
![]() $\unicode[STIX]{x1D709}_{i}\in X_{i}$
be a lift of
$\unicode[STIX]{x1D709}_{i}\in X_{i}$
be a lift of
![]() $\unicode[STIX]{x1D709}_{i-1}$
such that the toroidal index (see Definition 7.4) at
$\unicode[STIX]{x1D709}_{i-1}$
such that the toroidal index (see Definition 7.4) at
![]() $\unicode[STIX]{x1D709}_{i}$
is the same as the toroidal index at
$\unicode[STIX]{x1D709}_{i}$
is the same as the toroidal index at
![]() $\unicode[STIX]{x1D709}_{i-1}$
. Then all components of
$\unicode[STIX]{x1D709}_{i-1}$
. Then all components of
![]() $\boldsymbol{D}_{i}$
are divisorially independent at
$\boldsymbol{D}_{i}$
are divisorially independent at
![]() $\unicode[STIX]{x1D709}_{i}$
. In particular, all components of
$\unicode[STIX]{x1D709}_{i}$
. In particular, all components of
![]() $\boldsymbol{D}_{n}$
are independent at
$\boldsymbol{D}_{n}$
are independent at
![]() $\unicode[STIX]{x1D709}_{n}$
in the sense of Definition 7.2.
$\unicode[STIX]{x1D709}_{n}$
in the sense of Definition 7.2.
Proof. Note that a divisor
![]() $E$
is independent at a point if and only if it is divisorially independent and the
$E$
is independent at a point if and only if it is divisorially independent and the
![]() $E$
-divisorial index is zero. This is an easy consequence of the definitions. Therefore, the last statement of the lemma follows from the second last statement.
$E$
-divisorial index is zero. This is an easy consequence of the definitions. Therefore, the last statement of the lemma follows from the second last statement.
We fix
![]() $i$
and assume that all components of
$i$
and assume that all components of
![]() $\boldsymbol{D}_{i}$
are divisorially independent at
$\boldsymbol{D}_{i}$
are divisorially independent at
![]() $\unicode[STIX]{x1D709}_{i}$
. We want to prove that all components of
$\unicode[STIX]{x1D709}_{i}$
. We want to prove that all components of
![]() $\boldsymbol{D}_{i+1}$
are divisorially independent at
$\boldsymbol{D}_{i+1}$
are divisorially independent at
![]() $\unicode[STIX]{x1D709}_{i+1}$
.
$\unicode[STIX]{x1D709}_{i+1}$
.
As usual, we may work locally and assume that
![]() $X_{i}$
is a basic toric stack. We use the same notation as in the proof of correctness of Algorithm D. We need only consider the patch corresponding to
$X_{i}$
is a basic toric stack. We use the same notation as in the proof of correctness of Algorithm D. We need only consider the patch corresponding to
![]() $p=1$
of the blow-up, since the toroidal index is lower at all other patches. But, at this patch, we have
$p=1$
of the blow-up, since the toroidal index is lower at all other patches. But, at this patch, we have
 $\widetilde{e}_{j}\in \boldsymbol{E}_{i+1}$
(or
$\widetilde{e}_{j}\in \boldsymbol{E}_{i+1}$
(or
 $\widetilde{e}_{j}\in \boldsymbol{D}_{i+1}$
) precisely when
$\widetilde{e}_{j}\in \boldsymbol{D}_{i+1}$
) precisely when
![]() $e_{j}\in \boldsymbol{E}_{i}$
(or
$e_{j}\in \boldsymbol{E}_{i}$
(or
 $e_{j}\in \boldsymbol{D}_{i}$
). Furthermore, we have
$e_{j}\in \boldsymbol{D}_{i}$
). Furthermore, we have
![]() $\widetilde{a}_{j}=a_{j}$
whenever
$\widetilde{a}_{j}=a_{j}$
whenever
![]() $e_{j}\neq \ast$
. From this it follows that the distinguished divisors are divisorially independent at
$e_{j}\neq \ast$
. From this it follows that the distinguished divisors are divisorially independent at
![]() $\unicode[STIX]{x1D709}_{i+1}$
provided that the distinguished divisors are divisorially independent at
$\unicode[STIX]{x1D709}_{i+1}$
provided that the distinguished divisors are divisorially independent at
![]() $\unicode[STIX]{x1D709}_{i}$
, as desired.◻
$\unicode[STIX]{x1D709}_{i}$
, as desired.◻
Example 8.5. Consider the standard pair
 $(X,\boldsymbol{E},\boldsymbol{D})$
from Example 8.3. Note that the divisors in
$(X,\boldsymbol{E},\boldsymbol{D})$
from Example 8.3. Note that the divisors in
![]() $\boldsymbol{E}$
are divisorially independent (see Definition 7.15) since the group
$\boldsymbol{E}$
are divisorially independent (see Definition 7.15) since the group
![]() $(C_{3})^{2}$
is a direct sum of the cyclic groups generated by the weights
$(C_{3})^{2}$
is a direct sum of the cyclic groups generated by the weights
![]() $a_{1}$
and
$a_{1}$
and
![]() $a_{2}$
of the coordinate functions
$a_{2}$
of the coordinate functions
![]() $x_{1}$
and
$x_{1}$
and
![]() $x_{2}$
, respectively. Hence, Lemma 8.4 applies. From Figure 8.2, we see that the
$x_{2}$
, respectively. Hence, Lemma 8.4 applies. From Figure 8.2, we see that the
![]() $a_{1}$
coefficient has been reduced to zero in the weights of the third and fourth coordinate functions in chart 3. Hence, the divisor
$a_{1}$
coefficient has been reduced to zero in the weights of the third and fourth coordinate functions in chart 3. Hence, the divisor
![]() $D_{3}$
is independent at this chart (see Definition 7.1). At all other terminal charts, i.e., the charts 4, 6, 7 and 8, the property of divisorial independence is destroyed. Note, however, that at these charts the toroidal index has dropped.
$D_{3}$
is independent at this chart (see Definition 7.1). At all other terminal charts, i.e., the charts 4, 6, 7 and 8, the property of divisorial independence is destroyed. Note, however, that at these charts the toroidal index has dropped.
Let
![]() $(X,\boldsymbol{E})$
be a standard pair. Recall that we do not require the components of the sequence
$(X,\boldsymbol{E})$
be a standard pair. Recall that we do not require the components of the sequence
![]() $\boldsymbol{E}$
to be connected (see Definition 2.1). This poses a small technical problem at the final stage of the destackification process. To deal with this, we introduce the concept of a refinement of the sequence
$\boldsymbol{E}$
to be connected (see Definition 2.1). This poses a small technical problem at the final stage of the destackification process. To deal with this, we introduce the concept of a refinement of the sequence
![]() $\boldsymbol{E}$
.
$\boldsymbol{E}$
.
Definition 8.6. Let
![]() $(X,\boldsymbol{E})$
and
$(X,\boldsymbol{E})$
and
![]() $(X,\boldsymbol{E}^{\prime })$
be standard pairs. Assume that the sequence
$(X,\boldsymbol{E}^{\prime })$
be standard pairs. Assume that the sequence
![]() $\boldsymbol{E}$
is indexed by the set
$\boldsymbol{E}$
is indexed by the set
 $[s]=\{1,\ldots ,s\}$
and
$[s]=\{1,\ldots ,s\}$
and
![]() $\boldsymbol{E}^{\prime }$
by the set
$\boldsymbol{E}^{\prime }$
by the set
 $[s^{\prime }]=\{1,\ldots ,s^{\prime }\}$
. We say that
$[s^{\prime }]=\{1,\ldots ,s^{\prime }\}$
. We say that
![]() $\boldsymbol{E}^{\prime }$
is a refinement of
$\boldsymbol{E}^{\prime }$
is a refinement of
![]() $\boldsymbol{E}$
if there exists a surjective function
$\boldsymbol{E}$
if there exists a surjective function
 $f:[s^{\prime }]\rightarrow [s]$
such that for each
$f:[s^{\prime }]\rightarrow [s]$
such that for each
![]() $i\in [s]$
, the component
$i\in [s]$
, the component
![]() $E^{i}$
in
$E^{i}$
in
![]() $\boldsymbol{E}$
is the disjoint union
$\boldsymbol{E}$
is the disjoint union
 $\bigcup _{j}(E^{\prime })^{j},$
with
$\bigcup _{j}(E^{\prime })^{j},$
with
 $(E^{\prime })^{j}\in \boldsymbol{E}^{\prime }$
, where the union is taken over the set
$(E^{\prime })^{j}\in \boldsymbol{E}^{\prime }$
, where the union is taken over the set
 $f^{-1}(\{i\})$
.
$f^{-1}(\{i\})$
.
The next proposition shows that, up to a refinement of the divisor
![]() $\boldsymbol{E}$
, a divisorial standard pair
$\boldsymbol{E}$
, a divisorial standard pair
![]() $(X,\boldsymbol{E})$
is destackified (cf. Definition 2.3) provided that the independency index vanishes everywhere.
$(X,\boldsymbol{E})$
is destackified (cf. Definition 2.3) provided that the independency index vanishes everywhere.
Proposition 8.7. Let
 $(X,\boldsymbol{E})/S$
be a divisorial stack over a quasi-compact scheme
$(X,\boldsymbol{E})/S$
be a divisorial stack over a quasi-compact scheme
![]() $S$
, and assume that the independency index is everywhere zero at
$S$
, and assume that the independency index is everywhere zero at
![]() $X$
. Let
$X$
. Let
 $\unicode[STIX]{x1D70B}:X\rightarrow X_{\text{cs}}$
be the coarse space. Then
$\unicode[STIX]{x1D70B}:X\rightarrow X_{\text{cs}}$
be the coarse space. Then
 $(X_{\text{cs}},\boldsymbol{E}_{\text{cs}})/S$
is a standard pair. In particular, the stack
$(X_{\text{cs}},\boldsymbol{E}_{\text{cs}})/S$
is a standard pair. In particular, the stack
![]() $X_{\text{cs}}$
is smooth and
$X_{\text{cs}}$
is smooth and
![]() $\boldsymbol{E}_{\text{cs}}$
has simple normal crossings.
$\boldsymbol{E}_{\text{cs}}$
has simple normal crossings.
Moreover, there exists a refinement
![]() $\boldsymbol{E}^{\prime }$
of
$\boldsymbol{E}^{\prime }$
of
![]() $\boldsymbol{E}$
, in the sense of Definition 8.6, such that the following holds.
$\boldsymbol{E}$
, in the sense of Definition 8.6, such that the following holds.
-
(i) The divisor
 $\boldsymbol{E}^{\prime }$
is the
$\boldsymbol{E}^{\prime }$
is the
 $\boldsymbol{d}$
th root of
$\boldsymbol{d}$
th root of
 $\unicode[STIX]{x1D70B}^{\ast }\boldsymbol{E}_{\text{cs}}^{\prime }$
for some sequence
$\unicode[STIX]{x1D70B}^{\ast }\boldsymbol{E}_{\text{cs}}^{\prime }$
for some sequence
 $\boldsymbol{d}$
of positive integers indexed by the components of
$\boldsymbol{d}$
of positive integers indexed by the components of
 $\boldsymbol{E}^{\prime }$
.
$\boldsymbol{E}^{\prime }$
. -
(ii) The canonical factorisation
 $X\rightarrow (X_{\text{cs}})_{\boldsymbol{d}^{-1}E_{\text{cs}}^{\prime }}\rightarrow E_{\text{cs}}$
makes
$X\rightarrow (X_{\text{cs}})_{\boldsymbol{d}^{-1}E_{\text{cs}}^{\prime }}\rightarrow E_{\text{cs}}$
makes
 $X$
a gerbe over the stack
$X$
a gerbe over the stack
 $(X_{\text{cs}})_{\boldsymbol{d}^{-1}E_{\text{cs}}^{\prime }}$
.
$(X_{\text{cs}})_{\boldsymbol{d}^{-1}E_{\text{cs}}^{\prime }}$
.
Proof. That
![]() $X_{\text{cs}}$
is smooth and that
$X_{\text{cs}}$
is smooth and that
![]() $\boldsymbol{E}_{\text{cs}}$
has normal crossings can be verified étale locally on
$\boldsymbol{E}_{\text{cs}}$
has normal crossings can be verified étale locally on
![]() $X_{\text{cs}}$
. Hence, we may assume that
$X_{\text{cs}}$
. Hence, we may assume that
![]() $X$
is a basic toric stack with homogeneous coordinates as in (8.1). We use the notation
$X$
is a basic toric stack with homogeneous coordinates as in (8.1). We use the notation
 $$\begin{eqnarray}{\mathcal{R}}:={\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}].\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{R}}:={\mathcal{O}}_{S}[x_{1},\ldots ,x_{r}].\end{eqnarray}$$
We choose the coordinates such that the components of
![]() $\boldsymbol{E}$
are
$\boldsymbol{E}$
are
![]() $V(x_{j})$
for
$V(x_{j})$
for
 $j\in \{1,\ldots ,s\}$
. Let
$j\in \{1,\ldots ,s\}$
. Let
 $A_{\text{rig}}=\langle a_{1},\ldots ,a_{r}\rangle$
. By the assumption that the independency index is everywhere zero, we have
$A_{\text{rig}}=\langle a_{1},\ldots ,a_{r}\rangle$
. By the assumption that the independency index is everywhere zero, we have
 $A_{\text{rig}}=\bigoplus _{j=1}^{r}A_{j}$
with each group
$A_{\text{rig}}=\bigoplus _{j=1}^{r}A_{j}$
with each group
![]() $A_{j}$
finite and cyclic. By the assumption that
$A_{j}$
finite and cyclic. By the assumption that
![]() $(X,\boldsymbol{E})$
is divisorial, the group
$(X,\boldsymbol{E})$
is divisorial, the group
![]() $A_{j}$
vanishes for each
$A_{j}$
vanishes for each
![]() $j>s$
.
$j>s$
.
Denote the order of
![]() $A_{j}$
by
$A_{j}$
by
![]() $d_{j}$
. Then the coarse space is the relative spectrum of the invariant ring
$d_{j}$
. Then the coarse space is the relative spectrum of the invariant ring
 $$\begin{eqnarray}{\mathcal{R}}^{\prime }:={\mathcal{O}}_{S}[x_{1}^{d_{1}},\ldots ,x_{s}^{d_{s}},x_{s+1},\ldots ,x_{r}].\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{R}}^{\prime }:={\mathcal{O}}_{S}[x_{1}^{d_{1}},\ldots ,x_{s}^{d_{s}},x_{s+1},\ldots ,x_{r}].\end{eqnarray}$$
In particular, the coarse space is smooth since this is a polynomial ring. The coarse space
![]() $E_{\text{cs}}^{j}$
of a component
$E_{\text{cs}}^{j}$
of a component
![]() $E^{j}$
of
$E^{j}$
of
![]() $\boldsymbol{E}$
corresponding to the
$\boldsymbol{E}$
corresponding to the
![]() $j$
th coordinate is
$j$
th coordinate is
![]() $V(x_{j}^{d_{j}})$
. Hence also
$V(x_{j}^{d_{j}})$
. Hence also
![]() $E_{\text{cs}}^{j}$
is smooth, and the divisors
$E_{\text{cs}}^{j}$
is smooth, and the divisors
 $E_{\text{cs}}^{j},\ldots ,E_{\text{cs}}^{j}$
have simple normal crossings. This proves that
$E_{\text{cs}}^{j},\ldots ,E_{\text{cs}}^{j}$
have simple normal crossings. This proves that
 $(X_{\text{cs}},\boldsymbol{E}_{\text{cs}})$
is a standard pair.
$(X_{\text{cs}},\boldsymbol{E}_{\text{cs}})$
is a standard pair.
From the local coordinates, we also see that
![]() $E^{j}$
is a
$E^{j}$
is a
![]() $d_{j}$
th root of
$d_{j}$
th root of
 $\unicode[STIX]{x1D70B}^{-1}(E_{\text{cs}}^{j})$
. Globally, the coefficient
$\unicode[STIX]{x1D70B}^{-1}(E_{\text{cs}}^{j})$
. Globally, the coefficient
![]() $d_{j}$
is locally constant on
$d_{j}$
is locally constant on
![]() $E^{j}$
. By refining
$E^{j}$
. By refining
![]() $\boldsymbol{E}$
such that
$\boldsymbol{E}$
such that
![]() $d_{j}$
becomes constant on each component, we may assume that
$d_{j}$
becomes constant on each component, we may assume that
![]() $E^{j}$
is the
$E^{j}$
is the
![]() $d_{j}$
th root of
$d_{j}$
th root of
 $\unicode[STIX]{x1D70B}^{-1}(E_{\text{cs}}^{i})$
globally, which proves (i). This gives the factorisation in (ii) by the universal property of root stacks. The fact that
$\unicode[STIX]{x1D70B}^{-1}(E_{\text{cs}}^{i})$
globally, which proves (i). This gives the factorisation in (ii) by the universal property of root stacks. The fact that
![]() $X$
is a gerbe over
$X$
is a gerbe over
 $(X_{\text{cs}})_{\boldsymbol{d}^{-1}E_{\text{cs}}}$
can again be verified locally. Here it follows from the sequence of homomorphisms between the local homogeneous coordinate rings of graded
$(X_{\text{cs}})_{\boldsymbol{d}^{-1}E_{\text{cs}}}$
can again be verified locally. Here it follows from the sequence of homomorphisms between the local homogeneous coordinate rings of graded
![]() ${\mathcal{O}}_{S}$
-algebras
${\mathcal{O}}_{S}$
-algebras
 $$\begin{eqnarray}(R^{\prime },0)\rightarrow (R,A_{\text{rig}})\rightarrow (R,A);\end{eqnarray}$$
$$\begin{eqnarray}(R^{\prime },0)\rightarrow (R,A_{\text{rig}})\rightarrow (R,A);\end{eqnarray}$$
here the first map corresponds to the root stack and the second map corresponds to the gerbe (cf. Remark 3.5). ◻
Remark 8.8. Let
![]() $(X,\boldsymbol{E})$
be a standard pair. It is easy to see that any refinement
$(X,\boldsymbol{E})$
be a standard pair. It is easy to see that any refinement
![]() $\boldsymbol{E}^{\prime }$
of
$\boldsymbol{E}^{\prime }$
of
![]() $\boldsymbol{E}$
can be obtained via a sequence of blow-ups, at least if we do not care about the ordering of
$\boldsymbol{E}$
can be obtained via a sequence of blow-ups, at least if we do not care about the ordering of
![]() $\boldsymbol{E}^{\prime }$
. Indeed, we only have to blow up a suitable subset of the components of
$\boldsymbol{E}^{\prime }$
. Indeed, we only have to blow up a suitable subset of the components of
![]() $\boldsymbol{E}^{\prime }$
one after another. Notice that each such blow-up is trivial in the sense that it does not modify
$\boldsymbol{E}^{\prime }$
one after another. Notice that each such blow-up is trivial in the sense that it does not modify
![]() $X$
since the centres of the blow-ups are effective Cartier divisors.
$X$
since the centres of the blow-ups are effective Cartier divisors.
Remark 8.9. A naive choice of refinement of
![]() $\boldsymbol{E}$
in Proposition 8.7 would be to take
$\boldsymbol{E}$
in Proposition 8.7 would be to take
![]() $\boldsymbol{E}^{\prime }$
such that each component of
$\boldsymbol{E}^{\prime }$
such that each component of
![]() $\boldsymbol{E}^{\prime }$
is connected. The problem with this choice is that it in general cannot be made functorial, even with respect to isomorphisms. To see this, let
$\boldsymbol{E}^{\prime }$
is connected. The problem with this choice is that it in general cannot be made functorial, even with respect to isomorphisms. To see this, let
![]() $X$
be a two-dimensional orbifold admitting a non-trivial involution
$X$
be a two-dimensional orbifold admitting a non-trivial involution
![]() $\unicode[STIX]{x1D70E}$
. Assume that
$\unicode[STIX]{x1D70E}$
. Assume that
![]() $P$
and
$P$
and
![]() $Q$
are distinct points on
$Q$
are distinct points on
![]() $X$
which are exchanged by
$X$
which are exchanged by
![]() $\unicode[STIX]{x1D70E}$
and that the corresponding points on
$\unicode[STIX]{x1D70E}$
and that the corresponding points on
![]() $X_{\text{cs}}$
are isolated singularities. Then it is easy to see that any functorial destackification algorithm must blow up the points
$X_{\text{cs}}$
are isolated singularities. Then it is easy to see that any functorial destackification algorithm must blow up the points
![]() $P$
and
$P$
and
![]() $Q$
simultaneously, which results in a disconnected divisor.
$Q$
simultaneously, which results in a disconnected divisor.
Remark 8.10. Let
![]() $(X,\boldsymbol{E})$
be a divisorial standard pair and assume that the independency index is everywhere vanishing. By Remark 8.8, there is a refinement
$(X,\boldsymbol{E})$
be a divisorial standard pair and assume that the independency index is everywhere vanishing. By Remark 8.8, there is a refinement
![]() $\boldsymbol{E}^{\prime }$
of
$\boldsymbol{E}^{\prime }$
of
![]() $\boldsymbol{E}$
as in Proposition 8.7, but, by Remark 8.9, some care must be taken when constructing a refinement algorithm in order to get the right functorial properties. A simple algorithm which works is to take each of the components
$\boldsymbol{E}$
as in Proposition 8.7, but, by Remark 8.9, some care must be taken when constructing a refinement algorithm in order to get the right functorial properties. A simple algorithm which works is to take each of the components
![]() $E^{i}$
of
$E^{i}$
of
![]() $\boldsymbol{E}$
and repeatedly blow up the locus where the order of the corresponding weight
$\boldsymbol{E}$
and repeatedly blow up the locus where the order of the corresponding weight
![]() $a_{i}$
in the toric type is maximal until the order becomes zero. This gives a refinement
$a_{i}$
in the toric type is maximal until the order becomes zero. This gives a refinement
![]() $\boldsymbol{E}^{\prime }$
such that the order of
$\boldsymbol{E}^{\prime }$
such that the order of
![]() $a_{i}$
is constant for each component
$a_{i}$
is constant for each component
![]() $(E^{\prime })^{i}$
of
$(E^{\prime })^{i}$
of
![]() $\boldsymbol{E}^{\prime }$
. We leave to the reader to verify that this gives an algorithm with the right functorial properties and that
$\boldsymbol{E}^{\prime }$
. We leave to the reader to verify that this gives an algorithm with the right functorial properties and that
![]() $\boldsymbol{E}^{\prime }$
is a suitable choice of refinement for the purpose of Proposition 8.7.
$\boldsymbol{E}^{\prime }$
is a suitable choice of refinement for the purpose of Proposition 8.7.
Algorithm E (Destackification).
The input of the algorithm is a divisorial stack
![]() $(X,\boldsymbol{E})$
over a quasi-compact base scheme
$(X,\boldsymbol{E})$
over a quasi-compact base scheme
![]() $S$
. The output of the algorithm is a destackification (see Definition 2.3)
$S$
. The output of the algorithm is a destackification (see Definition 2.3)
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}:(X_{n},\boldsymbol{E}_{n})\rightarrow \cdots \rightarrow (X_{0},\boldsymbol{E}_{0})=(X,\boldsymbol{E}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}:(X_{n},\boldsymbol{E}_{n})\rightarrow \cdots \rightarrow (X_{0},\boldsymbol{E}_{0})=(X,\boldsymbol{E}).\end{eqnarray}$$
The construction is functorial (see Definition 2.6) with respect to arbitrary base change
 $S^{\prime }\rightarrow S$
and with respect to morphisms
$S^{\prime }\rightarrow S$
and with respect to morphisms
 $X^{\prime }\rightarrow X$
which are either gerbes or smooth and stabiliser-preserving.
$X^{\prime }\rightarrow X$
which are either gerbes or smooth and stabiliser-preserving.
- E0.
-
[Initialise.] Let
 $i=0$
.
$i=0$
. - E1.
-
[Find the worst locus.] The main conormal invariant of the algorithm is the invariant
 $U(\boldsymbol{E}_{i})\rightarrow \mathbb{N}\times \mathbb{N}\times T(\boldsymbol{E}_{i})$
composed lexicographically, in the sense of Example 6.12, by the independency index (see Definition 7.1), the toroidal index (see Definition 7.4) and the divisorial type (see Definition 7.8). Let
$U(\boldsymbol{E}_{i})\rightarrow \mathbb{N}\times \mathbb{N}\times T(\boldsymbol{E}_{i})$
composed lexicographically, in the sense of Example 6.12, by the independency index (see Definition 7.1), the toroidal index (see Definition 7.4) and the divisorial type (see Definition 7.8). Let
 $Z_{i}$
be the locus in
$Z_{i}$
be the locus in
 $X_{i}$
where this invariant obtains its maximum. If
$X_{i}$
where this invariant obtains its maximum. If
 $Z_{i}=X_{i}$
, we perform the algorithm indicated in Remark 8.10 and then terminate.
$Z_{i}=X_{i}$
, we perform the algorithm indicated in Remark 8.10 and then terminate. - E2.
-
[Blow up
 $Z_{i}$
.] By construction of the main invariant in Step E1, the divisorial type is constant at
$Z_{i}$
.] By construction of the main invariant in Step E1, the divisorial type is constant at
 $Z_{i}$
. Let
$Z_{i}$
. Let
 $\boldsymbol{\unicode[STIX]{x1D6F4}}$
be the orbifold fan with ordered rays associated to this divisorial type in the sense of Remark 7.11. Let
$\boldsymbol{\unicode[STIX]{x1D6F4}}$
be the orbifold fan with ordered rays associated to this divisorial type in the sense of Remark 7.11. Let
 $(X_{i+1},\boldsymbol{E}_{i+1})\rightarrow (X_{i},\boldsymbol{E}_{i})$
be the blow-up of
$(X_{i+1},\boldsymbol{E}_{i+1})\rightarrow (X_{i},\boldsymbol{E}_{i})$
be the blow-up of
 $(X_{i},\boldsymbol{E}_{i})$
in the centre
$(X_{i},\boldsymbol{E}_{i})$
in the centre
 $Z_{i}$
. Denote the exceptional divisor by
$Z_{i}$
. Denote the exceptional divisor by
 $\boldsymbol{D}_{i+1}$
and mark it as a distinguished divisor. Also, let
$\boldsymbol{D}_{i+1}$
and mark it as a distinguished divisor. Also, let
 $\boldsymbol{\unicode[STIX]{x1D6F4}}_{i+1}$
be the star subdivision
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{i+1}$
be the star subdivision
 $\boldsymbol{\unicode[STIX]{x1D6F4}}^{\ast }(\unicode[STIX]{x1D70E})$
, where
$\boldsymbol{\unicode[STIX]{x1D6F4}}^{\ast }(\unicode[STIX]{x1D70E})$
, where
 $\unicode[STIX]{x1D70E}$
is the maximal cone in
$\unicode[STIX]{x1D70E}$
is the maximal cone in
 $\boldsymbol{\unicode[STIX]{x1D6F4}}$
. We label the exceptional ray
$\boldsymbol{\unicode[STIX]{x1D6F4}}$
. We label the exceptional ray
 $\unicode[STIX]{x1D6FF}$
by
$\unicode[STIX]{x1D6FF}$
by
 $\boldsymbol{D}_{i+1}$
, and give
$\boldsymbol{D}_{i+1}$
, and give
 $\boldsymbol{\unicode[STIX]{x1D6F4}}_{i+1}$
a distinguished structure by letting
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{i+1}$
a distinguished structure by letting
 $\{\unicode[STIX]{x1D6FF}\}$
be the set of distinguished rays. Increment
$\{\unicode[STIX]{x1D6FF}\}$
be the set of distinguished rays. Increment
 $i$
by 1.
$i$
by 1. - E3.
-
[Perform toric destackification.] Perform Algorithm A on
 $\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
, and denote the result by
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
, and denote the result by
 $\boldsymbol{\unicode[STIX]{x1D6F4}}_{i+k}\rightarrow \cdots \rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
.
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{i+k}\rightarrow \cdots \rightarrow \boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
. - E4.
-
[Perform corresponding stacky blow-ups.] Perform the corresponding stacky blow-ups on
 $(X_{i},\boldsymbol{E}_{i},\boldsymbol{D}_{i})$
to form the sequence
$(X_{i},\boldsymbol{E}_{i},\boldsymbol{D}_{i})$
to form the sequence  $$\begin{eqnarray}(X_{i+k},\boldsymbol{E}_{i+k},\boldsymbol{D}_{i+k})\rightarrow \cdots \rightarrow (X_{i},\boldsymbol{E}_{i},\boldsymbol{D}_{i}).\end{eqnarray}$$
$$\begin{eqnarray}(X_{i+k},\boldsymbol{E}_{i+k},\boldsymbol{D}_{i+k})\rightarrow \cdots \rightarrow (X_{i},\boldsymbol{E}_{i},\boldsymbol{D}_{i}).\end{eqnarray}$$
At each step, a star subdivision corresponds to a blow-up in the intersection of the divisors labelling the rays of the subdivided cone. Rooting a ray corresponds to the taking of a root stack of the same order in the corresponding distinguished divisor. Also, the ray–divisor correspondence is extended in each step such that the exceptional ray of each subdivision or root corresponds to the exceptional divisor of the corresponding stacky blow-up. Increment
 $i$
by
$i$
by
 $k$
.
$k$
. - E5.
-
[Eliminate divisorial index along distinguished divisors.] Perform Algorithm D on the triple
 $(X_{i},\boldsymbol{E}_{i},\boldsymbol{D}_{i})$
, and append the output of the algorithm to the blow-up sequence. Increment
$(X_{i},\boldsymbol{E}_{i},\boldsymbol{D}_{i})$
, and append the output of the algorithm to the blow-up sequence. Increment
 $i$
by the length of the output. After this step we forget the distinguished structure.
$i$
by the length of the output. After this step we forget the distinguished structure. - E6.
-
[Iterate.] Iterate from Step E1.
Proof of correctness of Algorithm E.
When the algorithm terminates, the independence index is constant (zero) at
![]() $X_{i}$
, according to the termination criterion in Step E1. Hence, by Proposition 8.7 and Remark 8.10, we only need to prove that the algorithm terminates.
$X_{i}$
, according to the termination criterion in Step E1. Hence, by Proposition 8.7 and Remark 8.10, we only need to prove that the algorithm terminates.
We will prove that the maximum of the conormal invariant composed by the independency index, the toroidal index and the divisorial type decreases strictly with each iteration of the main loop of the algorithm. Note that the independency index decreases weakly with each iteration since all blow-ups performed during the iteration have centres with intersect the transforms of the divisors which were independent at the start of the iteration transversally. It is easy to see that also the toroidal index decreases weakly at each blow-up.
We examine how the invariant described above is affected during a single iteration of the main loop. For notational convenience, we assume that
![]() $i=0$
at the start of the iteration and that
$i=0$
at the start of the iteration and that
![]() $i=n$
at the end of the iteration. Assume that we are in Step E1 of the algorithm, and let
$i=n$
at the end of the iteration. Assume that we are in Step E1 of the algorithm, and let
![]() $\unicode[STIX]{x1D709}$
be any point in
$\unicode[STIX]{x1D709}$
be any point in
![]() $Z_{0}$
. Since all blow-ups during a single iteration have centres lying above
$Z_{0}$
. Since all blow-ups during a single iteration have centres lying above
![]() $Z_{0}$
, it is enough to show that any point in
$Z_{0}$
, it is enough to show that any point in
![]() $X_{n}$
lying over
$X_{n}$
lying over
![]() $\unicode[STIX]{x1D709}$
has either strictly lower independence index, or strictly lower toroidal index, than
$\unicode[STIX]{x1D709}$
has either strictly lower independence index, or strictly lower toroidal index, than
![]() $\unicode[STIX]{x1D709}$
at the end of the iteration.
$\unicode[STIX]{x1D709}$
at the end of the iteration.
Using the notation from the beginning of the section, we denote the toric type at
![]() $\unicode[STIX]{x1D709}$
by
$\unicode[STIX]{x1D709}$
by
![]() $(A,\boldsymbol{v})$
, where
$(A,\boldsymbol{v})$
, where
 $\boldsymbol{v}=(v_{1},\ldots ,v_{r})$
and
$\boldsymbol{v}=(v_{1},\ldots ,v_{r})$
and
 $v_{j}=(a_{j},e_{j})$
. Choose the indexing of
$v_{j}=(a_{j},e_{j})$
. Choose the indexing of
![]() $\boldsymbol{v}$
such that, for some integers
$\boldsymbol{v}$
such that, for some integers
![]() $s,t$
satisfying
$s,t$
satisfying
 $1\leqslant s\leqslant t\leqslant r$
, the following holds.
$1\leqslant s\leqslant t\leqslant r$
, the following holds.
-
(i) The component
 $v_{j}$
is independent in the sense of Definition 7.1 if and only if
$v_{j}$
is independent in the sense of Definition 7.1 if and only if
 $j>t$
.
$j>t$
. -
(ii) For indices
 $j$
such that
$j$
such that
 $1\leqslant j\leqslant s$
, we have
$1\leqslant j\leqslant s$
, we have
 $e_{j}\in \boldsymbol{E}_{0}$
.
$e_{j}\in \boldsymbol{E}_{0}$
. -
(iii) For indices
 $j$
such that
$j$
such that
 $s<j\leqslant t$
, we have
$s<j\leqslant t$
, we have
 $e_{j}=\ast$
.
$e_{j}=\ast$
.
In particular, the independency index at
![]() $\unicode[STIX]{x1D709}$
is
$\unicode[STIX]{x1D709}$
is
![]() $t$
. Note that since
$t$
. Note that since
 $(X_{0},\boldsymbol{E}_{0})$
is assumed to be divisorial, we have
$(X_{0},\boldsymbol{E}_{0})$
is assumed to be divisorial, we have
![]() $a_{j}=0$
for each
$a_{j}=0$
for each
![]() $j>t$
such that
$j>t$
such that
![]() $e_{j}=\ast$
by the assumption that
$e_{j}=\ast$
by the assumption that
![]() $v_{j}$
is independent. This implies that the toroidal index at
$v_{j}$
is independent. This implies that the toroidal index at
![]() $\unicode[STIX]{x1D709}$
is
$\unicode[STIX]{x1D709}$
is
![]() $t-s$
. The set
$t-s$
. The set
![]() $J$
, as defined in (8.2), is equal to
$J$
, as defined in (8.2), is equal to
 $\{1,\ldots ,t\}$
.
$\{1,\ldots ,t\}$
.
The toroidal index and the independency index can be computed using local homogeneous coordinates, so we may just as well assume that
![]() $X_{0}$
is a basic toric stack. Using the indexing convention described above, the local homogeneous coordinates are given by
$X_{0}$
is a basic toric stack. Using the indexing convention described above, the local homogeneous coordinates are given by
 $$\begin{eqnarray}{\mathcal{R}}={\mathcal{O}}_{S}[x_{1},\ldots ,x_{s},x_{s+1},\ldots ,x_{t},x_{t+1},\ldots ,x_{r}].\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{R}}={\mathcal{O}}_{S}[x_{1},\ldots ,x_{s},x_{s+1},\ldots ,x_{t},x_{t+1},\ldots ,x_{r}].\end{eqnarray}$$
By our assumption that
![]() $v_{j}$
is independent for
$v_{j}$
is independent for
![]() $j>t$
, the group
$j>t$
, the group
 $A_{\text{rig}}=\langle a_{1},\ldots ,a_{r}\rangle \subset A$
splits as a direct sum
$A_{\text{rig}}=\langle a_{1},\ldots ,a_{r}\rangle \subset A$
splits as a direct sum
 $A_{\text{rig}}=A^{\prime }\oplus A^{\prime \prime }$
, where
$A_{\text{rig}}=A^{\prime }\oplus A^{\prime \prime }$
, where
 $A^{\prime }=\langle a_{1},\ldots ,a_{t}\rangle$
and
$A^{\prime }=\langle a_{1},\ldots ,a_{t}\rangle$
and
 $A^{\prime \prime }=\langle a_{t+1},\ldots ,a_{r}\rangle$
.
$A^{\prime \prime }=\langle a_{t+1},\ldots ,a_{r}\rangle$
.
After the blow-up in Step E2, the stack
![]() $X_{1}$
is covered by
$X_{1}$
is covered by
![]() $|J|=t$
patches. Choose any
$|J|=t$
patches. Choose any
![]() $p\in J$
and let
$p\in J$
and let
 $U_{1}\subset X_{1}$
be the corresponding coordinate patch. The coordinate ring of
$U_{1}\subset X_{1}$
be the corresponding coordinate patch. The coordinate ring of
![]() $U_{1}$
is given by
$U_{1}$
is given by
 $$\begin{eqnarray}\widetilde{{\mathcal{R}}}={\mathcal{O}}_{S}[\widetilde{x}_{1},\ldots ,\widetilde{x}_{s},\widetilde{x}_{s+1},\ldots ,\widetilde{x}_{t},\widetilde{x}_{t+1},\ldots ,\widetilde{x}_{r}]\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{{\mathcal{R}}}={\mathcal{O}}_{S}[\widetilde{x}_{1},\ldots ,\widetilde{x}_{s},\widetilde{x}_{s+1},\ldots ,\widetilde{x}_{t},\widetilde{x}_{t+1},\ldots ,\widetilde{x}_{r}]\end{eqnarray}$$
using the notation from (8.3). We define
 $\widetilde{A}_{\text{rig}}\subset \widetilde{A}$
and the subgroups
$\widetilde{A}_{\text{rig}}\subset \widetilde{A}$
and the subgroups
![]() $\widetilde{A}^{\prime }$
and
$\widetilde{A}^{\prime }$
and
![]() $\widetilde{A}^{\prime }$
similarly as above and note that
$\widetilde{A}^{\prime }$
similarly as above and note that
 $\widetilde{A}^{\prime }=A^{\prime }$
and
$\widetilde{A}^{\prime }=A^{\prime }$
and
 $\widetilde{A}^{\prime \prime }=A^{\prime \prime }$
.
$\widetilde{A}^{\prime \prime }=A^{\prime \prime }$
.
If
![]() $p>s$
, then
$p>s$
, then
![]() $\widetilde{e}_{p}\neq \ast$
whereas
$\widetilde{e}_{p}\neq \ast$
whereas
![]() $e_{p}=\ast$
, so the toroidal index at the patch is strictly lower than the toroidal index at
$e_{p}=\ast$
, so the toroidal index at the patch is strictly lower than the toroidal index at
![]() $\unicode[STIX]{x1D709}$
. Hence, we may assume that
$\unicode[STIX]{x1D709}$
. Hence, we may assume that
![]() $p\leqslant s$
.
$p\leqslant s$
.
Next we consider the toric stacks
![]() $X_{i}^{\prime }$
associated to the stacky fans
$X_{i}^{\prime }$
associated to the stacky fans
![]() $\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
. Recall that
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
. Recall that
![]() $X_{0}^{\prime }$
is the basic toric stack associated to the divisorial type of
$X_{0}^{\prime }$
is the basic toric stack associated to the divisorial type of
![]() $(A,\boldsymbol{v})$
. Note that the group
$(A,\boldsymbol{v})$
. Note that the group
![]() $A^{\prime }$
is generated by
$A^{\prime }$
is generated by
 $a_{1},\ldots ,a_{s}$
by the assumption that
$a_{1},\ldots ,a_{s}$
by the assumption that
 $(X_{0},\boldsymbol{E}_{0})$
is divisorial. It follows that the homogeneous coordinates for
$(X_{0},\boldsymbol{E}_{0})$
is divisorial. It follows that the homogeneous coordinates for
![]() $X_{0}^{\prime }$
are
$X_{0}^{\prime }$
are
 $$\begin{eqnarray}({\mathcal{R}}^{\prime }={\mathcal{O}}_{S}[x_{1},\ldots ,x_{s}],A^{\prime },(a_{1},\ldots ,a_{s})).\end{eqnarray}$$
$$\begin{eqnarray}({\mathcal{R}}^{\prime }={\mathcal{O}}_{S}[x_{1},\ldots ,x_{s}],A^{\prime },(a_{1},\ldots ,a_{s})).\end{eqnarray}$$
By the assumption that
![]() $p\leqslant s$
, the blow-up
$p\leqslant s$
, the blow-up
![]() $X_{1}^{\prime }$
contains a basic toric substack
$X_{1}^{\prime }$
contains a basic toric substack
 $U_{1}^{\prime }\subset X_{1}^{\prime }$
with homogeneous coordinates
$U_{1}^{\prime }\subset X_{1}^{\prime }$
with homogeneous coordinates
 $$\begin{eqnarray}(\widetilde{{\mathcal{R}}}^{\prime }={\mathcal{O}}_{S}[\widetilde{x}_{1},\ldots ,\widetilde{x}_{s}],\widetilde{A}^{\prime },(\widetilde{a}_{1},\ldots ,\widetilde{a}_{s})).\end{eqnarray}$$
$$\begin{eqnarray}(\widetilde{{\mathcal{R}}}^{\prime }={\mathcal{O}}_{S}[\widetilde{x}_{1},\ldots ,\widetilde{x}_{s}],\widetilde{A}^{\prime },(\widetilde{a}_{1},\ldots ,\widetilde{a}_{s})).\end{eqnarray}$$
Now execute the partial toric resolution in Step E3, and assume that it finishes in
![]() $k$
steps. Also, perform the corresponding stacky blow-ups in Step E4. For each stacky blow-up
$k$
steps. Also, perform the corresponding stacky blow-ups in Step E4. For each stacky blow-up
 $X_{i+1}\rightarrow X_{i}$
with
$X_{i+1}\rightarrow X_{i}$
with
 $1<i\leqslant k$
, we choose an arbitrary patch
$1<i\leqslant k$
, we choose an arbitrary patch
![]() $U_{i+1}$
lying over
$U_{i+1}$
lying over
![]() $U_{i}$
, with
$U_{i}$
, with
![]() $U_{i+1}$
being a basic toric stack. We assume by induction that
$U_{i+1}$
being a basic toric stack. We assume by induction that
![]() $U_{i}$
has homogeneous coordinates
$U_{i}$
has homogeneous coordinates
 $$\begin{eqnarray}(\widehat{{\mathcal{R}}}={\mathcal{O}}_{S}[\widehat{x}_{1},\ldots ,\widehat{x}_{r}],\widehat{A},(\widehat{a}_{1},\ldots ,\widehat{a}_{t},\widehat{a}_{t+1},\ldots ,\widehat{a}_{r}))\end{eqnarray}$$
$$\begin{eqnarray}(\widehat{{\mathcal{R}}}={\mathcal{O}}_{S}[\widehat{x}_{1},\ldots ,\widehat{x}_{r}],\widehat{A},(\widehat{a}_{1},\ldots ,\widehat{a}_{t},\widehat{a}_{t+1},\ldots ,\widehat{a}_{r}))\end{eqnarray}$$
satisfying the following conditions.
-
(i) The orbifold fan
 $\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
has a maximal cone whose corresponding basic toric stack
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
has a maximal cone whose corresponding basic toric stack
 $U_{i}^{\prime }$
has homogeneous coordinates
$U_{i}^{\prime }$
has homogeneous coordinates  $$\begin{eqnarray}({\mathcal{O}}_{S}[\widehat{x}_{1},\ldots ,\widehat{x}_{s}],\langle \widehat{a}_{1},\ldots ,\widehat{a}_{s}\rangle ,(\widehat{a}_{1},\ldots ,\widehat{a}_{s})).\end{eqnarray}$$
$$\begin{eqnarray}({\mathcal{O}}_{S}[\widehat{x}_{1},\ldots ,\widehat{x}_{s}],\langle \widehat{a}_{1},\ldots ,\widehat{a}_{s}\rangle ,(\widehat{a}_{1},\ldots ,\widehat{a}_{s})).\end{eqnarray}$$
-
(ii) The toric divisor on
 $U^{\prime }$
corresponding to
$U^{\prime }$
corresponding to
 $\widehat{x}_{j}$
corresponds to a component
$\widehat{x}_{j}$
corresponds to a component
 $E$
of
$E$
of
 $\boldsymbol{E}_{i}$
if and only if
$\boldsymbol{E}_{i}$
if and only if
 $V(\widehat{x}_{j})=E$
in
$V(\widehat{x}_{j})=E$
in
 $U_{i}$
.
$U_{i}$
. -
(iii) For each
 $j>s$
, the divisor
$j>s$
, the divisor
 $V(\widehat{x}_{j})$
on
$V(\widehat{x}_{j})$
on
 $U_{i}$
is either unmarked or independent.
$U_{i}$
is either unmarked or independent.
It is straightforward to verify that these properties are preserved under the stacky blow-ups described in Step E4. In particular, they hold for
![]() $U_{k+1}$
. By the exit condition of Algorithm A, any distinguished divisor
$U_{k+1}$
. By the exit condition of Algorithm A, any distinguished divisor
![]() $V(\widehat{x}_{j})$
on
$V(\widehat{x}_{j})$
on
![]() $U_{k+1}^{\prime }$
is independent. It follows that the corresponding divisor
$U_{k+1}^{\prime }$
is independent. It follows that the corresponding divisor
![]() $V(\widehat{x}_{j})$
on
$V(\widehat{x}_{j})$
on
![]() $U_{k+1}$
is divisorially independent at the points where the toroidal index has not dropped.
$U_{k+1}$
is divisorially independent at the points where the toroidal index has not dropped.
Now execute the subalgorithm in Step E5. From Lemma 8.4, we see that after this step all distinguished divisors are independent at points where the toroidal index has not dropped. Due to the first blow-up, there is at least one distinguished divisor going through every point lying over
![]() $\unicode[STIX]{x1D709}$
. Thus, at points where the toroidal index has not dropped, the independency index is at most
$\unicode[STIX]{x1D709}$
. Thus, at points where the toroidal index has not dropped, the independency index is at most
![]() $t-1$
, which concludes the proof.◻
$t-1$
, which concludes the proof.◻
Example 8.11. In a final example, we examine the output of Algorithm E when applied to the basic toric stack
![]() $(X,\boldsymbol{E})$
with homogeneous coordinates
$(X,\boldsymbol{E})$
with homogeneous coordinates
 $(k[x_{1},x_{2},x_{3}],A,\boldsymbol{a})$
. Here we let
$(k[x_{1},x_{2},x_{3}],A,\boldsymbol{a})$
. Here we let
 $A=C_{6}\times C_{2}$
,
$A=C_{6}\times C_{2}$
,
 $\boldsymbol{a}=((1,0),(5,1),(3,1))$
and
$\boldsymbol{a}=((1,0),(5,1),(3,1))$
and
 $\boldsymbol{E}=(E^{1},E^{2})$
with
$\boldsymbol{E}=(E^{1},E^{2})$
with
 $E^{1}=V(x_{1})$
and
$E^{1}=V(x_{1})$
and
 $E^{2}=V(x_{2})$
.
$E^{2}=V(x_{2})$
.
In Step E1, the origin
 $Z_{0}=V(x_{1},x_{2},x_{3})$
is identified as the most problematic locus. The divisorial type is given by the triple
$Z_{0}=V(x_{1},x_{2},x_{3})$
is identified as the most problematic locus. The divisorial type is given by the triple
 $(A,(a_{1},E^{1}),(a_{2},E^{2}))$
with the weights corresponding to
$(A,(a_{1},E^{1}),(a_{2},E^{2}))$
with the weights corresponding to
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
, respectively. Figure 8.3 shows the destackification of the corresponding orbifold fan, which is obtained by invoking Algorithm A from Step E3. This gives a combinatorial recipe for destackifying
$E_{2}$
, respectively. Figure 8.3 shows the destackification of the corresponding orbifold fan, which is obtained by invoking Algorithm A from Step E3. This gives a combinatorial recipe for destackifying
![]() $(X,\boldsymbol{E})$
; after the initial blow-up of
$(X,\boldsymbol{E})$
; after the initial blow-up of
![]() $Z_{0}$
, we blow up the intersections
$Z_{0}$
, we blow up the intersections
 $D^{1}\cap E^{2}$
and
$D^{1}\cap E^{2}$
and
 $E^{1}\cap D^{1}$
in turn. The resulting blow-up tree is shown in Figure 8.4. The key things to note are as follows.
$E^{1}\cap D^{1}$
in turn. The resulting blow-up tree is shown in Figure 8.4. The key things to note are as follows.
-
(i) If we forget the weight in the third column, i.e., the weight not corresponding to any divisor in
 $\boldsymbol{E}$
, in the charts 1–7 of Figure 8.4, we precisely get the blow-up tree described in Figure 8.3. Since all the distinguished divisors in the output of Algorithm A are guaranteed to be independent, the distinguished divisors in Figure 8.4 are guaranteed to be divisorially independent at the charts 3, 4, 6 and 7. Hence, these charts will improve after invoking Algorithm D from Step E5.
$\boldsymbol{E}$
, in the charts 1–7 of Figure 8.4, we precisely get the blow-up tree described in Figure 8.3. Since all the distinguished divisors in the output of Algorithm A are guaranteed to be independent, the distinguished divisors in Figure 8.4 are guaranteed to be divisorially independent at the charts 3, 4, 6 and 7. Hence, these charts will improve after invoking Algorithm D from Step E5. -
(ii) In the remaining terminal charts the toroidal index has dropped, which gives the desired improvement. Note that the blow-ups of the loci in charts 8 and 9 do nothing to further improve the situation; they are merely side effects of improving charts 2 and 5.

Figure 8.3. The left-hand picture shows the orbifold fan
![]() $\boldsymbol{\unicode[STIX]{x1D6F4}}_{i+k}$
directly after Step E3 in the first iteration of the main loop in Algorithm E for the input described in Example 8.11. The table to the right shows the corresponding blow-up tree. The weights are in the group
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{i+k}$
directly after Step E3 in the first iteration of the main loop in Algorithm E for the input described in Example 8.11. The table to the right shows the corresponding blow-up tree. The weights are in the group
 $C_{6}\times C_{2}$
and the divisors
$C_{6}\times C_{2}$
and the divisors
![]() $E^{i}$
and
$E^{i}$
and
![]() $D^{i}$
correspond to the rays
$D^{i}$
correspond to the rays
![]() $\unicode[STIX]{x1D70C}_{i}$
and
$\unicode[STIX]{x1D70C}_{i}$
and
![]() $\unicode[STIX]{x1D6FF}_{i}$
respectively from the fan in the left-hand picture.
$\unicode[STIX]{x1D6FF}_{i}$
respectively from the fan in the left-hand picture.

Figure 8.4. The blow-up tree produced by Steps E2–E4 of Algorithm E for the input described in Example 8.11. The weights are in the group
 $C_{6}\times C_{2}$
. The last two columns contain the independency index and the toroidal index, respectively. Note that the distinguished divisors
$C_{6}\times C_{2}$
. The last two columns contain the independency index and the toroidal index, respectively. Note that the distinguished divisors
![]() $D^{1}$
,
$D^{1}$
,
![]() $D^{2}$
and
$D^{2}$
and
![]() $D^{3}$
are divisorially independent (Definition 7.15) at charts 3, 4, 6 and 7.
$D^{3}$
are divisorially independent (Definition 7.15) at charts 3, 4, 6 and 7.
Acknowledgements
This project was suggested to me by my advisor, David Rydh. I am truly grateful for his guidance, enthusiasm and tireless support.
Appendix A Tame stacks
This appendix may be viewed as a supplement to § 3 of the article [Reference Abramovich, Olsson and VistoliAOV08]. We start by recalling some of the main concepts. Let
![]() $S$
be a scheme and let
$S$
be a scheme and let
![]() $X$
be an algebraic stack which is quasi-separated and locally of finite presentation over
$X$
be an algebraic stack which is quasi-separated and locally of finite presentation over
![]() $S$
. If
$S$
. If
![]() $X$
has finite inertia, there exists a coarse space
$X$
has finite inertia, there exists a coarse space
 $\unicode[STIX]{x1D70B}:X\rightarrow X_{\text{cs}}$
with the map
$\unicode[STIX]{x1D70B}:X\rightarrow X_{\text{cs}}$
with the map
![]() $\unicode[STIX]{x1D70B}$
being proper. Following [Reference Abramovich, Olsson and VistoliAOV08], we say that
$\unicode[STIX]{x1D70B}$
being proper. Following [Reference Abramovich, Olsson and VistoliAOV08], we say that
![]() $X$
is tame if the functor
$X$
is tame if the functor
 $\unicode[STIX]{x1D70B}_{\ast }\text{QCoh}\,X\rightarrow \text{QCoh}\,X_{\text{cs}}$
is exact. We call a group scheme
$\unicode[STIX]{x1D70B}_{\ast }\text{QCoh}\,X\rightarrow \text{QCoh}\,X_{\text{cs}}$
is exact. We call a group scheme
![]() $G\rightarrow S$
finite, linearly reductive if
$G\rightarrow S$
finite, linearly reductive if
![]() $G$
is finite, flat, locally of finite presentation and the fibres are linearly reductive. We say that an algebraic stack
$G$
is finite, flat, locally of finite presentation and the fibres are linearly reductive. We say that an algebraic stack
![]() $X$
has linearly reductive stabiliser at a point
$X$
has linearly reductive stabiliser at a point
![]() $\unicode[STIX]{x1D709}\in |X|$
if the stabiliser at one of, or equivalently any of, the
$\unicode[STIX]{x1D709}\in |X|$
if the stabiliser at one of, or equivalently any of, the
![]() $k$
-points representing
$k$
-points representing
![]() $\unicode[STIX]{x1D709}$
is linearly reductive.
$\unicode[STIX]{x1D709}$
is linearly reductive.
The following theorem is an extension of the main theorem of [Reference Abramovich, Olsson and VistoliAOV08].
Theorem A.1. Let
![]() $S$
be a scheme, and let
$S$
be a scheme, and let
![]() $X$
be an algebraic stack which is quasi-separated and locally of finite presentation over
$X$
be an algebraic stack which is quasi-separated and locally of finite presentation over
![]() $S$
. Assume that
$S$
. Assume that
![]() $X$
has finite inertia. Then the following conditions are equivalent.
$X$
has finite inertia. Then the following conditions are equivalent.
-
(a) The stack
 $X$
is tame.
$X$
is tame. -
(b) The stabilisers of
 $X$
are linearly reductive.
$X$
are linearly reductive. -
(c) There exist a covering
 $Y\rightarrow X_{\text{cs}}$
of the coarse space, which is faithfully flat and locally of finite presentation, a finite, linearly reductive group scheme
$Y\rightarrow X_{\text{cs}}$
of the coarse space, which is faithfully flat and locally of finite presentation, a finite, linearly reductive group scheme
 $G\rightarrow Y$
and a
$G\rightarrow Y$
and a
 $G$
-space
$G$
-space
 $U\rightarrow Y$
, which is finite and finitely presented, together with an isomorphism
$U\rightarrow Y$
, which is finite and finitely presented, together with an isomorphism  $$\begin{eqnarray}[U/G]\simeq Y\times _{X_{\text{cs}}}X.\end{eqnarray}$$
$$\begin{eqnarray}[U/G]\simeq Y\times _{X_{\text{cs}}}X.\end{eqnarray}$$
-
(d) The same as (c), but
 $Y\rightarrow X_{\text{cs}}$
can be assumed to be étale.
$Y\rightarrow X_{\text{cs}}$
can be assumed to be étale.
If, in addition, the morphism
![]() $X\rightarrow S$
is assumed to be smooth, the above conditions are equivalent to the following condition.
$X\rightarrow S$
is assumed to be smooth, the above conditions are equivalent to the following condition.
-
(e) The same as (d), but
 $U$
can be assumed to be smooth over
$U$
can be assumed to be smooth over
 $S$
.
$S$
.
The equivalence of the conditions (a)–(d) is [Reference Abramovich, Olsson and VistoliAOV08, Theorem 3.2]. Here we will prove that (e) is equivalent to the other conditions under the extra hypothesis, and give a simplification of the proof that (b) implies (d).
In [Reference Abramovich, Olsson and VistoliAOV08], it is proven that tame gerbes admit sections étale locally. The argument given is based on rigidification and the structure theory of linearly reductive groups. But, rather interestingly, the existence of an étale local section is a consequence of a much more elementary fact regarding gerbes in general.
Proposition A.2. Let
![]() $S$
be a scheme and let
$S$
be a scheme and let
![]() $X$
be an algebraic stack which is an fppf gerbe over
$X$
be an algebraic stack which is an fppf gerbe over
![]() $S$
. Then the structure morphism
$S$
. Then the structure morphism
 $\unicode[STIX]{x1D70B}:X\rightarrow S$
is smooth.
$\unicode[STIX]{x1D70B}:X\rightarrow S$
is smooth.
Proof. The question is local on the base in the fppf topology, so we may assume that
![]() $X$
is a classifying stack
$X$
is a classifying stack
![]() $\text{B}_{S}G$
for some group algebraic space
$\text{B}_{S}G$
for some group algebraic space
![]() $G$
which is flat and locally of finite presentation over
$G$
which is flat and locally of finite presentation over
![]() $S$
. In particular, we have an atlas
$S$
. In particular, we have an atlas
![]() $S\rightarrow X$
. Let
$S\rightarrow X$
. Let
 $U\rightarrow X$
be a smooth atlas. Then the fibre product
$U\rightarrow X$
be a smooth atlas. Then the fibre product
 $U^{\prime }=S\times _{X}U$
is an algebraic space which is smooth over
$U^{\prime }=S\times _{X}U$
is an algebraic space which is smooth over
![]() $S$
, and the projection
$S$
, and the projection
 $U^{\prime }\rightarrow U$
is faithfully flat and locally of finite presentation. Hence,
$U^{\prime }\rightarrow U$
is faithfully flat and locally of finite presentation. Hence,
![]() $U$
is also smooth over
$U$
is also smooth over
![]() $S$
by [Reference Dieudonné and GrothendieckEGAIV, Proposition 17.7.7], and it follows that
$S$
by [Reference Dieudonné and GrothendieckEGAIV, Proposition 17.7.7], and it follows that
![]() $X$
is smooth over
$X$
is smooth over
![]() $S$
.◻
$S$
.◻
In fact, from the proof we see that the structure morphism of a gerbe has all properties which are fppf local on the base and which descend fppf locally on the source. Note, however, that although for instance being étale is such a property when we restrict to morphisms of schemes, this is not the case when we consider morphisms of algebraic stacks. Indeed, the classifying stack
![]() $\text{B}\unicode[STIX]{x1D707}_{p}$
is not étale over the base if the base is a field of characteristic
$\text{B}\unicode[STIX]{x1D707}_{p}$
is not étale over the base if the base is a field of characteristic
![]() $p$
.
$p$
.
One of the fundamental properties of finite linearly reductive groups acting on algebraic spaces is that taking quotients of invariant closed subspaces coincides with taking schematic images. We give a formulation of this property in terms of tame stacks.
Proposition A.3. Let
![]() $X\rightarrow S$
be a tame stack over a scheme
$X\rightarrow S$
be a tame stack over a scheme
![]() $S$
and let
$S$
and let
 $\unicode[STIX]{x1D70B}:X\rightarrow X_{\text{cs}}$
be its coarse space. Let
$\unicode[STIX]{x1D70B}:X\rightarrow X_{\text{cs}}$
be its coarse space. Let
![]() $Z\subset X$
be a closed substack. Then the canonical map
$Z\subset X$
be a closed substack. Then the canonical map
 $Z\rightarrow \unicode[STIX]{x1D70B}(Z)$
to the schematic image of
$Z\rightarrow \unicode[STIX]{x1D70B}(Z)$
to the schematic image of
![]() $Z$
under
$Z$
under
![]() $\unicode[STIX]{x1D70B}$
is the coarse space of
$\unicode[STIX]{x1D70B}$
is the coarse space of
![]() $Z$
.
$Z$
.
Proof. The question may be verified after a faithfully flat base change of the coarse space. Thus, we may use Theorem A.1(c) to reduce to the case when
 $X_{\text{cs}}=\text{Spec}\,A$
for some ring
$X_{\text{cs}}=\text{Spec}\,A$
for some ring
![]() $A$
and
$A$
and
 $X=[U/G]$
, where
$X=[U/G]$
, where
![]() $G$
is a linearly reductive group scheme over
$G$
is a linearly reductive group scheme over
![]() $\text{Spec}\,A$
, and
$\text{Spec}\,A$
, and
 $U=\text{Spec}\,B$
, where
$U=\text{Spec}\,B$
, where
![]() $B$
is a finite
$B$
is a finite
![]() $A$
-algebra. Let
$A$
-algebra. Let
![]() $I\subset B$
be the
$I\subset B$
be the
![]() $G$
-invariant ideal defining
$G$
-invariant ideal defining
![]() $Z$
. Then the coarse space of
$Z$
. Then the coarse space of
![]() $Z$
is
$Z$
is
 $\text{Spec}\,(A/I)^{G}$
and the schematic image is given by
$\text{Spec}\,(A/I)^{G}$
and the schematic image is given by
 $\text{Spec}\,A^{G}/I^{G}$
. But the functor
$\text{Spec}\,A^{G}/I^{G}$
. But the functor
![]() $-^{G}$
is exact since the group
$-^{G}$
is exact since the group
![]() $G$
is linearly reductive, so
$G$
is linearly reductive, so
 $(A/I)^{G}=A^{G}/I^{G}$
, as desired.◻
$(A/I)^{G}=A^{G}/I^{G}$
, as desired.◻
Propositions A.2 and A.3 together imply the following corollary, which is a reformulation of [Reference Abramovich, Olsson and VistoliAOV08, Proposition 3.7]. This gives the simplification of the proof, that (b) implies (d) in Theorem A.1, that was promised earlier.
Corollary A.4. Let
![]() $X\rightarrow S$
be a tame stack over a scheme
$X\rightarrow S$
be a tame stack over a scheme
![]() $S$
and let
$S$
and let
 $\unicode[STIX]{x1D70B}:X\rightarrow X_{\text{cs}}$
be the coarse space. Then the residual field at each point
$\unicode[STIX]{x1D70B}:X\rightarrow X_{\text{cs}}$
be the coarse space. Then the residual field at each point
![]() $\unicode[STIX]{x1D709}\in |X|$
coincides with the residual field of the point
$\unicode[STIX]{x1D709}\in |X|$
coincides with the residual field of the point
![]() $\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709})$
. In particular, every
$\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709})$
. In particular, every
![]() $k$
-point in
$k$
-point in
![]() $X_{\text{cs}}$
, with
$X_{\text{cs}}$
, with
![]() $k$
a field, lifts to a
$k$
a field, lifts to a
![]() $K$
-point of
$K$
-point of
![]() $X$
for some separable field extension
$X$
for some separable field extension
![]() $K/k$
.
$K/k$
.
Proof. Let
 $k=\unicode[STIX]{x1D705}(\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709}))$
be the residue field of
$k=\unicode[STIX]{x1D705}(\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709}))$
be the residue field of
![]() $\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709})$
. Let
$\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709})$
. Let
 $X_{k}\rightarrow \text{Spec}\,k$
be the pull-back of
$X_{k}\rightarrow \text{Spec}\,k$
be the pull-back of
![]() $\unicode[STIX]{x1D70B}$
along
$\unicode[STIX]{x1D70B}$
along
 $\text{Spec}\,k{\hookrightarrow}X_{\text{cs}}$
. Then
$\text{Spec}\,k{\hookrightarrow}X_{\text{cs}}$
. Then
 $X_{k}\rightarrow \text{Spec}\,k$
is a coarse space by [Reference Abramovich, Olsson and VistoliAOV08, Corollary 3.3(a)]. Furthermore, the induced map
$X_{k}\rightarrow \text{Spec}\,k$
is a coarse space by [Reference Abramovich, Olsson and VistoliAOV08, Corollary 3.3(a)]. Furthermore, the induced map
 $X_{k}^{\text{red}}\rightarrow \text{Spec}\,k$
from the reduction of
$X_{k}^{\text{red}}\rightarrow \text{Spec}\,k$
from the reduction of
![]() $X_{k}$
is a coarse space by Proposition A.3, since the schematic image of
$X_{k}$
is a coarse space by Proposition A.3, since the schematic image of
![]() $X_{k}^{\text{red}}$
in
$X_{k}^{\text{red}}$
in
![]() $\text{Spec}\,k$
must be
$\text{Spec}\,k$
must be
![]() $\text{Spec}\,k$
itself. But the monomorphism
$\text{Spec}\,k$
itself. But the monomorphism
 $X_{k}^{\text{red}}{\hookrightarrow}X$
, being a monomorphism from a reduced, locally noetherian singleton, is the residual gerbe at
$X_{k}^{\text{red}}{\hookrightarrow}X$
, being a monomorphism from a reduced, locally noetherian singleton, is the residual gerbe at
![]() $\unicode[STIX]{x1D709}$
. Hence,
$\unicode[STIX]{x1D709}$
. Hence,
![]() $k$
is indeed the residue field at
$k$
is indeed the residue field at
![]() $\unicode[STIX]{x1D709}$
. By Proposition A.2, the map
$\unicode[STIX]{x1D709}$
. By Proposition A.2, the map
 $X_{k}^{\text{red}}\rightarrow \text{Spec}\,k$
is smooth, so it admits a section étale locally on
$X_{k}^{\text{red}}\rightarrow \text{Spec}\,k$
is smooth, so it admits a section étale locally on
![]() $\text{Spec}\,k$
. From this, the last statement of the proposition follows.◻
$\text{Spec}\,k$
. From this, the last statement of the proposition follows.◻
Before turning to condition (e) of Theorem A.1, we review what is meant by a fixed point for an action by an algebraic group
![]() $G$
. Note that it is insufficient to just study the action of the topological group
$G$
. Note that it is insufficient to just study the action of the topological group
![]() $|G|$
, as is illustrated by the following basic example.
$|G|$
, as is illustrated by the following basic example.
Example A.5. The group
![]() $\unicode[STIX]{x1D707}_{2}$
has a natural action on
$\unicode[STIX]{x1D707}_{2}$
has a natural action on
![]() $\text{Spec}\,\mathbb{C}$
over
$\text{Spec}\,\mathbb{C}$
over
![]() $\text{Spec}\,\mathbb{R}$
. Topologically, the space
$\text{Spec}\,\mathbb{R}$
. Topologically, the space
![]() $\text{Spec}\,\mathbb{C}$
has a single point, but it is not accurate to say that the point is fixed under the
$\text{Spec}\,\mathbb{C}$
has a single point, but it is not accurate to say that the point is fixed under the
![]() $\unicode[STIX]{x1D707}_{2}$
-action. Rather, we wish to think of
$\unicode[STIX]{x1D707}_{2}$
-action. Rather, we wish to think of
![]() $\unicode[STIX]{x1D707}_{2}$
as acting freely on
$\unicode[STIX]{x1D707}_{2}$
as acting freely on
![]() $\text{Spec}\,\mathbb{C}$
, making
$\text{Spec}\,\mathbb{C}$
, making
![]() $\text{Spec}\,\mathbb{C}$
a
$\text{Spec}\,\mathbb{C}$
a
![]() $\unicode[STIX]{x1D707}_{2}$
-torsor over
$\unicode[STIX]{x1D707}_{2}$
-torsor over
![]() $\text{Spec}\,\mathbb{R}$
. In this case, we can think of
$\text{Spec}\,\mathbb{R}$
. In this case, we can think of
![]() $\text{Spec}\,\mathbb{C}$
having two different geometric points
$\text{Spec}\,\mathbb{C}$
having two different geometric points
 $\text{Spec}\,\mathbb{C}\rightarrow \text{Spec}\,\mathbb{C}$
over
$\text{Spec}\,\mathbb{C}\rightarrow \text{Spec}\,\mathbb{C}$
over
![]() $\text{Spec}\,\mathbb{R}$
, neither of which is fixed under the
$\text{Spec}\,\mathbb{R}$
, neither of which is fixed under the
![]() $\unicode[STIX]{x1D707}_{2}$
-action.
$\unicode[STIX]{x1D707}_{2}$
-action.
If we are working with non-reduced group schemes, even this point of view does not work. This can be seen by instead considering the corresponding example over the function field
 $k=\mathbb{F}_{p}(X)$
, and the group
$k=\mathbb{F}_{p}(X)$
, and the group
![]() $\unicode[STIX]{x1D707}_{p}$
acting on
$\unicode[STIX]{x1D707}_{p}$
acting on
 $\text{Spec}\,k[Y]/(Y^{p}-X)$
over
$\text{Spec}\,k[Y]/(Y^{p}-X)$
over
![]() $\text{Spec}\,k$
.
$\text{Spec}\,k$
.
Instead we consider the correct, sheaf-theoretic definition based on the following proposition. We omit the proof, since it is an easy diagram chase.
Proposition A.6. Let
![]() $R\rightrightarrows U$
be a groupoid of sheaves on a site and let
$R\rightrightarrows U$
be a groupoid of sheaves on a site and let
 $\unicode[STIX]{x1D709}:T\rightarrow U$
be a generalised point. Then the following statements are equivalent.
$\unicode[STIX]{x1D709}:T\rightarrow U$
be a generalised point. Then the following statements are equivalent.
-
(i) For any morphism
 $T^{\prime }\rightarrow T$
, the restriction of
$T^{\prime }\rightarrow T$
, the restriction of
 $\unicode[STIX]{x1D709}$
to
$\unicode[STIX]{x1D709}$
to
 $T^{\prime }$
is the unique representative of its isomorphism class in the groupoid
$T^{\prime }$
is the unique representative of its isomorphism class in the groupoid
 $R(T^{\prime })\rightrightarrows U(T^{\prime })$
viewed as a small category.
$R(T^{\prime })\rightrightarrows U(T^{\prime })$
viewed as a small category. -
(ii) The graph
 $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}:T{\hookrightarrow}U\times T$
is invariant with respect to the groupoid
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}:T{\hookrightarrow}U\times T$
is invariant with respect to the groupoid
 $R\times T\rightrightarrows U\times T$
.
$R\times T\rightrightarrows U\times T$
.
If the groupoid
![]() $R\rightrightarrows U$
is an action groupoid for a group action
$R\rightrightarrows U$
is an action groupoid for a group action
 $G\times U\rightarrow U$
, then the above two statements are equivalent to the following statement.
$G\times U\rightarrow U$
, then the above two statements are equivalent to the following statement.
-
(iii) The canonical monomorphism
 $\text{Stab}\,(\unicode[STIX]{x1D709})\rightarrow G\times T$
of groups over
$\text{Stab}\,(\unicode[STIX]{x1D709})\rightarrow G\times T$
of groups over
 $T$
is an isomorphism.
$T$
is an isomorphism.
Definition A.7. Let
![]() $R\rightrightarrows U$
and
$R\rightrightarrows U$
and
 $\unicode[STIX]{x1D709}:T\rightarrow U$
be as in Proposition A.6. If the conditions given in the proposition are satisfied, we say that
$\unicode[STIX]{x1D709}:T\rightarrow U$
be as in Proposition A.6. If the conditions given in the proposition are satisfied, we say that
![]() $\unicode[STIX]{x1D709}$
is a fixed point for the groupoid
$\unicode[STIX]{x1D709}$
is a fixed point for the groupoid
![]() $R\rightrightarrows U$
. If the groupoid is algebraic and
$R\rightrightarrows U$
. If the groupoid is algebraic and
![]() $\unicode[STIX]{x1D709}\in |U|$
is a point in
$\unicode[STIX]{x1D709}\in |U|$
is a point in
![]() $U$
, we say that
$U$
, we say that
![]() $\unicode[STIX]{x1D709}$
is a fixed point if it may be represented by a morphism
$\unicode[STIX]{x1D709}$
is a fixed point if it may be represented by a morphism
 $\text{Spec}\,k\rightarrow U$
which is a fixed point in the above sense. It is easily verified that the choice of representative is irrelevant.
$\text{Spec}\,k\rightarrow U$
which is a fixed point in the above sense. It is easily verified that the choice of representative is irrelevant.
That condition (b) implies condition (d) of Theorem A.1 follows from the sharper [Reference Abramovich, Olsson and VistoliAOV08, Proposition 3.6]. In order to see that it also implies (e), we need to sharpen the formulation of the proposition somewhat more.
Proposition A.8. Let
![]() $S$
be a scheme and let
$S$
be a scheme and let
![]() $X$
be an algebraic stack having finite inertia and being quasi-separated and locally of finite presentation over
$X$
be an algebraic stack having finite inertia and being quasi-separated and locally of finite presentation over
![]() $S$
. Denote the coarse space by
$S$
. Denote the coarse space by
 $\unicode[STIX]{x1D70B}:X\rightarrow X_{\text{cs}}$
and let
$\unicode[STIX]{x1D70B}:X\rightarrow X_{\text{cs}}$
and let
![]() $\unicode[STIX]{x1D709}\in |X|$
be a point. If the stabiliser at
$\unicode[STIX]{x1D709}\in |X|$
be a point. If the stabiliser at
![]() $\unicode[STIX]{x1D709}$
is linearly reductive, then there exist an étale neighbourhood
$\unicode[STIX]{x1D709}$
is linearly reductive, then there exist an étale neighbourhood
 $Y\rightarrow X_{\text{cs}}$
of
$Y\rightarrow X_{\text{cs}}$
of
![]() $\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709})$
, a finite, linearly reductive group scheme
$\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709})$
, a finite, linearly reductive group scheme
![]() $G\rightarrow Y$
acting on a finite scheme
$G\rightarrow Y$
acting on a finite scheme
![]() $U\rightarrow Y$
of finite presentation and an isomorphism
$U\rightarrow Y$
of finite presentation and an isomorphism
 $[U/G]\simeq Y\times _{X_{\text{cs}}}X$
of algebraic stacks. Furthermore, the point
$[U/G]\simeq Y\times _{X_{\text{cs}}}X$
of algebraic stacks. Furthermore, the point
![]() $\unicode[STIX]{x1D709}$
lifts to a point
$\unicode[STIX]{x1D709}$
lifts to a point
![]() $\unicode[STIX]{x1D709}^{\prime }\in U$
which is fixed under the action of
$\unicode[STIX]{x1D709}^{\prime }\in U$
which is fixed under the action of
![]() $G$
.
$G$
.
All but the last sentence comes from the original statement, and although the last sentence is not explicitly stated, it follows from the proof. Indeed, the scheme
![]() $U\rightarrow Y$
is constructed in a way such that the diagram
$U\rightarrow Y$
is constructed in a way such that the diagram

becomes cartesian. Here
 $\unicode[STIX]{x1D709}:\text{Spec}\,k\rightarrow X$
is a morphism representing
$\unicode[STIX]{x1D709}:\text{Spec}\,k\rightarrow X$
is a morphism representing
![]() $\unicode[STIX]{x1D709}$
, the vertical maps are
$\unicode[STIX]{x1D709}$
, the vertical maps are
![]() $G$
-torsors and
$G$
-torsors and
![]() $G_{\unicode[STIX]{x1D709}}$
denotes the stabiliser at
$G_{\unicode[STIX]{x1D709}}$
denotes the stabiliser at
![]() $\unicode[STIX]{x1D709}$
. In particular, the point
$\unicode[STIX]{x1D709}$
. In particular, the point
![]() $\unicode[STIX]{x1D709}^{\prime }$
becomes the desired lifting according to the third condition of Proposition A.6 characterising fixed points. Finally, to see that this implies (e) in the case when
$\unicode[STIX]{x1D709}^{\prime }$
becomes the desired lifting according to the third condition of Proposition A.6 characterising fixed points. Finally, to see that this implies (e) in the case when
![]() $X$
is smooth over the base, we apply the following proposition.
$X$
is smooth over the base, we apply the following proposition.
Proposition A.9. Let
![]() $U$
be an algebraic space which is flat, locally of finite presentation and quasi-separated over a scheme
$U$
be an algebraic space which is flat, locally of finite presentation and quasi-separated over a scheme
![]() $S$
. Assume that
$S$
. Assume that
![]() $R\rightrightarrows U$
is a groupoid which is flat and locally of finite presentation, and assume that the stack quotient
$R\rightrightarrows U$
is a groupoid which is flat and locally of finite presentation, and assume that the stack quotient
![]() $[U/R]$
is smooth over
$[U/R]$
is smooth over
![]() $S$
. Then
$S$
. Then
![]() $U$
is smooth over
$U$
is smooth over
![]() $S$
at any point
$S$
at any point
![]() $\unicode[STIX]{x1D709}\in |U|$
which is a fixed point with respect to the groupoid
$\unicode[STIX]{x1D709}\in |U|$
which is a fixed point with respect to the groupoid
![]() $R\rightrightarrows U$
.
$R\rightrightarrows U$
.
Proof. Let
 $\unicode[STIX]{x1D709}:\text{Spec}\,k\rightarrow U$
be a geometric point representing
$\unicode[STIX]{x1D709}:\text{Spec}\,k\rightarrow U$
be a geometric point representing
![]() $\unicode[STIX]{x1D709}$
, and let
$\unicode[STIX]{x1D709}$
, and let
 $R_{k}\rightrightarrows U_{k}$
denote the pull-back of the groupoid along the morphism
$R_{k}\rightrightarrows U_{k}$
denote the pull-back of the groupoid along the morphism
 $\text{Spec}\,k\rightarrow U\rightarrow S$
. Since
$\text{Spec}\,k\rightarrow U\rightarrow S$
. Since
![]() $\unicode[STIX]{x1D709}$
is a fixed point, the graph
$\unicode[STIX]{x1D709}$
is a fixed point, the graph
 $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}:\text{Spec}\,k\rightarrow U_{k}$
is invariant in the groupoid. Hence, the diagram
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}:\text{Spec}\,k\rightarrow U_{k}$
is invariant in the groupoid. Hence, the diagram

is 2-cartesian. The graph
 $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}:\text{Spec}\,k\rightarrow U_{k}$
is a closed immersion since it is a rational point. Since the vertical maps in the diagram are faithfully flat and locally of finite presentation, it follows that also
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}:\text{Spec}\,k\rightarrow U_{k}$
is a closed immersion since it is a rational point. Since the vertical maps in the diagram are faithfully flat and locally of finite presentation, it follows that also
![]() $\unicode[STIX]{x1D704}$
is a closed immersion, by descent. The stack
$\unicode[STIX]{x1D704}$
is a closed immersion, by descent. The stack
 $[U_{k}/R_{k}]$
is smooth over
$[U_{k}/R_{k}]$
is smooth over
![]() $k$
since it is isomorphic to the pull-back
$k$
since it is isomorphic to the pull-back
 $[U/R]\times _{S}\text{Spec}\,k$
and smoothness is stable under base change. The stack
$[U/R]\times _{S}\text{Spec}\,k$
and smoothness is stable under base change. The stack
 $\text{B}_{k}\text{Stab}\,(\unicode[STIX]{x1D709})$
is smooth over
$\text{B}_{k}\text{Stab}\,(\unicode[STIX]{x1D709})$
is smooth over
![]() $k$
since it is a gerbe. It follows that
$k$
since it is a gerbe. It follows that
![]() $\unicode[STIX]{x1D704}$
is a regular immersion, so the same holds for the graph
$\unicode[STIX]{x1D704}$
is a regular immersion, so the same holds for the graph
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
, since the property of being a regular immersion is stable under flat base change. But then
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
, since the property of being a regular immersion is stable under flat base change. But then
![]() $U_{k}$
must be regular at
$U_{k}$
must be regular at
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
. Since
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
. Since
![]() $U$
is flat and of finite presentation over
$U$
is flat and of finite presentation over
![]() $S$
, it follows that
$S$
, it follows that
![]() $U\rightarrow S$
is smooth at
$U\rightarrow S$
is smooth at
![]() $\unicode[STIX]{x1D709}$
.◻
$\unicode[STIX]{x1D709}$
.◻
We conclude the section with a technical lemma, which is not related to tame stacks, about closed points on stacks. In general, rational points on algebraic stacks need not be closed. For instance, the stack
 $[\mathbb{A}_{k}^{1}/\mathbb{G}_{m}]$
has an open rational point. But stacks with finite stabilisers are better behaved.
$[\mathbb{A}_{k}^{1}/\mathbb{G}_{m}]$
has an open rational point. But stacks with finite stabilisers are better behaved.
Lemma A.10. Let
![]() $k$
be a field and
$k$
be a field and
![]() $X$
an algebraic stack which is locally of finite type and quasi-separated over
$X$
an algebraic stack which is locally of finite type and quasi-separated over
![]() $\text{Spec}\,k$
. If
$\text{Spec}\,k$
. If
![]() $X$
has point-wise finite stabilisers, then every point of finite type in
$X$
has point-wise finite stabilisers, then every point of finite type in
![]() $X$
is closed. In particular, all rational points of
$X$
is closed. In particular, all rational points of
![]() $X$
are closed.
$X$
are closed.
Proof. Let
![]() $\unicode[STIX]{x1D709}\in |X|$
be a point of finite type in
$\unicode[STIX]{x1D709}\in |X|$
be a point of finite type in
![]() $X$
, and let
$X$
, and let
 $f:\mathscr{G}_{\unicode[STIX]{x1D709}}{\hookrightarrow}X$
be the inclusion of the residual gerbe at
$f:\mathscr{G}_{\unicode[STIX]{x1D709}}{\hookrightarrow}X$
be the inclusion of the residual gerbe at
![]() $\unicode[STIX]{x1D709}$
. By the assumption that
$\unicode[STIX]{x1D709}$
. By the assumption that
![]() $\unicode[STIX]{x1D709}$
is a point of finite type, the monomorphism
$\unicode[STIX]{x1D709}$
is a point of finite type, the monomorphism
![]() $f$
is locally of finite type. We want to show that
$f$
is locally of finite type. We want to show that
![]() $f$
is a closed immersion.
$f$
is a closed immersion.
We may assume that
![]() $X$
is of finite type over
$X$
is of finite type over
![]() $k$
. Since
$k$
. Since
![]() $X$
is quasi-separated and has finite stabilisers, we can choose a quasi-finite, flat covering
$X$
is quasi-separated and has finite stabilisers, we can choose a quasi-finite, flat covering
 $U\rightarrow X$
with
$U\rightarrow X$
with
![]() $U$
affine [Reference RydhRyd11, Theorem 7.1]. Let
$U$
affine [Reference RydhRyd11, Theorem 7.1]. Let
 $U_{\unicode[STIX]{x1D709}}=U\times _{X}\mathscr{G}_{\unicode[STIX]{x1D709}}$
. Since
$U_{\unicode[STIX]{x1D709}}=U\times _{X}\mathscr{G}_{\unicode[STIX]{x1D709}}$
. Since
![]() $U_{\unicode[STIX]{x1D709}}$
is quasi-finite over the field
$U_{\unicode[STIX]{x1D709}}$
is quasi-finite over the field
![]() $k$
, it must also be finite over
$k$
, it must also be finite over
![]() $k$
. Since we assume that
$k$
. Since we assume that
![]() $U$
is affine, also the projection
$U$
is affine, also the projection
 $U_{\unicode[STIX]{x1D709}}\rightarrow U$
must be finite. It follows that
$U_{\unicode[STIX]{x1D709}}\rightarrow U$
must be finite. It follows that
![]() $f$
is a finite monomorphism and therefore a closed immersion.◻
$f$
is a finite monomorphism and therefore a closed immersion.◻
Appendix B The cotangent complex of toric stacks
We wish to compute the cotangent complex for a basic toric stack
![]() $X$
without torus factors over a scheme
$X$
without torus factors over a scheme
![]() $S$
. Assume that
$S$
. Assume that
![]() $X$
has homogeneous coordinates
$X$
has homogeneous coordinates
 $({\mathcal{O}}_{S}[x_{1},\ldots ,x_{n}],A,\boldsymbol{a})$
, where
$({\mathcal{O}}_{S}[x_{1},\ldots ,x_{n}],A,\boldsymbol{a})$
, where
 $A=\mathbb{Z}/q_{1}\mathbb{Z}\times \cdots \times \mathbb{Z}/q_{s}\mathbb{Z}$
and
$A=\mathbb{Z}/q_{1}\mathbb{Z}\times \cdots \times \mathbb{Z}/q_{s}\mathbb{Z}$
and
 $a_{i}=(a_{1i},\ldots ,a_{si})$
for
$a_{i}=(a_{1i},\ldots ,a_{si})$
for
 $1\leqslant i\leqslant n$
.
$1\leqslant i\leqslant n$
.
The quasi-coherent
![]() ${\mathcal{O}}_{X}$
-modules are in canonical one-to-one correspondence with the quasi-coherent
${\mathcal{O}}_{X}$
-modules are in canonical one-to-one correspondence with the quasi-coherent
![]() $A$
-graded
$A$
-graded
 ${\mathcal{O}}_{S}[x_{1},\ldots ,x_{n}]$
-modules. Given
${\mathcal{O}}_{S}[x_{1},\ldots ,x_{n}]$
-modules. Given
![]() $a\in A$
, we denote by
$a\in A$
, we denote by
 ${\mathcal{O}}_{X}(-a)$
the line bundle corresponding to the free
${\mathcal{O}}_{X}(-a)$
the line bundle corresponding to the free
 ${\mathcal{O}}_{S}[x_{1},\ldots ,x_{n}]$
-module of rank 1 generated in degree
${\mathcal{O}}_{S}[x_{1},\ldots ,x_{n}]$
-module of rank 1 generated in degree
![]() $a$
.
$a$
.
Proposition B.1. Let
![]() $X$
be a basic toric stack over a scheme
$X$
be a basic toric stack over a scheme
![]() $S$
, and assume that
$S$
, and assume that
![]() $X$
has homogeneous coordinates as described above. Then the cotangent complex
$X$
has homogeneous coordinates as described above. Then the cotangent complex
![]() $L_{X/S}$
is quasi-isomorphic to the perfect complex
$L_{X/S}$
is quasi-isomorphic to the perfect complex
 $$\begin{eqnarray}{\mathcal{O}}_{X}(-a_{1})\oplus \cdots \oplus {\mathcal{O}}_{X}(-a_{n})\oplus {\mathcal{O}}_{X}^{s}\rightarrow {\mathcal{O}}_{X}^{s}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}_{X}(-a_{1})\oplus \cdots \oplus {\mathcal{O}}_{X}(-a_{n})\oplus {\mathcal{O}}_{X}^{s}\rightarrow {\mathcal{O}}_{X}^{s}\end{eqnarray}$$
concentrated in cohomological degrees
![]() $[0,1]$
and with differential given by the matrix
$[0,1]$
and with differential given by the matrix
 $$\begin{eqnarray}\left(\begin{array}{@{}cccccc@{}}a_{11}x_{1} & \cdots \, & a_{1n}x_{n} & q_{1} & & 0\\ \vdots & \ddots & \vdots & & \ddots & \\ a_{s1}x_{1} & \cdots \, & a_{sn}x_{n} & 0 & & q_{s}\\ \end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cccccc@{}}a_{11}x_{1} & \cdots \, & a_{1n}x_{n} & q_{1} & & 0\\ \vdots & \ddots & \vdots & & \ddots & \\ a_{s1}x_{1} & \cdots \, & a_{sn}x_{n} & 0 & & q_{s}\\ \end{array}\right).\end{eqnarray}$$
Proof. Due to the base-change properties of the cotangent complex, we may just as well assume that
 $S=\text{Spec}\,\mathbb{Z}$
. Consider the
$S=\text{Spec}\,\mathbb{Z}$
. Consider the
![]() $\mathbb{Z}^{s}$
-graded coordinate ring
$\mathbb{Z}^{s}$
-graded coordinate ring
 ${\mathcal{O}}_{\mathbb{A}^{n}\times \mathbb{G}_{\text{m}}^{s}}=\mathbb{Z}[x_{1},\ldots ,x_{n},t_{1}^{\pm 1},\ldots ,t_{s}^{\pm 1}]$
of the space
${\mathcal{O}}_{\mathbb{A}^{n}\times \mathbb{G}_{\text{m}}^{s}}=\mathbb{Z}[x_{1},\ldots ,x_{n},t_{1}^{\pm 1},\ldots ,t_{s}^{\pm 1}]$
of the space
 $\mathbb{A}^{n}\times \mathbb{G}_{\text{m}}^{s}$
, with
$\mathbb{A}^{n}\times \mathbb{G}_{\text{m}}^{s}$
, with
![]() $x^{i}$
having degree
$x^{i}$
having degree
![]() $a_{i}$
, viewed as a vector of integers, and
$a_{i}$
, viewed as a vector of integers, and
![]() $t_{j}$
having degree
$t_{j}$
having degree
![]() $q_{j}$
. The grading corresponds to an action of the torus
$q_{j}$
. The grading corresponds to an action of the torus
![]() $\mathbb{G}_{\text{m}}^{s}$
. The stack quotient
$\mathbb{G}_{\text{m}}^{s}$
. The stack quotient
 $[\mathbb{A}^{n}\times \mathbb{G}_{m}^{s}/\mathbb{G}_{\text{m}}^{s}]$
is equivalent to
$[\mathbb{A}^{n}\times \mathbb{G}_{m}^{s}/\mathbb{G}_{\text{m}}^{s}]$
is equivalent to
![]() $X$
, with the equivalence induced by slicing the action groupoid
$X$
, with the equivalence induced by slicing the action groupoid
 $\mathbb{A}^{n}\times \mathbb{G}_{m}^{s}\times \mathbb{G}_{m}^{s}\rightrightarrows \mathbb{A}^{n}\times \mathbb{G}_{m}^{s}$
at the closed subscheme
$\mathbb{A}^{n}\times \mathbb{G}_{m}^{s}\times \mathbb{G}_{m}^{s}\rightrightarrows \mathbb{A}^{n}\times \mathbb{G}_{m}^{s}$
at the closed subscheme
 $V(t_{j}=1\mid 1\leqslant j\leqslant s)$
of
$V(t_{j}=1\mid 1\leqslant j\leqslant s)$
of
 $\mathbb{A}^{n}\times \mathbb{G}_{m}^{s}$
. Indeed, then we get the Morita equivalent groupoid
$\mathbb{A}^{n}\times \mathbb{G}_{m}^{s}$
. Indeed, then we get the Morita equivalent groupoid
 $\mathbb{A}^{n}\times \unicode[STIX]{x1D6E5}\rightrightarrows \mathbb{A}^{n}$
, with
$\mathbb{A}^{n}\times \unicode[STIX]{x1D6E5}\rightrightarrows \mathbb{A}^{n}$
, with
 $\unicode[STIX]{x1D6E5}=A^{\vee }$
, which is the presentation of
$\unicode[STIX]{x1D6E5}=A^{\vee }$
, which is the presentation of
![]() $X$
corresponding to the original
$X$
corresponding to the original
![]() $A$
-grading.
$A$
-grading.
The atlas introduced above gives us a cartesian square

of smooth morphisms. Here
![]() $\unicode[STIX]{x1D70B}$
denotes the projection on the first two factors and
$\unicode[STIX]{x1D70B}$
denotes the projection on the first two factors and
![]() $\unicode[STIX]{x1D6FC}$
denotes the action map. Choose coordinates
$\unicode[STIX]{x1D6FC}$
denotes the action map. Choose coordinates
 ${\mathcal{O}}_{\mathbb{A}^{n}\times \mathbb{G}_{\text{m}}^{s}\times \mathbb{G}_{\text{m}}^{s}}=\mathbb{Z}[x_{i},t_{j}^{\pm 1},u_{k}^{\pm 1}]$
. Then the action map corresponds to the ring homomorphism
${\mathcal{O}}_{\mathbb{A}^{n}\times \mathbb{G}_{\text{m}}^{s}\times \mathbb{G}_{\text{m}}^{s}}=\mathbb{Z}[x_{i},t_{j}^{\pm 1},u_{k}^{\pm 1}]$
. Then the action map corresponds to the ring homomorphism
![]() $\unicode[STIX]{x1D711}$
taking
$\unicode[STIX]{x1D711}$
taking
![]() $x_{i}$
to
$x_{i}$
to
 $x_{i}u_{1}^{a_{1i}}\cdots u_{s}^{a_{si}}$
and
$x_{i}u_{1}^{a_{1i}}\cdots u_{s}^{a_{si}}$
and
![]() $t_{i}$
to
$t_{i}$
to
![]() $t_{i}u_{i}^{q_{i}}$
. We get an induced map of differentials
$t_{i}u_{i}^{q_{i}}$
. We get an induced map of differentials
 $$\begin{eqnarray}d\unicode[STIX]{x1D711}:\unicode[STIX]{x1D6FC}^{\ast }\unicode[STIX]{x1D6FA}_{\mathbb{A}^{n}\times \mathbb{G}_{\text{m}}^{s}}\rightarrow \unicode[STIX]{x1D6FA}_{\mathbb{A}^{n}\times \mathbb{G}_{\text{m}}^{s}\times \mathbb{G}_{\text{m}}^{s}/\mathbb{A}^{n}\times \mathbb{G}_{\text{m}}^{s}}\end{eqnarray}$$
$$\begin{eqnarray}d\unicode[STIX]{x1D711}:\unicode[STIX]{x1D6FC}^{\ast }\unicode[STIX]{x1D6FA}_{\mathbb{A}^{n}\times \mathbb{G}_{\text{m}}^{s}}\rightarrow \unicode[STIX]{x1D6FA}_{\mathbb{A}^{n}\times \mathbb{G}_{\text{m}}^{s}\times \mathbb{G}_{\text{m}}^{s}/\mathbb{A}^{n}\times \mathbb{G}_{\text{m}}^{s}}\end{eqnarray}$$
given by
 $$\begin{eqnarray}dx_{i}\mapsto a_{1i}\unicode[STIX]{x1D711}(x_{i})u_{1}^{-1}du_{1}+\cdots +a_{si}\unicode[STIX]{x1D711}(x_{i})u_{s}^{-1}du_{s},\quad dt_{j}\mapsto q_{j}\unicode[STIX]{x1D711}(t_{j})u_{j}^{-1}du_{j}.\end{eqnarray}$$
$$\begin{eqnarray}dx_{i}\mapsto a_{1i}\unicode[STIX]{x1D711}(x_{i})u_{1}^{-1}du_{1}+\cdots +a_{si}\unicode[STIX]{x1D711}(x_{i})u_{s}^{-1}du_{s},\quad dt_{j}\mapsto q_{j}\unicode[STIX]{x1D711}(t_{j})u_{j}^{-1}du_{j}.\end{eqnarray}$$
Since the above square is cartesian and
![]() $\unicode[STIX]{x1D6FC}$
is flat, this descends to a map
$\unicode[STIX]{x1D6FC}$
is flat, this descends to a map
 $\unicode[STIX]{x1D6FA}_{\mathbb{A}^{n}\times \mathbb{G}_{m}}\rightarrow \unicode[STIX]{x1D6FA}_{\mathbb{A}^{n}\times \mathbb{G}_{m}/X}$
. We choose
$\unicode[STIX]{x1D6FA}_{\mathbb{A}^{n}\times \mathbb{G}_{m}}\rightarrow \unicode[STIX]{x1D6FA}_{\mathbb{A}^{n}\times \mathbb{G}_{m}/X}$
. We choose
 $(dx_{i},dt_{j})$
as a basis for the left-hand side. An easy calculation gives that the elements
$(dx_{i},dt_{j})$
as a basis for the left-hand side. An easy calculation gives that the elements
![]() $u_{i}^{-1}du$
descend to elements of
$u_{i}^{-1}du$
descend to elements of
 $\unicode[STIX]{x1D6FA}_{\mathbb{A}^{n}\times \mathbb{G}_{\text{m}}/X}$
, which we also denote by
$\unicode[STIX]{x1D6FA}_{\mathbb{A}^{n}\times \mathbb{G}_{\text{m}}/X}$
, which we also denote by
![]() $u_{i}^{-1}du$
. These elements form a basis for the right-hand side. With respect to these choices, the map is described by the matrix
$u_{i}^{-1}du$
. These elements form a basis for the right-hand side. With respect to these choices, the map is described by the matrix
 $$\begin{eqnarray}\left(\begin{array}{@{}cccccc@{}}a_{11}x_{1} & \cdots \, & a_{1n}x_{n} & t_{1}q_{1} & & 0\\ \vdots & \ddots & \vdots & & \ddots & \\ a_{s1}x_{1} & \cdots \, & a_{sn}x_{n} & 0 & & t_{s}q_{s}\\ \end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cccccc@{}}a_{11}x_{1} & \cdots \, & a_{1n}x_{n} & t_{1}q_{1} & & 0\\ \vdots & \ddots & \vdots & & \ddots & \\ a_{s1}x_{1} & \cdots \, & a_{sn}x_{n} & 0 & & t_{s}q_{s}\\ \end{array}\right).\end{eqnarray}$$
Now we may compute the cotangent complex with help of the distinguished triangle
 $$\begin{eqnarray}\unicode[STIX]{x1D6FA}_{\mathbb{A}^{n}\times \mathbb{G}_{\text{m}}^{s}}\rightarrow \unicode[STIX]{x1D6FA}_{\mathbb{A}^{n}\times \mathbb{G}_{\text{m}}^{s}/X}\rightarrow \mathbf{L}q^{\ast }L_{X}[1].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FA}_{\mathbb{A}^{n}\times \mathbb{G}_{\text{m}}^{s}}\rightarrow \unicode[STIX]{x1D6FA}_{\mathbb{A}^{n}\times \mathbb{G}_{\text{m}}^{s}/X}\rightarrow \mathbf{L}q^{\ast }L_{X}[1].\end{eqnarray}$$
Hence, the derived pull-back
![]() $\mathbf{L}q^{\ast }L_{X}$
is given by a two-term complex
$\mathbf{L}q^{\ast }L_{X}$
is given by a two-term complex
 $\unicode[STIX]{x1D6FA}_{\mathbb{A}^{n}\times \mathbb{G}_{\text{m}}^{s}}\rightarrow \unicode[STIX]{x1D6FA}_{\mathbb{A}^{n}\times \mathbb{G}_{\text{m}}^{s}/X}[-1]$
with differential as in the matrix above. This is graded by
$\unicode[STIX]{x1D6FA}_{\mathbb{A}^{n}\times \mathbb{G}_{\text{m}}^{s}}\rightarrow \unicode[STIX]{x1D6FA}_{\mathbb{A}^{n}\times \mathbb{G}_{\text{m}}^{s}/X}[-1]$
with differential as in the matrix above. This is graded by
![]() $\mathbb{Z}^{s}$
, with
$\mathbb{Z}^{s}$
, with
 $|dx_{i}|=a_{i}$
,
$|dx_{i}|=a_{i}$
,
 $|dt_{j}|=q_{j}$
and
$|dt_{j}|=q_{j}$
and
 $|u_{k}^{-1}du_{k}|=0$
, which reflects that the complex lives over
$|u_{k}^{-1}du_{k}|=0$
, which reflects that the complex lives over
![]() $[\mathbb{A}^{n}/\unicode[STIX]{x1D6E5}]$
. We obtain the original homogeneous coordinates by slicing at
$[\mathbb{A}^{n}/\unicode[STIX]{x1D6E5}]$
. We obtain the original homogeneous coordinates by slicing at
 $V(t_{j}=1\mid 1\leqslant j\leqslant s)$
as described before, which gives the result stated in the proposition.◻
$V(t_{j}=1\mid 1\leqslant j\leqslant s)$
as described before, which gives the result stated in the proposition.◻
Note that if the product
![]() $q_{1}\cdots q_{s}$
is invertible in
$q_{1}\cdots q_{s}$
is invertible in
![]() ${\mathcal{O}}_{S}$
, then this complex is quasi-isomorphic to the
${\mathcal{O}}_{S}$
, then this complex is quasi-isomorphic to the
![]() ${\mathcal{O}}_{X}$
-module
${\mathcal{O}}_{X}$
-module
 $$\begin{eqnarray}\mathscr{H}^{0}(L_{X/S})={\mathcal{O}}_{X}(-a_{1})\oplus \cdots \oplus {\mathcal{O}}_{X}(-a_{n}).\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{H}^{0}(L_{X/S})={\mathcal{O}}_{X}(-a_{1})\oplus \cdots \oplus {\mathcal{O}}_{X}(-a_{n}).\end{eqnarray}$$
The fibre of this module in a point
![]() $\unicode[STIX]{x1D709}$
, together with the natural action of the stabiliser, coincides with the conormal representation at
$\unicode[STIX]{x1D709}$
, together with the natural action of the stabiliser, coincides with the conormal representation at
![]() $\unicode[STIX]{x1D709}$
. If
$\unicode[STIX]{x1D709}$
. If
![]() $q_{1}\cdots q_{s}$
is not invertible, this need not be true. Consider, for instance,
$q_{1}\cdots q_{s}$
is not invertible, this need not be true. Consider, for instance,
 $X=[\mathbb{A}_{S}^{1}/\unicode[STIX]{x1D707}_{q}]$
, where
$X=[\mathbb{A}_{S}^{1}/\unicode[STIX]{x1D707}_{q}]$
, where
 $S=\text{Spec}\,k$
with
$S=\text{Spec}\,k$
with
![]() $k$
a field of characteristic
$k$
a field of characteristic
![]() $p$
and
$p$
and
![]() $q=0$
in
$q=0$
in
![]() $k$
. If
$k$
. If
![]() $\unicode[STIX]{x1D707}_{q}$
is acting with weight
$\unicode[STIX]{x1D707}_{q}$
is acting with weight
![]() $a$
, we have
$a$
, we have
 $$\begin{eqnarray}\mathscr{H}^{0}(L_{X/S})=\left\{\begin{array}{@{}ll@{}}{\mathcal{O}}_{X}(-a)\oplus {\mathcal{O}}_{X} & \text{if }a=0\text{ in }k,\\ {\mathcal{O}}_{X} & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{H}^{0}(L_{X/S})=\left\{\begin{array}{@{}ll@{}}{\mathcal{O}}_{X}(-a)\oplus {\mathcal{O}}_{X} & \text{if }a=0\text{ in }k,\\ {\mathcal{O}}_{X} & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
We see that, in general, the information about the weight is lost. If one wishes to preserve this information, it is better to look at
![]() $[L_{X/S}]$
or, equivalently, the alternating sum
$[L_{X/S}]$
or, equivalently, the alternating sum
 $[\mathscr{H}^{0}(L_{X/S})]-[\mathscr{H}^{1}(L_{X/S})]$
in the
$[\mathscr{H}^{0}(L_{X/S})]-[\mathscr{H}^{1}(L_{X/S})]$
in the
![]() $K$
-group.
$K$
-group.
Appendix C Cotangent complex interpretation
In this appendix, we take a brief look at an alternative way to look at the conormal representation in terms of the cotangent complex. An advantage with this point of view is that we can use various distinguished triangles for the cotangent complex in our computations.
Given an algebraic stack
![]() $X$
, we consider the triangulated category
$X$
, we consider the triangulated category
 $\text{Perf}(X)$
. This is the full subcategory of the derived category of
$\text{Perf}(X)$
. This is the full subcategory of the derived category of
![]() $X$
whose objects are represented by perfect complexes. Its associated Grothendieck group is denoted by
$X$
whose objects are represented by perfect complexes. Its associated Grothendieck group is denoted by
 $\text{K}_{0}(\text{Perf}(X))$
. A morphism
$\text{K}_{0}(\text{Perf}(X))$
. A morphism
 $f:X\rightarrow Y$
gives a morphism
$f:X\rightarrow Y$
gives a morphism
 $f^{\ast }\text{K}_{0}(\text{Perf}(Y))\rightarrow \text{K}_{0}(\text{Perf}(X))$
induced by the derived pull-back. If
$f^{\ast }\text{K}_{0}(\text{Perf}(Y))\rightarrow \text{K}_{0}(\text{Perf}(X))$
induced by the derived pull-back. If
![]() $X$
is smooth over a field, then
$X$
is smooth over a field, then
 $\text{K}_{0}(\text{Perf}(X))$
is canonically isomorphic to the Grothendieck group
$\text{K}_{0}(\text{Perf}(X))$
is canonically isomorphic to the Grothendieck group
 $\text{K}_{0}(\text{Coh}(X))$
of coherent
$\text{K}_{0}(\text{Coh}(X))$
of coherent
![]() ${\mathcal{O}}_{X}$
-modules.
${\mathcal{O}}_{X}$
-modules.
In the particular situation described in the beginning of § 6, we have a 2-commutative diagram

where the square is 2-cartesian. Denote the composition
![]() $f\circ \unicode[STIX]{x1D704}$
by
$f\circ \unicode[STIX]{x1D704}$
by
![]() $g$
. By using the distinguished triangle for composition and the base-change property for cotangent complexes, we get the identities
$g$
. By using the distinguished triangle for composition and the base-change property for cotangent complexes, we get the identities
 $$\begin{eqnarray}\unicode[STIX]{x1D704}^{\ast }[L_{X_{\bar{k}}/\bar{k}}]-[L_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/\bar{k}}]+[L_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}]=0,\quad [L_{X_{\bar{k}}/\bar{k}}]=f^{\ast }[L_{X/S}]\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}^{\ast }[L_{X_{\bar{k}}/\bar{k}}]-[L_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/\bar{k}}]+[L_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}]=0,\quad [L_{X_{\bar{k}}/\bar{k}}]=f^{\ast }[L_{X/S}]\end{eqnarray}$$
in
 $\text{K}_{0}(\text{Perf}(\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}))$
. Since the immersion
$\text{K}_{0}(\text{Perf}(\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}))$
. Since the immersion
 $\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}{\hookrightarrow}X_{\bar{k}}$
is regular, the cotangent complex
$\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}{\hookrightarrow}X_{\bar{k}}$
is regular, the cotangent complex
 $L_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}$
is quasi-isomorphic to the complex having
$L_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}$
is quasi-isomorphic to the complex having
 ${\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}$
concentrated in degree
${\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}$
concentrated in degree
![]() $-1$
. Together with the identities above, this implies that
$-1$
. Together with the identities above, this implies that
 $$\begin{eqnarray}[{\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}]=-[L_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}]=g^{\ast }[L_{X/S}]-[L_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/\bar{k}}]\end{eqnarray}$$
$$\begin{eqnarray}[{\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}]=-[L_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}]=g^{\ast }[L_{X/S}]-[L_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/\bar{k}}]\end{eqnarray}$$
in
 $\text{K}_{0}(\text{Perf}(\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}))$
. If
$\text{K}_{0}(\text{Perf}(\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}))$
. If
![]() $\bar{k}$
has characteristic 0, the complex
$\bar{k}$
has characteristic 0, the complex
![]() $L_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/\bar{k}}$
vanishes since
$L_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/\bar{k}}$
vanishes since
![]() $\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
is étale over
$\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
is étale over
![]() $\bar{k}$
. In positive characteristic, the complex
$\bar{k}$
. In positive characteristic, the complex
![]() $L_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/\bar{k}}$
need not vanish, but its class in the Grothendieck group always vanishes. This can be seen from the explicit formula derived in Appendix B. In particular, we have the identity
$L_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/\bar{k}}$
need not vanish, but its class in the Grothendieck group always vanishes. This can be seen from the explicit formula derived in Appendix B. In particular, we have the identity
 $[{\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}]=g^{\ast }[L_{X/S}]$
. We summarise the result in the following proposition.
$[{\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}]=g^{\ast }[L_{X/S}]$
. We summarise the result in the following proposition.
Proposition C.1. Let
 $(X,\boldsymbol{E})/S$
be a standard pair with diagonalisable stabilisers. Furthermore, let
$(X,\boldsymbol{E})/S$
be a standard pair with diagonalisable stabilisers. Furthermore, let
 $\unicode[STIX]{x1D709}:\text{Spec}\,\bar{k}\rightarrow X$
be a geometric point,
$\unicode[STIX]{x1D709}:\text{Spec}\,\bar{k}\rightarrow X$
be a geometric point,
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
the stabiliser at
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
the stabiliser at
![]() $\unicode[STIX]{x1D709}$
and
$\unicode[STIX]{x1D709}$
and
 $g:\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}\rightarrow X$
the induced morphism. Then we have the identity
$g:\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}\rightarrow X$
the induced morphism. Then we have the identity
 $$\begin{eqnarray}[{\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}]=g^{\ast }[L_{X/S}]\end{eqnarray}$$
$$\begin{eqnarray}[{\mathcal{N}}_{\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}/X_{\bar{k}}}]=g^{\ast }[L_{X/S}]\end{eqnarray}$$
in the group
 $\text{K}_{0}(\text{Perf}(\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}))$
, which we have identified with
$\text{K}_{0}(\text{Perf}(\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}))$
, which we have identified with
 $\text{K}_{0}(\text{Coh}(\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}))$
.
$\text{K}_{0}(\text{Coh}(\text{B}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}))$
.