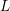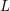1 Introduction
Soit
![]() $N\geqslant 3$
un entier. Soit
$N\geqslant 3$
un entier. Soit
![]() $Y(N)$
la courbe modulaire ouverte et
$Y(N)$
la courbe modulaire ouverte et
![]() $E$
la courbe elliptique universelle sur
$E$
la courbe elliptique universelle sur
![]() $Y(N)$
. Pour un entier
$Y(N)$
. Pour un entier
![]() $n\geqslant 0$
, notons
$n\geqslant 0$
, notons
![]() $E^{n}$
la puissance fibrée
$E^{n}$
la puissance fibrée
![]() $n$
-ième de
$n$
-ième de
![]() $E$
au-dessus de
$E$
au-dessus de
![]() $Y(N)$
. Pour tout
$Y(N)$
. Pour tout
![]() $u\in (\mathbf{Z}/N\mathbf{Z})^{2}$
, avec
$u\in (\mathbf{Z}/N\mathbf{Z})^{2}$
, avec
![]() $u\neq 0$
si
$u\neq 0$
si
![]() $n=0$
, Beilinson a défini le symbole d’Eisenstein
$n=0$
, Beilinson a défini le symbole d’Eisenstein
Le symbole d’Eisenstein est à la base de la preuve par Beilinson et Deninger–Scholl de la conjecture de Beilinson pour les valeurs non critiques des fonctions
![]() $L$
des formes modulaires.
$L$
des formes modulaires.
Plus précisément, donnons-nous un entier
![]() $k\geqslant 0$
, et choisissons une décomposition
$k\geqslant 0$
, et choisissons une décomposition
![]() $k=k_{1}+k_{2}$
avec
$k=k_{1}+k_{2}$
avec
![]() $k_{1},k_{2}\geqslant 0$
. Considérons les projections canoniques
$k_{1},k_{2}\geqslant 0$
. Considérons les projections canoniques

Soient
![]() $u_{1},u_{2}\in (\mathbf{Z}/N\mathbf{Z})^{2}$
, avec
$u_{1},u_{2}\in (\mathbf{Z}/N\mathbf{Z})^{2}$
, avec
![]() $u_{i}\neq 0$
si
$u_{i}\neq 0$
si
![]() $k_{i}=0$
. Généralisant les constructions de Beilinson et Deninger–Scholl, Gealy [Reference GealyGea05] définit un élément dans la cohomologie motivique de
$k_{i}=0$
. Généralisant les constructions de Beilinson et Deninger–Scholl, Gealy [Reference GealyGea05] définit un élément dans la cohomologie motivique de
![]() $E^{k}$
,
$E^{k}$
,
Dans le cas
![]() $k=0$
, on retrouve les éléments de Beilinson–Kato (cup-produits d’unités de Siegel) dans le
$k=0$
, on retrouve les éléments de Beilinson–Kato (cup-produits d’unités de Siegel) dans le
![]() $K_{2}$
de la courbe modulaire
$K_{2}$
de la courbe modulaire
![]() $Y(N)$
. Considérons le régulateur de Beilinson à valeurs dans la cohomologie de Deligne–Beilinson
$Y(N)$
. Considérons le régulateur de Beilinson à valeurs dans la cohomologie de Deligne–Beilinson
et l’application analogue pour la compactification lisse
![]() $\overline{E}^{k}$
de
$\overline{E}^{k}$
de
![]() $E^{k}$
définie par Deligne. Soit
$E^{k}$
définie par Deligne. Soit
![]() $f$
une forme parabolique primitive de poids
$f$
une forme parabolique primitive de poids
![]() $k+2$
pour le groupe
$k+2$
pour le groupe
![]() $\unicode[STIX]{x1D6E4}_{1}(N)$
. Notons
$\unicode[STIX]{x1D6E4}_{1}(N)$
. Notons
![]() $K_{f}$
le corps des coefficients de
$K_{f}$
le corps des coefficients de
![]() $f$
, et
$f$
, et
![]() $\unicode[STIX]{x1D714}_{f}\in \unicode[STIX]{x1D6FA}^{k+1}(\overline{E}^{k})\otimes K_{f}$
la forme différentielle associée à
$\unicode[STIX]{x1D714}_{f}\in \unicode[STIX]{x1D6FA}^{k+1}(\overline{E}^{k})\otimes K_{f}$
la forme différentielle associée à
![]() $f$
. Classiquement, le régulateur de Beilinson associé à
$f$
. Classiquement, le régulateur de Beilinson associé à
![]() $f$
est défini au moyen de l’accouplement issu de la dualité de Poincaré
$f$
est défini au moyen de l’accouplement issu de la dualité de Poincaré
En utilisant les éléments (1), Deninger et Scholl [Reference Deninger and SchollDS91] et Gealy [Reference GealyGea05] montrent qu’il existe un élément
![]() $x$
de
$x$
de
![]() $H_{{\mathcal{M}}}^{k+2}(\overline{E}^{k},\mathbf{Q}(k+2))\otimes K_{f}$
tel que
$H_{{\mathcal{M}}}^{k+2}(\overline{E}^{k},\mathbf{Q}(k+2))\otimes K_{f}$
tel que
où
![]() $\unicode[STIX]{x1D6FA}_{f}^{+}$
est la période réelle de
$\unicode[STIX]{x1D6FA}_{f}^{+}$
est la période réelle de
![]() $f$
. Le calcul est basé sur la méthode de Rankin–Selberg. Cela permet de démontrer la conjecture de Beilinson pour la valeur spéciale
$f$
. Le calcul est basé sur la méthode de Rankin–Selberg. Cela permet de démontrer la conjecture de Beilinson pour la valeur spéciale
![]() $L(f,k+2)$
.
$L(f,k+2)$
.
Dans cet article, nous proposons une approche nouvelle, et totalement explicite, pour calculer le régulateur. Au lieu d’intégrer le régulateur de Beilinson contre une forme parabolique, nous pouvons l’intégrer le long des
![]() $(k+1)$
-cycles explicites fournis par la théorie de Shokurov [Reference ŠokurovŠok80]. Plus précisément, considérons le cycle de Shokurov
$(k+1)$
-cycles explicites fournis par la théorie de Shokurov [Reference ŠokurovŠok80]. Plus précisément, considérons le cycle de Shokurov
![]() $X^{k}\{0,\infty \}$
(voir la § 4). Dans la § 6, nous définissons une forme différentielle explicite
$X^{k}\{0,\infty \}$
(voir la § 4). Dans la § 6, nous définissons une forme différentielle explicite
![]() $\text{Eis}_{{\mathcal{D}}}^{k_{1},k_{2}}(u_{1},u_{2})$
représentant le régulateur de Beilinson de
$\text{Eis}_{{\mathcal{D}}}^{k_{1},k_{2}}(u_{1},u_{2})$
représentant le régulateur de Beilinson de
![]() $\text{Eis}^{k_{1},k_{2}}(u_{1},u_{2})$
. Considérons alors l’intégrale
$\text{Eis}^{k_{1},k_{2}}(u_{1},u_{2})$
. Considérons alors l’intégrale
Contrairement au cas
![]() $k=0$
, l’intégrale (2) ne converge pas absolument en général. Pour remédier à ce problème, nous introduisons un paramètre complexe
$k=0$
, l’intégrale (2) ne converge pas absolument en général. Pour remédier à ce problème, nous introduisons un paramètre complexe
![]() $s\in \mathbf{C}$
et considérons l’intégrale
$s\in \mathbf{C}$
et considérons l’intégrale
Nous montrons que l’intégrale (3) converge pour
![]() $\Re (s)\ll 0$
et se prolonge en une fonction méromorphe sur
$\Re (s)\ll 0$
et se prolonge en une fonction méromorphe sur
![]() $\mathbf{C}$
, holomorphe en
$\mathbf{C}$
, holomorphe en
![]() $s=0$
. Définissons alors l’intégrale régularisée
$s=0$
. Définissons alors l’intégrale régularisée
comme la valeur en
![]() $s=0$
de cette fonction.
$s=0$
de cette fonction.
Soit
![]() ${\mathcal{H}}$
le demi-plan de Poincaré. Pour
${\mathcal{H}}$
le demi-plan de Poincaré. Pour
![]() $\ell \geqslant 1$
,
$\ell \geqslant 1$
,
![]() $a,b\in \mathbf{Z}/N\mathbf{Z}$
, définissons la série d’Eisenstein
$a,b\in \mathbf{Z}/N\mathbf{Z}$
, définissons la série d’Eisenstein
avec
 $$\begin{eqnarray}\displaystyle a_{0}(G_{a,b}^{(1)})=\left\{\begin{array}{@{}ll@{}}\displaystyle 0\quad & \text{si }a=b=0,\\ \displaystyle \frac{1}{2}-\biggl\{\frac{b}{N}\biggr\}\quad & \text{si }a=0\text{ et }b\neq 0,\\ \displaystyle \frac{1}{2}-\biggl\{\frac{a}{N}\biggr\}\quad & \text{si }a\neq 0\text{ et }b=0,\\ \displaystyle 0\quad & \text{si }a\neq 0\text{et }b\neq 0,\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a_{0}(G_{a,b}^{(1)})=\left\{\begin{array}{@{}ll@{}}\displaystyle 0\quad & \text{si }a=b=0,\\ \displaystyle \frac{1}{2}-\biggl\{\frac{b}{N}\biggr\}\quad & \text{si }a=0\text{ et }b\neq 0,\\ \displaystyle \frac{1}{2}-\biggl\{\frac{a}{N}\biggr\}\quad & \text{si }a\neq 0\text{ et }b=0,\\ \displaystyle 0\quad & \text{si }a\neq 0\text{et }b\neq 0,\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
et pour
![]() $\ell \geqslant 2$
,
$\ell \geqslant 2$
,
 $$\begin{eqnarray}\displaystyle a_{0}(G_{a,b}^{(\ell )})=\left\{\begin{array}{@{}ll@{}}\displaystyle -N^{\ell -1}\frac{B_{\ell }(\{a/N\})}{\ell }\quad & \text{si }b=0,\\ 0\quad & \text{si }b\neq 0,\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a_{0}(G_{a,b}^{(\ell )})=\left\{\begin{array}{@{}ll@{}}\displaystyle -N^{\ell -1}\frac{B_{\ell }(\{a/N\})}{\ell }\quad & \text{si }b=0,\\ 0\quad & \text{si }b\neq 0,\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
où
![]() $\{x\}=x-\lfloor x\rfloor$
désigne la partie fractionnaire de
$\{x\}=x-\lfloor x\rfloor$
désigne la partie fractionnaire de
![]() $x$
, et
$x$
, et
![]() $B_{\ell }$
est le
$B_{\ell }$
est le
![]() $\ell$
-ième polynôme de Bernoulli. La fonction
$\ell$
-ième polynôme de Bernoulli. La fonction
![]() $G_{a,b}^{(\ell )}$
est une forme modulaire (quasi-modulaire si
$G_{a,b}^{(\ell )}$
est une forme modulaire (quasi-modulaire si
![]() $\ell =2$
et
$\ell =2$
et
![]() $a=0$
) de poids
$a=0$
) de poids
![]() $\ell$
pour le groupe
$\ell$
pour le groupe
![]() $\unicode[STIX]{x1D6E4}_{1}(N^{2})$
.
$\unicode[STIX]{x1D6E4}_{1}(N^{2})$
.
Étant donnée une forme modulaire
![]() $F=\sum _{n=0}^{\infty }a_{n}q^{n}$
pour
$F=\sum _{n=0}^{\infty }a_{n}q^{n}$
pour
![]() $\unicode[STIX]{x1D6E4}_{1}(M)$
, notons
$\unicode[STIX]{x1D6E4}_{1}(M)$
, notons
la fonction
![]() $L$
complétée de
$L$
complétée de
![]() $F$
, et notons
$F$
, et notons
![]() $\unicode[STIX]{x1D6EC}^{\ast }(F,0)$
la valeur régularisée de
$\unicode[STIX]{x1D6EC}^{\ast }(F,0)$
la valeur régularisée de
![]() $\unicode[STIX]{x1D6EC}(F,s)$
en
$\unicode[STIX]{x1D6EC}(F,s)$
en
![]() $s=0$
(voir la définition 3.13).
$s=0$
(voir la définition 3.13).
En utilisant la méthode de Rogers–Zudilin, nous montrons le résultat suivant.
Théorème 1.1. Soit
![]() $k\geqslant 0$
un entier, et soient
$k\geqslant 0$
un entier, et soient
![]() $k_{1},k_{2}\geqslant 0$
tels que
$k_{1},k_{2}\geqslant 0$
tels que
![]() $k=k_{1}+k_{2}$
. Soit
$k=k_{1}+k_{2}$
. Soit
![]() $N\geqslant 3$
un entier, et soient
$N\geqslant 3$
un entier, et soient
![]() $u_{1}=(a_{1},b_{1})$
,
$u_{1}=(a_{1},b_{1})$
,
![]() $u_{2}=(a_{2},b_{2})\in (\mathbf{Z}/N\mathbf{Z})^{2}$
. Supposons
$u_{2}=(a_{2},b_{2})\in (\mathbf{Z}/N\mathbf{Z})^{2}$
. Supposons
![]() $u_{i}\neq (0,0)$
si
$u_{i}\neq (0,0)$
si
![]() $k_{i}=0$
, et
$k_{i}=0$
, et
![]() $b_{i}\neq 0$
si
$b_{i}\neq 0$
si
![]() $k_{i}=1$
. Alors
$k_{i}=1$
. Alors
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X^{k}\{0,\infty \}}^{\ast }\text{Eis}_{{\mathcal{D}}}^{k_{1},k_{2}}(u_{1},u_{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(k_{1}+2)(k_{2}+2)}{2N^{k+2}}(2\unicode[STIX]{x1D70B})^{k+1}i^{k_{1}-k_{2}+1}\unicode[STIX]{x1D6EC}^{\ast }(G_{b_{2},a_{1}}^{(k_{2}+1)}G_{b_{1},-a_{2}}^{(k_{1}+1)}-G_{b_{2},-a_{1}}^{(k_{2}+1)}G_{b_{1},a_{2}}^{(k_{1}+1)},0).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X^{k}\{0,\infty \}}^{\ast }\text{Eis}_{{\mathcal{D}}}^{k_{1},k_{2}}(u_{1},u_{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(k_{1}+2)(k_{2}+2)}{2N^{k+2}}(2\unicode[STIX]{x1D70B})^{k+1}i^{k_{1}-k_{2}+1}\unicode[STIX]{x1D6EC}^{\ast }(G_{b_{2},a_{1}}^{(k_{2}+1)}G_{b_{1},-a_{2}}^{(k_{1}+1)}-G_{b_{2},-a_{1}}^{(k_{2}+1)}G_{b_{1},a_{2}}^{(k_{1}+1)},0).\end{eqnarray}$$
Remarques 1.2. (i) Lorsque
![]() $k_{1}=k_{2}=0$
, on retrouve la formule pour le régulateur du cup-produit de deux unités modulaires [Reference ZudilinZud14, Reference BrunaultBru16].
$k_{1}=k_{2}=0$
, on retrouve la formule pour le régulateur du cup-produit de deux unités modulaires [Reference ZudilinZud14, Reference BrunaultBru16].
(ii) La forme modulaire de poids
![]() $k+2$
apparaissant dans le membre de droite de (5) est à coefficients rationnels. Il est naturel de se demander si toute forme parabolique primitive est combinaison linéaire de telles formes modulaires.
$k+2$
apparaissant dans le membre de droite de (5) est à coefficients rationnels. Il est naturel de se demander si toute forme parabolique primitive est combinaison linéaire de telles formes modulaires.
(iii) Si
![]() $\unicode[STIX]{x1D6FE}$
est un
$\unicode[STIX]{x1D6FE}$
est un
![]() $(k+1)$
-cycle de la forme
$(k+1)$
-cycle de la forme
![]() $\unicode[STIX]{x1D6FE}=\sum _{i}n_{i}(X^{k}\{0,\infty \})|g_{i}$
avec
$\unicode[STIX]{x1D6FE}=\sum _{i}n_{i}(X^{k}\{0,\infty \})|g_{i}$
avec
![]() $n_{i}\in \mathbf{Z}$
et
$n_{i}\in \mathbf{Z}$
et
![]() $g_{i}\in \text{GL}_{2}(\mathbf{Z}/N\mathbf{Z})$
, alors on peut calculer l’intégrale de
$g_{i}\in \text{GL}_{2}(\mathbf{Z}/N\mathbf{Z})$
, alors on peut calculer l’intégrale de
![]() $\text{Eis}_{{\mathcal{D}}}^{k_{1},k_{2}}(u_{1},u_{2})$
le long de
$\text{Eis}_{{\mathcal{D}}}^{k_{1},k_{2}}(u_{1},u_{2})$
le long de
![]() $\unicode[STIX]{x1D6FE}$
au moyen de la formule
$\unicode[STIX]{x1D6FE}$
au moyen de la formule
(iv) Soit
![]() $F_{u_{1},u_{2}}=G_{b_{2},a_{1}}^{(k_{2}+1)}G_{b_{1},-a_{2}}^{(k_{1}+1)}-G_{b_{2},-a_{1}}^{(k_{2}+1)}G_{b_{1},a_{2}}^{(k_{1}+1)}$
la forme modulaire apparaissant dans le membre de droite de (5). Alors
$F_{u_{1},u_{2}}=G_{b_{2},a_{1}}^{(k_{2}+1)}G_{b_{1},-a_{2}}^{(k_{1}+1)}-G_{b_{2},-a_{1}}^{(k_{2}+1)}G_{b_{1},a_{2}}^{(k_{1}+1)}$
la forme modulaire apparaissant dans le membre de droite de (5). Alors
![]() $\tilde{F}_{u_{1},u_{2}}(\unicode[STIX]{x1D70F})=F_{u_{1},u_{2}}(\unicode[STIX]{x1D70F}/N)$
est modulaire pour le groupe
$\tilde{F}_{u_{1},u_{2}}(\unicode[STIX]{x1D70F})=F_{u_{1},u_{2}}(\unicode[STIX]{x1D70F}/N)$
est modulaire pour le groupe
![]() $\unicode[STIX]{x1D6E4}(N)$
. Supposons de plus
$\unicode[STIX]{x1D6E4}(N)$
. Supposons de plus
![]() $\det (u_{1},u_{2})=0$
, c’est-à-dire
$\det (u_{1},u_{2})=0$
, c’est-à-dire
![]() $a_{1}b_{2}-a_{2}b_{1}=0$
. Alors
$a_{1}b_{2}-a_{2}b_{1}=0$
. Alors
![]() $F_{u_{1},u_{2}}\in \mathbf{Q}[[q^{N}]]$
, de sorte que
$F_{u_{1},u_{2}}\in \mathbf{Q}[[q^{N}]]$
, de sorte que
![]() $\tilde{F}_{u_{1},u_{2}}(\unicode[STIX]{x1D70F}+1)=\tilde{F}_{u_{1},u_{2}}(\unicode[STIX]{x1D70F})$
, et donc
$\tilde{F}_{u_{1},u_{2}}(\unicode[STIX]{x1D70F}+1)=\tilde{F}_{u_{1},u_{2}}(\unicode[STIX]{x1D70F})$
, et donc
![]() $\tilde{F}_{u_{1},u_{2}}\in M_{k+2}(\unicode[STIX]{x1D6E4}_{1}(N))$
. Remarquons en outre que pour tout
$\tilde{F}_{u_{1},u_{2}}\in M_{k+2}(\unicode[STIX]{x1D6E4}_{1}(N))$
. Remarquons en outre que pour tout
![]() $g\in \text{GL}_{2}(\mathbf{Z}/N\mathbf{Z})$
, avec
$g\in \text{GL}_{2}(\mathbf{Z}/N\mathbf{Z})$
, avec
![]() $u_{i}g\neq (\ast ,0)$
si
$u_{i}g\neq (\ast ,0)$
si
![]() $k_{i}=1$
, on a
$k_{i}=1$
, on a
![]() $\det (u_{1}g,u_{2}g)=0$
et donc
$\det (u_{1}g,u_{2}g)=0$
et donc
![]() $\tilde{F}_{u_{1}g,u_{2}g}\in M_{k+2}(\unicode[STIX]{x1D6E4}_{1}(N))$
.
$\tilde{F}_{u_{1}g,u_{2}g}\in M_{k+2}(\unicode[STIX]{x1D6E4}_{1}(N))$
.
(v) Dans le cas où
![]() $k_{i}=1$
et
$k_{i}=1$
et
![]() $b_{i}=0$
, on a un résultat partiel pour le calcul du régulateur, voir le théorème 9.5.
$b_{i}=0$
, on a un résultat partiel pour le calcul du régulateur, voir le théorème 9.5.
Cet article est organisé comme suit. Dans les §§ 2 et 3, nous introduisons les notations concernant la fonction zêta de Hurwitz et les séries d’Eisenstein–Kronecker, et rappelons les résultats principaux les concernant. Dans les §§ 4 et 5, nous rappelons la définition des cycles de Shokurov et la formule donnant la réalisation du symbole d’Eisenstein. Dans la § 6, nous définissons les éléments de Deninger–Scholl et explicitons leurs réalisations en cohomologie de Deligne–Beilinson. Dans la § 7, nous exposons la méthode de Rogers–Zudilin dans un cadre suffisamment général. Dans la § 8, nous calculons le développement de Fourier de certaines séries d’Eisenstein analytiques réelles. Enfin, nous effectuons le calcul proprement dit du régulateur dans la § 9.
Ce travail doit beaucoup à Anton Mellit et Don Zagier, qui ont les premiers proposé une formulation analytique générale de l’astuce de Rogers–Zudilin. Je remercie Anton Mellit de m’avoir invité à l’université de Köln en novembre 2011, et pour les discussions très constructives que nous avons eues. Je remercie Odile Lecacheux pour des échanges très stimulants autour de ces questions, Loïc Merel pour avoir porté mon attention sur les cycles de Shokurov, Wadim Zudilin pour ses encouragements lors de la rédaction, et Michael Neururer pour ses commentaires et la relecture de ce texte. Enfin, je remercie le rapporteur pour ses remarques utiles pour l’amélioration de ce texte.
2 Fonction zêta de Hurwitz
Pour
![]() $x\in \mathbf{R}/\mathbf{Z}$
, on définit la fonction zêta de Hurwitz
$x\in \mathbf{R}/\mathbf{Z}$
, on définit la fonction zêta de Hurwitz
et la fonction zêta périodique
On a donc
![]() $\unicode[STIX]{x1D701}(0,s)=\hat{\unicode[STIX]{x1D701}}(0,s)=\unicode[STIX]{x1D701}(s)$
. La fonction
$\unicode[STIX]{x1D701}(0,s)=\hat{\unicode[STIX]{x1D701}}(0,s)=\unicode[STIX]{x1D701}(s)$
. La fonction
![]() $s\mapsto \unicode[STIX]{x1D701}(x,s)$
se prolonge en une fonction méromorphe sur
$s\mapsto \unicode[STIX]{x1D701}(x,s)$
se prolonge en une fonction méromorphe sur
![]() $\mathbf{C}$
, avec un unique pôle simple en
$\mathbf{C}$
, avec un unique pôle simple en
![]() $s=1$
, de résidu égal à
$s=1$
, de résidu égal à
![]() $1$
[Reference Knopp and RobinsKR01, Corollary 2(a)].
$1$
[Reference Knopp and RobinsKR01, Corollary 2(a)].
Définition 2.1. Pour
![]() $x\in \mathbf{R}/\mathbf{Z}$
, on pose
$x\in \mathbf{R}/\mathbf{Z}$
, on pose
Pour
![]() $x\in \mathbf{R}/\mathbf{Z}$
,
$x\in \mathbf{R}/\mathbf{Z}$
,
![]() $x\neq 0$
, la fonction
$x\neq 0$
, la fonction
![]() $s\mapsto \hat{\unicode[STIX]{x1D701}}(x,s)$
se prolonge en une fonction holomorphe sur
$s\mapsto \hat{\unicode[STIX]{x1D701}}(x,s)$
se prolonge en une fonction holomorphe sur
![]() $\mathbf{C}$
[Reference Knopp and RobinsKR01, Corollary 2(c)]. Pour tout entier
$\mathbf{C}$
[Reference Knopp and RobinsKR01, Corollary 2(c)]. Pour tout entier
![]() $N\geqslant 1$
, en notant
$N\geqslant 1$
, en notant
![]() $\unicode[STIX]{x1D701}_{N}=e^{2i\unicode[STIX]{x1D70B}/N}$
, on a les relations suivantes
$\unicode[STIX]{x1D701}_{N}=e^{2i\unicode[STIX]{x1D70B}/N}$
, on a les relations suivantes
 $$\begin{eqnarray}\displaystyle & \displaystyle \mathop{\sum }_{x\in \mathbf{Z}/N\mathbf{Z}}\unicode[STIX]{x1D701}_{N}^{xu}\unicode[STIX]{x1D701}\biggl(\frac{x}{N},s\biggr)=N^{s}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{u}{N},s\biggr), & \displaystyle \nonumber\\ \displaystyle & \mathop{\sum }_{x\in \mathbf{Z}/N\mathbf{Z}}\unicode[STIX]{x1D701}_{N}^{xu}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{x}{N},s\biggr)=N^{1-s}\unicode[STIX]{x1D701}\biggl(-\frac{u}{N},s\biggr). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathop{\sum }_{x\in \mathbf{Z}/N\mathbf{Z}}\unicode[STIX]{x1D701}_{N}^{xu}\unicode[STIX]{x1D701}\biggl(\frac{x}{N},s\biggr)=N^{s}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{u}{N},s\biggr), & \displaystyle \nonumber\\ \displaystyle & \mathop{\sum }_{x\in \mathbf{Z}/N\mathbf{Z}}\unicode[STIX]{x1D701}_{N}^{xu}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{x}{N},s\biggr)=N^{1-s}\unicode[STIX]{x1D701}\biggl(-\frac{u}{N},s\biggr). & \displaystyle \nonumber\end{eqnarray}$$
La formule de Hurwitz [Reference Knopp and RobinsKR01, (2), Corollary 2(b)] est une équation fonctionnelle reliant
![]() $\unicode[STIX]{x1D701}$
et
$\unicode[STIX]{x1D701}$
et
![]() $\hat{\unicode[STIX]{x1D701}}$
,
$\hat{\unicode[STIX]{x1D701}}$
,
Rappelons maintenant les résultats concernant les valeurs spéciales de
![]() $\unicode[STIX]{x1D701}$
et
$\unicode[STIX]{x1D701}$
et
![]() $\hat{\unicode[STIX]{x1D701}}$
aux entiers. Les polynômes de Bernoulli
$\hat{\unicode[STIX]{x1D701}}$
aux entiers. Les polynômes de Bernoulli
![]() $B_{n}(x)$
sont définis par
$B_{n}(x)$
sont définis par
On a
![]() $B_{0}(x)=1$
,
$B_{0}(x)=1$
,
![]() $B_{1}(x)=x-\frac{1}{2}$
,
$B_{1}(x)=x-\frac{1}{2}$
,
![]() $B_{2}(x)=x^{2}-x+\frac{1}{6}$
.
$B_{2}(x)=x^{2}-x+\frac{1}{6}$
.
Pour
![]() $x\in \mathbf{R}$
, on note
$x\in \mathbf{R}$
, on note
![]() $\{x\}=x-\lfloor x\rfloor$
la partie fractionnaire de
$\{x\}=x-\lfloor x\rfloor$
la partie fractionnaire de
![]() $x$
.
$x$
.
Pour
![]() $x\in \mathbf{R}/\mathbf{Z}$
et
$x\in \mathbf{R}/\mathbf{Z}$
et
![]() $n\geqslant 2$
, on a
$n\geqslant 2$
, on a
On en déduit, pour
![]() $x\in \mathbf{R}/\mathbf{Z}$
et
$x\in \mathbf{R}/\mathbf{Z}$
et
![]() $n\geqslant 2$
,
$n\geqslant 2$
,
Pour
![]() $x\in \mathbf{R}/\mathbf{Z}$
, on a
$x\in \mathbf{R}/\mathbf{Z}$
, on a
On déduit de la formule de Hurwitz que pour
![]() $x\in \mathbf{R}/\mathbf{Z}$
,
$x\in \mathbf{R}/\mathbf{Z}$
,
![]() $x\neq 0$
, on a
$x\neq 0$
, on a
Notons les relations suivantes : pour tout
![]() $n\geqslant 1$
et tout
$n\geqslant 1$
et tout
![]() $x\in \mathbf{R}/\mathbf{Z}$
, avec
$x\in \mathbf{R}/\mathbf{Z}$
, avec
![]() $x\neq 0$
si
$x\neq 0$
si
![]() $n=1$
, on a
$n=1$
, on a
Définition 2.2. Pour
![]() $u\in \mathbf{Z}/N\mathbf{Z}$
, définissons les fonctions
$u\in \mathbf{Z}/N\mathbf{Z}$
, définissons les fonctions
![]() $\unicode[STIX]{x1D6FF}_{u},\hat{\unicode[STIX]{x1D6FF}}_{u}:\mathbf{Z}/N\mathbf{Z}\rightarrow \mathbf{C}$
par
$\unicode[STIX]{x1D6FF}_{u},\hat{\unicode[STIX]{x1D6FF}}_{u}:\mathbf{Z}/N\mathbf{Z}\rightarrow \mathbf{C}$
par
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FF}_{u}(n)=\left\{\begin{array}{@{}ll@{}}1\quad & \text{si }n\equiv u\;(\text{mod}\;N),\\ 0\quad & \text{si }n\not \equiv u\;(\text{mod}\;N),\end{array}\right. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \hat{\unicode[STIX]{x1D6FF}}_{u}(n)=\mathop{\sum }_{x\in \mathbf{Z}/N\mathbf{Z}}\unicode[STIX]{x1D6FF}_{u}(x)\unicode[STIX]{x1D701}_{N}^{-xn}=\unicode[STIX]{x1D701}_{N}^{-un}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FF}_{u}(n)=\left\{\begin{array}{@{}ll@{}}1\quad & \text{si }n\equiv u\;(\text{mod}\;N),\\ 0\quad & \text{si }n\not \equiv u\;(\text{mod}\;N),\end{array}\right. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \hat{\unicode[STIX]{x1D6FF}}_{u}(n)=\mathop{\sum }_{x\in \mathbf{Z}/N\mathbf{Z}}\unicode[STIX]{x1D6FF}_{u}(x)\unicode[STIX]{x1D701}_{N}^{-xn}=\unicode[STIX]{x1D701}_{N}^{-un}. & \displaystyle \nonumber\end{eqnarray}$$
3 Séries d’Eisenstein–Kronecker
Nous définissons dans cette section les séries d’Eisenstein–Kronecker classiques [Reference ColmezCol04, § 1.3], [Reference KatoKat04, § 3], [Reference SchoenebergSch74, ch. VII], [Reference WeilWei99, ch. VIII].
Pour
![]() $k\geqslant 0$
un entier,
$k\geqslant 0$
un entier,
![]() $\unicode[STIX]{x1D70F}\in {\mathcal{H}}$
,
$\unicode[STIX]{x1D70F}\in {\mathcal{H}}$
,
![]() $z,u\in \mathbf{C}$
, on pose
$z,u\in \mathbf{C}$
, on pose
 $$\begin{eqnarray}\displaystyle {\mathcal{K}}_{k}(s,\unicode[STIX]{x1D70F},z,u)=\frac{\unicode[STIX]{x1D6E4}(s)}{(-2i\unicode[STIX]{x1D70B})^{k}}\biggl(\frac{\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}}}{2i\unicode[STIX]{x1D70B}}\biggr)^{s-k}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D714}\in \mathbf{Z}+\unicode[STIX]{x1D70F}\mathbf{Z} \\ \unicode[STIX]{x1D714}\neq -z}}\frac{\overline{\unicode[STIX]{x1D714}+z}^{k}}{|\unicode[STIX]{x1D714}+z|^{2s}}\exp \biggl(\frac{2i\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D714}\overline{u}-\overline{\unicode[STIX]{x1D714}}u)}{\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}}}\biggr). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{K}}_{k}(s,\unicode[STIX]{x1D70F},z,u)=\frac{\unicode[STIX]{x1D6E4}(s)}{(-2i\unicode[STIX]{x1D70B})^{k}}\biggl(\frac{\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}}}{2i\unicode[STIX]{x1D70B}}\biggr)^{s-k}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D714}\in \mathbf{Z}+\unicode[STIX]{x1D70F}\mathbf{Z} \\ \unicode[STIX]{x1D714}\neq -z}}\frac{\overline{\unicode[STIX]{x1D714}+z}^{k}}{|\unicode[STIX]{x1D714}+z|^{2s}}\exp \biggl(\frac{2i\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D714}\overline{u}-\overline{\unicode[STIX]{x1D714}}u)}{\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}}}\biggr). & & \displaystyle \nonumber\end{eqnarray}$$
Cette série converge pour
![]() $s\in \mathbf{C}$
,
$s\in \mathbf{C}$
,
![]() $\Re (s)>1+k/2$
, et possède un prolongement méromorphe au plan complexe, holomorphe sur
$\Re (s)>1+k/2$
, et possède un prolongement méromorphe au plan complexe, holomorphe sur
![]() $\mathbf{C}$
sauf éventuellement des pôles simples en
$\mathbf{C}$
sauf éventuellement des pôles simples en
![]() $s=0$
(si
$s=0$
(si
![]() $k=0$
et
$k=0$
et
![]() $z\in \mathbf{Z}+\unicode[STIX]{x1D70F}\mathbf{Z}$
) et en
$z\in \mathbf{Z}+\unicode[STIX]{x1D70F}\mathbf{Z}$
) et en
![]() $s=1$
(si
$s=1$
(si
![]() $k=0$
et
$k=0$
et
![]() $u\in \mathbf{Z}+\unicode[STIX]{x1D70F}\mathbf{Z}$
). La fonction
$u\in \mathbf{Z}+\unicode[STIX]{x1D70F}\mathbf{Z}$
). La fonction
![]() ${\mathcal{K}}_{k}(s,\unicode[STIX]{x1D70F},z,u)$
est périodique en
${\mathcal{K}}_{k}(s,\unicode[STIX]{x1D70F},z,u)$
est périodique en
![]() $u$
de période
$u$
de période
![]() $\mathbf{Z}+\unicode[STIX]{x1D70F}\mathbf{Z}$
, et vérifie
$\mathbf{Z}+\unicode[STIX]{x1D70F}\mathbf{Z}$
, et vérifie
En particulier la fonction
![]() $z\mapsto {\mathcal{K}}_{k}(s,\unicode[STIX]{x1D70F},z,0)$
est
$z\mapsto {\mathcal{K}}_{k}(s,\unicode[STIX]{x1D70F},z,0)$
est
![]() $(\mathbf{Z}+\unicode[STIX]{x1D70F}\mathbf{Z})$
-périodique. La fonction
$(\mathbf{Z}+\unicode[STIX]{x1D70F}\mathbf{Z})$
-périodique. La fonction
![]() ${\mathcal{K}}_{k}$
vérifie l’équation fonctionnelle [Reference WeilWei99, ch. VIII, (32)]
${\mathcal{K}}_{k}$
vérifie l’équation fonctionnelle [Reference WeilWei99, ch. VIII, (32)]
Pour
![]() $k\geqslant 1$
,
$k\geqslant 1$
,
![]() $N\geqslant 1$
un entier,
$N\geqslant 1$
un entier,
![]() $a,b\in \mathbf{Z}/N\mathbf{Z}$
,
$a,b\in \mathbf{Z}/N\mathbf{Z}$
,
![]() $\unicode[STIX]{x1D70F}\in {\mathcal{H}}$
, on pose
$\unicode[STIX]{x1D70F}\in {\mathcal{H}}$
, on pose
Pour
![]() $\unicode[STIX]{x1D70F}\in {\mathcal{H}}$
et
$\unicode[STIX]{x1D70F}\in {\mathcal{H}}$
et
![]() $\unicode[STIX]{x1D6FC}\in \mathbf{Q}_{{>}0}$
, on pose
$\unicode[STIX]{x1D6FC}\in \mathbf{Q}_{{>}0}$
, on pose
![]() $q^{\unicode[STIX]{x1D6FC}}=e^{2i\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70F}}$
.
$q^{\unicode[STIX]{x1D6FC}}=e^{2i\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70F}}$
.
Lemme 3.1. Supposons
![]() $k\geqslant 1$
,
$k\geqslant 1$
,
![]() $k\neq 2$
. La fonction
$k\neq 2$
. La fonction
![]() $E_{a,b}^{(k)}$
est une série d’Eisenstein de poids
$E_{a,b}^{(k)}$
est une série d’Eisenstein de poids
![]() $k$
pour le groupe
$k$
pour le groupe
![]() $\unicode[STIX]{x1D6E4}(N)$
, et son
$\unicode[STIX]{x1D6E4}(N)$
, et son
![]() $q$
-développement est donné par
$q$
-développement est donné par
avec
 $$\begin{eqnarray}\displaystyle a_{0}(E_{a,b}^{(1)})=\left\{\begin{array}{@{}ll@{}}\displaystyle 0\quad & \text{si }a=b=0,\\ \displaystyle \frac{1}{2}\frac{1+\unicode[STIX]{x1D701}_{N}^{b}}{1-\unicode[STIX]{x1D701}_{N}^{b}}\quad & \text{si }a=0\text{ et }b\neq 0,\\ \displaystyle \frac{1}{2}-\biggl\{\frac{a}{N}\biggr\}\quad & \text{si }a\neq 0,\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a_{0}(E_{a,b}^{(1)})=\left\{\begin{array}{@{}ll@{}}\displaystyle 0\quad & \text{si }a=b=0,\\ \displaystyle \frac{1}{2}\frac{1+\unicode[STIX]{x1D701}_{N}^{b}}{1-\unicode[STIX]{x1D701}_{N}^{b}}\quad & \text{si }a=0\text{ et }b\neq 0,\\ \displaystyle \frac{1}{2}-\biggl\{\frac{a}{N}\biggr\}\quad & \text{si }a\neq 0,\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
et pour
![]() $k\geqslant 3$
,
$k\geqslant 3$
,
 $$\begin{eqnarray}\displaystyle a_{0}(E_{a,b}^{(k)})=\left\{\begin{array}{@{}ll@{}}\displaystyle \hat{\unicode[STIX]{x1D701}}\biggl(\frac{b}{N},1-k\biggr)\quad & \text{si }a=0,\\ 0\quad & \text{si }a\neq 0.\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a_{0}(E_{a,b}^{(k)})=\left\{\begin{array}{@{}ll@{}}\displaystyle \hat{\unicode[STIX]{x1D701}}\biggl(\frac{b}{N},1-k\biggr)\quad & \text{si }a=0,\\ 0\quad & \text{si }a\neq 0.\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
Lemme 3.2. Supposons
![]() $k=2$
. La fonction
$k=2$
. La fonction
![]() $E_{a,b}^{(2)}$
est de classe
$E_{a,b}^{(2)}$
est de classe
![]() ${\mathcal{C}}^{\infty }$
sur
${\mathcal{C}}^{\infty }$
sur
![]() ${\mathcal{H}}$
. Elle est modulaire de poids
${\mathcal{H}}$
. Elle est modulaire de poids
![]() $2$
pour le groupe
$2$
pour le groupe
![]() $\unicode[STIX]{x1D6E4}(N)$
, et son développement de Fourier est donné par
$\unicode[STIX]{x1D6E4}(N)$
, et son développement de Fourier est donné par
 $$\begin{eqnarray}\displaystyle E_{a,b}^{(2)}(\unicode[STIX]{x1D70F})=a_{0}(E_{a,b}^{(2)})+\frac{1}{4\unicode[STIX]{x1D70B}\Im (\unicode[STIX]{x1D70F})}+\mathop{\sum }_{\substack{ m,n\geqslant 1 \\ m\equiv a(N)}}n\unicode[STIX]{x1D701}_{N}^{bn}q^{mn/N}+\mathop{\sum }_{\substack{ m,n\geqslant 1 \\ m\equiv -a(N)}}n\unicode[STIX]{x1D701}_{N}^{-bn}q^{mn/N} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{a,b}^{(2)}(\unicode[STIX]{x1D70F})=a_{0}(E_{a,b}^{(2)})+\frac{1}{4\unicode[STIX]{x1D70B}\Im (\unicode[STIX]{x1D70F})}+\mathop{\sum }_{\substack{ m,n\geqslant 1 \\ m\equiv a(N)}}n\unicode[STIX]{x1D701}_{N}^{bn}q^{mn/N}+\mathop{\sum }_{\substack{ m,n\geqslant 1 \\ m\equiv -a(N)}}n\unicode[STIX]{x1D701}_{N}^{-bn}q^{mn/N} & & \displaystyle \nonumber\end{eqnarray}$$
avec
 $$\begin{eqnarray}\displaystyle a_{0}(E_{a,b}^{(2)})=\left\{\begin{array}{@{}ll@{}}\displaystyle \hat{\unicode[STIX]{x1D701}}\biggl(\frac{b}{N},-1\biggr)\quad & \text{si }a=0,\\ \displaystyle -\frac{1}{12}\quad & \text{si }a\neq 0.\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a_{0}(E_{a,b}^{(2)})=\left\{\begin{array}{@{}ll@{}}\displaystyle \hat{\unicode[STIX]{x1D701}}\biggl(\frac{b}{N},-1\biggr)\quad & \text{si }a=0,\\ \displaystyle -\frac{1}{12}\quad & \text{si }a\neq 0.\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
En particulier
![]() $E_{a,b}^{(2)}-E_{0,0}^{(2)}$
est une série d’Eisenstein de poids
$E_{a,b}^{(2)}-E_{0,0}^{(2)}$
est une série d’Eisenstein de poids
![]() $2$
pour le groupe
$2$
pour le groupe
![]() $\unicode[STIX]{x1D6E4}(N)$
.
$\unicode[STIX]{x1D6E4}(N)$
.
Lemme 3.3. Supposons
![]() $k\geqslant 1$
, et
$k\geqslant 1$
, et
![]() $(a,b)\neq (0,0)$
dans le cas
$(a,b)\neq (0,0)$
dans le cas
![]() $k=2$
. La fonction
$k=2$
. La fonction
![]() $F_{a,b}^{(k)}$
est une série d’Eisenstein de poids
$F_{a,b}^{(k)}$
est une série d’Eisenstein de poids
![]() $k$
pour le groupe
$k$
pour le groupe
![]() $\unicode[STIX]{x1D6E4}(N)$
, et son
$\unicode[STIX]{x1D6E4}(N)$
, et son
![]() $q$
-développement est donné par
$q$
-développement est donné par
 $$\begin{eqnarray}\displaystyle F_{a,b}^{(k)}=a_{0}(F_{a,b}^{(k)})+N^{1-k}\biggl(\mathop{\sum }_{\substack{ m,n\geqslant 1 \\ n\equiv a(N)}}\unicode[STIX]{x1D701}_{N}^{bm}n^{k-1}q^{mn/N}+(-1)^{k}\mathop{\sum }_{\substack{ m,n\geqslant 1 \\ n\equiv -a(N)}}\unicode[STIX]{x1D701}_{N}^{-bm}n^{k-1}q^{mn/N}\biggr). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{a,b}^{(k)}=a_{0}(F_{a,b}^{(k)})+N^{1-k}\biggl(\mathop{\sum }_{\substack{ m,n\geqslant 1 \\ n\equiv a(N)}}\unicode[STIX]{x1D701}_{N}^{bm}n^{k-1}q^{mn/N}+(-1)^{k}\mathop{\sum }_{\substack{ m,n\geqslant 1 \\ n\equiv -a(N)}}\unicode[STIX]{x1D701}_{N}^{-bm}n^{k-1}q^{mn/N}\biggr). & & \displaystyle \nonumber\end{eqnarray}$$
avec
 $$\begin{eqnarray}\displaystyle a_{0}(F_{a,b}^{(1)})=\left\{\begin{array}{@{}ll@{}}\displaystyle 0\quad & \text{si }a=b=0,\\ \displaystyle \frac{1}{2}\frac{1+\unicode[STIX]{x1D701}_{N}^{b}}{1-\unicode[STIX]{x1D701}_{N}^{b}}\quad & \text{si }a=0\text{ et }b\neq 0,\\ \displaystyle \frac{1}{2}-\biggl\{\frac{a}{N}\biggr\}\quad & \text{si }a\neq 0,\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a_{0}(F_{a,b}^{(1)})=\left\{\begin{array}{@{}ll@{}}\displaystyle 0\quad & \text{si }a=b=0,\\ \displaystyle \frac{1}{2}\frac{1+\unicode[STIX]{x1D701}_{N}^{b}}{1-\unicode[STIX]{x1D701}_{N}^{b}}\quad & \text{si }a=0\text{ et }b\neq 0,\\ \displaystyle \frac{1}{2}-\biggl\{\frac{a}{N}\biggr\}\quad & \text{si }a\neq 0,\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
et pour
![]() $k\geqslant 2$
,
$k\geqslant 2$
,
Lemme 3.4 [Reference KatoKat04, Lemma 3.7(1)(iii)].
Soit
![]() $k\geqslant 1$
un entier. Soit
$k\geqslant 1$
un entier. Soit
![]() $(a,b)\in (\mathbf{Z}/N\mathbf{Z})^{2}$
, avec
$(a,b)\in (\mathbf{Z}/N\mathbf{Z})^{2}$
, avec
![]() $(a,b)\neq (0,0)$
dans le cas
$(a,b)\neq (0,0)$
dans le cas
![]() $k=2$
. Alors pour tout
$k=2$
. Alors pour tout
![]() $g\in \text{SL}_{2}(\mathbf{Z})$
, on a
$g\in \text{SL}_{2}(\mathbf{Z})$
, on a
![]() $F_{a,b}^{(k)}|_{k}g=F_{(a,b)g}^{(k)}$
.
$F_{a,b}^{(k)}|_{k}g=F_{(a,b)g}^{(k)}$
.
Nous allons maintenant définir des séries d’Eisenstein dont le
![]() $q$
-développement est rationnel.
$q$
-développement est rationnel.
Définition 3.5. Pour
![]() $k\geqslant 1$
,
$k\geqslant 1$
,
![]() $a,b\in \mathbf{Z}/N\mathbf{Z}$
, on pose
$a,b\in \mathbf{Z}/N\mathbf{Z}$
, on pose
avec
 $$\begin{eqnarray}\displaystyle a_{0}(G_{a,b}^{(1)})=\left\{\begin{array}{@{}ll@{}}\displaystyle 0\quad & \text{si }a=b=0,\\ \displaystyle \frac{1}{2}-\biggl\{\frac{b}{N}\biggr\}\quad & \text{si }a=0\text{ et }b\neq 0,\\ \displaystyle \frac{1}{2}-\biggl\{\frac{a}{N}\biggr\}\quad & \text{si }a\neq 0\text{ et }b=0,\\ \displaystyle 0\quad & \text{si }a\neq 0\text{et }b\neq 0,\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a_{0}(G_{a,b}^{(1)})=\left\{\begin{array}{@{}ll@{}}\displaystyle 0\quad & \text{si }a=b=0,\\ \displaystyle \frac{1}{2}-\biggl\{\frac{b}{N}\biggr\}\quad & \text{si }a=0\text{ et }b\neq 0,\\ \displaystyle \frac{1}{2}-\biggl\{\frac{a}{N}\biggr\}\quad & \text{si }a\neq 0\text{ et }b=0,\\ \displaystyle 0\quad & \text{si }a\neq 0\text{et }b\neq 0,\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
et pour
![]() $k\geqslant 2$
,
$k\geqslant 2$
,
 $$\begin{eqnarray}\displaystyle a_{0}(G_{a,b}^{(k)})=\left\{\begin{array}{@{}ll@{}}\displaystyle -N^{k-1}\frac{B_{k}(\{a/N\})}{k}\quad & \text{si }b=0,\\ \displaystyle 0\quad & \text{si }b\neq 0.\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a_{0}(G_{a,b}^{(k)})=\left\{\begin{array}{@{}ll@{}}\displaystyle -N^{k-1}\frac{B_{k}(\{a/N\})}{k}\quad & \text{si }b=0,\\ \displaystyle 0\quad & \text{si }b\neq 0.\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
Lemme 3.6. Soit
![]() $k\geqslant 1$
, avec
$k\geqslant 1$
, avec
![]() $a\neq 0$
si
$a\neq 0$
si
![]() $k=2$
. Alors la fonction
$k=2$
. Alors la fonction
![]() $G_{a,b}^{(k)}(\unicode[STIX]{x1D70F}/N)$
est modulaire de poids
$G_{a,b}^{(k)}(\unicode[STIX]{x1D70F}/N)$
est modulaire de poids
![]() $k$
pour
$k$
pour
![]() $\unicode[STIX]{x1D6E4}(N)$
.
$\unicode[STIX]{x1D6E4}(N)$
.
Démonstration.
On vérifie l’identité
Par inversion de Fourier, il vient
Le résultat suit alors du lemme 3.3. ◻
Lemme 3.7. Si
![]() $G(\unicode[STIX]{x1D70F}/N)$
est modulaire de poids
$G(\unicode[STIX]{x1D70F}/N)$
est modulaire de poids
![]() $k$
pour le groupe
$k$
pour le groupe
![]() $\unicode[STIX]{x1D6E4}(N)$
, alors
$\unicode[STIX]{x1D6E4}(N)$
, alors
![]() $G(\unicode[STIX]{x1D70F})$
est modulaire de poids
$G(\unicode[STIX]{x1D70F})$
est modulaire de poids
![]() $k$
pour le groupe
$k$
pour le groupe
![]() $\unicode[STIX]{x1D6E4}_{1}(N^{2})$
.
$\unicode[STIX]{x1D6E4}_{1}(N^{2})$
.
Démonstration.
Cela résulte de l’inclusion
![]() $\big(\!\begin{smallmatrix}N & 0\\ 0 & 1\end{smallmatrix}\!\big)\unicode[STIX]{x1D6E4}_{1}(N^{2})\big(\!\begin{smallmatrix}N & 0\\ 0 & 1\end{smallmatrix}\!\big)^{-1}\subset \unicode[STIX]{x1D6E4}(N)$
.◻
$\big(\!\begin{smallmatrix}N & 0\\ 0 & 1\end{smallmatrix}\!\big)\unicode[STIX]{x1D6E4}_{1}(N^{2})\big(\!\begin{smallmatrix}N & 0\\ 0 & 1\end{smallmatrix}\!\big)^{-1}\subset \unicode[STIX]{x1D6E4}(N)$
.◻
On en déduit le lemme suivant.
Lemme 3.8. Soit
![]() $k\geqslant 1$
, avec
$k\geqslant 1$
, avec
![]() $a\neq 0$
si
$a\neq 0$
si
![]() $k=2$
. Alors
$k=2$
. Alors
![]() $G_{a,b}^{(k)}$
est une forme modulaire de poids
$G_{a,b}^{(k)}$
est une forme modulaire de poids
![]() $k$
pour
$k$
pour
![]() $\unicode[STIX]{x1D6E4}_{1}(N^{2})$
.
$\unicode[STIX]{x1D6E4}_{1}(N^{2})$
.
Rappelons que l’involution d’Atkin–Lehner
![]() $W_{N}$
sur
$W_{N}$
sur
![]() $M_{k}(\unicode[STIX]{x1D6E4}_{1}(N))$
est définie par
$M_{k}(\unicode[STIX]{x1D6E4}_{1}(N))$
est définie par
Définition 3.9. Pour
![]() $k\geqslant 1$
,
$k\geqslant 1$
,
![]() $a,b\in \mathbf{Z}/N\mathbf{Z}$
, on pose
$a,b\in \mathbf{Z}/N\mathbf{Z}$
, on pose
avec
 $$\begin{eqnarray}\displaystyle a_{0}(H_{a,b}^{(1)})=\left\{\begin{array}{@{}ll@{}}\displaystyle 0\quad & \text{si }a=b=0,\\ \displaystyle -\frac{1}{2}\frac{1+\unicode[STIX]{x1D701}_{N}^{b}}{1-\unicode[STIX]{x1D701}_{N}^{b}}\quad & \text{si }a=0\text{ et }b\neq 0,\\ \displaystyle -\frac{1}{2}\frac{1+\unicode[STIX]{x1D701}_{N}^{a}}{1-\unicode[STIX]{x1D701}_{N}^{a}}\quad & \text{si }a\neq 0\text{ et }b=0,\\ \displaystyle -\frac{1}{2}\biggl(\frac{1+\unicode[STIX]{x1D701}_{N}^{a}}{1-\unicode[STIX]{x1D701}_{N}^{a}}+\frac{1+\unicode[STIX]{x1D701}_{N}^{b}}{1-\unicode[STIX]{x1D701}_{N}^{b}}\biggr)\quad & \text{si }a\neq 0\text{ et }b\neq 0,\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a_{0}(H_{a,b}^{(1)})=\left\{\begin{array}{@{}ll@{}}\displaystyle 0\quad & \text{si }a=b=0,\\ \displaystyle -\frac{1}{2}\frac{1+\unicode[STIX]{x1D701}_{N}^{b}}{1-\unicode[STIX]{x1D701}_{N}^{b}}\quad & \text{si }a=0\text{ et }b\neq 0,\\ \displaystyle -\frac{1}{2}\frac{1+\unicode[STIX]{x1D701}_{N}^{a}}{1-\unicode[STIX]{x1D701}_{N}^{a}}\quad & \text{si }a\neq 0\text{ et }b=0,\\ \displaystyle -\frac{1}{2}\biggl(\frac{1+\unicode[STIX]{x1D701}_{N}^{a}}{1-\unicode[STIX]{x1D701}_{N}^{a}}+\frac{1+\unicode[STIX]{x1D701}_{N}^{b}}{1-\unicode[STIX]{x1D701}_{N}^{b}}\biggr)\quad & \text{si }a\neq 0\text{ et }b\neq 0,\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
et pour
![]() $k\geqslant 2$
,
$k\geqslant 2$
,
Notons l’identité
![]() $H_{-a,-b}^{(k)}=(-1)^{k}H_{a,b}^{(k)}$
.
$H_{-a,-b}^{(k)}=(-1)^{k}H_{a,b}^{(k)}$
.
Lemme 3.10. Soit
![]() $k\geqslant 1$
,
$k\geqslant 1$
,
![]() $a,b\in \mathbf{Z}/N\mathbf{Z}$
. Dans le cas
$a,b\in \mathbf{Z}/N\mathbf{Z}$
. Dans le cas
![]() $k=2$
, supposons
$k=2$
, supposons
![]() $a\neq 0$
. Alors
$a\neq 0$
. Alors
En particulier
![]() $H_{a,b}^{(k)}$
est une forme modulaire de poids
$H_{a,b}^{(k)}$
est une forme modulaire de poids
![]() $k$
pour
$k$
pour
![]() $\unicode[STIX]{x1D6E4}_{1}(N^{2})$
.
$\unicode[STIX]{x1D6E4}_{1}(N^{2})$
.
Démonstration.
Le cas
![]() $k=1$
est traité dans [Reference BrunaultBru16, Lemma 13]. Supposons donc
$k=1$
est traité dans [Reference BrunaultBru16, Lemma 13]. Supposons donc
![]() $k\geqslant 2$
, avec
$k\geqslant 2$
, avec
![]() $a\neq 0$
si
$a\neq 0$
si
![]() $k=2$
. Par définition, on a
$k=2$
. Par définition, on a
 $$\begin{eqnarray}\displaystyle W_{N^{2}}(G_{a,b}^{(k)})(\unicode[STIX]{x1D70F}) & = & \displaystyle i^{k}N^{-k}\unicode[STIX]{x1D70F}^{-k}G_{a,b}^{(k)}\biggl(-\frac{1}{N^{2}\unicode[STIX]{x1D70F}}\biggr)\nonumber\\ \displaystyle & = & \displaystyle i^{k}N^{-k}\unicode[STIX]{x1D70F}^{-k}N^{k-2}\mathop{\sum }_{c\in \mathbf{Z}/N\mathbf{Z}}\unicode[STIX]{x1D701}_{N}^{-bc}F_{a,c}^{(k)}\biggl(-\frac{1}{N\unicode[STIX]{x1D70F}}\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle W_{N^{2}}(G_{a,b}^{(k)})(\unicode[STIX]{x1D70F}) & = & \displaystyle i^{k}N^{-k}\unicode[STIX]{x1D70F}^{-k}G_{a,b}^{(k)}\biggl(-\frac{1}{N^{2}\unicode[STIX]{x1D70F}}\biggr)\nonumber\\ \displaystyle & = & \displaystyle i^{k}N^{-k}\unicode[STIX]{x1D70F}^{-k}N^{k-2}\mathop{\sum }_{c\in \mathbf{Z}/N\mathbf{Z}}\unicode[STIX]{x1D701}_{N}^{-bc}F_{a,c}^{(k)}\biggl(-\frac{1}{N\unicode[STIX]{x1D70F}}\biggr).\nonumber\end{eqnarray}$$
D’après le lemme 3.4, il vient
 $$\begin{eqnarray}\displaystyle W_{N^{2}}(G_{a,b}^{(k)})(\unicode[STIX]{x1D70F}) & = & \displaystyle i^{k}N^{-k}\unicode[STIX]{x1D70F}^{-k}N^{k-2}\mathop{\sum }_{c\in \mathbf{Z}/N\mathbf{Z}}\unicode[STIX]{x1D701}_{N}^{-bc}(N\unicode[STIX]{x1D70F})^{k}F_{c,-a}^{(k)}(N\unicode[STIX]{x1D70F})\nonumber\\ \displaystyle & = & \displaystyle i^{k}N^{k-2}\mathop{\sum }_{c\in \mathbf{Z}/N\mathbf{Z}}\unicode[STIX]{x1D701}_{N}^{-bc}F_{c,-a}^{(k)}(N\unicode[STIX]{x1D70F}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle W_{N^{2}}(G_{a,b}^{(k)})(\unicode[STIX]{x1D70F}) & = & \displaystyle i^{k}N^{-k}\unicode[STIX]{x1D70F}^{-k}N^{k-2}\mathop{\sum }_{c\in \mathbf{Z}/N\mathbf{Z}}\unicode[STIX]{x1D701}_{N}^{-bc}(N\unicode[STIX]{x1D70F})^{k}F_{c,-a}^{(k)}(N\unicode[STIX]{x1D70F})\nonumber\\ \displaystyle & = & \displaystyle i^{k}N^{k-2}\mathop{\sum }_{c\in \mathbf{Z}/N\mathbf{Z}}\unicode[STIX]{x1D701}_{N}^{-bc}F_{c,-a}^{(k)}(N\unicode[STIX]{x1D70F}).\nonumber\end{eqnarray}$$
En utilisant le développement de Fourier de
![]() $F^{(k)}$
(lemme 3.3), on obtient
$F^{(k)}$
(lemme 3.3), on obtient
 $$\begin{eqnarray}\displaystyle W_{N^{2}}(G_{a,b}^{(k)})(\unicode[STIX]{x1D70F}) & = & \displaystyle i^{k}N^{k-2}\mathop{\sum }_{c\in \mathbf{Z}/N\mathbf{Z}}\unicode[STIX]{x1D701}_{N}^{-bc}a_{0}(F_{c,-a}^{(k)})\nonumber\\ \displaystyle & & \displaystyle +\,i^{k}N^{k-2}\mathop{\sum }_{c\in \mathbf{Z}/N\mathbf{Z}}\unicode[STIX]{x1D701}_{N}^{-bc}N^{1-k}\mathop{\sum }_{m,n\geqslant 1}(\hat{\unicode[STIX]{x1D6FF}}_{a}(m)\unicode[STIX]{x1D6FF}_{c}(n)+(-1)^{k}\hat{\unicode[STIX]{x1D6FF}}_{-a}(m)\unicode[STIX]{x1D6FF}_{-c}(n))n^{k-1}q^{mn}\nonumber\\ \displaystyle & = & \displaystyle i^{k}N^{k-2}\mathop{\sum }_{c\in \mathbf{Z}/N\mathbf{Z}}\unicode[STIX]{x1D701}_{N}^{-bc}\unicode[STIX]{x1D701}\biggl(\frac{c}{N},1-k\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{i^{k}}{N}\mathop{\sum }_{m,n\geqslant 1}(\hat{\unicode[STIX]{x1D6FF}}_{a}(m)\hat{\unicode[STIX]{x1D6FF}}_{b}(n)+(-1)^{k}\hat{\unicode[STIX]{x1D6FF}}_{-a}(m)\hat{\unicode[STIX]{x1D6FF}}_{-b}(n))n^{k-1}q^{mn}\nonumber\\ \displaystyle & = & \displaystyle \frac{i^{k}}{N}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b}{N},1-k\biggr)+\mathop{\sum }_{m,n\geqslant 1}(\hat{\unicode[STIX]{x1D6FF}}_{a}(m)\hat{\unicode[STIX]{x1D6FF}}_{b}(n)+(-1)^{k}\hat{\unicode[STIX]{x1D6FF}}_{-a}(m)\hat{\unicode[STIX]{x1D6FF}}_{-b}(n))n^{k-1}q^{mn}\biggr).\Box \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle W_{N^{2}}(G_{a,b}^{(k)})(\unicode[STIX]{x1D70F}) & = & \displaystyle i^{k}N^{k-2}\mathop{\sum }_{c\in \mathbf{Z}/N\mathbf{Z}}\unicode[STIX]{x1D701}_{N}^{-bc}a_{0}(F_{c,-a}^{(k)})\nonumber\\ \displaystyle & & \displaystyle +\,i^{k}N^{k-2}\mathop{\sum }_{c\in \mathbf{Z}/N\mathbf{Z}}\unicode[STIX]{x1D701}_{N}^{-bc}N^{1-k}\mathop{\sum }_{m,n\geqslant 1}(\hat{\unicode[STIX]{x1D6FF}}_{a}(m)\unicode[STIX]{x1D6FF}_{c}(n)+(-1)^{k}\hat{\unicode[STIX]{x1D6FF}}_{-a}(m)\unicode[STIX]{x1D6FF}_{-c}(n))n^{k-1}q^{mn}\nonumber\\ \displaystyle & = & \displaystyle i^{k}N^{k-2}\mathop{\sum }_{c\in \mathbf{Z}/N\mathbf{Z}}\unicode[STIX]{x1D701}_{N}^{-bc}\unicode[STIX]{x1D701}\biggl(\frac{c}{N},1-k\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{i^{k}}{N}\mathop{\sum }_{m,n\geqslant 1}(\hat{\unicode[STIX]{x1D6FF}}_{a}(m)\hat{\unicode[STIX]{x1D6FF}}_{b}(n)+(-1)^{k}\hat{\unicode[STIX]{x1D6FF}}_{-a}(m)\hat{\unicode[STIX]{x1D6FF}}_{-b}(n))n^{k-1}q^{mn}\nonumber\\ \displaystyle & = & \displaystyle \frac{i^{k}}{N}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b}{N},1-k\biggr)+\mathop{\sum }_{m,n\geqslant 1}(\hat{\unicode[STIX]{x1D6FF}}_{a}(m)\hat{\unicode[STIX]{x1D6FF}}_{b}(n)+(-1)^{k}\hat{\unicode[STIX]{x1D6FF}}_{-a}(m)\hat{\unicode[STIX]{x1D6FF}}_{-b}(n))n^{k-1}q^{mn}\biggr).\Box \nonumber\end{eqnarray}$$
Dans le cas du poids
![]() $2$
, on a également les résultats suivants.
$2$
, on a également les résultats suivants.
Lemme 3.11. Soient
![]() $b,b^{\prime }\in \mathbf{Z}/N\mathbf{Z}$
. La fonction
$b,b^{\prime }\in \mathbf{Z}/N\mathbf{Z}$
. La fonction
![]() $G_{0,b^{\prime }}^{(2)}(\unicode[STIX]{x1D70F}/N)-G_{0,b}^{(2)}(\unicode[STIX]{x1D70F}/N)$
est une forme modulaire de poids
$G_{0,b^{\prime }}^{(2)}(\unicode[STIX]{x1D70F}/N)-G_{0,b}^{(2)}(\unicode[STIX]{x1D70F}/N)$
est une forme modulaire de poids
![]() $2$
pour
$2$
pour
![]() $\unicode[STIX]{x1D6E4}(N)$
. En particulier
$\unicode[STIX]{x1D6E4}(N)$
. En particulier
![]() $G_{0,b^{\prime }}^{(2)}-G_{0,b}^{(2)}$
est modulaire pour
$G_{0,b^{\prime }}^{(2)}-G_{0,b}^{(2)}$
est modulaire pour
![]() $\unicode[STIX]{x1D6E4}_{1}(N^{2})$
. De plus on a
$\unicode[STIX]{x1D6E4}_{1}(N^{2})$
. De plus on a
En particulier
![]() $H_{0,b^{\prime }}^{(2)}-H_{0,b}^{(2)}$
est une forme modulaire de poids
$H_{0,b^{\prime }}^{(2)}-H_{0,b}^{(2)}$
est une forme modulaire de poids
![]() $2$
pour
$2$
pour
![]() $\unicode[STIX]{x1D6E4}_{1}(N^{2})$
.
$\unicode[STIX]{x1D6E4}_{1}(N^{2})$
.
Démonstration.
Le caractère modulaire de
![]() $G_{0,b^{\prime }}^{(2)}-G_{0,b}^{(2)}$
résulte de la formule explicite
$G_{0,b^{\prime }}^{(2)}-G_{0,b}^{(2)}$
résulte de la formule explicite
 $$\begin{eqnarray}\displaystyle G_{0,b^{\prime }}^{(2)}(\unicode[STIX]{x1D70F}/N)-G_{0,b}^{(2)}(\unicode[STIX]{x1D70F}/N)=\mathop{\sum }_{\substack{ c\in \mathbf{Z}/N\mathbf{Z} \\ c\neq 0}}(\unicode[STIX]{x1D701}_{N}^{-b^{\prime }c}-\unicode[STIX]{x1D701}_{N}^{-bc})F_{0,c}^{(2)}(\unicode[STIX]{x1D70F}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle G_{0,b^{\prime }}^{(2)}(\unicode[STIX]{x1D70F}/N)-G_{0,b}^{(2)}(\unicode[STIX]{x1D70F}/N)=\mathop{\sum }_{\substack{ c\in \mathbf{Z}/N\mathbf{Z} \\ c\neq 0}}(\unicode[STIX]{x1D701}_{N}^{-b^{\prime }c}-\unicode[STIX]{x1D701}_{N}^{-bc})F_{0,c}^{(2)}(\unicode[STIX]{x1D70F}). & & \displaystyle \nonumber\end{eqnarray}$$
Pour terminer cette section, nous déterminons la fonction
![]() $L$
associée à
$L$
associée à
![]() $H_{a,b}^{(k)}$
(voir [Reference KatoKat04, 3.10] pour le cas des séries
$H_{a,b}^{(k)}$
(voir [Reference KatoKat04, 3.10] pour le cas des séries
![]() $E_{a,b}^{(k)}$
et
$E_{a,b}^{(k)}$
et
![]() $F_{a,b}^{(k)}$
).
$F_{a,b}^{(k)}$
).
Rappelons que si
![]() $f=\sum _{n=0}^{\infty }a_{n}(f)q^{n}$
est une forme modulaire de poids
$f=\sum _{n=0}^{\infty }a_{n}(f)q^{n}$
est une forme modulaire de poids
![]() $k\geqslant 1$
pour
$k\geqslant 1$
pour
![]() $\unicode[STIX]{x1D6E4}_{1}(N)$
, alors la fonction
$\unicode[STIX]{x1D6E4}_{1}(N)$
, alors la fonction
![]() $L$
de
$L$
de
![]() $f$
est définie par
$f$
est définie par
![]() $L(f,s)=\sum _{n=1}^{\infty }a_{n}(f)n^{-s}$
pour
$L(f,s)=\sum _{n=1}^{\infty }a_{n}(f)n^{-s}$
pour
![]() $\Re (s)>k$
.
$\Re (s)>k$
.
Définition 3.12. Pour
![]() $f\in M_{k}(\unicode[STIX]{x1D6E4}_{1}(N))$
, on pose
$f\in M_{k}(\unicode[STIX]{x1D6E4}_{1}(N))$
, on pose
![]() $f^{\ast }=f-a_{0}(f)$
.
$f^{\ast }=f-a_{0}(f)$
.
La fonction
![]() $L$
complétée de
$L$
complétée de
![]() $f$
est définie par
$f$
est définie par
Elle se prolonge en une fonction méromorphe sur
![]() $\mathbf{C}$
qui vérifie l’équation fonctionnelle
$\mathbf{C}$
qui vérifie l’équation fonctionnelle
De plus, la fonction
![]() $\unicode[STIX]{x1D6EC}(f,s)+a_{0}(f)/s+a_{0}(W_{N}f)/(k-s)$
est holomorphe sur
$\unicode[STIX]{x1D6EC}(f,s)+a_{0}(f)/s+a_{0}(W_{N}f)/(k-s)$
est holomorphe sur
![]() $\mathbf{C}$
[Reference MiyakeMiy06, Theorem 4.3.5].
$\mathbf{C}$
[Reference MiyakeMiy06, Theorem 4.3.5].
Définition 3.13. Les valeurs régularisées de
![]() $\unicode[STIX]{x1D6EC}(f,s)$
en
$\unicode[STIX]{x1D6EC}(f,s)$
en
![]() $s=0$
et
$s=0$
et
![]() $s=k$
sont définies par
$s=k$
sont définies par
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6EC}^{\ast }(f,0):=\lim _{s\rightarrow 0}\biggl(\unicode[STIX]{x1D6EC}(f,s)+\frac{a_{0}(f)}{s}\biggr), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6EC}^{\ast }(f,k):=\lim _{s\rightarrow k}\biggl(\unicode[STIX]{x1D6EC}(f,s)+\frac{a_{0}(W_{N}f)}{k-s}\biggr). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6EC}^{\ast }(f,0):=\lim _{s\rightarrow 0}\biggl(\unicode[STIX]{x1D6EC}(f,s)+\frac{a_{0}(f)}{s}\biggr), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6EC}^{\ast }(f,k):=\lim _{s\rightarrow k}\biggl(\unicode[STIX]{x1D6EC}(f,s)+\frac{a_{0}(W_{N}f)}{k-s}\biggr). & \displaystyle \nonumber\end{eqnarray}$$
Notons que
![]() $\unicode[STIX]{x1D6EC}^{\ast }(f,k)=\unicode[STIX]{x1D6EC}^{\ast }(W_{N}f,0)$
pour tout
$\unicode[STIX]{x1D6EC}^{\ast }(f,k)=\unicode[STIX]{x1D6EC}^{\ast }(W_{N}f,0)$
pour tout
![]() $f\in M_{k}(\unicode[STIX]{x1D6E4}_{1}(N))$
.
$f\in M_{k}(\unicode[STIX]{x1D6E4}_{1}(N))$
.
Lemme 3.14. Soit
![]() $k\geqslant 1$
et
$k\geqslant 1$
et
![]() $a,b\in \mathbf{Z}/N\mathbf{Z}$
, avec
$a,b\in \mathbf{Z}/N\mathbf{Z}$
, avec
![]() $a\neq 0$
si
$a\neq 0$
si
![]() $k=2$
. Alors
$k=2$
. Alors
Dans le cas
![]() $k=2$
, soient
$k=2$
, soient
![]() $b,b^{\prime }\in \mathbf{Z}/N\mathbf{Z}$
. Alors
$b,b^{\prime }\in \mathbf{Z}/N\mathbf{Z}$
. Alors
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EC}(H_{0,b^{\prime }}^{(2)}-H_{0,b}^{(2)},s) & = & \displaystyle N^{s}(2\unicode[STIX]{x1D70B})^{-s}\unicode[STIX]{x1D6E4}(s)\unicode[STIX]{x1D701}(s)(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b^{\prime }}{N},s-1\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b^{\prime }}{N},s-1\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b}{N},s-1\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b}{N},s-1\biggr)\!).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EC}(H_{0,b^{\prime }}^{(2)}-H_{0,b}^{(2)},s) & = & \displaystyle N^{s}(2\unicode[STIX]{x1D70B})^{-s}\unicode[STIX]{x1D6E4}(s)\unicode[STIX]{x1D701}(s)(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b^{\prime }}{N},s-1\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b^{\prime }}{N},s-1\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b}{N},s-1\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b}{N},s-1\biggr)\!).\nonumber\end{eqnarray}$$
Démonstration.
Cela résulte des définitions. ◻
4 Cycles de Shokurov
Soit
![]() $N\geqslant 3$
un entier. Soit
$N\geqslant 3$
un entier. Soit
![]() $Y(N)$
le courbe modulaire de niveau
$Y(N)$
le courbe modulaire de niveau
![]() $N$
définie sur
$N$
définie sur
![]() $\mathbf{Q}$
, et soit
$\mathbf{Q}$
, et soit
![]() $E$
la courbe elliptique universelle au-dessus de
$E$
la courbe elliptique universelle au-dessus de
![]() $Y(N)$
. Fixons un entier
$Y(N)$
. Fixons un entier
![]() $n\geqslant 0$
. Notons
$n\geqslant 0$
. Notons
![]() $E^{n}$
la puissance fibrée
$E^{n}$
la puissance fibrée
![]() $n$
-ième de
$n$
-ième de
![]() $E$
au-dessus de
$E$
au-dessus de
![]() $Y(N)$
. C’est une variété abélienne de dimension relative
$Y(N)$
. C’est une variété abélienne de dimension relative
![]() $n$
sur
$n$
sur
![]() $Y(N)$
. Les points complexes de
$Y(N)$
. Les points complexes de
![]() $E^{n}$
sont décrits par l’isomorphisme [Reference DeningerDen97, (3.6)]
$E^{n}$
sont décrits par l’isomorphisme [Reference DeningerDen97, (3.6)]
On note
![]() $\unicode[STIX]{x1D70E}=\big(\!\begin{smallmatrix}0 & -1\\ 1 & 0\end{smallmatrix}\!\big)$
. Pour tout entier
$\unicode[STIX]{x1D70E}=\big(\!\begin{smallmatrix}0 & -1\\ 1 & 0\end{smallmatrix}\!\big)$
. Pour tout entier
![]() $0\leqslant j\leqslant n$
, on définit le cycle de Shokurov
$0\leqslant j\leqslant n$
, on définit le cycle de Shokurov
C’est un
![]() $(n+1)$
-cycle sur
$(n+1)$
-cycle sur
![]() $E^{n}(\mathbf{C})$
, muni de l’orientation produit. Il est naturellement fibré au-dessus du symbole modulaire
$E^{n}(\mathbf{C})$
, muni de l’orientation produit. Il est naturellement fibré au-dessus du symbole modulaire
![]() $\{0,\infty \}$
. Notons
$\{0,\infty \}$
. Notons
![]() $f_{j}:X^{j}Y^{n-j}\{0,\infty \}\rightarrow \{0,\infty \}$
cette fibration.
$f_{j}:X^{j}Y^{n-j}\{0,\infty \}\rightarrow \{0,\infty \}$
cette fibration.
Définition 4.1. Pour
![]() $y>0$
, on note
$y>0$
, on note
![]() $\unicode[STIX]{x1D6FE}_{y,j}$
la fibre de
$\unicode[STIX]{x1D6FE}_{y,j}$
la fibre de
![]() $f_{j}$
au-dessus du point
$f_{j}$
au-dessus du point
![]() $iy$
.
$iy$
.
On a donc
5 Symbole d’Eisenstein
On note
![]() $X(N)$
la compactification de
$X(N)$
la compactification de
![]() $Y(N)$
, et on note
$Y(N)$
, et on note
![]() $X^{\infty }=X(N)-Y(N)$
l’ensemble des pointes de
$X^{\infty }=X(N)-Y(N)$
l’ensemble des pointes de
![]() $X(N)$
, vu comme sous-schéma fermé de
$X(N)$
, vu comme sous-schéma fermé de
![]() $X(N)$
. On a une bijection
$X(N)$
. On a une bijection
où
![]() $P$
est le sous-groupe algébrique de
$P$
est le sous-groupe algébrique de
![]() $\text{SL}_{2}$
formé des matrices de la forme
$\text{SL}_{2}$
formé des matrices de la forme
![]() $\pm \big(\!\begin{smallmatrix}1 & \ast \\ 0 & 1\end{smallmatrix}\!\big)$
. Pour tout entier
$\pm \big(\!\begin{smallmatrix}1 & \ast \\ 0 & 1\end{smallmatrix}\!\big)$
. Pour tout entier
![]() $n\geqslant 0$
, on définit
$n\geqslant 0$
, on définit
Ce groupe est (non canoniquement) isomorphe au groupe des diviseurs sur
![]() $X^{\infty }$
.
$X^{\infty }$
.
Fixons un entier
![]() $n\geqslant 0$
. On dispose d’une application résidu
$n\geqslant 0$
. On dispose d’une application résidu
généralisant l’application diviseur pour
![]() $n=0$
. Notons
$n=0$
. Notons
![]() $V_{0}$
le sous-groupe de
$V_{0}$
le sous-groupe de
![]() $\mathbf{Q}[X^{\infty }]^{(0)}$
formé des diviseurs de degré
$\mathbf{Q}[X^{\infty }]^{(0)}$
formé des diviseurs de degré
![]() $0$
, et notons
$0$
, et notons
![]() $V_{n}=\mathbf{Q}[X^{\infty }]^{(n)}$
pour
$V_{n}=\mathbf{Q}[X^{\infty }]^{(n)}$
pour
![]() $n\geqslant 1$
. L’image de l’application
$n\geqslant 1$
. L’image de l’application
![]() $\text{Res}^{n}$
est égale à
$\text{Res}^{n}$
est égale à
![]() $V_{n}$
(généralisation du théorème de Manin–Drinfeld). Le symbole d’Eisenstein, construit par Beilinson, est une application canonique
$V_{n}$
(généralisation du théorème de Manin–Drinfeld). Le symbole d’Eisenstein, construit par Beilinson, est une application canonique
telle que ![]()
Notons
![]() $\unicode[STIX]{x1D714}^{n}:\mathbf{Q}[(\mathbf{Z}/N\mathbf{Z})^{2}]\rightarrow \mathbf{Q}[X^{\infty }]^{(n)}$
l’application horosphérique, définie par
$\unicode[STIX]{x1D714}^{n}:\mathbf{Q}[(\mathbf{Z}/N\mathbf{Z})^{2}]\rightarrow \mathbf{Q}[X^{\infty }]^{(n)}$
l’application horosphérique, définie par
Dans le cas
![]() $n=0$
, l’application
$n=0$
, l’application
![]() $\unicode[STIX]{x1D714}^{0}$
induit une surjection de
$\unicode[STIX]{x1D714}^{0}$
induit une surjection de
![]() $\mathbf{Q}[(\mathbf{Z}/N\mathbf{Z})^{2}\backslash \{0\}]$
dans
$\mathbf{Q}[(\mathbf{Z}/N\mathbf{Z})^{2}\backslash \{0\}]$
dans
![]() $V_{0}$
; dans le cas
$V_{0}$
; dans le cas
![]() $n\geqslant 1$
, l’application
$n\geqslant 1$
, l’application
![]() $\unicode[STIX]{x1D714}^{n}$
est surjective [Reference Schappacher and SchollSS91, 7.5] (la preuve donnée dans cet article marche également pour
$\unicode[STIX]{x1D714}^{n}$
est surjective [Reference Schappacher and SchollSS91, 7.5] (la preuve donnée dans cet article marche également pour
![]() $n=0$
).
$n=0$
).
Définition 5.1. Soit
![]() $u\in (\mathbf{Z}/N\mathbf{Z})^{2}$
. Dans le cas
$u\in (\mathbf{Z}/N\mathbf{Z})^{2}$
. Dans le cas
![]() $n=0$
, on suppose
$n=0$
, on suppose
![]() $u\neq 0$
. On définit
$u\neq 0$
. On définit
où
![]() $\unicode[STIX]{x1D719}_{u}$
est la fonction caractéristique de
$\unicode[STIX]{x1D719}_{u}$
est la fonction caractéristique de
![]() $\{u\}$
.
$\{u\}$
.
Notons que
![]() $\text{Eis}^{0}(u)$
n’est autre que l’unité de Siegel
$\text{Eis}^{0}(u)$
n’est autre que l’unité de Siegel
![]() $g_{u}\otimes (2/N)$
[Reference KatoKat04, § 1].
$g_{u}\otimes (2/N)$
[Reference KatoKat04, § 1].
Par définition, on a
![]() $\text{Res}^{n}(\text{Eis}^{n}(u))=\unicode[STIX]{x1D714}^{n}(\unicode[STIX]{x1D719}_{u})$
; l’application horosphérique donne donc les résidus des symboles d’Eisenstein.
$\text{Res}^{n}(\text{Eis}^{n}(u))=\unicode[STIX]{x1D714}^{n}(\unicode[STIX]{x1D719}_{u})$
; l’application horosphérique donne donc les résidus des symboles d’Eisenstein.
Le groupe
![]() $G=\text{GL}_{2}(\mathbf{Z}/N\mathbf{Z})$
agit à gauche sur
$G=\text{GL}_{2}(\mathbf{Z}/N\mathbf{Z})$
agit à gauche sur
![]() $E^{n}$
. Sur les points complexes, cette action est induite par
$E^{n}$
. Sur les points complexes, cette action est induite par
![]() $\unicode[STIX]{x1D6FE}\cdot (\unicode[STIX]{x1D70F},z,g)=(\unicode[STIX]{x1D70F},z,g^{t}\unicode[STIX]{x1D6FE})$
. On en déduit une action à droite de
$\unicode[STIX]{x1D6FE}\cdot (\unicode[STIX]{x1D70F},z,g)=(\unicode[STIX]{x1D70F},z,g^{t}\unicode[STIX]{x1D6FE})$
. On en déduit une action à droite de
![]() $G$
sur
$G$
sur
![]() $H_{{\mathcal{M}}}^{n+1}(E^{n},\mathbf{Q}(n+1))$
. Les applications
$H_{{\mathcal{M}}}^{n+1}(E^{n},\mathbf{Q}(n+1))$
. Les applications
![]() $\text{Res}^{n}$
et
$\text{Res}^{n}$
et ![]() étant
étant
![]() $G$
-équivariantes, on a le lemme suivant.
$G$
-équivariantes, on a le lemme suivant.
Lemme 5.2. Pour tout
![]() $g\in G$
, et pour tout
$g\in G$
, et pour tout
![]() $u\in (\mathbf{Z}/N\mathbf{Z})^{2}$
(avec
$u\in (\mathbf{Z}/N\mathbf{Z})^{2}$
(avec
![]() $u\neq 0$
si
$u\neq 0$
si
![]() $n=0$
), on a
$n=0$
), on a
Dans la suite de cette section, nous rappelons la description explicite de la réalisation du symbole d’Eisenstein en cohomologie de Deligne [Reference BeilinsonBei86, Reference DeningerDen97, Reference Deninger and SchollDS91].
Commençons par quelques rappels sur la cohomologie de Deligne
![]() $H_{{\mathcal{D}}}^{i}(X/\mathbf{R},\mathbf{R}(j))$
associée à un schéma
$H_{{\mathcal{D}}}^{i}(X/\mathbf{R},\mathbf{R}(j))$
associée à un schéma
![]() $X$
lisse et quasi-projectif sur
$X$
lisse et quasi-projectif sur
![]() $\mathbf{R}$
. Notons
$\mathbf{R}$
. Notons
![]() ${\mathcal{S}}^{\cdot }(X,\mathbf{R}(n))$
le complexe des formes différentielles
${\mathcal{S}}^{\cdot }(X,\mathbf{R}(n))$
le complexe des formes différentielles
![]() ${\mathcal{C}}^{\infty }$
sur
${\mathcal{C}}^{\infty }$
sur
![]() $X(\mathbf{C})$
à valeurs dans
$X(\mathbf{C})$
à valeurs dans
![]() $\mathbf{R}(n)=(2i\unicode[STIX]{x1D70B})^{n}\mathbf{R}$
vérifiant
$\mathbf{R}(n)=(2i\unicode[STIX]{x1D70B})^{n}\mathbf{R}$
vérifiant
![]() $c^{\ast }\unicode[STIX]{x1D714}=(-1)^{n}\unicode[STIX]{x1D714}$
, où
$c^{\ast }\unicode[STIX]{x1D714}=(-1)^{n}\unicode[STIX]{x1D714}$
, où
![]() $c$
désigne la conjugaison complexe sur
$c$
désigne la conjugaison complexe sur
![]() $X(\mathbf{C})$
. Par la résolution des singularités, il existe une compactification lisse
$X(\mathbf{C})$
. Par la résolution des singularités, il existe une compactification lisse
![]() $\overline{X}$
de
$\overline{X}$
de
![]() $X$
telle que
$X$
telle que
![]() $X^{\infty }:=\overline{X}-X$
soit un diviseur à croisements normaux. Pour un entier
$X^{\infty }:=\overline{X}-X$
soit un diviseur à croisements normaux. Pour un entier
![]() $m\geqslant 0$
, notons
$m\geqslant 0$
, notons
![]() $\unicode[STIX]{x1D6FA}_{\overline{X}}^{m}\langle X^{\infty }\rangle$
le
$\unicode[STIX]{x1D6FA}_{\overline{X}}^{m}\langle X^{\infty }\rangle$
le
![]() $\mathbf{C}$
-espace vectoriel des
$\mathbf{C}$
-espace vectoriel des
![]() $m$
-formes holomorphes sur
$m$
-formes holomorphes sur
![]() $X(\mathbf{C})$
à singularités logarithmiques le long de
$X(\mathbf{C})$
à singularités logarithmiques le long de
![]() $X^{\infty }(\mathbf{C})$
. Pour toute forme différentielle
$X^{\infty }(\mathbf{C})$
. Pour toute forme différentielle
![]() $\unicode[STIX]{x1D6FC}$
et tout entier
$\unicode[STIX]{x1D6FC}$
et tout entier
![]() $n\in \mathbf{Z}$
, notons
$n\in \mathbf{Z}$
, notons
![]() $\unicode[STIX]{x1D70B}_{n}(\unicode[STIX]{x1D6FC})=\frac{1}{2}(\unicode[STIX]{x1D6FC}+(-1)^{n}\overline{\unicode[STIX]{x1D6FC}})$
.
$\unicode[STIX]{x1D70B}_{n}(\unicode[STIX]{x1D6FC})=\frac{1}{2}(\unicode[STIX]{x1D6FC}+(-1)^{n}\overline{\unicode[STIX]{x1D6FC}})$
.
Proposition 5.3 [Reference Deninger and SchollDS91, (2.5.1)].
Pour tout entier
![]() $n\geqslant 0$
, on a un isomorphisme
$n\geqslant 0$
, on a un isomorphisme
Pour décrire la réalisation du symbole d’Eisenstein en cohomologie de Deligne, considérons maintenant l’application régulateur notée ![]() définie par Beilinson,
définie par Beilinson,
D’après la proposition 5.3, les éléments de
![]() $H_{{\mathcal{D}}}^{n+1}(E^{n}/\mathbf{R},\mathbf{R}(n+1))$
sont représentés par des
$H_{{\mathcal{D}}}^{n+1}(E^{n}/\mathbf{R},\mathbf{R}(n+1))$
sont représentés par des
![]() $n$
-formes différentielles sur
$n$
-formes différentielles sur
![]() $E^{n}(\mathbf{C})$
. Nous noterons
$E^{n}(\mathbf{C})$
. Nous noterons
![]() $(\unicode[STIX]{x1D70F};z_{1},\ldots ,z_{n};g)$
les coordonnées naturelles sur
$(\unicode[STIX]{x1D70F};z_{1},\ldots ,z_{n};g)$
les coordonnées naturelles sur
![]() $E^{n}(\mathbf{C})$
, avec
$E^{n}(\mathbf{C})$
, avec
![]() $\unicode[STIX]{x1D70F}\in {\mathcal{H}}$
,
$\unicode[STIX]{x1D70F}\in {\mathcal{H}}$
,
![]() $z_{i}\in \mathbf{C}$
,
$z_{i}\in \mathbf{C}$
,
![]() $g\in \text{GL}_{2}(\mathbf{Z}/N\mathbf{Z})$
, et nous poserons
$g\in \text{GL}_{2}(\mathbf{Z}/N\mathbf{Z})$
, et nous poserons
![]() $q=e^{2i\unicode[STIX]{x1D70B}\unicode[STIX]{x1D70F}}$
. Pour tous entiers
$q=e^{2i\unicode[STIX]{x1D70B}\unicode[STIX]{x1D70F}}$
. Pour tous entiers
![]() $a,b\geqslant 0$
tels que
$a,b\geqslant 0$
tels que
![]() $a+b=n$
, définissons la
$a+b=n$
, définissons la
![]() $n$
-forme différentielle sur
$n$
-forme différentielle sur
![]() $\mathbf{C}^{n}$
,
$\mathbf{C}^{n}$
,
D’après [Reference DeningerDen97, (3.12), (3.28)] et [Reference Huber and KingsHK99, Remark after Lemma 7.1], on a la proposition suivante.
Proposition 5.4. Soit
![]() $u\in (\mathbf{Z}/N\mathbf{Z})^{2}$
, avec
$u\in (\mathbf{Z}/N\mathbf{Z})^{2}$
, avec
![]() $u\neq 0$
dans le cas
$u\neq 0$
dans le cas
![]() $n=0$
. L’élément
$n=0$
. L’élément ![]() est représenté par une
est représenté par une
![]() $n$
-forme différentielle
$n$
-forme différentielle
![]() $\text{Eis}_{{\mathcal{D}}}^{n}(u)$
vérifiant
$\text{Eis}_{{\mathcal{D}}}^{n}(u)$
vérifiant
De plus, on a
où
![]() $\text{Eis}_{\text{hol}}^{n}(u)$
est la série d’Eisenstein holomorphe de poids
$\text{Eis}_{\text{hol}}^{n}(u)$
est la série d’Eisenstein holomorphe de poids
![]() $n+2$
définie par
$n+2$
définie par
Remarque 5.5. Pour
![]() $n=0$
, les séries intervenant dans
$n=0$
, les séries intervenant dans
![]() $\text{Eis}_{{\mathcal{D}}}^{0}(u)$
et
$\text{Eis}_{{\mathcal{D}}}^{0}(u)$
et
![]() $\text{Eis}_{\text{hol}}^{0}(u)$
ne convergent pas absolument et on a recours à la sommation d’Eisenstein ou de Kronecker pour leur donner un sens [Reference WeilWei99, ch. VIII, § 9].
$\text{Eis}_{\text{hol}}^{0}(u)$
ne convergent pas absolument et on a recours à la sommation d’Eisenstein ou de Kronecker pour leur donner un sens [Reference WeilWei99, ch. VIII, § 9].
6 Éléments de Deninger–Scholl
Dans cette section, nous rappelons la définition des éléments de Deninger–Scholl et calculons explicitement leurs réalisations en cohomologie de Deligne.
Soit
![]() $k\geqslant 0$
un entier. On choisit une décomposition
$k\geqslant 0$
un entier. On choisit une décomposition
![]() $k=k_{1}+k_{2}$
avec
$k=k_{1}+k_{2}$
avec
![]() $k_{1},k_{2}\geqslant 0$
. Considérons les projections canoniques
$k_{1},k_{2}\geqslant 0$
. Considérons les projections canoniques
![]() $p_{1}:E^{k_{1}+k_{2}}\rightarrow E^{k_{1}}$
et
$p_{1}:E^{k_{1}+k_{2}}\rightarrow E^{k_{1}}$
et
![]() $p_{2}:E^{k_{1}+k_{2}}\rightarrow E^{k_{2}}$
. Les éléments suivants, définis par Gealy dans [Reference GealyGea05], sont une généralisation des éléments de Beilinson–Kato et Deninger–Scholl.
$p_{2}:E^{k_{1}+k_{2}}\rightarrow E^{k_{2}}$
. Les éléments suivants, définis par Gealy dans [Reference GealyGea05], sont une généralisation des éléments de Beilinson–Kato et Deninger–Scholl.
Définition 6.1. Soient
![]() $u_{1},u_{2}\in (\mathbf{Z}/N\mathbf{Z})^{2}$
. Dans le cas où
$u_{1},u_{2}\in (\mathbf{Z}/N\mathbf{Z})^{2}$
. Dans le cas où
![]() $k_{i}=0$
, on suppose
$k_{i}=0$
, on suppose
![]() $u_{i}\neq 0$
. On pose
$u_{i}\neq 0$
. On pose
Dans le cas
![]() $k=0$
, on retrouve les éléments de Beilinson–Kato dans le
$k=0$
, on retrouve les éléments de Beilinson–Kato dans le
![]() $K_{2}$
de la courbe modulaire
$K_{2}$
de la courbe modulaire
![]() $Y(N)$
[Reference KatoKat04]. Notons également la relation
$Y(N)$
[Reference KatoKat04]. Notons également la relation
![]() $\text{Eis}^{0,k}(u_{2},u_{1})=(-1)^{k+1}\,\text{Eis}^{k,0}(u_{1},u_{2})$
, qui découle du caractère commutatif gradué du cup-produit [Reference Deninger and SchollDS91, (1.3), Theorem (2)].
$\text{Eis}^{0,k}(u_{2},u_{1})=(-1)^{k+1}\,\text{Eis}^{k,0}(u_{1},u_{2})$
, qui découle du caractère commutatif gradué du cup-produit [Reference Deninger and SchollDS91, (1.3), Theorem (2)].
Pour décrire la réalisation de ces éléments en cohomologie de Deligne, considérons le régulateur de Beilinson
Les éléments de
![]() $H_{{\mathcal{D}}}^{k+2}(E^{k}/\mathbf{R},\mathbf{R}(k+2))$
sont représentés par des
$H_{{\mathcal{D}}}^{k+2}(E^{k}/\mathbf{R},\mathbf{R}(k+2))$
sont représentés par des
![]() $(k+1)$
-formes différentielles fermées sur
$(k+1)$
-formes différentielles fermées sur
![]() $E^{k}(\mathbf{C})$
. En effet, comme
$E^{k}(\mathbf{C})$
. En effet, comme
![]() $E^{k}$
est de dimension
$E^{k}$
est de dimension
![]() $k+1$
, il n’y a pas de
$k+1$
, il n’y a pas de
![]() $(k+2)$
-forme holomorphe sur
$(k+2)$
-forme holomorphe sur
![]() $E^{k}(\mathbf{C})$
, et la proposition 5.3 entraîne un isomorphisme
$E^{k}(\mathbf{C})$
, et la proposition 5.3 entraîne un isomorphisme
Lemme 6.2. L’élément ![]() est représenté par la forme différentielle fermée
est représenté par la forme différentielle fermée
Démonstration.
Cela résulte de la proposition 5.4 et de la formule pour le cup-produit en cohomologie de Deligne [Reference Deninger and SchollDS91, (2.5)]. ◻
7 La méthode de Rogers–Zudilin
Rogers et Zudilin [Reference Rogers and ZudilinRZ12] ont introduit une nouvelle méthode permettant de calculer certaines mesures de Mahler en termes de valeurs de fonctions
![]() $L$
. Cette méthode est basée sur un changement de variables astucieux dans une intégrale le long du symbole modulaire
$L$
. Cette méthode est basée sur un changement de variables astucieux dans une intégrale le long du symbole modulaire
![]() $\{0,\infty \}$
. Dans cette section, nous expliquons cette méthode dans un cadre assez général (voir également l’interprétation proposée dans [Reference Diamantis, Neururer and StrömbergDNS15]). L’identité obtenue (proposition 7.2) est la clé de notre calcul du régulateur.
$\{0,\infty \}$
. Dans cette section, nous expliquons cette méthode dans un cadre assez général (voir également l’interprétation proposée dans [Reference Diamantis, Neururer and StrömbergDNS15]). L’identité obtenue (proposition 7.2) est la clé de notre calcul du régulateur.
Introduisons, pour des fonctions
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}:\mathbf{Z}/N\mathbf{Z}\rightarrow \mathbf{C}$
et des nombres complexes
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}:\mathbf{Z}/N\mathbf{Z}\rightarrow \mathbf{C}$
et des nombres complexes
![]() $t,u\in \mathbf{C}$
, la série suivante
$t,u\in \mathbf{C}$
, la série suivante
Cette série définit une fonction holomorphe sur
![]() ${\mathcal{H}}$
.
${\mathcal{H}}$
.
Lemme 7.1. Pour
![]() $s\in \mathbf{C}$
,
$s\in \mathbf{C}$
,
![]() $\Re (s)\gg 0$
, la fonction
$\Re (s)\gg 0$
, la fonction
![]() $y\mapsto S_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{t,u}(iy)y^{s-1}$
est intégrable sur
$y\mapsto S_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{t,u}(iy)y^{s-1}$
est intégrable sur
![]() $]\!0,+\infty \![$
, et on a
$]\!0,+\infty \![$
, et on a
Pour
![]() $s\in \mathbf{C}$
,
$s\in \mathbf{C}$
,
![]() $\Re (s)\ll 0$
, la fonction
$\Re (s)\ll 0$
, la fonction
![]() $y\mapsto S_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{t,u}(i/y)y^{s-1}$
est intégrable sur
$y\mapsto S_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{t,u}(i/y)y^{s-1}$
est intégrable sur
![]() $]\!0,+\infty \![$
, et on a
$]\!0,+\infty \![$
, et on a
Démonstration (Voir [Reference Diamantis, Neururer and StrömbergDNS15, § 3]).
La fonction
![]() $S_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{t,u}(iy)$
décroît exponentiellement lorsque
$S_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{t,u}(iy)$
décroît exponentiellement lorsque
![]() $y\rightarrow +\infty$
, et croît au plus polynomialement en
$y\rightarrow +\infty$
, et croît au plus polynomialement en
![]() $1/y$
lorsque
$1/y$
lorsque
![]() $y\rightarrow 0$
. La première intégrale converge donc pour
$y\rightarrow 0$
. La première intégrale converge donc pour
![]() $\Re (s)\gg 0$
, et une simple interversion somme-intégrale mène alors au résultat. La seconde assertion résulte d’un calcul similaire.◻
$\Re (s)\gg 0$
, et une simple interversion somme-intégrale mène alors au résultat. La seconde assertion résulte d’un calcul similaire.◻
Nous pouvons maintenant énoncer la proposition-clé à la base de la méthode de Rogers–Zudilin.
Proposition 7.2. Soient
![]() $t_{1},u_{1},t_{2},u_{2},s\in \mathbf{C}$
des nombres complexes, et soient
$t_{1},u_{1},t_{2},u_{2},s\in \mathbf{C}$
des nombres complexes, et soient
![]() $\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FD}_{2}:\mathbf{Z}/N\mathbf{Z}\rightarrow \mathbf{C}$
des fonctions. On a
$\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FD}_{2}:\mathbf{Z}/N\mathbf{Z}\rightarrow \mathbf{C}$
des fonctions. On a
Démonstration.
Voir [Reference Diamantis, Neururer and StrömbergDNS15, Theorem 3.2]. ◻
8 Quelques développements de Fourier
Dans cette section, nous calculons le développement de Fourier de la réalisation du symbole d’Eisenstein en cohomologie de Deligne. Commençons par rappeler le développement de Fourier de
![]() $\text{Eis}_{\text{hol}}^{n}(u)$
, qui a en fait déjà été déterminé dans la § 3.
$\text{Eis}_{\text{hol}}^{n}(u)$
, qui a en fait déjà été déterminé dans la § 3.
Proposition 8.1. Soit
![]() $n\geqslant 0$
un entier, et soit
$n\geqslant 0$
un entier, et soit
![]() $u\in (\mathbf{Z}/N\mathbf{Z})^{2}$
(avec
$u\in (\mathbf{Z}/N\mathbf{Z})^{2}$
(avec
![]() $u\neq 0$
si
$u\neq 0$
si
![]() $n=0$
). Alors
$n=0$
). Alors
Démonstration.
Par définition, on a
 $$\begin{eqnarray}\displaystyle \sum ^{\prime }_{(c,d)\in \mathbf{Z}^{2}}\frac{\unicode[STIX]{x1D701}_{N}^{c(gu)_{1}+d(gu)_{2}}}{(c\unicode[STIX]{x1D70F}+d)^{n+2}} & = & \displaystyle \frac{(-2i\unicode[STIX]{x1D70B})^{n+2}}{(n+1)!}{\mathcal{K}}_{n+2}\biggl(n+2,\unicode[STIX]{x1D70F},0,\frac{-(gu)_{2}\unicode[STIX]{x1D70F}+(gu)_{1}}{N}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \frac{(-2i\unicode[STIX]{x1D70B})^{n+2}}{(n+1)!}F_{-(gu)_{2},(gu)_{1}}^{(n+2)}(\unicode[STIX]{x1D70F})\nonumber\\ \displaystyle & = & \displaystyle \frac{(-2i\unicode[STIX]{x1D70B})^{n+2}}{(n+1)!}F_{\unicode[STIX]{x1D70E}gu}^{(n+2)}(\unicode[STIX]{x1D70F}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \sum ^{\prime }_{(c,d)\in \mathbf{Z}^{2}}\frac{\unicode[STIX]{x1D701}_{N}^{c(gu)_{1}+d(gu)_{2}}}{(c\unicode[STIX]{x1D70F}+d)^{n+2}} & = & \displaystyle \frac{(-2i\unicode[STIX]{x1D70B})^{n+2}}{(n+1)!}{\mathcal{K}}_{n+2}\biggl(n+2,\unicode[STIX]{x1D70F},0,\frac{-(gu)_{2}\unicode[STIX]{x1D70F}+(gu)_{1}}{N}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \frac{(-2i\unicode[STIX]{x1D70B})^{n+2}}{(n+1)!}F_{-(gu)_{2},(gu)_{1}}^{(n+2)}(\unicode[STIX]{x1D70F})\nonumber\\ \displaystyle & = & \displaystyle \frac{(-2i\unicode[STIX]{x1D70B})^{n+2}}{(n+1)!}F_{\unicode[STIX]{x1D70E}gu}^{(n+2)}(\unicode[STIX]{x1D70F}).\nonumber\end{eqnarray}$$
On en déduit le résultat. ◻
La forme différentielle
![]() $\text{Eis}_{{\mathcal{D}}}^{n}(u)$
étant invariante par
$\text{Eis}_{{\mathcal{D}}}^{n}(u)$
étant invariante par
![]() $\unicode[STIX]{x1D70F}\mapsto \unicode[STIX]{x1D70F}+N$
, elle possède un développement de Fourier en la variable
$\unicode[STIX]{x1D70F}\mapsto \unicode[STIX]{x1D70F}+N$
, elle possède un développement de Fourier en la variable
![]() $q^{1/N}=e^{2i\unicode[STIX]{x1D70B}\unicode[STIX]{x1D70F}/N}$
.
$q^{1/N}=e^{2i\unicode[STIX]{x1D70B}\unicode[STIX]{x1D70F}/N}$
.
Introduisons, pour des entiers
![]() $a,b\geqslant 0$
, et
$a,b\geqslant 0$
, et
![]() $u=(u_{1},u_{2})\in (\mathbf{Z}/N\mathbf{Z})^{2}$
, les séries d’Eisenstein analytiques réelles suivantes
$u=(u_{1},u_{2})\in (\mathbf{Z}/N\mathbf{Z})^{2}$
, les séries d’Eisenstein analytiques réelles suivantes
 $$\begin{eqnarray}\displaystyle & \displaystyle E_{u}^{a,b}(\unicode[STIX]{x1D70F})=\sum ^{\prime }_{(m,n)\equiv (u_{1},u_{2})(N)}\frac{1}{(m\unicode[STIX]{x1D70F}+n)^{a+1}(m\overline{\unicode[STIX]{x1D70F}}+n)^{b+1}}\quad (\unicode[STIX]{x1D70F}\in {\mathcal{H}}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle F_{u}^{a,b}(\unicode[STIX]{x1D70F})=\sum ^{\prime }_{(m,n)\in \mathbf{Z}^{2}}\frac{\unicode[STIX]{x1D701}_{N}^{mu_{1}+nu_{2}}}{(m\unicode[STIX]{x1D70F}+n)^{a+1}(m\overline{\unicode[STIX]{x1D70F}}+n)^{b+1}}\quad (\unicode[STIX]{x1D70F}\in {\mathcal{H}}). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle E_{u}^{a,b}(\unicode[STIX]{x1D70F})=\sum ^{\prime }_{(m,n)\equiv (u_{1},u_{2})(N)}\frac{1}{(m\unicode[STIX]{x1D70F}+n)^{a+1}(m\overline{\unicode[STIX]{x1D70F}}+n)^{b+1}}\quad (\unicode[STIX]{x1D70F}\in {\mathcal{H}}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle F_{u}^{a,b}(\unicode[STIX]{x1D70F})=\sum ^{\prime }_{(m,n)\in \mathbf{Z}^{2}}\frac{\unicode[STIX]{x1D701}_{N}^{mu_{1}+nu_{2}}}{(m\unicode[STIX]{x1D70F}+n)^{a+1}(m\overline{\unicode[STIX]{x1D70F}}+n)^{b+1}}\quad (\unicode[STIX]{x1D70F}\in {\mathcal{H}}). & \displaystyle \nonumber\end{eqnarray}$$
On a donc
D’après la proposition 5.4 et la définition de
![]() $F_{u}^{a,b}$
, on a
$F_{u}^{a,b}$
, on a
Pour des entiers
![]() $k,\ell \in \mathbf{Z}$
et des fonctions
$k,\ell \in \mathbf{Z}$
et des fonctions
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}:\mathbf{Z}/N\mathbf{Z}\rightarrow \mathbf{C}$
, nous poserons également
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}:\mathbf{Z}/N\mathbf{Z}\rightarrow \mathbf{C}$
, nous poserons également
Proposition 8.2. Pour
![]() $a,b\geqslant 0$
et
$a,b\geqslant 0$
et
![]() $u_{1},u_{2}\in \mathbf{Z}/N\mathbf{Z}$
, on a
$u_{1},u_{2}\in \mathbf{Z}/N\mathbf{Z}$
, on a
 $$\begin{eqnarray}\displaystyle E_{(u_{1},u_{2})}^{a,b}(\unicode[STIX]{x1D70F}) & = & \displaystyle \unicode[STIX]{x1D6FF}_{0}(u_{1})N^{-a-b-2}\biggl(\unicode[STIX]{x1D701}\biggl(\frac{u_{2}}{N},a+b+2\biggr)+(-1)^{a+b}\unicode[STIX]{x1D701}\biggl(-\frac{u_{2}}{N},a+b+2\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{b}\frac{2i\unicode[STIX]{x1D70B}}{N^{a+b+2}}\left(\begin{array}{@{}c@{}}a+b\\ a\end{array}\right) (\unicode[STIX]{x1D701}\biggl(\frac{u_{1}}{N},a+b+1\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{a+b}\unicode[STIX]{x1D701}\biggl(-\frac{u_{1}}{N},a+b+1\biggr)\!)(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(-1)^{b+1}}{b!}\mathop{\sum }_{j=0}^{a}\frac{(a+b-j)!}{j!(a-j)!}\biggl(-\frac{2i\unicode[STIX]{x1D70B}}{N}\biggr)^{j+1}(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1+j} (S_{\unicode[STIX]{x1D6FF}_{u_{1}},\hat{\unicode[STIX]{x1D6FF}}_{-u_{2}}}^{j-a-b-1,j}(\unicode[STIX]{x1D70F})\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{a+b}S_{\unicode[STIX]{x1D6FF}_{-u_{1}},\hat{\unicode[STIX]{x1D6FF}}_{u_{2}}}^{j-a-b-1,j}(\unicode[STIX]{x1D70F}))\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(-1)^{b+1}}{a!}\mathop{\sum }_{j=0}^{b}\frac{(a+b-j)!}{j!(b-j)!}\biggl(-\frac{2i\unicode[STIX]{x1D70B}}{N}\biggr)^{j+1}(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1+j} (\overline{S}_{\unicode[STIX]{x1D6FF}_{u_{1}},\hat{\unicode[STIX]{x1D6FF}}_{-u_{2}}}^{j-a-b-1,j}(\unicode[STIX]{x1D70F})\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{a+b}\overline{S}_{\unicode[STIX]{x1D6FF}_{-u_{1}},\hat{\unicode[STIX]{x1D6FF}}_{u_{2}}}^{j-a-b-1,j}(\unicode[STIX]{x1D70F})).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{(u_{1},u_{2})}^{a,b}(\unicode[STIX]{x1D70F}) & = & \displaystyle \unicode[STIX]{x1D6FF}_{0}(u_{1})N^{-a-b-2}\biggl(\unicode[STIX]{x1D701}\biggl(\frac{u_{2}}{N},a+b+2\biggr)+(-1)^{a+b}\unicode[STIX]{x1D701}\biggl(-\frac{u_{2}}{N},a+b+2\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{b}\frac{2i\unicode[STIX]{x1D70B}}{N^{a+b+2}}\left(\begin{array}{@{}c@{}}a+b\\ a\end{array}\right) (\unicode[STIX]{x1D701}\biggl(\frac{u_{1}}{N},a+b+1\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{a+b}\unicode[STIX]{x1D701}\biggl(-\frac{u_{1}}{N},a+b+1\biggr)\!)(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(-1)^{b+1}}{b!}\mathop{\sum }_{j=0}^{a}\frac{(a+b-j)!}{j!(a-j)!}\biggl(-\frac{2i\unicode[STIX]{x1D70B}}{N}\biggr)^{j+1}(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1+j} (S_{\unicode[STIX]{x1D6FF}_{u_{1}},\hat{\unicode[STIX]{x1D6FF}}_{-u_{2}}}^{j-a-b-1,j}(\unicode[STIX]{x1D70F})\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{a+b}S_{\unicode[STIX]{x1D6FF}_{-u_{1}},\hat{\unicode[STIX]{x1D6FF}}_{u_{2}}}^{j-a-b-1,j}(\unicode[STIX]{x1D70F}))\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(-1)^{b+1}}{a!}\mathop{\sum }_{j=0}^{b}\frac{(a+b-j)!}{j!(b-j)!}\biggl(-\frac{2i\unicode[STIX]{x1D70B}}{N}\biggr)^{j+1}(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1+j} (\overline{S}_{\unicode[STIX]{x1D6FF}_{u_{1}},\hat{\unicode[STIX]{x1D6FF}}_{-u_{2}}}^{j-a-b-1,j}(\unicode[STIX]{x1D70F})\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{a+b}\overline{S}_{\unicode[STIX]{x1D6FF}_{-u_{1}},\hat{\unicode[STIX]{x1D6FF}}_{u_{2}}}^{j-a-b-1,j}(\unicode[STIX]{x1D70F})).\end{eqnarray}$$
Démonstration.
On suit la méthode classique [Reference SchoenebergSch74, ch. III, § 2] pour déterminer le développement de Fourier des séries d’Eisenstein. Pour
![]() $a,b\geqslant 0$
,
$a,b\geqslant 0$
,
![]() $\unicode[STIX]{x1D70F}\in \mathbf{C}-\mathbf{R}$
et
$\unicode[STIX]{x1D70F}\in \mathbf{C}-\mathbf{R}$
et
![]() $x\in \mathbf{R}$
, posons
$x\in \mathbf{R}$
, posons
Cette série converge et définit une fonction
![]() $1$
-périodique de
$1$
-périodique de
![]() $x$
. Rappelons le calcul classique de son développement de Fourier
$x$
. Rappelons le calcul classique de son développement de Fourier
Lemme 8.3. On a
 $$\begin{eqnarray}\displaystyle c_{r}(\unicode[STIX]{x1D719}_{a,b,\unicode[STIX]{x1D70F}})=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{(-1)^{b}}{b!}2i\unicode[STIX]{x1D70B}\mathop{\sum }_{j=0}^{a}(-1)^{j}\frac{(a+b-j)!}{j!(a-j)!}(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1+j}(2i\unicode[STIX]{x1D70B}r)^{j}e^{2i\unicode[STIX]{x1D70B}r\unicode[STIX]{x1D70F}}\quad & \text{si }\unicode[STIX]{x1D70F}\in {\mathcal{H}},r\geqslant 1,\\ \displaystyle \frac{(-1)^{b}}{a!}2i\unicode[STIX]{x1D70B}\mathop{\sum }_{j=0}^{b}\frac{(a+b-j)!}{j!(b-j)!}(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1+j}(2i\unicode[STIX]{x1D70B}r)^{j}e^{2i\unicode[STIX]{x1D70B}r\overline{\unicode[STIX]{x1D70F}}}\quad & \text{si }\unicode[STIX]{x1D70F}\in {\mathcal{H}},r\leqslant -1,\\ \displaystyle (-1)^{b}2i\unicode[STIX]{x1D70B}\left(\begin{array}{@{}c@{}}a+b\\ a\end{array}\right)(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1}\quad & \text{si }\unicode[STIX]{x1D70F}\in {\mathcal{H}},r=0,\\ (-1)^{a+b}c_{-r}(\unicode[STIX]{x1D719}_{a,b,-\unicode[STIX]{x1D70F}})\quad & \text{si }\unicode[STIX]{x1D70F}\in -{\mathcal{H}}.\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{r}(\unicode[STIX]{x1D719}_{a,b,\unicode[STIX]{x1D70F}})=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{(-1)^{b}}{b!}2i\unicode[STIX]{x1D70B}\mathop{\sum }_{j=0}^{a}(-1)^{j}\frac{(a+b-j)!}{j!(a-j)!}(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1+j}(2i\unicode[STIX]{x1D70B}r)^{j}e^{2i\unicode[STIX]{x1D70B}r\unicode[STIX]{x1D70F}}\quad & \text{si }\unicode[STIX]{x1D70F}\in {\mathcal{H}},r\geqslant 1,\\ \displaystyle \frac{(-1)^{b}}{a!}2i\unicode[STIX]{x1D70B}\mathop{\sum }_{j=0}^{b}\frac{(a+b-j)!}{j!(b-j)!}(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1+j}(2i\unicode[STIX]{x1D70B}r)^{j}e^{2i\unicode[STIX]{x1D70B}r\overline{\unicode[STIX]{x1D70F}}}\quad & \text{si }\unicode[STIX]{x1D70F}\in {\mathcal{H}},r\leqslant -1,\\ \displaystyle (-1)^{b}2i\unicode[STIX]{x1D70B}\left(\begin{array}{@{}c@{}}a+b\\ a\end{array}\right)(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1}\quad & \text{si }\unicode[STIX]{x1D70F}\in {\mathcal{H}},r=0,\\ (-1)^{a+b}c_{-r}(\unicode[STIX]{x1D719}_{a,b,-\unicode[STIX]{x1D70F}})\quad & \text{si }\unicode[STIX]{x1D70F}\in -{\mathcal{H}}.\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
Démonstration.
Voir [Reference ShimuraShi75, Lemma 1] et [Reference SturmStu80, Lemma 5]. ◻
Exprimons maintenant
![]() $E_{u}^{a,b}$
en termes de
$E_{u}^{a,b}$
en termes de
![]() $\unicode[STIX]{x1D719}_{a,b,\unicode[STIX]{x1D70F}}$
. On a
$\unicode[STIX]{x1D719}_{a,b,\unicode[STIX]{x1D70F}}$
. On a
 $$\begin{eqnarray}\displaystyle E_{(u_{1},u_{2})}^{a,b}(\unicode[STIX]{x1D70F}) & = & \displaystyle \unicode[STIX]{x1D6FF}_{u_{1}=0}\sum ^{\prime }_{n\equiv u_{2}(N)}\frac{1}{n^{a+b+2}}+\mathop{\sum }_{\substack{ m\equiv u_{1}(N) \\ m\neq 0}}\mathop{\sum }_{n\in \mathbf{Z}}\frac{1}{(m\unicode[STIX]{x1D70F}+u_{2}+Nn)^{a+1}(m\overline{\unicode[STIX]{x1D70F}}+u_{2}+Nn)^{b+1}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FF}_{u_{1}=0}\biggl(\mathop{\sum }_{\substack{ n\geqslant 1 \\ n\equiv u_{2}(N)}}\frac{1}{n^{a+b+2}}+\mathop{\sum }_{\substack{ n\leqslant -1 \\ n\equiv u_{2}(N)}}\frac{1}{n^{a+b+2}}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,N^{-a-b-2}\mathop{\sum }_{\substack{ m\equiv u_{1}(N) \\ m\neq 0}}\mathop{\sum }_{n\in \mathbf{Z}}\frac{1}{((m\unicode[STIX]{x1D70F}+u_{2})/N+n)^{a+1}((m\overline{\unicode[STIX]{x1D70F}}+u_{2})/N+n)^{b+1}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FF}_{u_{1}=0}\biggl(\mathop{\sum }_{\substack{ n\geqslant 1 \\ n\equiv u_{2}(N)}}\frac{1}{n^{a+b+2}}+(-1)^{a+b}\mathop{\sum }_{\substack{ n\geqslant 1 \\ n\equiv -u_{2}(N)}}\frac{1}{n^{a+b+2}}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,N^{-a-b-2}\mathop{\sum }_{\substack{ m\equiv u_{1}(N) \\ m\neq 0}}\unicode[STIX]{x1D719}_{a,b,(m\unicode[STIX]{x1D70F}+u_{2})/N}(0)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FF}_{u_{1}=0}N^{-a-b-2}\biggl(\mathop{\sum }_{\substack{ x>0 \\ x\equiv (u_{2}/N)(1)}}\frac{1}{x^{a+b+2}}+(-1)^{a+b}\mathop{\sum }_{\substack{ x>0 \\ x\equiv -(u_{2}/N)(1)}}\frac{1}{x^{a+b+2}}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,N^{-a-b-2}\mathop{\sum }_{\substack{ m\equiv u_{1}(N) \\ m\neq 0}}\mathop{\sum }_{r\in \mathbf{Z}}c_{r}(\unicode[STIX]{x1D719}_{a,b,(m\unicode[STIX]{x1D70F}+u_{2})/N})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FF}_{u_{1}=0}N^{-a-b-2}\biggl(\unicode[STIX]{x1D701}\biggl(\frac{u_{2}}{N},a+b+2\biggr)+(-1)^{a+b}\unicode[STIX]{x1D701}\biggl(-\frac{u_{2}}{N},a+b+2\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,N^{-a-b-2} (\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv u_{1}(N)}}\mathop{\sum }_{r\in \mathbf{Z}}c_{r}(\unicode[STIX]{x1D719}_{a,b,(m\unicode[STIX]{x1D70F}+u_{2})/N})\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{a+b}\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv -u_{1}(N)}}\mathop{\sum }_{r\in \mathbf{Z}}c_{r}(\unicode[STIX]{x1D719}_{a,b,(m\unicode[STIX]{x1D70F}-u_{2})/N})\!).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{(u_{1},u_{2})}^{a,b}(\unicode[STIX]{x1D70F}) & = & \displaystyle \unicode[STIX]{x1D6FF}_{u_{1}=0}\sum ^{\prime }_{n\equiv u_{2}(N)}\frac{1}{n^{a+b+2}}+\mathop{\sum }_{\substack{ m\equiv u_{1}(N) \\ m\neq 0}}\mathop{\sum }_{n\in \mathbf{Z}}\frac{1}{(m\unicode[STIX]{x1D70F}+u_{2}+Nn)^{a+1}(m\overline{\unicode[STIX]{x1D70F}}+u_{2}+Nn)^{b+1}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FF}_{u_{1}=0}\biggl(\mathop{\sum }_{\substack{ n\geqslant 1 \\ n\equiv u_{2}(N)}}\frac{1}{n^{a+b+2}}+\mathop{\sum }_{\substack{ n\leqslant -1 \\ n\equiv u_{2}(N)}}\frac{1}{n^{a+b+2}}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,N^{-a-b-2}\mathop{\sum }_{\substack{ m\equiv u_{1}(N) \\ m\neq 0}}\mathop{\sum }_{n\in \mathbf{Z}}\frac{1}{((m\unicode[STIX]{x1D70F}+u_{2})/N+n)^{a+1}((m\overline{\unicode[STIX]{x1D70F}}+u_{2})/N+n)^{b+1}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FF}_{u_{1}=0}\biggl(\mathop{\sum }_{\substack{ n\geqslant 1 \\ n\equiv u_{2}(N)}}\frac{1}{n^{a+b+2}}+(-1)^{a+b}\mathop{\sum }_{\substack{ n\geqslant 1 \\ n\equiv -u_{2}(N)}}\frac{1}{n^{a+b+2}}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,N^{-a-b-2}\mathop{\sum }_{\substack{ m\equiv u_{1}(N) \\ m\neq 0}}\unicode[STIX]{x1D719}_{a,b,(m\unicode[STIX]{x1D70F}+u_{2})/N}(0)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FF}_{u_{1}=0}N^{-a-b-2}\biggl(\mathop{\sum }_{\substack{ x>0 \\ x\equiv (u_{2}/N)(1)}}\frac{1}{x^{a+b+2}}+(-1)^{a+b}\mathop{\sum }_{\substack{ x>0 \\ x\equiv -(u_{2}/N)(1)}}\frac{1}{x^{a+b+2}}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,N^{-a-b-2}\mathop{\sum }_{\substack{ m\equiv u_{1}(N) \\ m\neq 0}}\mathop{\sum }_{r\in \mathbf{Z}}c_{r}(\unicode[STIX]{x1D719}_{a,b,(m\unicode[STIX]{x1D70F}+u_{2})/N})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FF}_{u_{1}=0}N^{-a-b-2}\biggl(\unicode[STIX]{x1D701}\biggl(\frac{u_{2}}{N},a+b+2\biggr)+(-1)^{a+b}\unicode[STIX]{x1D701}\biggl(-\frac{u_{2}}{N},a+b+2\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,N^{-a-b-2} (\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv u_{1}(N)}}\mathop{\sum }_{r\in \mathbf{Z}}c_{r}(\unicode[STIX]{x1D719}_{a,b,(m\unicode[STIX]{x1D70F}+u_{2})/N})\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{a+b}\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv -u_{1}(N)}}\mathop{\sum }_{r\in \mathbf{Z}}c_{r}(\unicode[STIX]{x1D719}_{a,b,(m\unicode[STIX]{x1D70F}-u_{2})/N})\!).\nonumber\end{eqnarray}$$
On distingue ensuite suivant la valeur de
![]() $r$
, ce qui donne
$r$
, ce qui donne
 $$\begin{eqnarray}\displaystyle & & \displaystyle E_{(u_{1},u_{2})}^{a,b}(\unicode[STIX]{x1D70F})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6FF}_{u_{1}=0}N^{-a-b-2}\biggl(\unicode[STIX]{x1D701}\biggl(\frac{u_{2}}{N},a+b+2\biggr)+(-1)^{a+b}\unicode[STIX]{x1D701}\biggl(-\frac{u_{2}}{N},a+b+2\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,N^{-a-b-2}\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv u_{1}(N)}}(-1)^{b}2i\unicode[STIX]{x1D70B}\left(\begin{array}{@{}c@{}}a+b\\ a\end{array}\right)\biggl(\frac{m\unicode[STIX]{x1D70F}-m\overline{\unicode[STIX]{x1D70F}}}{N}\biggr)^{-a-b-1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{a+b}N^{-a-b-2}\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv -u_{1}(N)}}(-1)^{b}2i\unicode[STIX]{x1D70B}\left(\begin{array}{@{}c@{}}a+b\\ a\end{array}\right)\biggl(\frac{m\unicode[STIX]{x1D70F}-m\overline{\unicode[STIX]{x1D70F}}}{N}\biggr)^{-a-b-1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,N^{-a-b-2}\biggl(\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv u_{1}(N)}}\mathop{\sum }_{r\geqslant 1}c_{r}(\unicode[STIX]{x1D719}_{a,b,(m\unicode[STIX]{x1D70F}+u_{2})/N})+(-1)^{a+b}\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv -u_{1}(N)}}\mathop{\sum }_{r\geqslant 1}c_{r}(\unicode[STIX]{x1D719}_{a,b,(m\unicode[STIX]{x1D70F}-u_{2})/N})\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,N^{-a-b-2} (\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv u_{1}(N)}}\mathop{\sum }_{r\leqslant -1}c_{r}(\unicode[STIX]{x1D719}_{a,b,(m\unicode[STIX]{x1D70F}+u_{2})/N})+(-1)^{a+b}\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv -u_{1}(N)}}\mathop{\sum }_{r\leqslant -1}c_{r}(\unicode[STIX]{x1D719}_{a,b,(m\unicode[STIX]{x1D70F}-u_{2})/N})\!).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle E_{(u_{1},u_{2})}^{a,b}(\unicode[STIX]{x1D70F})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6FF}_{u_{1}=0}N^{-a-b-2}\biggl(\unicode[STIX]{x1D701}\biggl(\frac{u_{2}}{N},a+b+2\biggr)+(-1)^{a+b}\unicode[STIX]{x1D701}\biggl(-\frac{u_{2}}{N},a+b+2\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,N^{-a-b-2}\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv u_{1}(N)}}(-1)^{b}2i\unicode[STIX]{x1D70B}\left(\begin{array}{@{}c@{}}a+b\\ a\end{array}\right)\biggl(\frac{m\unicode[STIX]{x1D70F}-m\overline{\unicode[STIX]{x1D70F}}}{N}\biggr)^{-a-b-1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{a+b}N^{-a-b-2}\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv -u_{1}(N)}}(-1)^{b}2i\unicode[STIX]{x1D70B}\left(\begin{array}{@{}c@{}}a+b\\ a\end{array}\right)\biggl(\frac{m\unicode[STIX]{x1D70F}-m\overline{\unicode[STIX]{x1D70F}}}{N}\biggr)^{-a-b-1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,N^{-a-b-2}\biggl(\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv u_{1}(N)}}\mathop{\sum }_{r\geqslant 1}c_{r}(\unicode[STIX]{x1D719}_{a,b,(m\unicode[STIX]{x1D70F}+u_{2})/N})+(-1)^{a+b}\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv -u_{1}(N)}}\mathop{\sum }_{r\geqslant 1}c_{r}(\unicode[STIX]{x1D719}_{a,b,(m\unicode[STIX]{x1D70F}-u_{2})/N})\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,N^{-a-b-2} (\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv u_{1}(N)}}\mathop{\sum }_{r\leqslant -1}c_{r}(\unicode[STIX]{x1D719}_{a,b,(m\unicode[STIX]{x1D70F}+u_{2})/N})+(-1)^{a+b}\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv -u_{1}(N)}}\mathop{\sum }_{r\leqslant -1}c_{r}(\unicode[STIX]{x1D719}_{a,b,(m\unicode[STIX]{x1D70F}-u_{2})/N})\!).\nonumber\end{eqnarray}$$
En utilisant l’expression des coefficients de Fourier de
![]() $\unicode[STIX]{x1D719}_{a,b,\unicode[STIX]{x1D70F}}$
, il vient
$\unicode[STIX]{x1D719}_{a,b,\unicode[STIX]{x1D70F}}$
, il vient
 $$\begin{eqnarray}\displaystyle E_{(u_{1},u_{2})}^{a,b}(\unicode[STIX]{x1D70F}) & = & \displaystyle \unicode[STIX]{x1D6FF}_{u_{1}=0}N^{-a-b-2}\biggl(\unicode[STIX]{x1D701}\biggl(\frac{u_{2}}{N},a+b+2\biggr)+(-1)^{a+b}\unicode[STIX]{x1D701}\biggl(-\frac{u_{2}}{N},a+b+2\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{b}\frac{2i\unicode[STIX]{x1D70B}}{N^{a+b+2}}\left(\begin{array}{@{}c@{}}a+b\\ a\end{array}\right) (\unicode[STIX]{x1D701}\biggl(\frac{u_{1}}{N},a+b+1\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{a+b}\unicode[STIX]{x1D701}\biggl(-\frac{u_{1}}{N},a+b+1\biggr)\!)(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1}\nonumber\\ \displaystyle & & \displaystyle +\,N^{-a-b-2}\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv u_{1}(N)}}\mathop{\sum }_{r\geqslant 1}\frac{(-1)^{b}}{b!}2i\unicode[STIX]{x1D70B}\mathop{\sum }_{j=0}^{a}(-1)^{j}\frac{(a+b-j)!}{j!(a-j)!}\biggl(\frac{m(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})}{N}\biggr)^{-a-b-1+j}\nonumber\\ \displaystyle & & \displaystyle \cdot \,(2i\unicode[STIX]{x1D70B}r)^{j}e^{2i\unicode[STIX]{x1D70B}r((m\unicode[STIX]{x1D70F}+u_{2})/N)}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(-1)^{a+b}}{N^{a+b+2}}\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv -u_{1}(N)}}\mathop{\sum }_{r\geqslant 1}\frac{(-1)^{b}}{b!}2i\unicode[STIX]{x1D70B}\mathop{\sum }_{j=0}^{a}(-1)^{j}\frac{(a+b-j)!}{j!(a-j)!}\biggl(\frac{m(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})}{N}\biggr)^{-a-b-1+j}\nonumber\\ \displaystyle & & \displaystyle \cdot \,(2i\unicode[STIX]{x1D70B}r)^{j}e^{2i\unicode[STIX]{x1D70B}r((m\unicode[STIX]{x1D70F}-u_{2})/N)}\nonumber\\ \displaystyle & & \displaystyle +\,N^{-a-b-2}\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv u_{1}(N)}}\mathop{\sum }_{r\leqslant -1}\frac{(-1)^{b}}{a!}2i\unicode[STIX]{x1D70B}\mathop{\sum }_{j=0}^{b}\frac{(a+b-j)!}{j!(b-j)!}\biggl(\frac{m(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})}{N}\biggr)^{-a-b-1+j}\nonumber\\ \displaystyle & & \displaystyle \cdot \,(2i\unicode[STIX]{x1D70B}r)^{j}e^{2i\unicode[STIX]{x1D70B}r((m\overline{\unicode[STIX]{x1D70F}}+u_{2})/N)}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(-1)^{a+b}}{N^{a+b+2}}\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv -u_{1}(N)}}\mathop{\sum }_{r\leqslant -1}\frac{(-1)^{b}}{a!}2i\unicode[STIX]{x1D70B}\mathop{\sum }_{j=0}^{b}\frac{(a+b-j)!}{j!(b-j)!}\biggl(\frac{m(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})}{N}\biggr)^{-a-b-1+j}\nonumber\\ \displaystyle & & \displaystyle \cdot \,(2i\unicode[STIX]{x1D70B}r)^{j}e^{2i\unicode[STIX]{x1D70B}r((m\overline{\unicode[STIX]{x1D70F}}-u_{2})/N)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{(u_{1},u_{2})}^{a,b}(\unicode[STIX]{x1D70F}) & = & \displaystyle \unicode[STIX]{x1D6FF}_{u_{1}=0}N^{-a-b-2}\biggl(\unicode[STIX]{x1D701}\biggl(\frac{u_{2}}{N},a+b+2\biggr)+(-1)^{a+b}\unicode[STIX]{x1D701}\biggl(-\frac{u_{2}}{N},a+b+2\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{b}\frac{2i\unicode[STIX]{x1D70B}}{N^{a+b+2}}\left(\begin{array}{@{}c@{}}a+b\\ a\end{array}\right) (\unicode[STIX]{x1D701}\biggl(\frac{u_{1}}{N},a+b+1\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{a+b}\unicode[STIX]{x1D701}\biggl(-\frac{u_{1}}{N},a+b+1\biggr)\!)(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1}\nonumber\\ \displaystyle & & \displaystyle +\,N^{-a-b-2}\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv u_{1}(N)}}\mathop{\sum }_{r\geqslant 1}\frac{(-1)^{b}}{b!}2i\unicode[STIX]{x1D70B}\mathop{\sum }_{j=0}^{a}(-1)^{j}\frac{(a+b-j)!}{j!(a-j)!}\biggl(\frac{m(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})}{N}\biggr)^{-a-b-1+j}\nonumber\\ \displaystyle & & \displaystyle \cdot \,(2i\unicode[STIX]{x1D70B}r)^{j}e^{2i\unicode[STIX]{x1D70B}r((m\unicode[STIX]{x1D70F}+u_{2})/N)}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(-1)^{a+b}}{N^{a+b+2}}\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv -u_{1}(N)}}\mathop{\sum }_{r\geqslant 1}\frac{(-1)^{b}}{b!}2i\unicode[STIX]{x1D70B}\mathop{\sum }_{j=0}^{a}(-1)^{j}\frac{(a+b-j)!}{j!(a-j)!}\biggl(\frac{m(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})}{N}\biggr)^{-a-b-1+j}\nonumber\\ \displaystyle & & \displaystyle \cdot \,(2i\unicode[STIX]{x1D70B}r)^{j}e^{2i\unicode[STIX]{x1D70B}r((m\unicode[STIX]{x1D70F}-u_{2})/N)}\nonumber\\ \displaystyle & & \displaystyle +\,N^{-a-b-2}\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv u_{1}(N)}}\mathop{\sum }_{r\leqslant -1}\frac{(-1)^{b}}{a!}2i\unicode[STIX]{x1D70B}\mathop{\sum }_{j=0}^{b}\frac{(a+b-j)!}{j!(b-j)!}\biggl(\frac{m(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})}{N}\biggr)^{-a-b-1+j}\nonumber\\ \displaystyle & & \displaystyle \cdot \,(2i\unicode[STIX]{x1D70B}r)^{j}e^{2i\unicode[STIX]{x1D70B}r((m\overline{\unicode[STIX]{x1D70F}}+u_{2})/N)}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(-1)^{a+b}}{N^{a+b+2}}\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv -u_{1}(N)}}\mathop{\sum }_{r\leqslant -1}\frac{(-1)^{b}}{a!}2i\unicode[STIX]{x1D70B}\mathop{\sum }_{j=0}^{b}\frac{(a+b-j)!}{j!(b-j)!}\biggl(\frac{m(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})}{N}\biggr)^{-a-b-1+j}\nonumber\\ \displaystyle & & \displaystyle \cdot \,(2i\unicode[STIX]{x1D70B}r)^{j}e^{2i\unicode[STIX]{x1D70B}r((m\overline{\unicode[STIX]{x1D70F}}-u_{2})/N)}.\nonumber\end{eqnarray}$$
On obtient
 $$\begin{eqnarray}\displaystyle & & \displaystyle E_{(u_{1},u_{2})}^{a,b}(\unicode[STIX]{x1D70F})\nonumber\\ \displaystyle & & \displaystyle \hspace{2.5pt}=\unicode[STIX]{x1D6FF}_{u_{1}=0}N^{-a-b-2}\biggl(\unicode[STIX]{x1D701}\biggl(\frac{u_{2}}{N},a+b+2\biggr)+(-1)^{a+b}\unicode[STIX]{x1D701}\biggl(-\frac{u_{2}}{N},a+b+2\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad +\,(-1)^{b}\frac{2i\unicode[STIX]{x1D70B}}{N^{a+b+2}}\left(\begin{array}{@{}c@{}}a+b\\ a\end{array}\right)\biggl(\unicode[STIX]{x1D701}\biggl(\frac{u_{1}}{N},a+b+1\biggr)+(-1)^{a+b}\unicode[STIX]{x1D701}\biggl(-\frac{u_{1}}{N},a+b+1\biggr)\biggr)(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1}\nonumber\\ \displaystyle & & \displaystyle \hspace{2.5pt}\quad +\,\frac{(-1)^{b+1}}{b!}\mathop{\sum }_{j=0}^{a}\frac{(a+b-j)!}{j!(a-j)!}\biggl(-\frac{2i\unicode[STIX]{x1D70B}}{N}\biggr)^{j+1}(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1+j}\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv u_{1}(N)}}\mathop{\sum }_{r\geqslant 1}m^{-a-b-1+j}r^{j}\unicode[STIX]{x1D701}_{N}^{ru_{2}}q^{mr/N}\nonumber\\ \displaystyle & & \displaystyle \hspace{2.5pt}\quad +\,\frac{(-1)^{a+1}}{b!}\mathop{\sum }_{j=0}^{a}\frac{(a+b-j)!}{j!(a-j)!}\biggl(-\frac{2i\unicode[STIX]{x1D70B}}{N}\biggr)^{j+1}(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1+j}\!\!\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv -u_{1}(N)}}\!\!\mathop{\sum }_{r\geqslant 1}m^{-a-b-1+j}r^{j}\unicode[STIX]{x1D701}_{N}^{-ru_{2}}q^{mr/N}\nonumber\\ \displaystyle & & \displaystyle \hspace{2.5pt}\quad +\,\frac{(-1)^{b+1}}{a!}\mathop{\sum }_{j=0}^{b}\frac{(a+b-j)!}{j!(b-j)!}\biggl(-\frac{2i\unicode[STIX]{x1D70B}}{N}\biggr)^{j+1}(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1+j}\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv u_{1}(N)}}\mathop{\sum }_{r\geqslant 1}m^{-a-b-1+j}r^{j}\unicode[STIX]{x1D701}_{N}^{-ru_{2}}\overline{q}^{mr/N}\nonumber\\ \displaystyle & & \displaystyle \hspace{2.5pt}\quad +\,\frac{(-1)^{a+1}}{a!}\mathop{\sum }_{j=0}^{b}\frac{(a+b-j)!}{j!(b-j)!}\biggl(-\frac{2i\unicode[STIX]{x1D70B}}{N}\biggr)^{j+1}(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1+j}\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv -u_{1}(N)}}\mathop{\sum }_{r\geqslant 1}m^{-a-b-1+j}r^{j}\unicode[STIX]{x1D701}_{N}^{ru_{2}}\overline{q}^{mr/N}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle E_{(u_{1},u_{2})}^{a,b}(\unicode[STIX]{x1D70F})\nonumber\\ \displaystyle & & \displaystyle \hspace{2.5pt}=\unicode[STIX]{x1D6FF}_{u_{1}=0}N^{-a-b-2}\biggl(\unicode[STIX]{x1D701}\biggl(\frac{u_{2}}{N},a+b+2\biggr)+(-1)^{a+b}\unicode[STIX]{x1D701}\biggl(-\frac{u_{2}}{N},a+b+2\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad +\,(-1)^{b}\frac{2i\unicode[STIX]{x1D70B}}{N^{a+b+2}}\left(\begin{array}{@{}c@{}}a+b\\ a\end{array}\right)\biggl(\unicode[STIX]{x1D701}\biggl(\frac{u_{1}}{N},a+b+1\biggr)+(-1)^{a+b}\unicode[STIX]{x1D701}\biggl(-\frac{u_{1}}{N},a+b+1\biggr)\biggr)(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1}\nonumber\\ \displaystyle & & \displaystyle \hspace{2.5pt}\quad +\,\frac{(-1)^{b+1}}{b!}\mathop{\sum }_{j=0}^{a}\frac{(a+b-j)!}{j!(a-j)!}\biggl(-\frac{2i\unicode[STIX]{x1D70B}}{N}\biggr)^{j+1}(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1+j}\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv u_{1}(N)}}\mathop{\sum }_{r\geqslant 1}m^{-a-b-1+j}r^{j}\unicode[STIX]{x1D701}_{N}^{ru_{2}}q^{mr/N}\nonumber\\ \displaystyle & & \displaystyle \hspace{2.5pt}\quad +\,\frac{(-1)^{a+1}}{b!}\mathop{\sum }_{j=0}^{a}\frac{(a+b-j)!}{j!(a-j)!}\biggl(-\frac{2i\unicode[STIX]{x1D70B}}{N}\biggr)^{j+1}(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1+j}\!\!\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv -u_{1}(N)}}\!\!\mathop{\sum }_{r\geqslant 1}m^{-a-b-1+j}r^{j}\unicode[STIX]{x1D701}_{N}^{-ru_{2}}q^{mr/N}\nonumber\\ \displaystyle & & \displaystyle \hspace{2.5pt}\quad +\,\frac{(-1)^{b+1}}{a!}\mathop{\sum }_{j=0}^{b}\frac{(a+b-j)!}{j!(b-j)!}\biggl(-\frac{2i\unicode[STIX]{x1D70B}}{N}\biggr)^{j+1}(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1+j}\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv u_{1}(N)}}\mathop{\sum }_{r\geqslant 1}m^{-a-b-1+j}r^{j}\unicode[STIX]{x1D701}_{N}^{-ru_{2}}\overline{q}^{mr/N}\nonumber\\ \displaystyle & & \displaystyle \hspace{2.5pt}\quad +\,\frac{(-1)^{a+1}}{a!}\mathop{\sum }_{j=0}^{b}\frac{(a+b-j)!}{j!(b-j)!}\biggl(-\frac{2i\unicode[STIX]{x1D70B}}{N}\biggr)^{j+1}(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1+j}\mathop{\sum }_{\substack{ m\geqslant 1 \\ m\equiv -u_{1}(N)}}\mathop{\sum }_{r\geqslant 1}m^{-a-b-1+j}r^{j}\unicode[STIX]{x1D701}_{N}^{ru_{2}}\overline{q}^{mr/N}\nonumber\end{eqnarray}$$
d’où le résultat. ◻
Proposition 8.4. Pour
![]() $a,b\geqslant 0$
et
$a,b\geqslant 0$
et
![]() $u_{1},u_{2}\in \mathbf{Z}/N\mathbf{Z}$
, on a
$u_{1},u_{2}\in \mathbf{Z}/N\mathbf{Z}$
, on a
 $$\begin{eqnarray}\displaystyle F_{(u_{1},u_{2})}^{a,b}(\unicode[STIX]{x1D70F}) & = & \displaystyle \hat{\unicode[STIX]{x1D701}}\biggl(\frac{u_{2}}{N},a+b+2\biggr)+(-1)^{a+b}\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{u_{2}}{N},a+b+2\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{b}2i\unicode[STIX]{x1D70B}\left(\begin{array}{@{}c@{}}a+b\\ a\end{array}\right)\unicode[STIX]{x1D6FF}_{0}(u_{2})(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1} (\hat{\unicode[STIX]{x1D701}}\biggl(\frac{u_{1}}{N},a+b+1\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{a+b}\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{u_{1}}{N},a+b+1\biggr)\!)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(-1)^{b+1}}{b!}\mathop{\sum }_{j=0}^{a}\frac{(a+b-j)!}{j!(a-j)!}\biggl(-\frac{2i\unicode[STIX]{x1D70B}}{N}\biggr)^{j+1}(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1+j}N(S_{\hat{\unicode[STIX]{x1D6FF}}_{-u_{1}},\unicode[STIX]{x1D6FF}_{-u_{2}}}^{j-a-b-1,j}(\unicode[STIX]{x1D70F})\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{a+b}S_{\hat{\unicode[STIX]{x1D6FF}}_{u_{1}},\unicode[STIX]{x1D6FF}_{u_{2}}}^{j-a-b-1,j}(\unicode[STIX]{x1D70F}))\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(-1)^{b+1}}{a!}\mathop{\sum }_{j=0}^{b}\frac{(a+b-j)!}{j!(b-j)!}\biggl(-\frac{2i\unicode[STIX]{x1D70B}}{N}\biggr)^{j+1}(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1+j}N(\overline{S}_{\hat{\unicode[STIX]{x1D6FF}}_{u_{1}},\unicode[STIX]{x1D6FF}_{u_{2}}}^{j-a-b-1,j}(\unicode[STIX]{x1D70F})\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{a+b}\overline{S}_{\hat{\unicode[STIX]{x1D6FF}}_{-u_{1}},\unicode[STIX]{x1D6FF}_{-u_{2}}}^{j-a-b-1,j}(\unicode[STIX]{x1D70F})).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{(u_{1},u_{2})}^{a,b}(\unicode[STIX]{x1D70F}) & = & \displaystyle \hat{\unicode[STIX]{x1D701}}\biggl(\frac{u_{2}}{N},a+b+2\biggr)+(-1)^{a+b}\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{u_{2}}{N},a+b+2\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{b}2i\unicode[STIX]{x1D70B}\left(\begin{array}{@{}c@{}}a+b\\ a\end{array}\right)\unicode[STIX]{x1D6FF}_{0}(u_{2})(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1} (\hat{\unicode[STIX]{x1D701}}\biggl(\frac{u_{1}}{N},a+b+1\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{a+b}\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{u_{1}}{N},a+b+1\biggr)\!)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(-1)^{b+1}}{b!}\mathop{\sum }_{j=0}^{a}\frac{(a+b-j)!}{j!(a-j)!}\biggl(-\frac{2i\unicode[STIX]{x1D70B}}{N}\biggr)^{j+1}(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1+j}N(S_{\hat{\unicode[STIX]{x1D6FF}}_{-u_{1}},\unicode[STIX]{x1D6FF}_{-u_{2}}}^{j-a-b-1,j}(\unicode[STIX]{x1D70F})\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{a+b}S_{\hat{\unicode[STIX]{x1D6FF}}_{u_{1}},\unicode[STIX]{x1D6FF}_{u_{2}}}^{j-a-b-1,j}(\unicode[STIX]{x1D70F}))\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(-1)^{b+1}}{a!}\mathop{\sum }_{j=0}^{b}\frac{(a+b-j)!}{j!(b-j)!}\biggl(-\frac{2i\unicode[STIX]{x1D70B}}{N}\biggr)^{j+1}(\unicode[STIX]{x1D70F}-\overline{\unicode[STIX]{x1D70F}})^{-a-b-1+j}N(\overline{S}_{\hat{\unicode[STIX]{x1D6FF}}_{u_{1}},\unicode[STIX]{x1D6FF}_{u_{2}}}^{j-a-b-1,j}(\unicode[STIX]{x1D70F})\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{a+b}\overline{S}_{\hat{\unicode[STIX]{x1D6FF}}_{-u_{1}},\unicode[STIX]{x1D6FF}_{-u_{2}}}^{j-a-b-1,j}(\unicode[STIX]{x1D70F})).\end{eqnarray}$$
On déduit le développement de Fourier de
![]() $\text{Eis}_{{\mathcal{D}}}^{n}(u)$
de la formule (20) et de la proposition 8.4.
$\text{Eis}_{{\mathcal{D}}}^{n}(u)$
de la formule (20) et de la proposition 8.4.
9 Calcul du régulateur
Le calcul de l’intégrale de
![]() $\text{Eis}_{{\mathcal{D}}}^{k_{1},k_{2}}(u_{1},u_{2})$
le long du cycle de Shokurov
$\text{Eis}_{{\mathcal{D}}}^{k_{1},k_{2}}(u_{1},u_{2})$
le long du cycle de Shokurov
![]() $X^{k}\{0,\infty \}$
procède en trois étapes. Dans un premier temps, nous intégrons
$X^{k}\{0,\infty \}$
procède en trois étapes. Dans un premier temps, nous intégrons
![]() $\text{Eis}_{{\mathcal{D}}}^{k_{1},k_{2}}(u_{1},u_{2})$
sur les fibres
$\text{Eis}_{{\mathcal{D}}}^{k_{1},k_{2}}(u_{1},u_{2})$
sur les fibres
![]() $\unicode[STIX]{x1D6FE}_{y,k}$
du cycle de Shokurov. Dans un deuxième temps, nous intégrons le résultat obtenu le long du symbole modulaire
$\unicode[STIX]{x1D6FE}_{y,k}$
du cycle de Shokurov. Dans un deuxième temps, nous intégrons le résultat obtenu le long du symbole modulaire
![]() $\{0,\infty \}$
, à l’aide de la méthode de Rogers–Zudilin. L’expression obtenue (33) comporte six termes : un terme principal (noté
$\{0,\infty \}$
, à l’aide de la méthode de Rogers–Zudilin. L’expression obtenue (33) comporte six termes : un terme principal (noté
![]() $A$
) et cinq termes supplémentaires (notés
$A$
) et cinq termes supplémentaires (notés
![]() $B$
à
$B$
à
![]() $F$
) provenant des termes constants des séries d’Eisenstein. Dans un troisième temps, nous montrons que tous les termes supplémentaires se simplifient.
$F$
) provenant des termes constants des séries d’Eisenstein. Dans un troisième temps, nous montrons que tous les termes supplémentaires se simplifient.
Soit
![]() $p:E^{k}(\mathbf{C})\rightarrow Y(N)(\mathbf{C})$
la projection canonique. On a une application naturelle
$p:E^{k}(\mathbf{C})\rightarrow Y(N)(\mathbf{C})$
la projection canonique. On a une application naturelle
![]() $\unicode[STIX]{x1D708}:{\mathcal{H}}\rightarrow Y(N)(\mathbf{C})$
donnée par
$\unicode[STIX]{x1D708}:{\mathcal{H}}\rightarrow Y(N)(\mathbf{C})$
donnée par
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D70F})=[(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E})]$
, qui nous permet de voir le chemin
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D70F})=[(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E})]$
, qui nous permet de voir le chemin
![]() $\{0,\infty \}$
comme une sous-variété de
$\{0,\infty \}$
comme une sous-variété de
![]() $Y(N)(\mathbf{C})$
. Considérons la sous-variété
$Y(N)(\mathbf{C})$
. Considérons la sous-variété
![]() $W=p^{-1}(\{0,\infty \})$
de
$W=p^{-1}(\{0,\infty \})$
de
![]() $E^{k}(\mathbf{C})$
. On a
$E^{k}(\mathbf{C})$
. On a
Soient
![]() $u_{1}=(a_{1},b_{1})$
,
$u_{1}=(a_{1},b_{1})$
,
![]() $u_{2}=(a_{2},b_{2})\in (\mathbf{Z}/N\mathbf{Z})^{2}$
. Nous allons calculer la restriction de
$u_{2}=(a_{2},b_{2})\in (\mathbf{Z}/N\mathbf{Z})^{2}$
. Nous allons calculer la restriction de
![]() $\text{Eis}_{{\mathcal{D}}}^{k_{1},k_{2}}(u_{1},u_{2})$
à
$\text{Eis}_{{\mathcal{D}}}^{k_{1},k_{2}}(u_{1},u_{2})$
à
![]() $W$
. D’après la proposition 5.4, on a
$W$
. D’après la proposition 5.4, on a
Comme
![]() $\text{Eis}_{{\mathcal{D}}}^{k_{1}}(u_{1})$
est invariante par
$\text{Eis}_{{\mathcal{D}}}^{k_{1}}(u_{1})$
est invariante par
![]() $\unicode[STIX]{x1D70E}:(\unicode[STIX]{x1D70F},z,g)\mapsto (-1/\unicode[STIX]{x1D70F},z/\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}g)$
, il vient
$\unicode[STIX]{x1D70E}:(\unicode[STIX]{x1D70F},z,g)\mapsto (-1/\unicode[STIX]{x1D70F},z/\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}g)$
, il vient
 $$\begin{eqnarray}\displaystyle \text{Eis}_{{\mathcal{D}}}^{k_{1}}(u_{1}) & = & \displaystyle \unicode[STIX]{x1D70E}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{1}}(u_{1})\nonumber\\ \displaystyle & = & \displaystyle -\frac{k_{1}!(k_{1}+2)}{2\unicode[STIX]{x1D70B}N}\Im \biggl(-\frac{1}{\unicode[STIX]{x1D70F}}\biggr)\mathop{\sum }_{a=0}^{k_{1}}F_{\unicode[STIX]{x1D70E}gu_{1}}^{a,k_{1}-a}\biggl(-\frac{1}{\unicode[STIX]{x1D70F}}\biggr)\unicode[STIX]{x1D70F}^{-a}\overline{\unicode[STIX]{x1D70F}}^{-k_{1}+a}\unicode[STIX]{x1D713}_{a,k_{1}-a}\hspace{0.6em}{\rm mod}\hspace{0.2em}d\unicode[STIX]{x1D70F},d\overline{\unicode[STIX]{x1D70F}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Eis}_{{\mathcal{D}}}^{k_{1}}(u_{1}) & = & \displaystyle \unicode[STIX]{x1D70E}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{1}}(u_{1})\nonumber\\ \displaystyle & = & \displaystyle -\frac{k_{1}!(k_{1}+2)}{2\unicode[STIX]{x1D70B}N}\Im \biggl(-\frac{1}{\unicode[STIX]{x1D70F}}\biggr)\mathop{\sum }_{a=0}^{k_{1}}F_{\unicode[STIX]{x1D70E}gu_{1}}^{a,k_{1}-a}\biggl(-\frac{1}{\unicode[STIX]{x1D70F}}\biggr)\unicode[STIX]{x1D70F}^{-a}\overline{\unicode[STIX]{x1D70F}}^{-k_{1}+a}\unicode[STIX]{x1D713}_{a,k_{1}-a}\hspace{0.6em}{\rm mod}\hspace{0.2em}d\unicode[STIX]{x1D70F},d\overline{\unicode[STIX]{x1D70F}}.\nonumber\end{eqnarray}$$
En restreignant à
![]() $W$
, il vient
$W$
, il vient
 $$\begin{eqnarray}\displaystyle p_{1}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{1}}(u_{1})|_{W} & = & \displaystyle -\frac{k_{1}!(k_{1}+2)}{2\unicode[STIX]{x1D70B}N}y^{-1}\mathop{\sum }_{a=0}^{k_{1}}F_{-u_{1}}^{a,k_{1}-a}\biggl(\frac{i}{y}\biggr)(iy)^{-a}(-iy)^{-k_{1}+a}p_{1}^{\ast }\unicode[STIX]{x1D713}_{a,k_{1}-a}\hspace{0.6em}{\rm mod}\hspace{0.2em}dy\nonumber\\ \displaystyle & = & \displaystyle -\frac{k_{1}!(k_{1}+2)}{2\unicode[STIX]{x1D70B}N}y^{-1}(iy)^{-k_{1}}\mathop{\sum }_{a=0}^{k_{1}}F_{-u_{1}}^{a,k_{1}-a}\biggl(\frac{i}{y}\biggr)(-1)^{-k_{1}+a}p_{1}^{\ast }\unicode[STIX]{x1D713}_{a,k_{1}-a}\hspace{0.6em}{\rm mod}\hspace{0.2em}dy.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle p_{1}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{1}}(u_{1})|_{W} & = & \displaystyle -\frac{k_{1}!(k_{1}+2)}{2\unicode[STIX]{x1D70B}N}y^{-1}\mathop{\sum }_{a=0}^{k_{1}}F_{-u_{1}}^{a,k_{1}-a}\biggl(\frac{i}{y}\biggr)(iy)^{-a}(-iy)^{-k_{1}+a}p_{1}^{\ast }\unicode[STIX]{x1D713}_{a,k_{1}-a}\hspace{0.6em}{\rm mod}\hspace{0.2em}dy\nonumber\\ \displaystyle & = & \displaystyle -\frac{k_{1}!(k_{1}+2)}{2\unicode[STIX]{x1D70B}N}y^{-1}(iy)^{-k_{1}}\mathop{\sum }_{a=0}^{k_{1}}F_{-u_{1}}^{a,k_{1}-a}\biggl(\frac{i}{y}\biggr)(-1)^{-k_{1}+a}p_{1}^{\ast }\unicode[STIX]{x1D713}_{a,k_{1}-a}\hspace{0.6em}{\rm mod}\hspace{0.2em}dy.\end{eqnarray}$$
En utilisant la proposition 8.4, il vient
 $$\begin{eqnarray}\displaystyle F_{-u_{1}}^{a,k_{1}-a}\biggl(\frac{i}{y}\biggr) & = & \displaystyle \unicode[STIX]{x1D6FC}_{1}+(-1)^{k_{1}-a}\left(\begin{array}{@{}c@{}}k_{1}\\ a\end{array}\right)\unicode[STIX]{x1D6FD}_{1}y^{k_{1}+1}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(-1)^{k_{1}+1-a}}{(k_{1}-a)!}N\mathop{\sum }_{\ell =0}^{a}\frac{(k_{1}-\ell )!}{\ell !(a-\ell )!}\biggl(-\frac{2i\unicode[STIX]{x1D70B}}{N}\biggr)^{\ell +1}\biggl(\frac{2i}{y}\biggr)^{-k_{1}-1+\ell } (S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}}^{\ell -k_{1}-1,\ell }\biggl(\frac{i}{y}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{k_{1}}S_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{-b_{1}}}^{\ell -k_{1}-1,\ell }\biggl(\frac{i}{y}\biggr)\!)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(-1)^{k_{1}+1-a}}{a!}N\mathop{\sum }_{\ell =0}^{k_{1}-a}\frac{(k_{1}-\ell )!}{\ell !(k_{1}-a-\ell )!}\biggl(-\frac{2i\unicode[STIX]{x1D70B}}{N}\biggr)^{\ell +1}\biggl(\frac{2i}{y}\biggr)^{-k_{1}-1+\ell } (\overline{S}_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{-b_{1}}}^{\ell -k_{1}-1,\ell }\biggl(\frac{i}{y}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{k_{1}}\overline{S}_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}}^{\ell -k_{1}-1,\ell }\biggl(\frac{i}{y}\biggr)\!)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{-u_{1}}^{a,k_{1}-a}\biggl(\frac{i}{y}\biggr) & = & \displaystyle \unicode[STIX]{x1D6FC}_{1}+(-1)^{k_{1}-a}\left(\begin{array}{@{}c@{}}k_{1}\\ a\end{array}\right)\unicode[STIX]{x1D6FD}_{1}y^{k_{1}+1}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(-1)^{k_{1}+1-a}}{(k_{1}-a)!}N\mathop{\sum }_{\ell =0}^{a}\frac{(k_{1}-\ell )!}{\ell !(a-\ell )!}\biggl(-\frac{2i\unicode[STIX]{x1D70B}}{N}\biggr)^{\ell +1}\biggl(\frac{2i}{y}\biggr)^{-k_{1}-1+\ell } (S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}}^{\ell -k_{1}-1,\ell }\biggl(\frac{i}{y}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{k_{1}}S_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{-b_{1}}}^{\ell -k_{1}-1,\ell }\biggl(\frac{i}{y}\biggr)\!)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(-1)^{k_{1}+1-a}}{a!}N\mathop{\sum }_{\ell =0}^{k_{1}-a}\frac{(k_{1}-\ell )!}{\ell !(k_{1}-a-\ell )!}\biggl(-\frac{2i\unicode[STIX]{x1D70B}}{N}\biggr)^{\ell +1}\biggl(\frac{2i}{y}\biggr)^{-k_{1}-1+\ell } (\overline{S}_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{-b_{1}}}^{\ell -k_{1}-1,\ell }\biggl(\frac{i}{y}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{k_{1}}\overline{S}_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}}^{\ell -k_{1}-1,\ell }\biggl(\frac{i}{y}\biggr)\!)\nonumber\end{eqnarray}$$
avec
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FC}_{1}=\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k_{1}+2\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k_{1}+2\biggr), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6FD}_{1}=2i\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FF}_{b_{1}=0}(2i)^{-k_{1}-1}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},k_{1}+1\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},k_{1}+1\biggr)\biggr). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FC}_{1}=\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k_{1}+2\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k_{1}+2\biggr), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6FD}_{1}=2i\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FF}_{b_{1}=0}(2i)^{-k_{1}-1}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},k_{1}+1\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},k_{1}+1\biggr)\biggr). & \displaystyle \nonumber\end{eqnarray}$$
En reportant dans (23), il vient
avec
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D702}_{1} & = & \displaystyle (-1)^{k_{1}+1}\frac{k_{1}!(k_{1}+2)}{2^{k_{1}+3}\unicode[STIX]{x1D70B}}\mathop{\sum }_{\ell =0}^{k_{1}}\biggl(S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}}^{\ell -k_{1}-1,\ell }\biggl(\frac{i}{y}\biggr)+(-1)^{k_{1}}S_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{-b_{1}}}^{\ell -k_{1}-1,\ell }\biggl(\frac{i}{y}\biggr)\biggr)\unicode[STIX]{x1D6FA}_{\ell }\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{k_{1}+1}\frac{k_{1}!(k_{1}+2)}{2^{k_{1}+3}\unicode[STIX]{x1D70B}}\mathop{\sum }_{\ell =0}^{k_{1}}\biggl(\overline{S}_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{-b_{1}}}^{\ell -k_{1}-1,\ell }\biggl(\frac{i}{y}\biggr)+(-1)^{k_{1}}\overline{S}_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}}^{\ell -k_{1}-1,\ell }\biggl(\frac{i}{y}\biggr)\biggr)\overline{\unicode[STIX]{x1D6FA}_{\ell }}\hspace{0.6em}{\rm mod}\hspace{0.2em}dy\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D702}_{1} & = & \displaystyle (-1)^{k_{1}+1}\frac{k_{1}!(k_{1}+2)}{2^{k_{1}+3}\unicode[STIX]{x1D70B}}\mathop{\sum }_{\ell =0}^{k_{1}}\biggl(S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}}^{\ell -k_{1}-1,\ell }\biggl(\frac{i}{y}\biggr)+(-1)^{k_{1}}S_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{-b_{1}}}^{\ell -k_{1}-1,\ell }\biggl(\frac{i}{y}\biggr)\biggr)\unicode[STIX]{x1D6FA}_{\ell }\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{k_{1}+1}\frac{k_{1}!(k_{1}+2)}{2^{k_{1}+3}\unicode[STIX]{x1D70B}}\mathop{\sum }_{\ell =0}^{k_{1}}\biggl(\overline{S}_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{-b_{1}}}^{\ell -k_{1}-1,\ell }\biggl(\frac{i}{y}\biggr)+(-1)^{k_{1}}\overline{S}_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}}^{\ell -k_{1}-1,\ell }\biggl(\frac{i}{y}\biggr)\biggr)\overline{\unicode[STIX]{x1D6FA}_{\ell }}\hspace{0.6em}{\rm mod}\hspace{0.2em}dy\end{eqnarray}$$
où l’on a posé, pour tout
![]() $0\leqslant \ell \leqslant k_{1}$
,
$0\leqslant \ell \leqslant k_{1}$
,
D’autre part, en utilisant la proposition 8.1, on a
 $$\begin{eqnarray}\displaystyle p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{2}}(u_{2}) & = & \displaystyle (-1)^{k_{2}+1}\frac{k_{2}+2}{N}(2i\unicode[STIX]{x1D70B})^{k_{2}}F_{\unicode[STIX]{x1D70E}gu_{2}}^{(k_{2}+2)}(\unicode[STIX]{x1D70F})\,\frac{dq}{q}\wedge p_{2}^{\ast }\unicode[STIX]{x1D713}_{k_{2},0}\nonumber\\ \displaystyle & = & \displaystyle (-1)^{k_{2}+1}\frac{k_{2}+2}{N}(2i\unicode[STIX]{x1D70B})^{k_{2}+1}F_{\unicode[STIX]{x1D70E}gu_{2}}^{(k_{2}+2)}(\unicode[STIX]{x1D70F})\,d\unicode[STIX]{x1D70F}\wedge p_{2}^{\ast }\unicode[STIX]{x1D713}_{k_{2},0}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{2}}(u_{2}) & = & \displaystyle (-1)^{k_{2}+1}\frac{k_{2}+2}{N}(2i\unicode[STIX]{x1D70B})^{k_{2}}F_{\unicode[STIX]{x1D70E}gu_{2}}^{(k_{2}+2)}(\unicode[STIX]{x1D70F})\,\frac{dq}{q}\wedge p_{2}^{\ast }\unicode[STIX]{x1D713}_{k_{2},0}\nonumber\\ \displaystyle & = & \displaystyle (-1)^{k_{2}+1}\frac{k_{2}+2}{N}(2i\unicode[STIX]{x1D70B})^{k_{2}+1}F_{\unicode[STIX]{x1D70E}gu_{2}}^{(k_{2}+2)}(\unicode[STIX]{x1D70F})\,d\unicode[STIX]{x1D70F}\wedge p_{2}^{\ast }\unicode[STIX]{x1D713}_{k_{2},0}\nonumber\end{eqnarray}$$
d’où
puis
Lemme 9.1. Soit
![]() $0\leqslant a\leqslant k_{1}$
un entier. On a
$0\leqslant a\leqslant k_{1}$
un entier. On a
Démonstration.
Cela résulte d’un calcul direct. ◻
Lemme 9.2. Pour tout entier
![]() $0\leqslant \ell \leqslant k_{1}$
, on a
$0\leqslant \ell \leqslant k_{1}$
, on a
 $$\begin{eqnarray}\displaystyle & \displaystyle \int _{\unicode[STIX]{x1D6FE}_{y,k}}\unicode[STIX]{x1D6FA}_{\ell }\wedge p_{2}^{\ast }\unicode[STIX]{x1D713}_{k_{2},0}=\left\{\begin{array}{@{}ll@{}}\displaystyle 0\quad & \text{si }\ell <k_{1},\\ \displaystyle \frac{i^{k}}{k_{1}!}\biggl(\frac{4\unicode[STIX]{x1D70B}}{N}\biggr)^{k_{1}+1}y^{k_{2}}\quad & \text{si }\ell =k_{1},\end{array}\right. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \int _{\unicode[STIX]{x1D6FE}_{y,k}}\unicode[STIX]{x1D6FA}_{\ell }\wedge p_{2}^{\ast }\unicode[STIX]{x1D713}_{0,k_{2}}=\left\{\begin{array}{@{}ll@{}}\displaystyle 0\quad & \text{si }\ell <k_{1},\\ \displaystyle (-1)^{k_{2}}\frac{i^{k}}{k_{1}!}\biggl(\frac{4\unicode[STIX]{x1D70B}}{N}\biggr)^{k_{1}+1}y^{k_{2}}\quad & \text{si }\ell =k_{1},\end{array}\right. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \int _{\unicode[STIX]{x1D6FE}_{y,k}}\overline{\unicode[STIX]{x1D6FA}_{\ell }}\wedge p_{2}^{\ast }\unicode[STIX]{x1D713}_{k_{2},0}=\left\{\begin{array}{@{}ll@{}}0\quad & \text{si }\ell <k_{1},\\ \displaystyle (-1)^{k_{1}}\frac{i^{k}}{k_{1}!}\biggl(\frac{4\unicode[STIX]{x1D70B}}{N}\biggr)^{k_{1}+1}y^{k_{2}}\quad & \text{si }\ell =k_{1},\end{array}\right. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \int _{\unicode[STIX]{x1D6FE}_{y,k}}\overline{\unicode[STIX]{x1D6FA}_{\ell }}\wedge p_{2}^{\ast }\unicode[STIX]{x1D713}_{0,k_{2}}=\left\{\begin{array}{@{}ll@{}}\displaystyle 0\quad & \text{si }\ell <k_{1},\\ \displaystyle (-1)^{k}\frac{i^{k}}{k_{1}!}\biggl(\frac{4\unicode[STIX]{x1D70B}}{N}\biggr)^{k_{1}+1}y^{k_{2}}\quad & \text{si }\ell =k_{1}.\end{array}\right. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \int _{\unicode[STIX]{x1D6FE}_{y,k}}\unicode[STIX]{x1D6FA}_{\ell }\wedge p_{2}^{\ast }\unicode[STIX]{x1D713}_{k_{2},0}=\left\{\begin{array}{@{}ll@{}}\displaystyle 0\quad & \text{si }\ell <k_{1},\\ \displaystyle \frac{i^{k}}{k_{1}!}\biggl(\frac{4\unicode[STIX]{x1D70B}}{N}\biggr)^{k_{1}+1}y^{k_{2}}\quad & \text{si }\ell =k_{1},\end{array}\right. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \int _{\unicode[STIX]{x1D6FE}_{y,k}}\unicode[STIX]{x1D6FA}_{\ell }\wedge p_{2}^{\ast }\unicode[STIX]{x1D713}_{0,k_{2}}=\left\{\begin{array}{@{}ll@{}}\displaystyle 0\quad & \text{si }\ell <k_{1},\\ \displaystyle (-1)^{k_{2}}\frac{i^{k}}{k_{1}!}\biggl(\frac{4\unicode[STIX]{x1D70B}}{N}\biggr)^{k_{1}+1}y^{k_{2}}\quad & \text{si }\ell =k_{1},\end{array}\right. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \int _{\unicode[STIX]{x1D6FE}_{y,k}}\overline{\unicode[STIX]{x1D6FA}_{\ell }}\wedge p_{2}^{\ast }\unicode[STIX]{x1D713}_{k_{2},0}=\left\{\begin{array}{@{}ll@{}}0\quad & \text{si }\ell <k_{1},\\ \displaystyle (-1)^{k_{1}}\frac{i^{k}}{k_{1}!}\biggl(\frac{4\unicode[STIX]{x1D70B}}{N}\biggr)^{k_{1}+1}y^{k_{2}}\quad & \text{si }\ell =k_{1},\end{array}\right. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \int _{\unicode[STIX]{x1D6FE}_{y,k}}\overline{\unicode[STIX]{x1D6FA}_{\ell }}\wedge p_{2}^{\ast }\unicode[STIX]{x1D713}_{0,k_{2}}=\left\{\begin{array}{@{}ll@{}}\displaystyle 0\quad & \text{si }\ell <k_{1},\\ \displaystyle (-1)^{k}\frac{i^{k}}{k_{1}!}\biggl(\frac{4\unicode[STIX]{x1D70B}}{N}\biggr)^{k_{1}+1}y^{k_{2}}\quad & \text{si }\ell =k_{1}.\end{array}\right. & \displaystyle \nonumber\end{eqnarray}$$
Démonstration.
On applique le lemme 9.1 avec
![]() $m=k=k_{1}+k_{2}$
, ce qui donne
$m=k=k_{1}+k_{2}$
, ce qui donne
 $$\begin{eqnarray}\displaystyle \int _{\unicode[STIX]{x1D6FE}_{y,k}}\unicode[STIX]{x1D6FA}_{\ell }\wedge p_{2}^{\ast }\unicode[STIX]{x1D713}_{k_{2},0} & = & \displaystyle \frac{(k_{1}-\ell )!}{\ell !}\biggl(\frac{4\unicode[STIX]{x1D70B}}{N}\biggr)^{\ell +1}y^{-\ell }\mathop{\sum }_{a=\ell }^{k_{1}}\frac{1}{(k_{1}-a)!(a-\ell )!}\int _{\unicode[STIX]{x1D6FE}_{y,k}}p_{1}^{\ast }\unicode[STIX]{x1D713}_{a,k_{1}-a}\wedge p_{2}^{\ast }\unicode[STIX]{x1D713}_{k_{2},0}\nonumber\\ \displaystyle & = & \displaystyle \frac{(k_{1}-\ell )!}{\ell !}\biggl(\frac{4\unicode[STIX]{x1D70B}}{N}\biggr)^{\ell +1}y^{-\ell }\mathop{\sum }_{a=\ell }^{k_{1}}\frac{(-1)^{k_{1}-a}(iy)^{k}}{(k_{1}-a)!(a-\ell )!}\nonumber\\ \displaystyle & = & \displaystyle \frac{(k_{1}-\ell )!}{\ell !}\biggl(\frac{4\unicode[STIX]{x1D70B}}{N}\biggr)^{\ell +1}y^{-\ell }(iy)^{k}\mathop{\sum }_{a=0}^{k_{1}-\ell }\frac{(-1)^{k_{1}-\ell -a}}{(k_{1}-\ell -a)!a!}\nonumber\\ \displaystyle & = & \displaystyle \left\{\begin{array}{@{}ll@{}}\displaystyle 0\quad & \text{si }\ell <k_{1},\\ \displaystyle \frac{i^{k}}{k_{1}!}\biggl(\frac{4\unicode[STIX]{x1D70B}}{N}\biggr)^{k_{1}+1}y^{k_{2}}\quad & \text{si }\ell =k_{1}.\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{\unicode[STIX]{x1D6FE}_{y,k}}\unicode[STIX]{x1D6FA}_{\ell }\wedge p_{2}^{\ast }\unicode[STIX]{x1D713}_{k_{2},0} & = & \displaystyle \frac{(k_{1}-\ell )!}{\ell !}\biggl(\frac{4\unicode[STIX]{x1D70B}}{N}\biggr)^{\ell +1}y^{-\ell }\mathop{\sum }_{a=\ell }^{k_{1}}\frac{1}{(k_{1}-a)!(a-\ell )!}\int _{\unicode[STIX]{x1D6FE}_{y,k}}p_{1}^{\ast }\unicode[STIX]{x1D713}_{a,k_{1}-a}\wedge p_{2}^{\ast }\unicode[STIX]{x1D713}_{k_{2},0}\nonumber\\ \displaystyle & = & \displaystyle \frac{(k_{1}-\ell )!}{\ell !}\biggl(\frac{4\unicode[STIX]{x1D70B}}{N}\biggr)^{\ell +1}y^{-\ell }\mathop{\sum }_{a=\ell }^{k_{1}}\frac{(-1)^{k_{1}-a}(iy)^{k}}{(k_{1}-a)!(a-\ell )!}\nonumber\\ \displaystyle & = & \displaystyle \frac{(k_{1}-\ell )!}{\ell !}\biggl(\frac{4\unicode[STIX]{x1D70B}}{N}\biggr)^{\ell +1}y^{-\ell }(iy)^{k}\mathop{\sum }_{a=0}^{k_{1}-\ell }\frac{(-1)^{k_{1}-\ell -a}}{(k_{1}-\ell -a)!a!}\nonumber\\ \displaystyle & = & \displaystyle \left\{\begin{array}{@{}ll@{}}\displaystyle 0\quad & \text{si }\ell <k_{1},\\ \displaystyle \frac{i^{k}}{k_{1}!}\biggl(\frac{4\unicode[STIX]{x1D70B}}{N}\biggr)^{k_{1}+1}y^{k_{2}}\quad & \text{si }\ell =k_{1}.\end{array}\right.\nonumber\end{eqnarray}$$
Les autres cas se traitent de manière similaire. ◻
On intègre
![]() $\unicode[STIX]{x1D702}_{0}\wedge \unicode[STIX]{x1D70B}_{k_{2}+1}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{2}}(u_{2}))$
sur les fibres de
$\unicode[STIX]{x1D702}_{0}\wedge \unicode[STIX]{x1D70B}_{k_{2}+1}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{2}}(u_{2}))$
sur les fibres de
![]() $X^{k}\{0,\infty \}\rightarrow \{0,\infty \}$
grâce au lemme 9.1, ce qui donne
$X^{k}\{0,\infty \}\rightarrow \{0,\infty \}$
grâce au lemme 9.1, ce qui donne
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D6FE}_{y,k}}\unicode[STIX]{x1D702}_{0}\wedge \unicode[STIX]{x1D70B}_{k_{2}+1}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{2}}(u_{2}))\nonumber\\ \displaystyle & & \displaystyle \quad =-(-1)^{k_{1}}\frac{k_{1}!(k_{1}+2)}{2\unicode[STIX]{x1D70B}N}i^{-k_{1}}\cdot i\frac{k_{2}+2}{2N}(-2i\unicode[STIX]{x1D70B})^{k_{2}+1}\,dy\mathop{\sum }_{a=0}^{k_{1}}\left((-1)^{k_{1}-a}\unicode[STIX]{x1D6FC}_{1}y^{-k_{1}-1}+\left(\begin{array}{@{}c@{}}k_{1}\\ a\end{array}\right)\unicode[STIX]{x1D6FD}_{1}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\int _{\unicode[STIX]{x1D6FE}_{y,k}}p_{1}^{\ast }\unicode[STIX]{x1D713}_{a,k_{1}-a}\wedge (F_{-u_{2}}^{(k_{2}+2)}(iy)p_{2}^{\ast }\unicode[STIX]{x1D713}_{k_{2},0}-\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy)p_{2}^{\ast }\unicode[STIX]{x1D713}_{0,k_{2}})\nonumber\\ \displaystyle & & \displaystyle \quad =-(-1)^{k_{1}}\frac{k_{1}!(k_{1}+2)}{2\unicode[STIX]{x1D70B}N}i^{-k_{1}}\cdot i\frac{k_{2}+2}{2N}(-2i\unicode[STIX]{x1D70B})^{k_{2}+1}\,dy\mathop{\sum }_{a=0}^{k_{1}}\left((-1)^{k_{1}-a}\unicode[STIX]{x1D6FC}_{1}y^{-k_{1}-1}+\left(\begin{array}{@{}c@{}}k_{1}\\ a\end{array}\right)\unicode[STIX]{x1D6FD}_{1}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,(F_{-u_{2}}^{(k_{2}+2)}(iy)(-1)^{k_{1}-a}(iy)^{k}-\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy)(-1)^{k-a}(iy)^{k})\nonumber\\ \displaystyle & & \displaystyle \quad =-(-1)^{k_{1}}\frac{k_{1}!(k_{1}+2)}{2\unicode[STIX]{x1D70B}N}i^{-k_{1}}\cdot i\frac{k_{2}+2}{2N}(-2i\unicode[STIX]{x1D70B})^{k_{2}+1}\mathop{\sum }_{a=0}^{k_{1}}\left((-1)^{k_{1}-a}\unicode[STIX]{x1D6FC}_{1}y^{-k_{1}-1}+\left(\begin{array}{@{}c@{}}k_{1}\\ a\end{array}\right)\unicode[STIX]{x1D6FD}_{1}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,(-1)^{k_{1}-a}(iy)^{k}(F_{-u_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy))\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =-(-1)^{k_{1}}\frac{k_{1}!(k_{1}+2)}{2\unicode[STIX]{x1D70B}N}i^{k_{2}+1}\frac{k_{2}+2}{2N}(-2i\unicode[STIX]{x1D70B})^{k_{2}+1}\mathop{\sum }_{a=0}^{k_{1}}\left(\unicode[STIX]{x1D6FC}_{1}y^{k_{2}-1}+(-1)^{k_{1}-a}\left(\begin{array}{@{}c@{}}k_{1}\\ a\end{array}\right)\unicode[STIX]{x1D6FD}_{1}y^{k}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,(F_{-u_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy))\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =-(-1)^{k_{1}}\frac{k_{1}!(k_{1}+2)(k_{2}+2)}{2N^{2}}(2\unicode[STIX]{x1D70B})^{k_{2}}((k_{1}+1)\unicode[STIX]{x1D6FC}_{1}y^{k_{2}-1}+\unicode[STIX]{x1D6FF}_{k_{1}=0}\unicode[STIX]{x1D6FD}_{1}y^{k})\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,(F_{-u_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy))\,dy.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D6FE}_{y,k}}\unicode[STIX]{x1D702}_{0}\wedge \unicode[STIX]{x1D70B}_{k_{2}+1}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{2}}(u_{2}))\nonumber\\ \displaystyle & & \displaystyle \quad =-(-1)^{k_{1}}\frac{k_{1}!(k_{1}+2)}{2\unicode[STIX]{x1D70B}N}i^{-k_{1}}\cdot i\frac{k_{2}+2}{2N}(-2i\unicode[STIX]{x1D70B})^{k_{2}+1}\,dy\mathop{\sum }_{a=0}^{k_{1}}\left((-1)^{k_{1}-a}\unicode[STIX]{x1D6FC}_{1}y^{-k_{1}-1}+\left(\begin{array}{@{}c@{}}k_{1}\\ a\end{array}\right)\unicode[STIX]{x1D6FD}_{1}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\int _{\unicode[STIX]{x1D6FE}_{y,k}}p_{1}^{\ast }\unicode[STIX]{x1D713}_{a,k_{1}-a}\wedge (F_{-u_{2}}^{(k_{2}+2)}(iy)p_{2}^{\ast }\unicode[STIX]{x1D713}_{k_{2},0}-\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy)p_{2}^{\ast }\unicode[STIX]{x1D713}_{0,k_{2}})\nonumber\\ \displaystyle & & \displaystyle \quad =-(-1)^{k_{1}}\frac{k_{1}!(k_{1}+2)}{2\unicode[STIX]{x1D70B}N}i^{-k_{1}}\cdot i\frac{k_{2}+2}{2N}(-2i\unicode[STIX]{x1D70B})^{k_{2}+1}\,dy\mathop{\sum }_{a=0}^{k_{1}}\left((-1)^{k_{1}-a}\unicode[STIX]{x1D6FC}_{1}y^{-k_{1}-1}+\left(\begin{array}{@{}c@{}}k_{1}\\ a\end{array}\right)\unicode[STIX]{x1D6FD}_{1}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,(F_{-u_{2}}^{(k_{2}+2)}(iy)(-1)^{k_{1}-a}(iy)^{k}-\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy)(-1)^{k-a}(iy)^{k})\nonumber\\ \displaystyle & & \displaystyle \quad =-(-1)^{k_{1}}\frac{k_{1}!(k_{1}+2)}{2\unicode[STIX]{x1D70B}N}i^{-k_{1}}\cdot i\frac{k_{2}+2}{2N}(-2i\unicode[STIX]{x1D70B})^{k_{2}+1}\mathop{\sum }_{a=0}^{k_{1}}\left((-1)^{k_{1}-a}\unicode[STIX]{x1D6FC}_{1}y^{-k_{1}-1}+\left(\begin{array}{@{}c@{}}k_{1}\\ a\end{array}\right)\unicode[STIX]{x1D6FD}_{1}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,(-1)^{k_{1}-a}(iy)^{k}(F_{-u_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy))\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =-(-1)^{k_{1}}\frac{k_{1}!(k_{1}+2)}{2\unicode[STIX]{x1D70B}N}i^{k_{2}+1}\frac{k_{2}+2}{2N}(-2i\unicode[STIX]{x1D70B})^{k_{2}+1}\mathop{\sum }_{a=0}^{k_{1}}\left(\unicode[STIX]{x1D6FC}_{1}y^{k_{2}-1}+(-1)^{k_{1}-a}\left(\begin{array}{@{}c@{}}k_{1}\\ a\end{array}\right)\unicode[STIX]{x1D6FD}_{1}y^{k}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,(F_{-u_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy))\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =-(-1)^{k_{1}}\frac{k_{1}!(k_{1}+2)(k_{2}+2)}{2N^{2}}(2\unicode[STIX]{x1D70B})^{k_{2}}((k_{1}+1)\unicode[STIX]{x1D6FC}_{1}y^{k_{2}-1}+\unicode[STIX]{x1D6FF}_{k_{1}=0}\unicode[STIX]{x1D6FD}_{1}y^{k})\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,(F_{-u_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy))\,dy.\end{eqnarray}$$
On intègre
![]() $\unicode[STIX]{x1D702}_{1}\wedge \unicode[STIX]{x1D70B}_{k_{2}+1}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{2}}(u_{2}))$
sur les fibres de
$\unicode[STIX]{x1D702}_{1}\wedge \unicode[STIX]{x1D70B}_{k_{2}+1}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{2}}(u_{2}))$
sur les fibres de
![]() $X^{k}\{0,\infty \}\rightarrow \{0,\infty \}$
grâce au lemme 9.2, ce qui donne
$X^{k}\{0,\infty \}\rightarrow \{0,\infty \}$
grâce au lemme 9.2, ce qui donne
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D6FE}_{y,k}}\unicode[STIX]{x1D702}_{1}\wedge \unicode[STIX]{x1D70B}_{k_{2}+1}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{2}}(u_{2}))\nonumber\\ \displaystyle & & \displaystyle \quad =-i^{k_{1}}\frac{(k_{1}+2)(k_{2}+2)}{4N^{k_{1}+2}}(2\unicode[STIX]{x1D70B})^{k_{1}+k_{2}+1}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\biggl(S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)+(-1)^{k_{1}}S_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{-b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)+(-1)^{k_{1}}\overline{S}_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{-b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)+\overline{S}_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,(F_{-u_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy))y^{k_{2}}\,dy.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D6FE}_{y,k}}\unicode[STIX]{x1D702}_{1}\wedge \unicode[STIX]{x1D70B}_{k_{2}+1}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{2}}(u_{2}))\nonumber\\ \displaystyle & & \displaystyle \quad =-i^{k_{1}}\frac{(k_{1}+2)(k_{2}+2)}{4N^{k_{1}+2}}(2\unicode[STIX]{x1D70B})^{k_{1}+k_{2}+1}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\biggl(S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)+(-1)^{k_{1}}S_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{-b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)+(-1)^{k_{1}}\overline{S}_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{-b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)+\overline{S}_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,(F_{-u_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy))y^{k_{2}}\,dy.\end{eqnarray}$$
Puisque
![]() $\overline{S}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{k,\ell }(i/y)=S_{\overline{\unicode[STIX]{x1D6FC}},\overline{\unicode[STIX]{x1D6FD}}}^{k,\ell }(i/y)$
et comme
$\overline{S}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{k,\ell }(i/y)=S_{\overline{\unicode[STIX]{x1D6FC}},\overline{\unicode[STIX]{x1D6FD}}}^{k,\ell }(i/y)$
et comme
![]() $\overline{\unicode[STIX]{x1D6FF}_{a}}=\unicode[STIX]{x1D6FF}_{a}$
et
$\overline{\unicode[STIX]{x1D6FF}_{a}}=\unicode[STIX]{x1D6FF}_{a}$
et
![]() $\overline{\hat{\unicode[STIX]{x1D6FF}}_{a}}=\hat{\unicode[STIX]{x1D6FF}}_{-a}$
, il vient
$\overline{\hat{\unicode[STIX]{x1D6FF}}_{a}}=\hat{\unicode[STIX]{x1D6FF}}_{-a}$
, il vient
 $$\begin{eqnarray}\displaystyle & & \displaystyle S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)+(-1)^{k_{1}}S_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{-b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)+(-1)^{k_{1}}\overline{S}_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{-b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)+\overline{S}_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)+(-1)^{k_{1}}S_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{-b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)+(-1)^{k_{1}}S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}},\unicode[STIX]{x1D6FF}_{-b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)+S_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}}+\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}+(-1)^{k_{1}}\unicode[STIX]{x1D6FF}_{-b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)+(-1)^{k_{1}}S_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{-b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)+(-1)^{k_{1}}\overline{S}_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{-b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)+\overline{S}_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)+(-1)^{k_{1}}S_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{-b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)+(-1)^{k_{1}}S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}},\unicode[STIX]{x1D6FF}_{-b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)+S_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}}+\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}+(-1)^{k_{1}}\unicode[STIX]{x1D6FF}_{-b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr).\nonumber\end{eqnarray}$$
En mettant ensemble (28) et (29), il vient
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D6FE}_{y,k}}p_{1}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{1}}(u_{1})\wedge \unicode[STIX]{x1D70B}_{k_{2}+1}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{2}}(u_{2}))\nonumber\\ \displaystyle & & \displaystyle \quad =(-1)^{k_{1}+1}\frac{k_{1}!(k_{1}+2)(k_{2}+2)}{2N^{2}}(2\unicode[STIX]{x1D70B})^{k_{2}} (\,(k_{1}+1)\unicode[STIX]{x1D6FC}_{1}y^{k_{2}-1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D6FF}_{k_{1}=0}\unicode[STIX]{x1D6FD}_{1}y^{k_{2}} )(F_{-u_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy))\,dy\nonumber\\ \displaystyle & & \displaystyle \qquad -\,i^{k_{1}}\frac{(k_{1}+2)(k_{2}+2)}{4N^{k_{1}+2}}(2\unicode[STIX]{x1D70B})^{k_{1}+k_{2}+1}S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}}+\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}+(-1)^{k_{1}}\unicode[STIX]{x1D6FF}_{-b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)(F_{-u_{2}}^{(k_{2}+2)}(iy)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{k_{2}+1}\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy))y^{k_{2}}\,dy.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D6FE}_{y,k}}p_{1}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{1}}(u_{1})\wedge \unicode[STIX]{x1D70B}_{k_{2}+1}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{2}}(u_{2}))\nonumber\\ \displaystyle & & \displaystyle \quad =(-1)^{k_{1}+1}\frac{k_{1}!(k_{1}+2)(k_{2}+2)}{2N^{2}}(2\unicode[STIX]{x1D70B})^{k_{2}} (\,(k_{1}+1)\unicode[STIX]{x1D6FC}_{1}y^{k_{2}-1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D6FF}_{k_{1}=0}\unicode[STIX]{x1D6FD}_{1}y^{k_{2}} )(F_{-u_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy))\,dy\nonumber\\ \displaystyle & & \displaystyle \qquad -\,i^{k_{1}}\frac{(k_{1}+2)(k_{2}+2)}{4N^{k_{1}+2}}(2\unicode[STIX]{x1D70B})^{k_{1}+k_{2}+1}S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}}+\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}+(-1)^{k_{1}}\unicode[STIX]{x1D6FF}_{-b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)(F_{-u_{2}}^{(k_{2}+2)}(iy)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{k_{2}+1}\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy))y^{k_{2}}\,dy.\nonumber\end{eqnarray}$$
D’autre part, d’après le lemme 3.3, le terme constant de la série d’Eisenstein
![]() $F_{-u_{2}}^{(k_{2}+2)}$
est réel, et on a
$F_{-u_{2}}^{(k_{2}+2)}$
est réel, et on a
 $$\begin{eqnarray}\displaystyle & & \displaystyle F_{-u_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D701}\biggl(-\frac{a_{2}}{N},-k_{2}-1\biggr)+(-1)^{k_{2}+1}\unicode[STIX]{x1D701}\biggl(-\frac{a_{2}}{N},-k_{2}-1\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,N^{-k_{2}-1}\biggl(\mathop{\sum }_{\substack{ m,n\geqslant 1 \\ n\equiv -a_{2}(N)}}\unicode[STIX]{x1D701}_{N}^{-b_{2}m}n^{k_{2}+1}e^{-(2\unicode[STIX]{x1D70B}mny)/N}+(-1)^{k_{2}}\mathop{\sum }_{\substack{ m,n\geqslant 1 \\ n\equiv a_{2}(N)}}\unicode[STIX]{x1D701}_{N}^{b_{2}m}n^{k_{2}+1}e^{-(2\unicode[STIX]{x1D70B}mny)/N}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{k_{2}+1}N^{-k_{2}-1} (\mathop{\sum }_{\substack{ m,n\geqslant 1 \\ n\equiv -a_{2}(N)}}\unicode[STIX]{x1D701}_{N}^{b_{2}m}n^{k_{2}+1}e^{-(2\unicode[STIX]{x1D70B}mny)/N}+(-1)^{k_{2}}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\mathop{\sum }_{\substack{ m,n\geqslant 1 \\ n\equiv a_{2}(N)}}\unicode[STIX]{x1D701}_{N}^{-b_{2}m}n^{k_{2}+1}e^{-(2\unicode[STIX]{x1D70B}mny)/N}\! )\nonumber\\ \displaystyle & & \displaystyle \quad =(1+(-1)^{k_{2}+1})\unicode[STIX]{x1D701}\biggl(-\frac{a_{2}}{N},-k_{2}-1\biggr)+N^{-k_{2}-1}S_{\hat{\unicode[STIX]{x1D6FF}}_{b_{2}}+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D6FF}}_{-b_{2}},\unicode[STIX]{x1D6FF}_{-a_{2}}-\unicode[STIX]{x1D6FF}_{a_{2}}}^{0,k_{2}+1}(iy).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle F_{-u_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D701}\biggl(-\frac{a_{2}}{N},-k_{2}-1\biggr)+(-1)^{k_{2}+1}\unicode[STIX]{x1D701}\biggl(-\frac{a_{2}}{N},-k_{2}-1\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,N^{-k_{2}-1}\biggl(\mathop{\sum }_{\substack{ m,n\geqslant 1 \\ n\equiv -a_{2}(N)}}\unicode[STIX]{x1D701}_{N}^{-b_{2}m}n^{k_{2}+1}e^{-(2\unicode[STIX]{x1D70B}mny)/N}+(-1)^{k_{2}}\mathop{\sum }_{\substack{ m,n\geqslant 1 \\ n\equiv a_{2}(N)}}\unicode[STIX]{x1D701}_{N}^{b_{2}m}n^{k_{2}+1}e^{-(2\unicode[STIX]{x1D70B}mny)/N}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{k_{2}+1}N^{-k_{2}-1} (\mathop{\sum }_{\substack{ m,n\geqslant 1 \\ n\equiv -a_{2}(N)}}\unicode[STIX]{x1D701}_{N}^{b_{2}m}n^{k_{2}+1}e^{-(2\unicode[STIX]{x1D70B}mny)/N}+(-1)^{k_{2}}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\mathop{\sum }_{\substack{ m,n\geqslant 1 \\ n\equiv a_{2}(N)}}\unicode[STIX]{x1D701}_{N}^{-b_{2}m}n^{k_{2}+1}e^{-(2\unicode[STIX]{x1D70B}mny)/N}\! )\nonumber\\ \displaystyle & & \displaystyle \quad =(1+(-1)^{k_{2}+1})\unicode[STIX]{x1D701}\biggl(-\frac{a_{2}}{N},-k_{2}-1\biggr)+N^{-k_{2}-1}S_{\hat{\unicode[STIX]{x1D6FF}}_{b_{2}}+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D6FF}}_{-b_{2}},\unicode[STIX]{x1D6FF}_{-a_{2}}-\unicode[STIX]{x1D6FF}_{a_{2}}}^{0,k_{2}+1}(iy).\nonumber\end{eqnarray}$$
Lemme 9.3. Pour
![]() $s\in \mathbf{C}$
,
$s\in \mathbf{C}$
,
![]() $\Re (s)<0$
, la fonction
$\Re (s)<0$
, la fonction
![]() $y\mapsto (F_{-u_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy))y^{s-1}$
est intégrable sur
$y\mapsto (F_{-u_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy))y^{s-1}$
est intégrable sur
![]() $]\!0,+\infty \![$
, et on a
$]\!0,+\infty \ $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }(F_{-u_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy))y^{s}\,\frac{dy}{y}=i^{k_{2}+2}(2\unicode[STIX]{x1D70B})^{s-k_{2}-2}\unicode[STIX]{x1D6E4}(-s+k_{2}+2)\nonumber\\ \displaystyle & & \displaystyle \quad \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},-s+k_{2}+2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},-s+k_{2}+2\biggr)\biggr)(\unicode[STIX]{x1D701}\biggl(-\frac{b_{2}}{N},-s+1\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad +\,(-1)^{k_{2}+1}\unicode[STIX]{x1D701}\biggl(\frac{b_{2}}{N},-s+1\biggr)\!).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }(F_{-u_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy))y^{s}\,\frac{dy}{y}=i^{k_{2}+2}(2\unicode[STIX]{x1D70B})^{s-k_{2}-2}\unicode[STIX]{x1D6E4}(-s+k_{2}+2)\nonumber\\ \displaystyle & & \displaystyle \quad \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},-s+k_{2}+2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},-s+k_{2}+2\biggr)\biggr)(\unicode[STIX]{x1D701}\biggl(-\frac{b_{2}}{N},-s+1\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad +\,(-1)^{k_{2}+1}\unicode[STIX]{x1D701}\biggl(\frac{b_{2}}{N},-s+1\biggr)\!).\nonumber\end{eqnarray}$$
Démonstration.
L’hypothèse
![]() $\Re (s)<0$
entraîne que l’intégrale converge lorsque
$\Re (s)<0$
entraîne que l’intégrale converge lorsque
![]() $y\rightarrow +\infty$
. On a
$y\rightarrow +\infty$
. On a
![]() $\overline{F}_{-a_{2},-b_{2}}^{(k_{2}+2)}(iy)=F_{-a_{2},b_{2}}^{(k_{2}+2)}(iy)$
. Pour montrer l’intégrabilité lorsque
$\overline{F}_{-a_{2},-b_{2}}^{(k_{2}+2)}(iy)=F_{-a_{2},b_{2}}^{(k_{2}+2)}(iy)$
. Pour montrer l’intégrabilité lorsque
![]() $y\rightarrow 0$
, on effectue le changement de variables
$y\rightarrow 0$
, on effectue le changement de variables
![]() $y\mapsto 1/y$
et on utilise le lemme 3.4 avec
$y\mapsto 1/y$
et on utilise le lemme 3.4 avec
![]() $g=\unicode[STIX]{x1D70E}$
, ce qui donne
$g=\unicode[STIX]{x1D70E}$
, ce qui donne
Il en résulte
 $$\begin{eqnarray}\displaystyle & & \displaystyle (F_{-a_{2},-b_{2}}^{(k_{2}+2)}(i/y)+(-1)^{k_{2}+1}F_{-a_{2},b_{2}}^{(k_{2}+2)}(i/y))y^{-s-1}\nonumber\\ \displaystyle & & \displaystyle \quad =(iy)^{k_{2}+2}(F_{-b_{2},a_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}F_{b_{2},a_{2}}^{(k_{2}+2)}(iy))y^{-s-1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (F_{-a_{2},-b_{2}}^{(k_{2}+2)}(i/y)+(-1)^{k_{2}+1}F_{-a_{2},b_{2}}^{(k_{2}+2)}(i/y))y^{-s-1}\nonumber\\ \displaystyle & & \displaystyle \quad =(iy)^{k_{2}+2}(F_{-b_{2},a_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}F_{b_{2},a_{2}}^{(k_{2}+2)}(iy))y^{-s-1}.\nonumber\end{eqnarray}$$
Le terme constant de la série d’Eisenstein
![]() $F_{-b_{2},a_{2}}^{(k_{2}+2)}+(-1)^{k_{2}+1}F_{b_{2},a_{2}}^{(k_{2}+2)}$
est nul, ce qui montre la convergence de l’intégrale de départ pour
$F_{-b_{2},a_{2}}^{(k_{2}+2)}+(-1)^{k_{2}+1}F_{b_{2},a_{2}}^{(k_{2}+2)}$
est nul, ce qui montre la convergence de l’intégrale de départ pour
![]() $\Re (s)<0$
. Par changement de variables dans cette même intégrale, on obtient
$\Re (s)<0$
. Par changement de variables dans cette même intégrale, on obtient
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }(F_{-u_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy))y^{s}\,\frac{dy}{y}\nonumber\\ \displaystyle & & \displaystyle \quad =i^{k_{2}+2}\int _{0}^{\infty }(F_{-b_{2},a_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}F_{b_{2},a_{2}}^{(k_{2}+2)}(iy))y^{-s+k_{2}+2}\,\frac{dy}{y}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }(F_{-u_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy))y^{s}\,\frac{dy}{y}\nonumber\\ \displaystyle & & \displaystyle \quad =i^{k_{2}+2}\int _{0}^{\infty }(F_{-b_{2},a_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}F_{b_{2},a_{2}}^{(k_{2}+2)}(iy))y^{-s+k_{2}+2}\,\frac{dy}{y}.\nonumber\end{eqnarray}$$
D’après le lemme 3.3, on a
 $$\begin{eqnarray}\displaystyle & & \displaystyle F_{-b_{2},a_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}F_{b_{2},a_{2}}^{(k_{2}+2)}(iy)\nonumber\\ \displaystyle & & \displaystyle \quad =N^{-k_{2}-1}(S_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{2}},\unicode[STIX]{x1D6FF}_{-b_{2}}}^{0,k_{2}+1}(iy)+(-1)^{k_{2}}S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{2}},\unicode[STIX]{x1D6FF}_{b_{2}}}^{0,k_{2}+1}(iy)+(-1)^{k_{2}+1}S_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{2}},\unicode[STIX]{x1D6FF}_{b_{2}}}^{0,k_{2}+1}(iy)-S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{2}},\unicode[STIX]{x1D6FF}_{-b_{2}}}^{0,k_{2}+1}(iy))\nonumber\\ \displaystyle & & \displaystyle \quad =N^{-k_{2}-1}S_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{2}}-\hat{\unicode[STIX]{x1D6FF}}_{a_{2}},\unicode[STIX]{x1D6FF}_{-b_{2}}+(-1)^{k_{2}+1}\unicode[STIX]{x1D6FF}_{b_{2}}}^{0,k_{2}+1}(iy).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle F_{-b_{2},a_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}F_{b_{2},a_{2}}^{(k_{2}+2)}(iy)\nonumber\\ \displaystyle & & \displaystyle \quad =N^{-k_{2}-1}(S_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{2}},\unicode[STIX]{x1D6FF}_{-b_{2}}}^{0,k_{2}+1}(iy)+(-1)^{k_{2}}S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{2}},\unicode[STIX]{x1D6FF}_{b_{2}}}^{0,k_{2}+1}(iy)+(-1)^{k_{2}+1}S_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{2}},\unicode[STIX]{x1D6FF}_{b_{2}}}^{0,k_{2}+1}(iy)-S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{2}},\unicode[STIX]{x1D6FF}_{-b_{2}}}^{0,k_{2}+1}(iy))\nonumber\\ \displaystyle & & \displaystyle \quad =N^{-k_{2}-1}S_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{2}}-\hat{\unicode[STIX]{x1D6FF}}_{a_{2}},\unicode[STIX]{x1D6FF}_{-b_{2}}+(-1)^{k_{2}+1}\unicode[STIX]{x1D6FF}_{b_{2}}}^{0,k_{2}+1}(iy).\nonumber\end{eqnarray}$$
Grâce au lemme 7.1, on en déduit
 $$\begin{eqnarray}\displaystyle & & \displaystyle i^{k_{2}+2}\int _{0}^{\infty }(F_{-b_{2},a_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}F_{b_{2},a_{2}}^{(k_{2}+2)}(iy))y^{-s+k_{2}+2}\,\frac{dy}{y}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{i^{k_{2}+2}}{N^{k_{2}+1}}\int _{0}^{\infty }S_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{2}}-\hat{\unicode[STIX]{x1D6FF}}_{a_{2}},\unicode[STIX]{x1D6FF}_{-b_{2}}+(-1)^{k_{2}+1}\unicode[STIX]{x1D6FF}_{b_{2}}}^{0,k_{2}+1}(iy)y^{-s+k_{2}+2}\,\frac{dy}{y}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{i^{k_{2}+2}}{N^{k_{2}+1}}\biggl(\frac{2\unicode[STIX]{x1D70B}}{N}\biggr)^{s-k_{2}-2}\unicode[STIX]{x1D6E4}(s-k_{2}+2)L(\hat{\unicode[STIX]{x1D6FF}}_{-a_{2}}-\hat{\unicode[STIX]{x1D6FF}}_{a_{2}},-s+k_{2}+2)L(\unicode[STIX]{x1D6FF}_{-b_{2}}+(-1)^{k_{2}+1}\unicode[STIX]{x1D6FF}_{b_{2}},-s+1)\nonumber\\ \displaystyle & & \displaystyle \quad =i^{k_{2}+2}(2\unicode[STIX]{x1D70B})^{s-k_{2}-2}\unicode[STIX]{x1D6E4}(-s+k_{2}+2)\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},-s+k_{2}+2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},-s+k_{2}+2\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\biggl(\unicode[STIX]{x1D701}\biggl(-\frac{b_{2}}{N},-s+1\biggr)+(-1)^{k_{2}+1}\unicode[STIX]{x1D701}\biggl(\frac{b_{2}}{N},-s+1\biggr)\biggr).\Box \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle i^{k_{2}+2}\int _{0}^{\infty }(F_{-b_{2},a_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}F_{b_{2},a_{2}}^{(k_{2}+2)}(iy))y^{-s+k_{2}+2}\,\frac{dy}{y}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{i^{k_{2}+2}}{N^{k_{2}+1}}\int _{0}^{\infty }S_{\hat{\unicode[STIX]{x1D6FF}}_{-a_{2}}-\hat{\unicode[STIX]{x1D6FF}}_{a_{2}},\unicode[STIX]{x1D6FF}_{-b_{2}}+(-1)^{k_{2}+1}\unicode[STIX]{x1D6FF}_{b_{2}}}^{0,k_{2}+1}(iy)y^{-s+k_{2}+2}\,\frac{dy}{y}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{i^{k_{2}+2}}{N^{k_{2}+1}}\biggl(\frac{2\unicode[STIX]{x1D70B}}{N}\biggr)^{s-k_{2}-2}\unicode[STIX]{x1D6E4}(s-k_{2}+2)L(\hat{\unicode[STIX]{x1D6FF}}_{-a_{2}}-\hat{\unicode[STIX]{x1D6FF}}_{a_{2}},-s+k_{2}+2)L(\unicode[STIX]{x1D6FF}_{-b_{2}}+(-1)^{k_{2}+1}\unicode[STIX]{x1D6FF}_{b_{2}},-s+1)\nonumber\\ \displaystyle & & \displaystyle \quad =i^{k_{2}+2}(2\unicode[STIX]{x1D70B})^{s-k_{2}-2}\unicode[STIX]{x1D6E4}(-s+k_{2}+2)\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},-s+k_{2}+2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},-s+k_{2}+2\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\biggl(\unicode[STIX]{x1D701}\biggl(-\frac{b_{2}}{N},-s+1\biggr)+(-1)^{k_{2}+1}\unicode[STIX]{x1D701}\biggl(\frac{b_{2}}{N},-s+1\biggr)\biggr).\Box \nonumber\end{eqnarray}$$
Pour
![]() $\Re (s)\ll 0$
, on en déduit
$\Re (s)\ll 0$
, on en déduit
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X^{k}\{0,\infty \}}y^{s}p_{1}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{1}}(u_{1})\wedge \unicode[STIX]{x1D70B}_{k_{2}+1}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{2}}(u_{2}))\nonumber\\ \displaystyle & & \displaystyle \quad =(-1)^{k_{1}+1}k_{1}!\frac{(k_{1}+2)(k_{2}+2)}{2N^{2}}(2\unicode[STIX]{x1D70B})^{k_{2}}\int _{0}^{\infty }(F_{-u_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy))\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,((k_{1}+1)\unicode[STIX]{x1D6FC}_{1}y^{k_{2}-1}+\unicode[STIX]{x1D6FF}_{k_{1}=0}\unicode[STIX]{x1D6FD}_{1}y^{k_{2}})y^{s}\,dy\nonumber\\ \displaystyle & & \displaystyle \qquad -\,i^{k_{1}}\frac{(k_{1}+2)(k_{2}+2)}{4N^{k_{1}+2}}(2\unicode[STIX]{x1D70B})^{k_{1}+k_{2}+1}\int _{0}^{\infty }S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}}+\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}+(-1)^{k_{1}}\unicode[STIX]{x1D6FF}_{-b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\biggl((1+(-1)^{k_{2}+1})\unicode[STIX]{x1D701}\biggl(-\frac{a_{2}}{N},-k_{2}-1\biggr)+N^{-k_{2}-1}S_{\hat{\unicode[STIX]{x1D6FF}}_{b_{2}}+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D6FF}}_{-b_{2}},\unicode[STIX]{x1D6FF}_{-a_{2}}-\unicode[STIX]{x1D6FF}_{a_{2}}}^{0,k_{2}+1}(iy)\biggr)y^{s+k_{2}}\,dy.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X^{k}\{0,\infty \}}y^{s}p_{1}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{1}}(u_{1})\wedge \unicode[STIX]{x1D70B}_{k_{2}+1}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{2}}(u_{2}))\nonumber\\ \displaystyle & & \displaystyle \quad =(-1)^{k_{1}+1}k_{1}!\frac{(k_{1}+2)(k_{2}+2)}{2N^{2}}(2\unicode[STIX]{x1D70B})^{k_{2}}\int _{0}^{\infty }(F_{-u_{2}}^{(k_{2}+2)}(iy)+(-1)^{k_{2}+1}\overline{F}_{-u_{2}}^{(k_{2}+2)}(iy))\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,((k_{1}+1)\unicode[STIX]{x1D6FC}_{1}y^{k_{2}-1}+\unicode[STIX]{x1D6FF}_{k_{1}=0}\unicode[STIX]{x1D6FD}_{1}y^{k_{2}})y^{s}\,dy\nonumber\\ \displaystyle & & \displaystyle \qquad -\,i^{k_{1}}\frac{(k_{1}+2)(k_{2}+2)}{4N^{k_{1}+2}}(2\unicode[STIX]{x1D70B})^{k_{1}+k_{2}+1}\int _{0}^{\infty }S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}}+\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\unicode[STIX]{x1D6FF}_{b_{1}}+(-1)^{k_{1}}\unicode[STIX]{x1D6FF}_{-b_{1}}}^{-1,k_{1}}\biggl(\frac{i}{y}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\biggl((1+(-1)^{k_{2}+1})\unicode[STIX]{x1D701}\biggl(-\frac{a_{2}}{N},-k_{2}-1\biggr)+N^{-k_{2}-1}S_{\hat{\unicode[STIX]{x1D6FF}}_{b_{2}}+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D6FF}}_{-b_{2}},\unicode[STIX]{x1D6FF}_{-a_{2}}-\unicode[STIX]{x1D6FF}_{a_{2}}}^{0,k_{2}+1}(iy)\biggr)y^{s+k_{2}}\,dy.\nonumber\end{eqnarray}$$
En appliquant les lemmes 7.1, 9.3 et la proposition 7.2, on obtient
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X^{k}\{0,\infty \}}y^{s}p_{1}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{1}}(u_{1})\wedge \unicode[STIX]{x1D70B}_{k_{2}+1}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{2}}(u_{2}))\nonumber\\ \displaystyle & & \displaystyle \quad =(-1)^{k_{1}}\frac{(k_{1}+2)!(k_{2}+2)}{2N^{2}}(2i\unicode[STIX]{x1D70B})^{k_{2}}\unicode[STIX]{x1D6FC}_{1}(2\unicode[STIX]{x1D70B})^{s-2}\unicode[STIX]{x1D6E4}(-s+2)\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},-s+2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},-s+2\biggr)\biggr)(\unicode[STIX]{x1D701}\biggl(-\frac{b_{2}}{N},-s-k_{2}+1\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{k_{2}+1}\unicode[STIX]{x1D701}\biggl(\frac{b_{2}}{N},-s-k_{2}+1\biggr)\!)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D6FF}_{k_{1}=0}\unicode[STIX]{x1D6FD}_{1}\frac{k_{2}+2}{N^{2}}(2i\unicode[STIX]{x1D70B})^{k_{2}}(2\unicode[STIX]{x1D70B})^{s-1}\unicode[STIX]{x1D6E4}(-s+1)\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},-s+1\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},-s+1\biggr)\biggr)\biggl(\unicode[STIX]{x1D701}\biggl(-\frac{b_{2}}{N},-s-k_{2}\biggr)+(-1)^{k_{2}+1}\unicode[STIX]{x1D701}\biggl(\frac{b_{2}}{N},-s-k_{2}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,i^{k_{1}}\frac{(k_{1}+2)(k_{2}+2)}{4N^{k_{1}+2}}(2\unicode[STIX]{x1D70B})^{k_{1}+k_{2}+1}(1+(-1)^{k_{2}+1})\unicode[STIX]{x1D701}\biggl(-\frac{a_{2}}{N},-k_{2}-1\biggr)\biggl(\frac{2\unicode[STIX]{x1D70B}}{N}\biggr)^{s+k_{2}+1}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\unicode[STIX]{x1D6E4}(-s-k_{2}-1)\cdot \biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},-s-k_{2}\biggr)+\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},-s-k_{2}\biggr)\biggr)N^{s+k+1} (\unicode[STIX]{x1D701}\biggl(\frac{b_{1}}{N},-s-k-1\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{k_{1}}\unicode[STIX]{x1D701}\biggl(-\frac{b_{1}}{N},-s-k-1\biggr)\!)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,i^{k_{1}}\frac{(k_{1}+2)(k_{2}+2)}{4N^{k_{1}+2}}(2\unicode[STIX]{x1D70B})^{k_{1}+k_{2}+1}N^{-k_{2}-1}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\int _{0}^{\infty }S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}}+\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\hat{\unicode[STIX]{x1D6FF}}_{b_{2}}+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D6FF}}_{-b_{2}}}^{s+k_{2},0}(iy)S_{\unicode[STIX]{x1D6FF}_{b_{1}}+(-1)^{k_{1}}\unicode[STIX]{x1D6FF}_{-b_{1}},\unicode[STIX]{x1D6FF}_{-a_{2}}-\unicode[STIX]{x1D6FF}_{a_{2}}}^{k_{1},-s}\biggl(\frac{i}{y}\biggr)y^{s+k_{2}}\,dy.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X^{k}\{0,\infty \}}y^{s}p_{1}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{1}}(u_{1})\wedge \unicode[STIX]{x1D70B}_{k_{2}+1}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{2}}(u_{2}))\nonumber\\ \displaystyle & & \displaystyle \quad =(-1)^{k_{1}}\frac{(k_{1}+2)!(k_{2}+2)}{2N^{2}}(2i\unicode[STIX]{x1D70B})^{k_{2}}\unicode[STIX]{x1D6FC}_{1}(2\unicode[STIX]{x1D70B})^{s-2}\unicode[STIX]{x1D6E4}(-s+2)\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},-s+2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},-s+2\biggr)\biggr)(\unicode[STIX]{x1D701}\biggl(-\frac{b_{2}}{N},-s-k_{2}+1\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{k_{2}+1}\unicode[STIX]{x1D701}\biggl(\frac{b_{2}}{N},-s-k_{2}+1\biggr)\!)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D6FF}_{k_{1}=0}\unicode[STIX]{x1D6FD}_{1}\frac{k_{2}+2}{N^{2}}(2i\unicode[STIX]{x1D70B})^{k_{2}}(2\unicode[STIX]{x1D70B})^{s-1}\unicode[STIX]{x1D6E4}(-s+1)\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},-s+1\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},-s+1\biggr)\biggr)\biggl(\unicode[STIX]{x1D701}\biggl(-\frac{b_{2}}{N},-s-k_{2}\biggr)+(-1)^{k_{2}+1}\unicode[STIX]{x1D701}\biggl(\frac{b_{2}}{N},-s-k_{2}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,i^{k_{1}}\frac{(k_{1}+2)(k_{2}+2)}{4N^{k_{1}+2}}(2\unicode[STIX]{x1D70B})^{k_{1}+k_{2}+1}(1+(-1)^{k_{2}+1})\unicode[STIX]{x1D701}\biggl(-\frac{a_{2}}{N},-k_{2}-1\biggr)\biggl(\frac{2\unicode[STIX]{x1D70B}}{N}\biggr)^{s+k_{2}+1}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\unicode[STIX]{x1D6E4}(-s-k_{2}-1)\cdot \biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},-s-k_{2}\biggr)+\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},-s-k_{2}\biggr)\biggr)N^{s+k+1} (\unicode[STIX]{x1D701}\biggl(\frac{b_{1}}{N},-s-k-1\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{k_{1}}\unicode[STIX]{x1D701}\biggl(-\frac{b_{1}}{N},-s-k-1\biggr)\!)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,i^{k_{1}}\frac{(k_{1}+2)(k_{2}+2)}{4N^{k_{1}+2}}(2\unicode[STIX]{x1D70B})^{k_{1}+k_{2}+1}N^{-k_{2}-1}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\int _{0}^{\infty }S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}}+\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\hat{\unicode[STIX]{x1D6FF}}_{b_{2}}+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D6FF}}_{-b_{2}}}^{s+k_{2},0}(iy)S_{\unicode[STIX]{x1D6FF}_{b_{1}}+(-1)^{k_{1}}\unicode[STIX]{x1D6FF}_{-b_{1}},\unicode[STIX]{x1D6FF}_{-a_{2}}-\unicode[STIX]{x1D6FF}_{a_{2}}}^{k_{1},-s}\biggl(\frac{i}{y}\biggr)y^{s+k_{2}}\,dy.\end{eqnarray}$$
L’expression précédente est une fonction méromorphe de
![]() $s$
, et tous les termes qui la composent sont holomorphes au voisinage de
$s$
, et tous les termes qui la composent sont holomorphes au voisinage de
![]() $s=0$
, excepté les termes suivants
:
$s=0$
, excepté les termes suivants
:
-
(i) L’expression
 $\unicode[STIX]{x1D701}(\pm b_{2}/N,-s-k_{2}+1)$
a un pôle simple lorsque
$\unicode[STIX]{x1D701}(\pm b_{2}/N,-s-k_{2}+1)$
a un pôle simple lorsque
 $k_{2}=0$
. Mais dans ce cas est holomorphe en
$k_{2}=0$
. Mais dans ce cas est holomorphe en $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}\biggl(-\frac{b_{2}}{N},-s-k_{2}+1\biggr)+(-1)^{k_{2}+1}\unicode[STIX]{x1D701}\biggl(\frac{b_{2}}{N},-s-k_{2}+1\biggr)=\unicode[STIX]{x1D701}\biggl(-\frac{b_{2}}{N},-s+1\biggr)-\unicode[STIX]{x1D701}\biggl(\frac{b_{2}}{N},-s+1\biggr) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}\biggl(-\frac{b_{2}}{N},-s-k_{2}+1\biggr)+(-1)^{k_{2}+1}\unicode[STIX]{x1D701}\biggl(\frac{b_{2}}{N},-s-k_{2}+1\biggr)=\unicode[STIX]{x1D701}\biggl(-\frac{b_{2}}{N},-s+1\biggr)-\unicode[STIX]{x1D701}\biggl(\frac{b_{2}}{N},-s+1\biggr) & & \displaystyle \nonumber\end{eqnarray}$$
 $s=0$
; sa valeur est
$s=0$
; sa valeur est
 $\unicode[STIX]{x1D701}^{\ast }(-b_{2}/N,1)-\unicode[STIX]{x1D701}^{\ast }(b_{2}/N,1)$
.
$\unicode[STIX]{x1D701}^{\ast }(-b_{2}/N,1)-\unicode[STIX]{x1D701}^{\ast }(b_{2}/N,1)$
.
-
(ii) Le facteur
 $\unicode[STIX]{x1D6E4}(-s-k_{2}-1)$
a un pôle simple. Mais ce terme n’intervient que si
$\unicode[STIX]{x1D6E4}(-s-k_{2}-1)$
a un pôle simple. Mais ce terme n’intervient que si
 $k_{2}$
est impair, et dans ce cas on a
$k_{2}$
est impair, et dans ce cas on a  $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}\biggl(\frac{b_{1}}{N},-k-1\biggr)+(-1)^{k_{1}}\unicode[STIX]{x1D701}\biggl(-\frac{b_{1}}{N},-k-1\biggr)=-\frac{B_{k+2}(\{b_{1}/N\})}{k+2}+(-1)^{k}\frac{B_{k+2}(\{-b_{1}/N\})}{k+2}=0. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}\biggl(\frac{b_{1}}{N},-k-1\biggr)+(-1)^{k_{1}}\unicode[STIX]{x1D701}\biggl(-\frac{b_{1}}{N},-k-1\biggr)=-\frac{B_{k+2}(\{b_{1}/N\})}{k+2}+(-1)^{k}\frac{B_{k+2}(\{-b_{1}/N\})}{k+2}=0. & & \displaystyle \nonumber\end{eqnarray}$$
L’expression précédente est donc holomorphe en
![]() $s=0$
. Nous allons calculer l’intégrale (30) pour
$s=0$
. Nous allons calculer l’intégrale (30) pour
![]() $s=0$
, soit
$s=0$
, soit
Pour cela, nous aurons besoin du lemme suivant [Reference BrunaultBru16, Lemmas 8 and 9].
Lemme 9.4. Soit
![]() $f=\sum _{n=0}^{\infty }a_{n}q^{n}\in M_{k}(\unicode[STIX]{x1D6E4}_{1}(M))$
et
$f=\sum _{n=0}^{\infty }a_{n}q^{n}\in M_{k}(\unicode[STIX]{x1D6E4}_{1}(M))$
et
![]() $g=\sum _{n=0}^{\infty }b_{n}q^{n}\in M_{\ell }(\unicode[STIX]{x1D6E4}_{1}(M))$
avec
$g=\sum _{n=0}^{\infty }b_{n}q^{n}\in M_{\ell }(\unicode[STIX]{x1D6E4}_{1}(M))$
avec
![]() $k,\ell \geqslant 1$
. Soit
$k,\ell \geqslant 1$
. Soit
![]() $h=W_{M}(g)$
. Alors on a
$h=W_{M}(g)$
. Alors on a
En particulier, on a
En faisant le changement de variables
![]() $y\rightarrow Ny$
dans
$y\rightarrow Ny$
dans
![]() $I$
, on a
$I$
, on a
Par définition, on a
 $$\begin{eqnarray}\displaystyle & \displaystyle S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}}+\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\hat{\unicode[STIX]{x1D6FF}}_{b_{2}}+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D6FF}}_{-b_{2}}}^{k_{2},0}(iNy)=H_{b_{2},a_{1}}^{(k_{2}+1),\ast }(iy)+H_{b_{2},-a_{1}}^{(k_{2}+1),\ast }(iy), & \displaystyle \nonumber\\ \displaystyle & \displaystyle S_{\unicode[STIX]{x1D6FF}_{b_{1}}+(-1)^{k_{1}}\unicode[STIX]{x1D6FF}_{-b_{1}},\unicode[STIX]{x1D6FF}_{-a_{2}}-\unicode[STIX]{x1D6FF}_{a_{2}}}^{k_{1},0}\biggl(\frac{i}{Ny}\biggr)=G_{b_{1},-a_{2}}^{(k_{1}+1),\ast }\biggl(\frac{i}{N^{2}y}\biggr)-G_{b_{1},a_{2}}^{(k_{1}+1),\ast }\biggl(\frac{i}{N^{2}y}\biggr). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle S_{\hat{\unicode[STIX]{x1D6FF}}_{a_{1}}+\hat{\unicode[STIX]{x1D6FF}}_{-a_{1}},\hat{\unicode[STIX]{x1D6FF}}_{b_{2}}+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D6FF}}_{-b_{2}}}^{k_{2},0}(iNy)=H_{b_{2},a_{1}}^{(k_{2}+1),\ast }(iy)+H_{b_{2},-a_{1}}^{(k_{2}+1),\ast }(iy), & \displaystyle \nonumber\\ \displaystyle & \displaystyle S_{\unicode[STIX]{x1D6FF}_{b_{1}}+(-1)^{k_{1}}\unicode[STIX]{x1D6FF}_{-b_{1}},\unicode[STIX]{x1D6FF}_{-a_{2}}-\unicode[STIX]{x1D6FF}_{a_{2}}}^{k_{1},0}\biggl(\frac{i}{Ny}\biggr)=G_{b_{1},-a_{2}}^{(k_{1}+1),\ast }\biggl(\frac{i}{N^{2}y}\biggr)-G_{b_{1},a_{2}}^{(k_{1}+1),\ast }\biggl(\frac{i}{N^{2}y}\biggr). & \displaystyle \nonumber\end{eqnarray}$$
En utilisant le lemme 9.4 avec
![]() $M=N^{2}$
,
$M=N^{2}$
,
![]() $f=H_{b_{2},a_{1}}^{(k_{2}+1)}+H_{b_{2},-a_{1}}^{(k_{2}+1)}$
et
$f=H_{b_{2},a_{1}}^{(k_{2}+1)}+H_{b_{2},-a_{1}}^{(k_{2}+1)}$
et
![]() $g=G_{b_{1},-a_{2}}^{(k_{1}+1)}-G_{b_{1},a_{2}}^{(k_{1}+1)}$
, il vient
$g=G_{b_{1},-a_{2}}^{(k_{1}+1)}-G_{b_{1},a_{2}}^{(k_{1}+1)}$
, il vient
avec
 $$\begin{eqnarray}\displaystyle I_{1} & = & \displaystyle \unicode[STIX]{x1D6EC}^{\ast }(f\cdot W_{N^{2}}(g),k+2)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6EC}^{\ast }(W_{N^{2}}(f)\cdot g,0)\nonumber\\ \displaystyle & = & \displaystyle i^{-k_{2}-1}N\unicode[STIX]{x1D6EC}^{\ast }((G_{b_{2},a_{1}}^{(k_{2}+1)}+G_{b_{2},-a_{1}}^{(k_{2}+1)})(G_{b_{1},-a_{2}}^{(k_{1}+1)}-G_{b_{1},a_{2}}^{(k_{1}+1)}),0),\nonumber\\ \displaystyle I_{2} & = & \displaystyle -a_{0}(f)\unicode[STIX]{x1D6EC}(W_{N^{2}}(g),k+2),\nonumber\\ \displaystyle I_{3} & = & \displaystyle -a_{0}(g)\unicode[STIX]{x1D6EC}^{\ast }(f,k_{2}+1).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{1} & = & \displaystyle \unicode[STIX]{x1D6EC}^{\ast }(f\cdot W_{N^{2}}(g),k+2)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6EC}^{\ast }(W_{N^{2}}(f)\cdot g,0)\nonumber\\ \displaystyle & = & \displaystyle i^{-k_{2}-1}N\unicode[STIX]{x1D6EC}^{\ast }((G_{b_{2},a_{1}}^{(k_{2}+1)}+G_{b_{2},-a_{1}}^{(k_{2}+1)})(G_{b_{1},-a_{2}}^{(k_{1}+1)}-G_{b_{1},a_{2}}^{(k_{1}+1)}),0),\nonumber\\ \displaystyle I_{2} & = & \displaystyle -a_{0}(f)\unicode[STIX]{x1D6EC}(W_{N^{2}}(g),k+2),\nonumber\\ \displaystyle I_{3} & = & \displaystyle -a_{0}(g)\unicode[STIX]{x1D6EC}^{\ast }(f,k_{2}+1).\nonumber\end{eqnarray}$$
Calcul de
![]() $I_{2}$
. Grâce aux lemmes 3.10 et 3.14, on a
$I_{2}$
. Grâce aux lemmes 3.10 et 3.14, on a
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EC}(W_{N^{2}}(g),k+2) & = & \displaystyle \frac{i^{k_{1}+1}}{N}\unicode[STIX]{x1D6EC}(H_{b_{1},-a_{2}}^{(k_{1}+1)}-H_{b_{1},a_{2}}^{(k_{1}+1)},k+2)\nonumber\\ \displaystyle & = & \displaystyle \frac{i^{k_{1}+1}}{N}N^{k+2}(2\unicode[STIX]{x1D70B})^{-k-2}\unicode[STIX]{x1D6E4}(k+2)\nonumber\\ \displaystyle & & \displaystyle \cdot \,(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2\biggr)\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},k_{2}+2\biggr)+(-1)^{k_{1}+1}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2\biggr)\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},k_{2}+2\biggr)\nonumber\\ \displaystyle & & \displaystyle -\,\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2\biggr)\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},k_{2}+2\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2\biggr)\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},k_{2}+2\biggr)\!)\nonumber\\ \displaystyle & = & \displaystyle i^{k_{1}+1}N^{k+1}(2\unicode[STIX]{x1D70B})^{-k-2}(k+1)!\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},k_{2}+2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},k_{2}+2\biggr)\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EC}(W_{N^{2}}(g),k+2) & = & \displaystyle \frac{i^{k_{1}+1}}{N}\unicode[STIX]{x1D6EC}(H_{b_{1},-a_{2}}^{(k_{1}+1)}-H_{b_{1},a_{2}}^{(k_{1}+1)},k+2)\nonumber\\ \displaystyle & = & \displaystyle \frac{i^{k_{1}+1}}{N}N^{k+2}(2\unicode[STIX]{x1D70B})^{-k-2}\unicode[STIX]{x1D6E4}(k+2)\nonumber\\ \displaystyle & & \displaystyle \cdot \,(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2\biggr)\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},k_{2}+2\biggr)+(-1)^{k_{1}+1}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2\biggr)\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},k_{2}+2\biggr)\nonumber\\ \displaystyle & & \displaystyle -\,\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2\biggr)\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},k_{2}+2\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2\biggr)\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},k_{2}+2\biggr)\!)\nonumber\\ \displaystyle & = & \displaystyle i^{k_{1}+1}N^{k+1}(2\unicode[STIX]{x1D70B})^{-k-2}(k+1)!\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},k_{2}+2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},k_{2}+2\biggr)\biggr).\nonumber\end{eqnarray}$$
On obtient donc
 $$\begin{eqnarray}\displaystyle I_{2} & = & \displaystyle -i^{k_{1}+1}N^{k+1}(2\unicode[STIX]{x1D70B})^{-k-2}(k+1)!a_{0}(H_{b_{2},a_{1}}^{(k_{2}+1)}+H_{b_{2},-a_{1}}^{(k_{2}+1)})\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2\biggr)\biggr)\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},k_{2}+2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},k_{2}+2\biggr)\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{2} & = & \displaystyle -i^{k_{1}+1}N^{k+1}(2\unicode[STIX]{x1D70B})^{-k-2}(k+1)!a_{0}(H_{b_{2},a_{1}}^{(k_{2}+1)}+H_{b_{2},-a_{1}}^{(k_{2}+1)})\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2\biggr)\biggr)\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},k_{2}+2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},k_{2}+2\biggr)\biggr).\nonumber\end{eqnarray}$$
Calcul de
![]() $I_{3}$
. Si
$I_{3}$
. Si
![]() $k_{1}\geqslant 1$
et
$k_{1}\geqslant 1$
et
![]() $a_{2}\neq 0$
, alors
$a_{2}\neq 0$
, alors
![]() $a_{0}(g)=0$
. Si
$a_{0}(g)=0$
. Si
![]() $a_{2}=0$
, alors
$a_{2}=0$
, alors
![]() $g=0$
. On peut donc supposer
$g=0$
. On peut donc supposer
![]() $k_{1}=0$
et
$k_{1}=0$
et
![]() $a_{2}\neq 0$
. Si
$a_{2}\neq 0$
. Si
![]() $b_{1}\neq 0$
, alors
$b_{1}\neq 0$
, alors
![]() $a_{0}(g)=0$
. On peut donc supposer
$a_{0}(g)=0$
. On peut donc supposer
![]() $b_{1}=0$
. Alors
$b_{1}=0$
. Alors
De plus
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EC}(f,s) & = & \displaystyle N^{s}(2\unicode[STIX]{x1D70B})^{-s}\unicode[STIX]{x1D6E4}(s)(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{2}}{N},s\biggr)\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},s-k_{2}\biggr)+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{2}}{N},s\biggr)\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},s-k_{2}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{2}}{N},s\biggr)\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},s-k_{2}\biggr)+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{2}}{N},s\biggr)\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},s-k_{2}\biggr)\!)\nonumber\\ \displaystyle & = & \displaystyle N^{s}(2\unicode[STIX]{x1D70B})^{-s}\unicode[STIX]{x1D6E4}(s)\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{2}}{N},s\biggr)+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{2}}{N},s\biggr)\biggr)\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},s-k_{2}\biggr)+\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},s-k_{2}\biggr)\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EC}(f,s) & = & \displaystyle N^{s}(2\unicode[STIX]{x1D70B})^{-s}\unicode[STIX]{x1D6E4}(s)(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{2}}{N},s\biggr)\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},s-k_{2}\biggr)+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{2}}{N},s\biggr)\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},s-k_{2}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{2}}{N},s\biggr)\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},s-k_{2}\biggr)+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{2}}{N},s\biggr)\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},s-k_{2}\biggr)\!)\nonumber\\ \displaystyle & = & \displaystyle N^{s}(2\unicode[STIX]{x1D70B})^{-s}\unicode[STIX]{x1D6E4}(s)\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{2}}{N},s\biggr)+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{2}}{N},s\biggr)\biggr)\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},s-k_{2}\biggr)+\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},s-k_{2}\biggr)\biggr).\nonumber\end{eqnarray}$$
Comme
![]() $a_{1}\neq 0$
, les fonctions
$a_{1}\neq 0$
, les fonctions
![]() $\hat{\unicode[STIX]{x1D701}}(a_{1}/N,s)$
et
$\hat{\unicode[STIX]{x1D701}}(a_{1}/N,s)$
et
![]() $\hat{\unicode[STIX]{x1D701}}(-a_{1}/N,s)$
sont holomorphes sur
$\hat{\unicode[STIX]{x1D701}}(-a_{1}/N,s)$
sont holomorphes sur
![]() $\mathbf{C}$
, d’où
$\mathbf{C}$
, d’où
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EC}^{\ast }(f,k_{2}+1) & = & \displaystyle \unicode[STIX]{x1D6EC}(f,k_{2}+1)=N^{k_{2}+1}(2\unicode[STIX]{x1D70B})^{-k_{2}-1}k_{2}!\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{2}}{N},k_{2}+1\biggr)+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{2}}{N},k_{2}+1\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},1\biggr)+\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},1\biggr)\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EC}^{\ast }(f,k_{2}+1) & = & \displaystyle \unicode[STIX]{x1D6EC}(f,k_{2}+1)=N^{k_{2}+1}(2\unicode[STIX]{x1D70B})^{-k_{2}-1}k_{2}!\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{2}}{N},k_{2}+1\biggr)+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{2}}{N},k_{2}+1\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},1\biggr)+\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},1\biggr)\biggr).\nonumber\end{eqnarray}$$
On a alors
 $$\begin{eqnarray}\displaystyle I_{3} & = & \displaystyle \unicode[STIX]{x1D6FF}_{k_{1}=0}\unicode[STIX]{x1D6FF}_{a_{2}\neq 0}\unicode[STIX]{x1D6FF}_{b_{1}=0}N^{k_{2}+1}(2\unicode[STIX]{x1D70B})^{-k_{2}-1}k_{2}!\biggl(1-2\biggl\{\frac{a_{2}}{N}\biggr\}\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{2}}{N},k_{2}+1\biggr)+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{2}}{N},k_{2}+1\biggr)\biggr)\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},1\biggr)+\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},1\biggr)\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{3} & = & \displaystyle \unicode[STIX]{x1D6FF}_{k_{1}=0}\unicode[STIX]{x1D6FF}_{a_{2}\neq 0}\unicode[STIX]{x1D6FF}_{b_{1}=0}N^{k_{2}+1}(2\unicode[STIX]{x1D70B})^{-k_{2}-1}k_{2}!\biggl(1-2\biggl\{\frac{a_{2}}{N}\biggr\}\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{2}}{N},k_{2}+1\biggr)+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{2}}{N},k_{2}+1\biggr)\biggr)\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},1\biggr)+\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},1\biggr)\biggr).\nonumber\end{eqnarray}$$
Alors l’intégrale régularisée de
![]() $p_{1}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{1}}(u_{1})\wedge \unicode[STIX]{x1D70B}_{k_{2}+1}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{2}}(u_{2}))$
le long de
$p_{1}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{1}}(u_{1})\wedge \unicode[STIX]{x1D70B}_{k_{2}+1}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{2}}(u_{2}))$
le long de
![]() $X^{k}\{0,\infty \}$
est donnée par
$X^{k}\{0,\infty \}$
est donnée par
avec
 $$\begin{eqnarray}\displaystyle A & = & \displaystyle A^{k_{1},k_{2}}(u_{1},u_{2})\nonumber\\ \displaystyle & = & \displaystyle i^{k_{1}-k_{2}+1}\frac{(k_{1}+2)(k_{2}+2)}{4N^{k_{1}+k_{2}+2}}(2\unicode[STIX]{x1D70B})^{k_{1}+k_{2}+1}\unicode[STIX]{x1D6EC}^{\ast }((G_{b_{2},a_{1}}^{(k_{2}+1)}+G_{b_{2},-a_{1}}^{(k_{2}+1)})(G_{b_{1},-a_{2}}^{(k_{1}+1)}-G_{b_{1},a_{2}}^{(k_{1}+1)}),0),\nonumber\\ \displaystyle B & = & \displaystyle B^{k_{1},k_{2}}(u_{1},u_{2})\nonumber\\ \displaystyle & = & \displaystyle (-1)^{k_{1}}\frac{(k_{1}+2)!(k_{2}+2)}{8\unicode[STIX]{x1D70B}^{2}N^{2}}(2i\unicode[STIX]{x1D70B})^{k_{2}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k_{1}+2\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k_{1}+2\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},2\biggr)\biggr)\biggl(\unicode[STIX]{x1D701}^{(\ast )}\biggl(-\frac{b_{2}}{N},-k_{2}+1\biggr)+(-1)^{k_{2}+1}\unicode[STIX]{x1D701}^{(\ast )}\biggl(\frac{b_{2}}{N},-k_{2}+1\biggr)\biggr),\nonumber\\ \displaystyle C & = & \displaystyle C^{k_{1},k_{2}}(u_{1},u_{2})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FF}_{k_{1}=0}\unicode[STIX]{x1D6FF}_{b_{1}=0}\unicode[STIX]{x1D6FF}_{a_{2}\neq 0}\frac{k_{2}+2}{2N^{2}}(2i\unicode[STIX]{x1D70B})^{k_{2}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},1\biggr)+\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},1\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},1\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},1\biggr)\biggr)\biggl(\unicode[STIX]{x1D701}\biggl(-\frac{b_{2}}{N},-k_{2}\biggr)+(-1)^{k_{2}+1}\unicode[STIX]{x1D701}\biggl(\frac{b_{2}}{N},-k_{2}\biggr)\biggr),\nonumber\\ \displaystyle D & = & \displaystyle D^{k_{1},k_{2}}(u_{1},u_{2})\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x1D6FF}_{k_{2}\equiv 1(2)}i^{k_{1}}\frac{(k_{1}+2)(k_{2}+2)}{2N^{2}}(2\unicode[STIX]{x1D70B})^{k_{1}+2k_{2}+2}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},-k_{2}\biggr)+\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},-k_{2}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\unicode[STIX]{x1D701}\biggl(-\frac{a_{2}}{N},-k_{2}-1\biggr)\cdot \lim _{s\rightarrow 0}\biggl(\unicode[STIX]{x1D6E4}(s-k_{2}-1)\biggl(\unicode[STIX]{x1D701}\biggl(\frac{b_{1}}{N},s-k-1\biggr)+(-1)^{k_{1}}\unicode[STIX]{x1D701}\biggl(-\frac{b_{1}}{N},s-k-1\biggr)\biggr)\biggr),\nonumber\\ \displaystyle E & = & \displaystyle E^{k_{1},k_{2}}(u_{1},u_{2})\nonumber\\ \displaystyle & = & \displaystyle -i^{k_{1}}\frac{(k_{1}+2)(k_{2}+2)}{4N^{k_{1}+2}}(2\unicode[STIX]{x1D70B})^{k_{1}+k_{2}+1}N^{-k_{2}-1}I_{2}\nonumber\\ \displaystyle & = & \displaystyle (-1)^{k_{1}}i\frac{(k_{1}+2)(k_{2}+2)(k+1)!}{8\unicode[STIX]{x1D70B}N^{2}}a_{0}(H_{b_{2},a_{1}}^{(k_{2}+1)}+H_{b_{2},-a_{1}}^{(k_{2}+1)})\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2\biggr)\biggr)\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},k_{2}+2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},k_{2}+2\biggr)\biggr),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A & = & \displaystyle A^{k_{1},k_{2}}(u_{1},u_{2})\nonumber\\ \displaystyle & = & \displaystyle i^{k_{1}-k_{2}+1}\frac{(k_{1}+2)(k_{2}+2)}{4N^{k_{1}+k_{2}+2}}(2\unicode[STIX]{x1D70B})^{k_{1}+k_{2}+1}\unicode[STIX]{x1D6EC}^{\ast }((G_{b_{2},a_{1}}^{(k_{2}+1)}+G_{b_{2},-a_{1}}^{(k_{2}+1)})(G_{b_{1},-a_{2}}^{(k_{1}+1)}-G_{b_{1},a_{2}}^{(k_{1}+1)}),0),\nonumber\\ \displaystyle B & = & \displaystyle B^{k_{1},k_{2}}(u_{1},u_{2})\nonumber\\ \displaystyle & = & \displaystyle (-1)^{k_{1}}\frac{(k_{1}+2)!(k_{2}+2)}{8\unicode[STIX]{x1D70B}^{2}N^{2}}(2i\unicode[STIX]{x1D70B})^{k_{2}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k_{1}+2\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k_{1}+2\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},2\biggr)\biggr)\biggl(\unicode[STIX]{x1D701}^{(\ast )}\biggl(-\frac{b_{2}}{N},-k_{2}+1\biggr)+(-1)^{k_{2}+1}\unicode[STIX]{x1D701}^{(\ast )}\biggl(\frac{b_{2}}{N},-k_{2}+1\biggr)\biggr),\nonumber\\ \displaystyle C & = & \displaystyle C^{k_{1},k_{2}}(u_{1},u_{2})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FF}_{k_{1}=0}\unicode[STIX]{x1D6FF}_{b_{1}=0}\unicode[STIX]{x1D6FF}_{a_{2}\neq 0}\frac{k_{2}+2}{2N^{2}}(2i\unicode[STIX]{x1D70B})^{k_{2}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},1\biggr)+\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},1\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},1\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},1\biggr)\biggr)\biggl(\unicode[STIX]{x1D701}\biggl(-\frac{b_{2}}{N},-k_{2}\biggr)+(-1)^{k_{2}+1}\unicode[STIX]{x1D701}\biggl(\frac{b_{2}}{N},-k_{2}\biggr)\biggr),\nonumber\\ \displaystyle D & = & \displaystyle D^{k_{1},k_{2}}(u_{1},u_{2})\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x1D6FF}_{k_{2}\equiv 1(2)}i^{k_{1}}\frac{(k_{1}+2)(k_{2}+2)}{2N^{2}}(2\unicode[STIX]{x1D70B})^{k_{1}+2k_{2}+2}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},-k_{2}\biggr)+\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},-k_{2}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\unicode[STIX]{x1D701}\biggl(-\frac{a_{2}}{N},-k_{2}-1\biggr)\cdot \lim _{s\rightarrow 0}\biggl(\unicode[STIX]{x1D6E4}(s-k_{2}-1)\biggl(\unicode[STIX]{x1D701}\biggl(\frac{b_{1}}{N},s-k-1\biggr)+(-1)^{k_{1}}\unicode[STIX]{x1D701}\biggl(-\frac{b_{1}}{N},s-k-1\biggr)\biggr)\biggr),\nonumber\\ \displaystyle E & = & \displaystyle E^{k_{1},k_{2}}(u_{1},u_{2})\nonumber\\ \displaystyle & = & \displaystyle -i^{k_{1}}\frac{(k_{1}+2)(k_{2}+2)}{4N^{k_{1}+2}}(2\unicode[STIX]{x1D70B})^{k_{1}+k_{2}+1}N^{-k_{2}-1}I_{2}\nonumber\\ \displaystyle & = & \displaystyle (-1)^{k_{1}}i\frac{(k_{1}+2)(k_{2}+2)(k+1)!}{8\unicode[STIX]{x1D70B}N^{2}}a_{0}(H_{b_{2},a_{1}}^{(k_{2}+1)}+H_{b_{2},-a_{1}}^{(k_{2}+1)})\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2\biggr)\biggr)\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},k_{2}+2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},k_{2}+2\biggr)\biggr),\nonumber\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle F & = & \displaystyle F^{k_{1},k_{2}}(u_{1},u_{2})\nonumber\\ \displaystyle & = & \displaystyle -i^{k_{1}}\frac{(k_{1}+2)(k_{2}+2)}{4N^{k_{1}+2}}(2\unicode[STIX]{x1D70B})^{k_{1}+k_{2}+1}N^{-k_{2}-1}I_{3}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FF}_{k_{1}=0}\unicode[STIX]{x1D6FF}_{b_{1}=0}\unicode[STIX]{x1D6FF}_{a_{2}\neq 0}\frac{k_{2}!(k_{2}+2)}{2N^{2}}\biggl(2\biggl\{\frac{a_{2}}{N}\biggr\}-1\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{2}}{N},k_{2}+1\biggr)+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{2}}{N},k_{2}+1\biggr)\biggr)\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},1\biggr)+\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},1\biggr)\biggr).\hspace{72.0pt}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F & = & \displaystyle F^{k_{1},k_{2}}(u_{1},u_{2})\nonumber\\ \displaystyle & = & \displaystyle -i^{k_{1}}\frac{(k_{1}+2)(k_{2}+2)}{4N^{k_{1}+2}}(2\unicode[STIX]{x1D70B})^{k_{1}+k_{2}+1}N^{-k_{2}-1}I_{3}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FF}_{k_{1}=0}\unicode[STIX]{x1D6FF}_{b_{1}=0}\unicode[STIX]{x1D6FF}_{a_{2}\neq 0}\frac{k_{2}!(k_{2}+2)}{2N^{2}}\biggl(2\biggl\{\frac{a_{2}}{N}\biggr\}-1\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{2}}{N},k_{2}+1\biggr)+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{2}}{N},k_{2}+1\biggr)\biggr)\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},1\biggr)+\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},1\biggr)\biggr).\hspace{72.0pt}\nonumber\end{eqnarray}$$
Dans la formule pour
![]() $B$
, le symbole
$B$
, le symbole
![]() $\unicode[STIX]{x1D701}^{(\ast )}$
indique que l’on prend la valeur régularisée lorsque
$\unicode[STIX]{x1D701}^{(\ast )}$
indique que l’on prend la valeur régularisée lorsque
![]() $k_{2}=0$
.
$k_{2}=0$
.
Montrons maintenant que les termes
![]() $C$
et
$C$
et
![]() $F$
se simplifient. D’après la formule (8), on a
$F$
se simplifient. D’après la formule (8), on a
D’autre part, en appliquant la formule de Hurwitz (6) en
![]() $s=k_{2}+1$
, il vient
$s=k_{2}+1$
, il vient
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}\biggl(-\frac{b_{2}}{N},-k_{2}\biggr) & = & \displaystyle \frac{k_{2}!}{(2\unicode[STIX]{x1D70B})^{k_{2}+1}}\biggl((-i)^{k_{2}+1}\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{2}}{N},k_{2}+1\biggr)+i^{k_{2}+1}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{2}}{N},k_{2}+1\biggr)\biggr)\nonumber\\ \displaystyle & = & \displaystyle (-i)^{k_{2}+1}\frac{k_{2}!}{(2\unicode[STIX]{x1D70B})^{k_{2}+1}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{2}}{N},k_{2}+1\biggr)+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{2}}{N},k_{2}+1\biggr)\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}\biggl(-\frac{b_{2}}{N},-k_{2}\biggr) & = & \displaystyle \frac{k_{2}!}{(2\unicode[STIX]{x1D70B})^{k_{2}+1}}\biggl((-i)^{k_{2}+1}\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{2}}{N},k_{2}+1\biggr)+i^{k_{2}+1}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{2}}{N},k_{2}+1\biggr)\biggr)\nonumber\\ \displaystyle & = & \displaystyle (-i)^{k_{2}+1}\frac{k_{2}!}{(2\unicode[STIX]{x1D70B})^{k_{2}+1}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{2}}{N},k_{2}+1\biggr)+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{2}}{N},k_{2}+1\biggr)\biggr).\nonumber\end{eqnarray}$$
De même, on a
On en déduit
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}\biggl(-\frac{b_{2}}{N},-k_{2}\biggr)+(-1)^{k_{2}+1}\unicode[STIX]{x1D701}\biggl(\frac{b_{2}}{N},-k_{2}\biggr) & = & \displaystyle 2\frac{(-i)^{k_{2}+1}k_{2}!}{(2\unicode[STIX]{x1D70B})^{k_{2}+1}} (\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{2}}{N},k_{2}+1\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{2}}{N},k_{2}+1\biggr)\!).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}\biggl(-\frac{b_{2}}{N},-k_{2}\biggr)+(-1)^{k_{2}+1}\unicode[STIX]{x1D701}\biggl(\frac{b_{2}}{N},-k_{2}\biggr) & = & \displaystyle 2\frac{(-i)^{k_{2}+1}k_{2}!}{(2\unicode[STIX]{x1D70B})^{k_{2}+1}} (\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{2}}{N},k_{2}+1\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{2}}{N},k_{2}+1\biggr)\!).\end{eqnarray}$$
En reportant (34) et (35) dans le terme
![]() $C$
, on obtient
$C$
, on obtient
 $$\begin{eqnarray}\displaystyle C & = & \displaystyle \unicode[STIX]{x1D6FF}_{k_{1}=0}\unicode[STIX]{x1D6FF}_{b_{1}=0}\unicode[STIX]{x1D6FF}_{a_{2}\neq 0}\frac{k_{2}+2}{2N^{2}}(2i\unicode[STIX]{x1D70B})^{k_{2}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},1\biggr)+\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},1\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,2i\unicode[STIX]{x1D70B}\biggl(\frac{1}{2}-\biggl\{\frac{a_{2}}{N}\biggr\}\biggr)2\frac{(-i)^{k_{2}+1}k_{2}!}{(2\unicode[STIX]{x1D70B})^{k_{2}+1}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{2}}{N},k_{2}+1\biggr)+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{2}}{N},k_{2}+1\biggr)\biggr)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FF}_{k_{1}=0}\unicode[STIX]{x1D6FF}_{b_{1}=0}\unicode[STIX]{x1D6FF}_{a_{2}\neq 0}\frac{k_{2}!(k_{2}+2)}{2N^{2}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},1\biggr)+\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},1\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(1-2\biggl\{\frac{a_{2}}{N}\biggr\}\biggr)\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{2}}{N},k_{2}+1\biggr)+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{2}}{N},k_{2}+1\biggr)\biggr)\nonumber\\ \displaystyle & = & \displaystyle -F.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C & = & \displaystyle \unicode[STIX]{x1D6FF}_{k_{1}=0}\unicode[STIX]{x1D6FF}_{b_{1}=0}\unicode[STIX]{x1D6FF}_{a_{2}\neq 0}\frac{k_{2}+2}{2N^{2}}(2i\unicode[STIX]{x1D70B})^{k_{2}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},1\biggr)+\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},1\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,2i\unicode[STIX]{x1D70B}\biggl(\frac{1}{2}-\biggl\{\frac{a_{2}}{N}\biggr\}\biggr)2\frac{(-i)^{k_{2}+1}k_{2}!}{(2\unicode[STIX]{x1D70B})^{k_{2}+1}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{2}}{N},k_{2}+1\biggr)+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{2}}{N},k_{2}+1\biggr)\biggr)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FF}_{k_{1}=0}\unicode[STIX]{x1D6FF}_{b_{1}=0}\unicode[STIX]{x1D6FF}_{a_{2}\neq 0}\frac{k_{2}!(k_{2}+2)}{2N^{2}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},1\biggr)+\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},1\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(1-2\biggl\{\frac{a_{2}}{N}\biggr\}\biggr)\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{2}}{N},k_{2}+1\biggr)+(-1)^{k_{2}+1}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{2}}{N},k_{2}+1\biggr)\biggr)\nonumber\\ \displaystyle & = & \displaystyle -F.\nonumber\end{eqnarray}$$
Nous allons maintenant simplifier d’autres termes, en distinguant les cas suivant
![]() $k_{2}$
.
$k_{2}$
.
Premier cas:
![]() $k_{2}=0$
.
$k_{2}=0$
.
On a alors
![]() $D=0$
. Nous allons montrer que
$D=0$
. Nous allons montrer que
![]() $B+E=0$
. On a
$B+E=0$
. On a
 $$\begin{eqnarray}\displaystyle B & = & \displaystyle (-1)^{k_{1}}\frac{(k_{1}+2)!}{4\unicode[STIX]{x1D70B}^{2}N^{2}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k_{1}+2\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k_{1}+2\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},2\biggr)\biggr)\biggl(\unicode[STIX]{x1D701}^{\ast }\biggl(-\frac{b_{2}}{N},1\biggr)-\unicode[STIX]{x1D701}^{\ast }\biggl(\frac{b_{2}}{N},1\biggr)\biggr)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B & = & \displaystyle (-1)^{k_{1}}\frac{(k_{1}+2)!}{4\unicode[STIX]{x1D70B}^{2}N^{2}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k_{1}+2\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k_{1}+2\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},2\biggr)\biggr)\biggl(\unicode[STIX]{x1D701}^{\ast }\biggl(-\frac{b_{2}}{N},1\biggr)-\unicode[STIX]{x1D701}^{\ast }\biggl(\frac{b_{2}}{N},1\biggr)\biggr)\nonumber\end{eqnarray}$$
et
 $$\begin{eqnarray}\displaystyle E & = & \displaystyle (-1)^{k_{1}}i\frac{(k_{1}+2)!}{4\unicode[STIX]{x1D70B}N^{2}}a_{0}(H_{b_{2},a_{1}}^{(1)}+H_{b_{2},-a_{1}}^{(1)})\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k_{1}+2\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k_{1}+2\biggr)\biggr)\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},2\biggr)\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E & = & \displaystyle (-1)^{k_{1}}i\frac{(k_{1}+2)!}{4\unicode[STIX]{x1D70B}N^{2}}a_{0}(H_{b_{2},a_{1}}^{(1)}+H_{b_{2},-a_{1}}^{(1)})\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k_{1}+2\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k_{1}+2\biggr)\biggr)\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},2\biggr)\biggr).\nonumber\end{eqnarray}$$
Si
![]() $b_{2}=0$
, alors
$b_{2}=0$
, alors
![]() $H_{0,a_{1}}^{(1)}+H_{0,-a_{1}}^{(1)}=0$
et donc
$H_{0,a_{1}}^{(1)}+H_{0,-a_{1}}^{(1)}=0$
et donc
![]() $B=E=0$
. Nous pouvons donc supposer
$B=E=0$
. Nous pouvons donc supposer
![]() $b_{2}\neq 0$
. D’après la formule (9), on a
$b_{2}\neq 0$
. D’après la formule (9), on a
D’après la définition 3.9 et en utilisant l’identité
il vient
En reportant dans
![]() $B$
et
$B$
et
![]() $E$
, on obtient
$E$
, on obtient
![]() $B+E=0$
. Au final, on a donc dans ce cas
$B+E=0$
. Au final, on a donc dans ce cas
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X^{k}\{0,\infty \}}^{\ast }p_{1}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{1}}(u_{1})\wedge \unicode[STIX]{x1D70B}_{k_{2}+1}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{2}}(u_{2}))=A\nonumber\\ \displaystyle & & \displaystyle \quad =i^{k_{1}+1}\frac{(k_{1}+2)}{2N^{k_{1}+2}}(2\unicode[STIX]{x1D70B})^{k_{1}+1}\unicode[STIX]{x1D6EC}^{\ast }((G_{b_{2},a_{1}}^{(1)}+G_{b_{2},-a_{1}}^{(1)})(G_{b_{1},-a_{2}}^{(k_{1}+1)}-G_{b_{1},a_{2}}^{(k_{1}+1)}),0).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X^{k}\{0,\infty \}}^{\ast }p_{1}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{1}}(u_{1})\wedge \unicode[STIX]{x1D70B}_{k_{2}+1}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{2}}(u_{2}))=A\nonumber\\ \displaystyle & & \displaystyle \quad =i^{k_{1}+1}\frac{(k_{1}+2)}{2N^{k_{1}+2}}(2\unicode[STIX]{x1D70B})^{k_{1}+1}\unicode[STIX]{x1D6EC}^{\ast }((G_{b_{2},a_{1}}^{(1)}+G_{b_{2},-a_{1}}^{(1)})(G_{b_{1},-a_{2}}^{(k_{1}+1)}-G_{b_{1},a_{2}}^{(k_{1}+1)}),0).\nonumber\end{eqnarray}$$
Second cas:
![]() $k_{2}\geqslant 1$
.
$k_{2}\geqslant 1$
.
Puisque
![]() $\unicode[STIX]{x1D701}(-b_{2}/N,-k_{2}+1)=(-1)^{k_{2}}\unicode[STIX]{x1D701}(b_{2}/N,-k_{2}+1)$
, on a
$\unicode[STIX]{x1D701}(-b_{2}/N,-k_{2}+1)=(-1)^{k_{2}}\unicode[STIX]{x1D701}(b_{2}/N,-k_{2}+1)$
, on a
![]() $B=0$
(lorsque
$B=0$
(lorsque
![]() $k_{2}=1$
, on utilise ici l’hypothèse
$k_{2}=1$
, on utilise ici l’hypothèse
![]() $b_{2}\neq 0$
).
$b_{2}\neq 0$
).
Comparons les termes
![]() $D$
et
$D$
et
![]() $E$
. On a
$E$
. On a
 $$\begin{eqnarray}\displaystyle E & = & \displaystyle (-1)^{k_{1}}i\frac{(k_{1}+2)(k_{2}+2)(k+1)!}{8\unicode[STIX]{x1D70B}N^{2}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},-k_{2}\biggr)+\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},-k_{2}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2\biggr)\biggr)\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},k_{2}+2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},k_{2}+2\biggr)\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E & = & \displaystyle (-1)^{k_{1}}i\frac{(k_{1}+2)(k_{2}+2)(k+1)!}{8\unicode[STIX]{x1D70B}N^{2}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},-k_{2}\biggr)+\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},-k_{2}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2\biggr)\biggr)\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},k_{2}+2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},k_{2}+2\biggr)\biggr).\nonumber\end{eqnarray}$$
D’après (11), on a
![]() $\hat{\unicode[STIX]{x1D701}}(-a_{1}/N,-k_{2})+\hat{\unicode[STIX]{x1D701}}(a_{1}/N,-k_{2})=0$
si
$\hat{\unicode[STIX]{x1D701}}(-a_{1}/N,-k_{2})+\hat{\unicode[STIX]{x1D701}}(a_{1}/N,-k_{2})=0$
si
![]() $k_{2}$
est pair. Donc
$k_{2}$
est pair. Donc
![]() $E=0$
dès que
$E=0$
dès que
![]() $k_{2}$
est pair, et nous supposons désormais
$k_{2}$
est pair, et nous supposons désormais
![]() $k_{2}$
impair. Par la formule d’Hurwitz en
$k_{2}$
impair. Par la formule d’Hurwitz en
![]() $s=k_{2}+2$
, on obtient
$s=k_{2}+2$
, on obtient
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}\biggl(-\frac{a_{2}}{N},-k_{2}-1\biggr) & = & \displaystyle \frac{(k_{2}+1)!}{(2\unicode[STIX]{x1D70B})^{k_{2}+2}}\biggl((-i)^{k_{2}+2}\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},k_{2}+2\biggr)+i^{k_{2}+2}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},k_{2}+2\biggr)\biggr)\nonumber\\ \displaystyle & = & \displaystyle \frac{i^{k_{2}+2}(k_{2}+1)!}{(2\unicode[STIX]{x1D70B})^{k_{2}+2}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},k_{2}+2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},k_{2}+2\biggr)\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}\biggl(-\frac{a_{2}}{N},-k_{2}-1\biggr) & = & \displaystyle \frac{(k_{2}+1)!}{(2\unicode[STIX]{x1D70B})^{k_{2}+2}}\biggl((-i)^{k_{2}+2}\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},k_{2}+2\biggr)+i^{k_{2}+2}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},k_{2}+2\biggr)\biggr)\nonumber\\ \displaystyle & = & \displaystyle \frac{i^{k_{2}+2}(k_{2}+1)!}{(2\unicode[STIX]{x1D70B})^{k_{2}+2}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},k_{2}+2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},k_{2}+2\biggr)\biggr).\nonumber\end{eqnarray}$$
Appliquons maintenant la formule d’Hurwitz aux termes à l’intérieur de la limite dans
![]() $D$
. Il vient
$D$
. Il vient
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}\biggl(\frac{b_{1}}{N},s-k-1\biggr) & = & \displaystyle \frac{\unicode[STIX]{x1D6E4}(k+2-s)}{(2\unicode[STIX]{x1D70B})^{k+2-s}} (e^{-(i\unicode[STIX]{x1D70B}/2)(k+2-s)}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2-s\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,e^{(i\unicode[STIX]{x1D70B}/2)(k+2-s)}\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2-s\biggr)\!),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}\biggl(\frac{b_{1}}{N},s-k-1\biggr) & = & \displaystyle \frac{\unicode[STIX]{x1D6E4}(k+2-s)}{(2\unicode[STIX]{x1D70B})^{k+2-s}} (e^{-(i\unicode[STIX]{x1D70B}/2)(k+2-s)}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2-s\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,e^{(i\unicode[STIX]{x1D70B}/2)(k+2-s)}\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2-s\biggr)\!),\nonumber\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}\biggl(-\frac{b_{1}}{N},s-k-1\biggr) & = & \displaystyle \frac{\unicode[STIX]{x1D6E4}(k+2-s)}{(2\unicode[STIX]{x1D70B})^{k+2-s}} (e^{-(i\unicode[STIX]{x1D70B}/2)(k+2-s)}\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2-s\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,e^{(i\unicode[STIX]{x1D70B}/2)(k+2-s)}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2-s\biggr)\!),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}\biggl(-\frac{b_{1}}{N},s-k-1\biggr) & = & \displaystyle \frac{\unicode[STIX]{x1D6E4}(k+2-s)}{(2\unicode[STIX]{x1D70B})^{k+2-s}} (e^{-(i\unicode[STIX]{x1D70B}/2)(k+2-s)}\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2-s\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,e^{(i\unicode[STIX]{x1D70B}/2)(k+2-s)}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2-s\biggr)\!),\nonumber\end{eqnarray}$$
d’où l’on déduit
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D701}\biggl(\frac{b_{1}}{N},s-k-1\biggr)+(-1)^{k_{1}}\unicode[STIX]{x1D701}\biggl(-\frac{b_{1}}{N},s-k-1\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\unicode[STIX]{x1D6E4}(k+2-s)}{(2\unicode[STIX]{x1D70B})^{k+2-s}} (e^{-(i\unicode[STIX]{x1D70B}/2)(k+2-s)}(1-e^{-i\unicode[STIX]{x1D70B}s})\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2-s\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,e^{(i\unicode[STIX]{x1D70B}/2)(k+2-s)}(1-e^{i\unicode[STIX]{x1D70B}s})\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2-s\biggr)\!).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D701}\biggl(\frac{b_{1}}{N},s-k-1\biggr)+(-1)^{k_{1}}\unicode[STIX]{x1D701}\biggl(-\frac{b_{1}}{N},s-k-1\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\unicode[STIX]{x1D6E4}(k+2-s)}{(2\unicode[STIX]{x1D70B})^{k+2-s}} (e^{-(i\unicode[STIX]{x1D70B}/2)(k+2-s)}(1-e^{-i\unicode[STIX]{x1D70B}s})\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2-s\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,e^{(i\unicode[STIX]{x1D70B}/2)(k+2-s)}(1-e^{i\unicode[STIX]{x1D70B}s})\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2-s\biggr)\!).\nonumber\end{eqnarray}$$
Lorsque
![]() $s\rightarrow 0$
, on a
$s\rightarrow 0$
, on a
![]() $\unicode[STIX]{x1D6E4}(s-k_{2}-1)\sim (1/(k_{2}+1)!)s^{-1}$
et
$\unicode[STIX]{x1D6E4}(s-k_{2}-1)\sim (1/(k_{2}+1)!)s^{-1}$
et
![]() $1-e^{\pm i\unicode[STIX]{x1D70B}s}\sim \mp i\unicode[STIX]{x1D70B}s$
d’où
$1-e^{\pm i\unicode[STIX]{x1D70B}s}\sim \mp i\unicode[STIX]{x1D70B}s$
d’où
 $$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{s\rightarrow 0}\biggl(\unicode[STIX]{x1D6E4}(s-k_{2}-1)\biggl(\unicode[STIX]{x1D701}\biggl(\frac{b_{1}}{N},s-k-1\biggr)+(-1)^{k_{1}}\unicode[STIX]{x1D701}\biggl(-\frac{b_{1}}{N},s-k-1\biggr)\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(k+1)!}{(k_{2}+1)!(2\unicode[STIX]{x1D70B})^{k+2}}\biggl((-i)^{k+2}i\unicode[STIX]{x1D70B}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2\biggr)+i^{k+2}(-i\unicode[STIX]{x1D70B})\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(k+1)!(-i)^{k+2}i\unicode[STIX]{x1D70B}}{(k_{2}+1)!(2\unicode[STIX]{x1D70B})^{k+2}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2\biggr)\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{s\rightarrow 0}\biggl(\unicode[STIX]{x1D6E4}(s-k_{2}-1)\biggl(\unicode[STIX]{x1D701}\biggl(\frac{b_{1}}{N},s-k-1\biggr)+(-1)^{k_{1}}\unicode[STIX]{x1D701}\biggl(-\frac{b_{1}}{N},s-k-1\biggr)\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(k+1)!}{(k_{2}+1)!(2\unicode[STIX]{x1D70B})^{k+2}}\biggl((-i)^{k+2}i\unicode[STIX]{x1D70B}\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2\biggr)+i^{k+2}(-i\unicode[STIX]{x1D70B})\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(k+1)!(-i)^{k+2}i\unicode[STIX]{x1D70B}}{(k_{2}+1)!(2\unicode[STIX]{x1D70B})^{k+2}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2\biggr)\biggr).\nonumber\end{eqnarray}$$
En reportant dans
![]() $D$
, on obtient
$D$
, on obtient
 $$\begin{eqnarray}\displaystyle D & = & \displaystyle -i^{k_{1}}\frac{(k_{1}+2)(k_{2}+2)}{2N^{2}}(2\unicode[STIX]{x1D70B})^{k_{1}+2k_{2}+2}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},-k_{2}\biggr)+\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},-k_{2}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\frac{i^{k_{2}+2}(k_{2}+1)!}{(2\unicode[STIX]{x1D70B})^{k_{2}+2}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},k_{2}+2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},k_{2}+2\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\frac{(k+1)!(-i)^{k+2}i\unicode[STIX]{x1D70B}}{(k_{2}+1)!(2\unicode[STIX]{x1D70B})^{k+2}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2\biggr)\biggr)\nonumber\\ \displaystyle & = & \displaystyle -i\frac{(k_{1}+2)(k_{2}+2)(k+1)!}{8\unicode[STIX]{x1D70B}N^{2}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},-k_{2}\biggr)+\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},-k_{2}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},k_{2}+2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},k_{2}+2\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2\biggr)\biggr)\nonumber\\ \displaystyle & = & \displaystyle -E.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D & = & \displaystyle -i^{k_{1}}\frac{(k_{1}+2)(k_{2}+2)}{2N^{2}}(2\unicode[STIX]{x1D70B})^{k_{1}+2k_{2}+2}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},-k_{2}\biggr)+\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},-k_{2}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\frac{i^{k_{2}+2}(k_{2}+1)!}{(2\unicode[STIX]{x1D70B})^{k_{2}+2}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},k_{2}+2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},k_{2}+2\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\frac{(k+1)!(-i)^{k+2}i\unicode[STIX]{x1D70B}}{(k_{2}+1)!(2\unicode[STIX]{x1D70B})^{k+2}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2\biggr)\biggr)\nonumber\\ \displaystyle & = & \displaystyle -i\frac{(k_{1}+2)(k_{2}+2)(k+1)!}{8\unicode[STIX]{x1D70B}N^{2}}\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{1}}{N},-k_{2}\biggr)+\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{1}}{N},-k_{2}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{a_{2}}{N},k_{2}+2\biggr)-\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{a_{2}}{N},k_{2}+2\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(\hat{\unicode[STIX]{x1D701}}\biggl(\frac{b_{1}}{N},k+2\biggr)+(-1)^{k_{1}}\hat{\unicode[STIX]{x1D701}}\biggl(-\frac{b_{1}}{N},k+2\biggr)\biggr)\nonumber\\ \displaystyle & = & \displaystyle -E.\nonumber\end{eqnarray}$$
Au final, on a donc dans ce cas
Dans tous les cas, on a donc
Démonstration du théorème 1.1.
Rappelons que la forme différentielle
![]() $\text{Eis}_{{\mathcal{D}}}^{k_{1},k_{2}}(u_{1},u_{2})$
est donnée par
$\text{Eis}_{{\mathcal{D}}}^{k_{1},k_{2}}(u_{1},u_{2})$
est donnée par
 $$\begin{eqnarray}\displaystyle \text{Eis}_{{\mathcal{D}}}^{k_{1},k_{2}}(u_{1},u_{2}) & = & \displaystyle p_{1}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{1}}(u_{1})\wedge \unicode[STIX]{x1D70B}_{k_{2}+1}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{2}}(u_{2}))\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{k_{1}+1}\unicode[STIX]{x1D70B}_{k_{1}+1}(p_{1}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{1}}(u_{1}))\wedge p_{2}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{2}}(u_{2})\nonumber\\ \displaystyle & = & \displaystyle p_{1}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{1}}(u_{1})\wedge \unicode[STIX]{x1D70B}_{k_{2}+1}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{2}}(u_{2}))\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{(k_{1}+1)(k_{2}+1)}p_{2}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{2}}(u_{2})\wedge \unicode[STIX]{x1D70B}_{k_{1}+1}(p_{1}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{1}}(u_{1})).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Eis}_{{\mathcal{D}}}^{k_{1},k_{2}}(u_{1},u_{2}) & = & \displaystyle p_{1}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{1}}(u_{1})\wedge \unicode[STIX]{x1D70B}_{k_{2}+1}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{2}}(u_{2}))\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{k_{1}+1}\unicode[STIX]{x1D70B}_{k_{1}+1}(p_{1}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{1}}(u_{1}))\wedge p_{2}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{2}}(u_{2})\nonumber\\ \displaystyle & = & \displaystyle p_{1}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{1}}(u_{1})\wedge \unicode[STIX]{x1D70B}_{k_{2}+1}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{2}}(u_{2}))\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{(k_{1}+1)(k_{2}+1)}p_{2}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{2}}(u_{2})\wedge \unicode[STIX]{x1D70B}_{k_{1}+1}(p_{1}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{1}}(u_{1})).\nonumber\end{eqnarray}$$
Notons
![]() $\unicode[STIX]{x1D703}:E^{k}\rightarrow E^{k}$
l’isomorphisme défini par
$\unicode[STIX]{x1D703}:E^{k}\rightarrow E^{k}$
l’isomorphisme défini par
Cet isomorphisme laisse stable le cycle de Shokurov
![]() $X^{k}\{0,\infty \}$
en multipliant l’orientation par
$X^{k}\{0,\infty \}$
en multipliant l’orientation par
![]() $(-1)^{k_{1}k_{2}}$
. Il vient donc
$(-1)^{k_{1}k_{2}}$
. Il vient donc
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X^{k}\{0,\infty \}}^{\ast }p_{2}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{2}}(u_{2})\wedge \unicode[STIX]{x1D70B}_{k_{1}+1}(p_{1}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{1}}(u_{1}))\nonumber\\ \displaystyle & & \displaystyle \quad =(-1)^{k_{1}k_{2}}\int _{X^{k}\{0,\infty \}}^{\ast }\unicode[STIX]{x1D703}^{\ast }(p_{2}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{2}}(u_{2})\wedge \unicode[STIX]{x1D70B}_{k_{1}+1}(p_{1}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{1}}(u_{1})))\nonumber\\ \displaystyle & & \displaystyle \quad =(-1)^{k_{1}k_{2}}A^{k_{2},k_{1}}(u_{2},u_{1}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X^{k}\{0,\infty \}}^{\ast }p_{2}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{2}}(u_{2})\wedge \unicode[STIX]{x1D70B}_{k_{1}+1}(p_{1}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{1}}(u_{1}))\nonumber\\ \displaystyle & & \displaystyle \quad =(-1)^{k_{1}k_{2}}\int _{X^{k}\{0,\infty \}}^{\ast }\unicode[STIX]{x1D703}^{\ast }(p_{2}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k_{2}}(u_{2})\wedge \unicode[STIX]{x1D70B}_{k_{1}+1}(p_{1}^{\ast }\,\text{Eis}_{\text{hol}}^{k_{1}}(u_{1})))\nonumber\\ \displaystyle & & \displaystyle \quad =(-1)^{k_{1}k_{2}}A^{k_{2},k_{1}}(u_{2},u_{1}).\nonumber\end{eqnarray}$$
On obtient ainsi
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X^{k}\{0,\infty \}}^{\ast }\text{Eis}_{{\mathcal{D}}}^{k_{1},k_{2}}(u_{1},u_{2})\nonumber\\ \displaystyle & & \displaystyle \quad =A^{k_{1},k_{2}}(u_{1},u_{2})+(-1)^{k_{1}+k_{2}+1}A^{k_{2},k_{1}}(u_{2},u_{1})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(k_{1}+2)(k_{2}+2)}{4N^{k+2}}(2\unicode[STIX]{x1D70B})^{k+1} (i^{k_{1}-k_{2}+1}\unicode[STIX]{x1D6EC}^{\ast }((G_{b_{2},a_{1}}^{(k_{2}+1)}+G_{b_{2},-a_{1}}^{(k_{2}+1)})(G_{b_{1},-a_{2}}^{(k_{1}+1)}-G_{b_{1},a_{2}}^{(k_{1}+1)}),0)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{k_{1}+k_{2}+1}i^{k_{2}-k_{1}+1}\unicode[STIX]{x1D6EC}^{\ast }((G_{b_{1},a_{2}}^{(k_{1}+1)}+G_{b_{1},-a_{2}}^{(k_{1}+1)})(G_{b_{2},-a_{1}}^{(k_{2}+1)}-G_{b_{2},a_{1}}^{(k_{2}+1)}),0))\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(k_{1}+2)(k_{2}+2)}{4N^{k+2}}(2\unicode[STIX]{x1D70B})^{k+1}i^{k_{1}-k_{2}+1}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\unicode[STIX]{x1D6EC}^{\ast }((G_{b_{2},a_{1}}^{(k_{2}+1)}+G_{b_{2},-a_{1}}^{(k_{2}+1)})(G_{b_{1},-a_{2}}^{(k_{1}+1)}-G_{b_{1},a_{2}}^{(k_{1}+1)})-(G_{b_{1},a_{2}}^{(k_{1}+1)}+G_{b_{1},-a_{2}}^{(k_{1}+1)})(G_{b_{2},-a_{1}}^{(k_{2}+1)}-G_{b_{2},a_{1}}^{(k_{2}+1)}),0)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(k_{1}+2)(k_{2}+2)}{2N^{k+2}}(2\unicode[STIX]{x1D70B})^{k+1}i^{k_{1}-k_{2}+1}\unicode[STIX]{x1D6EC}^{\ast }(G_{b_{2},a_{1}}^{(k_{2}+1)}G_{b_{1},-a_{2}}^{(k_{1}+1)}-G_{b_{2},-a_{1}}^{(k_{2}+1)}G_{b_{1},a_{2}}^{(k_{1}+1)},0).\Box \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X^{k}\{0,\infty \}}^{\ast }\text{Eis}_{{\mathcal{D}}}^{k_{1},k_{2}}(u_{1},u_{2})\nonumber\\ \displaystyle & & \displaystyle \quad =A^{k_{1},k_{2}}(u_{1},u_{2})+(-1)^{k_{1}+k_{2}+1}A^{k_{2},k_{1}}(u_{2},u_{1})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(k_{1}+2)(k_{2}+2)}{4N^{k+2}}(2\unicode[STIX]{x1D70B})^{k+1} (i^{k_{1}-k_{2}+1}\unicode[STIX]{x1D6EC}^{\ast }((G_{b_{2},a_{1}}^{(k_{2}+1)}+G_{b_{2},-a_{1}}^{(k_{2}+1)})(G_{b_{1},-a_{2}}^{(k_{1}+1)}-G_{b_{1},a_{2}}^{(k_{1}+1)}),0)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(-1)^{k_{1}+k_{2}+1}i^{k_{2}-k_{1}+1}\unicode[STIX]{x1D6EC}^{\ast }((G_{b_{1},a_{2}}^{(k_{1}+1)}+G_{b_{1},-a_{2}}^{(k_{1}+1)})(G_{b_{2},-a_{1}}^{(k_{2}+1)}-G_{b_{2},a_{1}}^{(k_{2}+1)}),0))\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(k_{1}+2)(k_{2}+2)}{4N^{k+2}}(2\unicode[STIX]{x1D70B})^{k+1}i^{k_{1}-k_{2}+1}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\unicode[STIX]{x1D6EC}^{\ast }((G_{b_{2},a_{1}}^{(k_{2}+1)}+G_{b_{2},-a_{1}}^{(k_{2}+1)})(G_{b_{1},-a_{2}}^{(k_{1}+1)}-G_{b_{1},a_{2}}^{(k_{1}+1)})-(G_{b_{1},a_{2}}^{(k_{1}+1)}+G_{b_{1},-a_{2}}^{(k_{1}+1)})(G_{b_{2},-a_{1}}^{(k_{2}+1)}-G_{b_{2},a_{1}}^{(k_{2}+1)}),0)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(k_{1}+2)(k_{2}+2)}{2N^{k+2}}(2\unicode[STIX]{x1D70B})^{k+1}i^{k_{1}-k_{2}+1}\unicode[STIX]{x1D6EC}^{\ast }(G_{b_{2},a_{1}}^{(k_{2}+1)}G_{b_{1},-a_{2}}^{(k_{1}+1)}-G_{b_{2},-a_{1}}^{(k_{2}+1)}G_{b_{1},a_{2}}^{(k_{1}+1)},0).\Box \nonumber\end{eqnarray}$$
Nous terminons par un résultat partiel pour le calcul du régulateur dans le cas où
![]() $k_{i}=1$
et
$k_{i}=1$
et
![]() $b_{i}=0$
.
$b_{i}=0$
.
Théorème 9.5. Soit
![]() $k\geqslant 0$
un entier. Soit
$k\geqslant 0$
un entier. Soit
![]() $N\geqslant 3$
un entier, et soient
$N\geqslant 3$
un entier, et soient
![]() $a,a^{\prime },b,c\in \mathbf{Z}/N\mathbf{Z}$
. Supposons
$a,a^{\prime },b,c\in \mathbf{Z}/N\mathbf{Z}$
. Supposons
![]() $(a,b),(a^{\prime },b)\neq (0,0)$
si
$(a,b),(a^{\prime },b)\neq (0,0)$
si
![]() $k=0$
, et
$k=0$
, et
![]() $b\neq 0$
si
$b\neq 0$
si
![]() $k=1$
. Alors
$k=1$
. Alors
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X^{k+1}\{0,\infty \}}^{\ast }\text{Eis}_{{\mathcal{D}}}^{k,1}((a,b),(c,0))-\text{Eis}_{{\mathcal{D}}}^{k,1}((a^{\prime },b),(c,0))\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{3(k+2)}{2N^{k+3}}(2\unicode[STIX]{x1D70B})^{k+2}i^{k}\unicode[STIX]{x1D6EC}^{\ast }((G_{0,a}^{(2)}-G_{0,a^{\prime }}^{(2)})G_{b,-c}^{(k+1)}-(G_{0,-a}^{(2)}-G_{0,-a^{\prime }}^{(2)})G_{b,c}^{(k+1)},0).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X^{k+1}\{0,\infty \}}^{\ast }\text{Eis}_{{\mathcal{D}}}^{k,1}((a,b),(c,0))-\text{Eis}_{{\mathcal{D}}}^{k,1}((a^{\prime },b),(c,0))\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{3(k+2)}{2N^{k+3}}(2\unicode[STIX]{x1D70B})^{k+2}i^{k}\unicode[STIX]{x1D6EC}^{\ast }((G_{0,a}^{(2)}-G_{0,a^{\prime }}^{(2)})G_{b,-c}^{(k+1)}-(G_{0,-a}^{(2)}-G_{0,-a^{\prime }}^{(2)})G_{b,c}^{(k+1)},0).\nonumber\end{eqnarray}$$
Notons que les séries d’Eisenstein
![]() $G_{0,a}^{(2)}$
sont seulement quasi-modulaires, mais que les différences
$G_{0,a}^{(2)}$
sont seulement quasi-modulaires, mais que les différences
![]() $G_{0,a}^{(2)}-G_{0,a^{\prime }}^{(2)}$
sont modulaires.
$G_{0,a}^{(2)}-G_{0,a^{\prime }}^{(2)}$
sont modulaires.
Démonstration.
On a comme dans le calcul précédent
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X^{k+1}\{0,\infty \}}^{\ast }p_{1}^{\ast }(\text{Eis}_{{\mathcal{D}}}^{k}(a,b)-\text{Eis}_{{\mathcal{D}}}^{k}(a^{\prime },b))\wedge \unicode[STIX]{x1D70B}_{2}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{1}(c,0))\nonumber\\ \displaystyle & & \displaystyle \quad =A^{k,1}((a,b),(c,0))-A^{k,1}((a^{\prime },b),(c,0))+B^{k,1}((a,b),(c,0))-B^{k,1}((a^{\prime },b),(c,0))\nonumber\\ \displaystyle & & \displaystyle \qquad +\,C^{k,1}((a,b),(c,0))-C^{k,1}((a^{\prime },b),(c,0))+D^{k,1}((a,b),(c,0))-D^{k,1}((a^{\prime },b),(c,0))\nonumber\\ \displaystyle & & \displaystyle \qquad +\,E^{k,1}((a,b),(c,0))-E^{k,1}((a^{\prime },b),(c,0))+F^{k,1}((a,b),(c,0))-F^{k,1}((a^{\prime },b),(c,0)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X^{k+1}\{0,\infty \}}^{\ast }p_{1}^{\ast }(\text{Eis}_{{\mathcal{D}}}^{k}(a,b)-\text{Eis}_{{\mathcal{D}}}^{k}(a^{\prime },b))\wedge \unicode[STIX]{x1D70B}_{2}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{1}(c,0))\nonumber\\ \displaystyle & & \displaystyle \quad =A^{k,1}((a,b),(c,0))-A^{k,1}((a^{\prime },b),(c,0))+B^{k,1}((a,b),(c,0))-B^{k,1}((a^{\prime },b),(c,0))\nonumber\\ \displaystyle & & \displaystyle \qquad +\,C^{k,1}((a,b),(c,0))-C^{k,1}((a^{\prime },b),(c,0))+D^{k,1}((a,b),(c,0))-D^{k,1}((a^{\prime },b),(c,0))\nonumber\\ \displaystyle & & \displaystyle \qquad +\,E^{k,1}((a,b),(c,0))-E^{k,1}((a^{\prime },b),(c,0))+F^{k,1}((a,b),(c,0))-F^{k,1}((a^{\prime },b),(c,0)).\nonumber\end{eqnarray}$$
Comme
![]() $B^{k,1}((a,b),(c,0))$
ne dépend pas de
$B^{k,1}((a,b),(c,0))$
ne dépend pas de
![]() $a$
, on a
$a$
, on a
![]() $B^{k,1}((a,b),(c,0))-B^{k,1}((a^{\prime },b),(c,0))=0$
. On a également
$B^{k,1}((a,b),(c,0))-B^{k,1}((a^{\prime },b),(c,0))=0$
. On a également
Par ailleurs les termes
![]() $D$
et
$D$
et
![]() $E$
ne font pas intervenir
$E$
ne font pas intervenir
![]() $b_{2}$
, donc le calcul précédent montre que
$b_{2}$
, donc le calcul précédent montre que
Il reste
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X^{k+1}\{0,\infty \}}^{\ast }p_{1}^{\ast }(\text{Eis}_{{\mathcal{D}}}^{k}(a,b)-\text{Eis}_{{\mathcal{D}}}^{k}(a^{\prime },b))\wedge \unicode[STIX]{x1D70B}_{2}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{1}(c,0))\nonumber\\ \displaystyle & & \displaystyle \quad =A^{k,1}((a,b),(c,0))-A^{k,1}((a^{\prime },b),(c,0))\nonumber\\ \displaystyle & & \displaystyle \quad =i^{k}\frac{3(k+2)}{4N^{k+3}}(2\unicode[STIX]{x1D70B})^{k+2}\unicode[STIX]{x1D6EC}^{\ast }((G_{0,a}^{(2)}-G_{0,a^{\prime }}^{(2)}+G_{0,-a}^{(2)}-G_{0,-a^{\prime }}^{(2)})(G_{b,-c}^{(k+1)}-G_{b,c}^{(k+1)}),0).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X^{k+1}\{0,\infty \}}^{\ast }p_{1}^{\ast }(\text{Eis}_{{\mathcal{D}}}^{k}(a,b)-\text{Eis}_{{\mathcal{D}}}^{k}(a^{\prime },b))\wedge \unicode[STIX]{x1D70B}_{2}(p_{2}^{\ast }\,\text{Eis}_{\text{hol}}^{1}(c,0))\nonumber\\ \displaystyle & & \displaystyle \quad =A^{k,1}((a,b),(c,0))-A^{k,1}((a^{\prime },b),(c,0))\nonumber\\ \displaystyle & & \displaystyle \quad =i^{k}\frac{3(k+2)}{4N^{k+3}}(2\unicode[STIX]{x1D70B})^{k+2}\unicode[STIX]{x1D6EC}^{\ast }((G_{0,a}^{(2)}-G_{0,a^{\prime }}^{(2)}+G_{0,-a}^{(2)}-G_{0,-a^{\prime }}^{(2)})(G_{b,-c}^{(k+1)}-G_{b,c}^{(k+1)}),0).\end{eqnarray}$$
D’autre part, en notant
![]() $q_{1}:E^{1+k}\rightarrow E$
et
$q_{1}:E^{1+k}\rightarrow E$
et
![]() $q_{2}:E^{1+k}\rightarrow E^{k}$
les deux projections canoniques, il vient
$q_{2}:E^{1+k}\rightarrow E^{k}$
les deux projections canoniques, il vient
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X^{k+1}\{0,\infty \}}^{\ast }q_{1}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{1}(c,0)\wedge \unicode[STIX]{x1D70B}_{k+1}(q_{2}^{\ast }(\text{Eis}_{\text{hol}}^{k}(a,b)-\text{Eis}_{\text{hol}}^{k}(a^{\prime },b)))\nonumber\\ \displaystyle & & \displaystyle \quad =A^{1,k}((c,0),(a,b))-A^{1,k}((c,0),(a^{\prime },b))+B^{1,k}((c,0),(a,b))-B^{1,k}((c,0),(a^{\prime },b))\nonumber\\ \displaystyle & & \displaystyle \qquad +\,C^{1,k}((c,0),(a,b))-C^{1,k}((c,0),(a^{\prime },b))+D^{1,k}((c,0),(a,b))-D^{1,k}((c,0),(a^{\prime },b))\nonumber\\ \displaystyle & & \displaystyle \qquad +\,E^{1,k}((c,0),(a,b))-E^{1,k}((c,0),(a^{\prime },b))+F^{1,k}((c,0),(a,b))-F^{1,k}((c,0),(a^{\prime },b)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X^{k+1}\{0,\infty \}}^{\ast }q_{1}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{1}(c,0)\wedge \unicode[STIX]{x1D70B}_{k+1}(q_{2}^{\ast }(\text{Eis}_{\text{hol}}^{k}(a,b)-\text{Eis}_{\text{hol}}^{k}(a^{\prime },b)))\nonumber\\ \displaystyle & & \displaystyle \quad =A^{1,k}((c,0),(a,b))-A^{1,k}((c,0),(a^{\prime },b))+B^{1,k}((c,0),(a,b))-B^{1,k}((c,0),(a^{\prime },b))\nonumber\\ \displaystyle & & \displaystyle \qquad +\,C^{1,k}((c,0),(a,b))-C^{1,k}((c,0),(a^{\prime },b))+D^{1,k}((c,0),(a,b))-D^{1,k}((c,0),(a^{\prime },b))\nonumber\\ \displaystyle & & \displaystyle \qquad +\,E^{1,k}((c,0),(a,b))-E^{1,k}((c,0),(a^{\prime },b))+F^{1,k}((c,0),(a,b))-F^{1,k}((c,0),(a^{\prime },b)).\nonumber\end{eqnarray}$$
On vérifie directement que tous les termes
![]() $B$
à
$B$
à
![]() $F$
sont nuls, et il reste
$F$
sont nuls, et il reste
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X^{k+1}\{0,\infty \}}^{\ast }q_{1}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{1}(c,0)\wedge \unicode[STIX]{x1D70B}_{k+1}(q_{2}^{\ast }(\text{Eis}_{\text{hol}}^{k}(a,b)-\text{Eis}_{\text{hol}}^{k}(a^{\prime },b)))\nonumber\\ \displaystyle & & \displaystyle \quad =A^{1,k}((c,0),(a,b))-A^{1,k}((c,0),(a^{\prime },b))\nonumber\\ \displaystyle & & \displaystyle \quad =i^{2-k}\frac{3(k+2)}{4N^{k+3}}(2\unicode[STIX]{x1D70B})^{k+2}\unicode[STIX]{x1D6EC}^{\ast }((G_{0,-a}^{(2)}-G_{0,-a^{\prime }}^{(2)}-G_{0,a}^{(2)}+G_{0,a^{\prime }}^{(2)})(G_{b,c}^{(k+1)}+G_{b,-c}^{(k+1)}),0).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X^{k+1}\{0,\infty \}}^{\ast }q_{1}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{1}(c,0)\wedge \unicode[STIX]{x1D70B}_{k+1}(q_{2}^{\ast }(\text{Eis}_{\text{hol}}^{k}(a,b)-\text{Eis}_{\text{hol}}^{k}(a^{\prime },b)))\nonumber\\ \displaystyle & & \displaystyle \quad =A^{1,k}((c,0),(a,b))-A^{1,k}((c,0),(a^{\prime },b))\nonumber\\ \displaystyle & & \displaystyle \quad =i^{2-k}\frac{3(k+2)}{4N^{k+3}}(2\unicode[STIX]{x1D70B})^{k+2}\unicode[STIX]{x1D6EC}^{\ast }((G_{0,-a}^{(2)}-G_{0,-a^{\prime }}^{(2)}-G_{0,a}^{(2)}+G_{0,a^{\prime }}^{(2)})(G_{b,c}^{(k+1)}+G_{b,-c}^{(k+1)}),0).\end{eqnarray}$$
D’après (36) et (37), on obtient finalement
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X^{k+1}\{0,\infty \}}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k,1}((a,b),(c,0))-\text{Eis}_{{\mathcal{D}}}^{k,1}((a^{\prime },b),(c,0))\nonumber\\ \displaystyle & & \displaystyle \quad =A^{k,1}((a,b),(c,0))-A^{k,1}((a^{\prime },b),(c,0))+(-1)^{k}(A^{1,k}((c,0),(a,b))-A^{1,k}((c,0),(a^{\prime },b)))\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{3(k+2)}{2N^{k+3}}(2\unicode[STIX]{x1D70B})^{k+2}i^{k}\unicode[STIX]{x1D6EC}^{\ast }((G_{0,a}^{(2)}-G_{0,a^{\prime }}^{(2)})G_{b,-c}^{(k+1)}-(G_{0,-a}^{(2)}-G_{0,-a^{\prime }}^{(2)})G_{b,c}^{(k+1)},0).\Box \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X^{k+1}\{0,\infty \}}^{\ast }\,\text{Eis}_{{\mathcal{D}}}^{k,1}((a,b),(c,0))-\text{Eis}_{{\mathcal{D}}}^{k,1}((a^{\prime },b),(c,0))\nonumber\\ \displaystyle & & \displaystyle \quad =A^{k,1}((a,b),(c,0))-A^{k,1}((a^{\prime },b),(c,0))+(-1)^{k}(A^{1,k}((c,0),(a,b))-A^{1,k}((c,0),(a^{\prime },b)))\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{3(k+2)}{2N^{k+3}}(2\unicode[STIX]{x1D70B})^{k+2}i^{k}\unicode[STIX]{x1D6EC}^{\ast }((G_{0,a}^{(2)}-G_{0,a^{\prime }}^{(2)})G_{b,-c}^{(k+1)}-(G_{0,-a}^{(2)}-G_{0,-a^{\prime }}^{(2)})G_{b,c}^{(k+1)},0).\Box \nonumber\end{eqnarray}$$