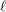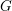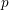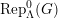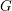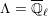Introduction
Soient
![]() $k$
un corps local non archimédien et
$k$
un corps local non archimédien et
![]() $\mathbf{G}$
un groupe réductif connexe défini sur
$\mathbf{G}$
un groupe réductif connexe défini sur
![]() $k$
. Notons
$k$
. Notons
![]() $G:=\mathbf{G}(k)$
. Soit
$G:=\mathbf{G}(k)$
. Soit
![]() $\ell$
un nombre premier,
$\ell$
un nombre premier,
![]() $\ell \neq p$
, et posons
$\ell \neq p$
, et posons
![]() $\unicode[STIX]{x1D6EC}=\overline{\mathbb{Q}}_{\ell }$
ou
$\unicode[STIX]{x1D6EC}=\overline{\mathbb{Q}}_{\ell }$
ou
![]() $\overline{\mathbb{Z}}_{\ell }$
. On appelle
$\overline{\mathbb{Z}}_{\ell }$
. On appelle
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}(G)$
la catégorie abélienne des représentations lisses de
$\text{Rep}_{\unicode[STIX]{x1D6EC}}(G)$
la catégorie abélienne des représentations lisses de
![]() $G$
à coefficients dans
$G$
à coefficients dans
![]() $\unicode[STIX]{x1D6EC}$
et
$\unicode[STIX]{x1D6EC}$
et
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{0}(G)$
la sous-catégorie pleine des représentations de niveau 0.
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{0}(G)$
la sous-catégorie pleine des représentations de niveau 0.
Pour
![]() $\unicode[STIX]{x1D6EC}=\overline{\mathbb{Q}}_{\ell }$
le théorème de décomposition de Bernstein nous fournit une décomposition de
$\unicode[STIX]{x1D6EC}=\overline{\mathbb{Q}}_{\ell }$
le théorème de décomposition de Bernstein nous fournit une décomposition de
![]() $\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}(G)$
en un produit de blocs (c’est à dire de sous-catégories indécomposables). Le cas
$\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}(G)$
en un produit de blocs (c’est à dire de sous-catégories indécomposables). Le cas
![]() $\unicode[STIX]{x1D6EC}=\overline{\mathbb{Z}}_{\ell }$
est quant à lui assez peu connu. Pour
$\unicode[STIX]{x1D6EC}=\overline{\mathbb{Z}}_{\ell }$
est quant à lui assez peu connu. Pour
![]() $\mathbf{G}=\text{GL}_{n}$
, Vignéras a obtenu dans [Reference VignérasVig98] une décomposition de la catégorie
$\mathbf{G}=\text{GL}_{n}$
, Vignéras a obtenu dans [Reference VignérasVig98] une décomposition de la catégorie
![]() $\text{Rep}_{\overline{\mathbb{F}}_{\ell }}(\text{GL}_{n}(k))$
en blocs (voir aussi les travaux de Sécherre et Stevens [Reference Sécherre and StevensSS16]). Celle-ci a permis par la suite à Helm [Reference HelmHel16] d’obtenir une décomposition de
$\text{Rep}_{\overline{\mathbb{F}}_{\ell }}(\text{GL}_{n}(k))$
en blocs (voir aussi les travaux de Sécherre et Stevens [Reference Sécherre and StevensSS16]). Celle-ci a permis par la suite à Helm [Reference HelmHel16] d’obtenir une décomposition de
![]() $\text{Rep}_{\overline{\mathbb{Z}}_{\ell }}(\text{GL}_{n}(k))$
. Prenons une classe d’équivalence inertielle de paires
$\text{Rep}_{\overline{\mathbb{Z}}_{\ell }}(\text{GL}_{n}(k))$
. Prenons une classe d’équivalence inertielle de paires
![]() $(L,\unicode[STIX]{x1D70B})$
où
$(L,\unicode[STIX]{x1D70B})$
où
![]() $L$
est un Levi de
$L$
est un Levi de
![]() $\text{GL}_{n}(k)$
et
$\text{GL}_{n}(k)$
et
![]() $\unicode[STIX]{x1D70B}$
est une représentation supercuspidale irréductible de
$\unicode[STIX]{x1D70B}$
est une représentation supercuspidale irréductible de
![]() $L$
sur
$L$
sur
![]() $\overline{\mathbb{F}}_{\ell }$
. Définissons alors
$\overline{\mathbb{F}}_{\ell }$
. Définissons alors
![]() $\text{Rep}_{\overline{\mathbb{Z}}_{\ell }}(\text{GL}_{n}(k))_{[L,\unicode[STIX]{x1D70B}]}$
la sous-catégorie pleine de
$\text{Rep}_{\overline{\mathbb{Z}}_{\ell }}(\text{GL}_{n}(k))_{[L,\unicode[STIX]{x1D70B}]}$
la sous-catégorie pleine de
![]() $\text{Rep}_{\overline{\mathbb{Z}}_{\ell }}(\text{GL}_{n}(k))$
dont les objets sont les
$\text{Rep}_{\overline{\mathbb{Z}}_{\ell }}(\text{GL}_{n}(k))$
dont les objets sont les
![]() $\unicode[STIX]{x1D6F1}$
tels que tous les sous-quotients simples de
$\unicode[STIX]{x1D6F1}$
tels que tous les sous-quotients simples de
![]() $\unicode[STIX]{x1D6F1}$
ont un ‘support supercuspidal inertiel mod
$\unicode[STIX]{x1D6F1}$
ont un ‘support supercuspidal inertiel mod
![]() $\ell$
’ donné par
$\ell$
’ donné par
![]() $(L,\unicode[STIX]{x1D70B})$
. Les blocs de
$(L,\unicode[STIX]{x1D70B})$
. Les blocs de
![]() $\text{Rep}_{\overline{\mathbb{Z}}_{\ell }}(\text{GL}_{n}(k))$
sont exactement les sous-catégories
$\text{Rep}_{\overline{\mathbb{Z}}_{\ell }}(\text{GL}_{n}(k))$
sont exactement les sous-catégories
![]() $\text{Rep}_{\overline{\mathbb{Z}}_{\ell }}(\text{GL}_{n}(k))_{[L,\unicode[STIX]{x1D70B}]}$
.
$\text{Rep}_{\overline{\mathbb{Z}}_{\ell }}(\text{GL}_{n}(k))_{[L,\unicode[STIX]{x1D70B}]}$
.
Ces méthodes sont basées sur ‘l’unicité du support supercuspidal’, qui est vraie pour
![]() $\text{GL}_{n}$
mais ne l’est pas en général. Un contre exemple dans
$\text{GL}_{n}$
mais ne l’est pas en général. Un contre exemple dans
![]() $\text{Sp}_{8}$
sur un corps fini a été trouvé récemment par Dudas puis a été relevé sur un corps
$\text{Sp}_{8}$
sur un corps fini a été trouvé récemment par Dudas puis a été relevé sur un corps
![]() $p$
-adique par Dat dans [Reference DatDat].
$p$
-adique par Dat dans [Reference DatDat].
Dans le cas du niveau 0, Dat propose (voir [Reference DatDat16]) une nouvelle construction des blocs de
![]() $\text{GL}_{n}(k)$
en utilisant la théorie de Deligne–Lusztig et des systèmes d’idempotents sur l’immeuble de Bruhat–Tits semi-simple (comme dans l’article de Meyer et Solleveld [Reference Meyer and SolleveldMS10]). Il réinterprète également dans [Reference DatDat17] les paramétrisations des décompositions précédentes de
$\text{GL}_{n}(k)$
en utilisant la théorie de Deligne–Lusztig et des systèmes d’idempotents sur l’immeuble de Bruhat–Tits semi-simple (comme dans l’article de Meyer et Solleveld [Reference Meyer and SolleveldMS10]). Il réinterprète également dans [Reference DatDat17] les paramétrisations des décompositions précédentes de
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}(\text{GL}_{n}(k))$
en termes ‘duaux’. Introduisons quelques notations pour un énoncé plus précis.
$\text{Rep}_{\unicode[STIX]{x1D6EC}}(\text{GL}_{n}(k))$
en termes ‘duaux’. Introduisons quelques notations pour un énoncé plus précis.
On suppose que
![]() $\mathbf{G}$
est déployé sur l’extension non-ramifiée maximale de
$\mathbf{G}$
est déployé sur l’extension non-ramifiée maximale de
![]() $k$
, c’est à dire que
$k$
, c’est à dire que
![]() $\mathbf{G}$
est une forme intérieure d’un groupe non-ramifié. Soient
$\mathbf{G}$
est une forme intérieure d’un groupe non-ramifié. Soient
![]() $W_{k}$
le groupe de Weil absolu de
$W_{k}$
le groupe de Weil absolu de
![]() $k$
et
$k$
et
![]() $I_{k}$
le sous-groupe d’inertie. Le groupe
$I_{k}$
le sous-groupe d’inertie. Le groupe
![]() $\unicode[STIX]{x1D6E4}:=\text{Gal}(\bar{k}/k)/I_{k}$
est topologiquement engendré par le Frobenius inverse
$\unicode[STIX]{x1D6E4}:=\text{Gal}(\bar{k}/k)/I_{k}$
est topologiquement engendré par le Frobenius inverse
![]() $\text{Frob}$
. Via le choix d’un épinglage de
$\text{Frob}$
. Via le choix d’un épinglage de
![]() $\widehat{\mathbf{G}}$
, le dual de
$\widehat{\mathbf{G}}$
, le dual de
![]() $\mathbf{G}$
sur
$\mathbf{G}$
sur
![]() $\overline{\mathbb{Q}}_{\ell }$
,
$\overline{\mathbb{Q}}_{\ell }$
,
![]() $\text{Frob}$
induit un automorphisme que l’on nomme
$\text{Frob}$
induit un automorphisme que l’on nomme
![]() $\widehat{\unicode[STIX]{x1D717}}$
sur
$\widehat{\unicode[STIX]{x1D717}}$
sur
![]() $\widehat{\mathbf{G}}$
. On note
$\widehat{\mathbf{G}}$
. On note
![]() $\unicode[STIX]{x1D6F7}(\text{}\text{G})$
l’ensemble des morphismes admissibles
$\unicode[STIX]{x1D6F7}(\text{}\text{G})$
l’ensemble des morphismes admissibles
![]() $\unicode[STIX]{x1D719}:W_{k}^{\prime }\,\rightarrow \,^{L}\text{}\text{G}(\overline{\mathbb{Q}}_{\ell })$
modulo les automorphismes intérieurs par des éléments de
$\unicode[STIX]{x1D719}:W_{k}^{\prime }\,\rightarrow \,^{L}\text{}\text{G}(\overline{\mathbb{Q}}_{\ell })$
modulo les automorphismes intérieurs par des éléments de
![]() $\widehat{\text{}\text{G}}(\overline{\mathbb{Q}}_{\ell })$
, où
$\widehat{\text{}\text{G}}(\overline{\mathbb{Q}}_{\ell })$
, où
![]() $W_{k}^{\prime }=W_{k}\ltimes \overline{\mathbb{Q}}_{\ell }$
désigne le groupe de Weil–Deligne et
$W_{k}^{\prime }=W_{k}\ltimes \overline{\mathbb{Q}}_{\ell }$
désigne le groupe de Weil–Deligne et
![]() $^{L}\text{}\text{G}(\overline{\mathbb{Q}}_{\ell }):=\langle \widehat{\unicode[STIX]{x1D717}}\rangle \ltimes \widehat{\text{}\text{G}}(\overline{\mathbb{Q}}_{\ell })$
le groupe de Langlands dual. Posons
$^{L}\text{}\text{G}(\overline{\mathbb{Q}}_{\ell }):=\langle \widehat{\unicode[STIX]{x1D717}}\rangle \ltimes \widehat{\text{}\text{G}}(\overline{\mathbb{Q}}_{\ell })$
le groupe de Langlands dual. Posons
![]() $I_{k}^{\unicode[STIX]{x1D6EC}}:=I_{k}$
si
$I_{k}^{\unicode[STIX]{x1D6EC}}:=I_{k}$
si
![]() $\unicode[STIX]{x1D6EC}=\overline{\mathbb{Q}}_{\ell }$
et
$\unicode[STIX]{x1D6EC}=\overline{\mathbb{Q}}_{\ell }$
et
![]() $I_{k}^{\unicode[STIX]{x1D6EC}}:=I_{k}^{(\ell )}$
, le sous-groupe fermé maximal de
$I_{k}^{\unicode[STIX]{x1D6EC}}:=I_{k}^{(\ell )}$
, le sous-groupe fermé maximal de
![]() $I_{k}$
de pro-ordre premier à
$I_{k}$
de pro-ordre premier à
![]() $\ell$
, si
$\ell$
, si
![]() $\unicode[STIX]{x1D6EC}=\overline{\mathbb{Z}}_{\ell }$
. Pour
$\unicode[STIX]{x1D6EC}=\overline{\mathbb{Z}}_{\ell }$
. Pour
![]() $I$
un sous-groupe de
$I$
un sous-groupe de
![]() $W_{k}$
, définissons
$W_{k}$
, définissons
![]() $\unicode[STIX]{x1D6F7}(I,\text{}\text{G})$
l’ensemble des classes de
$\unicode[STIX]{x1D6F7}(I,\text{}\text{G})$
l’ensemble des classes de
![]() $\widehat{\text{}\text{G}}$
-conjugaison de morphismes continus
$\widehat{\text{}\text{G}}$
-conjugaison de morphismes continus
![]() $I\rightarrow ^{L}\text{}\text{G}(\overline{\mathbb{Q}}_{\ell })$
qui admettent une extension à un
$I\rightarrow ^{L}\text{}\text{G}(\overline{\mathbb{Q}}_{\ell })$
qui admettent une extension à un
![]() $L$
-morphisme de
$L$
-morphisme de
![]() $\unicode[STIX]{x1D6F7}(\text{}\text{G})$
. On s’intéressera principalement à
$\unicode[STIX]{x1D6F7}(\text{}\text{G})$
. On s’intéressera principalement à
![]() $\unicode[STIX]{x1D6F7}(I_{k}^{\unicode[STIX]{x1D6EC}},\text{}\text{G})$
. Enfin, si
$\unicode[STIX]{x1D6F7}(I_{k}^{\unicode[STIX]{x1D6EC}},\text{}\text{G})$
. Enfin, si
![]() $I$
contient l’inertie sauvage, posons
$I$
contient l’inertie sauvage, posons
![]() $\unicode[STIX]{x1D6F7}_{m}(I,\text{}\text{G})$
les éléments de
$\unicode[STIX]{x1D6F7}_{m}(I,\text{}\text{G})$
les éléments de
![]() $\unicode[STIX]{x1D6F7}(I,\text{}\text{G})$
qui sont triviaux sur l’inertie sauvage.
$\unicode[STIX]{x1D6F7}(I,\text{}\text{G})$
qui sont triviaux sur l’inertie sauvage.
Il y a alors une bijection entre les blocs de Bernstein pour
![]() $\text{GL}_{n}(k)$
et les éléments de
$\text{GL}_{n}(k)$
et les éléments de
![]() $\unicode[STIX]{x1D6F7}(I_{k},\text{GL}_{n})$
ainsi qu’entre les blocs de Vignéras–Helm et
$\unicode[STIX]{x1D6F7}(I_{k},\text{GL}_{n})$
ainsi qu’entre les blocs de Vignéras–Helm et
![]() $\unicode[STIX]{x1D6F7}(I_{k}^{(\ell )},\text{GL}_{n})$
, nous donnant ainsi une décomposition en blocs
$\unicode[STIX]{x1D6F7}(I_{k}^{(\ell )},\text{GL}_{n})$
, nous donnant ainsi une décomposition en blocs
De plus les facteurs apparaissant dans
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{0}(\text{GL}_{n}(k))$
, la sous-catégorie de niveau 0, correspondent aux
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{0}(\text{GL}_{n}(k))$
, la sous-catégorie de niveau 0, correspondent aux
![]() $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\text{GL}_{n})$
.
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\text{GL}_{n})$
.
La méthode de Vignéras ne pouvant s’appliquer dans le cas général, nous nous proposons ici de généraliser la construction de systèmes d’idempotents via la théorie de Deligne–Lusztig pour obtenir des décompositions de
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{0}(G)$
. Nous obtenons ainsi une décomposition analogue à celle de Dat (voir §§ 3 et 4).
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{0}(G)$
. Nous obtenons ainsi une décomposition analogue à celle de Dat (voir §§ 3 et 4).
Théorème. Soit
![]() $\mathbf{G}$
un groupe réductif connexe défini sur
$\mathbf{G}$
un groupe réductif connexe défini sur
![]() $k$
et déployé sur une extension non-ramifiée de
$k$
et déployé sur une extension non-ramifiée de
![]() $k$
. Alors la catégorie de niveau
$k$
. Alors la catégorie de niveau
![]() $0$
se décompose en
$0$
se décompose en
De plus, les catégories
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
vérifient les propriétés suivantes
:
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
vérifient les propriétés suivantes
:
(i) Lien entre
 $\overline{\mathbb{Z}}_{\ell }$
et
$\overline{\mathbb{Z}}_{\ell }$
et
 $\overline{\mathbb{Q}}_{\ell }$
: Soit
$\overline{\mathbb{Q}}_{\ell }$
: Soit
 $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{(\ell )},\mathbf{G})$
, alors
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{(\ell )},\mathbf{G})$
, alors
 $\text{Rep}_{\overline{\mathbb{Z}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)\cap \text{Rep}_{\overline{\mathbb{Q}}_{\ell }}(G)=\prod _{\unicode[STIX]{x1D719}^{\prime }}\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}^{\prime }}(G)$
où le produit est pris sur les
$\text{Rep}_{\overline{\mathbb{Z}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)\cap \text{Rep}_{\overline{\mathbb{Q}}_{\ell }}(G)=\prod _{\unicode[STIX]{x1D719}^{\prime }}\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}^{\prime }}(G)$
où le produit est pris sur les
 $\unicode[STIX]{x1D719}^{\prime }\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{G})$
tels que
$\unicode[STIX]{x1D719}^{\prime }\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{G})$
tels que
 $\unicode[STIX]{x1D719}_{\mid I_{k}^{(\ell )}}^{\prime }\sim \unicode[STIX]{x1D719}$
.
$\unicode[STIX]{x1D719}_{\mid I_{k}^{(\ell )}}^{\prime }\sim \unicode[STIX]{x1D719}$
.(ii) Représentations irréductibles de
 $\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
: Soit
$\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
: Soit
 $\unicode[STIX]{x1D70B}\in \text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)$
. Alors
$\unicode[STIX]{x1D70B}\in \text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)$
. Alors
 $\unicode[STIX]{x1D70B}\in \text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
si et seulement s’il existe
$\unicode[STIX]{x1D70B}\in \text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
si et seulement s’il existe
 $\mathbf{T}$
un tore maximal non-ramifié de
$\mathbf{T}$
un tore maximal non-ramifié de
 $\mathbf{G}$
,
$\mathbf{G}$
,
 $\unicode[STIX]{x1D719}_{\mathbf{T}}\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{T})$
et
$\unicode[STIX]{x1D719}_{\mathbf{T}}\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{T})$
et
 $x$
un sommet de l’immeuble de
$x$
un sommet de l’immeuble de
 $G$
(sur
$G$
(sur
 $k$
) qui est dans l’appartement de
$k$
) qui est dans l’appartement de
 $\mathbf{T}$
(sur
$\mathbf{T}$
(sur
 $K$
) tels que
$K$
) tels que(a)
 $\langle \unicode[STIX]{x1D70B}^{G_{x}^{+}},{\mathcal{R}}_{\unicode[STIX]{x1D64F}_{x}}^{\overline{\text{G}}_{x}}(\unicode[STIX]{x1D703}_{\boldsymbol{ T}})\rangle \neq 0$
$\langle \unicode[STIX]{x1D70B}^{G_{x}^{+}},{\mathcal{R}}_{\unicode[STIX]{x1D64F}_{x}}^{\overline{\text{G}}_{x}}(\unicode[STIX]{x1D703}_{\boldsymbol{ T}})\rangle \neq 0$
(b)
 $\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D719}_{\mathbf{T}}\sim \unicode[STIX]{x1D719}$
$\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D719}_{\mathbf{T}}\sim \unicode[STIX]{x1D719}$
où
 $\unicode[STIX]{x1D704}$
est un plongement
$\unicode[STIX]{x1D704}$
est un plongement
 $\unicode[STIX]{x1D704}:^{L}\mathbf{T}{\hookrightarrow}^{L}\mathbf{G}$
,
$\unicode[STIX]{x1D704}:^{L}\mathbf{T}{\hookrightarrow}^{L}\mathbf{G}$
,
 $G_{x}^{\circ }$
est le sous-groupe parahorique en
$G_{x}^{\circ }$
est le sous-groupe parahorique en
 $x$
,
$x$
,
 $G_{x}^{+}$
son pro-p-radical,
$G_{x}^{+}$
son pro-p-radical,
 $\overline{\mathsf{G}}_{x}\simeq G_{x}^{\circ }/G_{x}^{+}$
le quotient réductif,
$\overline{\mathsf{G}}_{x}\simeq G_{x}^{\circ }/G_{x}^{+}$
le quotient réductif,
 $\unicode[STIX]{x1D64F}_{x}$
est le tore induit par
$\unicode[STIX]{x1D64F}_{x}$
est le tore induit par
 $\mathbf{T}$
sur
$\mathbf{T}$
sur
 $\overline{\mathsf{G}}_{x}$
,
$\overline{\mathsf{G}}_{x}$
,
 ${\mathcal{R}}_{\unicode[STIX]{x1D64F}_{x}}^{\overline{\text{G}}_{x}}$
est l’induction de Deligne–Lusztig et
${\mathcal{R}}_{\unicode[STIX]{x1D64F}_{x}}^{\overline{\text{G}}_{x}}$
est l’induction de Deligne–Lusztig et
 $\unicode[STIX]{x1D703}_{\mathbf{T}}$
est le caractère de niveau 0 de
$\unicode[STIX]{x1D703}_{\mathbf{T}}$
est le caractère de niveau 0 de
 $\mathbf{T}^{F}$
correspondant à
$\mathbf{T}^{F}$
correspondant à
 $\unicode[STIX]{x1D719}_{\mathbf{T}}$
via la correspondance de Langlands pour les tores restreinte à l’inertie.
$\unicode[STIX]{x1D719}_{\mathbf{T}}$
via la correspondance de Langlands pour les tores restreinte à l’inertie.(Notons que l’on obtient également une description de
 $\text{Rep}_{\overline{\mathbb{Z}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)\cap \text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)$
grâce au
$\text{Rep}_{\overline{\mathbb{Z}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)\cap \text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)$
grâce au
 $(1)$
.)
$(1)$
.)(iii) Compatibilité à l’induction et à la restriction parabolique : Soient
 $\mathbf{P}$
un sous-groupe parabolique de
$\mathbf{P}$
un sous-groupe parabolique de
 $\mathbf{G}$
ayant pour facteur de Levi
$\mathbf{G}$
ayant pour facteur de Levi
 $\mathbf{M}$
et
$\mathbf{M}$
et
 $\unicode[STIX]{x1D704}:^{L}\mathbf{M}{\hookrightarrow}^{L}\mathbf{G}$
un plongement.
$\unicode[STIX]{x1D704}:^{L}\mathbf{M}{\hookrightarrow}^{L}\mathbf{G}$
un plongement.(a) Soit
 $\unicode[STIX]{x1D719}_{M}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{M})$
, alors
$\unicode[STIX]{x1D719}_{M}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{M})$
, alors
 $i_{P}^{G}(\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}_{M}}(M))\subseteq \text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D719}_{M}}(G)$
, où
$i_{P}^{G}(\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}_{M}}(M))\subseteq \text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D719}_{M}}(G)$
, où
 $i_{P}^{G}$
désigne l’induction parabolique.
$i_{P}^{G}$
désigne l’induction parabolique.(b) Soit
 $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
, alors
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
, alors
 $r_{P}^{G}(\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G))\subseteq \prod _{\unicode[STIX]{x1D719}_{M}}\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}_{M}}(M)$
, où
$r_{P}^{G}(\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G))\subseteq \prod _{\unicode[STIX]{x1D719}_{M}}\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}_{M}}(M)$
, où
 $r_{P}^{G}$
désigne la restriction parabolique et le produit est pris sur les
$r_{P}^{G}$
désigne la restriction parabolique et le produit est pris sur les
 $\unicode[STIX]{x1D719}_{M}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{M})$
tels que
$\unicode[STIX]{x1D719}_{M}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{M})$
tels que
 $\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D719}_{M}\sim \unicode[STIX]{x1D719}$
.
$\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D719}_{M}\sim \unicode[STIX]{x1D719}$
.(c) Soit
 $\unicode[STIX]{x1D719}_{M}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{M})$
. Posons
$\unicode[STIX]{x1D719}_{M}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{M})$
. Posons
 $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D719}_{M}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
et notons
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D719}_{M}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
et notons
 $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
le centralisateur dans
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
le centralisateur dans
 $\widehat{\mathbf{G}}$
de l’image de
$\widehat{\mathbf{G}}$
de l’image de
 $\unicode[STIX]{x1D719}$
. Alors si
$\unicode[STIX]{x1D719}$
. Alors si
 $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})\subseteq \unicode[STIX]{x1D704}(\widehat{\mathbf{M}})$
le foncteur
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})\subseteq \unicode[STIX]{x1D704}(\widehat{\mathbf{M}})$
le foncteur
 $i_{P}^{G}$
réalise une équivalence de catégories entre
$i_{P}^{G}$
réalise une équivalence de catégories entre
 $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}_{M}}(M)$
et
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}_{M}}(M)$
et
 $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
.
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
.
On s’attend à ce que cette décomposition soit compatible à la correspondance de Langlands. Nous le vérifions dans le cas des groupes classiques.
Théorème. Supposons que
![]() $\mathbf{G}$
est un groupe classique non-ramifié,
$\mathbf{G}$
est un groupe classique non-ramifié,
![]() $\unicode[STIX]{x1D6EC}=\overline{\mathbb{Q}}_{\ell }$
,
$\unicode[STIX]{x1D6EC}=\overline{\mathbb{Q}}_{\ell }$
,
![]() $k$
est de caractéristique nulle et de caractéristique résiduelle impaire. On obtient alors également les propriétés suivantes.
$k$
est de caractéristique nulle et de caractéristique résiduelle impaire. On obtient alors également les propriétés suivantes.
(i) Compatibilité à la correspondance de Langlands : Soient
 $\unicode[STIX]{x1D70B}\in \text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)$
une représentation irréductible de niveau 0 et
$\unicode[STIX]{x1D70B}\in \text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)$
une représentation irréductible de niveau 0 et
 $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{G})$
. Notons
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{G})$
. Notons
 $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70B}}$
le paramètre de Langlands associé à
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70B}}$
le paramètre de Langlands associé à
 $\unicode[STIX]{x1D70B}$
via la correspondance de Langlands locale pour les groupes classiques [Reference Harris and TaylorHT01, Reference HenniartHen00, Reference ArthurArt13, Reference MokMok15, Reference Kaletha, Minguez, Shin and WhiteKMSW14]. Alors
$\unicode[STIX]{x1D70B}$
via la correspondance de Langlands locale pour les groupes classiques [Reference Harris and TaylorHT01, Reference HenniartHen00, Reference ArthurArt13, Reference MokMok15, Reference Kaletha, Minguez, Shin and WhiteKMSW14]. Alors  $$\begin{eqnarray}\unicode[STIX]{x1D70B}\in \text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)\Leftrightarrow \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70B}|I_{k}}\sim \unicode[STIX]{x1D719}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}\in \text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)\Leftrightarrow \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70B}|I_{k}}\sim \unicode[STIX]{x1D719}.\end{eqnarray}$$
(ii) Blocs stables : Soit
 $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{G})$
tel que
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{G})$
tel que
 $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
soit connexe. Alors
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
soit connexe. Alors
 $\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
est un ‘bloc stable’ (c’est-à-dire, correspond à un idempotent primitif du centre de Bernstein stable au sens de Haines [Reference HainesHai14]).
$\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
est un ‘bloc stable’ (c’est-à-dire, correspond à un idempotent primitif du centre de Bernstein stable au sens de Haines [Reference HainesHai14]).
Contrairement au cas de
![]() $\text{GL}_{n}$
les catégories
$\text{GL}_{n}$
les catégories
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
ne sont pas des facteurs indécomposables en général. Dans un prochain article, en cours d’écriture, nous expliquerons comment pousser la méthode utilisée ici, pour obtenir une décomposition minimale construite à partir de systèmes d’idempotents et de la théorie de Deligne–Lusztig. Nous interpréterons également cette nouvelle décomposition à l’aide d’invariants cohomologiques.
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
ne sont pas des facteurs indécomposables en général. Dans un prochain article, en cours d’écriture, nous expliquerons comment pousser la méthode utilisée ici, pour obtenir une décomposition minimale construite à partir de systèmes d’idempotents et de la théorie de Deligne–Lusztig. Nous interpréterons également cette nouvelle décomposition à l’aide d’invariants cohomologiques.
Dans cet article nous nous limitons à l’étude de
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{0}(G)$
la catégorie de niveau 0. On peut cependant espérer que les travaux menés sur la théorie des types permettront d’en déduire des résultats sur
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{0}(G)$
la catégorie de niveau 0. On peut cependant espérer que les travaux menés sur la théorie des types permettront d’en déduire des résultats sur
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}(G)$
. En effet Chinello montre dans [Reference ChinelloChi17] que l’on a une équivalence de catégories entre chaque bloc de
$\text{Rep}_{\unicode[STIX]{x1D6EC}}(G)$
. En effet Chinello montre dans [Reference ChinelloChi17] que l’on a une équivalence de catégories entre chaque bloc de
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}(\text{GL}_{n}(k))$
et un bloc de niveau 0 de
$\text{Rep}_{\unicode[STIX]{x1D6EC}}(\text{GL}_{n}(k))$
et un bloc de niveau 0 de
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{0}(G^{\prime })$
où
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{0}(G^{\prime })$
où
![]() $G^{\prime }$
est un groupe de la forme
$G^{\prime }$
est un groupe de la forme
![]() $G^{\prime }=\prod _{i=1}^{r}\text{GL}_{n_{i}}(D_{i})$
avec pour
$G^{\prime }=\prod _{i=1}^{r}\text{GL}_{n_{i}}(D_{i})$
avec pour
![]() $i\in \{1,\ldots ,r\}$
,
$i\in \{1,\ldots ,r\}$
,
![]() $n_{i}$
un entier et
$n_{i}$
un entier et
![]() $D_{i}$
une algèbre à division centrale de dimension finie sur un corps
$D_{i}$
une algèbre à division centrale de dimension finie sur un corps
![]() $p$
-adique. Des travaux en cours de Stevens et Kurinczuk tentent d’étendre ces résultats à un
$p$
-adique. Des travaux en cours de Stevens et Kurinczuk tentent d’étendre ces résultats à un
![]() $G$
plus général.
$G$
plus général.
Cet article se compose de 4 parties. La partie 1 rappelle les résultats sur les systèmes cohérents d’idempotents. Dans la seconde partie nous expliquons comment construire des idempotents à partir de la théorie de Deligne–Lusztig. Nous associons aux paramètres de l’inertie modérés des systèmes cohérents dans la troisième partie pour obtenir la décomposition du théorème précédent. La dernière partie a pour but de montrer les propriétés des facteurs directs ainsi obtenus. Les quatre premières propriétés découlent de la construction de ces catégories et la dernière repose sur les travaux de Moeglin [Reference MoeglinMoe14], Moussaoui [Reference MoussaouiMou17a], Haines [Reference HainesHai14], Lust et Stevens [Reference Lust and StevensLS16].
Notations
Soit
![]() $k$
un corps local non archimédien et
$k$
un corps local non archimédien et
![]() $\mathfrak{f}$
son corps résiduel. Notons
$\mathfrak{f}$
son corps résiduel. Notons
![]() $q=|\mathfrak{f}|$
. On fixe une clôture algébrique
$q=|\mathfrak{f}|$
. On fixe une clôture algébrique
![]() $\overline{k}$
de
$\overline{k}$
de
![]() $k$
et on note
$k$
et on note
![]() $K$
l’extension non-ramifiée maximale de
$K$
l’extension non-ramifiée maximale de
![]() $k$
dans
$k$
dans
![]() $\overline{k}$
. On appellera
$\overline{k}$
. On appellera
![]() $\mathfrak{o}_{k}$
(resp.
$\mathfrak{o}_{k}$
(resp.
![]() $\mathfrak{o}_{K}$
) l’anneau des entiers de
$\mathfrak{o}_{K}$
) l’anneau des entiers de
![]() $k$
(resp.
$k$
(resp.
![]() $K$
). Notons également
$K$
). Notons également
![]() $\mathfrak{F}$
le corps résiduel de
$\mathfrak{F}$
le corps résiduel de
![]() $K$
qui est alors une clôture algébrique de
$K$
qui est alors une clôture algébrique de
![]() $\mathfrak{f}$
.
$\mathfrak{f}$
.
On adopte les conventions d’écriture suivantes.
![]() $\text{}\text{G}$
désignera un groupe réductif connexe défini sur
$\text{}\text{G}$
désignera un groupe réductif connexe défini sur
![]() $k$
que l’on identifiera avec
$k$
que l’on identifiera avec
![]() $\text{}\text{G}(\overline{k})$
et l’on notera
$\text{}\text{G}(\overline{k})$
et l’on notera
![]() $G:=\text{}\text{G}(k)$
et
$G:=\text{}\text{G}(k)$
et
![]() $G^{nr}:=\text{}\text{G}(K)$
. On appellera
$G^{nr}:=\text{}\text{G}(K)$
. On appellera
![]() $\widehat{\mathbf{G}}$
son groupe dual sur
$\widehat{\mathbf{G}}$
son groupe dual sur
![]() $\overline{\mathbb{Q}}_{\ell }$
. Pour les groupes réductifs connexes sur
$\overline{\mathbb{Q}}_{\ell }$
. Pour les groupes réductifs connexes sur
![]() $\mathfrak{f}$
, nous utiliserons la police d’écriture
$\mathfrak{f}$
, nous utiliserons la police d’écriture
![]() $\text{G}$
et l’on identifiera
$\text{G}$
et l’on identifiera
![]() $\text{G}$
avec
$\text{G}$
avec
![]() $\text{G}(\mathfrak{F})$
et de même on note
$\text{G}(\mathfrak{F})$
et de même on note
![]() $\mathsf{G}:=\text{G}(\mathfrak{f})$
. Le groupe dual de
$\mathsf{G}:=\text{G}(\mathfrak{f})$
. Le groupe dual de
![]() $\text{}\text{G}$
sur
$\text{}\text{G}$
sur
![]() $\mathfrak{F}$
sera noté
$\mathfrak{F}$
sera noté
![]() $\text{G}^{\ast }$
.
$\text{G}^{\ast }$
.
Si
![]() $H$
désigne l’ensemble des points d’un groupe algébrique à valeur dans un corps alors
$H$
désigne l’ensemble des points d’un groupe algébrique à valeur dans un corps alors
![]() $H_{ss}$
désigne l’ensemble des classes de conjugaison semi-simples dans
$H_{ss}$
désigne l’ensemble des classes de conjugaison semi-simples dans
![]() $H$
.
$H$
.
On fixe dans tout ce papier un système compatible de racines de l’unité
![]() $(\mathbb{Q}/\mathbb{Z})_{p^{\prime }}\overset{\backsim }{\rightarrow }\mathfrak{F}^{\times }$
et
$(\mathbb{Q}/\mathbb{Z})_{p^{\prime }}\overset{\backsim }{\rightarrow }\mathfrak{F}^{\times }$
et
![]() $(\mathbb{Q}/\mathbb{Z})_{p^{\prime }}{\hookrightarrow}\overline{\mathbb{Z}}_{\ell }^{\times }$
.
$(\mathbb{Q}/\mathbb{Z})_{p^{\prime }}{\hookrightarrow}\overline{\mathbb{Z}}_{\ell }^{\times }$
.
Dans la suite
![]() $\text{}\text{G}$
désignera un groupe réductif connexe défini sur
$\text{}\text{G}$
désignera un groupe réductif connexe défini sur
![]() $k$
.
$k$
.
1 Système cohérent d’idempotents
Les diverses décompositions obtenues dans cet article sont construites à partir de systèmes cohérents d’idempotents. Cette partie à pour but de rappeler leur définition ainsi que les premières propriétés.
Soit
![]() $K_{1}$
une extension non-ramifiée de
$K_{1}$
une extension non-ramifiée de
![]() $k$
. On note
$k$
. On note
![]() $BT(K_{1})$
l’immeuble de Bruhat–Tits semi-simple associé à
$BT(K_{1})$
l’immeuble de Bruhat–Tits semi-simple associé à
![]() $\mathbf{G}(K_{1})$
. L’immeuble est un complexe polysimplicial et l’on note
$\mathbf{G}(K_{1})$
. L’immeuble est un complexe polysimplicial et l’on note
![]() $BT_{0}(K_{1})$
pour l’ensemble des polysimplexes de dimension 0, c’est à dire les sommets. Dans la suite on utilisera des lettres latines
$BT_{0}(K_{1})$
pour l’ensemble des polysimplexes de dimension 0, c’est à dire les sommets. Dans la suite on utilisera des lettres latines
![]() $x,y,\ldots$
pour parler des sommets et des lettres grecques pour parler des polysimplexes généraux
$x,y,\ldots$
pour parler des sommets et des lettres grecques pour parler des polysimplexes généraux
![]() $\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F},\ldots \,$
. L’immeuble
$\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F},\ldots \,$
. L’immeuble
![]() $BT(K_{1})$
est partiellement ordonné par la relation d’ordre
$BT(K_{1})$
est partiellement ordonné par la relation d’ordre
![]() $\unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D70F}$
si
$\unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D70F}$
si
![]() $\unicode[STIX]{x1D70E}$
est une facette de
$\unicode[STIX]{x1D70E}$
est une facette de
![]() $\unicode[STIX]{x1D70F}$
. Un ensemble de polysimplexes
$\unicode[STIX]{x1D70F}$
. Un ensemble de polysimplexes
![]() $\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D70E}_{k}$
est dit adjacent s’il existe un polysimplexe
$\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D70E}_{k}$
est dit adjacent s’il existe un polysimplexe
![]() $\unicode[STIX]{x1D70E}$
tel que
$\unicode[STIX]{x1D70E}$
tel que
![]() $\forall i\in 1,\ldots ,k$
,
$\forall i\in 1,\ldots ,k$
,
![]() $\unicode[STIX]{x1D70E}_{i}\leqslant \unicode[STIX]{x1D70E}$
. Si
$\unicode[STIX]{x1D70E}_{i}\leqslant \unicode[STIX]{x1D70E}$
. Si
![]() $x$
et
$x$
et
![]() $y$
sont deux sommets adjacents on notera
$y$
sont deux sommets adjacents on notera
![]() $[x,y]$
le plus petit polysimplexe contenant
$[x,y]$
le plus petit polysimplexe contenant
![]() $x\cup y$
. Notons également, pour
$x\cup y$
. Notons également, pour
![]() $\unicode[STIX]{x1D70E}$
,
$\unicode[STIX]{x1D70E}$
,
![]() $\unicode[STIX]{x1D70F}$
deux polysimplexes,
$\unicode[STIX]{x1D70F}$
deux polysimplexes,
![]() $H(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F})$
l’enveloppe polysimpliciale de
$H(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F})$
l’enveloppe polysimpliciale de
![]() $\unicode[STIX]{x1D70E}$
et
$\unicode[STIX]{x1D70E}$
et
![]() $\unicode[STIX]{x1D70F}$
, c’est à dire l’intersection de tous les appartements contenant
$\unicode[STIX]{x1D70F}$
, c’est à dire l’intersection de tous les appartements contenant
![]() $\unicode[STIX]{x1D70E}\cup \unicode[STIX]{x1D70F}$
.
$\unicode[STIX]{x1D70E}\cup \unicode[STIX]{x1D70F}$
.
Pour simplifier les notations nous noterons
![]() $BT:=BT(k)$
et
$BT:=BT(k)$
et
![]() $BT_{0}:=BT_{0}(k)$
.
$BT_{0}:=BT_{0}(k)$
.
Soit
![]() $R$
un anneau commutatif dans lequel
$R$
un anneau commutatif dans lequel
![]() $p$
est inversible. On munit
$p$
est inversible. On munit
![]() $G$
d’une mesure de Haar et on note
$G$
d’une mesure de Haar et on note
![]() ${\mathcal{H}}_{R}(G)$
l’algèbre de Hecke à coefficients dans
${\mathcal{H}}_{R}(G)$
l’algèbre de Hecke à coefficients dans
![]() $R$
, c’est à dire l’algèbre des fonctions de
$R$
, c’est à dire l’algèbre des fonctions de
![]() $G$
dans
$G$
dans
![]() $R$
localement constantes et à support compact.
$R$
localement constantes et à support compact.
Définition 1.0.1. On dit qu’un système d’idempotents
![]() $e=(e_{x})_{x\in BT_{0}}$
de
$e=(e_{x})_{x\in BT_{0}}$
de
![]() ${\mathcal{H}}_{R}(G)$
est cohérent si les propriétés suivantes sont satisfaites
:
${\mathcal{H}}_{R}(G)$
est cohérent si les propriétés suivantes sont satisfaites
:
(i)
 $e_{x}e_{y}=e_{y}e_{x}$
lorsque
$e_{x}e_{y}=e_{y}e_{x}$
lorsque
 $x$
et
$x$
et
 $y$
sont adjacents ;
$y$
sont adjacents ;(ii)
 $e_{x}e_{z}e_{y}=e_{x}e_{y}$
lorsque
$e_{x}e_{z}e_{y}=e_{x}e_{y}$
lorsque
 $z\in H(x,y)$
et
$z\in H(x,y)$
et
 $z$
est adjacent à
$z$
est adjacent à
 $x$
;
$x$
;(iii)
 $e_{gx}=ge_{x}g^{-1}$
quel que soit
$e_{gx}=ge_{x}g^{-1}$
quel que soit
 $x\in BT_{0}$
et
$x\in BT_{0}$
et
 $g\in G$
.
$g\in G$
.
Soit
![]() $\text{Rep}_{R}(G)$
la catégorie abélienne des représentations lisses de
$\text{Rep}_{R}(G)$
la catégorie abélienne des représentations lisses de
![]() $G$
à coefficients dans
$G$
à coefficients dans
![]() $R$
. Grâce à un résultat de Meyer et Solleveld on a théorème suivant.
$R$
. Grâce à un résultat de Meyer et Solleveld on a théorème suivant.
Théorème 1.0.2 [MS10, Theorem 3.1]. Soit
![]() $e=(e_{x})_{x\in BT_{0}}$
un système cohérent d’idempotents, alors la sous-catégorie pleine
$e=(e_{x})_{x\in BT_{0}}$
un système cohérent d’idempotents, alors la sous-catégorie pleine
![]() $\text{Rep}_{R}^{e}(G)$
des objets
$\text{Rep}_{R}^{e}(G)$
des objets
![]() $V$
de
$V$
de
![]() $\text{Rep}_{R}(G)$
tels que
$\text{Rep}_{R}(G)$
tels que
![]() $V=\sum _{x\in BT_{0}}e_{x}V$
est une sous-catégorie de Serre.
$V=\sum _{x\in BT_{0}}e_{x}V$
est une sous-catégorie de Serre.
Soit
![]() $\unicode[STIX]{x1D70E}\in BT$
. Notons
$\unicode[STIX]{x1D70E}\in BT$
. Notons
![]() $G_{\unicode[STIX]{x1D70E}}$
le fixateur de
$G_{\unicode[STIX]{x1D70E}}$
le fixateur de
![]() $\unicode[STIX]{x1D70E}$
. Celui-ci contient un sous-groupe appelé sous-groupe parahorique, que l’on note
$\unicode[STIX]{x1D70E}$
. Celui-ci contient un sous-groupe appelé sous-groupe parahorique, que l’on note
![]() $G_{\unicode[STIX]{x1D70E}}^{\circ }$
, qui est le ‘fixateur connexe’ de
$G_{\unicode[STIX]{x1D70E}}^{\circ }$
, qui est le ‘fixateur connexe’ de
![]() $\unicode[STIX]{x1D70E}$
. Enfin on note
$\unicode[STIX]{x1D70E}$
. Enfin on note
![]() $G_{\unicode[STIX]{x1D70E}}^{+}$
le pro-
$G_{\unicode[STIX]{x1D70E}}^{+}$
le pro-
![]() $p$
-radical (pro-
$p$
-radical (pro-
![]() $p$
-sous-groupe distingué maximal) de
$p$
-sous-groupe distingué maximal) de
![]() $G_{\unicode[STIX]{x1D70E}}^{\circ }$
.
$G_{\unicode[STIX]{x1D70E}}^{\circ }$
.
Si
![]() $x$
est un sommet de l’immeuble
$x$
est un sommet de l’immeuble
![]() $BT$
alors
$BT$
alors
![]() $G_{x}^{+}$
détermine un idempotent
$G_{x}^{+}$
détermine un idempotent
![]() $e_{x}^{+}\in {\mathcal{H}}_{\mathbb{Z}[1/p]}(G_{x})$
.
$e_{x}^{+}\in {\mathcal{H}}_{\mathbb{Z}[1/p]}(G_{x})$
.
Proposition 1.0.3 [Reference Meyer and SolleveldMS10, § 2.2].
Le système d’idempotents
![]() $(e_{x}^{+})_{x\in BT_{0}}$
est cohérent.
$(e_{x}^{+})_{x\in BT_{0}}$
est cohérent.
On a de plus que, pour tout polysimplexe
![]() $\unicode[STIX]{x1D70E}$
, l’idempotent
$\unicode[STIX]{x1D70E}$
, l’idempotent
![]() $e_{\unicode[STIX]{x1D70E}}^{+}:=\prod _{x\in \unicode[STIX]{x1D70E}}e_{x}^{+}$
est l’idempotent associé à
$e_{\unicode[STIX]{x1D70E}}^{+}:=\prod _{x\in \unicode[STIX]{x1D70E}}e_{x}^{+}$
est l’idempotent associé à
![]() $G_{\unicode[STIX]{x1D70E}}^{+}$
.
$G_{\unicode[STIX]{x1D70E}}^{+}$
.
Lemme 1.0.4. Soient
![]() $x,y\in BT_{0}$
deux sommets. Alors il existe une suite de sommets
$x,y\in BT_{0}$
deux sommets. Alors il existe une suite de sommets
![]() $x_{0}=x,x_{1},\ldots ,x_{\ell }=y$
joignant
$x_{0}=x,x_{1},\ldots ,x_{\ell }=y$
joignant
![]() $x$
à
$x$
à
![]() $y$
, telle que pour tout
$y$
, telle que pour tout
![]() $i\in \{0,\ldots ,l-1\}$
,
$i\in \{0,\ldots ,l-1\}$
,
![]() $x_{i+1}$
est adjacent à
$x_{i+1}$
est adjacent à
![]() $x_{i}$
et
$x_{i}$
et
![]() $x_{i+1}\in H(x_{i},y)$
.
$x_{i+1}\in H(x_{i},y)$
.
Démonstration.
Pour
![]() $x_{1}$
, il suffit de prendre un sommet dans
$x_{1}$
, il suffit de prendre un sommet dans
![]() $H(x,y)$
qui est adjacent à
$H(x,y)$
qui est adjacent à
![]() $x$
et tel que la distance de
$x$
et tel que la distance de
![]() $x_{1}$
à
$x_{1}$
à
![]() $y$
est strictement inférieure à celle de
$y$
est strictement inférieure à celle de
![]() $x$
à
$x$
à
![]() $y$
. En ré-appliquant ce résultat à
$y$
. En ré-appliquant ce résultat à
![]() $x_{1}$
et
$x_{1}$
et
![]() $y$
on construit
$y$
on construit
![]() $x_{2}$
et ainsi de suite pour obtenir le résultat voulu par récurrence.◻
$x_{2}$
et ainsi de suite pour obtenir le résultat voulu par récurrence.◻
Définition 1.0.5. On dit qu’un système
![]() $(e_{\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}\in BT}$
est 0-cohérent si
$(e_{\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}\in BT}$
est 0-cohérent si
(i)
 $e_{gx}=ge_{x}g^{-1}$
quel que soit
$e_{gx}=ge_{x}g^{-1}$
quel que soit
 $x\in BT_{0}$
et
$x\in BT_{0}$
et
 $g\in G$
;
$g\in G$
;(ii)
 $e_{\unicode[STIX]{x1D70E}}=e_{\unicode[STIX]{x1D70E}}^{+}e_{x}=e_{x}e_{\unicode[STIX]{x1D70E}}^{+}$
pour
$e_{\unicode[STIX]{x1D70E}}=e_{\unicode[STIX]{x1D70E}}^{+}e_{x}=e_{x}e_{\unicode[STIX]{x1D70E}}^{+}$
pour
 $x\in BT_{0}$
et
$x\in BT_{0}$
et
 $\unicode[STIX]{x1D70E}\in BT$
tels que
$\unicode[STIX]{x1D70E}\in BT$
tels que
 $x\leqslant \unicode[STIX]{x1D70E}$
.
$x\leqslant \unicode[STIX]{x1D70E}$
.
En s’inspirant de [Reference DatDat16, §3.2.1] on montre la proposition suivante.
Proposition 1.0.6. Soit
![]() $(e_{\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}\in BT}$
un système d’idempotents 0-cohérent, alors le système d’idempotents
$(e_{\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}\in BT}$
un système d’idempotents 0-cohérent, alors le système d’idempotents
![]() $(e_{x})_{x\in BT_{0}}$
est cohérent.
$(e_{x})_{x\in BT_{0}}$
est cohérent.
On a de plus, pour
![]() $x,y\in BT_{0}$
,
$x,y\in BT_{0}$
,
![]() $e_{x}^{+}e_{y}=e_{x}e_{y}$
.
$e_{x}^{+}e_{y}=e_{x}e_{y}$
.
Démonstration.
Il ne reste à vérifier que les conditions (i) et (ii) de la définition 1.0.1.
Commençons par vérifier la propriété (i) de 1.0.1 : Soient
![]() $x$
et
$x$
et
![]() $y$
deux sommets adjacents et
$y$
deux sommets adjacents et
![]() $\unicode[STIX]{x1D70E}$
le polysimplexe
$\unicode[STIX]{x1D70E}$
le polysimplexe
![]() $[x,y]$
. On sait déjà que
$[x,y]$
. On sait déjà que
![]() $e_{x}^{+}e_{y}^{+}=e_{\unicode[STIX]{x1D70E}}^{+}=e_{\unicode[STIX]{x1D70E}}^{+}e_{\unicode[STIX]{x1D70E}}^{+}$
. Ainsi
$e_{x}^{+}e_{y}^{+}=e_{\unicode[STIX]{x1D70E}}^{+}=e_{\unicode[STIX]{x1D70E}}^{+}e_{\unicode[STIX]{x1D70E}}^{+}$
. Ainsi
Ce qui montre la propriété (i) de 1.0.1.
Examinons maintenant la propriété (ii) de 1.0.1 : Soient
![]() $x$
,
$x$
,
![]() $y$
et
$y$
et
![]() $z$
des sommets de
$z$
des sommets de
![]() $BT$
tels que
$BT$
tels que
![]() $z$
soit dans l’enveloppe polysimpliciale de
$z$
soit dans l’enveloppe polysimpliciale de
![]() $\{x,y\}$
et
$\{x,y\}$
et
![]() $z$
adjacent à
$z$
adjacent à
![]() $x$
. Par la proposition 1.0.3 on sait que
$x$
. Par la proposition 1.0.3 on sait que
![]() $e_{x}^{+}e_{y}^{+}=e_{x}^{+}e_{z}^{+}e_{y}^{+}$
. Par ce qui précède
$e_{x}^{+}e_{y}^{+}=e_{x}^{+}e_{z}^{+}e_{y}^{+}$
. Par ce qui précède
![]() $e_{[x,z]}=e_{x}e_{z}$
et on a
$e_{[x,z]}=e_{x}e_{z}$
et on a
Le système d’idempotents
![]() $(e_{x})_{x\in BT_{0}}$
est cohérent.
$(e_{x})_{x\in BT_{0}}$
est cohérent.
Montrons maintenant que
![]() $e_{x}^{+}e_{y}=e_{x}e_{y}$
.
$e_{x}^{+}e_{y}=e_{x}e_{y}$
.
Si
![]() $x$
et
$x$
et
![]() $y$
sont adjacents on obtient que
$y$
sont adjacents on obtient que
Dans le cas général choisissons grâce au lemme 1.0.4 une suite de sommets
![]() $x_{0}=x,x_{1},\ldots ,x_{\ell }=y$
joignant
$x_{0}=x,x_{1},\ldots ,x_{\ell }=y$
joignant
![]() $x$
à
$x$
à
![]() $y$
, telle que pour tout
$y$
, telle que pour tout
![]() $i\in \{0,\ldots ,l-1\}$
,
$i\in \{0,\ldots ,l-1\}$
,
![]() $x_{i+1}$
est adjacent à
$x_{i+1}$
est adjacent à
![]() $x_{i}$
et
$x_{i}$
et
![]() $x_{i+1}\in H(x_{i},y)$
. Alors
$x_{i+1}\in H(x_{i},y)$
. Alors
 $$\begin{eqnarray}\displaystyle e_{x}^{+}e_{y} & = & \displaystyle e_{x}^{+}e_{y}^{+}e_{y}=e_{x}^{+}e_{x_{1}}^{+}e_{y}^{+}e_{y}=\cdots =e_{x}^{+}e_{x_{1}}^{+}\cdots e_{x_{l-1}}^{+}e_{y}^{+}e_{y}\nonumber\\ \displaystyle & = & \displaystyle e_{x}^{+}e_{x_{1}}^{+}\cdots e_{x_{l-1}}^{+}e_{y}=e_{x}^{+}e_{x_{1}}^{+}\cdots e_{x_{l-1}}e_{y}=\cdots =e_{x}e_{x_{1}}\cdots e_{x_{l-1}}e_{y}\nonumber\\ \displaystyle & = & \displaystyle e_{x}e_{x_{1}}\cdots e_{x_{l-2}}e_{y}=\cdots =e_{x}e_{x_{1}}e_{y}=e_{x}e_{y}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle e_{x}^{+}e_{y} & = & \displaystyle e_{x}^{+}e_{y}^{+}e_{y}=e_{x}^{+}e_{x_{1}}^{+}e_{y}^{+}e_{y}=\cdots =e_{x}^{+}e_{x_{1}}^{+}\cdots e_{x_{l-1}}^{+}e_{y}^{+}e_{y}\nonumber\\ \displaystyle & = & \displaystyle e_{x}^{+}e_{x_{1}}^{+}\cdots e_{x_{l-1}}^{+}e_{y}=e_{x}^{+}e_{x_{1}}^{+}\cdots e_{x_{l-1}}e_{y}=\cdots =e_{x}e_{x_{1}}\cdots e_{x_{l-1}}e_{y}\nonumber\\ \displaystyle & = & \displaystyle e_{x}e_{x_{1}}\cdots e_{x_{l-2}}e_{y}=\cdots =e_{x}e_{x_{1}}e_{y}=e_{x}e_{y}.\nonumber\end{eqnarray}$$
(La première ligne découle de la propriété (ii) de 1.0.1 appliquée aux
![]() $e_{x}^{+}$
. Pour la seconde, on utilise le fait que
$e_{x}^{+}$
. Pour la seconde, on utilise le fait que
![]() $e_{x_{i}}^{+}e_{x_{i+1}}=e_{x_{i}}e_{x_{i+1}}$
car
$e_{x_{i}}^{+}e_{x_{i+1}}=e_{x_{i}}e_{x_{i+1}}$
car
![]() $x_{i}$
et
$x_{i}$
et
![]() $x_{i+1}$
sont adjacents. Enfin pour la dernière on applique que
$x_{i+1}$
sont adjacents. Enfin pour la dernière on applique que
![]() $e_{x_{i}}e_{x_{i+1}}e_{y}=e_{x_{i}}e_{y}$
car
$e_{x_{i}}e_{x_{i+1}}e_{y}=e_{x_{i}}e_{y}$
car
![]() $x_{i+1}$
est adjacent à
$x_{i+1}$
est adjacent à
![]() $x_{i}$
et
$x_{i}$
et
![]() $x_{i+1}\in H(x_{i},y)$
.)
$x_{i+1}\in H(x_{i},y)$
.)
Ainsi
2 Construction d’idempotents
Nous expliquons ici comment construire des idempotents sur l’immeuble à partir de la théorie de Deligne–Lusztig ainsi que les conditions qu’ils doivent vérifier pour obtenir un système cohérent.
2.1 Théorie de Deligne–Lusztig
Rappelons brièvement le fonctionnement de la théorie de Deligne–Lusztig. Dans cette section les groupes algébriques considérés seront sur
![]() $\mathfrak{F}$
et
$\mathfrak{F}$
et
![]() $\ell$
est un nombre premier différent de
$\ell$
est un nombre premier différent de
![]() $p$
.
$p$
.
Soit
![]() $\text{G}$
un groupe réductif défini sur
$\text{G}$
un groupe réductif défini sur
![]() $\mathfrak{f}$
. Soit
$\mathfrak{f}$
. Soit
![]() $\text{P}$
un sous-groupe parabolique de radical unipotent
$\text{P}$
un sous-groupe parabolique de radical unipotent
![]() $\text{U}$
et supposons que
$\text{U}$
et supposons que
![]() $\text{P}$
contienne un Levi
$\text{P}$
contienne un Levi
![]() $F$
-stable
$F$
-stable
![]() $\text{L}$
. On associe alors à ces données la variété de Deligne–Lusztig
$\text{L}$
. On associe alors à ces données la variété de Deligne–Lusztig
![]() $Y_{\text{P}}$
définie par
$Y_{\text{P}}$
définie par
C’est une variété définie sur
![]() $\mathfrak{F}$
avec une action à gauche de
$\mathfrak{F}$
avec une action à gauche de
![]() $\mathsf{G}:=\text{G}^{F}$
donnée par
$\mathsf{G}:=\text{G}^{F}$
donnée par
![]() $(\unicode[STIX]{x1D6FE},g\text{U})\mapsto \unicode[STIX]{x1D6FE}g\text{U}$
et une action à droite de
$(\unicode[STIX]{x1D6FE},g\text{U})\mapsto \unicode[STIX]{x1D6FE}g\text{U}$
et une action à droite de
![]() $\mathsf{L}:=\text{L}^{F}$
donnée par
$\mathsf{L}:=\text{L}^{F}$
donnée par
![]() $(g\text{U},\unicode[STIX]{x1D6FF})\mapsto g\unicode[STIX]{x1D6FF}\text{U}$
. Le complexe cohomologique
$(g\text{U},\unicode[STIX]{x1D6FF})\mapsto g\unicode[STIX]{x1D6FF}\text{U}$
. Le complexe cohomologique
![]() $R\unicode[STIX]{x1D6E4}_{c}(Y_{\text{P}},\overline{\mathbb{Z}}_{\ell })$
est alors un complexe de
$R\unicode[STIX]{x1D6E4}_{c}(Y_{\text{P}},\overline{\mathbb{Z}}_{\ell })$
est alors un complexe de
![]() $(\overline{\mathbb{Z}}_{\ell }[G],\overline{\mathbb{Z}}_{\ell }[L])$
-bimodules et induit deux foncteurs adjoints
$(\overline{\mathbb{Z}}_{\ell }[G],\overline{\mathbb{Z}}_{\ell }[L])$
-bimodules et induit deux foncteurs adjoints
où
![]() $D^{b}$
signifie ‘catégorie dérivée bornée’.
$D^{b}$
signifie ‘catégorie dérivée bornée’.
Nous avons fixé des systèmes compatibles de racines de l’unité
![]() $(\mathbb{Q}/\mathbb{Z})_{p^{\prime }}\overset{\backsim }{\longrightarrow }\mathfrak{F}^{\times }$
et
$(\mathbb{Q}/\mathbb{Z})_{p^{\prime }}\overset{\backsim }{\longrightarrow }\mathfrak{F}^{\times }$
et
![]() $(\mathbb{Q}/\mathbb{Z})_{p^{\prime }}{\hookrightarrow}\overline{\mathbb{Z}}_{\ell }^{\times }$
. Si
$(\mathbb{Q}/\mathbb{Z})_{p^{\prime }}{\hookrightarrow}\overline{\mathbb{Z}}_{\ell }^{\times }$
. Si
![]() $\text{T}$
est un tore défini sur
$\text{T}$
est un tore défini sur
![]() $\mathfrak{f}$
et
$\mathfrak{f}$
et
![]() $\text{T}^{\ast }$
est son tore dual, aussi défini sur
$\text{T}^{\ast }$
est son tore dual, aussi défini sur
![]() $\mathfrak{f}$
, alors les deux applications précédentes permettent de définir une bijection
$\mathfrak{f}$
, alors les deux applications précédentes permettent de définir une bijection
![]() $\text{T}^{\ast F}\rightarrow \text{Hom}(T,\overline{\mathbb{Z}}_{\ell }^{\times })$
. Ainsi un élément
$\text{T}^{\ast F}\rightarrow \text{Hom}(T,\overline{\mathbb{Z}}_{\ell }^{\times })$
. Ainsi un élément
![]() $t\in \text{T}^{\ast F}$
détermine un caractère
$t\in \text{T}^{\ast F}$
détermine un caractère
![]() $\widehat{t}:T\rightarrow \overline{\mathbb{Z}}_{\ell }^{\times }$
.
$\widehat{t}:T\rightarrow \overline{\mathbb{Z}}_{\ell }^{\times }$
.
Soit
![]() $s$
une classe de conjugaison semi-simple dans
$s$
une classe de conjugaison semi-simple dans
![]() $\mathsf{G}^{\ast }:=\text{G}^{\ast F}$
. Une représentation irréductible
$\mathsf{G}^{\ast }:=\text{G}^{\ast F}$
. Une représentation irréductible
![]() $\unicode[STIX]{x1D70B}\in \text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(\mathsf{G})$
appartient à la série rationnelle attachée à
$\unicode[STIX]{x1D70B}\in \text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(\mathsf{G})$
appartient à la série rationnelle attachée à
![]() $s$
s’il existe un tore
$s$
s’il existe un tore
![]() $F$
-stable
$F$
-stable
![]() $\text{T}$
dans
$\text{T}$
dans
![]() $\text{G}$
, un élément
$\text{G}$
, un élément
![]() $t\in \text{T}^{\ast F}$
qui appartienne à
$t\in \text{T}^{\ast F}$
qui appartienne à
![]() $s$
et un Borel
$s$
et un Borel
![]() $\text{B}$
contenant
$\text{B}$
contenant
![]() $\text{T}$
tel que
$\text{T}$
tel que
![]() $\unicode[STIX]{x1D70B}$
apparaisse avec une multiplicité non nulle dans
$\unicode[STIX]{x1D70B}$
apparaisse avec une multiplicité non nulle dans
![]() $[{\mathcal{R}}_{\text{T}\subset \text{B}}^{\text{G}}(\widehat{t})]$
(où la notation
$[{\mathcal{R}}_{\text{T}\subset \text{B}}^{\text{G}}(\widehat{t})]$
(où la notation
![]() $[\cdot ]$
signifie que l’on prend l’image du complexe dans le groupe de Grothendieck). On note alors
$[\cdot ]$
signifie que l’on prend l’image du complexe dans le groupe de Grothendieck). On note alors
![]() ${\mathcal{E}}(\mathsf{G},s)$
l’ensemble des telles séries rationnelles et par
${\mathcal{E}}(\mathsf{G},s)$
l’ensemble des telles séries rationnelles et par
![]() $e_{s,\overline{\mathbb{Q}}_{\ell }}^{\mathsf{G}}\in \overline{\mathbb{Q}}_{\ell }[\mathsf{G}]$
l’idempotent central les sélectionnant.
$e_{s,\overline{\mathbb{Q}}_{\ell }}^{\mathsf{G}}\in \overline{\mathbb{Q}}_{\ell }[\mathsf{G}]$
l’idempotent central les sélectionnant.
Proposition 2.1.1.
(i) [Reference Cabanes and EnguehardCE04, théorème 8.23] Nous avons
 $1=\sum _{s}e_{s,\overline{\mathbb{Q}}_{\ell }}^{\mathsf{G}}$
dans
$1=\sum _{s}e_{s,\overline{\mathbb{Q}}_{\ell }}^{\mathsf{G}}$
dans
 $\overline{\mathbb{Q}}_{\ell }[\mathsf{G}]$
.
$\overline{\mathbb{Q}}_{\ell }[\mathsf{G}]$
.(ii) [Reference Bonnafé and RouquierBR03, théorème A
 $^{\prime }$
et remarque 11.3] Si
$^{\prime }$
et remarque 11.3] Si
 $s$
se compose d’éléments
$s$
se compose d’éléments
 $\ell$
-réguliers, alors nous avons un idempotent
$\ell$
-réguliers, alors nous avons un idempotent
 $e_{s,\overline{\mathbb{Z}}_{\ell }}^{\mathsf{G}}=\sum _{s^{\prime }\backsim _{\ell }s}e_{s^{\prime },\overline{\mathbb{Q}}_{\ell }}^{\mathsf{G}}\in \overline{\mathbb{Z}}_{\ell }[\mathsf{G}]$
, où
$e_{s,\overline{\mathbb{Z}}_{\ell }}^{\mathsf{G}}=\sum _{s^{\prime }\backsim _{\ell }s}e_{s^{\prime },\overline{\mathbb{Q}}_{\ell }}^{\mathsf{G}}\in \overline{\mathbb{Z}}_{\ell }[\mathsf{G}]$
, où
 $s^{\prime }\backsim _{\ell }s$
signifie que
$s^{\prime }\backsim _{\ell }s$
signifie que
 $s$
est la partie
$s$
est la partie
 $\ell$
-régulière de
$\ell$
-régulière de
 $s^{\prime }$
.
$s^{\prime }$
.
Soit
![]() $\text{L}$
un Levi
$\text{L}$
un Levi
![]() $F$
-stable de
$F$
-stable de
![]() $\text{G}$
contenu dans un parabolique
$\text{G}$
contenu dans un parabolique
![]() $\text{P}$
. Une classe de conjugaison
$\text{P}$
. Une classe de conjugaison
![]() $t$
dans
$t$
dans
![]() $\mathsf{L}^{\ast }$
donne une classe de conjugaison
$\mathsf{L}^{\ast }$
donne une classe de conjugaison
![]() $s$
dans
$s$
dans
![]() $\mathsf{G}^{\ast }$
. Ainsi nous avons une application
$\mathsf{G}^{\ast }$
. Ainsi nous avons une application
![]() $\unicode[STIX]{x1D711}_{\mathsf{L}^{\ast },\mathsf{G}^{\ast }}$
à fibres finies définie par
$\unicode[STIX]{x1D711}_{\mathsf{L}^{\ast },\mathsf{G}^{\ast }}$
à fibres finies définie par
Soit
![]() $\unicode[STIX]{x1D6EC}=\overline{\mathbb{Q}}_{\ell }$
ou
$\unicode[STIX]{x1D6EC}=\overline{\mathbb{Q}}_{\ell }$
ou
![]() $\overline{\mathbb{Z}}_{\ell }$
. Construisons alors un idempotent
$\overline{\mathbb{Z}}_{\ell }$
. Construisons alors un idempotent
![]() $e_{s,\unicode[STIX]{x1D6EC}}^{\mathsf{L}}:=\sum _{t\in \unicode[STIX]{x1D711}_{\mathsf{L}^{\ast },\mathsf{G}^{\ast }}^{-1}(s)}e_{t,\unicode[STIX]{x1D6EC}}^{\mathsf{L}}$
.
$e_{s,\unicode[STIX]{x1D6EC}}^{\mathsf{L}}:=\sum _{t\in \unicode[STIX]{x1D711}_{\mathsf{L}^{\ast },\mathsf{G}^{\ast }}^{-1}(s)}e_{t,\unicode[STIX]{x1D6EC}}^{\mathsf{L}}$
.
Dans le cas où
![]() $\text{P}$
est lui-même
$\text{P}$
est lui-même
![]() $F$
-stable, on note
$F$
-stable, on note
![]() $\text{U}$
le radical unipotent de
$\text{U}$
le radical unipotent de
![]() $\text{P}$
et
$\text{P}$
et
![]() $\mathsf{U}=\text{U}^{F}$
. Notons
$\mathsf{U}=\text{U}^{F}$
. Notons
![]() $e_{\mathsf{U}}:=(1/|\mathsf{U}|)\sum _{x\in \mathsf{U}}\unicode[STIX]{x1D7D9}_{x}$
l’idempotent réalisant la moyenne sur
$e_{\mathsf{U}}:=(1/|\mathsf{U}|)\sum _{x\in \mathsf{U}}\unicode[STIX]{x1D7D9}_{x}$
l’idempotent réalisant la moyenne sur
![]() $\mathsf{U}$
. Alors on a la proposition suivante.
$\mathsf{U}$
. Alors on a la proposition suivante.
Proposition 2.1.2 [Reference DatDat16, § 2.1.4].
où
![]() $e_{s,\unicode[STIX]{x1D6EC}}^{\mathsf{P}}$
est un idempotent central dans
$e_{s,\unicode[STIX]{x1D6EC}}^{\mathsf{P}}$
est un idempotent central dans
![]() $\unicode[STIX]{x1D6EC}[\mathsf{P}]$
.
$\unicode[STIX]{x1D6EC}[\mathsf{P}]$
.
Soient
![]() $\text{G}^{\prime }$
un autre groupe réductif défini sur
$\text{G}^{\prime }$
un autre groupe réductif défini sur
![]() $\mathfrak{f}$
et
$\mathfrak{f}$
et
![]() $\unicode[STIX]{x1D711}:\text{G}\rightarrow \text{G}^{\prime }$
un isomorphisme compatible avec les
$\unicode[STIX]{x1D711}:\text{G}\rightarrow \text{G}^{\prime }$
un isomorphisme compatible avec les
![]() $F$
-structures. Alors
$F$
-structures. Alors
![]() $\unicode[STIX]{x1D711}$
induit une bijection (voir annexe A)
$\unicode[STIX]{x1D711}$
induit une bijection (voir annexe A)
Lemme 2.1.3. On a
Démonstration.
Par construction un élément
![]() $t\in \text{T}^{\ast F}$
appartenant à
$t\in \text{T}^{\ast F}$
appartenant à
![]() $s$
est envoyé sur
$s$
est envoyé sur
![]() $\unicode[STIX]{x1D711}^{\ast }(t)$
appartenant à
$\unicode[STIX]{x1D711}^{\ast }(t)$
appartenant à
![]() $\unicode[STIX]{x1D711}^{\ast }(s)$
. Ainsi
$\unicode[STIX]{x1D711}^{\ast }(s)$
. Ainsi
![]() $\unicode[STIX]{x1D711}$
envoie
$\unicode[STIX]{x1D711}$
envoie
![]() ${\mathcal{E}}(\mathsf{G},s)$
sur
${\mathcal{E}}(\mathsf{G},s)$
sur
![]() ${\mathcal{E}}(\mathsf{G}^{\prime },\unicode[STIX]{x1D711}^{\ast }(s))$
et on a le résultat.◻
${\mathcal{E}}(\mathsf{G}^{\prime },\unicode[STIX]{x1D711}^{\ast }(s))$
et on a le résultat.◻
2.2 Construction d’idempotents sur l’immeuble
Maintenant que l’on sait fabriquer des idempotents sur les groupes finis, il nous faut les relever en des idempotents sur le groupe
![]() $p$
-adique. On utilise pour cela le fait que les sous-groupes parahoriques
$p$
-adique. On utilise pour cela le fait que les sous-groupes parahoriques
![]() $G_{\unicode[STIX]{x1D70E}}^{\circ }$
admettent un modèle entier et que le quotient
$G_{\unicode[STIX]{x1D70E}}^{\circ }$
admettent un modèle entier et que le quotient
![]() $G_{\unicode[STIX]{x1D70E}}^{\circ }/G_{\unicode[STIX]{x1D70E}}^{+}$
est alors l’ensemble des points d’un groupe réductif connexe à valeur dans un corps fini.
$G_{\unicode[STIX]{x1D70E}}^{\circ }/G_{\unicode[STIX]{x1D70E}}^{+}$
est alors l’ensemble des points d’un groupe réductif connexe à valeur dans un corps fini.
Soit
![]() $\unicode[STIX]{x1D70E}$
un polysimplexe dans
$\unicode[STIX]{x1D70E}$
un polysimplexe dans
![]() $BT$
. D’après [Reference TitsTit79, § 3.4] il existe un schéma en groupes affine lisse
$BT$
. D’après [Reference TitsTit79, § 3.4] il existe un schéma en groupes affine lisse
![]() ${\mathcal{G}}_{\unicode[STIX]{x1D70E}}$
défini sur
${\mathcal{G}}_{\unicode[STIX]{x1D70E}}$
défini sur
![]() $\mathfrak{o}_{k}$
, unique à isomorphisme près, tel que
$\mathfrak{o}_{k}$
, unique à isomorphisme près, tel que
(i) la fibre générique
 ${\mathcal{G}}_{\unicode[STIX]{x1D70E},k}$
de
${\mathcal{G}}_{\unicode[STIX]{x1D70E},k}$
de
 ${\mathcal{G}}_{\unicode[STIX]{x1D70E}}$
est
${\mathcal{G}}_{\unicode[STIX]{x1D70E}}$
est
 $G$
;
$G$
;(ii) pour toute extension galoisienne non-ramifiée
 $K_{1}$
de
$K_{1}$
de
 $k$
,
$k$
,
 ${\mathcal{G}}_{\unicode[STIX]{x1D70E}}(\mathfrak{o}_{K_{1}})$
est le sous-groupe compact maximal de
${\mathcal{G}}_{\unicode[STIX]{x1D70E}}(\mathfrak{o}_{K_{1}})$
est le sous-groupe compact maximal de
 $\mathbf{G}(K_{1})_{\unicode[STIX]{x1D70E}}$
, où
$\mathbf{G}(K_{1})_{\unicode[STIX]{x1D70E}}$
, où
 $\unicode[STIX]{x1D70E}$
est identifié avec son image canonique dans
$\unicode[STIX]{x1D70E}$
est identifié avec son image canonique dans
 $BT(K_{1})$
.
$BT(K_{1})$
.
L’application de réduction modulo
![]() $p$
fournit un morphisme surjectif
$p$
fournit un morphisme surjectif
![]() $G_{\unicode[STIX]{x1D70E}}={\mathcal{G}}_{\unicode[STIX]{x1D70E}}(\mathfrak{o}_{k})\rightarrow \tilde{\mathsf{G}}_{\unicode[STIX]{x1D70E}}:=\tilde{\text{}\text{G}}_{\unicode[STIX]{x1D70E}}^{F}$
, où
$G_{\unicode[STIX]{x1D70E}}={\mathcal{G}}_{\unicode[STIX]{x1D70E}}(\mathfrak{o}_{k})\rightarrow \tilde{\mathsf{G}}_{\unicode[STIX]{x1D70E}}:=\tilde{\text{}\text{G}}_{\unicode[STIX]{x1D70E}}^{F}$
, où
![]() $\tilde{\text{G}}_{\unicode[STIX]{x1D70E}}$
, la fibre spéciale de
$\tilde{\text{G}}_{\unicode[STIX]{x1D70E}}$
, la fibre spéciale de
![]() ${\mathcal{G}}_{\unicode[STIX]{x1D70E}}$
, est un groupe algébrique défini sur
${\mathcal{G}}_{\unicode[STIX]{x1D70E}}$
, est un groupe algébrique défini sur
![]() $\mathfrak{f}$
. On note
$\mathfrak{f}$
. On note
![]() ${\mathcal{G}}_{\unicode[STIX]{x1D70E}}^{\circ }$
la composante neutre de
${\mathcal{G}}_{\unicode[STIX]{x1D70E}}^{\circ }$
la composante neutre de
![]() ${\mathcal{G}}_{\unicode[STIX]{x1D70E}}$
et
${\mathcal{G}}_{\unicode[STIX]{x1D70E}}$
et
![]() $\tilde{\text{G}}_{\unicode[STIX]{x1D70E}}^{\circ }$
celle de
$\tilde{\text{G}}_{\unicode[STIX]{x1D70E}}^{\circ }$
celle de
![]() $\tilde{\text{G}}_{\unicode[STIX]{x1D70E}}$
. D’après [Reference Bruhat and TitsBT84, § 5.2.6], on a
$\tilde{\text{G}}_{\unicode[STIX]{x1D70E}}$
. D’après [Reference Bruhat and TitsBT84, § 5.2.6], on a
![]() $G_{\unicode[STIX]{x1D70E}}^{\circ }={\mathcal{G}}_{\unicode[STIX]{x1D70E}}^{\circ }(\mathfrak{o}_{k})$
. D’où un morphisme surjectif
$G_{\unicode[STIX]{x1D70E}}^{\circ }={\mathcal{G}}_{\unicode[STIX]{x1D70E}}^{\circ }(\mathfrak{o}_{k})$
. D’où un morphisme surjectif
![]() $G_{\unicode[STIX]{x1D70E}}^{\circ }\rightarrow \tilde{\mathsf{G}}_{\unicode[STIX]{x1D70E}}^{\circ }$
.
$G_{\unicode[STIX]{x1D70E}}^{\circ }\rightarrow \tilde{\mathsf{G}}_{\unicode[STIX]{x1D70E}}^{\circ }$
.
Notons
![]() $\overline{\text{}\text{G}}_{\unicode[STIX]{x1D70E}}$
le quotient réductif de
$\overline{\text{}\text{G}}_{\unicode[STIX]{x1D70E}}$
le quotient réductif de
![]() $\tilde{\text{}\text{G}}_{\unicode[STIX]{x1D70E}}^{\circ }$
. On a donc un morphisme surjectif
$\tilde{\text{}\text{G}}_{\unicode[STIX]{x1D70E}}^{\circ }$
. On a donc un morphisme surjectif
![]() $G_{\unicode[STIX]{x1D70E}}^{\circ }\rightarrow \overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}$
de noyau
$G_{\unicode[STIX]{x1D70E}}^{\circ }\rightarrow \overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}$
de noyau
![]() $G_{\unicode[STIX]{x1D70E}}^{+}$
, d’où un isomorphisme :
$G_{\unicode[STIX]{x1D70E}}^{+}$
, d’où un isomorphisme :
Soit
![]() $s\in (\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}^{\ast })_{ss}$
(rappelons que
$s\in (\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}^{\ast })_{ss}$
(rappelons que
![]() $\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}^{\ast }=\overline{\text{G}}_{\unicode[STIX]{x1D70E}}^{\ast F}$
) d’ordre inversible dans
$\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}^{\ast }=\overline{\text{G}}_{\unicode[STIX]{x1D70E}}^{\ast F}$
) d’ordre inversible dans
![]() $\unicode[STIX]{x1D6EC}$
, on peut alors tirer en arrière par cet isomorphisme l’idempotent
$\unicode[STIX]{x1D6EC}$
, on peut alors tirer en arrière par cet isomorphisme l’idempotent
![]() $e_{s,\unicode[STIX]{x1D6EC}}^{\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}}$
en un idempotent
$e_{s,\unicode[STIX]{x1D6EC}}^{\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}}$
en un idempotent
![]() $e_{\unicode[STIX]{x1D70E}}^{s,\unicode[STIX]{x1D6EC}}\in \unicode[STIX]{x1D6EC}[G_{\unicode[STIX]{x1D70E}}^{\circ }/G_{\unicode[STIX]{x1D70E}}^{+}]\subset {\mathcal{H}}_{\unicode[STIX]{x1D6EC}}(G_{\unicode[STIX]{x1D70E}})$
.
$e_{\unicode[STIX]{x1D70E}}^{s,\unicode[STIX]{x1D6EC}}\in \unicode[STIX]{x1D6EC}[G_{\unicode[STIX]{x1D70E}}^{\circ }/G_{\unicode[STIX]{x1D70E}}^{+}]\subset {\mathcal{H}}_{\unicode[STIX]{x1D6EC}}(G_{\unicode[STIX]{x1D70E}})$
.
Soit
![]() $x\in BT_{0}$
. Si l’on considère la sous-partie de l’immeuble constituée des polysimplexes
$x\in BT_{0}$
. Si l’on considère la sous-partie de l’immeuble constituée des polysimplexes
![]() $\unicode[STIX]{x1D70F}$
tels que
$\unicode[STIX]{x1D70F}$
tels que
![]() $x\leqslant \unicode[STIX]{x1D70F}$
alors d’après [Reference TitsTit79, § 3.5.4], on obtient l’immeuble sphérique (‘immeuble des sous-groupes
$x\leqslant \unicode[STIX]{x1D70F}$
alors d’après [Reference TitsTit79, § 3.5.4], on obtient l’immeuble sphérique (‘immeuble des sous-groupes
![]() $\mathfrak{f}$
-paraboliques’) de
$\mathfrak{f}$
-paraboliques’) de
![]() $\overline{\mathsf{G}}_{x}$
.
$\overline{\mathsf{G}}_{x}$
.
Soit
![]() $\unicode[STIX]{x1D70E}\in BT$
tel que
$\unicode[STIX]{x1D70E}\in BT$
tel que
![]() $x\leqslant \unicode[STIX]{x1D70E}$
. Alors
$x\leqslant \unicode[STIX]{x1D70E}$
. Alors
![]() $G_{\unicode[STIX]{x1D70E}}^{\circ }\subset G_{x}^{\circ }$
. On a ainsi un morphisme
$G_{\unicode[STIX]{x1D70E}}^{\circ }\subset G_{x}^{\circ }$
. On a ainsi un morphisme
![]() $G_{\unicode[STIX]{x1D70E}}^{\circ }\rightarrow G_{x}^{\circ }\rightarrow \overline{\mathsf{G}}_{x}$
. Notons
$G_{\unicode[STIX]{x1D70E}}^{\circ }\rightarrow G_{x}^{\circ }\rightarrow \overline{\mathsf{G}}_{x}$
. Notons
![]() $\mathsf{P}_{\unicode[STIX]{x1D70E}}$
l’image de
$\mathsf{P}_{\unicode[STIX]{x1D70E}}$
l’image de
![]() $G_{\unicode[STIX]{x1D70E}}^{\circ }$
dans
$G_{\unicode[STIX]{x1D70E}}^{\circ }$
dans
![]() $\overline{\mathsf{G}}_{x}$
qui est un sous-groupe parabolique et
$\overline{\mathsf{G}}_{x}$
qui est un sous-groupe parabolique et
![]() $\mathsf{U}_{\unicode[STIX]{x1D70E}}$
son radical unipotent. L’image réciproque de
$\mathsf{U}_{\unicode[STIX]{x1D70E}}$
son radical unipotent. L’image réciproque de
![]() $\mathsf{U}_{\unicode[STIX]{x1D70E}}$
dans
$\mathsf{U}_{\unicode[STIX]{x1D70E}}$
dans
![]() $G_{\unicode[STIX]{x1D70E}}^{\circ }$
est
$G_{\unicode[STIX]{x1D70E}}^{\circ }$
est
![]() $G_{\unicode[STIX]{x1D70E}}^{+}$
. Ceci fournit donc un isomorphisme
$G_{\unicode[STIX]{x1D70E}}^{+}$
. Ceci fournit donc un isomorphisme
![]() $G_{\unicode[STIX]{x1D70E}}/G_{\unicode[STIX]{x1D70E}}^{+}\simeq \overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}\simeq \mathsf{P}_{\unicode[STIX]{x1D70E}}/\mathsf{U}_{\unicode[STIX]{x1D70E}}$
.
$G_{\unicode[STIX]{x1D70E}}/G_{\unicode[STIX]{x1D70E}}^{+}\simeq \overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}\simeq \mathsf{P}_{\unicode[STIX]{x1D70E}}/\mathsf{U}_{\unicode[STIX]{x1D70E}}$
.
Considérons
![]() $\mathsf{M}_{\unicode[STIX]{x1D70E}}^{\ast }$
un sous-groupe de Levi de
$\mathsf{M}_{\unicode[STIX]{x1D70E}}^{\ast }$
un sous-groupe de Levi de
![]() $\overline{\mathsf{G}}_{x}^{\ast }$
relevant
$\overline{\mathsf{G}}_{x}^{\ast }$
relevant
![]() $\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}^{\ast }$
. Dans le § 2.1, nous avons défini une application
$\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}^{\ast }$
. Dans le § 2.1, nous avons défini une application
![]() $\unicode[STIX]{x1D711}_{\mathsf{M}_{\unicode[STIX]{x1D70E}}^{\ast },\overline{\mathsf{G}}_{x}^{\ast }}:(\mathsf{M}_{\unicode[STIX]{x1D70E}}^{\ast })_{ss}\rightarrow (\overline{\mathsf{G}}_{x}^{\ast })_{ss}$
. Cette application est indépendante du choix du relèvement de
$\unicode[STIX]{x1D711}_{\mathsf{M}_{\unicode[STIX]{x1D70E}}^{\ast },\overline{\mathsf{G}}_{x}^{\ast }}:(\mathsf{M}_{\unicode[STIX]{x1D70E}}^{\ast })_{ss}\rightarrow (\overline{\mathsf{G}}_{x}^{\ast })_{ss}$
. Cette application est indépendante du choix du relèvement de
![]() $\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}^{\ast }$
et nous définit donc une application
$\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}^{\ast }$
et nous définit donc une application
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E},x}^{\ast }:(\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}^{\ast })_{ss}\rightarrow (\overline{\mathsf{G}}_{x}^{\ast })_{ss}$
. On définit alors pour
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E},x}^{\ast }:(\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}^{\ast })_{ss}\rightarrow (\overline{\mathsf{G}}_{x}^{\ast })_{ss}$
. On définit alors pour
![]() $s\in (\overline{\mathsf{G}}_{x}^{\ast })_{ss}$
d’ordre inversible dans
$s\in (\overline{\mathsf{G}}_{x}^{\ast })_{ss}$
d’ordre inversible dans
![]() $\unicode[STIX]{x1D6EC}$
, l’idempotent
$\unicode[STIX]{x1D6EC}$
, l’idempotent
![]() $e_{\unicode[STIX]{x1D70E}}^{s,\unicode[STIX]{x1D6EC}}:=\sum _{t\in \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E},x}^{\ast -1}(s)}e_{\unicode[STIX]{x1D70E}}^{t,\unicode[STIX]{x1D6EC}}$
.
$e_{\unicode[STIX]{x1D70E}}^{s,\unicode[STIX]{x1D6EC}}:=\sum _{t\in \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E},x}^{\ast -1}(s)}e_{\unicode[STIX]{x1D70E}}^{t,\unicode[STIX]{x1D6EC}}$
.
Proposition 2.2.1. Soient
![]() $x\in BT_{0}$
,
$x\in BT_{0}$
,
![]() $\unicode[STIX]{x1D70E}\in BT$
tel que
$\unicode[STIX]{x1D70E}\in BT$
tel que
![]() $x\leqslant \unicode[STIX]{x1D70E}$
et
$x\leqslant \unicode[STIX]{x1D70E}$
et
![]() $s\in (\overline{\mathsf{G}}_{x}^{\ast })_{ss}$
d’ordre inversible dans
$s\in (\overline{\mathsf{G}}_{x}^{\ast })_{ss}$
d’ordre inversible dans
![]() $\unicode[STIX]{x1D6EC}$
.Alors
$\unicode[STIX]{x1D6EC}$
.Alors
![]() $e_{\unicode[STIX]{x1D70E}}^{+}e_{x}^{s,\unicode[STIX]{x1D6EC}}=e_{x}^{s,\unicode[STIX]{x1D6EC}}e_{\unicode[STIX]{x1D70E}}^{+}=e_{\unicode[STIX]{x1D70E}}^{s,\unicode[STIX]{x1D6EC}}$
.
$e_{\unicode[STIX]{x1D70E}}^{+}e_{x}^{s,\unicode[STIX]{x1D6EC}}=e_{x}^{s,\unicode[STIX]{x1D6EC}}e_{\unicode[STIX]{x1D70E}}^{+}=e_{\unicode[STIX]{x1D70E}}^{s,\unicode[STIX]{x1D6EC}}$
.
Démonstration.
D’après la proposition 2.1.2 on a
![]() $e_{s,\unicode[STIX]{x1D6EC}}^{\overline{\mathsf{G}}_{x}}e_{\mathsf{U}_{\unicode[STIX]{x1D70E}}}=e_{\mathsf{U}_{\unicode[STIX]{x1D70E}}}e_{s,\unicode[STIX]{x1D6EC}}^{\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}}$
dans
$e_{s,\unicode[STIX]{x1D6EC}}^{\overline{\mathsf{G}}_{x}}e_{\mathsf{U}_{\unicode[STIX]{x1D70E}}}=e_{\mathsf{U}_{\unicode[STIX]{x1D70E}}}e_{s,\unicode[STIX]{x1D6EC}}^{\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}}$
dans
![]() $\unicode[STIX]{x1D6EC}[\overline{\mathsf{G}}_{x}]$
. Lorsque l’on tire en arrière ces idempotents par l’isomorphisme
$\unicode[STIX]{x1D6EC}[\overline{\mathsf{G}}_{x}]$
. Lorsque l’on tire en arrière ces idempotents par l’isomorphisme
![]() $G_{x}^{\circ }/G_{x}^{+}\overset{{\sim}}{\longrightarrow }\overline{\mathsf{G}}_{x}$
, on obtient dans
$G_{x}^{\circ }/G_{x}^{+}\overset{{\sim}}{\longrightarrow }\overline{\mathsf{G}}_{x}$
, on obtient dans
![]() $\unicode[STIX]{x1D6EC}[G_{x}^{\circ }/G_{x}^{+}]$
:
$\unicode[STIX]{x1D6EC}[G_{x}^{\circ }/G_{x}^{+}]$
:
Maintenant comme
![]() $e_{\unicode[STIX]{x1D70E}}^{+}e_{\unicode[STIX]{x1D70E}}^{s,\unicode[STIX]{x1D6EC}}=e_{\unicode[STIX]{x1D70E}}^{s,\unicode[STIX]{x1D6EC}}$
et
$e_{\unicode[STIX]{x1D70E}}^{+}e_{\unicode[STIX]{x1D70E}}^{s,\unicode[STIX]{x1D6EC}}=e_{\unicode[STIX]{x1D70E}}^{s,\unicode[STIX]{x1D6EC}}$
et
![]() $e_{\unicode[STIX]{x1D70E}}^{+}e_{x}^{s,\unicode[STIX]{x1D6EC}}=e_{x}^{s,\unicode[STIX]{x1D6EC}}e_{\unicode[STIX]{x1D70E}}^{+}$
on a le résultat.◻
$e_{\unicode[STIX]{x1D70E}}^{+}e_{x}^{s,\unicode[STIX]{x1D6EC}}=e_{x}^{s,\unicode[STIX]{x1D6EC}}e_{\unicode[STIX]{x1D70E}}^{+}$
on a le résultat.◻
2.3 Systèmes 0-cohérents de classes de conjugaison
À partir d’un polysimplexe
![]() $\unicode[STIX]{x1D70E}$
et d’une classe de conjugaison semi-simple
$\unicode[STIX]{x1D70E}$
et d’une classe de conjugaison semi-simple
![]() $s$
nous savons maintenant construire un idempotent
$s$
nous savons maintenant construire un idempotent
![]() $e_{\unicode[STIX]{x1D70E}}^{s,\unicode[STIX]{x1D6EC}}$
. On décrit alors dans cette partie les conditions que l’on doit imposer pour que le système d’idempotents formé à partir des
$e_{\unicode[STIX]{x1D70E}}^{s,\unicode[STIX]{x1D6EC}}$
. On décrit alors dans cette partie les conditions que l’on doit imposer pour que le système d’idempotents formé à partir des
![]() $e_{\unicode[STIX]{x1D70E}}^{s,\unicode[STIX]{x1D6EC}}$
soit un système 0-cohérent.
$e_{\unicode[STIX]{x1D70E}}^{s,\unicode[STIX]{x1D6EC}}$
soit un système 0-cohérent.
Soient
![]() $g\in G$
et
$g\in G$
et
![]() $\unicode[STIX]{x1D70E}\in BT$
, on a
$\unicode[STIX]{x1D70E}\in BT$
, on a
![]() $gG_{\unicode[STIX]{x1D70E}}^{\circ }g^{-1}=G_{g\unicode[STIX]{x1D70E}}^{\circ }$
et
$gG_{\unicode[STIX]{x1D70E}}^{\circ }g^{-1}=G_{g\unicode[STIX]{x1D70E}}^{\circ }$
et
![]() $gG_{\unicode[STIX]{x1D70E}}^{+}g^{-1}=G_{g\unicode[STIX]{x1D70E}}^{+}$
, d’où
$gG_{\unicode[STIX]{x1D70E}}^{+}g^{-1}=G_{g\unicode[STIX]{x1D70E}}^{+}$
, d’où
![]() $g(G_{\unicode[STIX]{x1D70E}}^{\circ }/G_{\unicode[STIX]{x1D70E}}^{+})g^{-1}\simeq G_{g\unicode[STIX]{x1D70E}}^{\circ }/G_{g\unicode[STIX]{x1D70E}}^{+}$
. D’après [Reference Bruhat and TitsBT84, 4.6.30], la conjugaison par
$g(G_{\unicode[STIX]{x1D70E}}^{\circ }/G_{\unicode[STIX]{x1D70E}}^{+})g^{-1}\simeq G_{g\unicode[STIX]{x1D70E}}^{\circ }/G_{g\unicode[STIX]{x1D70E}}^{+}$
. D’après [Reference Bruhat and TitsBT84, 4.6.30], la conjugaison par
![]() $g$
se prolonge en un isomorphisme du
$g$
se prolonge en un isomorphisme du
![]() $\mathfrak{o}_{k}$
-schéma en groupes
$\mathfrak{o}_{k}$
-schéma en groupes
![]() ${\mathcal{G}}_{\unicode[STIX]{x1D70E}}^{\circ }$
sur le
${\mathcal{G}}_{\unicode[STIX]{x1D70E}}^{\circ }$
sur le
![]() $\mathfrak{o}_{k}$
-schéma en groupes
$\mathfrak{o}_{k}$
-schéma en groupes
![]() ${\mathcal{G}}_{g\unicode[STIX]{x1D70E}}^{\circ }$
et donc induit un isomorphisme
${\mathcal{G}}_{g\unicode[STIX]{x1D70E}}^{\circ }$
et donc induit un isomorphisme
![]() $\unicode[STIX]{x1D711}_{g,\unicode[STIX]{x1D70E}}:\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}\overset{{\sim}}{\rightarrow }\overline{\mathsf{G}}_{g\unicode[STIX]{x1D70E}}$
. On obtient alors, comme dans l’annexe A, un isomorphisme sur les classes de conjugaison semi-simples des groupes duaux
$\unicode[STIX]{x1D711}_{g,\unicode[STIX]{x1D70E}}:\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}\overset{{\sim}}{\rightarrow }\overline{\mathsf{G}}_{g\unicode[STIX]{x1D70E}}$
. On obtient alors, comme dans l’annexe A, un isomorphisme sur les classes de conjugaison semi-simples des groupes duaux
Pour
![]() $\unicode[STIX]{x1D70E}\in BT$
, on note
$\unicode[STIX]{x1D70E}\in BT$
, on note
Définition 2.3.1. Soit
![]() $S=(S_{\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}\in BT}$
un système d’ensembles de classes de conjugaison avec
$S=(S_{\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}\in BT}$
un système d’ensembles de classes de conjugaison avec
![]() $S_{\unicode[STIX]{x1D70E}}\subseteq (\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}^{\ast })_{ss,\unicode[STIX]{x1D6EC}}$
. On dit que
$S_{\unicode[STIX]{x1D70E}}\subseteq (\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}^{\ast })_{ss,\unicode[STIX]{x1D6EC}}$
. On dit que
![]() $S$
est 0-cohérent si
$S$
est 0-cohérent si
(i)
 $\unicode[STIX]{x1D711}_{g,x}^{\ast }(S_{x})=S_{gx}$
quel que soit
$\unicode[STIX]{x1D711}_{g,x}^{\ast }(S_{x})=S_{gx}$
quel que soit
 $x\in BT_{0}$
et
$x\in BT_{0}$
et
 $g\in G$
;
$g\in G$
;(ii)
 $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E},x}^{\ast -1}(S_{x})=S_{\unicode[STIX]{x1D70E}}$
pour
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E},x}^{\ast -1}(S_{x})=S_{\unicode[STIX]{x1D70E}}$
pour
 $x\in BT_{0}$
et
$x\in BT_{0}$
et
 $\unicode[STIX]{x1D70E}\in BT$
tels que
$\unicode[STIX]{x1D70E}\in BT$
tels que
 $x\leqslant \unicode[STIX]{x1D70E}$
.
$x\leqslant \unicode[STIX]{x1D70E}$
.
Soit
![]() $S=(S_{\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}\in BT}$
un système 0-cohérent. Soit
$S=(S_{\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}\in BT}$
un système 0-cohérent. Soit
![]() $\unicode[STIX]{x1D70E}\in BT$
, on définit alors
$\unicode[STIX]{x1D70E}\in BT$
, on définit alors
![]() $e_{\unicode[STIX]{x1D70E}}^{S,\unicode[STIX]{x1D6EC}}=\sum _{s\in S_{\unicode[STIX]{x1D70E}}}e_{\unicode[STIX]{x1D70E}}^{s,\unicode[STIX]{x1D6EC}}$
.
$e_{\unicode[STIX]{x1D70E}}^{S,\unicode[STIX]{x1D6EC}}=\sum _{s\in S_{\unicode[STIX]{x1D70E}}}e_{\unicode[STIX]{x1D70E}}^{s,\unicode[STIX]{x1D6EC}}$
.
Proposition 2.3.2. Le système
![]() $(e_{\unicode[STIX]{x1D70E}}^{S,\unicode[STIX]{x1D6EC}})_{\unicode[STIX]{x1D70E}\in BT}$
est 0-cohérent.
$(e_{\unicode[STIX]{x1D70E}}^{S,\unicode[STIX]{x1D6EC}})_{\unicode[STIX]{x1D70E}\in BT}$
est 0-cohérent.
Démonstration.
Commençons par vérifier la condition (i) :
Soient
![]() $x\in BT_{0}$
et
$x\in BT_{0}$
et
![]() $g\in G$
. On a la commutativité du diagramme suivant
$g\in G$
. On a la commutativité du diagramme suivant

Le lemme 2.1.3 nous dit que
![]() $\unicode[STIX]{x1D711}_{g,x}(e_{s,\unicode[STIX]{x1D6EC}}^{\overline{\mathsf{G}}_{x}})=e_{\unicode[STIX]{x1D711}_{g,x}^{\ast }(s),\unicode[STIX]{x1D6EC}}^{\overline{\mathsf{G}}_{gx}}$
. Ainsi
$\unicode[STIX]{x1D711}_{g,x}(e_{s,\unicode[STIX]{x1D6EC}}^{\overline{\mathsf{G}}_{x}})=e_{\unicode[STIX]{x1D711}_{g,x}^{\ast }(s),\unicode[STIX]{x1D6EC}}^{\overline{\mathsf{G}}_{gx}}$
. Ainsi
Passons maintenant à la condition (ii) :
Soient
![]() $x\in BT_{0}$
et
$x\in BT_{0}$
et
![]() $\unicode[STIX]{x1D70E}\in BT$
tels que
$\unicode[STIX]{x1D70E}\in BT$
tels que
![]() $x\leqslant \unicode[STIX]{x1D70E}$
.
$x\leqslant \unicode[STIX]{x1D70E}$
.
Par la proposition 2.2.1 on a
![]() $e_{\unicode[STIX]{x1D70E}}^{+}e_{x}^{s,\unicode[STIX]{x1D6EC}}=\sum _{t\in \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E},x}^{\ast -1}(s)}e_{\unicode[STIX]{x1D70E}}^{t,\unicode[STIX]{x1D6EC}}$
. Donc
$e_{\unicode[STIX]{x1D70E}}^{+}e_{x}^{s,\unicode[STIX]{x1D6EC}}=\sum _{t\in \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E},x}^{\ast -1}(s)}e_{\unicode[STIX]{x1D70E}}^{t,\unicode[STIX]{x1D6EC}}$
. Donc
On note
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}(G)$
la catégorie abélienne des représentations lisses de
$\text{Rep}_{\unicode[STIX]{x1D6EC}}(G)$
la catégorie abélienne des représentations lisses de
![]() $G$
à coefficients dans
$G$
à coefficients dans
![]() $\unicode[STIX]{x1D6EC}$
. Notons
$\unicode[STIX]{x1D6EC}$
. Notons
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{0}(G)$
la sous-catégorie des représentations de niveau 0, c’est à dire la sous-catégorie découpée par le système d’idempotents
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{0}(G)$
la sous-catégorie des représentations de niveau 0, c’est à dire la sous-catégorie découpée par le système d’idempotents
![]() $(e_{x}^{+})_{x\in BT_{0}}$
.
$(e_{x}^{+})_{x\in BT_{0}}$
.
Soit
![]() $S=(S_{\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}\in BT}$
un système 0-cohérent, il définit alors un système
$S=(S_{\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}\in BT}$
un système 0-cohérent, il définit alors un système
![]() $(e_{\unicode[STIX]{x1D70E}}^{S,\unicode[STIX]{x1D6EC}})_{\unicode[STIX]{x1D70E}\in BT}$
0-cohérent et forme donc, d’après le théorème 1.0.2, une catégorie
$(e_{\unicode[STIX]{x1D70E}}^{S,\unicode[STIX]{x1D6EC}})_{\unicode[STIX]{x1D70E}\in BT}$
0-cohérent et forme donc, d’après le théorème 1.0.2, une catégorie
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{S}(G)$
.
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{S}(G)$
.
Définition 2.3.3. Soient
![]() $S_{1}=(S_{1,\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}\in BT}$
et
$S_{1}=(S_{1,\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}\in BT}$
et
![]() $S_{2}=(S_{2,\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}\in BT}$
deux systèmes de classes de conjugaison. On définit alors
$S_{2}=(S_{2,\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}\in BT}$
deux systèmes de classes de conjugaison. On définit alors
![]() $S_{1}\cup S_{2}:=(S_{1,\unicode[STIX]{x1D70E}}\cup S_{2,\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}\in BT}$
et
$S_{1}\cup S_{2}:=(S_{1,\unicode[STIX]{x1D70E}}\cup S_{2,\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}\in BT}$
et
![]() $S_{1}\cap S_{2}:=(S_{1,\unicode[STIX]{x1D70E}}\cap S_{2,\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}\in BT}$
. On dit que
$S_{1}\cap S_{2}:=(S_{1,\unicode[STIX]{x1D70E}}\cap S_{2,\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}\in BT}$
. On dit que
![]() $S_{2}\subseteq S_{1}$
si pour tout
$S_{2}\subseteq S_{1}$
si pour tout
![]() $\unicode[STIX]{x1D70E}\in BT$
$\unicode[STIX]{x1D70E}\in BT$
![]() $S_{2,\unicode[STIX]{x1D70E}}\subseteq S_{1,\unicode[STIX]{x1D70E}}$
. Enfin, si
$S_{2,\unicode[STIX]{x1D70E}}\subseteq S_{1,\unicode[STIX]{x1D70E}}$
. Enfin, si
![]() $S_{2}\subseteq S_{1}$
, on note
$S_{2}\subseteq S_{1}$
, on note
![]() $S_{1}\backslash S_{2}:=(S_{1,\unicode[STIX]{x1D70E}}\backslash S_{2,\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}\in BT}$
.
$S_{1}\backslash S_{2}:=(S_{1,\unicode[STIX]{x1D70E}}\backslash S_{2,\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}\in BT}$
.
Lemme 2.3.4. Soient
![]() $S_{1}$
et
$S_{1}$
et
![]() $S_{2}$
deux systèmes 0-cohérents tels que
$S_{2}$
deux systèmes 0-cohérents tels que
![]() $S_{1}\cap S_{2}=\emptyset$
. Alors les catégories
$S_{1}\cap S_{2}=\emptyset$
. Alors les catégories
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{S_{1}}(G)$
et
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{S_{1}}(G)$
et
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{S_{2}}(G)$
sont orthogonales.
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{S_{2}}(G)$
sont orthogonales.
Démonstration.
Soit
![]() $V$
un objet de
$V$
un objet de
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{S_{1}}(G)$
. Nous devons montrer que pour tout sommet de l’immeuble
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{S_{1}}(G)$
. Nous devons montrer que pour tout sommet de l’immeuble
![]() $x$
, on a
$x$
, on a
![]() $e_{x}^{S_{2}}V=0$
. Fixons un tel
$e_{x}^{S_{2}}V=0$
. Fixons un tel
![]() $x$
. Par définition
$x$
. Par définition
![]() $V=\sum _{y\in BT_{0}}e_{y}^{S_{1}}V$
, donc
$V=\sum _{y\in BT_{0}}e_{y}^{S_{1}}V$
, donc
![]() $e_{x}^{S_{2}}V=\sum _{y\in BT_{0}}e_{x}^{S_{2}}e_{y}^{S_{1}}V$
. Soit
$e_{x}^{S_{2}}V=\sum _{y\in BT_{0}}e_{x}^{S_{2}}e_{y}^{S_{1}}V$
. Soit
![]() $y\in BT_{0}$
. Comme
$y\in BT_{0}$
. Comme
![]() $(e_{\unicode[STIX]{x1D70E}}^{S_{1}})_{\unicode[STIX]{x1D70E}\in BT}$
est 0-cohérent, on sait par 1.0.6 que
$(e_{\unicode[STIX]{x1D70E}}^{S_{1}})_{\unicode[STIX]{x1D70E}\in BT}$
est 0-cohérent, on sait par 1.0.6 que
![]() $e_{x}^{+}e_{y}^{S_{1}}=e_{x}^{S_{1}}e_{y}^{S_{1}}$
et on a que
$e_{x}^{+}e_{y}^{S_{1}}=e_{x}^{S_{1}}e_{y}^{S_{1}}$
et on a que
Or si
![]() $s$
et
$s$
et
![]() $s^{\prime }$
sont deux éléments distincts de
$s^{\prime }$
sont deux éléments distincts de
![]() $(\widehat{\overline{\mathsf{G}}}_{x})_{ss}$
d’ordre inversible dans
$(\widehat{\overline{\mathsf{G}}}_{x})_{ss}$
d’ordre inversible dans
![]() $\unicode[STIX]{x1D6EC}$
,
$\unicode[STIX]{x1D6EC}$
,
![]() $e_{x}^{s,\unicode[STIX]{x1D6EC}}e_{x}^{s^{\prime },\unicode[STIX]{x1D6EC}}=0$
donc
$e_{x}^{s,\unicode[STIX]{x1D6EC}}e_{x}^{s^{\prime },\unicode[STIX]{x1D6EC}}=0$
donc
![]() $e_{x}^{S_{2}}e_{x}^{S_{1}}=0$
et on a le résultat.◻
$e_{x}^{S_{2}}e_{x}^{S_{1}}=0$
et on a le résultat.◻
Proposition 2.3.5. Soient
![]() $S_{1},\ldots ,S_{n}$
des systèmes 0-cohérents tels que
$S_{1},\ldots ,S_{n}$
des systèmes 0-cohérents tels que
![]() $S_{i}\cap S_{j}=\emptyset$
si
$S_{i}\cap S_{j}=\emptyset$
si
![]() $i\neq j$
et
$i\neq j$
et
![]() $\bigcup _{i=1}^{n}S_{i}=((\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}^{\ast })_{ss,\unicode[STIX]{x1D6EC}})_{\unicode[STIX]{x1D70E}\in BT}$
. Alors la catégorie de niveau
$\bigcup _{i=1}^{n}S_{i}=((\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}^{\ast })_{ss,\unicode[STIX]{x1D6EC}})_{\unicode[STIX]{x1D70E}\in BT}$
. Alors la catégorie de niveau
![]() $0$
se décompose en
$0$
se décompose en
Démonstration.
D’après le lemme 2.3.4 nous savons déjà que les catégories
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{S_{i}}(G)$
sont deux à deux orthogonales. Prenons maintenant
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{S_{i}}(G)$
sont deux à deux orthogonales. Prenons maintenant
![]() $V$
un objet de
$V$
un objet de
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{0}(G)$
. Par définition,
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{0}(G)$
. Par définition,
![]() $V=\sum _{x\in BT_{0}}e_{x}^{+}V$
. Fixons un sommet
$V=\sum _{x\in BT_{0}}e_{x}^{+}V$
. Fixons un sommet
![]() $x\in BT_{0}$
. D’après 2.1.1, on a
$x\in BT_{0}$
. D’après 2.1.1, on a
![]() $e_{x}^{+}=\sum _{s\in (\widehat{\overline{\mathsf{G}}}_{x})_{ss}}e_{x}^{s,\overline{\mathbb{Q}}_{\ell }}$
. Ainsi
$e_{x}^{+}=\sum _{s\in (\widehat{\overline{\mathsf{G}}}_{x})_{ss}}e_{x}^{s,\overline{\mathbb{Q}}_{\ell }}$
. Ainsi
![]() $e_{x}^{+}=\sum _{i=1}^{n}e_{x}^{S_{i}}$
. On en déduit que
$e_{x}^{+}=\sum _{i=1}^{n}e_{x}^{S_{i}}$
. On en déduit que
Or
![]() $\sum _{x\in BT_{0}}e_{x}^{S_{i}}V$
est un objet de
$\sum _{x\in BT_{0}}e_{x}^{S_{i}}V$
est un objet de
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{S_{i}}(G)$
d’après [Reference Meyer and SolleveldMS10] proposition 3.2, d’où le résultat.◻
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{S_{i}}(G)$
d’après [Reference Meyer and SolleveldMS10] proposition 3.2, d’où le résultat.◻
3 Paramètres de l’inertie modérés
Dans toute cette section on suppose de plus que
![]() $\text{}\text{G}$
est
$\text{}\text{G}$
est
![]() $K$
-déployé. Cela signifie que
$K$
-déployé. Cela signifie que
![]() $\mathbf{G}$
est une forme intérieure d’un groupe non-ramifié. On souhaite obtenir une décomposition de
$\mathbf{G}$
est une forme intérieure d’un groupe non-ramifié. On souhaite obtenir une décomposition de
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{0}(G)$
indexée par les paramètres de l’inertie modérés
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{0}(G)$
indexée par les paramètres de l’inertie modérés
![]() $\unicode[STIX]{x1D719}$
. Pour cela on construit un procédé permettant d’associer à chaque
$\unicode[STIX]{x1D719}$
. Pour cela on construit un procédé permettant d’associer à chaque
![]() $\unicode[STIX]{x1D719}$
un système de classes de conjugaison 0-cohérent.
$\unicode[STIX]{x1D719}$
un système de classes de conjugaison 0-cohérent.
3.1 Classes de conjugaison dans
 $\text{G}^{\ast }$
$\text{G}^{\ast }$
Commençons par définir les paramètres de l’inertie modérés et montrons que l’on peut décrire ceux-ci en terme de classes de conjugaison semi-simples dans
![]() $\text{G}^{\ast }$
.
$\text{G}^{\ast }$
.
On notera
![]() ${\mathcal{G}}_{k}=\text{Gal}(\overline{k}/k)$
le groupe de Galois absolu de
${\mathcal{G}}_{k}=\text{Gal}(\overline{k}/k)$
le groupe de Galois absolu de
![]() $k$
,
$k$
,
![]() $W_{k}$
le groupe de Weil absolu de
$W_{k}$
le groupe de Weil absolu de
![]() $k$
et
$k$
et
![]() $I_{k}$
le sous-groupe d’inertie. Le groupe
$I_{k}$
le sous-groupe d’inertie. Le groupe
![]() $\unicode[STIX]{x1D6E4}:={\mathcal{G}}_{k}/I_{k}$
est topologiquement engendré par un élément
$\unicode[STIX]{x1D6E4}:={\mathcal{G}}_{k}/I_{k}$
est topologiquement engendré par un élément
![]() $\text{Frob}$
dont l’inverse induit l’automorphisme
$\text{Frob}$
dont l’inverse induit l’automorphisme
![]() $x\mapsto x^{q}$
sur
$x\mapsto x^{q}$
sur
![]() $\mathfrak{F}$
. Ainsi
$\mathfrak{F}$
. Ainsi
![]() $K=\overline{k}^{I_{k}}$
et
$K=\overline{k}^{I_{k}}$
et
![]() $k=K^{\text{Frob}}$
. L’action de
$k=K^{\text{Frob}}$
. L’action de
![]() ${\mathcal{G}}_{k}$
sur
${\mathcal{G}}_{k}$
sur
![]() $\mathbf{G}$
donne une action de
$\mathbf{G}$
donne une action de
![]() $\unicode[STIX]{x1D6E4}$
sur
$\unicode[STIX]{x1D6E4}$
sur
![]() $\mathbf{G}(K)$
, complètement déterminée par un automorphisme
$\mathbf{G}(K)$
, complètement déterminée par un automorphisme
![]() $F\in \text{Aut}(\mathbf{G}(K))$
donné par l’action de
$F\in \text{Aut}(\mathbf{G}(K))$
donné par l’action de
![]() $\text{Frob}$
. On a alors
$\text{Frob}$
. On a alors
![]() $G=\mathbf{G}(K)^{F}$
.
$G=\mathbf{G}(K)^{F}$
.
Soit
![]() $\mathbf{T}$
un
$\mathbf{T}$
un
![]() $k$
-tore maximal
$k$
-tore maximal
![]() $K$
-déployé maximalement déployé, alors
$K$
-déployé maximalement déployé, alors
![]() $I_{k}$
agit trivialement sur
$I_{k}$
agit trivialement sur
![]() $X_{\ast }(\mathbf{T})$
, le groupe des co-caractères de
$X_{\ast }(\mathbf{T})$
, le groupe des co-caractères de
![]() $\mathbf{T}$
, et l’action de
$\mathbf{T}$
, et l’action de
![]() ${\mathcal{G}}_{k}$
sur
${\mathcal{G}}_{k}$
sur
![]() $X_{\ast }(\mathbf{T})$
se factorise à travers
$X_{\ast }(\mathbf{T})$
se factorise à travers
![]() $\unicode[STIX]{x1D6E4}$
. Notons alors
$\unicode[STIX]{x1D6E4}$
. Notons alors
![]() $\unicode[STIX]{x1D717}$
l’automorphisme de
$\unicode[STIX]{x1D717}$
l’automorphisme de
![]() $X_{\ast }(\mathbf{T})$
induit par
$X_{\ast }(\mathbf{T})$
induit par
![]() $F$
. La dualité entre
$F$
. La dualité entre
![]() $X_{\ast }(\mathbf{T})$
et
$X_{\ast }(\mathbf{T})$
et
![]() $X^{\ast }(\mathbf{T})$
permet d’associer de façon naturelle à
$X^{\ast }(\mathbf{T})$
permet d’associer de façon naturelle à
![]() $\unicode[STIX]{x1D717}$
un automorphisme
$\unicode[STIX]{x1D717}$
un automorphisme
![]() $\widehat{\unicode[STIX]{x1D717}}\in \text{Aut}(X^{\ast }(\mathbf{T}))$
. Cet automorphisme s’étend alors alors en un automorphisme
$\widehat{\unicode[STIX]{x1D717}}\in \text{Aut}(X^{\ast }(\mathbf{T}))$
. Cet automorphisme s’étend alors alors en un automorphisme
![]() $\widehat{\unicode[STIX]{x1D717}}\otimes 1$
de
$\widehat{\unicode[STIX]{x1D717}}\otimes 1$
de
![]() $\widehat{\mathbf{T}}(\overline{\mathbb{Q}}_{\ell }):=X^{\ast }(\mathbf{T})\otimes \overline{\mathbb{Q}}_{\ell }^{\times }$
que nous noterons encore
$\widehat{\mathbf{T}}(\overline{\mathbb{Q}}_{\ell }):=X^{\ast }(\mathbf{T})\otimes \overline{\mathbb{Q}}_{\ell }^{\times }$
que nous noterons encore
![]() $\widehat{\unicode[STIX]{x1D717}}$
. Fixons un épinglage
$\widehat{\unicode[STIX]{x1D717}}$
. Fixons un épinglage
![]() $(\widehat{\mathbf{G}},\widehat{\mathbf{B}},\widehat{\mathbf{T}},\{x_{\unicode[STIX]{x1D6FC}}\}_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}})$
de
$(\widehat{\mathbf{G}},\widehat{\mathbf{B}},\widehat{\mathbf{T}},\{x_{\unicode[STIX]{x1D6FC}}\}_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}})$
de
![]() $\widehat{\mathbf{G}}$
où
$\widehat{\mathbf{G}}$
où
![]() $\widehat{\mathbf{B}}$
est un Borel contenant
$\widehat{\mathbf{B}}$
est un Borel contenant
![]() $\widehat{\mathbf{T}}$
. Celui-ci permet de prolonger
$\widehat{\mathbf{T}}$
. Celui-ci permet de prolonger
![]() $\widehat{\unicode[STIX]{x1D717}}$
en un automorphisme
$\widehat{\unicode[STIX]{x1D717}}$
en un automorphisme
![]() $\widehat{\unicode[STIX]{x1D717}}\in \text{Aut}(\widehat{\mathbf{G}})$
.
$\widehat{\unicode[STIX]{x1D717}}\in \text{Aut}(\widehat{\mathbf{G}})$
.
On note
![]() $P_{k}$
le groupe d’inertie sauvage, c’est à dire le pro-
$P_{k}$
le groupe d’inertie sauvage, c’est à dire le pro-
![]() $p$
sous-groupe maximal de
$p$
sous-groupe maximal de
![]() $I_{k}$
. Le groupe d’inertie modérée est le quotient
$I_{k}$
. Le groupe d’inertie modérée est le quotient
![]() $I_{k}/P_{k}$
et le groupe de Weil modéré est le quotient
$I_{k}/P_{k}$
et le groupe de Weil modéré est le quotient
![]() $W_{k}/P_{k}$
. On note
$W_{k}/P_{k}$
. On note
![]() $W_{k}^{\prime }=W_{k}\ltimes \overline{\mathbb{Q}}_{\ell }$
le groupe de Weil–Deligne.
$W_{k}^{\prime }=W_{k}\ltimes \overline{\mathbb{Q}}_{\ell }$
le groupe de Weil–Deligne.
Définition 3.1.1. Un morphisme
![]() $\unicode[STIX]{x1D711}:W_{k}^{\prime }\,\rightarrow \,^{L}\text{}\text{G}(\overline{\mathbb{Q}}_{\ell }):=\langle \widehat{\unicode[STIX]{x1D717}}\rangle \ltimes \widehat{\text{}\text{G}}(\overline{\mathbb{Q}}_{\ell })$
est dit admissible si
$\unicode[STIX]{x1D711}:W_{k}^{\prime }\,\rightarrow \,^{L}\text{}\text{G}(\overline{\mathbb{Q}}_{\ell }):=\langle \widehat{\unicode[STIX]{x1D717}}\rangle \ltimes \widehat{\text{}\text{G}}(\overline{\mathbb{Q}}_{\ell })$
est dit admissible si
(i) le diagramme suivant commute :

(ii)
 $\unicode[STIX]{x1D711}$
est continue,
$\unicode[STIX]{x1D711}$
est continue,
 $\unicode[STIX]{x1D711}(\overline{\mathbb{Q}}_{\ell })$
est unipotent dans
$\unicode[STIX]{x1D711}(\overline{\mathbb{Q}}_{\ell })$
est unipotent dans
 $\widehat{\text{}\text{G}}(\overline{\mathbb{Q}}_{\ell })$
, et
$\widehat{\text{}\text{G}}(\overline{\mathbb{Q}}_{\ell })$
, et
 $\unicode[STIX]{x1D711}$
envoie
$\unicode[STIX]{x1D711}$
envoie
 $W_{k}$
sur des éléments semi-simples de
$W_{k}$
sur des éléments semi-simples de
 $\,^{L}\text{}\text{G}(\overline{\mathbb{Q}}_{\ell })$
(un élément de
$\,^{L}\text{}\text{G}(\overline{\mathbb{Q}}_{\ell })$
(un élément de
 $\,^{L}\text{}\text{G}(\overline{\mathbb{Q}}_{\ell })$
est semi-simple si sa projection dans
$\,^{L}\text{}\text{G}(\overline{\mathbb{Q}}_{\ell })$
est semi-simple si sa projection dans
 $\langle \widehat{\unicode[STIX]{x1D717}}\rangle /n\langle \widehat{\unicode[STIX]{x1D717}}\rangle \ltimes \widehat{\text{}\text{G}}(\overline{\mathbb{Q}}_{\ell })$
est semi-simple, où
$\langle \widehat{\unicode[STIX]{x1D717}}\rangle /n\langle \widehat{\unicode[STIX]{x1D717}}\rangle \ltimes \widehat{\text{}\text{G}}(\overline{\mathbb{Q}}_{\ell })$
est semi-simple, où
 $n$
est l’ordre de
$n$
est l’ordre de
 $\widehat{\unicode[STIX]{x1D717}}$
).
$\widehat{\unicode[STIX]{x1D717}}$
).
On note alors
![]() $\unicode[STIX]{x1D6F7}(\text{}\text{G})$
l’ensemble des morphismes admissibles
$\unicode[STIX]{x1D6F7}(\text{}\text{G})$
l’ensemble des morphismes admissibles
![]() $\unicode[STIX]{x1D711}:W_{k}^{\prime }\rightarrow \,^{L}\text{}\text{G}(\overline{\mathbb{Q}}_{\ell })$
modulo les automorphismes intérieurs par des éléments de
$\unicode[STIX]{x1D711}:W_{k}^{\prime }\rightarrow \,^{L}\text{}\text{G}(\overline{\mathbb{Q}}_{\ell })$
modulo les automorphismes intérieurs par des éléments de
![]() $\widehat{\text{}\text{G}}(\overline{\mathbb{Q}}_{\ell })$
.
$\widehat{\text{}\text{G}}(\overline{\mathbb{Q}}_{\ell })$
.
Soit
![]() $I$
un sous-groupe de
$I$
un sous-groupe de
![]() $W_{k}$
. On note alors
$W_{k}$
. On note alors
![]() $\unicode[STIX]{x1D6F7}(I,\text{}\text{G})$
l’ensemble des classes de
$\unicode[STIX]{x1D6F7}(I,\text{}\text{G})$
l’ensemble des classes de
![]() $\widehat{\text{}\text{G}}$
-conjugaison des morphismes continus
$\widehat{\text{}\text{G}}$
-conjugaison des morphismes continus
![]() $I\rightarrow ^{L}\text{}\text{G}(\overline{\mathbb{Q}}_{\ell })$
(où
$I\rightarrow ^{L}\text{}\text{G}(\overline{\mathbb{Q}}_{\ell })$
(où
![]() $\overline{\mathbb{Q}}_{\ell }$
est muni de la topologie discrète) qui admettent une extension à un
$\overline{\mathbb{Q}}_{\ell }$
est muni de la topologie discrète) qui admettent une extension à un
![]() $L$
-morphisme de
$L$
-morphisme de
![]() $\unicode[STIX]{x1D6F7}(\text{}\text{G})$
. Dans ce qui suit nous allons nous intéresser principalement aux paramètres de Langlands inertiels
$\unicode[STIX]{x1D6F7}(\text{}\text{G})$
. Dans ce qui suit nous allons nous intéresser principalement aux paramètres de Langlands inertiels
![]() $\unicode[STIX]{x1D6F7}(I_{k},\text{}\text{G})$
.
$\unicode[STIX]{x1D6F7}(I_{k},\text{}\text{G})$
.
Définition 3.1.2. Si
![]() $I$
contient
$I$
contient
![]() $P_{k}$
, l’inertie sauvage, on dit qu’un paramètre
$P_{k}$
, l’inertie sauvage, on dit qu’un paramètre
![]() $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}(I,\text{}\text{G})$
est modéré s’il est trivial sur
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}(I,\text{}\text{G})$
est modéré s’il est trivial sur
![]() $P_{k}$
, et on note
$P_{k}$
, et on note
![]() $\unicode[STIX]{x1D6F7}_{m}(I,\text{}\text{G})$
pour l’ensemble des paramètres de
$\unicode[STIX]{x1D6F7}_{m}(I,\text{}\text{G})$
pour l’ensemble des paramètres de
![]() $I$
modérés.
$I$
modérés.
Intéressons nous à
![]() $\unicode[STIX]{x1D6F7}_{m}(I_{k},\text{}\text{G})$
. Comme
$\unicode[STIX]{x1D6F7}_{m}(I_{k},\text{}\text{G})$
. Comme
![]() $I_{k}/P_{k}$
est procyclique de pro-ordre premier à
$I_{k}/P_{k}$
est procyclique de pro-ordre premier à
![]() $p$
un morphisme continu
$p$
un morphisme continu
![]() $I_{k}/P_{k}\rightarrow \widehat{\text{}\text{G}}(\overline{\mathbb{Q}}_{\ell })$
est donné par le choix d’un élément
$I_{k}/P_{k}\rightarrow \widehat{\text{}\text{G}}(\overline{\mathbb{Q}}_{\ell })$
est donné par le choix d’un élément
![]() $s$
d’ordre fini premier à
$s$
d’ordre fini premier à
![]() $p$
. Nous avons la décomposition
$p$
. Nous avons la décomposition
![]() $W_{k}/P_{k}=\langle \text{Frob}\rangle \ltimes (I_{k}/P_{k})$
, où pour
$W_{k}/P_{k}=\langle \text{Frob}\rangle \ltimes (I_{k}/P_{k})$
, où pour
![]() $x\in (I_{k}/P_{k})$
,
$x\in (I_{k}/P_{k})$
,
![]() $\text{Frob }^{-1}x\text{ Frob}=x^{q}$
. Un paramètre de Langlands doit envoyer
$\text{Frob }^{-1}x\text{ Frob}=x^{q}$
. Un paramètre de Langlands doit envoyer
![]() $\text{Frob}$
sur
$\text{Frob}$
sur
![]() $\widehat{\unicode[STIX]{x1D717}}f$
où
$\widehat{\unicode[STIX]{x1D717}}f$
où
![]() $f$
est un élément semi-simple de
$f$
est un élément semi-simple de
![]() $\widehat{\text{}\text{G}}(\overline{\mathbb{Q}}_{\ell })$
. Un tel morphisme s’étend donc à
$\widehat{\text{}\text{G}}(\overline{\mathbb{Q}}_{\ell })$
. Un tel morphisme s’étend donc à
![]() $W_{k}/P_{k}$
si
$W_{k}/P_{k}$
si
![]() $\text{Ad}(f)\circ \widehat{\unicode[STIX]{x1D717}}\circ s^{q}=s$
, où
$\text{Ad}(f)\circ \widehat{\unicode[STIX]{x1D717}}\circ s^{q}=s$
, où
![]() $\text{Ad}(f)$
désigne la conjugaison par
$\text{Ad}(f)$
désigne la conjugaison par
![]() $f$
. Ainsi à un paramètre inertiel modéré
$f$
. Ainsi à un paramètre inertiel modéré
![]() $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\text{}\text{G})$
on peut associer une classe de conjugaison semi-simple dans
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\text{}\text{G})$
on peut associer une classe de conjugaison semi-simple dans
![]() $\widehat{\text{}\text{G}}(\overline{\mathbb{Q}}_{\ell })$
stable sous
$\widehat{\text{}\text{G}}(\overline{\mathbb{Q}}_{\ell })$
stable sous
![]() $\widehat{\unicode[STIX]{x1D717}}\circ \unicode[STIX]{x1D713}$
où
$\widehat{\unicode[STIX]{x1D717}}\circ \unicode[STIX]{x1D713}$
où
![]() $\unicode[STIX]{x1D713}$
est l’élévation à la puissance
$\unicode[STIX]{x1D713}$
est l’élévation à la puissance
![]() $q$
-ième. On a donc une application
$q$
-ième. On a donc une application
![]() $\unicode[STIX]{x1D6F7}_{m}(I_{k},\text{}\text{G})\rightarrow (\widehat{\text{}\text{G}}(\overline{\mathbb{Q}}_{\ell })_{ss})^{\widehat{\unicode[STIX]{x1D717}}\circ \unicode[STIX]{x1D713}}$
. Or nous savons que
$\unicode[STIX]{x1D6F7}_{m}(I_{k},\text{}\text{G})\rightarrow (\widehat{\text{}\text{G}}(\overline{\mathbb{Q}}_{\ell })_{ss})^{\widehat{\unicode[STIX]{x1D717}}\circ \unicode[STIX]{x1D713}}$
. Or nous savons que
![]() $(\widehat{\text{}\text{T}}(\overline{\mathbb{Q}}_{\ell })/W_{0})\overset{{\sim}}{\longrightarrow }\widehat{\text{}\text{G}}(\overline{\mathbb{Q}}_{\ell })_{ss}$
, où
$(\widehat{\text{}\text{T}}(\overline{\mathbb{Q}}_{\ell })/W_{0})\overset{{\sim}}{\longrightarrow }\widehat{\text{}\text{G}}(\overline{\mathbb{Q}}_{\ell })_{ss}$
, où
![]() $W_{0}:=N(\mathbf{T})/\mathbf{T}$
désigne le groupe de Weyl de
$W_{0}:=N(\mathbf{T})/\mathbf{T}$
désigne le groupe de Weyl de
![]() $\mathbf{T}$
, ce qui nous permet de définir l’application
$\mathbf{T}$
, ce qui nous permet de définir l’application
![]() $\unicode[STIX]{x1D6F7}_{m}(I_{k},\text{}\text{G})\rightarrow (\widehat{\text{}\text{T}}(\overline{\mathbb{Q}}_{\ell })/W_{0})^{\widehat{\unicode[STIX]{x1D717}}\circ \unicode[STIX]{x1D713}}$
. Réciproquement, prenons un élément de
$\unicode[STIX]{x1D6F7}_{m}(I_{k},\text{}\text{G})\rightarrow (\widehat{\text{}\text{T}}(\overline{\mathbb{Q}}_{\ell })/W_{0})^{\widehat{\unicode[STIX]{x1D717}}\circ \unicode[STIX]{x1D713}}$
. Réciproquement, prenons un élément de
![]() $(\widehat{\text{}\text{T}}(\overline{\mathbb{Q}}_{\ell })/W_{0})^{\widehat{\unicode[STIX]{x1D717}}\circ \unicode[STIX]{x1D713}}$
. Ceci nous fournit un élément semi-simple
$(\widehat{\text{}\text{T}}(\overline{\mathbb{Q}}_{\ell })/W_{0})^{\widehat{\unicode[STIX]{x1D717}}\circ \unicode[STIX]{x1D713}}$
. Ceci nous fournit un élément semi-simple
![]() $s$
tel que
$s$
tel que
![]() $\widehat{\unicode[STIX]{x1D717}}\circ \unicode[STIX]{x1D713}(s)=w\cdot s$
, où
$\widehat{\unicode[STIX]{x1D717}}\circ \unicode[STIX]{x1D713}(s)=w\cdot s$
, où
![]() $w\in W_{0}$
. Soit
$w\in W_{0}$
. Soit
![]() $f$
un relèvement de
$f$
un relèvement de
![]() $w$
, qui est alors un élément semi-simple, on a alors
$w$
, qui est alors un élément semi-simple, on a alors
![]() $\widehat{\unicode[STIX]{x1D717}}\circ \unicode[STIX]{x1D713}(s)=\text{Ad}(f)(s)$
, donc on obtient un
$\widehat{\unicode[STIX]{x1D717}}\circ \unicode[STIX]{x1D713}(s)=\text{Ad}(f)(s)$
, donc on obtient un
![]() $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\text{}\text{G})$
. Ceci nous montre que l’on a une correspondance
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\text{}\text{G})$
. Ceci nous montre que l’on a une correspondance
Soit
![]() $s\in (\widehat{\text{}\text{T}}(\overline{\mathbb{Q}}_{\ell })/W_{0})^{\widehat{\unicode[STIX]{x1D717}}\circ \unicode[STIX]{x1D713}}$
, on peut représenter
$s\in (\widehat{\text{}\text{T}}(\overline{\mathbb{Q}}_{\ell })/W_{0})^{\widehat{\unicode[STIX]{x1D717}}\circ \unicode[STIX]{x1D713}}$
, on peut représenter
![]() $s$
par
$s$
par
![]() $s=(a_{1},\ldots ,a_{n})$
, avec
$s=(a_{1},\ldots ,a_{n})$
, avec
![]() $a_{i}\in \overline{\mathbb{Q}}_{\ell }^{\times }$
(
$a_{i}\in \overline{\mathbb{Q}}_{\ell }^{\times }$
(
![]() $\widehat{\text{}\text{T}}\simeq \mathbb{G}_{m}^{n}$
). Soit
$\widehat{\text{}\text{T}}\simeq \mathbb{G}_{m}^{n}$
). Soit
![]() $k\in \mathbb{N}$
, par définition on a
$k\in \mathbb{N}$
, par définition on a
![]() $\widehat{\unicode[STIX]{x1D717}}^{k}(s^{p^{k}})=s$
dans
$\widehat{\unicode[STIX]{x1D717}}^{k}(s^{p^{k}})=s$
dans
![]() $(\widehat{\text{}\text{T}}(\overline{\mathbb{Q}}_{\ell })/W_{0})^{\widehat{\unicode[STIX]{x1D717}}\circ \unicode[STIX]{x1D713}}$
. Comme
$(\widehat{\text{}\text{T}}(\overline{\mathbb{Q}}_{\ell })/W_{0})^{\widehat{\unicode[STIX]{x1D717}}\circ \unicode[STIX]{x1D713}}$
. Comme
![]() $\widehat{\unicode[STIX]{x1D717}}$
est d’ordre fini, disons
$\widehat{\unicode[STIX]{x1D717}}$
est d’ordre fini, disons
![]() $N$
,
$N$
,
![]() $s^{p^{N}}=s$
dans
$s^{p^{N}}=s$
dans
![]() $(\widehat{\text{}\text{T}}(\overline{\mathbb{Q}}_{\ell })/W_{0})^{\widehat{\unicode[STIX]{x1D717}}\circ \unicode[STIX]{x1D713}}$
. Donc il existe
$(\widehat{\text{}\text{T}}(\overline{\mathbb{Q}}_{\ell })/W_{0})^{\widehat{\unicode[STIX]{x1D717}}\circ \unicode[STIX]{x1D713}}$
. Donc il existe
![]() $w\in W_{0}$
tel que
$w\in W_{0}$
tel que
![]() $(a_{1}^{p^{N}},\ldots ,a_{n}^{p^{N}})=w\cdot (a_{1},\ldots ,a_{n})$
. Or
$(a_{1}^{p^{N}},\ldots ,a_{n}^{p^{N}})=w\cdot (a_{1},\ldots ,a_{n})$
. Or
![]() $W_{0}$
est de cardinal fini, donc il existe
$W_{0}$
est de cardinal fini, donc il existe
![]() $k\in \mathbb{N}^{\ast }$
, tel que
$k\in \mathbb{N}^{\ast }$
, tel que
![]() $(a_{1}^{p^{kN}},\ldots ,a_{n}^{p^{kN}})=(a_{1},\ldots ,a_{n})$
. Ainsi
$(a_{1}^{p^{kN}},\ldots ,a_{n}^{p^{kN}})=(a_{1},\ldots ,a_{n})$
. Ainsi
![]() $\forall i\in \{1,\ldots ,n\}$
,
$\forall i\in \{1,\ldots ,n\}$
,
![]() $a_{i}^{p^{kN}-1}=1$
. Les
$a_{i}^{p^{kN}-1}=1$
. Les
![]() $a_{i}$
sont donc des racines
$a_{i}$
sont donc des racines
![]() $p^{\prime }$
-ièmes de l’unité (racines de l’unité d’ordre premier à
$p^{\prime }$
-ièmes de l’unité (racines de l’unité d’ordre premier à
![]() $p$
).
$p$
).
Notre groupe
![]() $\mathbf{G}$
étant
$\mathbf{G}$
étant
![]() $K$
-déployé, il possède une forme intérieure non-ramifiée. Cette dernière permet de définir sur
$K$
-déployé, il possède une forme intérieure non-ramifiée. Cette dernière permet de définir sur
![]() $\text{}\text{G}^{\ast }$
, le groupe dual de
$\text{}\text{G}^{\ast }$
, le groupe dual de
![]() $\mathbf{G}$
sur
$\mathbf{G}$
sur
![]() $\mathfrak{F}$
, une
$\mathfrak{F}$
, une
![]() $\mathfrak{f}$
-structure (et donc un Frobenius
$\mathfrak{f}$
-structure (et donc un Frobenius
![]() $F$
) en choissant un sommet hyperspécial dans l’immeuble. Le choix d’un système compatible de racines de l’unité (que l’on a fixé au début dans les notations) permet d’identifier
$F$
) en choissant un sommet hyperspécial dans l’immeuble. Le choix d’un système compatible de racines de l’unité (que l’on a fixé au début dans les notations) permet d’identifier
(Nous rappelons que
![]() $\widehat{\mathbf{T}}$
désigne le dual de
$\widehat{\mathbf{T}}$
désigne le dual de
![]() $\mathbf{T}$
sur
$\mathbf{T}$
sur
![]() $\overline{\mathbb{Q}}_{\ell }$
et
$\overline{\mathbb{Q}}_{\ell }$
et
![]() $\text{T}^{\ast }$
celui sur
$\text{T}^{\ast }$
celui sur
![]() $\mathfrak{F}$
. Ainsi
$\mathfrak{F}$
. Ainsi
![]() $\widehat{\mathbf{T}}(\overline{\mathbb{Q}}_{\ell })=X^{\ast }(\mathbf{T})\otimes \overline{\mathbb{Q}}_{\ell }^{\times }$
et
$\widehat{\mathbf{T}}(\overline{\mathbb{Q}}_{\ell })=X^{\ast }(\mathbf{T})\otimes \overline{\mathbb{Q}}_{\ell }^{\times }$
et
![]() $\text{T}^{\ast }(\mathfrak{F})=X^{\ast }(\mathbf{T})\otimes \mathfrak{F}^{\times }$
.)
$\text{T}^{\ast }(\mathfrak{F})=X^{\ast }(\mathbf{T})\otimes \mathfrak{F}^{\times }$
.)
Or l’action de
![]() $\widehat{\unicode[STIX]{x1D717}}\circ \unicode[STIX]{x1D713}$
sur
$\widehat{\unicode[STIX]{x1D717}}\circ \unicode[STIX]{x1D713}$
sur
![]() $\text{T}^{\ast }(\mathfrak{F})$
correspond à l’action du Frobenius
$\text{T}^{\ast }(\mathfrak{F})$
correspond à l’action du Frobenius
![]() $F$
(voir annexe B, ici
$F$
(voir annexe B, ici
![]() $\widehat{\unicode[STIX]{x1D717}}=\unicode[STIX]{x1D70F}_{X}^{-1}$
). Ainsi
$\widehat{\unicode[STIX]{x1D717}}=\unicode[STIX]{x1D70F}_{X}^{-1}$
). Ainsi
En résumé nous avons montré la proposition suivante.
Proposition 3.1.3. La discussion précédente nous fournit une identification :
Dans le but d’étudier les représentations à coefficients dans
![]() $\overline{\mathbb{Z}}_{\ell }$
nous avons besoin de restreindre
$\overline{\mathbb{Z}}_{\ell }$
nous avons besoin de restreindre
![]() $\unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{G})$
. Introduisons
$\unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{G})$
. Introduisons
![]() $I_{k}^{(\ell )}:=\text{ker}\{I_{k}\rightarrow \mathbb{Z}_{\ell }(1)\}$
qui est le sous-groupe fermé maximal de
$I_{k}^{(\ell )}:=\text{ker}\{I_{k}\rightarrow \mathbb{Z}_{\ell }(1)\}$
qui est le sous-groupe fermé maximal de
![]() $I_{k}$
de pro-ordre premier à
$I_{k}$
de pro-ordre premier à
![]() $\ell$
. Sous l’identification de la proposition 3.1.3,
$\ell$
. Sous l’identification de la proposition 3.1.3,
![]() $\unicode[STIX]{x1D6F7}_{m}(I_{k}^{(\ell )},\mathbf{G})$
correspond aux
$\unicode[STIX]{x1D6F7}_{m}(I_{k}^{(\ell )},\mathbf{G})$
correspond aux
![]() $s\in (\widehat{\text{G}}(\mathfrak{F})_{ss})^{F}$
d’ordre premier à
$s\in (\widehat{\text{G}}(\mathfrak{F})_{ss})^{F}$
d’ordre premier à
![]() $\ell$
.
$\ell$
.
Pour unifier les notations, notons
![]() $I_{k}^{\unicode[STIX]{x1D6EC}}$
qui vaut
$I_{k}^{\unicode[STIX]{x1D6EC}}$
qui vaut
![]() $I_{k}$
si
$I_{k}$
si
![]() $\unicode[STIX]{x1D6EC}=\overline{\mathbb{Q}}_{\ell }$
et
$\unicode[STIX]{x1D6EC}=\overline{\mathbb{Q}}_{\ell }$
et
![]() $I_{k}^{(\ell )}$
si
$I_{k}^{(\ell )}$
si
![]() $\unicode[STIX]{x1D6EC}=\overline{\mathbb{Z}}_{\ell }$
. On obtient alors la proposition suivante.
$\unicode[STIX]{x1D6EC}=\overline{\mathbb{Z}}_{\ell }$
. On obtient alors la proposition suivante.
Proposition 3.1.4. L’identification de la proposition 3.1.3 se restreint en :
3.2 Classes de conjugaison dans les quotients réductifs des groupes parahoriques
Nous venons de voir que l’on pouvait identifier les paramètres de l’inertie modérés avec des classes de conjugaison semi-simples dans
![]() $\text{G}^{\ast }$
. Pour obtenir des systèmes 0-cohérents nous avons besoin de classes de conjugaison dans les quotients réductifs des groupes parahoriques. Nous construisons alors dans cette section un système d’applications compatibles
$\text{G}^{\ast }$
. Pour obtenir des systèmes 0-cohérents nous avons besoin de classes de conjugaison dans les quotients réductifs des groupes parahoriques. Nous construisons alors dans cette section un système d’applications compatibles
![]() $((\overline{\text{G}}_{\unicode[STIX]{x1D70E}}^{\ast })_{ss})^{F}\rightarrow (\text{G}^{\ast }(\mathfrak{F})_{ss})^{F}$
, pour
$((\overline{\text{G}}_{\unicode[STIX]{x1D70E}}^{\ast })_{ss})^{F}\rightarrow (\text{G}^{\ast }(\mathfrak{F})_{ss})^{F}$
, pour
![]() $\unicode[STIX]{x1D70E}\in BT$
.
$\unicode[STIX]{x1D70E}\in BT$
.
Soit
![]() $\mathbf{S}$
un tore déployé maximal, tel que
$\mathbf{S}$
un tore déployé maximal, tel que
![]() $\unicode[STIX]{x1D70E}\in {\mathcal{A}}(\mathbf{S},k)$
, où
$\unicode[STIX]{x1D70E}\in {\mathcal{A}}(\mathbf{S},k)$
, où
![]() ${\mathcal{A}}(\mathbf{S},k)$
est l’appartement associé à
${\mathcal{A}}(\mathbf{S},k)$
est l’appartement associé à
![]() $\text{}\text{S}$
dans
$\text{}\text{S}$
dans
![]() $BT$
. Notons
$BT$
. Notons
![]() $\mathbf{T}$
un
$\mathbf{T}$
un
![]() $k$
-tore maximal
$k$
-tore maximal
![]() $K$
-déployé contenant
$K$
-déployé contenant
![]() $\mathbf{S}$
(qui existe par [Reference Bruhat and TitsBT84, 5.1.12]). De plus par [Reference TitsTit79, 2.6.1]
$\mathbf{S}$
(qui existe par [Reference Bruhat and TitsBT84, 5.1.12]). De plus par [Reference TitsTit79, 2.6.1]
![]() ${\mathcal{A}}(\mathbf{S},k)=BT\cap {\mathcal{A}}(\mathbf{T},K)$
. Notons
${\mathcal{A}}(\mathbf{S},k)=BT\cap {\mathcal{A}}(\mathbf{T},K)$
. Notons
![]() $\unicode[STIX]{x1D70E}_{1}$
l’image canonique de
$\unicode[STIX]{x1D70E}_{1}$
l’image canonique de
![]() $\unicode[STIX]{x1D70E}$
dans
$\unicode[STIX]{x1D70E}$
dans
![]() $BT(K)$
.
$BT(K)$
.
Notons
![]() $W$
le groupe de Weyl affine de
$W$
le groupe de Weyl affine de
![]() $\mathbf{G}(K)$
,
$\mathbf{G}(K)$
,
![]() $W_{0}=N(\mathbf{T})/\mathbf{T}$
, le groupe de Weyl de
$W_{0}=N(\mathbf{T})/\mathbf{T}$
, le groupe de Weyl de
![]() $\mathbf{G}(K)$
et
$\mathbf{G}(K)$
et
![]() $W_{\unicode[STIX]{x1D70E}_{1}}$
le groupe engendré par les réflexions des hyperplans contenant
$W_{\unicode[STIX]{x1D70E}_{1}}$
le groupe engendré par les réflexions des hyperplans contenant
![]() $\unicode[STIX]{x1D70E}_{1}$
dans
$\unicode[STIX]{x1D70E}_{1}$
dans
![]() $BT(K)$
. Nous avons
$BT(K)$
. Nous avons
![]() $W=W_{0}\ltimes T/^{\circ }T$
, où
$W=W_{0}\ltimes T/^{\circ }T$
, où
![]() $^{\circ }T$
désigne le sous-groupe borné maximal de
$^{\circ }T$
désigne le sous-groupe borné maximal de
![]() $T$
. De plus
$T$
. De plus
![]() $W_{\unicode[STIX]{x1D70E}_{1}}$
est un sous-groupe de
$W_{\unicode[STIX]{x1D70E}_{1}}$
est un sous-groupe de
![]() $W$
, on a donc une application
$W$
, on a donc une application
![]() $W_{\unicode[STIX]{x1D70E}_{1}}\rightarrow W\rightarrow W_{0}$
. Le noyau du morphisme
$W_{\unicode[STIX]{x1D70E}_{1}}\rightarrow W\rightarrow W_{0}$
. Le noyau du morphisme
![]() $W=W_{0}\ltimes T/^{\circ }T\rightarrow W_{0}$
est un groupe sans torsion. Or
$W=W_{0}\ltimes T/^{\circ }T\rightarrow W_{0}$
est un groupe sans torsion. Or
![]() $W_{\unicode[STIX]{x1D70E}_{1}}$
est un groupe fini donc l’application
$W_{\unicode[STIX]{x1D70E}_{1}}$
est un groupe fini donc l’application
![]() $W_{\unicode[STIX]{x1D70E}_{1}}\rightarrow W_{0}$
est injective et nous permet de voir
$W_{\unicode[STIX]{x1D70E}_{1}}\rightarrow W_{0}$
est injective et nous permet de voir
![]() $W_{\unicode[STIX]{x1D70E}_{1}}$
comme un sous-groupe de
$W_{\unicode[STIX]{x1D70E}_{1}}$
comme un sous-groupe de
![]() $W_{0}$
.
$W_{0}$
.
Par [Reference TitsTit79, 3.4.3],
![]() ${\mathcal{G}}_{\unicode[STIX]{x1D70E}_{1}}$
est obtenu à partir de
${\mathcal{G}}_{\unicode[STIX]{x1D70E}_{1}}$
est obtenu à partir de
![]() ${\mathcal{G}}_{\unicode[STIX]{x1D70E}}$
par changement de base. En particulier
${\mathcal{G}}_{\unicode[STIX]{x1D70E}}$
par changement de base. En particulier
![]() $\overline{\text{}\text{G}}_{\unicode[STIX]{x1D70E}_{1}}=\overline{\text{}\text{G}}_{\unicode[STIX]{x1D70E}}\times _{\mathfrak{f}}\mathfrak{F}$
.
$\overline{\text{}\text{G}}_{\unicode[STIX]{x1D70E}_{1}}=\overline{\text{}\text{G}}_{\unicode[STIX]{x1D70E}}\times _{\mathfrak{f}}\mathfrak{F}$
.
Le tore
![]() $\mathbf{S}$
(resp.
$\mathbf{S}$
(resp.
![]() $\mathbf{T}$
) se prolonge en un tore de
$\mathbf{T}$
) se prolonge en un tore de
![]() ${\mathcal{G}}_{\unicode[STIX]{x1D70E}}$
,
${\mathcal{G}}_{\unicode[STIX]{x1D70E}}$
,
![]() ${\mathcal{S}}_{\unicode[STIX]{x1D70E}}$
(resp.
${\mathcal{S}}_{\unicode[STIX]{x1D70E}}$
(resp.
![]() ${\mathcal{T}}_{\unicode[STIX]{x1D70E}}$
), défini sur
${\mathcal{T}}_{\unicode[STIX]{x1D70E}}$
), défini sur
![]() $\mathfrak{o}_{k}$
de fibre générique
$\mathfrak{o}_{k}$
de fibre générique
![]() ${\mathcal{S}}_{\unicode[STIX]{x1D70E},k}=S$
(resp.
${\mathcal{S}}_{\unicode[STIX]{x1D70E},k}=S$
(resp.
![]() ${\mathcal{T}}_{\unicode[STIX]{x1D70E},k}=T$
). Notons
${\mathcal{T}}_{\unicode[STIX]{x1D70E},k}=T$
). Notons
![]() $\mathsf{S}_{\unicode[STIX]{x1D70E}}$
(resp.
$\mathsf{S}_{\unicode[STIX]{x1D70E}}$
(resp.
![]() $\mathsf{T}_{\unicode[STIX]{x1D70E}}$
) la fibre spéciale de
$\mathsf{T}_{\unicode[STIX]{x1D70E}}$
) la fibre spéciale de
![]() ${\mathcal{S}}_{\unicode[STIX]{x1D70E}}$
(resp.
${\mathcal{S}}_{\unicode[STIX]{x1D70E}}$
(resp.
![]() ${\mathcal{T}}_{\unicode[STIX]{x1D70E}}$
). Alors
${\mathcal{T}}_{\unicode[STIX]{x1D70E}}$
). Alors
![]() $\mathsf{T}_{\unicode[STIX]{x1D70E}}$
est un tore maximal de
$\mathsf{T}_{\unicode[STIX]{x1D70E}}$
est un tore maximal de
![]() $\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}$
défini sur
$\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}$
défini sur
![]() $\mathfrak{f}$
. De plus on a que
$\mathfrak{f}$
. De plus on a que
![]() $\text{}\text{T}_{\unicode[STIX]{x1D70E}_{1}}=\text{}\text{T}_{\unicode[STIX]{x1D70E}}\times _{\mathfrak{f}}\mathfrak{F}$
.
$\text{}\text{T}_{\unicode[STIX]{x1D70E}_{1}}=\text{}\text{T}_{\unicode[STIX]{x1D70E}}\times _{\mathfrak{f}}\mathfrak{F}$
.
Le groupe des caractères de
![]() $\mathsf{T}_{\unicode[STIX]{x1D70E}_{1}}$
,
$\mathsf{T}_{\unicode[STIX]{x1D70E}_{1}}$
,
![]() $X^{\ast }(\text{}\text{T}_{\unicode[STIX]{x1D70E}_{1}})$
, est canoniquement isomorphe à
$X^{\ast }(\text{}\text{T}_{\unicode[STIX]{x1D70E}_{1}})$
, est canoniquement isomorphe à
![]() $X=X^{\ast }(\mathbf{T})$
, on les identifiera désormais. De plus, par [Reference TitsTit79, 3.5.1], le groupe de Weyl de
$X=X^{\ast }(\mathbf{T})$
, on les identifiera désormais. De plus, par [Reference TitsTit79, 3.5.1], le groupe de Weyl de
![]() $\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}_{1}}$
associé à
$\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}_{1}}$
associé à
![]() $\mathsf{T}_{\unicode[STIX]{x1D70E}_{1}}$
est
$\mathsf{T}_{\unicode[STIX]{x1D70E}_{1}}$
est
![]() $W_{\unicode[STIX]{x1D70E}_{1}}$
. L’action de
$W_{\unicode[STIX]{x1D70E}_{1}}$
. L’action de
![]() $W_{\unicode[STIX]{x1D70E}_{1}}$
sur
$W_{\unicode[STIX]{x1D70E}_{1}}$
sur
![]() $X^{\ast }(\mathsf{T}_{\unicode[STIX]{x1D70E}_{1}})$
coïncide avec l’action de l’image de
$X^{\ast }(\mathsf{T}_{\unicode[STIX]{x1D70E}_{1}})$
coïncide avec l’action de l’image de
![]() $W_{\unicode[STIX]{x1D70E}_{1}}\rightarrow W_{0}$
sur
$W_{\unicode[STIX]{x1D70E}_{1}}\rightarrow W_{0}$
sur
![]() $X^{\ast }(\mathbf{T})$
.
$X^{\ast }(\mathbf{T})$
.
On obtient alors :
Le morphisme
![]() $W_{\unicode[STIX]{x1D70E}_{1}}\rightarrow W_{0}$
induit
$W_{\unicode[STIX]{x1D70E}_{1}}\rightarrow W_{0}$
induit
Et de même que précédemment, on a un isomorphisme
On vient donc de construire une application
Lemme 3.2.1. L’application
![]() $\tilde{\unicode[STIX]{x1D713}}_{\unicode[STIX]{x1D70E}}$
est indépendante du choix du tore
$\tilde{\unicode[STIX]{x1D713}}_{\unicode[STIX]{x1D70E}}$
est indépendante du choix du tore
![]() $\text{}\text{S}$
.
$\text{}\text{S}$
.
Démonstration.
Soit
![]() $\text{}\text{S}^{\prime }$
un autre tore déployé maximal tel que
$\text{}\text{S}^{\prime }$
un autre tore déployé maximal tel que
![]() $\unicode[STIX]{x1D70E}\in {\mathcal{A}}(\text{}\text{S}^{\prime })$
. Nous utiliserons la notation ’ pour les éléments se rapportant à
$\unicode[STIX]{x1D70E}\in {\mathcal{A}}(\text{}\text{S}^{\prime })$
. Nous utiliserons la notation ’ pour les éléments se rapportant à
![]() $\text{}\text{S}^{\prime }$
.
$\text{}\text{S}^{\prime }$
.
D’après [Reference Bruhat and TitsBT84, 4.6.28],
![]() $G_{\unicode[STIX]{x1D70E}_{1}}^{\circ }$
permute transitivement les appartements de
$G_{\unicode[STIX]{x1D70E}_{1}}^{\circ }$
permute transitivement les appartements de
![]() $BT(K)$
contenant
$BT(K)$
contenant
![]() $\unicode[STIX]{x1D70E}_{1}$
. Ainsi,
$\unicode[STIX]{x1D70E}_{1}$
. Ainsi,
![]() $\text{}\text{T}$
et
$\text{}\text{T}$
et
![]() $\text{}\text{T}^{\prime }$
sont conjugués par un élément
$\text{}\text{T}^{\prime }$
sont conjugués par un élément
![]() $g\in G_{\unicode[STIX]{x1D70E}_{1}}^{\circ }$
, c’est à dire
$g\in G_{\unicode[STIX]{x1D70E}_{1}}^{\circ }$
, c’est à dire
![]() $\text{}\text{T}^{\prime }=g\text{}\text{T}g^{-1}$
. Comme
$\text{}\text{T}^{\prime }=g\text{}\text{T}g^{-1}$
. Comme
![]() $\mathbf{T}$
et
$\mathbf{T}$
et
![]() $\mathbf{T}^{\prime }$
sont deux
$\mathbf{T}^{\prime }$
sont deux
![]() $k$
-tores,
$k$
-tores,
![]() $g$
vérifie que
$g$
vérifie que
![]() $g^{-1}F(g)\in N(\mathbf{G},\mathbf{T})$
, le normalisateur de
$g^{-1}F(g)\in N(\mathbf{G},\mathbf{T})$
, le normalisateur de
![]() $\mathbf{T}$
dans
$\mathbf{T}$
dans
![]() $\mathbf{G}$
. La conjugaison par
$\mathbf{G}$
. La conjugaison par
![]() $g$
,
$g$
,
![]() $\text{Ad}(g)$
, induit alors un isomorphisme
$\text{Ad}(g)$
, induit alors un isomorphisme
![]() $X\longrightarrow X^{\prime }:=X^{\ast }(\mathbf{T}^{\prime })$
. De plus comme elle envoie
$X\longrightarrow X^{\prime }:=X^{\ast }(\mathbf{T}^{\prime })$
. De plus comme elle envoie
![]() ${\mathcal{A}}(\text{}\text{T},K)$
sur
${\mathcal{A}}(\text{}\text{T},K)$
sur
![]() ${\mathcal{A}}(\text{}\text{T}^{\prime },K)$
et que les morphismes
${\mathcal{A}}(\text{}\text{T}^{\prime },K)$
et que les morphismes
![]() $W_{\unicode[STIX]{x1D70E}_{1}}\longrightarrow W_{0}$
et
$W_{\unicode[STIX]{x1D70E}_{1}}\longrightarrow W_{0}$
et
![]() $W_{\unicode[STIX]{x1D70E}_{1}}^{\prime }\longrightarrow W_{0}^{\prime }$
sont définis à partir des racines, on a le diagramme commutatif
$W_{\unicode[STIX]{x1D70E}_{1}}^{\prime }\longrightarrow W_{0}^{\prime }$
sont définis à partir des racines, on a le diagramme commutatif

et donc le diagramme commutatif

L’application
![]() $G_{\unicode[STIX]{x1D70E}_{1}}^{\circ }\rightarrow \overline{\text{G}}_{\unicode[STIX]{x1D70E}}$
envoie
$G_{\unicode[STIX]{x1D70E}_{1}}^{\circ }\rightarrow \overline{\text{G}}_{\unicode[STIX]{x1D70E}}$
envoie
![]() $g$
sur un élément que l’on note
$g$
sur un élément que l’on note
![]() $\overline{g}$
. De plus nous savons que l’action par conjugaison par
$\overline{g}$
. De plus nous savons que l’action par conjugaison par
![]() $\overline{g}$
qui envoie
$\overline{g}$
qui envoie
![]() $X_{\ast }(\text{}\text{T}_{\unicode[STIX]{x1D70E}})$
sur
$X_{\ast }(\text{}\text{T}_{\unicode[STIX]{x1D70E}})$
sur
![]() $X_{\ast }(\text{}\text{T}_{\unicode[STIX]{x1D70E}}^{\prime })$
coïncide avec l’action par conjugaison par
$X_{\ast }(\text{}\text{T}_{\unicode[STIX]{x1D70E}}^{\prime })$
coïncide avec l’action par conjugaison par
![]() $g$
qui envoie
$g$
qui envoie
![]() $X$
sur
$X$
sur
![]() $X^{\prime }$
.
$X^{\prime }$
.
La conjugaison par
![]() $\overline{g}\in \overline{\text{G}}_{\unicode[STIX]{x1D70E}}$
d’un coté et par
$\overline{g}\in \overline{\text{G}}_{\unicode[STIX]{x1D70E}}$
d’un coté et par
![]() $g\in \mathbf{G}$
de l’autre, induit les deux diagrammes commutatifs suivants (lemme A.0.2) :
$g\in \mathbf{G}$
de l’autre, induit les deux diagrammes commutatifs suivants (lemme A.0.2) :

On obtient alors que le diagramme suivant commute :

Ce qui nous montre le résultat. ◻
3.3 Classes de conjugaison dans un groupe fini
La partie précédente nous fournit des classes de conjugaison semi-simples géométriques d’un groupe réductif connexe fini. Nous sommes plus intéressé par des classes de conjugaison rationnelles. On rappelle alors ici le lien entre les deux.
Dans cette sous-section
![]() $\text{G}$
désigne un groupe réductif connexe défini sur
$\text{G}$
désigne un groupe réductif connexe défini sur
![]() $\mathfrak{f}$
. Pour un élément semi-simple
$\mathfrak{f}$
. Pour un élément semi-simple
![]() $x\in \text{G}$
, on note
$x\in \text{G}$
, on note
![]() $[x]$
sa classe de conjugaison,
$[x]$
sa classe de conjugaison,
![]() $[x]\in \text{G}_{ss}$
.
$[x]\in \text{G}_{ss}$
.
Lemme 3.3.1. Soit
![]() $s\in (\text{G}_{ss})^{F}$
. Alors il existe
$s\in (\text{G}_{ss})^{F}$
. Alors il existe
![]() $x\in \mathsf{G}:=\text{G}^{F}$
tel que
$x\in \mathsf{G}:=\text{G}^{F}$
tel que
![]() $s=[x]$
.
$s=[x]$
.
Démonstration.
![]() $s=[y]$
avec
$s=[y]$
avec
![]() $y\in \text{G}$
. La classe de conjugaison
$y\in \text{G}$
. La classe de conjugaison
![]() $s$
étant
$s$
étant
![]() $F$
-stable, il existe
$F$
-stable, il existe
![]() $g\in \text{G}$
tel que
$g\in \text{G}$
tel que
![]() $F(y)=g^{-1}yg$
. L’application de Lang,
$F(y)=g^{-1}yg$
. L’application de Lang,
![]() $\text{Lan}:\text{G}\rightarrow \text{G}$
définie par
$\text{Lan}:\text{G}\rightarrow \text{G}$
définie par
![]() $\text{Lan}(g)=g^{-1}F(g)$
est surjective d’après [Reference Cabanes and EnguehardCE04] Théorème 7.1. Ainsi, il existe
$\text{Lan}(g)=g^{-1}F(g)$
est surjective d’après [Reference Cabanes and EnguehardCE04] Théorème 7.1. Ainsi, il existe
![]() $h\in \text{G}$
tel que
$h\in \text{G}$
tel que
![]() $g=h^{-1}F(h)$
. Alors
$g=h^{-1}F(h)$
. Alors
Ainsi
![]() $x=hyh^{-1}$
convient.◻
$x=hyh^{-1}$
convient.◻
Corollaire 3.3.2. L’application
![]() $\mathsf{G}_{ss}{\twoheadrightarrow}(\text{G}_{ss})^{F}$
est surjective.
$\mathsf{G}_{ss}{\twoheadrightarrow}(\text{G}_{ss})^{F}$
est surjective.
3.4 Systèmes 0-cohérents de classes de conjugaison associés aux paramètres de l’inertie modérés
On met bout à bout les résultats des sous-sections précédentes pour obtenir une application qui à un paramètre inertiel modéré associe un système de classes de conjugaison 0-cohérent.
En composant la proposition 3.3.2, l’application
![]() $\tilde{\unicode[STIX]{x1D713}}_{\unicode[STIX]{x1D70E}}$
et la proposition 3.1.3, on obtient une application
$\tilde{\unicode[STIX]{x1D713}}_{\unicode[STIX]{x1D70E}}$
et la proposition 3.1.3, on obtient une application
Soient
![]() $\unicode[STIX]{x1D70E},\unicode[STIX]{x1D714}\in BT$
tels que
$\unicode[STIX]{x1D70E},\unicode[STIX]{x1D714}\in BT$
tels que
![]() $\unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D714}$
. Nous avons vu que
$\unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D714}$
. Nous avons vu que
![]() $\overline{\mathsf{G}}_{\unicode[STIX]{x1D714}}$
est un Levi de
$\overline{\mathsf{G}}_{\unicode[STIX]{x1D714}}$
est un Levi de
![]() $\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}$
. Ceci nous donne donc, comme dans le § 2.1, une application
$\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}$
. Ceci nous donne donc, comme dans le § 2.1, une application
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D714},\unicode[STIX]{x1D70E}}^{\ast }:(\overline{\mathsf{G}}_{\unicode[STIX]{x1D714}}^{\ast })_{ss}\rightarrow (\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}^{\ast })_{ss}$
.
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D714},\unicode[STIX]{x1D70E}}^{\ast }:(\overline{\mathsf{G}}_{\unicode[STIX]{x1D714}}^{\ast })_{ss}\rightarrow (\overline{\mathsf{G}}_{\unicode[STIX]{x1D70E}}^{\ast })_{ss}$
.
Lemme 3.4.1. Soient
![]() $\unicode[STIX]{x1D70E},\unicode[STIX]{x1D714}\in BT$
tels que
$\unicode[STIX]{x1D70E},\unicode[STIX]{x1D714}\in BT$
tels que
![]() $\unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D714}$
. Alors
$\unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D714}$
. Alors
Démonstration.
![]() $W_{\unicode[STIX]{x1D714}_{1}}$
est le groupe engendré par les réflexions des hyperplans contenant
$W_{\unicode[STIX]{x1D714}_{1}}$
est le groupe engendré par les réflexions des hyperplans contenant
![]() $\unicode[STIX]{x1D714}_{1}$
où
$\unicode[STIX]{x1D714}_{1}$
où
![]() $\unicode[STIX]{x1D714}_{1}$
est l’image canonique de
$\unicode[STIX]{x1D714}_{1}$
est l’image canonique de
![]() $\unicode[STIX]{x1D714}$
dans
$\unicode[STIX]{x1D714}$
dans
![]() $BT(K)$
. Or
$BT(K)$
. Or
![]() $\unicode[STIX]{x1D70E}_{1}\leqslant \unicode[STIX]{x1D714}_{1}$
, donc un hyperplan contenant
$\unicode[STIX]{x1D70E}_{1}\leqslant \unicode[STIX]{x1D714}_{1}$
, donc un hyperplan contenant
![]() $\unicode[STIX]{x1D714}_{1}$
contient aussi
$\unicode[STIX]{x1D714}_{1}$
contient aussi
![]() $\unicode[STIX]{x1D70E}_{1}$
et
$\unicode[STIX]{x1D70E}_{1}$
et
![]() $W_{\unicode[STIX]{x1D714}_{1}}$
est un sous-groupe de
$W_{\unicode[STIX]{x1D714}_{1}}$
est un sous-groupe de
![]() $W_{\unicode[STIX]{x1D70E}_{1}}$
. Ainsi le diagramme commutatif
$W_{\unicode[STIX]{x1D70E}_{1}}$
. Ainsi le diagramme commutatif

induit le diagramme commutatif

D’où la commutativité de

et on a le résultat voulu. ◻
Soient
![]() $g\in G$
et
$g\in G$
et
![]() $\unicode[STIX]{x1D70E}\in BT$
, nous avons déjà vu (au début du § 2.3) que la conjugaison par
$\unicode[STIX]{x1D70E}\in BT$
, nous avons déjà vu (au début du § 2.3) que la conjugaison par
![]() $g$
induisait deux applications
$g$
induisait deux applications
Lemme 3.4.2. Soient
![]() $g\in G$
et
$g\in G$
et
![]() $\unicode[STIX]{x1D70E}\in BT$
alors
$\unicode[STIX]{x1D70E}\in BT$
alors
Démonstration.
Soit
![]() $\mathbf{S}$
un tore déployé maximal tel que
$\mathbf{S}$
un tore déployé maximal tel que
![]() $\unicode[STIX]{x1D70E}\in {\mathcal{A}}(\mathbf{S})$
. Alors si l’on pose
$\unicode[STIX]{x1D70E}\in {\mathcal{A}}(\mathbf{S})$
. Alors si l’on pose
![]() $\mathbf{S}^{\prime }=\text{Ad}(g)(\mathbf{S})$
,
$\mathbf{S}^{\prime }=\text{Ad}(g)(\mathbf{S})$
,
![]() $\mathbf{S}^{\prime }$
est un tore déployé maximal tel que
$\mathbf{S}^{\prime }$
est un tore déployé maximal tel que
![]() $g\unicode[STIX]{x1D70E}\in {\mathcal{A}}(\mathbf{S}^{\prime })$
. La conjugaison par
$g\unicode[STIX]{x1D70E}\in {\mathcal{A}}(\mathbf{S}^{\prime })$
. La conjugaison par
![]() $g$
induit un isomorphisme de
$g$
induit un isomorphisme de
![]() $X$
vers
$X$
vers
![]() $X^{\prime }$
. Le lemme A.0.1 nous donne le diagramme commutatif suivant :
$X^{\prime }$
. Le lemme A.0.1 nous donne le diagramme commutatif suivant :

La conjugaison par
![]() $g$
envoie les racines affines pour
$g$
envoie les racines affines pour
![]() $\mathbf{S}$
s’annulant sur
$\mathbf{S}$
s’annulant sur
![]() $\unicode[STIX]{x1D70E}_{1}$
sur les racines affines pour
$\unicode[STIX]{x1D70E}_{1}$
sur les racines affines pour
![]() $\mathbf{S}^{\prime }$
s’annulant sur
$\mathbf{S}^{\prime }$
s’annulant sur
![]() $g\unicode[STIX]{x1D70E}_{1}$
. On a donc le diagramme commutatif suivant
$g\unicode[STIX]{x1D70E}_{1}$
. On a donc le diagramme commutatif suivant

et

Enfin la conjugaison par
![]() $g$
étant un isomorphisme intérieur sur
$g$
étant un isomorphisme intérieur sur
![]() $G$
, le diagramme ci-dessous commute (lemme A.0.2)
$G$
, le diagramme ci-dessous commute (lemme A.0.2)

Mis bout à bout ces diagrammes donnent la commutativité de

ce qui finit la preuve. ◻
Construisons maintenant un système 0-cohérent de classes de conjugaison.
Définition 3.4.3. Soient
![]() $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
et
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
et
![]() $\unicode[STIX]{x1D70E}\in BT$
. On définit le système de classes de conjugaison
$\unicode[STIX]{x1D70E}\in BT$
. On définit le système de classes de conjugaison
![]() $S_{\unicode[STIX]{x1D719}}=(S_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}\in BT}$
par
$S_{\unicode[STIX]{x1D719}}=(S_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D70E}})_{\unicode[STIX]{x1D70E}\in BT}$
par
Proposition 3.4.4. Soit
![]() $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
. Le système
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
. Le système
![]() $S_{\unicode[STIX]{x1D719}}$
est 0-cohérent.
$S_{\unicode[STIX]{x1D719}}$
est 0-cohérent.
Ainsi par la proposition 2.3.5, si l’on note
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G):=\text{Rep}_{\unicode[STIX]{x1D6EC}}^{S_{\unicode[STIX]{x1D719}}}(G)$
, alors
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G):=\text{Rep}_{\unicode[STIX]{x1D6EC}}^{S_{\unicode[STIX]{x1D719}}}(G)$
, alors
Théorème 3.4.5. Soit
![]() $\mathbf{G}$
un groupe réductif connexe défini sur
$\mathbf{G}$
un groupe réductif connexe défini sur
![]() $k$
et
$k$
et
![]() $K$
-déployé. Alors la catégorie de niveau
$K$
-déployé. Alors la catégorie de niveau
![]() $0$
se décompose en
$0$
se décompose en
Notons que si
![]() $\mathbf{G}$
est quasi-déployé alors il est non-ramifié et possède donc un sommet hyperspécial
$\mathbf{G}$
est quasi-déployé alors il est non-ramifié et possède donc un sommet hyperspécial
![]() $o$
. Dans ce cas, l’application
$o$
. Dans ce cas, l’application
![]() $\tilde{\unicode[STIX]{x1D713}}_{o}$
est bijective, donc
$\tilde{\unicode[STIX]{x1D713}}_{o}$
est bijective, donc
![]() $\unicode[STIX]{x1D713}_{o}$
est surjective et
$\unicode[STIX]{x1D713}_{o}$
est surjective et
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
est non vide pour tout
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
est non vide pour tout
![]() $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
. Cependant, lorsque
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
. Cependant, lorsque
![]() $\mathbf{G}$
n’est pas quasi-déployé, les catégories
$\mathbf{G}$
n’est pas quasi-déployé, les catégories
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
peuvent être vides. Nous devons rajouter une condition de ‘relevance’ pour avoir
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
peuvent être vides. Nous devons rajouter une condition de ‘relevance’ pour avoir
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
non vide, ce que nous détaillerons dans la partie 4.3.
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
non vide, ce que nous détaillerons dans la partie 4.3.
4 Propriétés de
 $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
Fixons dans toute cette section un paramètre inertiel modéré
![]() $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
. Le but de cette section est d’étudier quelques propriétés vérifiées par
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
. Le but de cette section est d’étudier quelques propriétés vérifiées par
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
. Rappelons qu’à
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
. Rappelons qu’à
![]() $\unicode[STIX]{x1D719}$
nous avons associé dans la partie 3.4 un système 0-cohérent de classes de conjugaison
$\unicode[STIX]{x1D719}$
nous avons associé dans la partie 3.4 un système 0-cohérent de classes de conjugaison
![]() $S_{\unicode[STIX]{x1D719}}$
, qui permet de définir
$S_{\unicode[STIX]{x1D719}}$
, qui permet de définir
![]() $e_{\unicode[STIX]{x1D719}}=(e_{\unicode[STIX]{x1D719},x})_{x\in BT_{0}}$
un système 0-cohérent d’idempotents défini par
$e_{\unicode[STIX]{x1D719}}=(e_{\unicode[STIX]{x1D719},x})_{x\in BT_{0}}$
un système 0-cohérent d’idempotents défini par
![]() $e_{\unicode[STIX]{x1D719},x}=\sum _{s\in S_{\unicode[STIX]{x1D719},x}}e_{x}^{s,\unicode[STIX]{x1D6EC}}$
.
$e_{\unicode[STIX]{x1D719},x}=\sum _{s\in S_{\unicode[STIX]{x1D719},x}}e_{x}^{s,\unicode[STIX]{x1D6EC}}$
.
4.1 Lien entre les décompositions sur
 $\overline{\mathbb{Z}}_{\ell }$
et
$\overline{\mathbb{Z}}_{\ell }$
et
 $\overline{\mathbb{Q}}_{\ell }$
$\overline{\mathbb{Q}}_{\ell }$
Au vu de la construction de
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
il est assez simple de comprendre le lien entre
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
il est assez simple de comprendre le lien entre
![]() $\unicode[STIX]{x1D6EC}=\overline{\mathbb{Z}}_{\ell }$
et
$\unicode[STIX]{x1D6EC}=\overline{\mathbb{Z}}_{\ell }$
et
![]() $\unicode[STIX]{x1D6EC}=\overline{\mathbb{Q}}_{\ell }$
ce que nous faisons ici.
$\unicode[STIX]{x1D6EC}=\overline{\mathbb{Q}}_{\ell }$
ce que nous faisons ici.
Considérons ici que
![]() $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{(\ell )},\mathbf{G})$
. Soit
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{(\ell )},\mathbf{G})$
. Soit
![]() $x\in BT_{0}$
et notons
$x\in BT_{0}$
et notons
![]() $S_{\unicode[STIX]{x1D719},x}^{\prime }$
l’ensemble des
$S_{\unicode[STIX]{x1D719},x}^{\prime }$
l’ensemble des
![]() $s^{\prime }\in (\overline{\mathsf{G}}_{x}^{\ast })_{ss}$
dont
$s^{\prime }\in (\overline{\mathsf{G}}_{x}^{\ast })_{ss}$
dont
![]() $s$
la partie
$s$
la partie
![]() $\ell$
-régulière de
$\ell$
-régulière de
![]() $s^{\prime }$
est dans
$s^{\prime }$
est dans
![]() $S_{\unicode[STIX]{x1D719},x}$
. Alors par construction,
$S_{\unicode[STIX]{x1D719},x}$
. Alors par construction,
![]() $e_{\unicode[STIX]{x1D719},x}=\sum _{s\in S_{\unicode[STIX]{x1D719},x}}e_{x}^{s,\overline{\mathbb{Z}}_{\ell }}=\sum _{s^{\prime }\in S_{\unicode[STIX]{x1D719},x}^{\prime }}e_{x}^{s,\overline{\mathbb{Q}}_{\ell }}$
. Prenons
$e_{\unicode[STIX]{x1D719},x}=\sum _{s\in S_{\unicode[STIX]{x1D719},x}}e_{x}^{s,\overline{\mathbb{Z}}_{\ell }}=\sum _{s^{\prime }\in S_{\unicode[STIX]{x1D719},x}^{\prime }}e_{x}^{s,\overline{\mathbb{Q}}_{\ell }}$
. Prenons
![]() $s^{\prime }\in (\overline{\mathsf{G}}_{x}^{\ast })_{ss}$
et nommons
$s^{\prime }\in (\overline{\mathsf{G}}_{x}^{\ast })_{ss}$
et nommons
![]() $\unicode[STIX]{x1D719}^{\prime }\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{G})$
le paramètre inertiel qui lui est associé, c’est à dire
$\unicode[STIX]{x1D719}^{\prime }\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{G})$
le paramètre inertiel qui lui est associé, c’est à dire
![]() $\unicode[STIX]{x1D719}^{\prime }:=\unicode[STIX]{x1D713}_{x}(s^{\prime })$
. Soit
$\unicode[STIX]{x1D719}^{\prime }:=\unicode[STIX]{x1D713}_{x}(s^{\prime })$
. Soit
![]() $s\in S_{\unicode[STIX]{x1D719},x}$
(donc
$s\in S_{\unicode[STIX]{x1D719},x}$
(donc
![]() $\unicode[STIX]{x1D713}_{x}(s)=\unicode[STIX]{x1D719}$
),
$\unicode[STIX]{x1D713}_{x}(s)=\unicode[STIX]{x1D719}$
),
![]() $s$
est la partie
$s$
est la partie
![]() $\ell$
-régulière de
$\ell$
-régulière de
![]() $s^{\prime }$
si et seulement si
$s^{\prime }$
si et seulement si
![]() $\unicode[STIX]{x1D719}_{\mid I_{k}^{(\ell )}}^{\prime }\sim \unicode[STIX]{x1D719}$
. Le lien entre les décompositions sur
$\unicode[STIX]{x1D719}_{\mid I_{k}^{(\ell )}}^{\prime }\sim \unicode[STIX]{x1D719}$
. Le lien entre les décompositions sur
![]() $\overline{\mathbb{Z}}_{\ell }$
et
$\overline{\mathbb{Z}}_{\ell }$
et
![]() $\overline{\mathbb{Q}}_{\ell }$
est alors clair.
$\overline{\mathbb{Q}}_{\ell }$
est alors clair.
Proposition 4.1.1. Soit
![]() $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{(\ell )},\mathbf{G})$
, alors
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{(\ell )},\mathbf{G})$
, alors
où le produit est pris sur les
![]() $\unicode[STIX]{x1D719}^{\prime }\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{G})$
tels que
$\unicode[STIX]{x1D719}^{\prime }\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{G})$
tels que
![]() $\unicode[STIX]{x1D719}_{\mid I_{k}^{(\ell )}}^{\prime }\sim \unicode[STIX]{x1D719}$
.
$\unicode[STIX]{x1D719}_{\mid I_{k}^{(\ell )}}^{\prime }\sim \unicode[STIX]{x1D719}$
.
4.2 Représentations irréductibles de
 $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
Nous souhaitons dans cette partie décrire les représentations irréductibles qui sont dans
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
.
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
.
Soit
![]() $\mathbf{T}$
un tore maximal non-ramifié de
$\mathbf{T}$
un tore maximal non-ramifié de
![]() $\mathbf{G}$
(
$\mathbf{G}$
(
![]() $\mathbf{T}$
est un
$\mathbf{T}$
est un
![]() $k$
-tore
$k$
-tore
![]() $K$
-déployé maximal de
$K$
-déployé maximal de
![]() $\mathbf{G}$
). Nommons
$\mathbf{G}$
). Nommons
![]() $\mathbf{T}_{0}$
le tore de référence utilisé pour définir
$\mathbf{T}_{0}$
le tore de référence utilisé pour définir
![]() $\widehat{\unicode[STIX]{x1D717}}$
et
$\widehat{\unicode[STIX]{x1D717}}$
et
![]() $\widehat{\mathbf{G}}$
. Le tore
$\widehat{\mathbf{G}}$
. Le tore
![]() $\mathbf{T}$
étant non-ramifié il existe
$\mathbf{T}$
étant non-ramifié il existe
![]() $g\in G^{nr}$
tel que
$g\in G^{nr}$
tel que
![]() $T^{nr}=^{g}T_{0}^{nr}$
. Dans ce cas
$T^{nr}=^{g}T_{0}^{nr}$
. Dans ce cas
![]() $g^{-1}F(g)\in N(T_{0}^{nr},G^{nr})$
et définit un élément
$g^{-1}F(g)\in N(T_{0}^{nr},G^{nr})$
et définit un élément
![]() $w\in W_{0}$
. Ainsi
$w\in W_{0}$
. Ainsi
![]() $^{L}\mathbf{T}\simeq \langle w\widehat{\unicode[STIX]{x1D717}}\rangle \ltimes \widehat{\mathbf{T}}_{0}(\overline{\mathbb{Q}}_{\ell })$
. Le choix d’un relèvement
$^{L}\mathbf{T}\simeq \langle w\widehat{\unicode[STIX]{x1D717}}\rangle \ltimes \widehat{\mathbf{T}}_{0}(\overline{\mathbb{Q}}_{\ell })$
. Le choix d’un relèvement
![]() ${\dot{w}}\in N(\widehat{\mathbf{T}}_{0},\widehat{\mathbf{G}})$
de
${\dot{w}}\in N(\widehat{\mathbf{T}}_{0},\widehat{\mathbf{G}})$
de
![]() $w$
permet alors de définir un plongement
$w$
permet alors de définir un plongement
![]() $^{L}\mathbf{T}{\hookrightarrow}^{L}\mathbf{G}$
par
$^{L}\mathbf{T}{\hookrightarrow}^{L}\mathbf{G}$
par
![]() $\widehat{\mathbf{T}}_{0}(\overline{\mathbb{Q}}_{\ell })\subseteq \widehat{\mathbf{G}}(\overline{\mathbb{Q}}_{\ell })$
et
$\widehat{\mathbf{T}}_{0}(\overline{\mathbb{Q}}_{\ell })\subseteq \widehat{\mathbf{G}}(\overline{\mathbb{Q}}_{\ell })$
et
![]() $w\widehat{\unicode[STIX]{x1D717}}\mapsto ({\dot{w}},\widehat{\unicode[STIX]{x1D717}})$
. Ce plongement dépend (même à
$w\widehat{\unicode[STIX]{x1D717}}\mapsto ({\dot{w}},\widehat{\unicode[STIX]{x1D717}})$
. Ce plongement dépend (même à
![]() $\widehat{\mathbf{G}}(\overline{\mathbb{Q}}_{\ell })$
-conjugaison près) du choix du relèvement de
$\widehat{\mathbf{G}}(\overline{\mathbb{Q}}_{\ell })$
-conjugaison près) du choix du relèvement de
![]() $w$
. Il induit cependant une application
$w$
. Il induit cependant une application
qui elle est indépendante des choix effectués car les paramètres inertiels sont à valeurs dans
![]() $\widehat{\mathbf{T}}_{0}(\overline{\mathbb{Q}}_{\ell })$
(ou
$\widehat{\mathbf{T}}_{0}(\overline{\mathbb{Q}}_{\ell })$
(ou
![]() $\widehat{\mathbf{G}}(\overline{\mathbb{Q}}_{\ell })$
).
$\widehat{\mathbf{G}}(\overline{\mathbb{Q}}_{\ell })$
).
Soit
![]() $\unicode[STIX]{x1D719}_{\mathbf{T}}\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{T})$
. Notons
$\unicode[STIX]{x1D719}_{\mathbf{T}}\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{T})$
. Notons
![]() $X:=X^{\ast }(\mathbf{T})$
. Nous avons vu dans les §§ 3.2 et 3.1 que l’on a une bijection
$X:=X^{\ast }(\mathbf{T})$
. Nous avons vu dans les §§ 3.2 et 3.1 que l’on a une bijection
![]() $\unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{T})\simeq (X\otimes _{\mathbb{Z}}\mathfrak{F}^{\times })^{F}$
. Soit
$\unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{T})\simeq (X\otimes _{\mathbb{Z}}\mathfrak{F}^{\times })^{F}$
. Soit
![]() $x\in {\mathcal{A}}(\mathbf{T},K)\cap BT_{0}$
. Nous savons que l’on a également un isomorphisme
$x\in {\mathcal{A}}(\mathbf{T},K)\cap BT_{0}$
. Nous savons que l’on a également un isomorphisme
![]() $(X\otimes _{\mathbb{Z}}\mathfrak{F}^{\times })^{F}\simeq (\text{T}_{x}^{\ast })^{F}\simeq \text{Hom}(\text{}\text{T}_{x}^{F},\overline{\mathbb{Q}}_{\ell }^{\times })$
. On associe donc à
$(X\otimes _{\mathbb{Z}}\mathfrak{F}^{\times })^{F}\simeq (\text{T}_{x}^{\ast })^{F}\simeq \text{Hom}(\text{}\text{T}_{x}^{F},\overline{\mathbb{Q}}_{\ell }^{\times })$
. On associe donc à
![]() $\unicode[STIX]{x1D719}_{\mathbf{T}}$
de manière bijective un caractère
$\unicode[STIX]{x1D719}_{\mathbf{T}}$
de manière bijective un caractère
![]() $\unicode[STIX]{x1D703}_{\mathbf{T}}:\text{}\text{T}_{x}^{F}\rightarrow \overline{\mathbb{Q}}_{\ell }^{\times }$
, qui se relève en un caractère de niveau 0 :
$\unicode[STIX]{x1D703}_{\mathbf{T}}:\text{}\text{T}_{x}^{F}\rightarrow \overline{\mathbb{Q}}_{\ell }^{\times }$
, qui se relève en un caractère de niveau 0 :
![]() $\unicode[STIX]{x1D703}_{\mathbf{T}}:^{0}\text{}\text{T}^{F}\rightarrow \overline{\mathbb{Q}}_{\ell }^{\times }$
. L’association qui à
$\unicode[STIX]{x1D703}_{\mathbf{T}}:^{0}\text{}\text{T}^{F}\rightarrow \overline{\mathbb{Q}}_{\ell }^{\times }$
. L’association qui à
![]() $\unicode[STIX]{x1D719}_{\mathbf{T}}$
donne
$\unicode[STIX]{x1D719}_{\mathbf{T}}$
donne
![]() $\unicode[STIX]{x1D703}_{\mathbf{T}}$
est alors la correspondance de Langlands locale pour les tores restreinte à l’inertie.
$\unicode[STIX]{x1D703}_{\mathbf{T}}$
est alors la correspondance de Langlands locale pour les tores restreinte à l’inertie.
Théorème 4.2.1. Soit
![]() $\unicode[STIX]{x1D70B}\in \text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)$
. Alors
$\unicode[STIX]{x1D70B}\in \text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)$
. Alors
![]() $\unicode[STIX]{x1D70B}\in \text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
si et seulement s’il existe
$\unicode[STIX]{x1D70B}\in \text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
si et seulement s’il existe
![]() $\mathbf{T}$
un tore maximal non-ramifié de
$\mathbf{T}$
un tore maximal non-ramifié de
![]() $\mathbf{G}$
,
$\mathbf{G}$
,
![]() $\unicode[STIX]{x1D719}_{\mathbf{T}}\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{T})$
et
$\unicode[STIX]{x1D719}_{\mathbf{T}}\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{T})$
et
![]() $x\in {\mathcal{A}}(\mathbf{T},K)\cap BT_{0}$
tels que
$x\in {\mathcal{A}}(\mathbf{T},K)\cap BT_{0}$
tels que
![]() $\unicode[STIX]{x1D704}(\unicode[STIX]{x1D719}_{\mathbf{T}})\sim \unicode[STIX]{x1D719}$
et
$\unicode[STIX]{x1D704}(\unicode[STIX]{x1D719}_{\mathbf{T}})\sim \unicode[STIX]{x1D719}$
et
![]() $\langle \unicode[STIX]{x1D70B}^{G_{x}^{+}},{\mathcal{R}}_{\text{}\text{T}_{x}}^{\overline{\text{G}}_{x}}(\unicode[STIX]{x1D703}_{\boldsymbol{ T}})\rangle \neq 0$
(où
$\langle \unicode[STIX]{x1D70B}^{G_{x}^{+}},{\mathcal{R}}_{\text{}\text{T}_{x}}^{\overline{\text{G}}_{x}}(\unicode[STIX]{x1D703}_{\boldsymbol{ T}})\rangle \neq 0$
(où
![]() $\unicode[STIX]{x1D70B}^{G_{x}^{+}}$
est vue comme une représentation de
$\unicode[STIX]{x1D70B}^{G_{x}^{+}}$
est vue comme une représentation de
![]() $\overline{\mathsf{G}}_{x}\simeq G_{x}^{\circ }/G_{x}^{+}$
et
$\overline{\mathsf{G}}_{x}\simeq G_{x}^{\circ }/G_{x}^{+}$
et
![]() ${\mathcal{R}}_{\text{}\text{T}_{x}}^{\overline{\text{G}}_{x}}$
désigne l’induction de Deligne–Lusztig).
${\mathcal{R}}_{\text{}\text{T}_{x}}^{\overline{\text{G}}_{x}}$
désigne l’induction de Deligne–Lusztig).
Démonstration.
Par définition de
![]() $\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
, comme
$\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
, comme
![]() $\unicode[STIX]{x1D70B}$
est une représentation irréductible,
$\unicode[STIX]{x1D70B}$
est une représentation irréductible,
![]() $\unicode[STIX]{x1D70B}\in \text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
si et seulement s’il existe
$\unicode[STIX]{x1D70B}\in \text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
si et seulement s’il existe
![]() $x\in BT_{0}$
tel que
$x\in BT_{0}$
tel que
![]() $e_{\unicode[STIX]{x1D719},x}\unicode[STIX]{x1D70B}^{G_{x}^{+}}\neq 0$
. Soit
$e_{\unicode[STIX]{x1D719},x}\unicode[STIX]{x1D70B}^{G_{x}^{+}}\neq 0$
. Soit
![]() $x\in BT_{0}$
, alors par construction
$x\in BT_{0}$
, alors par construction
![]() $e_{\unicode[STIX]{x1D719},x}\unicode[STIX]{x1D70B}^{G_{x}^{+}}\neq 0$
est équivalent à l’existence d’une classe de conjugaison rationnelle semi-simple
$e_{\unicode[STIX]{x1D719},x}\unicode[STIX]{x1D70B}^{G_{x}^{+}}\neq 0$
est équivalent à l’existence d’une classe de conjugaison rationnelle semi-simple
![]() $s\in S_{\unicode[STIX]{x1D719},x}$
telle que
$s\in S_{\unicode[STIX]{x1D719},x}$
telle que
![]() $e_{s,\overline{\mathbb{Q}}_{\ell }}^{\overline{\mathsf{G}}_{x}}\unicode[STIX]{x1D70B}^{G_{x}^{+}}\neq 0$
. Soit
$e_{s,\overline{\mathbb{Q}}_{\ell }}^{\overline{\mathsf{G}}_{x}}\unicode[STIX]{x1D70B}^{G_{x}^{+}}\neq 0$
. Soit
![]() $\text{T}_{x}$
un
$\text{T}_{x}$
un
![]() $\mathfrak{f}$
-tore maximal de
$\mathfrak{f}$
-tore maximal de
![]() $\overline{\text{G}}_{x}$
tel que
$\overline{\text{G}}_{x}$
tel que
![]() $s\in (\text{T}_{x}^{\ast })^{F}$
. Relevons
$s\in (\text{T}_{x}^{\ast })^{F}$
. Relevons
![]() $\text{T}_{x}$
en
$\text{T}_{x}$
en
![]() $\mathbf{T}$
un tore maximal non-ramifié de
$\mathbf{T}$
un tore maximal non-ramifié de
![]() $\mathbf{G}$
. Nous avons que
$\mathbf{G}$
. Nous avons que
![]() $\unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{T})\simeq (X\otimes _{\mathbb{Z}}\mathfrak{F}^{\times })^{F}\simeq (\text{T}_{x}^{\ast })^{F}$
et donc
$\unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{T})\simeq (X\otimes _{\mathbb{Z}}\mathfrak{F}^{\times })^{F}\simeq (\text{T}_{x}^{\ast })^{F}$
et donc
![]() $s$
correspond à
$s$
correspond à
![]() $\unicode[STIX]{x1D719}_{\mathbf{T}}$
un paramètre inertiel modéré de
$\unicode[STIX]{x1D719}_{\mathbf{T}}$
un paramètre inertiel modéré de
![]() $\mathbf{T}$
. La discussion qui précède le théorème montre que
$\mathbf{T}$
. La discussion qui précède le théorème montre que
![]() $s$
est également associé au caractère
$s$
est également associé au caractère
![]() $\unicode[STIX]{x1D703}_{\mathbf{T}}:\text{}\text{T}_{x}^{F}\rightarrow \overline{\mathbb{Q}}_{\ell }^{\times }$
. Le § 2.1 nous dit alors que
$\unicode[STIX]{x1D703}_{\mathbf{T}}:\text{}\text{T}_{x}^{F}\rightarrow \overline{\mathbb{Q}}_{\ell }^{\times }$
. Le § 2.1 nous dit alors que
![]() $e_{s,\overline{\mathbb{Q}}_{\ell }}^{\overline{\mathsf{G}}_{x}}\unicode[STIX]{x1D70B}^{G_{x}^{+}}\neq 0$
si et seulement si
$e_{s,\overline{\mathbb{Q}}_{\ell }}^{\overline{\mathsf{G}}_{x}}\unicode[STIX]{x1D70B}^{G_{x}^{+}}\neq 0$
si et seulement si
![]() $\langle \unicode[STIX]{x1D70B}^{G_{x}^{+}},{\mathcal{R}}_{\text{}\text{T}_{x}}^{\overline{\text{G}}_{x}}(\unicode[STIX]{x1D703}_{\boldsymbol{ T}})\rangle \neq 0$
.
$\langle \unicode[STIX]{x1D70B}^{G_{x}^{+}},{\mathcal{R}}_{\text{}\text{T}_{x}}^{\overline{\text{G}}_{x}}(\unicode[STIX]{x1D703}_{\boldsymbol{ T}})\rangle \neq 0$
.
On vient donc de montrer que
![]() $\unicode[STIX]{x1D70B}\in \text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
si et seulement s’il existe
$\unicode[STIX]{x1D70B}\in \text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
si et seulement s’il existe
![]() $\mathbf{T}$
un tore maximal non-ramifié de
$\mathbf{T}$
un tore maximal non-ramifié de
![]() $\mathbf{G}$
,
$\mathbf{G}$
,
![]() $x\in {\mathcal{A}}(\mathbf{T},K)\cap BT_{0}$
,
$x\in {\mathcal{A}}(\mathbf{T},K)\cap BT_{0}$
,
![]() $\unicode[STIX]{x1D719}_{\mathbf{T}}\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{T})$
correspondant à
$\unicode[STIX]{x1D719}_{\mathbf{T}}\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{T})$
correspondant à
![]() $s\in S_{\unicode[STIX]{x1D719},x}$
tels que
$s\in S_{\unicode[STIX]{x1D719},x}$
tels que
![]() $\langle \unicode[STIX]{x1D70B}^{G_{x}^{+}},{\mathcal{R}}_{\text{}\text{T}_{x}}^{\overline{\text{G}}_{x}}(\unicode[STIX]{x1D703}_{\boldsymbol{ T}})\rangle \neq 0$
. Pour achever la preuve du théorème il ne nous reste donc qu’à montrer que
$\langle \unicode[STIX]{x1D70B}^{G_{x}^{+}},{\mathcal{R}}_{\text{}\text{T}_{x}}^{\overline{\text{G}}_{x}}(\unicode[STIX]{x1D703}_{\boldsymbol{ T}})\rangle \neq 0$
. Pour achever la preuve du théorème il ne nous reste donc qu’à montrer que
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D704}(\unicode[STIX]{x1D719}_{\mathbf{T}})$
. Or cela découle du diagramme commutatif suivant
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D704}(\unicode[STIX]{x1D719}_{\mathbf{T}})$
. Or cela découle du diagramme commutatif suivant

Notons que le théorème précédent n’est énoncé que pour
![]() $\unicode[STIX]{x1D6EC}=\overline{\mathbb{Q}}_{\ell }$
puisque l’on peut en déduire une description de
$\unicode[STIX]{x1D6EC}=\overline{\mathbb{Q}}_{\ell }$
puisque l’on peut en déduire une description de
![]() $\text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)\cap \text{Rep}_{\overline{\mathbb{Z}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
grâce à la proposition 4.1.1. Notons également que pour
$\text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)\cap \text{Rep}_{\overline{\mathbb{Z}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
grâce à la proposition 4.1.1. Notons également que pour
![]() $\unicode[STIX]{x1D6EC}=\overline{\mathbb{Z}}_{\ell }$
, les objets simples de
$\unicode[STIX]{x1D6EC}=\overline{\mathbb{Z}}_{\ell }$
, les objets simples de
![]() $\text{Rep}_{\overline{\mathbb{Z}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
sont
:
$\text{Rep}_{\overline{\mathbb{Z}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
sont
:
(i) Les objets simples de caractéristique 0 qui sont les
 $\unicode[STIX]{x1D70B}\in \text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)\cap \text{Rep}_{\overline{\mathbb{Z}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
qui ne sont pas entières.
$\unicode[STIX]{x1D70B}\in \text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)\cap \text{Rep}_{\overline{\mathbb{Z}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
qui ne sont pas entières.(ii) Les objets simples de caractéristique
 $\ell$
qui sont les sous-quotients simples des réductions modulo
$\ell$
qui sont les sous-quotients simples des réductions modulo
 $\ell$
des
$\ell$
des
 $\unicode[STIX]{x1D70B}\in \text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)\cap \text{Rep}_{\overline{\mathbb{Z}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
qui sont entières (voir le lemme 6.8 de [Reference DatDat05], les hypothèses peuvent être supprimées ici car on est en niveau 0).
$\unicode[STIX]{x1D70B}\in \text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)\cap \text{Rep}_{\overline{\mathbb{Z}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
qui sont entières (voir le lemme 6.8 de [Reference DatDat05], les hypothèses peuvent être supprimées ici car on est en niveau 0).
4.3 Condition de relevance
Nous avons noté précédemment que si
![]() $\mathbf{G}$
n’est pas quasi-déployé alors les catégories
$\mathbf{G}$
n’est pas quasi-déployé alors les catégories
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
peuvent être vides. Nous allons montrer dans cette partie que
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
peuvent être vides. Nous allons montrer dans cette partie que
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
est non vide si et seulement si
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
est non vide si et seulement si
![]() $\unicode[STIX]{x1D719}$
est relevant, au sens suivant.
$\unicode[STIX]{x1D719}$
est relevant, au sens suivant.
Définition 4.3.1. Soit
![]() $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
un paramètre inertiel. On dit que
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
un paramètre inertiel. On dit que
![]() $\unicode[STIX]{x1D719}$
est relevant s’il existe
$\unicode[STIX]{x1D719}$
est relevant s’il existe
![]() $\unicode[STIX]{x1D711}^{\prime }\in \unicode[STIX]{x1D6F7}(\mathbf{G})$
une extension de
$\unicode[STIX]{x1D711}^{\prime }\in \unicode[STIX]{x1D6F7}(\mathbf{G})$
une extension de
![]() $\unicode[STIX]{x1D719}$
à
$\unicode[STIX]{x1D719}$
à
![]() $W_{k}^{\prime }$
qui est relevant, c’est à dire que si l’image de
$W_{k}^{\prime }$
qui est relevant, c’est à dire que si l’image de
![]() $\unicode[STIX]{x1D711}^{\prime }$
est contenue dans un Levi de
$\unicode[STIX]{x1D711}^{\prime }$
est contenue dans un Levi de
![]() $^{L}\mathbf{G}$
alors ce dernier est relevant (au sens de [Reference BorelBor79, 3.4]).
$^{L}\mathbf{G}$
alors ce dernier est relevant (au sens de [Reference BorelBor79, 3.4]).
Soit
![]() $\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D6F7}(W_{k},\mathbf{G})$
et posons
$\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D6F7}(W_{k},\mathbf{G})$
et posons
![]() $\unicode[STIX]{x1D719}:=\unicode[STIX]{x1D711}_{|I_{k}^{\unicode[STIX]{x1D6EC}}}$
. Pour
$\unicode[STIX]{x1D719}:=\unicode[STIX]{x1D711}_{|I_{k}^{\unicode[STIX]{x1D6EC}}}$
. Pour
![]() $w\in W_{k}$
, l’action par conjugaison de
$w\in W_{k}$
, l’action par conjugaison de
![]() $\unicode[STIX]{x1D711}(w)$
normalise
$\unicode[STIX]{x1D711}(w)$
normalise
![]() $\unicode[STIX]{x1D719}(I_{k}^{\unicode[STIX]{x1D6EC}})$
donc normalise également
$\unicode[STIX]{x1D719}(I_{k}^{\unicode[STIX]{x1D6EC}})$
donc normalise également
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})^{\circ }$
, le centralisateur connexe de l’image de
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})^{\circ }$
, le centralisateur connexe de l’image de
![]() $\unicode[STIX]{x1D719}$
dans
$\unicode[STIX]{x1D719}$
dans
![]() $\widehat{\mathbf{G}}$
. On définit alors
$\widehat{\mathbf{G}}$
. On définit alors
qui est un Levi de
![]() $^{L}\mathbf{G}$
dont la partie connexe est
$^{L}\mathbf{G}$
dont la partie connexe est
![]() $M_{\unicode[STIX]{x1D711}}:=C_{\widehat{\mathbf{G}}}(Z(C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})^{\circ })^{\unicode[STIX]{x1D711}(W_{k}),\circ })$
.
$M_{\unicode[STIX]{x1D711}}:=C_{\widehat{\mathbf{G}}}(Z(C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})^{\circ })^{\unicode[STIX]{x1D711}(W_{k}),\circ })$
.
Lemme 4.3.2. Soit
![]() $\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D6F7}(W_{k},\mathbf{G})$
. Alors toute extension
$\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D6F7}(W_{k},\mathbf{G})$
. Alors toute extension
![]() $\unicode[STIX]{x1D711}^{\prime }\in \unicode[STIX]{x1D6F7}(\mathbf{G})$
de
$\unicode[STIX]{x1D711}^{\prime }\in \unicode[STIX]{x1D6F7}(\mathbf{G})$
de
![]() $\unicode[STIX]{x1D711}$
à
$\unicode[STIX]{x1D711}$
à
![]() $W_{k}^{\prime }$
se factorise par
$W_{k}^{\prime }$
se factorise par
![]() ${\mathcal{M}}_{\unicode[STIX]{x1D711}}$
. De plus il existe un
${\mathcal{M}}_{\unicode[STIX]{x1D711}}$
. De plus il existe un
![]() $\unicode[STIX]{x1D711}^{\prime }\in \unicode[STIX]{x1D6F7}(\mathbf{G})$
étendant
$\unicode[STIX]{x1D711}^{\prime }\in \unicode[STIX]{x1D6F7}(\mathbf{G})$
étendant
![]() $\unicode[STIX]{x1D719}:=\unicode[STIX]{x1D711}_{|I_{k}}$
ne se factorisant par aucun sous Levi propre de
$\unicode[STIX]{x1D719}:=\unicode[STIX]{x1D711}_{|I_{k}}$
ne se factorisant par aucun sous Levi propre de
![]() ${\mathcal{M}}_{\unicode[STIX]{x1D711}}$
.
${\mathcal{M}}_{\unicode[STIX]{x1D711}}$
.
Démonstration.
Ici, on écrira plutôt
![]() $W_{k}^{\prime }$
sous la forme
$W_{k}^{\prime }$
sous la forme
![]() $W_{k}\times \text{SL}_{2}$
. On prendra garde cependant à prendre la bonne ‘restriction’ de
$W_{k}\times \text{SL}_{2}$
. On prendra garde cependant à prendre la bonne ‘restriction’ de
![]() $W_{k}\times \text{SL}_{2}$
à
$W_{k}\times \text{SL}_{2}$
à
![]() $W_{k}$
qui est donnée par le plongement
$W_{k}$
qui est donnée par le plongement
![]() $W_{k}{\hookrightarrow}W_{k}\times \text{SL}_{2}$
,
$W_{k}{\hookrightarrow}W_{k}\times \text{SL}_{2}$
,
![]() $w\mapsto (w,\text{diag}(|w|^{1/2},|w|^{-1/2}))$
. Néanmoins, cela ne fait pas de différence lorsque l’on prend les restrictions à l’inertie.
$w\mapsto (w,\text{diag}(|w|^{1/2},|w|^{-1/2}))$
. Néanmoins, cela ne fait pas de différence lorsque l’on prend les restrictions à l’inertie.
Prenons
![]() $\unicode[STIX]{x1D711}^{\prime }\in \unicode[STIX]{x1D6F7}(G)$
une extension de
$\unicode[STIX]{x1D711}^{\prime }\in \unicode[STIX]{x1D6F7}(G)$
une extension de
![]() $\unicode[STIX]{x1D711}$
. Par définition
$\unicode[STIX]{x1D711}$
. Par définition
![]() ${\mathcal{M}}_{\unicode[STIX]{x1D711}}$
contient
${\mathcal{M}}_{\unicode[STIX]{x1D711}}$
contient
![]() $\unicode[STIX]{x1D711}(W_{k})$
. De plus,
$\unicode[STIX]{x1D711}(W_{k})$
. De plus,
![]() $\unicode[STIX]{x1D711}^{\prime }(\text{SL}_{2})$
est contenue dans
$\unicode[STIX]{x1D711}^{\prime }(\text{SL}_{2})$
est contenue dans
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})^{\circ }$
donc
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})^{\circ }$
donc
![]() $\unicode[STIX]{x1D711}^{\prime }(\text{SL}_{2})\subseteq {\mathcal{M}}_{\unicode[STIX]{x1D711}}$
et par conséquent
$\unicode[STIX]{x1D711}^{\prime }(\text{SL}_{2})\subseteq {\mathcal{M}}_{\unicode[STIX]{x1D711}}$
et par conséquent
![]() $\unicode[STIX]{x1D711}^{\prime }(W_{k}^{\prime })\subseteq {\mathcal{M}}_{\unicode[STIX]{x1D711}}$
.
$\unicode[STIX]{x1D711}^{\prime }(W_{k}^{\prime })\subseteq {\mathcal{M}}_{\unicode[STIX]{x1D711}}$
.
Construisons maintenant un
![]() $\unicode[STIX]{x1D711}^{\prime }$
ne se factorisant par aucun sous Levi propre de
$\unicode[STIX]{x1D711}^{\prime }$
ne se factorisant par aucun sous Levi propre de
![]() ${\mathcal{M}}_{\unicode[STIX]{x1D711}}$
. Un Levi minimal de
${\mathcal{M}}_{\unicode[STIX]{x1D711}}$
. Un Levi minimal de
![]() ${\mathcal{M}}_{\unicode[STIX]{x1D711}}$
factorisant
${\mathcal{M}}_{\unicode[STIX]{x1D711}}$
factorisant
![]() $\unicode[STIX]{x1D711}^{\prime }$
est obtenu en prenant le centralisateur dans
$\unicode[STIX]{x1D711}^{\prime }$
est obtenu en prenant le centralisateur dans
![]() ${\mathcal{M}}_{\unicode[STIX]{x1D711}}$
d’un tore maximal de
${\mathcal{M}}_{\unicode[STIX]{x1D711}}$
d’un tore maximal de
![]() $C_{M_{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D711}^{\prime })^{\circ }$
. Ainsi pour prouver la propriété demandée, il nous suffit de fabriquer un
$C_{M_{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D711}^{\prime })^{\circ }$
. Ainsi pour prouver la propriété demandée, il nous suffit de fabriquer un
![]() $\unicode[STIX]{x1D711}^{\prime }$
tel que
$\unicode[STIX]{x1D711}^{\prime }$
tel que
![]() $C_{M_{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D711}^{\prime })^{\circ }\subseteq Z({\mathcal{M}}_{\unicode[STIX]{x1D711}})$
.
$C_{M_{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D711}^{\prime })^{\circ }\subseteq Z({\mathcal{M}}_{\unicode[STIX]{x1D711}})$
.
Soit
![]() $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}(I_{k},\mathbf{G})$
. Prenons
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}(I_{k},\mathbf{G})$
. Prenons
![]() $\unicode[STIX]{x1D711}$
étendant
$\unicode[STIX]{x1D711}$
étendant
![]() $\unicode[STIX]{x1D719}$
tel que l’automorphisme semi-simple
$\unicode[STIX]{x1D719}$
tel que l’automorphisme semi-simple
![]() $\unicode[STIX]{x1D703}$
de conjugaison par
$\unicode[STIX]{x1D703}$
de conjugaison par
![]() $\unicode[STIX]{x1D711}(\text{Frob})$
préserve un épinglage
$\unicode[STIX]{x1D711}(\text{Frob})$
préserve un épinglage
![]() $(C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})^{\circ },\mathbf{B},\mathbf{T},\{x_{\unicode[STIX]{x1D6FC}}\}_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}})$
de
$(C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})^{\circ },\mathbf{B},\mathbf{T},\{x_{\unicode[STIX]{x1D6FC}}\}_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}})$
de
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})^{\circ }$
. On définit
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})^{\circ }$
. On définit
![]() $\unicode[STIX]{x1D711}_{|W_{k}}^{\prime }=\unicode[STIX]{x1D711}$
(ici on considère la restriction naïve de
$\unicode[STIX]{x1D711}_{|W_{k}}^{\prime }=\unicode[STIX]{x1D711}$
(ici on considère la restriction naïve de
![]() $W_{k}\times \text{SL}_{2}$
à
$W_{k}\times \text{SL}_{2}$
à
![]() $W_{k}$
) et
$W_{k}$
) et
![]() $\unicode[STIX]{x1D711}_{|\text{SL}_{2}}^{\prime }:\text{SL}_{2}\rightarrow C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D711})^{\circ }$
le morphisme principal de
$\unicode[STIX]{x1D711}_{|\text{SL}_{2}}^{\prime }:\text{SL}_{2}\rightarrow C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D711})^{\circ }$
le morphisme principal de
![]() $\text{SL}_{2}$
à valeur dans
$\text{SL}_{2}$
à valeur dans
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D711})^{\circ }$
associé à l’épinglage choisi. Nous avons alors que
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D711})^{\circ }$
associé à l’épinglage choisi. Nous avons alors que
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D711}^{\prime })^{\circ }=C_{C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D711})^{\circ }}(\unicode[STIX]{x1D711}_{|\text{SL}_{2}}^{\prime })^{\circ }=Z(C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D711})^{\circ })^{\circ }$
. Pour achever la preuve il ne reste donc qu’à montrer que
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D711}^{\prime })^{\circ }=C_{C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D711})^{\circ }}(\unicode[STIX]{x1D711}_{|\text{SL}_{2}}^{\prime })^{\circ }=Z(C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D711})^{\circ })^{\circ }$
. Pour achever la preuve il ne reste donc qu’à montrer que
![]() $Z(C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D711})^{\circ })^{\circ }=Z(C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})^{\circ })^{\unicode[STIX]{x1D711}(W_{k}),\circ }$
. En effet, on aura alors le résultat voulu puisque
$Z(C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D711})^{\circ })^{\circ }=Z(C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})^{\circ })^{\unicode[STIX]{x1D711}(W_{k}),\circ }$
. En effet, on aura alors le résultat voulu puisque
![]() $C_{M_{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D711}^{\prime })^{\circ }\subseteq C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D711}^{\prime })^{\circ }=Z(C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})^{\circ })^{\unicode[STIX]{x1D711}(W_{k}),\circ }\subseteq Z({\mathcal{M}}_{\unicode[STIX]{x1D711}})$
.
$C_{M_{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D711}^{\prime })^{\circ }\subseteq C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D711}^{\prime })^{\circ }=Z(C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})^{\circ })^{\unicode[STIX]{x1D711}(W_{k}),\circ }\subseteq Z({\mathcal{M}}_{\unicode[STIX]{x1D711}})$
.
Notons que
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})=C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D711})^{\unicode[STIX]{x1D703}}$
. Pour simplifier les notations on pose
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})=C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D711})^{\unicode[STIX]{x1D703}}$
. Pour simplifier les notations on pose
![]() $H=C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
. Il nous reste donc à prouver que
$H=C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
. Il nous reste donc à prouver que
![]() $Z(H^{\unicode[STIX]{x1D703},\circ })^{\circ }=Z(H^{\circ })^{\unicode[STIX]{x1D703},\circ }$
. Calculons les centres ici présents. Nous avons que
$Z(H^{\unicode[STIX]{x1D703},\circ })^{\circ }=Z(H^{\circ })^{\unicode[STIX]{x1D703},\circ }$
. Calculons les centres ici présents. Nous avons que
![]() $Z(H^{\circ })=\bigcap _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}\ker (\unicode[STIX]{x1D6FC})$
et par conséquent
$Z(H^{\circ })=\bigcap _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}\ker (\unicode[STIX]{x1D6FC})$
et par conséquent
![]() $Z(H^{\circ })^{\unicode[STIX]{x1D703},\circ }=((\bigcap _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}\ker (\unicode[STIX]{x1D6FC}))\cap T^{\unicode[STIX]{x1D703},\circ })^{\circ }$
. Comme
$Z(H^{\circ })^{\unicode[STIX]{x1D703},\circ }=((\bigcap _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}\ker (\unicode[STIX]{x1D6FC}))\cap T^{\unicode[STIX]{x1D703},\circ })^{\circ }$
. Comme
![]() $\unicode[STIX]{x1D703}$
préserve un épinglage, on a également grâce au théorème 1.8 (v) de [Reference Digne and MichelDM94],
$\unicode[STIX]{x1D703}$
préserve un épinglage, on a également grâce au théorème 1.8 (v) de [Reference Digne and MichelDM94],
![]() $Z(H^{\unicode[STIX]{x1D703},\circ })=\bigcap _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}/\unicode[STIX]{x1D703}}\ker (\unicode[STIX]{x1D6FC}_{|T^{\unicode[STIX]{x1D703},\circ }})=\bigcap _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}/\unicode[STIX]{x1D703}}\ker (\unicode[STIX]{x1D6FC})\cap T^{\unicode[STIX]{x1D703},\circ }$
, d’où le résultat voulu.◻
$Z(H^{\unicode[STIX]{x1D703},\circ })=\bigcap _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}/\unicode[STIX]{x1D703}}\ker (\unicode[STIX]{x1D6FC}_{|T^{\unicode[STIX]{x1D703},\circ }})=\bigcap _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}/\unicode[STIX]{x1D703}}\ker (\unicode[STIX]{x1D6FC})\cap T^{\unicode[STIX]{x1D703},\circ }$
, d’où le résultat voulu.◻
On appelle tore maximal de
![]() $^{L}\mathbf{G}$
un sous-groupe
$^{L}\mathbf{G}$
un sous-groupe
![]() ${\mathcal{T}}$
de
${\mathcal{T}}$
de
![]() $^{L}\mathbf{G}$
qui se surjecte sur
$^{L}\mathbf{G}$
qui se surjecte sur
![]() $\langle \widehat{\unicode[STIX]{x1D717}}\rangle$
et dont l’intersection
$\langle \widehat{\unicode[STIX]{x1D717}}\rangle$
et dont l’intersection
![]() ${\mathcal{T}}^{\circ }$
avec
${\mathcal{T}}^{\circ }$
avec
![]() $\widehat{\mathbf{G}}$
est un tore maximal de
$\widehat{\mathbf{G}}$
est un tore maximal de
![]() $\widehat{\mathbf{G}}$
. Pour un tel tore, on notera
$\widehat{\mathbf{G}}$
. Pour un tel tore, on notera
![]() $\widehat{\mathbf{T}}:={\mathcal{T}}^{\circ }$
sa partie connexe. Nous avons la suite exacte suivante :
$\widehat{\mathbf{T}}:={\mathcal{T}}^{\circ }$
sa partie connexe. Nous avons la suite exacte suivante :
![]() $\widehat{\mathbf{T}}{\hookrightarrow}{\mathcal{T}}{\twoheadrightarrow}\langle \widehat{\unicode[STIX]{x1D717}}\rangle$
. Le tore
$\widehat{\mathbf{T}}{\hookrightarrow}{\mathcal{T}}{\twoheadrightarrow}\langle \widehat{\unicode[STIX]{x1D717}}\rangle$
. Le tore
![]() ${\mathcal{T}}$
agit par conjugaison sur
${\mathcal{T}}$
agit par conjugaison sur
![]() $\widehat{\mathbf{T}}$
et donc, on en déduit une action de
$\widehat{\mathbf{T}}$
et donc, on en déduit une action de
![]() $\langle \widehat{\unicode[STIX]{x1D717}}\rangle$
sur
$\langle \widehat{\unicode[STIX]{x1D717}}\rangle$
sur
![]() $\widehat{\mathbf{T}}$
qui nous permet de définir une
$\widehat{\mathbf{T}}$
qui nous permet de définir une
![]() $k$
-structure sur
$k$
-structure sur
![]() $\mathbf{T}$
le dual de
$\mathbf{T}$
le dual de
![]() $\widehat{\mathbf{T}}$
. On dira qu’un tore maximal
$\widehat{\mathbf{T}}$
. On dira qu’un tore maximal
![]() ${\mathcal{T}}$
est relevant si le plongement
${\mathcal{T}}$
est relevant si le plongement
![]() $\widehat{\mathbf{T}}{\hookrightarrow}\widehat{\mathbf{G}}$
correspond dualement à un
$\widehat{\mathbf{T}}{\hookrightarrow}\widehat{\mathbf{G}}$
correspond dualement à un
![]() $k$
-plongement
$k$
-plongement
![]() $\mathbf{T}{\hookrightarrow}\mathbf{G}$
. Enfin, on dira que
$\mathbf{T}{\hookrightarrow}\mathbf{G}$
. Enfin, on dira que
![]() ${\mathcal{T}}$
est elliptique dans
${\mathcal{T}}$
est elliptique dans
![]() $^{L}\mathbf{G}$
si
$^{L}\mathbf{G}$
si
![]() ${\mathcal{T}}$
n’est contenu dans aucun Levi propre
${\mathcal{T}}$
n’est contenu dans aucun Levi propre
![]() ${\mathcal{M}}$
de
${\mathcal{M}}$
de
![]() $^{L}\mathbf{G}$
ou de façon équivalente si
$^{L}\mathbf{G}$
ou de façon équivalente si
![]() $Z({\mathcal{T}})^{\circ }=Z(\,^{L}\mathbf{G})^{\circ }$
.
$Z({\mathcal{T}})^{\circ }=Z(\,^{L}\mathbf{G})^{\circ }$
.
Lemme 4.3.3. Soit
![]() ${\mathcal{M}}$
un Levi de
${\mathcal{M}}$
un Levi de
![]() $^{L}\mathbf{G}$
.
$^{L}\mathbf{G}$
.
(i) Si
 ${\mathcal{M}}$
contient
${\mathcal{M}}$
contient
 ${\mathcal{T}}$
, un tore maximal relevant, alors
${\mathcal{T}}$
, un tore maximal relevant, alors
 ${\mathcal{M}}$
est relevant.
${\mathcal{M}}$
est relevant.(ii) Si
 ${\mathcal{M}}$
est relevant et
${\mathcal{M}}$
est relevant et
 ${\mathcal{T}}$
est un tore maximal elliptique de
${\mathcal{T}}$
est un tore maximal elliptique de
 ${\mathcal{M}}$
alors
${\mathcal{M}}$
alors
 ${\mathcal{T}}$
est relevant.
${\mathcal{T}}$
est relevant.
Démonstration.
(i) (Dat) Notons
![]() $({\mathcal{M}}^{\circ })_{ab}$
l’abélianisé de
$({\mathcal{M}}^{\circ })_{ab}$
l’abélianisé de
![]() ${\mathcal{M}}^{\circ }$
qui est un tore. Le groupe
${\mathcal{M}}^{\circ }$
qui est un tore. Le groupe
![]() ${\mathcal{M}}$
agit par conjugaison sur
${\mathcal{M}}$
agit par conjugaison sur
![]() ${\mathcal{M}}^{\circ }$
donc sur
${\mathcal{M}}^{\circ }$
donc sur
![]() $({\mathcal{M}}^{\circ })_{ab}$
. Cette action est triviale sur
$({\mathcal{M}}^{\circ })_{ab}$
. Cette action est triviale sur
![]() ${\mathcal{M}}^{\circ }$
donc nous donne une action de
${\mathcal{M}}^{\circ }$
donc nous donne une action de
![]() $\langle \widehat{\unicode[STIX]{x1D717}}\rangle$
sur
$\langle \widehat{\unicode[STIX]{x1D717}}\rangle$
sur
![]() $({\mathcal{M}}^{\circ })_{ab}$
. Le plongement
$({\mathcal{M}}^{\circ })_{ab}$
. Le plongement
![]() ${\mathcal{T}}^{\circ }\rightarrow {\mathcal{M}}^{\circ }$
induit alors un morphisme
${\mathcal{T}}^{\circ }\rightarrow {\mathcal{M}}^{\circ }$
induit alors un morphisme
![]() $\langle \widehat{\unicode[STIX]{x1D717}}\rangle$
-équivariant
$\langle \widehat{\unicode[STIX]{x1D717}}\rangle$
-équivariant
![]() ${\mathcal{T}}^{\circ }\rightarrow ({\mathcal{M}}^{\circ })_{ab}$
. On obtient ainsi dualement un
${\mathcal{T}}^{\circ }\rightarrow ({\mathcal{M}}^{\circ })_{ab}$
. On obtient ainsi dualement un
![]() $k$
-plongement
$k$
-plongement
![]() $\mathbf{S}{\hookrightarrow}\mathbf{T}$
. Si
$\mathbf{S}{\hookrightarrow}\mathbf{T}$
. Si
![]() ${\mathcal{T}}$
est relevant, on peut choisir un plongement
${\mathcal{T}}$
est relevant, on peut choisir un plongement
![]() $\mathbf{T}{\hookrightarrow}\mathbf{G}$
rationnel, et alors
$\mathbf{T}{\hookrightarrow}\mathbf{G}$
rationnel, et alors
![]() $C_{\mathbf{G}}(\mathbf{S})$
est un Levi rationnel, dual de
$C_{\mathbf{G}}(\mathbf{S})$
est un Levi rationnel, dual de
![]() ${\mathcal{M}}$
, qui est donc relevant.
${\mathcal{M}}$
, qui est donc relevant.
(ii) Le tore
![]() ${\mathcal{T}}$
de
${\mathcal{T}}$
de
![]() ${\mathcal{M}}$
nous fournit dualement un plongement
${\mathcal{M}}$
nous fournit dualement un plongement
![]() $\mathbf{T}{\hookrightarrow}\mathbf{M}_{qd}$
, où
$\mathbf{T}{\hookrightarrow}\mathbf{M}_{qd}$
, où
![]() $\mathbf{M}_{qd}$
est la forme quasi-déployée de
$\mathbf{M}_{qd}$
est la forme quasi-déployée de
![]() $\mathbf{M}$
, un
$\mathbf{M}$
, un
![]() $k$
-sous-groupe de Levi de
$k$
-sous-groupe de Levi de
![]() $\mathbf{G}$
dual de
$\mathbf{G}$
dual de
![]() $\widehat{\mathbf{M}}$
. Comme
$\widehat{\mathbf{M}}$
. Comme
![]() ${\mathcal{T}}$
est elliptique, le rang déployé de
${\mathcal{T}}$
est elliptique, le rang déployé de
![]() $\mathbf{T}$
est le même que celui du centre de
$\mathbf{T}$
est le même que celui du centre de
![]() $\mathbf{M}_{qd}$
, et par conséquent
$\mathbf{M}_{qd}$
, et par conséquent
![]() $\mathbf{T}$
est elliptique. Ainsi, il se plonge dans toutes les formes intérieures de
$\mathbf{T}$
est elliptique. Ainsi, il se plonge dans toutes les formes intérieures de
![]() $\mathbf{M}_{qd}$
(voir par exemple [Reference KalethaKal16, lemme 3.2.1]) donc en particulier dans
$\mathbf{M}_{qd}$
(voir par exemple [Reference KalethaKal16, lemme 3.2.1]) donc en particulier dans
![]() $\mathbf{M}$
et donc
$\mathbf{M}$
et donc
![]() ${\mathcal{T}}$
est relevant.◻
${\mathcal{T}}$
est relevant.◻
Lemme 4.3.4. Soit
![]() $\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D6F7}(W_{k},\mathbf{G})$
. Notons
$\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D6F7}(W_{k},\mathbf{G})$
. Notons
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D711}_{|I_{k}}$
et posons
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D711}_{|I_{k}}$
et posons
![]() ${\mathcal{C}}:=C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})^{\circ }\unicode[STIX]{x1D711}(W_{k})$
qui est un sous-groupe de
${\mathcal{C}}:=C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})^{\circ }\unicode[STIX]{x1D711}(W_{k})$
qui est un sous-groupe de
![]() $^{L}\mathbf{G}$
. Alors il existe
$^{L}\mathbf{G}$
. Alors il existe
![]() ${\mathcal{T}}\subseteq {\mathcal{C}}$
un sous-tore maximal de
${\mathcal{T}}\subseteq {\mathcal{C}}$
un sous-tore maximal de
![]() ${\mathcal{C}}$
tel que
${\mathcal{C}}$
tel que
![]() $Z({\mathcal{T}})^{\circ }=Z({\mathcal{C}})^{\circ }$
.
$Z({\mathcal{T}})^{\circ }=Z({\mathcal{C}})^{\circ }$
.
Démonstration.
Notons
![]() $\unicode[STIX]{x1D703}$
la conjugaison par
$\unicode[STIX]{x1D703}$
la conjugaison par
![]() $\unicode[STIX]{x1D711}(\text{Frob})$
qui est un automorphisme semi-simple de
$\unicode[STIX]{x1D711}(\text{Frob})$
qui est un automorphisme semi-simple de
![]() $C:=C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})^{\circ }$
. Prenons alors
$C:=C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})^{\circ }$
. Prenons alors
![]() $(\widehat{\mathbf{T}},\widehat{\mathbf{B}})$
une paire de Borel de
$(\widehat{\mathbf{T}},\widehat{\mathbf{B}})$
une paire de Borel de
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})^{\circ }$
stable sous
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})^{\circ }$
stable sous
![]() $\unicode[STIX]{x1D703}$
(existe par [Reference SteinbergSte68, théorème 7.5]). Nous pouvons écrire
$\unicode[STIX]{x1D703}$
(existe par [Reference SteinbergSte68, théorème 7.5]). Nous pouvons écrire
![]() ${\mathcal{C}}$
sous la forme
${\mathcal{C}}$
sous la forme
![]() ${\mathcal{C}}:=C\rtimes \langle \unicode[STIX]{x1D703}\rangle$
. On forme alors
${\mathcal{C}}:=C\rtimes \langle \unicode[STIX]{x1D703}\rangle$
. On forme alors
![]() ${\mathcal{T}}:=\widehat{\mathbf{T}}\rtimes \langle \unicode[STIX]{x1D703}\rangle$
qui est un tore maximal de
${\mathcal{T}}:=\widehat{\mathbf{T}}\rtimes \langle \unicode[STIX]{x1D703}\rangle$
qui est un tore maximal de
![]() ${\mathcal{C}}$
. Nous allons modifier
${\mathcal{C}}$
. Nous allons modifier
![]() ${\mathcal{T}}$
pour le rendre elliptique. Toute section
${\mathcal{T}}$
pour le rendre elliptique. Toute section
![]() $\unicode[STIX]{x1D702}$
de la suite exacte
$\unicode[STIX]{x1D702}$
de la suite exacte
![]() $N_{C}(\widehat{\mathbf{T}}){\hookrightarrow}N_{{\mathcal{C}}}(\widehat{\mathbf{T}}){\twoheadrightarrow}\langle \unicode[STIX]{x1D703}\rangle$
(la notation
$N_{C}(\widehat{\mathbf{T}}){\hookrightarrow}N_{{\mathcal{C}}}(\widehat{\mathbf{T}}){\twoheadrightarrow}\langle \unicode[STIX]{x1D703}\rangle$
(la notation
![]() $N_{C}(\widehat{\mathbf{T}})$
signifie le normalisateur de
$N_{C}(\widehat{\mathbf{T}})$
signifie le normalisateur de
![]() $\widehat{\mathbf{T}}$
dans
$\widehat{\mathbf{T}}$
dans
![]() $C$
et idem pour
$C$
et idem pour
![]() $N_{{\mathcal{C}}}(\widehat{\mathbf{T}})$
avec
$N_{{\mathcal{C}}}(\widehat{\mathbf{T}})$
avec
![]() ${\mathcal{C}}$
) nous permet de définir un tore maximal
${\mathcal{C}}$
) nous permet de définir un tore maximal
![]() ${\mathcal{T}}_{\unicode[STIX]{x1D702}}$
par
${\mathcal{T}}_{\unicode[STIX]{x1D702}}$
par
![]() ${\mathcal{T}}_{\unicode[STIX]{x1D702}}:=\widehat{\mathbf{T}}\cdot \unicode[STIX]{x1D702}(\langle \unicode[STIX]{x1D703}\rangle )$
. Une section
${\mathcal{T}}_{\unicode[STIX]{x1D702}}:=\widehat{\mathbf{T}}\cdot \unicode[STIX]{x1D702}(\langle \unicode[STIX]{x1D703}\rangle )$
. Une section
![]() $\unicode[STIX]{x1D702}$
est donnée par
$\unicode[STIX]{x1D702}$
est donnée par
![]() $\unicode[STIX]{x1D702}(\unicode[STIX]{x1D703})=n_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D703}$
où
$\unicode[STIX]{x1D702}(\unicode[STIX]{x1D703})=n_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D703}$
où
![]() $n_{\unicode[STIX]{x1D703}}\in N_{C}(\widehat{\mathbf{T}})$
. On prend alors pour
$n_{\unicode[STIX]{x1D703}}\in N_{C}(\widehat{\mathbf{T}})$
. On prend alors pour
![]() $n_{\unicode[STIX]{x1D703}}$
un élément de
$n_{\unicode[STIX]{x1D703}}$
un élément de
![]() $\unicode[STIX]{x1D703}$
-coxeter, c’est à dire un élément du groupe de Weyl formé en prenant un produit de réflexions simples, une pour chaque orbite sous
$\unicode[STIX]{x1D703}$
-coxeter, c’est à dire un élément du groupe de Weyl formé en prenant un produit de réflexions simples, une pour chaque orbite sous
![]() $\unicode[STIX]{x1D703}$
. Il découle alors du lemme 7.4(i) de [Reference SpringerSpr74] que le tore que l’on obtient est elliptique, ce qui achève la preuve.◻
$\unicode[STIX]{x1D703}$
. Il découle alors du lemme 7.4(i) de [Reference SpringerSpr74] que le tore que l’on obtient est elliptique, ce qui achève la preuve.◻
Rappelons nous que dans le § 4.2 nous avons fixé un tore maximal de référence
![]() $\mathbf{T}_{0}$
, qui nous a permis d’associer à
$\mathbf{T}_{0}$
, qui nous a permis d’associer à
![]() $\mathbf{T}$
, un tore maximal non-ramifié de
$\mathbf{T}$
, un tore maximal non-ramifié de
![]() $\mathbf{G}$
, un élément
$\mathbf{G}$
, un élément
![]() $w\in W_{0}$
, un tore
$w\in W_{0}$
, un tore
![]() $\,^{L}\mathbf{T}=\widehat{\mathbf{T}}_{0}\rtimes \langle w\widehat{\unicode[STIX]{x1D717}}\rangle$
et un plongement
$\,^{L}\mathbf{T}=\widehat{\mathbf{T}}_{0}\rtimes \langle w\widehat{\unicode[STIX]{x1D717}}\rangle$
et un plongement
![]() $\unicode[STIX]{x1D704}:\,^{L}\mathbf{T}{\hookrightarrow}\,^{L}\mathbf{G}$
en choisissant un relèvement
$\unicode[STIX]{x1D704}:\,^{L}\mathbf{T}{\hookrightarrow}\,^{L}\mathbf{G}$
en choisissant un relèvement
![]() ${\dot{w}}\in N(\widehat{\mathbf{T}}_{0},\widehat{\mathbf{G}})$
de
${\dot{w}}\in N(\widehat{\mathbf{T}}_{0},\widehat{\mathbf{G}})$
de
![]() $w$
.
$w$
.
Proposition 4.3.5. Soit
![]() $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{G})$
. Alors les propositions suivantes sont équivalentes
:
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{G})$
. Alors les propositions suivantes sont équivalentes
:
(i)
 $\unicode[STIX]{x1D719}$
est relevant ;
$\unicode[STIX]{x1D719}$
est relevant ;(ii) il existe
 $\mathbf{T}$
un tore maximal non-ramifié de
$\mathbf{T}$
un tore maximal non-ramifié de
 $\mathbf{G}$
et
$\mathbf{G}$
et
 $\unicode[STIX]{x1D719}_{T}\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{T})$
tel que
$\unicode[STIX]{x1D719}_{T}\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{T})$
tel que
 $\unicode[STIX]{x1D719}\sim \unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D719}_{T}$
où
$\unicode[STIX]{x1D719}\sim \unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D719}_{T}$
où
 $\unicode[STIX]{x1D704}:\,^{L}\mathbf{T}{\hookrightarrow}\,^{L}\mathbf{G}$
;
$\unicode[STIX]{x1D704}:\,^{L}\mathbf{T}{\hookrightarrow}\,^{L}\mathbf{G}$
;(iii)
 $\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
est non vide.
$\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
est non vide.
Démonstration.
L’équivalence
![]() $(2)\Leftrightarrow (3)$
est donnée par le théorème 4.2.1. Montrons
$(2)\Leftrightarrow (3)$
est donnée par le théorème 4.2.1. Montrons
![]() $(1)\Leftrightarrow (2)$
.
$(1)\Leftrightarrow (2)$
.
Supposons
![]() $\unicode[STIX]{x1D719}$
relevant. Par définition, il existe
$\unicode[STIX]{x1D719}$
relevant. Par définition, il existe
![]() $\unicode[STIX]{x1D711}^{\prime }:W_{k}^{\prime }\rightarrow \,^{L}\mathbf{G}$
relevant qui étend
$\unicode[STIX]{x1D711}^{\prime }:W_{k}^{\prime }\rightarrow \,^{L}\mathbf{G}$
relevant qui étend
![]() $\unicode[STIX]{x1D719}$
. Notons
$\unicode[STIX]{x1D719}$
. Notons
![]() $\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}_{|W_{k}}^{\prime }$
. Alors le lemme 4.3.2 nous dit que
$\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}_{|W_{k}}^{\prime }$
. Alors le lemme 4.3.2 nous dit que
![]() ${\mathcal{M}}_{\unicode[STIX]{x1D711}}$
factorise
${\mathcal{M}}_{\unicode[STIX]{x1D711}}$
factorise
![]() $\unicode[STIX]{x1D711}^{\prime }$
et est donc un Levi relevant. Le lemme 4.3.4 nous fournit
$\unicode[STIX]{x1D711}^{\prime }$
et est donc un Levi relevant. Le lemme 4.3.4 nous fournit
![]() ${\mathcal{T}}$
un tore maximal de
${\mathcal{T}}$
un tore maximal de
![]() ${\mathcal{C}}:=C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})^{\circ }\unicode[STIX]{x1D711}(W_{k})$
tel que
${\mathcal{C}}:=C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})^{\circ }\unicode[STIX]{x1D711}(W_{k})$
tel que
![]() $Z({\mathcal{T}})^{\circ }=Z({\mathcal{C}})^{\circ }$
. Comme
$Z({\mathcal{T}})^{\circ }=Z({\mathcal{C}})^{\circ }$
. Comme
![]() ${\mathcal{C}}\subseteq {\mathcal{M}}_{\unicode[STIX]{x1D711}}$
on a également que
${\mathcal{C}}\subseteq {\mathcal{M}}_{\unicode[STIX]{x1D711}}$
on a également que
![]() ${\mathcal{T}}$
est un tore maximal de
${\mathcal{T}}$
est un tore maximal de
![]() ${\mathcal{M}}_{\unicode[STIX]{x1D711}}$
. Maintenant
${\mathcal{M}}_{\unicode[STIX]{x1D711}}$
. Maintenant
![]() $Z({\mathcal{T}})^{\circ }=Z({\mathcal{C}})^{\circ }\subseteq Z({\mathcal{M}}_{\unicode[STIX]{x1D711}})^{\circ }$
et comme
$Z({\mathcal{T}})^{\circ }=Z({\mathcal{C}})^{\circ }\subseteq Z({\mathcal{M}}_{\unicode[STIX]{x1D711}})^{\circ }$
et comme
![]() ${\mathcal{T}}$
est un tore maximal de
${\mathcal{T}}$
est un tore maximal de
![]() ${\mathcal{M}}_{\unicode[STIX]{x1D711}}$
on a aussi
${\mathcal{M}}_{\unicode[STIX]{x1D711}}$
on a aussi
![]() $Z({\mathcal{M}}_{\unicode[STIX]{x1D711}})^{\circ }\subseteq Z({\mathcal{T}})^{\circ }$
et par conséquent
$Z({\mathcal{M}}_{\unicode[STIX]{x1D711}})^{\circ }\subseteq Z({\mathcal{T}})^{\circ }$
et par conséquent
![]() $Z({\mathcal{M}}_{\unicode[STIX]{x1D711}})^{\circ }=Z({\mathcal{T}})^{\circ }$
, c’est à dire que
$Z({\mathcal{M}}_{\unicode[STIX]{x1D711}})^{\circ }=Z({\mathcal{T}})^{\circ }$
, c’est à dire que
![]() ${\mathcal{T}}$
est un tore maximal elliptique de
${\mathcal{T}}$
est un tore maximal elliptique de
![]() ${\mathcal{M}}_{\unicode[STIX]{x1D711}}$
. Le lemme 4.3.3
${\mathcal{M}}_{\unicode[STIX]{x1D711}}$
. Le lemme 4.3.3
![]() $(2)$
nous dit alors que
$(2)$
nous dit alors que
![]() ${\mathcal{T}}$
est un tore relevant. De plus comme
${\mathcal{T}}$
est un tore relevant. De plus comme
![]() ${\mathcal{T}}\subseteq {\mathcal{C}}$
, ce tore factorise
${\mathcal{T}}\subseteq {\mathcal{C}}$
, ce tore factorise
![]() $\unicode[STIX]{x1D719}$
et l’on a
$\unicode[STIX]{x1D719}$
et l’on a
![]() $(2)$
.
$(2)$
.
Supposons maintenant qu’il existe
![]() $\mathbf{T}\,\subseteq \,\mathbf{G}$
un tore maximal non-ramifié de
$\mathbf{T}\,\subseteq \,\mathbf{G}$
un tore maximal non-ramifié de
![]() $\mathbf{G}$
et
$\mathbf{G}$
et
![]() $\unicode[STIX]{x1D719}_{T}\,\in \,\unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{T})$
tel que
$\unicode[STIX]{x1D719}_{T}\,\in \,\unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{T})$
tel que
![]() $\unicode[STIX]{x1D719}\sim \unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D719}_{T}$
. On rappelle que
$\unicode[STIX]{x1D719}\sim \unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D719}_{T}$
. On rappelle que
![]() $^{L}\mathbf{T}=\widehat{\mathbf{T}}_{0}\rtimes \langle w\widehat{\unicode[STIX]{x1D717}}\rangle$
. Le paramètre
$^{L}\mathbf{T}=\widehat{\mathbf{T}}_{0}\rtimes \langle w\widehat{\unicode[STIX]{x1D717}}\rangle$
. Le paramètre
![]() $\unicode[STIX]{x1D719}_{T}$
se prolonge en
$\unicode[STIX]{x1D719}_{T}$
se prolonge en
![]() $\unicode[STIX]{x1D711}_{T}\in \unicode[STIX]{x1D6F7}(W_{k},\mathbf{T})$
et on pose
$\unicode[STIX]{x1D711}_{T}\in \unicode[STIX]{x1D6F7}(W_{k},\mathbf{T})$
et on pose
![]() $\unicode[STIX]{x1D711}=\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D711}_{T}\in \unicode[STIX]{x1D6F7}(W_{k},G)$
qui est une extension de
$\unicode[STIX]{x1D711}=\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D711}_{T}\in \unicode[STIX]{x1D6F7}(W_{k},G)$
qui est une extension de
![]() $\unicode[STIX]{x1D719}$
à
$\unicode[STIX]{x1D719}$
à
![]() $W_{k}$
. Ainsi
$W_{k}$
. Ainsi
![]() $\text{Im}(\unicode[STIX]{x1D719})\subseteq \widehat{T}_{0}$
, donc
$\text{Im}(\unicode[STIX]{x1D719})\subseteq \widehat{T}_{0}$
, donc
![]() $\widehat{T}_{0}\subseteq C_{\widehat{G}}(\unicode[STIX]{x1D719})^{\circ }$
et donc
$\widehat{T}_{0}\subseteq C_{\widehat{G}}(\unicode[STIX]{x1D719})^{\circ }$
et donc
![]() $\widehat{T}_{0}\subseteq {\mathcal{M}}_{\unicode[STIX]{x1D719}}$
. Nous avons également que
$\widehat{T}_{0}\subseteq {\mathcal{M}}_{\unicode[STIX]{x1D719}}$
. Nous avons également que
![]() ${\dot{w}}\unicode[STIX]{x1D717}=\unicode[STIX]{x1D711}(\text{Frob})\in {\mathcal{M}}_{\unicode[STIX]{x1D719}}$
. Ainsi
${\dot{w}}\unicode[STIX]{x1D717}=\unicode[STIX]{x1D711}(\text{Frob})\in {\mathcal{M}}_{\unicode[STIX]{x1D719}}$
. Ainsi
![]() $\unicode[STIX]{x1D704}(\,^{L}\mathbf{T})\subseteq {\mathcal{M}}_{\unicode[STIX]{x1D719}}$
et le lemme 4.3.3
$\unicode[STIX]{x1D704}(\,^{L}\mathbf{T})\subseteq {\mathcal{M}}_{\unicode[STIX]{x1D719}}$
et le lemme 4.3.3
![]() $(1)$
nous dit alors que
$(1)$
nous dit alors que
![]() ${\mathcal{M}}_{\unicode[STIX]{x1D719}}$
est relevant. De plus, le lemme 4.3.2 nous construit
${\mathcal{M}}_{\unicode[STIX]{x1D719}}$
est relevant. De plus, le lemme 4.3.2 nous construit
![]() $\unicode[STIX]{x1D711}^{\prime }\in \unicode[STIX]{x1D6F7}(G)$
un paramètre étendant
$\unicode[STIX]{x1D711}^{\prime }\in \unicode[STIX]{x1D6F7}(G)$
un paramètre étendant
![]() $\unicode[STIX]{x1D719}$
et tel que
$\unicode[STIX]{x1D719}$
et tel que
![]() ${\mathcal{M}}_{\unicode[STIX]{x1D711}}$
soit un Levi minimal contenant son image. Comme
${\mathcal{M}}_{\unicode[STIX]{x1D711}}$
soit un Levi minimal contenant son image. Comme
![]() ${\mathcal{M}}_{\unicode[STIX]{x1D711}}$
est relevant, on en déduit que
${\mathcal{M}}_{\unicode[STIX]{x1D711}}$
est relevant, on en déduit que
![]() $\unicode[STIX]{x1D711}^{\prime }$
est relevant et donc que
$\unicode[STIX]{x1D711}^{\prime }$
est relevant et donc que
![]() $\unicode[STIX]{x1D719}$
est relevant.◻
$\unicode[STIX]{x1D719}$
est relevant.◻
Théorème 4.3.6. Soit
![]() $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
. Alors
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
. Alors
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
est non vide si et seulement si
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
est non vide si et seulement si
![]() $\unicode[STIX]{x1D719}$
est relevant.
$\unicode[STIX]{x1D719}$
est relevant.
Démonstration.
La proposition 4.3.5 nous donne le résultat lorsque
![]() $\unicode[STIX]{x1D6EC}=\overline{\mathbb{Q}}_{\ell }$
. Pour le cas général, notons que par la proposition 4.1.1,
$\unicode[STIX]{x1D6EC}=\overline{\mathbb{Q}}_{\ell }$
. Pour le cas général, notons que par la proposition 4.1.1,
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
est non vide si et seulement s’il existe
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
est non vide si et seulement s’il existe
![]() $\unicode[STIX]{x1D719}^{\prime }\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{G})$
tel que
$\unicode[STIX]{x1D719}^{\prime }\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{G})$
tel que
![]() $\unicode[STIX]{x1D719}_{|I_{k}^{\prime \unicode[STIX]{x1D6EC}}}\sim \unicode[STIX]{x1D719}$
et
$\unicode[STIX]{x1D719}_{|I_{k}^{\prime \unicode[STIX]{x1D6EC}}}\sim \unicode[STIX]{x1D719}$
et
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
est non vide, si et seulement s’il existe
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
est non vide, si et seulement s’il existe
![]() $\unicode[STIX]{x1D719}^{\prime }\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{G})$
relevant prolongeant
$\unicode[STIX]{x1D719}^{\prime }\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{G})$
relevant prolongeant
![]() $\unicode[STIX]{x1D719}$
, si et seulement si
$\unicode[STIX]{x1D719}$
, si et seulement si
![]() $\unicode[STIX]{x1D719}$
est relevant.◻
$\unicode[STIX]{x1D719}$
est relevant.◻
4.4 Compatibilité à l’induction et à la restriction parabolique
Cette sous-partie à pour but d’étudier le comportement des catégories
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
vis à vis de l’induction et de la restriction parabolique.
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
vis à vis de l’induction et de la restriction parabolique.
Jusqu’à présent, nous avons considéré l’immeuble de Bruhat–Tits semi-simple, puisque celui-ci est muni d’une structure de complexe polysimplicial. Cependant dans cette section, nous souhaitons comparer l’immeuble d’un Levi et celui de
![]() $G$
. L’immeuble de Bruhat–Tits ‘étendu’ semble alors plus approprié. Cela ne fait pas une grosse différence. En effet nous traitions la structure polysimpliciale de façon purement combinatoire. De plus, les idempotents
$G$
. L’immeuble de Bruhat–Tits ‘étendu’ semble alors plus approprié. Cela ne fait pas une grosse différence. En effet nous traitions la structure polysimpliciale de façon purement combinatoire. De plus, les idempotents
![]() $e_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D70E}}$
auraient très bien pu être définis pour un point quelconque
$e_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D70E}}$
auraient très bien pu être définis pour un point quelconque
![]() $x$
de l’immeuble, on aurait alors eu que
$x$
de l’immeuble, on aurait alors eu que
![]() $e_{\unicode[STIX]{x1D719},x}=e_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D70E}}$
, où
$e_{\unicode[STIX]{x1D719},x}=e_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D70E}}$
, où
![]() $\unicode[STIX]{x1D70E}$
est le plus petit polysimplexe contenant
$\unicode[STIX]{x1D70E}$
est le plus petit polysimplexe contenant
![]() $x$
. Ainsi, dans cette partie seulement, on utilisera l’immeuble de Bruhat–Tits ‘étendu’, que l’on notera
$x$
. Ainsi, dans cette partie seulement, on utilisera l’immeuble de Bruhat–Tits ‘étendu’, que l’on notera
![]() $BT^{e}(G)$
.
$BT^{e}(G)$
.
Soit
![]() $\mathbf{P}$
un
$\mathbf{P}$
un
![]() $k$
-sous-groupe parabolique de
$k$
-sous-groupe parabolique de
![]() $\mathbf{G}$
de quotient de Levi
$\mathbf{G}$
de quotient de Levi
![]() $\mathbf{M}$
défini sur
$\mathbf{M}$
défini sur
![]() $k$
. Prenons
$k$
. Prenons
![]() $\mathbf{S}$
un tore déployé maximal de
$\mathbf{S}$
un tore déployé maximal de
![]() $\mathbf{G}$
contenu dans
$\mathbf{G}$
contenu dans
![]() $\mathbf{P}$
et notons
$\mathbf{P}$
et notons
![]() $\mathbf{T}$
son centralisateur dans
$\mathbf{T}$
son centralisateur dans
![]() $\mathbf{G}$
. Il existe alors un unique relèvement de
$\mathbf{G}$
. Il existe alors un unique relèvement de
![]() $\mathbf{M}$
en un sous-groupe de
$\mathbf{M}$
en un sous-groupe de
![]() $\mathbf{G}$
contenant
$\mathbf{G}$
contenant
![]() $\mathbf{T}$
. Notons
$\mathbf{T}$
. Notons
![]() $\unicode[STIX]{x1D711}$
le système de racines de
$\unicode[STIX]{x1D711}$
le système de racines de
![]() $G$
relativement à
$G$
relativement à
![]() $S$
et
$S$
et
![]() $\unicode[STIX]{x1D711}_{M}\subseteq \unicode[STIX]{x1D711}$
celui de
$\unicode[STIX]{x1D711}_{M}\subseteq \unicode[STIX]{x1D711}$
celui de
![]() $M$
. L’appartement
$M$
. L’appartement
![]() ${\mathcal{A}}_{M}^{e}(\mathbf{S},k)$
de
${\mathcal{A}}_{M}^{e}(\mathbf{S},k)$
de
![]() $BT^{e}(M)$
relativement à
$BT^{e}(M)$
relativement à
![]() $\mathbf{S}$
est égal à
$\mathbf{S}$
est égal à
![]() ${\mathcal{A}}^{e}:={\mathcal{A}}^{e}(\mathbf{S},k)$
mais en ne gardant que les murs associés aux racines affines dont la partie vectorielle est dans
${\mathcal{A}}^{e}:={\mathcal{A}}^{e}(\mathbf{S},k)$
mais en ne gardant que les murs associés aux racines affines dont la partie vectorielle est dans
![]() $\unicode[STIX]{x1D711}_{M}$
. Soit
$\unicode[STIX]{x1D711}_{M}$
. Soit
![]() $x\in {\mathcal{A}}$
, alors
$x\in {\mathcal{A}}$
, alors
![]() $M_{x}^{\circ }=M\cap G_{x}^{\circ }$
et
$M_{x}^{\circ }=M\cap G_{x}^{\circ }$
et
![]() $M_{x}^{+}=M\cap G_{x}^{+}$
(voir [Reference Moy and PrasadMP96, § 4.3]). Rappelons que l’on a déjà défini
$M_{x}^{+}=M\cap G_{x}^{+}$
(voir [Reference Moy and PrasadMP96, § 4.3]). Rappelons que l’on a déjà défini
![]() $\overline{\mathsf{M}}_{x}\simeq M_{x}^{\circ }/M_{x}^{+}$
et posons
$\overline{\mathsf{M}}_{x}\simeq M_{x}^{\circ }/M_{x}^{+}$
et posons
![]() $\overline{\mathsf{P}}_{x}$
l’image de
$\overline{\mathsf{P}}_{x}$
l’image de
![]() $P_{x}:=P\cap G_{x}^{\circ }$
dans
$P_{x}:=P\cap G_{x}^{\circ }$
dans
![]() $\overline{\mathsf{G}}_{x}$
.
$\overline{\mathsf{G}}_{x}$
.
Lemme 4.4.1.
![]() $\overline{\mathsf{P}}_{x}$
est un sous-groupe parabolique de
$\overline{\mathsf{P}}_{x}$
est un sous-groupe parabolique de
![]() $\overline{\mathsf{G}}_{x}$
de quotient de Levi
$\overline{\mathsf{G}}_{x}$
de quotient de Levi
![]() $\overline{\mathsf{M}}_{x}$
.
$\overline{\mathsf{M}}_{x}$
.
Démonstration.
Notons
![]() $\unicode[STIX]{x1D711}_{P}$
le sous-ensemble de
$\unicode[STIX]{x1D711}_{P}$
le sous-ensemble de
![]() $\unicode[STIX]{x1D711}$
des racines
$\unicode[STIX]{x1D711}$
des racines
![]() $\unicode[STIX]{x1D6FC}$
telles que
$\unicode[STIX]{x1D6FC}$
telles que
![]() $P$
soit engendré par
$P$
soit engendré par
![]() $T$
et les
$T$
et les
![]() $U_{\unicode[STIX]{x1D6FC}}$
,
$U_{\unicode[STIX]{x1D6FC}}$
,
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D711}_{P}$
. Notons maintenant
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D711}_{P}$
. Notons maintenant
![]() $\unicode[STIX]{x1D711}_{x}$
(resp.
$\unicode[STIX]{x1D711}_{x}$
(resp.
![]() $\unicode[STIX]{x1D711}_{P,x}$
, resp.
$\unicode[STIX]{x1D711}_{P,x}$
, resp.
![]() $\unicode[STIX]{x1D711}_{M,x}$
) les racines affines passant par
$\unicode[STIX]{x1D711}_{M,x}$
) les racines affines passant par
![]() $x$
et dont la partie vectorielle est dans
$x$
et dont la partie vectorielle est dans
![]() $\unicode[STIX]{x1D711}$
(resp.
$\unicode[STIX]{x1D711}$
(resp.
![]() $\unicode[STIX]{x1D711}_{P}$
, resp.
$\unicode[STIX]{x1D711}_{P}$
, resp.
![]() $\unicode[STIX]{x1D711}_{M}$
). Alors
$\unicode[STIX]{x1D711}_{M}$
). Alors
![]() $\unicode[STIX]{x1D711}_{x}$
(resp.
$\unicode[STIX]{x1D711}_{x}$
(resp.
![]() $\unicode[STIX]{x1D711}_{P,x}$
, resp.
$\unicode[STIX]{x1D711}_{P,x}$
, resp.
![]() $\unicode[STIX]{x1D711}_{M,x}$
) est le système de racine de
$\unicode[STIX]{x1D711}_{M,x}$
) est le système de racine de
![]() $\overline{\mathsf{G}}_{x}$
(resp.
$\overline{\mathsf{G}}_{x}$
(resp.
![]() $\overline{\mathsf{P}}_{x}$
, resp.
$\overline{\mathsf{P}}_{x}$
, resp.
![]() $\overline{\mathsf{M}}_{x}$
) relativement à
$\overline{\mathsf{M}}_{x}$
) relativement à
![]() $S_{x}$
. Choisissons maintenant une forme linéaire
$S_{x}$
. Choisissons maintenant une forme linéaire
![]() $f:X^{\ast }(\mathbf{S})\rightarrow \mathbb{R}$
telle que
$f:X^{\ast }(\mathbf{S})\rightarrow \mathbb{R}$
telle que
![]() $\unicode[STIX]{x1D711}_{P}=\{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D711},f(\unicode[STIX]{x1D6FC})\geqslant 0\}$
et
$\unicode[STIX]{x1D711}_{P}=\{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D711},f(\unicode[STIX]{x1D6FC})\geqslant 0\}$
et
![]() $\unicode[STIX]{x1D711}_{M}=\{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D711},f(\unicode[STIX]{x1D6FC})=0\}$
. Les sous-ensembles
$\unicode[STIX]{x1D711}_{M}=\{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D711},f(\unicode[STIX]{x1D6FC})=0\}$
. Les sous-ensembles
![]() $\unicode[STIX]{x1D711}_{P,x}$
et
$\unicode[STIX]{x1D711}_{P,x}$
et
![]() $\unicode[STIX]{x1D711}_{M,x}$
vérifient alors
$\unicode[STIX]{x1D711}_{M,x}$
vérifient alors
![]() $\unicode[STIX]{x1D711}_{P,x}=\{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D711}_{x},f(\unicode[STIX]{x1D6FC})\geqslant 0\}$
et
$\unicode[STIX]{x1D711}_{P,x}=\{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D711}_{x},f(\unicode[STIX]{x1D6FC})\geqslant 0\}$
et
![]() $\unicode[STIX]{x1D711}_{M,x}=\{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D711}_{x},f(\unicode[STIX]{x1D6FC})=0\}$
, ce qui montre que
$\unicode[STIX]{x1D711}_{M,x}=\{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D711}_{x},f(\unicode[STIX]{x1D6FC})=0\}$
, ce qui montre que
![]() $\overline{\mathsf{P}}_{x}$
est bien un parabolique de
$\overline{\mathsf{P}}_{x}$
est bien un parabolique de
![]() $\overline{\mathsf{G}}_{x}$
de quotient de Levi
$\overline{\mathsf{G}}_{x}$
de quotient de Levi
![]() $\overline{\mathsf{M}}_{x}$
.◻
$\overline{\mathsf{M}}_{x}$
.◻
Considérons
![]() $\widehat{\mathbf{M}}$
un dual de
$\widehat{\mathbf{M}}$
un dual de
![]() $\mathbf{M}$
sur
$\mathbf{M}$
sur
![]() $\overline{\mathbb{Q}}_{\ell }$
muni d’un plongement
$\overline{\mathbb{Q}}_{\ell }$
muni d’un plongement
![]() $\unicode[STIX]{x1D704}:^{L}\mathbf{M}{\hookrightarrow}^{L}\mathbf{G}$
(voir [Reference BorelBor79, § 3.4]), qui induit une application
$\unicode[STIX]{x1D704}:^{L}\mathbf{M}{\hookrightarrow}^{L}\mathbf{G}$
(voir [Reference BorelBor79, § 3.4]), qui induit une application
![]() $\unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{M})\rightarrow \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
.
$\unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{M})\rightarrow \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
.
Commençons par vérifier la compatibilité à la restriction parabolique.
Théorème 4.4.2. Soit
![]() $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
. Alors pour tout sous-groupe parabolique
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
. Alors pour tout sous-groupe parabolique
![]() $\mathbf{P}$
de
$\mathbf{P}$
de
![]() $\mathbf{G}$
ayant pour facteur de Levi
$\mathbf{G}$
ayant pour facteur de Levi
![]() $\mathbf{M}$
, on a
$\mathbf{M}$
, on a
où le produit est pris sur les
![]() $\unicode[STIX]{x1D719}_{M}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{M})$
tels que
$\unicode[STIX]{x1D719}_{M}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{M})$
tels que
![]() $\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D719}_{M}\sim \unicode[STIX]{x1D719}$
et
$\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D719}_{M}\sim \unicode[STIX]{x1D719}$
et
![]() $r_{P}^{G}$
désigne la restriction parabolique.
$r_{P}^{G}$
désigne la restriction parabolique.
Démonstration.
Soit
![]() $V\in \text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
. La restriction parabolique préserve le niveau donc
$V\in \text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
. La restriction parabolique préserve le niveau donc
![]() $r_{P}^{G}(V)\in \text{Rep}_{\unicode[STIX]{x1D6EC}}^{0}(M)$
. Il nous suffit donc de montrer que pour
$r_{P}^{G}(V)\in \text{Rep}_{\unicode[STIX]{x1D6EC}}^{0}(M)$
. Il nous suffit donc de montrer que pour
![]() $x\in {\mathcal{A}}_{M}^{e}$
et
$x\in {\mathcal{A}}_{M}^{e}$
et
![]() $\unicode[STIX]{x1D719}^{\prime }\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{M})$
tel que
$\unicode[STIX]{x1D719}^{\prime }\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{M})$
tel que
![]() $\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D719}^{\prime }\neq \unicode[STIX]{x1D719}$
, on a
$\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D719}^{\prime }\neq \unicode[STIX]{x1D719}$
, on a
![]() $e_{\unicode[STIX]{x1D719}^{\prime },x}r_{P}^{G}(V)=0$
.
$e_{\unicode[STIX]{x1D719}^{\prime },x}r_{P}^{G}(V)=0$
.
Nous avons
![]() $r_{P}^{G}(V)^{M_{x}^{+}}\simeq r_{\overline{\mathsf{P}}_{x}}^{\overline{\mathsf{G}}_{x}}(V^{G_{x}^{+}})$
(voir [Reference DatDat09, propositions 3.1 et 6.2]), donc
$r_{P}^{G}(V)^{M_{x}^{+}}\simeq r_{\overline{\mathsf{P}}_{x}}^{\overline{\mathsf{G}}_{x}}(V^{G_{x}^{+}})$
(voir [Reference DatDat09, propositions 3.1 et 6.2]), donc
![]() $e_{\unicode[STIX]{x1D719}^{\prime },x}r_{P}^{G}(V)^{M_{x}^{+}}\simeq e_{\unicode[STIX]{x1D719}^{\prime },x}r_{\overline{\mathsf{P}}_{x}}^{\overline{\mathsf{G}}_{x}}(V^{G_{x}^{+}})\simeq e_{\unicode[STIX]{x1D719}^{\prime },x}r_{\overline{\mathsf{P}}_{x}}^{\overline{\mathsf{G}}_{x}}(e_{\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D719}^{\prime },x}(V^{G_{x}^{+}}))$
(la dernière égalité provient de 2.1.2). Or par hypothèse
$e_{\unicode[STIX]{x1D719}^{\prime },x}r_{P}^{G}(V)^{M_{x}^{+}}\simeq e_{\unicode[STIX]{x1D719}^{\prime },x}r_{\overline{\mathsf{P}}_{x}}^{\overline{\mathsf{G}}_{x}}(V^{G_{x}^{+}})\simeq e_{\unicode[STIX]{x1D719}^{\prime },x}r_{\overline{\mathsf{P}}_{x}}^{\overline{\mathsf{G}}_{x}}(e_{\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D719}^{\prime },x}(V^{G_{x}^{+}}))$
(la dernière égalité provient de 2.1.2). Or par hypothèse
![]() $\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D719}^{\prime }\neq \unicode[STIX]{x1D719}$
donc
$\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D719}^{\prime }\neq \unicode[STIX]{x1D719}$
donc
![]() $e_{\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D719}^{\prime },x}(V^{G_{x}^{+}})=0$
d’où le résultat.◻
$e_{\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D719}^{\prime },x}(V^{G_{x}^{+}})=0$
d’où le résultat.◻
Passons maintenant à l’induction parabolique.
Théorème 4.4.3. Soit
![]() $\unicode[STIX]{x1D719}_{M}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{M})$
et notons
$\unicode[STIX]{x1D719}_{M}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{M})$
et notons
![]() $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
son image par
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
son image par
![]() $\unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{M})\rightarrow \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
. Alors pour tout sous-groupe parabolique
$\unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{M})\rightarrow \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
. Alors pour tout sous-groupe parabolique
![]() $\mathbf{P}$
de
$\mathbf{P}$
de
![]() $\mathbf{G}$
ayant pour facteur de Levi
$\mathbf{G}$
ayant pour facteur de Levi
![]() $\mathbf{M}$
, on a
$\mathbf{M}$
, on a
où
![]() $i_{P}^{G}$
désigne l’induction parabolique.
$i_{P}^{G}$
désigne l’induction parabolique.
Démonstration.
Cela découle du théorème 4.4.2 et du fait que
![]() $r_{P}^{G}$
est adjoint à gauche de
$r_{P}^{G}$
est adjoint à gauche de
![]() $i_{P}^{G}$
.◻
$i_{P}^{G}$
.◻
Proposition 4.4.4. Soit
![]() $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
. Alors si
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
. Alors si
![]() $\unicode[STIX]{x1D719}$
est discret (c’est-à-dire ne se factorise pas par un Levi rationnel propre) toutes les représentations de
$\unicode[STIX]{x1D719}$
est discret (c’est-à-dire ne se factorise pas par un Levi rationnel propre) toutes les représentations de
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
sont cuspidales et toutes les représentations irréductibles de
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
sont cuspidales et toutes les représentations irréductibles de
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
sont supercuspidales.
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
sont supercuspidales.
De plus, si
![]() $\mathbf{G}$
est quasi-déployé, on a la réciproque pour la cuspidalité, c’est à dire que
$\mathbf{G}$
est quasi-déployé, on a la réciproque pour la cuspidalité, c’est à dire que
![]() $\unicode[STIX]{x1D719}$
est discret si et seulement si
$\unicode[STIX]{x1D719}$
est discret si et seulement si
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
ne contient que des cuspidales.
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
ne contient que des cuspidales.
Démonstration.
La cuspidalité découle immédiatement du théorème 4.4.2. Pour la supercuspidalité, remarquons que si
![]() $\unicode[STIX]{x1D719}$
est discret, alors le théorème 4.4.3 montre qu’une induite n’as pas de composante dans
$\unicode[STIX]{x1D719}$
est discret, alors le théorème 4.4.3 montre qu’une induite n’as pas de composante dans
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
et donc n’a pas de sous-quotient irréductible dans
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
et donc n’a pas de sous-quotient irréductible dans
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
.
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
.
Maintenant si
![]() $\mathbf{G}$
est quasi-déployé et que
$\mathbf{G}$
est quasi-déployé et que
![]() $\unicode[STIX]{x1D719}$
n’est pas discret, alors
$\unicode[STIX]{x1D719}$
n’est pas discret, alors
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
contient des induites d’après le théorème 4.4.3 (nous utilisons l’hypothèse quasi-déployé pour dire que ces facteurs sont non-nuls).◻
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
contient des induites d’après le théorème 4.4.3 (nous utilisons l’hypothèse quasi-déployé pour dire que ces facteurs sont non-nuls).◻
Si
![]() $\mathbf{G}$
n’est pas quasi-déployé l’équivalence peut être fausse, comme le montre l’exemple de
$\mathbf{G}$
n’est pas quasi-déployé l’équivalence peut être fausse, comme le montre l’exemple de
![]() $G=D^{\times }$
où
$G=D^{\times }$
où
![]() $D$
est une
$D$
est une
![]() $k$
-algèbre à division de dimension finie. Alors toutes les représentations sont cuspidales, en particulier
$k$
-algèbre à division de dimension finie. Alors toutes les représentations sont cuspidales, en particulier
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{1}(G)$
ne contient que des cuspidales.
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{1}(G)$
ne contient que des cuspidales.
Avoir
![]() $\unicode[STIX]{x1D719}$
discret n’est pas une condition nécessaire pour avoir des cuspidales (supercuspidales) dans
$\unicode[STIX]{x1D719}$
discret n’est pas une condition nécessaire pour avoir des cuspidales (supercuspidales) dans
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
. En effet, toute cuspidale unipotente se retrouvera dans
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
. En effet, toute cuspidale unipotente se retrouvera dans
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{1}(G)$
.
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{1}(G)$
.
Soit
![]() $\unicode[STIX]{x1D719}_{M}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{M})$
et posons
$\unicode[STIX]{x1D719}_{M}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{M})$
et posons
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D719}_{M}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
. Nous venons de voir que
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D704}\circ \unicode[STIX]{x1D719}_{M}\in \unicode[STIX]{x1D6F7}_{m}(I_{k}^{\unicode[STIX]{x1D6EC}},\mathbf{G})$
. Nous venons de voir que
![]() $i_{P}^{G}$
réalise un foncteur
$i_{P}^{G}$
réalise un foncteur
La catégorie
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}_{M}}(M)$
est un facteur direct de
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}_{M}}(M)$
est un facteur direct de
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{0}(M)$
, on a donc un foncteur
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{0}(M)$
, on a donc un foncteur
![]() $e_{\unicode[STIX]{x1D719}_{M}}:\text{Rep}_{\unicode[STIX]{x1D6EC}}^{0}(M)\rightarrow \text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}_{M}}(M)$
. Définissons
$e_{\unicode[STIX]{x1D719}_{M}}:\text{Rep}_{\unicode[STIX]{x1D6EC}}^{0}(M)\rightarrow \text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}_{M}}(M)$
. Définissons
![]() $r_{P}^{G,\unicode[STIX]{x1D719}_{M}}:=e_{\unicode[STIX]{x1D719}_{M}}\circ r_{P}^{G}$
, de sorte que
$r_{P}^{G,\unicode[STIX]{x1D719}_{M}}:=e_{\unicode[STIX]{x1D719}_{M}}\circ r_{P}^{G}$
, de sorte que
![]() $r_{P}^{G,\unicode[STIX]{x1D719}_{M}}$
soit un foncteur
$r_{P}^{G,\unicode[STIX]{x1D719}_{M}}$
soit un foncteur
Lemme 4.4.5. Le foncteur
![]() $r_{P}^{G,\unicode[STIX]{x1D719}_{M}}$
est adjoint à gauche de
$r_{P}^{G,\unicode[STIX]{x1D719}_{M}}$
est adjoint à gauche de
![]() $i_{P}^{G}$
.
$i_{P}^{G}$
.
Démonstration.
Soient
![]() $V\in \text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
et
$V\in \text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
et
![]() $W\in \text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}_{M}}(M)$
. Nous savons déjà que
$W\in \text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}_{M}}(M)$
. Nous savons déjà que
![]() $r_{P}^{G}$
est adjoint à gauche de
$r_{P}^{G}$
est adjoint à gauche de
![]() $i_{P}^{G}$
, donc
$i_{P}^{G}$
, donc
![]() $\text{Hom}(r_{P}^{G}(V),W)=\text{Hom}(V,i_{P}^{G}(W))$
. Maintenant
$\text{Hom}(r_{P}^{G}(V),W)=\text{Hom}(V,i_{P}^{G}(W))$
. Maintenant
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}_{M}}(M)$
est un facteur direct de
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}_{M}}(M)$
est un facteur direct de
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{0}(M)$
de sorte que
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{0}(M)$
de sorte que
![]() $\text{Hom}(r_{P}^{G}(V),W)=\text{Hom}(r_{P}^{G,\unicode[STIX]{x1D719}_{M}}(V),W)$
et on a le résultat.◻
$\text{Hom}(r_{P}^{G}(V),W)=\text{Hom}(r_{P}^{G,\unicode[STIX]{x1D719}_{M}}(V),W)$
et on a le résultat.◻
Théorème 4.4.6. Notons
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
le centralisateur dans
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
le centralisateur dans
![]() $\widehat{\mathbf{G}}$
de l’image de
$\widehat{\mathbf{G}}$
de l’image de
![]() $\unicode[STIX]{x1D719}$
. Alors si
$\unicode[STIX]{x1D719}$
. Alors si
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})\subseteq \unicode[STIX]{x1D704}(\widehat{\mathbf{M}})$
la paire de foncteurs adjoints
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})\subseteq \unicode[STIX]{x1D704}(\widehat{\mathbf{M}})$
la paire de foncteurs adjoints
![]() $(i_{P}^{G},r_{P}^{G,\unicode[STIX]{x1D719}_{M}})$
réalise une équivalence de catégories entre
$(i_{P}^{G},r_{P}^{G,\unicode[STIX]{x1D719}_{M}})$
réalise une équivalence de catégories entre
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}_{M}}(M)$
et
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}_{M}}(M)$
et
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
.
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
.
Démonstration.
Soit
![]() $V\in \text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}_{M}}(M)$
. Par adjonction, nous avons une application
$V\in \text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}_{M}}(M)$
. Par adjonction, nous avons une application
![]() $r_{\mathbf{P}}^{\mathbf{G}}i_{\mathbf{P}}^{\mathbf{G}}(V)\rightarrow V$
. Le lemme géométrique nous dit qu’elle est surjective et que son noyau
$r_{\mathbf{P}}^{\mathbf{G}}i_{\mathbf{P}}^{\mathbf{G}}(V)\rightarrow V$
. Le lemme géométrique nous dit qu’elle est surjective et que son noyau
![]() $W$
, admet une filtration dont les composantes du gradué associé sont isomorphes à
$W$
, admet une filtration dont les composantes du gradué associé sont isomorphes à
![]() $(i_{M\cap \,^{w}P}^{M}\circ w\circ r_{\,^{w^{-1}}P\cap M}^{M})(V)$
, où
$(i_{M\cap \,^{w}P}^{M}\circ w\circ r_{\,^{w^{-1}}P\cap M}^{M})(V)$
, où
![]() $w$
parcourt un ensemble
$w$
parcourt un ensemble
![]() ${\mathcal{W}}^{P}$
de représentants particuliers dans
${\mathcal{W}}^{P}$
de représentants particuliers dans
![]() $G$
des doubles classes
$G$
des doubles classes
![]() $W_{M,0}\backslash W_{0}/W_{M,0}$
ne contenant pas la classe triviale (
$W_{M,0}\backslash W_{0}/W_{M,0}$
ne contenant pas la classe triviale (
![]() $W_{M,0}$
est le groupe de Weyl de
$W_{M,0}$
est le groupe de Weyl de
![]() $\mathbf{M}$
). Nous souhaitons montrer que
$\mathbf{M}$
). Nous souhaitons montrer que
![]() $e_{\unicode[STIX]{x1D719}_{M}}(W)=0$
.
$e_{\unicode[STIX]{x1D719}_{M}}(W)=0$
.
Prenons donc
![]() $w\in {\mathcal{W}}^{P}$
et montrons que
$w\in {\mathcal{W}}^{P}$
et montrons que
Identifions les paramètres inertiels avec des classes de conjugaison semi-simples
![]() $F$
-stables. Ainsi
$F$
-stables. Ainsi
![]() $\unicode[STIX]{x1D719}_{M}$
correspond à
$\unicode[STIX]{x1D719}_{M}$
correspond à
![]() $s\in (\text{M}_{ss}^{\ast })^{F}$
et on note
$s\in (\text{M}_{ss}^{\ast })^{F}$
et on note
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{s}(M)$
pour
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{s}(M)$
pour
![]() $\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}_{M}}(M)$
. Par le théorème 4.4.2
$\text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}_{M}}(M)$
. Par le théorème 4.4.2
où
![]() $\{s_{1},\ldots ,s_{n}\}$
est l’image réciproque de
$\{s_{1},\ldots ,s_{n}\}$
est l’image réciproque de
![]() $\{s\}$
par l’application
$\{s\}$
par l’application
![]() $((\,^{w^{-1}}\text{M}\cap \text{M})_{ss}^{\ast })^{F}\rightarrow (\text{M}_{ss}^{\ast })^{F}$
. Donc
$((\,^{w^{-1}}\text{M}\cap \text{M})_{ss}^{\ast })^{F}\rightarrow (\text{M}_{ss}^{\ast })^{F}$
. Donc
Enfin par le théorème 4.4.3
où
![]() $\{t_{1},\ldots ,t_{m}\}$
est l’image de
$\{t_{1},\ldots ,t_{m}\}$
est l’image de
![]() $\{\,^{w}s_{1},\ldots ,\,^{w}s_{n}\}$
par l’application
$\{\,^{w}s_{1},\ldots ,\,^{w}s_{n}\}$
par l’application
![]() $((\text{M}\cap ^{w}\text{M})_{ss}^{\ast })^{F}\rightarrow (\text{M}_{ss}^{\ast })^{F}$
.
$((\text{M}\cap ^{w}\text{M})_{ss}^{\ast })^{F}\rightarrow (\text{M}_{ss}^{\ast })^{F}$
.
On veut donc montrer qu’aucun des
![]() $t_{i}$
n’est égal à
$t_{i}$
n’est égal à
![]() $s$
. Supposons le contraire et que l’on ait un
$s$
. Supposons le contraire et que l’on ait un
![]() $i$
tel que
$i$
tel que
![]() $t_{i}=s$
. Par construction,
$t_{i}=s$
. Par construction,
![]() $t_{i}$
est dans l’une des classes de conjugaison sur
$t_{i}$
est dans l’une des classes de conjugaison sur
![]() $\text{M}^{\ast }$
des
$\text{M}^{\ast }$
des
![]() $^{w}(s_{j})$
, donc il existe
$^{w}(s_{j})$
, donc il existe
![]() $g\in \text{M}^{\ast }$
et
$g\in \text{M}^{\ast }$
et
![]() $j\in \{1,\ldots ,n\}$
tels que
$j\in \{1,\ldots ,n\}$
tels que
![]() $t_{i}=^{gw}(s_{j})$
. De même par construction des
$t_{i}=^{gw}(s_{j})$
. De même par construction des
![]() $s_{j}$
, il existe
$s_{j}$
, il existe
![]() $h\in \text{M}^{\ast }$
tel que
$h\in \text{M}^{\ast }$
tel que
![]() $s_{j}=^{h}s$
. Donc
$s_{j}=^{h}s$
. Donc
![]() $s=t_{i}=^{gwh}(s)$
et
$s=t_{i}=^{gwh}(s)$
et
![]() $gwh\in C_{\text{G}^{\ast }}(s)\subseteq \text{M}^{\ast }$
(par hypothèse), ce qui est absurde car
$gwh\in C_{\text{G}^{\ast }}(s)\subseteq \text{M}^{\ast }$
(par hypothèse), ce qui est absurde car
![]() $w\notin \text{M}^{\ast }$
. Ceci nous montre que
$w\notin \text{M}^{\ast }$
. Ceci nous montre que
![]() $e_{\unicode[STIX]{x1D719}_{M}}(W)=0$
et donc que
$e_{\unicode[STIX]{x1D719}_{M}}(W)=0$
et donc que
![]() $r_{\mathbf{P}}^{\mathbf{G},\unicode[STIX]{x1D719}_{M}}i_{\mathbf{P}}^{\mathbf{G}}(V)\overset{{\sim}}{\rightarrow }V$
est un isomorphisme.
$r_{\mathbf{P}}^{\mathbf{G},\unicode[STIX]{x1D719}_{M}}i_{\mathbf{P}}^{\mathbf{G}}(V)\overset{{\sim}}{\rightarrow }V$
est un isomorphisme.
Montrons maintenant que le foncteur
![]() $r_{\mathbf{P}}^{\mathbf{G},\unicode[STIX]{x1D719}_{M}}$
est conservatif. Ceci nous permettra de conclure grâce au lemme 4.4.7 ci-dessous. Comme les catégories considérées sont abéliennes et que
$r_{\mathbf{P}}^{\mathbf{G},\unicode[STIX]{x1D719}_{M}}$
est conservatif. Ceci nous permettra de conclure grâce au lemme 4.4.7 ci-dessous. Comme les catégories considérées sont abéliennes et que
![]() $r_{\mathbf{P}}^{\mathbf{G},\unicode[STIX]{x1D719}_{M}}$
est exact, il nous suffit de montrer que si
$r_{\mathbf{P}}^{\mathbf{G},\unicode[STIX]{x1D719}_{M}}$
est exact, il nous suffit de montrer que si
![]() $V\neq 0$
alors
$V\neq 0$
alors
![]() $r_{\mathbf{P}}^{\mathbf{G},\unicode[STIX]{x1D719}_{M}}(V)\neq 0$
.
$r_{\mathbf{P}}^{\mathbf{G},\unicode[STIX]{x1D719}_{M}}(V)\neq 0$
.
Prenons donc
![]() $V\in \text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
tel que
$V\in \text{Rep}_{\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}}(G)$
tel que
![]() $V\neq 0$
. Il existe
$V\neq 0$
. Il existe
![]() $x\in {\mathcal{A}}^{e}$
tel que
$x\in {\mathcal{A}}^{e}$
tel que
![]() $e_{\unicode[STIX]{x1D719},x}V\neq 0$
. Notons
$e_{\unicode[STIX]{x1D719},x}V\neq 0$
. Notons
![]() $s\in (\text{M}_{ss}^{\ast })^{F}$
la classe de conjugaison semi-simple correspondant à
$s\in (\text{M}_{ss}^{\ast })^{F}$
la classe de conjugaison semi-simple correspondant à
![]() $\unicode[STIX]{x1D719}_{M}$
. Comme
$\unicode[STIX]{x1D719}_{M}$
. Comme
![]() $e_{\unicode[STIX]{x1D719},x}V\neq 0$
, il existe
$e_{\unicode[STIX]{x1D719},x}V\neq 0$
, il existe
![]() $s_{x}\in (\overline{\mathsf{M}}_{x}^{\ast })_{ss}$
dont l’image par
$s_{x}\in (\overline{\mathsf{M}}_{x}^{\ast })_{ss}$
dont l’image par
![]() $(\overline{\text{M}}_{x}^{\ast })_{ss}^{F}\rightarrow (\text{M}_{ss}^{\ast })^{F}$
est
$(\overline{\text{M}}_{x}^{\ast })_{ss}^{F}\rightarrow (\text{M}_{ss}^{\ast })^{F}$
est
![]() $s$
et telle que
$s$
et telle que
![]() $e_{s_{x},\unicode[STIX]{x1D6EC}}^{\overline{\mathsf{G}}_{x}}V^{G_{x}^{+}}\neq 0$
. L’hypothèse
$e_{s_{x},\unicode[STIX]{x1D6EC}}^{\overline{\mathsf{G}}_{x}}V^{G_{x}^{+}}\neq 0$
. L’hypothèse
![]() $C_{\text{G}^{\ast }}(s)\subseteq \text{M}^{\ast }$
peut se retraduire, si l’on voit
$C_{\text{G}^{\ast }}(s)\subseteq \text{M}^{\ast }$
peut se retraduire, si l’on voit
![]() $s$
comme un élément de
$s$
comme un élément de
![]() $\text{T}^{\ast }$
, de la manière suivante : si
$\text{T}^{\ast }$
, de la manière suivante : si
![]() $w\in W_{0}$
est tel que
$w\in W_{0}$
est tel que
![]() $ws=s$
alors
$ws=s$
alors
![]() $w\in W_{M,0}$
. Or l’application
$w\in W_{M,0}$
. Or l’application
![]() $(\overline{\text{M}}_{x}^{\ast })_{ss}\rightarrow (\text{M}_{ss}^{\ast })$
est définie par
$(\overline{\text{M}}_{x}^{\ast })_{ss}\rightarrow (\text{M}_{ss}^{\ast })$
est définie par
![]() $\text{T}_{x}^{\ast }/W_{M,x}\rightarrow \text{T}^{\ast }/W_{M,0}$
et comme
$\text{T}_{x}^{\ast }/W_{M,x}\rightarrow \text{T}^{\ast }/W_{M,0}$
et comme
![]() $W_{M,x}=W_{M,0}\cap W_{x}$
on en déduit que
$W_{M,x}=W_{M,0}\cap W_{x}$
on en déduit que
![]() $s_{x}$
vérifie les mêmes hypothèses que
$s_{x}$
vérifie les mêmes hypothèses que
![]() $s$
, c’est à dire
$s$
, c’est à dire
![]() $C_{\overline{\text{G}}_{x}^{\ast }}(s_{x})\subseteq \overline{\text{M}}_{x}^{\ast }$
.
$C_{\overline{\text{G}}_{x}^{\ast }}(s_{x})\subseteq \overline{\text{M}}_{x}^{\ast }$
.
Maintenant, nous avons vu dans la preuve du théorème 4.4.2 que
En notant
![]() $r_{\overline{\mathsf{P}}_{x}}^{\overline{\mathsf{G}}_{x},s_{x}}$
le foncteur
$r_{\overline{\mathsf{P}}_{x}}^{\overline{\mathsf{G}}_{x},s_{x}}$
le foncteur
![]() $e_{s_{x},\unicode[STIX]{x1D6EC}}^{\overline{\mathsf{M}}_{x}}r_{\overline{\mathsf{P}}_{x}}^{\overline{\mathsf{G}}_{x}}$
, on a
$e_{s_{x},\unicode[STIX]{x1D6EC}}^{\overline{\mathsf{M}}_{x}}r_{\overline{\mathsf{P}}_{x}}^{\overline{\mathsf{G}}_{x}}$
, on a
Comme
![]() $C_{\overline{\text{G}}_{x}^{\ast }}(s_{x})\subseteq \overline{\text{M}}_{x}^{\ast }$
le théorème B’ de [Reference Bonnafé and RouquierBR03] nous dit que
$C_{\overline{\text{G}}_{x}^{\ast }}(s_{x})\subseteq \overline{\text{M}}_{x}^{\ast }$
le théorème B’ de [Reference Bonnafé and RouquierBR03] nous dit que
![]() $r_{\overline{\mathsf{P}}_{x}}^{\overline{\mathsf{G}}_{x},s_{x}}$
réalise une équivalence de catégories. En particulier il est conservatif et comme
$r_{\overline{\mathsf{P}}_{x}}^{\overline{\mathsf{G}}_{x},s_{x}}$
réalise une équivalence de catégories. En particulier il est conservatif et comme
![]() $e_{s_{x},\unicode[STIX]{x1D6EC}}^{\overline{\mathsf{G}}_{x}}(V^{G_{x}^{+}})\neq 0$
on a
$e_{s_{x},\unicode[STIX]{x1D6EC}}^{\overline{\mathsf{G}}_{x}}(V^{G_{x}^{+}})\neq 0$
on a
et donc
![]() $r_{\mathbf{P}}^{\mathbf{G},\unicode[STIX]{x1D719}_{M}}(V)\neq 0$
ce qui achève la preuve.◻
$r_{\mathbf{P}}^{\mathbf{G},\unicode[STIX]{x1D719}_{M}}(V)\neq 0$
ce qui achève la preuve.◻
Lemme 4.4.7. Soient
![]() ${\mathcal{C}}$
,
${\mathcal{C}}$
,
![]() ${\mathcal{D}}$
deux catégories et
${\mathcal{D}}$
deux catégories et
![]() $F:{\mathcal{C}}\rightarrow {\mathcal{D}}$
un foncteur. Si
$F:{\mathcal{C}}\rightarrow {\mathcal{D}}$
un foncteur. Si
![]() $F$
est conservatif et admet un adjoint à droite (ou à gauche) pleinement fidèle, alors
$F$
est conservatif et admet un adjoint à droite (ou à gauche) pleinement fidèle, alors
![]() $F$
réalise une équivalence de catégories.
$F$
réalise une équivalence de catégories.
Démonstration.
Soit
![]() $G$
un adjoint à droite. Le cas d’un adjoint à gauche se traite de la même manière par dualité. Le foncteur
$G$
un adjoint à droite. Le cas d’un adjoint à gauche se traite de la même manière par dualité. Le foncteur
![]() $G$
étant pleinement fidèle, le morphisme
$G$
étant pleinement fidèle, le morphisme
![]() $\unicode[STIX]{x1D6FC}:FG\rightarrow \text{id}_{{\mathcal{D}}}$
est un isomorphisme naturel. Nous devons montrer que
$\unicode[STIX]{x1D6FC}:FG\rightarrow \text{id}_{{\mathcal{D}}}$
est un isomorphisme naturel. Nous devons montrer que
![]() $\unicode[STIX]{x1D6FD}:\text{id}_{{\mathcal{C}}}\rightarrow GF$
est également un isomorphisme. Par les axiomes d’adjonctions, la composition
$\unicode[STIX]{x1D6FD}:\text{id}_{{\mathcal{C}}}\rightarrow GF$
est également un isomorphisme. Par les axiomes d’adjonctions, la composition
est
![]() $\text{id}_{F(x)}$
pour tout
$\text{id}_{F(x)}$
pour tout
![]() $x\in {\mathcal{C}}$
. Comme
$x\in {\mathcal{C}}$
. Comme
![]() $\unicode[STIX]{x1D6FC}$
est déjà un isomorphisme, on en déduit que
$\unicode[STIX]{x1D6FC}$
est déjà un isomorphisme, on en déduit que
![]() $F(\unicode[STIX]{x1D6FD}_{x})$
est un isomorphisme, et donc que
$F(\unicode[STIX]{x1D6FD}_{x})$
est un isomorphisme, et donc que
![]() $\unicode[STIX]{x1D6FD}_{x}$
est un isomorphisme puisque
$\unicode[STIX]{x1D6FD}_{x}$
est un isomorphisme puisque
![]() $F$
est conservatif.◻
$F$
est conservatif.◻
4.5 Compatibilité à la correspondance de Langlands
Dans cette partie nous prendrons
![]() $\unicode[STIX]{x1D6EC}=\overline{\mathbb{Q}}_{\ell }$
et
$\unicode[STIX]{x1D6EC}=\overline{\mathbb{Q}}_{\ell }$
et
![]() $k$
de caractéristique nulle. La correspondance de Langlands locale prédit une application à fibres finies
$k$
de caractéristique nulle. La correspondance de Langlands locale prédit une application à fibres finies
![]() $\text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)\rightarrow \unicode[STIX]{x1D6F7}(\mathbf{G})$
,
$\text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)\rightarrow \unicode[STIX]{x1D6F7}(\mathbf{G})$
,
![]() $\unicode[STIX]{x1D70B}\mapsto \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70B}}$
. Dans des cas où elle est connue, nous souhaitons vérifier que la décomposition du théorème 3.4.5 est bien compatible à cette dernière, c’est à dire que si
$\unicode[STIX]{x1D70B}\mapsto \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70B}}$
. Dans des cas où elle est connue, nous souhaitons vérifier que la décomposition du théorème 3.4.5 est bien compatible à cette dernière, c’est à dire que si
![]() $\unicode[STIX]{x1D70B}\in \text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)$
est une représentation de niveau 0 alors
$\unicode[STIX]{x1D70B}\in \text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)$
est une représentation de niveau 0 alors
![]() $\unicode[STIX]{x1D70B}\in \text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
avec
$\unicode[STIX]{x1D70B}\in \text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
avec
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70B}|I_{k}}\sim \unicode[STIX]{x1D719}$
.
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70B}|I_{k}}\sim \unicode[STIX]{x1D719}$
.
La correspondance de Langlands est connue dans plusieurs cas dont : les tores (prouvé par Langlands lui-même), les représentations unipotentes des groupes
![]() $p$
-adiques adjoints [Reference LusztigLus95, Reference LusztigLus02] et les groupes classiques [Reference Harris and TaylorHT01, Reference HenniartHen00, Reference ArthurArt13, Reference MokMok15, Reference Kaletha, Minguez, Shin and WhiteKMSW14]. La compatibilité à la correspondance de Langlands pour les tores est contenue dans le théorème 4.2.1. Pour ce qui est des représentations unipotentes, par construction, elle appartiennent toutes à
$p$
-adiques adjoints [Reference LusztigLus95, Reference LusztigLus02] et les groupes classiques [Reference Harris and TaylorHT01, Reference HenniartHen00, Reference ArthurArt13, Reference MokMok15, Reference Kaletha, Minguez, Shin and WhiteKMSW14]. La compatibilité à la correspondance de Langlands pour les tores est contenue dans le théorème 4.2.1. Pour ce qui est des représentations unipotentes, par construction, elle appartiennent toutes à
![]() $\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{1}(G)$
. Par conséquent, dans cette section nous examinerons le cas des groupes classiques. Notons que
$\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{1}(G)$
. Par conséquent, dans cette section nous examinerons le cas des groupes classiques. Notons que
![]() $\mathbf{G}=\text{GL}_{n}$
a déjà été fait dans [Reference DatDat16, § 3.2.6], on se concentrera ici sur les autres cas. Dans le but d’utiliser les résultats de [Reference Lust and StevensLS16], nous supposerons de plus que
$\mathbf{G}=\text{GL}_{n}$
a déjà été fait dans [Reference DatDat16, § 3.2.6], on se concentrera ici sur les autres cas. Dans le but d’utiliser les résultats de [Reference Lust and StevensLS16], nous supposerons de plus que
![]() $k$
est de caractéristique résiduelle impaire.
$k$
est de caractéristique résiduelle impaire.
Commençons par expliquer ce que l’on entend par un groupe classique. Soit
![]() $k^{\prime }$
une extension de degré au plus 2 de
$k^{\prime }$
une extension de degré au plus 2 de
![]() $k$
et
$k$
et
![]() $\mathfrak{f}^{\prime }$
son corps résiduel. Notons
$\mathfrak{f}^{\prime }$
son corps résiduel. Notons
![]() $\unicode[STIX]{x1D70E}$
le générateur du groupe de Galois de
$\unicode[STIX]{x1D70E}$
le générateur du groupe de Galois de
![]() $k^{\prime }/k$
et
$k^{\prime }/k$
et
![]() $N_{k^{\prime }/k}:k^{\prime \times }\rightarrow k^{\times }$
l’application norme. Fixons un signe
$N_{k^{\prime }/k}:k^{\prime \times }\rightarrow k^{\times }$
l’application norme. Fixons un signe
![]() $\unicode[STIX]{x1D700}=\pm 1$
et soit
$\unicode[STIX]{x1D700}=\pm 1$
et soit
![]() $(V,h)$
un espace
$(V,h)$
un espace
![]() $k^{\prime }/k$
-
$k^{\prime }/k$
-
![]() $\unicode[STIX]{x1D700}$
-hermitien non-dégénéré. Dans cette partie
$\unicode[STIX]{x1D700}$
-hermitien non-dégénéré. Dans cette partie
![]() $G:=U(V)^{\circ }$
est la composante connexe du groupe des
$G:=U(V)^{\circ }$
est la composante connexe du groupe des
![]() $k$
-points du groupe réductif déterminé par
$k$
-points du groupe réductif déterminé par
![]() $(V,h)$
, c’est à dire
$(V,h)$
, c’est à dire
![]() $U(V):=\{g\in \text{Aut}_{k^{\prime }}(V),h(gv,gw)=h(v,w)\text{ pour tout }v,w\in V\}$
et
$U(V):=\{g\in \text{Aut}_{k^{\prime }}(V),h(gv,gw)=h(v,w)\text{ pour tout }v,w\in V\}$
et
![]() $U(V)^{\circ }:=\{g\in U(V),N_{k^{\prime }/k}\,\text{det}_{k^{\prime }}(g)=1\}$
.
$U(V)^{\circ }:=\{g\in U(V),N_{k^{\prime }/k}\,\text{det}_{k^{\prime }}(g)=1\}$
.
La correspondance de Langlands pour les groupes classiques (restreinte à
![]() $W_{k}$
) est compatible à l’induction parabolique (voir [Reference MoussaouiMou17a, théorème 4.9]). Il en est de même pour
$W_{k}$
) est compatible à l’induction parabolique (voir [Reference MoussaouiMou17a, théorème 4.9]). Il en est de même pour
![]() $\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
d’après le § 4.4. Nous pouvons ainsi nous restreindre ici aux représentations irréductibles cuspidales. On pose
$\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
d’après le § 4.4. Nous pouvons ainsi nous restreindre ici aux représentations irréductibles cuspidales. On pose
![]() ${\mathcal{A}}(G)$
l’ensemble des classes d’équivalence des représentations irréductibles cuspidales de
${\mathcal{A}}(G)$
l’ensemble des classes d’équivalence des représentations irréductibles cuspidales de
![]() $G$
et
$G$
et
![]() ${\mathcal{A}}_{[0]}(G)$
le sous-ensemble des représentations de niveau 0. Soit
${\mathcal{A}}_{[0]}(G)$
le sous-ensemble des représentations de niveau 0. Soit
![]() $\unicode[STIX]{x1D70C}$
une représentation irréductible cuspidale de
$\unicode[STIX]{x1D70C}$
une représentation irréductible cuspidale de
![]() $\text{GL}_{n}(k^{\prime })$
. On définit la représentation
$\text{GL}_{n}(k^{\prime })$
. On définit la représentation
![]() $\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}$
de
$\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}$
de
![]() $\text{GL}_{n}(k^{\prime })$
par
$\text{GL}_{n}(k^{\prime })$
par
![]() $\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}(g)=\unicode[STIX]{x1D70C}(\,^{t}\unicode[STIX]{x1D70E}(g^{-1}))$
, où
$\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}(g)=\unicode[STIX]{x1D70C}(\,^{t}\unicode[STIX]{x1D70E}(g^{-1}))$
, où
![]() $^{t}g$
désigne la transposée de
$^{t}g$
désigne la transposée de
![]() $g$
. On dit alors que
$g$
. On dit alors que
![]() $\unicode[STIX]{x1D70C}$
est auto-duale si
$\unicode[STIX]{x1D70C}$
est auto-duale si
![]() $\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}\simeq \unicode[STIX]{x1D70C}$
et on pose
$\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}\simeq \unicode[STIX]{x1D70C}$
et on pose
![]() ${\mathcal{A}}_{n}^{\unicode[STIX]{x1D70E}}(k^{\prime })$
l’ensemble des représentations irréductibles cuspidales auto-duales de
${\mathcal{A}}_{n}^{\unicode[STIX]{x1D70E}}(k^{\prime })$
l’ensemble des représentations irréductibles cuspidales auto-duales de
![]() $\text{GL}_{n}(k^{\prime })$
,
$\text{GL}_{n}(k^{\prime })$
,
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D70E}}(k^{\prime }):=\bigcup _{n\geqslant 1}{\mathcal{A}}_{n}^{\unicode[STIX]{x1D70E}}(k^{\prime })$
et
${\mathcal{A}}^{\unicode[STIX]{x1D70E}}(k^{\prime }):=\bigcup _{n\geqslant 1}{\mathcal{A}}_{n}^{\unicode[STIX]{x1D70E}}(k^{\prime })$
et
![]() ${\mathcal{A}}_{[0]}^{\unicode[STIX]{x1D70E}}(k^{\prime })$
le sous-ensemble de
${\mathcal{A}}_{[0]}^{\unicode[STIX]{x1D70E}}(k^{\prime })$
le sous-ensemble de
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D70E}}(k^{\prime })$
composé des représentations de niveau 0.
${\mathcal{A}}^{\unicode[STIX]{x1D70E}}(k^{\prime })$
composé des représentations de niveau 0.
Notons
![]() $H=H^{-}\oplus H^{+}$
le plan hyperbolique, c’est à dire,
$H=H^{-}\oplus H^{+}$
le plan hyperbolique, c’est à dire,
![]() $H^{\pm }$
est un
$H^{\pm }$
est un
![]() $k^{\prime }$
-espace vectoriel de dimension 1 de base
$k^{\prime }$
-espace vectoriel de dimension 1 de base
![]() $e_{\pm }$
et
$e_{\pm }$
et
![]() $H$
est muni de la forme
$H$
est muni de la forme
![]() $h_{H}$
donnée par
$h_{H}$
donnée par
![]() $h_{H}(\unicode[STIX]{x1D706}_{-}e_{-}+\unicode[STIX]{x1D706}_{+}e_{+},\unicode[STIX]{x1D707}_{-}e_{-}+\unicode[STIX]{x1D707}_{+}e_{+})=\unicode[STIX]{x1D706}_{-}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D707}_{+})+\unicode[STIX]{x1D700}\unicode[STIX]{x1D706}_{+}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D707}_{-})$
. Pour un entier
$h_{H}(\unicode[STIX]{x1D706}_{-}e_{-}+\unicode[STIX]{x1D706}_{+}e_{+},\unicode[STIX]{x1D707}_{-}e_{-}+\unicode[STIX]{x1D707}_{+}e_{+})=\unicode[STIX]{x1D706}_{-}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D707}_{+})+\unicode[STIX]{x1D700}\unicode[STIX]{x1D706}_{+}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D707}_{-})$
. Pour un entier
![]() $n\geqslant 0$
, on pose
$n\geqslant 0$
, on pose
![]() $V_{n}:=V\oplus nH$
muni de la forme
$V_{n}:=V\oplus nH$
muni de la forme
![]() $h_{n}:=h\oplus h_{H}\oplus \cdots \oplus h_{H}$
et
$h_{n}:=h\oplus h_{H}\oplus \cdots \oplus h_{H}$
et
![]() $G_{n}:=U(V_{n})^{\circ }$
. Le stabilisateur dans
$G_{n}:=U(V_{n})^{\circ }$
. Le stabilisateur dans
![]() $G_{n}$
de la décomposition
$G_{n}$
de la décomposition
![]() $V_{n}=nH^{-}\oplus V\oplus nH^{+}$
est un sous-groupe de Levi
$V_{n}=nH^{-}\oplus V\oplus nH^{+}$
est un sous-groupe de Levi
![]() $M_{n}$
de
$M_{n}$
de
![]() $G_{n}$
et l’on a un isomorphisme
$G_{n}$
et l’on a un isomorphisme
![]() $M_{n}\simeq \text{GL}_{n}(k^{\prime })\times G$
. Le stabilisateur de
$M_{n}\simeq \text{GL}_{n}(k^{\prime })\times G$
. Le stabilisateur de
![]() $nH^{-}$
est quand à lui un sous-groupe parabolique
$nH^{-}$
est quand à lui un sous-groupe parabolique
![]() $P_{n}$
de
$P_{n}$
de
![]() $G_{n}$
de facteur de Levi
$G_{n}$
de facteur de Levi
![]() $M_{n}$
. Ainsi si
$M_{n}$
. Ainsi si
![]() $\unicode[STIX]{x1D70C}\in {\mathcal{A}}_{n}^{\unicode[STIX]{x1D70E}}(k^{\prime })$
et
$\unicode[STIX]{x1D70C}\in {\mathcal{A}}_{n}^{\unicode[STIX]{x1D70E}}(k^{\prime })$
et
![]() $\unicode[STIX]{x1D70B}\in {\mathcal{A}}(G)$
, on peut former
$\unicode[STIX]{x1D70B}\in {\mathcal{A}}(G)$
, on peut former
![]() $\unicode[STIX]{x1D70C}\otimes \unicode[STIX]{x1D70B}$
que l’on considère comme une représentation de
$\unicode[STIX]{x1D70C}\otimes \unicode[STIX]{x1D70B}$
que l’on considère comme une représentation de
![]() $M_{n}$
. Définissons pour
$M_{n}$
. Définissons pour
![]() $s\in \mathbb{C}$
,
$s\in \mathbb{C}$
,
![]() $I(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70B},s):=i_{P_{n}}^{G_{n}}\unicode[STIX]{x1D70C}|\text{det}(\cdot )|_{k^{\prime }}^{s}\,\otimes \unicode[STIX]{x1D70B}$
.
$I(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70B},s):=i_{P_{n}}^{G_{n}}\unicode[STIX]{x1D70C}|\text{det}(\cdot )|_{k^{\prime }}^{s}\,\otimes \unicode[STIX]{x1D70B}$
.
Théorème 4.5.1 [Sil80, théorème 1.6]. Si
![]() $I(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70B},s)$
est réductible pour un certain
$I(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70B},s)$
est réductible pour un certain
![]() $s\in \mathbb{R}$
alors il existe un unique réel positif
$s\in \mathbb{R}$
alors il existe un unique réel positif
![]() $s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})$
tel que,
$s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})$
tel que,
![]() $I(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70B},s)$
est réductible si et seulement si
$I(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70B},s)$
est réductible si et seulement si
![]() $s=\pm s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})$
.
$s=\pm s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})$
.
Si
![]() $I(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70B},s)$
est irréductible pour tout
$I(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70B},s)$
est irréductible pour tout
![]() $s\in \mathbb{R}$
, on pose alors
$s\in \mathbb{R}$
, on pose alors
![]() $s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})=0$
. Définissons alors l’ensemble de Jordans
$s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})=0$
. Définissons alors l’ensemble de Jordans
![]() $\text{Jord}(\unicode[STIX]{x1D70B})$
par
$\text{Jord}(\unicode[STIX]{x1D70B})$
par
Rappelons que comme
![]() $G$
est un groupe classique on a la correspondance de Langlands locale,
$G$
est un groupe classique on a la correspondance de Langlands locale,
![]() $\text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)\rightarrow \unicode[STIX]{x1D6F7}(\mathbf{G})$
,
$\text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)\rightarrow \unicode[STIX]{x1D6F7}(\mathbf{G})$
,
![]() $\unicode[STIX]{x1D70B}\mapsto \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70B}}$
. Jusqu’à présent nos paramètres de Langlands
$\unicode[STIX]{x1D70B}\mapsto \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70B}}$
. Jusqu’à présent nos paramètres de Langlands
![]() $\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D6F7}(\mathbf{G})$
étaient de la forme
$\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D6F7}(\mathbf{G})$
étaient de la forme
![]() $\unicode[STIX]{x1D711}:W_{k}^{\prime }\rightarrow \,^{L}\text{}\text{G}(\overline{\mathbb{Q}}_{\ell })$
avec
$\unicode[STIX]{x1D711}:W_{k}^{\prime }\rightarrow \,^{L}\text{}\text{G}(\overline{\mathbb{Q}}_{\ell })$
avec
![]() $W_{k}^{\prime }=W_{k}\ltimes \overline{\mathbb{Q}}_{\ell }$
. Dans cette section seulement, on considére une autre version du groupe de Weil–Deligne :
$W_{k}^{\prime }=W_{k}\ltimes \overline{\mathbb{Q}}_{\ell }$
. Dans cette section seulement, on considére une autre version du groupe de Weil–Deligne :
![]() $W_{k}^{\prime }\simeq W_{k}\times \text{SL}_{2}(\overline{\mathbb{Q}}_{\ell })$
. Ainsi les paramètres de Langlands sont de la forme
$W_{k}^{\prime }\simeq W_{k}\times \text{SL}_{2}(\overline{\mathbb{Q}}_{\ell })$
. Ainsi les paramètres de Langlands sont de la forme
![]() $\unicode[STIX]{x1D711}:W_{k}\times \text{SL}_{2}(\overline{\mathbb{Q}}_{\ell })\rightarrow \,^{L}\mathbf{G}$
. Notons
$\unicode[STIX]{x1D711}:W_{k}\times \text{SL}_{2}(\overline{\mathbb{Q}}_{\ell })\rightarrow \,^{L}\mathbf{G}$
. Notons
![]() $N_{\widehat{\mathbf{G}}}$
la dimension de l’espace vectoriel sur lequel agit naturellement
$N_{\widehat{\mathbf{G}}}$
la dimension de l’espace vectoriel sur lequel agit naturellement
![]() $\widehat{\mathbf{G}}$
. Alors si
$\widehat{\mathbf{G}}$
. Alors si
![]() $\unicode[STIX]{x1D711}:W_{k}\times \text{SL}_{2}(\overline{\mathbb{Q}}_{\ell })\rightarrow \,^{L}\mathbf{G}$
est un paramètre de Langlands, on notera
$\unicode[STIX]{x1D711}:W_{k}\times \text{SL}_{2}(\overline{\mathbb{Q}}_{\ell })\rightarrow \,^{L}\mathbf{G}$
est un paramètre de Langlands, on notera
![]() $\tilde{\unicode[STIX]{x1D711}}:W_{k^{\prime }}\times \text{SL}_{2}(\overline{\mathbb{Q}}_{\ell })\rightarrow \text{GL}_{N_{\widehat{\mathbf{G}}}}(\overline{\mathbb{Q}}_{\ell })$
l’application obtenue en restreignant
$\tilde{\unicode[STIX]{x1D711}}:W_{k^{\prime }}\times \text{SL}_{2}(\overline{\mathbb{Q}}_{\ell })\rightarrow \text{GL}_{N_{\widehat{\mathbf{G}}}}(\overline{\mathbb{Q}}_{\ell })$
l’application obtenue en restreignant
![]() $\unicode[STIX]{x1D711}$
à
$\unicode[STIX]{x1D711}$
à
![]() $W_{k^{\prime }}$
et en la composant avec
$W_{k^{\prime }}$
et en la composant avec
![]() $\widehat{\mathbf{G}}{\hookrightarrow}\text{GL}_{N_{\widehat{\mathbf{G}}}}(\overline{\mathbb{Q}}_{\ell })$
. Il est attendu (et connu au moins dans le cas où
$\widehat{\mathbf{G}}{\hookrightarrow}\text{GL}_{N_{\widehat{\mathbf{G}}}}(\overline{\mathbb{Q}}_{\ell })$
. Il est attendu (et connu au moins dans le cas où
![]() $\mathbf{G}$
est quasi-déployé, voir par exemple [Reference MoeglinMoe14]) que le paramètre
$\mathbf{G}$
est quasi-déployé, voir par exemple [Reference MoeglinMoe14]) que le paramètre
![]() $\tilde{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D70B}}$
soit décrit grâce à l’ensemble de Jordan
$\tilde{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D70B}}$
soit décrit grâce à l’ensemble de Jordan
![]() $\text{Jord}(\unicode[STIX]{x1D70B})$
de la façon suivante.
$\text{Jord}(\unicode[STIX]{x1D70B})$
de la façon suivante.
Théorème 4.5.2 [Reference MoeglinMoe14]. Si
![]() $\mathbf{G}$
est un groupe classique quasi-déployé et
$\mathbf{G}$
est un groupe classique quasi-déployé et
![]() $\unicode[STIX]{x1D70B}\in {\mathcal{A}}(G)$
, on a
$\unicode[STIX]{x1D70B}\in {\mathcal{A}}(G)$
, on a
où
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}$
est la représentation irréductible de
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}$
est la représentation irréductible de
![]() $W_{k^{\prime }}$
correspondant à
$W_{k^{\prime }}$
correspondant à
![]() $\unicode[STIX]{x1D70C}$
via la correspondance de Langlands locale pour
$\unicode[STIX]{x1D70C}$
via la correspondance de Langlands locale pour
![]() $\text{GL}_{n}$
et
$\text{GL}_{n}$
et
![]() $st_{m}$
est la représentation irréductible
$st_{m}$
est la représentation irréductible
![]() $m$
-dimensionnelle de
$m$
-dimensionnelle de
![]() $\text{SL}_{2}(\overline{\mathbb{Q}}_{\ell })$
.
$\text{SL}_{2}(\overline{\mathbb{Q}}_{\ell })$
.
Le résultat précédent étant connu dans le cas où
![]() $\mathbf{G}$
est quasi-déployé et le théorème 3.4.5 nécessitant l’hypothèse
$\mathbf{G}$
est quasi-déployé et le théorème 3.4.5 nécessitant l’hypothèse
![]() $K$
-déployé, nous nous limiterons ici au cas où
$K$
-déployé, nous nous limiterons ici au cas où
![]() $\mathbf{G}$
est un groupe classique non-ramifié, c’est à dire un groupe spécial orthogonal impair
$\mathbf{G}$
est un groupe classique non-ramifié, c’est à dire un groupe spécial orthogonal impair
![]() $\text{SO}_{2n+1}$
, un groupe spécial orthogonal pair
$\text{SO}_{2n+1}$
, un groupe spécial orthogonal pair
![]() $\text{SO}_{2n}$
(groupe spécial orthogonal déployé) ou
$\text{SO}_{2n}$
(groupe spécial orthogonal déployé) ou
![]() $\text{SO}_{2n}^{\ast }$
(groupe spécial orthogonal quasi-déployé associé à une extension quadratique non-ramifiée
$\text{SO}_{2n}^{\ast }$
(groupe spécial orthogonal quasi-déployé associé à une extension quadratique non-ramifiée
![]() $k^{\prime }/k$
), un groupe symplectique
$k^{\prime }/k$
), un groupe symplectique
![]() $\text{Sp}_{2n}$
ou un groupe unitaire
$\text{Sp}_{2n}$
ou un groupe unitaire
![]() $U_{n}(k^{\prime }/k)$
où
$U_{n}(k^{\prime }/k)$
où
![]() $k^{\prime }$
est une extension non-ramifiée de
$k^{\prime }$
est une extension non-ramifiée de
![]() $k$
.
$k$
.
Pour comprendre
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70B}}$
nous avons donc besoin de comprendre
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70B}}$
nous avons donc besoin de comprendre
![]() $\text{Jord}(\unicode[STIX]{x1D70B})$
et en particulier
$\text{Jord}(\unicode[STIX]{x1D70B})$
et en particulier
![]() $s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})$
. Nous allons pour cela nous appuyer sur les résultats obtenus dans [Reference Lust and StevensLS16].
$s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})$
. Nous allons pour cela nous appuyer sur les résultats obtenus dans [Reference Lust and StevensLS16].
Soit
![]() $\unicode[STIX]{x1D70B}\in {\mathcal{A}}_{[0]}(G)$
. Il existe alors
$\unicode[STIX]{x1D70B}\in {\mathcal{A}}_{[0]}(G)$
. Il existe alors
![]() $x\in BT_{0}$
et
$x\in BT_{0}$
et
![]() $s\in (\overline{\mathsf{G}}_{x}^{\ast })_{ss}$
tels que
$s\in (\overline{\mathsf{G}}_{x}^{\ast })_{ss}$
tels que
![]() $e_{s,\overline{\mathbb{Q}}_{\ell }}^{\overline{\mathsf{G}}_{x}}\unicode[STIX]{x1D70B}^{G_{x}^{+}}$
. Comme nous sommes dans le cas où
$e_{s,\overline{\mathbb{Q}}_{\ell }}^{\overline{\mathsf{G}}_{x}}\unicode[STIX]{x1D70B}^{G_{x}^{+}}$
. Comme nous sommes dans le cas où
![]() $\mathbf{G}$
est un groupe classique, le groupe
$\mathbf{G}$
est un groupe classique, le groupe
![]() $\overline{\mathsf{G}}_{x}$
se décompose en un produit de deux groupes
$\overline{\mathsf{G}}_{x}$
se décompose en un produit de deux groupes
![]() $\overline{\mathsf{G}}_{x}\simeq \overline{\mathsf{G}}_{x,1}\times \overline{\mathsf{G}}_{x,2}$
, où les
$\overline{\mathsf{G}}_{x}\simeq \overline{\mathsf{G}}_{x,1}\times \overline{\mathsf{G}}_{x,2}$
, où les
![]() $\overline{\mathsf{G}}_{x,i}$
sont des groupes classiques (voir par exemple [Reference Lust and StevensLS16, § 2]). Ainsi
$\overline{\mathsf{G}}_{x,i}$
sont des groupes classiques (voir par exemple [Reference Lust and StevensLS16, § 2]). Ainsi
![]() $s$
correspond via cet isomorphisme à
$s$
correspond via cet isomorphisme à
![]() $(s_{1},s_{2})$
où
$(s_{1},s_{2})$
où
![]() $s_{i}\in (\overline{\mathsf{G}}_{x,i}^{\ast })_{ss}$
. Soit
$s_{i}\in (\overline{\mathsf{G}}_{x,i}^{\ast })_{ss}$
. Soit
![]() $P\in \mathfrak{f}^{\prime }[X]$
un polynôme unitaire. Désignons par
$P\in \mathfrak{f}^{\prime }[X]$
un polynôme unitaire. Désignons par
![]() $\unicode[STIX]{x1D70F}$
le générateur du groupe de Galois
$\unicode[STIX]{x1D70F}$
le générateur du groupe de Galois
![]() $\text{Gal}(\mathfrak{f}^{\prime }/\mathfrak{f})$
. On définit
$\text{Gal}(\mathfrak{f}^{\prime }/\mathfrak{f})$
. On définit
![]() $P^{\unicode[STIX]{x1D70F}}(X):=\unicode[STIX]{x1D70F}(P(0))^{-1}X^{\text{deg}(P)}\unicode[STIX]{x1D70F}(P)(1/X)$
et on dit que
$P^{\unicode[STIX]{x1D70F}}(X):=\unicode[STIX]{x1D70F}(P(0))^{-1}X^{\text{deg}(P)}\unicode[STIX]{x1D70F}(P)(1/X)$
et on dit que
![]() $P$
est auto-dual si
$P$
est auto-dual si
![]() $P=P^{\unicode[STIX]{x1D70F}}$
. Le polynôme caractéristique
$P=P^{\unicode[STIX]{x1D70F}}$
. Le polynôme caractéristique
![]() $P_{s_{i}}$
de
$P_{s_{i}}$
de
![]() $s_{i}$
est alors un polynôme unitaire auto-dual et on l’écrit (comme dans [Reference Lust and StevensLS16, § 7])
$s_{i}$
est alors un polynôme unitaire auto-dual et on l’écrit (comme dans [Reference Lust and StevensLS16, § 7])
![]() $P_{s_{i}}(X)=\prod _{P}P(X)^{a_{P}^{(i)}}$
, où le produit est pris sur l’ensemble des polynômes unitaires irréductibles auto-duaux sur
$P_{s_{i}}(X)=\prod _{P}P(X)^{a_{P}^{(i)}}$
, où le produit est pris sur l’ensemble des polynômes unitaires irréductibles auto-duaux sur
![]() $\mathfrak{f}^{\prime }$
(une telle écriture est possible car la série de Deligne–Lusztig associée à
$\mathfrak{f}^{\prime }$
(une telle écriture est possible car la série de Deligne–Lusztig associée à
![]() $s_{i}$
contient une représentation cuspidale et que si
$s_{i}$
contient une représentation cuspidale et que si
![]() $P_{s_{i}}$
contenait un facteur de la forme
$P_{s_{i}}$
contenait un facteur de la forme
![]() $P(X)P^{\unicode[STIX]{x1D70F}}(X)$
avec
$P(X)P^{\unicode[STIX]{x1D70F}}(X)$
avec
![]() $P$
irreductible et
$P$
irreductible et
![]() $P\neq P^{\unicode[STIX]{x1D70F}}$
alors le centralisateur de
$P\neq P^{\unicode[STIX]{x1D70F}}$
alors le centralisateur de
![]() $s_{i}$
dans
$s_{i}$
dans
![]() $(\overline{\mathsf{G}}_{x,i}^{\ast })_{ss}$
serait contenu dans un Levi rationnel propre).
$(\overline{\mathsf{G}}_{x,i}^{\ast })_{ss}$
serait contenu dans un Levi rationnel propre).
Soit
![]() $\unicode[STIX]{x1D70C}$
une représentation irréductible cuspidale auto-duale de niveau zero d’un certain
$\unicode[STIX]{x1D70C}$
une représentation irréductible cuspidale auto-duale de niveau zero d’un certain
![]() $\text{GL}_{n}(k^{\prime })$
. Notons
$\text{GL}_{n}(k^{\prime })$
. Notons
![]() $G^{\prime }\,=\,\text{GL}_{n}(k^{\prime })$
. Comme précédemment nous avons l’existence d’un
$G^{\prime }\,=\,\text{GL}_{n}(k^{\prime })$
. Comme précédemment nous avons l’existence d’un
![]() $y\in BT_{0}(\mathbf{G}^{\prime },k^{\prime })$
et d’une classe de conjugaison semi-simple
$y\in BT_{0}(\mathbf{G}^{\prime },k^{\prime })$
et d’une classe de conjugaison semi-simple
![]() $s_{\unicode[STIX]{x1D70C}}\,\in \,(\overline{\mathsf{G}}_{y}^{\prime \ast })_{ss}$
telle que
$s_{\unicode[STIX]{x1D70C}}\,\in \,(\overline{\mathsf{G}}_{y}^{\prime \ast })_{ss}$
telle que
![]() $e_{s_{\unicode[STIX]{x1D70C}},\overline{\mathbb{Q}}_{\ell }}^{\overline{\mathsf{G}}_{y}^{\prime }}\unicode[STIX]{x1D70C}^{G_{y}^{\prime +}}$
. Notons qu’ici
$e_{s_{\unicode[STIX]{x1D70C}},\overline{\mathbb{Q}}_{\ell }}^{\overline{\mathsf{G}}_{y}^{\prime }}\unicode[STIX]{x1D70C}^{G_{y}^{\prime +}}$
. Notons qu’ici
![]() $\overline{\mathsf{G}}_{y}^{\prime \ast }\simeq \text{GL}_{n}(\mathfrak{f}^{\prime })$
. Associons de même à
$\overline{\mathsf{G}}_{y}^{\prime \ast }\simeq \text{GL}_{n}(\mathfrak{f}^{\prime })$
. Associons de même à
![]() $s_{\unicode[STIX]{x1D70C}}$
son polynôme caractéristique
$s_{\unicode[STIX]{x1D70C}}$
son polynôme caractéristique
![]() $Q$
qui est un polynôme unitaire irréductible auto-dual de degré
$Q$
qui est un polynôme unitaire irréductible auto-dual de degré
![]() $n$
.
$n$
.
Théorème 4.5.3 [Reference Lust and StevensLS16, §8]. Notons
![]() $\unicode[STIX]{x1D70C}^{\prime }\in {\mathcal{A}}_{n}^{\unicode[STIX]{x1D70E}}(k^{\prime })$
l’unique (à équivalence près) twist non-ramifié (non-équivalent) de
$\unicode[STIX]{x1D70C}^{\prime }\in {\mathcal{A}}_{n}^{\unicode[STIX]{x1D70E}}(k^{\prime })$
l’unique (à équivalence près) twist non-ramifié (non-équivalent) de
![]() $\unicode[STIX]{x1D70C}$
qui est auto-dual. Alors pour
$\unicode[STIX]{x1D70C}$
qui est auto-dual. Alors pour
![]() $\mathbf{G}$
un groupe classique non-ramifié, on a
$\mathbf{G}$
un groupe classique non-ramifié, on a
sauf si
![]() $\mathbf{G}=\text{Sp}_{2n}$
et
$\mathbf{G}=\text{Sp}_{2n}$
et
![]() $Q(X)=X-1$
où dans ce cas on a
$Q(X)=X-1$
où dans ce cas on a
Les résultats dans [Reference Lust and StevensLS16] sont exprimés en termes de polynômes auto-duaux. Nous nous utilisons plutôt des classes de conjugaisons semi-simples. Nous souhaitons donc faire le lien entre les deux.
Soit
![]() $\text{}\text{H}$
un groupe du type
$\text{}\text{H}$
un groupe du type
![]() $\text{GL}_{n}$
,
$\text{GL}_{n}$
,
![]() $\text{Sp}_{2n}$
,
$\text{Sp}_{2n}$
,
![]() $\text{SO}_{2n+1}$
ou
$\text{SO}_{2n+1}$
ou
![]() $\text{SO}_{2n}$
sur
$\text{SO}_{2n}$
sur
![]() $\mathfrak{F}$
. On considère son plongement naturel
$\mathfrak{F}$
. On considère son plongement naturel
![]() $\text{}\text{H}\subseteq \text{GL}_{N}$
où
$\text{}\text{H}\subseteq \text{GL}_{N}$
où
![]() $N$
est en entier naturel (
$N$
est en entier naturel (
![]() $N=n$
pour
$N=n$
pour
![]() $\text{GL}_{n}$
,
$\text{GL}_{n}$
,
![]() $N=2n+1$
pour
$N=2n+1$
pour
![]() $\text{SO}_{2n+1}$
et
$\text{SO}_{2n+1}$
et
![]() $N=2n$
pour
$N=2n$
pour
![]() $\text{Sp}_{2n}$
ou
$\text{Sp}_{2n}$
ou
![]() $\text{SO}_{2n}$
). Soit
$\text{SO}_{2n}$
). Soit
![]() $s\in \text{}\text{H}_{ss}$
une classe de conjugaison semi-simple. Celle-ci donne lieu à une classe de conjugaison semi-simple de
$s\in \text{}\text{H}_{ss}$
une classe de conjugaison semi-simple. Celle-ci donne lieu à une classe de conjugaison semi-simple de
![]() $\text{GL}_{N}$
et l’on peut considérer
$\text{GL}_{N}$
et l’on peut considérer
![]() $P$
son polynôme caractéristique.
$P$
son polynôme caractéristique.
Lemme 4.5.4. Une classe de conjugaison géométrique semi-simple
![]() $s\in \text{}\text{H}_{ss}$
est caractérisée par son polynôme caractéristique
$s\in \text{}\text{H}_{ss}$
est caractérisée par son polynôme caractéristique
![]() $P$
.
$P$
.
Démonstration.
Traitons
![]() $\text{H}=\text{Sp}_{2n}$
, les autres cas étant similaires. On a donc
$\text{H}=\text{Sp}_{2n}$
, les autres cas étant similaires. On a donc
![]() $N=2n$
. Soit
$N=2n$
. Soit
![]() $\text{T}$
le tore déployé de
$\text{T}$
le tore déployé de
![]() $\text{Sp}_{2n}$
, c’est à dire
$\text{Sp}_{2n}$
, c’est à dire
![]() $\text{T}=\text{Diag}(a_{1},\ldots ,a_{n},a_{n}^{-1},\ldots ,a_{1}^{-1})$
,
$\text{T}=\text{Diag}(a_{1},\ldots ,a_{n},a_{n}^{-1},\ldots ,a_{1}^{-1})$
,
![]() $a_{i}\in \mathfrak{F}$
. Nous pouvons supposer que
$a_{i}\in \mathfrak{F}$
. Nous pouvons supposer que
![]() $s\in \text{T}$
et donc écrire
$s\in \text{T}$
et donc écrire
![]() $s=(a_{1},\ldots ,a_{2n})$
avec
$s=(a_{1},\ldots ,a_{2n})$
avec
![]() $a_{n+i}=a_{n-i+1}^{-1}$
pour
$a_{n+i}=a_{n-i+1}^{-1}$
pour
![]() $1\leqslant i\leqslant n$
. Prenons
$1\leqslant i\leqslant n$
. Prenons
![]() $s^{\prime }=(b_{1},\ldots ,b_{2n})\in \text{T}$
une autre classe de conjugaison semi-simple géométrique de
$s^{\prime }=(b_{1},\ldots ,b_{2n})\in \text{T}$
une autre classe de conjugaison semi-simple géométrique de
![]() $\text{}\text{H}$
ayant pour polynôme caractéristique
$\text{}\text{H}$
ayant pour polynôme caractéristique
![]() $P$
. Nous souhaitons donc montrer que
$P$
. Nous souhaitons donc montrer que
![]() $s$
et
$s$
et
![]() $s^{\prime }$
sont conjuguées dans
$s^{\prime }$
sont conjuguées dans
![]() $\text{}\text{H}$
. Comme ce sont deux éléments de
$\text{}\text{H}$
. Comme ce sont deux éléments de
![]() $\text{T}$
cela est équivalent au fait qu’il existe
$\text{T}$
cela est équivalent au fait qu’il existe
![]() $w\in W_{\text{H}}^{0}$
, le groupe de Weyl de
$w\in W_{\text{H}}^{0}$
, le groupe de Weyl de
![]() $\text{H}$
, tel que
$\text{H}$
, tel que
![]() $w\cdot s^{\prime }=s$
. Rappelons que
$w\cdot s^{\prime }=s$
. Rappelons que
![]() $W_{\text{H}}^{0}\simeq {\mathcal{S}}_{n}\ltimes (\mathbb{Z}/2\mathbb{Z})^{n}$
. Comme
$W_{\text{H}}^{0}\simeq {\mathcal{S}}_{n}\ltimes (\mathbb{Z}/2\mathbb{Z})^{n}$
. Comme
![]() $s$
et
$s$
et
![]() $s^{\prime }$
ont même polynôme caractéristique, il existe une permutation
$s^{\prime }$
ont même polynôme caractéristique, il existe une permutation
![]() $\unicode[STIX]{x1D70E}\in {\mathcal{S}}_{2n}$
telle que
$\unicode[STIX]{x1D70E}\in {\mathcal{S}}_{2n}$
telle que
![]() $b_{i}=a_{\unicode[STIX]{x1D70E}(i)}$
. Comme
$b_{i}=a_{\unicode[STIX]{x1D70E}(i)}$
. Comme
![]() $s\in \text{T}$
,
$s\in \text{T}$
,
![]() $\{a_{\unicode[STIX]{x1D70E}(1)},\ldots ,a_{\unicode[STIX]{x1D70E}(2n)}\}=\{a_{1}^{\pm },\ldots ,a_{n}^{\pm }\}$
(comptés avec multiplicités), donc il existe
$\{a_{\unicode[STIX]{x1D70E}(1)},\ldots ,a_{\unicode[STIX]{x1D70E}(2n)}\}=\{a_{1}^{\pm },\ldots ,a_{n}^{\pm }\}$
(comptés avec multiplicités), donc il existe
![]() $i\in \{1,\ldots ,n\}$
tel que
$i\in \{1,\ldots ,n\}$
tel que
![]() $a_{\unicode[STIX]{x1D70E}(1)}=a_{i}^{\pm }$
. Posons
$a_{\unicode[STIX]{x1D70E}(1)}=a_{i}^{\pm }$
. Posons
![]() $\unicode[STIX]{x1D70F}(1)=i$
. Comme
$\unicode[STIX]{x1D70F}(1)=i$
. Comme
![]() $s^{\prime }\in \text{T}$
,
$s^{\prime }\in \text{T}$
,
![]() $a_{\unicode[STIX]{x1D70E}(2n)}=b_{2n}=b_{1}^{-1}=a_{\unicode[STIX]{x1D70E}(1)}^{-1}$
, donc
$a_{\unicode[STIX]{x1D70E}(2n)}=b_{2n}=b_{1}^{-1}=a_{\unicode[STIX]{x1D70E}(1)}^{-1}$
, donc
![]() $\{a_{\unicode[STIX]{x1D70E}(2)},\ldots ,a_{\unicode[STIX]{x1D70E}(2n-1)}\}=\{a_{i}^{\pm },1\leqslant i\leqslant n,i\neq \unicode[STIX]{x1D70F}(1)\}$
. On construit donc par récurrence une permutation
$\{a_{\unicode[STIX]{x1D70E}(2)},\ldots ,a_{\unicode[STIX]{x1D70E}(2n-1)}\}=\{a_{i}^{\pm },1\leqslant i\leqslant n,i\neq \unicode[STIX]{x1D70F}(1)\}$
. On construit donc par récurrence une permutation
![]() $\unicode[STIX]{x1D70F}\in {\mathcal{S}}_{n}$
telle que
$\unicode[STIX]{x1D70F}\in {\mathcal{S}}_{n}$
telle que
![]() $a_{\unicode[STIX]{x1D70E}(i)}=a_{\unicode[STIX]{x1D70F}(i)}^{\pm }$
, pour
$a_{\unicode[STIX]{x1D70E}(i)}=a_{\unicode[STIX]{x1D70F}(i)}^{\pm }$
, pour
![]() $1\leqslant i\leqslant n$
. Dit autrement, on vient de fabriquer un élément
$1\leqslant i\leqslant n$
. Dit autrement, on vient de fabriquer un élément
![]() $w\in W_{\text{H}}^{0}\simeq {\mathcal{S}}_{n}\ltimes (\mathbb{Z}/2\mathbb{Z})^{n}$
tel que
$w\in W_{\text{H}}^{0}\simeq {\mathcal{S}}_{n}\ltimes (\mathbb{Z}/2\mathbb{Z})^{n}$
tel que
![]() $b_{i}=a_{\unicode[STIX]{x1D70E}(i)}=w\cdot a_{i}$
, donc tel que
$b_{i}=a_{\unicode[STIX]{x1D70E}(i)}=w\cdot a_{i}$
, donc tel que
![]() $s^{\prime }=w\cdot s$
ce qui achève la preuve.◻
$s^{\prime }=w\cdot s$
ce qui achève la preuve.◻
Soit
![]() $x\in BT_{0}$
et
$x\in BT_{0}$
et
![]() $s\in (\overline{\mathsf{G}}_{x}^{\ast })_{ss}$
. La classe de conjugaison
$s\in (\overline{\mathsf{G}}_{x}^{\ast })_{ss}$
. La classe de conjugaison
![]() $s$
correspond comme précédemment à
$s$
correspond comme précédemment à
![]() $(s_{1},s_{2})$
,
$(s_{1},s_{2})$
,
![]() $s_{i}\in (\overline{\mathsf{G}}_{x,i}^{\ast })_{ss}$
qui ont pour polynômes caractéristiques
$s_{i}\in (\overline{\mathsf{G}}_{x,i}^{\ast })_{ss}$
qui ont pour polynômes caractéristiques
![]() $P_{s_{1}}$
et
$P_{s_{1}}$
et
![]() $P_{s_{2}}$
. Dans le § 3.2 on a construit une application
$P_{s_{2}}$
. Dans le § 3.2 on a construit une application
![]() $\tilde{\unicode[STIX]{x1D713}}_{x}:((\overline{\text{G}}_{x}^{\ast })_{ss})^{F}\rightarrow (\text{G}^{\ast }(\mathfrak{F})_{ss})^{F}$
. Nommons
$\tilde{\unicode[STIX]{x1D713}}_{x}:((\overline{\text{G}}_{x}^{\ast })_{ss})^{F}\rightarrow (\text{G}^{\ast }(\mathfrak{F})_{ss})^{F}$
. Nommons
![]() $\tilde{s}:=\tilde{\unicode[STIX]{x1D713}}_{x}(s)$
l’image de
$\tilde{s}:=\tilde{\unicode[STIX]{x1D713}}_{x}(s)$
l’image de
![]() $s$
par cette application.
$s$
par cette application.
Lemme 4.5.5. Notons
![]() $P_{\tilde{s}}$
le polynôme caractéristique de
$P_{\tilde{s}}$
le polynôme caractéristique de
![]() $\tilde{s}$
alors on a
:
$\tilde{s}$
alors on a
:
(i) si
 $\mathbf{G}\neq \text{Sp}_{2n}$
:
$\mathbf{G}\neq \text{Sp}_{2n}$
:
 $P_{\tilde{s}}(X)=P_{s_{1}}(X)P_{s_{2}}(X)$
;
$P_{\tilde{s}}(X)=P_{s_{1}}(X)P_{s_{2}}(X)$
;(ii) si
 $\mathbf{G}=\text{Sp}_{2n}$
:
$\mathbf{G}=\text{Sp}_{2n}$
:
 $P_{\tilde{s}}(X)=P_{s_{1}}(X)P_{s_{2}}(X)/(X-1)$
.
$P_{\tilde{s}}(X)=P_{s_{1}}(X)P_{s_{2}}(X)/(X-1)$
.
Démonstration.
Traitons par exemple le cas où
![]() $\mathbf{G}=\text{Sp}_{2n}$
est un groupe symplectique. Dans ce cas
$\mathbf{G}=\text{Sp}_{2n}$
est un groupe symplectique. Dans ce cas
![]() $\overline{\mathsf{G}}_{x_{i}}=\text{Sp}_{2n_{i}}(\mathfrak{f})$
(avec
$\overline{\mathsf{G}}_{x_{i}}=\text{Sp}_{2n_{i}}(\mathfrak{f})$
(avec
![]() $n_{1}+n_{2}=n$
). On a
$n_{1}+n_{2}=n$
). On a
![]() $\text{}\text{G}^{\ast }=\text{SO}_{2n+1}$
et
$\text{}\text{G}^{\ast }=\text{SO}_{2n+1}$
et
![]() $\overline{\text{}\text{G}}_{x_{i}}^{\ast }=\text{SO}_{2n_{i}+1}$
. Notons
$\overline{\text{}\text{G}}_{x_{i}}^{\ast }=\text{SO}_{2n_{i}+1}$
. Notons
![]() $\text{T}^{\ast }$
le tore déployé de
$\text{T}^{\ast }$
le tore déployé de
![]() $\text{}\text{G}^{\ast }$
et
$\text{}\text{G}^{\ast }$
et
![]() $\text{T}_{i}^{\ast }$
celui de
$\text{T}_{i}^{\ast }$
celui de
![]() $\overline{\text{}\text{G}}_{x_{i}}^{\ast }$
. On peut alors considérer que
$\overline{\text{}\text{G}}_{x_{i}}^{\ast }$
. On peut alors considérer que
![]() $\tilde{s}\in \text{}\text{G}^{\ast }$
,
$\tilde{s}\in \text{}\text{G}^{\ast }$
,
![]() $s_{i}\in \text{T}_{i}^{\ast }$
et donc écrire
$s_{i}\in \text{T}_{i}^{\ast }$
et donc écrire
On obtient alors que
d’où le résultat. On fait de même avec les autres cas. ◻
Théorème 4.5.6. Supposons que
![]() $\mathbf{G}$
est un groupe classique non-ramifié,
$\mathbf{G}$
est un groupe classique non-ramifié,
![]() $k$
de caractéristique nulle et
$k$
de caractéristique nulle et
![]() $p\neq 2$
. Soient
$p\neq 2$
. Soient
![]() $\unicode[STIX]{x1D70B}\in \text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)$
une représentation de niveau 0 et
$\unicode[STIX]{x1D70B}\in \text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)$
une représentation de niveau 0 et
![]() $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{G})$
tel que
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{G})$
tel que
![]() $\unicode[STIX]{x1D70B}\in \text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
. Notons
$\unicode[STIX]{x1D70B}\in \text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
. Notons
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70B}}$
le paramètre de Langlands associé à
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70B}}$
le paramètre de Langlands associé à
![]() $\unicode[STIX]{x1D70B}$
via la correspondance de Langlands locale pour les groupes classiques. Alors
$\unicode[STIX]{x1D70B}$
via la correspondance de Langlands locale pour les groupes classiques. Alors
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70B}|I_{k}}\sim \unicode[STIX]{x1D719}$
.
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70B}|I_{k}}\sim \unicode[STIX]{x1D719}$
.
Démonstration.
Le § 4.4 permet de nous ramener au cas où
![]() $\unicode[STIX]{x1D70B}$
est cuspidale. Le théorème 4.5.2 nous dit alors
$\unicode[STIX]{x1D70B}$
est cuspidale. Le théorème 4.5.2 nous dit alors
![]() $\tilde{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D70B}}=\bigoplus _{(\unicode[STIX]{x1D70C},m)\in \text{Jord}(\unicode[STIX]{x1D70B})}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}\otimes st_{m}$
donc
$\tilde{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D70B}}=\bigoplus _{(\unicode[STIX]{x1D70C},m)\in \text{Jord}(\unicode[STIX]{x1D70B})}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}\otimes st_{m}$
donc
![]() $\tilde{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D70B}|I_{k}}=\bigoplus _{(\unicode[STIX]{x1D70C},m)\in \text{Jord}(\unicode[STIX]{x1D70B})}m\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}|I_{k}}$
. Comme
$\tilde{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D70B}|I_{k}}=\bigoplus _{(\unicode[STIX]{x1D70C},m)\in \text{Jord}(\unicode[STIX]{x1D70B})}m\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}|I_{k}}$
. Comme
![]() $\sum _{m,(\unicode[STIX]{x1D70C},m)\in \text{Jord}(\unicode[STIX]{x1D70B})}m=\lfloor s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})^{2}\rfloor$
(où
$\sum _{m,(\unicode[STIX]{x1D70C},m)\in \text{Jord}(\unicode[STIX]{x1D70B})}m=\lfloor s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})^{2}\rfloor$
(où
![]() $\lfloor \cdot \rfloor$
désigne la partie entière inférieure) on obtient
$\lfloor \cdot \rfloor$
désigne la partie entière inférieure) on obtient
![]() $\tilde{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D70B}|I_{k}}=\bigoplus _{\unicode[STIX]{x1D70C}\in {\mathcal{A}}_{[0]}^{\unicode[STIX]{x1D70E}}(k)}\lfloor s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})^{2}\rfloor \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}|I_{k}}$
. Notons
$\tilde{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D70B}|I_{k}}=\bigoplus _{\unicode[STIX]{x1D70C}\in {\mathcal{A}}_{[0]}^{\unicode[STIX]{x1D70E}}(k)}\lfloor s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})^{2}\rfloor \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}|I_{k}}$
. Notons
![]() $[\unicode[STIX]{x1D70C}]$
la classe d’inertie de
$[\unicode[STIX]{x1D70C}]$
la classe d’inertie de
![]() $\unicode[STIX]{x1D70C}$
de sorte que
$\unicode[STIX]{x1D70C}$
de sorte que
![]() $[\unicode[STIX]{x1D70C}]\cap {\mathcal{A}}^{\unicode[STIX]{x1D70E}}(k^{\prime })=\{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70C}^{\prime }\}$
. Les deux paramètres de Langlands
$[\unicode[STIX]{x1D70C}]\cap {\mathcal{A}}^{\unicode[STIX]{x1D70E}}(k^{\prime })=\{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70C}^{\prime }\}$
. Les deux paramètres de Langlands
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}$
et
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}$
et
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}^{\prime }}$
ont la même restriction à l’inertie donc
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}^{\prime }}$
ont la même restriction à l’inertie donc
![]() $\tilde{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D70B}|I_{k}}=\bigoplus _{[\unicode[STIX]{x1D70C}]}(\lfloor s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})^{2}\rfloor +\lfloor s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C}^{\prime })^{2}\rfloor )\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}|I_{k}}$
. Notons
$\tilde{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D70B}|I_{k}}=\bigoplus _{[\unicode[STIX]{x1D70C}]}(\lfloor s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})^{2}\rfloor +\lfloor s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C}^{\prime })^{2}\rfloor )\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}|I_{k}}$
. Notons
![]() $t\in (\text{G}_{ss}^{\ast })^{F}$
la classe de conjugaison semi-simple associée à
$t\in (\text{G}_{ss}^{\ast })^{F}$
la classe de conjugaison semi-simple associée à
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70B}|I_{k}}$
.
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70B}|I_{k}}$
.
Reprenons les notations précédentes,
![]() $\unicode[STIX]{x1D70B}$
nous fournit un
$\unicode[STIX]{x1D70B}$
nous fournit un
![]() $x\in BT_{0}$
et un
$x\in BT_{0}$
et un
![]() $s\in (\overline{\mathsf{G}}_{x}^{\ast })_{ss}$
correspondant à
$s\in (\overline{\mathsf{G}}_{x}^{\ast })_{ss}$
correspondant à
![]() $(s_{1},s_{2})$
,
$(s_{1},s_{2})$
,
![]() $s_{i}\in (\overline{\mathsf{G}}_{x,i}^{\ast })_{ss}$
. On définit également
$s_{i}\in (\overline{\mathsf{G}}_{x,i}^{\ast })_{ss}$
. On définit également
![]() $\tilde{s}\in (\text{}\text{G}_{ss}^{\ast })^{F}$
par
$\tilde{s}\in (\text{}\text{G}_{ss}^{\ast })^{F}$
par
![]() $\tilde{s}:=\tilde{\unicode[STIX]{x1D713}}_{x}(s)$
. Par définition
$\tilde{s}:=\tilde{\unicode[STIX]{x1D713}}_{x}(s)$
. Par définition
![]() $\tilde{s}$
est la classe de conjugaison semi-simple
$\tilde{s}$
est la classe de conjugaison semi-simple
![]() $F$
-stable associée à
$F$
-stable associée à
![]() $\unicode[STIX]{x1D719}$
. Il nous faut donc montrer que
$\unicode[STIX]{x1D719}$
. Il nous faut donc montrer que
![]() $t=\tilde{s}$
. Le lemme 4.5.4 nous dit qu’il suffit de montrer que
$t=\tilde{s}$
. Le lemme 4.5.4 nous dit qu’il suffit de montrer que
![]() $P_{t}=P_{\tilde{s}}$
où
$P_{t}=P_{\tilde{s}}$
où
![]() $P_{t}$
et
$P_{t}$
et
![]() $P_{\tilde{s}}$
sont les polynômes caractéristiques de
$P_{\tilde{s}}$
sont les polynômes caractéristiques de
![]() $t$
et
$t$
et
![]() $\tilde{s}$
.
$\tilde{s}$
.
Si
![]() $\unicode[STIX]{x1D70C}\in {\mathcal{A}}_{[0]}^{\unicode[STIX]{x1D70E}}(k)$
, on a vu qu’on pouvait lui associer une classe de conjugaison semi-simple
$\unicode[STIX]{x1D70C}\in {\mathcal{A}}_{[0]}^{\unicode[STIX]{x1D70E}}(k)$
, on a vu qu’on pouvait lui associer une classe de conjugaison semi-simple
![]() $s_{\unicode[STIX]{x1D70C}}$
et l’on note
$s_{\unicode[STIX]{x1D70C}}$
et l’on note
![]() $Q$
son polynôme caractéristique. La compatibilité à Langlands dans le cas
$Q$
son polynôme caractéristique. La compatibilité à Langlands dans le cas
![]() $\mathbf{G}=\text{GL}_{n}$
, démontré dans [Reference DatDat16, §3.2.6], montre que
$\mathbf{G}=\text{GL}_{n}$
, démontré dans [Reference DatDat16, §3.2.6], montre que
![]() $Q$
est bien le polynôme caractéristique de la classe de conjugaison semi-simple
$Q$
est bien le polynôme caractéristique de la classe de conjugaison semi-simple
![]() $F$
-stable associée à
$F$
-stable associée à
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}\mid I_{k}}$
.
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}\mid I_{k}}$
.
Le théorème 4.5.3 et le lemme 4.5.5 permettent alors de conclure. Traitons par exemple la cas
![]() $\mathbf{G}=\text{Sp}_{2n}$
. Nous avons
$\mathbf{G}=\text{Sp}_{2n}$
. Nous avons
![]() $\tilde{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D70B}|I_{k}}=\bigoplus _{[\unicode[STIX]{x1D70C}]}(\lfloor s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})^{2}\rfloor +\lfloor s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C}^{\prime })^{2}\rfloor )\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}|I_{k}}$
. Le théorème 4.5.3 nous donne alors
$\tilde{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D70B}|I_{k}}=\bigoplus _{[\unicode[STIX]{x1D70C}]}(\lfloor s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})^{2}\rfloor +\lfloor s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C}^{\prime })^{2}\rfloor )\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}|I_{k}}$
. Le théorème 4.5.3 nous donne alors
![]() $\lfloor s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})^{2}\rfloor +\lfloor s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C}^{\prime })^{2}\rfloor =a_{Q}^{(1)}+a_{Q}^{(2)}$
si
$\lfloor s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})^{2}\rfloor +\lfloor s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C}^{\prime })^{2}\rfloor =a_{Q}^{(1)}+a_{Q}^{(2)}$
si
![]() $Q(X)\neq X-1$
et
$Q(X)\neq X-1$
et
![]() $\lfloor s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})^{2}\rfloor +\lfloor s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C}^{\prime })^{2}\rfloor =a_{(X-1)}^{(1)}+a_{(X-1)}^{(2)}-1$
si
$\lfloor s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C})^{2}\rfloor +\lfloor s_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70C}^{\prime })^{2}\rfloor =a_{(X-1)}^{(1)}+a_{(X-1)}^{(2)}-1$
si
![]() $Q(X)=X-1$
. Donc
$Q(X)=X-1$
. Donc
 $$\begin{eqnarray}\displaystyle P_{t}(X) & = & \displaystyle (X-1)^{(a_{(X-1)}^{(1)}+a_{(X-1)}^{(2)}-1)}\mathop{\prod }_{Q(X)\neq X-1}Q(X)^{(a_{Q}^{(1)}+a_{Q}^{(2)})}\nonumber\\ \displaystyle & = & \displaystyle 1/(X-1)\biggl(\mathop{\prod }_{Q}Q^{a_{Q}^{(1)}}\biggr)\biggl(\mathop{\prod }_{Q}Q^{a_{Q}^{(2)}}\biggr)\nonumber\\ \displaystyle & = & \displaystyle 1/(X-1)P_{s_{1}}(X)P_{s_{2}}(X).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{t}(X) & = & \displaystyle (X-1)^{(a_{(X-1)}^{(1)}+a_{(X-1)}^{(2)}-1)}\mathop{\prod }_{Q(X)\neq X-1}Q(X)^{(a_{Q}^{(1)}+a_{Q}^{(2)})}\nonumber\\ \displaystyle & = & \displaystyle 1/(X-1)\biggl(\mathop{\prod }_{Q}Q^{a_{Q}^{(1)}}\biggr)\biggl(\mathop{\prod }_{Q}Q^{a_{Q}^{(2)}}\biggr)\nonumber\\ \displaystyle & = & \displaystyle 1/(X-1)P_{s_{1}}(X)P_{s_{2}}(X).\nonumber\end{eqnarray}$$
Le lemme 4.5.5 montre alors que
![]() $P_{t}=P_{\tilde{s}}$
qui est le résultat recherché.◻
$P_{t}=P_{\tilde{s}}$
qui est le résultat recherché.◻
Le théorème de décomposition de Bernstein fournit une partition des irréductibles
![]() $\text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)=\bigsqcup _{\mathfrak{s}\in {\mathcal{B}}(G)}\text{Irr}_{\mathfrak{s}}(G)$
, où
$\text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)=\bigsqcup _{\mathfrak{s}\in {\mathcal{B}}(G)}\text{Irr}_{\mathfrak{s}}(G)$
, où
![]() ${\mathcal{B}}(G)$
désigne l’ensemble des classes d’inertie de données cuspidales. En supposant vraie la correspondance de Langlands locale, on obtient une autre partition
${\mathcal{B}}(G)$
désigne l’ensemble des classes d’inertie de données cuspidales. En supposant vraie la correspondance de Langlands locale, on obtient une autre partition
![]() $\text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)=\bigsqcup _{\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D6F7}(\mathbf{G})}\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D711}}$
, où
$\text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)=\bigsqcup _{\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D6F7}(\mathbf{G})}\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D711}}$
, où
![]() $\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D711}}$
est le
$\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D711}}$
est le
![]() $L$
-paquet associé au paramètre
$L$
-paquet associé au paramètre
![]() $\unicode[STIX]{x1D711}$
. Haines introduit dans [Reference HainesHai14] la notion de ‘centre de Bernstein stable’ qui permet de comparer ces deux décompositions.
$\unicode[STIX]{x1D711}$
. Haines introduit dans [Reference HainesHai14] la notion de ‘centre de Bernstein stable’ qui permet de comparer ces deux décompositions.
Soit
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6F7}(W_{k},\mathbf{G})$
et
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6F7}(W_{k},\mathbf{G})$
et
![]() $\mathfrak{i}$
sa classe d’inertie (on rappelle la définition de l’équivalence inertielle de Haines en C.0.1). On définit un paquet inertiel par
$\mathfrak{i}$
sa classe d’inertie (on rappelle la définition de l’équivalence inertielle de Haines en C.0.1). On définit un paquet inertiel par
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{\mathfrak{i}}^{+}:=\bigsqcup _{\substack{ \unicode[STIX]{x1D711}\in \unicode[STIX]{x1D6F7}(\mathbf{G}) \\ \unicode[STIX]{x1D711}_{|W_{k}}\in \mathfrak{i}}}\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D711}}(G).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{\mathfrak{i}}^{+}:=\bigsqcup _{\substack{ \unicode[STIX]{x1D711}\in \unicode[STIX]{x1D6F7}(\mathbf{G}) \\ \unicode[STIX]{x1D711}_{|W_{k}}\in \mathfrak{i}}}\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D711}}(G).\end{eqnarray}$$
Supposons que l’on ait la correspondance de Langlands locale pour
![]() $G$
ainsi que ses sous-groupes de Levi, la compatibilité à l’induction parabolique et à certains isomorphismes (voir [Reference HainesHai14] définition 5.2.1 pour plus de détails). Alors on peut définir une application
$G$
ainsi que ses sous-groupes de Levi, la compatibilité à l’induction parabolique et à certains isomorphismes (voir [Reference HainesHai14] définition 5.2.1 pour plus de détails). Alors on peut définir une application
![]() ${\mathcal{L}}_{i}$
qui à une classe d’inertie de données cuspidales
${\mathcal{L}}_{i}$
qui à une classe d’inertie de données cuspidales
![]() $\mathfrak{s}=[L,\unicode[STIX]{x1D70E}]\in {\mathcal{B}}(G)$
associe
$\mathfrak{s}=[L,\unicode[STIX]{x1D70E}]\in {\mathcal{B}}(G)$
associe
![]() ${\mathcal{L}}_{i}(\mathfrak{s})$
la classe d’inertie du paramètre de Weil
${\mathcal{L}}_{i}(\mathfrak{s})$
la classe d’inertie du paramètre de Weil
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}|W_{k}}$
. Les paquets inertiels permettent de comparer les décompositions
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}|W_{k}}$
. Les paquets inertiels permettent de comparer les décompositions
![]() $\text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)=\bigsqcup _{\mathfrak{s}\in {\mathcal{B}}(G)}\text{Irr}_{\mathfrak{s}}(G)=\bigsqcup _{\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D6F7}(\mathbf{G})}\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D711}}$
.
$\text{Irr}_{\overline{\mathbb{Q}}_{\ell }}(G)=\bigsqcup _{\mathfrak{s}\in {\mathcal{B}}(G)}\text{Irr}_{\mathfrak{s}}(G)=\bigsqcup _{\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D6F7}(\mathbf{G})}\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D711}}$
.
Théorème 4.5.7 [Reference MoussaouiMou17b, théorème 2.9]. Soient
![]() $G$
un groupe classique déployé et
$G$
un groupe classique déployé et
![]() $\mathfrak{i}$
une classe d’inertie de paramètres de Weil. Alors
$\mathfrak{i}$
une classe d’inertie de paramètres de Weil. Alors
Revenons à l’étude de
![]() $\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
.
$\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
.
Théorème 4.5.8. Soient
![]() $\mathbf{G}$
un groupe classique non-ramifié,
$\mathbf{G}$
un groupe classique non-ramifié,
![]() $k$
de caractéristique nulle,
$k$
de caractéristique nulle,
![]() $p\neq 2$
et
$p\neq 2$
et
![]() $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{G})$
un paramètre inertiel modéré. Alors si
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}_{m}(I_{k},\mathbf{G})$
un paramètre inertiel modéré. Alors si
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
, le centralisateur de
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
, le centralisateur de
![]() $\unicode[STIX]{x1D719}(I_{k})$
dans
$\unicode[STIX]{x1D719}(I_{k})$
dans
![]() $\widehat{\mathbf{G}}$
, est connexe
$\widehat{\mathbf{G}}$
, est connexe
où
![]() $\mathfrak{i}$
est la classe d’inertie formée des paramètres de Weil qui étendent
$\mathfrak{i}$
est la classe d’inertie formée des paramètres de Weil qui étendent
![]() $\unicode[STIX]{x1D719}$
.
$\unicode[STIX]{x1D719}$
.
Dit autrement,
![]() $\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
est un ‘bloc stable’ (c’est-à-dire, correspond à un idempotent primitif du centre de Bernstein stable au sens de Haines [Reference HainesHai14]).
$\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
est un ‘bloc stable’ (c’est-à-dire, correspond à un idempotent primitif du centre de Bernstein stable au sens de Haines [Reference HainesHai14]).
Démonstration.
La proposition C.0.2 montre que si
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
est connexe, alors l’ensemble des
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
est connexe, alors l’ensemble des
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6F7}(W_{k},\mathbf{G})$
tels que
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6F7}(W_{k},\mathbf{G})$
tels que
![]() $\unicode[STIX]{x1D706}_{|I_{k}}\sim \unicode[STIX]{x1D719}$
forme une classe d’équivalence inertielle. De plus, le théorème 4.5.6 montre que la construction de
$\unicode[STIX]{x1D706}_{|I_{k}}\sim \unicode[STIX]{x1D719}$
forme une classe d’équivalence inertielle. De plus, le théorème 4.5.6 montre que la construction de
![]() $\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}$
est compatible avec la correspondance de Langlands, d’où le résultat.◻
$\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}$
est compatible avec la correspondance de Langlands, d’où le résultat.◻
Lorsque
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
n’est pas connexe,
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
n’est pas connexe,
![]() $\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
est une somme de ‘blocs stables’. Nous expliquerons dans un prochain article comment décomposer naturellement la catégorie
$\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
est une somme de ‘blocs stables’. Nous expliquerons dans un prochain article comment décomposer naturellement la catégorie
![]() $\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
en ‘blocs stables’.
$\text{Rep}_{\overline{\mathbb{Q}}_{\ell }}^{\unicode[STIX]{x1D719}}(G)$
en ‘blocs stables’.
Remerciements
Je tiens à remercier Jean-François Dat pour son aide précieuse concernant la rédaction de cet article.
Annexe A Rappels sur le groupe dual
Soient
![]() $\unicode[STIX]{x1D6FA}$
un corps algébriquement clos et
$\unicode[STIX]{x1D6FA}$
un corps algébriquement clos et
![]() $\mathbf{G}$
,
$\mathbf{G}$
,
![]() $\mathbf{G}^{\prime }$
deux groupes réductifs définis sur
$\mathbf{G}^{\prime }$
deux groupes réductifs définis sur
![]() $\unicode[STIX]{x1D6FA}$
. Prenons
$\unicode[STIX]{x1D6FA}$
. Prenons
![]() $\unicode[STIX]{x1D711}:\mathbf{G}\rightarrow \mathbf{G}^{\prime }$
un isomorphisme. Choisissons
$\unicode[STIX]{x1D711}:\mathbf{G}\rightarrow \mathbf{G}^{\prime }$
un isomorphisme. Choisissons
![]() $\text{}\text{T}$
un tore maximal de
$\text{}\text{T}$
un tore maximal de
![]() $\mathbf{G}$
et notons
$\mathbf{G}$
et notons
![]() $\mathbf{T}^{\prime }=\unicode[STIX]{x1D711}(\mathbf{T})$
qui est un tore maximal de
$\mathbf{T}^{\prime }=\unicode[STIX]{x1D711}(\mathbf{T})$
qui est un tore maximal de
![]() $\mathbf{G}^{\prime }$
. On associe à
$\mathbf{G}^{\prime }$
. On associe à
![]() $\mathbf{G}$
et
$\mathbf{G}$
et
![]() $\mathbf{T}$
une donnée radicielle
$\mathbf{T}$
une donnée radicielle
![]() $\unicode[STIX]{x1D719}(\mathbf{G},\mathbf{T})=(X,X^{\vee },\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\vee })$
où
$\unicode[STIX]{x1D719}(\mathbf{G},\mathbf{T})=(X,X^{\vee },\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}^{\vee })$
où
![]() $X=X^{\ast }(\mathbf{T})$
est le groupe des caractère de
$X=X^{\ast }(\mathbf{T})$
est le groupe des caractère de
![]() $\mathbf{T}$
,
$\mathbf{T}$
,
![]() $X^{\vee }=X_{\ast }(\mathbf{T})$
est le groupe des co-caractères,
$X^{\vee }=X_{\ast }(\mathbf{T})$
est le groupe des co-caractères,
![]() $\unicode[STIX]{x1D719}$
est l’ensemble des racines et
$\unicode[STIX]{x1D719}$
est l’ensemble des racines et
![]() $\unicode[STIX]{x1D719}^{\vee }$
l’ensemble des co-racines. À partir de
$\unicode[STIX]{x1D719}^{\vee }$
l’ensemble des co-racines. À partir de
![]() $\unicode[STIX]{x1D719}(\mathbf{G},\mathbf{T})$
on forme la donnée radicielle duale
$\unicode[STIX]{x1D719}(\mathbf{G},\mathbf{T})$
on forme la donnée radicielle duale
![]() $\widehat{\unicode[STIX]{x1D719}(\mathbf{G},\mathbf{T})}$
définie par
$\widehat{\unicode[STIX]{x1D719}(\mathbf{G},\mathbf{T})}$
définie par
![]() $\widehat{\unicode[STIX]{x1D719}(\mathbf{G},\mathbf{T})}=(X^{\vee },X,\unicode[STIX]{x1D719}^{\vee },\unicode[STIX]{x1D719})$
. D’après [Reference SpringerSpr79] théorème 2.9 nous savons qu’il existe un groupe réductif
$\widehat{\unicode[STIX]{x1D719}(\mathbf{G},\mathbf{T})}=(X^{\vee },X,\unicode[STIX]{x1D719}^{\vee },\unicode[STIX]{x1D719})$
. D’après [Reference SpringerSpr79] théorème 2.9 nous savons qu’il existe un groupe réductif
![]() $\widehat{\mathbf{G}}$
et un tore
$\widehat{\mathbf{G}}$
et un tore
![]() $\widehat{\mathbf{T}}$
tel que
$\widehat{\mathbf{T}}$
tel que
![]() $\unicode[STIX]{x1D719}(\widehat{\mathbf{G}},\widehat{\mathbf{T}})=\widehat{\unicode[STIX]{x1D719}(\mathbf{G},\mathbf{T})}$
. De façon analogue il existe
$\unicode[STIX]{x1D719}(\widehat{\mathbf{G}},\widehat{\mathbf{T}})=\widehat{\unicode[STIX]{x1D719}(\mathbf{G},\mathbf{T})}$
. De façon analogue il existe
![]() $\widehat{\mathbf{G}}^{\prime }$
et
$\widehat{\mathbf{G}}^{\prime }$
et
![]() $\widehat{\mathbf{T}}^{\prime }$
tel que
$\widehat{\mathbf{T}}^{\prime }$
tel que
![]() $\unicode[STIX]{x1D719}(\widehat{\mathbf{G}}^{\prime },\widehat{\mathbf{T}}^{\prime })=\widehat{\unicode[STIX]{x1D719}(\mathbf{G}^{\prime },\mathbf{T}^{\prime })}$
.
$\unicode[STIX]{x1D719}(\widehat{\mathbf{G}}^{\prime },\widehat{\mathbf{T}}^{\prime })=\widehat{\unicode[STIX]{x1D719}(\mathbf{G}^{\prime },\mathbf{T}^{\prime })}$
.
L’isomorphisme
![]() $\unicode[STIX]{x1D711}:\mathbf{G}\rightarrow \mathbf{G}^{\prime }$
induit un isomorphisme
$\unicode[STIX]{x1D711}:\mathbf{G}\rightarrow \mathbf{G}^{\prime }$
induit un isomorphisme
![]() $f(\unicode[STIX]{x1D711}):\unicode[STIX]{x1D719}(\mathbf{G}^{\prime },\mathbf{T}^{\prime })\rightarrow \unicode[STIX]{x1D719}(\mathbf{G},\mathbf{T})$
. Nous avons alors aussi l’isogénie
$f(\unicode[STIX]{x1D711}):\unicode[STIX]{x1D719}(\mathbf{G}^{\prime },\mathbf{T}^{\prime })\rightarrow \unicode[STIX]{x1D719}(\mathbf{G},\mathbf{T})$
. Nous avons alors aussi l’isogénie
![]() $^{t}f(\unicode[STIX]{x1D711}):\widehat{\unicode[STIX]{x1D719}(\mathbf{G}^{\prime },\mathbf{T}^{\prime })}\rightarrow \widehat{\unicode[STIX]{x1D719}(\mathbf{G},\mathbf{T})}$
, c’est à dire
$^{t}f(\unicode[STIX]{x1D711}):\widehat{\unicode[STIX]{x1D719}(\mathbf{G}^{\prime },\mathbf{T}^{\prime })}\rightarrow \widehat{\unicode[STIX]{x1D719}(\mathbf{G},\mathbf{T})}$
, c’est à dire
![]() $^{t}f(\unicode[STIX]{x1D711}):\unicode[STIX]{x1D719}(\widehat{\mathbf{G}}^{\prime },\widehat{\mathbf{T}}^{\prime })\rightarrow \unicode[STIX]{x1D719}(\widehat{\mathbf{G}},\widehat{\mathbf{T}})$
. Le théorème 2.9 de [Reference SpringerSpr79] nous dit également qu’il existe un isomorphisme
$^{t}f(\unicode[STIX]{x1D711}):\unicode[STIX]{x1D719}(\widehat{\mathbf{G}}^{\prime },\widehat{\mathbf{T}}^{\prime })\rightarrow \unicode[STIX]{x1D719}(\widehat{\mathbf{G}},\widehat{\mathbf{T}})$
. Le théorème 2.9 de [Reference SpringerSpr79] nous dit également qu’il existe un isomorphisme
![]() $\widehat{\unicode[STIX]{x1D711}}:\widehat{\mathbf{G}}^{\prime }\rightarrow \widehat{\mathbf{G}}$
qui envoie
$\widehat{\unicode[STIX]{x1D711}}:\widehat{\mathbf{G}}^{\prime }\rightarrow \widehat{\mathbf{G}}$
qui envoie
![]() $\widehat{\mathbf{T}}^{\prime }$
sur
$\widehat{\mathbf{T}}^{\prime }$
sur
![]() $\widehat{\mathbf{T}}$
et tel que
$\widehat{\mathbf{T}}$
et tel que
![]() $f(\widehat{\unicode[STIX]{x1D711}})=^{t}f(\unicode[STIX]{x1D711})$
. Ce
$f(\widehat{\unicode[STIX]{x1D711}})=^{t}f(\unicode[STIX]{x1D711})$
. Ce
![]() $\widehat{\unicode[STIX]{x1D711}}$
n’est pas unique et deux tels
$\widehat{\unicode[STIX]{x1D711}}$
n’est pas unique et deux tels
![]() $\widehat{\unicode[STIX]{x1D711}}$
diffèrent par un automorphisme
$\widehat{\unicode[STIX]{x1D711}}$
diffèrent par un automorphisme
![]() $\text{Int}(\hat{t}^{\prime })$
où
$\text{Int}(\hat{t}^{\prime })$
où
![]() $\hat{t}^{\prime }\in \widehat{\mathbf{T}}^{\prime }$
.
$\hat{t}^{\prime }\in \widehat{\mathbf{T}}^{\prime }$
.
Nous savons que
![]() $\widehat{\mathbf{T}}\simeq X_{\ast }(\widehat{\mathbf{T}})\otimes _{\mathbb{Z}}\unicode[STIX]{x1D6FA}^{\times }=X\otimes _{\mathbb{Z}}\unicode[STIX]{x1D6FA}^{\times }$
et de même
$\widehat{\mathbf{T}}\simeq X_{\ast }(\widehat{\mathbf{T}})\otimes _{\mathbb{Z}}\unicode[STIX]{x1D6FA}^{\times }=X\otimes _{\mathbb{Z}}\unicode[STIX]{x1D6FA}^{\times }$
et de même
![]() $\widehat{\mathbf{T}}^{\prime }\simeq X^{\prime }\otimes _{\mathbb{Z}}\unicode[STIX]{x1D6FA}^{\times }$
. Par définition de
$\widehat{\mathbf{T}}^{\prime }\simeq X^{\prime }\otimes _{\mathbb{Z}}\unicode[STIX]{x1D6FA}^{\times }$
. Par définition de
![]() $\widehat{\unicode[STIX]{x1D711}}$
, le morphisme
$\widehat{\unicode[STIX]{x1D711}}$
, le morphisme
![]() $\widehat{\unicode[STIX]{x1D711}}:\widehat{\mathbf{T}}^{\prime }\rightarrow \widehat{\mathbf{T}}$
est donné par
$\widehat{\unicode[STIX]{x1D711}}:\widehat{\mathbf{T}}^{\prime }\rightarrow \widehat{\mathbf{T}}$
est donné par
![]() $f(\unicode[STIX]{x1D711})\otimes \text{id}:X^{\prime }\otimes _{\mathbb{Z}}\unicode[STIX]{x1D6FA}^{\times }\rightarrow X\otimes _{\mathbb{Z}}\unicode[STIX]{x1D6FA}^{\times }$
. Nous avons donc le diagramme commutatif suivant :
$f(\unicode[STIX]{x1D711})\otimes \text{id}:X^{\prime }\otimes _{\mathbb{Z}}\unicode[STIX]{x1D6FA}^{\times }\rightarrow X\otimes _{\mathbb{Z}}\unicode[STIX]{x1D6FA}^{\times }$
. Nous avons donc le diagramme commutatif suivant :

Le morphisme
![]() $\widehat{\unicode[STIX]{x1D711}}$
est défini à conjugaison intérieure près, ainsi si l’on passe aux classes de conjugaison celui ci est bien défini. De plus on sait que
$\widehat{\unicode[STIX]{x1D711}}$
est défini à conjugaison intérieure près, ainsi si l’on passe aux classes de conjugaison celui ci est bien défini. De plus on sait que
![]() $\widehat{\mathbf{G}}_{ss}\simeq (\widehat{\mathbf{T}}/W)$
où
$\widehat{\mathbf{G}}_{ss}\simeq (\widehat{\mathbf{T}}/W)$
où
![]() $W$
est le groupe de Weyl de
$W$
est le groupe de Weyl de
![]() $\widehat{\mathbf{G}}$
relativement à
$\widehat{\mathbf{G}}$
relativement à
![]() $\widehat{\mathbf{T}}$
. Ainsi on obtient
$\widehat{\mathbf{T}}$
. Ainsi on obtient
Lemme A.0.1. Avec les notations précédentes on a un diagramme commutatif

Si maintenant on prend
![]() $\mathbf{G}^{\prime }=\mathbf{G}$
et
$\mathbf{G}^{\prime }=\mathbf{G}$
et
![]() $\unicode[STIX]{x1D711}\in \text{Aut}(\mathbf{G})$
. Nous pouvons identifier de manière canonique
$\unicode[STIX]{x1D711}\in \text{Aut}(\mathbf{G})$
. Nous pouvons identifier de manière canonique
![]() $\widehat{\mathbf{G}}_{ss}$
et
$\widehat{\mathbf{G}}_{ss}$
et
![]() $\widehat{\mathbf{G}}_{ss}^{\prime }$
de la façon suivante. Il existe un
$\widehat{\mathbf{G}}_{ss}^{\prime }$
de la façon suivante. Il existe un
![]() $g\in \mathbf{G}$
tel que
$g\in \mathbf{G}$
tel que
![]() $\mathbf{T}^{\prime }=\text{Ad}(g)(\mathbf{T})$
. L’automorphisme
$\mathbf{T}^{\prime }=\text{Ad}(g)(\mathbf{T})$
. L’automorphisme
![]() $\text{Ad}(g)$
induit donc un isomorphisme
$\text{Ad}(g)$
induit donc un isomorphisme
![]() $f$
de
$f$
de
![]() $X^{\prime }$
dans
$X^{\prime }$
dans
![]() $X$
et un isomorphisme canonique
$X$
et un isomorphisme canonique
(comme on a quotienté par le groupe de Weyl,
![]() $f\otimes \text{id}$
ne dépend pas du choix de
$f\otimes \text{id}$
ne dépend pas du choix de
![]() $g$
).
$g$
).
Le lemme A.0.1 nous fournit un isomorphisme canonique
![]() $\widehat{f}_{ss}$
entre
$\widehat{f}_{ss}$
entre
![]() $\widehat{\mathbf{G}}_{ss}$
et
$\widehat{\mathbf{G}}_{ss}$
et
![]() $\widehat{\mathbf{G}}_{ss}^{\prime }$
. Via cette identification, l’automorphisme
$\widehat{\mathbf{G}}_{ss}^{\prime }$
. Via cette identification, l’automorphisme
![]() $\unicode[STIX]{x1D711}$
donne lieu à un isomorphisme
$\unicode[STIX]{x1D711}$
donne lieu à un isomorphisme
![]() $\widehat{\unicode[STIX]{x1D711}}_{ss}\in \text{Aut}(\widehat{\mathbf{G}}_{ss})$
. Ce dernier est défini par le diagramme commutatif suivant
$\widehat{\unicode[STIX]{x1D711}}_{ss}\in \text{Aut}(\widehat{\mathbf{G}}_{ss})$
. Ce dernier est défini par le diagramme commutatif suivant

Il correspond donc à l’automorphisme de
![]() $X$
:
$X$
:
![]() $f\circ f(\unicode[STIX]{x1D711})$
. Une autre façon de voir les choses est la suivante.
$f\circ f(\unicode[STIX]{x1D711})$
. Une autre façon de voir les choses est la suivante.
Fixons un épinglage
![]() $(\mathbf{G},\mathbf{B},\mathbf{T},\{u_{\unicode[STIX]{x1D6FC}}\}_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}})$
. On a alors une suite exacte scindée
$(\mathbf{G},\mathbf{B},\mathbf{T},\{u_{\unicode[STIX]{x1D6FC}}\}_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}})$
. On a alors une suite exacte scindée
L’automorphisme
![]() $f\circ f(\unicode[STIX]{x1D711})$
correspond à l’image de
$f\circ f(\unicode[STIX]{x1D711})$
correspond à l’image de
![]() $\unicode[STIX]{x1D711}$
par l’application
$\unicode[STIX]{x1D711}$
par l’application
![]() $\text{Aut}(\mathbf{G})\longrightarrow \text{Out}(\mathbf{G})$
. Son image par
$\text{Aut}(\mathbf{G})\longrightarrow \text{Out}(\mathbf{G})$
. Son image par
![]() $\text{Out}(\mathbf{G})\rightarrow \text{Out}(\widehat{\mathbf{G}})$
est
$\text{Out}(\mathbf{G})\rightarrow \text{Out}(\widehat{\mathbf{G}})$
est
![]() $^{t}(f\circ f(\unicode[STIX]{x1D711}))$
. On peut donc prendre pour
$^{t}(f\circ f(\unicode[STIX]{x1D711}))$
. On peut donc prendre pour
![]() $\widehat{\unicode[STIX]{x1D711}}$
l’image de
$\widehat{\unicode[STIX]{x1D711}}$
l’image de
![]() $^{t}(f\circ f(\unicode[STIX]{x1D711}))$
par
$^{t}(f\circ f(\unicode[STIX]{x1D711}))$
par
![]() $\text{Out}(\widehat{\mathbf{G}})\rightarrow \text{Aut}(\widehat{\mathbf{G}})$
. L’automorphisme
$\text{Out}(\widehat{\mathbf{G}})\rightarrow \text{Aut}(\widehat{\mathbf{G}})$
. L’automorphisme
![]() $\widehat{\unicode[STIX]{x1D711}}_{ss}$
recherché est alors l’application induite par
$\widehat{\unicode[STIX]{x1D711}}_{ss}$
recherché est alors l’application induite par
![]() $\widehat{\unicode[STIX]{x1D711}}$
sur les classes de conjugaison semi-simples.
$\widehat{\unicode[STIX]{x1D711}}$
sur les classes de conjugaison semi-simples.
Lemme A.0.2. On a un diagramme commutatif

où
![]() $\widehat{\unicode[STIX]{x1D711}}$
est l’image de
$\widehat{\unicode[STIX]{x1D711}}$
est l’image de
![]() $\unicode[STIX]{x1D711}$
par l’application
$\unicode[STIX]{x1D711}$
par l’application
![]() $\text{Aut}(\mathbf{G})\rightarrow \text{Out}(\mathbf{G})\rightarrow \text{Out}(\widehat{\mathbf{G}})\rightarrow \text{Aut}(\widehat{\mathbf{G}})$
. En particulier, si
$\text{Aut}(\mathbf{G})\rightarrow \text{Out}(\mathbf{G})\rightarrow \text{Out}(\widehat{\mathbf{G}})\rightarrow \text{Aut}(\widehat{\mathbf{G}})$
. En particulier, si
![]() $\unicode[STIX]{x1D711}\in \text{Int}(\mathbf{G})$
,
$\unicode[STIX]{x1D711}\in \text{Int}(\mathbf{G})$
,
![]() $\widehat{\unicode[STIX]{x1D711}}_{ss}=\text{id}$
.
$\widehat{\unicode[STIX]{x1D711}}_{ss}=\text{id}$
.
Annexe B Rappels sur le Frobenius
Soit
![]() $\text{G}$
un groupe réductif connexe défini sur
$\text{G}$
un groupe réductif connexe défini sur
![]() $\mathfrak{F}$
. Une structure sur
$\mathfrak{F}$
. Une structure sur
![]() $\mathfrak{f}$
donne lieu à un endomorphisme de Frobenius noté
$\mathfrak{f}$
donne lieu à un endomorphisme de Frobenius noté
![]() $F:\text{G}\rightarrow \text{G}$
, tel que les
$F:\text{G}\rightarrow \text{G}$
, tel que les
![]() $\mathfrak{f}$
-points de
$\mathfrak{f}$
-points de
![]() $\text{G}$
soient
$\text{G}$
soient
![]() $\mathsf{G}:=\text{G}^{F}=\text{G}(\mathfrak{f})$
. Celui-ci est défini de la manière suivante.
$\mathsf{G}:=\text{G}^{F}=\text{G}(\mathfrak{f})$
. Celui-ci est défini de la manière suivante.
![]() $\text{G}$
possède une
$\text{G}$
possède une
![]() $\mathfrak{f}$
-structure si et seulement si son algèbre des fonctions, que l’on note
$\mathfrak{f}$
-structure si et seulement si son algèbre des fonctions, que l’on note
![]() $A$
, vérifie
$A$
, vérifie
![]() $A=A_{0}\otimes _{\mathfrak{f}}\mathfrak{F}$
où
$A=A_{0}\otimes _{\mathfrak{f}}\mathfrak{F}$
où
![]() $A_{0}$
est une
$A_{0}$
est une
![]() $\mathfrak{f}$
-algèbre. L’endomorphisme de Frobenius
$\mathfrak{f}$
-algèbre. L’endomorphisme de Frobenius
![]() $F:\text{G}\rightarrow \text{G}$
est alors défini par son co-morphisme
$F:\text{G}\rightarrow \text{G}$
est alors défini par son co-morphisme
![]() $F^{\ast }\in \operatorname{End}(A_{0}\otimes _{\mathfrak{f}}\mathfrak{F})$
qui a
$F^{\ast }\in \operatorname{End}(A_{0}\otimes _{\mathfrak{f}}\mathfrak{F})$
qui a
![]() $x\otimes \unicode[STIX]{x1D706}$
associe
$x\otimes \unicode[STIX]{x1D706}$
associe
![]() $x^{q}\otimes \unicode[STIX]{x1D706}$
.
$x^{q}\otimes \unicode[STIX]{x1D706}$
.
Le groupe de Galois
![]() $\operatorname{Gal}(\mathfrak{F}/\mathfrak{f})$
agit également sur
$\operatorname{Gal}(\mathfrak{F}/\mathfrak{f})$
agit également sur
![]() $A_{0}\otimes _{\mathfrak{f}}\mathfrak{F}$
par
$A_{0}\otimes _{\mathfrak{f}}\mathfrak{F}$
par
![]() $x\otimes \unicode[STIX]{x1D706}\mapsto x\otimes \unicode[STIX]{x1D706}^{q}$
et donc induit une action que l’on note
$x\otimes \unicode[STIX]{x1D706}\mapsto x\otimes \unicode[STIX]{x1D706}^{q}$
et donc induit une action que l’on note
![]() $\unicode[STIX]{x1D70F}$
sur
$\unicode[STIX]{x1D70F}$
sur
![]() $\text{G}$
.
$\text{G}$
.
Nous avons besoin de comprendre un peu plus en détail comment ces deux actions agissent lorsque
![]() $\text{G}=\text{T}$
est un tore défini sur
$\text{G}=\text{T}$
est un tore défini sur
![]() $\mathfrak{f}$
. Notons
$\mathfrak{f}$
. Notons
![]() $X=X^{\ast }(\text{T})=\text{Hom}(\text{T},\mathbb{G}_{m})$
le groupe des caractères de
$X=X^{\ast }(\text{T})=\text{Hom}(\text{T},\mathbb{G}_{m})$
le groupe des caractères de
![]() $\text{T}$
. On a
$\text{T}$
. On a
![]() $X\simeq \text{Hom}_{\text{alg}-\text{Hopf}}(\mathfrak{F}[t,t^{-1}],A)$
et donc
$X\simeq \text{Hom}_{\text{alg}-\text{Hopf}}(\mathfrak{F}[t,t^{-1}],A)$
et donc
![]() $\unicode[STIX]{x1D70F}$
et
$\unicode[STIX]{x1D70F}$
et
![]() $F$
se prolongent en des actions sur
$F$
se prolongent en des actions sur
![]() $X$
. Notons
$X$
. Notons
![]() $\unicode[STIX]{x1D70F}_{X}$
l’action de
$\unicode[STIX]{x1D70F}_{X}$
l’action de
![]() $\unicode[STIX]{x1D70F}$
induit sur
$\unicode[STIX]{x1D70F}$
induit sur
![]() $X$
.
$X$
.
Soit
![]() $\unicode[STIX]{x1D6FC}\in X$
et calculons
$\unicode[STIX]{x1D6FC}\in X$
et calculons
![]() $\unicode[STIX]{x1D70F}_{X}\cdot F\cdot \unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D70F}_{X}\cdot F\cdot \unicode[STIX]{x1D6FC}$
.
On voit donc que
![]() $\unicode[STIX]{x1D70F}_{X}\cdot F\cdot \unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}^{q}$
. Notons
$\unicode[STIX]{x1D70F}_{X}\cdot F\cdot \unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}^{q}$
. Notons
![]() $\unicode[STIX]{x1D713}$
l’élévation à la puissance
$\unicode[STIX]{x1D713}$
l’élévation à la puissance
![]() $q$
. Comme
$q$
. Comme
![]() $\text{T}\simeq \text{Hom}(X,\mathfrak{F}^{\times })$
, ces actions se transfèrent en des actions sur
$\text{T}\simeq \text{Hom}(X,\mathfrak{F}^{\times })$
, ces actions se transfèrent en des actions sur
![]() $\text{T}$
. A quoi correspond
$\text{T}$
. A quoi correspond
![]() $\unicode[STIX]{x1D713}$
? Prenons
$\unicode[STIX]{x1D713}$
? Prenons
![]() $u:X\rightarrow \mathfrak{F}^{\times }$
alors
$u:X\rightarrow \mathfrak{F}^{\times }$
alors
Donc
![]() $\unicode[STIX]{x1D713}$
agit comme l’élévation à la puissance
$\unicode[STIX]{x1D713}$
agit comme l’élévation à la puissance
![]() $q$
sur
$q$
sur
![]() $\text{T}$
. Finalement on trouve que l’action de
$\text{T}$
. Finalement on trouve que l’action de
![]() $F$
sur
$F$
sur
![]() $\text{T}$
est donnée par
$\text{T}$
est donnée par
![]() $F=\unicode[STIX]{x1D70F}_{X}^{-1}\circ \unicode[STIX]{x1D713}$
.
$F=\unicode[STIX]{x1D70F}_{X}^{-1}\circ \unicode[STIX]{x1D713}$
.
Annexe C Équivalence inertielle pour les paramètres de Langlands
Nous rappelons dans cette section la définition de classe inertielle introduite par Haines dans [Reference HainesHai14]. Nous montrons également une proposition, utile pour le théorème 4.5.8, qui relie une classe inertielle aux paramètres de l’inertie.
Soit
![]() $\mathbf{G}$
un groupe réductif connexe défini sur
$\mathbf{G}$
un groupe réductif connexe défini sur
![]() $k$
un corps
$k$
un corps
![]() $p$
-adique. On considère ici des représentations à coefficients complexes.
$p$
-adique. On considère ici des représentations à coefficients complexes.
Commençons par rappeler la notion de parabolique standard et de Levi standard de
![]() $^{L}\mathbf{G}$
, définis dans [Reference BorelBor79, paragraphes 3.3 et 3.4]. Fixons des données
$^{L}\mathbf{G}$
, définis dans [Reference BorelBor79, paragraphes 3.3 et 3.4]. Fixons des données
![]() $\widehat{\mathbf{T}}_{0}\subseteq \widehat{\mathbf{B}}_{0}\subseteq \widehat{\mathbf{G}}$
, composées d’un tore maximal et d’un Borel, stables sous l’action du groupe de Galois. On dit alors qu’un sous-groupe parabolique
$\widehat{\mathbf{T}}_{0}\subseteq \widehat{\mathbf{B}}_{0}\subseteq \widehat{\mathbf{G}}$
, composées d’un tore maximal et d’un Borel, stables sous l’action du groupe de Galois. On dit alors qu’un sous-groupe parabolique
![]() ${\mathcal{P}}$
de
${\mathcal{P}}$
de
![]() $^{L}\mathbf{G}$
est standard si
$^{L}\mathbf{G}$
est standard si
![]() ${\mathcal{P}}\supseteq ^{L}\mathbf{B}_{0}$
. Sa composante neutre
${\mathcal{P}}\supseteq ^{L}\mathbf{B}_{0}$
. Sa composante neutre
![]() ${\mathcal{P}}^{\circ }:={\mathcal{P}}\cap \widehat{\mathbf{G}}$
est alors un sous-groupe parabolique standard de
${\mathcal{P}}^{\circ }:={\mathcal{P}}\cap \widehat{\mathbf{G}}$
est alors un sous-groupe parabolique standard de
![]() $\widehat{\mathbf{G}}$
contenant
$\widehat{\mathbf{G}}$
contenant
![]() $\widehat{\mathbf{B}}_{0}$
et on a
$\widehat{\mathbf{B}}_{0}$
et on a
![]() ${\mathcal{P}}={\mathcal{P}}^{\circ }\rtimes W_{k}$
. Soit
${\mathcal{P}}={\mathcal{P}}^{\circ }\rtimes W_{k}$
. Soit
![]() ${\mathcal{M}}^{\circ }$
l’unique Levi de
${\mathcal{M}}^{\circ }$
l’unique Levi de
![]() ${\mathcal{P}}^{\circ }$
contenant
${\mathcal{P}}^{\circ }$
contenant
![]() $\widehat{\mathbf{T}}_{0}$
. Alors
$\widehat{\mathbf{T}}_{0}$
. Alors
![]() ${\mathcal{M}}:=N_{{\mathcal{P}}}({\mathcal{M}}^{\circ })$
est un sous-groupe de Levi de
${\mathcal{M}}:=N_{{\mathcal{P}}}({\mathcal{M}}^{\circ })$
est un sous-groupe de Levi de
![]() ${\mathcal{P}}$
et
${\mathcal{P}}$
et
![]() ${\mathcal{M}}={\mathcal{M}}^{\circ }\rtimes W_{k}$
. Les sous-groupes de Levi de
${\mathcal{M}}={\mathcal{M}}^{\circ }\rtimes W_{k}$
. Les sous-groupes de Levi de
![]() $^{L}\mathbf{G}$
construits de cette manière sont appelés standards. Tout sous-groupe de Levi de
$^{L}\mathbf{G}$
construits de cette manière sont appelés standards. Tout sous-groupe de Levi de
![]() $^{L}\mathbf{G}$
est
$^{L}\mathbf{G}$
est
![]() $\widehat{\mathbf{G}}$
-conjugué à un Levi standard, et pour
$\widehat{\mathbf{G}}$
-conjugué à un Levi standard, et pour
![]() ${\mathcal{M}}$
un Levi standard de
${\mathcal{M}}$
un Levi standard de
![]() $^{L}\mathbf{G}$
, on note
$^{L}\mathbf{G}$
, on note
![]() $\{{\mathcal{M}}\}$
l’ensemble des sous-groupes de Levi standards qui sont
$\{{\mathcal{M}}\}$
l’ensemble des sous-groupes de Levi standards qui sont
![]() $\widehat{\mathbf{G}}$
-conjugués à
$\widehat{\mathbf{G}}$
-conjugués à
![]() ${\mathcal{M}}$
.
${\mathcal{M}}$
.
Soit
![]() $\unicode[STIX]{x1D706}:W_{k}\rightarrow \,^{L}\mathbf{G}$
un morphisme admissible. L’image de
$\unicode[STIX]{x1D706}:W_{k}\rightarrow \,^{L}\mathbf{G}$
un morphisme admissible. L’image de
![]() $\unicode[STIX]{x1D706}$
est alors contenue dans un Levi minimal de
$\unicode[STIX]{x1D706}$
est alors contenue dans un Levi minimal de
![]() $^{L}\mathbf{G}$
, bien défini à conjugaison par un élément de
$^{L}\mathbf{G}$
, bien défini à conjugaison par un élément de
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D706})^{\circ }$
, où
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D706})^{\circ }$
, où
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D706})$
désigne le centralisateur de
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D706})$
désigne le centralisateur de
![]() $\unicode[STIX]{x1D706}(W_{k})$
dans
$\unicode[STIX]{x1D706}(W_{k})$
dans
![]() $\widehat{\mathbf{G}}$
(voir [Reference BorelBor79, proposition 3.6]). Notons
$\widehat{\mathbf{G}}$
(voir [Reference BorelBor79, proposition 3.6]). Notons
![]() $(\unicode[STIX]{x1D706})_{\widehat{\mathbf{G}}}$
la classe de
$(\unicode[STIX]{x1D706})_{\widehat{\mathbf{G}}}$
la classe de
![]() $\widehat{\mathbf{G}}$
-conjugaison de
$\widehat{\mathbf{G}}$
-conjugaison de
![]() $\unicode[STIX]{x1D706}$
. Alors
$\unicode[STIX]{x1D706}$
. Alors
![]() $\unicode[STIX]{x1D706}$
donne lieu à une unique classe de Levi standards
$\unicode[STIX]{x1D706}$
donne lieu à une unique classe de Levi standards
![]() $\{{\mathcal{M}}_{\unicode[STIX]{x1D706}}\}$
telle qu’il existe
$\{{\mathcal{M}}_{\unicode[STIX]{x1D706}}\}$
telle qu’il existe
![]() $\unicode[STIX]{x1D706}^{+}\in (\unicode[STIX]{x1D706})_{\widehat{\mathbf{G}}}$
dont l’image est contenue minimalement dans
$\unicode[STIX]{x1D706}^{+}\in (\unicode[STIX]{x1D706})_{\widehat{\mathbf{G}}}$
dont l’image est contenue minimalement dans
![]() ${\mathcal{M}}_{\unicode[STIX]{x1D706}}$
, pour un
${\mathcal{M}}_{\unicode[STIX]{x1D706}}$
, pour un
![]() ${\mathcal{M}}_{\unicode[STIX]{x1D706}}$
dans cette classe.
${\mathcal{M}}_{\unicode[STIX]{x1D706}}$
dans cette classe.
Définition C.0.1 [Reference HainesHai14, définition 5.3.3]. Soient
![]() $\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}:W_{k}\rightarrow \,^{L}\mathbf{G}$
deux paramètres admissibles. On dit que
$\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}:W_{k}\rightarrow \,^{L}\mathbf{G}$
deux paramètres admissibles. On dit que
![]() $\unicode[STIX]{x1D706}_{1}$
et
$\unicode[STIX]{x1D706}_{1}$
et
![]() $\unicode[STIX]{x1D706}_{2}$
sont inertiellement équivalents si
$\unicode[STIX]{x1D706}_{2}$
sont inertiellement équivalents si
(i)
 $\{{\mathcal{M}}_{\unicode[STIX]{x1D706}_{1}}\}=\{{\mathcal{M}}_{\unicode[STIX]{x1D706}_{2}}\}$
;
$\{{\mathcal{M}}_{\unicode[STIX]{x1D706}_{1}}\}=\{{\mathcal{M}}_{\unicode[STIX]{x1D706}_{2}}\}$
;(ii) il existe
 ${\mathcal{M}}\in \{{\mathcal{M}}_{\unicode[STIX]{x1D706}_{1}}\}$
,
${\mathcal{M}}\in \{{\mathcal{M}}_{\unicode[STIX]{x1D706}_{1}}\}$
,
 $\unicode[STIX]{x1D706}_{1}^{+}\in (\unicode[STIX]{x1D706}_{1})_{\widehat{\mathbf{G}}}$
et
$\unicode[STIX]{x1D706}_{1}^{+}\in (\unicode[STIX]{x1D706}_{1})_{\widehat{\mathbf{G}}}$
et
 $\unicode[STIX]{x1D706}_{2}^{+}\in (\unicode[STIX]{x1D706}_{2})_{\widehat{\mathbf{G}}}$
dont les images sont minimalement contenues dans
$\unicode[STIX]{x1D706}_{2}^{+}\in (\unicode[STIX]{x1D706}_{2})_{\widehat{\mathbf{G}}}$
dont les images sont minimalement contenues dans
 ${\mathcal{M}}$
, et
${\mathcal{M}}$
, et
 $z\in H^{1}(\langle \widehat{\unicode[STIX]{x1D717}}\rangle ,(Z({\mathcal{M}}^{\circ })^{I_{k}})^{\circ })$
vérifiant
$z\in H^{1}(\langle \widehat{\unicode[STIX]{x1D717}}\rangle ,(Z({\mathcal{M}}^{\circ })^{I_{k}})^{\circ })$
vérifiant  $$\begin{eqnarray}(z\unicode[STIX]{x1D706}_{1}^{+})_{{\mathcal{M}}^{\circ }}=(\unicode[STIX]{x1D706}_{2}^{+})_{{\mathcal{M}}^{\circ }}.\end{eqnarray}$$
$$\begin{eqnarray}(z\unicode[STIX]{x1D706}_{1}^{+})_{{\mathcal{M}}^{\circ }}=(\unicode[STIX]{x1D706}_{2}^{+})_{{\mathcal{M}}^{\circ }}.\end{eqnarray}$$
Proposition C.0.2. Soit
![]() $\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}(I_{k},\mathbf{G})$
tel que
$\unicode[STIX]{x1D719}\in \unicode[STIX]{x1D6F7}(I_{k},\mathbf{G})$
tel que
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
, le centralisateur de
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
, le centralisateur de
![]() $\unicode[STIX]{x1D719}(I_{k})$
dans
$\unicode[STIX]{x1D719}(I_{k})$
dans
![]() $\widehat{\mathbf{G}}$
, est connexe. Alors l’ensemble des
$\widehat{\mathbf{G}}$
, est connexe. Alors l’ensemble des
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6F7}(W_{k},\mathbf{G})$
tels que
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6F7}(W_{k},\mathbf{G})$
tels que
![]() $\unicode[STIX]{x1D706}_{|I_{k}}\sim \unicode[STIX]{x1D719}$
forme une classe d’équivalence inertielle.
$\unicode[STIX]{x1D706}_{|I_{k}}\sim \unicode[STIX]{x1D719}$
forme une classe d’équivalence inertielle.
Démonstration.
Remarquons tout d’abord que deux paramètres admissibles de
![]() $W_{k}$
inertiellement équivalents ont des restrictions à l’inertie conjuguées. Prenons donc deux paramètres admissibles
$W_{k}$
inertiellement équivalents ont des restrictions à l’inertie conjuguées. Prenons donc deux paramètres admissibles
![]() $\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}:W_{k}\rightarrow \,^{L}\mathbf{G}$
tels que
$\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}:W_{k}\rightarrow \,^{L}\mathbf{G}$
tels que
![]() $\unicode[STIX]{x1D706}_{1|I_{k}}\sim \unicode[STIX]{x1D706}_{2|I_{k}}\sim \unicode[STIX]{x1D719}$
et montrons qu’ils sont inertiellement équivalents. Quitte à conjuguer par
$\unicode[STIX]{x1D706}_{1|I_{k}}\sim \unicode[STIX]{x1D706}_{2|I_{k}}\sim \unicode[STIX]{x1D719}$
et montrons qu’ils sont inertiellement équivalents. Quitte à conjuguer par
![]() $\widehat{\mathbf{G}}$
, on peut supposer que
$\widehat{\mathbf{G}}$
, on peut supposer que
![]() $\unicode[STIX]{x1D706}_{1|I_{k}}=\unicode[STIX]{x1D706}_{2|I_{k}}=\unicode[STIX]{x1D719}$
. Fixons
$\unicode[STIX]{x1D706}_{1|I_{k}}=\unicode[STIX]{x1D706}_{2|I_{k}}=\unicode[STIX]{x1D719}$
. Fixons
![]() $(\widehat{\mathbf{T}},\widehat{\mathbf{B}})$
une paire constituée d’un tore maximal et d’un Borel de
$(\widehat{\mathbf{T}},\widehat{\mathbf{B}})$
une paire constituée d’un tore maximal et d’un Borel de
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
.
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
.
Comme
![]() $\unicode[STIX]{x1D706}_{1|I_{k}}=\unicode[STIX]{x1D719}$
, pour
$\unicode[STIX]{x1D706}_{1|I_{k}}=\unicode[STIX]{x1D719}$
, pour
![]() $w\in W_{k}$
,
$w\in W_{k}$
,
![]() $\unicode[STIX]{x1D706}_{1}(w)$
normalise
$\unicode[STIX]{x1D706}_{1}(w)$
normalise
![]() $\unicode[STIX]{x1D719}(I_{k})$
donc normalise également
$\unicode[STIX]{x1D719}(I_{k})$
donc normalise également
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
. En faisant agir
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
. En faisant agir
![]() $w$
par conjugaison par
$w$
par conjugaison par
![]() $\unicode[STIX]{x1D706}_{1}(w)$
on obtient une action
$\unicode[STIX]{x1D706}_{1}(w)$
on obtient une action
![]() $\text{Ad}_{\unicode[STIX]{x1D706}_{1}}:W_{k}/I_{k}\rightarrow \text{Aut}(C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719}))$
. La conjugaison par
$\text{Ad}_{\unicode[STIX]{x1D706}_{1}}:W_{k}/I_{k}\rightarrow \text{Aut}(C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719}))$
. La conjugaison par
![]() $\unicode[STIX]{x1D706}_{1}(\text{Frob})$
,
$\unicode[STIX]{x1D706}_{1}(\text{Frob})$
,
![]() $\text{Ad}_{\unicode[STIX]{x1D706}_{1}}(\text{Frob})$
est donc un automorphisme semi-simple de
$\text{Ad}_{\unicode[STIX]{x1D706}_{1}}(\text{Frob})$
est donc un automorphisme semi-simple de
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
, que l’on notera
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
, que l’on notera
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}$
. Par le théorème 7.5 de [Reference SteinbergSte68] il existe une paire
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}$
. Par le théorème 7.5 de [Reference SteinbergSte68] il existe une paire
![]() $(\mathbf{T}_{1},\mathbf{B}_{1})$
constituée d’un tore maximal et d’un Borel de
$(\mathbf{T}_{1},\mathbf{B}_{1})$
constituée d’un tore maximal et d’un Borel de
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
tous les deux
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
tous les deux
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}$
-stables. Quitte à conjuguer
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}$
-stables. Quitte à conjuguer
![]() $\unicode[STIX]{x1D706}_{1}$
par un élément de
$\unicode[STIX]{x1D706}_{1}$
par un élément de
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
, on peut supposer que
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
, on peut supposer que
![]() $(\mathbf{T}_{1},\mathbf{B}_{1})=(\widehat{\mathbf{T}},\widehat{\mathbf{B}})$
, c’est à dire que
$(\mathbf{T}_{1},\mathbf{B}_{1})=(\widehat{\mathbf{T}},\widehat{\mathbf{B}})$
, c’est à dire que
![]() $\widehat{\mathbf{T}}$
et
$\widehat{\mathbf{T}}$
et
![]() $\widehat{\mathbf{B}}$
sont
$\widehat{\mathbf{B}}$
sont
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}$
-stables. On fait de même pour
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}$
-stables. On fait de même pour
![]() $\unicode[STIX]{x1D706}_{2}$
et donc
$\unicode[STIX]{x1D706}_{2}$
et donc
![]() $\widehat{\mathbf{T}}$
et
$\widehat{\mathbf{T}}$
et
![]() $\widehat{\mathbf{B}}$
sont également
$\widehat{\mathbf{B}}$
sont également
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{2}}$
-stables.
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{2}}$
-stables.
Posons
![]() ${\mathcal{M}}_{\unicode[STIX]{x1D706}_{1}}:=C_{^{L}\mathbf{G}}([\widehat{\mathbf{T}}^{\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}}]^{\circ })$
. Comme
${\mathcal{M}}_{\unicode[STIX]{x1D706}_{1}}:=C_{^{L}\mathbf{G}}([\widehat{\mathbf{T}}^{\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}}]^{\circ })$
. Comme
![]() $(\widehat{\mathbf{T}}^{\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}})^{\circ }$
est un tore maximal de
$(\widehat{\mathbf{T}}^{\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}})^{\circ }$
est un tore maximal de
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D706}_{1})^{\circ }$
[Reference Digne and MichelDM94, théorème 1.8(iii)],
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D706}_{1})^{\circ }$
[Reference Digne and MichelDM94, théorème 1.8(iii)],
![]() ${\mathcal{M}}_{\unicode[STIX]{x1D706}_{1}}$
est un Levi minimal contenant l’image de
${\mathcal{M}}_{\unicode[STIX]{x1D706}_{1}}$
est un Levi minimal contenant l’image de
![]() $\unicode[STIX]{x1D706}_{1}$
[Reference BorelBor79, proposition 3.6]. Adoptons les même notations pour
$\unicode[STIX]{x1D706}_{1}$
[Reference BorelBor79, proposition 3.6]. Adoptons les même notations pour
![]() $\unicode[STIX]{x1D706}_{2}$
.
$\unicode[STIX]{x1D706}_{2}$
.
Écrivons pour
![]() $w\in W_{k}$
,
$w\in W_{k}$
,
![]() $\unicode[STIX]{x1D706}_{2}(w)=\unicode[STIX]{x1D702}(w)\unicode[STIX]{x1D706}_{1}(w)$
avec
$\unicode[STIX]{x1D706}_{2}(w)=\unicode[STIX]{x1D702}(w)\unicode[STIX]{x1D706}_{1}(w)$
avec
![]() $\unicode[STIX]{x1D702}(w)\in \widehat{\mathbf{G}}$
. Alors
$\unicode[STIX]{x1D702}(w)\in \widehat{\mathbf{G}}$
. Alors
![]() $\unicode[STIX]{x1D702}$
est un cocycle à valeurs dans
$\unicode[STIX]{x1D702}$
est un cocycle à valeurs dans
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
pour l’action
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
pour l’action
![]() $\text{Ad}_{\unicode[STIX]{x1D706}_{1}}$
, c’est-à-dire
$\text{Ad}_{\unicode[STIX]{x1D706}_{1}}$
, c’est-à-dire
![]() $\unicode[STIX]{x1D702}\in Z_{\text{Ad}_{\unicode[STIX]{x1D706}_{1}}}^{1}(W_{k}/I_{k},C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719}))$
. Comme la paire
$\unicode[STIX]{x1D702}\in Z_{\text{Ad}_{\unicode[STIX]{x1D706}_{1}}}^{1}(W_{k}/I_{k},C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719}))$
. Comme la paire
![]() $(\widehat{\mathbf{T}},\widehat{\mathbf{B}})$
est à la fois
$(\widehat{\mathbf{T}},\widehat{\mathbf{B}})$
est à la fois
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}$
-stable et
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}$
-stable et
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{2}}$
-stable,
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{2}}$
-stable,
![]() $\unicode[STIX]{x1D702}(\text{Frob})$
est dans le normalisateur dans
$\unicode[STIX]{x1D702}(\text{Frob})$
est dans le normalisateur dans
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
de la paire
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
de la paire
![]() $(\widehat{\mathbf{T}},\widehat{\mathbf{B}})$
qui est égal à
$(\widehat{\mathbf{T}},\widehat{\mathbf{B}})$
qui est égal à
![]() $\widehat{\mathbf{T}}$
. Puisque
$\widehat{\mathbf{T}}$
. Puisque
![]() $\unicode[STIX]{x1D702}(\text{Frob})\in \widehat{\mathbf{T}}$
, on a en particulier que
$\unicode[STIX]{x1D702}(\text{Frob})\in \widehat{\mathbf{T}}$
, on a en particulier que
![]() $\widehat{\mathbf{T}}^{\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}}=\widehat{\mathbf{T}}^{\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{2}}}$
et donc
$\widehat{\mathbf{T}}^{\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}}=\widehat{\mathbf{T}}^{\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{2}}}$
et donc
![]() ${\mathcal{M}}_{\unicode[STIX]{x1D706}_{1}}={\mathcal{M}}_{\unicode[STIX]{x1D706}_{2}}$
. Notons maintenant
${\mathcal{M}}_{\unicode[STIX]{x1D706}_{1}}={\mathcal{M}}_{\unicode[STIX]{x1D706}_{2}}$
. Notons maintenant
![]() ${\mathcal{M}}:={\mathcal{M}}_{\unicode[STIX]{x1D706}_{1}}={\mathcal{M}}_{\unicode[STIX]{x1D706}_{2}}$
.
${\mathcal{M}}:={\mathcal{M}}_{\unicode[STIX]{x1D706}_{1}}={\mathcal{M}}_{\unicode[STIX]{x1D706}_{2}}$
.
La suite exacte
![]() $1\rightarrow {\mathcal{M}}^{\circ }\rightarrow {\mathcal{M}}\rightarrow \langle \widehat{\unicode[STIX]{x1D717}}\rangle \rightarrow 1$
et le choix d’une section permettent de définir une action de
$1\rightarrow {\mathcal{M}}^{\circ }\rightarrow {\mathcal{M}}\rightarrow \langle \widehat{\unicode[STIX]{x1D717}}\rangle \rightarrow 1$
et le choix d’une section permettent de définir une action de
![]() $\langle \widehat{\unicode[STIX]{x1D717}}\rangle$
sur
$\langle \widehat{\unicode[STIX]{x1D717}}\rangle$
sur
![]() ${\mathcal{M}}^{\circ }$
. Par conjugaison, elle induit une action de
${\mathcal{M}}^{\circ }$
. Par conjugaison, elle induit une action de
![]() $\langle \widehat{\unicode[STIX]{x1D717}}\rangle$
sur
$\langle \widehat{\unicode[STIX]{x1D717}}\rangle$
sur
![]() $Z({\mathcal{M}}^{\circ })$
qui est alors indépendante du choix de la section. On a donc une action canonique de
$Z({\mathcal{M}}^{\circ })$
qui est alors indépendante du choix de la section. On a donc une action canonique de
![]() $\langle \widehat{\unicode[STIX]{x1D717}}\rangle$
sur
$\langle \widehat{\unicode[STIX]{x1D717}}\rangle$
sur
![]() $Z({\mathcal{M}}^{\circ })$
.
$Z({\mathcal{M}}^{\circ })$
.
On aurait pu conjuguer
![]() $\unicode[STIX]{x1D719}$
dès le départ pour avoir
$\unicode[STIX]{x1D719}$
dès le départ pour avoir
![]() ${\mathcal{M}}$
standard. Il nous suffit donc pour montrer que
${\mathcal{M}}$
standard. Il nous suffit donc pour montrer que
![]() $\unicode[STIX]{x1D706}_{1}$
et
$\unicode[STIX]{x1D706}_{1}$
et
![]() $\unicode[STIX]{x1D706}_{2}$
sont inertiellement équivalents de montrer l’existence d’un
$\unicode[STIX]{x1D706}_{2}$
sont inertiellement équivalents de montrer l’existence d’un
![]() $z\in H^{1}(\langle \widehat{\unicode[STIX]{x1D717}}\rangle ,(Z({\mathcal{M}}^{\circ })^{I_{k}})^{\circ })$
tel que
$z\in H^{1}(\langle \widehat{\unicode[STIX]{x1D717}}\rangle ,(Z({\mathcal{M}}^{\circ })^{I_{k}})^{\circ })$
tel que
![]() $(z\unicode[STIX]{x1D706}_{1})_{{\mathcal{M}}^{\circ }}=(\unicode[STIX]{x1D706}_{2})_{{\mathcal{M}}^{\circ }}$
. Soit
$(z\unicode[STIX]{x1D706}_{1})_{{\mathcal{M}}^{\circ }}=(\unicode[STIX]{x1D706}_{2})_{{\mathcal{M}}^{\circ }}$
. Soit
![]() $t\in \widehat{\mathbf{T}}$
, alors
$t\in \widehat{\mathbf{T}}$
, alors
![]() $^{t}\unicode[STIX]{x1D706}_{2}=\unicode[STIX]{x1D702}^{\prime }\unicode[STIX]{x1D706}_{1}$
avec
$^{t}\unicode[STIX]{x1D706}_{2}=\unicode[STIX]{x1D702}^{\prime }\unicode[STIX]{x1D706}_{1}$
avec
![]() $\unicode[STIX]{x1D702}^{\prime }=t^{-1}\unicode[STIX]{x1D702}\text{Ad}_{\unicode[STIX]{x1D706}_{1}}(t)$
. Ainsi, pour finir la preuve de la proposition, il nous suffit de montrer qu’il existe
$\unicode[STIX]{x1D702}^{\prime }=t^{-1}\unicode[STIX]{x1D702}\text{Ad}_{\unicode[STIX]{x1D706}_{1}}(t)$
. Ainsi, pour finir la preuve de la proposition, il nous suffit de montrer qu’il existe
![]() $t\in \widehat{\mathbf{T}}$
tel que
$t\in \widehat{\mathbf{T}}$
tel que
![]() $t^{-1}\unicode[STIX]{x1D702}(\text{Frob})\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}(t)\in (Z({\mathcal{M}}^{\circ })^{I_{k}})^{\circ }$
. Or comme
$t^{-1}\unicode[STIX]{x1D702}(\text{Frob})\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}(t)\in (Z({\mathcal{M}}^{\circ })^{I_{k}})^{\circ }$
. Or comme
![]() $(\widehat{\mathbf{T}}^{\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}})^{\circ }\subseteq (Z({\mathcal{M}}^{\circ })^{I_{k}})^{\circ }$
cela découle du lemme C.0.3 ci-dessous. Pour pouvoir appliquer ce dernier, il nous reste à vérifier que
$(\widehat{\mathbf{T}}^{\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}})^{\circ }\subseteq (Z({\mathcal{M}}^{\circ })^{I_{k}})^{\circ }$
cela découle du lemme C.0.3 ci-dessous. Pour pouvoir appliquer ce dernier, il nous reste à vérifier que
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}$
induit un automorphisme d’ordre fini sur
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}$
induit un automorphisme d’ordre fini sur
![]() $X_{\ast }(\widehat{\mathbf{T}})$
. Par dualité, il suffit de vérifier que
$X_{\ast }(\widehat{\mathbf{T}})$
. Par dualité, il suffit de vérifier que
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}$
a une action d’ordre fini sur le groupe des caractère
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}$
a une action d’ordre fini sur le groupe des caractère
![]() $X^{\ast }(\widehat{\mathbf{T}})$
. Pour cela nous allons montrer la finitude de l’action de
$X^{\ast }(\widehat{\mathbf{T}})$
. Pour cela nous allons montrer la finitude de l’action de
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}$
sur
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}$
sur
![]() $Q$
, le réseau engendré par les racines, puis sur le centre
$Q$
, le réseau engendré par les racines, puis sur le centre
![]() $Z(C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719}))$
. Comme le groupe des caractères de
$Z(C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719}))$
. Comme le groupe des caractères de
![]() $Z(C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719}))$
est
$Z(C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719}))$
est
![]() $X^{\ast }(\widehat{\mathbf{T}})/Q$
[Reference SpringerSpr79, 2.15], on en déduit la finitude de l’action sur
$X^{\ast }(\widehat{\mathbf{T}})/Q$
[Reference SpringerSpr79, 2.15], on en déduit la finitude de l’action sur
![]() $X^{\ast }(\widehat{\mathbf{T}})$
.
$X^{\ast }(\widehat{\mathbf{T}})$
.
L’automorphisme
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}$
de
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}$
de
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
stabilise
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
stabilise
![]() $\widehat{\mathbf{T}}$
, donc agit sur l’ensemble des racines de
$\widehat{\mathbf{T}}$
, donc agit sur l’ensemble des racines de
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
par rapport à
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
par rapport à
![]() $\widehat{\mathbf{T}}$
. Cet ensemble étant fini, cette action est également d’ordre fini. Il nous reste à étudier l’action de
$\widehat{\mathbf{T}}$
. Cet ensemble étant fini, cette action est également d’ordre fini. Il nous reste à étudier l’action de
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}$
sur
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}$
sur
![]() $Z(C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719}))$
le centre de
$Z(C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719}))$
le centre de
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
. D’après [Reference DatDat17, lemme 2.1.1], il existe
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
. D’après [Reference DatDat17, lemme 2.1.1], il existe
![]() $n\in \mathbb{N}^{\ast }$
et
$n\in \mathbb{N}^{\ast }$
et
![]() $\unicode[STIX]{x1D706}:W_{k}\rightarrow \,^{L}\mathbf{G}$
une extension de
$\unicode[STIX]{x1D706}:W_{k}\rightarrow \,^{L}\mathbf{G}$
une extension de
![]() $\unicode[STIX]{x1D719}$
telle que
$\unicode[STIX]{x1D719}$
telle que
![]() $\unicode[STIX]{x1D706}(n\text{Frob})=(1,n\widehat{\unicode[STIX]{x1D717}})$
. En particulier
$\unicode[STIX]{x1D706}(n\text{Frob})=(1,n\widehat{\unicode[STIX]{x1D717}})$
. En particulier
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}}$
a une action d’ordre fini sur
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}}$
a une action d’ordre fini sur
![]() $Z(C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719}))$
. Or nous avons vu que deux paramètres de
$Z(C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719}))$
. Or nous avons vu que deux paramètres de
![]() $W_{k}$
qui étendent
$W_{k}$
qui étendent
![]() $\unicode[STIX]{x1D719}$
diffèrent par un cocycle à valeur dans
$\unicode[STIX]{x1D719}$
diffèrent par un cocycle à valeur dans
![]() $C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
, donc l’action sur le centre
$C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719})$
, donc l’action sur le centre
![]() $Z(C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719}))$
est indépendante du choix de l’extension de
$Z(C_{\widehat{\mathbf{G}}}(\unicode[STIX]{x1D719}))$
est indépendante du choix de l’extension de
![]() $\unicode[STIX]{x1D719}$
. Par conséquent
$\unicode[STIX]{x1D719}$
. Par conséquent
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}$
a une action d’ordre fini sur le centre et on a le résultat.◻
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}_{1}}$
a une action d’ordre fini sur le centre et on a le résultat.◻
Lemme C.0.3. Soient
![]() $\mathbf{T}$
un tore sur
$\mathbf{T}$
un tore sur
![]() $\mathbb{C}$
et
$\mathbb{C}$
et
![]() $\unicode[STIX]{x1D703}\in \text{Aut}(\mathbf{T})$
. On note
$\unicode[STIX]{x1D703}\in \text{Aut}(\mathbf{T})$
. On note
![]() $X_{\ast }:=X_{\ast }(\mathbf{T})$
l’ensemble des co-caractères et on suppose que
$X_{\ast }:=X_{\ast }(\mathbf{T})$
l’ensemble des co-caractères et on suppose que
![]() $\unicode[STIX]{x1D703}$
induit un automorphisme d’ordre fini sur
$\unicode[STIX]{x1D703}$
induit un automorphisme d’ordre fini sur
![]() $X_{\ast }$
. Posons
$X_{\ast }$
. Posons
![]() $L_{\unicode[STIX]{x1D703}}$
l’application
$L_{\unicode[STIX]{x1D703}}$
l’application
![]() $L_{\unicode[STIX]{x1D703}}:\mathbf{T}\rightarrow \mathbf{T}$
,
$L_{\unicode[STIX]{x1D703}}:\mathbf{T}\rightarrow \mathbf{T}$
,
![]() $t\mapsto t^{-1}\unicode[STIX]{x1D703}(t)$
. Alors
$t\mapsto t^{-1}\unicode[STIX]{x1D703}(t)$
. Alors
![]() $\mathbf{T}=L_{\unicode[STIX]{x1D703}}(\mathbf{T})\cdot (\mathbf{T}^{\unicode[STIX]{x1D703}})^{\circ }$
.
$\mathbf{T}=L_{\unicode[STIX]{x1D703}}(\mathbf{T})\cdot (\mathbf{T}^{\unicode[STIX]{x1D703}})^{\circ }$
.
Démonstration.
Le groupe des co-caractères de
![]() $(\mathbf{T}^{\unicode[STIX]{x1D703}})^{\circ }$
vaut
$(\mathbf{T}^{\unicode[STIX]{x1D703}})^{\circ }$
vaut
![]() $X_{\ast }((\mathbf{T}^{\unicode[STIX]{x1D703}})^{\circ })=X_{\ast }^{\unicode[STIX]{x1D703}}$
. On définit
$X_{\ast }((\mathbf{T}^{\unicode[STIX]{x1D703}})^{\circ })=X_{\ast }^{\unicode[STIX]{x1D703}}$
. On définit
![]() $L_{\unicode[STIX]{x1D703}}^{X}:X_{\ast }\rightarrow X_{\ast }$
par
$L_{\unicode[STIX]{x1D703}}^{X}:X_{\ast }\rightarrow X_{\ast }$
par
![]() $L_{\unicode[STIX]{x1D703}}^{X}(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D706}-\unicode[STIX]{x1D703}(\unicode[STIX]{x1D706})$
. Alors
$L_{\unicode[STIX]{x1D703}}^{X}(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D706}-\unicode[STIX]{x1D703}(\unicode[STIX]{x1D706})$
. Alors
![]() $X_{\ast }(L_{\unicode[STIX]{x1D703}}(\mathbf{T}))\supseteq \text{Im}(L_{\unicode[STIX]{x1D703}}^{X})$
.
$X_{\ast }(L_{\unicode[STIX]{x1D703}}(\mathbf{T}))\supseteq \text{Im}(L_{\unicode[STIX]{x1D703}}^{X})$
.
Posons
![]() $X_{\ast ,\mathbb{Q}}:=X_{\ast }\otimes \mathbb{Q}$
et de même
$X_{\ast ,\mathbb{Q}}:=X_{\ast }\otimes \mathbb{Q}$
et de même
![]() $L_{\unicode[STIX]{x1D703},\mathbb{Q}}^{X}:X_{\ast ,\mathbb{Q}}\rightarrow X_{\ast ,\mathbb{Q}}$
. Comme
$L_{\unicode[STIX]{x1D703},\mathbb{Q}}^{X}:X_{\ast ,\mathbb{Q}}\rightarrow X_{\ast ,\mathbb{Q}}$
. Comme
![]() $\unicode[STIX]{x1D703}$
est d’ordre fini,
$\unicode[STIX]{x1D703}$
est d’ordre fini,
![]() $\unicode[STIX]{x1D703}$
est un endormorphisme semi-simple du
$\unicode[STIX]{x1D703}$
est un endormorphisme semi-simple du
![]() $\mathbb{Q}$
-espace vectoriel
$\mathbb{Q}$
-espace vectoriel
![]() $X_{\ast ,\mathbb{Q}}$
. Ainsi, on a la décomposition
$X_{\ast ,\mathbb{Q}}$
. Ainsi, on a la décomposition
![]() $X_{\ast ,\mathbb{Q}}=X_{\ast ,\mathbb{Q}}^{\unicode[STIX]{x1D703}}\oplus \text{Im}(L_{\unicode[STIX]{x1D703},\mathbb{Q}}^{X})$
. On en déduit que
$X_{\ast ,\mathbb{Q}}=X_{\ast ,\mathbb{Q}}^{\unicode[STIX]{x1D703}}\oplus \text{Im}(L_{\unicode[STIX]{x1D703},\mathbb{Q}}^{X})$
. On en déduit que
![]() $X_{\ast }^{\unicode[STIX]{x1D703}}+\text{Im}(L_{\unicode[STIX]{x1D703}}^{X})$
est d’indice fini dans
$X_{\ast }^{\unicode[STIX]{x1D703}}+\text{Im}(L_{\unicode[STIX]{x1D703}}^{X})$
est d’indice fini dans
![]() $X_{\ast }$
et donc, comme
$X_{\ast }$
et donc, comme
![]() $\mathbb{C}^{\ast }$
est divisible, que l’application
$\mathbb{C}^{\ast }$
est divisible, que l’application
![]() $(X_{\ast }^{\unicode[STIX]{x1D703}}\otimes \mathbb{C}^{\ast })\times (\text{Im}(L_{\unicode[STIX]{x1D703}}^{X})\otimes \mathbb{C}^{\ast })\rightarrow X_{\ast }\otimes \mathbb{C}^{\ast }$
est surjective. En particulier l’application
$(X_{\ast }^{\unicode[STIX]{x1D703}}\otimes \mathbb{C}^{\ast })\times (\text{Im}(L_{\unicode[STIX]{x1D703}}^{X})\otimes \mathbb{C}^{\ast })\rightarrow X_{\ast }\otimes \mathbb{C}^{\ast }$
est surjective. En particulier l’application
![]() $(X_{\ast }((\mathbf{T}^{\unicode[STIX]{x1D703}})^{\circ })\otimes \mathbb{C}^{\ast })\times (X_{\ast }(L_{\unicode[STIX]{x1D703}}(\mathbf{T}))\otimes \mathbb{C}^{\ast })\rightarrow X_{\ast }\otimes \mathbb{C}^{\ast }$
est surjective, d’où le résultat. ◻
$(X_{\ast }((\mathbf{T}^{\unicode[STIX]{x1D703}})^{\circ })\otimes \mathbb{C}^{\ast })\times (X_{\ast }(L_{\unicode[STIX]{x1D703}}(\mathbf{T}))\otimes \mathbb{C}^{\ast })\rightarrow X_{\ast }\otimes \mathbb{C}^{\ast }$
est surjective, d’où le résultat. ◻