Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-26T23:34:16.825Z Has data issue: false hasContentIssue false
  • English
  • Français

Manning’s formula and Strickler’s scaling explained by a co-spectral budget model

Published online by Cambridge University Press:  12 January 2017

S. Bonetti ,
G. Manoli ,
C. Manes ,
A. Porporato  and
G. G. Katul
S. Bonetti
Affiliation:
Pratt School of Engineering, Duke University, Durham, NC 27708, USA
G. Manoli
Affiliation:
Institute of Environmental Engineering, ETH Zurich, 8093 Zurich, Switzerland Nicholas School of the Environment, Duke University, Durham, NC 27708, USA
C. Manes*
Affiliation:
Department of Environment, Land and Infrastructure Engineering, Politecnico di Torino, 10129 Torino, Italy
A. Porporato
Affiliation:
Pratt School of Engineering, Duke University, Durham, NC 27708, USA Nicholas School of the Environment, Duke University, Durham, NC 27708, USA
G. G. Katul
Affiliation:
Pratt School of Engineering, Duke University, Durham, NC 27708, USA Nicholas School of the Environment, Duke University, Durham, NC 27708, USA
*
†Email address for correspondence: costantino.manes@polito.it
Get access Rights & Permissions [Opens in a new window]

Abstract

Manning’s empirical formula in conjunction with Strickler’s scaling is widely used to predict the bulk velocity 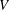$V$ from the hydraulic radius 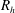$R_{h}$, the roughness size $r$ and the slope of the energy grade line 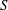$S$ in uniform channel and pipe flows at high bulk Reynolds numbers. Despite their importance in science and engineering, both Manning’s and Strickler’s formulations have waited for decades before finding a theoretical explanation. This was provided, for the first time, by Gioia & Bombardelli (Phys. Rev. Lett., vol. 88, 2002, 014501), labelled as GB02, using phenomenological arguments. Perhaps their most remarkable finding was the link between the Strickler and the Kolmogorov scaling exponents, the latter pertaining to velocity fluctuations in the inertial subrange of the turbulence spectrum and presumed to be universal. In this work, the GB02 analysis is first revisited, showing that GB02 employed several ad hoc scaling assumptions for the turbulent kinetic energy dissipation rate and, although implicitly, for the mean velocity gradient adjacent to the roughness elements. The similarity constants arising from the GB02 scaling assumptions were presumed to be independent of 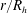$r/R_{h}$, which is inconsistent with well-known flow properties in the near-wall region of turbulent wall flows. Because of the dependence of these similarity constants on 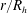$r/R_{h}$, this existing theory requires the validity of the Strickler scaling to cancel the dependence of these constants on 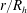$r/R_{h}$ so as to arrive at the Strickler scaling and Manning’s formula. Here, the GB02 approach is corroborated using a co-spectral budget (CSB) model for the wall shear stress formulated at the cross-over between the roughness sublayer and the log region. Assuming a simplified shape for the spectrum of the vertical velocity 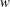$w$, the proposed CSB model (subject to another simplifying assumption that production is balanced by pressure–velocity interaction) allows Manning’s formula to be derived. To substantiate this approach, numerical solutions to the CSB over the entire flow depth using different spectral shapes for 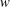$w$ are carried out for a wide range of 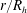$r/R_{h}$. The results from this analysis support the simplifying hypotheses used to derive Manning’s equation. The derived equation provides a formulation for $n$ that agrees with reported values in the literature over seven decades of $r$ variations. While none of the investigated spectral shapes allows the recovery of the Strickler scaling, the numerical solutions of the CSB reproduce the Nikuradse data in the fully rough regime, thereby confirming that the Strickler scaling represents only an approximate fit for the friction factor for granular roughness.

JFM classification

Waves/Free-surface Flows: Channel flow Waves/Free-surface Flows: Hydraulics Turbulent Flows: Turbulence theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 812 , 10 February 2017 , pp. 1189 - 1212
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H. & Antonia, R. A. 2016 Relationship between the energy dissipation function and the skin friction law in a turbulent channel flow. J. Fluid Mech. 798, 140–164.Google Scholar
Barenblatt, G. I. 1996 Scaling, Self-similarity, and Intermediate Asymptotics: Dimensional Analysis and Intermediate Asymptotics, vol. 14. Cambridge University Press.Google Scholar
Bathurst, J. C. 1985 Flow resistance estimation in mountain rivers. ASCE J. Hydraul. Engng 111 (4), 625–643.Google Scholar
Bathurst, J. C., Simons, D. B. & Li, R.-M. 1981 Resistance equation for large-scale roughness. ASCE J. Hydraul. Div. 107 (12), 1593–1613.Google Scholar
Bos, W. J. T., Touil, H., Shao, L. & Bertogli, J. P. 2004 On the behavior of the velocity–scalar cross correlation spectrum in the inertial range. Phys. Fluids 16, 3818–3923.Google Scholar
Brown, G. O. 2002 The history of the Darcy–Weisbach equation for pipe flow resistance. Environ. Water Resour. History 38 (7), 34–43.Google Scholar
Brutsaert, W. 1975 The roughness length for water vapor sensible heat, and other scalars. J. Atmos. Sci. 32 (10), 2028–2031.Google Scholar
Brutsaert, W. B. 1982 Evaporation into the Atmosphere: Theory, History and Applications. Springer.CrossRefGoogle Scholar
Brutsaert, W. B.(Ed.) 2005 Hydrology: An Introduction. Cambridge University Press.Google Scholar
Cheng, N.-S. 2011 Representative roughness height of submerged vegetation. Water Resour. Res. 47 (8), W08517.Google Scholar
Choi, K. S. & Lumley, J. L. 2000 The return to isotropy of homogeneous turbulence. J. Fluid Mech. 436, 59–84.Google Scholar
Chow, V. T.(Ed.) 1959 Open Channel Hydraulics. McGraw-Hill.Google Scholar
Chung, M. K. & Kim, S. K. 1995 A nonlinear return-to-isotropy model with Reynolds number and anisotropy dependency. Phys. Fluids 7 (6), 1425–1437.CrossRefGoogle Scholar
Colosimo, C., Copertino, V. A. & Veltri, M. 1988 Friction factor evaluation in gravel-bed rivers. ASCE J. Hydraul. Engng 114 (8), 861–876.CrossRefGoogle Scholar
Corrsin, S. 1964 Further generalization of Onsager’s cascade model for turbulent spectra. Phys. Fluids 7, 1156–1159.CrossRefGoogle Scholar
Dunn, C., López, F. & García, M. H. 1996 Mean flow and turbulence in a laboratory channel with simulated vegetation. Hydraul. Engng 51.Google Scholar
Ferguson, R. 2010 Time to abandon the Manning equation? Earth Surf. Process. Landf. 35 (15), 1873–1876.Google Scholar
Frisch, U.(Ed.) 1995 Turbulence. Cambridge University Press.Google Scholar
Gatski, T. B. & Jongen, T. 2000 Nonlinear eddy viscosity and algebraic stress models for solving complex turbulent flows. Prog. Aerosp. Sci. 36 (8), 655–682.Google Scholar
Gatski, T. B. & Speziale, C. G. 1993 On explicit algebraic stress models for complex turbulent flows. J. Fluid Mech. 254, 59–78.Google Scholar
Gauckler, P. 1867 Etudes Théoriques et Pratiques sur l’Ecoulement et le Mouvement des Eaux. Gauthier-Villars.Google Scholar
Ghisalberti, M. & Nepf, H. M. 2004 The limited growth of vegetated shear layers. Water Resour. Res. 40 (7), W07502.Google Scholar
Gioia, G. & Bombardelli, F. 2002 Scaling and similarity in rough channel flows. Phys. Rev. Lett. 88, 014501.Google ScholarPubMed
Gioia, G. & Chakraborty, P. 2006 Turbulent friction in rough pipes and the energy spectrum of the phenomenological theory. Phys. Rev. Lett. 96, 044502.Google Scholar
Gioia, G., Guttenberg, N., Goldenfeld, N. & Chakraborty, P. 2010 Spectral theory of the turbulent mean-velocity profile. Phys. Rev. Lett. 105 (18), 184501.Google Scholar
Girimaji, S. S. 1996 Fully explicit and self-consistent algebraic Reynolds stress model. Theor. Comput. Fluid Dyn. 8 (6), 387–402.Google Scholar
Hey, R. D. 1979 Flow resistance in gravel-bed rivers. ASCE J. Hydraul. Div. 105 (4), 365–379.Google Scholar
Jacob, B., Biferale, L., Iuso, G. & Casciola, C. M. 2004 Anisotropic fluctuations in turbulent shear flows. Phys. Fluids 16 (11), 4135–4142.Google Scholar
Jacob, B., Casciola, C. M., Talamelli, A. & Alfredsson, P. H. 2008 Scaling of mixed structure functions in turbulent boundary layers. Phys. Fluids 20 (4), 045101.CrossRefGoogle Scholar
Johansson, A. V. & Wallin, S. 1996 A new explicit algebraic Reynolds stress model. In Advances in Turbulence VI, pp. 31–34. Springer.Google Scholar
Jongen, T. & Gatski, T. B. 1998 General explicit algebraic stress relations and best approximation for three-dimensional flows. Intl J. Engng Sci. 36 (7), 739–763.CrossRefGoogle Scholar
Katul, G. & Manes, C. 2014 Cospectral budget of turbulence explains the bulk properties of smooth pipe flow. Phys. Rev. E 90, 063008.Google Scholar
Katul, G. G., Geron, C. D., Hsieh, C.-I., Vidakovic, B. & Guenther, A. B. 1998 Active turbulence and scalar transport near the forest–atmosphere interface. J. Appl. Meteorol. 37 (12), 1533–1546.Google Scholar
Katul, G., Wiberg, P., Albertson, J. D. & Hornberger, G. 2002 A mixing layer theory for flow resistance in shallow streams. Water Resour. Res. 38, 1250.Google Scholar
Katul, G. G., Manes, C., Porporato, A., Bou-Zeid, E. & Chamecki, M. 2015 Bottlenecks in turbulent kinetic energy spectra predicted from structure function inflections using the von Kármán–Howarth equation. Phys. Rev. E 92 (3), 033009.Google Scholar
Katul, G. G., Porporato, A., Manes, C. & Meneveau, C. 2013 Co-spectrum and mean velocity in turbulent boundary layers. Phys. Fluids 25 (9), 091702.Google Scholar
Kolmogorov, A. N. 1941 Dissipation of energy under locally isotropic turbulence. Dokl. Akad. Nauk. SSSR 32, 16–18.Google Scholar
Konings, A. G., Katul, G. G. & Thompson, S. E. 2012 A phenomenological model for the flow resistance over submerged vegetation. Water Resour. Res. 48 (2), W02522.Google Scholar
Kunkel, G. J. & Marusic, I. 2006 Study of the near-wall-turbulent region of the high-Reynolds-number boundary layer using an atmospheric flow. ASCE J. Fluid Mech. 548, 375–402.Google Scholar
Launder, B. E., Reece, G. J. & Rodi, W. 1975 Progress in the development of Reynolds-stress turbulence closure. J. Fluid Mech. 68, 537–566.Google Scholar
López, F. & García, M. H. 2001 Mean flow and turbulence structure of open-channel flow through non-emergent vegetation. ASCE J. Hydraul. Engng 127 (5), 392–402.Google Scholar
Lumley, J. L. 1967 Similarity and the turbulent energy spectrum. Phys. Fluids 10, 855–858.Google Scholar
Lumley, J. L. 1978 Computational modeling of turbulent flows. Adv. Appl. Mech. 18 (123), 213.Google Scholar
Manes, C., Poggi, D. & Ridolfi, L. 2011 Turbulent boundary layers over permeable walls: scaling and near-wall structure. J. Fluid Mech. 687, 141–170.Google Scholar
Manes, C., Pokrajac, D. & McEwan, I. 2007 Double-averaged open-channel flows with small relative submergence. ASCE J. Hydraul. Engng 133, 896–904.Google Scholar
Manning, R. 1891 On the flow of water in open channels and pipes. Trans. Inst. Civil Eng. Ireland 20, 161–207.Google Scholar
McColl, K. A., Katul, G. G., Gentine, P. & Entekhabi, D. 2016 Mean-velocity profile of smooth channel flow explained by a cospectral budget model with wall-blockage. Phys. Fluids 28 (3), 035107.Google Scholar
McKeon, B. J. & Morrison, J. F. 2007 Asymptotic scaling in turbulent pipe flow. Phil. Trans. R. Soc. Lond. A 365, 771–787.Google ScholarPubMed
McKeon, B. J., Zagarola, M. V. & Smits, A. J. 2005 A new friction factor relationship for fully developed pipe flow. J. Fluid Mech. 538, 429–443.Google Scholar
Meijer, D. G. & Van Velzen, E. H. 1999 Prototype-scale flume experiments on hydraulic roughness of submerged vegetation. In Conference Proceedings of the 28th International IAHR Conference, Graz. Institute for Hydraulics and Hydrology, Technical University Graz.Google Scholar
Mellor, G. L. & Yamada, T. 1982 Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. 20 (4), 851–875.Google Scholar
Murphy, E., Ghisalberti, M. & Nepf, H. 2007 Model and laboratory study of dispersion in flows with submerged vegetation. Water Resour. Res. 43 (5), W05438.Google Scholar
Nezu, I. & Sanjou, M. 2008 Turburence structure and coherent motion in vegetated canopy open-channel flows. J. Hydro-environment Res. 2 (2), 62–90.Google Scholar
Nickels, T. B., Marusic, I., Hafez, S., Hutchins, N. & Chong, M. S. 2007 Some predictions of the attached eddy model for a high Reynolds number boundary layer. Phil. Trans. R. Soc. Lond. A 365 (1852), 807–822.Google ScholarPubMed
Onsager, L. 1949 Statistical hydrodynamics. Il Nuovo Cimento 6, 279–287.Google Scholar
Panchev, S.(Ed.) 1971 Random Functions and Turbulence. Pergamon.Google Scholar
Poggi, D., Porporato, A. & Ridolfi, L. 2002 An experimental contribution to near-wall measurements by means of a special laser Doppler anemometry technique. Exp. Fluids 32, 366–375.Google Scholar
Poggi, D., Porporato, A., Ridolfi, L., Albertson, J. D. & Katul, G. G. 2004 The effect of vegetation density on canopy sub-layer turbulence. Boundary-Layer Meteorol. 111 (3), 565–587.Google Scholar
Pope, S. B. 1975 A more general effective-viscosity hypothesis. J. Fluid Mech. 72 (02), 331–340.Google Scholar
Pope, S. B.(Ed.) 2000 Turbulent Flows. Cambridge Univeristy Press.Google Scholar
Powell, R. W. 1960 History of Manning’s formula. J. Geophys. Res. 65, 1310–1311.Google Scholar
Raupach, M. R. 1981 Conditional statistics of Reynolds stress in rough-wall and smooth-wall turbulent boundary layers. J. Fluid Mech. 108, 363–382.CrossRefGoogle Scholar
Raupach, M. R., Antonia, R. A. & Rajagopalan, S. 1991 Rough-wall turbulent boundary layers. Appl. Mech. Rev. 44 (1), 1–25.Google Scholar
Raupach, M. R., Hughes, D. E. & Cleugh, H. A. 2006 Momentum absorption in rough-wall boundary layers with sparse roughness elements in random and clustered distributions. Boundary-Layer Meteorol. 120 (2), 201–218.Google Scholar
Rotta, J. C. 1962 Turbulent boundary layers in incompressible flow. Prog. Aerosp. Sci. 2 (1), 1–95.Google Scholar
Rung, T., Thiele, F. & Fu, S. 1998 On the realizability of nonlinear stress–strain relationships for Reynolds stress closures. Flow Turbul. Combust. 60 (4), 333–359.Google Scholar
Saddoughi, S. & Veeravalli, S. 1994 Local isotropy in turbulent boundary layers at high Reynolds number flow. J. Fluid Mech. 268, 333–372.Google Scholar
Sarkar, S. & Speziale, C. G. 1990 A simple nonlinear model for the return to isotropy in turbulence. Phys. Fluids A 2 (1), 84–93.CrossRefGoogle Scholar
Schmitt, F. G. 2007 Direct test of a nonlinear constitutive equation for simple turbulent shear flows using DNS data. Commun. Nonlinear Sci. Numer. Simul. 12 (7), 1251–1264.Google Scholar
Schumann, U. 1977 Realizability of Reynolds-stress turbulence models. Phys. Fluids 20 (5), 721–725.Google Scholar
Shih, T.-H., Zhu, J. & Lumley, J. L. 1995 A new Reynolds stress algebraic equation model. Comput. Meth. Appl. Mech. Engng 125 (1), 287–302.Google Scholar
Taulbee, D. B. 1992 An improved algebraic Reynolds stress model and corresponding nonlinear stress model. Phys. Fluids A 4 (11), 2555–2561.Google Scholar
Tennekes, H. & Lumley, J. L.(Eds) 1972 A First Course in Turbulence. MIT Press.Google Scholar
Willcocks, W. & Holt, R.(Eds) 1899 Elementary Hydraulics. National Printing Office.Google Scholar
Yang, B. H. & Joseph, D. D. 2009 Virtual Nikuradse. J. Turbul. 10 (11), 1–28.Google Scholar
Yang, W. & Choi, S.-U. 2010 A two-layer approach for depth-limited open-channel flows with submerged vegetation. J. Hydraul. Res. 48 (4), 466–475.Google Scholar
Zhao, R. & Smits, A. J. 2007 Scaling of the wall-normal turbulence component in high-Reynolds-number pipe flow. J. Fluid Mech. 576, 457–473.Google Scholar