Hostname: page-component-848d4c4894-wzw2p Total loading time: 0 Render date: 2024-05-07T22:36:50.156Z Has data issue: false hasContentIssue false
  • English
  • Français

COHOMOLOGY AND OVERCONVERGENCE FOR REPRESENTATIONS OF POWERS OF GALOIS GROUPS

Part of: Homological methods (field theory) Algebraic number theory: local and $p$-adic fields Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  11 April 2019

Aprameyo Pal  and
Gergely Zábrádi Open the ORCID record for Gergely Zábrádi [Opens in a new window]
Aprameyo Pal
Affiliation:
Universität Duisburg-Essen, Fakultät für Mathematik, Thea-Leymann-Straße 9, D-45127Essen, Germany (aprameyo.pal@uni-due.de)
Gergely Zábrádi
Affiliation:
Eötvös Loránd University, Institute of Mathematics, Pázmány Péter sétány 1/C, H-1117Budapest, Hungary Alfréd Rényi Institute of Mathematics, Hungarian Academy of Sciences, POB 127, BudapestH-1364, Hungary MTA Rényi Intézet Lendület Automorphic Research Group, Hungary (zger@cs.elte.hu)
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the Galois cohomology groups of 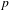$p$-adic representations of a direct power of $\operatorname{Gal}(\overline{\mathbb{Q}_{p}}/\mathbb{Q}_{p})$ can be computed via the generalization of Herr’s complex to multivariable 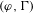$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$-modules. Using Tate duality and a pairing for multivariable 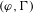$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$-modules we extend this to analogues of the Iwasawa cohomology. We show that all $p$-adic representations of a direct power of 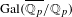$\operatorname{Gal}(\overline{\mathbb{Q}_{p}}/\mathbb{Q}_{p})$ are overconvergent and, moreover, passing to overconvergent multivariable 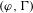$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$-modules is an equivalence of categories. Finally, we prove that the overconvergent Herr complex also computes the Galois cohomology groups.

Keywords

(𝜑, 𝛤)-modulesp-adic Galois representationsoverconvergenceHerr’s complex

MSC classification

Primary: 11S25: Galois cohomology
Secondary: 11S20: Galois theory 11S37: Langlands-Weil conjectures, nonabelian class field theory 11F80: Galois representations 12G05: Galois cohomology
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 2 , March 2021 , pp. 361 - 421
Check for updates
Copyright
© Cambridge University Press 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balister, P. and Howson, S., Note on Nakayama’s lemma for compact 𝛬-modules, Asian J. Math. 1(2) (1997), 224–229.CrossRefGoogle Scholar
Benois, D., On Iwasawa theory of crystalline representations, Duke Math. J. 104 (2000), 211–267.CrossRefGoogle Scholar
Benois, D. and Berger, L., Théorie d’Iwasawa des représentations cristallines. II, Comment. Math. Helv. 83 (2008), 603–677.10.4171/CMH/138CrossRefGoogle Scholar
Berger, L., Multivariable Lubin–Tate (𝜑, 𝛤)-modules and filtered 𝜑-modules, Math. Res. Lett. 20(3) (2013), 409–428.CrossRefGoogle Scholar
Berger, L., Multivariable Lubin–Tate (𝜑, 𝛤)-modules and locally analytic vectors, Duke Math. J. 165(18) (2016), 3567–3595.CrossRefGoogle Scholar
Berger, L. and Fourquaux, L., Iwasawa theory and F-analytic Lubin–Tate (𝜑, 𝛤)-modules, Doc. Math. 22 (2017), 999–1030.Google Scholar
Berger, L., Schneider, P. and Xie, B., Rigid character groups, Lubin–Tate theory, and (𝜑, 𝛤)-modules, Mem. Amer. Math. Soc. (2015), to appear, preprint version.Google Scholar
Bley, W. and Cobbe, A., Equivariant epsilon constant conjectures for weakly ramified extensions, Math. Z. 283 (2016), 1217–1244.CrossRefGoogle Scholar
Breuil, Ch., Induction parabolique et (𝜑, 𝛤)-modules, Algebra Number Theory 9(10) (2015), 2241–2291.CrossRefGoogle Scholar
Breuil, Ch. and Herzig, F., Ordinary representations of G (ℚp) and fundamental algebraic representations, Duke Math. J. 164 (2015), 1271–1352.CrossRefGoogle Scholar
Breuil, Ch., Herzig, F. and Schraen, B., 2016, paper in preparation.Google Scholar
Carter, A., Kedlaya, K. S. and Zábrádi, G., Drinfeld’s lemma for perfectoid spaces and overconvergence of multivariate $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$-modules, preprint, 2018. arXiv:1808.03964.Google Scholar
Cherbonnier, F. and Colmez, P., Représentations p-adiques surconvergentes, Invent. Math. 133 (1998), 581–611.10.1007/s002220050255CrossRefGoogle Scholar
Cherbonnier, F. and Colmez, P., Théorie d’Iwasawa des représentations p-adiques d’un corps local, J. Amer. Math. Soc. 12(1) (1999), 241–268.CrossRefGoogle Scholar
Colmez, P., Fontaine’s rings and $p$-adic $L$-functions, https://webusers.imj-prg.fr/∼pierre.colmez/tsinghua.pdf, 2004. Lecture notes from Tsinghua.Google Scholar
Colmez, P., (𝜑, 𝛤)-modules et représentations du mirabolique de GL 2(ℚp), Astérisque 330 (2010), 61–153.Google Scholar
Colmez, P., Représentations localement analytiques de GL 2(ℚp) et (𝜑, 𝛤)-modules, Represent. Theory 20 (2016), 187–248.CrossRefGoogle Scholar
Fulton, W., A note on weakly complete algebras, Bull. Amer. Math. Soc. 75 (1969), 591–593.CrossRefGoogle Scholar
Greenberg, R., Introduction to Iwasawa theory for elliptic curves, in Arithmetic Algebraic Geometry, Park City Lecture Notes, pp. 407–464 (American Mathematical Society, Providence, RI, 2009).Google Scholar
Herr, L., Sur la cohomologie galoisienne des corps p-adiques, Bull. Soc. Math. France 126 (1998), 563–600.CrossRefGoogle Scholar
Kedlaya, K., Slope filtrations for relative Frobenius, Astérisque 319 (2008), 259–301.Google Scholar
Kedlaya, K., Some slope theory for multivariate Robba rings, preprint, 2013,arXiv:1311.7468.Google Scholar
Kedlaya, K., New methods for (𝜑, 𝛤)-modules, Res. Math. Sci. 2(20) (2015), (Robert Coleman memorial issue).Google Scholar
Kedlaya, K., Sheaves, Stacks, and Shtukas, Lecture Notes for the 2017 Arizona Winter School on perfectoid spaces, preprint, 2018, http://swc.math.arizona.edu/aws/2017/2017KedlayaNotes.pdf.Google Scholar
Liu, R., Cohomology and duality for (𝜑, 𝛤)-modules over the Robba ring, Int. Math. Res. Not. IMRN 2007 (2007), page rnm150.CrossRefGoogle Scholar
Martin-Peinador, E., A reflexible admissible topological group must be locally compact, Proc. Amer. Math. Soc. 123 (1995), 3563–3566.CrossRefGoogle Scholar
Nakamura, K., Iwasawa theory of de Rham (𝜑, 𝛤)-modules over Robba ring, J. Inst. Math. Jussieu 13 (2014), 65–118.CrossRefGoogle Scholar
Nakamura, K., A generalization of Kato’s local 𝜀-conjecture for (𝜑, 𝛤)-modules over the Robba ring, Algebra Number Theory 11 (2017), 319–404.CrossRefGoogle Scholar
Nakamura, K., Local 𝜀-isomorphisms for rank two p-adic representations of Gal(ℚp/ℚp) and a functional equation of Kato’s Euler system, Cambridge J. Math. 5 (2017), 281–368.CrossRefGoogle Scholar
Neukirch, J., Schmidt, A. and Wingberg, K., Cohomology of Number Fields, 2nd ed. (Springer, Heidelberg, 2007).Google Scholar
Schneider, P., p-Adic Lie Groups, Grundlehren der mathematischen Wissenschaften, Volume 344 (Springer, Heidelberg, 2011).CrossRefGoogle Scholar
Schneider, P. and Venjakob, O., Coates–Wiles homomorphisms and Iwasawa cohomology for Lubin–Tate extensions, in Elliptic Curves, Modular Forms and Iwasawa Theory (ed. Loeffler, D. and Zerbes, S.), Proc. Math. & Stat., Volume 188, pp. 401–468 (Springer, 2016), in honour of J. Coates’ 70th birthday.CrossRefGoogle Scholar
Scholze, P. and Weinstein, J., Berkeley lectures on $p$-adic geometry, http://www.math.uni-bonn.de/people/scholze/Berkeley.pdf, 2018.Google Scholar
Weibel, Ch., An Introduction to Homological Algebra, Cambridge Studies in Advanced Mathematics, Volume 38 (Cambridge University Press, Cambridge, 1994).CrossRefGoogle Scholar
Zábrádi, G., Generalized Robba rings (with an appendix by P. Schneider), Israel J. Math. 191(2) (2012), 817–887.CrossRefGoogle Scholar
Zábrádi, G., Multivariable (𝜑, 𝛤)-modules and smooth o-torsion representations, Selecta Math. 24(2) (2018), 935–995.CrossRefGoogle Scholar
Zábrádi, G., Multivariable (𝜑, 𝛤)-modules and products of Galois groups, Math. Res. Lett. 25(2) (2018), 687–721.CrossRefGoogle Scholar