Hostname: page-component-848d4c4894-nr4z6 Total loading time: 0 Render date: 2024-05-05T17:56:27.125Z Has data issue: false hasContentIssue false
  • English
  • Français

Robustness of vortex populations in the two-dimensional inverse energy cascade

Published online by Cambridge University Press:  10 July 2018

B. H. Burgess Open the ORCID record for B. H. Burgess [Opens in a new window]  and
R. K. Scott
B. H. Burgess*
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews KY16 9SS, UK
R. K. Scott
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews KY16 9SS, UK
*
†Email address for correspondence: bhb3@st-andrews.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We study how the properties of forcing and dissipation affect the scaling behaviour of the vortex population in the two-dimensional turbulent inverse energy cascade. When the flow is forced at scales intermediate between the domain and dissipation scales, the growth rates of the largest vortex area and the spectral peak length scale are robust to all simulation parameters. For white-in-time forcing the number density distribution of vortex areas follows the scaling theory predictions of Burgess & Scott (J. Fluid Mech., vol. 811, 2017, pp. 742–756) and shows little sensitivity either to the forcing bandwidth or to the nature of the small-scale dissipation: both narrowband and broadband forcing generate nearly identical vortex populations, as do Laplacian diffusion and hyperdiffusion. The greatest differences arise in comparing simulations with correlated forcing to those with white-in-time forcing: in flows with correlated forcing the intermediate range in the vortex number density steepens significantly past the predicted scale-invariant 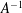$A^{-1}$ scaling. We also study the impact of the forcing Reynolds number $Re_{f}$, a measure of the relative importance of nonlinear terms and dissipation at the forcing scale, on vortex formation and the scaling of the number density. As 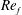$Re_{f}$ decreases, the flow changes from one dominated by intense circular vortices surrounded by filaments to a less structured flow in which vortex formation becomes progressively more suppressed and the filamentary nature of the surrounding vorticity field is lost. However, even at very small 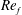$Re_{f}$, and in the absence of intense coherent vortex formation, regions of anomalously high vorticity merge and grow in area as predicted by the scaling theory, generating a three-part number density similar to that found at higher $Re_{f}$. At late enough stages the aggregation process results in the formation of long-lived circular vortices, demonstrating a strong tendency to vortex formation, and via a route distinct from the axisymmetrization of forcing extrema seen at higher 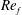$Re_{f}$. Our results establish coherent vortices as a robust feature of the two-dimensional inverse energy cascade, and provide clues as to the dynamical mechanisms shaping their statistics.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulence theory Vortex Flows: Vortex Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 850 , 10 September 2018 , pp. 844 - 874
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bartello, P. & Warn, T. 1996 Self-similarity of decaying two-dimensional turbulence. J. Fluid Mech. 326, 357–372.Google Scholar
Batchelor, G. K. 1969 Computation of the energy spectrum in homogeneous two-dimensional turbulence. Phys. Fluids 12, 233–239.Google Scholar
Benzi, R., Collela, M., Briscolini, M. & Santangelo, P. 1992 A simple point vortex model for two-dimensional decaying turbulence. Phys. Fluids A 4, 1036–1039.Google Scholar
Benzi, R., Patarnello, S. & Santangelo, P. 1988 Self-similar coherent structures in two-dimensional decaying turbulence. J. Phys. A: Math. Gen. 5, 1221–1237.Google Scholar
Berges, J. & Mesterhazy, D. 2012 Introduction to the nonequilibrium functional renormalization group. Nucl. Phys. B Proc. Suppl. 00 228, 37–60.Google Scholar
Borue, V. 1994 Inverse energy cascade in stationary two-dimensional homogeneous turbulence. Phys. Rev. Lett. 72, 1475–1478.Google Scholar
Buckingham, E. 1914 On physically similar systems; illustrations of the use of dimensional equations. Phys. Rev. 4, 345–376.Google Scholar
Buckingham, E. 1915 The principle of similitude. Nature 96, 396–397.Google Scholar
Burgess, B. H. & Scott, R. K. 2017 Scaling theory for vortices in the two-dimensional inverse energy cascade. J. Fluid Mech. 811, 742–756.Google Scholar
Burgess, B. H., Scott, R. K. & Shepherd, T. G. 2015 Kraichnan–Leith–Batchelor similarity theory and two-dimensional inverse cascades. J. Fluid Mech. 767, 467–496.Google Scholar
Carnevale, G. F., McWilliams, J. C., Pomeau, Y., Weiss, J. B. & Young, W. R. 1991 Evolution of vortex statistics in two-dimensional turbulence. Phys. Rev. Lett. 66, 2735–2738.Google Scholar
Davidson, P. 2004 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Dritschel, D. G. 1992 Quantification of the inelastic interaction of unequal vortices in two-dimensional vortex dynamics. Phys. Fluids A 4, 1737–1744.Google Scholar
Dritschel, D. G., Scott, R. K., Macaskill, C., Gottwald, G. A. & Tran, C. V. 2008 Unifying scaling theory for vortex dynamics in two-dimensional turbulence. Phys. Rev. Lett. 101, 094501.Google Scholar
Fontane, J., Dritschel, D. G. & Scott, R. K. 2013 Vortical control of forced two-dimensional turbulence. Phys. Fluids 25, 015101.Google Scholar
Haller, G., Hadjighasem, A., Farazmand, M. & Huhn, F. 2016 Defining coherent vortices objectively from the vorticity. J. Fluid Mech. 795, 136–173.Google Scholar
Hou, T. Y. & Li, R. 2006 Dynamic depletion of vortex stretching and non-blowup of the 3-D incompressible Euler equations. J. Nonlinear Sci. 16, 639–664.Google Scholar
Hua, B. L. & Klein, P. 1998 An exact criterion for the stirring properties of nearly two-dimensional turbulence. Physica D 113, 98–110.Google Scholar
Jimenez, J. 1994 Hyperviscous vorticities. J. Fluid Mech. 279, 169–176.Google Scholar
Kraichnan, R. H. 1967 Inertial ranges in two-dimensional turbulence. Phys. Fluids 10, 1417–1423.Google Scholar
Kraichnan, R. H. 1971 Inertial range transfer in two- and three-dimensional turbulence. J. Fluid Mech. 47, 525–535.Google Scholar
Kraichnan, R. H. 1975 Statistical dynamics of two-dimensional flow. J. Fluid Mech. 67, 155–175.Google Scholar
Liu, S. & Scott, R. K. 2015 The onset of the barotropic sudden warming in a global model. Q. J. R. Meteorol. Soc. 141, 2944–2955.Google Scholar
Lowe, A. J. & Davidson, P. A. 2005 The evolution of freely decaying, isotropic, two-dimensional turbulence. Eur. J. Mech. (B/Fluids) 24, 314–327.Google Scholar
Mariotti, A., Legras, B. & Dritschel, D. G. 1994 Vortex stripping and the erosion of coherent structures in two-dimensional flows. Phys. Fluids 6, 3954–3962.Google Scholar
Okubo, A. 1970 Horizontal dispersion of floatable particles in the vicinity of velocity singularities such as convergences. Deep-Sea Res. 17, 445–454.Google Scholar
Roos, M. 2015 Introduction to Cosmology, fourth edn. Wiley.Google Scholar
Scott, R. K. 2007 Nonrobustness of the two-dimensional turbulent inverse cascade. Phys. Rev. E 75, 046301.Google Scholar
Smith, L. M. & Yakhot, V. 1993 Bose condensation and small-scale structure generation in a random force driven 2D turbulence. Phys. Rev. Lett. 71, 352–355.Google Scholar
Tabeling, P. 2002 Two-dimensional turbulence: a physicist approach. Phys. Rep. 362, 1–62.Google Scholar
Thompson, A. F. & Young, W. R. 2006 Scaling baroclinic eddy fluxes: vortices and energy balance. J. Phys. Oceanogr. 36, 720–738.Google Scholar
Vallgren, A. 2011 Infrared Reynolds number dependency of the two-dimensional inverse energy cascade. J. Fluid Mech. 667, 463–473.Google Scholar
Virasoro, M. A. 1981 Variational principle for two-dimensional incompressible hydrodynamics and quasigeostrophic flows. Phys. Rev. Lett. 47, 1181–1183.Google Scholar
Weiss, J. B. 1991 The dynamics of enstrophy transfer in two-dimensional hydrodynamics. Physica D 48, 273–294.Google Scholar
Weiss, J. B. & McWilliams, J. C. 1993 Temporal scaling behavior of decaying two-dimensional turbulence. Phys. Fluids 5, 608–621.Google Scholar
Zabusky, N. J. 1979 Contour dynamics for the Euler equations in two dimensions. J. Comput. Phys. 30, 96–106.Google Scholar