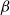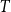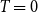1. Introduction
Network models play an important role in different scientific fields (Chakrabarti & Faloutsos, Reference Chakrabarti and Faloutsos2006). From the perspective of network science, models can be used to explain observed behavior in the real world. To mention one example, Watts and Strogatz (Reference Watts and Strogatz1998) observed that few random long-range connections suffice to guarantee a small diameter. This explains why many real-world networks exhibit the small-world property despite heavily favoring local over long-range connections. From the perspective of computer science, and specifically algorithmics, realistic random networks can provide input instances for graph algorithms. This facilitates theoretical approaches (e.g., average-case analysis), as well as extensive empirical evaluations by providing an abundance of benchmark instances, solving the pervasive scarcity of real-world instances.
There are some crucial features that make a network model useful. The generated instances have to resemble real-world networks. The model should be as simple and natural as possible to facilitate theoretical analysis and to prevent untypical artifacts. And it should be possible to efficiently draw networks from the model. This is particularly important for the empirical analysis of model properties and for generating benchmark instances.
A model that has proven itself useful in recent years is the hyperbolic random graph (HRG) model (Krioukov et al., Reference Krioukov, Papadopoulos, Kitsak, Vahdat and Boguñá2010). HRGs are generated by drawing vertex positions uniformly at random from a disk in the hyperbolic plane. Two vertices are joined by an edge if and only if their distance lies below a certain threshold, see Section 2.2. HRGs resemble real-world networks with respect to crucial properties. Most notable are the power-law degree distribution (Gugelmann et al., Reference Gugelmann, Panagiotou and Peter2012) (i.e., the number of vertices of degree
![]() $k$
is roughly proportional to
$k$
is roughly proportional to
![]() $k^{-\beta }$
with
$k^{-\beta }$
with
![]() $\beta \in (2, 3)$
), the high clustering coefficient (Gugelmann et al., Reference Gugelmann, Panagiotou and Peter2012) (i.e., two vertices are more likely to be connected if they have a common neighbor), and the small diameter (Friedrich & Krohmer, Reference Friedrich and Krohmer2018; Müller & Staps, Reference Müller and Staps2017). Moreover, HRGs are accessible for theoretical analysis (see, e.g., Gugelmann et al., Reference Gugelmann, Panagiotou and Peter2012; Friedrich & Krohmer, Reference Friedrich and Krohmer2018; Müller & Staps, Reference Müller and Staps2017; Bläsius et al., Reference Bläsius, Freiberger, Friedrich, Katzmann, Montenegro-Retana and Thieffry2018a). Finally, there is a multitude of efficient generators with different emphases (Aldecoa et al., Reference Aldecoa, Orsini and Krioukov2015; von Looz et al., Reference von Looz, Meyerhenke and Prutkin2015; von Looz & Meyerhenke, Reference von Looz and Meyerhenke2016; von Looz et al., Reference von Looz, Özdayi, Laue and Meyerhenke2016; Penschuck, Reference Penschuck2017; Funke et al., Reference Funke, Lamm, Sanders, Schulz, Strash and von Looz2018, Reference Funke, Lamm, Meyer, Penschuck, Sanders, Schulz and von Looz2019), see Section 1.2 for a discussion.
$\beta \in (2, 3)$
), the high clustering coefficient (Gugelmann et al., Reference Gugelmann, Panagiotou and Peter2012) (i.e., two vertices are more likely to be connected if they have a common neighbor), and the small diameter (Friedrich & Krohmer, Reference Friedrich and Krohmer2018; Müller & Staps, Reference Müller and Staps2017). Moreover, HRGs are accessible for theoretical analysis (see, e.g., Gugelmann et al., Reference Gugelmann, Panagiotou and Peter2012; Friedrich & Krohmer, Reference Friedrich and Krohmer2018; Müller & Staps, Reference Müller and Staps2017; Bläsius et al., Reference Bläsius, Freiberger, Friedrich, Katzmann, Montenegro-Retana and Thieffry2018a). Finally, there is a multitude of efficient generators with different emphases (Aldecoa et al., Reference Aldecoa, Orsini and Krioukov2015; von Looz et al., Reference von Looz, Meyerhenke and Prutkin2015; von Looz & Meyerhenke, Reference von Looz and Meyerhenke2016; von Looz et al., Reference von Looz, Özdayi, Laue and Meyerhenke2016; Penschuck, Reference Penschuck2017; Funke et al., Reference Funke, Lamm, Sanders, Schulz, Strash and von Looz2018, Reference Funke, Lamm, Meyer, Penschuck, Sanders, Schulz and von Looz2019), see Section 1.2 for a discussion.
Closely related to HRGs is the geometric inhomogeneous random graph (GIRG) model (Bringmann et al., Reference Bringmann, Keusch and Lengler2019). Here, every vertex has a position on the
![]() $d$
-dimensional torus and a weight following a power law. Two vertices are then connected if and only if their distance on the torus is smaller than a threshold based on the product of their weights. When using positions on the circle (
$d$
-dimensional torus and a weight following a power law. Two vertices are then connected if and only if their distance on the torus is smaller than a threshold based on the product of their weights. When using positions on the circle (
![]() $d = 1$
), GIRGs approximate HRGs in the following sense: the processes of generating a HRG and a GIRG can be coupled such that it suffices to decrease and increase the average degree of the GIRG by only a constant factor to obtain a subgraph and a supergraph of the corresponding HRG, respectively. Compared to HRGs, GIRGs are potentially easier to analyze, generalize nicely to higher dimensions, and the weights allow to directly adjust the degree distribution.
$d = 1$
), GIRGs approximate HRGs in the following sense: the processes of generating a HRG and a GIRG can be coupled such that it suffices to decrease and increase the average degree of the GIRG by only a constant factor to obtain a subgraph and a supergraph of the corresponding HRG, respectively. Compared to HRGs, GIRGs are potentially easier to analyze, generalize nicely to higher dimensions, and the weights allow to directly adjust the degree distribution.
Above, we described the idealized threshold variants of the models, where two vertices are connected if and only if their distance is small enough. Arguably more realistic are the binomial variants, which allow longer edges and shorter non-edges with a small probability. This is achieved with an additional parameter
![]() $T$
, called temperature. For
$T$
, called temperature. For
![]() $T \to 0$
, the binomial and threshold variants coincide. Many publications focus on the threshold case, as it is typically simpler. This is particularly true for generation algorithms: in the threshold variants, one can ignore all vertex pairs with sufficient distance, which can be done using geometric data structures. In the binomial case, any pair of vertices could be adjacent, and the search space cannot be reduced as easily. For practical purposes, however, a non-zero temperature is crucial as real-world networks are generally assumed to have positive temperature allowing so-called weak ties (Granovetter, Reference Granovetter1973), that is, edges between nodes that have no strong reason to be connected and where the endpoints do not have many common neighbors. Moreover, from an algorithmic perspective, the threshold variants typically produce particularly well-behaved instances, while a higher temperature leads to more difficult problem inputs. Thus, to obtain benchmark instances of varying difficulty, generators for the binomial variants are key.
$T \to 0$
, the binomial and threshold variants coincide. Many publications focus on the threshold case, as it is typically simpler. This is particularly true for generation algorithms: in the threshold variants, one can ignore all vertex pairs with sufficient distance, which can be done using geometric data structures. In the binomial case, any pair of vertices could be adjacent, and the search space cannot be reduced as easily. For practical purposes, however, a non-zero temperature is crucial as real-world networks are generally assumed to have positive temperature allowing so-called weak ties (Granovetter, Reference Granovetter1973), that is, edges between nodes that have no strong reason to be connected and where the endpoints do not have many common neighbors. Moreover, from an algorithmic perspective, the threshold variants typically produce particularly well-behaved instances, while a higher temperature leads to more difficult problem inputs. Thus, to obtain benchmark instances of varying difficulty, generators for the binomial variants are key.
1.1 Contribution and outline
Based on the algorithm by Bringmann et al. (Reference Bringmann, Keusch and Lengler2019), we provide an efficient and flexible GIRG generator. It includes the binomial case and allows higher dimensions. Its expected running time is linear in the graph size. To the best of our knowledge, this is the first efficient generator for the GIRG model. Moreover, we adapt the algorithm to the HRG model, including the binomial variant. Compared to existing HRG generators (most of which only support the threshold variant), our implementation is the fastest sequential HRG generator.
A refactoring of the original GIRG algorithm (Bringmann et al., Reference Bringmann, Keusch and Lengler2019) allows us to parallelize our generators. They do not use multiple processors as effectively as the threshold-HRG generator by Penschuck (Reference Penschuck2017), which was specifically tailored toward parallelism. However, in a setting realistic for commodity hardware (8 cores, 16 threads), we still achieve comparable run times.
Our generators come as an open-source C++ libraryFootnote 1 with documentation, command-line interface, unit tests, and OpenMP (Board, 2018) parallelization using shared memory.
Besides the efficient generators, we have three secondary contributions. (1) We provide a comprehensible description of the sampling algorithm that should make it easy to understand how the algorithm works, why it works, and how it can be implemented. Although the core idea of the algorithm is not new (Bringmann et al., Reference Bringmann, Keusch and Lengler2019), the previous description is somewhat technical. (2) The expected average degree can be controlled via an input parameter. However, the dependence of the average degree on the actual parameter is non-trivial. In fact, given the average degree, there is no closed formula to determine the parameter. We provide a linear-time algorithm to estimate it. (3) We investigate how GIRGs and HRGs actually relate to each other by measuring how much the average degree of the GIRG has to be decreased and increased to obtain a subgraph and supergraph of the HRG, respectively. We find that a GIRG with only slightly lower average degree already yields a subgraph. In fact, our experiments indicate that the gap between average degrees vanishes for growing
![]() $n$
, that is, the GIRG subgraph is lacking only a sublinear fraction of edges. On the other hand, one has to increase the average degree significantly to obtain a GIRG supergraph.
$n$
, that is, the GIRG subgraph is lacking only a sublinear fraction of edges. On the other hand, one has to increase the average degree significantly to obtain a GIRG supergraph.
In the following, we first discuss our main contribution in the context of existing HRG generators. In Section 2, we formally define the GIRG and HRG models. Afterwards we describe the sampling algorithm in Section 3. In Section 4, we discuss implementation details, including the parameter estimation for the average degree (Section 4.3) as well as multiple performance improvements. Section 5 contains our experiments: we investigate the scaling behavior of our generator in Section 5.1, compare our HRG generator to existing ones in Section 5.2, and compare GIRGs to HRGs in Section 5.3.
1.2 Comparison with existing generators
Concerning HRGs, most previous algorithms only support the threshold case, see Table 1. A quadtree data structure was used to achieve the first subquadratic threshold generator (QuadTree) (von Looz et al., Reference von Looz, Meyerhenke and Prutkin2015). It was later improved leading to the algorithm currently implemented in NetworKit (NkGen) (von Looz et al., Reference von Looz, Özdayi, Laue and Meyerhenke2016). A later re-implementation by Penschuck (Reference Penschuck2017) improves it by about a factor of 2 (NkOpt). However, the main contribution of Penschuck (Reference Penschuck2017) was a new generator that features sublinear memory and near optimal parallelization (HyperGen). Up to date, HyperGen was the fastest threshold-HRG generator on a single processor. Our generator, HyperGIRGs, improves by a factor of
![]() $1.3$
–
$1.3$
–
![]() $2$
(depending on the parameters) but scales worse for more processors. Finally, Funke et al. (Reference Funke, Lamm, Sanders, Schulz, Strash and von Looz2018) provide a generator designed for a distributed setting (RHG) and later combine it with the streaming technique of HyperGen to generate enormous instances (sRHG) (Funke et al., Reference Funke, Lamm, Meyer, Penschuck, Sanders, Schulz and von Looz2019).
$2$
(depending on the parameters) but scales worse for more processors. Finally, Funke et al. (Reference Funke, Lamm, Sanders, Schulz, Strash and von Looz2018) provide a generator designed for a distributed setting (RHG) and later combine it with the streaming technique of HyperGen to generate enormous instances (sRHG) (Funke et al., Reference Funke, Lamm, Meyer, Penschuck, Sanders, Schulz and von Looz2019).
Table 1. Existing hyperbolic random graph generators. The columns show the names used throughout the paper; the authors and reference (journal if available); whether the generator supports the binomial model; and the asymptotic running time. The time bounds hold in the worst case (wc), with high probability (whp), in expectation (exp), or empirically (emp)

The published generators for the binomial model are the trivial quadratic algorithm (Aldecoa et al., Reference Aldecoa, Orsini and Krioukov2015) and an
![]() $O((n^{3/2} + m) \log n)$
algorithm (von Looz & Meyerhenke, Reference von Looz and Meyerhenke2016) based on the above-mentioned quadtree data structure (von Looz et al., Reference von Looz, Meyerhenke and Prutkin2015). The latter is part of NetworkKit; we call it NkQuad. In his thesis, v. Looz adapted NkGen for the binomial model resulting in the NkGenBin algorithm (Looz, Reference Looz2019) Moreover, the code for a hyperbolic embedding algorithm (Bläsius et al., Reference Bläsius, Friedrich, Krohmer and Laue2018b) includes a HRG generator implemented by Bringmann based on the GIRG algorithm (Bringmann et al., Reference Bringmann, Keusch and Lengler2019); we call it Embedder in the following. Embedder has been widely ignored as a high performance generator. This is because it was somewhat hidden, and it is heavily outperformed by other threshold generators. Experiments show that our generator HyperGIRGs is much faster than NkQuad, which is to be expected considering the asymptotic running time. Moreover, on a single processor, we outperform Embedder by an order of magnitude for
$O((n^{3/2} + m) \log n)$
algorithm (von Looz & Meyerhenke, Reference von Looz and Meyerhenke2016) based on the above-mentioned quadtree data structure (von Looz et al., Reference von Looz, Meyerhenke and Prutkin2015). The latter is part of NetworkKit; we call it NkQuad. In his thesis, v. Looz adapted NkGen for the binomial model resulting in the NkGenBin algorithm (Looz, Reference Looz2019) Moreover, the code for a hyperbolic embedding algorithm (Bläsius et al., Reference Bläsius, Friedrich, Krohmer and Laue2018b) includes a HRG generator implemented by Bringmann based on the GIRG algorithm (Bringmann et al., Reference Bringmann, Keusch and Lengler2019); we call it Embedder in the following. Embedder has been widely ignored as a high performance generator. This is because it was somewhat hidden, and it is heavily outperformed by other threshold generators. Experiments show that our generator HyperGIRGs is much faster than NkQuad, which is to be expected considering the asymptotic running time. Moreover, on a single processor, we outperform Embedder by an order of magnitude for
![]() $T = 0$
and by a factor of
$T = 0$
and by a factor of
![]() $4$
for higher temperatures. As Embedder does not support parallelization, this speedup increases for multiple processors. Finally, we are two to three times faster than NkGenBin, which was shown to perform slightly better than Embedder for
$4$
for higher temperatures. As Embedder does not support parallelization, this speedup increases for multiple processors. Finally, we are two to three times faster than NkGenBin, which was shown to perform slightly better than Embedder for
![]() $T\gt 0$
(Looz, Reference Looz2019).
$T\gt 0$
(Looz, Reference Looz2019).
We are not aware of a previous GIRG generator.
2. Models
2.1 Geometric inhomogeneous random graphs
GIRGs (Bringmann et al., Reference Bringmann, Keusch and Lengler2019) combine elements from random geometric graphs (Gilbert, Reference Gilbert1961) and Chung-Lu graphs (Chung & Lu, Reference Chung and Lu2002a, Reference Chung and Lu2002b). Let
![]() $V = \{1,\dots,n\}$
be a set of vertices with positive weights
$V = \{1,\dots,n\}$
be a set of vertices with positive weights
![]() $w_1,\dots,w_n$
following a power law with exponent
$w_1,\dots,w_n$
following a power law with exponent
![]() $\beta \gt 2$
. Let
$\beta \gt 2$
. Let
![]() $W$
be their sum. Let
$W$
be their sum. Let
![]() $\mathbb{T}^d$
be the
$\mathbb{T}^d$
be the
![]() $d$
-dimensional torus for a fixed dimension
$d$
-dimensional torus for a fixed dimension
![]() $d\geq 1$
represented by the
$d\geq 1$
represented by the
![]() $d$
-dimensional cube
$d$
-dimensional cube
![]() $[0,1]^d$
where opposite boundaries are identified. For each vertex
$[0,1]^d$
where opposite boundaries are identified. For each vertex
![]() $v \in V$
, let
$v \in V$
, let
![]() $x_v\in \mathbb{T}^d$
be a point drawn uniformly and independently at random. For
$x_v\in \mathbb{T}^d$
be a point drawn uniformly and independently at random. For
![]() $x,y \in \mathbb{T}^d$
let
$x,y \in \mathbb{T}^d$
let
![]() $||x-y||$
denote the
$||x-y||$
denote the
![]() $L_\infty$
-norm on the torus, that is,
$L_\infty$
-norm on the torus, that is,
![]() $||x-y|| = \max _{1\leq i\leq d} \min \{|x_i-y_i|, 1-|x_i-y_i|\}$
. Two vertices
$||x-y|| = \max _{1\leq i\leq d} \min \{|x_i-y_i|, 1-|x_i-y_i|\}$
. Two vertices
![]() $u\neq v$
are independently connected with probability
$u\neq v$
are independently connected with probability
![]() $p_{uv}$
. For a positive temperature
$p_{uv}$
. For a positive temperature
![]() $0 \lt T \lt 1$
,
$0 \lt T \lt 1$
,
 \begin{equation} p_{uv} = \min \left \{ 1, c\left ( \frac{w_uw_v/W}{{||x_u - x_v||}^d} \right )^{1/T} \right \} \end{equation}
\begin{equation} p_{uv} = \min \left \{ 1, c\left ( \frac{w_uw_v/W}{{||x_u - x_v||}^d} \right )^{1/T} \right \} \end{equation}
while for
![]() $T=0$
a threshold variant of the model is obtained with
$T=0$
a threshold variant of the model is obtained with
 \begin{align*} p_{uv} = \begin{cases} 1 & \text{if } ||x_u - x_v|| \leq c(w_uw_v/W)^{1/d}, \\ 0 & \text{else.} \end{cases} \end{align*}
\begin{align*} p_{uv} = \begin{cases} 1 & \text{if } ||x_u - x_v|| \leq c(w_uw_v/W)^{1/d}, \\ 0 & \text{else.} \end{cases} \end{align*}
The constant
![]() $c\gt 0$
controls the expected average degree. We note that the above formulation slightly deviates from the original definition, see Section 2.3 for more details.
$c\gt 0$
controls the expected average degree. We note that the above formulation slightly deviates from the original definition, see Section 2.3 for more details.
2.2 Hyperbolic random graphs
HRGs (Krioukov et al., Reference Krioukov, Papadopoulos, Kitsak, Vahdat and Boguñá2010) are generated by sampling random positions in the hyperbolic plane and connecting vertices that are close. More formally, let
![]() $V = \{1,\dots,n\}$
be a set of vertices. Let
$V = \{1,\dots,n\}$
be a set of vertices. Let
![]() $\alpha \gt 1/2$
and
$\alpha \gt 1/2$
and
![]() $C \in \mathbb{R}$
be two constants, where
$C \in \mathbb{R}$
be two constants, where
![]() $\alpha$
controls the power-law degree distribution with exponent
$\alpha$
controls the power-law degree distribution with exponent
![]() $\beta = 2\alpha{+}1 \gt 2$
, and
$\beta = 2\alpha{+}1 \gt 2$
, and
![]() $C$
determines the average degree
$C$
determines the average degree
![]() $\bar d$
. For each vertex
$\bar d$
. For each vertex
![]() $v \in V$
, we sample a random point
$v \in V$
, we sample a random point
![]() $p_v = (r_v, \theta _v)$
in the hyperbolic plane, using polar coordinates. Its angular coordinate
$p_v = (r_v, \theta _v)$
in the hyperbolic plane, using polar coordinates. Its angular coordinate
![]() $\theta _v$
is chosen uniformly from
$\theta _v$
is chosen uniformly from
![]() $[0, 2\pi )$
while its radius
$[0, 2\pi )$
while its radius
![]() $0 \le r_v \lt R$
with
$0 \le r_v \lt R$
with
![]() $R = 2\log (n) + C$
is drawn according to the density function
$R = 2\log (n) + C$
is drawn according to the density function
In the threshold case of HRGs, two vertices
![]() $u \not = v$
are connected if and only if their distance is below
$u \not = v$
are connected if and only if their distance is below
![]() $R$
. The hyperbolic distance
$R$
. The hyperbolic distance
![]() $d(p_u, p_v)$
is defined as
$d(p_u, p_v)$
is defined as
where the angle difference
![]() $\theta _u - \theta _v$
is modulo
$\theta _u - \theta _v$
is modulo
![]() $\pi$
.
$\pi$
.
The binomial variant adds a temperature
![]() $T \in [0, 1]$
to control the clustering, with lower temperatures leading to higher clustering. Two nodes
$T \in [0, 1]$
to control the clustering, with lower temperatures leading to higher clustering. Two nodes
![]() $u,v \in V$
are then connected with probability
$u,v \in V$
are then connected with probability
![]() $p_T(d(p_u, p_v))$
where
$p_T(d(p_u, p_v))$
where
For
![]() $T \rightarrow 0$
, the two definitions (threshold and binomial) coincide.
$T \rightarrow 0$
, the two definitions (threshold and binomial) coincide.
2.3 Comparison of GIRGs and HRGs
Bringmann et al. (Reference Bringmann, Keusch and Lengler2019) show that the HRG model can be seen as a special case of the GIRG model in the following sense. Let
![]() $d_{\mathrm{HRG}}$
be the average degree of a HRG. Then there exist GIRGs with average degree
$d_{\mathrm{HRG}}$
be the average degree of a HRG. Then there exist GIRGs with average degree
![]() $d_{\mathrm{GIRG}}$
and
$d_{\mathrm{GIRG}}$
and
![]() $D_{\mathrm{GIRG}}$
with
$D_{\mathrm{GIRG}}$
with
![]() ${d_{\mathrm{GIRG}}} \le{d_{\mathrm{HRG}}} \le{D_{\mathrm{GIRG}}}$
such that they are sub- and supergraphs of the HRG, respectively. Moreover,
${d_{\mathrm{GIRG}}} \le{d_{\mathrm{HRG}}} \le{D_{\mathrm{GIRG}}}$
such that they are sub- and supergraphs of the HRG, respectively. Moreover,
![]() $d_{\mathrm{GIRG}}$
and
$d_{\mathrm{GIRG}}$
and
![]() $D_{\mathrm{GIRG}}$
differ only by a constant factor. Formally, this is achieved by using the big-
$D_{\mathrm{GIRG}}$
differ only by a constant factor. Formally, this is achieved by using the big-
![]() $O$
notation instead of a single constant
$O$
notation instead of a single constant
![]() $c$
for the connection probability. We call this the generic GIRG framework. It basically captures any specific model whose connection probabilities differ from Equation (1) by only a constant factor. From a theoretical point of view, this is useful as proving something for the generic GIRG framework also proves it for any manifestation, including HRGs.
$c$
for the connection probability. We call this the generic GIRG framework. It basically captures any specific model whose connection probabilities differ from Equation (1) by only a constant factor. From a theoretical point of view, this is useful as proving something for the generic GIRG framework also proves it for any manifestation, including HRGs.
To see how HRGs fit into the generic GIRG framework, consider the following mapping (Bringmann et al., Reference Bringmann, Keusch and Lengler2019). Radii are mapped to weights
![]() $w_v = e^{(R-r_v)/2}$
, and angles are scaled to fit on a
$w_v = e^{(R-r_v)/2}$
, and angles are scaled to fit on a
![]() $1$
-dimensional torus
$1$
-dimensional torus
![]() $x_v = \theta _v/ (2\pi )$
. One can then see that the hyperbolic connection probability
$x_v = \theta _v/ (2\pi )$
. One can then see that the hyperbolic connection probability
![]() $p_T(d)$
under the provided mapping deviates from Equation (1) by only a constant. Thus,
$p_T(d)$
under the provided mapping deviates from Equation (1) by only a constant. Thus,
![]() $c$
in Equation (1) can be chosen such that all GIRG probabilities are larger or smaller than the corresponding HRG probabilities, leading to the two average degrees
$c$
in Equation (1) can be chosen such that all GIRG probabilities are larger or smaller than the corresponding HRG probabilities, leading to the two average degrees
![]() $d_{\mathrm{GIRG}}$
and
$d_{\mathrm{GIRG}}$
and
![]() $D_{\mathrm{GIRG}}$
mentioned above. Bringmann et al. (Reference Bringmann, Keusch and Lengler2019) note that the two constants, which they hide in the big-
$D_{\mathrm{GIRG}}$
mentioned above. Bringmann et al. (Reference Bringmann, Keusch and Lengler2019) note that the two constants, which they hide in the big-
![]() $O$
notation, do not have to match. They leave it open if they match, converge asymptotically, or how large the interval between them is in practice. We investigate this empirically in Section 5.3.
$O$
notation, do not have to match. They leave it open if they match, converge asymptotically, or how large the interval between them is in practice. We investigate this empirically in Section 5.3.
3. Sampling algorithm
As mentioned in the introduction, the core of our sampling algorithm is based on the algorithm by Bringmann et al. (Reference Bringmann, Keusch and Lengler2019). In the following, we first give a description of the core ideas and then work out the details that lead to an efficient implementation.
To explain the idea, we make two temporary assumptions and relax them in Sections 3.1 and 3.2, respectively. For now, assume that all weights are equal and consider only the threshold variant
![]() $T = 0$
. The task is to find all vertex pairs that form an edge, that is, their distance is below the threshold
$T = 0$
. The task is to find all vertex pairs that form an edge, that is, their distance is below the threshold
![]() $c(w_uw_v/W)^{1/d}$
. Since all weights are equal, the threshold in this restricted scenario is the same for all vertex pairs. One approach to quickly identify adjacent vertices is to partition the ground space into a grid of cells. The size of the cells should be chosen, such that (1) the cells are as small as possible and (2) the diameter of cells is larger than the threshold
$c(w_uw_v/W)^{1/d}$
. Since all weights are equal, the threshold in this restricted scenario is the same for all vertex pairs. One approach to quickly identify adjacent vertices is to partition the ground space into a grid of cells. The size of the cells should be chosen, such that (1) the cells are as small as possible and (2) the diameter of cells is larger than the threshold
![]() $c(w_uw_v/W)^{1/d}$
. The latter implies that only vertices in neighboring cells can be connected, thus narrowing down the search space. The former ensures that neighboring cells contain as few vertex pairs as possible reducing the number of comparisons. Figure 1a shows an example of such a grid for a
$c(w_uw_v/W)^{1/d}$
. The latter implies that only vertices in neighboring cells can be connected, thus narrowing down the search space. The former ensures that neighboring cells contain as few vertex pairs as possible reducing the number of comparisons. Figure 1a shows an example of such a grid for a
![]() $2$
-dimensional ground space.
$2$
-dimensional ground space.

Figure 1.
(a, b) The grid used by weight bucket pairs with a connection probability threshold between
![]() $2^{-3}$
and
$2^{-3}$
and
![]() $2^{-4}$
in two dimensions. (a) Each pair of colored cells represent neighbors. Note that the ground space is a torus and a cell is also a neighbor to itself. (b) The eight gray cells represent multiple distant cell pairs, which are replaced by one pair consisting of the red outlined parent cell pair. (c) Linearization of the cells on level 1 (left) and 2 (right) for
$2^{-4}$
in two dimensions. (a) Each pair of colored cells represent neighbors. Note that the ground space is a torus and a cell is also a neighbor to itself. (b) The eight gray cells represent multiple distant cell pairs, which are replaced by one pair consisting of the red outlined parent cell pair. (c) Linearization of the cells on level 1 (left) and 2 (right) for
![]() $d = 2$
.
$d = 2$
.
3.1 Inhomogeneous weights
Assume that we have vertices with two different weights
![]() $w_1, w_2$
, rather than one. As before, the cells should still be as small as possible while having a diameter larger than the connection threshold. However, there are three different thresholds now, one for each combination of weights. To resolve this, we can group the vertices by weight and use three differently sized grids to find the edges between them.
$w_1, w_2$
, rather than one. As before, the cells should still be as small as possible while having a diameter larger than the connection threshold. However, there are three different thresholds now, one for each combination of weights. To resolve this, we can group the vertices by weight and use three differently sized grids to find the edges between them.
As GIRGs require not only two but many weights, considering one grid for every weight pair is infeasible. The solution is to discretize the weights by grouping ranges of weights into weight buckets. When searching for edges between vertices in two weight buckets, the pair of largest weights in these buckets provides the threshold for the cell diameter. This choice of the cell diameter satisfies property (2). Property (1) is violated only slightly, if the weight range within the bucket is not too large. Thus, each combination of two weight buckets uses a grid of cells, whose granularity is based on the maximum weight in the respective buckets.
As a tradeoff, we choose
![]() $\lceil \log _2 n \rceil$
many buckets which yields a sublinear number of grids. Moreover, the largest and smallest weights in a bucket are at most a factor of two apart. Thus, the diameter of a cell is too large by at most a factor of four.
$\lceil \log _2 n \rceil$
many buckets which yields a sublinear number of grids. Moreover, the largest and smallest weights in a bucket are at most a factor of two apart. Thus, the diameter of a cell is too large by at most a factor of four.
With this approach, a single vertex has to appear in grids of different granularity. To do this in an efficient manner, we recursively divide the space into ever smaller grid cells, leading to a hierarchical subdivision of the space. This hierarchy is naturally described by a tree. For a
![]() $2$
-dimensional ground space, each node has four children, which is why we call it quadtree. Note that each level of the quadtree represents a grid of different granularity. Moreover, the side length of a grid cell on level
$2$
-dimensional ground space, each node has four children, which is why we call it quadtree. Note that each level of the quadtree represents a grid of different granularity. Moreover, the side length of a grid cell on level
![]() $\ell$
is
$\ell$
is
![]() $2^{-\ell }$
. For a pair
$2^{-\ell }$
. For a pair
![]() $(i, j)$
of weight buckets, we then choose the level that fits best for the corresponding weights, that is, the deepest level such that the diameter of each grid cell is above the connection threshold for the largest weights in bucket
$(i, j)$
of weight buckets, we then choose the level that fits best for the corresponding weights, that is, the deepest level such that the diameter of each grid cell is above the connection threshold for the largest weights in bucket
![]() $i$
and
$i$
and
![]() $j$
, respectively. We call this level the comparison level, denoted by
$j$
, respectively. We call this level the comparison level, denoted by
![]() $CL(i, j)$
. It suffices to insert vertices of a bucket into the deepest level among all its comparison levels. This level is called the insertion level and we denote it by
$CL(i, j)$
. It suffices to insert vertices of a bucket into the deepest level among all its comparison levels. This level is called the insertion level and we denote it by
![]() $I(i)$
. In Section 3.4, we discuss in detail how to efficiently access all vertices in a given grid cell belonging to a given weight bucket.
$I(i)$
. In Section 3.4, we discuss in detail how to efficiently access all vertices in a given grid cell belonging to a given weight bucket.
3.2 Binomial variant of the model
For
![]() $T \gt 0$
, neighboring cell pairs are still easy to handle: a constant fraction of vertex pairs will have an edge and one can sample them by explicitly checking every pair. For distant cell pairs and a fixed pair of weight buckets, the distance between the cells yields an upper bound on the connection probability of included vertices, see Equation (1). The probability bound depends on both, the weight buckets and the cell pair distance, using the maximum weight within the buckets and the minimum distance between points in the cells. We note that the individual connection probabilities are only a constant factor smaller than the upper bound.
$T \gt 0$
, neighboring cell pairs are still easy to handle: a constant fraction of vertex pairs will have an edge and one can sample them by explicitly checking every pair. For distant cell pairs and a fixed pair of weight buckets, the distance between the cells yields an upper bound on the connection probability of included vertices, see Equation (1). The probability bound depends on both, the weight buckets and the cell pair distance, using the maximum weight within the buckets and the minimum distance between points in the cells. We note that the individual connection probabilities are only a constant factor smaller than the upper bound.
Knowing this, we can use geometric jumps to skip most vertex pairs (Ahrens & Dieter, Reference Ahrens and Dieter1985). The approach works as follows. Assume that we want to create an edge with probability
![]() $\overline{p}$
for each vertex pair. For this process, we define the random variable
$\overline{p}$
for each vertex pair. For this process, we define the random variable
![]() $X$
to be the number of vertex pairs we see until we add the next edge. Then
$X$
to be the number of vertex pairs we see until we add the next edge. Then
![]() $X$
follows a geometric distribution. Thus, instead of throwing a coin for each vertex pair, we can do a single experiment that samples
$X$
follows a geometric distribution. Thus, instead of throwing a coin for each vertex pair, we can do a single experiment that samples
![]() $X$
from the geometric distribution and then skip
$X$
from the geometric distribution and then skip
![]() $X$
vertex pairs ahead. Since not all vertex pairs reach the upper bound
$X$
vertex pairs ahead. Since not all vertex pairs reach the upper bound
![]() $\overline{p}$
, we accept encountered pairs with probability
$\overline{p}$
, we accept encountered pairs with probability
![]() $p_{uv}/\overline{p}$
to get correct results.
$p_{uv}/\overline{p}$
to get correct results.
Although distant cell pairs are handled efficiently, their number is still quadratic, most of which yield no edges. To circumvent this problem, the sampling algorithm, yet again, uses a quadtree. In the quadratic set of cell pairs to compare for one weight bucket pair, non-neighboring cells are grouped together along the quadtree hierarchy. They are replaced by their parents as shown in Figure 1b until their parents become neighbors.
In conclusion, for each pair of weight buckets
![]() $(i,j)$
the following two types of cell pairs have to be processed: any two neighboring cell pairs on the comparison level
$(i,j)$
the following two types of cell pairs have to be processed: any two neighboring cell pairs on the comparison level
![]() $CL(i, j)$
and any distant cell pair with level larger or equal
$CL(i, j)$
and any distant cell pair with level larger or equal
![]() $CL(i, j)$
that has neighboring parents. The resulting set of distant and neighboring cell pairs for a fixed bucket pair partitions
$CL(i, j)$
that has neighboring parents. The resulting set of distant and neighboring cell pairs for a fixed bucket pair partitions
![]() $\mathbb{T}^d\times \mathbb{T}^d$
.
$\mathbb{T}^d\times \mathbb{T}^d$
.
3.3 Efficiently iterating over cell pairs
The previous description sketches the algorithm as originally published. Here, we propose a refactoring that greatly simplifies the implementation and enables parallelization. We attribute a significant amount of HyperGIRGs’ speedup over Embedder to this change.
Instead of first iterating over all bucket pairs and then over all corresponding cell pairs, we reverse this order. This removes the need to repeatedly determine the cell pairs to process for a given bucket pair. Instead it suffices to find the bucket pairs that process a given cell pair. This only depends on the level of the two cells and their type (neighboring or distant). Inverting the mapping from bucket pairs to cell pairs in the previous section yields the following. A neighboring cell pair on level
![]() $\ell$
is processed for bucket pairs with a comparison level of exactly
$\ell$
is processed for bucket pairs with a comparison level of exactly
![]() $\ell$
. A distant cell pair on level
$\ell$
. A distant cell pair on level
![]() $\ell$
(with neighboring parents) is processed for bucket pairs with a comparison level larger than or equal to
$\ell$
(with neighboring parents) is processed for bucket pairs with a comparison level larger than or equal to
![]() $\ell$
. Thus, for each level of the quadtree we must enumerate all neighboring cell pairs, as well as distant cell pairs with neighboring parents. Algorithm 1 recursively enumerates exactly these cell pairs.
$\ell$
. Thus, for each level of the quadtree we must enumerate all neighboring cell pairs, as well as distant cell pairs with neighboring parents. Algorithm 1 recursively enumerates exactly these cell pairs.

3.4 Efficient access to vertices by bucket and cell
A crucial part of the algorithm is to quickly access the set of vertices restricted to a weight bucket
![]() $i$
and a cell
$i$
and a cell
![]() $A$
, which we denote by
$A$
, which we denote by
![]() $V_i^A$
. To this end, we linearize the cells of each level as illustrated in Figure 1c. This linearization is called Morton code (Morton, Reference Morton1966) or z-order curve (Orenstein & Merrett, Reference Orenstein and Merrett1984). It has the nice properties that (1) for each cell in level
$V_i^A$
. To this end, we linearize the cells of each level as illustrated in Figure 1c. This linearization is called Morton code (Morton, Reference Morton1966) or z-order curve (Orenstein & Merrett, Reference Orenstein and Merrett1984). It has the nice properties that (1) for each cell in level
![]() $\ell$
, its descendants in level
$\ell$
, its descendants in level
![]() $\ell ' \gt \ell$
in the quadtree appear consecutively and (2) it is easy to convert between a cells position in the linear order and its
$\ell ' \gt \ell$
in the quadtree appear consecutively and (2) it is easy to convert between a cells position in the linear order and its
![]() $d$
-dimensional coordinates (see Section 4.2).
$d$
-dimensional coordinates (see Section 4.2).
We sort the vertices of a fixed weight bucket
![]() $i$
by the Morton code of their containing cell on the insertion level
$i$
by the Morton code of their containing cell on the insertion level
![]() $I(i)$
, using arbitrary tie-breaking for vertices in the same cell. This has the effect that for any cell
$I(i)$
, using arbitrary tie-breaking for vertices in the same cell. This has the effect that for any cell
![]() $A$
with
$A$
with
![]() $\text{level}(A) \le I(i)$
, the vertices of
$\text{level}(A) \le I(i)$
, the vertices of
![]() $V_i^A$
appear consecutive. Thus, to efficiently enumerate them, it suffices to know for each cell
$V_i^A$
appear consecutive. Thus, to efficiently enumerate them, it suffices to know for each cell
![]() $A$
the index of the first vertex in
$A$
the index of the first vertex in
![]() $V_i^A$
. This can be precomputed using prefix sums leading to the following lemma.
$V_i^A$
. This can be precomputed using prefix sums leading to the following lemma.
Lemma 1.
After linear preprocessing, for all cells
![]() $A$
and weight buckets
$A$
and weight buckets
![]() $i$
with
$i$
with
![]() $\text{level}(A) \leq I(i)$
, vertices in the set
$\text{level}(A) \leq I(i)$
, vertices in the set
![]() $V_i^A$
can be enumerated in
$V_i^A$
can be enumerated in
![]() $\mathcal{O}(|V_i^A|)$
.
$\mathcal{O}(|V_i^A|)$
.
Proof. As mentioned above, we have to sort the vertices
![]() $V_i$
of each weight bucket
$V_i$
of each weight bucket
![]() $i$
according to the index (Morton code) of the containing cell. Clearly, the
$i$
according to the index (Morton code) of the containing cell. Clearly, the
![]() $d$
-dimensional coordinates of the cell containing a given vertex are obtained in constant time by rounding. From this one can obtain the index in constant time (also see Section 4.2). This can be done using, for example, bucket sort with respect to this index to sort the vertices. In the following, we refer to this sorted array with
$d$
-dimensional coordinates of the cell containing a given vertex are obtained in constant time by rounding. From this one can obtain the index in constant time (also see Section 4.2). This can be done using, for example, bucket sort with respect to this index to sort the vertices. In the following, we refer to this sorted array with
![]() $V_i$
.
$V_i$
.
Besides these sorted arrays
![]() $V_i$
of vertices, one for each weight bucket
$V_i$
of vertices, one for each weight bucket
![]() $i$
, we store for each cell
$i$
, we store for each cell
![]() $C$
at level
$C$
at level
![]() $I(i)$
the number of vertices preceding the vertices in cell
$I(i)$
the number of vertices preceding the vertices in cell
![]() $C$
. Note that this is simply the prefix sum of the number of vertices in all cells that come before cell
$C$
. Note that this is simply the prefix sum of the number of vertices in all cells that come before cell
![]() $C$
. Denote this prefix sum of cell
$C$
. Denote this prefix sum of cell
![]() $C$
with
$C$
with
![]() $P_C$
.
$P_C$
.
Now let
![]() $i$
be a weight bucket and let
$i$
be a weight bucket and let
![]() $A$
be a cell identifying the requested set of vertices
$A$
be a cell identifying the requested set of vertices
![]() $V_i^A$
(with
$V_i^A$
(with
![]() $\text{level}(A) \leq I(i)$
). Let
$\text{level}(A) \leq I(i)$
). Let
![]() $C_1, \dots, C_j$
be the descendants of cell
$C_1, \dots, C_j$
be the descendants of cell
![]() $A$
at level
$A$
at level
![]() $I(i)$
, appearing in this order according to the Morton code. Recall that the vertices in
$I(i)$
, appearing in this order according to the Morton code. Recall that the vertices in
![]() $C_1, \dots, C_j$
appear consecutive in the sorted array
$C_1, \dots, C_j$
appear consecutive in the sorted array
![]() $V_i$
. Thus,
$V_i$
. Thus,
![]() $V_i^A$
is given by the range
$V_i^A$
is given by the range
![]() $[P_{C_1},\dots, P_{C_{j+1}})$
in
$[P_{C_1},\dots, P_{C_{j+1}})$
in
![]() $V_i$
.
$V_i$
.
In terms of running time, each weight bucket requires
![]() $\mathcal{O}(|V_i| + 2^{d\cdot I(i)})$
time for bucket sort and
$\mathcal{O}(|V_i| + 2^{d\cdot I(i)})$
time for bucket sort and
![]() $\mathcal{O}(2^{d\cdot I(i)})$
time for the prefix sums, where
$\mathcal{O}(2^{d\cdot I(i)})$
time for the prefix sums, where
![]() $2^{d\cdot I(i)}$
is the number of cells in the insertion level
$2^{d\cdot I(i)}$
is the number of cells in the insertion level
![]() $I(i)$
. Over all weight buckets, the term
$I(i)$
. Over all weight buckets, the term
![]() $|V_i|$
sums up to
$|V_i|$
sums up to
![]() $|V|$
and Bringmann et al. (Reference Bringmann, Keusch and Lengler2019) show that the same holds for
$|V|$
and Bringmann et al. (Reference Bringmann, Keusch and Lengler2019) show that the same holds for
![]() $2^{d\cdot I(i)}$
.
$2^{d\cdot I(i)}$
.
3.5 Adapting the algorithm to HRGs
One possibility to generate HRGs with this algorithm would be to convert hyperbolic points to GIRG coordinates according to Section 2.3 and use the algorithm as is. However, the generic GIRG framework captures HRGs only up to constant factor deviations in connection probabilities. In fact, we find that using only one scaling constant as in Equation (1) is insufficient to exactly represent the corresponding HRG probabilities (see Section 5.3).
To generate exact HRGs, we adapt the algorithm to work with hyperbolic data in the first place, as was done in Bläsius et al. (Reference Bläsius, Friedrich, Krohmer and Laue2018b). Concretely, we sample and store only hyperbolic coordinates instead of mapping them to GIRG data, use the hyperbolic distance function to determine distance between vertices and cells, control the expected average degree with an estimate for the radius
![]() $R$
of the hyperbolic disc, use the exact hyperbolic connection probability
$R$
of the hyperbolic disc, use the exact hyperbolic connection probability
![]() $p_T$
, and trivially find the comparison and insertion levels instead of using the closed form for canonical GIRGs. The resulting implementation is called HyperGIRGs.
$p_T$
, and trivially find the comparison and insertion levels instead of using the closed form for canonical GIRGs. The resulting implementation is called HyperGIRGs.
4. Implementation details
The description in the previous section is an idealized version of the algorithm. For an actual implementation, there are some gaps to fill in. Omitting many minor tweaks, we want to mention implementation details and optimizations that are crucial to achieve a good practical run time in the following.
4.1 Avoiding double counting buckets, cells, and vertices
The algorithm as described in Section 3 iterates over pairs of buckets, cells, and vertices. All three entities need to be handled correctly to avoid visiting vertex or cell pairs multiple times. Consider the cell pairs
![]() $(A,B)$
and
$(A,B)$
and
![]() $(B,A)$
as well as two bucket pairs
$(B,A)$
as well as two bucket pairs
![]() $(i,j)$
and
$(i,j)$
and
![]() $(j,i)$
that process them. When the bucket pair
$(j,i)$
that process them. When the bucket pair
![]() $(i,j)$
processes
$(i,j)$
processes
![]() $(A,B)$
it samples edges between
$(A,B)$
it samples edges between
![]() $V_i^A$
and
$V_i^A$
and
![]() $V_j^B$
while the bucket pair
$V_j^B$
while the bucket pair
![]() $(j,i)$
processes
$(j,i)$
processes
![]() $(B,A)$
to sample edges between
$(B,A)$
to sample edges between
![]() $V_j^B$
and
$V_j^B$
and
![]() $V_i^A$
. Meaning these edges are sampled twice, once in each direction. Since we want undirected edges this introduces double counting. To solve this, one can restrict the algorithm to cell pairs
$V_i^A$
. Meaning these edges are sampled twice, once in each direction. Since we want undirected edges this introduces double counting. To solve this, one can restrict the algorithm to cell pairs
![]() $A\leq B$
(or to bucket pairs
$A\leq B$
(or to bucket pairs
![]() $i\leq j$
). In any case, bucket pairs
$i\leq j$
). In any case, bucket pairs
![]() $(i, i)$
require special treatment for cell pairs of the form
$(i, i)$
require special treatment for cell pairs of the form
![]() $(A, A)$
. Then, only edges between vertices
$(A, A)$
. Then, only edges between vertices
![]() $u\lt v$
should be checked, because this call samples edges within a set of vertices instead of between two disjoined vertex sets. If self-loops are desired, the constraint can be relaxed to
$u\lt v$
should be checked, because this call samples edges within a set of vertices instead of between two disjoined vertex sets. If self-loops are desired, the constraint can be relaxed to
![]() $u\leq v$
.
$u\leq v$
.
4.2 Efficiently encoding and decoding Morton codes
Recall from Section 3.4 that we linearize the
![]() $d$
-dimensional grid of cells using Morton code. As vertex positions are given as
$d$
-dimensional grid of cells using Morton code. As vertex positions are given as
![]() $d$
-dimensional coordinates, we have to convert the coordinates to Morton codes (i.e., the index in the linearization) and vice versa. This is done by bitwise interleaving of the coordinates. For example, the
$d$
-dimensional coordinates, we have to convert the coordinates to Morton codes (i.e., the index in the linearization) and vice versa. This is done by bitwise interleaving of the coordinates. For example, the
![]() $2$
-dimensional Morton code of the four-bit coordinates
$2$
-dimensional Morton code of the four-bit coordinates
![]() $a=a_3a_2a_1a_0$
and
$a=a_3a_2a_1a_0$
and
![]() $b=b_3b_2b_1b_0$
is
$b=b_3b_2b_1b_0$
is
![]() $a_3b_3a_2b_2a_1b_1a_0b_0$
.
$a_3b_3a_2b_2a_1b_1a_0b_0$
.
Implementation wise, the encoding approaches are as follows.
-
FOR, FOR OPT. Set each bit of the result with shifts and bitwise operations (FOR). Since we know the level of a cell, we know the number of relevant bits in each coordinate. Considering only relevant bits improves performance significantly (FOR OPT).
-
MASKS. For details on this method, we refer to the open-source library libmorton (Baert, Reference Baert2018) and the authors related blog posts.Footnote 2
-
LUT. A lookup table computed at compile timeFootnote 3 can be used. The input is divided into chunks; a precomputed result for each chunk is obtained and shifted into place.
-
BMI2. The Parallel Bits Deposit/Extract assembler instructions from Intels Bit Manipulation Instruction Set 2 (Intel, 2019) provide a solution with one assembler instruction per input coordinate. BMI2 is available on Intel CPUs since 2013 and supported by recent AMD CPUs (Zen).
All approaches except LUT support a complementary decoding operation. We measured the approaches, excluding LUT, on an Intel i7-8550U processor (see Figure 2) and an AMD Ryzen7-2700X (see Figure 3). On Intel, BMI2 is consistently the fastest and at least an order of magnitude faster than FOR. Surprisingly, FOR OPT is not monotone in the number of bits per coordinate for dimensions below 5. Inspection of the generated assemblyFootnote 4 reveals that the compiler employed SIMD instructions. On AMD, BMI2 is the slowest. Our GIRG generator uses BMI2 if enabled and the loop with early termination (FOR OPT) otherwise.

Figure 2. Performance of Morton code generation in dimensions 2–5 on an Intel processor. Input coordinates are limited to
![]() $\lfloor 32/d\rfloor$
bits each, because the result is saved as a 32 bit integer.
$\lfloor 32/d\rfloor$
bits each, because the result is saved as a 32 bit integer.

Figure 3. Performance of Morton code generation in dimensions 2–5 on an AMD processor. Input coordinates are limited to
![]() $\lfloor 32/d\rfloor$
bits each, because the result is saved as a 32 bit integer.
$\lfloor 32/d\rfloor$
bits each, because the result is saved as a 32 bit integer.
4.3 Estimating the average degree parameter
Here, we describe how to estimate the parameter
![]() $c$
in Equation (1) to achieve a given expected average degree.Footnote
5
This section covers the estimation for the binomial version of the model
$c$
in Equation (1) to achieve a given expected average degree.Footnote
5
This section covers the estimation for the binomial version of the model
![]() $T\gt 0$
. The calculations for the threshold case
$T\gt 0$
. The calculations for the threshold case
![]() $T=0$
are analogous (and simpler). We estimate the constant based on the actual weights, not on their probability distribution. This leads to lower variance and allows user-defined weights.
$T=0$
are analogous (and simpler). We estimate the constant based on the actual weights, not on their probability distribution. This leads to lower variance and allows user-defined weights.
We start with an arbitrary constant
![]() $c$
, calculate the resulting expected average degree
$c$
, calculate the resulting expected average degree
![]() ${\mathbb{E}}[\bar{d}]$
, and adjust
${\mathbb{E}}[\bar{d}]$
, and adjust
![]() $c$
accordingly, using a modified binary search. This is possible, as
$c$
accordingly, using a modified binary search. This is possible, as
![]() ${\mathbb{E}}[\bar{d}]$
is monotone in
${\mathbb{E}}[\bar{d}]$
is monotone in
![]() $c$
. We derive an exact formula for
$c$
. We derive an exact formula for
![]() ${\mathbb{E}}[\bar{d}]$
, depending on
${\mathbb{E}}[\bar{d}]$
, depending on
![]() $c$
and the weights. It cannot simply be solved for
$c$
and the weights. It cannot simply be solved for
![]() $c$
, which is why we use binary search instead of a closed expression.
$c$
, which is why we use binary search instead of a closed expression.
For the binary search, we need to efficiently evaluate
![]() ${\mathbb{E}}[\bar{d}]$
for different values of
${\mathbb{E}}[\bar{d}]$
for different values of
![]() $c$
. Let
$c$
. Let
![]() $X_{uv}$
be a random indicator variable for the existence of the edge
$X_{uv}$
be a random indicator variable for the existence of the edge
![]() $uv$
with fixed weights but unknown positions. The expected average degree can be expressed as
$uv$
with fixed weights but unknown positions. The expected average degree can be expressed as
 \begin{equation} \mathbb{E}[\bar{d}] = \frac{1}{n} \cdot \mathbb{E}\left [\sum _{u\in V} \sum _{v\neq u} X_{uv} \right ] = \frac{1}{n} \sum _{u\in V} \sum _{v\neq u} \mathbb{E}[X_{uv}] \end{equation}
\begin{equation} \mathbb{E}[\bar{d}] = \frac{1}{n} \cdot \mathbb{E}\left [\sum _{u\in V} \sum _{v\neq u} X_{uv} \right ] = \frac{1}{n} \sum _{u\in V} \sum _{v\neq u} \mathbb{E}[X_{uv}] \end{equation}
with the expectation of a single edge being
 \begin{align*} \mathbb{E}[X_{uv}] = \mathbb{E}\left [ \min \left \{1, c \cdot \left ( \frac{w_uw_v/W}{{||x_u - x_v||}^d} \right )^{1/T} \right \} \right ] = \mathbb{E}\left [ \min \left \{1, \left ( \frac{c^{\frac{T}{d}} \left ( \frac{w_uw_v}{W} \right )^{\frac{1}{d}}}{||x_u - x_v||} \right )^{d/T} \right \} \right ]. \end{align*}
\begin{align*} \mathbb{E}[X_{uv}] = \mathbb{E}\left [ \min \left \{1, c \cdot \left ( \frac{w_uw_v/W}{{||x_u - x_v||}^d} \right )^{1/T} \right \} \right ] = \mathbb{E}\left [ \min \left \{1, \left ( \frac{c^{\frac{T}{d}} \left ( \frac{w_uw_v}{W} \right )^{\frac{1}{d}}}{||x_u - x_v||} \right )^{d/T} \right \} \right ]. \end{align*}
This is potentially problematic, as the formula for
![]() ${\mathbb{E}}[\bar{d}]$
sums over all vertex pairs. The issue preventing us from simplifying this formula is the minimum in the connection probability. We split it into short edges and long edges based on whether the minimum takes effect or not, that is, whether the numerator of the connection probability, call it
${\mathbb{E}}[\bar{d}]$
sums over all vertex pairs. The issue preventing us from simplifying this formula is the minimum in the connection probability. We split it into short edges and long edges based on whether the minimum takes effect or not, that is, whether the numerator of the connection probability, call it
![]() $k=c^{\frac{T}{d}} \left ( \frac{w_uw_v}{W} \right )^{1/d}$
, is bigger than the distance in the denominator. If
$k=c^{\frac{T}{d}} \left ( \frac{w_uw_v}{W} \right )^{1/d}$
, is bigger than the distance in the denominator. If
![]() $||x_u - x_v||\leq k$
, we have a short edge and the vertices are so close together that they will definitely be connected. Else, we have a long edge with
$||x_u - x_v||\leq k$
, we have a short edge and the vertices are so close together that they will definitely be connected. Else, we have a long edge with
![]() $k\lt ||x_u - x_v||$
; thus, we can drop the minimum. We get
$k\lt ||x_u - x_v||$
; thus, we can drop the minimum. We get
 \begin{align*} \mathbb{E}[X_{uv}] = \mathrm{Pr}(||x_u - x_v|| \leq k) + \mathrm{Pr}(k \lt ||x_u - x_v||) \cdot \mathbb{E}\left [ c\cdot \left ( \frac{w_uw_v/W}{{||x_u - x_v||}^d} \right )^{1/T} \mid k \lt ||x_u - x_v|| \right ]. \end{align*}
\begin{align*} \mathbb{E}[X_{uv}] = \mathrm{Pr}(||x_u - x_v|| \leq k) + \mathrm{Pr}(k \lt ||x_u - x_v||) \cdot \mathbb{E}\left [ c\cdot \left ( \frac{w_uw_v/W}{{||x_u - x_v||}^d} \right )^{1/T} \mid k \lt ||x_u - x_v|| \right ]. \end{align*}
For any constant
![]() $t\leq 0.5$
,
$t\leq 0.5$
,
![]() $\mathrm{Pr}(||x_u - x_v||\leq t) = (2t)^d$
, which is the fraction of the ground space which is covered by a hypercube with radius
$\mathrm{Pr}(||x_u - x_v||\leq t) = (2t)^d$
, which is the fraction of the ground space which is covered by a hypercube with radius
![]() $t$
. The probability for a short edge becomes
$t$
. The probability for a short edge becomes
 \begin{equation} \mathrm{Pr}(||x_u - x_v|| \leq k) = \begin{cases} (2k)^d = 2^dc^T \left ( \frac{w_uw_v}{W} \right ) & \text{if } k\leq 0.5 \\ 1 & \text{else}\\ \end{cases} \end{equation}
\begin{equation} \mathrm{Pr}(||x_u - x_v|| \leq k) = \begin{cases} (2k)^d = 2^dc^T \left ( \frac{w_uw_v}{W} \right ) & \text{if } k\leq 0.5 \\ 1 & \text{else}\\ \end{cases} \end{equation}
For long edges, one must also distinguish between
![]() $k\gt 0.5$
and
$k\gt 0.5$
and
![]() $k\leq 0.5$
because the distance on a unit torus with the
$k\leq 0.5$
because the distance on a unit torus with the
![]() $L_{\infty }$
-norm is at most 0.5. Thus for
$L_{\infty }$
-norm is at most 0.5. Thus for
![]() $k\gt 0.5$
, the probability for a long edge
$k\gt 0.5$
, the probability for a long edge
![]() $\mathrm{Pr}(k \lt ||x_u - x_v||)$
becomes zero independent of the distance. For
$\mathrm{Pr}(k \lt ||x_u - x_v||)$
becomes zero independent of the distance. For
![]() $k\leq 0.5$
, we can simplify the formula for long edges by integrating over all possible values of
$k\leq 0.5$
, we can simplify the formula for long edges by integrating over all possible values of
![]() $||x_u - x_v||$
. The probability density function of
$||x_u - x_v||$
. The probability density function of
![]() $||x_u - x_v||$
between 0 and 0.5 is the derivative of
$||x_u - x_v||$
between 0 and 0.5 is the derivative of
![]() $(2x)^d$
, namely
$(2x)^d$
, namely
![]() $d2^dx^{d-1}$
. Using this we get
$d2^dx^{d-1}$
. Using this we get
 \begin{align}& \mathrm{Pr}(k \lt ||x_u - x_v||) \cdot \mathbb{E}\left [ c \cdot \left ( \frac{w_uw_v/W}{{||x_u - x_v||}^d} \right )^{1/T} \mid k \lt ||x_u - x_v|| \right ] \nonumber\\ &\quad= \mathrm{Pr}(k \lt ||x_u - x_v||) \cdot \frac{ \int _k^{0.5}c \cdot \left ( \frac{w_uw_v/W}{x^d} \right )^{1/T} \cdot d2^dx^{d-1}\,\mathrm{d}x }{\mathrm{Pr}(k \lt ||x_u - x_v||)} \nonumber \\ &\quad= c \left (\frac{w_uw_v}{W}\right )^{1/T} d 2^d \int _k^{0.5} x^{d-1-d/T}\,\mathrm{d}x \nonumber \\ &\quad= c \left (\frac{w_uw_v}{W}\right )^{1/T} d 2^d \left [ \frac{1}{d(1-1/T)} \cdot x^{d-d/T} \right ]_k^{0.5} \nonumber \\ &\quad= c \left (\frac{w_uw_v}{W}\right )^{1/T} \frac{d 2^d}{d(1-1/T)} \left ( \left (\frac{1}{2}\right )^{d-d/T} - k^{d(1-1/T)} \right ) \nonumber \\ &\quad= c \left (\frac{w_uw_v}{W}\right )^{1/T} \frac{2^d}{1-1/T} \left ( \frac{2^{d/T}}{2^d} - \left ( c^{\frac{T}{d}} \left ( \frac{w_uw_v}{W} \right )^{1/d} \right )^{d(1-1/T)} \right ) \nonumber \\ &\quad= c \left (\frac{w_uw_v}{W}\right )^{1/T} \frac{2^{d/T}}{1-1/T} - c \left (\frac{w_uw_v}{W}\right )^{1/T} \frac{2^d}{1-1/T} c^{T-1} \left ( \frac{w_uw_v}{W} \right )^{1-1/T} \nonumber \\ &\quad= c \left (\frac{w_uw_v}{W}\right )^{1/T} \frac{2^{d/T}}{1-1/T} - c^T \left (\frac{w_uw_v}{W}\right ) \frac{2^d}{1-1/T}.\end{align}
\begin{align}& \mathrm{Pr}(k \lt ||x_u - x_v||) \cdot \mathbb{E}\left [ c \cdot \left ( \frac{w_uw_v/W}{{||x_u - x_v||}^d} \right )^{1/T} \mid k \lt ||x_u - x_v|| \right ] \nonumber\\ &\quad= \mathrm{Pr}(k \lt ||x_u - x_v||) \cdot \frac{ \int _k^{0.5}c \cdot \left ( \frac{w_uw_v/W}{x^d} \right )^{1/T} \cdot d2^dx^{d-1}\,\mathrm{d}x }{\mathrm{Pr}(k \lt ||x_u - x_v||)} \nonumber \\ &\quad= c \left (\frac{w_uw_v}{W}\right )^{1/T} d 2^d \int _k^{0.5} x^{d-1-d/T}\,\mathrm{d}x \nonumber \\ &\quad= c \left (\frac{w_uw_v}{W}\right )^{1/T} d 2^d \left [ \frac{1}{d(1-1/T)} \cdot x^{d-d/T} \right ]_k^{0.5} \nonumber \\ &\quad= c \left (\frac{w_uw_v}{W}\right )^{1/T} \frac{d 2^d}{d(1-1/T)} \left ( \left (\frac{1}{2}\right )^{d-d/T} - k^{d(1-1/T)} \right ) \nonumber \\ &\quad= c \left (\frac{w_uw_v}{W}\right )^{1/T} \frac{2^d}{1-1/T} \left ( \frac{2^{d/T}}{2^d} - \left ( c^{\frac{T}{d}} \left ( \frac{w_uw_v}{W} \right )^{1/d} \right )^{d(1-1/T)} \right ) \nonumber \\ &\quad= c \left (\frac{w_uw_v}{W}\right )^{1/T} \frac{2^{d/T}}{1-1/T} - c \left (\frac{w_uw_v}{W}\right )^{1/T} \frac{2^d}{1-1/T} c^{T-1} \left ( \frac{w_uw_v}{W} \right )^{1-1/T} \nonumber \\ &\quad= c \left (\frac{w_uw_v}{W}\right )^{1/T} \frac{2^{d/T}}{1-1/T} - c^T \left (\frac{w_uw_v}{W}\right ) \frac{2^d}{1-1/T}.\end{align}
We add the
![]() $k\leq 0.5$
cases of short and long edges [Equations (6) and (7)], that is
$k\leq 0.5$
cases of short and long edges [Equations (6) and (7)], that is
 \begin{align}& 2^dc^T \left ( \frac{w_uw_v}{W} \right ) + c \left (\frac{w_uw_v}{W}\right )^{1/T} \frac{2^{d/T}}{1-1/T} - c^T \left (\frac{w_uw_v}{W}\right ) \frac{2^d}{1-1/T} \nonumber \\ &\quad= 2^dc^T \left ( \frac{w_uw_v}{W} \right )\left (1+\frac{1}{1/T-1}\right ) - c \left (\frac{w_uw_v}{W}\right )^{1/T} \frac{2^{d/T}}{1/T-1} \nonumber \\ &\quad= c^{T}\frac{2^d}{1-T} \left ( \frac{w_uw_v}{W} \right ) - c \frac{2^{d/T}}{1/T-1} \left (\frac{w_uw_v}{W}\right )^{1/T},\end{align}
\begin{align}& 2^dc^T \left ( \frac{w_uw_v}{W} \right ) + c \left (\frac{w_uw_v}{W}\right )^{1/T} \frac{2^{d/T}}{1-1/T} - c^T \left (\frac{w_uw_v}{W}\right ) \frac{2^d}{1-1/T} \nonumber \\ &\quad= 2^dc^T \left ( \frac{w_uw_v}{W} \right )\left (1+\frac{1}{1/T-1}\right ) - c \left (\frac{w_uw_v}{W}\right )^{1/T} \frac{2^{d/T}}{1/T-1} \nonumber \\ &\quad= c^{T}\frac{2^d}{1-T} \left ( \frac{w_uw_v}{W} \right ) - c \frac{2^{d/T}}{1/T-1} \left (\frac{w_uw_v}{W}\right )^{1/T},\end{align}
to concisely express the expectation for
![]() $X_{uv}$
as
$X_{uv}$
as
 \begin{equation} \mathbb{E}[X_{uv}] = \begin{cases} c^{T}\frac{2^d}{1-T} \left ( \frac{w_uw_v}{W} \right ) - c \frac{2^{d/T}}{1/T-1} \left (\frac{w_uw_v}{W}\right )^{1/T} & \text{if } k\leq 0.5 \\ 1 & \text{if } k\gt 0.5\\ \end{cases} \end{equation}
\begin{equation} \mathbb{E}[X_{uv}] = \begin{cases} c^{T}\frac{2^d}{1-T} \left ( \frac{w_uw_v}{W} \right ) - c \frac{2^{d/T}}{1/T-1} \left (\frac{w_uw_v}{W}\right )^{1/T} & \text{if } k\leq 0.5 \\ 1 & \text{if } k\gt 0.5\\ \end{cases} \end{equation}
Unfortunately, we still cannot simplify the expected average degree into a form that can be computed in subquadratic time because of the case distinction in Equation (9). To circumvent this, we compute
![]() $\mathbb{E}[\bar d]$
for all vertex pairs as if
$\mathbb{E}[\bar d]$
for all vertex pairs as if
![]() $k\leq 0.5$
(call it
$k\leq 0.5$
(call it
![]() $Q_{\mathrm{over}}$
), then add an error term
$Q_{\mathrm{over}}$
), then add an error term
![]() $Q_{\mathrm{error}}$
to cancel out the pairs we treated wrongly, and add the correct value for those pairs. This results in
$Q_{\mathrm{error}}$
to cancel out the pairs we treated wrongly, and add the correct value for those pairs. This results in
![]() $\mathbb{E}[\bar d] = Q_{\mathrm{over}} + Q_{\mathrm{error}}$
.
$\mathbb{E}[\bar d] = Q_{\mathrm{over}} + Q_{\mathrm{error}}$
.
Plugging the
![]() $k\leq 0.5$
case of Equation (9) into Equation (5) and pulling constants out of the sum yield
$k\leq 0.5$
case of Equation (9) into Equation (5) and pulling constants out of the sum yield
 \begin{equation} Q_{\mathrm{over}} \cdot n = c^T\frac{2^d}{1-T} \sum _{u\in V}\sum _{v\neq u} \left ( \frac{w_uw_v}{W} \right ) - c \frac{2^{d/T}}{1/T-1} \sum _{u\in V}\sum _{v\neq u} \left (\frac{w_uw_v}{W}\right )^{1/T} \\ \end{equation}
\begin{equation} Q_{\mathrm{over}} \cdot n = c^T\frac{2^d}{1-T} \sum _{u\in V}\sum _{v\neq u} \left ( \frac{w_uw_v}{W} \right ) - c \frac{2^{d/T}}{1/T-1} \sum _{u\in V}\sum _{v\neq u} \left (\frac{w_uw_v}{W}\right )^{1/T} \\ \end{equation}
There are still quadratic sums in Equation (10), but those can be simplified to
 \begin{align*} \sum _{u\in V}\sum _{v\neq u} \left ( \frac{w_uw_v}{W} \right ) = \sum _{u\in V}\sum _{v\in V}\frac{w_uw_v}{W} - \sum _{v\in V}\frac{w_v^2}{W} = W - \sum _{v\in V}\frac{w_v^2}{W} \end{align*}
\begin{align*} \sum _{u\in V}\sum _{v\neq u} \left ( \frac{w_uw_v}{W} \right ) = \sum _{u\in V}\sum _{v\in V}\frac{w_uw_v}{W} - \sum _{v\in V}\frac{w_v^2}{W} = W - \sum _{v\in V}\frac{w_v^2}{W} \end{align*}
and
 \begin{align*} \sum _{u\in V}\sum _{v\neq u} \left (\frac{w_uw_v}{W}\right )^{1/T} &= \sum _{u\in V}\sum _{v\in V} \left (\frac{w_uw_v}{W}\right )^{1/T} - \sum _{v\in V}\left (\frac{w_v^2}{W}\right )^{1/T}\\ &= \frac{1}{W^{1/T}} \left ( \sum _{u\in V}\sum _{v\in V} (w_uw_v)^{1/T} - \sum _{v\in V}w_v^{2/T}\right ) \\ &= \frac{1}{W^{1/T}} \left ( \left ( \sum _{v\in V}w_v^{1/T} \right )^2 - \sum _{v\in V}w_v^{2/T}\right ). \end{align*}
\begin{align*} \sum _{u\in V}\sum _{v\neq u} \left (\frac{w_uw_v}{W}\right )^{1/T} &= \sum _{u\in V}\sum _{v\in V} \left (\frac{w_uw_v}{W}\right )^{1/T} - \sum _{v\in V}\left (\frac{w_v^2}{W}\right )^{1/T}\\ &= \frac{1}{W^{1/T}} \left ( \sum _{u\in V}\sum _{v\in V} (w_uw_v)^{1/T} - \sum _{v\in V}w_v^{2/T}\right ) \\ &= \frac{1}{W^{1/T}} \left ( \left ( \sum _{v\in V}w_v^{1/T} \right )^2 - \sum _{v\in V}w_v^{2/T}\right ). \end{align*}
To obtain the error term
![]() $Q_{\mathrm{error}}$
, let
$Q_{\mathrm{error}}$
, let
![]() $E_S$
be the set of vertex pairs
$E_S$
be the set of vertex pairs
![]() $(u,v)$
with
$(u,v)$
with
![]() $0.5 \lt k$
. So
$0.5 \lt k$
. So
![]() $Q_{\mathrm{error}}$
subtracts the
$Q_{\mathrm{error}}$
subtracts the
![]() $k\leq 0.5$
case and adds the
$k\leq 0.5$
case and adds the
![]() $k\gt 0.5$
case given in Equation (9) for all vertex pairs in
$k\gt 0.5$
case given in Equation (9) for all vertex pairs in
![]() $E_S$
, thus
$E_S$
, thus
 \begin{equation} Q_{\mathrm{error}} \cdot n = |E_S| - \sum _{(u,v)\in E_S} \left ( c^T\frac{2^d}{1-T} \left ( \frac{w_uw_v}{W} \right ) - c \frac{2^{d/T}}{1/T-1} \left (\frac{w_uw_v}{W}\right )^{1/T}\right ). \end{equation}
\begin{equation} Q_{\mathrm{error}} \cdot n = |E_S| - \sum _{(u,v)\in E_S} \left ( c^T\frac{2^d}{1-T} \left ( \frac{w_uw_v}{W} \right ) - c \frac{2^{d/T}}{1/T-1} \left (\frac{w_uw_v}{W}\right )^{1/T}\right ). \end{equation}
Now we are ready to find the constant
![]() $c$
for a desired average degree using binary search over the monotone function
$c$
for a desired average degree using binary search over the monotone function
![]() $f(c) = \mathbb{E}[\bar d] = Q_{\mathrm{over}} + Q_{\mathrm{error}}$
. The function
$f(c) = \mathbb{E}[\bar d] = Q_{\mathrm{over}} + Q_{\mathrm{error}}$
. The function
![]() $f$
is given by Equation (10) (using simplified sums) and adding the error
$f$
is given by Equation (10) (using simplified sums) and adding the error
![]() $Q_{\mathrm{error}}$
from Equation (11) for vertex pairs with
$Q_{\mathrm{error}}$
from Equation (11) for vertex pairs with
![]() $k\gt 0.5$
.
$k\gt 0.5$
.
 \begin{align*} \begin{aligned} f(c) &= c^T \cdot \frac{2^d}{n(1-T)} \left ( W - \sum _{v\in V}\frac{w_v^2}{W} \right ) \\ &\quad- c \cdot \frac{2^{d/T}}{n(1/T-1)} \cdot \frac{1}{W^{1/T}} \left ( \left ( \sum _{v\in V}w_v^{1/T} \right )^2 - \sum _{v\in V}w_v^{2/T}\right ) \\ &\quad- \frac{1}{n} \sum _{(u,v)\in E_S} \left ( c^T\frac{2^d}{1-T} \left ( \frac{w_uw_v}{W} \right ) - c \frac{2^{d/T}}{1/T-1} \left (\frac{w_uw_v}{W}\right )^{1/T} - 1 \right ) \end{aligned} \end{align*}
\begin{align*} \begin{aligned} f(c) &= c^T \cdot \frac{2^d}{n(1-T)} \left ( W - \sum _{v\in V}\frac{w_v^2}{W} \right ) \\ &\quad- c \cdot \frac{2^{d/T}}{n(1/T-1)} \cdot \frac{1}{W^{1/T}} \left ( \left ( \sum _{v\in V}w_v^{1/T} \right )^2 - \sum _{v\in V}w_v^{2/T}\right ) \\ &\quad- \frac{1}{n} \sum _{(u,v)\in E_S} \left ( c^T\frac{2^d}{1-T} \left ( \frac{w_uw_v}{W} \right ) - c \frac{2^{d/T}}{1/T-1} \left (\frac{w_uw_v}{W}\right )^{1/T} - 1 \right ) \end{aligned} \end{align*}
The binary search would now take
![]() $O(n)$
time to compute the sums that are independent of
$O(n)$
time to compute the sums that are independent of
![]() $c$
and
$c$
and
![]() $O(1+|E_S|)$
per evaluation of
$O(1+|E_S|)$
per evaluation of
![]() $f(c)$
. This assumes that
$f(c)$
. This assumes that
![]() $E_S$
can be found efficiently, which may add additionally overhead to the precomputation, for example, by sorting. In the following, we further reduce the time to evaluate
$E_S$
can be found efficiently, which may add additionally overhead to the precomputation, for example, by sorting. In the following, we further reduce the time to evaluate
![]() $f(c)$
from
$f(c)$
from
![]() $O(|E_S|)$
to
$O(|E_S|)$
to
![]() $O(|S|)$
with
$O(|S|)$
with
![]() $S$
being the set of vertices with at least one occurrence in
$S$
being the set of vertices with at least one occurrence in
![]() $E_S$
.
$E_S$
.
For a vertex
![]() $v\in V$
, let
$v\in V$
, let
![]() $E_S(v) = \{u \in V \mid uv \in E_S\}$
be the set of partners in
$E_S(v) = \{u \in V \mid uv \in E_S\}$
be the set of partners in
![]() $E_S$
. We rewrite the sum in the
$E_S$
. We rewrite the sum in the
![]() $Q_{\mathrm{error}}$
part of
$Q_{\mathrm{error}}$
part of
![]() $f(c)$
as follows:
$f(c)$
as follows:
 \begin{align*} \begin{aligned} &\sum _{(u,v)\in E_S} \left ( c^T\frac{2^d}{1-T} \left ( \frac{w_uw_v}{W} \right ) - c \frac{2^{d/T}}{1/T-1} \left (\frac{w_uw_v}{W}\right )^{1/T} - 1 \right )\\ &\quad=\sum _{v\in S} \sum _{u\in E_S(v)}\left ( c^T\frac{2^d}{1-T} \left ( \frac{w_uw_v}{W} \right ) - c \frac{2^{d/T}}{1/T-1} \left (\frac{w_uw_v}{W}\right )^{1/T} - 1 \right )\\ &\quad=\sum _{v\in S} \left ( c^T\frac{2^d}{1-T} \left ( \frac{w_v}{W} \right ) \sum _{u\in E_S(v)} (w_u) - c \frac{2^{d/T}}{1/T-1} \left (\frac{w_v}{W}\right )^{1/T} \sum _{u\in E_S(v)} (w_u^{1/T}) - \sum _{u\in E_S(v)} 1 \right ) \end{aligned} \end{align*}
\begin{align*} \begin{aligned} &\sum _{(u,v)\in E_S} \left ( c^T\frac{2^d}{1-T} \left ( \frac{w_uw_v}{W} \right ) - c \frac{2^{d/T}}{1/T-1} \left (\frac{w_uw_v}{W}\right )^{1/T} - 1 \right )\\ &\quad=\sum _{v\in S} \sum _{u\in E_S(v)}\left ( c^T\frac{2^d}{1-T} \left ( \frac{w_uw_v}{W} \right ) - c \frac{2^{d/T}}{1/T-1} \left (\frac{w_uw_v}{W}\right )^{1/T} - 1 \right )\\ &\quad=\sum _{v\in S} \left ( c^T\frac{2^d}{1-T} \left ( \frac{w_v}{W} \right ) \sum _{u\in E_S(v)} (w_u) - c \frac{2^{d/T}}{1/T-1} \left (\frac{w_v}{W}\right )^{1/T} \sum _{u\in E_S(v)} (w_u^{1/T}) - \sum _{u\in E_S(v)} 1 \right ) \end{aligned} \end{align*}
We reduce the running time by exploiting that for any two vertices
![]() $u,v\in S$
,
$u,v\in S$
,
![]() $w_u \leq w_v$
implies
$w_u \leq w_v$
implies
![]() $E_S(u) \subseteq E_S(v)$
. Thus, if we iterate the vertices in
$E_S(u) \subseteq E_S(v)$
. Thus, if we iterate the vertices in
![]() $S$
by increasing weight, we can reuse the computations for the last vertex by maintaining
$S$
by increasing weight, we can reuse the computations for the last vertex by maintaining
![]() $E_S(v)$
and the associated sums incrementally. Therefore, we partially sort the weights for all vertices in
$E_S(v)$
and the associated sums incrementally. Therefore, we partially sort the weights for all vertices in
![]() $S$
. Since the upper and lower bounds for the binary search are found with an exponential search, the size of
$S$
. Since the upper and lower bounds for the binary search are found with an exponential search, the size of
![]() $S$
might grow until the upper bound is found. We lazily extend a sorted prefix of the weight array while raising the upper bound. We assume
$S$
might grow until the upper bound is found. We lazily extend a sorted prefix of the weight array while raising the upper bound. We assume
![]() $S$
to be very small compared to
$S$
to be very small compared to
![]() $n$
and thus consider this overhead dominated by the other precomputations.
$n$
and thus consider this overhead dominated by the other precomputations.
4.4 Avoiding expensive mathematical operations for HRGs
HRGs introduce many computationally expensive mathematical operations like the hyperbolic cosine. We significantly improve the performance of the generator by avoiding or reusing the results of those operations.
For the threshold model, an edge exists if the distance
![]() $d$
is smaller than
$d$
is smaller than
![]() $R$
. Considering how the hyperbolic distance is defined (Section 2.2), reformulating it to
$R$
. Considering how the hyperbolic distance is defined (Section 2.2), reformulating it to
![]() $\cosh (d) \lt \cosh (R)$
avoids the expensive
$\cosh (d) \lt \cosh (R)$
avoids the expensive
![]() $\text{arccosh}$
, while
$\text{arccosh}$
, while
![]() $\cosh (R)$
remains constant during execution and can thus be precomputed. Similar to recent threshold-HRG generators, we compute intermediate values per vertex such that
$\cosh (R)$
remains constant during execution and can thus be precomputed. Similar to recent threshold-HRG generators, we compute intermediate values per vertex such that
![]() $\cosh (d)$
can be computed using only multiplication and addition (Funke et al., Reference Funke, Lamm, Meyer, Penschuck, Sanders, Schulz and von Looz2019; Penschuck, Reference Penschuck2017).
$\cosh (d)$
can be computed using only multiplication and addition (Funke et al., Reference Funke, Lamm, Meyer, Penschuck, Sanders, Schulz and von Looz2019; Penschuck, Reference Penschuck2017).
For the binomial model, evaluating the connection probability
![]() $p_T(d)$
from the optimized
$p_T(d)$
from the optimized
![]() $\cosh (d)$
is a performance bottleneck and made up half of the total run time. Evaluating
$\cosh (d)$
is a performance bottleneck and made up half of the total run time. Evaluating
![]() $p_T(d)$
includes an expensive exponential function and cannot avoid the
$p_T(d)$
includes an expensive exponential function and cannot avoid the
![]() $\text{arccosh}$
like in the threshold model. We use a technique that we call a distance filter to reduce the frequency of the operation resulting in a speedup of approximately factor two.
$\text{arccosh}$
like in the threshold model. We use a technique that we call a distance filter to reduce the frequency of the operation resulting in a speedup of approximately factor two.
To explain how the distance filter works (also see Figure 4a), consider the straightforward way to sample an edge. That is, one samples a uniform random value
![]() $u \in [0,1]$
and creates the edge if and only if
$u \in [0,1]$
and creates the edge if and only if
![]() $u \lt p_T(d)$
. Since
$u \lt p_T(d)$
. Since
![]() $p_T$
is monotonically decreasing, an alternative check would be
$p_T$
is monotonically decreasing, an alternative check would be
![]() $p_T^{-1}(u) \gt d$
. The distance filter improves this by precomputing the inverse
$p_T^{-1}(u) \gt d$
. The distance filter improves this by precomputing the inverse
![]() $p_T^{-1}(u)$
for equidistant values in
$p_T^{-1}(u)$
for equidistant values in
![]() $[0, 1]$
. This let us, for small ranges in
$[0, 1]$
. This let us, for small ranges in
![]() $[0, 1]$
, quickly access the corresponding range of distances. Then, the process of sampling an edge becomes the following. We first sample
$[0, 1]$
, quickly access the corresponding range of distances. Then, the process of sampling an edge becomes the following. We first sample
![]() $u \in [0, 1]$
, which falls in a range between two precomputed values, which in turn yields a range of distances. If the actual distance lies below that range, there has to be an edge and if it lies above, there is no edge. Only if it lies in the range, we actually have to compute the probability
$u \in [0, 1]$
, which falls in a range between two precomputed values, which in turn yields a range of distances. If the actual distance lies below that range, there has to be an edge and if it lies above, there is no edge. Only if it lies in the range, we actually have to compute the probability
![]() $p_T(d)$
and do the check the straightforward way. Since
$p_T(d)$
and do the check the straightforward way. Since
![]() $u$
is uniformly distributed, the probability to hit the interval where
$u$
is uniformly distributed, the probability to hit the interval where
![]() $p_T(d)$
has to be evaluated is
$p_T(d)$
has to be evaluated is
![]() $1/k$
, where
$1/k$
, where
![]() $k$
is the number of precomputed entries. Our generator uses
$k$
is the number of precomputed entries. Our generator uses
![]() $k=100$
which is large enough to amortize the few times we have to compute
$k=100$
which is large enough to amortize the few times we have to compute
![]() $p_T(d)$
but still small enough to avoid cache misses. Additionally, we avoid the
$p_T(d)$
but still small enough to avoid cache misses. Additionally, we avoid the
![]() $\text{arccosh}$
by directly storing
$\text{arccosh}$
by directly storing
![]() $\cosh [p_T^{-1}(x)]$
in the filter.
$\cosh [p_T^{-1}(x)]$
in the filter.

Figure 4. Distance filter (left) and tasks for parallelization in the
![]() $1$
-dimensional case (right).
$1$
-dimensional case (right).
4.5 Parallelization
This section describes how the sampling algorithm can be parallelized. The presented approach applies to the GIRG and HRG implementations. The algorithm has five steps: generate weights, generate positions, estimate the average degree constant, precompute the geometric data structure, and sample edges. The first two are trivial to parallelize. For estimating the constants, we parallelize the dominant computations with linear running time.
For the preprocessing, we have to do three subtasks: compute for each vertex its containing cells on its insertion level, sort the vertices according to their Morton code index, and compute the prefix sum for all cells. We parallelize all three tasks and optimize them by handling all weight buckets together, sorting by weight bucket first and Morton code second. This is done by encoding this criterion into integers that are sorted with parallel radix sort. Then, the vertices of a weight bucket form a contiguous subsequence in the sorted array. Moreover, they are sorted by cell, allowing parallel computation of the prefix sums for all cells in the insertion level of the weight bucket.
To sample the edges, we make use of the fact that we iterate over cell pairs in a recursive manner. This can be parallelized by cutting the recursion tree at a certain level and distributing the loose ends among multiple processors. This works well, as the recursion tree is symmetric, leading to multiple tasks of similar load. As the number of run time intensive tasks is a power of
![]() $2$
, it works particularly well if the number of processors is also a power of
$2$
, it works particularly well if the number of processors is also a power of
![]() $2$
and experiments suggest a near optimal scaling in this case.
$2$
and experiments suggest a near optimal scaling in this case.
In detail, we parallelize the edge sampling as follows. Each thread has a local random generator. We use static scheduling to produce deterministic results even for the binomial model. However, the ordering of edges in the edge list varies, because each thread locally buffers generated edges before writing them while locking a mutex. We distinguish two stages of execution. The first stage is to “saw off” the recursion tree at a certain level and collect the omitted recursive calls as tasks to execute in stage two. A task is represented by a cell pair from which to pick up the execution later. One thread collects the tasks by traversing the recursion tree without sampling any edges (omitting lines 1–6 in Algorithm 1). Meanwhile, the other threads process the pairs that the main thread passed through, that is, the work in the top of the recursion tree before the saw-off point. When all tasks are collected stage two begins. In stage two, the threads pick up the “loose ends” of the cut recursion tree. There are three different types of tasks with varying load. For
![]() $1$
-dimensional geometry, level
$1$
-dimensional geometry, level
![]() $\ell \gt 2$
, and assuming a number of threads that is constant in
$\ell \gt 2$
, and assuming a number of threads that is constant in
![]() $n$
, the types of tasks are the following. There are
$n$
, the types of tasks are the following. There are
![]() $2^\ell$
heavy tasks given by a neighboring cell pair of the form
$2^\ell$
heavy tasks given by a neighboring cell pair of the form
![]() $(A,A)$
. Their number of recursive calls grows exponentially with each subsequent level implying a load of
$(A,A)$
. Their number of recursive calls grows exponentially with each subsequent level implying a load of
![]() $O(n)$
. There are
$O(n)$
. There are
![]() $2^\ell$
light tasks given by a neighboring cell pair of the form
$2^\ell$
light tasks given by a neighboring cell pair of the form
![]() $(A,A+1)$
. They produce four recursive calls per subsequent level implying a load of
$(A,A+1)$
. They produce four recursive calls per subsequent level implying a load of
![]() $O(\log n)$
. Finally, there are
$O(\log n)$
. Finally, there are
![]() $3\cdot 2^{\ell -1}$
constant tasks given by a distant cell pair. They invoke no recursive calls at all. The number of distant cell pairs in a level is explained by Figure 4b. For each cell
$3\cdot 2^{\ell -1}$
constant tasks given by a distant cell pair. They invoke no recursive calls at all. The number of distant cell pairs in a level is explained by Figure 4b. For each cell
![]() $B$
in level
$B$
in level
![]() $\ell -1$
with children
$\ell -1$
with children
![]() $A$
and
$A$
and
![]() $A+1$
, the distant cell pairs in level
$A+1$
, the distant cell pairs in level
![]() $\ell$
are
$\ell$
are
![]() $(A,A+2), (A, A+3), (A+1, A+3)$
.
$(A,A+2), (A, A+3), (A+1, A+3)$
.
Since heavy tasks dominate the run time during stage two, we distribute heavy tasks evenly among all threads. This is why the approach scales best when the number of threads is a power of two. The level where we saw off the recursion tree is a tuning parameter of the generator. We choose it, such that there are two heavy tasks per thread to reduce load imbalance if one thread stalls. To apply the same scheduling approach to higher dimensions it suffices to know that the load of tasks remains similar and the number of heavy tasks is
![]() $2^{\ell d}$
.
$2^{\ell d}$
.
5. Experimental evaluation
We perform three types of experiments. In Section 5.1, we investigate the scaling behavior of our GIRG generator, broken down into the different tasks performed by the algorithm. In Section 5.2, we compare our HRG generator with existing generators. In Section 5.3, we experimentally investigate the difference between HRGs and their GIRG counterpart. Whenever a data point represents the mean over multiple iterations, our plots include error bars that indicate the standard deviation. Besides the implementation itself, all benchmarks and analysis scripts are also accessible in our source repository.
5.1 Scaling of the GIRG generator
We investigate the scaling of the generator, broken down into five steps. (1) (Weights) Generate power-law weights. (2) (Positions) Generate points on
![]() $\mathbb{T}^d$
. (3) (Binary) Estimate the constant controlling the average degree. (4) (Pre) Preprocess the geometric data structure (Section 3.4). (5) (Edges) Sample edges between all vertex pairs as described in Algorithm 1.
$\mathbb{T}^d$
. (3) (Binary) Estimate the constant controlling the average degree. (4) (Pre) Preprocess the geometric data structure (Section 3.4). (5) (Edges) Sample edges between all vertex pairs as described in Algorithm 1.
Figure 5 shows the sequential run time over the number of nodes
![]() $n$
(top left), number of edges
$n$
(top left), number of edges
![]() $m$
(top right), temperature
$m$
(top right), temperature
![]() $T$
(bottom right), and dimension
$T$
(bottom right), and dimension
![]() $d$
(bottom right). The performance is measured in nanoseconds per edge. Each data point represents the mean over 10 iterations. To make the measurements independent of the graph representation, we do not save the edges into RAM but accumulate a checksum instead. Note that the top right plot increases the average degree, resulting in a decreased time per edge.
$d$
(bottom right). The performance is measured in nanoseconds per edge. Each data point represents the mean over 10 iterations. To make the measurements independent of the graph representation, we do not save the edges into RAM but accumulate a checksum instead. Note that the top right plot increases the average degree, resulting in a decreased time per edge.

Figure 5. Sequential run time for the steps of the GIRG sampling algorithm averaged over 10 iterations. Each plot varies a different model parameter deviating from a base configuration
![]() $d=1$
,
$d=1$
,
![]() $n=2^{15}$
,
$n=2^{15}$
,
![]() $T=0$
,
$T=0$
,
![]() $\beta =2.5$
, and
$\beta =2.5$
, and
![]() $\bar d=10$
. The base configuration is indicated by a dashed vertical line.
$\bar d=10$
. The base configuration is indicated by a dashed vertical line.
The empirical run times match the theoretical bounds: it is linear in
![]() $n$
and
$n$
and
![]() $m$
, grows exponentially in the dimension
$m$
, grows exponentially in the dimension
![]() $d$
, and is unaffected by the temperature
$d$
, and is unaffected by the temperature
![]() $T$
. The overall time is dominated by the edge sampling. Generating the weights includes expensive exponential functions, making it the slowest step after edge sampling. Generating the positions is significantly faster even for higher dimensions. For the parameter estimation using binary search, one can see that the run time never exceeds the time to generate the weights. For non-zero temperature
$T$
. The overall time is dominated by the edge sampling. Generating the weights includes expensive exponential functions, making it the slowest step after edge sampling. Generating the positions is significantly faster even for higher dimensions. For the parameter estimation using binary search, one can see that the run time never exceeds the time to generate the weights. For non-zero temperature
![]() $T$
, the performance of the binary search is similar to the generation of the weights, as it also requires exponential functions. The lower run times per edge for the increasing number of edges (top right) show that the run time is dominated by the number of nodes
$T$
, the performance of the binary search is similar to the generation of the weights, as it also requires exponential functions. The lower run times per edge for the increasing number of edges (top right) show that the run time is dominated by the number of nodes
![]() $n$
. Only for very high average degrees, the cost per edge outgrows the cost per vertex.
$n$
. Only for very high average degrees, the cost per edge outgrows the cost per vertex.
5.2 HRG run time comparison
We evaluate the run time performance of HyperGIRGs compared to the generators in Table 1, excluding the generators with high asymptotic run time as well as RHG and sRHG, which are designed for distributed machines. Executed on a single compute node, the performance of the faster sRHG is comparable to HyperGen (Funke et al., Reference Funke, Lamm, Meyer, Penschuck, Sanders, Schulz and von Looz2019). To avoid systematic biases between different graph representations, the implementations are modifiedFootnote 6 not to store the resulting graph. Instead, only the number of edges produced is counted and we ensure that the computation of incident nodes is not optimized away by the compiler.
We used different machines for our sequential and parallel experiments. The former are done on an Intel Xeon Skylake CP Gold 6144 with 192 GB RAM and the latter on an Intel Xeon E5-2630 v3 with 8 cores (16 threads) and 64 GB RAM.
For threshold graphs, our generator HyperGIRGs is consistently faster than the competitors, independent of the parameter choices, see Figure 6a and 6b. Only for unrealistic average degrees (1 K), HyperGen slightly outperforms HyperGIRGs.

Figure 6. Comparison of HRG generators averaged over five iterations. (a, b) Threshold variant for different average degrees
![]() $\bar{d}$
and power-law exponents
$\bar{d}$
and power-law exponents
![]() $\beta$
. (c) Binomial variant with temperature
$\beta$
. (c) Binomial variant with temperature
![]() $T = 0.5$
. (d) The same configuration as (b) but utilizing multiple cores.
$T = 0.5$
. (d) The same configuration as (b) but utilizing multiple cores.
For higher temperatures, we compare our algorithm with the three other non-quadratic generators NkQuad (included in NetworKit), NkGenBin, and Embedder, see Figure 6c. One can clearly see the worse asymptotic running time of NkQuad. HyperGIRGs is consistently four times faster than Embedder and 2–3 times faster than NkGenBin for graphs that are not too small. We note that Embedder uses a different estimation for
![]() $R$
, which leads to an insignificant left shift of the corresponding curve.
$R$
, which leads to an insignificant left shift of the corresponding curve.
Figure 6d shows measurements for parallel experiments using 16 threads. The parameters coincide with Figure 6b. Embedder does not support parallelization and is outperformed even more by the other generators. For sufficiently large graphs, the fastest generator in this multi-core setting is HyperGen, which is specifically tailored toward parallel execution. Nonetheless, HyperGIRGs shows comparable performance and overtakes the other two generators NkGen and NkOpt. We note that even on parallel machines, the sequential performance is of high importance: one often needs a large collection of graphs rather than a single huge instance. In this case, it is more efficient to run multiple instances of a sequential generator in parallel.
5.3 Difference between HRGs and GIRGs
Recall from Section 2.3 that a HRG with average degree
![]() $d_{\mathrm{HRG}}$
has a corresponding GIRG sub- and supergraphs with average degrees
$d_{\mathrm{HRG}}$
has a corresponding GIRG sub- and supergraphs with average degrees
![]() $d_{\mathrm{GIRG}}$
and
$d_{\mathrm{GIRG}}$
and
![]() $D_{\mathrm{GIRG}}$
, respectively.
$D_{\mathrm{GIRG}}$
, respectively.
We experimentally determine, for given HRGs, the values for
![]() $d_{\mathrm{GIRG}}$
by decreasing the average degree of the corresponding GIRGs until it is a subgraph of the HRG. Analogously, we determine the value for
$d_{\mathrm{GIRG}}$
by decreasing the average degree of the corresponding GIRGs until it is a subgraph of the HRG. Analogously, we determine the value for
![]() $D_{\mathrm{GIRG}}$
. We focus on the threshold variant of the models, as this makes the coupling between HRGs and GIRGs much simpler (the graph is uniquely determined by the coordinates). Figure 7a shows
$D_{\mathrm{GIRG}}$
. We focus on the threshold variant of the models, as this makes the coupling between HRGs and GIRGs much simpler (the graph is uniquely determined by the coordinates). Figure 7a shows
![]() $d_{\mathrm{GIRG}}$
and
$d_{\mathrm{GIRG}}$
and
![]() $D_{\mathrm{GIRG}}$
, compared to
$D_{\mathrm{GIRG}}$
, compared to
![]() $d_{\mathrm{HRG}}$
for growing
$d_{\mathrm{HRG}}$
for growing
![]() $n$
. One can see that
$n$
. One can see that
![]() $d_{\mathrm{GIRG}}$
and
$d_{\mathrm{GIRG}}$
and
![]() $D_{\mathrm{GIRG}}$
are actually quite far apart. They in particular do not converge to the same value for growing
$D_{\mathrm{GIRG}}$
are actually quite far apart. They in particular do not converge to the same value for growing
![]() $n$
. However, at least
$n$
. However, at least
![]() $d_{\mathrm{GIRG}}$
seems to approach
$d_{\mathrm{GIRG}}$
seems to approach
![]() $d_{\mathrm{HRG}}$
. This indicates that every HRG corresponds to a GIRG subgraph that is missing only a sublinear fraction of edges. On the other hand, the average degree of the GIRG has to be increased by a lot to actually contain all edges also contained in the HRG.
$d_{\mathrm{HRG}}$
. This indicates that every HRG corresponds to a GIRG subgraph that is missing only a sublinear fraction of edges. On the other hand, the average degree of the GIRG has to be increased by a lot to actually contain all edges also contained in the HRG.

Figure 7. Relation between the HRG and the GIRG model. (a) The values for
![]() $d_{\mathrm{HRG}}$
,
$d_{\mathrm{HRG}}$
,
![]() $d_{\mathrm{GIRG}}$
,
$d_{\mathrm{GIRG}}$
,
![]() $D_{\mathrm{GIRG}}$
averaged over 50 iterations. (b) The number of missing (
$D_{\mathrm{GIRG}}$
averaged over 50 iterations. (b) The number of missing (
![]() $\text{HRG}\setminus \text{GIRG}$
) and additional (
$\text{HRG}\setminus \text{GIRG}$
) and additional (
![]() $\text{GIRG} \setminus \text{HRG}$
) edges depending on the expected degree of the corresponding GIRG. It can be interpreted as a cross-section of one iteration in (a).
$\text{GIRG} \setminus \text{HRG}$
) edges depending on the expected degree of the corresponding GIRG. It can be interpreted as a cross-section of one iteration in (a).
Figure 7b gives a more detailed view for a single HRG. Depending on the average degree of the GIRG, it shows how many edges the GIRG lacks and how many edges the GIRG has in addition to the HRG. For degree
![]() $100$
, the GIRG contains about 38 K additional and lacks about 42 K edges. These are rather small numbers compared to the 5 million edges of the graphs.
$100$
, the GIRG contains about 38 K additional and lacks about 42 K edges. These are rather small numbers compared to the 5 million edges of the graphs.
6. Conclusion
We provide the first efficient implementation of a geometric inhomogeneous graph generator and a special case adaption for HRGs that constitutes the fastest sequential HRG generator to date. Our code is publicly available. We describe the sampling algorithms along with crucial implementation details such as optimizations, parallelization strategies, and the non-trivial estimation of input parameters to control the average degree of the resulting graphs. Moreover, we relate the GIRG and HRG model and find that, although a straightforward inclusion does not hold, they are sufficiently similar in practice. For example, a HRG with about 5 million edges and its corresponding GIRG equivalent have 99.24% of their edges in common.
Competing interests
None.