Hostname: page-component-848d4c4894-mwx4w Total loading time: 0 Render date: 2024-06-14T19:30:45.367Z Has data issue: false hasContentIssue false
  • English
  • Français

Analytical solution for laminar entrance flow in circular pipes

Published online by Cambridge University Press:  25 January 2024

Taig Young Kim Open the ORCID record for Taig Young Kim [Opens in a new window]
Taig Young Kim*
Affiliation:
Department of Mechanical Eng., Tech University of Korea, 237 Sangideahak-ro, Siheung-si, Gyeonggi-do 15073, South Korea
*
†Email address for correspondence: tagikim@tukorea.ac.kr
Get access Rights & Permissions [Opens in a new window]

Abstract

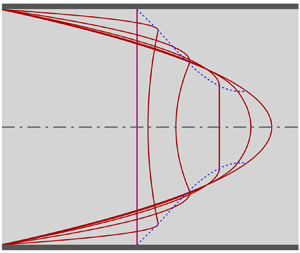
This study introduces an analytical solution for the laminar entrance flow in circular pipes, aiming to confirm the occurrence of velocity overshoot. Velocity overshoot is characterised by the maximum axial velocity appearing near the pipe wall instead of the central axis. Similar to the previous studies, the analytical solution is derived from the parabolised Navier–Stokes equation; however, the specific approach used in linearising the momentum equation has not been attempted before. The accuracy of this analytical solution has been verified through a comprehensive comparison with various published experimental data. The existence of velocity overshoot at a short distance from the inlet, which is evident in numerous numerical calculations based on the full Navier–Stokes equations and corroborated by recent magnetic resonance (MR) velocimetry experiments, is identified analytically for the first time. The parabolised Navier–Stokes equation has inherent self-similarity with respect to the Reynolds number, implying that $Re$ is incorporated into the dimensionless variables rather than serving as an independent flow parameter. According to both MR velocimetry measurements and the present analytical solution, the self-similarity is not valid immediately following the pipe inlet, and this becomes more evident as $Re$ decreases; hence, the analytical solution derived from the parabolised Navier–Stokes equation cannot accurately predict the evolution of the velocity profile within this region near the pipe inlet.

JFM classification

Boundary Layers: Pipe flow boundary layer Mathematical Foundations: General fluid mechanics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 979 , 25 January 2024 , A51
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Al-Nassri, S.A. & Unny, T. 1981 Developing laminar flow in the inlet length of a smooth pipe. Appl. Sci. Res. 36, 313–332.Google Scholar
Atkinson, B., Brocklebank, M.P., Card, C.C.H. & Smith, J.M. 1969 Low Reynolds number developing flows. AIChE J. 15, 548–553.Google Scholar
Atkinson, B., Kemblowski, Z. & Smith, J.M. 1967 Measurements of velocity profile in developing liquid flows. AIChE J. 13, 17–20.Google Scholar
Berman, N.S. & Santos, V.A. 1969 Laminar velocity profiles in developing flows using a laser doppler technique. AIChE J. 15, 323–327.Google Scholar
Boussinesq, J. 1981 Calcul de la moindre longeur que doit avoir un tube circulaire, èvasè á son entrèe, pour qu'un règime sensiblement uniforme s'y ètablisse, et de la dèpense de charge qu'y entraine l’ètablissement de ce règime. Comptes Rendus 113, 49–51.Google Scholar
Campbell, W.D. & Slattery, J.C. 1963 Flow in the entrance region of a tube. Trans. ASME J. Basic Engng 85, 41–46.Google Scholar
Dombrowski, N., Foumeny, E.A., Ookawara, S. & Riza, A. 1993 The influence of Reynolds number on the entry length and pressure drop for laminar pipe flow. Can. J. Chem. Engng 71, 427–476.Google Scholar
Durst, F., Ray, S., Ünsal, B. & Bayoumi, O.A. 2005 The development lengths of laminar pipe and channel flows. J. Fluids Engng 127, 1154–1160.Google Scholar
Emery, A.F. & Chen, C.S. 1968 An experimental investigation of possible methods to reduce laminar entry lengths. Trans. ASME J. Basic Engng 90, 134–137.Google Scholar
Fargie, D. & Martin, B.W. 1971 Developing laminar flow in a pipe of circular cross-section. Proc. R. Soc. Lond. A 321, 461–476.Google Scholar
Friedmann, M., Gillis, J. & Liron, N. 1968 Laminar flow in a pipe at low and moderate Reynolds numbers. Appl. Sci. Res. 19, 426–438.Google Scholar
Gupta, R.C. 1977 Laminar flow in the entrance of a tube. Appl. Sci. Res. 33, 1–10.Google Scholar
Langhaar, H.L. 1942 Steady flow in the transition length of a straight tube. Trans. ASME J. Appl. Mech. 9, 55–58.Google Scholar
Lorenzini, G. & Saro, O. 1999 Finite element solution for velocity and temperature in developing laminar pipe flow. WIT Trans. Model. Sim. 21, 315–324.Google Scholar
Mohanty, A.K. & Asthana, S.B.L. 1978 Laminar flow in the entrance region of a smooth pipe. J. Fluid Mech. 90, 433–447.CrossRefGoogle Scholar
Nikuradse, J. 1950 Laws of flow in rough pipes. NASA Tech. Mem. 1292.Google Scholar
Pagliarini, G. 1989 Steady laminar heat transfer in the entry region of circular tubes with axial diffusion of heat and momentum. Intl J. Heat Mass Transfer 32, 1037–1052.Google Scholar
Pfenninger, W. 1952 Experiments with laminar flow in the inlet length of a tube at high Reynolds numbers with and without boundary-layer suction. Northrop Corporation, Norair Division Rep.Google Scholar
Reci, A., Sederman, A. & Gladden, L.F. 2018 Experimental evidence of velocity profile inversion in developing laminar flow using magnetic resonance velocimetry. J. Fluid Mech. 851, 547–557.Google Scholar
Reshotko, E. 1958 Experimental study of the stability of pipe flow. I. Development of an axially symmetric Poiseuille flow. Prog. Rep. 20-364. Jet Prop. Lab. California.Google Scholar
dos Santos, R.G. & Figueiredo, J.R. 2007 Laminar elliptic flow in the entrance region of tubes. J. Braz. Soc. Mech. Sci. Engng 29, 233–239.Google Scholar
Schiller, L. 1922 Die entwicklung der laminaren geschwindigkeitsverteilung. Z. Angew. Math. Mech. 2, 96–106.Google Scholar
Schlichting, H. 1969 Boundary-Layer Theory, 7th edn. McGraw-Hill.Google Scholar
Shapiro, A.H., Siegel, R. & Kline, S.J. 1954 Friction factor in the laminar entry length of a smooth tube. In Proc. 2nd U.S. National Congress Appl. Mech., pp. 733–741. ASME.Google Scholar
Smith, S.R. & Cui, Z.F. 2004 Analysis of developing laminar pipe flow – an application to gas slug enhanced hollow fibre ultrafiltration. Chem. Engng Sci. 59, 5975–5986.Google Scholar
Sparrow, E.M., Lin, S.H. & Lundgren, T.S. 1964 Flow development in the hydrodynamic entrance region of tubes and ducts. Phys. Fluids 7, 338–347.Google Scholar
Wagner, M.H. 1975 Developing flow in circular conduits: transition from plug flow to tube flow. J. Fluid Mech. 72, 257–268.Google Scholar
Wiginton, C.L. & Wendt, R.L. 1969 Flow in the entrance region of ducts. Phys. Fluids 12, 465–466.Google Scholar