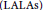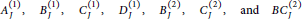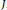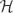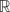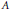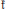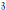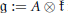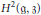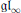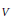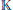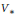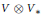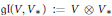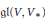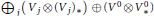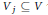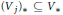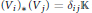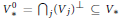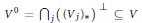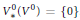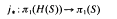The closest infinite-dimensional relatives of compact Lie algebras are Hilbert-Lie algebras, i.e., real Hilbert spaces with a Lie algebra structure for which the scalar product is invariant. Locally affine Lie algebras 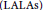 $\left( \text{LALAs} \right)$ correspond to double extensions of (twisted) loop algebras over simple Hilbert-Lie algebras
$\left( \text{LALAs} \right)$ correspond to double extensions of (twisted) loop algebras over simple Hilbert-Lie algebras  $\mathfrak{k}$, also called affinisations of
$\mathfrak{k}$, also called affinisations of  $\mathfrak{k}$. They possess a root space decomposition whose corresponding root system is a locally affine root system of one of the 7 families
$\mathfrak{k}$. They possess a root space decomposition whose corresponding root system is a locally affine root system of one of the 7 families
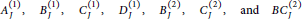 $$A_{J}^{\left( 1 \right)},\,B_{J}^{\left( 1 \right)},\,C_{J}^{\left( 1 \right)},\,D_{J}^{\left( 1 \right)},\,B_{J}^{\left( 2 \right)},\,C_{J}^{\left( 2 \right)},\,\,\text{and}\,BC_{J}^{\left( 2 \right)}$$
$$A_{J}^{\left( 1 \right)},\,B_{J}^{\left( 1 \right)},\,C_{J}^{\left( 1 \right)},\,D_{J}^{\left( 1 \right)},\,B_{J}^{\left( 2 \right)},\,C_{J}^{\left( 2 \right)},\,\,\text{and}\,BC_{J}^{\left( 2 \right)}$$
for some infinite set 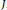 $J$. To each of these types corresponds a “minimal ” affinisation of some simple Hilbert-Lie algebra
$J$. To each of these types corresponds a “minimal ” affinisation of some simple Hilbert-Lie algebra  $\mathfrak{k}$, which we call standard.
$\mathfrak{k}$, which we call standard.
In this paper, we give for each affinisation  $\mathfrak{g}$ of a simple Hilbert-Lie algebra
$\mathfrak{g}$ of a simple Hilbert-Lie algebra  $\mathfrak{k}$ an explicit isomorphism from
$\mathfrak{k}$ an explicit isomorphism from  $\mathfrak{g}$ to one of the standard affinisations of
$\mathfrak{g}$ to one of the standard affinisations of  $\mathfrak{k}$. The existence of such an isomorphism could also be derived from the classiffication of locally affine root systems, but for representation theoretic purposes it is crucial to obtain it explicitly as a deformation between two twists that is compatible with the root decompositions. We illustrate this by applying our isomorphism theorem to the study of positive energy highest weight representations of
$\mathfrak{k}$. The existence of such an isomorphism could also be derived from the classiffication of locally affine root systems, but for representation theoretic purposes it is crucial to obtain it explicitly as a deformation between two twists that is compatible with the root decompositions. We illustrate this by applying our isomorphism theorem to the study of positive energy highest weight representations of  $\mathfrak{g}$. In subsequent work, this paper will be used to obtain a complete classification of the positive energy highest weight representations of affinisations of
$\mathfrak{g}$. In subsequent work, this paper will be used to obtain a complete classification of the positive energy highest weight representations of affinisations of  $\mathfrak{k}$.
$\mathfrak{k}$.
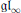 $\mathfrak{g}{{\mathfrak{l}}_{\infty }}$
$\mathfrak{g}{{\mathfrak{l}}_{\infty }}$