Hostname: page-component-76fb5796d-5g6vh Total loading time: 0 Render date: 2024-04-28T08:09:22.564Z Has data issue: false hasContentIssue false
  • English
  • Français

Bose-Einstein-type statistics, order statistics and planar random motions with three directions

Part of: Special processes Hyperbolic equations and systems Nonparametric inference Combinatorial probability

Published online by Cambridge University Press:  01 July 2016

S. Leorato  and
E. Orsingher
S. Leorato*
Affiliation:
University of Rome ‘La Sapienza'
E. Orsingher*
Affiliation:
University of Rome ‘La Sapienza'
*
∗ Postal address: Dipartimento di Statistica, Probabilità e Statistiche Applicate, University of Rome ‘La Sapienza’, Piazzale Aldo Moro, 5, 00185 Rome, Italy.
∗ Postal address: Dipartimento di Statistica, Probabilità e Statistiche Applicate, University of Rome ‘La Sapienza’, Piazzale Aldo Moro, 5, 00185 Rome, Italy.
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study different types of planar random motions (performed with constant velocity) with three directions, defined by the vectors dj = (cos(2πj/3), sin(2πj/3)) for j = 0, 1, 2, changing at Poisson-paced times. We examine the cyclic motion (where the change of direction is deterministic), the completely uniform motion (where at each Poisson event each direction can be taken with probability 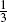) and the symmetrically deviating case (where the particle can choose all directions except that taken before the Poisson event). For each of the above random motions we derive the explicit distribution of the position of the particle, by using an approach based on order statistics. We prove that the densities obtained are solutions of the partial differential equations governing the processes. We are also able to give the explicit distributions on the boundary and, for the case of the symmetrically deviating motion, we can write it as the distribution of a telegraph process. For the symmetrically deviating motion we use a generalization of the Bose-Einstein statistics in order to determine the distribution of the triple (N0, N1, N2) (conditional on N(t) = k, with N0 + N1 + N2 = N(t) + 1, where N(t) is the number of Poisson events in [0, t]), where Nj denotes the number of times the direction dj (j = 0, 1, 2) is taken. Possible extensions to four directions or more are briefly considered.

Keywords

Bose-Einstein statisticsorder statisticsBessel functionbeta distributionmultinomial distributiontelegraph processplanar random motionhyperbolic equationgamma function

MSC classification

Primary: 60K99: None of the above, but in this section
Secondary: 62G30: Order statistics; empirical distribution functions 35L25: Higher-order hyperbolic equations 60C05: Combinatorial probability
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 36 , Issue 3 , September 2004 , pp. 937 - 970
Copyright
Copyright © Applied Probability Trust 2004 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beghin, L., Nieddu, L. and Orsingher, E. (2001). Probabilistic analysis of the telegrapher's process with drift by means of relativistic transformations. J. Appl. Math. Stoch. Anal. 14, 11–25.Google Scholar
Bizley, M. T. L. (1970). A generalization of Nanjundiah's identity. Amer. Math. Monthly 77, 863–865.CrossRefGoogle Scholar
David, H. A. and Nagaraja, H. N. (2003). Order Statistics, 3rd edn. John Wiley, Hoboken, NJ.CrossRefGoogle Scholar
Di Crescenzo, A. (2002). Exact transient analysis of a planar motion with three directions. Stoch. Stoch. Reports 72, 175–189.Google Scholar
Foong, S. K. (1997). Functional integration and wave propagation. In Functional Integration (Cargése, 1996; NATO Adv. Sci. Inst. Ser. B Phys. 361), Plenum, New York, pp. 97–130.CrossRefGoogle Scholar
Johnson, N. L. and Kotz, S. (1977). Urn Models and Their Application. John Wiley, New York.Google Scholar
Kolesnik, A. D. (1991). Markov equations of random evolutions. , University of Kiev (in Russian).Google Scholar
Kolesnik, A. D. and Orsingher, E. (2001). Analysis of a two-dimensional random walk with finite velocity and reflection. Teor. Veroyat. i Primen. 46, 138–147 (in Russian). English translation: Theory Prob. Appl. 46 (2002), 132–140.Google Scholar
Leorato, S., Orsingher, E. and Scavino, M. (2003). An alternating motion with stops and the related planar, cyclic motion with four directions. Adv. Appl. Prob. 35, 1153–1168.CrossRefGoogle Scholar
Orsingher, E. (2000). Exact joint distribution in a model of planar random motion. Stoch. Stoch. Reports 69, 1–10.Google Scholar
Orsingher, E. (2002). Bessel functions of third order and the distribution of cyclic planar motions with three directions. Stoch. Stoch. Reports 74, 617–631.Google Scholar
Orsingher, E. and Ratanov, N. (2002). Planar random motions with drift. J. Appl. Math. Stoch. Anal. 15, 205–221.Google Scholar
Orsingher, E. and San Martini, A. (1995). Planar random evolution with three directions. In Exploring Stochastic Laws, VSP, Utrecht, pp. 357–366.Google Scholar
Pinsky, M. A. (1991). Lectures on Random Evolution. World Scientific, River Edge, NJ.CrossRefGoogle Scholar
Samoilenko, I. V. (2001a). Analytical theory of Markov random evolutions in ℝn . , University of Kiev (in Russian).Google Scholar
Samoilenko, I. V. (2001b). Markovian random evolution in ℝn . Random Operators Stoch. Equat. 9, 139–160.Google Scholar