Published online by Cambridge University Press: 01 August 2014
In this paper problems of social choice in general, and political choice in particular, are considered in light of uncertainty. The space of social alternatives in this formulation includes not only pure social states, but lotteries or probability distributions over those states as well. In the context of candidate strategy selection in a spatial model of political choice, candidate strategy sets are represented by pure strategies—points in the space of alternatives—and ambiguous strategies—lotteries over those points. Questions about optimal strategy choice and the equilibrium properties of these choices are then entertained. Duncan Black's theorem about the dominance of the median preference is generalized, and further contingencies in which the theorem is false are specified. The substantive foci of these results are: (1) the conditions in which seekers of political office will rationally choose to appear equivocal in their policy intentions; and (2) the role of institutional structure in defining equilibrium.
Several closely related papers including the one presented here have benefitted from close readings and careful criticism by a number of people. For their efforts I acknowledge and thank Richard Niemi, Alvin Rabushka, William Riker, John Sprague, and Herbert Weisberg, as well as the anonymous referees of this paper. A Washington University Faculty Summer Research Grant provided time to prepare and revise various drafts of this paper.
1 Biddle, Nicholas, Correspondenc, McGrane, R. C., ed. (Boston:Houghton, Mifflin, 1919), p. 256 Google Scholar. Cited in Schlesinger, Arthur M. Jr., The Age of Jackson (Boston: Little, Brown, 1945), p. 211 Google Scholar. I thank Professor Robert Lineberry for bringing this citation to my attention.
2 For example, William Leuchtenberg reports the following remarks by a Harding advisor during the 1920 presidential campaign: “From his deathbed, Boies Penrose the Pennsylvania machine politician advised: ‘Keep Warren at home. Don't let him make speeches. If he goes out on tour somebody's sure to ask him questions, and Warren's just the sort of damned fool that will try to answer them.’” Leuchtenberg, William E., The Perils of Prosperity, 1914–1932 (Chicago: University of Chicago Press, 1958), p. 88 Google Scholar. I thank Risé S. Shepsle for this citation.
3 Sartori, Giovanni, Democratic Theory (Detroit: Wayne State University Press 1962), p. 207 (emphasis added)Google Scholar.
4 Herring, Pendleton, The Politics of Democracy: American Parties in Action, 2nd ed. (New York: Norton, 1965), p. 188 Google Scholar.
5 Key, V. O. Jr., Public Opinion and American Democracy (New York: Knopf, 1961), p. 424 Google Scholar.
6 Key, V. O. Jr., Politics, Parties and Pressure Groups, 4th ed. (New York: Crowell, 1958), p. 241 Google Scholar.
7 Downs, Anthony, An Economic Theory of Democracy (New York: Harper & Row, 1957), p. 136 Google Scholar.
8 Downs, p. 136.
9 For an effort to explicate the role of ambiguity in the context of administrative decision making, a paper recently brought to my attention is Wolpert's, Julian “Consequences of Inadvertent and Purposeful Ambiguity in Locational Strategies,” presented at the 65th Annual Meeting of the American Political Science Association, New York 1969 Google Scholar.
10 Three monographs provide a sampling of this literature. See Borch, Karl Henrik, The Economics of Uncertainty (Princeton: Princeton University Press, 1968)Google Scholar; Raiffa, Howard, Decision Analysis (Reading, Mass.: Addison-Wesley, 1968)Google ScholarPubMed; and Arrow, Kenneth J., Essays on the Theory of Risk-Bearing (Chicago: Markham, 1971)Google Scholar.
11 The importance of these inquiries is suggested in a passage from a paper by Arrow:
There is no need to enlarge upon the importance of a realistic theory explaining how individuals choose among alternate courses of action when the consequences of their actions are incompletely known to them. It is no exaggeration to say that every choice made by human beings would meet this description if attention were paid to the ultimate implications. Risk and the human reactions to it have been called upon to explain everything from the purchase of chances in a “numbers” game to the capitalist structure of our economy; according to Professor Frank Knight, even human consciousness itself would disappear in the absence of uncertainty.
See Arrow, Kenneth J., “Alternative Approaches to the Theory of Choice in Risk-Taking Situations,” Econometrica, 19 (10 1951), 404 CrossRefGoogle Scholar. Also see Knight, Frank H., Risk, Uncertainty, and Profit (New York: Houghton-Mifflin, 1921)Google Scholar.
12 This statement needs some qualification if the specialized literature in the field of constitutional choice—essentially the social choice of a social decision process under conditions of uncertainty—is included. See, for example, Buchanan, James M. and Tullock, Gordon, The Calculus of Consent (Ann Arbor: University of Michigan Press, 1962)CrossRefGoogle Scholar; and Rae, Douglas W., “Decision Rules and Individual Values in Constitutional Choice,” American Political Science Review, 63 (03 1969), 40–56 CrossRefGoogle Scholar.
13 If alternatives A and B are on the agenda, then each citizen either prefers A to B, B to A, or is indifferent between them.
14 Whereas connectivity is a dyadic property, transitivity imposes constraints on triads of alternatives. Thus, for the dyad (A, B), if a citizen prefers A to B or is indifferent; if, for the dyad (B, C), he prefers B to C or is indifferent; then it cannot be the case that he prefers C to A when the dyad (A, C) is offered. That is, for (A, B, C), A ≥ B and B ≥ C → ∼ (C > A), where ≥ is the symbol for preference or indifference.
15 Downs, , Economic Theory of Democracy, p. 30 Google Scholar.
16 Downs, p. 28.
17 Stokes, Donald E., “Spatial Models of Party Competition,” American Political Science Review, 57 (06 1963), 368–377 (quoted at p. 368)CrossRefGoogle Scholar.
18 However, one is not required to suppose this dimension is ideological in nature, as Downs does. The prospects for relaxing this assumption are extremely good, as has been indicated by the multidimensional generalizations of Downs in the research of scholars at Carnegie-Mellon University. For a summary of this work, see Davis, Otto, Hinich, Melvin, and Ordeshook, Peter, “An Expository Development of a Mathematical Model of the Electoral Process,” American Political Science Review, 64 (06 1970), 426–448 CrossRefGoogle Scholar; and Hinich, Melvin, Ledyard, John, and Ordeshook, Peter, “A Theory of Electoral Equilibrium: A Spatial Analysis Based on the Theory of Games” (Carnegie-Mellon University, 1971, unpublished manuscript)Google Scholar.
19 In fact, it may be shown that the competitive situation in an unbounded space may be transformed to a bounded space with no effect on strategic considerations. See Shepsle, Kenneth A., Essays on Risky Choice in Electoral Competition (unpublished doctoral dissertation, University of Rochester, 1970)Google Scholar, Chap. 4. Also see Samberg, Robert G., “Collective Decision-Making in a Bounded Prospect Space,” a paper delivered at the Sixty-sixth Annual Meeting of the American Political Science Association, Los Angeles, 1970 Google Scholar.
20 For early discussion of the single-peakedness concept, see Black, Duncan, The Theory of Committees and Elections (Cambridge: Cambridge University Press, 1958)Google Scholar. For a generalization of single-peakedness, see Sen, Amartya, “A Possibility Theorem on Majority Decisions,” Econometrica, 34 (04 1966), 491–499 CrossRefGoogle Scholar.
21 The term is adapted from Ward, Benjamin, “Majority Voting and Alternative Forms of Public Enterprise,” in Margolis, Julius, ed., The Public Economy of Urban Communities (Baltimore: The Johns Hopkins University Press, 1965), pp. 112–126 Google Scholar.
22 For an examination of the dynamics of building a majority coalition, and a less “mechanistic” treatment of the voter, see Brams, Steven, “Positive Coalition Theory: The Relationship Between Postulated Goals and Derived Behavior,” in Cotter, Cornelius P. et al., eds., Political Science Annual: Conflict, Competition, and Coalitions, IV (Indianapolis: Bobbs-Merrill, 1972)Google Scholar, forthcoming. “Sophisticated voting” as treated in Farquharson, Robin, Theory of Voting (New Haven: Yale University Press, 1969)Google Scholar is also not considered here. Voters consult only their own preference schedules in making their voting choice. They do not engage in speculation or calculation about the behavior of other voters. In the context of two-candidate elections (which is all we consider in this paper), with single-peaked preference functions and universal participation (A.5), “sophisticated voting” is not crucial. For electoral contingencies in which it is important, see, in addition to Farquharson, , Kramer, Gerald H., “Sophisticated Voting Over Multidimensional Choice Spaces,” a paper delivered at the Meetings of the Public Choice Society, Blacksburg, Virginia, 1971 Google Scholar.
23 Garvey, Gerald, “The Theory of Party Equilibrium,” American Political Science Review, 60 (03 1966), 29–38 CrossRefGoogle Scholar; Hinich, Melvin and Ordeshook, Peter, “Abstentions and Equilibrium in the Electoral Process,” Public Choice, 7 (Fall 1969), 81–106 CrossRefGoogle Scholar; Kramer, Gerald H., “A Decision-Theoretic Analysis of a Problem in Political Campaigning,” in Bernd, Joseph L., ed., Mathematical Applications in Political Science, II (Dallas: Southern Methodist University Press, 1966), pp. 137–160 Google Scholar.
24 We do not need to be more explicit in stating this assumption since, in the remainder of this paper, we shall be concerned only with winning strategies—those strategies that are “dominant” in a sense to be specified below.
25
Decision theories ordinarily distinguish among contingencies of certainty, risk, and uncertainty. In the case of certainty, each action or choice is known to lead to a specific (set of) outcome(s). In contingencies of risk, each action is probabilistically related to outcomes in the sense that action ai, results in outcome oj with probability pij. Thus, for the set of outcomes O = {o1, o2, …, on}, the ith action or choice is a lottery ticket: ai = ( pi1 o1, pi2 o2, …, Pin on), where the usual probability constraints on the Pi's apply. In the case of uncertainty, each action is probabilistically related to outcomes, but the nature of the relationship depends on an unknown parameter θ, labeled “the state of nature.” Thus, a1 = ![]() o1,
o1, ![]() o2, …,
o2, …, ![]() on). We have argued elsewhere that the three-part distinction above is, for our purposes, somewhat artificial, and that we may conceive of all contingencies as falling under the rubric of risk—a known probability distribution over outcomes. We shall, however, often use the common parlance, referring (somewhat confusingly, we admit) to uncertainty. Let us reiterate that we shall always mean risk. See
Shepsle, Kenneth A., “Parties, Voters, and the Risk Environment: A Mathematical Treatment of Electoral Competition Under Uncertainty,” in Probability Models of Collective Decision-Making, Niemi, Richard G. and Weisberg, Herbert F., eds. (Columbus: Charles E. Merrill), forthcomingGoogle Scholar.
on). We have argued elsewhere that the three-part distinction above is, for our purposes, somewhat artificial, and that we may conceive of all contingencies as falling under the rubric of risk—a known probability distribution over outcomes. We shall, however, often use the common parlance, referring (somewhat confusingly, we admit) to uncertainty. Let us reiterate that we shall always mean risk. See
Shepsle, Kenneth A., “Parties, Voters, and the Risk Environment: A Mathematical Treatment of Electoral Competition Under Uncertainty,” in Probability Models of Collective Decision-Making, Niemi, Richard G. and Weisberg, Herbert F., eds. (Columbus: Charles E. Merrill), forthcomingGoogle Scholar.
26 Schoenberger, Robert, “Campaign Strategy and Party Loyalty: The Electoral Relevance of Candidate Decision-Making in the 1964 Congressional Elections,” American Political Science Review, 63 (06 1969), 515–520 (quotation at pp. 519–520)CrossRefGoogle Scholar.
27 In fact, throughout this essay we refer to competition among candidates rather than teams of activists.
28 It should be noted here that, by virtue of A.4 and A.5, voters do not concern themselves, in a strategic fashion, with the effect of their vote on the aggregate outcome. Rather they treat the voting decision as one of individual decision making, maximizing expected utility. Thus, the voter's information about the intentions of other voters (an additional source of uncertainty) is not germane in this model. For an initial examination of the voting decision in contingencies of strategic interaction among voters, see Riker, William H. and Ordeshook, Peter C., “A Theory of the Calculus of Voting,” American Political Science Review, 62 (03 1968), 25–42 CrossRefGoogle Scholar.
29 This is analogous to the assumption of free entry and exit in economic models. For an interesting point of view on this assumption, see Hirschman, Albert O., Exit, Voice and Loyalty: Responses to Decline in Firms, Organizations, and States (Cambridge: Harvard University Press, 1970)Google Scholar.
30 More recently efforts have been made to deal with this question in a more systematic fashion. See Peter Aranson and Peter Ordeshook, “Spatial Strategies for Sequential Elections,” in Niemi and Weisberg, Probability Models; James S. Coleman, “The Positions of Political Parties in Elections.” in Niemi and Weisberg; Otto A. Davis and Melvin J. Hinich, “Spatial Competition Under Constrained Choice,” in Niemi and Weisberg.
31 That image, however, may be (instantaneously) altered by a dramatic act, e.g., a halt in the bombing of North Viet Nam in 1968.
32 Stokes, “Spatial Models.”
33 Quite obviously, C.1 and C.2 are somewhat arbitrary. Moreover, in an historically dynamic world the ability of incumbents to appear equivocal renders C.1 overly restrictive. Attempts to relax them are given in Shepsle, Essays …, Chap. 3. For the purposes of this essay, however, they provide a well-specified electoral contingency suitable for analysis.
34 Down's reliance on the distribution of most-preferred points in the electorate, and not on the functional form of utility schedules, prevented him from correctly specifying the possibilities of a strategy of ambiguity. For an early treatment of the importance of utility function form in decision making under risk and uncertainty, as well as some fascinating economic applications, see the classic paper by Friedman, Milton and Savage, L. J., “The Utility Analysis of Choices Involving Risk,” Journal of Political Economy, 56 (1948), 279–304 CrossRefGoogle Scholar.
35 The expectation of a gamble p(x), p̄, is the expected value (not to be confused with the expected utility) of that gamble: p̄ = ∑ xp(x) for discrete probability distributions and p̄ = ∫ xp(x)dx for continuous distributions. In the example above y is the expectation of (½ x, ½ z) by construction, i.e., it is the midpoint of [x, z]. The three voter types may be defined mathematically:
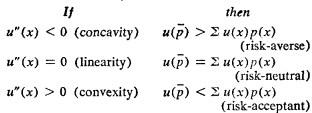
36 For further results see Kenneth A. Shepsle, “Parties, Voters, and the Risk Environment,” passim.
37 Two other arrangements are possible in twoparty competition. The first, in which two incumbents face each other (by virtue, say, of redistricting so that two elected officials, formerly representing distinct constituencies, now must compete with each other to represent a single constituency), is simply the original Downsian model in which constraint C.1 applies to both candidates. The second, in which two challengers face each other, is somewhat more complex. In this case, which might occur when an incumbent does not seek re-election or fails to obtain his party's nomination, and when his replacement is not considered his hand-picked successor, both candidates are governed by constraint C.2. This case is treated briefly in Shepsle, “Parties …” In a future paper, I expect to examine this case in greater detail.
38 The nonuniqueness of winning strategies poses no theoretical problems. The candidate simply chooses from among those strategies the one which maximizes votes (A.6). If two or more winning strategies are vote-maximizing, then any arbitrary standard may be employed for final selection. The question of mathematical existence, however, raises interesting theoretical possibilities to be explored below. Several observations are appropriate here. First, it is obvious that both candidates cannot possess winning strategies. Otherwise some majority would have to prefer x*εS I (the incumbent's alleged winning strategy), to all y εS II, on the one hand, while some other majority prefers y*εS II (the challenger's alleged winning strategy) to all x εS I, on the other. But this condition is contradictory, since any two majorities contain at least one person in common. Second, it is possible that neither candidate possesses a winning strategy. In this case, as in two-person zero-sum games without pure strategy saddle points, a problem in conjectural variation arises. Although there are optimal mixed strategies (technically, ε- optimal since this is an infinite game), this will not be our concern. In this essay the concern is the set of conditions under which winning strategies exist. In the last section of the paper the “non-existence problem” is addressed. There the relationship between winning strategies and electoral equilibrium is considered. On the relationship between spatial models and the theory of infinite games, the reader may consult Shepsle, Essays …, Chap. 4; and Hinich, Ledyard, and Ordeshook, “A Theory of Electoral Equilibrium.” For an examination of social choice situations with ambiguous alternatives in which no winning strategy exists, see Zeckhauser, Richard, “Majority Rule with Lotteries on Alternatives,” Quarterly Journal of Economics, 83 (11 1969), 696–703 CrossRefGoogle Scholar; and Shepsle, Kenneth A., “Uncertainty and Electoral Competition: The Search for Equilibria,” a paper presented at the Mathematical Collective Decisions Seminar, Hilton Head Island, South Carolina, 08, 1971 Google Scholar.
39 This result is discussed in Black, , The Theory of Committees and Elections, pp. 14–18 Google Scholar. This discussion parallels that of Downs, Economic Theory of Democracy, Chap. 8.
40 For technical definitions, see Pratt, John W., Raiffa, Howard, and Schlaifer, Robert, “The Foundations of Decision Under Uncertainty: An Elementary Exposition,” Journal of the American Statistics Association, 59 (1964), 353–375 CrossRefGoogle Scholar.
41 What is required here is a serious discussion of the “units problem.” This problem is usually avoided in the spatial modeling literature, but when the shape of preference functions is under consideration, it is particularly important to have the units of the strategy space specified. See Shepsle, “Uncertainty and Electoral Competition.”
42 For a mathematical definition of intensity based on reactions to risk, see Rabushka, Alvin and Shepsle, Kenneth A., Politics in Plural Societies: A Theory of Democratic Instability (Columbus: Charles E. Merrill, 1972), Chap. 2Google Scholar.
43 As well, we may now assess the probable success of campaign rhetoric that encourages the electorate to resist changing horses in midstream: it is successful when voters are not risk-acceptant on the issue in question.
44 On the importance of commitment in more general strategic situations, see Schelling, Thomas C., The Strategy of Conflict (New York: Oxford University Press, 1963)Google Scholar, passim.
45 Davis, Otto A. and Hinich, Melvin J., “A Mathematical Model of Policy Formation in a Democratic Society,” in Mathematical Applications … Bernd, J., ed., Vol. II, pp. 175–208 Google Scholar; “Some Results Related to a Mathematical Model of Policy Formation in a Democratic Society,” in Bernd, , Vol. III, pp. 14–38 Google Scholar; “On the Power and Importance of the Mean Preference in a Mathematical Model of Democratic Choice,” Public Choice, 5 (Fall 1968), 59–72 CrossRefGoogle Scholar.
46 See Kenneth A. Shepsle, “Intensity, Salience, and the Risk Environment: Some Theoretical Aspects of Conflict in the Plural Society,” a paper presented at the Conference on Theories of Collective Behavior, Fels Center of Government, University of Pennsylvania, December, 1970. For an empirical application of this notion of intensity, see Rabushka and Shepsle, Politics in Plural Societies.
47 Note that the median-defeating strategies p(x)εS II need not be unique. This lack of uniqueness, however, is inconsequential for our argument.
48 Since x med εS II, strategy x* is not threatened by it, so that we do not technically have a contingency of collective intransitivity. But a median-defeating strategy p*(x)εS II can be found, distributed entirely in an interval of length ε about x med, for arbitrarily small ε. It may then be shown that p*(x) defeats x*. If this p*(x) is invulnerable, then a collective intransitivity is averted. However, if for any median-defeating strategy in SII there is an x* which in turn defeats it, then a nonequilibrium situation is insured. It is of theoretical interest to specify the conditions under which these events transpire. Our intentions in what follows are more modest and these fundamental theoretical issues are left as open questions.
49 Zeckhauser, “Majority Rule.”
50 Elsewhere I have examined Zeckhauser's Theorem for electoral profiles with nonsingle peaked preferences, proving that equilibrium situations in these contingencies may exist. See Shepsle, Kenneth A., “A Note on Zeckhauser's ‘Majority Rule with Lotteries on Alternatives’: The Case of the Paradox of Voting,” Quarterly Journal of Economics, 84 (11 1970), 705–710 CrossRefGoogle Scholar; and “The Paradox of Voting and Uncertainty,” in Niemi and Weisberg, forthcoming.
51 See footnote 48.
52 See Kemeny, John G., Snell, J. Laurie, and Thompson, Gerald L., Introduction to Finite Mathematics, 2nd ed. (New York: Prentice-Hall, 1966), p. 82 Google Scholar.
53 In particular, see Shepsle, “Uncertainty and Electoral Competition …”
54 See Downs, Economic Theory of Democracy, Chap. 8, and Davis, Hinich, and Ordeshook, “An Expository Development of a Mathematical Model of the Electoral Process.”
55 Downs, p. 136.
56 In “Parties, Voters, and the Risk Environment …,” I conjectured that under the conditions of Theorem 3 there does exist a winning strategy in the challenger's strategy set. However, the more recent generalized version of Zeckhauser's Theorem makes that conjecture questionable, or at least incompletely specified. For a recent rather general mathematical treatment of the question of social choice under conditions of uncertainty, see Fishburn, Peter, “Lotteries and Social Choice,” a paper presented at the Mathematical Collective Decisions Seminar, Hilton Head Island, South Carolina, 08, 1971 Google Scholar.
57 For an interesting essay that deals with candidate uncertainty about the parameters of the voter distribution and the effect of this on the decision to allocate resources for information collection, see Gilbert, Jane, “Who Gets Information, Where, and When” (University of Rochester, 1970, unpublished manuscript)Google Scholar.
Comments
No Comments have been published for this article.