No CrossRef data available.
Article contents
A COMPACT QUALITATIVE UNCERTAINTY PRINCIPLE FOR SOME NONUNIMODULAR GROUPS
Published online by Cambridge University Press: 28 November 2018
Abstract
Let 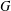 $G$ be a separable locally compact group with type
$G$ be a separable locally compact group with type 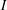 $I$ left regular representation,
$I$ left regular representation, 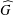 $\widehat{G}$ its dual,
$\widehat{G}$ its dual, 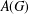 $A(G)$ its Fourier algebra and
$A(G)$ its Fourier algebra and 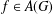 $f\in A(G)$ with compact support. If
$f\in A(G)$ with compact support. If 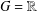 $G=\mathbb{R}$ and the Fourier transform of
$G=\mathbb{R}$ and the Fourier transform of 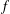 $f$ is compactly supported, then, by a classical Paley–Wiener theorem,
$f$ is compactly supported, then, by a classical Paley–Wiener theorem, 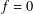 $f=0$. There are extensions of this theorem for abelian and some unimodular groups. In this paper, we prove that if
$f=0$. There are extensions of this theorem for abelian and some unimodular groups. In this paper, we prove that if 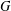 $G$ has no (nonempty) open compact subsets,
$G$ has no (nonempty) open compact subsets, 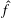 $\hat{f}$, the regularised Fourier cotransform of
$\hat{f}$, the regularised Fourier cotransform of 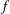 $f$, is compactly supported and
$f$, is compactly supported and 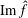 $\text{Im}\,\hat{f}$ is finite dimensional, then
$\text{Im}\,\hat{f}$ is finite dimensional, then 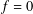 $f=0$. In connection with this result, we characterise locally compact abelian groups whose identity components are noncompact.
$f=0$. In connection with this result, we characterise locally compact abelian groups whose identity components are noncompact.
Keywords
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 99 , Issue 1 , February 2019 , pp. 114 - 120
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © 2018 Australian Mathematical Publishing Association Inc.
Footnotes
This project has been funded with support from the Lebanese University.

