Article contents
Representing Multipliers of the Fourier Algebra on Non-Commutative Lp Spaces
Published online by Cambridge University Press: 20 November 2018
Abstract
We show that the multiplier algebra of the Fourier algebra on a locally compact group  $G$ can be isometrically represented on a direct sum on non-commutative
$G$ can be isometrically represented on a direct sum on non-commutative 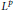 ${{L}^{p}}$ spaces associated with the right von Neumann algebra of
${{L}^{p}}$ spaces associated with the right von Neumann algebra of  $G$. The resulting image is the idealiser of the image of the Fourier algebra. If these spaces are given their canonical operator space structure, then we get a completely isometric representation of the completely bounded multiplier algebra. We make a careful study of the noncommutative
$G$. The resulting image is the idealiser of the image of the Fourier algebra. If these spaces are given their canonical operator space structure, then we get a completely isometric representation of the completely bounded multiplier algebra. We make a careful study of the noncommutative 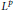 ${{L}^{p}}$ spaces we construct and show that they are completely isometric to those considered recently by Forrest, Lee, and Samei. We improve a result of theirs about module homomorphisms. We suggest a definition of a Figa-Talamanca–Herz algebra built out of these non-commutative
${{L}^{p}}$ spaces we construct and show that they are completely isometric to those considered recently by Forrest, Lee, and Samei. We improve a result of theirs about module homomorphisms. We suggest a definition of a Figa-Talamanca–Herz algebra built out of these non-commutative 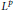 ${{L}^{p}}$ spaces, say
${{L}^{p}}$ spaces, say 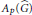 ${{A}_{p}}(\hat{G})$. It is shown that
${{A}_{p}}(\hat{G})$. It is shown that 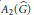 ${{A}_{2}}(\hat{G})$ is isometric to
${{A}_{2}}(\hat{G})$ is isometric to 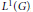 ${{L}^{1}}(G)$, generalising the abelian situation.
${{L}^{1}}(G)$, generalising the abelian situation.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2011
References
- 5
- Cited by


