Hostname: page-component-6766d58669-tq7bh Total loading time: 0 Render date: 2026-05-15T23:23:49.364Z Has data issue: false hasContentIssue false
  • English
  • Français

A Short Note on the Continuous Rokhlin Property and the Universal Coefficient Theorem in E-theory

Published online by Cambridge University Press:  20 November 2018

Gábor Szabó
Gábor Szabó*
Affiliation:
Westfälische Wilhelms-Universität, Fachbereich Mathematik, Einsteinstrasse 62, 48149 Münster, Germany. e-mail: gabor.szabo@uni-muenster.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the 'Save PDF' action button.

Let 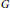$G$ be a metrizable compact group, 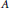$A$ a separable 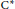${{\text{C}}^{*}}$ -algebra, and 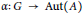$\alpha :G\,\to \,\text{Aut}\left( A \right)$ a strongly continuous action. Provided that $\alpha $ satisfies the continuous Rokhlin property, we show that the property of satisfying the 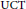$\text{UCT}$ in $E$ -theory passes from 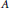$A$ to the crossed product 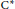${{\text{C}}^{*}}$ -algebra 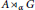$\mathcal{A}{{\rtimes }_{\alpha }}\,G$ and the fixed point algebra 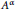${{A}^{\alpha }}$ . This extends a similar result by Gardella for 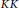$KK$ -theory in the case of unital 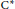${{\text{C}}^{*}}$ -algebras but with a shorter and less technical proof. For circle actions on separable unital 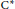${{\text{C}}^{*}}$ -algebras with the continuous Rokhlin property, we establish a connection between the $E$ -theory equivalence class of 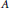$A$ and that of its fixed point algebra 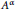${{A}^{\alpha }}$ .

Keywords

46L5519K35Rokhlin propertyUCTKK-theoryE-theorycircle actions

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 2 , 01 June 2015 , pp. 374 - 380
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Blackadar, B., K-theory for Operator Algebras. Second éd., Mathematical Sciences Research Institute Publications, 5, Cambridge University Press, Cambridge, 1998.Google Scholar
[2] Pack, T. and Maréchal, O., Sur la classification des symétries des C*-algebres UHF. Canad. J. Math. 31 (1979), no. 3, pp. 496–523. http://dx.doi.org/10.4153/CJM-1979-055-7 Google Scholar
[3] Gardella, E., Classification theorems for circle actions on Kirchberg algebras. I. arxiv:1405.2469Google Scholar
[4] Gardella, E., Classification theorems for circle actions on Kirchberg algebras. IL arxiv:1406.1208Google Scholar
[5] Guentner, E., Higson, N., and Trout, J., Equivariant E-theory for C* -algebras. Mem. Amer. Math. Soc. 148 (2000), no. 703.Google Scholar
[6] Herman, R. H. and R.|Jones, V. F., Period two automorphisms of UHF C*-algebras. J. Funct. Anal. 45 (1982), no. 2, 169–176. http://dx.doi.Org/10.1016/0022-1236(82)90016-7 Google Scholar
[7] Herman, R. H. and Jones, V. F. R., Models of finite group actions. Math. Scand. 52 (1983), no. 2, 312–320.Google Scholar
[8] Hirshberg, I. and Winter, W., Rokhlin actions and self-absorbing C* -algebras. Pacific J. Math. 233 (2007), no. 1, 125–143. http://dx.doi.org/10.2140/pjm.2007.233.125 Google Scholar
[9] Izumi, M., Finite group actions on C* -algebras with the Rohlin property. I. Duke Math. J. 122 (2004), no. 2, 233–280. http://dx.doi.org/10.1215/S0012-7094-04-12221-3 Google Scholar
[10] Izumi, M., Finite group actions on C*-algebras with the Rohlin property. II. Adv. Math. 184 (2004), no. 1, 119–160. http://dx.doi.org/10.1016/S0001-8708(03)00140-3 Google Scholar
[11] Kirchberg, E., Central sequences in C*-algebras and strongly purely infinite algebras. In: Operator algebras: The Abel Symposium 2004, Abel Symp,.l, Springer, Berlin, 2006, pp. 175–231.Google Scholar
[12] Nawata, N., Finite group actions on certain stably projectionless C*-algebras with the Rohlin property. Trans. Amer. Math. Soc, to appear. arxiv:1308.0429Google Scholar
[13] Santiago, L., Crossed products by actions of finite groups with the Rokhlin property.arxiv:1401.6852Google Scholar
[14] Skandalis, G., Le bifoncteur de Kasparov n'est pas exact. C. R. Acad. Sci. Paris Sér I Math. 313 (1991), no. 13, 939–941.Google Scholar