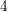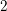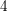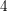1 Introduction
Let
![]() $F$
be a field and
$F$
be a field and
![]() $\overline{F}$
a separable closure of
$\overline{F}$
a separable closure of
![]() $F$
. The absolute Galois group of
$F$
. The absolute Galois group of
![]() $F$
, denoted
$F$
, denoted
![]() $G_{F}:=\operatorname{Gal}(\overline{F}/F)$
is an object of great interest in algebra and number theory. Many aspects of modern Galois theory, in one way or another, aim to understand the structural properties of
$G_{F}:=\operatorname{Gal}(\overline{F}/F)$
is an object of great interest in algebra and number theory. Many aspects of modern Galois theory, in one way or another, aim to understand the structural properties of
![]() $G_{F}$
. Recent major results in Galois cohomology show that such absolute Galois groups are extremely rare among all profinite groups. The most notable restriction on absolute Galois groups arises from the Bloch–Kato conjecture, which is now a theorem due to Rost and Voevodsky; see [Reference VoevodskyVoe11, Reference RostRos98, Reference Suslin and JoukhovitskiSJ06, Reference Haesemeyer and WeibelHW09, Reference WeibelWei09]. In particular, if
$G_{F}$
. Recent major results in Galois cohomology show that such absolute Galois groups are extremely rare among all profinite groups. The most notable restriction on absolute Galois groups arises from the Bloch–Kato conjecture, which is now a theorem due to Rost and Voevodsky; see [Reference VoevodskyVoe11, Reference RostRos98, Reference Suslin and JoukhovitskiSJ06, Reference Haesemeyer and WeibelHW09, Reference WeibelWei09]. In particular, if
![]() $F$
contains a primitive
$F$
contains a primitive
![]() $p$
th root of unity, then
$p$
th root of unity, then
![]() $\operatorname{H}^{\ast }(G_{F},\mathbb{Z}/p)$
is a quadratic algebra. More explicitly, this means that
$\operatorname{H}^{\ast }(G_{F},\mathbb{Z}/p)$
is a quadratic algebra. More explicitly, this means that
![]() $\operatorname{H}^{\ast }(G_{F},\mathbb{Z}/p)$
is generated by elements of
$\operatorname{H}^{\ast }(G_{F},\mathbb{Z}/p)$
is generated by elements of
![]() $\operatorname{H}^{1}(G_{F},\mathbb{Z}/p)$
, and the relations are generated only by those relations appearing in degree
$\operatorname{H}^{1}(G_{F},\mathbb{Z}/p)$
, and the relations are generated only by those relations appearing in degree
![]() $2$
. This is a very strong restriction on the group-theoretical structure of
$2$
. This is a very strong restriction on the group-theoretical structure of
![]() $G_{F}$
. Recently, other explicit structural restrictions on absolute Galois groups started to arise, based on the notion of Massey products in the context of Galois cohomology.
$G_{F}$
. Recently, other explicit structural restrictions on absolute Galois groups started to arise, based on the notion of Massey products in the context of Galois cohomology.
We will recall the definition of Massey products below, but we briefly note that, given
![]() $x_{1},\ldots ,x_{n}\in \operatorname{H}^{1}(G_{F},\mathbb{Z}/p)$
where
$x_{1},\ldots ,x_{n}\in \operatorname{H}^{1}(G_{F},\mathbb{Z}/p)$
where
![]() $p$
is a prime, the
$p$
is a prime, the
![]() $n$
-Massey product, denoted
$n$
-Massey product, denoted
![]() $\langle x_{1},\ldots ,x_{n}\rangle$
, is a (possibly empty) subset of
$\langle x_{1},\ldots ,x_{n}\rangle$
, is a (possibly empty) subset of
![]() $\operatorname{H}^{2}(G_{F},\mathbb{Z}/p)$
. In the case
$\operatorname{H}^{2}(G_{F},\mathbb{Z}/p)$
. In the case
![]() $n=2$
, one has a simple description in terms of the cup-product as
$n=2$
, one has a simple description in terms of the cup-product as
![]() $\langle x_{1},x_{2}\rangle =\{x_{1}\cup x_{2}\}$
. Just as the cup-product
$\langle x_{1},x_{2}\rangle =\{x_{1}\cup x_{2}\}$
. Just as the cup-product
![]() $x_{1}\cup x_{2}$
provides an obstruction to the existence of Heisenberg extensions of
$x_{1}\cup x_{2}$
provides an obstruction to the existence of Heisenberg extensions of
![]() $F$
(of degree
$F$
(of degree
![]() $p^{3}$
), the
$p^{3}$
), the
![]() $n$
-Massey product provides as obstruction for the existence of higher
$n$
-Massey product provides as obstruction for the existence of higher
![]() $\mathbb{Z}/p$
-unipotent extensions. In this respect, we are primarily interested in situations where the
$\mathbb{Z}/p$
-unipotent extensions. In this respect, we are primarily interested in situations where the
![]() $n$
-Massey product
$n$
-Massey product
![]() $\langle x_{1},\ldots ,x_{n}\rangle$
contains
$\langle x_{1},\ldots ,x_{n}\rangle$
contains
![]() $0$
. In this article, when
$0$
. In this article, when
![]() $\langle x_{1},\ldots ,x_{n}\rangle$
contains
$\langle x_{1},\ldots ,x_{n}\rangle$
contains
![]() $0$
, we will simply say that ‘
$0$
, we will simply say that ‘
![]() $\langle x_{1},\ldots ,x_{n}\rangle$
vanishes.’
$\langle x_{1},\ldots ,x_{n}\rangle$
vanishes.’
In the breakthrough paper on the subject, Hopkins and Wickelgren [Reference Hopkins and WickelgrenHW15] proved that, given
![]() $x_{1},x_{2},x_{3}\in \operatorname{H}^{1}(G_{F},\mathbb{Z}/p)$
, the triple Massey product
$x_{1},x_{2},x_{3}\in \operatorname{H}^{1}(G_{F},\mathbb{Z}/p)$
, the triple Massey product
![]() $\langle x_{1},x_{2},x_{3}\rangle$
always vanishes whenever it is non-empty, in the case where
$\langle x_{1},x_{2},x_{3}\rangle$
always vanishes whenever it is non-empty, in the case where
![]() $F$
is a number field and
$F$
is a number field and
![]() $p=2$
. This result was later extended by Mináč and Tân to arbitrary fields and
$p=2$
. This result was later extended by Mináč and Tân to arbitrary fields and
![]() $p=2$
[Reference Mináč and TânMT17c] partially based on ideas appearing in [Reference Gao, Leep, Mináč and SmithGLMS03], and to arbitrary primes
$p=2$
[Reference Mináč and TânMT17c] partially based on ideas appearing in [Reference Gao, Leep, Mináč and SmithGLMS03], and to arbitrary primes
![]() $p$
with
$p$
with
![]() $F$
a global field [Reference Mináč and TânMT15b].
$F$
a global field [Reference Mináč and TânMT15b].
The end of 2014 and early 2015 saw a surge of activity on triple Massey products of elements of
![]() $\operatorname{H}^{1}(G_{F},\mathbb{Z}/p)$
, significantly extending the results mentioned above. Matzri [Reference MatzriMat11] was first to announce his proof, extending these results to all primes
$\operatorname{H}^{1}(G_{F},\mathbb{Z}/p)$
, significantly extending the results mentioned above. Matzri [Reference MatzriMat11] was first to announce his proof, extending these results to all primes
![]() $p$
and all fields
$p$
and all fields
![]() $F$
which contain
$F$
which contain
![]() $\unicode[STIX]{x1D707}_{p}$
. Shortly thereafter, the arguments from [Reference MatzriMat11] were refined by Efrat and Matzri, and this work was eventually published in [Reference Efrat and MatzriEM17]. At around the same time as when [Reference Efrat and MatzriEM17] was posted, Mináč and Tân [Reference Mináč and TânMT16] also released their proof that triple Massey products of elements of
$\unicode[STIX]{x1D707}_{p}$
. Shortly thereafter, the arguments from [Reference MatzriMat11] were refined by Efrat and Matzri, and this work was eventually published in [Reference Efrat and MatzriEM17]. At around the same time as when [Reference Efrat and MatzriEM17] was posted, Mináč and Tân [Reference Mináč and TânMT16] also released their proof that triple Massey products of elements of
![]() $\operatorname{H}^{1}(G_{F},\mathbb{Z}/p)$
always vanish when defined, while also removing the condition that
$\operatorname{H}^{1}(G_{F},\mathbb{Z}/p)$
always vanish when defined, while also removing the condition that
![]() $F$
must contain
$F$
must contain
![]() $\unicode[STIX]{x1D707}_{p}$
. Motivated by these results, Mináč and Tân [Reference Mináč and TânMT17c, Reference Mináč and TânMT16, Reference Mináč and TânMT15a] eventually formulated the so-called
$\unicode[STIX]{x1D707}_{p}$
. Motivated by these results, Mináč and Tân [Reference Mináč and TânMT17c, Reference Mináč and TânMT16, Reference Mináč and TânMT15a] eventually formulated the so-called
![]() $n$
-Massey vanishing conjecture, which states that for an arbitrary field
$n$
-Massey vanishing conjecture, which states that for an arbitrary field
![]() $F$
, the
$F$
, the
![]() $n$
-Massey products of elements of
$n$
-Massey products of elements of
![]() $\operatorname{H}^{1}(G_{F},\mathbb{Z}/p)$
always vanish whenever they are non-empty.
$\operatorname{H}^{1}(G_{F},\mathbb{Z}/p)$
always vanish whenever they are non-empty.
The case of number fields has always played a particularly important role in this context, as will be outlined in the historical discussion below. In this respect, the present paper presents the first significant result concerning vanishing of
![]() $4$
-Massey products in Galois cohomology. Namely, this paper proves the following result.
$4$
-Massey products in Galois cohomology. Namely, this paper proves the following result.
Main Theorem. Let
![]() $F$
be a number field, and let
$F$
be a number field, and let
![]() $x_{1},x_{2},x_{3},x_{4}\in \operatorname{H}^{1}(G_{F},\mathbb{Z}/2)$
be given. If the Massey product
$x_{1},x_{2},x_{3},x_{4}\in \operatorname{H}^{1}(G_{F},\mathbb{Z}/2)$
be given. If the Massey product
![]() $\langle x_{1},x_{2},x_{3},x_{4}\rangle$
is non-empty, then it vanishes.
$\langle x_{1},x_{2},x_{3},x_{4}\rangle$
is non-empty, then it vanishes.
To achieve this, we construct a ‘splitting variety’ for the problem at hand, which works over any field of characteristic not
![]() $2$
, and which is compatible with base-change. More precisely, given a field
$2$
, and which is compatible with base-change. More precisely, given a field
![]() $F$
of characteristic not
$F$
of characteristic not
![]() $2$
and
$2$
and
![]() $x_{1},x_{2},x_{3},x_{4}\in \operatorname{H}^{1}(G_{F},\mathbb{Z}/2)$
, we construct an
$x_{1},x_{2},x_{3},x_{4}\in \operatorname{H}^{1}(G_{F},\mathbb{Z}/2)$
, we construct an
![]() $F$
-variety
$F$
-variety
![]() $\mathscr{X}_{F}$
such that the following are equivalent:
$\mathscr{X}_{F}$
such that the following are equivalent:
(1) the set of
 $F$
-rational points
$F$
-rational points
 $\mathscr{X}_{F}(F)$
is non-empty;
$\mathscr{X}_{F}(F)$
is non-empty;(2) the
 $4$
-Massey product
$4$
-Massey product
 $\langle x_{1},x_{2},x_{3},x_{4}\rangle$
vanishes.
$\langle x_{1},x_{2},x_{3},x_{4}\rangle$
vanishes.
Furthermore, this construction is compatible with base-change, in the sense that for all
![]() $L/F$
, one has
$L/F$
, one has
![]() $\mathscr{X}_{F}\otimes _{F}L=\mathscr{X}_{L}$
.
$\mathscr{X}_{F}\otimes _{F}L=\mathscr{X}_{L}$
.
The study of the geometry and arithmetic of this variety falls within the reach of the recent results in [Reference Harpaz and WittenbergHW16]. Hence, when
![]() $F$
is a number field, it turns out to be possible to prove that (a variant of)
$F$
is a number field, it turns out to be possible to prove that (a variant of)
![]() $\mathscr{X}_{F}$
satisfies a local-to-global principle for the existence of rational points, as soon as the corresponding Brauer–Manin obstruction vanishes. In the proof of Theorem 6.1, we arrange the existence of local points satisfying certain additional conditions which force the corresponding Brauer–Manin obstruction to vanish; this proves the modulo-
$\mathscr{X}_{F}$
satisfies a local-to-global principle for the existence of rational points, as soon as the corresponding Brauer–Manin obstruction vanishes. In the proof of Theorem 6.1, we arrange the existence of local points satisfying certain additional conditions which force the corresponding Brauer–Manin obstruction to vanish; this proves the modulo-
![]() $2$
case of the
$2$
case of the
![]() $4$
-Massey vanishing conjecture over number fields. Moreover, it turns out that the Brauer–Manin obstruction always vanishes in ‘generic’ situations, which allows us to prove a stronger version of our result in such cases (see Theorem C).
$4$
-Massey vanishing conjecture over number fields. Moreover, it turns out that the Brauer–Manin obstruction always vanishes in ‘generic’ situations, which allows us to prove a stronger version of our result in such cases (see Theorem C).
The overall strategy we take in this paper is similar to the approach taken by Wickelgren and Hopkins [Reference Hopkins and WickelgrenHW15], primarily because of the fact that we use splitting varieties. However, their methods are highly specialized to the case of triple Massey products. Indeed, working with
![]() $n$
-Massey products for
$n$
-Massey products for
![]() $n\geqslant 4$
is substantially harder, especially with respect to their definability and indeterminacy (see the discussion below). Moreover, there is a technical, yet fundamental difference between the two approaches arising from the additional conditions one must arrange for the local points of the splitting variety. The details and new tools we develop here are therefore completely different and more technically involved than those in [Reference Hopkins and WickelgrenHW15].
$n\geqslant 4$
is substantially harder, especially with respect to their definability and indeterminacy (see the discussion below). Moreover, there is a technical, yet fundamental difference between the two approaches arising from the additional conditions one must arrange for the local points of the splitting variety. The details and new tools we develop here are therefore completely different and more technically involved than those in [Reference Hopkins and WickelgrenHW15].
We want to say more about the context, and the history of the subject. Massey products were first introduced in the context of algebraic topology by Massey [Reference MasseyMas58], as a collection of ‘higher-order cohomology operations’ defined in terms of the cochain algebra. For example, Massey products of elements of
![]() $\operatorname{H}^{1}$
play a central role in (rational) homotopy theory, as being the most basic obstruction to 1-formality of manifolds – see the work of Deligne, Griffiths, Morgan and Sullivan [Reference Deligne, Griffiths, Morgan and SullivanDGMS75, Reference SullivanSul77, Reference MorganMor78, Reference MorganMor86]. Massey products in Galois cohomology were first systematically considered over number fields by Morishita [Reference MorishitaMor02, Reference MorishitaMor04], Vogel [Reference VogelVog05] and Sharifi [Reference SharifiSha07]. These papers were primarily focused on Galois groups of extensions with restricted ramification over number fields, where Massey products have interesting connections with topics from Iwasawa theory, Milnor invariants, and Rédei symbols. Understanding Massey products in the Galois cohomology of number fields is particularly important, as they also show up in the context of Grothendieck’s section conjecture; see Wickelgren [Reference WickelgrenWic09, Reference WickelgrenWic12, Reference WickelgrenWic12]. More generally, Massey products in Galois cohomology play an important role in understanding the structure of nilpotent quotients of absolute Galois groups. Therefore, a detailed understanding of Massey products in Galois cohomology could lead to significant generalizations of results in [Reference Efrat and MináčEM11, Reference Mináč and Spira.Min96] from the two-step nilpotent setting to more general settings.
$\operatorname{H}^{1}$
play a central role in (rational) homotopy theory, as being the most basic obstruction to 1-formality of manifolds – see the work of Deligne, Griffiths, Morgan and Sullivan [Reference Deligne, Griffiths, Morgan and SullivanDGMS75, Reference SullivanSul77, Reference MorganMor78, Reference MorganMor86]. Massey products in Galois cohomology were first systematically considered over number fields by Morishita [Reference MorishitaMor02, Reference MorishitaMor04], Vogel [Reference VogelVog05] and Sharifi [Reference SharifiSha07]. These papers were primarily focused on Galois groups of extensions with restricted ramification over number fields, where Massey products have interesting connections with topics from Iwasawa theory, Milnor invariants, and Rédei symbols. Understanding Massey products in the Galois cohomology of number fields is particularly important, as they also show up in the context of Grothendieck’s section conjecture; see Wickelgren [Reference WickelgrenWic09, Reference WickelgrenWic12, Reference WickelgrenWic12]. More generally, Massey products in Galois cohomology play an important role in understanding the structure of nilpotent quotients of absolute Galois groups. Therefore, a detailed understanding of Massey products in Galois cohomology could lead to significant generalizations of results in [Reference Efrat and MináčEM11, Reference Mináč and Spira.Min96] from the two-step nilpotent setting to more general settings.
The investigation of Massey products in Galois cohomology of arbitrary fields has recently started progressing very rapidly. This surge started with the work of Hopkins and Wickelgren [Reference Hopkins and WickelgrenHW15], and further progressed by Mináč and Tân [Reference Mináč and TânMT17b, Reference Mináč and TânMT17c, Reference Mináč and TânMT16, Reference Mináč and TânMT17a] and Efrat and Matzri [Reference Efrat and MatzriEM15, Reference Efrat and MatzriEM17, Reference EfratEfr14, Reference MatzriMat11]. In fact, ideas related to vanishing of modulo-
![]() $2$
triple Massey products already appeared in 2003 by Gao, Leep, Mináč and Smith [Reference Gao, Leep, Mináč and SmithGLMS03], albeit using different terminology. However, it is important to note that all of the results mentioned above were restricted to studying triple Massey products.
$2$
triple Massey products already appeared in 2003 by Gao, Leep, Mináč and Smith [Reference Gao, Leep, Mináč and SmithGLMS03], albeit using different terminology. However, it is important to note that all of the results mentioned above were restricted to studying triple Massey products.
Until now, the cases of the
![]() $n$
-Massey vanishing conjecture for
$n$
-Massey vanishing conjecture for
![]() $n\geqslant 4$
have remained completely open. Already in the case
$n\geqslant 4$
have remained completely open. Already in the case
![]() $n=4$
, having a non-empty
$n=4$
, having a non-empty
![]() $4$
-Massey product forces the vanishing of a new invariant defined by Isaksen [Reference IsaksenIsa15]. In particular, prior to the present paper there was not even a strategy for approaching the
$4$
-Massey product forces the vanishing of a new invariant defined by Isaksen [Reference IsaksenIsa15]. In particular, prior to the present paper there was not even a strategy for approaching the
![]() $4$
-Massey vanishing conjecture.
$4$
-Massey vanishing conjecture.
We now introduce the basic concepts, and the precise notation, needed to state the main results of the paper.
1.1 Basic notation
Throughout the paper,
![]() $F$
will denote a field of characteristic not
$F$
will denote a field of characteristic not
![]() $2$
. We will use the usual notation
$2$
. We will use the usual notation
![]() $\operatorname{H}^{\ast }(F,A):=\operatorname{H}^{\ast }(G_{F},A)$
for the Galois cohomology of
$\operatorname{H}^{\ast }(F,A):=\operatorname{H}^{\ast }(G_{F},A)$
for the Galois cohomology of
![]() $F$
with coefficients in the
$F$
with coefficients in the
![]() $G_{F}$
-module
$G_{F}$
-module
![]() $A$
.
$A$
.
Recall that Kummer theory yields a canonical isomorphism
For an element
![]() $x\in F^{\times }$
, we write
$x\in F^{\times }$
, we write
![]() $[x]$
for its class in
$[x]$
for its class in
![]() $F^{\times }/F^{\times 2}$
, and
$F^{\times }/F^{\times 2}$
, and
![]() $\unicode[STIX]{x1D712}_{x}\in \operatorname{H}^{1}(F,\mathbb{F}_{2})$
for the image of
$\unicode[STIX]{x1D712}_{x}\in \operatorname{H}^{1}(F,\mathbb{F}_{2})$
for the image of
![]() $[x]$
under the Kummer isomorphism. We will usually consider
$[x]$
under the Kummer isomorphism. We will usually consider
![]() $\unicode[STIX]{x1D712}_{x}$
as a (continuous) homomorphism
$\unicode[STIX]{x1D712}_{x}$
as a (continuous) homomorphism
via the canonical identification
![]() $\operatorname{H}^{1}(F,\mathbb{F}_{2})=\operatorname{Hom}^{\text{cont}}(G_{F},\mathbb{F}_{2})$
.
$\operatorname{H}^{1}(F,\mathbb{F}_{2})=\operatorname{Hom}^{\text{cont}}(G_{F},\mathbb{F}_{2})$
.
Given
![]() $a,b\in F^{\times }$
, we will usually write
$a,b\in F^{\times }$
, we will usually write
![]() $(a,b)_{F}$
(or
$(a,b)_{F}$
(or
![]() $(a,b)$
when
$(a,b)$
when
![]() $F$
is understood) for the cup-product
$F$
is understood) for the cup-product
![]() $\unicode[STIX]{x1D712}_{a}\,\cup \,\unicode[STIX]{x1D712}_{b}\in \operatorname{H}^{2}(F,\mathbb{F}_{2})$
. This notation borrows from the fact that
$\unicode[STIX]{x1D712}_{a}\,\cup \,\unicode[STIX]{x1D712}_{b}\in \operatorname{H}^{2}(F,\mathbb{F}_{2})$
. This notation borrows from the fact that
![]() $\operatorname{H}^{2}(F,\mathbb{F}_{2})$
is canonically isomorphic to the
$\operatorname{H}^{2}(F,\mathbb{F}_{2})$
is canonically isomorphic to the
![]() $2$
-torsion of
$2$
-torsion of
![]() $\operatorname{Br}(F)$
, and that the class of the quaternion algebra
$\operatorname{Br}(F)$
, and that the class of the quaternion algebra
![]() $(a,b)_{F}$
corresponds to
$(a,b)_{F}$
corresponds to
![]() $\unicode[STIX]{x1D712}_{a}\cup \unicode[STIX]{x1D712}_{b}$
via this identification.
$\unicode[STIX]{x1D712}_{a}\cup \unicode[STIX]{x1D712}_{b}$
via this identification.
1.2 The groups
 $\mathbb{U}_{n}(\mathbb{F}_{2})$
$\mathbb{U}_{n}(\mathbb{F}_{2})$
The group
![]() $\mathbb{U}_{n}(\mathbb{F}_{2})$
, for
$\mathbb{U}_{n}(\mathbb{F}_{2})$
, for
![]() $n\geqslant 2$
, is composed of the
$n\geqslant 2$
, is composed of the
![]() $n\times n$
upper-triangular matrices with entries in
$n\times n$
upper-triangular matrices with entries in
![]() $\mathbb{F}_{2}$
with
$\mathbb{F}_{2}$
with
![]() $1$
s along the diagonal. The group
$1$
s along the diagonal. The group
![]() $\mathbb{U}_{n}(\mathbb{F}_{2})$
is endowed with
$\mathbb{U}_{n}(\mathbb{F}_{2})$
is endowed with
![]() $n-1$
homomorphisms
$n-1$
homomorphisms
defined as
![]() $s_{i}(g)=g_{i,i+1}$
(the
$s_{i}(g)=g_{i,i+1}$
(the
![]() $i$
th near-diagonal component of
$i$
th near-diagonal component of
![]() $g$
).
$g$
).
The center
![]() ${\mathcal{Z}}(\mathbb{U}_{n}(\mathbb{F}_{2}))$
of
${\mathcal{Z}}(\mathbb{U}_{n}(\mathbb{F}_{2}))$
of
![]() $\mathbb{U}_{n}(\mathbb{F}_{2})$
consists of those matrices whose only possibly non-zero coefficient above the diagonal is in the top-right corner. In particular, the map
$\mathbb{U}_{n}(\mathbb{F}_{2})$
consists of those matrices whose only possibly non-zero coefficient above the diagonal is in the top-right corner. In particular, the map
![]() $g\mapsto g_{1,n}$
induces an isomorphism
$g\mapsto g_{1,n}$
induces an isomorphism
![]() ${\mathcal{Z}}(\mathbb{U}_{n}(\mathbb{F}_{2}))\cong \mathbb{F}_{2}$
. We write
${\mathcal{Z}}(\mathbb{U}_{n}(\mathbb{F}_{2}))\cong \mathbb{F}_{2}$
. We write
![]() $\overline{\mathbb{U}}_{n}(\mathbb{F}_{2}):=\mathbb{U}_{n}(\mathbb{F}_{2})/{\mathcal{Z}}(\mathbb{U}_{n}(\mathbb{F}_{2}))$
, and consider
$\overline{\mathbb{U}}_{n}(\mathbb{F}_{2}):=\mathbb{U}_{n}(\mathbb{F}_{2})/{\mathcal{Z}}(\mathbb{U}_{n}(\mathbb{F}_{2}))$
, and consider
![]() $\mathbb{U}_{n}(\mathbb{F}_{2})$
as an extension of
$\mathbb{U}_{n}(\mathbb{F}_{2})$
as an extension of
![]() $\overline{\mathbb{U}}_{n}(\mathbb{F}_{2})$
by
$\overline{\mathbb{U}}_{n}(\mathbb{F}_{2})$
by
![]() $\mathbb{F}_{2}$
. Furthermore, we denote by
$\mathbb{F}_{2}$
. Furthermore, we denote by
![]() $\unicode[STIX]{x1D709}_{n}$
the element of
$\unicode[STIX]{x1D709}_{n}$
the element of
![]() $\operatorname{H}^{2}(\overline{\mathbb{U}}_{n}(\mathbb{F}_{2}),\mathbb{F}_{2})$
associated to this extension.
$\operatorname{H}^{2}(\overline{\mathbb{U}}_{n}(\mathbb{F}_{2}),\mathbb{F}_{2})$
associated to this extension.
1.3 Massey products
Let
![]() $\unicode[STIX]{x1D6E4}$
be a profinite group, and let
$\unicode[STIX]{x1D6E4}$
be a profinite group, and let
![]() $x_{1},\ldots ,x_{n}\in \operatorname{H}^{1}(\unicode[STIX]{x1D6E4},\mathbb{F}_{2})$
be given. In this context, we say that the
$x_{1},\ldots ,x_{n}\in \operatorname{H}^{1}(\unicode[STIX]{x1D6E4},\mathbb{F}_{2})$
be given. In this context, we say that the
![]() $n$
-Massey product
$n$
-Massey product
![]() $\langle x_{1},\ldots ,x_{n}\rangle$
is defined provided that there exists a homomorphism
$\langle x_{1},\ldots ,x_{n}\rangle$
is defined provided that there exists a homomorphism
![]() $\unicode[STIX]{x1D711}:\unicode[STIX]{x1D6E4}\rightarrow \overline{\mathbb{U}}_{n+1}(\mathbb{F}_{2})$
such that
$\unicode[STIX]{x1D711}:\unicode[STIX]{x1D6E4}\rightarrow \overline{\mathbb{U}}_{n+1}(\mathbb{F}_{2})$
such that
![]() $x_{i}=s_{i}\circ \unicode[STIX]{x1D711}$
for
$x_{i}=s_{i}\circ \unicode[STIX]{x1D711}$
for
![]() $i=1,\ldots ,n$
. Furthermore, in this case we say that
$i=1,\ldots ,n$
. Furthermore, in this case we say that
![]() $\unicode[STIX]{x1D711}$
is a defining system for the
$\unicode[STIX]{x1D711}$
is a defining system for the
![]() $n$
-Massey product
$n$
-Massey product
![]() $\langle x_{1},\ldots ,x_{n}\rangle$
.
$\langle x_{1},\ldots ,x_{n}\rangle$
.
The
![]() $n$
-Massey product associated to the defining system
$n$
-Massey product associated to the defining system
![]() $\unicode[STIX]{x1D711}$
, denoted by
$\unicode[STIX]{x1D711}$
, denoted by
![]() $\langle x_{1},\ldots ,x_{n}\rangle _{\unicode[STIX]{x1D711}}$
, is defined to be
$\langle x_{1},\ldots ,x_{n}\rangle _{\unicode[STIX]{x1D711}}$
, is defined to be
![]() $\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D709}_{n+1}\in \operatorname{H}^{2}(\unicode[STIX]{x1D6E4},\mathbb{F}_{2})$
, the pull-back of
$\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D709}_{n+1}\in \operatorname{H}^{2}(\unicode[STIX]{x1D6E4},\mathbb{F}_{2})$
, the pull-back of
![]() $\unicode[STIX]{x1D709}_{n+1}$
along
$\unicode[STIX]{x1D709}_{n+1}$
along
![]() $\unicode[STIX]{x1D711}$
. Note that
$\unicode[STIX]{x1D711}$
. Note that
![]() $\langle x_{1},\ldots ,x_{n}\rangle _{\unicode[STIX]{x1D711}}=0$
if and only if the map
$\langle x_{1},\ldots ,x_{n}\rangle _{\unicode[STIX]{x1D711}}=0$
if and only if the map
![]() $\unicode[STIX]{x1D711}:\unicode[STIX]{x1D6E4}\rightarrow \overline{\mathbb{U}}_{n+1}(\mathbb{F}_{2})$
lifts to a homomorphism
$\unicode[STIX]{x1D711}:\unicode[STIX]{x1D6E4}\rightarrow \overline{\mathbb{U}}_{n+1}(\mathbb{F}_{2})$
lifts to a homomorphism
![]() $\widetilde{\unicode[STIX]{x1D711}}:\unicode[STIX]{x1D6E4}\rightarrow \mathbb{U}_{n+1}(\mathbb{F}_{2})$
.
$\widetilde{\unicode[STIX]{x1D711}}:\unicode[STIX]{x1D6E4}\rightarrow \mathbb{U}_{n+1}(\mathbb{F}_{2})$
.
Finally, the
![]() $n$
-Massey product
$n$
-Massey product
![]() $\langle x_{1},\ldots ,x_{n}\rangle$
is defined as the set
$\langle x_{1},\ldots ,x_{n}\rangle$
is defined as the set
where
![]() $\unicode[STIX]{x1D711}$
varies over all defining systems for
$\unicode[STIX]{x1D711}$
varies over all defining systems for
![]() $\langle x_{1},\ldots ,x_{n}\rangle$
. In particular, the
$\langle x_{1},\ldots ,x_{n}\rangle$
. In particular, the
![]() $n$
-Massey product
$n$
-Massey product
![]() $\langle x_{1},\ldots ,x_{n}\rangle$
is non-empty if and only if it is defined. As mentioned above we will be primarily interested in situations where the
$\langle x_{1},\ldots ,x_{n}\rangle$
is non-empty if and only if it is defined. As mentioned above we will be primarily interested in situations where the
![]() $n$
-Massey product
$n$
-Massey product
![]() $\langle x_{1},\ldots ,x_{n}\rangle$
contains
$\langle x_{1},\ldots ,x_{n}\rangle$
contains
![]() $0$
, and we say that ‘
$0$
, and we say that ‘
![]() $\langle x_{1},\ldots ,x_{n}\rangle$
vanishes’ in such situations. Note that, when we say ‘
$\langle x_{1},\ldots ,x_{n}\rangle$
vanishes’ in such situations. Note that, when we say ‘
![]() $\langle x_{1},\ldots ,x_{n}\rangle$
vanishes’ we are also implying that
$\langle x_{1},\ldots ,x_{n}\rangle$
vanishes’ we are also implying that
![]() $\langle x_{1},\ldots ,x_{n}\rangle$
is defined (as
$\langle x_{1},\ldots ,x_{n}\rangle$
is defined (as
![]() $\langle x_{1},\ldots ,x_{n}\rangle$
is non-empty).
$\langle x_{1},\ldots ,x_{n}\rangle$
is non-empty).
Remark.
We have presented the definition of defining systems and Massey products in the context of group cohomology from the point of view of embedding problems. This is nevertheless equivalent to the classical (highly technical) definitions, by the work of Dwyer [Reference DwyerDwy75]. For our purposes, Massey products are defined as above.
We will simplify the notation somewhat in the context of Galois cohomology. Namely, given
![]() $a_{1},\ldots ,a_{n}\in F^{\times }$
, we write
$a_{1},\ldots ,a_{n}\in F^{\times }$
, we write
![]() $\langle a_{1},\ldots ,a_{n}\rangle$
instead of
$\langle a_{1},\ldots ,a_{n}\rangle$
instead of
![]() $\langle \unicode[STIX]{x1D712}_{a_{1}},\ldots ,\unicode[STIX]{x1D712}_{a_{n}}\rangle$
. We will follow this convention when talking about defining systems as well as Massey products themselves.
$\langle \unicode[STIX]{x1D712}_{a_{1}},\ldots ,\unicode[STIX]{x1D712}_{a_{n}}\rangle$
. We will follow this convention when talking about defining systems as well as Massey products themselves.
1.4 Main results
We are now prepared to state our main theorems which characterize the vanishing of
![]() $4$
-Massey products in modulo-
$4$
-Massey products in modulo-
![]() $2$
Galois cohomology.
$2$
Galois cohomology.
Theorem A. Let
![]() $F$
be a field of characteristic not
$F$
be a field of characteristic not
![]() $2$
. Let
$2$
. Let
![]() $a,b,c,d\in F^{\times }$
be given, choose square roots
$a,b,c,d\in F^{\times }$
be given, choose square roots
![]() $\sqrt{a}$
respectively
$\sqrt{a}$
respectively
![]() $\sqrt{d}$
of
$\sqrt{d}$
of
![]() $a$
respectively
$a$
respectively
![]() $d$
in an algebraic closure of
$d$
in an algebraic closure of
![]() $F$
, and put
$F$
, and put
![]() $E:=F[\sqrt{a},\sqrt{d}]$
. Then the following are equivalent.
$E:=F[\sqrt{a},\sqrt{d}]$
. Then the following are equivalent.
(1) The
 $4$
-Massey product
$4$
-Massey product
 $\langle a,b,c,d\rangle$
vanishes (i.e. it is defined and contains
$\langle a,b,c,d\rangle$
vanishes (i.e. it is defined and contains
 $0$
).
$0$
).(2) There exist
 $B\in F[\sqrt{a}]$
,
$B\in F[\sqrt{a}]$
,
 $C\in F[\sqrt{d}]$
and
$C\in F[\sqrt{d}]$
and
 $z_{1},z_{2}\in F^{\times }$
such that the following conditions hold:
$z_{1},z_{2}\in F^{\times }$
such that the following conditions hold:(a) one has
 $\operatorname{N}_{F[\sqrt{a}]/F}(B)=b\cdot z_{1}^{2}$
and
$\operatorname{N}_{F[\sqrt{a}]/F}(B)=b\cdot z_{1}^{2}$
and
 $\operatorname{N}_{F[\sqrt{d}]/F}(C)=c\cdot z_{2}^{2}$
;
$\operatorname{N}_{F[\sqrt{d}]/F}(C)=c\cdot z_{2}^{2}$
;(b) one has
 $(B,C)_{E}=0$
,
$(B,C)_{E}=0$
,
 $(B,c)_{F[\sqrt{a}]}=0$
,
$(B,c)_{F[\sqrt{a}]}=0$
,
 $(b,C)_{F[\sqrt{d}]}=0$
and
$(b,C)_{F[\sqrt{d}]}=0$
and
 $(b,c)_{F}=0$
.
$(b,c)_{F}=0$
.
(3) There exist
 $B\in F[\sqrt{a}]$
,
$B\in F[\sqrt{a}]$
,
 $C\in F[\sqrt{d}]$
and
$C\in F[\sqrt{d}]$
and
 $z_{1},z_{2}\in F^{\times }$
such that the following conditions hold:
$z_{1},z_{2}\in F^{\times }$
such that the following conditions hold:(a) one has
 $\operatorname{N}_{F[\sqrt{a}]/F}(B)=b\cdot z_{1}^{2}$
and
$\operatorname{N}_{F[\sqrt{a}]/F}(B)=b\cdot z_{1}^{2}$
and
 $\operatorname{N}_{F[\sqrt{d}]/F}(C)=c\cdot z_{2}^{2}$
;
$\operatorname{N}_{F[\sqrt{d}]/F}(C)=c\cdot z_{2}^{2}$
;(b) one has
 $(B,C)_{E}=(B,c)_{E}=(b,C)_{E}=(b,c)_{E}=0$
.
$(B,C)_{E}=(B,c)_{E}=(b,C)_{E}=(b,c)_{E}=0$
.
Note that condition (2) of Theorem A can be readily described in terms of polynomial equations over
![]() $F$
, hence defining an (affine)
$F$
, hence defining an (affine)
![]() $F$
-variety. Theorem A then shows that this variety has an
$F$
-variety. Theorem A then shows that this variety has an
![]() $F$
-point if and only if
$F$
-point if and only if
![]() $\langle a,b,c,d\rangle$
vanishes. Note, however, that these equations depend on whether
$\langle a,b,c,d\rangle$
vanishes. Note, however, that these equations depend on whether
![]() $a$
,
$a$
,
![]() $d$
, and/or
$d$
, and/or
![]() $ad$
are squares in
$ad$
are squares in
![]() $F$
(the definition involves a Weil-restriction from
$F$
(the definition involves a Weil-restriction from
![]() $F[\sqrt{a},\sqrt{d}]$
to
$F[\sqrt{a},\sqrt{d}]$
to
![]() $F$
); in other words, the variety is not compatible with base-change to extensions of
$F$
); in other words, the variety is not compatible with base-change to extensions of
![]() $F$
. This is undesirable, as compatibility with base-change will be an important property towards the end of the paper. With some additional work, we are able to obtain the following characterization theorem which provides us with our desired uniform polynomial equations.
$F$
. This is undesirable, as compatibility with base-change will be an important property towards the end of the paper. With some additional work, we are able to obtain the following characterization theorem which provides us with our desired uniform polynomial equations.
Theorem B. Let
![]() $F$
be a field of characteristic not
$F$
be a field of characteristic not
![]() $2$
and let
$2$
and let
![]() $a,b,c,d\in F^{\times }$
be given. Consider the finite étale
$a,b,c,d\in F^{\times }$
be given. Consider the finite étale
![]() $F$
-algebra
$F$
-algebra
Then the following are equivalent.
(1) The
 $4$
-Massey product
$4$
-Massey product
 $\langle a,b,c,d\rangle$
vanishes.
$\langle a,b,c,d\rangle$
vanishes.(2) There exist
 $x_{1},y_{1},x_{2},y_{2}\in F$
,
$x_{1},y_{1},x_{2},y_{2}\in F$
,
 $z_{1},z_{2}\in F^{\times }$
and
$z_{1},z_{2}\in F^{\times }$
and
 $u,v\in {\mathcal{E}}$
such that the following equations are satisfied:
$u,v\in {\mathcal{E}}$
such that the following equations are satisfied:(a) one has
 $x_{1}^{2}-y_{1}^{2}\cdot a=b\cdot z_{1}^{2}$
and
$x_{1}^{2}-y_{1}^{2}\cdot a=b\cdot z_{1}^{2}$
and
 $x_{2}^{2}-y_{2}^{2}\cdot d=c\cdot z_{2}^{2}$
;
$x_{2}^{2}-y_{2}^{2}\cdot d=c\cdot z_{2}^{2}$
;(b) one has
 $u^{2}-\widetilde{B}v^{2}=\widetilde{C}$
in
$u^{2}-\widetilde{B}v^{2}=\widetilde{C}$
in
 ${\mathcal{E}}$
, where
${\mathcal{E}}$
, where
 $\widetilde{B}=x_{1}+y_{1}\cdot X\in {\mathcal{E}}$
and
$\widetilde{B}=x_{1}+y_{1}\cdot X\in {\mathcal{E}}$
and
 $\widetilde{C}=x_{2}+y_{2}\cdot Y\in {\mathcal{E}}$
.
$\widetilde{C}=x_{2}+y_{2}\cdot Y\in {\mathcal{E}}$
.
Note that the polynomial equations described by condition (2) of Theorem B actually have the same shape over any field which contains
![]() $a,b,c,d$
. The
$a,b,c,d$
. The
![]() $F$
-variety defined by these equations is what we will eventually call the splitting variety for
$F$
-variety defined by these equations is what we will eventually call the splitting variety for
![]() $\langle a,b,c,d\rangle$
.
$\langle a,b,c,d\rangle$
.
It is important to note that both Theorems A and B will play a key role in this paper. Indeed, condition (2) of Theorem A has an immediate and direct formulation involving cup-products in modulo-2 Galois cohomology (we exhibit some direct applications, over any field, in § 4). On the other hand, condition (2) of Theorem B defines a splitting variety whose geometry is remarkably simple. In generic situations, it satisfies the Hasse principle for the existence of rational points; in all cases, the local-to-global principle is governed by the Brauer–Manin obstruction, which takes a simple form here. See Theorem A.1 in the appendix for a detailed statement. We thereby obtain a more precise version of the Theorem announced above.
Theorem C. Let
![]() $F$
be a number field, and let
$F$
be a number field, and let
![]() $a,b,c,d\in F^{\times }$
be given. Then the following are equivalent:
$a,b,c,d\in F^{\times }$
be given. Then the following are equivalent:
(1) the
 $4$
-Massey product
$4$
-Massey product
 $\langle a,b,c,d\rangle$
vanishes;
$\langle a,b,c,d\rangle$
vanishes;(2) the
 $4$
-Massey product
$4$
-Massey product
 $\langle a,b,c,d\rangle$
is defined.
$\langle a,b,c,d\rangle$
is defined.
If furthermore
![]() $ad$
,
$ad$
,
![]() $ab$
,
$ab$
,
![]() $cd$
are all non-squares in
$cd$
are all non-squares in
![]() $F$
, then the above conditions are further equivalent to the following:
$F$
, then the above conditions are further equivalent to the following:
(3) one has
 $(a,b)_{F}=(b,c)_{F}=(c,d)_{F}=0$
.
$(a,b)_{F}=(b,c)_{F}=(c,d)_{F}=0$
.
Theorem C will be proved in Theorems 6.1 and 6.2 below. It is natural to ask whether the implication
![]() $(3)\;\Longrightarrow \;(1)$
holds in general. It turns out that this implication fails in general, even over number fields. See Remark 6.3, Example A.15, and the surrounding discussions for more details.
$(3)\;\Longrightarrow \;(1)$
holds in general. It turns out that this implication fails in general, even over number fields. See Remark 6.3, Example A.15, and the surrounding discussions for more details.
Organization of the paper
After some preliminaries in the next section, we prove Theorem A in § 3. In § 4, we give some first applications of Theorem A by proving a few cases of the 4-Massey vanishing conjecture by hand, over arbitrary fields. Then in § 5 we introduce the splitting variety
![]() $\mathscr{X}_{F}$
, as well as a variant
$\mathscr{X}_{F}$
, as well as a variant
![]() $X_{F}$
which will simplify some calculations. The next section, that is § 6, gives a proof of Theorem C. Finally in § 7 we make some of our constructions explicit, and explain concretely how to get a Galois extension with group
$X_{F}$
which will simplify some calculations. The next section, that is § 6, gives a proof of Theorem C. Finally in § 7 we make some of our constructions explicit, and explain concretely how to get a Galois extension with group
![]() $\mathbb{U}_{5}(\mathbb{F}_{2})$
when
$\mathbb{U}_{5}(\mathbb{F}_{2})$
when
![]() $\langle a,b,c,d\rangle$
vanishes and
$\langle a,b,c,d\rangle$
vanishes and
![]() $a,b,c,d$
are linearly independent modulo squares; incidentally, this gives an alternative, more pedestrian proof for the implication
$a,b,c,d$
are linearly independent modulo squares; incidentally, this gives an alternative, more pedestrian proof for the implication
![]() $(3)\;\Longrightarrow \;(1)$
in Theorem A in this case.
$(3)\;\Longrightarrow \;(1)$
in Theorem A in this case.
An appendix by Wittenberg shows that the variety
![]() $X_{F}$
satisfies the local-to-global principle alluded to above, which is of course a crucial ingredient for Theorem C.
$X_{F}$
satisfies the local-to-global principle alluded to above, which is of course a crucial ingredient for Theorem C.
2 Preliminaries
2.1 The groups
 $\mathbb{U}_{3}(\mathbb{F}_{2})$
and
$\mathbb{U}_{3}(\mathbb{F}_{2})$
and
 $\mathbb{U}_{5}(\mathbb{F}_{2})$
$\mathbb{U}_{5}(\mathbb{F}_{2})$
We shall need special notation for these two groups. First note that we define the dihedral group of order
![]() $8$
to be
$8$
to be
![]() $\mathbb{U}_{3}(\mathbb{F}_{2})$
, and we may write
$\mathbb{U}_{3}(\mathbb{F}_{2})$
, and we may write
![]() $D_{4}=\mathbb{U}_{3}(\mathbb{F}_{2})$
. An element
$D_{4}=\mathbb{U}_{3}(\mathbb{F}_{2})$
. An element
![]() $g\in D_{4}$
is a matrix of the form
$g\in D_{4}$
is a matrix of the form
 $$\begin{eqnarray}g=\left(\begin{array}{@{}ccc@{}}1 & s_{1}(g) & t(g)\\ 0 & 1 & s_{2}(g)\\ 0 & 0 & 1\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}g=\left(\begin{array}{@{}ccc@{}}1 & s_{1}(g) & t(g)\\ 0 & 1 & s_{2}(g)\\ 0 & 0 & 1\end{array}\right).\end{eqnarray}$$
Thus
![]() $D_{4}$
is equipped with maps
$D_{4}$
is equipped with maps
![]() $s_{1},s_{2},t:D_{4}\rightarrow \mathbb{F}_{2}$
. (The letter
$s_{1},s_{2},t:D_{4}\rightarrow \mathbb{F}_{2}$
. (The letter
![]() $t$
is for ‘top’.) Note that the first two are group homomorphisms, but
$t$
is for ‘top’.) Note that the first two are group homomorphisms, but
![]() $t$
is not. Our favourite generators are the involutions
$t$
is not. Our favourite generators are the involutions
![]() $\unicode[STIX]{x1D70E}_{1}$
and
$\unicode[STIX]{x1D70E}_{1}$
and
![]() $\unicode[STIX]{x1D70E}_{2}$
, with
$\unicode[STIX]{x1D70E}_{2}$
, with
![]() $s_{i}(\unicode[STIX]{x1D70E}_{i})=1$
and
$s_{i}(\unicode[STIX]{x1D70E}_{i})=1$
and
![]() $s_{j}(\unicode[STIX]{x1D70E}_{i})=t(\unicode[STIX]{x1D70E}_{i})=0$
for
$s_{j}(\unicode[STIX]{x1D70E}_{i})=t(\unicode[STIX]{x1D70E}_{i})=0$
for
![]() $j\neq i$
.
$j\neq i$
.
Similarly, an element
![]() $g\in \mathbb{U}_{5}(\mathbb{F}_{2})$
will be written
$g\in \mathbb{U}_{5}(\mathbb{F}_{2})$
will be written
 $$\begin{eqnarray}\left(\begin{array}{@{}ccccc@{}}1 & s_{1}(g) & t_{1}(g) & u_{1}(g) & z(g)\\ 0 & 1 & s_{2}(g) & u_{3}(g) & u_{2}(g)\\ 0 & 0 & 1 & s_{3}(g) & t_{2}(g)\\ 0 & 0 & 0 & 1 & s_{4}(g)\\ 0 & 0 & 0 & 0 & 1\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccccc@{}}1 & s_{1}(g) & t_{1}(g) & u_{1}(g) & z(g)\\ 0 & 1 & s_{2}(g) & u_{3}(g) & u_{2}(g)\\ 0 & 0 & 1 & s_{3}(g) & t_{2}(g)\\ 0 & 0 & 0 & 1 & s_{4}(g)\\ 0 & 0 & 0 & 0 & 1\end{array}\right).\end{eqnarray}$$
This endows
![]() $\mathbb{U}_{5}(\mathbb{F}_{2})$
with maps
$\mathbb{U}_{5}(\mathbb{F}_{2})$
with maps
![]() $s_{1},\ldots ,z:\mathbb{U}_{5}(\mathbb{F}_{2})\rightarrow \mathbb{F}_{2}$
, and
$s_{1},\ldots ,z:\mathbb{U}_{5}(\mathbb{F}_{2})\rightarrow \mathbb{F}_{2}$
, and
![]() $s_{i}$
is a group homomorphism for
$s_{i}$
is a group homomorphism for
![]() $1\leqslant i\leqslant 4$
.
$1\leqslant i\leqslant 4$
.
More generally the group
![]() $\mathbb{U}_{n}(\mathbb{F}_{2})$
has homomorphisms
$\mathbb{U}_{n}(\mathbb{F}_{2})$
has homomorphisms
![]() $s_{i}:\mathbb{U}_{n}(\mathbb{F}_{2})\rightarrow \mathbb{F}_{2}$
for
$s_{i}:\mathbb{U}_{n}(\mathbb{F}_{2})\rightarrow \mathbb{F}_{2}$
for
![]() $1\leqslant i\leqslant n-1$
, already mentioned in the Introduction, obtained by looking at the entries on what we call the near-diagonal. If we define elements
$1\leqslant i\leqslant n-1$
, already mentioned in the Introduction, obtained by looking at the entries on what we call the near-diagonal. If we define elements
![]() $\unicode[STIX]{x1D70E}_{i}$
by requiring
$\unicode[STIX]{x1D70E}_{i}$
by requiring
![]() $s_{i}(\unicode[STIX]{x1D70E}_{i})=1$
while all the other entries of
$s_{i}(\unicode[STIX]{x1D70E}_{i})=1$
while all the other entries of
![]() $\unicode[STIX]{x1D70E}_{i}$
above the diagonal are
$\unicode[STIX]{x1D70E}_{i}$
above the diagonal are
![]() $0$
, then each
$0$
, then each
![]() $\unicode[STIX]{x1D70E}_{i}$
is an involution, and these generate
$\unicode[STIX]{x1D70E}_{i}$
is an involution, and these generate
![]() $\mathbb{U}_{n}(\mathbb{F}_{2})$
.
$\mathbb{U}_{n}(\mathbb{F}_{2})$
.
We note that
![]() $\mathbb{U}_{n}(\mathbb{F}_{2})$
has an automorphism which exchanges
$\mathbb{U}_{n}(\mathbb{F}_{2})$
has an automorphism which exchanges
![]() $\unicode[STIX]{x1D70E}_{i}$
with
$\unicode[STIX]{x1D70E}_{i}$
with
![]() $\unicode[STIX]{x1D70E}_{n-i}$
. Most of our considerations respect this symmetry, and this motivates the notation above for
$\unicode[STIX]{x1D70E}_{n-i}$
. Most of our considerations respect this symmetry, and this motivates the notation above for
![]() $\mathbb{U}_{5}(\mathbb{F}_{2})$
. (The automorphism is given by ‘the transpose but along the other diagonal’, followed by
$\mathbb{U}_{5}(\mathbb{F}_{2})$
. (The automorphism is given by ‘the transpose but along the other diagonal’, followed by
![]() $g\mapsto g^{-1}$
.)
$g\mapsto g^{-1}$
.)
2.2 Around the group
 $D_{4}$
$D_{4}$
We write
![]() $s=(s_{1},s_{2}):D_{4}\rightarrow C_{2}\times C_{2}$
, where we have identified
$s=(s_{1},s_{2}):D_{4}\rightarrow C_{2}\times C_{2}$
, where we have identified
![]() $\mathbb{F}_{2}$
with the cyclic group of order
$\mathbb{F}_{2}$
with the cyclic group of order
![]() $2$
in multiplicative notation, written
$2$
in multiplicative notation, written
![]() $C_{2}$
. There is an exact sequence
$C_{2}$
. There is an exact sequence
the kernel of
![]() $s$
being generated by
$s$
being generated by
![]() $[\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}]$
(which is the element
$[\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}]$
(which is the element
![]() $g$
with
$g$
with
![]() $t(g)=1$
and
$t(g)=1$
and
![]() $s_{i}(g)=0$
,
$s_{i}(g)=0$
,
![]() $i=1,2$
).
$i=1,2$
).
The quotient group
![]() $C_{2}\times C_{2}$
is generated by the images of
$C_{2}\times C_{2}$
is generated by the images of
![]() $\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}$
, written
$\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}$
, written
![]() $\overline{\unicode[STIX]{x1D70E}}_{1},\overline{\unicode[STIX]{x1D70E}}_{2}$
. The cohomology group
$\overline{\unicode[STIX]{x1D70E}}_{1},\overline{\unicode[STIX]{x1D70E}}_{2}$
. The cohomology group
![]() $\operatorname{H}^{1}(C_{2}^{2},\mathbb{F}_{2})=\operatorname{Hom}(C_{2}^{2},\mathbb{F}_{2})$
is endowed with the dual basis
$\operatorname{H}^{1}(C_{2}^{2},\mathbb{F}_{2})=\operatorname{Hom}(C_{2}^{2},\mathbb{F}_{2})$
is endowed with the dual basis
![]() $\overline{s}_{1},\overline{s}_{2}$
. The next lemma is very well known.
$\overline{s}_{1},\overline{s}_{2}$
. The next lemma is very well known.
Lemma 2.1. The cohomology class of the above extension is
![]() $\overline{s}_{1}\overline{s}_{2}\in \operatorname{H}^{2}(C_{2}^{2},\mathbb{F}_{2})$
.
$\overline{s}_{1}\overline{s}_{2}\in \operatorname{H}^{2}(C_{2}^{2},\mathbb{F}_{2})$
.
We introduce the two elementary abelian subgroups
![]() $E_{1},E_{2}$
, where
$E_{1},E_{2}$
, where
![]() $E_{1}$
is the kernel of
$E_{1}$
is the kernel of
![]() $s_{2}$
and
$s_{2}$
and
![]() $E_{2}$
is the kernel of
$E_{2}$
is the kernel of
![]() $s_{1}$
(the switch is justified by the next lemma). A very useful observation is that
$s_{1}$
(the switch is justified by the next lemma). A very useful observation is that
![]() $t$
, when restricted to either of these, is a group homomorphism.
$t$
, when restricted to either of these, is a group homomorphism.
Lemma 2.2. The corestriction
carries
![]() $t|_{E_{i}}$
to
$t|_{E_{i}}$
to
![]() $s_{i}$
, for
$s_{i}$
, for
![]() $i=1,2$
. More generally if
$i=1,2$
. More generally if
![]() $\unicode[STIX]{x1D6E4}$
is any profinite group with a continuous homomorphism
$\unicode[STIX]{x1D6E4}$
is any profinite group with a continuous homomorphism
![]() $\unicode[STIX]{x1D711}:\unicode[STIX]{x1D6E4}\rightarrow D_{4}$
, and if
$\unicode[STIX]{x1D711}:\unicode[STIX]{x1D6E4}\rightarrow D_{4}$
, and if
![]() $H=\unicode[STIX]{x1D711}^{-1}(E_{i})$
is assumed to have index
$H=\unicode[STIX]{x1D711}^{-1}(E_{i})$
is assumed to have index
![]() $2$
in
$2$
in
![]() $\unicode[STIX]{x1D6E4}$
, then the corestriction
$\unicode[STIX]{x1D6E4}$
, then the corestriction
carries
![]() $t\circ \unicode[STIX]{x1D711}$
to
$t\circ \unicode[STIX]{x1D711}$
to
![]() $s_{i}\circ \unicode[STIX]{x1D711}$
, for
$s_{i}\circ \unicode[STIX]{x1D711}$
, for
![]() $i=1,2$
.
$i=1,2$
.
Proof. We recall some properties of the corestriction
where
![]() $N$
is a subgroup of finite index of the profinite group
$N$
is a subgroup of finite index of the profinite group
![]() $G$
, and
$G$
, and
![]() $M$
is a
$M$
is a
![]() $G$
-module. In fact, we only need to consider the case when
$G$
-module. In fact, we only need to consider the case when
![]() $M$
has a trivial action,
$M$
has a trivial action,
![]() $N$
is closed of index
$N$
is closed of index
![]() $2$
(and thus is normal) in
$2$
(and thus is normal) in
![]() $G$
, and
$G$
, and
![]() $i=1$
, so that
$i=1$
, so that
Here if
![]() $f:N\rightarrow M$
, then the map
$f:N\rightarrow M$
, then the map
![]() $\operatorname{cores}(f):G\rightarrow M$
is characterized as follows. Pick
$\operatorname{cores}(f):G\rightarrow M$
is characterized as follows. Pick
![]() $\unicode[STIX]{x1D70F}\in G\smallsetminus N$
. Then (i)
$\unicode[STIX]{x1D70F}\in G\smallsetminus N$
. Then (i)
![]() $\operatorname{cores}(f)(n)=f(n)+f(\unicode[STIX]{x1D70F}^{-1}n\unicode[STIX]{x1D70F})$
for
$\operatorname{cores}(f)(n)=f(n)+f(\unicode[STIX]{x1D70F}^{-1}n\unicode[STIX]{x1D70F})$
for
![]() $n\in N$
, and (ii)
$n\in N$
, and (ii)
![]() $\operatorname{cores}(f)(\unicode[STIX]{x1D70F})=f(\unicode[STIX]{x1D70F}^{2})$
. This follows from the material in [Reference TateTat76, § 2], for example.
$\operatorname{cores}(f)(\unicode[STIX]{x1D70F})=f(\unicode[STIX]{x1D70F}^{2})$
. This follows from the material in [Reference TateTat76, § 2], for example.
Let us use this for
![]() $N=E_{1}$
and
$N=E_{1}$
and
![]() $G=D_{4}$
. If
$G=D_{4}$
. If
 $$\begin{eqnarray}n=\left(\begin{array}{@{}ccc@{}}1 & a & b\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right)\quad \text{and}\quad \unicode[STIX]{x1D70F}=\left(\begin{array}{@{}ccc@{}}1 & c & d\\ 0 & 1 & 1\\ 0 & 0 & 1\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}n=\left(\begin{array}{@{}ccc@{}}1 & a & b\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right)\quad \text{and}\quad \unicode[STIX]{x1D70F}=\left(\begin{array}{@{}ccc@{}}1 & c & d\\ 0 & 1 & 1\\ 0 & 0 & 1\end{array}\right),\end{eqnarray}$$
then
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}^{-1}n\unicode[STIX]{x1D70F}=\left(\begin{array}{@{}ccc@{}}1 & a & a+b\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}^{-1}n\unicode[STIX]{x1D70F}=\left(\begin{array}{@{}ccc@{}}1 & a & a+b\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right).\end{eqnarray}$$
Moreover
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}^{2}=\left(\begin{array}{@{}ccc@{}}1 & 0 & c\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}^{2}=\left(\begin{array}{@{}ccc@{}}1 & 0 & c\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right).\end{eqnarray}$$
Thus
![]() $t(n)+t(\unicode[STIX]{x1D70F}^{-1}n\unicode[STIX]{x1D70F})=b+a+b=a=s_{1}(n)$
, and
$t(n)+t(\unicode[STIX]{x1D70F}^{-1}n\unicode[STIX]{x1D70F})=b+a+b=a=s_{1}(n)$
, and
![]() $t(\unicode[STIX]{x1D70F}^{2})=c=s_{1}(\unicode[STIX]{x1D70F})$
. Hence the first statement of the lemma for
$t(\unicode[STIX]{x1D70F}^{2})=c=s_{1}(\unicode[STIX]{x1D70F})$
. Hence the first statement of the lemma for
![]() $i=1$
. The other cases are treated similarly.◻
$i=1$
. The other cases are treated similarly.◻
2.3
 $D_{4}$
-extensions of fields
$D_{4}$
-extensions of fields
We proceed to apply the above observations in a Galois-theoretic context, but a couple of comments are in order. First, the group
![]() $D_{4}$
has an automorphism exchanging
$D_{4}$
has an automorphism exchanging
![]() $\unicode[STIX]{x1D70E}_{1}$
and
$\unicode[STIX]{x1D70E}_{1}$
and
![]() $\unicode[STIX]{x1D70E}_{2}$
, but the proposition below is not ‘symmetric’ in this way; it involves the subgroup
$\unicode[STIX]{x1D70E}_{2}$
, but the proposition below is not ‘symmetric’ in this way; it involves the subgroup
![]() $E_{2}$
and not
$E_{2}$
and not
![]() $E_{1}$
, for example (so that one could get a new proposition by exchanging the roles of various players). Second, when asked for a basis for
$E_{1}$
, for example (so that one could get a new proposition by exchanging the roles of various players). Second, when asked for a basis for
![]() $E_{2}$
, the reader would probably offer
$E_{2}$
, the reader would probably offer
![]() $[\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}],\unicode[STIX]{x1D70E}_{2}$
; however, later considerations with
$[\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}],\unicode[STIX]{x1D70E}_{2}$
; however, later considerations with
![]() $\mathbb{U}_{5}(\mathbb{F}_{2})$
compel us to work with
$\mathbb{U}_{5}(\mathbb{F}_{2})$
compel us to work with
![]() $\unicode[STIX]{x1D70E}_{2}[\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}],\unicode[STIX]{x1D70E}_{2}$
instead (specifically, we want Lemma 2.5 to have the simple form given below). This is reflected in the proposition below, since the dual basis of
$\unicode[STIX]{x1D70E}_{2}[\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}],\unicode[STIX]{x1D70E}_{2}$
instead (specifically, we want Lemma 2.5 to have the simple form given below). This is reflected in the proposition below, since the dual basis of
![]() $\operatorname{H}^{1}(E_{2},\mathbb{F}_{2})$
is
$\operatorname{H}^{1}(E_{2},\mathbb{F}_{2})$
is
![]() $t,s_{2}+t$
(or, in more complete notation,
$t,s_{2}+t$
(or, in more complete notation,
![]() $t|_{E_{2}},s_{2}|_{E_{2}}+t|_{E_{2}}$
).
$t|_{E_{2}},s_{2}|_{E_{2}}+t|_{E_{2}}$
).
Proposition 2.3. Let
![]() $F$
be a field of characteristic not
$F$
be a field of characteristic not
![]() $2$
and let
$2$
and let
![]() $a,b\in F^{\times }$
be given. Then the following are equivalent:
$a,b\in F^{\times }$
be given. Then the following are equivalent:
(1)
 $(a,b)_{F}=0$
;
$(a,b)_{F}=0$
;(2) there exists a continuous homomorphism
 $\unicode[STIX]{x1D711}:G_{F}\longrightarrow D_{4}$
such that
$\unicode[STIX]{x1D711}:G_{F}\longrightarrow D_{4}$
such that
 $s_{1}\circ \unicode[STIX]{x1D711}=\unicode[STIX]{x1D712}_{a}$
and
$s_{1}\circ \unicode[STIX]{x1D711}=\unicode[STIX]{x1D712}_{a}$
and
 $s_{2}\circ \unicode[STIX]{x1D711}=\unicode[STIX]{x1D712}_{b}$
;
$s_{2}\circ \unicode[STIX]{x1D711}=\unicode[STIX]{x1D712}_{b}$
;(3) there exist
 $x,y,z\in F$
such that
$x,y,z\in F$
such that
 $x^{2}-ay^{2}=bz^{2}$
, with
$x^{2}-ay^{2}=bz^{2}$
, with
 $z\neq 0$
.
$z\neq 0$
.
When the equivalent conditions hold and
![]() $B:=x+y\sqrt{a}$
, we will say that
$B:=x+y\sqrt{a}$
, we will say that
![]() $\unicode[STIX]{x1D711}$
from (2) and
$\unicode[STIX]{x1D711}$
from (2) and
![]() $x,y,z$
from (3) are consistent, provided that
$x,y,z$
from (3) are consistent, provided that
![]() $\unicode[STIX]{x1D712}_{bB}=t\circ \unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D712}_{bB}=t\circ \unicode[STIX]{x1D711}$
and
![]() $\unicode[STIX]{x1D712}_{B}=(s_{2}+t)\circ \unicode[STIX]{x1D711}$
as elements of
$\unicode[STIX]{x1D712}_{B}=(s_{2}+t)\circ \unicode[STIX]{x1D711}$
as elements of
![]() $\operatorname{H}^{1}(F[\sqrt{a}],\mathbb{F}_{2})$
. Then given any
$\operatorname{H}^{1}(F[\sqrt{a}],\mathbb{F}_{2})$
. Then given any
![]() $\unicode[STIX]{x1D711}$
as in (2), we can choose
$\unicode[STIX]{x1D711}$
as in (2), we can choose
![]() $x,y,z$
as in (3) which are consistent with
$x,y,z$
as in (3) which are consistent with
![]() $\unicode[STIX]{x1D711}$
. Conversely, given any
$\unicode[STIX]{x1D711}$
. Conversely, given any
![]() $x,y,z$
as in (3), we can choose
$x,y,z$
as in (3), we can choose
![]() $\unicode[STIX]{x1D711}$
as in (2) which is consistent with
$\unicode[STIX]{x1D711}$
as in (2) which is consistent with
![]() $x,y,z$
.
$x,y,z$
.
Again, this is essentially known, but we need the precise version given here. Note that it is necessary to deal with the cases when either
![]() $a$
or
$a$
or
![]() $b$
is a square, and that the proof below gives more concrete information in some situations. Also note that, as promised, the elements
$b$
is a square, and that the proof below gives more concrete information in some situations. Also note that, as promised, the elements
![]() $t,s_{2}+t$
, related to
$t,s_{2}+t$
, related to
![]() $E_{2}$
, make an uncanny appearance.
$E_{2}$
, make an uncanny appearance.
Proof. We can combine
![]() $\unicode[STIX]{x1D712}_{a}$
and
$\unicode[STIX]{x1D712}_{a}$
and
![]() $\unicode[STIX]{x1D712}_{b}$
into a homomorphism
$\unicode[STIX]{x1D712}_{b}$
into a homomorphism
![]() $G_{F}\rightarrow C_{2}\times C_{2}$
. The obstruction to lifting it to
$G_{F}\rightarrow C_{2}\times C_{2}$
. The obstruction to lifting it to
![]() $D_{4}$
is the cohomology class of the extension, so that Lemma 2.1 gives immediately the equivalence of (1) and (2).
$D_{4}$
is the cohomology class of the extension, so that Lemma 2.1 gives immediately the equivalence of (1) and (2).
We first conduct the rest of the proof under the following assumption.
Assumption.
Assume for the moment that
![]() $a$
is not a square in
$a$
is not a square in
![]() $F$
.
$F$
.
Suppose (2) holds. Note that
![]() $\unicode[STIX]{x1D711}^{-1}(E_{2})=G_{F[\sqrt{a}]}$
. Let
$\unicode[STIX]{x1D711}^{-1}(E_{2})=G_{F[\sqrt{a}]}$
. Let
![]() $B^{\prime }=x^{\prime }+y^{\prime }\sqrt{a}\in F[\sqrt{a}]$
be such that
$B^{\prime }=x^{\prime }+y^{\prime }\sqrt{a}\in F[\sqrt{a}]$
be such that
![]() $\unicode[STIX]{x1D712}_{B^{\prime }}=t\circ \unicode[STIX]{x1D711}|_{G_{F[\sqrt{a}]}}$
. Since
$\unicode[STIX]{x1D712}_{B^{\prime }}=t\circ \unicode[STIX]{x1D711}|_{G_{F[\sqrt{a}]}}$
. Since
![]() $a$
is not a square in
$a$
is not a square in
![]() $F$
, the subgroup
$F$
, the subgroup
![]() $G_{F[\sqrt{a}]}$
has index
$G_{F[\sqrt{a}]}$
has index
![]() $2$
in
$2$
in
![]() $G_{F}$
. Lemma 2.2 shows then that
$G_{F}$
. Lemma 2.2 shows then that
![]() $\operatorname{cores}(\unicode[STIX]{x1D712}_{B^{\prime }})=s_{2}\circ \unicode[STIX]{x1D711}=\unicode[STIX]{x1D712}_{b}$
. Now recall that under the identifications of
$\operatorname{cores}(\unicode[STIX]{x1D712}_{B^{\prime }})=s_{2}\circ \unicode[STIX]{x1D711}=\unicode[STIX]{x1D712}_{b}$
. Now recall that under the identifications of
![]() $\operatorname{H}^{1}(F,\mathbb{F}_{2})$
with
$\operatorname{H}^{1}(F,\mathbb{F}_{2})$
with
![]() $F^{\times }\!/F^{\times 2}$
and of
$F^{\times }\!/F^{\times 2}$
and of
![]() $\operatorname{H}^{1}(F[\sqrt{a}],\mathbb{F}_{2})$
with
$\operatorname{H}^{1}(F[\sqrt{a}],\mathbb{F}_{2})$
with
![]() $F[\sqrt{a}]^{\times }\!/F[\sqrt{a}]^{\times 2}$
, the corestriction becomes the usual norm
$F[\sqrt{a}]^{\times }\!/F[\sqrt{a}]^{\times 2}$
, the corestriction becomes the usual norm
![]() $N_{F[\sqrt{a}]/F}$
. It follows that
$N_{F[\sqrt{a}]/F}$
. It follows that
This gives (3), clearly, but we need to modify
![]() $B^{\prime }$
to get the consistency statement. And indeed, we put
$B^{\prime }$
to get the consistency statement. And indeed, we put
![]() $B=bB^{\prime }$
, so that
$B=bB^{\prime }$
, so that
![]() $B^{\prime }=bB$
modulo squares, and the result follows.
$B^{\prime }=bB$
modulo squares, and the result follows.
Next, we must prove that (3) implies (2), or equivalently (1). We may as well suppose that
![]() $a$
and
$a$
and
![]() $b$
are both not squares, for (1) holds trivially otherwise. The assumption is that
$b$
are both not squares, for (1) holds trivially otherwise. The assumption is that
![]() $b$
is a norm from
$b$
is a norm from
![]() $F[\sqrt{a}]$
, or in more cohomological terms, that
$F[\sqrt{a}]$
, or in more cohomological terms, that
![]() $\unicode[STIX]{x1D712}_{b}$
is the corestriction of an element from the subgroup
$\unicode[STIX]{x1D712}_{b}$
is the corestriction of an element from the subgroup
![]() $G_{F[\sqrt{a}]}$
. That the cup product
$G_{F[\sqrt{a}]}$
. That the cup product
![]() $\unicode[STIX]{x1D712}_{a}\unicode[STIX]{x1D712}_{b}=0$
then follows from the Arason exact sequence [Reference ArasonAra75].
$\unicode[STIX]{x1D712}_{a}\unicode[STIX]{x1D712}_{b}=0$
then follows from the Arason exact sequence [Reference ArasonAra75].
However, to prove the claimed consistency, a more explicit argument is needed. Assume
![]() $b$
is not a square. The element
$b$
is not a square. The element
![]() $B=x+y\sqrt{a}$
, where
$B=x+y\sqrt{a}$
, where
![]() $x,y$
are as in (3), is fixed up to squares by
$x,y$
are as in (3), is fixed up to squares by
![]() $\operatorname{Gal}(F[\sqrt{a},\sqrt{b}]/F)$
, as is readily checked. It follows that
$\operatorname{Gal}(F[\sqrt{a},\sqrt{b}]/F)$
, as is readily checked. It follows that
![]() $K=F[\sqrt{a},\sqrt{b},\sqrt{B}]$
is Galois over
$K=F[\sqrt{a},\sqrt{b},\sqrt{B}]$
is Galois over
![]() $F$
(by equivariant Kummer theory, if you will).
$F$
(by equivariant Kummer theory, if you will).
We distinguish two cases, and assume first that
![]() $a$
and
$a$
and
![]() $b$
are not equal modulo squares. We now introduce elements
$b$
are not equal modulo squares. We now introduce elements
![]() $\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}\in \operatorname{Gal}(K/F)$
which are dual to
$\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}\in \operatorname{Gal}(K/F)$
which are dual to
![]() $\sqrt{a},\sqrt{b}$
in the obvious sense. Direct computation shows that
$\sqrt{a},\sqrt{b}$
in the obvious sense. Direct computation shows that
![]() $\unicode[STIX]{x1D70E}_{1}^{2}=\unicode[STIX]{x1D70E}_{2}^{2}=1$
, and that
$\unicode[STIX]{x1D70E}_{1}^{2}=\unicode[STIX]{x1D70E}_{2}^{2}=1$
, and that
![]() $[\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}](\sqrt{B})=-\sqrt{B}$
, so that
$[\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}](\sqrt{B})=-\sqrt{B}$
, so that
![]() $[\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}]\neq 1$
. From this one draws readily that
$[\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}]\neq 1$
. From this one draws readily that
![]() $\operatorname{Gal}(K/F)\cong D_{4}$
and (again!) that (2) holds. Also, one computes that
$\operatorname{Gal}(K/F)\cong D_{4}$
and (again!) that (2) holds. Also, one computes that
![]() $\unicode[STIX]{x1D70E}_{2}(\sqrt{B})=\pm \sqrt{B}$
. We want to ensure that
$\unicode[STIX]{x1D70E}_{2}(\sqrt{B})=\pm \sqrt{B}$
. We want to ensure that
![]() $\unicode[STIX]{x1D70E}_{2}(\sqrt{B})=-\sqrt{B}$
, and to achieve this we replace
$\unicode[STIX]{x1D70E}_{2}(\sqrt{B})=-\sqrt{B}$
, and to achieve this we replace
![]() $\unicode[STIX]{x1D70E}_{2}$
by
$\unicode[STIX]{x1D70E}_{2}$
by
![]() $\unicode[STIX]{x1D70E}_{2}[\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}]$
if needed. Having done this, the elements
$\unicode[STIX]{x1D70E}_{2}[\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}]$
if needed. Having done this, the elements
![]() $\sqrt{B}$
,
$\sqrt{B}$
,
![]() $\sqrt{bB}$
are dual to
$\sqrt{bB}$
are dual to
![]() $\unicode[STIX]{x1D70E}_{2}$
,
$\unicode[STIX]{x1D70E}_{2}$
,
![]() $\unicode[STIX]{x1D70E}_{2}[\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}]$
, and one checks that the corresponding map
$\unicode[STIX]{x1D70E}_{2}[\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}]$
, and one checks that the corresponding map
![]() $\unicode[STIX]{x1D711}:G_{F}\rightarrow D_{4}$
has precisely the required consistency.
$\unicode[STIX]{x1D711}:G_{F}\rightarrow D_{4}$
has precisely the required consistency.
If
![]() $a=b$
modulo squares, one sees that
$a=b$
modulo squares, one sees that
![]() $\operatorname{Gal}(K/F)$
has order 4, so is abelian, and if
$\operatorname{Gal}(K/F)$
has order 4, so is abelian, and if
![]() $\unicode[STIX]{x1D70E}$
is the non-trivial element of
$\unicode[STIX]{x1D70E}$
is the non-trivial element of
![]() $\operatorname{Gal}(F[\sqrt{a}]/F)$
extended to
$\operatorname{Gal}(F[\sqrt{a}]/F)$
extended to
![]() $\operatorname{Gal}(K/F)$
, another direct calculation shows that
$\operatorname{Gal}(K/F)$
, another direct calculation shows that
![]() $\unicode[STIX]{x1D70E}$
does not have order
$\unicode[STIX]{x1D70E}$
does not have order
![]() $2$
. So
$2$
. So
![]() $\operatorname{Gal}(K/F)\cong C_{4}$
can be identified with the subgroup of
$\operatorname{Gal}(K/F)\cong C_{4}$
can be identified with the subgroup of
![]() $D_{4}$
generated by
$D_{4}$
generated by
![]() $\unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{2}$
, and (2) follows. Consistency is automatic.
$\unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{2}$
, and (2) follows. Consistency is automatic.
Finally, if
![]() $b$
is a square in
$b$
is a square in
![]() $F$
, we use the same extension
$F$
, we use the same extension
![]() $K=F[\sqrt{a},\sqrt{B}]$
of
$K=F[\sqrt{a},\sqrt{B}]$
of
![]() $F$
, but compute that
$F$
, but compute that
![]() $\operatorname{Gal}(K/F)\cong C_{2}^{2}$
. We identify this group with
$\operatorname{Gal}(K/F)\cong C_{2}^{2}$
. We identify this group with
![]() $E_{1}$
appropriately, yielding a consistent
$E_{1}$
appropriately, yielding a consistent
![]() $\unicode[STIX]{x1D711}$
.
$\unicode[STIX]{x1D711}$
.
The case when
![]() $a$
is a square.
$a$
is a square.
In this situation (1) holds trivially, and thus (2) also holds. As for (3), if
![]() $a=u^{2}$
then put
$a=u^{2}$
then put
and compute that
![]() $x_{0}^{2}-ay_{0}^{2}=b$
.
$x_{0}^{2}-ay_{0}^{2}=b$
.
Let us see how we can adjust
![]() $\unicode[STIX]{x1D711}$
from
$\unicode[STIX]{x1D711}$
from
![]() $x,y,z$
. Put
$x,y,z$
. Put
![]() $B=x+y\sqrt{a}\in F$
, and consider the characters
$B=x+y\sqrt{a}\in F$
, and consider the characters
![]() $\unicode[STIX]{x1D712}_{bB}$
and
$\unicode[STIX]{x1D712}_{bB}$
and
![]() $\unicode[STIX]{x1D712}_{b}$
, together defining a homomorphism
$\unicode[STIX]{x1D712}_{b}$
, together defining a homomorphism
![]() $G_{F}\rightarrow C_{2}\times C_{2}$
. Identifying Klein’s group with
$G_{F}\rightarrow C_{2}\times C_{2}$
. Identifying Klein’s group with
![]() $E_{2}$
sitting in
$E_{2}$
sitting in
![]() $D_{4}$
appropriately, we obtain
$D_{4}$
appropriately, we obtain
![]() $\unicode[STIX]{x1D711}:G_{F}\rightarrow D_{4}$
satisfying our requirements.
$\unicode[STIX]{x1D711}:G_{F}\rightarrow D_{4}$
satisfying our requirements.
Our very last step is to see how one can adjust
![]() $x,y,z$
from
$x,y,z$
from
![]() $\unicode[STIX]{x1D711}$
. First put
$\unicode[STIX]{x1D711}$
. First put
![]() $B_{0}=x_{0}+y_{0}\sqrt{a}\in F$
where
$B_{0}=x_{0}+y_{0}\sqrt{a}\in F$
where
![]() $x_{0}$
and
$x_{0}$
and
![]() $y_{0}$
are as above, which is a non-zero element since
$y_{0}$
are as above, which is a non-zero element since
![]() $B_{0}(x-y\sqrt{a})=b\neq 0$
. For
$B_{0}(x-y\sqrt{a})=b\neq 0$
. For
![]() $f\in F$
, put
$f\in F$
, put
![]() $x=(f/B_{0})x_{0}$
and
$x=(f/B_{0})x_{0}$
and
![]() $y=(f/B_{0})y_{0}$
, so that
$y=(f/B_{0})y_{0}$
, so that
![]() $x^{2}-ay^{2}=bz^{2}$
for some
$x^{2}-ay^{2}=bz^{2}$
for some
![]() $z\in F^{\times }$
, while
$z\in F^{\times }$
, while
![]() $B=x+y\sqrt{a}=f$
, an arbitrary element of
$B=x+y\sqrt{a}=f$
, an arbitrary element of
![]() $F$
. Of course
$F$
. Of course
![]() $\unicode[STIX]{x1D711}$
lands in the subgroup
$\unicode[STIX]{x1D711}$
lands in the subgroup
![]() $E_{2}$
, so we only need to pick
$E_{2}$
, so we only need to pick
![]() $f$
so that
$f$
so that
![]() $\unicode[STIX]{x1D712}_{f}=(s_{2}+t)\circ \unicode[STIX]{x1D711}=\unicode[STIX]{x1D712}_{B}$
; we have then (2) and (3) simultaneously and consistently.◻
$\unicode[STIX]{x1D712}_{f}=(s_{2}+t)\circ \unicode[STIX]{x1D711}=\unicode[STIX]{x1D712}_{B}$
; we have then (2) and (3) simultaneously and consistently.◻
2.4 The group
 $\mathbb{U}_{5}(\mathbb{F}_{2})$
and its subquotients
$\mathbb{U}_{5}(\mathbb{F}_{2})$
and its subquotients
Let
![]() $S$
(for ‘square’) be the subgroup of matrices of the form
$S$
(for ‘square’) be the subgroup of matrices of the form
 $$\begin{eqnarray}\left(\begin{array}{@{}ccccc@{}}1 & 0 & 0 & y_{1} & y_{2}\\ 0 & 1 & 0 & y_{3} & y_{4}\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccccc@{}}1 & 0 & 0 & y_{1} & y_{2}\\ 0 & 1 & 0 & y_{3} & y_{4}\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\end{array}\right).\end{eqnarray}$$
Then
![]() $S\cong C_{2}^{4}$
, and our favourite
$S\cong C_{2}^{4}$
, and our favourite
![]() $\mathbb{F}_{2}$
-basis, denoted
$\mathbb{F}_{2}$
-basis, denoted
![]() $e_{1},e_{2},e_{3},e_{4}$
, will be given by
$e_{1},e_{2},e_{3},e_{4}$
, will be given by
 $$\begin{eqnarray}\displaystyle & \displaystyle e_{1}=e=\left(\begin{array}{@{}ccccc@{}}1 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 1 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\end{array}\right),\quad e_{2}=\unicode[STIX]{x1D70E}_{1}e\unicode[STIX]{x1D70E}_{1}^{-1}=\left(\begin{array}{@{}ccccc@{}}1 & 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 1 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\end{array}\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle e_{3}=\unicode[STIX]{x1D70E}_{4}e\unicode[STIX]{x1D70E}_{4}^{-1}=\left(\begin{array}{@{}ccccc@{}}1 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 1 & 1\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\end{array}\right),\quad e_{4}=(\unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{4})e(\unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{4})^{-1}=\left(\begin{array}{@{}ccccc@{}}1 & 0 & 0 & 1 & 1\\ 0 & 1 & 0 & 1 & 1\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\end{array}\right). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle e_{1}=e=\left(\begin{array}{@{}ccccc@{}}1 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 1 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\end{array}\right),\quad e_{2}=\unicode[STIX]{x1D70E}_{1}e\unicode[STIX]{x1D70E}_{1}^{-1}=\left(\begin{array}{@{}ccccc@{}}1 & 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 1 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\end{array}\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle e_{3}=\unicode[STIX]{x1D70E}_{4}e\unicode[STIX]{x1D70E}_{4}^{-1}=\left(\begin{array}{@{}ccccc@{}}1 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 1 & 1\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\end{array}\right),\quad e_{4}=(\unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{4})e(\unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{4})^{-1}=\left(\begin{array}{@{}ccccc@{}}1 & 0 & 0 & 1 & 1\\ 0 & 1 & 0 & 1 & 1\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\end{array}\right). & \displaystyle \nonumber\end{eqnarray}$$
The centralizer of
![]() $S$
in
$S$
in
![]() $\mathbb{U}_{5}(\mathbb{F}_{2})$
, which we denote by
$\mathbb{U}_{5}(\mathbb{F}_{2})$
, which we denote by
![]() $\mathscr{C}(S)$
, is easily seen to be composed of the elements
$\mathscr{C}(S)$
, is easily seen to be composed of the elements
![]() $g$
for which
$g$
for which
![]() $s_{1}(g)=s_{4}(g)=0$
, that is
$s_{1}(g)=s_{4}(g)=0$
, that is
![]() $\mathscr{C}(S)=\ker s_{1}\cap \ker s_{4}$
. In particular
$\mathscr{C}(S)=\ker s_{1}\cap \ker s_{4}$
. In particular
![]() $\unicode[STIX]{x1D70E}_{2}$
and
$\unicode[STIX]{x1D70E}_{2}$
and
![]() $\unicode[STIX]{x1D70E}_{3}$
centralize
$\unicode[STIX]{x1D70E}_{3}$
centralize
![]() $S$
, and from the formulae above we see that
$S$
, and from the formulae above we see that
![]() $S$
is normal in
$S$
is normal in
![]() $\mathbb{U}_{5}(\mathbb{F}_{2})$
. We shall write
$\mathbb{U}_{5}(\mathbb{F}_{2})$
. We shall write
![]() $G=\mathbb{U}_{5}(\mathbb{F}_{2})/S$
, which we identify with
$G=\mathbb{U}_{5}(\mathbb{F}_{2})/S$
, which we identify with
![]() $D_{4}\times D_{4}$
, as we visibly may. The image of
$D_{4}\times D_{4}$
, as we visibly may. The image of
![]() $\mathscr{C}(S)$
in
$\mathscr{C}(S)$
in
![]() $G$
, that is
$G$
, that is
![]() $\mathscr{C}(S)/S$
, will be denoted by
$\mathscr{C}(S)/S$
, will be denoted by
![]() $N$
, a normal subgroup of
$N$
, a normal subgroup of
![]() $G$
.
$G$
.
One has
![]() $G/N=\mathbb{U}_{5}(\mathbb{F}_{2})/\mathscr{C}(S)=\langle \unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{4}\rangle \cong C_{2}^{2}$
(we shall often write
$G/N=\mathbb{U}_{5}(\mathbb{F}_{2})/\mathscr{C}(S)=\langle \unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{4}\rangle \cong C_{2}^{2}$
(we shall often write
![]() $\unicode[STIX]{x1D70E}_{i}$
for the image of this element in various quotients, whenever no confusion can arise). The next observation is now clear, but it is crucial.
$\unicode[STIX]{x1D70E}_{i}$
for the image of this element in various quotients, whenever no confusion can arise). The next observation is now clear, but it is crucial.
Lemma 2.4. The action of
![]() $G/N$
on
$G/N$
on
![]() $S$
, induced by conjugation, turns it into a free
$S$
, induced by conjugation, turns it into a free
![]() $\mathbb{F}_{2}[G/N]$
-module of rank
$\mathbb{F}_{2}[G/N]$
-module of rank
![]() $1$
. A specific isomorphism
$1$
. A specific isomorphism
![]() $\mathbb{F}_{2}[G/N]\rightarrow S$
is given by
$\mathbb{F}_{2}[G/N]\rightarrow S$
is given by
![]() $1\mapsto e$
, for example.
$1\mapsto e$
, for example.
The group
![]() $N$
itself also has a simple structure: one has
$N$
itself also has a simple structure: one has
![]() $N\cong C_{2}^{4}$
, a basis being
$N\cong C_{2}^{4}$
, a basis being
(A choice which respects the ambient ‘symmetry’ already alluded to.) The corresponding dual basis of
![]() $\operatorname{H}^{1}(N,\mathbb{F}_{2})$
will be denoted
$\operatorname{H}^{1}(N,\mathbb{F}_{2})$
will be denoted
![]() $x_{1},x_{2},x_{3},x_{4}$
. To bridge the notation with that of the previous sections, we regard
$x_{1},x_{2},x_{3},x_{4}$
. To bridge the notation with that of the previous sections, we regard
![]() $N$
as sitting in
$N$
as sitting in
![]() $D_{4}\times D_{4}$
, which itself possesses six maps
$D_{4}\times D_{4}$
, which itself possesses six maps
![]() $s_{1},s_{2},t_{1},s_{3},s_{4},t_{2}$
to
$s_{1},s_{2},t_{1},s_{3},s_{4},t_{2}$
to
![]() $\mathbb{F}_{2}$
, using names adapted from § 2.1. With this notation, one has
$\mathbb{F}_{2}$
, using names adapted from § 2.1. With this notation, one has
![]() $x_{1}=t_{1}$
,
$x_{1}=t_{1}$
,
![]() $x_{2}=s_{2}+t_{1}$
,
$x_{2}=s_{2}+t_{1}$
,
![]() $x_{3}=s_{3}+t_{2}$
, and
$x_{3}=s_{3}+t_{2}$
, and
![]() $x_{4}=t_{2}$
(where restrictions to
$x_{4}=t_{2}$
(where restrictions to
![]() $N$
are implicit).
$N$
are implicit).
Next we introduce some subgroups of
![]() $S$
, and use them to produce extensions of
$S$
, and use them to produce extensions of
![]() $N$
. These extensions turn out to control the entire situation, as will be explained. So we let
$N$
. These extensions turn out to control the entire situation, as will be explained. So we let
(The group
![]() $S_{4}$
which could be defined using the same logic will not play any role, as it happens. Also note that among these three, only
$S_{4}$
which could be defined using the same logic will not play any role, as it happens. Also note that among these three, only
![]() $S_{1}$
respects the ambient ‘symmetry’.)
$S_{1}$
respects the ambient ‘symmetry’.)
Lemma 2.5. Using the notation above, the following hold:
(1) the cohomology class of the extension
is $$\begin{eqnarray}0\longrightarrow S/S_{1}\cong \mathbb{F}_{2}\longrightarrow \mathscr{C}(S)/S_{1}\longrightarrow N\longrightarrow 1\end{eqnarray}$$
$$\begin{eqnarray}0\longrightarrow S/S_{1}\cong \mathbb{F}_{2}\longrightarrow \mathscr{C}(S)/S_{1}\longrightarrow N\longrightarrow 1\end{eqnarray}$$
 $x_{2}x_{3}$
;
$x_{2}x_{3}$
;(2) the cohomology class of the extension
is $$\begin{eqnarray}0\longrightarrow S/S_{2}\cong \mathbb{F}_{2}\longrightarrow \mathscr{C}(S)/S_{2}\longrightarrow N\longrightarrow 1\end{eqnarray}$$
$$\begin{eqnarray}0\longrightarrow S/S_{2}\cong \mathbb{F}_{2}\longrightarrow \mathscr{C}(S)/S_{2}\longrightarrow N\longrightarrow 1\end{eqnarray}$$
 $x_{1}x_{3}$
;
$x_{1}x_{3}$
;(3) the cohomology class of the extension
is $$\begin{eqnarray}0\longrightarrow S/S_{3}\cong \mathbb{F}_{2}\longrightarrow \mathscr{C}(S)/S_{3}\longrightarrow N\longrightarrow 1\end{eqnarray}$$
$$\begin{eqnarray}0\longrightarrow S/S_{3}\cong \mathbb{F}_{2}\longrightarrow \mathscr{C}(S)/S_{3}\longrightarrow N\longrightarrow 1\end{eqnarray}$$
 $x_{2}x_{4}$
.
$x_{2}x_{4}$
.
Proof. An element of
![]() $\mathscr{C}(S)$
has the form
$\mathscr{C}(S)$
has the form
 $$\begin{eqnarray}g=\left(\begin{array}{@{}ccccc@{}}1 & 0 & t_{1}(g) & u_{1}(g) & z(g)\\ 0 & 1 & s_{2}(g) & u_{3}(g) & u_{2}(g)\\ 0 & 0 & 1 & s_{3}(g) & t_{2}(g)\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}g=\left(\begin{array}{@{}ccccc@{}}1 & 0 & t_{1}(g) & u_{1}(g) & z(g)\\ 0 & 1 & s_{2}(g) & u_{3}(g) & u_{2}(g)\\ 0 & 0 & 1 & s_{3}(g) & t_{2}(g)\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\end{array}\right).\end{eqnarray}$$
Let us multiply two of these, say
![]() $g$
and
$g$
and
![]() $g^{\prime }$
, using the shorthand
$g^{\prime }$
, using the shorthand
![]() $s_{2}=s_{2}(g)$
and
$s_{2}=s_{2}(g)$
and
![]() $s_{2}^{\prime }=s_{2}(g^{\prime })$
, and so on:
$s_{2}^{\prime }=s_{2}(g^{\prime })$
, and so on:

We shall use the set-theoretic section
![]() $\sec :N\rightarrow \mathscr{C}(S)$
given by
$\sec :N\rightarrow \mathscr{C}(S)$
given by
 $$\begin{eqnarray}\sec (g)=\left(\begin{array}{@{}ccccc@{}}1 & 0 & t_{1}(g) & 0 & 0\\ 0 & 1 & s_{2}(g) & 0 & 0\\ 0 & 0 & 1 & s_{3}(g) & t_{2}(g)\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\sec (g)=\left(\begin{array}{@{}ccccc@{}}1 & 0 & t_{1}(g) & 0 & 0\\ 0 & 1 & s_{2}(g) & 0 & 0\\ 0 & 0 & 1 & s_{3}(g) & t_{2}(g)\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\end{array}\right).\end{eqnarray}$$
Let us prove (1). Using the section
![]() $N\rightarrow \mathscr{C}(S)/S_{1}$
induced by
$N\rightarrow \mathscr{C}(S)/S_{1}$
induced by
![]() $\sec$
, we end up with the bijection of sets
$\sec$
, we end up with the bijection of sets
![]() $\unicode[STIX]{x1D6F7}:S/S_{1}\times N\rightarrow \mathscr{C}(S)/S_{1}$
given by
$\unicode[STIX]{x1D6F7}:S/S_{1}\times N\rightarrow \mathscr{C}(S)/S_{1}$
given by
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}(x,g)=x\sec (g)=\left(\begin{array}{@{}ccccc@{}}1 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & x & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\end{array}\right)\times \sec (g)=\left(\begin{array}{@{}ccccc@{}}1 & 0 & t_{1}(g) & 0 & 0\\ 0 & 1 & s_{2}(g) & x & 0\\ 0 & 0 & 1 & s_{3}(g) & t_{2}(g)\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}(x,g)=x\sec (g)=\left(\begin{array}{@{}ccccc@{}}1 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & x & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\end{array}\right)\times \sec (g)=\left(\begin{array}{@{}ccccc@{}}1 & 0 & t_{1}(g) & 0 & 0\\ 0 & 1 & s_{2}(g) & x & 0\\ 0 & 0 & 1 & s_{3}(g) & t_{2}(g)\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\end{array}\right).\end{eqnarray}$$
Here we have used (∗) to perform the calculation. A caveat: in these expressions, we have identified
![]() $S/S_{1}$
with
$S/S_{1}$
with
![]() $\mathbb{F}_{2}$
(this can be done uniquely!), so that
$\mathbb{F}_{2}$
(this can be done uniquely!), so that
![]() $x\in S/S_{1}$
can be seen as an entry (
$x\in S/S_{1}$
can be seen as an entry (
![]() $0$
or
$0$
or
![]() $1$
) of a matrix. A second caveat is that the matrix displayed is understood modulo
$1$
) of a matrix. A second caveat is that the matrix displayed is understood modulo
![]() $S_{1}$
only.
$S_{1}$
only.
From the theory of group extensions, we have
![]() $\unicode[STIX]{x1D6F7}(x,g)\unicode[STIX]{x1D6F7}(y,g^{\prime })=\unicode[STIX]{x1D6F7}(x+y+c(g,g^{\prime }),gg^{\prime })$
, where the expression
$\unicode[STIX]{x1D6F7}(x,g)\unicode[STIX]{x1D6F7}(y,g^{\prime })=\unicode[STIX]{x1D6F7}(x+y+c(g,g^{\prime }),gg^{\prime })$
, where the expression
![]() $c(g,g^{\prime })$
, is what we are after, that is, it is a two-cocycle representing the cohomology class of the extension under scrutiny. So we compute, from (∗), that
$c(g,g^{\prime })$
, is what we are after, that is, it is a two-cocycle representing the cohomology class of the extension under scrutiny. So we compute, from (∗), that
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}(x,g)\unicode[STIX]{x1D6F7}(y,g^{\prime })=\left(\begin{array}{@{}ccccc@{}}1 & 0 & t_{1}+t_{1}^{\prime } & t_{1}s_{3}^{\prime } & t_{1}t_{2}^{\prime }\\ 0 & 1 & s_{2}+s_{2}^{\prime } & s_{2}s_{3}^{\prime }+x+y & s_{2}t_{2}^{\prime }\\ 0 & 0 & 1 & s_{3}+s_{3}^{\prime } & t_{2}+t_{2}^{\prime }\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}(x,g)\unicode[STIX]{x1D6F7}(y,g^{\prime })=\left(\begin{array}{@{}ccccc@{}}1 & 0 & t_{1}+t_{1}^{\prime } & t_{1}s_{3}^{\prime } & t_{1}t_{2}^{\prime }\\ 0 & 1 & s_{2}+s_{2}^{\prime } & s_{2}s_{3}^{\prime }+x+y & s_{2}t_{2}^{\prime }\\ 0 & 0 & 1 & s_{3}+s_{3}^{\prime } & t_{2}+t_{2}^{\prime }\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\end{array}\right).\end{eqnarray}$$
Another useful computational remark is that, in
![]() $S$
identified with the additive group of
$S$
identified with the additive group of
![]() $2\times 2$
-matrices, we have
$2\times 2$
-matrices, we have
Thus the last matrix displayed, viewed in
![]() $\mathscr{C}(S)/S_{1}$
, is also
$\mathscr{C}(S)/S_{1}$
, is also
 $$\begin{eqnarray}\left(\begin{array}{@{}ccccc@{}}1 & 0 & t_{1}+t_{1}^{\prime } & 0 & 0\\ 0 & 1 & s_{2}+s_{2}^{\prime } & x+y+s_{2}s_{3}^{\prime }+t_{1}s_{3}^{\prime }+s_{2}t_{2}^{\prime }+t_{1}t_{2}^{\prime } & 0\\ 0 & 0 & 1 & s_{3}+s_{3}^{\prime } & t_{2}+t_{2}^{\prime }\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccccc@{}}1 & 0 & t_{1}+t_{1}^{\prime } & 0 & 0\\ 0 & 1 & s_{2}+s_{2}^{\prime } & x+y+s_{2}s_{3}^{\prime }+t_{1}s_{3}^{\prime }+s_{2}t_{2}^{\prime }+t_{1}t_{2}^{\prime } & 0\\ 0 & 0 & 1 & s_{3}+s_{3}^{\prime } & t_{2}+t_{2}^{\prime }\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\end{array}\right).\end{eqnarray}$$
We conclude that, as predicted,
![]() $c(g,g^{\prime })=s_{2}(g)s_{3}(g^{\prime })+t_{1}(g)s_{3}(g^{\prime })+s_{2}(g)t_{2}(g^{\prime })+t_{1}(g)t_{2}(g^{\prime })=x_{2}(g)x_{3}(g^{\prime })$
, and
$c(g,g^{\prime })=s_{2}(g)s_{3}(g^{\prime })+t_{1}(g)s_{3}(g^{\prime })+s_{2}(g)t_{2}(g^{\prime })+t_{1}(g)t_{2}(g^{\prime })=x_{2}(g)x_{3}(g^{\prime })$
, and
![]() $c$
is indeed the cup-product of
$c$
is indeed the cup-product of
![]() $x_{2}$
and
$x_{2}$
and
![]() $x_{3}$
.
$x_{3}$
.
The proofs of (2) and (3) are similar. ◻
Remark 2.6. Note that in each case
![]() $\mathscr{C}(S)/S_{i}\cong C_{2}^{2}\times D_{4}$
.
$\mathscr{C}(S)/S_{i}\cong C_{2}^{2}\times D_{4}$
.
3 The fundamental cup-products
In this section, we prove Theorem A, as stated in the Introduction. We shall see that we are led naturally to another statement first, in which the following notation is used. When
![]() $a\in F$
, we put
$a\in F$
, we put
![]() $F_{a}=F[X]/(X^{2}-a)$
. When
$F_{a}=F[X]/(X^{2}-a)$
. When
![]() $e+fX\in F_{a}$
, we define its norm to be
$e+fX\in F_{a}$
, we define its norm to be
![]() $\operatorname{N}_{F_{a}/F}(e+fX)=e^{2}-af^{2}$
. When a square root
$\operatorname{N}_{F_{a}/F}(e+fX)=e^{2}-af^{2}$
. When a square root
![]() $\sqrt{a}$
has been chosen in some field containing
$\sqrt{a}$
has been chosen in some field containing
![]() $F$
, there is a homomorphism
$F$
, there is a homomorphism
![]() $F_{a}\rightarrow F[\sqrt{a}]$
mapping
$F_{a}\rightarrow F[\sqrt{a}]$
mapping
![]() $X$
to
$X$
to
![]() $\sqrt{a}$
. Of course when
$\sqrt{a}$
. Of course when
![]() $a$
is not a square in
$a$
is not a square in
![]() $F$
, this map is an isomorphism of extensions of
$F$
, this map is an isomorphism of extensions of
![]() $F$
, and the norm just introduced coincides with the usual norm map between fields. However, it is useful to work with
$F$
, and the norm just introduced coincides with the usual norm map between fields. However, it is useful to work with
![]() $F_{a}$
for those occasions when
$F_{a}$
for those occasions when
![]() $a$
is already a square in
$a$
is already a square in
![]() $F$
.
$F$
.
We start by the implication
![]() $(1)\;\Longrightarrow \;(2)$
from Theorem A.
$(1)\;\Longrightarrow \;(2)$
from Theorem A.
3.1 Proving that the four cup-products vanish
Theorem 3.1. Let
![]() $F$
be a field of characteristic not
$F$
be a field of characteristic not
![]() $2$
, let
$2$
, let
![]() $a,b,c,d\in F^{\times }$
be given and put
$a,b,c,d\in F^{\times }$
be given and put
![]() $E:=F[\sqrt{a},\sqrt{d}]$
. Suppose there exist a continuous homomorphism
$E:=F[\sqrt{a},\sqrt{d}]$
. Suppose there exist a continuous homomorphism
![]() $\overline{\unicode[STIX]{x1D711}}:G_{F}\rightarrow \overline{\mathbb{U}}_{5}(\mathbb{F}_{2})$
such that
$\overline{\unicode[STIX]{x1D711}}:G_{F}\rightarrow \overline{\mathbb{U}}_{5}(\mathbb{F}_{2})$
such that
![]() $\unicode[STIX]{x1D712}_{a}=s_{1}\circ \overline{\unicode[STIX]{x1D711}}$
,
$\unicode[STIX]{x1D712}_{a}=s_{1}\circ \overline{\unicode[STIX]{x1D711}}$
,
![]() $\unicode[STIX]{x1D712}_{b}=s_{2}\circ \overline{\unicode[STIX]{x1D711}}$
,
$\unicode[STIX]{x1D712}_{b}=s_{2}\circ \overline{\unicode[STIX]{x1D711}}$
,
![]() $\unicode[STIX]{x1D712}_{c}=s_{3}\circ \overline{\unicode[STIX]{x1D711}}$
, and
$\unicode[STIX]{x1D712}_{c}=s_{3}\circ \overline{\unicode[STIX]{x1D711}}$
, and
![]() $\unicode[STIX]{x1D712}_{d}=s_{4}\circ \overline{\unicode[STIX]{x1D711}}$
. (In other words, we assume that
$\unicode[STIX]{x1D712}_{d}=s_{4}\circ \overline{\unicode[STIX]{x1D711}}$
. (In other words, we assume that
![]() $\langle a,b,c,d\rangle$
is defined.) Then there exist
$\langle a,b,c,d\rangle$
is defined.) Then there exist
![]() $\widetilde{B}\in F_{a}$
and
$\widetilde{B}\in F_{a}$
and
![]() $\widetilde{C}\in F_{d}$
such that the following hold, where
$\widetilde{C}\in F_{d}$
such that the following hold, where
![]() $B$
denotes the image of
$B$
denotes the image of
![]() $\widetilde{B}$
under
$\widetilde{B}$
under
![]() $F_{a}\rightarrow F[\sqrt{a}]$
and
$F_{a}\rightarrow F[\sqrt{a}]$
and
![]() $C$
denotes the image of
$C$
denotes the image of
![]() $\widetilde{C}$
under
$\widetilde{C}$
under
![]() $F_{d}\rightarrow F[\sqrt{d}]$
.
$F_{d}\rightarrow F[\sqrt{d}]$
.
(1) One has
 $\operatorname{N}_{F_{a}/F}(\widetilde{B})=b$
modulo squares and
$\operatorname{N}_{F_{a}/F}(\widetilde{B})=b$
modulo squares and
 $\operatorname{N}_{F_{d}/F}(\widetilde{C})=c$
modulo squares.
$\operatorname{N}_{F_{d}/F}(\widetilde{C})=c$
modulo squares.(2) One has
 $(B,c)_{F[\sqrt{a}]}=0$
,
$(B,c)_{F[\sqrt{a}]}=0$
,
 $(b,C)_{F[\sqrt{d}]}=0$
, and
$(b,C)_{F[\sqrt{d}]}=0$
, and
 $(b,c)_{F}=0$
.
$(b,c)_{F}=0$
.(3) There is a class
 $u\in \operatorname{H}^{2}(F,\mathbb{F}_{2})$
whose image under the canonical restriction map
$u\in \operatorname{H}^{2}(F,\mathbb{F}_{2})$
whose image under the canonical restriction map
 $\operatorname{H}^{2}(F,\,\mathbb{F}_{2})\longrightarrow \operatorname{H}^{2}(E,\mathbb{F}_{2})$
is
$\operatorname{H}^{2}(F,\,\mathbb{F}_{2})\longrightarrow \operatorname{H}^{2}(E,\mathbb{F}_{2})$
is
 $(B,C)_{E}$
.
$(B,C)_{E}$
.(4) Suppose that
 $\overline{\unicode[STIX]{x1D711}}$
can be lifted to
$\overline{\unicode[STIX]{x1D711}}$
can be lifted to
 $\unicode[STIX]{x1D711}:G_{F}\rightarrow \mathbb{U}_{5}(\mathbb{F}_{2})$
. (In other words, assume that
$\unicode[STIX]{x1D711}:G_{F}\rightarrow \mathbb{U}_{5}(\mathbb{F}_{2})$
. (In other words, assume that
 $\langle a,b,c,d\rangle$
vanishes.) Then one has
$\langle a,b,c,d\rangle$
vanishes.) Then one has
 $(B,C)_{E}=0$
.
$(B,C)_{E}=0$
.
Note that the mere existence of
![]() $\widetilde{B}$
and
$\widetilde{B}$
and
![]() $\widetilde{C}$
implies also that
$\widetilde{C}$
implies also that
![]() $(a,b)_{F}=0$
and
$(a,b)_{F}=0$
and
![]() $(c,d)_{F}=0$
, by Proposition 2.3.
$(c,d)_{F}=0$
, by Proposition 2.3.
Proof. First we consider the composition
Projecting further onto the left factor, we make a first use of Proposition 2.3. We draw the existence of
![]() $x,y,z\in F$
satisfying
$x,y,z\in F$
satisfying
![]() $x^{2}-ay^{2}=bz^{2}$
, that is
$x^{2}-ay^{2}=bz^{2}$
, that is
![]() $\operatorname{N}_{F_{a}/F}(\widetilde{B})=bz^{2}$
, with
$\operatorname{N}_{F_{a}/F}(\widetilde{B})=bz^{2}$
, with
![]() $\widetilde{B}=x+yX\in F_{a}$
. If
$\widetilde{B}=x+yX\in F_{a}$
. If
![]() $B=x+y\sqrt{a}$
is the corresponding element, then the proposition says that we can arrange to have
$B=x+y\sqrt{a}$
is the corresponding element, then the proposition says that we can arrange to have
![]() $\unicode[STIX]{x1D712}_{bB}=t_{1}\circ \overline{\unicode[STIX]{x1D711}}=x_{1}\circ \overline{\unicode[STIX]{x1D711}}$
,
$\unicode[STIX]{x1D712}_{bB}=t_{1}\circ \overline{\unicode[STIX]{x1D711}}=x_{1}\circ \overline{\unicode[STIX]{x1D711}}$
,
![]() $\unicode[STIX]{x1D712}_{B}=(s_{2}+t_{1})\circ \overline{\unicode[STIX]{x1D711}}=x_{2}\circ \overline{\unicode[STIX]{x1D711}}$
. (We fully use the notation from § 2.4.)
$\unicode[STIX]{x1D712}_{B}=(s_{2}+t_{1})\circ \overline{\unicode[STIX]{x1D711}}=x_{2}\circ \overline{\unicode[STIX]{x1D711}}$
. (We fully use the notation from § 2.4.)
Using the right factor, we find elements
![]() $\widetilde{C}$
and
$\widetilde{C}$
and
![]() $C$
similarly, such that
$C$
similarly, such that
![]() $\unicode[STIX]{x1D712}_{C}=x_{3}\circ \overline{\unicode[STIX]{x1D711}}$
,
$\unicode[STIX]{x1D712}_{C}=x_{3}\circ \overline{\unicode[STIX]{x1D711}}$
,
![]() $\unicode[STIX]{x1D712}_{cC}=x_{4}\circ \overline{\unicode[STIX]{x1D711}}$
. This also proves the first assertion.
$\unicode[STIX]{x1D712}_{cC}=x_{4}\circ \overline{\unicode[STIX]{x1D711}}$
. This also proves the first assertion.
We prove that the cup-products vanish as announced in the second assertion, starting with
![]() $(b,c)_{F}=0$
(which of course does not depend on the choices for
$(b,c)_{F}=0$
(which of course does not depend on the choices for
![]() $B$
and
$B$
and
![]() $C$
). For this, consider the map
$C$
). For this, consider the map
which discards the top row and the rightmost column of an element of
![]() $\mathbb{U}_{5}(\mathbb{F}_{2})$
; this factors through
$\mathbb{U}_{5}(\mathbb{F}_{2})$
; this factors through
![]() $\overline{U}_{5}(\mathbb{F}_{2})$
. Postcomposing
$\overline{U}_{5}(\mathbb{F}_{2})$
. Postcomposing
![]() $\overline{\unicode[STIX]{x1D711}}$
with this, we draw from Proposition 2.3 that
$\overline{\unicode[STIX]{x1D711}}$
with this, we draw from Proposition 2.3 that
![]() $(b,c)_{F}=0$
, as required.
$(b,c)_{F}=0$
, as required.
Next we turn to the proof of
![]() $(B,c)_{F[\sqrt{a}]}=0$
, the cup-product
$(B,c)_{F[\sqrt{a}]}=0$
, the cup-product
![]() $(b,C)_{F[\sqrt{d}]}$
being treated in a similar way. Define a group homomorphism
$(b,C)_{F[\sqrt{d}]}$
being treated in a similar way. Define a group homomorphism
![]() $\unicode[STIX]{x1D70B}:\ker (s_{1})\subset \overline{\mathbb{U}}_{5}(\mathbb{F}_{2})\rightarrow \mathbb{U}_{3}(\mathbb{F}_{2})=D_{4}$
by
$\unicode[STIX]{x1D70B}:\ker (s_{1})\subset \overline{\mathbb{U}}_{5}(\mathbb{F}_{2})\rightarrow \mathbb{U}_{3}(\mathbb{F}_{2})=D_{4}$
by
 $$\begin{eqnarray}g\mapsto \left(\begin{array}{@{}ccc@{}}1 & t_{1}(g) & u_{1}(g)\\ 0 & 1 & s_{3}(g)\\ 0 & 0 & 1\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}g\mapsto \left(\begin{array}{@{}ccc@{}}1 & t_{1}(g) & u_{1}(g)\\ 0 & 1 & s_{3}(g)\\ 0 & 0 & 1\end{array}\right).\end{eqnarray}$$
One checks that
![]() $\unicode[STIX]{x1D70B}$
is well defined. Note that
$\unicode[STIX]{x1D70B}$
is well defined. Note that
![]() $\unicode[STIX]{x1D70B}\circ \overline{\unicode[STIX]{x1D711}}:G_{F[\sqrt{a}]}\rightarrow D_{4}$
is a lift for
$\unicode[STIX]{x1D70B}\circ \overline{\unicode[STIX]{x1D711}}:G_{F[\sqrt{a}]}\rightarrow D_{4}$
is a lift for
![]() $(t_{1}\circ \overline{\unicode[STIX]{x1D711}},s_{3}\circ \overline{\unicode[STIX]{x1D711}}):G_{F[\sqrt{a}]}\rightarrow \mathbb{F}_{2}\times \mathbb{F}_{2}$
(using that
$(t_{1}\circ \overline{\unicode[STIX]{x1D711}},s_{3}\circ \overline{\unicode[STIX]{x1D711}}):G_{F[\sqrt{a}]}\rightarrow \mathbb{F}_{2}\times \mathbb{F}_{2}$
(using that
![]() $G_{F[\sqrt{a}]}=\overline{\unicode[STIX]{x1D711}}^{-1}(\ker (s_{1}))$
). Therefore, we see from Proposition 2.3 that the cup product of
$G_{F[\sqrt{a}]}=\overline{\unicode[STIX]{x1D711}}^{-1}(\ker (s_{1}))$
). Therefore, we see from Proposition 2.3 that the cup product of
![]() $t_{1}\circ \overline{\unicode[STIX]{x1D711}}$
and
$t_{1}\circ \overline{\unicode[STIX]{x1D711}}$
and
![]() $s_{3}\circ \overline{\unicode[STIX]{x1D711}}$
is zero. This means, in alternative notation, that
$s_{3}\circ \overline{\unicode[STIX]{x1D711}}$
is zero. This means, in alternative notation, that
![]() $(Bb,c)_{F[\sqrt{a}]}=0$
, so
$(Bb,c)_{F[\sqrt{a}]}=0$
, so
![]() $(B,c)_{F[\sqrt{a}]}=0$
.
$(B,c)_{F[\sqrt{a}]}=0$
.
We now turn to the third assertion. Let
![]() $\unicode[STIX]{x1D6FC}$
be the cohomology class of the extension
$\unicode[STIX]{x1D6FC}$
be the cohomology class of the extension
Let us write down an explicit two-cocycle
![]() $\unicode[STIX]{x1D6FE}$
representing
$\unicode[STIX]{x1D6FE}$
representing
![]() $\unicode[STIX]{x1D6FC}$
. First, recall the functions
$\unicode[STIX]{x1D6FC}$
. First, recall the functions
![]() $s_{1},t_{1},\ldots :\mathbb{U}_{5}(\mathbb{F}_{2})\rightarrow \mathbb{F}_{2}$
introduced in § 2.1. Multiplying two matrices
$s_{1},t_{1},\ldots :\mathbb{U}_{5}(\mathbb{F}_{2})\rightarrow \mathbb{F}_{2}$
introduced in § 2.1. Multiplying two matrices
![]() $g,h\in \mathbb{U}_{5}(\mathbb{F}_{2})$
, the top-right coefficient must be
$g,h\in \mathbb{U}_{5}(\mathbb{F}_{2})$
, the top-right coefficient must be
![]() $z(g)+z(h)+\unicode[STIX]{x1D6FE}(g,h)$
, and we deduce
$z(g)+z(h)+\unicode[STIX]{x1D6FE}(g,h)$
, and we deduce
To obtain a two-cocycle representing the pull-back
![]() $\overline{\unicode[STIX]{x1D711}}^{\ast }(\unicode[STIX]{x1D6FC})\in \operatorname{H}^{2}(F,\mathbb{F}_{2})$
, we only need compose with
$\overline{\unicode[STIX]{x1D711}}^{\ast }(\unicode[STIX]{x1D6FC})\in \operatorname{H}^{2}(F,\mathbb{F}_{2})$
, we only need compose with
![]() $\overline{\unicode[STIX]{x1D711}}$
. Restricting to the subgroup
$\overline{\unicode[STIX]{x1D711}}$
. Restricting to the subgroup
![]() $G_{E}$
where
$G_{E}$
where
![]() $s_{1}\circ \overline{\unicode[STIX]{x1D711}}$
and
$s_{1}\circ \overline{\unicode[STIX]{x1D711}}$
and
![]() $s_{4}\circ \overline{\unicode[STIX]{x1D711}}$
both vanish, we obtain that
$s_{4}\circ \overline{\unicode[STIX]{x1D711}}$
both vanish, we obtain that
![]() $\overline{\unicode[STIX]{x1D711}}^{\ast }(\unicode[STIX]{x1D6FC})_{E}$
is represented by the two-cocyle
$\overline{\unicode[STIX]{x1D711}}^{\ast }(\unicode[STIX]{x1D6FC})_{E}$
is represented by the two-cocyle
It follows that
![]() $\overline{\unicode[STIX]{x1D711}}^{\ast }(\unicode[STIX]{x1D6FC})_{E}=t_{1}\circ \overline{\unicode[STIX]{x1D711}}\cup t_{2}\circ \overline{\unicode[STIX]{x1D711}}$
, the cup-product of the classes
$\overline{\unicode[STIX]{x1D711}}^{\ast }(\unicode[STIX]{x1D6FC})_{E}=t_{1}\circ \overline{\unicode[STIX]{x1D711}}\cup t_{2}\circ \overline{\unicode[STIX]{x1D711}}$
, the cup-product of the classes
![]() $t_{i}\circ \overline{\unicode[STIX]{x1D711}}\in \operatorname{H}^{1}(E,\mathbb{F}_{2})$
. Or in other words
$t_{i}\circ \overline{\unicode[STIX]{x1D711}}\in \operatorname{H}^{1}(E,\mathbb{F}_{2})$
. Or in other words
![]() $\overline{\unicode[STIX]{x1D711}}^{\ast }(\unicode[STIX]{x1D6FC})_{E}=(bB,cC)_{E}$
.
$\overline{\unicode[STIX]{x1D711}}^{\ast }(\unicode[STIX]{x1D6FC})_{E}=(bB,cC)_{E}$
.
Given that
![]() $(B,c)_{F[\sqrt{a}]}=0$
,
$(B,c)_{F[\sqrt{a}]}=0$
,
![]() $(b,C)_{F[\sqrt{d}]}=0$
, and
$(b,C)_{F[\sqrt{d}]}=0$
, and
![]() $(b,c)_{F}=0$
, it follows that one has
$(b,c)_{F}=0$
, it follows that one has
![]() $u=\unicode[STIX]{x1D711}^{\ast }(\unicode[STIX]{x1D6FC})\in \operatorname{H}^{2}(F,\mathbb{F}_{2})$
satisfies
$u=\unicode[STIX]{x1D711}^{\ast }(\unicode[STIX]{x1D6FC})\in \operatorname{H}^{2}(F,\mathbb{F}_{2})$
satisfies
![]() $u_{E}=(B,C)_{E}$
.
$u_{E}=(B,C)_{E}$
.
Finally, suppose that
![]() $\unicode[STIX]{x1D711}$
exists as in the fourth assertion. We note that
$\unicode[STIX]{x1D711}$
exists as in the fourth assertion. We note that
![]() $G_{E}=\unicode[STIX]{x1D711}^{-1}(\mathscr{C}(S))$
(again the notation
$G_{E}=\unicode[STIX]{x1D711}^{-1}(\mathscr{C}(S))$
(again the notation
![]() $\mathscr{C}(S)$
for the centralizer of
$\mathscr{C}(S)$
for the centralizer of
![]() $S$
is from § 2.4, and we had noted
$S$
is from § 2.4, and we had noted
![]() $\mathscr{C}(S)=\ker (s_{1})\,\cap \,\ker (s_{4})$
). The composition
$\mathscr{C}(S)=\ker (s_{1})\,\cap \,\ker (s_{4})$
). The composition
factors via
![]() $\mathscr{C}(S)/S_{i}$
(for
$\mathscr{C}(S)/S_{i}$
(for
![]() $i=1,2,3$
), so from the Lemma 2.5, we must have
$i=1,2,3$
), so from the Lemma 2.5, we must have
![]() $f^{\ast }(x_{2}x_{3})=0$
,
$f^{\ast }(x_{2}x_{3})=0$
,
![]() $f^{\ast }(x_{1}x_{3})=0$
and
$f^{\ast }(x_{1}x_{3})=0$
and
![]() $f^{\ast }(x_{2}x_{4})=0$
. But these translate as
$f^{\ast }(x_{2}x_{4})=0$
. But these translate as
![]() $(B,C)_{E}=0$
, which we were after, and
$(B,C)_{E}=0$
, which we were after, and
![]() $(bB,C)_{E}=0$
,
$(bB,C)_{E}=0$
,
![]() $(B,cC)_{E}=0$
, consistently with the above.◻
$(B,cC)_{E}=0$
, consistently with the above.◻
3.2 Shapiro’s lemma and the converse
Let
![]() $G$
be a finite group, let
$G$
be a finite group, let
![]() $N$
be a subgroup, and let
$N$
be a subgroup, and let
![]() $k$
be a field. For any
$k$
be a field. For any
![]() $kN$
-module
$kN$
-module
![]() $A$
, we let
$A$
, we let
![]() $\operatorname{Coind}_{N}^{G}(A)$
denote
$\operatorname{Coind}_{N}^{G}(A)$
denote
![]() $\operatorname{Hom}_{N}(kG,A)$
, which is a (left)
$\operatorname{Hom}_{N}(kG,A)$
, which is a (left)
![]() $kG$
-module with action
$kG$
-module with action
![]() $(\unicode[STIX]{x1D70E}\cdot f)(x)=f(x\unicode[STIX]{x1D70E})$
. (We are thinking of
$(\unicode[STIX]{x1D70E}\cdot f)(x)=f(x\unicode[STIX]{x1D70E})$
. (We are thinking of
![]() $G$
and
$G$
and
![]() $N$
as being the groups bearing those names in the discussion above, with
$N$
as being the groups bearing those names in the discussion above, with
![]() $k=\mathbb{F}_{2}$
, and
$k=\mathbb{F}_{2}$
, and
![]() $A$
having trivial action.) The well-known Shapiro’s lemma states the existence of an isomorphism
$A$
having trivial action.) The well-known Shapiro’s lemma states the existence of an isomorphism
More precisely, the map is obtained using
![]() $\operatorname{ev}:\operatorname{Coind}_{N}^{G}(A)\rightarrow A$
which evaluates at
$\operatorname{ev}:\operatorname{Coind}_{N}^{G}(A)\rightarrow A$
which evaluates at
![]() $1\in G$
, followed by restriction (in cohomology) to
$1\in G$
, followed by restriction (in cohomology) to
![]() $N$
. Note, if the class
$N$
. Note, if the class
![]() $\unicode[STIX]{x1D6FC}\in \operatorname{H}^{2}(G,\operatorname{Coind}_{N}^{G}(A))$
describes the extension
$\unicode[STIX]{x1D6FC}\in \operatorname{H}^{2}(G,\operatorname{Coind}_{N}^{G}(A))$
describes the extension
then
![]() $sh(\unicode[STIX]{x1D6FC})$
corresponds to
$sh(\unicode[STIX]{x1D6FC})$
corresponds to
as is easily verified.
In order to recognize that a given
![]() $G$
-module, say
$G$
-module, say
![]() $S$
, is isomorphic to
$S$
, is isomorphic to
![]() $\operatorname{Coind}_{N}^{G}(A)$
for some
$\operatorname{Coind}_{N}^{G}(A)$
for some
![]() $A$
, let us merely consider the case where
$A$
, let us merely consider the case where
![]() $A=k^{r}$
with trivial
$A=k^{r}$
with trivial
![]() $N$
-action, and assume that
$N$
-action, and assume that
![]() $N$
is normal in
$N$
is normal in
![]() $G$
to boot. Then
$G$
to boot. Then
![]() $\operatorname{Coind}_{N}^{G}(A)=(k[G/N]^{\ast })^{r}$
. The dual module
$\operatorname{Coind}_{N}^{G}(A)=(k[G/N]^{\ast })^{r}$
. The dual module
![]() $(k[G/N])^{\ast }$
is free of rank one, that is, it is isomorphic to
$(k[G/N])^{\ast }$
is free of rank one, that is, it is isomorphic to
![]() $k[G/N]$
. (Consider the map taking
$k[G/N]$
. (Consider the map taking
![]() $1\in G$
to
$1\in G$
to
![]() $\unicode[STIX]{x1D6FF}_{1}$
, the Dirac delta function at
$\unicode[STIX]{x1D6FF}_{1}$
, the Dirac delta function at
![]() $1$
. Thus,
$1$
. Thus,
![]() $\unicode[STIX]{x1D6FF}_{1}(N)=1$
and
$\unicode[STIX]{x1D6FF}_{1}(N)=1$
and
![]() $\unicode[STIX]{x1D6FF}_{1}(g\cdot N)=0$
if
$\unicode[STIX]{x1D6FF}_{1}(g\cdot N)=0$
if
![]() $g\notin N$
.) We conclude that
$g\notin N$
.) We conclude that
![]() $S$
is isomorphic to
$S$
is isomorphic to
![]() $\operatorname{Coind}_{N}^{G}(k^{r})$
if and only if
$\operatorname{Coind}_{N}^{G}(k^{r})$
if and only if
![]() $N$
acts trivially and we can find a basis for
$N$
acts trivially and we can find a basis for
![]() $S$
as a free
$S$
as a free
![]() $k[G/N]$
of rank
$k[G/N]$
of rank
![]() $r$
. If this basis is
$r$
. If this basis is
![]() $\unicode[STIX]{x1D700}_{1},\ldots ,\unicode[STIX]{x1D700}_{r}$
, then
$\unicode[STIX]{x1D700}_{1},\ldots ,\unicode[STIX]{x1D700}_{r}$
, then
![]() $\ker (ev)$
is the
$\ker (ev)$
is the
![]() $k$
-vector space spanned by
$k$
-vector space spanned by
![]() $g\unicode[STIX]{x1D700}_{i}$
, for
$g\unicode[STIX]{x1D700}_{i}$
, for
![]() $g\in G$
,
$g\in G$
,
![]() $g\neq 1$
,
$g\neq 1$
,
![]() $i=1,\ldots ,r$
.
$i=1,\ldots ,r$
.
For example, let
![]() $G,N,S$
recover their concrete meanings as in § 2.4 (all the accompanying notation will be used, too). Then Lemma 2.4 asserts that
$G,N,S$
recover their concrete meanings as in § 2.4 (all the accompanying notation will be used, too). Then Lemma 2.4 asserts that
![]() $S\cong \operatorname{Coind}_{N}^{G}(\mathbb{F}_{2})$
, in such a way that
$S\cong \operatorname{Coind}_{N}^{G}(\mathbb{F}_{2})$
, in such a way that
![]() $\ker (ev)$
is identified with
$\ker (ev)$
is identified with
![]() $S_{1}$
. As a result, the cohomology class of
$S_{1}$
. As a result, the cohomology class of
corresponds via
![]() $sh$
to the cohomology class of the first extension treated in Lemma 2.5, that is,
$sh$
to the cohomology class of the first extension treated in Lemma 2.5, that is,
![]() $x_{2}x_{3}$
.
$x_{2}x_{3}$
.
But
![]() $S$
can be regarded in another way. Consider the subgroup
$S$
can be regarded in another way. Consider the subgroup
![]() $G^{\prime }\subset G$
of elements mapping into
$G^{\prime }\subset G$
of elements mapping into
![]() $\langle \unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{4}\rangle$
under
$\langle \unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{4}\rangle$
under
![]() $G\rightarrow G/N$
(equivalently,
$G\rightarrow G/N$
(equivalently,
![]() $g\in G^{\prime }$
if
$g\in G^{\prime }$
if
![]() $s_{1}(g)=s_{4}(g)$
), and view
$s_{1}(g)=s_{4}(g)$
), and view
![]() $S$
as a
$S$
as a
![]() $G^{\prime }$
-module. Lemma 2.4 shows that
$G^{\prime }$
-module. Lemma 2.4 shows that
![]() $S$
is a free
$S$
is a free
![]() $\mathbb{F}_{2}[\langle \unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{4}\rangle ]=\mathbb{F}_{2}[G^{\prime }/N]$
-module, with basis
$\mathbb{F}_{2}[\langle \unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{4}\rangle ]=\mathbb{F}_{2}[G^{\prime }/N]$
-module, with basis
![]() $e_{1},e_{2}$
(or alternatively
$e_{1},e_{2}$
(or alternatively
![]() $e_{1},e_{3}$
). Thus we also have
$e_{1},e_{3}$
). Thus we also have
![]() $S\cong \operatorname{Coind}_{N}^{G^{\prime }}(\mathbb{F}_{2}\oplus \mathbb{F}_{2})$
, and
$S\cong \operatorname{Coind}_{N}^{G^{\prime }}(\mathbb{F}_{2}\oplus \mathbb{F}_{2})$
, and
![]() $\ker (ev)$
is spanned by
$\ker (ev)$
is spanned by
![]() $e_{3},e_{4}$
(or
$e_{3},e_{4}$
(or
![]() $e_{2},e_{4}$
in the alternative). Now the cohomology class of
$e_{2},e_{4}$
in the alternative). Now the cohomology class of
where
![]() $\mathbb{U}_{5}(\mathbb{F}_{2})^{\prime }$
is the preimage of
$\mathbb{U}_{5}(\mathbb{F}_{2})^{\prime }$
is the preimage of
![]() $G^{\prime }$
, is taken by Shapiro to that of the extension
$G^{\prime }$
, is taken by Shapiro to that of the extension
This extension is described by two classes in
![]() $\operatorname{H}^{2}(N,\mathbb{F}_{2})$
, corresponding to the exact sequences obtained by factoring out
$\operatorname{H}^{2}(N,\mathbb{F}_{2})$
, corresponding to the exact sequences obtained by factoring out
![]() $e_{1}$
and
$e_{1}$
and
![]() $e_{2}$
respectively. From Lemma 2.5, these are
$e_{2}$
respectively. From Lemma 2.5, these are
![]() $x_{1}x_{3}$
and
$x_{1}x_{3}$
and
![]() $x_{2}x_{3}$
respectively. With the alternative choice of basis for
$x_{2}x_{3}$
respectively. With the alternative choice of basis for
![]() $S$
, this discussion ends with
$S$
, this discussion ends with
![]() $x_{2}x_{4}$
and
$x_{2}x_{4}$
and
![]() $x_{2}x_{3}$
.
$x_{2}x_{3}$
.
There is a well-known version of Shapiro’s lemma for profinite groups (cf. [Reference Neukirch, Schmidt and WingbergNSW08, ch. 1, § 6]), which can be deduced from the version mentioned above using a straightforward limit argument. We record this version below in the context of Galois cohomology, since we will use it later on.
Lemma 3.2. Let
![]() $E/F$
be a finite Galois extension, let
$E/F$
be a finite Galois extension, let
![]() $A$
be a trivial, discrete
$A$
be a trivial, discrete
![]() $G_{E}$
-module, and consider
$G_{E}$
-module, and consider
![]() $\operatorname{Coind}_{G_{E}}^{G_{F}}(A)$
, a discrete
$\operatorname{Coind}_{G_{E}}^{G_{F}}(A)$
, a discrete
![]() $G_{F}$
-module. Then Shapiro’s map
$G_{F}$
-module. Then Shapiro’s map
defined as above, is an isomorphism.
With the preparations above, we can now prove our primary converse to Theorem 3.1.
Theorem 3.3. Let
![]() $F$
be a field of characteristic not
$F$
be a field of characteristic not
![]() $2$
, let
$2$
, let
![]() $a,b,c,d\in F^{\times }$
be given, and put
$a,b,c,d\in F^{\times }$
be given, and put
![]() $E:=F[\sqrt{a},\sqrt{d}]$
. Assume that there exist
$E:=F[\sqrt{a},\sqrt{d}]$
. Assume that there exist
![]() $\widetilde{B}\in F_{a}$
such that
$\widetilde{B}\in F_{a}$
such that
![]() $\operatorname{N}_{F_{a}/F}(\widetilde{B})=b$
modulo squares, and
$\operatorname{N}_{F_{a}/F}(\widetilde{B})=b$
modulo squares, and
![]() $\widetilde{C}\in F_{d}$
such that
$\widetilde{C}\in F_{d}$
such that
![]() $\operatorname{N}_{F_{d}/F}(\widetilde{C})=c$
modulo squares, with the following additional property: if
$\operatorname{N}_{F_{d}/F}(\widetilde{C})=c$
modulo squares, with the following additional property: if
![]() $B$
denotes the image of
$B$
denotes the image of
![]() $\widetilde{B}$
under
$\widetilde{B}$
under
![]() $F_{a}\rightarrow F[\sqrt{a}]$
and
$F_{a}\rightarrow F[\sqrt{a}]$
and
![]() $C$
denotes the image of
$C$
denotes the image of
![]() $\widetilde{C}$
under
$\widetilde{C}$
under
![]() $F_{d}\rightarrow F[\sqrt{d}]$
, then one has
$F_{d}\rightarrow F[\sqrt{d}]$
, then one has
![]() $(B,C)_{E}=(B,c)_{E}=(b,C)_{E}=(b,c)_{E}=0$
.
$(B,C)_{E}=(B,c)_{E}=(b,C)_{E}=(b,c)_{E}=0$
.
Then there exist a continuous homomorphism
![]() $\unicode[STIX]{x1D711}:G_{F}\rightarrow \mathbb{U}_{5}(\mathbb{F}_{2})$
such that
$\unicode[STIX]{x1D711}:G_{F}\rightarrow \mathbb{U}_{5}(\mathbb{F}_{2})$
such that
![]() $s_{1}\circ \unicode[STIX]{x1D711}=\unicode[STIX]{x1D712}_{a}$
,
$s_{1}\circ \unicode[STIX]{x1D711}=\unicode[STIX]{x1D712}_{a}$
,
![]() $s_{2}\circ \unicode[STIX]{x1D711}=\unicode[STIX]{x1D712}_{b}$
,
$s_{2}\circ \unicode[STIX]{x1D711}=\unicode[STIX]{x1D712}_{b}$
,
![]() $s_{3}\circ \unicode[STIX]{x1D711}=\unicode[STIX]{x1D712}_{c}$
and
$s_{3}\circ \unicode[STIX]{x1D711}=\unicode[STIX]{x1D712}_{c}$
and
![]() $s_{4}\circ \unicode[STIX]{x1D711}=\unicode[STIX]{x1D712}_{d}$
. In other words, the Massey product
$s_{4}\circ \unicode[STIX]{x1D711}=\unicode[STIX]{x1D712}_{d}$
. In other words, the Massey product
![]() $\langle a,b,c,d\rangle$
is defined and vanishes.
$\langle a,b,c,d\rangle$
is defined and vanishes.
Proof. We start by assuming that neither
![]() $a$
nor
$a$
nor
![]() $d$
is a square in
$d$
is a square in
![]() $F$
(we identify
$F$
(we identify
![]() $F_{a}$
and
$F_{a}$
and
![]() $F_{d}$
with
$F_{d}$
with
![]() $F[\sqrt{a}]$
and
$F[\sqrt{a}]$
and
![]() $F[\sqrt{d}]$
respectively). From Proposition 2.3 (applied twice), we obtain a homomorphism
$F[\sqrt{d}]$
respectively). From Proposition 2.3 (applied twice), we obtain a homomorphism
such that
![]() $s_{i}\circ f=\unicode[STIX]{x1D712}_{a},\unicode[STIX]{x1D712}_{b},\unicode[STIX]{x1D712}_{c},\unicode[STIX]{x1D712}_{d}$
according as
$s_{i}\circ f=\unicode[STIX]{x1D712}_{a},\unicode[STIX]{x1D712}_{b},\unicode[STIX]{x1D712}_{c},\unicode[STIX]{x1D712}_{d}$
according as
![]() $i=1,2,3,4$
, and also
$i=1,2,3,4$
, and also
![]() $f^{\ast }(x_{1})=\unicode[STIX]{x1D712}_{bB}$
,
$f^{\ast }(x_{1})=\unicode[STIX]{x1D712}_{bB}$
,
![]() $f^{\ast }(x_{2})=\unicode[STIX]{x1D712}_{B}$
,
$f^{\ast }(x_{2})=\unicode[STIX]{x1D712}_{B}$
,
![]() $f^{\ast }(x_{3})=\unicode[STIX]{x1D712}_{C}$
,
$f^{\ast }(x_{3})=\unicode[STIX]{x1D712}_{C}$
,
![]() $f^{\ast }(x_{4})=\unicode[STIX]{x1D712}_{cC}$
. If
$f^{\ast }(x_{4})=\unicode[STIX]{x1D712}_{cC}$
. If
![]() $\unicode[STIX]{x1D6FC}\in \operatorname{H}^{2}(D_{4}\times D_{4},S)$
is the class of the extension
$\unicode[STIX]{x1D6FC}\in \operatorname{H}^{2}(D_{4}\times D_{4},S)$
is the class of the extension
then its pull-back
![]() $f^{\ast }(\unicode[STIX]{x1D6FC})\in \operatorname{H}^{2}(F,S)$
is represented by the fibred-product of
$f^{\ast }(\unicode[STIX]{x1D6FC})\in \operatorname{H}^{2}(F,S)$
is represented by the fibred-product of
![]() $\mathbb{U}_{5}(\mathbb{F}_{2})$
with
$\mathbb{U}_{5}(\mathbb{F}_{2})$
with
![]() $G_{F}$
over
$G_{F}$
over
![]() $D_{4}\times D_{4}$
(via
$D_{4}\times D_{4}$
(via
![]() $f$
). To conclude the proof of the theorem, we will show that one has
$f$
). To conclude the proof of the theorem, we will show that one has
![]() $f^{\ast }(\unicode[STIX]{x1D6FC})=0$
, so that this fibred-product is a split extension of
$f^{\ast }(\unicode[STIX]{x1D6FC})=0$
, so that this fibred-product is a split extension of
![]() $G_{F}$
by
$G_{F}$
by
![]() $S$
. The composition of such a splitting with the projection to
$S$
. The composition of such a splitting with the projection to
![]() $\mathbb{U}_{5}(\mathbb{F}_{2})$
provides the necessary homomorphism
$\mathbb{U}_{5}(\mathbb{F}_{2})$
provides the necessary homomorphism
![]() $\unicode[STIX]{x1D711}$
.
$\unicode[STIX]{x1D711}$
.
Note that
![]() $G_{E}=f^{-1}(N)$
. Suppose first that
$G_{E}=f^{-1}(N)$
. Suppose first that
![]() $[E:F]=4$
. The
$[E:F]=4$
. The
![]() $G_{F}$
-module
$G_{F}$
-module
![]() $S$
is isomorphic to
$S$
is isomorphic to
![]() $\operatorname{Coind}_{G_{E}}^{G_{F}}(\mathbb{F}_{2})$
, the trivial module of
$\operatorname{Coind}_{G_{E}}^{G_{F}}(\mathbb{F}_{2})$
, the trivial module of
![]() $G_{E}$
(co)induced to
$G_{E}$
(co)induced to
![]() $G_{F}$
. Shapiro’s lemma applies, yielding the isomorphism
$G_{F}$
. Shapiro’s lemma applies, yielding the isomorphism
From the comments above and the naturality of Shapiro’s isomorphism, we see that
![]() $f^{\ast }(\unicode[STIX]{x1D6FC})$
is taken to
$f^{\ast }(\unicode[STIX]{x1D6FC})$
is taken to
![]() $f^{\ast }(x_{2}x_{3})=f^{\ast }(x_{2})f^{\ast }(x_{3})=(B,C)_{E}=0$
, so we are done in this case.
$f^{\ast }(x_{2}x_{3})=f^{\ast }(x_{2})f^{\ast }(x_{3})=(B,C)_{E}=0$
, so we are done in this case.
We turn to the case where
![]() $a=d$
mod squares and
$a=d$
mod squares and
![]() $[E:F]=2$
; another way to phrase this is by saying that the image of
$[E:F]=2$
; another way to phrase this is by saying that the image of
![]() $f$
lies within
$f$
lies within
![]() $G^{\prime }$
. Now the
$G^{\prime }$
. Now the
![]() $G_{F}$
-module
$G_{F}$
-module
![]() $S$
is isomorphic, although not canonically, to
$S$
is isomorphic, although not canonically, to
![]() $\operatorname{Coind}_{G_{E}}^{G_{F}}(\mathbb{F}_{2}\oplus \mathbb{F}_{2})$
: we have at least the two possibilities given in the discussion preceding the proof, and for definiteness say we pick the basis
$\operatorname{Coind}_{G_{E}}^{G_{F}}(\mathbb{F}_{2}\oplus \mathbb{F}_{2})$
: we have at least the two possibilities given in the discussion preceding the proof, and for definiteness say we pick the basis
![]() $e_{1},e_{2}$
.
$e_{1},e_{2}$
.
Now Shapiro’s lemma gives an isomorphism
This takes
![]() $f^{\ast }(\unicode[STIX]{x1D6FC})$
to a pair of cohomology classes, and again from naturality, they are
$f^{\ast }(\unicode[STIX]{x1D6FC})$
to a pair of cohomology classes, and again from naturality, they are
![]() $f^{\ast }(x_{2}x_{3})=(B,C)_{E}$
and
$f^{\ast }(x_{2}x_{3})=(B,C)_{E}$
and
![]() $f^{\ast }(x_{1}x_{3})=(bB,C)_{E}$
. These are both zero by assumption, and
$f^{\ast }(x_{1}x_{3})=(bB,C)_{E}$
. These are both zero by assumption, and
![]() $f^{\ast }(\unicode[STIX]{x1D6FC})=0$
also in this case.
$f^{\ast }(\unicode[STIX]{x1D6FC})=0$
also in this case.
Finally, suppose that
![]() $a$
is a square in
$a$
is a square in
![]() $F$
(a symmetric argument deals with the case when
$F$
(a symmetric argument deals with the case when
![]() $d$
is a square). A neat way to handle this is to use the Massey vanishing conjecture for
$d$
is a square). A neat way to handle this is to use the Massey vanishing conjecture for
![]() $n=3$
, (which is now a theorem, see [Reference MatzriMat11, Reference Efrat and MatzriEM17, Reference Mináč and TânMT17c, Reference Mináč and TânMT16]). First we claim that
$n=3$
, (which is now a theorem, see [Reference MatzriMat11, Reference Efrat and MatzriEM17, Reference Mináč and TânMT17c, Reference Mináč and TânMT16]). First we claim that
![]() $(b,c)_{F}=0$
. Indeed,
$(b,c)_{F}=0$
. Indeed,
![]() $(b,c)_{E}=0$
by assumption; if
$(b,c)_{E}=0$
by assumption; if
![]() $d$
is also a square in
$d$
is also a square in
![]() $F$
then
$F$
then
![]() $E=F$
, and otherwise
$E=F$
, and otherwise
![]() $E=F[\sqrt{d}]$
and
$E=F[\sqrt{d}]$
and
![]() $\operatorname{N}_{E/F}(C)=c$
mod squares, so
$\operatorname{N}_{E/F}(C)=c$
mod squares, so
![]() $(b,C)_{E}=0$
implies
$(b,C)_{E}=0$
implies
![]() $(b,c)_{F}=0$
by the projection formula in group cohomology. We also have
$(b,c)_{F}=0$
by the projection formula in group cohomology. We also have
![]() $(c,d)_{F}=0$
by Proposition 2.3. We deduce that the Massey product
$(c,d)_{F}=0$
by Proposition 2.3. We deduce that the Massey product
![]() $\langle b,c,d\rangle$
vanishes, and so that there is a continuous
$\langle b,c,d\rangle$
vanishes, and so that there is a continuous
![]() $\unicode[STIX]{x1D713}:G_{F}\rightarrow \mathbb{U}_{4}(\mathbb{F}_{2})$
compatible with
$\unicode[STIX]{x1D713}:G_{F}\rightarrow \mathbb{U}_{4}(\mathbb{F}_{2})$
compatible with
![]() $b,c,d$
. However, if we see
$b,c,d$
. However, if we see
![]() $\mathbb{U}_{4}(\mathbb{F}_{2})$
as the subgroup of
$\mathbb{U}_{4}(\mathbb{F}_{2})$
as the subgroup of
![]() $\mathbb{U}_{5}(\mathbb{F}_{2})$
consisting of those matrices whose first row is that of the identity matrix, we see that we have built
$\mathbb{U}_{5}(\mathbb{F}_{2})$
consisting of those matrices whose first row is that of the identity matrix, we see that we have built
![]() $G_{F}\rightarrow \mathbb{U}_{5}(\mathbb{F}_{2})$
compatible with
$G_{F}\rightarrow \mathbb{U}_{5}(\mathbb{F}_{2})$
compatible with
![]() $1,b,c,d$
, as required.◻
$1,b,c,d$
, as required.◻
Remark 3.4. It is possible to avoid relying on the Massey vanishing conjecture for
![]() $n=3$
if one wishes to do so. Here is a sketch. When
$n=3$
if one wishes to do so. Here is a sketch. When
![]() $d$
is not a square, use another argument based on Shapiro’s lemma, this time replacing
$d$
is not a square, use another argument based on Shapiro’s lemma, this time replacing
![]() $G^{\prime }$
by
$G^{\prime }$
by
![]() $G^{\prime \prime }$
, the subgroup of
$G^{\prime \prime }$
, the subgroup of
![]() $G$
of elements mapping to
$G$
of elements mapping to
![]() $\langle \unicode[STIX]{x1D70E}_{d}\rangle \subset G/N$
. When
$\langle \unicode[STIX]{x1D70E}_{d}\rangle \subset G/N$
. When
![]() $d$
is a square, define
$d$
is a square, define
![]() $f$
as in the first part of the proof; this time
$f$
as in the first part of the proof; this time
![]() $f$
takes values in
$f$
takes values in
![]() $N$
. The exact sequence
$N$
. The exact sequence
is central, and controlled by four cohomology classes in
![]() $\operatorname{H}^{2}(N,\mathbb{F}_{2})$
, pulling back to
$\operatorname{H}^{2}(N,\mathbb{F}_{2})$
, pulling back to
![]() $(B,C)$
,
$(B,C)$
,
![]() $(b,C)$
,
$(b,C)$
,
![]() $(B,c)$
and
$(B,c)$
and
![]() $(b,c)$
in
$(b,c)$
in
![]() $\operatorname{H}^{2}(F,\mathbb{F}_{2})$
under
$\operatorname{H}^{2}(F,\mathbb{F}_{2})$
under
![]() $f^{\ast }$
.
$f^{\ast }$
.
The proof of Theorem A is now almost complete. In fact, what we have is the following.
Theorem 3.5. Let
![]() $F$
be a field of characteristic not
$F$
be a field of characteristic not
![]() $2$
, and let
$2$
, and let
![]() $a,b,c,d\in F^{\times }$
be given. Then the following statements are equivalent.
$a,b,c,d\in F^{\times }$
be given. Then the following statements are equivalent.
(1) The Massey product
 $\langle a,b,c,d\rangle$
is defined and vanishes.
$\langle a,b,c,d\rangle$
is defined and vanishes.(2) There exist
 $\widetilde{B}\in F_{a}$
such that
$\widetilde{B}\in F_{a}$
such that
 $\operatorname{N}_{F_{a}/F}(\widetilde{B})=b$
modulo squares, and
$\operatorname{N}_{F_{a}/F}(\widetilde{B})=b$
modulo squares, and
 $\widetilde{C}\in F_{d}$
such that
$\widetilde{C}\in F_{d}$
such that
 $\operatorname{N}_{F_{d}/F}(\widetilde{C})=c$
modulo squares, with the following extra property. If
$\operatorname{N}_{F_{d}/F}(\widetilde{C})=c$
modulo squares, with the following extra property. If
 $B$
is the image of
$B$
is the image of
 $\widetilde{B}$
under
$\widetilde{B}$
under
 $F_{a}\rightarrow F[\sqrt{a}]$
and
$F_{a}\rightarrow F[\sqrt{a}]$
and
 $C$
is the image of
$C$
is the image of
 $\widetilde{C}$
under
$\widetilde{C}$
under
 $F_{d}\rightarrow F[\sqrt{d}]$
, then
$F_{d}\rightarrow F[\sqrt{d}]$
, then
 $(B,C)_{F[\sqrt{a},\sqrt{d}]}=0$
,
$(B,C)_{F[\sqrt{a},\sqrt{d}]}=0$
,
 $(B,c)_{F[\sqrt{a}]}=0$
,
$(B,c)_{F[\sqrt{a}]}=0$
,
 $(b,C)_{F[\sqrt{d}]}=0$
, and
$(b,C)_{F[\sqrt{d}]}=0$
, and
 $(b,c)_{F}=0$
.
$(b,c)_{F}=0$
.(3) There exist
 $\widetilde{B}\in F_{a}$
such that
$\widetilde{B}\in F_{a}$
such that
 $\operatorname{N}_{F_{a}/F}(\widetilde{B})=b$
modulo squares, and
$\operatorname{N}_{F_{a}/F}(\widetilde{B})=b$
modulo squares, and
 $\widetilde{C}\in F_{d}$
such that
$\widetilde{C}\in F_{d}$
such that
 $\operatorname{N}_{F_{d}/F}(\widetilde{C})=c$
modulo squares, with the following additional property: If
$\operatorname{N}_{F_{d}/F}(\widetilde{C})=c$
modulo squares, with the following additional property: If
 $B$
denotes the image of
$B$
denotes the image of
 $\widetilde{B}$
under
$\widetilde{B}$
under
 $F_{a}\rightarrow F[\sqrt{a}]$
and
$F_{a}\rightarrow F[\sqrt{a}]$
and
 $C$
denotes the image of
$C$
denotes the image of
 $\widetilde{C}$
under
$\widetilde{C}$
under
 $F_{d}\rightarrow F[\sqrt{d}]$
, then one has
$F_{d}\rightarrow F[\sqrt{d}]$
, then one has
 $(B,C)_{E}=(B,c)_{E}=(b,C)_{E}=(b,c)_{E}=0$
.
$(B,C)_{E}=(B,c)_{E}=(b,C)_{E}=(b,c)_{E}=0$
.
Proof. Theorem 3.1 shows the implication (1)
![]() $\;\Longrightarrow \;$
(2), while (2)
$\;\Longrightarrow \;$
(2), while (2)
![]() $\;\Longrightarrow \;$
(3) is trivial, and Theorem 3.3 shows (3)
$\;\Longrightarrow \;$
(3) is trivial, and Theorem 3.3 shows (3)
![]() $\;\Longrightarrow \;$
(1).◻
$\;\Longrightarrow \;$
(1).◻
The only difference with Theorem A is the presence of the elements
![]() $\widetilde{B}$
and
$\widetilde{B}$
and
![]() $\widetilde{C}$
instead of just
$\widetilde{C}$
instead of just
![]() $B,C$
. Clearly, if neither
$B,C$
. Clearly, if neither
![]() $a$
nor
$a$
nor
![]() $d$
is a square in
$d$
is a square in
![]() $F$
, then the two results are the same. On the other hand, when one of these two elements is a square, in fact when one of
$F$
, then the two results are the same. On the other hand, when one of these two elements is a square, in fact when one of
![]() $a,b,c,d$
is a square, things become very easy, as we proceed to show in the following subsection.
$a,b,c,d$
is a square, things become very easy, as we proceed to show in the following subsection.
3.3 Some trivial cases
Lemma 3.6. Let
![]() $F$
be a field of characteristic different from
$F$
be a field of characteristic different from
![]() $2$
and let
$2$
and let
![]() $a,b,c,d\in F^{\times }$
be given. Suppose that
$a,b,c,d\in F^{\times }$
be given. Suppose that
![]() $(a,b)_{F}=(b,c)_{F}=(c,d)_{F}=0$
. Finally, assume that one of
$(a,b)_{F}=(b,c)_{F}=(c,d)_{F}=0$
. Finally, assume that one of
![]() $a,b,c,d$
is a square in
$a,b,c,d$
is a square in
![]() $F$
. Then the Massey product
$F$
. Then the Massey product
![]() $\langle a,b,c,d\rangle$
is defined and vanishes.
$\langle a,b,c,d\rangle$
is defined and vanishes.
Proof. First assume that
![]() $a$
is a square, or equivalently
$a$
is a square, or equivalently
![]() $a=1$
. Then the argument given in the last paragraph of the proof of Theorem 3.3 shows that
$a=1$
. Then the argument given in the last paragraph of the proof of Theorem 3.3 shows that
![]() $0\in \langle a,b,c,d\rangle$
. The case when
$0\in \langle a,b,c,d\rangle$
. The case when
![]() $d=1$
is treated similarly.
$d=1$
is treated similarly.
On the other hand, suppose that
![]() $b=1$
. From
$b=1$
. From
![]() $(c,d)_{F}=0$
, we draw the existence of
$(c,d)_{F}=0$
, we draw the existence of
![]() $G_{F}\rightarrow \mathbb{U}_{3}(\mathbb{F}_{2})$
compatible with
$G_{F}\rightarrow \mathbb{U}_{3}(\mathbb{F}_{2})$
compatible with
![]() $c$
and
$c$
and
![]() $d$
, by Proposition 2.3. The element
$d$
, by Proposition 2.3. The element
![]() $a$
itself defines
$a$
itself defines
![]() $\unicode[STIX]{x1D712}_{a}:G_{F}\rightarrow \mathbb{F}_{2}\cong C_{2}$
. Since the subgroup of
$\unicode[STIX]{x1D712}_{a}:G_{F}\rightarrow \mathbb{F}_{2}\cong C_{2}$
. Since the subgroup of
![]() $\mathbb{U}_{5}(\mathbb{F}_{2})$
generated by
$\mathbb{U}_{5}(\mathbb{F}_{2})$
generated by
![]() $\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{3},\unicode[STIX]{x1D70E}_{4}$
is isomorphic to
$\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{3},\unicode[STIX]{x1D70E}_{4}$
is isomorphic to
![]() $C_{2}\times \mathbb{U}_{3}(\mathbb{F}_{2})$
, we see immediately that we may combine our two homomorphisms into one of the form
$C_{2}\times \mathbb{U}_{3}(\mathbb{F}_{2})$
, we see immediately that we may combine our two homomorphisms into one of the form
![]() $G_{F}\rightarrow \mathbb{U}_{5}(\mathbb{F}_{2})$
, showing that
$G_{F}\rightarrow \mathbb{U}_{5}(\mathbb{F}_{2})$
, showing that
![]() $0\in \langle a,1,b,c\rangle$
. The case when
$0\in \langle a,1,b,c\rangle$
. The case when
![]() $c=1$
is treated similarly.◻
$c=1$
is treated similarly.◻
Remark 3.7. The above proof, via the reference to the proof of Theorem 3.3, uses the Massey vanishing conjecture for
![]() $n=3$
. Without this, it is still a general fact about Massey products that
$n=3$
. Without this, it is still a general fact about Massey products that
![]() $\langle a,b,c,d\rangle$
vanishes when it is defined and one of them is a square [Reference FennFen83, Lemma 6.2.4]. However, the statement just given is stronger.
$\langle a,b,c,d\rangle$
vanishes when it is defined and one of them is a square [Reference FennFen83, Lemma 6.2.4]. However, the statement just given is stronger.
We proceed to show how we can improve the statement of Theorem 3.5 to that of Theorem A from the Introduction, so that the two are in fact equivalent. We have already mentioned that this is obvious when neither
![]() $a$
nor
$a$
nor
![]() $d$
is a square in
$d$
is a square in
![]() $F$
.
$F$
.
Let us call (1A), (2A), (3A) the conditions of Theorem A, and keep (1), (2), (3) for those of Theorem 3.5, which we know are equivalent. Note (1)
![]() $=$
(1A).
$=$
(1A).
Suppose
![]() $a$
is a square in
$a$
is a square in
![]() $F$
, but not
$F$
, but not
![]() $d$
. Assume condition (1A). We must show that condition (2A) holds. Indeed, from condition (2), we have the element
$d$
. Assume condition (1A). We must show that condition (2A) holds. Indeed, from condition (2), we have the element
![]() $C$
with
$C$
with
![]() $\operatorname{N}_{F[\sqrt{d}]/F}(C)=c$
mod squares, and satisfying
$\operatorname{N}_{F[\sqrt{d}]/F}(C)=c$
mod squares, and satisfying
![]() $(b,C)_{F[\sqrt{d}]}=0$
, and moreover
$(b,C)_{F[\sqrt{d}]}=0$
, and moreover
![]() $(b,c)_{F}=0$
. Now put
$(b,c)_{F}=0$
. Now put
![]() $B=b\in F=F[\sqrt{a}]$
, so that
$B=b\in F=F[\sqrt{a}]$
, so that
![]() $\operatorname{N}_{F[\sqrt{a}]/F}(B)=B=b$
. Then
$\operatorname{N}_{F[\sqrt{a}]/F}(B)=B=b$
. Then
![]() $(B,C)_{E}=(b,C)_{E}=0$
, while
$(B,C)_{E}=(b,C)_{E}=0$
, while
![]() $(B,c)_{F[\sqrt{a}]}=(b,c)_{F}=0$
. We do have condition (2A), and so also (3A).
$(B,c)_{F[\sqrt{a}]}=(b,c)_{F}=0$
. We do have condition (2A), and so also (3A).
Conversely, condition (3A) is enough to ensure that
![]() $(a,b)_{F}=(1,b)_{F}=0$
,
$(a,b)_{F}=(1,b)_{F}=0$
,
![]() $(b,c)_{F}=0$
(apply the projection formula to
$(b,c)_{F}=0$
(apply the projection formula to
![]() $(b,C)_{E}=0$
) and
$(b,C)_{E}=0$
) and
![]() $(c,d)_{F}=0$
(merely because
$(c,d)_{F}=0$
(merely because
![]() $C$
exists, cf. Proposition 2.3). So Lemma 3.6 applies and shows that condition (1A) holds.
$C$
exists, cf. Proposition 2.3). So Lemma 3.6 applies and shows that condition (1A) holds.
The situation when
![]() $a$
is not a square, but
$a$
is not a square, but
![]() $d$
is, is clearly similar.
$d$
is, is clearly similar.
Now suppose
![]() $a$
and
$a$
and
![]() $d$
are both squares. Suppose condition (1A) holds, and so also (2), and we have
$d$
are both squares. Suppose condition (1A) holds, and so also (2), and we have
![]() $(a,b)=(c,d)=0$
(because
$(a,b)=(c,d)=0$
(because
![]() $\widetilde{B}$
and
$\widetilde{B}$
and
![]() $\widetilde{C}$
exist, cf. remark after Theorem 3.1) and
$\widetilde{C}$
exist, cf. remark after Theorem 3.1) and
![]() $(b,c)=0$
. Thus condition (2A) holds with
$(b,c)=0$
. Thus condition (2A) holds with
![]() $B=b$
and
$B=b$
and
![]() $C=c$
, and (2A)
$C=c$
, and (2A)
![]() $=$
(3A) here. Conversely, condition (3A) contains the statement
$=$
(3A) here. Conversely, condition (3A) contains the statement
![]() $(b,c)=0$
, while
$(b,c)=0$
, while
![]() $(a,b)=(1,b)=0$
and
$(a,b)=(1,b)=0$
and
![]() $(c,d)=(c,1)=0$
, and we see by the last lemma that condition (1A) holds. We have therefore just proven Theorem A.
$(c,d)=(c,1)=0$
, and we see by the last lemma that condition (1A) holds. We have therefore just proven Theorem A.
Remark 3.8. Theorem 3.5 is heavier on notation than Theorem A, so we have deemed it unfit for the Introduction. However, the extra case-by-case considerations needed to establish the latter, as just given, are perhaps an indication that it is less natural. (Also, it relies more seriously on the Massey vanishing conjecture for
![]() $n=3$
, see Remark 3.4.) From now on, we shall refer to Theorem 3.5, rather than to Theorem A.
$n=3$
, see Remark 3.4.) From now on, we shall refer to Theorem 3.5, rather than to Theorem A.
3.4 Maps from profinite groups into
 $\mathbb{U}_{5}(\mathbb{F}_{2})$
$\mathbb{U}_{5}(\mathbb{F}_{2})$
A routine modification of the arguments given above produces the next result.
Theorem 3.9. Let
![]() $\unicode[STIX]{x1D6E4}$
be a profinite group, and let
$\unicode[STIX]{x1D6E4}$
be a profinite group, and let
![]() $\unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2},\unicode[STIX]{x1D712}_{3},\unicode[STIX]{x1D712}_{4}\in \operatorname{H}^{1}(\unicode[STIX]{x1D6E4},\mathbb{F}_{2})$
be given. Put
$\unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2},\unicode[STIX]{x1D712}_{3},\unicode[STIX]{x1D712}_{4}\in \operatorname{H}^{1}(\unicode[STIX]{x1D6E4},\mathbb{F}_{2})$
be given. Put
![]() $\unicode[STIX]{x1D6E4}_{1}:=\ker (\unicode[STIX]{x1D712}_{1})$
,
$\unicode[STIX]{x1D6E4}_{1}:=\ker (\unicode[STIX]{x1D712}_{1})$
,
![]() $\unicode[STIX]{x1D6E4}_{4}:=\ker (\unicode[STIX]{x1D712}_{4})$
, and
$\unicode[STIX]{x1D6E4}_{4}:=\ker (\unicode[STIX]{x1D712}_{4})$
, and
![]() $\unicode[STIX]{x1D6E4}_{14}:=\unicode[STIX]{x1D6E4}_{1}\cap \unicode[STIX]{x1D6E4}_{4}$
. The the following statements are equivalent.
$\unicode[STIX]{x1D6E4}_{14}:=\unicode[STIX]{x1D6E4}_{1}\cap \unicode[STIX]{x1D6E4}_{4}$
. The the following statements are equivalent.
(1) There exists a continuous homomorphism
 $\unicode[STIX]{x1D711}:\unicode[STIX]{x1D6E4}\rightarrow \mathbb{U}_{5}(\mathbb{F}_{2})$
such that
$\unicode[STIX]{x1D711}:\unicode[STIX]{x1D6E4}\rightarrow \mathbb{U}_{5}(\mathbb{F}_{2})$
such that
 $\unicode[STIX]{x1D712}_{i}=s_{i}\circ \unicode[STIX]{x1D711}$
for
$\unicode[STIX]{x1D712}_{i}=s_{i}\circ \unicode[STIX]{x1D711}$
for
 $i=1,2,3,4$
. In other words,
$i=1,2,3,4$
. In other words,
 $\langle \unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2},\unicode[STIX]{x1D712}_{3},\unicode[STIX]{x1D712}_{4}\rangle$
is defined and vanishes.
$\langle \unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2},\unicode[STIX]{x1D712}_{3},\unicode[STIX]{x1D712}_{4}\rangle$
is defined and vanishes.(2) There exist a continuous homomorphism
 $\unicode[STIX]{x1D6E4}\rightarrow D_{4}$
given by and another one given by
$\unicode[STIX]{x1D6E4}\rightarrow D_{4}$
given by and another one given by $$\begin{eqnarray}\unicode[STIX]{x1D6FE}\mapsto \left(\begin{array}{@{}ccc@{}}1 & \unicode[STIX]{x1D712}_{1}(\unicode[STIX]{x1D6FE}) & \unicode[STIX]{x1D701}_{1}(\unicode[STIX]{x1D6FE})\\ 0 & 1 & \unicode[STIX]{x1D712}_{2}(\unicode[STIX]{x1D6FE})\\ 0 & 0 & 1\end{array}\right),\end{eqnarray}$$
such that
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}\mapsto \left(\begin{array}{@{}ccc@{}}1 & \unicode[STIX]{x1D712}_{1}(\unicode[STIX]{x1D6FE}) & \unicode[STIX]{x1D701}_{1}(\unicode[STIX]{x1D6FE})\\ 0 & 1 & \unicode[STIX]{x1D712}_{2}(\unicode[STIX]{x1D6FE})\\ 0 & 0 & 1\end{array}\right),\end{eqnarray}$$
such that $$\begin{eqnarray}\unicode[STIX]{x1D6FE}\mapsto \left(\begin{array}{@{}ccc@{}}1 & \unicode[STIX]{x1D712}_{3}(\unicode[STIX]{x1D6FE}) & \unicode[STIX]{x1D701}_{2}(\unicode[STIX]{x1D6FE})\\ 0 & 1 & \unicode[STIX]{x1D712}_{4}(\unicode[STIX]{x1D6FE})\\ 0 & 0 & 1\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}\mapsto \left(\begin{array}{@{}ccc@{}}1 & \unicode[STIX]{x1D712}_{3}(\unicode[STIX]{x1D6FE}) & \unicode[STIX]{x1D701}_{2}(\unicode[STIX]{x1D6FE})\\ 0 & 1 & \unicode[STIX]{x1D712}_{4}(\unicode[STIX]{x1D6FE})\\ 0 & 0 & 1\end{array}\right),\end{eqnarray}$$
 $\unicode[STIX]{x1D701}_{1}|_{\unicode[STIX]{x1D6E4}_{14}}\cup \unicode[STIX]{x1D701}_{2}|_{\unicode[STIX]{x1D6E4}_{14}}=0$
,
$\unicode[STIX]{x1D701}_{1}|_{\unicode[STIX]{x1D6E4}_{14}}\cup \unicode[STIX]{x1D701}_{2}|_{\unicode[STIX]{x1D6E4}_{14}}=0$
,
 $\unicode[STIX]{x1D701}_{1}|_{\unicode[STIX]{x1D6E4}_{1}}\cup \unicode[STIX]{x1D712}_{3}|_{\unicode[STIX]{x1D6E4}_{1}}=0$
,
$\unicode[STIX]{x1D701}_{1}|_{\unicode[STIX]{x1D6E4}_{1}}\cup \unicode[STIX]{x1D712}_{3}|_{\unicode[STIX]{x1D6E4}_{1}}=0$
,
 $\unicode[STIX]{x1D712}_{2}|_{\unicode[STIX]{x1D6E4}_{4}}\cup \unicode[STIX]{x1D701}_{2}|_{\unicode[STIX]{x1D6E4}_{4}}=0$
,
$\unicode[STIX]{x1D712}_{2}|_{\unicode[STIX]{x1D6E4}_{4}}\cup \unicode[STIX]{x1D701}_{2}|_{\unicode[STIX]{x1D6E4}_{4}}=0$
,
 $\unicode[STIX]{x1D712}_{2}\cup \unicode[STIX]{x1D712}_{3}=0$
.
$\unicode[STIX]{x1D712}_{2}\cup \unicode[STIX]{x1D712}_{3}=0$
.(3)
 $\unicode[STIX]{x1D701}_{1}$
and
$\unicode[STIX]{x1D701}_{1}$
and
 $\unicode[STIX]{x1D701}_{2}$
exist as above and satisfy
$\unicode[STIX]{x1D701}_{2}$
exist as above and satisfy
 $\unicode[STIX]{x1D701}_{1}|_{\unicode[STIX]{x1D6E4}_{14}}\cup \unicode[STIX]{x1D701}_{2}|_{\unicode[STIX]{x1D6E4}_{14}}=\unicode[STIX]{x1D701}_{1}|_{\unicode[STIX]{x1D6E4}_{14}}\cup \unicode[STIX]{x1D712}_{3}|_{\unicode[STIX]{x1D6E4}_{14}}=\unicode[STIX]{x1D712}_{2}|_{\unicode[STIX]{x1D6E4}_{14}}\cup \unicode[STIX]{x1D701}_{2}|_{\unicode[STIX]{x1D6E4}_{14}}=\unicode[STIX]{x1D712}_{2}|_{\unicode[STIX]{x1D6E4}_{14}}\cup \unicode[STIX]{x1D712}_{3}|_{\unicode[STIX]{x1D6E4}_{14}}=0$
.
$\unicode[STIX]{x1D701}_{1}|_{\unicode[STIX]{x1D6E4}_{14}}\cup \unicode[STIX]{x1D701}_{2}|_{\unicode[STIX]{x1D6E4}_{14}}=\unicode[STIX]{x1D701}_{1}|_{\unicode[STIX]{x1D6E4}_{14}}\cup \unicode[STIX]{x1D712}_{3}|_{\unicode[STIX]{x1D6E4}_{14}}=\unicode[STIX]{x1D712}_{2}|_{\unicode[STIX]{x1D6E4}_{14}}\cup \unicode[STIX]{x1D701}_{2}|_{\unicode[STIX]{x1D6E4}_{14}}=\unicode[STIX]{x1D712}_{2}|_{\unicode[STIX]{x1D6E4}_{14}}\cup \unicode[STIX]{x1D712}_{3}|_{\unicode[STIX]{x1D6E4}_{14}}=0$
.
We shall have no use for this theorem in the sequel, so we leave the proof to the reader.
4 First applications
While our main objective in this paper is to prove the
![]() $4$
-Massey vanishing conjecture for number fields, there are a few cases which can be treated over any field. Usually, we use the following trick when working ‘by hand’. It will have a more theoretical use below, too.
$4$
-Massey vanishing conjecture for number fields, there are a few cases which can be treated over any field. Usually, we use the following trick when working ‘by hand’. It will have a more theoretical use below, too.
Proposition 4.1. Let
![]() $F$
be a field of characteristic not
$F$
be a field of characteristic not
![]() $2$
, and let
$2$
, and let
![]() $a,b,c,d\in F^{\times }$
. Let
$a,b,c,d\in F^{\times }$
. Let
![]() $\widetilde{B}_{0}\in F_{a}$
be any initial element such that
$\widetilde{B}_{0}\in F_{a}$
be any initial element such that
![]() $\operatorname{N}_{F_{a}/F}(\widetilde{B}_{0})=b$
, and likewise let
$\operatorname{N}_{F_{a}/F}(\widetilde{B}_{0})=b$
, and likewise let
![]() $\widetilde{C}_{0}\in F_{d}$
be any initial element such that
$\widetilde{C}_{0}\in F_{d}$
be any initial element such that
![]() $\operatorname{N}_{F_{d}/F}(\widetilde{C}_{0})=c$
. The following statements are equivalent:
$\operatorname{N}_{F_{d}/F}(\widetilde{C}_{0})=c$
. The following statements are equivalent:
(1) there exist
 $\widetilde{B}\in F_{a}$
with
$\widetilde{B}\in F_{a}$
with
 $\operatorname{N}_{F_{a}/F}(\widetilde{B})=bz_{1}^{2}$
, and
$\operatorname{N}_{F_{a}/F}(\widetilde{B})=bz_{1}^{2}$
, and
 $\widetilde{C}\in F_{d}$
with
$\widetilde{C}\in F_{d}$
with
 $\operatorname{N}_{F_{d}/F}(\widetilde{C})=cz_{2}^{2}$
, for some
$\operatorname{N}_{F_{d}/F}(\widetilde{C})=cz_{2}^{2}$
, for some
 $z_{1},z_{2}\in F^{\times }$
, such that we have simultaneously
$z_{1},z_{2}\in F^{\times }$
, such that we have simultaneously
 $(B,C)_{F[\sqrt{a},\sqrt{d}]}=0$
,
$(B,C)_{F[\sqrt{a},\sqrt{d}]}=0$
,
 $(B,c)_{F[\sqrt{a}]}=0$
,
$(B,c)_{F[\sqrt{a}]}=0$
,
 $(b,C)_{F[\sqrt{d}]}=0$
,
$(b,C)_{F[\sqrt{d}]}=0$
,
 $(b,c)_{F}=0$
, where
$(b,c)_{F}=0$
, where
 $B\in F[\sqrt{a}]$
and
$B\in F[\sqrt{a}]$
and
 $C\in F[\sqrt{d}]$
correspond to
$C\in F[\sqrt{d}]$
correspond to
 $\widetilde{B},\widetilde{C}$
respectively;
$\widetilde{B},\widetilde{C}$
respectively;(2) there exist
 $\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in F^{\times }$
such that
$\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in F^{\times }$
such that
 $\widetilde{B}=\unicode[STIX]{x1D6FD}\widetilde{B}_{0}$
and
$\widetilde{B}=\unicode[STIX]{x1D6FD}\widetilde{B}_{0}$
and
 $\widetilde{C}=\unicode[STIX]{x1D6FE}\widetilde{C}_{0}$
satisfy the previous condition.
$\widetilde{C}=\unicode[STIX]{x1D6FE}\widetilde{C}_{0}$
satisfy the previous condition.
Of course, by Theorem 3.5 these conditions are also equivalent to the vanishing of
![]() $\langle a,b,c,d\rangle$
, but the point of the proposition is to show that it makes sense to start with any
$\langle a,b,c,d\rangle$
, but the point of the proposition is to show that it makes sense to start with any
![]() $\widetilde{B}_{0},\widetilde{C}_{0}$
and then look for the ‘modifiers’
$\widetilde{B}_{0},\widetilde{C}_{0}$
and then look for the ‘modifiers’
![]() $\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}$
.
$\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}$
.
Proof. It is plain that (2) implies (1), so here is the non-trivial part. Assume that
![]() $\widetilde{B},\widetilde{C}$
exist as in the first part. We claim that we can in fact find
$\widetilde{B},\widetilde{C}$
exist as in the first part. We claim that we can in fact find
![]() $\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in F$
and
$\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in F$
and
![]() $\unicode[STIX]{x1D706}\in F[\sqrt{a}]$
,
$\unicode[STIX]{x1D706}\in F[\sqrt{a}]$
,
![]() $\unicode[STIX]{x1D707}\in F[\sqrt{d}]$
such that
$\unicode[STIX]{x1D707}\in F[\sqrt{d}]$
such that
![]() $B=\unicode[STIX]{x1D6FD}B_{0}\unicode[STIX]{x1D706}^{-2}$
and
$B=\unicode[STIX]{x1D6FD}B_{0}\unicode[STIX]{x1D706}^{-2}$
and
![]() $C=\unicode[STIX]{x1D6FE}C_{0}\unicode[STIX]{x1D707}^{-2}$
, where
$C=\unicode[STIX]{x1D6FE}C_{0}\unicode[STIX]{x1D707}^{-2}$
, where
![]() $B_{0}\in F[\sqrt{a}]$
and
$B_{0}\in F[\sqrt{a}]$
and
![]() $C_{0}\in F[\sqrt{d}]$
correspond to
$C_{0}\in F[\sqrt{d}]$
correspond to
![]() $\widetilde{B}_{0},\widetilde{C}_{0}$
respectively. Clearly this will give the result.
$\widetilde{B}_{0},\widetilde{C}_{0}$
respectively. Clearly this will give the result.
To prove the claim, we suppose first that
![]() $a$
is not a square in the field
$a$
is not a square in the field
![]() $F$
, and write
$F$
, and write
![]() $\operatorname{N}_{F[\sqrt{a}]/F}(Bz_{1}^{-1})=b=\operatorname{N}_{F[\sqrt{a}]/F}(B_{0})$
. Since we have
$\operatorname{N}_{F[\sqrt{a}]/F}(Bz_{1}^{-1})=b=\operatorname{N}_{F[\sqrt{a}]/F}(B_{0})$
. Since we have
![]() $\operatorname{N}_{F[\sqrt{a}]/F}(Bz_{1}^{-1}B_{0}^{-1})=1$
, by Hilbert’s Theorem 90 we have
$\operatorname{N}_{F[\sqrt{a}]/F}(Bz_{1}^{-1}B_{0}^{-1})=1$
, by Hilbert’s Theorem 90 we have
for some
![]() $\unicode[STIX]{x1D706}\in F[\sqrt{a}]$
, where
$\unicode[STIX]{x1D706}\in F[\sqrt{a}]$
, where
![]() $\unicode[STIX]{x1D70E}$
is the non-trivial element of
$\unicode[STIX]{x1D70E}$
is the non-trivial element of
![]() $\operatorname{Gal}(F[\sqrt{a}]/F)$
. Rewrite this
$\operatorname{Gal}(F[\sqrt{a}]/F)$
. Rewrite this
![]() $B=\unicode[STIX]{x1D6FD}B_{0}\unicode[STIX]{x1D706}^{-2}$
, with
$B=\unicode[STIX]{x1D6FD}B_{0}\unicode[STIX]{x1D706}^{-2}$
, with
![]() $\unicode[STIX]{x1D6FD}=z_{1}\unicode[STIX]{x1D706}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D706})\in F$
, and we are done.
$\unicode[STIX]{x1D6FD}=z_{1}\unicode[STIX]{x1D706}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D706})\in F$
, and we are done.
If on the other hand
![]() $a$
is a square in
$a$
is a square in
![]() $F$
, then
$F$
, then
![]() $B_{0},B\in F^{\times }$
, so we may put
$B_{0},B\in F^{\times }$
, so we may put
![]() $\unicode[STIX]{x1D6FD}=B/B_{0}$
and
$\unicode[STIX]{x1D6FD}=B/B_{0}$
and
![]() $\unicode[STIX]{x1D706}=1$
.
$\unicode[STIX]{x1D706}=1$
.
A similar argument works with
![]() $C,C_{0}$
.◻
$C,C_{0}$
.◻
We give a series of examples. These will demonstrate how, in practice, one looks for
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $\unicode[STIX]{x1D6FE}$
rather than
$\unicode[STIX]{x1D6FE}$
rather than
![]() $B$
and
$B$
and
![]() $C$
directly. Logically speaking, only the trivial implication of the last proposition is used, at this point (although knowing that the converse holds gives us confidence in the whole approach).
$C$
directly. Logically speaking, only the trivial implication of the last proposition is used, at this point (although knowing that the converse holds gives us confidence in the whole approach).
The elements
![]() $a$
and
$a$
and
![]() $d$
are always assumed not to be squares in
$d$
are always assumed not to be squares in
![]() $F$
, so we identify
$F$
, so we identify
![]() $F_{a}$
and
$F_{a}$
and
![]() $F[\sqrt{a}]$
, as well as
$F[\sqrt{a}]$
, as well as
![]() $F_{d}$
and
$F_{d}$
and
![]() $F[\sqrt{d}]$
, and
$F[\sqrt{d}]$
, and
![]() $\widetilde{B}_{0}=B_{0}$
,
$\widetilde{B}_{0}=B_{0}$
,
![]() $\widetilde{C}_{0}=C_{0}$
. As you have guessed, the characteristic is always not
$\widetilde{C}_{0}=C_{0}$
. As you have guessed, the characteristic is always not
![]() $2$
. We will make some forward references to the results of the next section, which reduce the number of conditions to check.
$2$
. We will make some forward references to the results of the next section, which reduce the number of conditions to check.
Example 4.2 (The abaa case).
In this example, we show that when
![]() $(a,b)=(a,a)=0$
, the Massey product
$(a,b)=(a,a)=0$
, the Massey product
![]() $\langle a,b,a,a\rangle$
is defined and vanishes, under the assumption that
$\langle a,b,a,a\rangle$
is defined and vanishes, under the assumption that
![]() $a\neq b$
modulo squares, and that
$a\neq b$
modulo squares, and that
![]() $a$
and
$a$
and
![]() $b$
are not squares.
$b$
are not squares.
Clearly we can find
![]() $B_{0}$
and
$B_{0}$
and
![]() $C_{0}$
as in the Proposition, by our assumption (and using Proposition 2.3, of course). We claim that
$C_{0}$
as in the Proposition, by our assumption (and using Proposition 2.3, of course). We claim that
![]() $B_{0}$
and
$B_{0}$
and
![]() $C_{0}$
form a basis for
$C_{0}$
form a basis for
![]() $F[\sqrt{a}]$
as an
$F[\sqrt{a}]$
as an
![]() $F$
-vector space. Indeed, if we had
$F$
-vector space. Indeed, if we had
![]() $\unicode[STIX]{x1D6FD}B_{0}=\unicode[STIX]{x1D6FE}C_{0}$
for
$\unicode[STIX]{x1D6FD}B_{0}=\unicode[STIX]{x1D6FE}C_{0}$
for
![]() $\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in F^{\times }$
, then by taking norms to
$\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in F^{\times }$
, then by taking norms to
![]() $F$
we would find that
$F$
we would find that
![]() $b=a$
modulo squares, a contradiction. Therefore there must exist
$b=a$
modulo squares, a contradiction. Therefore there must exist
![]() $\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in F$
such that
$\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in F$
such that
This implies
![]() $(\unicode[STIX]{x1D6FD}B_{0},\unicode[STIX]{x1D6FE}C_{0})_{F[\sqrt{a}]}=0$
. Moreover
$(\unicode[STIX]{x1D6FD}B_{0},\unicode[STIX]{x1D6FE}C_{0})_{F[\sqrt{a}]}=0$
. Moreover
![]() $(\unicode[STIX]{x1D6FD}B_{0},a)_{F[\sqrt{a}]}=(\unicode[STIX]{x1D6FD}B_{0},1)_{F[\sqrt{a}]}=0$
. By Lemma 5.5 below, the other cup-products vanish automatically (the reader will also enjoy looking for a direct argument). By Theorem 3.5, the Massey product is defined and vanishes.
$(\unicode[STIX]{x1D6FD}B_{0},a)_{F[\sqrt{a}]}=(\unicode[STIX]{x1D6FD}B_{0},1)_{F[\sqrt{a}]}=0$
. By Lemma 5.5 below, the other cup-products vanish automatically (the reader will also enjoy looking for a direct argument). By Theorem 3.5, the Massey product is defined and vanishes.
Example 4.3 (The aaaa case).
Now we complete the discussion of the previous example, and turn to the case when
![]() $a=b$
modulo squares (still assuming that
$a=b$
modulo squares (still assuming that
![]() $a$
is not a square). We show that
$a$
is not a square). We show that
![]() $(a,a)=0$
implies that
$(a,a)=0$
implies that
![]() $\langle a,a,a,a\rangle$
is defined and vanishes.
$\langle a,a,a,a\rangle$
is defined and vanishes.
Since
![]() $(a,a)=0$
, we draw the existence of
$(a,a)=0$
, we draw the existence of
![]() $B_{0}$
with
$B_{0}$
with
![]() $\operatorname{N}_{F[\sqrt{a}]/F}(B_{0})=a$
from Proposition 2.3. It is always true that
$\operatorname{N}_{F[\sqrt{a}]/F}(B_{0})=a$
from Proposition 2.3. It is always true that
![]() $(a,-a)=0$
, so we have
$(a,-a)=0$
, so we have
![]() $(a,-1)=0$
, implying that
$(a,-1)=0$
, implying that
![]() $a$
is a sum of two squares in
$a$
is a sum of two squares in
![]() $F$
. We invoke the ‘norm principle’ from [Reference Elman and LamEL76]: from the fact that
$F$
. We invoke the ‘norm principle’ from [Reference Elman and LamEL76]: from the fact that
![]() $\operatorname{N}_{F[\sqrt{a}]/F}(B_{0})$
is the product of two elements, namely
$\operatorname{N}_{F[\sqrt{a}]/F}(B_{0})$
is the product of two elements, namely
![]() $a$
and
$a$
and
![]() $1$
, which are each the sum of two squares in
$1$
, which are each the sum of two squares in
![]() $F$
, this principle implies that there exists
$F$
, this principle implies that there exists
![]() $\unicode[STIX]{x1D6FD}\in F^{\times }$
such that
$\unicode[STIX]{x1D6FD}\in F^{\times }$
such that
![]() $B=\unicode[STIX]{x1D6FD}B_{0}$
is the sum of two squares in
$B=\unicode[STIX]{x1D6FD}B_{0}$
is the sum of two squares in
![]() $F[\sqrt{a}]$
. In turn, this means that
$F[\sqrt{a}]$
. In turn, this means that
![]() $(B,-1)=0$
and so
$(B,-1)=0$
and so
![]() $(B,B)=0$
.
$(B,B)=0$
.
Obviously
![]() $(B,a)=(B,1)=0$
in the cohomology of
$(B,a)=(B,1)=0$
in the cohomology of
![]() $F[\sqrt{a}]$
since
$F[\sqrt{a}]$
since
![]() $a$
is a square there, so Theorem 3.5 applies (with
$a$
is a square there, so Theorem 3.5 applies (with
![]() $C=B$
).
$C=B$
).
Example 4.4 (The abad case).
One more example in the same style. We prove that
![]() $\langle a,b,a,d\rangle$
is defined and vanishes, under the following assumptions: none of
$\langle a,b,a,d\rangle$
is defined and vanishes, under the following assumptions: none of
![]() $a,b,d\in F^{\times }$
is a square, neither is
$a,b,d\in F^{\times }$
is a square, neither is
![]() $ad$
, and
$ad$
, and
![]() $(a,b)=(a,d)=0$
.
$(a,b)=(a,d)=0$
.
Pick
![]() $B_{0}$
such that
$B_{0}$
such that
![]() $\operatorname{N}_{F[\sqrt{a}]/F}(B_{0})=b$
and
$\operatorname{N}_{F[\sqrt{a}]/F}(B_{0})=b$
and
![]() $C_{0}$
such that
$C_{0}$
such that
![]() $\operatorname{N}_{F[\sqrt{d}]/F}(C_{0})=a$
. Furthermore, put
$\operatorname{N}_{F[\sqrt{d}]/F}(C_{0})=a$
. Furthermore, put
![]() $E=F[\sqrt{a},\sqrt{d}]$
. From the fact that
$E=F[\sqrt{a},\sqrt{d}]$
. From the fact that
![]() $\operatorname{N}_{E/F[\sqrt{a}]}(C/\sqrt{a})=1$
, we draw via Hilbert’s Theorem 90 the existence of
$\operatorname{N}_{E/F[\sqrt{a}]}(C/\sqrt{a})=1$
, we draw via Hilbert’s Theorem 90 the existence of
![]() $x\in E^{\times }$
such that
$x\in E^{\times }$
such that
![]() $Cx^{2}=\operatorname{N}_{E/F[\sqrt{a}]}(x)\sqrt{a}$
, and so in particular
$Cx^{2}=\operatorname{N}_{E/F[\sqrt{a}]}(x)\sqrt{a}$
, and so in particular
![]() $Cx^{2}\in F[\sqrt{a}]$
.
$Cx^{2}\in F[\sqrt{a}]$
.
Two cases can occur. First, assume that
![]() $B_{0}$
and
$B_{0}$
and
![]() $C_{0}x^{2}$
are linearly independent in
$C_{0}x^{2}$
are linearly independent in
![]() $F[\sqrt{a}]$
over
$F[\sqrt{a}]$
over
![]() $F$
. Then there exist
$F$
. Then there exist
![]() $\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in F$
such that
$\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in F$
such that
We can see easily that
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $\unicode[STIX]{x1D6FE}$
are both non-zero, for supposing otherwise would lead us to conclude, upon taking norms, that
$\unicode[STIX]{x1D6FE}$
are both non-zero, for supposing otherwise would lead us to conclude, upon taking norms, that
![]() $b$
or
$b$
or
![]() $a$
is a square in
$a$
is a square in
![]() $F$
. Thus
$F$
. Thus
Let us check that we can come to the same conclusion if we assume, alternatively, that
![]() $B_{0}=hC_{0}x^{2}$
for some
$B_{0}=hC_{0}x^{2}$
for some
![]() $h\in F^{\times }$
. Indeed, put
$h\in F^{\times }$
. Indeed, put
![]() $\unicode[STIX]{x1D6FD}=1$
and
$\unicode[STIX]{x1D6FD}=1$
and
![]() $\unicode[STIX]{x1D6FE}=-h$
and we do have
$\unicode[STIX]{x1D6FE}=-h$
and we do have
In either case, if we put
![]() $B=\unicode[STIX]{x1D6FD}B_{0}$
and
$B=\unicode[STIX]{x1D6FD}B_{0}$
and
![]() $C=\unicode[STIX]{x1D6FE}C_{0}$
, then
$C=\unicode[STIX]{x1D6FE}C_{0}$
, then
![]() $(B,C)_{E}=0$
. The other hypotheses required to apply Theorem 3.5 are redundant here, from Lemma 5.2 below (essentially because of the projection formula).
$(B,C)_{E}=0$
. The other hypotheses required to apply Theorem 3.5 are redundant here, from Lemma 5.2 below (essentially because of the projection formula).
5 Splitting varieties
5.1 The fundamental equation
Proposition 2.3 gives a necessary and sufficient condition for a cup-product to vanish in Galois cohomology, in terms of a simple polynomial equation. We shall see that the four cup-products of Theorem 3.5 are likewise controlled by a single polynomial equation, taking place in a certain finite étale
![]() $F$
-algebra, namely
$F$
-algebra, namely
More precisely, we establish the following.
Proposition 5.1. Let
![]() $a,b,c,d\in F^{\times }$
. Let
$a,b,c,d\in F^{\times }$
. Let
![]() $\widetilde{B}\in F_{a}\subset \mathscr{E}$
satisfy
$\widetilde{B}\in F_{a}\subset \mathscr{E}$
satisfy
![]() $\operatorname{N}_{F_{a}/F}(\widetilde{B})=bz_{1}^{2}$
, and let
$\operatorname{N}_{F_{a}/F}(\widetilde{B})=bz_{1}^{2}$
, and let
![]() $\widetilde{C}\in F_{d}\subset \mathscr{E}$
satisfy
$\widetilde{C}\in F_{d}\subset \mathscr{E}$
satisfy
![]() $\operatorname{N}_{F_{d}/F}(\widetilde{C})=cz_{2}^{2}$
, for some
$\operatorname{N}_{F_{d}/F}(\widetilde{C})=cz_{2}^{2}$
, for some
![]() $z_{1},z_{2}\in F^{\times }$
. Let
$z_{1},z_{2}\in F^{\times }$
. Let
![]() $B\in F[\sqrt{a}]$
and
$B\in F[\sqrt{a}]$
and
![]() $C\in F[\sqrt{d}]$
be the corresponding elements. Then the equation
$C\in F[\sqrt{d}]$
be the corresponding elements. Then the equation
has some solution with
![]() $u,v\in \mathscr{E}$
if and only if we have simultaneously
$u,v\in \mathscr{E}$
if and only if we have simultaneously
![]() $(B,C)_{F[\sqrt{a},\sqrt{d}]}=0$
,
$(B,C)_{F[\sqrt{a},\sqrt{d}]}=0$
,
![]() $(B,c)_{F[\sqrt{a}]}=0$
,
$(B,c)_{F[\sqrt{a}]}=0$
,
![]() $(b,C)_{F[\sqrt{d}]}=0$
,
$(b,C)_{F[\sqrt{d}]}=0$
,
![]() $(b,c)_{F}=0$
. Alternatively, the same holds with the equation
$(b,c)_{F}=0$
. Alternatively, the same holds with the equation
The proof will be done in a case-by-case manner (each time getting a slightly more precise statement than that in the proposition). A quick remark about the equivalence of the two equations, though: it is not a completely general fact, as for example the equation
![]() $u^{2}+2v^{2}=1$
has four solutions over
$u^{2}+2v^{2}=1$
has four solutions over
![]() $\mathbb{Z}/4\mathbb{Z}$
while
$\mathbb{Z}/4\mathbb{Z}$
while
![]() $u^{2}-v^{2}=2$
has no solution over the same ring. When working over a field of characteristic different from
$u^{2}-v^{2}=2$
has no solution over the same ring. When working over a field of characteristic different from
![]() $2$
however, the two problems are equivalent, as elementary computations reveal; since
$2$
however, the two problems are equivalent, as elementary computations reveal; since
![]() $\mathscr{E}$
is a direct sum of such fields, we may indeed use either equation. The second is symmetric in
$\mathscr{E}$
is a direct sum of such fields, we may indeed use either equation. The second is symmetric in
![]() $\widetilde{B}$
and
$\widetilde{B}$
and
![]() $\widetilde{C}$
, and will be used in the sequel, but the proofs in the remainder of this section will be dealing with the first.
$\widetilde{C}$
, and will be used in the sequel, but the proofs in the remainder of this section will be dealing with the first.
In the ‘generic case’ first, that is when
![]() $a$
and
$a$
and
![]() $d$
are linearly independent in
$d$
are linearly independent in
![]() $F^{\times }\!/F^{\times 2}$
, we can and we do identify
$F^{\times }\!/F^{\times 2}$
, we can and we do identify
![]() $\mathscr{E}$
with
$\mathscr{E}$
with
![]() $E=F[\sqrt{a},\sqrt{d}]$
. Moreover, we have the following simple situation.
$E=F[\sqrt{a},\sqrt{d}]$
. Moreover, we have the following simple situation.
Lemma 5.2. Let
![]() $\widetilde{B},B,\widetilde{C},C$
be as in the proposition. Suppose that
$\widetilde{B},B,\widetilde{C},C$
be as in the proposition. Suppose that
![]() $(B,C)_{E}=0$
.
$(B,C)_{E}=0$
.
(i) If neither
 $d$
nor
$d$
nor
 $ad$
is a square in
$ad$
is a square in
 $F$
, then we have
$F$
, then we have
 $(B,c)_{F[\sqrt{a}]}=0$
. If neither
$(B,c)_{F[\sqrt{a}]}=0$
. If neither
 $a$
nor
$a$
nor
 $ad$
is a square in
$ad$
is a square in
 $F$
, we have
$F$
, we have
 $(b,C)_{F[\sqrt{d}]}=0$
.
$(b,C)_{F[\sqrt{d}]}=0$
.(ii) If
 $(B,c)_{F[\sqrt{a}]}=0$
and
$(B,c)_{F[\sqrt{a}]}=0$
and
 $a$
is not a square in
$a$
is not a square in
 $F$
, we have
$F$
, we have
 $(b,c)_{F}=0$
. Likewise, if
$(b,c)_{F}=0$
. Likewise, if
 $(b,C)_{F[\sqrt{d}]}=0$
and
$(b,C)_{F[\sqrt{d}]}=0$
and
 $d$
is not a square in
$d$
is not a square in
 $F$
, we also conclude that
$F$
, we also conclude that
 $(b,c)_{F}=0$
.
$(b,c)_{F}=0$
.
In particular, when
![]() $[E:F]=4$
, the four cup-products from Theorem 3.5 vanish precisely when there are
$[E:F]=4$
, the four cup-products from Theorem 3.5 vanish precisely when there are
![]() $u,v\in E$
satisfying
$u,v\in E$
satisfying
Proof. If we suppose that
![]() $a$
is not a square in
$a$
is not a square in
![]() $F$
, then
$F$
, then
![]() $\operatorname{N}_{F[\sqrt{a}]/F}(B)=bz_{1}^{2}$
; if
$\operatorname{N}_{F[\sqrt{a}]/F}(B)=bz_{1}^{2}$
; if
![]() $ad$
is not a square either, than we can also write
$ad$
is not a square either, than we can also write
![]() $\operatorname{N}_{E/F[\sqrt{d}]}(B)=bz_{1}^{2}$
. Thus we can use the projection formula from group cohomology, asserting that
$\operatorname{N}_{E/F[\sqrt{d}]}(B)=bz_{1}^{2}$
. Thus we can use the projection formula from group cohomology, asserting that
where
![]() $\operatorname{cores}:\operatorname{H}^{2}(E,\mathbb{F}_{2})\rightarrow \operatorname{H}^{2}(F[\sqrt{d}],\mathbb{F}_{2})$
is the corestriction. Thus
$\operatorname{cores}:\operatorname{H}^{2}(E,\mathbb{F}_{2})\rightarrow \operatorname{H}^{2}(F[\sqrt{d}],\mathbb{F}_{2})$
is the corestriction. Thus
![]() $(B,C)_{E}=0$
does imply
$(B,C)_{E}=0$
does imply
![]() $(b,C)_{F[\sqrt{d}]}=0$
. The other case is treated similarly.
$(b,C)_{F[\sqrt{d}]}=0$
. The other case is treated similarly.
One also proves (ii) using the projection formula.
For the last statement, we invoke Proposition 2.3 which states that the proposed equation has a solution if and only if
![]() $(B,C)_{E}=0$
. By the first part, this implies that the other three cup-products also vanish.◻
$(B,C)_{E}=0$
. By the first part, this implies that the other three cup-products also vanish.◻
Now suppose that
![]() $a$
and
$a$
and
![]() $d$
are both squares in
$d$
are both squares in
![]() $F$
. Then we have four
$F$
. Then we have four
![]() $F$
-homomorphisms
$F$
-homomorphisms
![]() $p_{i}:\mathscr{E}\rightarrow F$
, for
$p_{i}:\mathscr{E}\rightarrow F$
, for
![]() $i=1,2,3,4$
, mapping
$i=1,2,3,4$
, mapping
![]() $X$
to
$X$
to
![]() $\pm \sqrt{a}$
and
$\pm \sqrt{a}$
and
![]() $Y$
to
$Y$
to
![]() $\pm \sqrt{d}$
. Together they induce an isomorphism
$\pm \sqrt{d}$
. Together they induce an isomorphism
![]() $\mathscr{E}\cong F\times F\times F\times F$
, by the Chinese remainder theorem. (Note that the map
$\mathscr{E}\cong F\times F\times F\times F$
, by the Chinese remainder theorem. (Note that the map
![]() $F\rightarrow \mathscr{E}$
which turns
$F\rightarrow \mathscr{E}$
which turns
![]() $\mathscr{E}$
naturally into an
$\mathscr{E}$
naturally into an
![]() $F$
-algebra is the diagonal embedding of
$F$
-algebra is the diagonal embedding of
![]() $F$
in
$F$
in
![]() $F^{4}$
, under this isomorphism.)
$F^{4}$
, under this isomorphism.)
Lemma 5.3. Suppose
![]() $a$
and
$a$
and
![]() $d$
are both squares in
$d$
are both squares in
![]() $F$
. Let
$F$
. Let
![]() $\widetilde{B},B,\widetilde{C},C$
be as in the proposition. Then
$\widetilde{B},B,\widetilde{C},C$
be as in the proposition. Then
has a solution with
![]() $u,v\in \mathscr{E}$
if and only if we have simultaneously
$u,v\in \mathscr{E}$
if and only if we have simultaneously
Proof. Applying
![]() $p_{i}$
with
$p_{i}$
with
![]() $i=1,2,3,4$
, the equation becomes equivalent to the four equations
$i=1,2,3,4$
, the equation becomes equivalent to the four equations
with unknowns
![]() $u_{i},v_{i}\in F$
. This is possible if and only if
$u_{i},v_{i}\in F$
. This is possible if and only if
![]() $(p_{i}(\widetilde{B}),p_{i}(\widetilde{C}))=0$
for
$(p_{i}(\widetilde{B}),p_{i}(\widetilde{C}))=0$
for
![]() $i=1,2,3,4$
. (Note that the calculations to follow will establish that
$i=1,2,3,4$
. (Note that the calculations to follow will establish that
![]() $p_{i}(B)\neq 0$
,
$p_{i}(B)\neq 0$
,
![]() $p_{i}(C)\neq 0$
for all
$p_{i}(C)\neq 0$
for all
![]() $i$
, so that the cup-products make sense.)
$i$
, so that the cup-products make sense.)
We need some notation. Let
![]() $B=x+y\sqrt{a}$
and
$B=x+y\sqrt{a}$
and
![]() $C=x^{\prime }+y^{\prime }\sqrt{d}$
, and introduce
$C=x^{\prime }+y^{\prime }\sqrt{d}$
, and introduce
![]() $B^{\prime }=x-y\sqrt{a}$
and
$B^{\prime }=x-y\sqrt{a}$
and
![]() $C^{\prime }=x^{\prime }-y^{\prime }\sqrt{d}$
, so that
$C^{\prime }=x^{\prime }-y^{\prime }\sqrt{d}$
, so that
![]() $BB^{\prime }=bz_{1}^{2}\neq 0$
, and likewise
$BB^{\prime }=bz_{1}^{2}\neq 0$
, and likewise
![]() $CC^{\prime }=cz_{2}^{2}\neq 0$
. To fix our ideas, we assume that the numbering of the homomorphisms
$CC^{\prime }=cz_{2}^{2}\neq 0$
. To fix our ideas, we assume that the numbering of the homomorphisms
![]() $p_{i}$
has been made such that
$p_{i}$
has been made such that
The four cup-products we consider are then
![]() $(B,C)$
,
$(B,C)$
,
![]() $(B^{\prime },C)$
,
$(B^{\prime },C)$
,
![]() $(B,C^{\prime })$
and
$(B,C^{\prime })$
and
![]() $(B^{\prime },C^{\prime })$
for
$(B^{\prime },C^{\prime })$
for
![]() $i=1,2,3,4$
respectively, all in the cohomology of
$i=1,2,3,4$
respectively, all in the cohomology of
![]() $F$
. However
$F$
. However
and similarly we draw
![]() $(B,c)=0$
and
$(B,c)=0$
and
![]() $(b,c)=0$
. One can also work backwards, clearly.◻
$(b,c)=0$
. One can also work backwards, clearly.◻
When
![]() $a$
is a square in
$a$
is a square in
![]() $F$
, but
$F$
, but
![]() $d$
is not, we view
$d$
is not, we view
![]() $\mathscr{E}$
as
$\mathscr{E}$
as
![]() $F[\sqrt{d}][X]/(X^{2}-a)\cong F[\sqrt{d}]\times F[\sqrt{d}]$
with its two
$F[\sqrt{d}][X]/(X^{2}-a)\cong F[\sqrt{d}]\times F[\sqrt{d}]$
with its two
![]() $F[\sqrt{d}]$
-homomorphisms
$F[\sqrt{d}]$
-homomorphisms
![]() $p_{1},p_{2}:\mathscr{E}\rightarrow F[\sqrt{d}]$
. The elements
$p_{1},p_{2}:\mathscr{E}\rightarrow F[\sqrt{d}]$
. The elements
![]() $Y$
and
$Y$
and
![]() $\sqrt{d}$
are identified. A reasoning similar to the above yields the following.
$\sqrt{d}$
are identified. A reasoning similar to the above yields the following.
Lemma 5.4. Suppose that
![]() $a$
is a square in
$a$
is a square in
![]() $F$
, and that
$F$
, and that
![]() $d$
is not. Let
$d$
is not. Let
![]() $\widetilde{B},B,\widetilde{C},C$
be as in the Proposition. Then the equation
$\widetilde{B},B,\widetilde{C},C$
be as in the Proposition. Then the equation
has a solution with
![]() $u,v\in \mathscr{E}$
if and only if we have simultaneously
$u,v\in \mathscr{E}$
if and only if we have simultaneously
![]() $(B,C)_{F[\sqrt{d}]}=(b,C)_{F[\sqrt{d}]}=0$
. When this is the case, we have automatically
$(B,C)_{F[\sqrt{d}]}=(b,C)_{F[\sqrt{d}]}=0$
. When this is the case, we have automatically
![]() $(B,c)_{F}=(b,c)_{F}=0$
from Lemma 5.2.
$(B,c)_{F}=(b,c)_{F}=0$
from Lemma 5.2.
Of course a similar result holds with the roles of
![]() $a$
and
$a$
and
![]() $d$
exchanged.
$d$
exchanged.
Finally we turn to the case when neither
![]() $a$
nor
$a$
nor
![]() $d$
is a square in
$d$
is a square in
![]() $F$
, but
$F$
, but
![]() $ad$
is. This is in fact similar to the previous case, except that we now have a choice. Namely, we can produce two
$ad$
is. This is in fact similar to the previous case, except that we now have a choice. Namely, we can produce two
![]() $F[\sqrt{d}]$
-homomorphisms
$F[\sqrt{d}]$
-homomorphisms
![]() $p_{1},p_{2}:\mathscr{E}\rightarrow F[\sqrt{d}]$
giving an isomorphism
$p_{1},p_{2}:\mathscr{E}\rightarrow F[\sqrt{d}]$
giving an isomorphism
![]() $\mathscr{E}\cong F[\sqrt{d}]\times F[\sqrt{d}]$
, identifying
$\mathscr{E}\cong F[\sqrt{d}]\times F[\sqrt{d}]$
, identifying
![]() $\sqrt{d}$
with
$\sqrt{d}$
with
![]() $Y$
all along; or, we can alternatively find two
$Y$
all along; or, we can alternatively find two
![]() $F[\sqrt{a}]$
-homomorphisms
$F[\sqrt{a}]$
-homomorphisms
![]() $p_{1}^{\prime },p_{2}^{\prime }:\mathscr{E}\rightarrow F[\sqrt{a}]$
, giving an isomorphism
$p_{1}^{\prime },p_{2}^{\prime }:\mathscr{E}\rightarrow F[\sqrt{a}]$
, giving an isomorphism
![]() $\mathscr{E}\cong F[\sqrt{a}]\times F[\sqrt{a}]$
, identifying
$\mathscr{E}\cong F[\sqrt{a}]\times F[\sqrt{a}]$
, identifying
![]() $X$
with
$X$
with
![]() $\sqrt{a}$
all along. These two isomorphisms are distinct, even if
$\sqrt{a}$
all along. These two isomorphisms are distinct, even if
![]() $a=d$
. Using one and then the other, we get the following.
$a=d$
. Using one and then the other, we get the following.
Lemma 5.5. Suppose that neither
![]() $a$
nor
$a$
nor
![]() $d$
is a square in
$d$
is a square in
![]() $F$
, but that
$F$
, but that
![]() $ad$
is. Let
$ad$
is. Let
![]() $\widetilde{B},B,\widetilde{C},C$
be as in the proposition. Then the equation
$\widetilde{B},B,\widetilde{C},C$
be as in the proposition. Then the equation
has a solution with
![]() $u,v\in \mathscr{E}$
if and only if we have simultaneously
$u,v\in \mathscr{E}$
if and only if we have simultaneously
![]() $(B,C)_{F[\sqrt{d}]}=(b,C)_{F[\sqrt{d}]}=0$
, if and only if we have simultaneously
$(B,C)_{F[\sqrt{d}]}=(b,C)_{F[\sqrt{d}]}=0$
, if and only if we have simultaneously
![]() $(B,C)_{F[\sqrt{a}]}=(B,c)_{F[\sqrt{a}]}=0$
. When this is the case, we have automatically
$(B,C)_{F[\sqrt{a}]}=(B,c)_{F[\sqrt{a}]}=0$
. When this is the case, we have automatically
![]() $(b,c)_{F}=0$
from Lemma 5.2.
$(b,c)_{F}=0$
from Lemma 5.2.
This completes the proof of the proposition. Given that the existence of
![]() $\widetilde{B}$
and
$\widetilde{B}$
and
![]() $\widetilde{C}$
is itself controlled by a simple polynomial equation, as in Proposition 2.3, the situation is now entirely rewritten in terms of the existence of a rational point on an algebraic variety.
$\widetilde{C}$
is itself controlled by a simple polynomial equation, as in Proposition 2.3, the situation is now entirely rewritten in terms of the existence of a rational point on an algebraic variety.
5.2 Splitting varieties
We proceed to translate our results into the language of algebraic geometry.
As ever, let
![]() $F$
be a field of characteristic not
$F$
be a field of characteristic not
![]() $2$
, let
$2$
, let
![]() $a,b,c,d\in F^{\times }$
, and put
$a,b,c,d\in F^{\times }$
, and put
Together, Theorem 3.5, Proposition 2.3 and Proposition 5.1 show that the vanishing of the Massey product
![]() $\langle a,b,c,d\rangle$
is equivalent to the existence of a solution to the following system of equations, with unknowns
$\langle a,b,c,d\rangle$
is equivalent to the existence of a solution to the following system of equations, with unknowns
![]() $x_{1},y_{1},z_{1},x_{2},y_{2},y_{3}\in F$
,
$x_{1},y_{1},z_{1},x_{2},y_{2},y_{3}\in F$
,
![]() $u,v\in \mathscr{E}$
:
$u,v\in \mathscr{E}$
:
(1)
 $x_{1}^{2}-ay_{1}^{2}=bz_{1}^{2}$
;
$x_{1}^{2}-ay_{1}^{2}=bz_{1}^{2}$
;(2)
 $x_{2}^{2}-dy_{2}^{2}=cz_{2}^{2}$
;
$x_{2}^{2}-dy_{2}^{2}=cz_{2}^{2}$
;(3)
 $u^{2}\widetilde{B}+v^{2}\widetilde{C}=1$
, where
$u^{2}\widetilde{B}+v^{2}\widetilde{C}=1$
, where
 $\widetilde{B}=x_{1}+y_{1}X\in \mathscr{E}$
and
$\widetilde{B}=x_{1}+y_{1}X\in \mathscr{E}$
and
 $\widetilde{C}=x_{2}+y_{2}Y\in \mathscr{E}$
.
$\widetilde{C}=x_{2}+y_{2}Y\in \mathscr{E}$
.
There is also the condition
![]() $z_{1}\neq 0$
,
$z_{1}\neq 0$
,
![]() $z_{2}\neq 0$
. Here
$z_{2}\neq 0$
. Here
![]() $u=u_{1}+u_{2}X+u_{3}Y+u_{4}XY$
, and likewise for
$u=u_{1}+u_{2}X+u_{3}Y+u_{4}XY$
, and likewise for
![]() $v$
, so that equation (3) can be written as four equations over
$v$
, so that equation (3) can be written as four equations over
![]() $F$
(carrying out the expansion in practice does not seem to clarify things).
$F$
(carrying out the expansion in practice does not seem to clarify things).
For technical reasons, related to Proposition 4.1, we change coordinates and work with the equations:
(i)
 $x_{1}^{2}-ay_{1}^{2}=b$
;
$x_{1}^{2}-ay_{1}^{2}=b$
;(ii)
 $x_{2}^{2}-dy_{2}^{2}=c$
;
$x_{2}^{2}-dy_{2}^{2}=c$
;(iii)
 $u^{2}\unicode[STIX]{x1D6FD}\widetilde{B}+v^{2}\unicode[STIX]{x1D6FE}\widetilde{C}=1$
, where
$u^{2}\unicode[STIX]{x1D6FD}\widetilde{B}+v^{2}\unicode[STIX]{x1D6FE}\widetilde{C}=1$
, where
 $\widetilde{B}=x_{1}+y_{1}X\in \mathscr{E}$
and
$\widetilde{B}=x_{1}+y_{1}X\in \mathscr{E}$
and
 $\widetilde{C}=x_{2}+y_{2}Y\in \mathscr{E}$
.
$\widetilde{C}=x_{2}+y_{2}Y\in \mathscr{E}$
.
Here
![]() $\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in F^{\times }$
are two new unknowns, and
$\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in F^{\times }$
are two new unknowns, and
![]() $z_{1},z_{2}$
have disappeared.
$z_{1},z_{2}$
have disappeared.
Equations (i), (ii), (iii) define an affine subvariety of
![]() $\mathbf{A}_{F}^{14}$
, the affine space of dimension 14 over
$\mathbf{A}_{F}^{14}$
, the affine space of dimension 14 over
![]() $F$
; we consider its intersection with the open subset defined by
$F$
; we consider its intersection with the open subset defined by
![]() $\unicode[STIX]{x1D6FD}\neq 0$
,
$\unicode[STIX]{x1D6FD}\neq 0$
,
![]() $\unicode[STIX]{x1D6FE}\neq 0$
, and call it
$\unicode[STIX]{x1D6FE}\neq 0$
, and call it
![]() $\mathscr{X}_{F}$
. Also, note that equation (i) implies that
$\mathscr{X}_{F}$
. Also, note that equation (i) implies that
![]() $\widetilde{B}$
is a unit of
$\widetilde{B}$
is a unit of
![]() $F_{a}:=F[X]/(X^{2}-a)$
, and similarly equation (ii) implies that
$F_{a}:=F[X]/(X^{2}-a)$
, and similarly equation (ii) implies that
![]() $\widetilde{C}$
is a unit of
$\widetilde{C}$
is a unit of
![]() $F_{d}:=F[Y]/(Y^{2}-d)$
. In particular, we can describe
$F_{d}:=F[Y]/(Y^{2}-d)$
. In particular, we can describe
![]() $\mathscr{X}_{F}$
in a more conceptual way using the Weil-restriction functors
$\mathscr{X}_{F}$
in a more conceptual way using the Weil-restriction functors
![]() $R_{\mathscr{E}|F}$
,
$R_{\mathscr{E}|F}$
,
![]() $R_{F_{a}|F}$
and
$R_{F_{a}|F}$
and
![]() $R_{F_{d}|F}$
. Namely, consider the
$R_{F_{d}|F}$
. Namely, consider the
![]() $F$
-variety:
$F$
-variety:
We view an
![]() $F$
-point of
$F$
-point of
![]() $\mathscr{Y}$
as a tuple
$\mathscr{Y}$
as a tuple
![]() $(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},u,v,\widetilde{B},\widetilde{C})$
, with
$(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},u,v,\widetilde{B},\widetilde{C})$
, with
![]() $\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in F^{\times }$
,
$\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in F^{\times }$
,
![]() $u,v\in \mathscr{E}$
,
$u,v\in \mathscr{E}$
,
![]() $\widetilde{B}\in F_{a}^{\times }$
and
$\widetilde{B}\in F_{a}^{\times }$
and
![]() $\widetilde{C}\in F_{d}^{\times }$
. Then
$\widetilde{C}\in F_{d}^{\times }$
. Then
![]() $\mathscr{X}_{F}$
is the closed subvariety of
$\mathscr{X}_{F}$
is the closed subvariety of
![]() $\mathscr{Y}$
defined by the three equations:
$\mathscr{Y}$
defined by the three equations:
We have the following trivial, yet crucial property: for an extension
![]() $L/F$
, we have
$L/F$
, we have
In particular, we have
![]() $\mathscr{X}_{F}(L)=\mathscr{X}_{L}(L)$
(using the standard notation for the set of rational points). As already noted, the set
$\mathscr{X}_{F}(L)=\mathscr{X}_{L}(L)$
(using the standard notation for the set of rational points). As already noted, the set
![]() $\mathscr{X}_{F}(F)$
is non-empty if and only if the Massey product
$\mathscr{X}_{F}(F)$
is non-empty if and only if the Massey product
![]() $\langle a,b,c,d\rangle$
is defined and vanishes in the cohomology of
$\langle a,b,c,d\rangle$
is defined and vanishes in the cohomology of
![]() $F$
. Now, it is obviously also true, but nicer, that for any field extension
$F$
. Now, it is obviously also true, but nicer, that for any field extension
![]() $L/F$
, the set
$L/F$
, the set
![]() $\mathscr{X}_{F}(L)$
is non-empty if and only if the Massey product
$\mathscr{X}_{F}(L)$
is non-empty if and only if the Massey product
![]() $\langle a,b,c,d\rangle$
is defined and vanishes in the cohomology of
$\langle a,b,c,d\rangle$
is defined and vanishes in the cohomology of
![]() $L$
. This is a property which is expected of a ‘splitting variety’ for the problem of the vanishing of
$L$
. This is a property which is expected of a ‘splitting variety’ for the problem of the vanishing of
![]() $\langle a,b,c,d\rangle$
.
$\langle a,b,c,d\rangle$
.
As it turns out, we can introduce a second splitting variety
![]() $X_{F}$
. It will depend on choices, and so is not canonically associated with the problem alone; on the other hand, the local-global principle is established in the appendix for
$X_{F}$
. It will depend on choices, and so is not canonically associated with the problem alone; on the other hand, the local-global principle is established in the appendix for
![]() $X_{F}$
rather than
$X_{F}$
rather than
![]() $\mathscr{X}_{F}$
. The construction will echo Proposition 4.1 rather precisely. Let
$\mathscr{X}_{F}$
. The construction will echo Proposition 4.1 rather precisely. Let
![]() $Z_{F}$
be the subvariety of
$Z_{F}$
be the subvariety of
![]() $R_{F_{a}/F}\mathbf{G}_{m}\times R_{F_{d}/F}\mathbf{G}_{m}$
, defined over
$R_{F_{a}/F}\mathbf{G}_{m}\times R_{F_{d}/F}\mathbf{G}_{m}$
, defined over
![]() $F$
be the equations
$F$
be the equations
There is an obvious morphism
![]() $\unicode[STIX]{x1D70B}:\mathscr{X}_{F}\rightarrow Z_{F}$
(forgetting
$\unicode[STIX]{x1D70B}:\mathscr{X}_{F}\rightarrow Z_{F}$
(forgetting
![]() $\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},u,v$
), and we will define
$\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},u,v$
), and we will define
![]() $X_{F}$
to be a fibre of
$X_{F}$
to be a fibre of
![]() $\unicode[STIX]{x1D70B}$
above an
$\unicode[STIX]{x1D70B}$
above an
![]() $F$
-rational point of
$F$
-rational point of
![]() $Z_{F}$
. That is, we will suppose from now on that
$Z_{F}$
. That is, we will suppose from now on that
![]() $(a,b)_{F}=(c,d)_{F}=0$
, and using Proposition 2.3 twice, we select
$(a,b)_{F}=(c,d)_{F}=0$
, and using Proposition 2.3 twice, we select
![]() $\widetilde{B}_{0}\in F_{a}$
and
$\widetilde{B}_{0}\in F_{a}$
and
![]() $\widetilde{C}_{0}\in F_{d}$
whose norms are
$\widetilde{C}_{0}\in F_{d}$
whose norms are
![]() $b$
and
$b$
and
![]() $c$
respectively; then we put
$c$
respectively; then we put
![]() $X_{F}=\unicode[STIX]{x1D70B}^{-1}(\widetilde{B}_{0},\widetilde{C}_{0})$
. The variety
$X_{F}=\unicode[STIX]{x1D70B}^{-1}(\widetilde{B}_{0},\widetilde{C}_{0})$
. The variety
![]() $X_{F}$
is thus defined by the equation
$X_{F}$
is thus defined by the equation
Note that our construction of
![]() $X_{F}$
depends on the choice of
$X_{F}$
depends on the choice of
![]() $\widetilde{B}_{0}$
and
$\widetilde{B}_{0}$
and
![]() $\widetilde{C}_{0}$
as above. In the sequel, this choice will always be clear from context, so we omit the
$\widetilde{C}_{0}$
as above. In the sequel, this choice will always be clear from context, so we omit the
![]() $\widetilde{B}_{0}$
,
$\widetilde{B}_{0}$
,
![]() $\widetilde{C}_{0}$
from the notation.
$\widetilde{C}_{0}$
from the notation.
It is clear that
![]() $X_{F}$
is also compatible with base-change, just like
$X_{F}$
is also compatible with base-change, just like
![]() $\mathscr{X}_{F}$
is. That it is also a splitting variety is part of the next theorem.
$\mathscr{X}_{F}$
is. That it is also a splitting variety is part of the next theorem.
Theorem 5.6. Let the notation be as above (in particular,
![]() $\widetilde{B}_{0}$
and
$\widetilde{B}_{0}$
and
![]() $\widetilde{C}_{0}$
have been chosen). Let
$\widetilde{C}_{0}$
have been chosen). Let
![]() $L/F$
be any field extension. The following statements are equivalent.
$L/F$
be any field extension. The following statements are equivalent.
(1) The Massey product
 $\langle a,b,c,d\rangle$
is defined and vanishes in the cohomology of
$\langle a,b,c,d\rangle$
is defined and vanishes in the cohomology of
 $L$
.
$L$
.(2) The variety
 $\mathscr{X}_{F}$
has an
$\mathscr{X}_{F}$
has an
 $L$
-rational point.
$L$
-rational point.(3) The variety
 $X_{F}$
has an
$X_{F}$
has an
 $L$
-rational point.
$L$
-rational point.
Moreover, let
![]() $\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in L$
. Then there is a rational point
$\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in L$
. Then there is a rational point
![]() $(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},u,v)\in X_{F}(L)$
if and only if we have
$(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},u,v)\in X_{F}(L)$
if and only if we have
![]() $(\unicode[STIX]{x1D6FD}B_{0},\unicode[STIX]{x1D6FE}C_{0})_{L[\sqrt{a},\sqrt{d}]}=0$
,
$(\unicode[STIX]{x1D6FD}B_{0},\unicode[STIX]{x1D6FE}C_{0})_{L[\sqrt{a},\sqrt{d}]}=0$
,
![]() $(\unicode[STIX]{x1D6FD}B_{0},c)_{L[\sqrt{a}]}=0$
,
$(\unicode[STIX]{x1D6FD}B_{0},c)_{L[\sqrt{a}]}=0$
,
![]() $(b,\unicode[STIX]{x1D6FE}C_{0})_{L[\sqrt{d}]}=0$
and
$(b,\unicode[STIX]{x1D6FE}C_{0})_{L[\sqrt{d}]}=0$
and
![]() $(b,c)_{L}=0$
simultaneously, where
$(b,c)_{L}=0$
simultaneously, where
![]() $B_{0}\in L[\sqrt{a}]$
corresponds to
$B_{0}\in L[\sqrt{a}]$
corresponds to
![]() $\widetilde{B}_{0}$
under the natural map
$\widetilde{B}_{0}$
under the natural map
![]() $F_{a}\rightarrow L[\sqrt{a}]$
, and likewise for
$F_{a}\rightarrow L[\sqrt{a}]$
, and likewise for
![]() $C_{0}\in L[\sqrt{d}]$
.
$C_{0}\in L[\sqrt{d}]$
.
Proof. Since
![]() $\mathscr{X}_{F}(L)=\mathscr{X}_{L}(L)$
, and similarly for
$\mathscr{X}_{F}(L)=\mathscr{X}_{L}(L)$
, and similarly for
![]() $X_{F}$
, we may as well (and we do) assume that
$X_{F}$
, we may as well (and we do) assume that
![]() $L=F$
. Then the equivalence is a mere reformulation of earlier material. To wit, Theorem 3.5 together with Proposition 5.1 shows the equivalence of (1) and (2), the variety
$L=F$
. Then the equivalence is a mere reformulation of earlier material. To wit, Theorem 3.5 together with Proposition 5.1 shows the equivalence of (1) and (2), the variety
![]() $\mathscr{X}_{F}$
being defined just for this purpose. The implication (3)
$\mathscr{X}_{F}$
being defined just for this purpose. The implication (3)
![]() $\;\Longrightarrow \;$
(2) is trivial. On the other hand, Proposition 4.1 gives (2)
$\;\Longrightarrow \;$
(2) is trivial. On the other hand, Proposition 4.1 gives (2)
![]() $\;\Longrightarrow \;$
(3) readily.
$\;\Longrightarrow \;$
(3) readily.
The ‘moreover’ statement is obtained by another application of Proposition 5.1. ◻
Having such a statement dealing with field extensions is necessary for us, as we intend to apply a local-global principle to prove the existence of rational points, and this requires an understanding of
![]() $X_{F}(F_{v})$
where
$X_{F}(F_{v})$
where
![]() $F_{v}$
is a completion of
$F_{v}$
is a completion of
![]() $F$
.
$F$
.
6 The
 $4$
-Massey vanishing conjecture for number fields
$4$
-Massey vanishing conjecture for number fields
In this section we finally prove the following.
Theorem 6.1. Let
![]() $F$
be a number field, and let
$F$
be a number field, and let
![]() $a,b,c,d\in F^{\times }$
be such that the Massey product
$a,b,c,d\in F^{\times }$
be such that the Massey product
![]() $\langle a,b,c,d\rangle$
is defined. Then
$\langle a,b,c,d\rangle$
is defined. Then
![]() $\langle a,b,c,d\rangle$
vanishes. In other words, the
$\langle a,b,c,d\rangle$
vanishes. In other words, the
![]() $4$
-Massey vanishing conjecture is true for number fields.
$4$
-Massey vanishing conjecture is true for number fields.
Proof. Since the Massey product is defined, we can apply Theorem 3.1, but some simplifying remarks are in order. First, we have
![]() $(a,b)=(b,c)=(c,d)=0$
, and so Lemma 3.6 takes care of the case when one of
$(a,b)=(b,c)=(c,d)=0$
, and so Lemma 3.6 takes care of the case when one of
![]() $a,b,c,d$
is a square in
$a,b,c,d$
is a square in
![]() $F$
; now we assume that none of them is a square, and in particular, we identify
$F$
; now we assume that none of them is a square, and in particular, we identify
![]() $F_{a}$
and
$F_{a}$
and
![]() $F[\sqrt{a}]$
, and we identify
$F[\sqrt{a}]$
, and we identify
![]() $F_{d}$
and
$F_{d}$
and
![]() $F[\sqrt{d}]$
. We do not distinguish between
$F[\sqrt{d}]$
. We do not distinguish between
![]() $\widetilde{B}$
and
$\widetilde{B}$
and
![]() $B$
, or between
$B$
, or between
![]() $\widetilde{C}$
and
$\widetilde{C}$
and
![]() $C$
, in the notation of Theorem 3.1. A second point is that we may replace once and for all
$C$
, in the notation of Theorem 3.1. A second point is that we may replace once and for all
![]() $b$
by
$b$
by
![]() $bz_{1}^{2}$
for
$bz_{1}^{2}$
for
![]() $z_{1}\in F^{\times }$
if we wish, as the class
$z_{1}\in F^{\times }$
if we wish, as the class
![]() $\unicode[STIX]{x1D712}_{b}\in \operatorname{H}^{1}(F,\mathbb{F}_{2})$
is not affected by this, and neither is the Massey product
$\unicode[STIX]{x1D712}_{b}\in \operatorname{H}^{1}(F,\mathbb{F}_{2})$
is not affected by this, and neither is the Massey product
![]() $\langle a,b,c,d\rangle$
. Likewise with
$\langle a,b,c,d\rangle$
. Likewise with
![]() $c$
.
$c$
.
With these precautions, the result of our application of Theorem 3.1 is this. We can find
![]() $B_{0}\in F[\sqrt{a}]$
and
$B_{0}\in F[\sqrt{a}]$
and
![]() $C_{0}\in F[\sqrt{d}]$
such that
$C_{0}\in F[\sqrt{d}]$
such that
![]() $\operatorname{N}_{F[\sqrt{a}]/F}(B_{0})=b$
and
$\operatorname{N}_{F[\sqrt{a}]/F}(B_{0})=b$
and
![]() $\operatorname{N}_{F[\sqrt{d}]/F}(C_{0})=c$
, while
$\operatorname{N}_{F[\sqrt{d}]/F}(C_{0})=c$
, while
![]() $(B_{0},c)_{F[\sqrt{a}]}=0$
and
$(B_{0},c)_{F[\sqrt{a}]}=0$
and
![]() $(b,C_{0})_{F[\sqrt{d}]}=0$
. Finally, we can find
$(b,C_{0})_{F[\sqrt{d}]}=0$
. Finally, we can find
![]() $u\in \operatorname{H}^{2}(F,\mathbb{F}_{2})$
whose restriction to
$u\in \operatorname{H}^{2}(F,\mathbb{F}_{2})$
whose restriction to
![]() $E$
is
$E$
is
![]() $(B_{0},C_{0})$
.
$(B_{0},C_{0})$
.
We select this
![]() $B_{0}$
and this
$B_{0}$
and this
![]() $C_{0}$
in order to construct the splitting variety
$C_{0}$
in order to construct the splitting variety
![]() $X_{F}$
, and we proceed to prove that
$X_{F}$
, and we proceed to prove that
![]() $X_{F}(F)$
is non-empty (by Theorem 5.6, we will then be done). From Theorem A.1, we see that it suffices to show that for each place
$X_{F}(F)$
is non-empty (by Theorem 5.6, we will then be done). From Theorem A.1, we see that it suffices to show that for each place
![]() $v$
of
$v$
of
![]() $F$
, we can find a rational point
$F$
, we can find a rational point
![]() $(\unicode[STIX]{x1D6FD}_{v},\unicode[STIX]{x1D6FE}_{v},u_{v},v_{v})$
in
$(\unicode[STIX]{x1D6FD}_{v},\unicode[STIX]{x1D6FE}_{v},u_{v},v_{v})$
in
![]() $X_{F}(F_{v})$
, in such a way that our various choices satisfy
$X_{F}(F_{v})$
, in such a way that our various choices satisfy
Here
![]() $\text{inv}_{v}$
is the unique isomorphism between
$\text{inv}_{v}$
is the unique isomorphism between
![]() $\operatorname{H}^{2}(F_{v},\mathbb{F}_{2})$
and
$\operatorname{H}^{2}(F_{v},\mathbb{F}_{2})$
and
![]() $\mathbb{F}_{2}$
. We turn to this, and in fact we shall arrange to have
$\mathbb{F}_{2}$
. We turn to this, and in fact we shall arrange to have
![]() $\text{inv}_{v}((\unicode[STIX]{x1D6FD}_{v},c)_{F_{v}})=0$
and
$\text{inv}_{v}((\unicode[STIX]{x1D6FD}_{v},c)_{F_{v}})=0$
and
![]() $\text{inv}_{v}((b,\unicode[STIX]{x1D6FE}_{v})_{F_{v}})=0$
at each place.
$\text{inv}_{v}((b,\unicode[STIX]{x1D6FE}_{v})_{F_{v}})=0$
at each place.
Let
![]() $v$
be a place. We see
$v$
be a place. We see
![]() $B_{0}$
and
$B_{0}$
and
![]() $C_{0}$
, chosen above, as elements of
$C_{0}$
, chosen above, as elements of
![]() $F_{v}[\sqrt{a}]$
and
$F_{v}[\sqrt{a}]$
and
![]() $F_{v}[\sqrt{d}]$
respectively, and we wish rely on the ‘moreover’ statement of Theorem 5.6 with
$F_{v}[\sqrt{d}]$
respectively, and we wish rely on the ‘moreover’ statement of Theorem 5.6 with
![]() $L=F_{v}$
.
$L=F_{v}$
.
First we treat the case when one of
![]() $a$
or
$a$
or
![]() $d$
is not a square in the completion
$d$
is not a square in the completion
![]() $F_{v}$
: either way, the field
$F_{v}$
: either way, the field
![]() $F_{v}[\sqrt{a},\sqrt{d}]$
is strictly larger than
$F_{v}[\sqrt{a},\sqrt{d}]$
is strictly larger than
![]() $F_{v}$
. However, it is a well-known fact from the theory of local fields that the restriction map
$F_{v}$
. However, it is a well-known fact from the theory of local fields that the restriction map
![]() $\operatorname{H}^{2}(F_{v},\mathbb{F}_{2})\rightarrow \operatorname{H}^{2}(F_{v}[\sqrt{a},\sqrt{d}],\mathbb{F}_{2})$
is then the zero map. Since
$\operatorname{H}^{2}(F_{v},\mathbb{F}_{2})\rightarrow \operatorname{H}^{2}(F_{v}[\sqrt{a},\sqrt{d}],\mathbb{F}_{2})$
is then the zero map. Since
![]() $(B_{0},C_{0})_{F_{v}[\sqrt{a},\sqrt{d}]}$
is the image of
$(B_{0},C_{0})_{F_{v}[\sqrt{a},\sqrt{d}]}$
is the image of
![]() $u_{F_{v}}\in \operatorname{H}^{2}(F_{v},\mathbb{F}_{2})$
(in the above notation), we have in fact
$u_{F_{v}}\in \operatorname{H}^{2}(F_{v},\mathbb{F}_{2})$
(in the above notation), we have in fact
![]() $(B_{0},C_{0})_{F_{v}[\sqrt{a},\sqrt{d}]}=0$
. For such a place, we take
$(B_{0},C_{0})_{F_{v}[\sqrt{a},\sqrt{d}]}=0$
. For such a place, we take
![]() $\unicode[STIX]{x1D6FD}_{v}=\unicode[STIX]{x1D6FE}_{v}=1$
. The four cup-products in (3) of Theorem 5.6 then vanish, so we have a rational point in
$\unicode[STIX]{x1D6FD}_{v}=\unicode[STIX]{x1D6FE}_{v}=1$
. The four cup-products in (3) of Theorem 5.6 then vanish, so we have a rational point in
![]() $X_{F}(F_{v})$
. In this case
$X_{F}(F_{v})$
. In this case
![]() $(\unicode[STIX]{x1D6FD}_{v},c)_{F_{v}}=0$
and
$(\unicode[STIX]{x1D6FD}_{v},c)_{F_{v}}=0$
and
![]() $(b,\unicode[STIX]{x1D6FE}_{v})_{F_{v}}=0$
, as promised.
$(b,\unicode[STIX]{x1D6FE}_{v})_{F_{v}}=0$
, as promised.
Now suppose alternatively that
![]() $a$
and
$a$
and
![]() $d$
are both squares in
$d$
are both squares in
![]() $F_{v}$
. Suppose our element
$F_{v}$
. Suppose our element
![]() $B_{0}$
was of the form
$B_{0}$
was of the form
![]() $B_{0}=x+y\sqrt{a}\in F[\sqrt{a}]\subset F_{v}$
, and let
$B_{0}=x+y\sqrt{a}\in F[\sqrt{a}]\subset F_{v}$
, and let
![]() $\unicode[STIX]{x1D6FD}_{v}=x-y\sqrt{a}\in F_{v}$
, so that
$\unicode[STIX]{x1D6FD}_{v}=x-y\sqrt{a}\in F_{v}$
, so that
![]() $\unicode[STIX]{x1D6FD}_{v}B_{0}=b$
. Likewise, write
$\unicode[STIX]{x1D6FD}_{v}B_{0}=b$
. Likewise, write
![]() $C_{0}=x^{\prime }+y^{\prime }\sqrt{d}$
and let
$C_{0}=x^{\prime }+y^{\prime }\sqrt{d}$
and let
![]() $\unicode[STIX]{x1D6FE}_{v}=x^{\prime }-y^{\prime }\sqrt{d}\in F_{v}$
, so
$\unicode[STIX]{x1D6FE}_{v}=x^{\prime }-y^{\prime }\sqrt{d}\in F_{v}$
, so
![]() $\unicode[STIX]{x1D6FE}_{v}C_{0}=c$
. The four cup-products mentioned in (3) of Theorem 5.6 are equal to
$\unicode[STIX]{x1D6FE}_{v}C_{0}=c$
. The four cup-products mentioned in (3) of Theorem 5.6 are equal to
![]() $(b,c)_{F_{v}}$
, so they all vanish, and there is an
$(b,c)_{F_{v}}$
, so they all vanish, and there is an
![]() $F_{v}$
-rational point. Moreover, we have
$F_{v}$
-rational point. Moreover, we have
as
![]() $(B_{0},c)_{F[\sqrt{a}]}=0$
. Similarly we draw
$(B_{0},c)_{F[\sqrt{a}]}=0$
. Similarly we draw
![]() $(b,\unicode[STIX]{x1D6FE}_{v})_{F_{v}}=0$
.◻
$(b,\unicode[STIX]{x1D6FE}_{v})_{F_{v}}=0$
.◻
The argument given in this proof establishes, in particular, that four-fold Massey products always vanish in the cohomology of local fields, when they are defined. This was of course known (we quote a strong version of this in the next proof), but here everything stays fairly concrete.
In many cases, we obtain an improved version of the conjecture.
Theorem 6.2. Let
![]() $F$
be a number field, and let
$F$
be a number field, and let
![]() $a,b,c,d\in F^{\times }$
be given. Suppose that none of
$a,b,c,d\in F^{\times }$
be given. Suppose that none of
![]() $ad$
,
$ad$
,
![]() $ab$
,
$ab$
,
![]() $cd$
is a square. Then the following are equivalent:
$cd$
is a square. Then the following are equivalent:
(1) the
 $4$
-Massey product
$4$
-Massey product
 $\langle a,b,c,d\rangle$
vanishes;
$\langle a,b,c,d\rangle$
vanishes;(2) the
 $4$
-Massey product
$4$
-Massey product
 $\langle a,b,c,d\rangle$
is defined;
$\langle a,b,c,d\rangle$
is defined;(3) one has
 $(a,b)_{F}=(b,c)_{F}=(c,d)_{F}=0$
.
$(a,b)_{F}=(b,c)_{F}=(c,d)_{F}=0$
.
Proof. The definitions are so arranged that
![]() $(1)\;\Longrightarrow \;(2)$
is a tautology, while
$(1)\;\Longrightarrow \;(2)$
is a tautology, while
![]() $(2)\;\Longrightarrow \;(3)$
is (a very small) part of Theorem 3.1 (and following remark). The non-trivial portion of the proof is
$(2)\;\Longrightarrow \;(3)$
is (a very small) part of Theorem 3.1 (and following remark). The non-trivial portion of the proof is
![]() $(3)\;\Longrightarrow \;(1)$
.
$(3)\;\Longrightarrow \;(1)$
.
Assume (3). From Theorem 5.6, we must prove that
![]() $X_{F}(F)$
is non-empty. By Theorem A.1 in the appendix, it suffices to show that for each place
$X_{F}(F)$
is non-empty. By Theorem A.1 in the appendix, it suffices to show that for each place
![]() $v$
of
$v$
of
![]() $F$
, we have
$F$
, we have
![]() $X_{F}(F_{v})\neq \varnothing$
. Applying Theorem 5.6 yet again, we now see that we must prove that the Massey product
$X_{F}(F_{v})\neq \varnothing$
. Applying Theorem 5.6 yet again, we now see that we must prove that the Massey product
![]() $\langle a,b,c,d\rangle$
is defined and vanishes in the cohomology of
$\langle a,b,c,d\rangle$
is defined and vanishes in the cohomology of
![]() $F_{v}$
. However, for a local field such as
$F_{v}$
. However, for a local field such as
![]() $F_{v}$
, it is known (see [Reference Mináč and TânMT17b, Proposition 4.1]) that the conditions
$F_{v}$
, it is known (see [Reference Mináč and TânMT17b, Proposition 4.1]) that the conditions
![]() $(a,b)_{F_{v}}=(b,c)_{F_{v}}=(c,d)_{F_{v}}=0$
(which hold here by restriction of the analogous identities over
$(a,b)_{F_{v}}=(b,c)_{F_{v}}=(c,d)_{F_{v}}=0$
(which hold here by restriction of the analogous identities over
![]() $F$
) are enough to imply this.◻
$F$
) are enough to imply this.◻
Remark 6.3. The implication
![]() $(3)\;\Longrightarrow \;(1)$
from Theorem 6.2 fails in general, if one removes the additional assumptions on
$(3)\;\Longrightarrow \;(1)$
from Theorem 6.2 fails in general, if one removes the additional assumptions on
![]() $ad$
,
$ad$
,
![]() $ab$
,
$ab$
,
![]() $cd$
. More precisely, Proposition A.12 and Remark A.14 provide necessary and sufficient conditions for the classes
$cd$
. More precisely, Proposition A.12 and Remark A.14 provide necessary and sufficient conditions for the classes
![]() $(\unicode[STIX]{x1D6FD},c)$
,
$(\unicode[STIX]{x1D6FD},c)$
,
![]() $(\unicode[STIX]{x1D6FE},b)$
and/or
$(\unicode[STIX]{x1D6FE},b)$
and/or
![]() $(\unicode[STIX]{x1D6FD},c)+(\unicode[STIX]{x1D6FE},b)$
, over the function field of
$(\unicode[STIX]{x1D6FD},c)+(\unicode[STIX]{x1D6FE},b)$
, over the function field of
![]() $X_{F}$
, to be unramified over
$X_{F}$
, to be unramified over
![]() $F$
(see the notation in § 5.2). When these conditions hold for one of these classes, a Brauer–Manin obstruction to the implication
$F$
(see the notation in § 5.2). When these conditions hold for one of these classes, a Brauer–Manin obstruction to the implication
![]() $(3)\;\Longrightarrow \;(1)$
may arise. See Example A.15, suggested by Y. Harpaz, for a concrete situation where (3) holds, so the variety
$(3)\;\Longrightarrow \;(1)$
may arise. See Example A.15, suggested by Y. Harpaz, for a concrete situation where (3) holds, so the variety
![]() $X_{F}$
has local points everywhere, but no
$X_{F}$
has local points everywhere, but no
![]() $F$
-rational point exists; that is, (1) fails. By Theorem 6.1, (2) also fails to hold. (In this case
$F$
-rational point exists; that is, (1) fails. By Theorem 6.1, (2) also fails to hold. (In this case
![]() $(\unicode[STIX]{x1D6FD},c)$
is unramified.) As we see from Theorem 6.2, this cannot happen in non-degenerate situations, where
$(\unicode[STIX]{x1D6FD},c)$
is unramified.) As we see from Theorem 6.2, this cannot happen in non-degenerate situations, where
![]() $[F(\sqrt{a},\sqrt{b},\sqrt{c},\sqrt{d}):F]=2^{4}$
.
$[F(\sqrt{a},\sqrt{b},\sqrt{c},\sqrt{d}):F]=2^{4}$
.
7 Explicit constructions
Suppose
![]() $a,b,c,d\in F^{\times }$
have linearly independent images in
$a,b,c,d\in F^{\times }$
have linearly independent images in
![]() $F^{\times }\!/F^{\times 2}$
. When the Massey product
$F^{\times }\!/F^{\times 2}$
. When the Massey product
![]() $\langle a,b,c,d\rangle$
vanishes, there is a certain map
$\langle a,b,c,d\rangle$
vanishes, there is a certain map
![]() $\unicode[STIX]{x1D711}:G_{F}\rightarrow \mathbb{U}_{5}(\mathbb{F}_{2})$
which is surjective when composed with
$\unicode[STIX]{x1D711}:G_{F}\rightarrow \mathbb{U}_{5}(\mathbb{F}_{2})$
which is surjective when composed with
![]() $\mathbb{U}_{5}(\mathbb{F}_{2})\rightarrow \mathbb{U}_{5}(\mathbb{F}_{2})/\unicode[STIX]{x1D6F7}(\mathbb{U}_{5}(\mathbb{F}_{2}))$
, the quotient modulo the Frattini subgroup, as follows from examining the notation (note that
$\mathbb{U}_{5}(\mathbb{F}_{2})\rightarrow \mathbb{U}_{5}(\mathbb{F}_{2})/\unicode[STIX]{x1D6F7}(\mathbb{U}_{5}(\mathbb{F}_{2}))$
, the quotient modulo the Frattini subgroup, as follows from examining the notation (note that
![]() $\unicode[STIX]{x1D6F7}(\mathbb{U}_{5}(\mathbb{F}_{2}))$
is the intersection of the kernels of the four maps
$\unicode[STIX]{x1D6F7}(\mathbb{U}_{5}(\mathbb{F}_{2}))$
is the intersection of the kernels of the four maps
![]() $s_{i}$
,
$s_{i}$
,
![]() $i=1,2,3,4$
). It follows that
$i=1,2,3,4$
). It follows that
![]() $\unicode[STIX]{x1D711}$
is itself surjective, and therefore, there exists an extension
$\unicode[STIX]{x1D711}$
is itself surjective, and therefore, there exists an extension
![]() $L/F$
such that
$L/F$
such that
![]() $\operatorname{Gal}(L/F)\cong \mathbb{U}_{5}(\mathbb{F}_{2})$
. The compatibility with
$\operatorname{Gal}(L/F)\cong \mathbb{U}_{5}(\mathbb{F}_{2})$
. The compatibility with
![]() $a,b,c,d$
means that
$a,b,c,d$
means that
![]() $F[\sqrt{a},\sqrt{b},\sqrt{c},\sqrt{d}]$
must be contained in
$F[\sqrt{a},\sqrt{b},\sqrt{c},\sqrt{d}]$
must be contained in
![]() $L$
, corresponding to the Frattini quotient via the Galois correspondence.
$L$
, corresponding to the Frattini quotient via the Galois correspondence.
This section is about constructing
![]() $L$
explicitly, under the condition that our usual four cup-products vanish – or equivalently, from Lemma 5.2, under the condition
$L$
explicitly, under the condition that our usual four cup-products vanish – or equivalently, from Lemma 5.2, under the condition
![]() $(B,C)_{E}=0$
. As it turns out, we end up giving an alternative, more explicit proof for Theorem 3.3, restricted to the ‘non-degenerate case’.
$(B,C)_{E}=0$
. As it turns out, we end up giving an alternative, more explicit proof for Theorem 3.3, restricted to the ‘non-degenerate case’.
Theorem 7.1. Let
![]() $F$
be a field of characteristic not
$F$
be a field of characteristic not
![]() $2$
, and let
$2$
, and let
![]() $a,b,c,d\in F^{\times }$
be elements such that
$a,b,c,d\in F^{\times }$
be elements such that
![]() $[a],[b],[c],[d]$
are linearly independent in
$[a],[b],[c],[d]$
are linearly independent in
![]() $F^{\times }\!/F^{\times 2}$
.
$F^{\times }\!/F^{\times 2}$
.
Assume that we can find
![]() $x,y\in F$
such that
$x,y\in F$
such that
and likewise assume that we can find
![]() $x^{\prime },y^{\prime }\in F$
such that
$x^{\prime },y^{\prime }\in F$
such that
Finally, put
![]() $B=x+y\sqrt{a}$
and
$B=x+y\sqrt{a}$
and
![]() $C=x^{\prime }+y^{\prime }\sqrt{d}$
, and assume that we can find
$C=x^{\prime }+y^{\prime }\sqrt{d}$
, and assume that we can find
![]() $u,v\in F[\sqrt{a},\sqrt{d}]$
such that
$u,v\in F[\sqrt{a},\sqrt{d}]$
such that
Under these assumptions, if we put
![]() $w=u+v\sqrt{B}$
, then the Galois closure
$w=u+v\sqrt{B}$
, then the Galois closure
![]() $L$
of
$L$
of
verifies
![]() $\operatorname{Gal}(L/F)\cong \mathbb{U}_{5}(\mathbb{F}_{2})$
.
$\operatorname{Gal}(L/F)\cong \mathbb{U}_{5}(\mathbb{F}_{2})$
.
The rest of this section is devoted to the proof. The argument is self-contained, but assumes the notation from §§ 2 and 3, and uses Shapiro’s lemma.
Lemma 7.2. Put
![]() $K=F[\sqrt{a},\sqrt{b},\sqrt{c},\sqrt{d},\sqrt{B},\sqrt{C}]$
. Then
$K=F[\sqrt{a},\sqrt{b},\sqrt{c},\sqrt{d},\sqrt{B},\sqrt{C}]$
. Then
![]() $K/F$
is Galois with
$K/F$
is Galois with
More precisely, the isomorphism can be chosen such that the standard generating involutions
![]() $\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2},\unicode[STIX]{x1D70E}_{3},\unicode[STIX]{x1D70E}_{4}\in D_{4}\times D_{4}$
, when viewed in
$\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2},\unicode[STIX]{x1D70E}_{3},\unicode[STIX]{x1D70E}_{4}\in D_{4}\times D_{4}$
, when viewed in
![]() $\operatorname{Gal}(K/F)$
, act on the elements of
$\operatorname{Gal}(K/F)$
, act on the elements of
![]() $K$
as follows.
$K$
as follows.

Finally,
![]() $\unicode[STIX]{x1D70E}_{1}$
and
$\unicode[STIX]{x1D70E}_{1}$
and
![]() $\unicode[STIX]{x1D70E}_{2}$
fix
$\unicode[STIX]{x1D70E}_{2}$
fix
![]() $\sqrt{c},\sqrt{d},\sqrt{C}$
, and vice-versa.
$\sqrt{c},\sqrt{d},\sqrt{C}$
, and vice-versa.
The
![]() $\star$
means that we do not insist on a value. One may show, for example, that
$\star$
means that we do not insist on a value. One may show, for example, that
![]() $\unicode[STIX]{x1D70E}_{1}(\sqrt{B})=\pm \sqrt{b}/\sqrt{B}$
, but the particular sign will not be relevant.
$\unicode[STIX]{x1D70E}_{1}(\sqrt{B})=\pm \sqrt{b}/\sqrt{B}$
, but the particular sign will not be relevant.
Proof. Let
![]() $K_{1}=F[\sqrt{a},\sqrt{b},\sqrt{B}]$
and
$K_{1}=F[\sqrt{a},\sqrt{b},\sqrt{B}]$
and
![]() $K_{2}=F[\sqrt{c},\sqrt{d},\sqrt{C}]$
. Then
$K_{2}=F[\sqrt{c},\sqrt{d},\sqrt{C}]$
. Then
![]() $K_{i}$
is a
$K_{i}$
is a
![]() $D_{4}$
-extension of
$D_{4}$
-extension of
![]() $F$
, for
$F$
, for
![]() $i=1,2$
, and the actions are as announced, for some choices of generating involutions for the dihedral groups: simply argue as in the proof of Proposition 2.3.
$i=1,2$
, and the actions are as announced, for some choices of generating involutions for the dihedral groups: simply argue as in the proof of Proposition 2.3.
In order to show that
![]() $K=K_{1}K_{2}$
is a
$K=K_{1}K_{2}$
is a
![]() $D_{4}\times D_{4}$
-extension, it suffices to show that
$D_{4}\times D_{4}$
-extension, it suffices to show that
![]() $K_{1}\cap K_{2}=F$
.
$K_{1}\cap K_{2}=F$
.
The extension of
![]() $F$
which corresponds to the Frattini quotient of
$F$
which corresponds to the Frattini quotient of
![]() $\operatorname{Gal}(K_{1}/F)$
respectively
$\operatorname{Gal}(K_{1}/F)$
respectively
![]() $\operatorname{Gal}(K_{2}/F)$
is
$\operatorname{Gal}(K_{2}/F)$
is
![]() $F[\sqrt{a},\sqrt{b}]$
, respectively
$F[\sqrt{a},\sqrt{b}]$
, respectively
![]() $F[\sqrt{c},\sqrt{d}]$
, so
$F[\sqrt{c},\sqrt{d}]$
, so
![]() $K_{1}\neq K_{2}$
. Thus
$K_{1}\neq K_{2}$
. Thus
![]() $K_{1}\cap K_{2}$
corresponds to a non-trivial normal subgroup of
$K_{1}\cap K_{2}$
corresponds to a non-trivial normal subgroup of
![]() $\operatorname{Gal}(K_{i}/F)$
, for
$\operatorname{Gal}(K_{i}/F)$
, for
![]() $i=1,2$
. Looking at the normal subgroups of
$i=1,2$
. Looking at the normal subgroups of
![]() $D_{4}$
, we see that
$D_{4}$
, we see that
![]() $K_{1}\cap K_{2}\subset F[\sqrt{a},\sqrt{b}]\cap F[\sqrt{c},\sqrt{d}]=F$
, which completes the proof.◻
$K_{1}\cap K_{2}\subset F[\sqrt{a},\sqrt{b}]\cap F[\sqrt{c},\sqrt{d}]=F$
, which completes the proof.◻
From now on we write
![]() $G$
for the group
$G$
for the group
![]() $D_{4}\times D_{4}$
, which we have just identified explicitly with
$D_{4}\times D_{4}$
, which we have just identified explicitly with
![]() $\operatorname{Gal}(K/F)$
. As above, we will write
$\operatorname{Gal}(K/F)$
. As above, we will write
![]() $N$
for the subgroup of
$N$
for the subgroup of
![]() $\operatorname{Gal}(K/F)$
generated by
$\operatorname{Gal}(K/F)$
generated by
![]() $\unicode[STIX]{x1D70E}_{2},[\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}],\unicode[STIX]{x1D70E}_{3},[\unicode[STIX]{x1D70E}_{4},\unicode[STIX]{x1D70E}_{3}]$
.
$\unicode[STIX]{x1D70E}_{2},[\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}],\unicode[STIX]{x1D70E}_{3},[\unicode[STIX]{x1D70E}_{4},\unicode[STIX]{x1D70E}_{3}]$
.
Lemma 7.3. The fixed field of
![]() $N$
within
$N$
within
![]() $K$
is
$K$
is
![]() $E=F[\sqrt{a},\sqrt{d}]$
.
$E=F[\sqrt{a},\sqrt{d}]$
.
Consider now
![]() $w=u+v\sqrt{B}$
as above, with
$w=u+v\sqrt{B}$
as above, with
![]() $u,v\in F[\sqrt{a},\sqrt{d}]$
, and let us study its class
$u,v\in F[\sqrt{a},\sqrt{d}]$
, and let us study its class
![]() $[w]\in K^{\times }\!/K^{\times 2}$
. Note that
$[w]\in K^{\times }\!/K^{\times 2}$
. Note that
![]() $w$
is clearly non-zero, since
$w$
is clearly non-zero, since
![]() $w(u-v\sqrt{B})=C\neq 0$
.
$w(u-v\sqrt{B})=C\neq 0$
.
Lemma 7.4. The element
![]() $[w]$
is fixed by
$[w]$
is fixed by
![]() $N$
.
$N$
.
Proof. The element
![]() $w$
is itself fixed by
$w$
is itself fixed by
![]() $\unicode[STIX]{x1D70E}_{3}$
and
$\unicode[STIX]{x1D70E}_{3}$
and
![]() $[\unicode[STIX]{x1D70E}_{4},\unicode[STIX]{x1D70E}_{3}]$
, as we see immediately from the tables. On the other hand
$[\unicode[STIX]{x1D70E}_{4},\unicode[STIX]{x1D70E}_{3}]$
, as we see immediately from the tables. On the other hand
![]() $\unicode[STIX]{x1D70E}_{2}(w)=u-v\sqrt{B}$
, and things have thus been arranged so that
$\unicode[STIX]{x1D70E}_{2}(w)=u-v\sqrt{B}$
, and things have thus been arranged so that
As a result
![]() $\unicode[STIX]{x1D70E}_{2}([w])=[w]$
. The element
$\unicode[STIX]{x1D70E}_{2}([w])=[w]$
. The element
![]() $[\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}]$
has the same effect on
$[\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2}]$
has the same effect on
![]() $w$
as
$w$
as
![]() $\unicode[STIX]{x1D70E}_{2}$
, so the same argument applies.◻
$\unicode[STIX]{x1D70E}_{2}$
, so the same argument applies.◻
We now let
![]() $W$
denote the
$W$
denote the
![]() $G$
-module spanned by
$G$
-module spanned by
![]() $[w]$
within
$[w]$
within
![]() $K^{\times }\!/K^{\times 2}$
. By the lemma this can be seen as a
$K^{\times }\!/K^{\times 2}$
. By the lemma this can be seen as a
![]() $G/N$
-module, and indeed it is the image of
$G/N$
-module, and indeed it is the image of
mapping
![]() $1\in G/N$
to
$1\in G/N$
to
![]() $[w]$
. We put
$[w]$
. We put
![]() $L=K[\sqrt{W}]$
, which is indeed the
$L=K[\sqrt{W}]$
, which is indeed the
![]() $L$
introduced in the theorem. Equivariant Kummer theory states that
$L$
introduced in the theorem. Equivariant Kummer theory states that
![]() $L/F$
is Galois, and that
$L/F$
is Galois, and that
![]() $\operatorname{Gal}(L/K)\cong W^{\ast }$
via the Kummer pairing. For future reference, let us recall that
$\operatorname{Gal}(L/K)\cong W^{\ast }$
via the Kummer pairing. For future reference, let us recall that
![]() $\unicode[STIX]{x1D70F}\in \operatorname{Gal}(L/K)$
is viewed as an element of
$\unicode[STIX]{x1D70F}\in \operatorname{Gal}(L/K)$
is viewed as an element of
![]() $W^{\ast }$
via
$W^{\ast }$
via
So we have an exact sequence
and we let
![]() $\unicode[STIX]{x1D6FC}\in \operatorname{H}^{2}(G,W^{\ast })$
denote the corresponding cohomology class. Consider the following commutative diagram.
$\unicode[STIX]{x1D6FC}\in \operatorname{H}^{2}(G,W^{\ast })$
denote the corresponding cohomology class. Consider the following commutative diagram.

Here is a word of explanation about the notation. First,
![]() $[w]^{\bot }=\{f\in W^{\ast }:f([w])=0\}$
. The map
$[w]^{\bot }=\{f\in W^{\ast }:f([w])=0\}$
. The map
![]() $sh$
is Shapiro’s isomorphism; the map
$sh$
is Shapiro’s isomorphism; the map
![]() $\unicode[STIX]{x1D70B}^{\ast }$
is the injection which is dual to the surjection
$\unicode[STIX]{x1D70B}^{\ast }$
is the injection which is dual to the surjection
![]() $\unicode[STIX]{x1D70B}:\mathbb{F}_{2}[G/N]\rightarrow W$
; the map
$\unicode[STIX]{x1D70B}:\mathbb{F}_{2}[G/N]\rightarrow W$
; the map
![]() $\widetilde{sh}$
is Shapiro-like, defined by using the projection
$\widetilde{sh}$
is Shapiro-like, defined by using the projection
![]() $W^{\ast }\rightarrow W^{\ast }/[w]^{\bot }$
and restriction to
$W^{\ast }\rightarrow W^{\ast }/[w]^{\bot }$
and restriction to
![]() $N$
; and the bottom map is seen as the identity, since
$N$
; and the bottom map is seen as the identity, since
![]() $W^{\ast }/[w]^{\bot }$
can be identified with
$W^{\ast }/[w]^{\bot }$
can be identified with
![]() $\mathbb{F}_{2}$
in a unique way (just like any group of order
$\mathbb{F}_{2}$
in a unique way (just like any group of order
![]() $2$
). Commutativity is clear.
$2$
). Commutativity is clear.
The cohomology class
![]() $\widetilde{sh}(\unicode[STIX]{x1D6FC})$
corresponds to the extension
$\widetilde{sh}(\unicode[STIX]{x1D6FC})$
corresponds to the extension
Let us elucidate a few things. First we have
Further,
It follows that if we put
![]() $L^{\prime }=K[\sqrt{w}]$
, then
$L^{\prime }=K[\sqrt{w}]$
, then
![]() $\operatorname{Gal}(L/L^{\prime })\cong [w]^{\bot }$
, and
$\operatorname{Gal}(L/L^{\prime })\cong [w]^{\bot }$
, and
Lemma 7.5. The Galois group
![]() $\operatorname{Gal}(L^{\prime }/E)$
is isomorphic to
$\operatorname{Gal}(L^{\prime }/E)$
is isomorphic to
![]() $C_{2}^{2}\times D_{4}$
.
$C_{2}^{2}\times D_{4}$
.
Proof. The element
![]() $w\in E[\sqrt{B}]$
satisfies
$w\in E[\sqrt{B}]$
satisfies
![]() $N_{E[\sqrt{B}]/E}(w)=C$
, and it follows that
$N_{E[\sqrt{B}]/E}(w)=C$
, and it follows that
is a
![]() $D_{4}$
-extension of
$D_{4}$
-extension of
![]() $E$
. (Here we do use the fact that
$E$
. (Here we do use the fact that
![]() $E[\sqrt{B},\sqrt{C}]$
is a
$E[\sqrt{B},\sqrt{C}]$
is a
![]() $C_{2}^{2}$
-extension of
$C_{2}^{2}$
-extension of
![]() $E$
, which we know from
$E$
, which we know from
![]() $\operatorname{Gal}(K/E)=N$
.)
$\operatorname{Gal}(K/E)=N$
.)
Of course
![]() $K/E$
is Galois with group
$K/E$
is Galois with group
![]() $N\cong C_{2}^{4}$
, so that
$N\cong C_{2}^{4}$
, so that
![]() $L^{\prime }=KM$
is Galois with group
$L^{\prime }=KM$
is Galois with group
Certainly we have
![]() $E[\sqrt{B},\sqrt{C}]\subset K\cap M$
, and the intersection
$E[\sqrt{B},\sqrt{C}]\subset K\cap M$
, and the intersection
![]() $K\cap M$
cannot in fact be larger, for (by counting dimensions, say) if it were we would have
$K\cap M$
cannot in fact be larger, for (by counting dimensions, say) if it were we would have
![]() $K\cap M=M$
; so
$K\cap M=M$
; so
![]() $M\subset K$
, a non-abelian extension contained in an abelian one, contradiction. So
$M\subset K$
, a non-abelian extension contained in an abelian one, contradiction. So
![]() $K\cap M=E[\sqrt{B},\sqrt{C}]$
.
$K\cap M=E[\sqrt{B},\sqrt{C}]$
.
Thus
![]() $\operatorname{Gal}(L^{\prime }/E)$
is of the form
$\operatorname{Gal}(L^{\prime }/E)$
is of the form
![]() $C_{2}^{4}\times _{C_{2}^{2}}D_{4}$
. Since the map
$C_{2}^{4}\times _{C_{2}^{2}}D_{4}$
. Since the map
![]() $C_{2}^{4}\rightarrow C_{2}^{2}$
is split, we see that this fibre product is in fact isomorphic to
$C_{2}^{4}\rightarrow C_{2}^{2}$
is split, we see that this fibre product is in fact isomorphic to
![]() $C_{2}^{2}\times D_{4}$
.◻
$C_{2}^{2}\times D_{4}$
.◻
From this last lemma, and its proof, it follows that (†) can be identified with the first exact sequence in Lemma 2.5, which implies that
![]() $\widetilde{sh}(\unicode[STIX]{x1D6FC})=x_{2}x_{3}$
. As a consequence, from the commutativity of the diagram above and the injectivity of Shapiro’s map, we see that
$\widetilde{sh}(\unicode[STIX]{x1D6FC})=x_{2}x_{3}$
. As a consequence, from the commutativity of the diagram above and the injectivity of Shapiro’s map, we see that
![]() $\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6FC})$
describes the extension
$\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D6FC})$
describes the extension
We conclude that
![]() $\operatorname{Gal}(L/F)$
is a subgroup of
$\operatorname{Gal}(L/F)$
is a subgroup of
![]() $\mathbb{U}_{5}(\mathbb{F}_{2})$
which maps onto the Frattini quotient
$\mathbb{U}_{5}(\mathbb{F}_{2})$
which maps onto the Frattini quotient
![]() $\operatorname{Gal}(F[\sqrt{a},\sqrt{b},\sqrt{c},\sqrt{d}]/F)$
. Thus
$\operatorname{Gal}(F[\sqrt{a},\sqrt{b},\sqrt{c},\sqrt{d}]/F)$
. Thus
![]() $\operatorname{Gal}(L/F)=\mathbb{U}_{5}(\mathbb{F}_{2})$
.
$\operatorname{Gal}(L/F)=\mathbb{U}_{5}(\mathbb{F}_{2})$
.
Example 7.6. Let us take
![]() $F=\mathbb{Q}$
and
$F=\mathbb{Q}$
and
![]() $a=11$
,
$a=11$
,
![]() $b=5$
,
$b=5$
,
![]() $c=79$
,
$c=79$
,
![]() $d=13$
. Let us try to look for solutions to (1)–(3). A little calculation with Hilbert symbols reveals that
$d=13$
. Let us try to look for solutions to (1)–(3). A little calculation with Hilbert symbols reveals that
![]() $(a,b)=(b,c)=(c,d)=0$
, and so Theorem 6.1 guarantees that such solutions do exist.
$(a,b)=(b,c)=(c,d)=0$
, and so Theorem 6.1 guarantees that such solutions do exist.
In practice though, the quickest way to look for
![]() $x,y,z\in \mathbb{Q}$
such that
$x,y,z\in \mathbb{Q}$
such that
is to pick random integers
![]() $y$
and
$y$
and
![]() $z$
until
$z$
until
![]() $11y^{2}+5z^{2}$
is a square. Let us fix an initial solution, say
$11y^{2}+5z^{2}$
is a square. Let us fix an initial solution, say
![]() $x_{0}=4$
,
$x_{0}=4$
,
![]() $y_{0}=z_{0}=1$
, and put
$y_{0}=z_{0}=1$
, and put
![]() $B_{0}=4+\sqrt{11}$
. Likewise
$B_{0}=4+\sqrt{11}$
. Likewise
![]() $C_{0}=14+3\sqrt{13}$
is an initial solution to equation (2).
$C_{0}=14+3\sqrt{13}$
is an initial solution to equation (2).
With these random values, there will likely be no solution to (3), since
![]() $(B_{0},C_{0})\neq 0$
in general. The next step is to pick random integers
$(B_{0},C_{0})\neq 0$
in general. The next step is to pick random integers
![]() $f,g\in \mathbb{Z}$
and check whether
$f,g\in \mathbb{Z}$
and check whether
![]() $(fB_{0},gC_{0})=0$
. Again, Proposition 4.1 justifies the existence of these; but there would be no harm in trying even if we did not know that. The most efficient method seems to be to compute the conductor of
$(fB_{0},gC_{0})=0$
. Again, Proposition 4.1 justifies the existence of these; but there would be no harm in trying even if we did not know that. The most efficient method seems to be to compute the conductor of
![]() $(fB_{0},gC_{0})$
, that is, the product of those prime ideals in the ring of integers of
$(fB_{0},gC_{0})$
, that is, the product of those prime ideals in the ring of integers of
![]() $E=\mathbb{Q}[\sqrt{11},\sqrt{13}]$
such that the cup product
$E=\mathbb{Q}[\sqrt{11},\sqrt{13}]$
such that the cup product
![]() $(fB_{0},gC_{0})$
maps to a non-zero class in the corresponding non-archimedean completion: this is an operation done quickly by the software PARI (which we have used through Sagemath). If the conductor is trivial, we use the more time-consuming methods of PARI to find a rational point on the conic defined by (3).
$(fB_{0},gC_{0})$
maps to a non-zero class in the corresponding non-archimedean completion: this is an operation done quickly by the software PARI (which we have used through Sagemath). If the conductor is trivial, we use the more time-consuming methods of PARI to find a rational point on the conic defined by (3).
Having found
![]() $f,g$
, we put
$f,g$
, we put
![]() $B=fB_{0}$
and
$B=fB_{0}$
and
![]() $C=gC_{0}$
(but also in principle
$C=gC_{0}$
(but also in principle
![]() $x=fx_{0},y=fy_{0},z=fz_{0}$
, and so on, thus changing our solutions to (1), (2), although these do not show up themselves in the statement of Theorem 7.1).
$x=fx_{0},y=fy_{0},z=fz_{0}$
, and so on, thus changing our solutions to (1), (2), although these do not show up themselves in the statement of Theorem 7.1).
In the case at hand, one search of the type just described has yielded the solutions
which verify
![]() $(B,C)=0$
. Indeed, equation (3) is solved by
$(B,C)=0$
. Indeed, equation (3) is solved by
![]() $w=u+v\sqrt{B}$
with
$w=u+v\sqrt{B}$
with
 $$\begin{eqnarray}\displaystyle u & = & \displaystyle \frac{2}{57\,319}\sqrt{13}(40\,730\,430\,348\,570\,235\,670\sqrt{11}-283\,850\,079\,471\,799\,786\,881)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{642\,122\,498\,218\,267\,058\,484}{57\,319}\sqrt{11}+\frac{143\,760\,709\,913\,945\,809\,313}{7396},\nonumber\\ \displaystyle v & = & \displaystyle \frac{4}{286\,595}\sqrt{13}(27\,413\,052\,840\,094\,197\,823\sqrt{11}-191\,041\,370\,339\,652\,873\,536)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{172\,868\,666\,747\,038\,399\,008}{57\,319}\sqrt{11}+\frac{193\,512\,315\,164\,122\,974\,131}{36\,980}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u & = & \displaystyle \frac{2}{57\,319}\sqrt{13}(40\,730\,430\,348\,570\,235\,670\sqrt{11}-283\,850\,079\,471\,799\,786\,881)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{642\,122\,498\,218\,267\,058\,484}{57\,319}\sqrt{11}+\frac{143\,760\,709\,913\,945\,809\,313}{7396},\nonumber\\ \displaystyle v & = & \displaystyle \frac{4}{286\,595}\sqrt{13}(27\,413\,052\,840\,094\,197\,823\sqrt{11}-191\,041\,370\,339\,652\,873\,536)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{172\,868\,666\,747\,038\,399\,008}{57\,319}\sqrt{11}+\frac{193\,512\,315\,164\,122\,974\,131}{36\,980}.\nonumber\end{eqnarray}$$
Acknowledgements
First and foremost, we have been in touch very frequently with Olivier Wittenberg while writing this paper. We thank him warmly for writing the appendix, and for various suggestions. We also thank Adriano Marmora for suggesting that we contact Olivier in the first place. Moreover, we warmly thank ![]() for his interest and insight, and for his extremely inspiring collaboration with the second author. It is a great pleasure to also thank B. I. Chetard, I. Efrat, Ch. Kapulkin, E. Matzri, C. McLeman, D. Neftin, M. Palaisti, C. Quadrelli and K. Wickelgren for inspiring discussions. Finally, we thank the referee for helpful comments regarding the exposition. JM is partially supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) grant R0370A01. AT was partially supported by EPSRC programme grant EP/M024830/1 Symmetries and Correspondences.
for his interest and insight, and for his extremely inspiring collaboration with the second author. It is a great pleasure to also thank B. I. Chetard, I. Efrat, Ch. Kapulkin, E. Matzri, C. McLeman, D. Neftin, M. Palaisti, C. Quadrelli and K. Wickelgren for inspiring discussions. Finally, we thank the referee for helpful comments regarding the exposition. JM is partially supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) grant R0370A01. AT was partially supported by EPSRC programme grant EP/M024830/1 Symmetries and Correspondences.
Appendix A Local-global principles and the splitting varieties
Olivier Wittenberg
The goal of this appendix is to establish a local-global principle, when
![]() $F$
is a number field, for the existence of a rational point on the variety
$F$
is a number field, for the existence of a rational point on the variety
![]() $X_{F}$
appearing in Theorem 5.6 of the paper (see Theorem A.1 below). I am indebted to the authors for sharing drafts of their paper with me, to Pierre Guillot for numerous discussions on
$X_{F}$
appearing in Theorem 5.6 of the paper (see Theorem A.1 below). I am indebted to the authors for sharing drafts of their paper with me, to Pierre Guillot for numerous discussions on
![]() $4$
-Massey products, and to Yonatan Harpaz for suggesting Example A.15.
$4$
-Massey products, and to Yonatan Harpaz for suggesting Example A.15.
A.1 Statements
Let
![]() $F$
be a field of characteristic
$F$
be a field of characteristic
![]() $0$
. For
$0$
. For
![]() $q,q^{\prime }\in F$
, we will write
$q,q^{\prime }\in F$
, we will write
![]() $F_{q}=F[t]/(t^{2}-q)$
and
$F_{q}=F[t]/(t^{2}-q)$
and
![]() $F_{q,q^{\prime }}=$
$F_{q,q^{\prime }}=$
![]() $F[t,t^{\prime }]/(t^{2}-q,{t^{\prime }}^{2}-q^{\prime })$
. Let us fix
$F[t,t^{\prime }]/(t^{2}-q,{t^{\prime }}^{2}-q^{\prime })$
. Let us fix
![]() $a,b,c,d\in F^{\ast }$
and
$a,b,c,d\in F^{\ast }$
and
![]() $B\in F_{a}^{\ast }$
,
$B\in F_{a}^{\ast }$
,
![]() $C\in F_{d}^{\ast }$
such that
$C\in F_{d}^{\ast }$
such that
![]() $N_{F_{a}/F}(B)=b$
and
$N_{F_{a}/F}(B)=b$
and
![]() $N_{F_{d}/F}(C)=c$
, and consider the closed subvariety
$N_{F_{d}/F}(C)=c$
, and consider the closed subvariety
defined by the equation
![]() $\unicode[STIX]{x1D6FD}Bx^{2}+\unicode[STIX]{x1D6FE}Cy^{2}=1$
, where
$\unicode[STIX]{x1D6FD}Bx^{2}+\unicode[STIX]{x1D6FE}Cy^{2}=1$
, where
![]() $R_{F_{a,d}/F}$
denotes the Weil restriction functor and
$R_{F_{a,d}/F}$
denotes the Weil restriction functor and
![]() $\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}$
are the coordinates of
$\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}$
are the coordinates of
![]() $\mathbf{G}_{m}^{2}$
while
$\mathbf{G}_{m}^{2}$
while
![]() $x,y$
are those of
$x,y$
are those of
![]() $R_{F_{a,d}/F}\mathbf{A}_{F_{a,d}}^{2}$
. (In the body of the paper, this variety is denoted by
$R_{F_{a,d}/F}\mathbf{A}_{F_{a,d}}^{2}$
. (In the body of the paper, this variety is denoted by
![]() $X_{F}$
rather than
$X_{F}$
rather than
![]() $X$
, and our
$X$
, and our
![]() $B,C$
play the rôle of the elements called
$B,C$
play the rôle of the elements called
![]() $B_{0},C_{0}$
there.)
$B_{0},C_{0}$
there.)
When
![]() $F$
is a number field, we denote by
$F$
is a number field, we denote by
![]() $\unicode[STIX]{x1D6FA}$
the set of its places, by
$\unicode[STIX]{x1D6FA}$
the set of its places, by
![]() $F_{v}$
the completion of
$F_{v}$
the completion of
![]() $F$
at
$F$
at
![]() $v\in \unicode[STIX]{x1D6FA}$
, and by
$v\in \unicode[STIX]{x1D6FA}$
, and by
![]() $(x,y)\in \{-1,1\}$
the Hilbert symbol of
$(x,y)\in \{-1,1\}$
the Hilbert symbol of
![]() $x,y\in F_{v}^{\ast }/F_{v}^{\ast 2}$
(see [Reference NeukirchNeu99, ch. V, § 3]).
$x,y\in F_{v}^{\ast }/F_{v}^{\ast 2}$
(see [Reference NeukirchNeu99, ch. V, § 3]).
Theorem A.1. Assume that
![]() $F$
is a number field. If none of
$F$
is a number field. If none of
![]() $ad$
,
$ad$
,
![]() $ab$
,
$ab$
,
![]() $cd$
is a square in
$cd$
is a square in
![]() $F$
, then
$F$
, then
![]() $X$
satisfies the Hasse principle:
$X$
satisfies the Hasse principle:
![]() $X(F)\neq \varnothing$
if and only if
$X(F)\neq \varnothing$
if and only if
![]() $X(F_{v})\neq \varnothing$
for all
$X(F_{v})\neq \varnothing$
for all
![]() $v\in \unicode[STIX]{x1D6FA}$
. In any case, the existence of a rational point on
$v\in \unicode[STIX]{x1D6FA}$
. In any case, the existence of a rational point on
![]() $X$
is equivalent to the existence of an element of
$X$
is equivalent to the existence of an element of
![]() $\prod _{v\in \unicode[STIX]{x1D6FA}}X(F_{v})$
whose
$\prod _{v\in \unicode[STIX]{x1D6FA}}X(F_{v})$
whose
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $\unicode[STIX]{x1D6FE}$
coordinates
$\unicode[STIX]{x1D6FE}$
coordinates
![]() $\unicode[STIX]{x1D6FD}_{v},\unicode[STIX]{x1D6FE}_{v}\in F_{v}^{\ast }$
satisfy
$\unicode[STIX]{x1D6FD}_{v},\unicode[STIX]{x1D6FE}_{v}\in F_{v}^{\ast }$
satisfy
In addition, if
![]() $X(F)\neq \varnothing$
, then
$X(F)\neq \varnothing$
, then
![]() $X(F)$
is dense in
$X(F)$
is dense in
![]() $X$
for the Zariski topology.
$X$
for the Zariski topology.
It is not hard to see that
![]() $X$
is smooth, irreducible, and geometrically rational. When
$X$
is smooth, irreducible, and geometrically rational. When
![]() $F$
is a number field, the existence of a rational point on
$F$
is a number field, the existence of a rational point on
![]() $X$
is therefore conjectured to be controlled by the Brauer–Manin obstruction (see [Reference Colliot-ThélèneCol92, § 4]). To establish Theorem A.1, we shall first deduce the validity of this conjecture, in the case of
$X$
is therefore conjectured to be controlled by the Brauer–Manin obstruction (see [Reference Colliot-ThélèneCol92, § 4]). To establish Theorem A.1, we shall first deduce the validity of this conjecture, in the case of
![]() $X$
, by an application of the fibration method (specifically, of [Reference Harpaz and WittenbergHW16, Theorem 9.31]). We shall then prove, in Theorem A.2 below, that the unramified Brauer group of
$X$
, by an application of the fibration method (specifically, of [Reference Harpaz and WittenbergHW16, Theorem 9.31]). We shall then prove, in Theorem A.2 below, that the unramified Brauer group of
![]() $X$
consists of constant classes, except when
$X$
consists of constant classes, except when
![]() $ad$
,
$ad$
,
![]() $ab$
, or
$ab$
, or
![]() $cd$
is a square, in which case the classes of the quaternion algebras
$cd$
is a square, in which case the classes of the quaternion algebras
![]() $(\unicode[STIX]{x1D6FD},c)$
and
$(\unicode[STIX]{x1D6FD},c)$
and
![]() $(\unicode[STIX]{x1D6FE},b)$
over
$(\unicode[STIX]{x1D6FE},b)$
over
![]() $F(X)$
may come into play. The combination of these two facts yields Theorem A.1. We note that Theorem A.2 is a purely algebraic statement: it holds over an arbitrary field
$F(X)$
may come into play. The combination of these two facts yields Theorem A.1. We note that Theorem A.2 is a purely algebraic statement: it holds over an arbitrary field
![]() $F$
of characteristic
$F$
of characteristic
![]() $0$
.
$0$
.
Theorem A.2. The natural map
![]() $\text{Br}(F)\rightarrow \text{Br}_{\text{nr}}(F(X)/F)$
is surjective if none of
$\text{Br}(F)\rightarrow \text{Br}_{\text{nr}}(F(X)/F)$
is surjective if none of
![]() $ad$
,
$ad$
,
![]() $ab$
,
$ab$
,
![]() $cd$
is a square in
$cd$
is a square in
![]() $F$
. In any case, its cokernel is killed by
$F$
. In any case, its cokernel is killed by
![]() $2$
and is contained in the subgroup of
$2$
and is contained in the subgroup of
![]() $\text{Coker}(\text{Br}(F)\rightarrow \text{Br}(F(X)))$
generated by the classes of the quaternion algebras
$\text{Coker}(\text{Br}(F)\rightarrow \text{Br}(F(X)))$
generated by the classes of the quaternion algebras
![]() $(\unicode[STIX]{x1D6FD},c)$
and
$(\unicode[STIX]{x1D6FD},c)$
and
![]() $(\unicode[STIX]{x1D6FE},b)$
over
$(\unicode[STIX]{x1D6FE},b)$
over
![]() $F(X)$
.
$F(X)$
.
We recall that the unramified Brauer group
![]() $\text{Br}_{\text{nr}}(K/F)$
of a finitely generated field extension
$\text{Br}_{\text{nr}}(K/F)$
of a finitely generated field extension
![]() $K/F$
is the intersection of the subgroups
$K/F$
is the intersection of the subgroups
![]() $\text{Im}(\text{Br}(A)\rightarrow \text{Br}(K))$
where
$\text{Im}(\text{Br}(A)\rightarrow \text{Br}(K))$
where
![]() $A$
ranges over the discrete valuation rings
$A$
ranges over the discrete valuation rings
![]() $F\subset A\subset K$
with quotient field
$F\subset A\subset K$
with quotient field
![]() $K$
. If
$K$
. If
![]() $F$
has characteristic
$F$
has characteristic
![]() $0$
and
$0$
and
![]() $K=F(S)$
for a smooth irreducible variety
$K=F(S)$
for a smooth irreducible variety
![]() $S$
, the group
$S$
, the group
![]() $\text{Br}(S)=\operatorname{H}_{\acute{\text{e}}\text{t}}^{2}(S,\mathbf{G}_{m})$
can be identified with the intersection of the subgroups
$\text{Br}(S)=\operatorname{H}_{\acute{\text{e}}\text{t}}^{2}(S,\mathbf{G}_{m})$
can be identified with the intersection of the subgroups
![]() $\text{Im}(\text{Br}(\mathscr{O}_{S,\unicode[STIX]{x1D709}})\rightarrow \text{Br}(K))$
where
$\text{Im}(\text{Br}(\mathscr{O}_{S,\unicode[STIX]{x1D709}})\rightarrow \text{Br}(K))$
where
![]() $\unicode[STIX]{x1D709}$
ranges over the codimension 1 points of
$\unicode[STIX]{x1D709}$
ranges over the codimension 1 points of
![]() $S$
; if
$S$
; if
![]() $S$
is proper, then
$S$
is proper, then
![]() $\text{Br}(S)=\text{Br}_{\text{nr}}(K/F)$
. See [Reference GrothendieckGro68, III, § 6], [Reference Colliot-Thélène and SansucCS07, § 5].
$\text{Br}(S)=\text{Br}_{\text{nr}}(K/F)$
. See [Reference GrothendieckGro68, III, § 6], [Reference Colliot-Thélène and SansucCS07, § 5].
Remark A.3. It is only for simplicity that we assume that
![]() $F$
has characteristic 0 in the statement of Theorem A.2: it allows us to refer to a smooth compactification of
$F$
has characteristic 0 in the statement of Theorem A.2: it allows us to refer to a smooth compactification of
![]() $X$
. When
$X$
. When
![]() $F$
has characteristic
$F$
has characteristic
![]() $p>2$
, the definition of
$p>2$
, the definition of
![]() $X$
still makes sense and Theorem A.2 remains true. Indeed, on the one hand, the proof given below easily adapts to show that the cokernel of
$X$
still makes sense and Theorem A.2 remains true. Indeed, on the one hand, the proof given below easily adapts to show that the cokernel of
![]() $\text{Br}(F)\rightarrow \text{Br}_{\text{nr}}(F(X)/F)$
satisfies the desired statement modulo its
$\text{Br}(F)\rightarrow \text{Br}_{\text{nr}}(F(X)/F)$
satisfies the desired statement modulo its
![]() $p$
-primary torsion subgroup, and, on the other hand, this cokernel is killed by a power of
$p$
-primary torsion subgroup, and, on the other hand, this cokernel is killed by a power of
![]() $2$
since
$2$
since
![]() $X$
becomes rational over
$X$
becomes rational over
![]() $F(\sqrt{a},\sqrt{b},\sqrt{c},\sqrt{d})$
(see [Reference SaltmanSal85, Proposition 1.7]). Presumably, the proof of Theorem A.1 should also work over a global field of characteristic
$F(\sqrt{a},\sqrt{b},\sqrt{c},\sqrt{d})$
(see [Reference SaltmanSal85, Proposition 1.7]). Presumably, the proof of Theorem A.1 should also work over a global field of characteristic
![]() $p>2$
; however, the results we use from [Reference Harpaz and WittenbergHW16] have not been written down in this setting.
$p>2$
; however, the results we use from [Reference Harpaz and WittenbergHW16] have not been written down in this setting.
A.2 Geometry
Following [Reference SkorobogatovSko96], we shall say that a scheme of finite type over a field is split if it possesses an irreducible component of multiplicity
![]() $1$
which is geometrically irreducible. In this preliminary section, we compactify
$1$
which is geometrically irreducible. In this preliminary section, we compactify
![]() $X$
to the total space of a fibration, over a proper base, with very few non-split fibres in codimension
$X$
to the total space of a fibration, over a proper base, with very few non-split fibres in codimension
![]() $1$
. This fibration will play a crucial rôle both in the proof of Theorem A.1 and in that of Theorem A.2. We then proceed to make further observations concerning its fibres (Proposition A.4 below), for use in the proof of Theorem A.2.
$1$
. This fibration will play a crucial rôle both in the proof of Theorem A.1 and in that of Theorem A.2. We then proceed to make further observations concerning its fibres (Proposition A.4 below), for use in the proof of Theorem A.2.
Let
![]() $X^{\prime \prime }\subset \mathbf{G}_{m}^{2}\times R_{F_{a,d}/F}\mathbf{P}_{F_{a,d}}^{2}$
denote the closed subvariety defined by
$X^{\prime \prime }\subset \mathbf{G}_{m}^{2}\times R_{F_{a,d}/F}\mathbf{P}_{F_{a,d}}^{2}$
denote the closed subvariety defined by
![]() $\unicode[STIX]{x1D6FD}Bx^{2}+\unicode[STIX]{x1D6FE}Cy^{2}=z^{2}$
, where
$\unicode[STIX]{x1D6FD}Bx^{2}+\unicode[STIX]{x1D6FE}Cy^{2}=z^{2}$
, where
![]() $\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}$
are the coordinates of
$\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}$
are the coordinates of
![]() $\mathbf{G}_{m}^{2}$
and
$\mathbf{G}_{m}^{2}$
and
![]() $x,y,z$
now denote the homogeneous coordinates of
$x,y,z$
now denote the homogeneous coordinates of
![]() $R_{F_{a,d}/F}\mathbf{P}_{F_{a,d}}^{2}$
. Clearly
$R_{F_{a,d}/F}\mathbf{P}_{F_{a,d}}^{2}$
. Clearly
![]() $X^{\prime \prime }$
is smooth and contains
$X^{\prime \prime }$
is smooth and contains
![]() $X$
as a dense open subset. Let us fix once and for all a smooth compactification
$X$
as a dense open subset. Let us fix once and for all a smooth compactification
![]() $X^{\prime \prime }\subset X^{\prime }$
such that the map
$X^{\prime \prime }\subset X^{\prime }$
such that the map
![]() $\unicode[STIX]{x1D711}:X^{\prime \prime }\rightarrow \mathbf{G}_{m}^{2}$
defined by
$\unicode[STIX]{x1D711}:X^{\prime \prime }\rightarrow \mathbf{G}_{m}^{2}$
defined by
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},[x:y:z])=(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})$
extends to a morphism
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},[x:y:z])=(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})$
extends to a morphism
![]() $\unicode[STIX]{x1D711}^{\prime }:X^{\prime }\rightarrow \mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1}$
. (We view
$\unicode[STIX]{x1D711}^{\prime }:X^{\prime }\rightarrow \mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1}$
. (We view
![]() $\mathbf{G}_{m}^{2}$
as an open subset of
$\mathbf{G}_{m}^{2}$
as an open subset of
![]() $\mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1}$
.) For
$\mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1}$
.) For
![]() $w\in F^{\ast }$
, let
$w\in F^{\ast }$
, let
![]() $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=w},\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FD}=w\unicode[STIX]{x1D6FE}}\in \mathbf{G}_{m}^{2}$
denote the generic points of the subvarieties of
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=w},\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FD}=w\unicode[STIX]{x1D6FE}}\in \mathbf{G}_{m}^{2}$
denote the generic points of the subvarieties of
![]() $\mathbf{G}_{m}^{2}$
defined by
$\mathbf{G}_{m}^{2}$
defined by
![]() $\unicode[STIX]{x1D6FE}=w$
and by
$\unicode[STIX]{x1D6FE}=w$
and by
![]() $\unicode[STIX]{x1D6FD}=w\unicode[STIX]{x1D6FE}$
, respectively. The next proposition lists sufficient conditions for the fibre of
$\unicode[STIX]{x1D6FD}=w\unicode[STIX]{x1D6FE}$
, respectively. The next proposition lists sufficient conditions for the fibre of
![]() $\unicode[STIX]{x1D711}$
(or, equivalently, of
$\unicode[STIX]{x1D711}$
(or, equivalently, of
![]() $\unicode[STIX]{x1D711}^{\prime }$
) above these points to contain a rational point (i.e. an
$\unicode[STIX]{x1D711}^{\prime }$
) above these points to contain a rational point (i.e. an
![]() $F(\mathbf{G}_{m})$
-point) for some
$F(\mathbf{G}_{m})$
-point) for some
![]() $w$
.
$w$
.
Proposition A.4. The following statements hold:
(1) if
 $c$
is a square in
$c$
is a square in
 $F$
or if
$F$
or if
 $d$
and
$d$
and
 $ac$
are squares in
$ac$
are squares in
 $F$
, then there exists
$F$
, then there exists
 $w\in F^{\ast }$
such that
$w\in F^{\ast }$
such that
 $\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=w})$
,
$\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=w})$
,
 $\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=aw})$
, and
$\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=aw})$
, and
 $\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=dw})$
contain a rational point;
$\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=dw})$
contain a rational point;(2) if
 $a=b=c=d$
in
$a=b=c=d$
in
 $F^{\ast }/F^{\ast 2}$
, then there exists
$F^{\ast }/F^{\ast 2}$
, then there exists
 $w\in F^{\ast }$
such that
$w\in F^{\ast }$
such that
 $\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FD}=w\unicode[STIX]{x1D6FE}})$
and
$\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FD}=w\unicode[STIX]{x1D6FE}})$
and
 $\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FD}=aw\unicode[STIX]{x1D6FE}})$
contain a rational point;
$\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FD}=aw\unicode[STIX]{x1D6FE}})$
contain a rational point;(3) in the case where
 $d$
and
$d$
and
 $ac$
are squares in
$ac$
are squares in
 $F$
, one can take
$F$
, one can take
 $w=C_{1}$
(or
$w=C_{1}$
(or
 $w=C_{2}$
) in (1), where
$w=C_{2}$
) in (1), where
 $C=(C_{1},C_{2})$
denotes the image of
$C=(C_{1},C_{2})$
denotes the image of
 $C$
by the isomorphism
$C$
by the isomorphism
 $F_{d}=F\times F$
induced by the choice of a square root of
$F_{d}=F\times F$
induced by the choice of a square root of
 $d$
.
$d$
.
Proof. We first assume that
![]() $c$
is a square in
$c$
is a square in
![]() $F$
and prove (1) in this case. As
$F$
and prove (1) in this case. As
![]() $N_{F_{d}/F}(C)=c$
is a square in
$N_{F_{d}/F}(C)=c$
is a square in
![]() $F$
, it follows from Hilbert’s Theorem 90 that there exists
$F$
, it follows from Hilbert’s Theorem 90 that there exists
![]() $w\in F^{\ast }$
such that
$w\in F^{\ast }$
such that
![]() $wC$
is a square in
$wC$
is a square in
![]() $F_{d}$
. Evaluating the function
$F_{d}$
. Evaluating the function
![]() $\unicode[STIX]{x1D6FE}C$
at any
$\unicode[STIX]{x1D6FE}C$
at any
![]() $\unicode[STIX]{x1D708}\in \{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=w},\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=aw},\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=dw}\}$
yields an element of
$\unicode[STIX]{x1D708}\in \{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=w},\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=aw},\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=dw}\}$
yields an element of
![]() $F(\unicode[STIX]{x1D708})\otimes _{F}F_{d}$
which becomes a square in
$F(\unicode[STIX]{x1D708})\otimes _{F}F_{d}$
which becomes a square in
![]() $F(\unicode[STIX]{x1D708})\otimes _{F}F_{a,d}$
, hence the claim.
$F(\unicode[STIX]{x1D708})\otimes _{F}F_{a,d}$
, hence the claim.
Let us now assume that
![]() $d$
and
$d$
and
![]() $ac$
are squares in
$ac$
are squares in
![]() $F$
, and prove (1) and (3) simultaneously. In this case, following the notation of (3), we have
$F$
, and prove (1) and (3) simultaneously. In this case, following the notation of (3), we have
![]() $C_{1}C\in F_{a,d}^{\ast 2}$
as
$C_{1}C\in F_{a,d}^{\ast 2}$
as
![]() $c$
is a square in
$c$
is a square in
![]() $F_{a}$
and as the decomposition
$F_{a}$
and as the decomposition
![]() $F_{a,d}=F_{a}\times F_{a}$
maps
$F_{a,d}=F_{a}\times F_{a}$
maps
![]() $C_{1}C$
to
$C_{1}C$
to
![]() $(C_{1}^{2},c)$
. Hence, with
$(C_{1}^{2},c)$
. Hence, with
![]() $w=C_{1}$
, the value of
$w=C_{1}$
, the value of
![]() $\unicode[STIX]{x1D6FE}C$
at any
$\unicode[STIX]{x1D6FE}C$
at any
![]() $\unicode[STIX]{x1D708}\in \{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=w},\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=aw},\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=dw}\}$
is again a square in
$\unicode[STIX]{x1D708}\in \{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=w},\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=aw},\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=dw}\}$
is again a square in
![]() $F(\unicode[STIX]{x1D708})\otimes _{F}F_{a,d}$
.
$F(\unicode[STIX]{x1D708})\otimes _{F}F_{a,d}$
.
Finally, let us assume that
![]() $a=b=c=d$
in
$a=b=c=d$
in
![]() $F^{\ast }/F^{\ast 2}$
and turn to (2). The choice of a square root of
$F^{\ast }/F^{\ast 2}$
and turn to (2). The choice of a square root of
![]() $ad$
determines isomorphisms
$ad$
determines isomorphisms ![]() and
and
![]() $F_{a,d}=F_{a}\times F_{a}$
. As
$F_{a,d}=F_{a}\times F_{a}$
. As
![]() $N_{F_{a}/F}(B\unicode[STIX]{x1D704}(C))=bc$
is a square in
$N_{F_{a}/F}(B\unicode[STIX]{x1D704}(C))=bc$
is a square in
![]() $F$
, Hilbert’s Theorem 90 ensures the existence of
$F$
, Hilbert’s Theorem 90 ensures the existence of
![]() $w\in F^{\ast }$
such that
$w\in F^{\ast }$
such that
![]() $-wB\unicode[STIX]{x1D704}(C)$
is a square in
$-wB\unicode[STIX]{x1D704}(C)$
is a square in
![]() $F_{a}$
. As
$F_{a}$
. As
![]() $c$
is a square in
$c$
is a square in
![]() $F_{a}$
, it follows that
$F_{a}$
, it follows that
![]() $-wBC$
is a square in
$-wBC$
is a square in
![]() $F_{a,d}$
and hence that the value of the function
$F_{a,d}$
and hence that the value of the function
![]() $-\unicode[STIX]{x1D6FE}C\unicode[STIX]{x1D6FD}B$
at any
$-\unicode[STIX]{x1D6FE}C\unicode[STIX]{x1D6FD}B$
at any
![]() $\unicode[STIX]{x1D708}\in \{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FD}=w\unicode[STIX]{x1D6FE}},\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FD}=aw\unicode[STIX]{x1D6FE}}\}$
is a square in
$\unicode[STIX]{x1D708}\in \{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FD}=w\unicode[STIX]{x1D6FE}},\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FD}=aw\unicode[STIX]{x1D6FE}}\}$
is a square in
![]() $F(\unicode[STIX]{x1D708})\otimes _{F}F_{a,d}$
. Hence, writing
$F(\unicode[STIX]{x1D708})\otimes _{F}F_{a,d}$
. Hence, writing
![]() $(\unicode[STIX]{x1D6FD}B,\unicode[STIX]{x1D6FE}C)$
for the class in
$(\unicode[STIX]{x1D6FD}B,\unicode[STIX]{x1D6FE}C)$
for the class in
![]() $\text{Br}(F(\unicode[STIX]{x1D708})\otimes _{F}F_{a,d})$
of the corresponding quaternion algebra, we have
$\text{Br}(F(\unicode[STIX]{x1D708})\otimes _{F}F_{a,d})$
of the corresponding quaternion algebra, we have
![]() $(\unicode[STIX]{x1D6FD}B,\unicode[STIX]{x1D6FE}C)=(-\unicode[STIX]{x1D6FE}C\unicode[STIX]{x1D6FD}B,\unicode[STIX]{x1D6FE}C)=0$
for any such
$(\unicode[STIX]{x1D6FD}B,\unicode[STIX]{x1D6FE}C)=(-\unicode[STIX]{x1D6FE}C\unicode[STIX]{x1D6FD}B,\unicode[STIX]{x1D6FE}C)=0$
for any such
![]() $\unicode[STIX]{x1D708}$
, or equivalently
$\unicode[STIX]{x1D708}$
, or equivalently
![]() $\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D708})$
possesses a rational point.◻
$\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D708})$
possesses a rational point.◻
A.3 Arithmetic
Let us deduce Theorem A.1 from Theorem A.2. The relevant arithmetic input is the following statement.
Theorem A.5. Let
![]() $Z$
be a smooth, proper, and irreducible variety over a number field
$Z$
be a smooth, proper, and irreducible variety over a number field
![]() $F$
. Let
$F$
. Let
![]() $n\geqslant 1$
be an integer and
$n\geqslant 1$
be an integer and
![]() $f:Z\rightarrow (\mathbf{P}_{F}^{1})^{n}$
be a dominant morphism. Assume that the geometric generic fibre of
$f:Z\rightarrow (\mathbf{P}_{F}^{1})^{n}$
be a dominant morphism. Assume that the geometric generic fibre of
![]() $f$
is rationally connected and that the fibre of
$f$
is rationally connected and that the fibre of
![]() $f$
above any codimension
$f$
above any codimension
![]() $1$
point of
$1$
point of
![]() $(\mathbf{P}_{F}^{1}\setminus \{0,\infty \})^{n}$
is split. Assume, in addition, that for any rational point
$(\mathbf{P}_{F}^{1}\setminus \{0,\infty \})^{n}$
is split. Assume, in addition, that for any rational point
![]() $t$
of a dense open subset of
$t$
of a dense open subset of
![]() $(\mathbf{P}_{F}^{1})^{n}$
, the set
$(\mathbf{P}_{F}^{1})^{n}$
, the set
![]() $Z_{t}(F)$
is dense in
$Z_{t}(F)$
is dense in
![]() $Z_{t}(\mathbf{A}_{F})^{\text{Br}(Z_{t})}$
, where
$Z_{t}(\mathbf{A}_{F})^{\text{Br}(Z_{t})}$
, where
![]() $Z_{t}=f^{-1}(t)$
. Then
$Z_{t}=f^{-1}(t)$
. Then
![]() $Z(F)$
is dense in
$Z(F)$
is dense in
![]() $Z(\mathbf{A}_{F})^{\text{Br}(Z)}$
.
$Z(\mathbf{A}_{F})^{\text{Br}(Z)}$
.
For
![]() $n=1$
, this is [Reference Harpaz and WittenbergHW16, Theorem 9.31]. In view of [Reference Graber, Harris and StarrGHS03, Corollary 1.3], Theorem A.5 for any
$n=1$
, this is [Reference Harpaz and WittenbergHW16, Theorem 9.31]. In view of [Reference Graber, Harris and StarrGHS03, Corollary 1.3], Theorem A.5 for any
![]() $n$
follows from the
$n$
follows from the
![]() $n=1$
case by a straightforward induction.
$n=1$
case by a straightforward induction.
To prove Theorem A.1, we apply Theorem A.5 to
![]() $\unicode[STIX]{x1D711}^{\prime }$
, with
$\unicode[STIX]{x1D711}^{\prime }$
, with
![]() $n=2$
. By our choice of
$n=2$
. By our choice of
![]() $X^{\prime \prime }$
, the fibres of
$X^{\prime \prime }$
, the fibres of
![]() $\unicode[STIX]{x1D711}^{\prime }$
above
$\unicode[STIX]{x1D711}^{\prime }$
above
![]() $(\mathbf{P}_{F}^{1}\setminus \{0,\infty \})^{2}$
are Weil restrictions of smooth projective conics. In particular, the geometric generic fibre of
$(\mathbf{P}_{F}^{1}\setminus \{0,\infty \})^{2}$
are Weil restrictions of smooth projective conics. In particular, the geometric generic fibre of
![]() $\unicode[STIX]{x1D711}^{\prime }$
is rational, hence rationally connected, and the codimension
$\unicode[STIX]{x1D711}^{\prime }$
is rational, hence rationally connected, and the codimension
![]() $1$
fibres of
$1$
fibres of
![]() $\unicode[STIX]{x1D711}^{\prime }$
above
$\unicode[STIX]{x1D711}^{\prime }$
above
![]() $(\mathbf{P}_{F}^{1}\setminus \{0,\infty \})^{2}$
are smooth and geometrically irreducible, hence split. To verify the arithmetic hypothesis on the closed fibres of
$(\mathbf{P}_{F}^{1}\setminus \{0,\infty \})^{2}$
are smooth and geometrically irreducible, hence split. To verify the arithmetic hypothesis on the closed fibres of
![]() $\unicode[STIX]{x1D711}^{\prime }$
, we note that if
$\unicode[STIX]{x1D711}^{\prime }$
, we note that if
![]() $Z_{t}$
is a Weil restriction, by a finite extension of number fields, of a smooth projective conic, and if
$Z_{t}$
is a Weil restriction, by a finite extension of number fields, of a smooth projective conic, and if
![]() $Z_{t}(\mathbf{A}_{F})\neq \varnothing$
, then the Hasse–Minkowski theorem implies that
$Z_{t}(\mathbf{A}_{F})\neq \varnothing$
, then the Hasse–Minkowski theorem implies that
![]() $Z_{t}(F)\neq \varnothing$
, from which it follows that the variety
$Z_{t}(F)\neq \varnothing$
, from which it follows that the variety
![]() $Z_{t}$
is rational over
$Z_{t}$
is rational over
![]() $F$
and hence that
$F$
and hence that
![]() $Z_{t}(F)$
is dense in
$Z_{t}(F)$
is dense in
![]() $Z_{t}(\mathbf{A}_{F})$
. All in all, we conclude that
$Z_{t}(\mathbf{A}_{F})$
. All in all, we conclude that
![]() $X^{\prime }(F)$
is dense in
$X^{\prime }(F)$
is dense in
![]() $X^{\prime }(\mathbf{A}_{F})^{\text{Br}(X^{\prime })}$
. Therefore
$X^{\prime }(\mathbf{A}_{F})^{\text{Br}(X^{\prime })}$
. Therefore
![]() $X(F)\neq \varnothing$
if and only if
$X(F)\neq \varnothing$
if and only if
![]() $X^{\prime }(\mathbf{A}_{F})^{\text{Br}(X^{\prime })}\cap \prod _{v\in \unicode[STIX]{x1D6FA}}X(F_{v})\neq \varnothing$
. By Theorem A.2, the latter condition is implied by the one which appears in the statement of Theorem A.1, which, in view of the quadratic reciprocity law, is itself implied by the existence of a rational point on
$X^{\prime }(\mathbf{A}_{F})^{\text{Br}(X^{\prime })}\cap \prod _{v\in \unicode[STIX]{x1D6FA}}X(F_{v})\neq \varnothing$
. By Theorem A.2, the latter condition is implied by the one which appears in the statement of Theorem A.1, which, in view of the quadratic reciprocity law, is itself implied by the existence of a rational point on
![]() $X$
. Thus the proof of Theorem A.1 is complete.
$X$
. Thus the proof of Theorem A.1 is complete.
A.4 Brauer groups
In the remainder of this appendix, we prove Theorem A.2. Hereafter
![]() $F$
denotes a field of characteristic
$F$
denotes a field of characteristic
![]() $0$
. We start with two general remarks about the Brauer group of Weil restrictions of conics and of trivial two-dimensional tori.
$0$
. We start with two general remarks about the Brauer group of Weil restrictions of conics and of trivial two-dimensional tori.
Proposition A.6. Let
![]() $k^{\prime }/k$
be a finite separable extension of fields. Let
$k^{\prime }/k$
be a finite separable extension of fields. Let
![]() $C$
be a smooth, projective conic over
$C$
be a smooth, projective conic over
![]() $k^{\prime }$
. If
$k^{\prime }$
. If
![]() $R_{k^{\prime }/k}C$
denotes the Weil restriction of
$R_{k^{\prime }/k}C$
denotes the Weil restriction of
![]() $C$
from
$C$
from
![]() $k^{\prime }$
to
$k^{\prime }$
to
![]() $k$
, the pull-back map
$k$
, the pull-back map
![]() $\text{Br}(k)\rightarrow \text{Br}(R_{k^{\prime }/k}C)$
is surjective.
$\text{Br}(k)\rightarrow \text{Br}(R_{k^{\prime }/k}C)$
is surjective.
Proof. Let
![]() $\overline{k}$
be a separable closure of
$\overline{k}$
be a separable closure of
![]() $k$
. The choice of a
$k$
. The choice of a
![]() $(k^{\prime }\otimes _{k}\overline{k})$
-point of
$(k^{\prime }\otimes _{k}\overline{k})$
-point of
![]() $C$
determines an isomorphism between
$C$
determines an isomorphism between
![]() $(R_{k^{\prime }/k}C)\otimes _{k}\overline{k}$
and the product of
$(R_{k^{\prime }/k}C)\otimes _{k}\overline{k}$
and the product of
![]() $[k^{\prime }:k]$
copies of
$[k^{\prime }:k]$
copies of
![]() $\mathbf{P}_{\overline{k}}^{1}$
indexed by the finite set
$\mathbf{P}_{\overline{k}}^{1}$
indexed by the finite set
![]() $\text{Spec}(k^{\prime }\otimes _{k}\overline{k})$
. It follows that
$\text{Spec}(k^{\prime }\otimes _{k}\overline{k})$
. It follows that
![]() $\text{Br}((R_{k^{\prime }/k}C)\otimes _{k}\overline{k})=0$
and that
$\text{Br}((R_{k^{\prime }/k}C)\otimes _{k}\overline{k})=0$
and that
![]() $\text{Pic}((R_{k^{\prime }/k}C)\otimes _{k}\overline{k})$
is isomorphic, as a Galois module, to
$\text{Pic}((R_{k^{\prime }/k}C)\otimes _{k}\overline{k})$
is isomorphic, as a Galois module, to
![]() $\mathbf{Z}^{\text{Spec}(k^{\prime }\otimes _{k}\overline{k})}$
. Hence, by Shapiro’s lemma, the terms
$\mathbf{Z}^{\text{Spec}(k^{\prime }\otimes _{k}\overline{k})}$
. Hence, by Shapiro’s lemma, the terms
![]() $E_{2}^{0,2}$
and
$E_{2}^{0,2}$
and
![]() $E_{2}^{1,1}$
of the Hochschild–Serre spectral sequence
$E_{2}^{1,1}$
of the Hochschild–Serre spectral sequence
vanish (see [Reference MilneMil80, ch. III, Proposition 4.9]). We conclude that
![]() $E_{2}^{2,0}=\text{Br}(k)$
surjects onto
$E_{2}^{2,0}=\text{Br}(k)$
surjects onto
![]() $\operatorname{H}_{\acute{\text{e}}\text{t}}^{2}(R_{k^{\prime }/k}C,\mathbf{G}_{m})=\text{Br}(R_{k^{\prime }/k}C)$
.◻
$\operatorname{H}_{\acute{\text{e}}\text{t}}^{2}(R_{k^{\prime }/k}C,\mathbf{G}_{m})=\text{Br}(R_{k^{\prime }/k}C)$
.◻
Given a field
![]() $k$
of characteristic different from
$k$
of characteristic different from
![]() $2$
(typically
$2$
(typically
![]() $k=F(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})$
or
$k=F(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})$
or
![]() $k=F(X)$
) and two elements
$k=F(X)$
) and two elements
![]() $x,y\in k^{\ast }$
, we denote by
$x,y\in k^{\ast }$
, we denote by
![]() $(x,y)$
the class, in
$(x,y)$
the class, in
![]() $\text{Br}(k)$
, of the corresponding quaternion algebra over
$\text{Br}(k)$
, of the corresponding quaternion algebra over
![]() $k$
.
$k$
.
Proposition A.7. Any
![]() $2$
-torsion element of
$2$
-torsion element of
![]() $\text{Br}((\mathbf{P}_{F}^{1}\setminus \{0,\infty \})^{2})$
can be written as
$\text{Br}((\mathbf{P}_{F}^{1}\setminus \{0,\infty \})^{2})$
can be written as
for some
![]() $r,s\in F^{\ast }$
, some
$r,s\in F^{\ast }$
, some
![]() $\unicode[STIX]{x1D700}\in \{0,1\}$
, and some
$\unicode[STIX]{x1D700}\in \{0,1\}$
, and some
![]() $\unicode[STIX]{x1D6FF}\in \text{Im}(\text{Br}(F)\rightarrow \text{Br}(F(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})))$
.
$\unicode[STIX]{x1D6FF}\in \text{Im}(\text{Br}(F)\rightarrow \text{Br}(F(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})))$
.
Proof. Let
![]() $D_{1}=\mathbf{A}_{F}^{1}\times \{0\}$
,
$D_{1}=\mathbf{A}_{F}^{1}\times \{0\}$
,
![]() $D_{2}=\{0\}\times \mathbf{A}_{F}^{1}$
,
$D_{2}=\{0\}\times \mathbf{A}_{F}^{1}$
,
![]() $D_{12}=D_{1}\cap D_{2}$
, and
$D_{12}=D_{1}\cap D_{2}$
, and
![]() $D_{i}^{0}=D_{i}\setminus D_{12}$
. By purity for étale cohomology, we have
$D_{i}^{0}=D_{i}\setminus D_{12}$
. By purity for étale cohomology, we have
![]() $\operatorname{H}_{\acute{\text{e}}\text{t},D_{12}}^{q}(\mathbf{A}_{F}^{2},\mathbf{Z}/2\mathbf{Z})=\operatorname{H}_{\acute{\text{e}}\text{t}}^{q-4}(D_{12},\mathbf{Z}/2\mathbf{Z})=\operatorname{H}^{q-4}(F,\mathbf{Z}/2\mathbf{Z})$
for any
$\operatorname{H}_{\acute{\text{e}}\text{t},D_{12}}^{q}(\mathbf{A}_{F}^{2},\mathbf{Z}/2\mathbf{Z})=\operatorname{H}_{\acute{\text{e}}\text{t}}^{q-4}(D_{12},\mathbf{Z}/2\mathbf{Z})=\operatorname{H}^{q-4}(F,\mathbf{Z}/2\mathbf{Z})$
for any
![]() $q$
, and
$q$
, and
![]() $\operatorname{H}_{\acute{\text{e}}\text{t},D_{1}^{0}\cup D_{2}^{0}}^{3}(\mathbf{A}_{F}^{2}\setminus D_{12},\mathbf{Z}/2\mathbf{Z})=\operatorname{H}_{\acute{\text{e}}\text{t}}^{1}(D_{1}^{0},\mathbf{Z}/2\mathbf{Z})\oplus \operatorname{H}_{\acute{\text{e}}\text{t}}^{1}(D_{2}^{0},\mathbf{Z}/2\mathbf{Z})$
(see [Reference MilneMil80, ch. VI, § 5]). The long exact sequence of a triple therefore yields an exact sequence
$\operatorname{H}_{\acute{\text{e}}\text{t},D_{1}^{0}\cup D_{2}^{0}}^{3}(\mathbf{A}_{F}^{2}\setminus D_{12},\mathbf{Z}/2\mathbf{Z})=\operatorname{H}_{\acute{\text{e}}\text{t}}^{1}(D_{1}^{0},\mathbf{Z}/2\mathbf{Z})\oplus \operatorname{H}_{\acute{\text{e}}\text{t}}^{1}(D_{2}^{0},\mathbf{Z}/2\mathbf{Z})$
(see [Reference MilneMil80, ch. VI, § 5]). The long exact sequence of a triple therefore yields an exact sequence
where the rightmost map is the sum of the residues at
![]() $0$
[Reference MilneMil80, ch. III, Remark 1.26]. Finally, let us consider the localisation exact sequence
$0$
[Reference MilneMil80, ch. III, Remark 1.26]. Finally, let us consider the localisation exact sequence
[Reference MilneMil80, ch. III, Proposition 1.25]. As any
![]() $2$
-torsion element of
$2$
-torsion element of
![]() $\text{Br}((\mathbf{P}_{F}^{1}\setminus \{0,\infty \})^{2})$
can be lifted to
$\text{Br}((\mathbf{P}_{F}^{1}\setminus \{0,\infty \})^{2})$
can be lifted to
![]() $\operatorname{H}_{\acute{\text{e}}\text{t}}^{2}(\mathbf{A}_{F}^{2}\setminus (D_{1}\cup D_{2}),\mathbf{Z}/2\mathbf{Z})$
and as
$\operatorname{H}_{\acute{\text{e}}\text{t}}^{2}(\mathbf{A}_{F}^{2}\setminus (D_{1}\cup D_{2}),\mathbf{Z}/2\mathbf{Z})$
and as
![]() $H^{1}(D_{i}^{0},\mathbf{Z}/2\mathbf{Z})\subset H^{1}(F(D_{i}),\mathbf{Z}/2\mathbf{Z})=F(D_{i})^{\ast }/F(D_{i})^{\ast 2}$
is generated by
$H^{1}(D_{i}^{0},\mathbf{Z}/2\mathbf{Z})\subset H^{1}(F(D_{i}),\mathbf{Z}/2\mathbf{Z})=F(D_{i})^{\ast }/F(D_{i})^{\ast 2}$
is generated by
![]() $F^{\ast }/F^{\ast 2}$
and by the class of
$F^{\ast }/F^{\ast 2}$
and by the class of
![]() $\unicode[STIX]{x1D6FD}$
(respectively
$\unicode[STIX]{x1D6FD}$
(respectively
![]() $\unicode[STIX]{x1D6FE}$
) if
$\unicode[STIX]{x1D6FE}$
) if
![]() $i=1$
(respectively
$i=1$
(respectively
![]() $i=2$
), we deduce from these two exact sequences that for an arbitrary
$i=2$
), we deduce from these two exact sequences that for an arbitrary
![]() $2$
-torsion class
$2$
-torsion class
![]() $\unicode[STIX]{x1D6FC}\in \text{Br}((\mathbf{P}_{F}^{1}\setminus \{0,\infty \})^{2})$
, the residues of
$\unicode[STIX]{x1D6FC}\in \text{Br}((\mathbf{P}_{F}^{1}\setminus \{0,\infty \})^{2})$
, the residues of
![]() $\unicode[STIX]{x1D6FC}$
at the generic points of
$\unicode[STIX]{x1D6FC}$
at the generic points of
![]() $D_{1}$
and
$D_{1}$
and
![]() $D_{2}$
, viewed as elements of
$D_{2}$
, viewed as elements of
![]() $F(D_{i})^{\ast }/F(D_{i})^{\ast 2}$
, are represented by elements of
$F(D_{i})^{\ast }/F(D_{i})^{\ast 2}$
, are represented by elements of
![]() $F(D_{i})^{\ast }$
of the shape
$F(D_{i})^{\ast }$
of the shape
![]() $\unicode[STIX]{x1D6FD}^{\unicode[STIX]{x1D700}}s$
and
$\unicode[STIX]{x1D6FD}^{\unicode[STIX]{x1D700}}s$
and
![]() $\unicode[STIX]{x1D6FE}^{\unicode[STIX]{x1D700}}r$
, respectively, for some
$\unicode[STIX]{x1D6FE}^{\unicode[STIX]{x1D700}}r$
, respectively, for some
![]() $r,s\in F^{\ast }$
and some
$r,s\in F^{\ast }$
and some
![]() $\unicode[STIX]{x1D700}\in \{0,1\}$
. The class
$\unicode[STIX]{x1D700}\in \{0,1\}$
. The class
![]() $(\unicode[STIX]{x1D6FD},r)+(\unicode[STIX]{x1D6FE},s)+\unicode[STIX]{x1D700}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})$
has the same residues as
$(\unicode[STIX]{x1D6FD},r)+(\unicode[STIX]{x1D6FE},s)+\unicode[STIX]{x1D700}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})$
has the same residues as
![]() $\unicode[STIX]{x1D6FC}$
at these two points. As
$\unicode[STIX]{x1D6FC}$
at these two points. As
![]() $\operatorname{H}_{\acute{\text{e}}\text{t}}^{2}(\mathbf{A}_{F}^{2},\mathbf{Z}/2\mathbf{Z})=\operatorname{H}^{2}(F,\mathbf{Z}/2\mathbf{Z})$
[Reference MilneMil80, ch. VI, Corollary 4.20], these two classes differ by a constant class, in view of the localisation exact sequence.◻
$\operatorname{H}_{\acute{\text{e}}\text{t}}^{2}(\mathbf{A}_{F}^{2},\mathbf{Z}/2\mathbf{Z})=\operatorname{H}^{2}(F,\mathbf{Z}/2\mathbf{Z})$
[Reference MilneMil80, ch. VI, Corollary 4.20], these two classes differ by a constant class, in view of the localisation exact sequence.◻
The following is a simple consequence of Propositions A.6 and A.7.
Proposition A.8. The cokernel of the natural map
![]() $\text{Br}(F)\rightarrow \text{Br}_{\text{nr}}(F(X)/F)$
is killed by
$\text{Br}(F)\rightarrow \text{Br}_{\text{nr}}(F(X)/F)$
is killed by
![]() $2$
. Its elements are represented by classes of the shape
$2$
. Its elements are represented by classes of the shape
for
![]() $r,s\in F^{\ast }$
and
$r,s\in F^{\ast }$
and
![]() $\unicode[STIX]{x1D700}\in \{0,1\}$
.
$\unicode[STIX]{x1D700}\in \{0,1\}$
.
Proof. The generic fibre of
![]() $\unicode[STIX]{x1D711}^{\prime }:X^{\prime }\rightarrow \mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1}$
is a Weil restriction of a smooth projective conic. Applying Proposition A.6 to it, we see that any element of
$\unicode[STIX]{x1D711}^{\prime }:X^{\prime }\rightarrow \mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1}$
is a Weil restriction of a smooth projective conic. Applying Proposition A.6 to it, we see that any element of
![]() $\text{Br}_{\text{nr}}(F(X)/F)=\text{Br}(X^{\prime })$
can be written as
$\text{Br}_{\text{nr}}(F(X)/F)=\text{Br}(X^{\prime })$
can be written as
![]() ${\unicode[STIX]{x1D711}^{\prime }}^{\ast }\unicode[STIX]{x1D6FC}$
for some
${\unicode[STIX]{x1D711}^{\prime }}^{\ast }\unicode[STIX]{x1D6FC}$
for some
![]() $\unicode[STIX]{x1D6FC}\in \text{Br}(F(\mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1}))$
. As
$\unicode[STIX]{x1D6FC}\in \text{Br}(F(\mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1}))$
. As
![]() ${\unicode[STIX]{x1D711}^{\prime }}^{\ast }\unicode[STIX]{x1D6FC}$
is unramified on
${\unicode[STIX]{x1D711}^{\prime }}^{\ast }\unicode[STIX]{x1D6FC}$
is unramified on
![]() $X^{\prime }$
and as the fibres of
$X^{\prime }$
and as the fibres of
![]() $\unicode[STIX]{x1D711}^{\prime }$
above
$\unicode[STIX]{x1D711}^{\prime }$
above
![]() $(\mathbf{P}_{F}^{1}\setminus \{0,\infty \})^{2}$
are split, the class
$(\mathbf{P}_{F}^{1}\setminus \{0,\infty \})^{2}$
are split, the class
![]() $\unicode[STIX]{x1D6FC}$
belongs to the subgroup
$\unicode[STIX]{x1D6FC}$
belongs to the subgroup
![]() $\text{Br}((\mathbf{P}_{F}^{1}\setminus \{0,\infty \})^{2})\subset \text{Br}(F(\mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1}))$
(see [Reference Colliot-Thélène and Swinnerton-DyerCS94, Proposition 1.1.1]). After adding a constant class to
$\text{Br}((\mathbf{P}_{F}^{1}\setminus \{0,\infty \})^{2})\subset \text{Br}(F(\mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1}))$
(see [Reference Colliot-Thélène and Swinnerton-DyerCS94, Proposition 1.1.1]). After adding a constant class to
![]() $\unicode[STIX]{x1D6FC}$
, we may assume that the value of
$\unicode[STIX]{x1D6FC}$
, we may assume that the value of
![]() $\unicode[STIX]{x1D6FC}$
at the point
$\unicode[STIX]{x1D6FC}$
at the point
![]() $(1,1)$
vanishes in
$(1,1)$
vanishes in
![]() $\text{Br}(F)$
. The next lemma then implies that
$\text{Br}(F)$
. The next lemma then implies that
![]() $2\unicode[STIX]{x1D6FC}=0$
[Reference Colliot-Thélène and Swinnerton-DyerCS94, Proposition 1.3.3]. Applying Proposition A.7 now completes the proof of Proposition A.8.◻
$2\unicode[STIX]{x1D6FC}=0$
[Reference Colliot-Thélène and Swinnerton-DyerCS94, Proposition 1.3.3]. Applying Proposition A.7 now completes the proof of Proposition A.8.◻
Lemma A.9. Let
![]() $i\in \{1,2\}$
,
$i\in \{1,2\}$
,
![]() $t\in \{0,\infty \}$
. Let
$t\in \{0,\infty \}$
. Let
![]() $\unicode[STIX]{x1D709}\in \mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1}$
be the generic point of the fibre, above
$\unicode[STIX]{x1D709}\in \mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1}$
be the generic point of the fibre, above
![]() $t$
, of the
$t$
, of the
![]() $i$
th projection
$i$
th projection
![]() $\mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1}\rightarrow \mathbf{P}_{F}^{1}$
. The residue of
$\mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1}\rightarrow \mathbf{P}_{F}^{1}$
. The residue of
![]() $\unicode[STIX]{x1D6FC}$
at
$\unicode[STIX]{x1D6FC}$
at
![]() $\unicode[STIX]{x1D709}$
is killed by
$\unicode[STIX]{x1D709}$
is killed by
![]() $2$
.
$2$
.
Proof. Let
![]() $K=F(\mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1})=F(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})$
and
$K=F(\mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1})=F(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})$
and
![]() $\mathscr{O}_{K}\subset K$
denote the local ring of
$\mathscr{O}_{K}\subset K$
denote the local ring of
![]() $\mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1}$
at
$\mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1}$
at
![]() $\unicode[STIX]{x1D709}$
. Let
$\unicode[STIX]{x1D709}$
. Let
![]() $K^{\prime }/K$
be the quadratic extension obtained by adjoining a square root of
$K^{\prime }/K$
be the quadratic extension obtained by adjoining a square root of
![]() $\unicode[STIX]{x1D6FD}$
if
$\unicode[STIX]{x1D6FD}$
if
![]() $i=1$
, or of
$i=1$
, or of
![]() $\unicode[STIX]{x1D6FE}$
if
$\unicode[STIX]{x1D6FE}$
if
![]() $i=2$
. Let
$i=2$
. Let
![]() $\mathscr{O}_{K^{\prime }}$
denote the integral closure of
$\mathscr{O}_{K^{\prime }}$
denote the integral closure of
![]() $\mathscr{O}_{K}$
in
$\mathscr{O}_{K}$
in
![]() $K^{\prime }$
. To prove the lemma, it suffices to check that the image of
$K^{\prime }$
. To prove the lemma, it suffices to check that the image of
![]() $\unicode[STIX]{x1D6FC}\in \text{Br}(K)$
in
$\unicode[STIX]{x1D6FC}\in \text{Br}(K)$
in
![]() $\text{Br}(K^{\prime })$
belongs to the subgroup
$\text{Br}(K^{\prime })$
belongs to the subgroup
![]() $\text{Br}(\mathscr{O}_{K^{\prime }})\subset \text{Br}(K^{\prime })$
(see [Reference Colliot-Thélène and Swinnerton-DyerCS94, Proposition 1.1.2]). For this, as
$\text{Br}(\mathscr{O}_{K^{\prime }})\subset \text{Br}(K^{\prime })$
(see [Reference Colliot-Thélène and Swinnerton-DyerCS94, Proposition 1.1.2]). For this, as
![]() ${\unicode[STIX]{x1D711}^{\prime }}^{\ast }\unicode[STIX]{x1D6FC}$
is unramified over
${\unicode[STIX]{x1D711}^{\prime }}^{\ast }\unicode[STIX]{x1D6FC}$
is unramified over
![]() $X^{\prime }$
, it suffices to check that the
$X^{\prime }$
, it suffices to check that the
![]() $K^{\prime }$
-variety
$K^{\prime }$
-variety
![]() $X^{\prime }\times _{\mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1}}\text{Spec}(K^{\prime })$
admits a proper regular model over
$X^{\prime }\times _{\mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1}}\text{Spec}(K^{\prime })$
admits a proper regular model over
![]() $\mathscr{O}_{K^{\prime }}$
whose special fibre is split ([Reference Colliot-Thélène and Swinnerton-DyerCS94, Proposition 1.1.1]; this property does not depend on the choice of the model [Reference SkorobogatovSko96, Corollary 1.2]). A look at the equations which define
$\mathscr{O}_{K^{\prime }}$
whose special fibre is split ([Reference Colliot-Thélène and Swinnerton-DyerCS94, Proposition 1.1.1]; this property does not depend on the choice of the model [Reference SkorobogatovSko96, Corollary 1.2]). A look at the equations which define
![]() $X^{\prime \prime }$
shows that
$X^{\prime \prime }$
shows that
![]() $X^{\prime }\times _{\mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1}}\text{Spec}(K^{\prime })$
even has good reduction over
$X^{\prime }\times _{\mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1}}\text{Spec}(K^{\prime })$
even has good reduction over
![]() $\mathscr{O}_{K^{\prime }}$
as it descends to a variety over
$\mathscr{O}_{K^{\prime }}$
as it descends to a variety over
![]() $F(\unicode[STIX]{x1D6FE})\subset \mathscr{O}_{K^{\prime }}$
if
$F(\unicode[STIX]{x1D6FE})\subset \mathscr{O}_{K^{\prime }}$
if
![]() $i=1$
, or over
$i=1$
, or over
![]() $F(\unicode[STIX]{x1D6FD})\subset \mathscr{O}_{K^{\prime }}$
if
$F(\unicode[STIX]{x1D6FD})\subset \mathscr{O}_{K^{\prime }}$
if
![]() $i=2$
.◻
$i=2$
.◻
To exploit the hypothesis that the classes under consideration are unramified, we shall repeatedly use the following tool.
Proposition A.10. Let
![]() $r,s\in F^{\ast }$
and
$r,s\in F^{\ast }$
and
![]() $\unicode[STIX]{x1D700}\in \{0,1\}$
be such that
$\unicode[STIX]{x1D700}\in \{0,1\}$
be such that
![]() $(\unicode[STIX]{x1D6FD},r)+(\unicode[STIX]{x1D6FE},s)+\unicode[STIX]{x1D700}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})\in \text{Br}_{\text{nr}}(F(X)/F)$
. Let
$(\unicode[STIX]{x1D6FD},r)+(\unicode[STIX]{x1D6FE},s)+\unicode[STIX]{x1D700}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})\in \text{Br}_{\text{nr}}(F(X)/F)$
. Let
![]() $w\in F^{\ast }$
.
$w\in F^{\ast }$
.
(1) If
 $\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=w})$
contains a rational point, then
$\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=w})$
contains a rational point, then
 $rw^{\unicode[STIX]{x1D700}}$
is a square in
$rw^{\unicode[STIX]{x1D700}}$
is a square in
 $F$
.
$F$
.(2) If
 $\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FD}=w\unicode[STIX]{x1D6FE}})$
contains a rational point, then
$\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FD}=w\unicode[STIX]{x1D6FE}})$
contains a rational point, then
 $rs(-w)^{\unicode[STIX]{x1D700}}$
is a square in
$rs(-w)^{\unicode[STIX]{x1D700}}$
is a square in
 $F$
.
$F$
.
Proof. Let
![]() $\unicode[STIX]{x1D708}\in \{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=w},\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FD}=w\unicode[STIX]{x1D6FE}}\}$
. Let
$\unicode[STIX]{x1D708}\in \{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=w},\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FD}=w\unicode[STIX]{x1D6FE}}\}$
. Let
![]() $\overline{\unicode[STIX]{x1D708}}$
denote the Zariski closure of
$\overline{\unicode[STIX]{x1D708}}$
denote the Zariski closure of
![]() $\unicode[STIX]{x1D708}$
in
$\unicode[STIX]{x1D708}$
in
![]() $\mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1}$
. Suppose that
$\mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1}$
. Suppose that
![]() $\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D708})$
contains a rational point. The inclusion
$\unicode[STIX]{x1D711}^{-1}(\unicode[STIX]{x1D708})$
contains a rational point. The inclusion
![]() $\overline{\unicode[STIX]{x1D708}}{\hookrightarrow}\mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1}$
then factors through
$\overline{\unicode[STIX]{x1D708}}{\hookrightarrow}\mathbf{P}_{F}^{1}\times \mathbf{P}_{F}^{1}$
then factors through
![]() $\unicode[STIX]{x1D711}^{\prime }$
. As
$\unicode[STIX]{x1D711}^{\prime }$
. As
![]() $(\unicode[STIX]{x1D6FD},r)+(\unicode[STIX]{x1D6FE},s)+\unicode[STIX]{x1D700}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})\in \text{Br}((\mathbf{P}_{F}^{1}\setminus \{0,\infty \})^{2})$
becomes, by assumption, unramified over
$(\unicode[STIX]{x1D6FD},r)+(\unicode[STIX]{x1D6FE},s)+\unicode[STIX]{x1D700}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})\in \text{Br}((\mathbf{P}_{F}^{1}\setminus \{0,\infty \})^{2})$
becomes, by assumption, unramified over
![]() $X^{\prime }$
when pulled back to
$X^{\prime }$
when pulled back to
![]() $X^{\prime \prime }$
, its value at
$X^{\prime \prime }$
, its value at
![]() $\unicode[STIX]{x1D708}$
must therefore belong to the subgroup
$\unicode[STIX]{x1D708}$
must therefore belong to the subgroup
![]() $\text{Br}(\overline{\unicode[STIX]{x1D708}})\subset \text{Br}(\unicode[STIX]{x1D708})$
. Letting
$\text{Br}(\overline{\unicode[STIX]{x1D708}})\subset \text{Br}(\unicode[STIX]{x1D708})$
. Letting
![]() $t$
denote the coordinate of
$t$
denote the coordinate of
![]() $\mathbf{P}_{F}^{1}$
, this means that when
$\mathbf{P}_{F}^{1}$
, this means that when
![]() $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=w}$
(respectively,
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FE}=w}$
(respectively,
![]() $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FD}=w\unicode[STIX]{x1D6FE}}$
), the class
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FD}=w\unicode[STIX]{x1D6FE}}$
), the class
![]() $(t,r)+(w,s)+\unicode[STIX]{x1D700}(t,w)$
(respectively,
$(t,r)+(w,s)+\unicode[STIX]{x1D700}(t,w)$
(respectively,
![]() $(wt,r)+(t,s)+\unicode[STIX]{x1D700}(wt,t)$
) in
$(wt,r)+(t,s)+\unicode[STIX]{x1D700}(wt,t)$
) in
![]() $\text{Br}(\mathbf{P}_{F}^{1}\setminus \{0,\infty \})$
must be unramified over
$\text{Br}(\mathbf{P}_{F}^{1}\setminus \{0,\infty \})$
must be unramified over
![]() $\mathbf{P}_{F}^{1}$
; hence the proposition.◻
$\mathbf{P}_{F}^{1}$
; hence the proposition.◻
The next three propositions complete the proof of Theorem A.2.
Proposition A.11. Let
![]() $r,s\in F^{\ast }$
. If the class
$r,s\in F^{\ast }$
. If the class
![]() $(\unicode[STIX]{x1D6FD},r)+(\unicode[STIX]{x1D6FE},s)+(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})\in \text{Br}(F(X))$
belongs to
$(\unicode[STIX]{x1D6FD},r)+(\unicode[STIX]{x1D6FE},s)+(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})\in \text{Br}(F(X))$
belongs to
![]() $\text{Br}_{\text{nr}}(F(X)/F)$
, then it belongs to the image of the natural map
$\text{Br}_{\text{nr}}(F(X)/F)$
, then it belongs to the image of the natural map
![]() $\text{Br}(F)\rightarrow \text{Br}(F(X))$
.
$\text{Br}(F)\rightarrow \text{Br}(F(X))$
.
Proof. We proceed in several steps.
Step 1: we claim that
![]() $ad$
is a square in
$ad$
is a square in
![]() $F$
.
$F$
.
Suppose that
![]() $ad$
is not a square in
$ad$
is not a square in
![]() $F$
. Then
$F$
. Then
![]() $a$
and
$a$
and
![]() $d$
are not both squares; by symmetry, we may assume that
$d$
are not both squares; by symmetry, we may assume that
![]() $a$
is not a square in
$a$
is not a square in
![]() $F$
; after replacing
$F$
; after replacing
![]() $F$
by
$F$
by
![]() $F(\sqrt{d})$
, we may then assume that
$F(\sqrt{d})$
, we may then assume that
![]() $d$
is a square in
$d$
is a square in
![]() $F$
. As
$F$
. As
![]() $a$
is not a square in
$a$
is not a square in
![]() $F$
, it cannot be a square in
$F$
, it cannot be a square in
![]() $F(\sqrt{c})$
and in
$F(\sqrt{c})$
and in
![]() $F(\sqrt{ac})$
at the same time. After replacing
$F(\sqrt{ac})$
at the same time. After replacing
![]() $F$
by one of these two extensions, we may therefore assume that
$F$
by one of these two extensions, we may therefore assume that
![]() $c$
or
$c$
or
![]() $ac$
is a square. The hypotheses of Proposition A.4(1) are now met. By Proposition A.10(1) applied twice, we deduce that
$ac$
is a square. The hypotheses of Proposition A.4(1) are now met. By Proposition A.10(1) applied twice, we deduce that
![]() $rw$
and
$rw$
and
![]() $raw$
are squares in
$raw$
are squares in
![]() $F$
, hence
$F$
, hence
![]() $a$
is a square in
$a$
is a square in
![]() $F$
, which is absurd.
$F$
, which is absurd.
Step 2: we claim that at least one of
![]() $d$
and
$d$
and
![]() $cd$
is a square in
$cd$
is a square in
![]() $F$
.
$F$
.
We may assume, after replacing
![]() $F$
with
$F$
with
![]() $F(\sqrt{c})$
, that
$F(\sqrt{c})$
, that
![]() $c$
is a square in
$c$
is a square in
![]() $F$
. Applying Propositions A.4(1) and A.10(1), we deduce that
$F$
. Applying Propositions A.4(1) and A.10(1), we deduce that
![]() $rw$
and
$rw$
and
![]() $rdw$
are squares in
$rdw$
are squares in
![]() $F$
; hence
$F$
; hence
![]() $d$
is a square in
$d$
is a square in
![]() $F$
.
$F$
.
Step 3: we claim that at least one of
![]() $a$
and
$a$
and
![]() $ab$
is a square in
$ab$
is a square in
![]() $F$
.
$F$
.
This follows from Step 2, by symmetry.
Step 4: if
![]() $a=b=c=d$
in
$a=b=c=d$
in
![]() $F^{\ast }/F^{\ast 2}$
, then
$F^{\ast }/F^{\ast 2}$
, then
![]() $a=b=c=d=1$
in
$a=b=c=d=1$
in
![]() $F^{\ast }/F^{\ast 2}$
.
$F^{\ast }/F^{\ast 2}$
.
Applying Propositions A.4(2) and A.10(2), we see that
![]() $-rsw$
and
$-rsw$
and
![]() $-rsaw$
are squares in
$-rsaw$
are squares in
![]() $F$
, hence
$F$
, hence
![]() $a$
is a square in
$a$
is a square in
![]() $F$
.
$F$
.
Putting Steps 1 to 4 together, we have now proved that
![]() $a$
and
$a$
and
![]() $d$
are squares in
$d$
are squares in
![]() $F$
. Let us write
$F$
. Let us write
![]() $B=(B_{1},B_{2})$
and
$B=(B_{1},B_{2})$
and
![]() $C=(C_{1},C_{2})$
according to the decompositions
$C=(C_{1},C_{2})$
according to the decompositions
![]() $F_{a}=F\times F$
and
$F_{a}=F\times F$
and
![]() $F_{d}=F\times F$
induced by the choice of square roots of
$F_{d}=F\times F$
induced by the choice of square roots of
![]() $a$
and
$a$
and
![]() $d$
.
$d$
.
Step 5: we claim that
![]() $s=B_{i}$
and
$s=B_{i}$
and
![]() $r=C_{j}$
in
$r=C_{j}$
in
![]() $F^{\ast }/F^{\ast 2}$
for some
$F^{\ast }/F^{\ast 2}$
for some
![]() $i,j\in \{1,2\}$
.
$i,j\in \{1,2\}$
.
By symmetry, it suffices to check that
![]() $r=C_{j}$
in
$r=C_{j}$
in
![]() $F^{\ast }/F^{\ast 2}$
for some
$F^{\ast }/F^{\ast 2}$
for some
![]() $j\in \{1,2\}$
. To this end, as
$j\in \{1,2\}$
. To this end, as
![]() $C_{1}C_{2}=c$
, we may replace
$C_{1}C_{2}=c$
, we may replace
![]() $F$
with
$F$
with
![]() $F(\sqrt{c})$
and assume that
$F(\sqrt{c})$
and assume that
![]() $c$
is a square in
$c$
is a square in
![]() $F$
. In this case, Propositions A.4(3) and A.10(1) together imply the claim.
$F$
. In this case, Propositions A.4(3) and A.10(1) together imply the claim.
As the equality
![]() $(\unicode[STIX]{x1D6FD}B_{i},\unicode[STIX]{x1D6FE}C_{j})=0$
holds in
$(\unicode[STIX]{x1D6FD}B_{i},\unicode[STIX]{x1D6FE}C_{j})=0$
holds in
![]() $\text{Br}(F(X))$
by the very definition of
$\text{Br}(F(X))$
by the very definition of
![]() $X$
, Step 5 implies that
$X$
, Step 5 implies that
![]() $(\unicode[STIX]{x1D6FD},r)+(\unicode[STIX]{x1D6FE},s)+(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})=(B_{i},C_{j})$
, which does come from
$(\unicode[STIX]{x1D6FD},r)+(\unicode[STIX]{x1D6FE},s)+(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})=(B_{i},C_{j})$
, which does come from
![]() $\text{Br}(F)$
.◻
$\text{Br}(F)$
.◻
Proposition A.12. Let
![]() $r,s\in F^{\ast }$
be such that
$r,s\in F^{\ast }$
be such that
![]() $(\unicode[STIX]{x1D6FD},r)+(\unicode[STIX]{x1D6FE},s)\in \text{Br}_{\text{nr}}(F(X)/F)$
. Then at least one of the following holds:
$(\unicode[STIX]{x1D6FD},r)+(\unicode[STIX]{x1D6FE},s)\in \text{Br}_{\text{nr}}(F(X)/F)$
. Then at least one of the following holds:
(1)
 $r$
and
$r$
and
 $s$
are squares in
$s$
are squares in
 $F$
;
$F$
;(2)
 $rc$
and
$rc$
and
 $s$
are squares in
$s$
are squares in
 $F$
, at least one of
$F$
, at least one of
 $a$
,
$a$
,
 $c$
,
$c$
,
 $ad$
,
$ad$
,
 $cd$
is a square in
$cd$
is a square in
 $F$
, and at least one of
$F$
, and at least one of
 $a$
,
$a$
,
 $b$
,
$b$
,
 $c$
,
$c$
,
 $d$
,
$d$
,
 $abc$
is a square in
$abc$
is a square in
 $F$
;
$F$
;(3)
 $r$
and
$r$
and
 $sb$
are squares in
$sb$
are squares in
 $F$
, at least one of
$F$
, at least one of
 $b$
,
$b$
,
 $d$
,
$d$
,
 $ad$
,
$ad$
,
 $ab$
is a square in
$ab$
is a square in
 $F$
, and at least one of
$F$
, and at least one of
 $a$
,
$a$
,
 $b$
,
$b$
,
 $c$
,
$c$
,
 $d$
,
$d$
,
 $bcd$
is a square in
$bcd$
is a square in
 $F$
;
$F$
;(4)
 $rc$
and
$rc$
and
 $sb$
are squares in
$sb$
are squares in
 $F$
, at least one of
$F$
, at least one of
 $a$
,
$a$
,
 $c$
,
$c$
,
 $ad$
,
$ad$
,
 $cd$
is a square in
$cd$
is a square in
 $F$
, and at least one of
$F$
, and at least one of
 $b$
,
$b$
,
 $d$
,
$d$
,
 $ad$
,
$ad$
,
 $ab$
is a square in
$ab$
is a square in
 $F$
.
$F$
.
Proof. Extending the scalars from
![]() $F$
to
$F$
to
![]() $F(\sqrt{c})$
and applying Propositions A.4(1) and A.10(1) shows that
$F(\sqrt{c})$
and applying Propositions A.4(1) and A.10(1) shows that
![]() $r$
is a square in
$r$
is a square in
![]() $F(\sqrt{c})$
, hence at least one of
$F(\sqrt{c})$
, hence at least one of
![]() $r$
and
$r$
and
![]() $rc$
is a square in
$rc$
is a square in
![]() $F$
. By symmetry, at least one of
$F$
. By symmetry, at least one of
![]() $s$
and
$s$
and
![]() $sb$
is a square in
$sb$
is a square in
![]() $F$
. The following two assertions and the symmetric assertions will now imply the proposition:
$F$
. The following two assertions and the symmetric assertions will now imply the proposition:
(i) if
 $rc$
is a square in
$rc$
is a square in
 $F$
, then at least one of
$F$
, then at least one of
 $a$
,
$a$
,
 $c$
,
$c$
,
 $ad$
,
$ad$
,
 $cd$
is a square in
$cd$
is a square in
 $F$
;
$F$
;(ii) if
 $rc$
and
$rc$
and
 $s$
are squares in
$s$
are squares in
 $F$
, then at least one of
$F$
, then at least one of
 $a$
,
$a$
,
 $b$
,
$b$
,
 $c$
,
$c$
,
 $d$
,
$d$
,
 $abc$
is a square in
$abc$
is a square in
 $F$
.
$F$
.
To prove (i), we may replace
![]() $F$
with
$F$
with
![]() $F(\sqrt{ac},\sqrt{d})$
and assume that
$F(\sqrt{ac},\sqrt{d})$
and assume that
![]() $ac$
and
$ac$
and
![]() $d$
are squares in
$d$
are squares in
![]() $F$
. Propositions A.4(1) and A.10(1) then imply that
$F$
. Propositions A.4(1) and A.10(1) then imply that
![]() $r$
is a square in
$r$
is a square in
![]() $F$
; if
$F$
; if
![]() $rc$
is a square in
$rc$
is a square in
![]() $F$
, it follows that
$F$
, it follows that
![]() $c$
is a square in
$c$
is a square in
![]() $F$
, as desired. To prove (ii), we may assume, in view of (i), that
$F$
, as desired. To prove (ii), we may assume, in view of (i), that
![]() $ad$
or
$ad$
or
![]() $cd$
is a square in
$cd$
is a square in
![]() $F$
. We may then replace
$F$
. We may then replace
![]() $F$
with
$F$
with
![]() $F(\sqrt{ab},\sqrt{ac})$
and assume that
$F(\sqrt{ab},\sqrt{ac})$
and assume that
![]() $ab$
and
$ab$
and
![]() $ac$
are squares in
$ac$
are squares in
![]() $F$
. In this case, Propositions A.4(2) and A.10(2) imply that
$F$
. In this case, Propositions A.4(2) and A.10(2) imply that
![]() $c$
is a square in
$c$
is a square in
![]() $F$
.◻
$F$
.◻
Proposition A.13. If
![]() $a$
or
$a$
or
![]() $c$
is a square in
$c$
is a square in
![]() $F$
, then
$F$
, then
![]() $(\unicode[STIX]{x1D6FD},c)\in \text{Im}(\text{Br}(F)\rightarrow \text{Br}(F(X)))$
. If
$(\unicode[STIX]{x1D6FD},c)\in \text{Im}(\text{Br}(F)\rightarrow \text{Br}(F(X)))$
. If
![]() $b$
or
$b$
or
![]() $d$
is a square in
$d$
is a square in
![]() $F$
, then
$F$
, then
![]() $(\unicode[STIX]{x1D6FE},b)\in \text{Im}(\text{Br}(F)\rightarrow \text{Br}(F(X)))$
.
$(\unicode[STIX]{x1D6FE},b)\in \text{Im}(\text{Br}(F)\rightarrow \text{Br}(F(X)))$
.
Proof. By symmetry, we need only check the first assertion. If
![]() $c$
is a square, it is trivial. Let us assume that
$c$
is a square, it is trivial. Let us assume that
![]() $a$
is a square in
$a$
is a square in
![]() $F$
and write
$F$
and write
![]() $B=(B_{1},B_{2})$
according to the decomposition
$B=(B_{1},B_{2})$
according to the decomposition
![]() $F_{a}=F\times F$
induced by the choice of a square root of
$F_{a}=F\times F$
induced by the choice of a square root of
![]() $a$
. The vanishing of the class
$a$
. The vanishing of the class
![]() $(\unicode[STIX]{x1D6FD}B,\unicode[STIX]{x1D6FE}C)\in \text{Br}(F(X)\otimes _{F}F_{a,d})$
, which holds by the very definition of
$(\unicode[STIX]{x1D6FD}B,\unicode[STIX]{x1D6FE}C)\in \text{Br}(F(X)\otimes _{F}F_{a,d})$
, which holds by the very definition of
![]() $X$
, is then equivalent to that of the two classes
$X$
, is then equivalent to that of the two classes
![]() $(\unicode[STIX]{x1D6FD}B_{i},\unicode[STIX]{x1D6FE}C)\in \text{Br}(F(X)\otimes _{F}F_{d})$
,
$(\unicode[STIX]{x1D6FD}B_{i},\unicode[STIX]{x1D6FE}C)\in \text{Br}(F(X)\otimes _{F}F_{d})$
,
![]() $i\in \{1,2\}$
. Taking the norm down to
$i\in \{1,2\}$
. Taking the norm down to
![]() $F(X)$
and applying the projection formula, we deduce that
$F(X)$
and applying the projection formula, we deduce that
![]() $(\unicode[STIX]{x1D6FD}B_{i},c)=0$
in
$(\unicode[STIX]{x1D6FD}B_{i},c)=0$
in
![]() $\text{Br}(F(X))$
for
$\text{Br}(F(X))$
for
![]() $i\in \{1,2\}$
. Hence
$i\in \{1,2\}$
. Hence
![]() $(\unicode[STIX]{x1D6FD},c)=(B_{i},c)$
, which does come from
$(\unicode[STIX]{x1D6FD},c)=(B_{i},c)$
, which does come from
![]() $\text{Br}(F)$
.◻
$\text{Br}(F)$
.◻
Remark A.14. Proposition A.12 provides necessary conditions for the classes
![]() $(\unicode[STIX]{x1D6FD},c)$
,
$(\unicode[STIX]{x1D6FD},c)$
,
![]() $(\unicode[STIX]{x1D6FE},b)$
and
$(\unicode[STIX]{x1D6FE},b)$
and
![]() $(\unicode[STIX]{x1D6FD},c)+(\unicode[STIX]{x1D6FE},b)$
to belong to
$(\unicode[STIX]{x1D6FD},c)+(\unicode[STIX]{x1D6FE},b)$
to belong to
![]() $\text{Br}_{\text{nr}}(F(X)/F)$
. It is possible to show, although we do not do it here, that these necessary conditions are in fact necessary and sufficient.
$\text{Br}_{\text{nr}}(F(X)/F)$
. It is possible to show, although we do not do it here, that these necessary conditions are in fact necessary and sufficient.
Example A.15. Let
![]() $F=\mathbf{Q}$
,
$F=\mathbf{Q}$
,
![]() $a=d=34$
,
$a=d=34$
,
![]() $b=2$
,
$b=2$
,
![]() $c=17$
,
$c=17$
,
![]() $B=6+\sqrt{34}$
,
$B=6+\sqrt{34}$
,
![]() $C=(17+2\sqrt{34})/3$
. It is easy to see that
$C=(17+2\sqrt{34})/3$
. It is easy to see that
![]() $X$
has points everywhere locally. Using the fact that at every place of
$X$
has points everywhere locally. Using the fact that at every place of
![]() $\mathbf{Q}$
, at least one of
$\mathbf{Q}$
, at least one of
![]() $2$
,
$2$
,
![]() $17$
, and
$17$
, and
![]() $34$
is a square, one can check that for any place
$34$
is a square, one can check that for any place
![]() $v$
of
$v$
of
![]() $\mathbf{Q}$
other than
$\mathbf{Q}$
other than
![]() $17$
(respectively, for
$17$
(respectively, for
![]() $v=17$
), if
$v=17$
), if
![]() $\unicode[STIX]{x1D6FD}_{v}\in F_{v}^{\ast }$
denotes the
$\unicode[STIX]{x1D6FD}_{v}\in F_{v}^{\ast }$
denotes the
![]() $\unicode[STIX]{x1D6FD}$
coordinate of any
$\unicode[STIX]{x1D6FD}$
coordinate of any
![]() $\mathbf{Q}_{v}$
-point of
$\mathbf{Q}_{v}$
-point of
![]() $X$
, the Hilbert symbol
$X$
, the Hilbert symbol
![]() $(\unicode[STIX]{x1D6FD}_{v},17)$
is trivial (respectively, is non-trivial). Hence
$(\unicode[STIX]{x1D6FD}_{v},17)$
is trivial (respectively, is non-trivial). Hence
![]() $X(\mathbf{Q})=\varnothing$
. Thus, in this case, the three classes
$X(\mathbf{Q})=\varnothing$
. Thus, in this case, the three classes
![]() $(a,b),(b,c),(c,d)\in \text{Br}(\mathbf{Q})$
vanish, but the Massey product
$(a,b),(b,c),(c,d)\in \text{Br}(\mathbf{Q})$
vanish, but the Massey product
![]() $\langle a,b,c,d\rangle$
is not defined, by Theorems 5.6 and 6.1. By Theorem 6.2, for such an example to exist, it is necessary that at least one of
$\langle a,b,c,d\rangle$
is not defined, by Theorems 5.6 and 6.1. By Theorem 6.2, for such an example to exist, it is necessary that at least one of
![]() $ad$
,
$ad$
,
![]() $ab$
,
$ab$
,
![]() $cd$
is a square.
$cd$
is a square.