Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zhu, C.
2009.
n-Groupoids and Stacky Groupoids.
International Mathematics Research Notices,
Dolgushev, Vasiliy
Tamarkin, Dmitry
and
Tsygan, Boris
2009.
Formality Theorems for Hochschild Complexes and Their Applications.
Letters in Mathematical Physics,
Vol. 90,
Issue. 1-3,
p.
103.
Zhu, Chenchang
2009.
Kan Replacement of Simplicial Manifolds.
Letters in Mathematical Physics,
Vol. 90,
Issue. 1-3,
p.
383.
Fregier, Y.
and
Wagemann, F.
2010.
On Hopf 2-algebras.
International Mathematics Research Notices,
Douglas, C. L.
Henriques, A. G.
and
Hill, M. A.
2010.
Homological Obstructions to String Orientations.
International Mathematics Research Notices,
BUIJS, Urtzi
FÉLIX, Yves
and
MURILLO, Aniceto
2011.
L∞ models of based mapping spaces.
Journal of the Mathematical Society of Japan,
Vol. 63,
Issue. 2,
Redden, Corbett
2011.
String structures and canonical 3-forms.
Pacific Journal of Mathematics,
Vol. 249,
Issue. 2,
p.
447.
Sheng, Yunhe
Liu, Zhangju
and
Zhu, Chenchang
2011.
Omni-Lie 2-algebras and their Dirac structures.
Journal of Geometry and Physics,
Vol. 61,
Issue. 2,
p.
560.
Wockel, Christoph
2011.
Principal 2-bundles and their gauge 2-groups.
Forum Mathematicum,
Vol. 23,
Issue. 3,
JURČO, BRANISLAV
2011.
NONABELIAN BUNDLE 2-GERBES.
International Journal of Geometric Methods in Modern Physics,
Vol. 08,
Issue. 01,
p.
49.
Mehta, Rajan Amit
and
Tang, Xiang
2011.
From double Lie groupoids to local Lie 2-groupoids.
Bulletin of the Brazilian Mathematical Society, New Series,
Vol. 42,
Issue. 4,
p.
651.
JURČO, BRANISLAV
2011.
CROSSED MODULE BUNDLE GERBES; CLASSIFICATION, STRING GROUP AND DIFFERENTIAL GEOMETRY.
International Journal of Geometric Methods in Modern Physics,
Vol. 08,
Issue. 05,
p.
1079.
Wockel, Christoph
2011.
Categorified central extensions, étale Lie 2-groups and Lieʼs Third Theorem for locally exponential Lie algebras.
Advances in Mathematics,
Vol. 228,
Issue. 4,
p.
2218.
Sheng, Yunhe
and
Zhu, Chenchang
2011.
Semidirect products of representations up to homotopy.
Pacific Journal of Mathematics,
Vol. 249,
Issue. 1,
p.
211.
SHENG, YUNHE
and
ZHU, CHENCHANG
2012.
INTEGRATION OF SEMIDIRECT PRODUCT LIE 2-ALGEBRAS.
International Journal of Geometric Methods in Modern Physics,
Vol. 09,
Issue. 05,
p.
1250043.
Sati, Hisham
Schreiber, Urs
and
Stasheff, Jim
2012.
Twisted Differential String and Fivebrane Structures.
Communications in Mathematical Physics,
Vol. 315,
Issue. 1,
p.
169.
Mylonas, Dionysios
Schupp, Peter
and
Szabo, Richard J.
2012.
Membrane sigma-models and quantization of non-geometric flux backgrounds.
Journal of High Energy Physics,
Vol. 2012,
Issue. 9,
Trentinaglia, Giorgio
and
Zhu, Chenchang
2012.
Strictification of étale stacky Lie groups.
Compositio Mathematica,
Vol. 148,
Issue. 3,
p.
807.
Ševera, Pavol
and
Li-Bland, David
2012.
Integration of exact Courant algebroids.
Electronic Research Announcements in Mathematical Sciences,
Vol. 19,
Issue. 0,
p.
58.
Jurčo, Branislav
2012.
From simplicial Lie algebras and hypercrossed complexes to differential graded Lie algebras via 1-jets.
Journal of Geometry and Physics,
Vol. 62,
Issue. 12,
p.
2389.
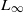 -algebras
-algebras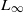 -algebras. When applied to an ordinary Lie algebra, our construction yields the simplicial classifying space of the corresponding simply connected Lie group. In the case of the string Lie 2-algebra of Baez and Crans, we obtain the simplicial nerve of their model of the string group.
-algebras. When applied to an ordinary Lie algebra, our construction yields the simplicial classifying space of the corresponding simply connected Lie group. In the case of the string Lie 2-algebra of Baez and Crans, we obtain the simplicial nerve of their model of the string group.

