Article contents
JASMIN-based Two-dimensional Adaptive Combined Preconditioner for Radiation Diffusion Equations in Inertial Fusion Research
Published online by Cambridge University Press: 07 September 2017
Abstract
We present a JASMIN-based two-dimensional parallel implementation of an adaptive combined preconditioner 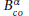 for the solution of linear problems arising in the finite volume discretisation of one-group and multi-group radiation diffusion equations. We first propose the attribute of patch-correlation for cells of a two-dimensional monolayer piecewise rectangular structured grid without any suspensions based on the patch hierarchy of JASMIN, classify and reorder these cells via their attributes, and derive the conversion of cell-permutations. Using two cell-permutations, we then construct some parallel incomplete LU factorisation and substitution algorithms, to provide our parallel
for the solution of linear problems arising in the finite volume discretisation of one-group and multi-group radiation diffusion equations. We first propose the attribute of patch-correlation for cells of a two-dimensional monolayer piecewise rectangular structured grid without any suspensions based on the patch hierarchy of JASMIN, classify and reorder these cells via their attributes, and derive the conversion of cell-permutations. Using two cell-permutations, we then construct some parallel incomplete LU factorisation and substitution algorithms, to provide our parallel 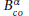 -GMRES solver with the help of the default BoomerAMG in the HYPRE library. Numerical results demonstrate that our proposed parallel incomplete LU preconditioner (ILU) is of higher efficiency than the counterpart in the Euclid library, and that the proposed parallel
-GMRES solver with the help of the default BoomerAMG in the HYPRE library. Numerical results demonstrate that our proposed parallel incomplete LU preconditioner (ILU) is of higher efficiency than the counterpart in the Euclid library, and that the proposed parallel 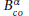 -GMRES solver is more robust and more efficient than the default BoomerAMG-GMRES solver.
-GMRES solver is more robust and more efficient than the default BoomerAMG-GMRES solver.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Global-Science Press 2017
References
- 2
- Cited by

