Time parallelization, also known as PinT (parallel-in-time), is a new research direction for the development of algorithms used for solving very large-scale evolution problems on highly parallel computing architectures. Despite the fact that interesting theoretical work on PinT appeared as early as 1964, it was not until 2004, when processor clock speeds reached their physical limit, that research in PinT took off. A distinctive characteristic of parallelization in time is that information flow only goes forward in time, meaning that time evolution processes seem necessarily to be sequential. Nevertheless, many algorithms have been developed for PinT computations over the past two decades, and they are often grouped into four basic classes according to how the techniques work and are used: shooting-type methods; waveform relaxation methods based on domain decomposition; multigrid methods in space–time; and direct time parallel methods. However, over the past few years, it has been recognized that highly successful PinT algorithms for parabolic problems struggle when applied to hyperbolic problems. We will therefore focus on this important aspect, first by providing a summary of the fundamental differences between parabolic and hyperbolic problems for time parallelization. We then group PinT algorithms into two basic groups. The first group contains four effective PinT techniques for hyperbolic problems: Schwarz waveform relaxation (SWR) with its relation to tent pitching; parallel integral deferred correction; ParaExp; and ParaDiag. While the methods in the first group also work well for parabolic problems, we then present PinT methods specifically designed for parabolic problems in the second group: Parareal; the parallel full approximation scheme in space–time (PFASST); multigrid reduction in time (MGRiT); and space–time multigrid (STMG). We complement our analysis with numerical illustrations using four time-dependent PDEs: the heat equation; the advection–diffusion equation; Burgers’ equation; and the second-order wave equation.

Floating-point numbers have an intuitive meaning when it comes to physics-based numerical computations, and they have thus become the most common way of approximating real numbers in computers. The IEEE-754 Standard has played a large part in making floating-point arithmetic ubiquitous today, by specifying its semantics in a strict yet useful way as early as 1985. In particular, floating-point operations should be performed as if their results were first computed with an infinite precision and then rounded to the target format. A consequence is that floating-point arithmetic satisfies the ‘standard model’ that is often used for analysing the accuracy of floating-point algorithms. But that is only scraping the surface, and floating-point arithmetic offers much more.

In this survey we recall the history of floating-point arithmetic as well as its specification mandated by the IEEE-754 Standard. We also recall what properties it entails and what every programmer should know when designing a floating-point algorithm. We provide various basic blocks that can be implemented with floating-point arithmetic. In particular, one can actually compute the rounding error caused by some floating-point operations, which paves the way to designing more accurate algorithms. More generally, properties of floating-point arithmetic make it possible to extend the accuracy of computations beyond working precision.

Low-rank tensor representations can provide highly compressed approximations of functions. These concepts, which essentially amount to generalizations of classical techniques of separation of variables, have proved to be particularly fruitful for functions of many variables. We focus here on problems where the target function is given only implicitly as the solution of a partial differential equation. A first natural question is under which conditions we should expect such solutions to be efficiently approximated in low-rank form. Due to the highly nonlinear nature of the resulting low-rank approximations, a crucial second question is at what expense such approximations can be computed in practice. This article surveys basic construction principles of numerical methods based on low-rank representations as well as the analysis of their convergence and computational complexity.

This work studies the average complexity of solving structured polynomial systems that are characterised by a low evaluation cost, as opposed to the dense random model previously used. Firstly, we design a continuation algorithm that computes, with high probability, an approximate zero of a polynomial system given only as black-box evaluation program. Secondly, we introduce a universal model of random polynomial systems with prescribed evaluation complexity L. Combining both, we show that we can compute an approximate zero of a random structured polynomial system with n equations of degree at most ${D}$ in n variables with only $\operatorname {poly}(n, {D}) L$ operations with high probability. This exceeds the expectations implicit in Smale’s 17th problem.

In numerical linear algebra, a well-established practice is to choose a norm that exploits the structure of the problem at hand to optimise accuracy or computational complexity. In numerical polynomial algebra, a single norm (attributed to Weyl) dominates the literature. This article initiates the use of $L_p$ norms for numerical algebraic geometry, with an emphasis on $L_{\infty }$. This classical idea yields strong improvements in the analysis of the number of steps performed by numerous iterative algorithms. In particular, we exhibit three algorithms where, despite the complexity of computing $L_{\infty }$-norm, the use of $L_p$-norms substantially reduces computational complexity: a subdivision-based algorithm in real algebraic geometry for computing the homology of semialgebraic sets, a well-known meshing algorithm in computational geometry and the computation of zeros of systems of complex quadratic polynomials (a particular case of Smale’s 17th problem).

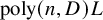
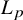
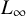
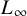
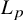
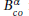We present a JASMIN-based two-dimensional parallel implementation of an adaptive combined preconditioner for the solution of linear problems arising in the finite volume discretisation of one-group and multi-group radiation diffusion equations. We first propose the attribute of patch-correlation for cells of a two-dimensional monolayer piecewise rectangular structured grid without any suspensions based on the patch hierarchy of JASMIN, classify and reorder these cells via their attributes, and derive the conversion of cell-permutations. Using two cell-permutations, we then construct some parallel incomplete LU factorisation and substitution algorithms, to provide our parallel -GMRES solver with the help of the default BoomerAMG in the HYPRE library. Numerical results demonstrate that our proposed parallel incomplete LU preconditioner (ILU) is of higher efficiency than the counterpart in the Euclid library, and that the proposed parallel -GMRES solver is more robust and more efficient than the default BoomerAMG-GMRES solver.

This paper presents a GPU-accelerated implementation of the Locally Optimal Block Preconditioned Conjugate Gradient (LOBPCG) method with an inexact nullspace filtering approach to find eigenvalues in electromagnetics analysis with higher-order FEM. The performance of the proposed approach is verified using the Kepler (Tesla K40c) graphics accelerator, and is compared to the performance of the implementation based on functions from the Intel MKL on the Intel Xeon (E5-2680 v3, 12 threads) central processing unit (CPU) executed in parallel mode. Compared to the CPU reference implementation based on the Intel MKL functions, the proposed GPU-based LOBPCG method with inexact nullspace filtering allowed us to achieve up to 2.9-fold acceleration.

In this paper, we study an exponential time differencing method for solving the gauge system of incompressible viscous flows governed by Stokes or Navier-Stokes equations. The momentum equation is decoupled from the kinematic equation at a discrete level and is then solved by exponential time stepping multistep schemes in our approach. We analyze the stability of the proposed method and rigorously prove that the first order exponential time differencing scheme is unconditionally stable for the Stokes problem. We also present a compact representation of the algorithm for problems on rectangular domains, which makes FFT-based solvers available for the resulting fully discretized system. Various numerical experiments in two and three dimensional spaces are carried out to demonstrate the accuracy and stability of the proposed method.

In many applications, the Gaussian convolution is approximately computed by means of recursive filters, with a significant improvement of computational efficiency. We are interested in theoretical and numerical issues related to such an use of recursive filters in a three-dimensional variational data assimilation (3Dvar) scheme as it appears in the software OceanVar. In that context, the main numerical problem consists in solving large linear systems with high efficiency, so that an iterative solver, namely the conjugate gradient method, is equipped with a recursive filter in order to compute matrix-vector multiplications that in fact are Gaussian convolutions. Here we present an error analysis that gives effective bounds for the perturbation on the solution of such linear systems, when is computed by means of recursive filters. We first prove that such a solution can be seen as the exact solution of a perturbed linear system. Then we study the related perturbation on the solution and we demonstrate that it can be bounded in terms of the difference between the two linear operators associated to the Gaussian convolution and the recursive filter, respectively. Moreover, we show through numerical experiments that the error on the solution, which exhibits a kind of edge effect, i.e. most of the error is localized in the first and last few entries of the computed solution, is due to the structure of the difference of the two linear operators.

We construct modulus-based synchronous multisplitting iteration methods to solve a large implicit complementarity problem on parallel multiprocessor systems, and prove their convergence. Numerical results confirm our theoretical analysis and show that these new methods are efficient.

An idea of designing oscillation-less and high-resolution hybrid schemes is proposed and several types of hybrid schemes based on this idea are presented on block-structured grids. The general framework, for designing various types of hybrid schemes, is established using a Multi-dimensional Optimal Order Detection (MOOD) method proposed by Clain, Diot and Loubère [1]. The methodology utilizes low dissipation or dispersion but less robust schemes to update the solution and then implements robust and high resolution schemes to deal with problematic situations. A wide range of computational methods including central scheme, MUSCL scheme, linear upwind scheme and Weighted Essentially Non Oscillatory (WENO) scheme have been applied in the current hybrid schemes framework. Detailed numerical studies on classical test cases for the Euler system are performed, addressing the issues of the resolution and non-oscillatory property around the discontinuities.

In this study an explicit Finite Difference Method (FDM) based scheme is developed to solve the Maxwell's equations in time domain for a lossless medium. This manuscript focuses on two unique aspects – the three dimensional time-accurate discretization of the hyperbolic system of Maxwell equations in three-point non-staggered grid stencil and it's application to parallel computing through the use of Graphics Processing Units (GPU). The proposed temporal scheme is symplectic, thus permitting conservation of all Hamiltonians in the Maxwell equation. Moreover, to enable accurate predictions over large time frames, a phase velocity preserving scheme is developed for treatment of the spatial derivative terms. As a result, the chosen time increment and grid spacing can be optimally coupled. An additional theoretical investigation into this pairing is also shown. Finally, the application of the proposed scheme to parallel computing using one Nvidia K20 Tesla GPU card is demonstrated. For the benchmarks performed, the parallel speedup when compared to a single core of an Intel i7-4820K CPU is approximately 190x.

In this paper we develop explicit fast exponential Runge-Kutta methods for the numerical solutions of a class of parabolic equations. By incorporating the linear splitting technique into the explicit exponential Runge-Kutta schemes, we are able to greatly improve the numerical stability. The proposed numerical methods could be fast implemented through use of decompositions of compact spatial difference operators on a regular mesh together with discrete fast Fourier transform techniques. The exponential Runge-Kutta schemes are easy to be adopted in adaptive temporal approximations with variable time step sizes, as well as applied to stiff nonlinearity and boundary conditions of different types. Linear stabilities of the proposed schemes and their comparison with other schemes are presented. We also numerically demonstrate accuracy, stability and robustness of the proposed method through some typical model problems.

As an exploratory study for structural deformation and thermodynamic response induced by spacecraft reentry aerodynamic force and thermal environment, a finite element algorithm is presented on the basis of the classic Fourier heat conductive law to simulate the dynamic thermoelasticity coupling performance of the material. The Newmark method and Crank-Nicolson scheme are utilized to discretize the dynamic thermoelasticity equation and heat conductive equation in the time domain, respectively, and the unconditionally stable implicit algorithm is constructed. Four types of finite-element computing schemes are devised and discussed to solve the thermodynamic coupling equation, all of which are implemented and compared in the computational examples including the one-dimensional transient heat conduction in considering and not considering the vibration, the transient heat flow for the infinite cylinder, and the dynamic coupling thermoelasticity around re-entry flat plate from hypersonic aerothermodynamic environment. The computational results show that the transient responses of temperature and displacement field generate lag phenomenon in case of considering the deformation effect on temperature field. Propagation, rebounding, attenuation and stabilized phenomena of elastic wave are also observed by the finite-element calculation of thermodynamic coupling problem considering vibration and damping, and the oscillation of the temperature field is simultaneously induced. As a result, the computational method and its application research platform have been founded to solve the transient thermodynamic coupling response problem of the structure in strong aerodynamic heating and force environment. By comparing various coupling calculations, it is demonstrated that the present algorithm could give a correct and reliable description of transient thermodynamic responses of structure, the rationality of the sequentially coupling method in engineering calculation is discussed, and the bending deformation mechanism produced by the thermodynamic coupling response from windward and leeward sides of flying body is revealed, which lays the foundation in developing the numerical method to solve material internal temperature distribution, structural deformation, and thermal damage induced by spacecraft dynamic thermoelasticity coupling response under uncontrolled reentry aerothermodynamic condition.

Computational scientists generally seek more accurate results in shorter times, and to achieve this a knowledge of evolving programming paradigms and hardware is important. In particular, optimising solvers for linear systems is a major challenge in scientific computation, and numerical algorithms must be modified or new ones created to fully use the parallel architecture of new computers. Parallel space discretisation solvers for Partial Differential Equations (PDE) such as Domain Decomposition Methods (DDM) are efficient and well documented. At first glance, parallelisation seems to be inconsistent with inherently sequential time evolution, but parallelisation is not limited to space directions. In this article, we present a new and simple method for time parallelisation, based on partial fraction decomposition of the inverse of some special matrices. We discuss its application to the heat equation and some limitations, in associated numerical experiments.

In this work, two approaches, based on the certified Reduced Basis method, have been developed for simulating the movement of nuclear reactor control rods, in time-dependent non-coercive settings featuring a 3D geometrical framework. In particular, in a first approach, a piece-wise affine transformation based on subdomains division has been implemented for modelling the movement of one control rod. In the second approach, a “staircase” strategy has been adopted for simulating the movement of all the three rods featured by the nuclear reactor chosen as case study. The neutron kinetics has been modelled according to the so-called multi-group neutron diffusion, which, in the present case, is a set of ten coupled parametrized parabolic equations (two energy groups for the neutron flux, and eight for the precursors). Both the reduced order models, developed according to the two approaches, provided a very good accuracy compared with high-fidelity results, assumed as “truth” solutions. At the same time, the computational speed-up in the Online phase, with respect to the fine “truth” finite element discretization, achievable by both the proposed approaches is at least of three orders of magnitude, allowing a real-time simulation of the rod movement and control.

The unified lattice Boltzmann model is extended to the quadtree grids for simulation of fluid flow through porous media. The unified lattice Boltzmann model is capable of simulating flow in porous media at various scales or in systems where multiple length scales coexist. The quadtree grid is able to provide a high-resolution approximation to complex geometries, with great flexibility to control local grid density. The combination of the unified lattice Boltzmann model and the quadtree grids results in an efficient numerical model for calculating permeability of multi-scale porous media. The model is used for permeability calculation for three systems, including a fractured system used in a previous study, a Voronoi tessellation system, and a computationally-generated pore structure of fractured shale. The results are compared with those obtained using the conventional lattice Boltzmann model or the unified lattice Boltzmann model on rectangular or uniform square grid. It is shown that the proposed model is an accurate and efficient tool for flow simulation in multi-scale porous media. In addition, for the fractured shale, the contribution of flow in matrix and fractures to the overall permeability of the fractured shale is studied systematically.

Mesh generation is a bottleneck for finite element simulations of biomolecules. A robust and efficient approach, based on the immersed boundary method proposed in [8], has been developed and implemented to generate large-scale mesh body-fitted to molecular shape for general parallel finite element simulations. The molecular Gaussian surface is adopted to represent the molecular surface, and is finally approximated by piecewise planes via the tool phgSurfaceCut in PHG [43], which is improved and can reliably handle complicated molecular surfaces, through mesh refinement steps. A coarse background mesh is imported first and then is distributed into each process using a mesh partitioning algorithm such as space filling curve [5] or METIS [22]. A bisection method is used for the mesh refinements according to the molecular PDB or PQR file which describes the biomolecular region. After mesh refinements, the mesh is optionally repartitioned and redistributed for load balancing. For finite element simulations, the modification of region mark and boundary types is done in parallel. Our parallel mesh generation method has been successfully applied to a sphere cavity model, a DNA fragment, a gramicidin A channel and a huge Dengue virus system. The results of numerical experiments show good parallel efficiency. Computations of electrostatic potential and solvation energy also validate the method. Moreover, the meshing process and adaptive finite element computation can be integrated as one PHG project to avoid the mesh importing and exporting costs, and improve the convenience of application as well.

Simulation of turbulent flows with shocks employing subgrid-scale (SGS) filtering may encounter a loss of accuracy in the vicinity of a shock. This paper addresses the accuracy improvement of LES of turbulent flows in two ways: (a) from the SGS model standpoint and (b) from the numerical method improvement standpoint. In an internal report, Kotov et al. ( “High Order Numerical Methods for large eddy simulation (LES) of Turbulent Flows with Shocks”, CTR Tech Brief, Oct. 2014, Stanford University), we performed a preliminary comparative study of different approaches to reduce the loss of accuracy within the framework of the dynamic Germano SGS model. The high order low dissipative method of Yee & Sjögreen (2009) using local flow sensors to control the amount of numerical dissipation where needed is used for the LES simulation. The considered improved dynamics model approaches include applying the one-sided SGS test filter of Sagaut & Germano (2005) and/or disabling the SGS terms at the shock location. For Mach 1.5 and 3 canonical shock-turbulence interaction problems, both of these approaches show a similar accuracy improvement to that of the full use of the SGS terms. The present study focuses on a five levels of grid refinement study to obtain the reference direct numerical simulation (DNS) solution for additional LES SGS comparison and approaches. One of the numerical accuracy improvements included here applies Harten's subcell resolution procedure to locate and sharpen the shock, and uses a one-sided test filter at the grid points adjacent to the exact shock location.