1. Introduction
Climate scientists broadly agree that the global climate is changing and that these changes will accelerate in coming decades (Christensen and Hewitson, Reference Christensen, Hewitson, Solomon, Qin, Manning, Chen, Merquis, Areryt, Tignor and Miller2007). However, estimates of the economic impacts of climate change vary widely, in large part due to uncertainty about adaptation (Mendelsohn et al., Reference Mendelsohn, Nordhaus and Shaw1994; Adams et al., Reference Adams, Hurd, Lenhart and Leary1998; Schlenker et al., Reference Schlenker, Hanemann and Fisher2005; Deschênes and Greenstone et al., Reference Deschênes and Greenstone2007; Schlenker and Roberts, Reference Schlenker and Roberts2009; Tol, Reference Tol2014). Rapid adaptation may curb economic damages, but slower adaptation will likely magnify them. Understanding adaptation is particularly crucial in developing countries and in the agricultural sector, as both are especially vulnerable to climate change (Parry, Reference Parry2007).
Recent scholarship has typically estimated climate change damages using year-to-year weather variation to compare economic outcomes under hotter versus cooler temperatures. This climate–economy relationship is then extrapolated to future climate change to estimate impacts (Deschênes and Greenstone et al., Reference Deschênes and Greenstone2007; Guiteras, Reference Guiteras2009; Schlenker and Roberts, Reference Schlenker and Roberts2009; Dell et al., Reference Dell, Jones and Olken2012; Burgess et al., Reference Burgess, Deschênes, Donaldson and Greenstone2014).Footnote 1 Since these calculations rely on annual weather variability, they do not account for possible adaptations that agents may undertake in response to sustained climate change. Therefore, to assess the accuracy of these estimates, it is vital to predict the likely extent of future adaptation.
In this paper, we exploit historical rainfall variation in India to estimate adaptation. Rather than analyzing year-to-year weather deviations, we focus on climate fluctuations that last several decades. The Indian monsoon undergoes multidecadal phases during which droughts or floods are more common. These monsoon phases induce persistent deviations in rainfall from decade to decade. We test whether farmers adapt their irrigation investments and crop portfolios in response to these persistent rainfall deviations. The monsoon regimes do not cause variation in temperature, so we do not analyze adaptation to temperature changes.
Figure 1 shows a moving average of India's summer rainfall, highlighting the monsoon phases. These phases induce persistent rainfall deviations and, hence, lagged rainfall provides information about future rainfall. Therefore, forward-looking farmers should adjust their agricultural decisions in response to recent weather.

Figure 1. Interdecadal variability of the Indian monsoon
Notes: This figure displays the 31-year moving average of India's summer monsoon rainfall, measured as a z-score deviation from the historical mean.
Source: The rainfall data are from the India Institute of Tropical Meteorology's Homogeneous Indian Monthly Rainfall Data Set (1871–2008). The figure is constructed based on the author's calculations.
Adaptation is tested for by analyzing whether agricultural decisions respond to lagged weather, looking specifically at irrigation investments and crop choice. We exploit the fact that the return to irrigation investment varies across wet versus dry growing seasons and that, similarly, the relative yields of different crops vary across wet versus dry growing seasons. The empirical strategy here is to regress irrigation assets and crop portfolios on rainfall from the past decade, while controlling for current rainfall, wealth, household fixed effects and year fixed effects. Regional variation in the timing of the decadal rainfall regimes, displayed in figure 2, allows for the inclusion of year fixed effects in the regressions and, hence, adaptation to rainfall can be separated from unrelated temporal changes in irrigation and crop choice.
Analyzing two agricultural data sets, evidence is found of both irrigation adaptation and crop adaptation. Each additional dry year in the past decade increases the probability that a farmer will invest in irrigation by 1.2 percentage points, relative to a baseline 5 per cent probability of investing.Footnote 2 Each additional dry year in the past decade reduces the average daily water need of a farmer's monsoon season crop portfolio by 0.2 mm/day, relative to an average water need of 8 mm/day.Footnote 3 In addition to testing for the presence of adaptation, the extent to which adaptation prevents profit losses is also measured. It is found that farmers are able to recover only a limited amount of their lost profits by adapting. Specifically, it is estimated that in the face of sustained adverse weather conditions, adaptation recovers no more than 9 per cent of lost profits.
In addition to contributing to the literature on climate change and agriculture in India (Guiteras, Reference Guiteras2009; Krishnamurthy, Reference Krishnamurthy2012; Fishman, Reference Fishman2016), this paper contributes to a rapidly growing literature on climate change adaptation. Dell et al., Reference Dell, Jones and Olken2014 present a helpful synthesis of this literature. Researchers have used a variety of techniques to identify the magnitude and efficacy of adaptation, including the Ricardian method or hedonic valuation method (Mendelsohn et al., Reference Mendelsohn, Nordhaus and Shaw1994; Fleischer et al., Reference Fleischer, Lichtman and Mendelsohn2008; Seo et al., Reference Seo, McCarl, McCarl and Mendelsohn2010; Kurukulasuriya et al., Reference Kurukulasuriya, Kala and Mendelsohn2011; da Cunha et al., Reference da Cunha, Coelho and Féres2014) and variants of the Ricardian method that incorporate panel data (Luis and Orlando, Reference Luis and Orlando2015) and structural agro-economic models (Kurukulasuriya and Mendelsohn, Reference Kurukulasuriya and Mendelsohn2008). Researchers have also analyzed adaptation by looking at long-run responses to one-time environmental shocks (Hornbeck, Reference Hornbeck2012; Deryugina, Reference Deryugina2013; Hornbeck and Naidu, Reference Hornbeck and Naidu2015), applying instrumental variables approaches that address the endogeneity of adaptation (Di Falco and Veronesi, Reference Di Falco and Veronesi2013; Di Falco and Veronesi, Reference Di Falco and Veronesi2014), using economic models that integrate biophysical modeling (Finger et al. Reference Finger, Hediger and Schmid2010), employing multinomial logit choice models (Seo and Mendelsohn, Reference Seo and Mendelsohn2008; Wang et al., Reference Wang, Mendelsohn and Dinar2010), testing whether new technologies have changed weather impacts over time (Barreca et al. Reference Barreca, Clay, Deschênes, Greenstone and Shapiro2015), analyzing differential weather impacts by the long-run frequency of the event (Deschênes and Greenstone, Reference Deschênes and Greenstone2011; Hsiang and Narita, Reference Hsiang and Narita2012), estimating correlations between farmer behavior and their perceptions of changes in climate (Bryan et al., Reference Bryan, Deressa, Gbetibouo and Ringler2009), and, lastly, using a ‘long-difference’ approach that compares short-run weather impacts with long-run impacts (Dell et al., Reference Dell, Jones and Olken2012; Burke and Emerick, Reference Burke and Emerick2016).
This paper contributes to the adaptation literature in multiple ways. First, this study is unique because it uses a household data set that spans several decades. The existing literature on adaptation uses either administrative data (Dell et al., Reference Dell, Jones and Olken2012), cross-sectional household data (Bryan et al., Reference Bryan, Deressa, Gbetibouo and Ringler2009; Mukherjee and Schwabe, Reference Mukherjee and Schwabe2015), or a short panel of household data that spans less than 10 years (Luis and Orlando, Reference Luis and Orlando2015). This paper is also unique because it estimates adaptation to large-scale, cyclical, decadal variation in climate that exhibits both spatial and temporal variation. The bulk of the existing literature on adaptation exploits either cross-sectional (spatial) variation in climate, a one-time shock to climate, or perceived changes in climate that are measured at a single point in time.
The unique data set and source of climate variation lead to a methodological contribution to the literature. Specifically, we can estimate how farmers adapt to medium-run (10–20 year) changes in climate that are occurring over the span of our data set, while controlling for unobserved heterogeneity. Put differently, the data allow us to look at how the behavior of a household changes across several decades, in response to time-varying changes in climate. The estimates of decade-to-decade adaptation are an important complement to the long-run adaptation estimates that are generated by methods that rely on purely spatial climate variation.Footnote 4 Conversely, the estimates in this study are also a complement to studies that estimate how farmers respond to recent perceived changes in climate. Typically, these studies use cross-sectional household data and focus only on behavior and climate perceptions from the past 10–20 years. The multidecadal household panel used in this paper, on the other hand, allows us to control for unobserved farmer heterogeneity and to analyze adaptation over several decades. In addition, a model is built that allows us to disentangle the effects of wealth and expectations. This is a methodological contribution because it allows us to test directly whether farmers are updating their beliefs about future rainfall in response to past rainfall, even in the absence of explicit data on farmers’ perceptions about climate change.
Several important limitations of this study should be acknowledged. First, this study only analyzes irrigation and crop choice. Data limitations do not permit the study of other potential adaptations, such as adjusting fertilizer and agricultural inputs (Duflo et al., Reference Duflo, Kremer and Robinson2011), shifting sowing dates (Giné et al., Reference Giné, Townsend and Vickery2009), purchasing crop insurance (Di Falco et al., Reference Di Falco, Adinolfi, Bozzola and Capitanio2014), switching out of agriculture (Rose, Reference Rose2001), or migrating (Fishman, Reference Fishman2015; Viswanathan and Kavi Kumar, Reference Viswanathan and Kavi Kumar2015). Secondly, since the monsoon regimes affect only precipitation, adaptation to temperature changes is not analyzed. Thirdly, since the household data set spans several decades, there is substantial, non-random attrition, which causes the analyzed sample to include households that are, on average, wealthier than a representative sample would be. Fourthly, there are potential threats to the exclusion restriction for the instrumental variables strategy, which are discussed in greater detail in section 5. Fifthly, due to data limitations, we are not fully able to rule out the possibility that depletion of water supplies or confounding factors, such as changes in agricultural technology or policies, are driving the results.
The paper is organized as follows. Section 2 describes the monsoon phases in greater detail. Section 3 presents a model of climate, irrigation, and crop choice. Section 4 describes the data, and section 5 proposes the empirical strategy. Section 6 presents the main results. Section 7 discusses several robustness tests that were performed and which are reported in an online appendix, available at https://doi.org/10.1017/ S1355770X17000195. Section 8 calculates the fraction of lost profits farmers recovered by adapting, and section 9 concludes.
2. Background on interdecadal rainfall variability
Indian agriculture depends heavily on the summer monsoon, which occurs during June, July, August and September (Krishna Kumar et al., Reference Krishna Kumar, Rupa Kumar, Ashrit, Deshpande and Hansen2004). Because India's climate is semi-arid, wetter monsoons increase agricultural output, and drier monsoons decrease it (Das, Reference Das1995; Jayachandran, Reference Jayachandran2006). Monsoon rainfall exhibits high interannual variability, as shown in figure A1 of online appendix 1. The monsoon also undergoes interdecadal variability, in the form of wet and dry phases that typically each last for about three decades (Pant and Kumar, Reference Pant and Kumar1997). Figure 1 in the main text smoothes national, annual rainfall with a moving average filter, to highlight the regimes.
The monsoon regimes cause average rainfall to vary more from decade to decade than it would if rainfall was independent and identically distributed (i.i.d.), as discussed in greater detail in online appendix 1. This persistent decadal variation means that lagged rainfall has predictive value for future rainfall. If rainfall were i.i.d., then lagged rainfall would not have this predictive element. Rational farmers should notice these persistent rainfall variations and update their future rainfall expectations in response. This updating could occur even if farmers were not aware of the existence of the monsoon regimes, per se. On the other hand, if rainfall were i.i.d., lagged rainfall would have no predictive value, and it would be irrational for farmers to update their rainfall expectations in response to it. The statistical significance of the decadal variations allows us to interpret a farmer's response to lagged rainfall as evidence of rational adaptation, rather than as an indicator of irrational behavior.Footnote 5
The monsoon regimes are not geographically homogeneous. There is significant spatial variation in the length and timing of the regimes (Subbaramayya and Naidu, Reference Subbaramayya and Naidu1992). In particular, rainfall in the southern peninsula and the easternmost region tends to be out of phase with the rest of the country (Wang, Reference Wang2006). Figure 2 displays smoothed rainfall graphs for India's five meteorological regions, highlighting the spatial variation. Providing more detail, online appendix 4 presents maps of district rainfall from the previous decade, for the three survey years of the REDS data set and at four decade intervals for the WB data set. We choose rainfall from the previous decade as a rough measure of the current monsoon regime (Kripalani and Kulkarni, Reference Kripalani and Kulkarni1997). The spatial variation in recent rainfall allows us to include year fixed effects in the regressions and, hence, distinguish rainfall adaptation from time trends in irrigation and crop choice.

Figure 2. Spatial variation of the interdecadal variability of the Indian monsoon
Notes: This figure graphs the 31-year moving average of the summer monsoon rainfall, measured in millimeters for India's five meteorological regions. The horizontal line represents mean rainfall for that region.
Source: The rainfall data are from the India Institute of Tropical Meteorology's Homogeneous Indian Monthly Rainfall Data Set (1871–2008). The figure is constructed based on the author's calculations.
3. Theoretical framework
We present climate and agricultural models and derive tests for adaptation.
3.1. Climate model
We model the monsoon regimes as a hidden Markov process. Let s t indicate the monsoon regime in year t, with s t =0 denoting a dry regime and s t =1 denoting a wet regime. Year t rainfall can be written as:
where θ0 is the average rainfall during a dry regime,
![]() $\theta_{0} + \delta$
is the average wet regime rainfall, and u
t
represents year-to-year rainfall variability. The monsoon regimes are persistent but not permanent, and they switch according to a Markov process. During a dry regime, the probability of switching to a wet regime during the next period is p
0. During a wet regime, the probability of switching to a dry regime is p
1. Each year, farmers observe r
t
and use this information to update their belief about the current regime state, which they do not observe. A farmer's belief about the current regime state determines his expectation of the next period's rainfall.
$\theta_{0} + \delta$
is the average wet regime rainfall, and u
t
represents year-to-year rainfall variability. The monsoon regimes are persistent but not permanent, and they switch according to a Markov process. During a dry regime, the probability of switching to a wet regime during the next period is p
0. During a wet regime, the probability of switching to a dry regime is p
1. Each year, farmers observe r
t
and use this information to update their belief about the current regime state, which they do not observe. A farmer's belief about the current regime state determines his expectation of the next period's rainfall.
3.2. Agricultural model
In this model, each farmer lives for two periods. In each period t, the farmer allocates his wealth, w t , between an irrigation asset, i t , and another agricultural asset, a t , such that a t +i t =w t .Footnote 6 The farmer also chooses a crop portfolio each period. The farmer has one unit of land, which he divides between a drought-tolerant crop and a crop that is relatively more sensitive to drought. Let ρ t be the area planted with the drought-tolerant crop, and let 1−ρ t be the drought-sensitive crop area.
Profits are determined by the asset mix, the crop portfolio, and rainfall r t . For tractability, we assume a quadratic profit function of the form:
 $$\eqalign{\pi_{t} &= \beta_{a}a_{t}+\beta_{i}i_{t}+\beta_{\rho}\rho_{t} + {1\over 2}\delta_{aa}a_{t}^{2}+{1\over 2}\delta_{ii}i_{t}^{2} +{1\over 2}\delta_{\rho\rho}\rho_{t}^{2}+\delta_{\rho i}\rho_{t}i_{t}+\delta_{ir}i_{t}r_{t} \cr &\quad + \delta_{\rho r}\rho_{t}r_{t}+\delta_{r}r_{t}+ \epsilon_t,}$$
$$\eqalign{\pi_{t} &= \beta_{a}a_{t}+\beta_{i}i_{t}+\beta_{\rho}\rho_{t} + {1\over 2}\delta_{aa}a_{t}^{2}+{1\over 2}\delta_{ii}i_{t}^{2} +{1\over 2}\delta_{\rho\rho}\rho_{t}^{2}+\delta_{\rho i}\rho_{t}i_{t}+\delta_{ir}i_{t}r_{t} \cr &\quad + \delta_{\rho r}\rho_{t}r_{t}+\delta_{r}r_{t}+ \epsilon_t,}$$
where π t is profits per acre and ε t is a mean zero productivity shock. To establish our adaptation tests, we assume that:
-
(1) Profits are increasing in rainfall (δ r >0). This assumption is consistent with earlier work on India (Jayachandran, Reference Jayachandran2006; Cole et al., Reference Cole, Healy and Werker2012), and is verified in online appendix 5.
-
(2) The return to irrigation is higher during periods of low rainfall (δ ir <0). This assumption is verified in online appendix 5.
-
(3) The drought-tolerant crop is less profitable, on average, than the drought-sensitive crop (
 $\beta_{\rho}\lt 0$
). This assumption is necessary to ensure that farmers do not plant all their land with the drought-tolerant crop.
$\beta_{\rho}\lt 0$
). This assumption is necessary to ensure that farmers do not plant all their land with the drought-tolerant crop. -
(4) Low rainfall reduces the profitability of the drought-tolerant crop less than it reduces the profitability of the drought-sensitive crop (
 $\delta_{\rho r}\lt 0$
). This assumption comprises our definition of the drought-tolerant crop.
$\delta_{\rho r}\lt 0$
). This assumption comprises our definition of the drought-tolerant crop.
3.3. Maximization problem
Each farmer maximizes:
subject to:
where 0<β<1. For tractability, we assume constant absolute risk aversion utility of the form
![]() $u(c_{t})=-e^{-\eta c_{t}}$
. The timing of the model is as follows. To begin, the farmer chooses his first-period assets and crop portfolio, based on initial wealth and rainfall expectations. Next, first-period rainfall occurs and first-period profits are determined. With these profits in hand, the farmer chooses how much to consume in the first period and how much wealth to bring into the second period. The farmer also chooses his second-period asset mix and crop portfolio. Lastly, second-period rainfall occurs, and second-period profits are determined.
$u(c_{t})=-e^{-\eta c_{t}}$
. The timing of the model is as follows. To begin, the farmer chooses his first-period assets and crop portfolio, based on initial wealth and rainfall expectations. Next, first-period rainfall occurs and first-period profits are determined. With these profits in hand, the farmer chooses how much to consume in the first period and how much wealth to bring into the second period. The farmer also chooses his second-period asset mix and crop portfolio. Lastly, second-period rainfall occurs, and second-period profits are determined.
3.4. Tests for adaptation
We now derive tests to determine whether farmers update their rainfall expectations in response to past rainfall and whether they adapt their agricultural decisions accordingly. We lack data on farmer rainfall expectations, but the structure of the model allows us to test for adaptation, even without explicit data on expectations. To clarify the analysis, we introduce the following notation. Let
![]() $\mu_{1}=E_{0}(r_{1})$
and
$\mu_{1}=E_{0}(r_{1})$
and
![]() $\mu_{2}=E_{1}(r_{2})$
denote rainfall expectations. Let
$\mu_{2}=E_{1}(r_{2})$
denote rainfall expectations. Let
![]() $w_{2}^{*}$
denote the optimal amount of wealth to bring into second-period wealth. Let
$w_{2}^{*}$
denote the optimal amount of wealth to bring into second-period wealth. Let
![]() $i_{2}^{*}$
and
$i_{2}^{*}$
and
![]() $\rho_{2}^{*}$
denote the optimal second-period irrigation and crop choice decisions. Note that
$\rho_{2}^{*}$
denote the optimal second-period irrigation and crop choice decisions. Note that
![]() $i_{2}^{*}$
and
$i_{2}^{*}$
and
![]() $\rho_{2}^{*}$
depend solely on μ2 and
$\rho_{2}^{*}$
depend solely on μ2 and
![]() $w_{2}^{*}$
. Furthermore,
$w_{2}^{*}$
. Furthermore,
![]() $w_{2}^{*}$
itself is a function of w
1, μ1, r
1 and μ2.
$w_{2}^{*}$
itself is a function of w
1, μ1, r
1 and μ2.
3.4.1. Tests for irrigation adaptation
To derive a test for irrigation adaptation, we take the derivative of second-period irrigation with respect to first-period rainfall. Rearranging terms, we get:
 $${di_{2}^{*}\over dr_{1}}=\underbrace{{\partial i_{2}^{*}\over \partial w_{2}}{\partial w_{2}^{*}\over \partial r_{1}}}_{{\rm wealth}\, {\rm effect}}+ \underbrace{ \left[{\partial i_{2}^{*}\over \partial w_{2}}{\partial w_{2}^{*}\over \partial \mu_2}+{\partial i_{2}^{*}\over \partial \mu_2}\right] }_{{\rm expectations}\, {\rm effect}} {d\mu_2\over dr_{1}}.$$
$${di_{2}^{*}\over dr_{1}}=\underbrace{{\partial i_{2}^{*}\over \partial w_{2}}{\partial w_{2}^{*}\over \partial r_{1}}}_{{\rm wealth}\, {\rm effect}}+ \underbrace{ \left[{\partial i_{2}^{*}\over \partial w_{2}}{\partial w_{2}^{*}\over \partial \mu_2}+{\partial i_{2}^{*}\over \partial \mu_2}\right] }_{{\rm expectations}\, {\rm effect}} {d\mu_2\over dr_{1}}.$$
The wealth effect term captures the impact that first-period rainfall has on second-period irrigation investment that occurs strictly via the impact of first-period rainfall on second-period wealth. The expectations effect term captures the impact that first-period rainfall has on second-period irrigation investment that occurs due to farmers updating their expectations of second-period rainfall. In online appendix 7, it is demonstrated that, for irrigation, the wealth effect is positive, and the expectations effect is negative.Footnote 7 Having separated the influences of wealth and expectations, two tests for irrigation adaptation are presented.
Proposition 3.1
If farmers increase their irrigation investment after low rainfall, this demonstrates adaptation:
![]() ${di_{2}^{*}\over dr_{1}}\lt 0$
implies
${di_{2}^{*}\over dr_{1}}\lt 0$
implies
![]() ${d\mu_{2}\over dr_{1}} \gt 0$
.
${d\mu_{2}\over dr_{1}} \gt 0$
.
Proposition 3.2
If, conditional on wealth, farmers increase their irrigation investment after low rainfall, this also demonstrates adaptation:
![]() $\left. {di_{2}^{*}\over dr_{1}} \right|_{w_{2}=constant} \lt 0$
implies
$\left. {di_{2}^{*}\over dr_{1}} \right|_{w_{2}=constant} \lt 0$
implies
![]() ${d\mu_{2}\over dr_{1}} \gt 0.$
${d\mu_{2}\over dr_{1}} \gt 0.$
Proposition 3.1 is an unconditional test that can be used even without data on wealth. Proposition 3.2, on the other hand, requires data on wealth but is a more powerful test than Proposition 3.1. If farmers are adapting, but the wealth effect dominates the expectation effect, then Proposition 3.2 will detect adaptation but Proposition 3.1 will not.
3.4.2. Test for crop adaptation
Lastly, we derive a test for crop adaptation. We take the derivative of the second-period drought-tolerant crop area with respect to first-period rainfall. Rearranging terms, we get:
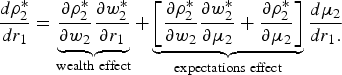 $${d\rho_{2}^{*}\over dr_{1}}= \underbrace{{\partial \rho_{2}^{*}\over \partial w_{2}}{\partial w_{2}^{*}\over \partial r_{1}}}_{{\rm wealth} \ {\rm effect}} + \underbrace{ \left[{\partial \rho_{2}^{*}\over \partial w_{2}}{\partial w_{2}^{*}\over \partial \mu_2}+{\partial \rho_{2}^{*}\over \partial \mu_2}\right] }_{{\rm expectations} \ {\rm effect}} {d\mu_2\over dr_{1}.}$$
$${d\rho_{2}^{*}\over dr_{1}}= \underbrace{{\partial \rho_{2}^{*}\over \partial w_{2}}{\partial w_{2}^{*}\over \partial r_{1}}}_{{\rm wealth} \ {\rm effect}} + \underbrace{ \left[{\partial \rho_{2}^{*}\over \partial w_{2}}{\partial w_{2}^{*}\over \partial \mu_2}+{\partial \rho_{2}^{*}\over \partial \mu_2}\right] }_{{\rm expectations} \ {\rm effect}} {d\mu_2\over dr_{1}.}$$
The wealth effect term captures the impact that first-period rainfall has on second-period crop choice that occurs strictly via the impact of first-period rainfall on second-period wealth. The expectations effect term captures the impact that first-period rainfall has on second-period crop choice that occurs due to farmers updating their expectations of second-period rainfall. In online appendix 7, it is demonstrated that, for crop choice, the wealth effect is negative and the sign of the expectation effect is ambiguous. Therefore, it is not possible to test for crop adaptation without controlling for wealth. Without a wealth control, a negative correlation between lagged rainfall and drought-tolerant crop areas could be occurring solely through a wealth channel and, hence, would not provide evidence of adaptation. On the other hand, if wealth is held constant, this removes the wealth effect and makes the sign of the expectations effect unambiguously negative, thereby generating the following test for adaptation:
Proposition 3.3
If, conditional on wealth, farmers plant a greater area of drought-tolerant crops after low rainfall, this demonstrates adaptation to climate:
![]() $\left. {d\rho_{2}^{*}\over dr_{1}} \right|_{w_{2}=constant} \lt 0$
, then
$\left. {d\rho_{2}^{*}\over dr_{1}} \right|_{w_{2}=constant} \lt 0$
, then
![]() ${d\mu_{2}\over dr_{1}} \gt 0.$
${d\mu_{2}\over dr_{1}} \gt 0.$
4. Data sources and summary statistics
We test our model with two agricultural data sets: a household panel and a district panel. The household panel–the Rural Economic and Demographic Survey (REDS)–was collected by the National Council of Applied Economic Research (NCAER). The data cover three rounds (1970/71, 1981/82 and 1998/99) and 259 villages across the 17 major states of India. The second and third rounds of the survey include data on the original households and households that split off from the original households, as well as a sample of new households. The analysis is restricted to households that either were surveyed in multiple rounds or split off from a previously surveyed household. Online appendix 2 displays a map with the locations of the REDS villages and gives more information on the sampling. Online appendix 3 discusses attrition in the REDS data set and its implications for our study. The REDS survey includes detailed data on irrigation, crop areas, assets, wealth, profits and inherited assets.
The district panel–the India Agriculture and Climate Data Set–was compiled by a World Bank research group and covers 271 districts across 14 states for each year between 1956 and 1987 (Sanghi et al. Reference Sanghi, Kumar and McKinsey1998). Online appendix 3 includes a map of the districts covered in the World Bank data set. The data set includes information on irrigated areas, crop areas, crop yields and prices, but does not include information about assets, wealth or profits.
Panel A in table 1 presents the summary statistics for agricultural variables of both data sets. For households, agricultural profits per acre are measured as crop receipts minus crop expenses, divided by the area of land cultivated. For the district data set, which lacks information on crop expenses, crop revenue per acre of land cultivated is used. For households, a dummy variable is created for irrigation investment that is equal to one if the household purchased materials, hired labor or used family labor to construct new irrigation assets, purchase new irrigation assets or improve existing irrigation assets during the 12 months prior to the survey interview. For the district data set, which lacks direct information on irrigation investment, irrigation investment is defined as the log of the 1-year change in the area of irrigated land. For households, wealth is measured as the sum of the value of irrigation assets, farm equipment, livestock, non-farm assets, housing, durable goods, farm inventory and financial assets minus debts, deflated to 1971 rupees. Online appendix 2 gives additional details about the construction of the agricultural variables.
Table 1. Summary statistics

Notes: The table displays mean coefficients, with standard deviations in parentheses. The household sample is restricted to farmers who cultivate land. See section 4 for details as to how the variables are constructed.
For both data sets, the water need of a crop portfolio is measured as the area-weighted average of the crop water need of the crops grown in a given year. We use the daily crop water need values (in centimeters per day) provided on the Agriinfo.in, 2015 website. These values, which are specific to the way that crops are grown in India, are presented in table 2. These numbers represent the average daily amount of water each crop needs, over the course of its growing season, in order to achieve optimal growth. An important caveat is that these values refer to optimal amounts, not necessarily what farmers apply in practice.
Table 2. Daily water requirements of common crops grown in India

Notes: The daily water requirement is measured in centimeters per day. Monsoon crops are crops who are grown during the summer monsoon season.
Sources: Agriinfo.in, 2015.
There are two main growing seasons in India: the kharif (or monsoon) season, which is the primary growing season and runs roughly from June to September, and the rabi (or winter) season, which is secondary and runs from October through February. The bulk of the rainfall comes during the monsoon season, but both kharif and rabi crops are affected by the quantity of monsoon rainfall. Rabi crops are affected because the monsoon affects soil moisture levels over the winter months, as well as surface water and groundwater supplies that are used to irrigate some winter crops. To address this seasonality, two different measures of crop water need are used: one that includes all crops grown during the year, and an alternate version that only includes the crops grown during the monsoon season. This captures the fact that monsoon crops are likely to be more strongly affected by monsoon rainfall than non-monsoon season crops. Due to the lack of season-specific crop planting data, crops are classified based on the season in which they are typically grown. The monsoon crops are cotton, maize, millet, peanut, pulses, rice, sorghum, soybean and sugarcane and the non-monsoon season crops are barley, mustard, oilseeds, potato and wheat.
The agricultural data is merged with gridded weather data from the Terrestrial Precipitation: Monthly Time Series (1900–2008), version 2.01, and the companion Terrestrial Air Temperature data set. The weather data for each 0.5-degree latitude–longitude grid point combines information from 20 nearby weather stations, using an interpolation algorithm based on the spherical version of Shepard's distance-weighting method. Current year growing season rainfall is measured as the z-score deviation from that location's historical mean.Footnote 8
To capture the decadal variability of the monsoon, a decadal rainfall variable is created that is the simple average of the rainfall z-scores from the past decade. We also use a specification where we measure lagged rainfall as the number of especially wet or dry years over the past decade. Following Jayachandran, Reference Jayachandran2006, the 20th percentile is used as the cutoff for a dry year and the 80th percentile as the cutoff for a wet year. Panel B of table 1 gives the means and standard deviations for the rainfall variables for the relevant years of the household and district surveys. Online appendix 2 gives additional details about the construction of the weather variables and online appendix 4 presents a detailed discussion of the variation of the decadal rainfall variables.
5. Empirical strategy
5.1. Tests for irrigation adaptation
In order to test for irrigation adaptation, we analyze how irrigation investment responds to lagged rainfall. For the household data set, a regression is run of the form
where the subscripts represent household i, village j, and year t. The dependent variable irr_inv
ijt
is a dummy variable equal to 1 if, during the recall period, a household purchased irrigation equipment or used labor to improve irrigation assets. The explanatory variables are past decade rainfall
![]() $decaderain_{jt}$
, current year rainfall rain
jt
, one-year lagged rainfall rain
jt−1, a year fixed effect λ
t
, a household fixed effect μ
ij
, and an error term ζ
ijt
.Footnote
9
The household survey follows households after household splits and after changes of the household head. Therefore, our household fixed effect is common to all parts of the household dynasty that have broken off from the original surveyed household, and can be thought of as a dynasty fixed effect.
$decaderain_{jt}$
, current year rainfall rain
jt
, one-year lagged rainfall rain
jt−1, a year fixed effect λ
t
, a household fixed effect μ
ij
, and an error term ζ
ijt
.Footnote
9
The household survey follows households after household splits and after changes of the household head. Therefore, our household fixed effect is common to all parts of the household dynasty that have broken off from the original surveyed household, and can be thought of as a dynasty fixed effect.
decaderain jt is measured in two ways. The first measure is a simple average of the rainfall z-scores from the past decade. The second measure tabulates the proportion of years in the past decade that were especially wet or dry. Following Jayachandran, Reference Jayachandran2006, the 20th percentile is used as the cut-off for a dry year and the 80th percentile as the cut-off for a wet year. The coefficient of interest is α1. Our model demonstrates that the sign of α1 is ambiguous and must be determined empirically. If the wealth effect dominates, then α1 will be positive. Irrigation investment will increase after wet decades, due to an accumulation of wealth and increased investment in all assets. On the other hand, if farmers are adapting to expected rainfall and the size of this effect is larger than the wealth effect, then we will find α1<0. Irrigation investment will increase after dry decades, due to farmers expecting more dry years in the future. Thus, finding α1<0 provides evidence of adaptation.Footnote 10
Current year rainfall is controlled for because farmers can invest in irrigation at any time during the year. Thus, a farmer's observation of current year rainfall (based on, say, the first half of the growing season) might directly affect his decision to invest in irrigation during that period. This response would not indicate adaptation to expected future year rainfall, but would simply reveal within-season adjustment to current year rainfall.Footnote 11
Propositions 3.1 and 3.2 demonstrate that we can test for irrigation adaptation with or without a wealth control. Thus, for completeness, we run a second household specification where we control for wealth. Once we have isolated the wealth effect, our model predicts that α1=0 if farmers are not adapting. On the other hand, if farmers are adapting, then α1<0.
Despite the dynasty fixed effect, there are two potential sources of endogeneity for wealth ijt . First, if the current period's productivity shocks are correlated with lagged productivity shocks, then wealth will be endogenous (because lagged productivity shocks affect wealth). Secondly, as above, if there is variation in farming ability within a dynasty, and farming ability is correlated (within the dynasty) with wealth, this will also cause endogeneity.
We employ an instrumental variables strategy that attempts to mitigate these endogeneity concerns. The REDS survey contains information, for each household and split-off household, about the amounts of wealth, land and irrigated land that were inherited at the time of household formation. Typically in India, at the time of a father's death, each son in the household will inherit land and become head of his own separate household (Fernando, Reference Fernando2014). We instrument for wealth
ijt
with
![]() $inhwealth_{ijt}$
, the amount of inherited wealth. Earlier work has used the same instrumental variables strategy (Foster and Rosenzweig, Reference Foster and Rosenzweig1995, Reference Foster and Rosenzweig2001; Reference Foster and Rosenzweig2010).
$inhwealth_{ijt}$
, the amount of inherited wealth. Earlier work has used the same instrumental variables strategy (Foster and Rosenzweig, Reference Foster and Rosenzweig1995, Reference Foster and Rosenzweig2001; Reference Foster and Rosenzweig2010).
Due to household splits, many dynasties include multiple household heads, which gives us variation in
![]() $inhwealth_{ijt}$
, even in the presence of the dynasty fixed effect.Footnote
12
We now discuss the exclusion restriction for our instruments and the extent to which these instruments reduce the endogeneity issues outlined above. First, consider the endogeneity that arises due to transient, current-period productivity shocks (that are not due to unobserved farmer ability). Because inheritances occurred in an earlier period, we should expect that inherited wealth should be less correlated with transient current period productivity shocks than current period wealth. Thus, we should expect the instruments to significantly reduce this source of endogeneity bias.
$inhwealth_{ijt}$
, even in the presence of the dynasty fixed effect.Footnote
12
We now discuss the exclusion restriction for our instruments and the extent to which these instruments reduce the endogeneity issues outlined above. First, consider the endogeneity that arises due to transient, current-period productivity shocks (that are not due to unobserved farmer ability). Because inheritances occurred in an earlier period, we should expect that inherited wealth should be less correlated with transient current period productivity shocks than current period wealth. Thus, we should expect the instruments to significantly reduce this source of endogeneity bias.
Secondly, consider the endogeneity that arises due to variations in farmer ability within a dynasty. Relative to this source of endogeneity, there is potential concern about whether the exclusion restriction holds. For example, if a son with higher farming ability inherits more wealth, then the exclusion restriction would be violated. However, there is evidence that inheritances may not be strongly correlated with variations in sons’ ability (Foster and Rosenzweig Reference Foster and Rosenzweig2002; Fernando, Reference Fernando2014),. Fernando, Reference Fernando2014 finds that the amount of inherited land is very strongly dictated by the number of sons in the family (and the total amount of land), and states that ‘equal division amongst sons [at the time of a father's death] is the norm’. If land is evenly divided, this is suggestive that non-land inheritances may also be divided roughly evenly. Note that even if there is purely equal division of inheritances among sons, changes across generations of household heads provide variation of the inheritances within each dynasty.
We cannot fully prove that contemporaneous variations in inheritances are uncorrelated with unobserved household ability, but to the extent that these inheritances are less correlated than current wealth and current irrigated land, our instrumental variables strategy should at least reduce the endogeneity bias. Due to potential concerns about the validity of the instrument, a non-instrumented version of the regression is run in online appendix 6.
For the district regression, irr_inv jt is defined as the log of the one-year change in the district's irrigated area, we use a district fixed effect, and we do not control for wealth. Proposition 3.1 demonstrates that we can test for irrigation adaptation, even in the absence of a wealth control. As with the household regression, finding α1<0 provides evidence of adaptation.
5.2. Test for crop adaptation
Lastly, we test for crop adaptation. We only perform this test with our household data set, and our regression is of the form:
where water_need ijt is the area-weighted water need of the farmer's crop portfolio. In one specification, we look at the area-weighted water need of all crops grown during the year. In a second specification, we look at the area-weighted water need of monsoon-season crops only. As mentioned above, we control for current year rainfall because farmers may have some knowledge of the current year's rainfall before they sow all of their crops. As in the irrigation regression, a response of crop choice to current year rainfall would indicate a within-season adjustment to rainfall, but would not provide evidence of adaptation to the expected future year rainfall.Footnote 13
We control for wealth ijt because, as demonstrated in section 3.4.2, without a control for wealth ijt , we could not interpret γ1 as evidence of adaptation. Wealth is endogenous and we instrument for it with inherited wealth. The validity of the instrument follows the same argument as above. Due to potential concerns about the validity of the instrument, we also run a non-instrumented version of the equation in online appendix 6. Finding γ1=0 demonstrates that farmers are not adapting their crop portfolios. Conversely, in the presence of adaptation, we expect to find γ1>0.
5.3. Standard error clustering
Standard errors are clustered at the weather grid-point level, which allows for serial correlation within dynasties and within districts (because any dynasty or district is always associated with the same weather grid point). In addition, this clustering allows for correlation in the error terms between adjacent households (or districts) that share the same value of rainfall due to the resolution of the rainfall data.
In online appendix 6, we verify that the results are robust to standard errors that allow for spatial correlation. This is important because lagged decadal rainfall exhibits substantial spatial correlation, as discussed in online appendix 4. To implement spatial clustering, we use code from Hsiang and Solow, (Reference Hsiang and Solow2010) and Fetzer, (Reference Fetzer2014). Guided by the autocorrelograms in online appendix 4, we allow for a spatial correlation within 800 km with a Bartlett (triangular) kernel and temporal correlation within a 30-year window.
6. Results
6.1. Tests for irrigation adaptation
Table 3 tests whether farmers adapt their irrigation investments in response to lagged rainfall. Recall that we can test for irrigation adaptation either with, or without, a wealth control. Columns 1 through 4 use the household data and, in columns 2 and 4, we control for wealth, which is instrumented for with inherited wealth. Columns 5 and 6 use the district data and do not control for wealth. In all columns, we find the coefficient of lagged rainfall is negative, which provides evidence of adaptation. In terms of magnitudes, column 4 demonstrates that a dry year in the preceding decade increases the probability of irrigation investment during the recall period by 1.2 percentage points. The baseline probability of investing in irrigation during the recall period is 5 per cent.Footnote 14 It is interesting to note that most of the irrigation adaptation effect is driven by dry shocks, rather than wet shocks (as seen in columns 3 and 4). Our theoretical model predicts that farmers should update their rainfall expectations equally much in response to wet or dry rainfall shocks. The larger observed response to dry shocks suggests that these shocks may be more salient to farmers. In addition, it suggests that farmers may be particularly concerned with protecting their farm profits (via irrigation investment) when they expect harmful dry years in the future.
Table 3. Testing for irrigation adaptation

Notes: Standard errors, in parentheses below the coefficients, allow for clustering within each latitude-longitude rainfall grid point. A dry shock is defined as rainfall below the 20th percentile and a wet shock is defined as rainfall above the 80th percentile. In columns 2 and 4, I instrument for wealth with inherited wealth. The first-stage F-statistics are reported in the table. Full first-stage regressions are also available upon request. F-test: the Staiger and Stock, Reference Staiger and Stock1997 rule of thumb is that instruments are ‘weak’ if the first-stage F is less than 10, and the Stock and Yogo, Reference Stock and Yogo2002 Weak ID test critical value for 2SLS bias being less than 10 per cent of OLS bias is 16.38. See section 4 for details on how the variables are constructed. *p<0.10, **p<0.05, ***p<0.01.
6.2. Test for crop adaptation
In table 4, we test for crop adaptation using the household data set. We control for wealth in all columns and instrument for it with inherited wealth.Footnote 15 Columns 1 and 2 look at the daily water need of all crops grown in the year, and columns 3 and 4 focus on the daily water need of monsoon season crops only. The monsoon season crops are cotton, maize, millet, peanut, pulses, rice, sorghum, soybean and sugarcane. The non-monsoon season crops are barley, mustard, oilseeds, potato and wheat. The columns that use the average rainfall specification are not significant. However, the columns that use the wet/dry shock rainfall specification are significant at the 1 per cent level for both all-season crops and monsoon season crops. The coefficient in column 2 indicates that each additional dry year in the past decade reduces the average water need of the crops planted by 0.16 mm/day, relative to an average water need of 7.3 mm/day. Restricting the analysis to monsoon season crops, we find that each additional dry year in the past decade reduces the average daily water need of a farmer's monsoon season crop portfolio by 0.2 mm/day, relative to an average water need of monsoon season crops of 8 mm/day.Footnote 16
Table 4. Testing for crop adaptation

Notes: Standard errors in parentheses allow for clustering within each latitude–longitude rainfall grid point. A dry shock is rainfall below the 20th percentile and a wet shock is rainfall above the 80th percentile. In all columns, we instrument for wealth with inherited wealth. The first-stage F-statistics are reported in the table. Full first-stage regressions are also available from the author. F-test: the Staiger and Stock, Reference Staiger and Stock1997 rule of thumb is that instruments are ‘weak’ if the first-stage F is less than 10, and the Stock and Yogo, Reference Stock and Yogo2002 Weak ID test critical value for 2SLS bias being less than 10% of OLS bias is 16.38. See section 4 for details on how the variables are constructed. *p<0.10, **p<0.05, ***p<0.01.
To further understand the crop adaptation results, individual crop regressions are run. In each column of table 5, the dependent variable is the proportion of land that is planted with a specific crop for the top eight crops by area in the REDS data set. These crops are (by area): rice, wheat, pulses, millet, cotton, sorghum, groundnut and maize. Consistent with the table 4 results, we find that after dry decades, farmers plant less rice (1.075 mm/day water need) and more pulses (3.50 mm/day water need). These are the crops with the highest and lowest water needs, respectively. In addition, after wet decades, farmers plant less millet (5.75 mm/day) and sorghum (5.75 mm/day), possibly because they are switching toward planting more (high water need) rice.
Table 5. Testing for crop adaptation: individual crops

Notes: Standard errors, in parentheses below the coefficients, allow for clustering within each latitude–longitude rainfall grid point. The dependent variable in each column is the proportion of total cultivated area planted with that crop. A dry shock is rainfall below the 20th percentile and a wet shock is rainfall above the 80th percentile. In all columns, we instrument for wealth with inherited wealth. The first-stage F-statistics are reported in the table. Full first-stage regressions are also available from the author. F-test: the Staiger and Stock, Reference Staiger and Stock1997 rule of thumb is that instruments are ‘weak’ if the first-stage F is less than 10, and the Stock and Yogo, Reference Stock and Yogo2002 Weak ID test critical value for 2SLS bias being less than 10% of OLS bias is 16.38. See section 4 for details on how the variables are constructed. *p<0.10, **p<0.05, ***p<0.01.
We also find that after wet decades, farmers plant more wheat (4.25 mm/day) and more cotton (5.25 mm/day). At first glance, these results seem counterintuitive because wheat and cotton have slightly lower water needs than millet and sorghum. However, wheat is grown during the rabi season, unlike millet and sorghum which are monsoon season crops. Compared to the other main rabi crops (barley and oilseeds), wheat has a higher water need. Thus our results indicate that after wet decades farmers shift their rabi crop portfolio towards higher water need crops. In a similar vein, cotton has a long growing season that spans both kharif and rabi. Famers may be growing more cotton after wet decades because they are planting more cotton, which is in the ground in both seasons, and growing less of the low water need rabi crops of barley and oilseeds.
Taken together, the irrigation and crop regressions suggest evidence that farmers are adapting in response to recent decadal rainfall. However, there are two important caveats to consider. First, our analysis treats irrigation investment and crop choice as two independent decisions, but in reality the two choices are interrelated. Our analysis is not able to completely disentangle the irrigation and crop choice decisions. A second caveat is that, due to attrition, the household sample in REDS is not nationally representative. Specifically, the famers in our sample have, on average, higher land areas, higher proportions of irrigated land and higher levels of non-land wealth than would be found in a representative sample. Thus, the adaptation results are an accurate representation of the behavior of this particular population, but our results may not hold more broadly.
7. Robustness
In online appendix 6, we investigate the robustness of our results.
First, we re-run our adaptation regressions using a fixed-effects specification that drops our instrumental variables strategy. In light of potential issues with our instruments, these results provide another set of estimates which may be of interest. In addition, using the non-IV specification allows us to estimate a new set of standard errors that allow for spatial correlation. This is important because, as indicated in online appendix 4, our lagged rainfall variable demonstrates significant spatial correlation. To implement these standard errors, we use code from Hsiang and Solow, (Reference Hsiang and Solow2010) and Fetzer, (Reference Fetzer2014). Guided by the autocorrelograms in online appendix 4, we allow for a correlation within 800 km using a Bartlett (triangular) kernel. The results are robust to these changes.
Secondly, we re-estimate our regressions using rainfall lag windows of 5 or 15 years, to verify that the choice of a 10-year window is not driving the results. The district irrigation regressions and the household crop regressions are robust to using alternate rainfall windows. In the household irrigation regressions, however, the signs of the coefficients of interest are preserved but are no longer statistically significant. We also present regressions in which we control for lagged rainfall separately for each year (rather than as an average). In this case, the coefficients are no longer individually statistically significant (likely because they are correlated with each other), but the set of rainfall lags is jointly significant.
Thirdly, we analyze how irrigation investment and crop choice are affected by lagged temperature shocks from the past decade. Temperature shocks affect profits and wealth. Therefore, we would expect to see wealth effects from lagged temperature on irrigation investment and crop choice. However, temperature does not undergo the persistent cycles that precipitation undergoes. Therefore, we would not expect to see an expectations effect for temperature. Our analysis corroborates this story: we find evidence of a temperature-induced wealth effect, but no evidence of a temperature-induced expectations effect.
Fourthly, we discuss the possibility that depletion of groundwater or surface water might be causing the relationship between irrigation investment and lagged rainfall that we have found. Using irrigated area (rather than irrigation investment) as the dependent variable, we find that the area of irrigated land increases after dry decades. As is discussed in greater detail in the appendix, this test provides some reassurance that water depletion is not driving the results, but it does not fully rule out that possibility.
Fifthly, we test whether the irrigation adaptation results might be due to public (government) investments rather than private (farmer) investments. In India, the bulk of direct public irrigation investments are large-scale dams. When we control for the presence of these dams, the irrigation adaptation results are preserved. However, government irrigation investment is an outcome variable and may be endogenous to the household investment decision. For this reason, our results are suggestive that the adaptation results are not driven by public investment, but do not definitively rule out that possibility.
Sixthly, we test whether changes in agricultural technology or policies might be confounding our results. We add controls for high-yielding variety crops, electrification rates, fertilizer prices, financial institutions, agricultural extension services, transportation infrastructure and government intervention in output markets. The irrigation and crop adaptation results are robust to adding these controls. However, these results are suggestive only, not definitive, since we are only able to control for a subset of possible confounders. Furthermore, the confounders that we do control for are potentially endogenous to the household irrigation and crop decisions.
Lastly, we run our regressions with region-by-year fixed effects. Due to the large-scale spatial correlation of the monsoons, it is possible that unobserved, time-varying confounding factors might be correlated with the lagged rainfall variables. Region-by-year fixed effects flexibly control for this. The district irrigation results and the household crop results are robust to the addition of these controls. The coefficients of interest are preserved in sign, magnitude and significance level. In the household irrigation regressions, however, the signs of the coefficients of interest are preserved but the magnitudes decrease by about 50 per cent and the coefficients are no longer statistically significant. The inclusion of region-by-year fixed effects is a stringent test since the household data set only spans three survey years. Therefore it is perhaps unsurprising that our household irrigation regressions are only weakly robust to the inclusion of these controls.
8. Effectiveness of adaptation
The preceding text finds evidence of adaptation; we now quantify its efficacy. What fraction of profits were farmers able to protect from adverse climate variations? To answer this question, we use the household data set to estimate the extent to which irrigation adaptation increased profits during 1971–1999.Footnote 17 Rainfall during this period was below average (as shown in figure 1), which reduced profits. On the other hand, farmers adapted to this below-average rainfall, by increasing their irrigation investments, which should have partially offset profit losses.
We take a two-step approach to estimate the efficacy of adaptation. First, we estimate the percentage of profits that were lost due to below-average rainfall during 1971–1999. Next, we estimate the percentage of these losses that were recovered due to increased irrigation investment. To calculate these percentage changes, we estimate profits π from three scenarios: a counterfactual scenario A, in which the drought did not occur; a counterfactual scenario B, in which the drought occurred but farmers did not adapt their irrigation; and the actual scenario C, in which the drought occurred and farmers adapted. The percentage of profits lost due to the below-average rainfall is
![]() ${\pi^{B}-\pi^{A}\over \pi^{A}}$
. The percentage of lost profits that were recovered by adaptation is
${\pi^{B}-\pi^{A}\over \pi^{A}}$
. The percentage of lost profits that were recovered by adaptation is
![]() ${\pi^{C}-\pi^{B}\over \pi^{B}-\pi^{A}}$
.
${\pi^{C}-\pi^{B}\over \pi^{B}-\pi^{A}}$
.
We observe π C only in the survey years (1971, 1982 and 1999). To estimate π C for the non-survey years, we regress survey-year profits on survey-year rainfall, temperature, irrigation and wealth:
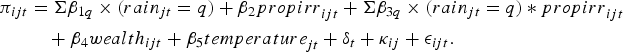 $$\eqalign{\pi_{ijt} &= \Sigma \beta_{1q}\times ({rain}_{jt}=q) + \beta_{2}{propirr}_{ijt}+ \Sigma \beta_{3q}\times ({rain}_{jt}=q) * {propirr}_{ijt} \cr & \quad + \beta_{4}{wealth}_{ijt}+\beta_{5}{temperature}_{jt} +\delta_{t}+\kappa_{ij}+\epsilon_{ijt}. }$$
$$\eqalign{\pi_{ijt} &= \Sigma \beta_{1q}\times ({rain}_{jt}=q) + \beta_{2}{propirr}_{ijt}+ \Sigma \beta_{3q}\times ({rain}_{jt}=q) * {propirr}_{ijt} \cr & \quad + \beta_{4}{wealth}_{ijt}+\beta_{5}{temperature}_{jt} +\delta_{t}+\kappa_{ij}+\epsilon_{ijt}. }$$
The variable rain
jt
=1,2,3,4,5 is a categorical variable representing the rainfall quintile for village j in year t and
![]() ${rain}_{jt}=3$
is the omitted category. The results of this regression are shown in table A2 of online appendix 5. We use the estimated coefficients and fixed effects to estimate non-survey-year profits:
${rain}_{jt}=3$
is the omitted category. The results of this regression are shown in table A2 of online appendix 5. We use the estimated coefficients and fixed effects to estimate non-survey-year profits:
 $$\eqalign{\pi^C_{ijt}& = \Sigma \beta_{1q}\times ({rain}_{jt}=q) + \beta_{2}\overline{{propirr}_{ijt}}+ \Sigma \beta_{3q}\times ({rain}_{jt}=q) * \overline{{propirr}_{ijt}} \cr & \quad + \beta_{4}\overline{{wealth}_{{ijt}}} + \beta_{5}{temperature}_{jt}+\overline{\delta_{t}}+\kappa_{ij},}$$
$$\eqalign{\pi^C_{ijt}& = \Sigma \beta_{1q}\times ({rain}_{jt}=q) + \beta_{2}\overline{{propirr}_{ijt}}+ \Sigma \beta_{3q}\times ({rain}_{jt}=q) * \overline{{propirr}_{ijt}} \cr & \quad + \beta_{4}\overline{{wealth}_{{ijt}}} + \beta_{5}{temperature}_{jt}+\overline{\delta_{t}}+\kappa_{ij},}$$
where
![]() $\overline{{propirr}_{ijt}}$
,
$\overline{{propirr}_{ijt}}$
,
![]() $\overline{{wealth}_{ijt}}$
and
$\overline{{wealth}_{ijt}}$
and
![]() $\overline{\delta_{t}}$
are linearly interpolated between survey rounds.
$\overline{\delta_{t}}$
are linearly interpolated between survey rounds.
To estimate π
B
, we compute
![]() $\widehat{{propirr}_{ijt}}$
, a counterfactual value of the proportion of irrigated land in the absence of adaptation. We use the coefficients from column 2 of table A10 in online appendix 6 to calculate the adaptive response of irrigation to lagged rainfall.Footnote
18
This table is analogous to the baseline irrigation adaptation specification (table 3) but uses the proportion of irrigated land as the dependent variable, rather than an irrigation investment dummy. The irrigation investment dummy captures precisely how the household is adjusting its irrigation this year. However, using it requires knowing what fraction of the farmer's land becomes irrigated when he invests in irrigation, since profits depend on the proportion of land irrigated. Thus, we instead use the proportion of irrigation, which is a coarser measure of adaptation. We use this regression to subtract a quantity of ‘adapted irrigation’ from
$\widehat{{propirr}_{ijt}}$
, a counterfactual value of the proportion of irrigated land in the absence of adaptation. We use the coefficients from column 2 of table A10 in online appendix 6 to calculate the adaptive response of irrigation to lagged rainfall.Footnote
18
This table is analogous to the baseline irrigation adaptation specification (table 3) but uses the proportion of irrigated land as the dependent variable, rather than an irrigation investment dummy. The irrigation investment dummy captures precisely how the household is adjusting its irrigation this year. However, using it requires knowing what fraction of the farmer's land becomes irrigated when he invests in irrigation, since profits depend on the proportion of land irrigated. Thus, we instead use the proportion of irrigation, which is a coarser measure of adaptation. We use this regression to subtract a quantity of ‘adapted irrigation’ from
![]() $\overline{{propirr}_{ijt}}$
, which gives us
$\overline{{propirr}_{ijt}}$
, which gives us
![]() $\widehat{{propirr}_{ijt}}$
, i.e., what irrigation would have been in the absence of adaptation.Footnote
19
We estimate
$\widehat{{propirr}_{ijt}}$
, i.e., what irrigation would have been in the absence of adaptation.Footnote
19
We estimate
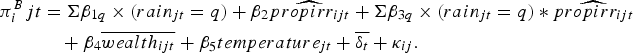 $$\eqalign{\pi^B_ijt &= \Sigma \beta_{1q}\times (rain_{jt}=q) + \beta_{2}\widehat{propirr_{ijt}}+ \Sigma \beta_{3q}\times (rain_{jt}=q)*\widehat{propirr_{ijt}} \cr & \quad + \beta_{4}\overline{wealth_{ijt}} + \beta_{5}temperature_{jt}+\overline{\delta_{t}}+\kappa_{ij}.}$$
$$\eqalign{\pi^B_ijt &= \Sigma \beta_{1q}\times (rain_{jt}=q) + \beta_{2}\widehat{propirr_{ijt}}+ \Sigma \beta_{3q}\times (rain_{jt}=q)*\widehat{propirr_{ijt}} \cr & \quad + \beta_{4}\overline{wealth_{ijt}} + \beta_{5}temperature_{jt}+\overline{\delta_{t}}+\kappa_{ij}.}$$
Lastly, to estimate π A , we calculate expected annual profits, using a 20 per cent chance of each rainfall quintile occurring. This calculation projects what expected profits would have been if rainfall were at its historical mean distribution. We estimate
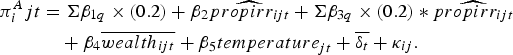 $$\eqalign{\pi^A_ijt &= \Sigma \beta_{1q}\times (0.2) + \beta_{2}\widehat{propirr_{ijt}}+ \Sigma \beta_{3q}\times (0.2) * \widehat{propirr_{ijt}} \cr & \quad + \beta_{4}\overline{wealth_{ijt}} + \beta_{5}{temperature}_{jt}+\overline{\delta_{t}}+\kappa_{ij}.}$$
$$\eqalign{\pi^A_ijt &= \Sigma \beta_{1q}\times (0.2) + \beta_{2}\widehat{propirr_{ijt}}+ \Sigma \beta_{3q}\times (0.2) * \widehat{propirr_{ijt}} \cr & \quad + \beta_{4}\overline{wealth_{ijt}} + \beta_{5}{temperature}_{jt}+\overline{\delta_{t}}+\kappa_{ij}.}$$
We use π A , π B and π C to calculate profit losses and recoveries. For each farmer, we sum total profits during 1971–1999, under each scenario. Using these profit estimates, we find that, on net, the dry regime decreased profits by 0.3 per cent. However, there is substantial heterogeneity and, for households with losses, the average loss was 7.9 per cent. We estimate that farmers with losses recovered, on average, only 9.4 per cent of their losses. Note that this estimate is an upper bound on the effectiveness of irrigation adaptation, because it does not incorporate the cost of the irrigation investments.
Our results demonstrate that farmer adaptation to persistent rainfall deviations was of limited efficacy. This suggests that adaptation to anthropogenic climate change may also be limited. However, there are four caveats to note. First, we only analyze irrigation adaptation. Farmers are likely to adapt via other channels as well, which will allow them to recapture additional profits. Secondly, extrapolating our results directly to future climate change is problematic, since future climate change will affect both rainfall and temperature. Thirdly, in addition to changing the demand for irrigation water, climate change will also affect the supply of irrigation water (Zaveri et al., Reference Zaveri, Grogan, Fisher-Vanden, Frolking, Lammers, Wrenn, Prusevich and Nicholas2016). In some regions, the available supply of irrigation water will decrease, potentially limiting the ability of farmers to increase their irrigation. Lastly, rich farmers with above-average land areas are over-represented in our sample. However, if we expect wealthier households to adapt more easily than poor households, then our estimate would overstate the efficacy of irrigation adaptation. Our results indicate that, even among richer households, irrigation adaptation was of limited benefit.
9. Conclusion
To accurately predict future climate change damages requires an accurate understanding of the ability of agents to adapt to changes in climate. In this paper, we exploit persistent rainfall variations in India over the past 50 years to test whether farmers adjust their irrigation and crop choice decisions in response to recent rainfall. Evidence is found of both irrigation adaptation and crop adaptation. However, analysis suggests that the efficacy of adaptation is limited; we estimate that adaptation recovers at most 9 per cent of lost profits. These results suggest that, in the context of the historical rainfall deviations that were analyzed, there are barriers to adaptation. This work does not elucidate the precise nature of these barriers. Other work, summarized by Jack, (Reference Jack2011), indicates that credit and information constraints, as well as inefficiencies in input, output, land, labor and risk markets, inhibit agricultural adaptation in a variety of situations. The specific barriers to climate change adaptation and, importantly, the institutions, technologies and policies that might remove these barriers, call for further exploration.
Supplementary material and methods
To view supplementary material for this article, please visit https://doi.org/10.1017/S1355770X17000195.











