Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Siboni, S
1998.
Some applications of symbolic dynamics techniques to toral skew endomorphisms.
Journal of Physics A: Mathematical and General,
Vol. 31,
Issue. 15,
p.
3665.
Denker, M.
and
Gordin, M.
1999.
Asymptotically gaussian distribution for random perturbations of rotations of the circle.
Journal of Mathematical Sciences,
Vol. 96,
Issue. 5,
p.
3493.
Вершик, Анатолий Моисеевич
Vershik, Anatolii Moiseevich
Горбульский, Александр Давидович
and
Gorbulsky, Alexander Davidovich
2007.
Масштабированная энтропия фильтраций $\sigma$-алгебр.
Теория вероятностей и ее применения,
Vol. 52,
Issue. 3,
p.
446.
Vershik, A. M.
and
Gorbulsky, A. D.
2008.
Scaled Entropy of Filtrations of $\sigma$-Fields.
Theory of Probability & Its Applications,
Vol. 52,
Issue. 3,
p.
493.
HAMDAN, D.
PARRY, W.
and
THOUVENOT, J.-P.
2008.
Shannon entropy for stationary processes and dynamical systems.
Ergodic Theory and Dynamical Systems,
Vol. 28,
Issue. 2,
p.
447.
POLLICOTT, M.
SHARP, R.
TUNCEL, S.
and
WALTERS, P.
2008.
The mathematical research of William Parry FRS.
Ergodic Theory and Dynamical Systems,
Vol. 28,
Issue. 2,
p.
321.
Mihailescu, Eugen
2012.
On some coding and mixing properties for a class of chaotic systems.
Monatshefte für Mathematik,
Vol. 167,
Issue. 2,
p.
241.
Mihailescu, Eugen
2013.
Higher dimensional expanding maps and toral extensions.
Proceedings of the American Mathematical Society,
Vol. 141,
Issue. 10,
p.
3467.
LEURIDAN, CHRISTOPHE
2021.
Bernoulliness of when is an irrational rotation: towards an explicit isomorphism.
Ergodic Theory and Dynamical Systems,
Vol. 41,
Issue. 7,
p.
2110.
LEURIDAN, CHRISTOPHE
2023.
When T is an irrational rotation, and are Bernoulli: explicit isomorphisms.
Ergodic Theory and Dynamical Systems,
p.
1.
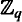 or the circle. We give conditions for the first kind to be isomorphic to the base itself and use this result to establish an isomorphism with the base for the second kind when a certain irrationalis very well approximated by rationals. A consequence is that there is a circle action of automorphisms commuting with theone-sided two-shift.
or the circle. We give conditions for the first kind to be isomorphic to the base itself and use this result to establish an isomorphism with the base for the second kind when a certain irrationalis very well approximated by rationals. A consequence is that there is a circle action of automorphisms commuting with theone-sided two-shift.

