Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hamenstädt, Ursula
1993.
Regularity of time-preserving conjugacies for contact Anosov flows withC1-Anosov splitting.
Ergodic Theory and Dynamical Systems,
Vol. 13,
Issue. 1,
p.
65.
Hamenstädt, Ursula
1994.
Regularity at infinity of compact negatively curved manifolds.
Ergodic Theory and Dynamical Systems,
Vol. 14,
Issue. 3,
p.
493.
Hamenstädt, Ursula
1994.
First European Congress of Mathematics Paris, July 6–10, 1992.
p.
73.
Besson, G�rard
Courtois, Gilles
and
Gallot, Sylvestre
1994.
Les vari�t�s hyperboliques sont des minima locaux de l'entropie topologique.
Inventiones Mathematicae,
Vol. 117,
Issue. 1,
p.
403.
Hamenstadt, Ursula
1994.
Anosov flows which are uniformly expanding at periodic points.
Ergodic Theory and Dynamical Systems,
Vol. 14,
Issue. 2,
p.
299.
Ledrappier, François
1995.
Proceedings of the International Congress of Mathematicians.
p.
1195.
Cao, Jianguo
1995.
Rigidity for non-compact surfaces of finite area and certain Kähler manifolds.
Ergodic Theory and Dynamical Systems,
Vol. 15,
Issue. 3,
p.
475.
Besson, G.
Courtois, G.
and
Gallot, S.
1995.
Entropies et rigidités des espaces localement symétriques de courbure strictement négative.
Geometric and Functional Analysis,
Vol. 5,
Issue. 5,
p.
731.
Hamenstädt, Ursula
1996.
Harmonic measures, Hausdorff measures and positive eigenfunctions.
Journal of Differential Geometry,
Vol. 44,
Issue. 1,
Yue, Chengbo
1996.
Quasiconformality in the geodesic flow of negatively curved manifolds.
Geometric and Functional Analysis,
Vol. 6,
Issue. 4,
p.
740.
Yue, Chengbo
1996.
The ergodic theory of discrete isometry groups on manifolds of variable negative curvature.
Transactions of the American Mathematical Society,
Vol. 348,
Issue. 12,
p.
4965.
Kim, Inkang
2001.
Marked length rigidity of rank one symmetric spaces and their product.
Topology,
Vol. 40,
Issue. 6,
p.
1295.
Knieper, Gerhard
2002.
Vol. 1,
Issue. ,
p.
453.
Croke, Christopher B.
2004.
Geometric Methods in Inverse Problems and PDE Control.
Vol. 137,
Issue. ,
p.
47.
Fanaï, Hamid-Reza
2005.
Conjugaison Géodésique en rang 1.
Bulletin of the Australian Mathematical Society,
Vol. 71,
Issue. 1,
p.
121.
Dankwart, Klaus
2014.
Rigidity of flat surfaces under the boundary measure.
Israel Journal of Mathematics,
Vol. 199,
Issue. 2,
p.
623.
Sambarino, A.
2016.
On entropy, regularity and rigidity for convex representations of hyperbolic manifolds.
Mathematische Annalen,
Vol. 364,
Issue. 1-2,
p.
453.
Butt, Karen
2024.
Approximate rigidity of the marked length spectrum.
Mathematics Research Reports,
Vol. 4,
Issue. ,
p.
63.
Biswas, Kingshook
2024.
Circumcenter extension of Moebius maps to CAT(-1) spaces.
Annales de l'Institut Fourier,
Vol. 74,
Issue. 1,
p.
235.
Biswas, Kingshook
2024.
Quasi-metric antipodal spaces and maximal Gromov hyperbolic spaces.
Geometriae Dedicata,
Vol. 218,
Issue. 2,
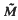 of M. This in term yields necessary and sufficient conditions for the existence of time preserving conjugacies of geodesic flows.
of M. This in term yields necessary and sufficient conditions for the existence of time preserving conjugacies of geodesic flows.

