Introduction
For more than five decades, networks of astronomers have been conducting the search for extra-terrestrial intelligence (SETI), up to now with no success. This means that of the immense amount of data that has been scanned (mainly radio signals) no message has been deliberately sent by ‘someone’ from other planetary systems. Drake's equation (see for example Drake & Sobel, Reference Drake and Sobel1994, pp. 51–52) implies that the universe hosts a vast amount of civilizations capable of inter-stellar radio communication. Yet, the absence of positive SETI beacons contradicts this idea. This contradiction between ‘theory’ and empirical observations is known as the Fermi–Hart paradox (Hart, Reference Hart1975). This ‘Great Silence’ (Brin, Reference Brin1983) implies that: there might not be intelligent life beyond Earth (e.g. the rare Earth hypothesis; Brownlee & Ward, Reference Ward and Brownlee2000), or that intelligent life exists, they are broadcasting, but we are missing the message, perhaps because of technological limitations, or any other reason, like life being sparse in the universe (Wesson, Reference Wesson1990; Ćirković & Vukotić, Reference Ćirković and Vukotić2008) (Conway Morris, Reference Conway Morris2003). Other interpretations to the cosmic silence are:
(1) There is no intelligent life beyond Earth at this moment.
(2) There is intelligent life beyond Earth, but they are far enough, say on the other side of the galaxy, or in another galaxy, but arose relatively recently. Since the information takes from up to 100 000 to millions of years to travel, signals have not reached earth.
(3) They are neither broadcasting nor listening, perhaps because they have not developed the necessary technology, or
(4) Because for any reason they are not interested in contacting other civilizations (Stephenson, Reference Stephenson1979; Brin, Reference Brin1983; Lem, Reference Lem2013, Ch. 3).
(5) There is intelligent life, they have the technology, but they are only listening and not broadcasting.
(6) Alien intelligent species could be employing totally different technologies (Sagan, Reference Sagan1973).
The first item in the list above leaves us with an unanswerable question about the existence of life (in so far that we do not send probes to selected locations). Items 2 and 3 relegate the search to future times, since at the moments there is not much we can do. Items 4–6 are scenarios that can be addressed, and are the subjects of the discussion I want embark.
In short, I present arguments and quantitative methods that support the active SETI, which involves messaging to extra-terrestrial intelligence (METI). So far, messages have been sent to selected locations in our galaxy and to a neighbouring galaxy M13 (Anonymous, 2006). Most of these messages have been only sporadic, while some of them have been resubmitted, although only a few times (Zaitsev, Reference Zaitsev2006). The closest star to which the broadcast was directed at is too far (∼33 light years) to expect any prompt response.
In this article, I introduce a quantitative model based on game theory, where different behavioural scenarios are considered. First, these scenarios help to explain the ‘Great Silence’, assuming that other civilizations might be listening – as we do – but is not broadcasting, at least not in a way that is detectable to us, as in the items 4–6 above.
The SETI community is divided in their opinions about whether to broadcast or not. One common argument is that under the uncertainty of the nature of a response, it is preferable to keep performing searches while staying silent.
To evaluate the potential hazards of sending a signal, Álmar and Shuch (Almár & Shuch, Reference Almár and Shuch2007) devised the San Marino scale (Fig. 1). Roughly speaking, the scale considers the intensity of the signal, how often it is repeated, its content, and its directionality. Thus, it gives a sensitive rule to decide whether to broadcast a message or not. Naturally, the San Marino scale does not consider (and cannot possibly do it) any potential outcome from the broadcast. Another tool is the Rio scale (Almár & Tarter, Reference Almár and Tarter2000), which measures the significance of any announcement of presumptive evidence of ETI (in the form of a radio signal or otherwise). Although the significance of these scales (as well as others such as the London scale; Almár, Reference Almár2011) takes into account different aspects such as social or economical, these do not explicitly account for a quantitative gain.

Fig. 1. The San Marino scale (colour on-line) measures the possibility of a potential hazard connected with any transmission. It is composed of two terms: the logarithm of intensity of the transmission relative to solar flux, ranging from 0 (less than the solar flux) to 5 (more than 105 times the solar flux), and on the nature of the message, assigning an index from 1 (a beacon without a message) up to 5 (intentional reply to an extra-terrestrial message) (Almár & Shuch, Reference Almár and Shuch2007; Shuch & Almár, Reference Shuch and Almár2007). A web-based San Marino scale calculator is accessible at http://iaaseti.org.
As in finance, any decision regarding an investment considers the risks, but is not only based solely on these. Instead, how an investment contributes to a portfolio return is of focal importance. Thus, I take a similar approach to active SETI by asking the question.
What are the expected benefits from engaging in a systematic and active SETI?
It is important to clarify that although SETI is a scientific subject, the question that I pose is not (yet) in itself a scientific one. Although based on assumptions that are in principle plausible, they might not be falsifiable as long as we do not detect any signal coming from extra-terrestrial intelligent societies (ETIS). However, a quantification – or estimation – of the gains is presented, in case we engage in the active SETI, and in case we do not and only search passively for SETI beacons. This is a novel framework for policy making in the SETI, and aims at an objective evaluation of the benefits and risks upon messaging.
To evaluate the possibilities of success of employing an active strategy, simple models can be considered. For example, among the most elementary forms are the two-player games (von Neumann & Morgenstern, Reference Von Neumann and Morgenstern1944). However, we ignore the nature of the ETIS, thus the space of possible ‘behaviours’ determining an action is obscure. Yet, we can make educated guesses about different hypothetical scenarios, and employ a framework of games with incomplete information (cf. Myerson Reference Myerson1991; Harsanyi, Reference Harsanyi1995). In other words, a framework is presented that consider distinct possible scenarios of ETIS’ behaviours, where each one has a certain probability of occurrence. In this way, it is possible to evaluate expected risks and benefits to address the question: should we embark in a systematic and active SETI, or should we only go on just listening for SETI signals? The framework proposed in this work goes beyond a yes/no answer taking instead a quantitative approach: how often should we broadcast? This question is tightly linked to the expected benefits. As it will be shown, the frequency of broadcasting events F B is (roughly) proportional to the inverse of the risk involved in messaging and proportional to the costs of METI. Thus, F B can be very small, but the immense number of stars that are being scanned suggests embarking into a systematic METI program. Indeed a METI program that systematically broadcast in all directions is discouraged. However, the results support that we can broadcast with frequency F B even if it is given that there are belligerent civilizations.
Searching for intelligent signals
‘It is just as unscientific to impute to remote intelligences wisdom and serenity as it is to impute to them irrational and murderous impulses. We must be prepared for either possibility and conduct our searches accordingly’ (Dyson, Reference Dyson1964).
In fact, it is extremely hard, if not impossible to make a judgment on what we can expect about the ‘intelligent nature’Footnote 1 of ETIS. On the other hand, there seem to be determinate conditions for intelligence to emerge. A critical understanding of any (anthropocentric) imputation to the intelligence of extra-terrestrial species should be judged under the light of the available theory. In as much as we would conclude that the wings of an organism have evolved because flying conferred an advantage to the ancestors of a species, so intelligence must be judged accordingly. Although human intelligence is by far the most prominent, several other species have also surprising levels of cognition, mathematical abilities, capacity to solve problems, memory, etc. Why did those traits evolve in different species? Admittedly, in most cases it is not an easy question to answer. But robust theories can explain why. If the causes and conditions for intelligence to evolve were restricted to only a few scenarios, we would in fact be forced to conclude that any ETIS would necessarily share with us, by pure convergence, analogous histories, as well as other analogous traits (Chela-Flores, Reference Chela-Flores2011, Chapters 11 and 12). But at the moments it is too soon to hypothesize on the subject.
This, however, is an adaptationist argument. Whether selection has been the actual drive for the emergence of intelligence in humans, genetic drift has been involved with more strength than selection, or if the pre-adaptations for intelligence were selected as side effects, we do not know. A popular way to understand the advantages of intelligence has been using the comparative method. Primates, cetaceans and other mammals, as well as some bird species, show considerable degrees of intelligence. This has sometimes been credited to convergent evolution. Nevertheless the understanding at the moments is that there are strong constraints in other species, which avoids or delays the increase in the amount of intelligence. This suggests that intelligence as ours is not likely to evolve again on Earth, certainly not soon. However, this principle of convergence has been repeated in astrobiology as if were a natural law; although the principle should not be underestimated (Chela-Flores, 2012, Chapter 12), we must not overestimate it either. Safe directions for speculations must be guided by experimental and empirical observations, which at the moments are not available in the SETI. We simply do not know whether life is to be founded outside Earth, and much less if intelligent life can evolve. Thus at the moment any speculation is, at best, wishful thinking, if not misleading.
If we would establish a METI project the chances of a response are necessarily favoured, opening the door for gathering knowledge about the possible existence, nature and willingness to communicate of ETIS, potentially establishing METI as a methodology to study other forms of evolution.
Simple games under different behavioural scenarios
Having that in mind that in searching for ‘intelligence’ we are actually searching for ETIS prone to be communicative, in proposing and analysing two scenarios, I will ascribe them with some anthropomorphic names. But these are intended only as mnemonic and operational labels, not as literal imputations or anticipation of the behaviours of ETIS.
By assumption the costs and rewards are taken as equivalent between us and the other communicative societies. On the one hand, we are a very young civilization, and is fairly unlikely that other civilizations are as young as ours (Almár, personal communication), which imposes a strong asymmetry not captured by the games considered in this article. On the other hand, the symmetry is justifiable in as long as the costs are proportional to ‘energetic expenditures’, although it might not be true in economical terms. However, regardless of the behavioural nature of the ETIS, this symmetric assumption allows us to measure: the chances that if we broadcast the outcome will be gainful, what is the expected outcome (gain or loss), and also how often we should broadcast.
Communicative societies
This mimics the current situation of the SETI institute that, although committed to its enterprise of finding ETI signals, is constrained by budget, political interests, etc. In this situation, the decision whether to search or search and broadcast (SB) is not strongly driven by any assessment of potential risks and benefits coming from exogenous sources. Thus, we can assign a zero gain to the SETI project, and say a cost −c, to the METI project. A similar situation applies to the ETIS, which for simplicity we assume to incur on equivalent costs. Detection of a signal would produce a gain ρ, which initially we set as unity (see Table 1 for a summary of mathematical symbols). The payoff matrix is resumed in Table 2.
Table 1. Mathematical symbols

Table 2. General payoff matrix for simple 2 player row-games
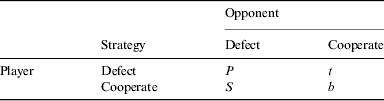
The prisoner's dilemma requires t + b > p > s, and is often parameterized as p = 0, b = 1, t = 2, s = 0. In this article, it is parameterized as p = 0, t = 1 + c, s = −c, b = 1, which does not change the properties of the game, but allows a natural extension to the other kinds of games discussed in the text.
Although detecting a signal will reward us in several ways, sending or not sending a message, makes absolutely no difference, since the gain is the same. However, the costs are higher when we send a message. Thus, even if the reward is higher than the costs the only equilibrium is just to listen (S), because overall, it is cheaper only to search for signals, than to SB a message.
For us, the human species (HS), gaining only depends on whether the ETIS broadcast or not – it is their decision whether to do it. But since our losses are anyway larger if we broadcast, it is better for us to pay less, irrespective if we gain by detecting their signals. As a result, we stay quiet, only listening.
If the situation were equivalent for the ETIS, then they would also decide to be quiet and search, just in case anyone broadcasts. The aftermath is that we end up both searching since it minimizes costs from both sides. This stable situation is known as a (strictly dominant) Nash equilibrium (Nash, Reference Nash1950): both parties are better off only defecting to broadcast, irrespective of the opponent's strategy. An assumption in these kinds of games is that there is no knowledge about the opponent's behaviour or tendency to choose among the strategies.
An extension of this situation arises when the benefits of mutual broadcast (ρ) are much bigger than when receiving a beacon aimed only to get our attention. For example, if we could exchange information with the ETIS, or receive some detailed information about their species or technology, etc. this could be a breakthrough for our society in many aspects. Thus, the reward ρ for actual communication with ETIS is larger than the net detection gain, i.e. ρ >1. In this case there are two pure Nash equilibria: the situation as in the previous scenario of only listening, denoted by the pair (S,S), is still a stable one, as is the communication strategy, where we both parties broadcast and listen (SB,SB). This particular kind of game, termed coordination game, is well known and vastly studied in the literature as a model for the evolution of cooperation (Cooper, Reference Cooper1999; Osborne, Reference Osborne2004 p. 31), and its payoff matrix is depicted in Table 3.
Table 3. Payoff matrix for games between communicative societies

c > 0 ρ > 1.
Belligerent societies
Perhaps the most feared set-up would be a Wellsian, science fiction situation in my opinion, where there is a notable penalty as a consequence of bidirectional broadcasting, for example, because of the possibility of being exploited, attacked, enslaved etc. by the ETIS. This fear seems to be profoundly implanted in us (culturally, historically and otherwise), to the level that the International Academy of Astronautics explicitly advocates peer international consultation before messaging back to any positive SETI signal (Billingham et al. Reference Billingham, Michaud, Tarter, Heidmann and Klein1991).
In this case, we can suppose a game where we pay a huge cost e for being exploited by the ETIS if they detect our signal at the same time that we do not detect theirs. However, if we both broadcast, then for example on the mutual fear of a belligerent move from the other party, only limited information will be shared leading to a basic gain ρ; this is reminiscent of a cold war-like situation. For example, only simple messages revealing our existence but without providing detailed information of our culture, habits, capabilities, technology or about any other resource would be shared. Table 4 resumes the payoff for this game.
Table 4. Payoff matrix for games between belligerent societies

e > > c > 0, c > 0, ρ > 1.
Once more, I assumed a symmetric game, but this need not to be the case. We could introduce an asymmetry in that, for example, we will not be belligerent as a first move. But this does not change the equilibrium. Hence, for simplicity, I will keep the game symmetric. The asymmetry can have an effect if we would consider a repeated game. But for the moments, I am not approaching this problem (although it is certainly interesting and highly relevant).
This last scenario has the same structure as the prisoner's dilemma game. The only Nash equilibrium for a one-shot game (played only once) is again to listen for signals but not to broadcast, (S,S).
The full game with incomplete information
In the analyses of the situations above there was a strong assumption, which is that in each case there was complete information about the reasons why the ETIS could take any strategy. In other words, the payoff matrices were taken as given. In practice, we have no clue which of the situations above (or any other) situations we could face. Thus to make a decision under this uncertainty, it is needed to consider a different structure for the game (Harsanyi, Reference Harsanyi1995). I will keep two artificial assumptions: (1) that we play a single shot game with (2) each of many other civilizations. In our financial analogy, this would be our portfolio. Both possibilities can be relaxed in subsequent works, but the intention of this article is to introduce the methodology by analysing a basic situation.
Before deriving the model in a detailed way, the rationale will be explained. If we knew the behavioural nature of other civilizations (at least qualitatively), there would not be major problem in making a decision whether to broadcast or not, as above. While game theory provides a good framework to model the behaviours, the occurrence of these behaviours is actually unknown. Given this uncertainty, we need to recur to a probabilistic rationalization of the problem. In other words, a frequency of occurrence will be assigned to each type of civilizations. This allows us to compute the average payoff. This average payoff is significant because we are attempting to communicate with (or at least detect) an arbitrary number of civilizations capable of interstellar communication, with varying behaviours (in this case we only consider two). Tentatively, only a proportion of these civilizations are attempting to communicate (i.e. they are broadcasting). These factors are already enough to establish a well-defined game, with which we could in theory, evaluate our strategy. Unfortunately, because to-date there has been no positive beacons we also ignore the distribution of the different types of civilizations, as well as the proportion of them that are broadcasting (if any of them actually occurs). A further way to deal with this uncertainty is to consider that these quantities are a draw from a probability distribution (which for simplicity here is taken as uniform), and compute the expectation of the payoffs. These expected payoffs are still functions of the costs and benefits of the basic games, and although they are independent of the frequencies of the types and the frequency of broadcasting societies, these quantities are not at all disregarded; they are averaged-out. This will convey us with a measure of potential costs and benefits, which allows addressing the question of METI in a quantitative way. In other words, more than a yes/no answer, with this tool a mixed strategy will be calculated, that is, the fraction of times that we should listen, and the fraction of times we should also broadcast.
Mathematical model
To evaluate what our strategy will be, we need to consider the prior probabilities r i, that the different scenarios (i = communicative, belligerent, etc.) can occur. We can compute the mean payoff of the game as
where V i(σ, σ′) is the payoff for the strategy (σ, σ′) of the type of ETIS i. Thus, this mean payoff matrix U is averaging over all the types and the entries are the averaged entries. We assume that V(S, S) = 0 and that V(S, SB) = t for all game types (Table 2). In the main example, we will consider only two types, namely communicative (Table 3) and belligerent (Table 4), but different choices are also possible. The mean payoff matrix involving these two types of scenarios is shown in Table 5.
Table 5. Matrix of average payoffs for a compound game

e >> c > 0, c > 0, ρ > 1.
We now assign a probability q for the ETIS playing SB and 1−q for playing S. This gives us our average payoff:
In our interest, we want to get the best of any situation, which means to choose which one among the two strategies is the best, given a set of parameters as well as the frequencies r and q. For this, we need to compute the boundary that makes, for example U(SB, q) > U(S, q), which can be computed explicitly by making U(SB, q*) = U(S, q*), which gives the general form:
The last equation would be the mixed Nash equilibrium if the game were being played rationally and with information about the occurrence of the different types. This assumption is waived in this article; instead, q is treated as a random variable, meaning that the frequency of societies that are broadcasting is contingent on unknown factors. Recall that the different entries in U are functions of the frequencies r, therefore q* is a surface parameterized by the variables r, which divides the unit hypercube formed by the variables r into two regions: the one above q*, mathematically written as Ω = {q:U(SB, q*) > U(S, q*)}, and the one below q*, denoted by Ωc. For instance, in the two-type game there is only one r, and the surface is only a curve given by
and is depicted in Fig. 2, where the shading emphasizes the region where U(SB, q) < U(S, q).

Fig. 2. The regions where U(SB, q) < U(S, q) (shaded in grey) are suggestive of adopting the S strategy, because the losses from broadcasting are big compared with the benefits. The white area above suggests adopting the strategy SB, since the gain is greater than when only searching. In this example c = 1, ρ = 200, e = 1000.
The game-theoretical approach commits to the assumption that the ETIS behave rationally, and from that assumption derives the mutually best selfish strategy. The next section introduces a probabilistic approach to deal with the unknown parameters r and q, in order to study how the expected returns of our portfolio behave, and compute our strategy under incomplete information.
Chance of profitable messaging and expected payoffs
At this point I treat q and r as a random variables, by assigning them a probability P(r, q). I define the chance of success Π as the proportion of the space of parameters where broadcasting results gainful. This is given by the proportion of the volume where U(SB, q) > U(S, q), that is the volume Ω above the surface q* (depicted in Fig. 2 for the two-type game). Then, we compute Π as the total volume as:
and similarly for the chance of a fruitless (or loss-making) effort, Πc. Here, n + 1 is the number of types (in the two type model, n = 1). Figure 3 shows how the chances where broadcasting is profitable change with some of the parameters. First consider a situation where the costs of the METI project are small, say unity or less, so that the rewards from mutual communication are always larger, i.e. c < ρ. In this situation, the chances of remuneration increase in a monotonous way with ρ, and as also shown in Fig. 2, it is desirable to broadcast in the whole space. The probability is ½ when ρ = 1 + 2e/5 (for large e), which supports the interpretation of Π as the chance of gainful calls: if the rewards are much higher than the costs, the probability increases to one monotonically. If c > ρ, then Π = 0.

Fig. 3. Proportion of the space where it is profitable to broadcast (Π). Π increases with the reward ρ as long as ρ > c, otherwise Π = 0. Solid line c = 0; dashed line c = 100. In both cases e = 1000.
With a similar approach as above, the average payoff on: Ω, U = (σ/Ω), can be defined as
for any strategy σ. In a similar way, we define U = (σ/Ωc). These quantities can be calculated in a closed form for the simple games considered here, but the actual expressions of these functions are neither simple nor revealing (see supplementary material (available at http://journals.cambridge.org/IJA) where the derivation is followed step by step, and is also checked with numerical integrations).
As σ takes two strategies and U is defined at the two regions, Ω and Ωc, it is a matrix. However, it does not represent an average player or anything alike, as the matrix U does; therefore U is not a payoff matrix of a game (in any region Ω either strategy can be played by the ETIS). Instead, U has to be interpreted in a statistical way. However, because it gives our expected payoff as a function of our actions we can employ it to compute the mixed strategy.
Mixed strategy
This section derives and states the central result of this article: the mixed strategy. This quantification follows from weighting the expected payoffs derived above with a frequency F B that we engage in broadcasting. Every time a star is scanned for SETI signals (under the assumption that it harvests a civilization capable of radio communication) there is a chance Π that it is profitable to broadcast. But we ignore whether that is the case. Our best action is to find F B such that we are equally well when we broadcast than when we do not. If we always broadcast, we are susceptible to pay a very high cost which overrides the gains. If we never broadcast we entirely rely on their willingness to communicate. There is a middle point set by equating the average payoff in each case, namely:
The left side of the equation is the average payoff if we were on the parameter region where we should broadcast; the right side of the equation is the average payoff if we were on the region where we should not broadcast.
Again, the explicit form of F B is elaborate (see supplementary material), but its form is shown in Fig. 4 for different parameters.

Fig. 4. A mixed strategy (frequency of METI events) exists when the rewards are smaller than a sixth of costs. For small values of reward, the mixed strategy is well approximated by Eq. (8). The mixed strategy decreases hyperbolically to zero, and for rewards that are greater than the costs of exploitation there is a pure strategy of only searching. In this example c = 1, and from top to bottom e = 103, 106, 109, 1012. Black lines: exact result; dashed grey lines: approximation.
F B decreases with ρ, and when ρ∼e/6 it vanishes. In words: as the rewards increase we should decrease the frequency of METI events. Crucially, when the rewards of communication are greater than a sixth of the risks, we should only search. This counter-intuitive outcome means that as the rewards get higher than the costs, our efforts to make profit can be relaxed. This result is also reflected in Fig. 3, which shows that as ρ increases, the probability of being in the gainful region of the games are greater than ½ and monotonically increases to one. Therefore, with less broadcast events, we are more certain of making a profit, and therefore it becomes less urgent to spend resources in broadcasting because we would have a notable income derived from less investment. The extreme limit of this situation would be realized if all civilizations were broadcasting: there would be little need for us to broadcast because only by scanning their messages we would get enough reward, and a few events of METI would constitute the bulk of the gains. An approximation for the mixed strategy is possible, which requires the assumption that ρ < e/6. In this case we find that for the two-type game
If ρ > e/6 there is only a pure strategy with F B = 0, that is, stay silent. This is the central result of this article. It is remarkable on its simplicity: generally speaking, if we consider that the costs of being exploited, e, are very high, then there is still a frequency of METI events that would not compromise us to the degree of such costs. Although F B might be very low, the large number of stars being surveyed results in a considerable amount of broadcast events (see Discussion section).
Payoff under the mixed strategy
Recall that by the structure of the game we spend c, but we gain the equivalent amount if we detect a signal effortlessly (plus a small reward from detection). Thus, it is important to keep in mind that these are neto gains (or losses), for they already discount the costs. The mixed strategy defines what will be the average payoff when adopting such a strategy, which is shown in Fig. 5(a) as a function of c, the cost of the project. In the limit when ρ < e/6 the expected gain is approximately

Fig. 5. Expected payoff U(F B) under the mixed strategy. (a) Roughly, U(F B) increases linearly with the cost of the METI project. Bottom curves and squares: ρ = 10; upper curves and bullets ρ = 500. (b) U(F B) increases logarithmically with the rewards for communication. Bottom curves and squares: c = 1. Upper curves and bullets: c = 10. Solid grey line: exact result, dashed line: approximation (Eq. 9), symbols: simulations. In all cases e = 104; the simulations results are averages over 106 replicas.
That is, the gain of METI is proportional to the cost of the project (Fig. 5(a)), and it increases slowly with the reward (Fig. 5(b)). Simulations of the games verify the result above; an averaging over 106 replicas was performed for each parameter combination (Fig. 5, see supplementary material for further details).
Discussion
The question about the need for SETI remains open. The SETI program has survived many fund cuts, and needed to compete for telescope time. More recently, tailored telescopes such as the Allen array have boosted the SETI (Welch et al. Reference Welch2009). Yet, technological innovations have not revealed any signal from ETIS. Nevertheless, the nature of the search has improved in time: more and narrower bandwidths, in parallel scanning have become the standard of SETI. A meticulous scanning is in progress aiming to detect weaker and farther putative signals, as well as undirected and unintentional leaked radiation from other civilizations. Necessarily, these technologies become more accurate and promising for the SETI program.
Is this enough? Arguably. An active search would open further doors in probably only a few decades. But instead of an active search, we have mostly remained quiet, a silence driven mostly of the fear for belligerent responses. This is, however, a weak argument. We might as well forbid domestic radio signals on the fear that leaked radiation would escape and get the attention of an ETIS. (If they are so advanced that they could exploit us, they could have or will detect our presence). Not embarking in an active search out of this fear of a response is like not developing further technologies out the fear that they will be misused (such as nuclear energy, transgenic organisms, or even the internet). Besides, the likelihood of exploitation – even if granting the existence of such belligerent societies – is rather small. The chances that our niches overlap are negligible and the idea that it would payoff (for them) to travel interstellar space to exploit a single or few resources is absurd for most scenarios.
Yet, in order to give a rational evaluation I have developed the analyses above, formulating the problem as a simple game theoretical model. I stress that the scenarios that I chose are rather arbitrary, albeit they somewhat represent the current ideas (or prejudices) about the unknown nature of possibly inexistent extra-terrestrial intelligences.
There is also another aspect not studied in this article: if there are in fact other civilizations that might be willing to communicate, they might be reluctant to do it so (as we are) on the fear of being exploited. An interesting follow-up to this question is: can we be the trigger an active communication? Indeed, the structure of the coordination game (Table 3) implies that if we broadcast, communicative societies would also broadcast. Suppose we can get the attention of an ETIS. What are the risks of a response and retaliation from different kinds of societies? These are questions that require a dynamical approach, since they rely on mutual exchange, and not in an average of one-shot games, and might include switching between different behavioural scenarios.
Notice that I have used the word risk in a sense analogous to economy, not as a measure of the hazard of the consequences of active SETI. Although the measures above should be sufficient to take a decision, these comprise only one particular aspect of SETI. Furthermore, the potential gains derived from communications with ETIS are somewhat uncorrelated to our a priori ideas about the hazards.
The San Marino scale (Fig. 1) measures the potential hazard connected to any transmission to extra-terrestrial intelligence (Almár & Shuch, Reference Almár and Shuch2007). Obviously, if we do not broadcast, there is no hazard. But, how risky is it to broadcast, in terms of the San Marino scale? The scale is derived from the index SMI = I + C, where I is related to the intensity of the signal (in log scale) and C is related to the content of the message (Fig. 1). The payoffs in Tables 2–4 are not set up in correlation with any of these. Yet, minimal assumptions about the intensity and nature of the message are built in the model. For instance, in order to message communicative societies we need sustained and intentional message, sent with intensity greater than that of the solar flux (in order to ensure that it can be detected). This gives a range from minor (SMI = 3) to high (SMI = 7). If we aim at a communicative society, we would include a message that is more informative, increasing the hazards by a unit. Naturally, intensifying the signal and revealing detailed information in all situations above can increase up to extraordinary hazards SMI = 10. Thus messaging seems indeed risky, although these risks might never change by delaying the action.
By daring more and more into space, by sending probes, by increasing our electromagnetic radiation spectrum and intensity, sooner or later we would reveal our existence, merely delaying our exposure to the risks. If we take a step forward and inquire, we can at least probe for the existence of other civilizations and about their nature. However, it is also important to consider that the spectrum and intensity of electromagnetic radiation is diminishing in time, due to technological advances that use less and less radio signalling (F. Drake, unpublished results). This of course diminishes our unintentional exposure, leaving it entirely our decision-making whether to be discovered or not.
This article introduced a novel framework for this decision-making. Although ecological and evolutionary arguments would dismiss the costs of being exploited as negligible (niche overlap and evolutionary convergence are somewhat unlikely), given the pervasiveness of the fear for a belligerent response in the SETI community, the possibility of this action has been seriously considered in the framework herein presented. Even then, the results still favour METI. Some tentative numbers can be plugged in. First of all, the scale should be standardized: it was mentioned that in an effortless detection our gain would be c + 1. The ‘1’ comes from the standard gain in a mutual communication after the costs have been recovered, and the c is what we saved from the spending of METI. Thus the ‘1’ sets the scale; say that the scaling factor is ϕ, then cϕ is the cost of METI minus the cost of SETI; the former would be considerably costlier than the latter. The costs of the Allen Telescope Array is about 50 million US$ (approximately 40 million €), so suppose that METI would cost from ten to hundred times that, say on the order of a billion EUR for a systematic search. If a positive beacon were detected, it would naturally boost the SETI project, even if the beacon does not contain much information. In the latter case, it would provide, say, grants. The most generous grants at the moments, from the European Actions provide up to a billion € (although not at once), so altogether ϕ(c + 1) ∼ 0.1–1 B€. Let us take the cost of being exploited as in the Iraq war (debated), but which is argued to be about a trillion dollars (1012, not at once). To be on the safe side, consider an order of magnitude above that, i.e. ϕe∼ 1013. Then the frequency of METI events should F B = 10−5–10−4. The SETI project minutely scans about 106 stars in the galactic plane within a radius of 1000 light years in frequencies between 1 and 10 GHz. This boils down to 10–100 stars to which we should message. Naturally, this is under the assumption that all of them harbour ETIS. Thus, if we correct by a factor of, say, 50–100, we get that we should message a couple of civilizations. Now, a less sensitive SETI surveys the inner galactic plane for about 1012 stars in the range of frequencies of 1420–1720 MHz (the ‘water window’). This gives a ‘corrected’ frequency of broadcasts of at least 105 METI events. Naturally broadcasting to that enormous number of stars demands sending messages to each of them, repeating them less frequently, which spreads the total power of the signal among that number of stars (which also diminishes the risks sensu the San Marino Scale), unlike the more sensitive broadcasts to the stars in the GHz SETI which concentrate the power into a few stars.
Concluding remarks
A paradigm change is necessary in SETI, and a systematic active search should be performed. Do the calculations above support this? First of all using the simple prisoner's dilemma game it was shown that if all civilizations choose the safe side and do not broadcast, the great silence would persist. Second, if we actually consider that the costs for being exploited are so high, it implies that it is as non-profitable to broadcast as not to do it, since it generates losses in any case. If that is indeed our assumption, then it entirely justifies shutting down the SETI project, since we do not expect to detect any positive beacon. However, the mixed games go beyond these assumptions and luckily justify both activities. Furthermore, it suggests that a mixed strategy should be performed, and a quantification for such a scenario has been derived.
As it often happens, game-theoretical models give counter-intuitive results and solutions. The mixed strategy derived here indicates that the more the communication would payoff, the less often we should broadcast. Conversely, when the rewards are lower than the cost of being exploited high, it is when it most desirable to broadcast. The paradox then is that if it is true that it is risky to message, as several SETI scientists hold, these fearing reasons are the ones that justify the METI project. However, it is true that it should not be an undisclosed broadcast.
The importance of framing the problem of METI as an economic one is twofold. On the one hand it is a justification for a continued funding of the SETI program. There are only a few research groups dedicated to this activity, and funding cuts to its central nodes is critical. This is unlike any other research field, where cutting the funding to some groups do not mean the death of the field. Moreover, I expect that, given that other civilizations exist, the program will eventually pay back. The second reason is to have a quantitative framework (which might be refined) in order to assess our potential role in an active communication at a larger scale. Notice that the payoffs are not necessarily in economical terms (although they may have an economic measure, as it was done in this article), thus the gains might be technological or intellectual, etc. Altogether this addresses the question of our relationship towards any possibly existing intelligent civilization, which may become a quantitative question upon detection. This includes an attractive possibility and the establishment of an unprecedented paradigm: it might be us who trigger an active communication among civilizations, and who define the nature of the game.
Acknowledgments
I am thankful to Professor Almár Ivan for his remarks on the manuscript and on the assumptions of the model, to Professor Szathmáry Eörs for a wonderful time at the Collegium Budapest where this and other ideas were conceived, to Professor Julián Chela-Flores for the discussions on the subject, and to Johannes Reiter for his observations and references on game theory. I would also like to acknowledge Professor Joanna Zylinska for kindly providing me with the translation of an important reference suggested by an anonymous referee.
Supplementary Material
For supplementary material for this article, please visit http://dx.doi.org/10.1017/S1473550412000407.












