Article contents
Acoustic microstreaming produced by two interacting gas bubbles undergoing axisymmetric shape oscillations
Published online by Cambridge University Press: 26 November 2021
Abstract
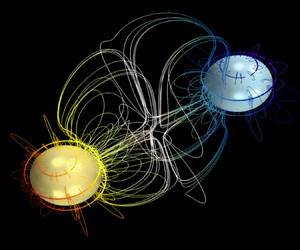
An analytical theory is developed that describes acoustic microstreaming produced by two interacting bubbles. The bubbles are assumed to undergo axisymmetric oscillation modes, which can include radial oscillations, translation and shape modes. Analytical solutions are derived in terms of complex amplitudes of oscillation modes, which means that the modal amplitudes are assumed to be known and serve as input data when the velocity field of acoustic microstreaming is calculated. No restrictions are imposed on the ratio of the bubble radii to the viscous penetration depth and the distance between the bubbles. The interaction between the bubbles is considered both when the linear velocity field is calculated and when the second-order velocity field of acoustic microstreaming is calculated. Capabilities of the analytical theory are illustrated by computational examples.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 6
- Cited by


