Article contents
Bifurcation analysis of steady natural convection in a tilted cubical cavity with adiabatic sidewalls
Published online by Cambridge University Press: 04 September 2014
Abstract
Natural convection in an inclined cubical cavity heated from two opposite walls maintained at different temperatures and with adiabatic sidewalls is investigated numerically. The cavity is inclined by an angle 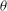 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\theta $ around a lower horizontal edge and the isothermal wall set at the higher temperature is the lower wall in the horizontal situation (
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\theta $ around a lower horizontal edge and the isothermal wall set at the higher temperature is the lower wall in the horizontal situation ( 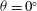 $\theta = 0^\circ $ ). A continuation method developed from a three-dimensional spectral finite-element code is applied to determine the bifurcation diagrams for steady flow solutions. The numerical technique is used to study the influence of
$\theta = 0^\circ $ ). A continuation method developed from a three-dimensional spectral finite-element code is applied to determine the bifurcation diagrams for steady flow solutions. The numerical technique is used to study the influence of 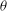 ${\theta }$ on the stability of the flow for moderate Rayleigh numbers in the range
${\theta }$ on the stability of the flow for moderate Rayleigh numbers in the range 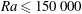 $\mathit{Ra} \leq 150\, 000$ , focusing on the Prandtl number
$\mathit{Ra} \leq 150\, 000$ , focusing on the Prandtl number 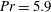 $\mathit{Pr} = 5.9$ . The results show that the inclination breaks the degeneracy of the stable solutions obtained at the first bifurcation point in the horizontal cubic cavity: (i) the transverse stable rolls, whose rotation vector is in the same direction as the inclination vector
$\mathit{Pr} = 5.9$ . The results show that the inclination breaks the degeneracy of the stable solutions obtained at the first bifurcation point in the horizontal cubic cavity: (i) the transverse stable rolls, whose rotation vector is in the same direction as the inclination vector 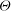 ${\boldsymbol{\Theta}}$ , start from
${\boldsymbol{\Theta}}$ , start from 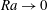 $\mathit{Ra} \to 0$ forming a leading branch and becoming more predominant with increasing
$\mathit{Ra} \to 0$ forming a leading branch and becoming more predominant with increasing 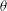 $\theta $ ; (ii) a disconnected branch consisting of transverse rolls, whose rotation vector is opposite to
$\theta $ ; (ii) a disconnected branch consisting of transverse rolls, whose rotation vector is opposite to 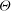 ${\boldsymbol{\Theta}}$ , develops from a saddle-node bifurcation, is stabilized at a pitchfork bifurcation, but globally disappears at a critical inclination angle; (iii) the semi-transverse stable rolls, whose rotation axis is perpendicular to
${\boldsymbol{\Theta}}$ , develops from a saddle-node bifurcation, is stabilized at a pitchfork bifurcation, but globally disappears at a critical inclination angle; (iii) the semi-transverse stable rolls, whose rotation axis is perpendicular to 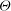 ${\boldsymbol{\Theta}}$ at
${\boldsymbol{\Theta}}$ at 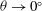 $\theta \to 0^\circ $ , develop from another saddle-node bifurcation, but the branch also disappears at a critical angle. We also found the stability thresholds for the stable diagonal-roll and four-roll solutions, which increase with
$\theta \to 0^\circ $ , develop from another saddle-node bifurcation, but the branch also disappears at a critical angle. We also found the stability thresholds for the stable diagonal-roll and four-roll solutions, which increase with 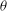 $\theta $ until they disappear at other critical angles. Finally, the families of stable solutions are presented in the
$\theta $ until they disappear at other critical angles. Finally, the families of stable solutions are presented in the 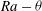 $\mathit{Ra}-\theta $ parameter space by determining the locus of the primary, secondary, saddle-node, and Hopf bifurcation points as a function of
$\mathit{Ra}-\theta $ parameter space by determining the locus of the primary, secondary, saddle-node, and Hopf bifurcation points as a function of 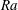 $\mathit{Ra}$ and
$\mathit{Ra}$ and 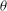 $\theta $ .
$\theta $ .
Information
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 32
- Cited by

