Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lei, Xianliang
Zhang, Qian
Zhang, Jun
and
Li, Huixiong
2017.
Experimental and Numerical Investigation of Convective Heat Transfer of Supercritical Carbon Dioxide at Low Mass Fluxes.
Applied Sciences,
Vol. 7,
Issue. 12,
p.
1260.
Patel, Ashish
Boersma, Bendiks J.
and
Pecnik, Rene
2017.
Scalar statistics in variable property turbulent channel flows.
Physical Review Fluids,
Vol. 2,
Issue. 8,
Irrenfried, C.
and
Steiner, H.
2017.
DNS based analytical P-function model for RANS with heat transfer at high Prandtl numbers.
International Journal of Heat and Fluid Flow,
Vol. 66,
Issue. ,
p.
217.
Pandey, Sandeep
Chu, Xu
and
Laurien, Eckart
2017.
Investigation of in-tube cooling of carbon dioxide at supercritical pressure by means of direct numerical simulation.
International Journal of Heat and Mass Transfer,
Vol. 114,
Issue. ,
p.
944.
Pecnik, Rene
and
Patel, Ashish
2017.
Scaling and modelling of turbulence in variable property channel flows.
Journal of Fluid Mechanics,
Vol. 823,
Issue. ,
Pandey, Sandeep
Chu, Xu
and
Laurien, Eckart
2018.
High Performance Computing in Science and Engineering ' 17.
p.
241.
Tao, Zhi
Cheng, Zeyuan
Zhu, Jianqin
Hu, Xizhuo
and
Wang, Longyun
2018.
Correction of low-Reynolds number turbulence model to hydrocarbon fuel at supercritical pressure.
Aerospace Science and Technology,
Vol. 77,
Issue. ,
p.
156.
Azih, Chukwudi
and
Yaras, Metin I.
2018.
Effects of spatial gradients in thermophysical properties on the topology of turbulence in heated channel flow of supercritical fluids.
Physics of Fluids,
Vol. 30,
Issue. 1,
Zhao, Pinghui
Liu, Jiaming
Ge, Zhihao
Li, Yuanjie
Zhao, Nian
and
Wan, Yuanxi
2018.
Direct numerical simulation of strongly heated air flows in a vertical pipe using a thermophysical property table.
International Journal of Heat and Mass Transfer,
Vol. 124,
Issue. ,
p.
1181.
Zhao, Pinghui
Zhu, Jiayin
Ge, Zhihao
Liu, Jiaming
and
Li, Yuanjie
2018.
Direct numerical simulation of turbulent mixed convection of LBE in heated upward pipe flows.
International Journal of Heat and Mass Transfer,
Vol. 126,
Issue. ,
p.
1275.
Ma, Peter C.
Yang, Xiang I. A.
and
Ihme, Matthias
2018.
Structure of wall-bounded flows at transcritical conditions.
Physical Review Fluids,
Vol. 3,
Issue. 3,
Pandey, Sandeep
Chu, Xu
Laurien, Eckart
and
Weigand, Bernhard
2018.
Buoyancy induced turbulence modulation in pipe flow at supercritical pressure under cooling conditions.
Physics of Fluids,
Vol. 30,
Issue. 6,
Liu, Jiaming
Jin, Yixuan
Zhao, Pinghui
Ge, Zhihao
Li, Yuanjie
and
Wan, Yuanxi
2019.
Analysis of heat transfer of supercritical water by direct numerical simulation of heated upward pipe flows.
International Journal of Thermal Sciences,
Vol. 138,
Issue. ,
p.
206.
Kawai, Soshi
2019.
Heated transcritical and unheated non-transcritical turbulent boundary layers at supercritical pressures.
Journal of Fluid Mechanics,
Vol. 865,
Issue. ,
p.
563.
Li, Zhouhang
Yao, Yecheng
Wang, Qinggong
Cai, Jingyong
Wu, Yuxin
and
Wang, Hua
2019.
Effect of internal helical-rib roughness on mixed convection flow and heat transfer in heated horizontal pipe flow of supercritical water.
International Journal of Heat and Mass Transfer,
Vol. 130,
Issue. ,
p.
1272.
Ren, Jie
Fu, Song
and
Pecnik, Rene
2019.
Linear instability of Poiseuille flows with highly non-ideal fluids.
Journal of Fluid Mechanics,
Vol. 859,
Issue. ,
p.
89.
Copping, Andrew W.
and
Yaras, Metin I.
2020.
A Critical Review of the Physics and Modeling of Deteriorated Heat Transfer in Supercritical Fluids.
Journal of Nuclear Engineering and Radiation Science,
Vol. 6,
Issue. 3,
Wan, Teng
Zhao, Pinghui
Liu, Jiaming
Wang, Chaozheng
and
Lei, Mingzhun
2020.
Mean velocity and temperature scaling for near-wall turbulence with heat transfer at supercritical pressure.
Physics of Fluids,
Vol. 32,
Issue. 5,
He, Jundi
Yan, Junjie
Wang, Wei
Jiang, Peixue
and
He, Shuisheng
2020.
Effects of buoyancy and thermophysical property variations on the flow of supercritical carbon dioxide.
International Journal of Heat and Fluid Flow,
Vol. 86,
Issue. ,
p.
108697.
Sufrà, Lorenzo
and
Steiner, Helfried
2020.
A Priori Assessment of Subgrid-Scale Models and Numerical Error in Forced Convective Flow at High Prandtl Numbers.
Flow, Turbulence and Combustion,
Vol. 105,
Issue. 2,
p.
377.
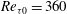 $Re_{{\it\tau}0}=360$ and Prandtl number at the inlet is
$Re_{{\it\tau}0}=360$ and Prandtl number at the inlet is  $Pr_{0}=3.19$ . The thermodynamic conditions are chosen such that the temperature range within the flow domain incorporates the pseudo-critical point where large variations in thermophysical properties occur. Two different thermal wall boundary conditions are studied: one that permits temperature fluctuations and one that does not allow temperature fluctuations at the wall (equivalent to cases where the thermal effusivity ratio approaches infinity and zero, respectively). Unlike for turbulent flows with constant thermophysical properties and Prandtl numbers above unity – where the effusivity ratio has a negligible influence on heat transfer – supercritical fluids shows a strong dependency on the effusivity ratio. We observe a reduction of 7 % in Nusselt number when the temperature fluctuations at the wall are suppressed. On the other hand, if temperature fluctuations are permitted, large property variations are induced that consequently cause an increase of wall-normal velocity fluctuations very close to the wall and thus an increased overall heat flux and skin friction.
$Pr_{0}=3.19$ . The thermodynamic conditions are chosen such that the temperature range within the flow domain incorporates the pseudo-critical point where large variations in thermophysical properties occur. Two different thermal wall boundary conditions are studied: one that permits temperature fluctuations and one that does not allow temperature fluctuations at the wall (equivalent to cases where the thermal effusivity ratio approaches infinity and zero, respectively). Unlike for turbulent flows with constant thermophysical properties and Prandtl numbers above unity – where the effusivity ratio has a negligible influence on heat transfer – supercritical fluids shows a strong dependency on the effusivity ratio. We observe a reduction of 7 % in Nusselt number when the temperature fluctuations at the wall are suppressed. On the other hand, if temperature fluctuations are permitted, large property variations are induced that consequently cause an increase of wall-normal velocity fluctuations very close to the wall and thus an increased overall heat flux and skin friction.

