Article contents
Stereo-PIV measurements of spatio-temporal turbulence correlations in an axisymmetric jet
Published online by Cambridge University Press: 30 July 2015
Abstract
Stereoscopic three-component particle image velocimetry (3C-PIV) measurements have been made in a turbulent round jet to investigate the spatio-temporal correlations that are the origin of aerodynamic noise. Restricting attention to subsonic, isothermal jets, measurements were taken in a water flow experiment where, for the same Reynolds number and nozzle size, the shortest time scale of the dynamically important turbulent structures is more than an order of magnitude greater that in equivalent airflow experiments, greatly facilitating time-resolved PIV measurements. Results obtained (for a jet nozzle diameter and velocity of 40 mm and 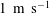 $1~\text{m}~\text{s}^{-1}$ , giving
$1~\text{m}~\text{s}^{-1}$ , giving 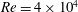 $\mathit{Re}=4\times 10^{4}$ ) show that, on the basis of both single-point statistics and two-point quantities (correlation functions, integral length scales) the present incompressible flow data are in excellent agreement with published compressible, subsonic airflow measurements. The 3C-PIV data are first compared to higher-spatial-resolution 2C-PIV data and observed to be in good agreement, although some deterioration in quality for higher-order correlations caused by high-frequency noise in the 3C-PIV data is noted. A filter method to correct for this is proposed, based on proper orthogonal decomposition (POD) of the 3C-PIV data. The corrected data are then used to construct correlation maps at the second- and fourth-order level for all velocity components. The present data are in accordance with existing hot-wire measurements, but provide significantly more detailed information on correlation components than has previously been available. The measured relative magnitudes of various components of the two-point fourth-order turbulence correlation coefficient (
$\mathit{Re}=4\times 10^{4}$ ) show that, on the basis of both single-point statistics and two-point quantities (correlation functions, integral length scales) the present incompressible flow data are in excellent agreement with published compressible, subsonic airflow measurements. The 3C-PIV data are first compared to higher-spatial-resolution 2C-PIV data and observed to be in good agreement, although some deterioration in quality for higher-order correlations caused by high-frequency noise in the 3C-PIV data is noted. A filter method to correct for this is proposed, based on proper orthogonal decomposition (POD) of the 3C-PIV data. The corrected data are then used to construct correlation maps at the second- and fourth-order level for all velocity components. The present data are in accordance with existing hot-wire measurements, but provide significantly more detailed information on correlation components than has previously been available. The measured relative magnitudes of various components of the two-point fourth-order turbulence correlation coefficient ( 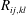 $R_{ij,kl}$ ) – the fundamental building block for free shear flow aerodynamic noise sources – are presented and represent a valuable source of validation data for acoustic source modelling. The relationship between fourth-order and second-order velocity correlations is also examined, based on an assumption of a quasi-Gaussian nearly normal p.d.f. for the velocity fluctuations. The present results indicate that this approximation shows reasonable agreement for the measured relative magnitudes of several correlation components; however, areas of discrepancy are identified, indicating the need for work on alternative models such as the shell turbulence concept of Afsar (Eur. J. Mech. (B/Fluids), vol. 31, 2012, pp. 129–139).
$R_{ij,kl}$ ) – the fundamental building block for free shear flow aerodynamic noise sources – are presented and represent a valuable source of validation data for acoustic source modelling. The relationship between fourth-order and second-order velocity correlations is also examined, based on an assumption of a quasi-Gaussian nearly normal p.d.f. for the velocity fluctuations. The present results indicate that this approximation shows reasonable agreement for the measured relative magnitudes of several correlation components; however, areas of discrepancy are identified, indicating the need for work on alternative models such as the shell turbulence concept of Afsar (Eur. J. Mech. (B/Fluids), vol. 31, 2012, pp. 129–139).
Information
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
Footnotes
Present address: Tata Technologies, Bristol BS16 1EJ, UK.
References
- 19
- Cited by

