Article contents
Interaction between hairy surfaces and turbulence for different surface time scales
Published online by Cambridge University Press: 27 December 2018
Abstract
Surfaces with filamentous structures are ubiquitous in nature on many different scales, ranging from forests to micrometre-sized cilia in organs. Hairy surfaces are elastic and porous, and it is not fully understood how they modify turbulence near a wall. The interaction between hairy surfaces and turbulent flows is here investigated numerically in a turbulent channel flow configuration at friction Reynolds number 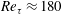 $Re_{\unicode[STIX]{x1D70F}}\approx 180$. We show that a filamentous bed of a given geometry can modify a turbulent flow very differently depending on the resonance frequency of the surface, which is determined by the elasticity and mass of the filaments. Filaments having resonance frequencies lower than the main frequency content of the turbulent wall-shear stress conform to slowly travelling elongated streaky structures, since they are too slow to adapt to fluid forces of higher frequencies. On the other hand, a bed consisting of stiff and low-mass filaments has a high resonance frequency and shows local regions of increased permeability, which results in large entrainment and a vast increase in drag.
$Re_{\unicode[STIX]{x1D70F}}\approx 180$. We show that a filamentous bed of a given geometry can modify a turbulent flow very differently depending on the resonance frequency of the surface, which is determined by the elasticity and mass of the filaments. Filaments having resonance frequencies lower than the main frequency content of the turbulent wall-shear stress conform to slowly travelling elongated streaky structures, since they are too slow to adapt to fluid forces of higher frequencies. On the other hand, a bed consisting of stiff and low-mass filaments has a high resonance frequency and shows local regions of increased permeability, which results in large entrainment and a vast increase in drag.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 13
- Cited by

