Article contents
Laminar vortex rings impinging onto porous walls with a constant porosity
Published online by Cambridge University Press: 05 January 2018
Abstract
For the first time, an experiment has been conducted to investigate synthetic jet laminar vortex rings impinging onto porous walls with different geometries by time-resolved particle image velocimetry. The geometry of the porous wall is changed by varying the hole diameter on the wall (from 1.0 mm to 3.0 mm) when surface porosity is kept constant (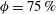 $\unicode[STIX]{x1D719}=75\,\%$). The finite-time Lyapunov exponent and phase-averaged vorticity field derived from particle image velocimetry data are presented to reveal the evolution of the vortical structures. A mechanism associated with vorticity cancellation is proposed to explain the formation of downstream transmitted vortex rings; and both the vortex ring trajectory and the time-mean flow feature are compared between different cases. It is found that the hole diameter significantly influences the evolution of the flow structures on both the upstream and downstream sides of the porous wall. In particular, for a porous wall with a small hole diameter (
$\unicode[STIX]{x1D719}=75\,\%$). The finite-time Lyapunov exponent and phase-averaged vorticity field derived from particle image velocimetry data are presented to reveal the evolution of the vortical structures. A mechanism associated with vorticity cancellation is proposed to explain the formation of downstream transmitted vortex rings; and both the vortex ring trajectory and the time-mean flow feature are compared between different cases. It is found that the hole diameter significantly influences the evolution of the flow structures on both the upstream and downstream sides of the porous wall. In particular, for a porous wall with a small hole diameter (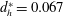 $d_{h}^{\ast }=0.067$, 0.10 and 0.133), the transmitted finger-type jets will reorganize into a well-formed transmitted vortex ring in the downstream flow. However, for the case of a large hole diameter of
$d_{h}^{\ast }=0.067$, 0.10 and 0.133), the transmitted finger-type jets will reorganize into a well-formed transmitted vortex ring in the downstream flow. However, for the case of a large hole diameter of 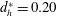 $d_{h}^{\ast }=0.20$, the transmitted vortex ring is not well formed because of insufficient vorticity cancellation. Additionally, the residual vorticity gradually evolves into discrete jet-like structures downstream, which further weaken the intensity of the transmitted vortex ring. Consequently, the transmitted flow structures for the
$d_{h}^{\ast }=0.20$, the transmitted vortex ring is not well formed because of insufficient vorticity cancellation. Additionally, the residual vorticity gradually evolves into discrete jet-like structures downstream, which further weaken the intensity of the transmitted vortex ring. Consequently, the transmitted flow structures for the 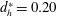 $d_{h}^{\ast }=0.20$ case would lose coherence more easily (or probably even transition to turbulence), resulting in a faster decay of the axial velocity and stronger entrainment of the transmitted jet. For all porous wall cases, the velocity profile of the transmitted jet exhibits self-similar behaviour in the far field (
$d_{h}^{\ast }=0.20$ case would lose coherence more easily (or probably even transition to turbulence), resulting in a faster decay of the axial velocity and stronger entrainment of the transmitted jet. For all porous wall cases, the velocity profile of the transmitted jet exhibits self-similar behaviour in the far field (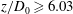 $z/D_{0}\geqslant 6.03$), which agrees well with the velocity distribution of free synthetic jets. With the help of the control-volume approach, the time-mean drag of the porous wall is evaluated experimentally for the first time. It is shown that the porous wall drag increases with the decrease in the hole diameter. Moreover, for a porous wall with a small hole diameter (
$z/D_{0}\geqslant 6.03$), which agrees well with the velocity distribution of free synthetic jets. With the help of the control-volume approach, the time-mean drag of the porous wall is evaluated experimentally for the first time. It is shown that the porous wall drag increases with the decrease in the hole diameter. Moreover, for a porous wall with a small hole diameter (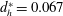 $d_{h}^{\ast }=0.067$, 0.10 and 0.133), it appears that the porous wall drag mainly derives from the viscous effect. However, as
$d_{h}^{\ast }=0.067$, 0.10 and 0.133), it appears that the porous wall drag mainly derives from the viscous effect. However, as 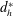 $d_{h}^{\ast }$ increases to 0.20, the form drag associated with the porous wall geometry becomes significant.
$d_{h}^{\ast }$ increases to 0.20, the form drag associated with the porous wall geometry becomes significant.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 28
- Cited by


