Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Vittoz, L.
Oger, G.
de Leffe, M.
and
Le Touzé, D.
2019.
Comparisons of weakly-compressible and truly incompressible approaches for viscous flow into a high-order Cartesian-grid finite volume framework.
Journal of Computational Physics: X,
Vol. 1,
Issue. ,
p.
100015.
Kurtulus, Dilek Funda
2019.
Unsteady aerodynamics of a pitching NACA 0012 airfoil at low Reynolds number.
International Journal of Micro Air Vehicles,
Vol. 11,
Issue. ,
p.
175682931989060.
Prasad Maddula, Satya
Bhargava, Vasishta
Prasad Padhy, Chinmaya
and
Khan, Md Akhtar
2020.
Computational analysis of NACA 0010 at moderate to high Reynolds number using 2D panel method.
MOJ Applied Bionics and Biomechanics,
Vol. 4,
Issue. 5,
p.
125.
Zhang, Kai
Hayostek, Shelby
Amitay, Michael
He, Wei
Theofilis, Vassilios
and
Taira, Kunihiko
2020.
On the formation of three-dimensional separated flows over wings under tip effects.
Journal of Fluid Mechanics,
Vol. 895,
Issue. ,
Durante, D.
Rossi, E.
and
Colagrossi, A.
2020.
Bifurcations and chaos transition of the flow over an airfoil at low Reynolds number varying the angle of attack.
Communications in Nonlinear Science and Numerical Simulation,
Vol. 89,
Issue. ,
p.
105285.
Durante, D.
Giannopoulou, O.
and
Colagrossi, A.
2021.
Regimes identification of the viscous flow past an elliptic cylinder for Reynolds number up to 10000.
Communications in Nonlinear Science and Numerical Simulation,
Vol. 102,
Issue. ,
p.
105902.
Yin, Bo
Guan, Yu
Wen, Ao
Karimi, Nader
and
Doranehgard, Mohammad Hossein
2021.
Numerical simulations of ultra-low-Re flow around two tandem airfoils in ground effect: isothermal and heated conditions.
Journal of Thermal Analysis and Calorimetry,
Vol. 145,
Issue. 4,
p.
2063.
Yuan, Wenyong
Laima, Shujin
Chen, Wen-Li
and
Li, Hui
2021.
External excitation effects on the flutter characteristics of a 2-DOF rigid rectangular panel.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 209,
Issue. ,
p.
104486.
Kurtulus, D. Funda
2021.
Vortex flow aerodynamics behind a symmetric airfoil at low angles of attack and Reynolds numbers.
International Journal of Micro Air Vehicles,
Vol. 13,
Issue. ,
p.
175682932110556.
Zhai, Xiangyu
Yin, Bo
Karimi, Nader
Gupta, Vikrant
Li, Larry K. B.
Guan, Yu
and
Ao, Wen
2021.
Lift characteristics of two tandem airfoils in the globally unstable wake of a heated cylinder.
Journal of Thermal Analysis and Calorimetry,
Vol. 145,
Issue. 4,
p.
2081.
Ribeiro, Jean Helder M.
Yeh, Chi-An
Zhang, Kai
and
Taira, Kunihiko
2022.
From biglobal to triglobal resolvent analysis: laminar separated flows over swept wings.
Zhang, Kai
Shah, Bharg
and
Bilgen, Onur
2022.
Low-Reynolds-Number Aerodynamic Characteristics of Airfoils with Piezocomposite Trailing Surfaces.
AIAA Journal,
Vol. 60,
Issue. 4,
p.
2701.
Burtsev, Anton
He, Wei
Zhang, Kai
Theofilis, Vassilios
Taira, Kunihiko
and
Amitay, Michael
2022.
Linear modal instabilities around post-stall swept finite wings at low Reynolds numbers.
Journal of Fluid Mechanics,
Vol. 944,
Issue. ,
Ribeiro, Jean Hélder Marques
Yeh, Chi-An
Zhang, Kai
and
Taira, Kunihiko
2022.
Wing sweep effects on laminar separated flows.
Journal of Fluid Mechanics,
Vol. 950,
Issue. ,
Bhargava, Vasishta
Maddula, Satya Prasad
Venkata Neigapula, Swamy Naidu
Khan, Md. Akhtar
Padhy, Chinmaya Prasad
and
Yagya Dutta, Dwivedi
2022.
Aerodynamic flow modelling of NACA 0010 using 2D panel and Jukouwski methods.
Aircraft Engineering and Aerospace Technology,
Vol. 94,
Issue. 6,
p.
965.
Rossi, E.
Durante, D.
Marrone, S.
and
Colagrossi, A.
2022.
A novel multi-resolution technique for solving complex vorticity patterns in planar viscous flows past bodies through the DVH method.
Computer Methods in Applied Mechanics and Engineering,
Vol. 396,
Issue. ,
p.
115082.
Reyes, M.
and
Mandujano, F.
2022.
Vortex induced vibrations of a cylinder at low mass ratio.
European Journal of Mechanics - B/Fluids,
Vol. 91,
Issue. ,
p.
66.
Zhang, Kai
and
Taira, Kunihiko
2022.
Aerodynamic characterization of low-aspect-ratio swept wings at Re=400.
Durante, D.
Pilloton, C.
and
Colagrossi, A.
2022.
Intermittency patterns in the chaotic transition of the planar flow past a circular cylinder.
Physical Review Fluids,
Vol. 7,
Issue. 5,
Wen, Shizheng
Lee, Michael W.
Bastos, Kai M. Kruger
Eldridge-Allegra, Ian K.
and
Dowell, Earl H.
2023.
Feature identification in complex fluid flows by convolutional neural networks.
Theoretical and Applied Mechanics Letters,
Vol. 13,
Issue. 6,
p.
100482.
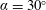 $\unicode[STIX]{x1D6FC}=30^{\circ }$
for which complex dynamics of the flow can take place in the different viscous regimes inspected. The Reynolds number ranges between
$\unicode[STIX]{x1D6FC}=30^{\circ }$
for which complex dynamics of the flow can take place in the different viscous regimes inspected. The Reynolds number ranges between
 $Re=100$
and
$Re=100$
and
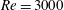 $Re=3000$
and, within this interval, numerous bifurcations of the solution are observed in terms of mean lift and drag coefficients, Strouhal number and downstream wake. An analysis of these bifurcations is provided and links are made between the wake structures observed. On this base the flow patterns can be classified in different modes similarly to the analysis by Kurtulus (Intl J. Micro Air Vehicles, vol. 7(3), 2015, pp. 301–326; vol. 8(2), 2016, pp. 109–139). A discussion of the vortical evolution of the flow in the vicinity of the suction side of the airfoil is also provided.
$Re=3000$
and, within this interval, numerous bifurcations of the solution are observed in terms of mean lift and drag coefficients, Strouhal number and downstream wake. An analysis of these bifurcations is provided and links are made between the wake structures observed. On this base the flow patterns can be classified in different modes similarly to the analysis by Kurtulus (Intl J. Micro Air Vehicles, vol. 7(3), 2015, pp. 301–326; vol. 8(2), 2016, pp. 109–139). A discussion of the vortical evolution of the flow in the vicinity of the suction side of the airfoil is also provided.


