Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ostilla-Mónico, Rodolfo
Verzicco, Roberto
and
Lohse, Detlef
2015.
Effects of the computational domain size on direct numerical simulations of Taylor-Couette turbulence with stationary outer cylinder.
Physics of Fluids,
Vol. 27,
Issue. 2,
Ostilla-Mónico, R.
Verzicco, R.
and
Lohse, D.
2016.
Turbulent Taylor–Couette flow with stationary inner cylinder.
Journal of Fluid Mechanics,
Vol. 799,
Issue. ,
Ostilla-Mónico, Rodolfo
Lohse, Detlef
and
Verzicco, Roberto
2016.
Effect of roll number on the statistics of turbulent Taylor-Couette flow.
Physical Review Fluids,
Vol. 1,
Issue. 5,
Spandan, Vamsi
Ostilla-Monico, Rodolfo
Lohse, Detlef
and
Verzicco, Roberto
2016.
Identifying coherent structures and vortex clusters in Taylor-Couette turbulence.
Journal of Physics: Conference Series,
Vol. 708,
Issue. ,
p.
012006.
van der Veen, Roeland C. A.
Huisman, Sander G.
Merbold, Sebastian
Harlander, Uwe
Egbers, Christoph
Lohse, Detlef
and
Sun, Chao
2016.
Taylor–Couette turbulence at radius ratio : scaling, flow structures and plumes.
Journal of Fluid Mechanics,
Vol. 799,
Issue. ,
p.
334.
Lasagna, D.
Tutty, O.R.
and
Chernyshenko, S.
2016.
Flow regimes in a simplified Taylor–Couette-type flow model.
European Journal of Mechanics - B/Fluids,
Vol. 57,
Issue. ,
p.
176.
Singh, Harminder
Suazo, Claudio Alberto Torres
and
Liné, Alain
2016.
Log law of the wall revisited in Taylor-Couette flows at intermediate Reynolds numbers.
Physical Review E,
Vol. 94,
Issue. 5,
Krug, Dominik
Yang, Xiang I. A.
de Silva, Charitha M.
Ostilla-Mónico, Rodolfo
Verzicco, Roberto
Marusic, Ivan
and
Lohse, Detlef
2017.
Statistics of turbulence in the energy-containing range of Taylor–Couette compared to canonical wall-bounded flows.
Journal of Fluid Mechanics,
Vol. 830,
Issue. ,
p.
797.
Zhu, Xiaojue
Verzicco, Roberto
and
Lohse, Detlef
2017.
Disentangling the origins of torque enhancement through wall roughness in Taylor–Couette turbulence.
Journal of Fluid Mechanics,
Vol. 812,
Issue. ,
p.
279.
Zhu, Xiaojue
Phillips, Everett
Spandan, Vamsi
Donners, John
Ruetsch, Gregory
Romero, Joshua
Ostilla-Mónico, Rodolfo
Yang, Yantao
Lohse, Detlef
Verzicco, Roberto
Fatica, Massimiliano
and
Stevens, Richard J.A.M.
2018.
AFiD-GPU: A versatile Navier–Stokes solver for wall-bounded turbulent flows on GPU clusters.
Computer Physics Communications,
Vol. 229,
Issue. ,
p.
199.
Luo, Guohu
Yao, Zhenqiang
and
Shen, Hong
2018.
A new hybrid turbulence model applied to highly turbulent Taylor-Couette flow.
Physics of Fluids,
Vol. 30,
Issue. 6,
Ostilla-Mónico, Rodolfo
Zhu, Xiaojue
and
Verzicco, Roberto
2018.
Exploring the large-scale structure of Taylor–Couette turbulence through Large-Eddy Simulations.
Journal of Physics: Conference Series,
Vol. 1001,
Issue. ,
p.
012017.
Costa, Pedro
2018.
A FFT-based finite-difference solver for massively-parallel direct numerical simulations of turbulent flows.
Computers & Mathematics with Applications,
Vol. 76,
Issue. 8,
p.
1853.
Zhu, Xiaojue
Verschoof, Ruben A.
Bakhuis, Dennis
Huisman, Sander G.
Verzicco, Roberto
Sun, Chao
and
Lohse, Detlef
2018.
Wall roughness induces asymptotic ultimate turbulence.
Nature Physics,
Vol. 14,
Issue. 4,
p.
417.
Sacco, Francesco
Verzicco, Roberto
and
Ostilla-Mónico, Rodolfo
2019.
Dynamics and evolution of turbulent Taylor rolls.
Journal of Fluid Mechanics,
Vol. 870,
Issue. ,
p.
970.
Kollmann, Wolfgang
2019.
Navier-Stokes Turbulence.
p.
333.
Froitzheim, Andreas
Ezeta, Rodrigo
Huisman, Sander G.
Merbold, Sebastian
Sun, Chao
Lohse, Detlef
and
Egbers, Christoph
2019.
Statistics, plumes and azimuthally travelling waves in ultimate Taylor–Couette turbulent vortices.
Journal of Fluid Mechanics,
Vol. 876,
Issue. ,
p.
733.
Berghout, Pieter
Zhu, Xiaojue
Chung, Daniel
Verzicco, Roberto
Stevens, Richard J. A. M.
and
Lohse, Detlef
2019.
Direct numerical simulations of Taylor–Couette turbulence: the effects of sand grain roughness.
Journal of Fluid Mechanics,
Vol. 873,
Issue. ,
p.
260.
Singh, Harminder
Bonnesoeur, Antoine
Besnard, Hugues
Houssin, Claude
Prigent, Arnaud
Crumeyrolle, Olivier
and
Mutabazi, Innocent
2019.
A large thermal turbulent Taylor-Couette (THETACO) facility for investigation of turbulence induced by simultaneous action of rotation and radial temperature gradient.
Review of Scientific Instruments,
Vol. 90,
Issue. 11,
Kollmann, Wolfgang
2019.
Navier-Stokes Turbulence.
p.
1.
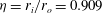 ${\it\eta}=r_{i}/r_{o}=0.909$, an aspect ratio of
${\it\eta}=r_{i}/r_{o}=0.909$, an aspect ratio of 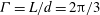 ${\it\Gamma}=L/d=2{\rm\pi}/3$, and a stationary outer cylinder. Three inner cylinder Reynolds numbers of
${\it\Gamma}=L/d=2{\rm\pi}/3$, and a stationary outer cylinder. Three inner cylinder Reynolds numbers of 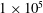 $1\times 10^{5}$,
$1\times 10^{5}$, 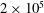 $2\times 10^{5}$ and
$2\times 10^{5}$ and 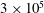 $3\times 10^{5}$ were simulated, corresponding to frictional Reynolds numbers between
$3\times 10^{5}$ were simulated, corresponding to frictional Reynolds numbers between 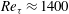 $Re_{{\it\tau}}\approx 1400$ and
$Re_{{\it\tau}}\approx 1400$ and 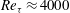 $Re_{{\it\tau}}\approx 4000$. An additional case with a large gap,
$Re_{{\it\tau}}\approx 4000$. An additional case with a large gap, 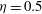 ${\it\eta}=0.5$ and driving of
${\it\eta}=0.5$ and driving of 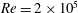 $Re=2\times 10^{5}$ was also investigated. Small-gap TC was found to be dominated by spatially fixed large-scale structures, known as Taylor rolls (TRs). TRs are attached to the boundary layer, and are active, i.e. they transport angular velocity through Reynolds stresses. An additional simulation was also conducted with inner cylinder Reynolds number of
$Re=2\times 10^{5}$ was also investigated. Small-gap TC was found to be dominated by spatially fixed large-scale structures, known as Taylor rolls (TRs). TRs are attached to the boundary layer, and are active, i.e. they transport angular velocity through Reynolds stresses. An additional simulation was also conducted with inner cylinder Reynolds number of 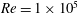 $Re=1\times 10^{5}$ and fixed outer cylinder with an externally imposed axial flow of comparable strength to the wind of the TRs. The axial flow was found to convect the TRs without any weakening effect. For small-gap TC flow, evidence was found for the existence of logarithmic velocity fluctuations, and of an overlap layer, in which the velocity fluctuations collapse in outer units. Profiles consistent with a logarithmic dependence were also found for the angular velocity in large-gap TC flow, albeit in a very reduced range of scales. Finally, the behaviour of both small- and large-gap TC flow was compared to other canonical flows. Small-gap TC flow has similar behaviour in the near-wall region to other canonical flows, while large-gap TC flow displays very different behaviour.
$Re=1\times 10^{5}$ and fixed outer cylinder with an externally imposed axial flow of comparable strength to the wind of the TRs. The axial flow was found to convect the TRs without any weakening effect. For small-gap TC flow, evidence was found for the existence of logarithmic velocity fluctuations, and of an overlap layer, in which the velocity fluctuations collapse in outer units. Profiles consistent with a logarithmic dependence were also found for the angular velocity in large-gap TC flow, albeit in a very reduced range of scales. Finally, the behaviour of both small- and large-gap TC flow was compared to other canonical flows. Small-gap TC flow has similar behaviour in the near-wall region to other canonical flows, while large-gap TC flow displays very different behaviour.


