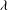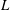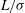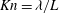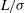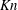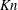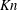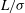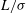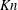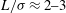1 Introduction
Gas transportation along micro/nanoscale channels exhibits unusual behaviour that cannot be captured by conventional computational fluid dynamics (Karniadakis, Beskok & Aluru Reference Karniadakis, Beskok and Aluru2005; Holt et al.
Reference Holt, Park, Wang, Stadermann, Artyukhin, Grigoropoulos, Noy and Bakajin2006). One well-known phenomenon is the Knudsen paradox (Knudsen Reference Knudsen1909): when a constant pressure difference drives flow along a narrow channel, the mass flow rate (MFR) displays a characteristic minimum as the inlet pressure is reduced, although the conventional Navier–Stokes equations simply predict a monotonic decreasing MFR. As the ratio of the gas molecular mean free path to the channel width (the Knudsen number,
![]() $Kn$
) becomes appreciable in narrow channels, the Boltzmann equation is commonly used to describe the collective motion of a dilute gas from the hydrodynamic to the free-molecular flow regimes (Chapman & Cowling Reference Chapman and Cowling1970). From numerical analysis of the Boltzmann equation (Ohwada, Sone & Aoki Reference Ohwada, Sone and Aoki1989a
), the Knudsen minimum may be understood as a consequence of the competition between the gas velocity slip at the channel wall and the effective shear viscosity, which both increase with the Knudsen number: while larger velocity slip increases the MFR, higher effective viscosity decreases the MFR by making the velocity profile flatter. The minimum MFR occurs at
$Kn$
) becomes appreciable in narrow channels, the Boltzmann equation is commonly used to describe the collective motion of a dilute gas from the hydrodynamic to the free-molecular flow regimes (Chapman & Cowling Reference Chapman and Cowling1970). From numerical analysis of the Boltzmann equation (Ohwada, Sone & Aoki Reference Ohwada, Sone and Aoki1989a
), the Knudsen minimum may be understood as a consequence of the competition between the gas velocity slip at the channel wall and the effective shear viscosity, which both increase with the Knudsen number: while larger velocity slip increases the MFR, higher effective viscosity decreases the MFR by making the velocity profile flatter. The minimum MFR occurs at
![]() $Kn\sim 1$
.
$Kn\sim 1$
.
Poiseuille flow with non-negligible Knudsen numbers has received much attention in recent years, due to the development of micro/nano-electromechanical systems (Karniadakis et al. Reference Karniadakis, Beskok and Aluru2005) and the shale gas revolution (Wang et al. Reference Wang, Chen, Jha and Rogers2014). The MFR obtained from the Boltzmann equation is a key parameter in the generalized Reynolds equation to describe gas-film lubrication problems such as the gas slide bearing (Fukui & Kaneko Reference Fukui and Kaneko1987, Reference Fukui and Kaneko1990; Cercignani, Lampis & Lorenzani Reference Cercignani, Lampis and Lorenzani2007), as well as in the upscaling methods used to predict the gas permeability of ultra-tight shale strata (Darabi et al. Reference Darabi, Ettehad, Javadpour and Sepehrnoori2012; Mehmani, Prodanović & Javadpour Reference Mehmani, Prodanović and Javadpour2013; Lunati & Lee Reference Lunati and Lee2014; Ma et al. Reference Ma, Sanchez, Wu, Couples and Jiang2014).
While the Boltzmann equation is a fundamental model for gas dynamics at low pressures, its applicability to a typical shale gas production scenario, with gas pressures of the order of
![]() $10^{6}{-}10^{7}$
Pa, is problematic (Ma et al.
Reference Ma, Sanchez, Wu, Couples and Jiang2014). This is because the Boltzmann equation is derived under the assumption that the mean free path is much larger than the molecular dimension, but this is not the case for large gas pressures. Instead, the Enskog equation, which takes into account the finite size of gas molecules and non-local collisions, has been developed for dense gases (Chapman & Cowling Reference Chapman and Cowling1970). Although the original equation is for hard-sphere molecules, long-range intermolecular attractive forces can be included through a mean-field theory (Grmela Reference Grmela1971; Karkheck & Stell Reference Karkheck and Stell1981), so that the van der Waals’ equation of state can be recovered. The extended Enskog equation has successfully described gas–liquid phase transitions, net condensation/evaporation and liquid menisci between two solid surfaces (Frezzotti, Gibelli & Lorenzani Reference Frezzotti, Gibelli and Lorenzani2005; Kon, Kobayashi & Watanabe Reference Kon, Kobayashi and Watanabe2014; Barbante, Frezzotti & Gibelli Reference Barbante, Frezzotti and Gibelli2015), with numerical results in good agreement with molecular dynamics simulations (Frezzotti Reference Frezzotti1998; Frezzotti et al.
Reference Frezzotti, Gibelli and Lorenzani2005).
$10^{6}{-}10^{7}$
Pa, is problematic (Ma et al.
Reference Ma, Sanchez, Wu, Couples and Jiang2014). This is because the Boltzmann equation is derived under the assumption that the mean free path is much larger than the molecular dimension, but this is not the case for large gas pressures. Instead, the Enskog equation, which takes into account the finite size of gas molecules and non-local collisions, has been developed for dense gases (Chapman & Cowling Reference Chapman and Cowling1970). Although the original equation is for hard-sphere molecules, long-range intermolecular attractive forces can be included through a mean-field theory (Grmela Reference Grmela1971; Karkheck & Stell Reference Karkheck and Stell1981), so that the van der Waals’ equation of state can be recovered. The extended Enskog equation has successfully described gas–liquid phase transitions, net condensation/evaporation and liquid menisci between two solid surfaces (Frezzotti, Gibelli & Lorenzani Reference Frezzotti, Gibelli and Lorenzani2005; Kon, Kobayashi & Watanabe Reference Kon, Kobayashi and Watanabe2014; Barbante, Frezzotti & Gibelli Reference Barbante, Frezzotti and Gibelli2015), with numerical results in good agreement with molecular dynamics simulations (Frezzotti Reference Frezzotti1998; Frezzotti et al.
Reference Frezzotti, Gibelli and Lorenzani2005).
For the Poiseuille flow of dense gases, there are three characteristic length scales: the mean free path, the channel width and the molecular diameter. The purpose of this paper is to investigate the influence of these competing length scales on the MFR in force-driven flow, through numerical solution of the Enskog equation. Our investigation is not, however, limited to elastic collisions between gas molecules, but is extended to dissipative collisions in dense granular gases, i.e. agitated ensembles of macroscopic grains modelled as inelastic hard discs or spheres (Brilliantov & Pöschel Reference Brilliantov and Pöschel2004; Aranson & Tsimring Reference Aranson and Tsimring2006). For simplicity, we consider the dense flow of hard discs in this paper, which is modelled by the generalized Enskog equation in § 2. In § 3, numerical results of the Enskog equation are presented, and analytical models are proposed to explain the unexpected behaviour of the MFR and the slip velocity. Finally, we draw conclusions in § 4.
2 The generalized Enskog equation for dense granular gases
Consider a granular gas composed of smooth hard discs of diameter
![]() ${\it\sigma}$
and mass
${\it\sigma}$
and mass
![]() $m$
, subject to an external acceleration
$m$
, subject to an external acceleration
![]() $a$
in the
$a$
in the
![]() $x$
direction, and confined between two infinite parallel plates of temperature
$x$
direction, and confined between two infinite parallel plates of temperature
![]() $T_{w}$
at
$T_{w}$
at
![]() $y=\pm (L+{\it\sigma})/2$
. Since the hard discs cannot fully occupy the region less than half a disc diameter away from a plate,
$y=\pm (L+{\it\sigma})/2$
. Since the hard discs cannot fully occupy the region less than half a disc diameter away from a plate,
![]() $L$
is regarded as the effective channel width. The impact of two hard discs conserves mass and momentum but not kinetic energy. Suppose
$L$
is regarded as the effective channel width. The impact of two hard discs conserves mass and momentum but not kinetic energy. Suppose
![]() $\boldsymbol{v}$
and
$\boldsymbol{v}$
and
![]() $\boldsymbol{v}_{\ast }$
are, respectively, the pre-collision velocities of a first and a second hard disc. The corresponding post-collision velocities
$\boldsymbol{v}_{\ast }$
are, respectively, the pre-collision velocities of a first and a second hard disc. The corresponding post-collision velocities
![]() $\boldsymbol{v}^{\prime }$
and
$\boldsymbol{v}^{\prime }$
and
![]() $\boldsymbol{v}_{\ast }^{\prime }$
are given by
$\boldsymbol{v}_{\ast }^{\prime }$
are given by
where
![]() $\boldsymbol{u}=\boldsymbol{v}-\boldsymbol{v}_{\ast }$
is the relative collision velocity,
$\boldsymbol{u}=\boldsymbol{v}-\boldsymbol{v}_{\ast }$
is the relative collision velocity,
![]() $\boldsymbol{k}$
is the unit vector from the centre of the first disc to the centre of the second at the time of their impact, and
$\boldsymbol{k}$
is the unit vector from the centre of the first disc to the centre of the second at the time of their impact, and
![]() ${\it\alpha}$
is the restitution coefficient characterizing the loss of the normal relative velocity, i.e.
${\it\alpha}$
is the restitution coefficient characterizing the loss of the normal relative velocity, i.e.
![]() $\boldsymbol{k}\boldsymbol{\cdot }(\boldsymbol{v}^{\prime }-\boldsymbol{v}_{\ast }^{\prime })=-{\it\alpha}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{u}$
. The collision is elastic when
$\boldsymbol{k}\boldsymbol{\cdot }(\boldsymbol{v}^{\prime }-\boldsymbol{v}_{\ast }^{\prime })=-{\it\alpha}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{u}$
. The collision is elastic when
![]() ${\it\alpha}=1$
and inelastic when
${\it\alpha}=1$
and inelastic when
![]() $0\leqslant {\it\alpha}<1$
.
$0\leqslant {\it\alpha}<1$
.
When the disc number density
![]() $n$
is small, so that the mean free path (
$n$
is small, so that the mean free path (
![]() $1/2\sqrt{2}n{\it\sigma}{\it\chi}(n)$
, where
$1/2\sqrt{2}n{\it\sigma}{\it\chi}(n)$
, where
![]() ${\it\chi}$
is the pair correlation function defined below) is much larger than the disc diameter, the dynamics of the dilute granular gas is modelled by the generalized Boltzmann equation (Goldstein & Shapiro Reference Goldstein and Shapiro1995). However, as the number density increases, the mean free path could become much smaller than the disc diameter, in which case the localized collision assumption in the Boltzmann equation is invalid and the finite area of the hard discs becomes important. The generalized Enskog equation (Esteban & Perthame Reference Esteban and Perthame1991; Brey, Dufty & Santos Reference Brey, Dufty and Santos1997; Bobylev, Carrillo & Gamba Reference Bobylev, Carrillo and Gamba2000) describes the flow of dense granular gases, where the velocity distribution function
${\it\chi}$
is the pair correlation function defined below) is much larger than the disc diameter, the dynamics of the dilute granular gas is modelled by the generalized Boltzmann equation (Goldstein & Shapiro Reference Goldstein and Shapiro1995). However, as the number density increases, the mean free path could become much smaller than the disc diameter, in which case the localized collision assumption in the Boltzmann equation is invalid and the finite area of the hard discs becomes important. The generalized Enskog equation (Esteban & Perthame Reference Esteban and Perthame1991; Brey, Dufty & Santos Reference Brey, Dufty and Santos1997; Bobylev, Carrillo & Gamba Reference Bobylev, Carrillo and Gamba2000) describes the flow of dense granular gases, where the velocity distribution function
![]() $f(y,\boldsymbol{v})$
, which is a function of the hard-disc velocity
$f(y,\boldsymbol{v})$
, which is a function of the hard-disc velocity
![]() $\boldsymbol{v}=(v_{x},v_{y})$
and spatial location
$\boldsymbol{v}=(v_{x},v_{y})$
and spatial location
![]() $y$
, is governed by
$y$
, is governed by
in which time is omitted because we are only interested in the steady-state profiles. Here
![]() $F=maL/2k_{B}T_{w}$
is the dimensionless acceleration,
$F=maL/2k_{B}T_{w}$
is the dimensionless acceleration,
![]() $k_{B}$
is the Boltzmann constant,
$k_{B}$
is the Boltzmann constant,
![]() $n_{0}$
is the average number density, and
$n_{0}$
is the average number density, and
![]() $\text{J}$
is the Jacobian of the transformation from
$\text{J}$
is the Jacobian of the transformation from
![]() $(\tilde{\boldsymbol{v}},\tilde{\boldsymbol{v}}_{\ast })$
into
$(\tilde{\boldsymbol{v}},\tilde{\boldsymbol{v}}_{\ast })$
into
![]() $(\boldsymbol{v},\boldsymbol{v}_{\ast })$
, where
$(\boldsymbol{v},\boldsymbol{v}_{\ast })$
, where
![]() $\tilde{\boldsymbol{v}}$
and
$\tilde{\boldsymbol{v}}$
and
![]() $\tilde{\boldsymbol{v}}_{\ast }$
are the pre-collision velocities producing post-collision velocities
$\tilde{\boldsymbol{v}}_{\ast }$
are the pre-collision velocities producing post-collision velocities
![]() $\boldsymbol{v}$
and
$\boldsymbol{v}$
and
![]() $\boldsymbol{v}_{\ast }$
. For hard-disc gases, collisions are instantaneous, and multiple encounters can be neglected (Chapman & Cowling Reference Chapman and Cowling1970). The binary collision is non-local, as the distance between the mass centres of the two colliding hard discs is the hard-disc diameter. Such non-local collisions are characterized by the product of the distribution function and a pair correlation function at different locations, i.e.
$\boldsymbol{v}_{\ast }$
. For hard-disc gases, collisions are instantaneous, and multiple encounters can be neglected (Chapman & Cowling Reference Chapman and Cowling1970). The binary collision is non-local, as the distance between the mass centres of the two colliding hard discs is the hard-disc diameter. Such non-local collisions are characterized by the product of the distribution function and a pair correlation function at different locations, i.e.
Here
![]() $k_{y}$
is the projection of
$k_{y}$
is the projection of
![]() $\boldsymbol{k}$
in the
$\boldsymbol{k}$
in the
![]() $y$
direction, and the pair correlation function
$y$
direction, and the pair correlation function
![]() ${\it\chi}$
is given by (Sanchez Reference Sanchez1994)
${\it\chi}$
is given by (Sanchez Reference Sanchez1994)
which, compared to other expressions (Henderson Reference Henderson1975; Baus & Colot Reference Baus and Colot1987), is accurate for the solid fraction
![]() ${\it\eta}={\rm\pi}{\it\sigma}^{2}nn_{0}/4$
up to the square-packing density
${\it\eta}={\rm\pi}{\it\sigma}^{2}nn_{0}/4$
up to the square-packing density
![]() ${\it\eta}={\rm\pi}/4$
.
${\it\eta}={\rm\pi}/4$
.
Note that in writing (2.2) the location
![]() $y$
is normalized by the effective channel width
$y$
is normalized by the effective channel width
![]() $L$
, the number density
$L$
, the number density
![]() $n$
is normalized by
$n$
is normalized by
![]() $n_{0}$
, velocity is normalized by the most probable speed
$n_{0}$
, velocity is normalized by the most probable speed
![]() $v_{m}=\sqrt{2k_{B}T_{w}/m}$
, temperature
$v_{m}=\sqrt{2k_{B}T_{w}/m}$
, temperature
![]() $T$
is normalized by
$T$
is normalized by
![]() $T_{w}$
, and the velocity distribution function
$T_{w}$
, and the velocity distribution function
![]() $f$
is normalized by
$f$
is normalized by
![]() $n_{0}/v_{m}^{2}$
. When the velocity distribution function is known, the normalized number density, flow velocity and temperature are given as follows:
$n_{0}/v_{m}^{2}$
. When the velocity distribution function is known, the normalized number density, flow velocity and temperature are given as follows:
![]() $n(y)=\int f(y,\boldsymbol{v})\,\text{d}\boldsymbol{v}$
,
$n(y)=\int f(y,\boldsymbol{v})\,\text{d}\boldsymbol{v}$
,
![]() $U_{x}(y)=\int f(y,\boldsymbol{v})v_{x}\,\text{d}\boldsymbol{v}/n(y)$
and
$U_{x}(y)=\int f(y,\boldsymbol{v})v_{x}\,\text{d}\boldsymbol{v}/n(y)$
and
![]() $T(y)=\int f(y,\boldsymbol{v})[(v_{x}-U_{x})^{2}+v_{y}^{2}]\,\text{d}\boldsymbol{v}/n(y)$
. The MFR, which is normalized by
$T(y)=\int f(y,\boldsymbol{v})[(v_{x}-U_{x})^{2}+v_{y}^{2}]\,\text{d}\boldsymbol{v}/n(y)$
. The MFR, which is normalized by
![]() $n_{0}mL^{2}a/v_{m}$
, is defined as
$n_{0}mL^{2}a/v_{m}$
, is defined as
where the integration range of the normalized
![]() $y$
is from
$y$
is from
![]() $-1/2$
to
$-1/2$
to
![]() $1/2$
because the centres of the hard discs are confined to this region such that macroscopic quantities outside of this region of
$1/2$
because the centres of the hard discs are confined to this region such that macroscopic quantities outside of this region of
![]() $y$
vanish.
$y$
vanish.
3 Numerical and analytical results
We solve the generalized Enskog equation (2.2) by using the fast spectral method (Wu, Zhang & Reese Reference Wu, Zhang and Reese2015) under the constraint
![]() $\int _{-1/2}^{1/2}n(y)\,\text{d}y=1$
, for various values of
$\int _{-1/2}^{1/2}n(y)\,\text{d}y=1$
, for various values of
![]() $L/{\it\sigma}$
and the global Knudsen number
$L/{\it\sigma}$
and the global Knudsen number
together with the diffuse boundary condition (Galvin, Hrenya & Wildman Reference Galvin, Hrenya and Wildman2007)
where
![]() $n_{w}=\pm 2\sqrt{{\rm\pi}}\int _{v_{y}\gtrless 0}v_{2}\,f(y=\pm 1/2,\boldsymbol{v})\,\text{d}\boldsymbol{v}$
. Note that the collisions in the Boltzmann equation are local, and the Boltzmann equation is recovered if we choose
$n_{w}=\pm 2\sqrt{{\rm\pi}}\int _{v_{y}\gtrless 0}v_{2}\,f(y=\pm 1/2,\boldsymbol{v})\,\text{d}\boldsymbol{v}$
. Note that the collisions in the Boltzmann equation are local, and the Boltzmann equation is recovered if we choose
![]() $g(y,\boldsymbol{k},\boldsymbol{v})$
in (2.3) as
$g(y,\boldsymbol{k},\boldsymbol{v})$
in (2.3) as
![]() $g(y,\boldsymbol{k},\boldsymbol{v})=f(y,\boldsymbol{v})$
and
$g(y,\boldsymbol{k},\boldsymbol{v})=f(y,\boldsymbol{v})$
and
![]() $Kn=1/2\sqrt{2}n_{0}{\it\sigma}L$
.
$Kn=1/2\sqrt{2}n_{0}{\it\sigma}L$
.

Figure 1. The mass flow rate as a function of the Knudsen number, for various values of
![]() $L/{\it\sigma}$
, when the collision between the hard discs is elastic. Dashed lines: numerical results of the Navier–Stokes equation (3.8) with the first-order velocity slip boundary condition (3.10). Dash-dotted lines: the asymptotic analytical solutions (3.5) as
$L/{\it\sigma}$
, when the collision between the hard discs is elastic. Dashed lines: numerical results of the Navier–Stokes equation (3.8) with the first-order velocity slip boundary condition (3.10). Dash-dotted lines: the asymptotic analytical solutions (3.5) as
![]() $Kn\rightarrow \infty$
; from top to bottom,
$Kn\rightarrow \infty$
; from top to bottom,
![]() $L/{\it\sigma}=1$
, 2 and 10.
$L/{\it\sigma}=1$
, 2 and 10.
3.1 Elastic collisions:
 ${\it\alpha}=1$
${\it\alpha}=1$
We consider the case where the external acceleration is very small (
![]() $F=0.0001$
). The Enskog equation (2.2) is solved from
$F=0.0001$
). The Enskog equation (2.2) is solved from
![]() ${\it\eta}\approx 0$
, until the maximum solid fraction reaches the square-packing limit. The MFR is shown in figure 1 as a function of the Knudsen number at several values of
${\it\eta}\approx 0$
, until the maximum solid fraction reaches the square-packing limit. The MFR is shown in figure 1 as a function of the Knudsen number at several values of
![]() $L/{\it\sigma}$
. For the Boltzmann equation, the Knudsen minimum is clearly seen at
$L/{\it\sigma}$
. For the Boltzmann equation, the Knudsen minimum is clearly seen at
![]() $Kn\sim 1$
, and when
$Kn\sim 1$
, and when
![]() $Kn<1$
(
$Kn<1$
(
![]() ${>}1$
), the MFR decreases (increases) monotonically with
${>}1$
), the MFR decreases (increases) monotonically with
![]() $Kn$
. For the Enskog equation, the MFR is significantly influenced by the tightness of the wall confinement. When the channel width is large (
$Kn$
. For the Enskog equation, the MFR is significantly influenced by the tightness of the wall confinement. When the channel width is large (
![]() $L/{\it\sigma}\geqslant 50$
), the MFR at
$L/{\it\sigma}\geqslant 50$
), the MFR at
![]() $Kn\geqslant 1$
is the same as that from the Boltzmann equation, while the MFR for
$Kn\geqslant 1$
is the same as that from the Boltzmann equation, while the MFR for
![]() $Kn<1$
is smaller than that from the Boltzmann equation, and the difference increases as
$Kn<1$
is smaller than that from the Boltzmann equation, and the difference increases as
![]() $Kn$
decreases. As
$Kn$
decreases. As
![]() $L/{\it\sigma}$
decreases, the MFR becomes smaller, and the difference from the Boltzmann result gradually extends to large Knudsen numbers. For
$L/{\it\sigma}$
decreases, the MFR becomes smaller, and the difference from the Boltzmann result gradually extends to large Knudsen numbers. For
![]() $L/{\it\sigma}>5$
, the MFR is not a monotonically decreasing function of
$L/{\it\sigma}>5$
, the MFR is not a monotonically decreasing function of
![]() $Kn$
in the slip flow regime (
$Kn$
in the slip flow regime (
![]() $Kn<0.1$
). Instead, there exists a specific value of
$Kn<0.1$
). Instead, there exists a specific value of
![]() $Kn$
at which the MFR is locally maximum, i.e.
$Kn$
at which the MFR is locally maximum, i.e.
![]() $Kn=0.02$
when
$Kn=0.02$
when
![]() $L/{\it\sigma}=30$
,
$L/{\it\sigma}=30$
,
![]() $Kn=0.05$
when
$Kn=0.05$
when
![]() $L/{\it\sigma}=15$
, and
$L/{\it\sigma}=15$
, and
![]() $Kn=0.08$
when
$Kn=0.08$
when
![]() $L/{\it\sigma}=10$
. For
$L/{\it\sigma}=10$
. For
![]() $L/{\it\sigma}\leqslant 5$
, the Knudsen minimum actually disappears, and the MFR only increases with the Knudsen number. Also, in the free-molecular regime (
$L/{\it\sigma}\leqslant 5$
, the Knudsen minimum actually disappears, and the MFR only increases with the Knudsen number. Also, in the free-molecular regime (
![]() $Kn>10$
), the MFR is larger than the Boltzmann prediction.
$Kn>10$
), the MFR is larger than the Boltzmann prediction.
We now examine the influence of the channel width on the MFR in the free-molecular regime. This regime occurs at small solid fractions. As with the Boltzmann equation, the normalized number density is unitary across the channel; however, the non-local collision in the Enskog equation makes the collision frequency spatially varying, which consequently affects the MFR. For small external accelerations, the distribution function can be linearized around the global equilibrium distribution function
![]() $f_{eq}(v)=\exp (-\boldsymbol{v}^{2})/{\rm\pi}$
as
$f_{eq}(v)=\exp (-\boldsymbol{v}^{2})/{\rm\pi}$
as
![]() $f(y,\boldsymbol{v})=f_{eq}(\boldsymbol{v})[1+h(y,\boldsymbol{v})]$
. The equilibrium collision frequency reads (as the pair correlation function is approximately 1)
$f(y,\boldsymbol{v})=f_{eq}(\boldsymbol{v})[1+h(y,\boldsymbol{v})]$
. The equilibrium collision frequency reads (as the pair correlation function is approximately 1)
where
![]() $H(y)$
is unitary for
$H(y)$
is unitary for
![]() $|y|\leqslant 1/2$
and zero otherwise. The mean collision frequency
$|y|\leqslant 1/2$
and zero otherwise. The mean collision frequency
![]() $\tilde{{\it\nu}}(y)=\int f_{eq}(\boldsymbol{v}){\it\nu}(y,\boldsymbol{v})\,\text{d}\boldsymbol{v}$
is plotted in figure 2 for various values of
$\tilde{{\it\nu}}(y)=\int f_{eq}(\boldsymbol{v}){\it\nu}(y,\boldsymbol{v})\,\text{d}\boldsymbol{v}$
is plotted in figure 2 for various values of
![]() $L/{\it\sigma}$
. For the Boltzmann equation with localized collisions, the mean collision frequency is a straight line with the value
$L/{\it\sigma}$
. For the Boltzmann equation with localized collisions, the mean collision frequency is a straight line with the value
![]() $2.507$
. For the Enskog equation, however, the non-local collision reduces the collision frequency in the region within one hard-disc diameter from the wall. For instance, the mean collision frequency at the wall for
$2.507$
. For the Enskog equation, however, the non-local collision reduces the collision frequency in the region within one hard-disc diameter from the wall. For instance, the mean collision frequency at the wall for
![]() $L/{\it\sigma}\geqslant 1$
is half that of the Boltzmann equation because half of the collision is shielded by the wall.
$L/{\it\sigma}\geqslant 1$
is half that of the Boltzmann equation because half of the collision is shielded by the wall.

Figure 2. The mean collision frequency
![]() $\tilde{{\it\nu}}(y,L/{\it\sigma})=\int f_{eq}(\boldsymbol{v}){\it\nu}(y,\boldsymbol{v})\,\text{d}\boldsymbol{v}$
for various values of
$\tilde{{\it\nu}}(y,L/{\it\sigma})=\int f_{eq}(\boldsymbol{v}){\it\nu}(y,\boldsymbol{v})\,\text{d}\boldsymbol{v}$
for various values of
![]() $L/{\it\sigma}$
, with
$L/{\it\sigma}$
, with
![]() $n_{0}\rightarrow 0$
. For symmetry, only half the spatial domain is plotted. Values of the spatially averaged mean collision frequency
$n_{0}\rightarrow 0$
. For symmetry, only half the spatial domain is plotted. Values of the spatially averaged mean collision frequency
![]() $\overline{{\it\nu}}=\int \tilde{{\it\nu}}(y)\,\text{d}y$
are 0.911, 1.709, 1.974, 2.107, 2.187, 2.347 and 2.428, when
$\overline{{\it\nu}}=\int \tilde{{\it\nu}}(y)\,\text{d}y$
are 0.911, 1.709, 1.974, 2.107, 2.187, 2.347 and 2.428, when
![]() $L/{\it\sigma}=1$
, 2, 3, 4, 5, 10 and 20, respectively.
$L/{\it\sigma}=1$
, 2, 3, 4, 5, 10 and 20, respectively.
When
![]() $Kn\rightarrow \infty$
, the collision term
$Kn\rightarrow \infty$
, the collision term
![]() $\text{J}{\it\alpha}^{-1}g(y,\boldsymbol{k},\tilde{\boldsymbol{v}}_{\ast })f(y,\tilde{\boldsymbol{v}})$
in (2.2) can be neglected (Cercignani Reference Cercignani and Laurmann1963; Takata & Funagane Reference Takata and Funagane2011). After linearization, the Enskog equation is approximated by the following equation for the deviational distribution function
$\text{J}{\it\alpha}^{-1}g(y,\boldsymbol{k},\tilde{\boldsymbol{v}}_{\ast })f(y,\tilde{\boldsymbol{v}})$
in (2.2) can be neglected (Cercignani Reference Cercignani and Laurmann1963; Takata & Funagane Reference Takata and Funagane2011). After linearization, the Enskog equation is approximated by the following equation for the deviational distribution function
![]() $h(y,\boldsymbol{v})$
:
$h(y,\boldsymbol{v})$
:
Here
![]() $\overline{{\it\nu}}=\int \tilde{{\it\nu}}(y)\,\text{d}y$
is the spatial average of the mean collision frequency, which decreases with
$\overline{{\it\nu}}=\int \tilde{{\it\nu}}(y)\,\text{d}y$
is the spatial average of the mean collision frequency, which decreases with
![]() $L/{\it\sigma}$
(see the caption of figure 2). With the diffuse boundary condition
$L/{\it\sigma}$
(see the caption of figure 2). With the diffuse boundary condition
![]() $h(y=\pm 1/2,v_{y}\lessgtr 0)=0$
, the final expression for the MFR at the asymptotic limit
$h(y=\pm 1/2,v_{y}\lessgtr 0)=0$
, the final expression for the MFR at the asymptotic limit
![]() $Kn\rightarrow \infty$
is
$Kn\rightarrow \infty$
is
where
![]() ${\it\gamma}\approx 0.577216$
is the Euler constant. This analytical solution is plotted in figure 1 as dash-dotted lines, where good agreement with fast spectral solutions of the Enskog equation (Wu et al.
Reference Wu, Zhang and Reese2015) can be seen when
${\it\gamma}\approx 0.577216$
is the Euler constant. This analytical solution is plotted in figure 1 as dash-dotted lines, where good agreement with fast spectral solutions of the Enskog equation (Wu et al.
Reference Wu, Zhang and Reese2015) can be seen when
![]() $Kn>30$
.
$Kn>30$
.
We turn to the flow in the hydrodynamic slip regime. The solid fraction
![]() ${\it\eta}$
is high, and the number density obtained from the Enskog equation is not uniform across the channel (unlike for the Boltzmann equation, where the normalized number density is unitary when the external acceleration is small). Substituting the local equilibrium distribution function
${\it\eta}$
is high, and the number density obtained from the Enskog equation is not uniform across the channel (unlike for the Boltzmann equation, where the normalized number density is unitary when the external acceleration is small). Substituting the local equilibrium distribution function
![]() $f(y,\boldsymbol{v})=n(y)f_{eq}(\boldsymbol{v})$
into (2.2), we obtain the following equation for the density variation:
$f(y,\boldsymbol{v})=n(y)f_{eq}(\boldsymbol{v})$
into (2.2), we obtain the following equation for the density variation:
which is numerically solved by an iterative method (Frezzotti Reference Frezzotti1997) under the constraint
![]() $\int _{-1/2}^{1/2}n(y)\,\text{d}y=1$
. Typical equilibrium density profiles are shown in figure 3. Near the wall, the density decreases monotonically under ultra-tight confinement (i.e.
$\int _{-1/2}^{1/2}n(y)\,\text{d}y=1$
. Typical equilibrium density profiles are shown in figure 3. Near the wall, the density decreases monotonically under ultra-tight confinement (i.e.
![]() $L/{\it\sigma}=2$
), but oscillates in the region within one to two hard-disc diameters from the wall when
$L/{\it\sigma}=2$
), but oscillates in the region within one to two hard-disc diameters from the wall when
![]() $L/{\it\sigma}$
is large (i.e.
$L/{\it\sigma}$
is large (i.e.
![]() $L/{\it\sigma}=10$
). Generally speaking, the larger the solid fraction, the larger the local disc density near the wall.
$L/{\it\sigma}=10$
). Generally speaking, the larger the solid fraction, the larger the local disc density near the wall.

Figure 3. Normalized density profiles of the dense gas under tight confinements (a)
![]() $L/{\it\sigma}=2$
and (b)
$L/{\it\sigma}=2$
and (b)
![]() $L/{\it\sigma}=10$
. The solid fractions, based on the average number density
$L/{\it\sigma}=10$
. The solid fractions, based on the average number density
![]() $n_{0}$
, are
$n_{0}$
, are
![]() ${\it\eta}=0.3$
, 0.2 and 0.1 for the solid, dashed and dash-dotted lines, respectively.
${\it\eta}=0.3$
, 0.2 and 0.1 for the solid, dashed and dash-dotted lines, respectively.
The density variation across the channel affects the gas slip velocity along the wall and the curvature of the velocity profile. To obtain quantitative estimates, we consider the Navier–Stokes equation with the first-order velocity slip boundary condition. Since the shear viscosity of the dense hard-disc system is (Garcia-Rojo, Luding & Brey Reference Garcia-Rojo, Luding and Brey2006)
the Navier–Stokes equation can be written as
where the effective Knudsen number is
and
![]() $b={\it\chi}(n){\it\eta}(n)$
. To exclude the effect of the wall on the shear viscosity, we choose
$b={\it\chi}(n){\it\eta}(n)$
. To exclude the effect of the wall on the shear viscosity, we choose
![]() $b(y)$
for
$b(y)$
for
![]() $y<-0.5+{\it\sigma}/L$
or
$y<-0.5+{\it\sigma}/L$
or
![]() $y>0.5-{\it\sigma}/L$
to be
$y>0.5-{\it\sigma}/L$
to be
![]() $b(y=0)$
.
$b(y=0)$
.
The first-order slip boundary condition at
![]() $y=\pm 1/2$
can be written as
$y=\pm 1/2$
can be written as
where the constant is set to be
![]() $C=1.11$
from the Boltzmann equation for hard-sphere molecules (Ohwada, Sone & Aoki Reference Ohwada, Sone and Aoki1989b
; Hadjiconstantinou Reference Hadjiconstantinou2003). Note that the second equation in (3.10) is derived from (3.8) using the symmetry condition
$C=1.11$
from the Boltzmann equation for hard-sphere molecules (Ohwada, Sone & Aoki Reference Ohwada, Sone and Aoki1989b
; Hadjiconstantinou Reference Hadjiconstantinou2003). Note that the second equation in (3.10) is derived from (3.8) using the symmetry condition
![]() $\partial V_{x}/\partial y=0$
at
$\partial V_{x}/\partial y=0$
at
![]() $y=0$
and the normalization condition
$y=0$
and the normalization condition
![]() $\int _{-1/2}^{1/2}n(y)\,\text{d}y=1$
.
$\int _{-1/2}^{1/2}n(y)\,\text{d}y=1$
.

Figure 4. Typical momentum profiles of the dense gas in the slip flow regime (
![]() $Kn=0.05$
). Solid symbols represent numerical solutions of the Navier–Stokes equation (3.8). The momentum profile from the Enskog equation is not a monotonically increasing function of
$Kn=0.05$
). Solid symbols represent numerical solutions of the Navier–Stokes equation (3.8). The momentum profile from the Enskog equation is not a monotonically increasing function of
![]() $y$
from the wall to the channel centre, because of the non-monotonic density variations.
$y$
from the wall to the channel centre, because of the non-monotonic density variations.
Although the slip velocity from the Enskog equation is smaller than that from the Boltzmann equation, the ‘momentum slip’, i.e.
![]() $V_{x}(\pm 0.5)n(\pm 0.5)$
, is the same for both equations. Therefore, the MFR predicted by the Enskog equation is smaller than that from the Boltzmann equation in the hydrodynamic flow regime because
$V_{x}(\pm 0.5)n(\pm 0.5)$
, is the same for both equations. Therefore, the MFR predicted by the Enskog equation is smaller than that from the Boltzmann equation in the hydrodynamic flow regime because
![]() $Kn_{e}>Kn$
, which makes the velocity profile by the Enskog equation much flatter than that by the Boltzmann equation. At the same
$Kn_{e}>Kn$
, which makes the velocity profile by the Enskog equation much flatter than that by the Boltzmann equation. At the same
![]() $Kn$
, as a smaller
$Kn$
, as a smaller
![]() $L/{\it\sigma}$
has a larger solid fraction
$L/{\it\sigma}$
has a larger solid fraction
![]() ${\it\eta}$
, and larger
${\it\eta}$
, and larger
![]() ${\it\eta}$
leads to larger
${\it\eta}$
leads to larger
![]() $Kn_{e}/Kn$
, the MFR decreases with the ratio
$Kn_{e}/Kn$
, the MFR decreases with the ratio
![]() $L/{\it\sigma}$
, as can be seen in figure 1. Typical momentum profiles in the hydrodynamic flow regime are shown in figure 4, where good agreement between the fast spectral solutions of the Enskog equation (Wu et al.
Reference Wu, Zhang and Reese2015) and the solutions of the Navier–Stokes equation can be found. We have also plotted the MFR from the Navier–Stokes equation in figure 1, showing that (3.8) is a good predictor of the MFR when
$L/{\it\sigma}$
, as can be seen in figure 1. Typical momentum profiles in the hydrodynamic flow regime are shown in figure 4, where good agreement between the fast spectral solutions of the Enskog equation (Wu et al.
Reference Wu, Zhang and Reese2015) and the solutions of the Navier–Stokes equation can be found. We have also plotted the MFR from the Navier–Stokes equation in figure 1, showing that (3.8) is a good predictor of the MFR when
![]() $Kn<0.1$
.
$Kn<0.1$
.

Figure 5. Macroscopic profiles of the dense gas for
![]() $Kn=0.237$
(
$Kn=0.237$
(
![]() ${\it\eta}=0.10$
, solid lines) and
${\it\eta}=0.10$
, solid lines) and
![]() $Kn=0.041$
(
$Kn=0.041$
(
![]() ${\it\eta}=0.35$
, dashed lines) when
${\it\eta}=0.35$
, dashed lines) when
![]() $L/{\it\sigma}=10$
. Although a larger value of
$L/{\it\sigma}=10$
. Although a larger value of
![]() ${\it\eta}$
means the momentum in the channel centre is larger, the significant dip in the density for larger
${\it\eta}$
means the momentum in the channel centre is larger, the significant dip in the density for larger
![]() ${\it\eta}$
reduces the local MFR, so that the two curves have the same overall MFR.
${\it\eta}$
reduces the local MFR, so that the two curves have the same overall MFR.
If
![]() $L/{\it\sigma}$
is fixed, the effective Knudsen number decreases as the solid fraction
$L/{\it\sigma}$
is fixed, the effective Knudsen number decreases as the solid fraction
![]() ${\it\eta}$
increases, hence the MFR should increase with the solid fraction and decrease with the global Knudsen number. From figure 1 we see that this is true in most cases. However, there is a critical point after which the MFR decreases although
${\it\eta}$
increases, hence the MFR should increase with the solid fraction and decrease with the global Knudsen number. From figure 1 we see that this is true in most cases. However, there is a critical point after which the MFR decreases although
![]() ${\it\eta}$
increases (and the MFR decreases with decreasing
${\it\eta}$
increases (and the MFR decreases with decreasing
![]() $Kn$
): for instance, see the curve of
$Kn$
): for instance, see the curve of
![]() $L/{\it\sigma}=10$
for
$L/{\it\sigma}=10$
for
![]() $Kn<0.08$
in figure 1, although the variation is quite small. This is because, at large
$Kn<0.08$
in figure 1, although the variation is quite small. This is because, at large
![]() ${\it\eta}$
, there is a significant dip in the number density at
${\it\eta}$
, there is a significant dip in the number density at
![]() $y\approx \pm (0.5-{\it\sigma}/L)$
, and this density dip may reduce the overall MFR. An illustrative example is shown in figure 5.
$y\approx \pm (0.5-{\it\sigma}/L)$
, and this density dip may reduce the overall MFR. An illustrative example is shown in figure 5.

Figure 6. MFR varying with
![]() $L/{\it\sigma}$
for the dense gas when
$L/{\it\sigma}$
for the dense gas when
![]() $Kn=0.5$
and
$Kn=0.5$
and
![]() $Kn=1$
.
$Kn=1$
.
Finally, we consider the transitional flow regime, which usually has a global Knudsen number ranging from approximately 0.1 to 10. Neither the hydrodynamic nor the free-molecular theories can explain the flow behaviour. Even for the Boltzmann equation, the regularized 26-moment equation of Gu & Emerson (Reference Gu and Emerson2009) can only give accurate results up to
![]() $Kn\sim 1$
. Since the MFR increases with decreasing
$Kn\sim 1$
. Since the MFR increases with decreasing
![]() $L/{\it\sigma}$
in the free-molecular flow regime, and the MFR increases with
$L/{\it\sigma}$
in the free-molecular flow regime, and the MFR increases with
![]() $L/{\it\sigma}$
in the hydrodynamic regime, in the transitional regime there should exist a specific value of
$L/{\it\sigma}$
in the hydrodynamic regime, in the transitional regime there should exist a specific value of
![]() $L/{\it\sigma}$
at which the MFR is minimum for a particular
$L/{\it\sigma}$
at which the MFR is minimum for a particular
![]() $Kn$
. Numerical results confirm that this minimum MFR occurs at
$Kn$
. Numerical results confirm that this minimum MFR occurs at
![]() $L/{\it\sigma}\approx 2{-}3$
in the transitional regime (see figure 6).
$L/{\it\sigma}\approx 2{-}3$
in the transitional regime (see figure 6).
3.2 Inelastic collisions:
 $0\leqslant {\it\alpha}<1$
$0\leqslant {\it\alpha}<1$
In the dilute limit
![]() ${\it\eta}\rightarrow 0$
, the behaviour of the MFR was studied by Alam, Mahajan & Shivanna (Reference Alam, Mahajan and Shivanna2015) using molecular dynamics simulations, and an anomalous velocity slip (i.e. the slip velocity decreases as
${\it\eta}\rightarrow 0$
, the behaviour of the MFR was studied by Alam, Mahajan & Shivanna (Reference Alam, Mahajan and Shivanna2015) using molecular dynamics simulations, and an anomalous velocity slip (i.e. the slip velocity decreases as
![]() $Kn$
increases) was observed. Here we investigate the origin of this anomalous velocity slip, and calculate the MFR of dilute-to-dense granular gases.
$Kn$
increases) was observed. Here we investigate the origin of this anomalous velocity slip, and calculate the MFR of dilute-to-dense granular gases.

Figure 7. Normalized density (a,b) and temperature (c,d) profiles of the dense granular gas under tight confinements (a,c)
![]() $L/{\it\sigma}=2$
and (b,d)
$L/{\it\sigma}=2$
and (b,d)
![]() $L/{\it\sigma}=10$
, for different values of the restitution coefficient. The normalized acceleration is
$L/{\it\sigma}=10$
, for different values of the restitution coefficient. The normalized acceleration is
![]() $F=0.0001$
.
$F=0.0001$
.
We first choose a small external acceleration (
![]() $F=0.0001$
). As the restitution coefficient
$F=0.0001$
). As the restitution coefficient
![]() ${\it\alpha}$
decreases, the gas temperature decreases monotonically from the wall to the channel centre, and the gas density near the wall (at the channel centre) decreases (increases); see figure 7. At large
${\it\alpha}$
decreases, the gas temperature decreases monotonically from the wall to the channel centre, and the gas density near the wall (at the channel centre) decreases (increases); see figure 7. At large
![]() $L/{\it\sigma}$
and small
$L/{\it\sigma}$
and small
![]() ${\it\alpha}$
, the gas concentrates in the channel centre and its density could even be larger than that near the wall. At fixed
${\it\alpha}$
, the gas concentrates in the channel centre and its density could even be larger than that near the wall. At fixed
![]() ${\it\alpha}$
, the decrease in the gas temperature gets larger when the solid fraction increases due to the increased number of dissipative collisions.
${\it\alpha}$
, the decrease in the gas temperature gets larger when the solid fraction increases due to the increased number of dissipative collisions.

Figure 8. (a,c,e) The slip velocity and (b,d,f) the MFR of a dense granular gas for different values of the restitution coefficient
![]() ${\it\alpha}$
, when
${\it\alpha}$
, when
![]() $L/{\it\sigma}=2$
(a,b), 10 (c,d) and 30 (e,f), and the normalized acceleration is
$L/{\it\sigma}=2$
(a,b), 10 (c,d) and 30 (e,f), and the normalized acceleration is
![]() $F=0.0001$
. In (a,c,e) the lines are the velocity slip obtained from numerical solution of the generalized Enskog equation (2.2). Symbols are calculated from the numerical results according to (3.11).
$F=0.0001$
. In (a,c,e) the lines are the velocity slip obtained from numerical solution of the generalized Enskog equation (2.2). Symbols are calculated from the numerical results according to (3.11).
The anomalous velocity slip can be explained qualitatively using the shear viscosity (3.7), although the true viscosity is a function of the restitution coefficient (Garzó & Dufty Reference Garzó and Dufty1999; Lutsko Reference Lutsko2005). Taking into account the temperature variation across the channel, the slip velocity (3.10) may be extended to
At fixed
![]() $L/{\it\sigma}$
and fixed solid fraction
$L/{\it\sigma}$
and fixed solid fraction
![]() ${\it\eta}$
(i.e. the Knudsen number is fixed), both the gas density at the wall and the ratio of the bulk gas temperature to the near-wall gas temperature
${\it\eta}$
(i.e. the Knudsen number is fixed), both the gas density at the wall and the ratio of the bulk gas temperature to the near-wall gas temperature
![]() $T(0)/T(\pm 1/2)$
decreases with the restitution coefficient (see figure 7). Therefore, the velocity slip increases as the restitution coefficient decreases; see figure 8. On the other hand, for fixed
$T(0)/T(\pm 1/2)$
decreases with the restitution coefficient (see figure 7). Therefore, the velocity slip increases as the restitution coefficient decreases; see figure 8. On the other hand, for fixed
![]() $L/{\it\sigma}$
and large values of
$L/{\it\sigma}$
and large values of
![]() ${\it\alpha}$
, the temperature ratio
${\it\alpha}$
, the temperature ratio
![]() $T(0)/T(\pm 1/2)$
decreases but the near-wall gas density increases with the solid fraction, such that the slip velocity decreases with
$T(0)/T(\pm 1/2)$
decreases but the near-wall gas density increases with the solid fraction, such that the slip velocity decreases with
![]() $Kn$
, for example, when
$Kn$
, for example, when
![]() $L/{\it\sigma}=10$
and
$L/{\it\sigma}=10$
and
![]() ${\it\alpha}>0.9$
. When
${\it\alpha}>0.9$
. When
![]() ${\it\alpha}$
is small, however, the decrease of
${\it\alpha}$
is small, however, the decrease of
![]() $T(0)/T(\pm 1/2)$
with respect to the solid fraction is rapid, and the slip velocity increases with decreasing
$T(0)/T(\pm 1/2)$
with respect to the solid fraction is rapid, and the slip velocity increases with decreasing
![]() $Kn$
in the slip flow regime (this is the so-called anomalous velocity slip); for instance, see figure 8 for
$Kn$
in the slip flow regime (this is the so-called anomalous velocity slip); for instance, see figure 8 for
![]() ${\it\alpha}=0.8$
and
${\it\alpha}=0.8$
and
![]() $L/{\it\sigma}=10$
. For intermediate values of
$L/{\it\sigma}=10$
. For intermediate values of
![]() ${\it\alpha}$
, it is possible for the slip velocity to remain constant if the decrease of the temperature ratio
${\it\alpha}$
, it is possible for the slip velocity to remain constant if the decrease of the temperature ratio
![]() $\sqrt{T(0)/T(\pm 1/2)}$
and the increase of the near-wall density cancel each other (see figure 8 for
$\sqrt{T(0)/T(\pm 1/2)}$
and the increase of the near-wall density cancel each other (see figure 8 for
![]() ${\it\alpha}=0.9$
and
${\it\alpha}=0.9$
and
![]() $L/{\it\sigma}=10$
).
$L/{\it\sigma}=10$
).

Figure 9. The influence of the external acceleration on the MFR at
![]() $L/{\it\sigma}=30$
, when the restitution coefficient is
$L/{\it\sigma}=30$
, when the restitution coefficient is
![]() ${\it\alpha}=0.9$
. The normalized acceleration is
${\it\alpha}=0.9$
. The normalized acceleration is
![]() $F=0.0001$
(triangles),
$F=0.0001$
(triangles),
![]() $F=0.5$
(circles) and
$F=0.5$
(circles) and
![]() $F=1$
(pentagrams). Inset: temperature and momentum profiles in the slip (first row) and transitional (second row) flow regimes.
$F=1$
(pentagrams). Inset: temperature and momentum profiles in the slip (first row) and transitional (second row) flow regimes.
The variation of the MFR with the restitution coefficient is also shown in figure 8. In the free-molecular flow regime, the MFR is insensitive to the restitution coefficient since there are essentially no collisions between the hard discs. In the transitional and slip flow regimes, when
![]() $Kn$
is fixed, the MFR increases as
$Kn$
is fixed, the MFR increases as
![]() ${\it\alpha}$
decreases. One reason for this increase in MFR is that the velocity slip (and momentum slip) increases when
${\it\alpha}$
decreases. One reason for this increase in MFR is that the velocity slip (and momentum slip) increases when
![]() ${\it\alpha}$
decreases. Another reason is that the effective Knudsen number (roughly
${\it\alpha}$
decreases. Another reason is that the effective Knudsen number (roughly
![]() $\sqrt{T(y=0)}Kn_{e}$
) decreases with
$\sqrt{T(y=0)}Kn_{e}$
) decreases with
![]() ${\it\alpha}$
, which consequently makes the velocity profile steeper and increases the MFR. Interestingly, for
${\it\alpha}$
, which consequently makes the velocity profile steeper and increases the MFR. Interestingly, for
![]() $L/{\it\sigma}=2$
the Knudsen minimum, which vanishes for elastic collisions, re-emerges when the collisions between hard discs are inelastic.
$L/{\it\sigma}=2$
the Knudsen minimum, which vanishes for elastic collisions, re-emerges when the collisions between hard discs are inelastic.
Finally, we consider the influence of large external accelerations (i.e.
![]() $F\sim 1$
) on the MFR. For granular gases driven by a gravitational force, a large value of
$F\sim 1$
) on the MFR. For granular gases driven by a gravitational force, a large value of
![]() $F$
is possible because of the large disc size and mass, and the small thermal velocity (Tij & Santos Reference Tij and Santos2004). Figure 9 shows that the normalized MFR reduces with increasing external acceleration. This is consistent with results from Boltzmann-type kinetic equations (Aoki, Takata & Nakanishi Reference Aoki, Takata and Nakanishi2002; Meng et al.
Reference Meng, Wu, Reese and Zhang2013). Generally speaking, because of the viscous heating, a larger external acceleration results in a higher gas temperature and consequently a larger effective Knudsen number
$F$
is possible because of the large disc size and mass, and the small thermal velocity (Tij & Santos Reference Tij and Santos2004). Figure 9 shows that the normalized MFR reduces with increasing external acceleration. This is consistent with results from Boltzmann-type kinetic equations (Aoki, Takata & Nakanishi Reference Aoki, Takata and Nakanishi2002; Meng et al.
Reference Meng, Wu, Reese and Zhang2013). Generally speaking, because of the viscous heating, a larger external acceleration results in a higher gas temperature and consequently a larger effective Knudsen number
![]() $Kn_{e}$
. In the slip flow regime, a larger
$Kn_{e}$
. In the slip flow regime, a larger
![]() $Kn_{e}$
has a flatter velocity profile and hence smaller MFR (see the first row in the inset of figure 9). Near the free-molecular flow regime, the slip velocity
$Kn_{e}$
has a flatter velocity profile and hence smaller MFR (see the first row in the inset of figure 9). Near the free-molecular flow regime, the slip velocity
![]() $U_{x}(y=\pm 1/2)$
is proportional to
$U_{x}(y=\pm 1/2)$
is proportional to
![]() $\sqrt{T(y=\pm 1/2)}$
, and since
$\sqrt{T(y=\pm 1/2)}$
, and since
![]() $\sqrt{T(y=\pm 1/2)}/F$
decreases as the normalized external acceleration
$\sqrt{T(y=\pm 1/2)}/F$
decreases as the normalized external acceleration
![]() $F$
increases, the normalized velocity slip
$F$
increases, the normalized velocity slip
![]() $V_{x}(y=\pm 1/2)=U_{x}(y=\pm 1/2)/F$
decreases as
$V_{x}(y=\pm 1/2)=U_{x}(y=\pm 1/2)/F$
decreases as
![]() $F$
increases (see the second row in the inset of figure 9), and so the MFR decreases because the normalized density profile is nearly unitary across the channel when
$F$
increases (see the second row in the inset of figure 9), and so the MFR decreases because the normalized density profile is nearly unitary across the channel when
![]() $Kn$
is large. Similar effects of the external force on the MFR are also observed at other values of
$Kn$
is large. Similar effects of the external force on the MFR are also observed at other values of
![]() $L/{\it\sigma}$
and
$L/{\it\sigma}$
and
![]() ${\it\alpha}$
.
${\it\alpha}$
.
4 Conclusions
Through both numerical solution of the generalized Enskog equation and analytical approaches, we have investigated the force-driven Poiseuille flow of a gas between two parallel plates. The dilute-to-dense gas exhibited new flow physics due to the competition of three characteristic length scales: the mean free path, the channel width and the molecular diameter.
For elastic collisions in the hard-disc gas, we found the following. (i) In the slip flow regime, the normalized MFR becomes smaller as the confinement (i.e.
![]() $L/{\it\sigma}$
) becomes tighter, for a fixed Knudsen number. In the limit of
$L/{\it\sigma}$
) becomes tighter, for a fixed Knudsen number. In the limit of
![]() $L/{\it\sigma}\rightarrow \infty$
, the MFR approaches that of the Boltzmann equation (in which the binary collisions are localized in space). When
$L/{\it\sigma}\rightarrow \infty$
, the MFR approaches that of the Boltzmann equation (in which the binary collisions are localized in space). When
![]() $L/{\it\sigma}$
is fixed, the variation of the MFR with the Knudsen number is not monotonic. As the Knudsen number decreases from 0.1, the MFR first increases and then decreases; the maximum MFR occurs when the average solid fraction is approximately
$L/{\it\sigma}$
is fixed, the variation of the MFR with the Knudsen number is not monotonic. As the Knudsen number decreases from 0.1, the MFR first increases and then decreases; the maximum MFR occurs when the average solid fraction is approximately
![]() $0.3$
. We explained this exotic behaviour using the Navier–Stokes equation with a first-order velocity slip boundary condition. (ii) In the free-molecular flow regime, for a fixed Knudsen number, the MFR increases as
$0.3$
. We explained this exotic behaviour using the Navier–Stokes equation with a first-order velocity slip boundary condition. (ii) In the free-molecular flow regime, for a fixed Knudsen number, the MFR increases as
![]() $L/{\it\sigma}$
is reduced, but in the limit
$L/{\it\sigma}$
is reduced, but in the limit
![]() $L/{\it\sigma}\rightarrow \infty$
the MFR is reduced to that of the Boltzmann equation. Our simple treatment of the average collision frequency accurately captures the influence of the tight wall confinement. (iii) In the transitional flow regime, for a fixed Knudsen number, the variation of the MFR with
$L/{\it\sigma}\rightarrow \infty$
the MFR is reduced to that of the Boltzmann equation. Our simple treatment of the average collision frequency accurately captures the influence of the tight wall confinement. (iii) In the transitional flow regime, for a fixed Knudsen number, the variation of the MFR with
![]() $L/{\it\sigma}$
is not monotonic, and the minimum MFR is achieved at
$L/{\it\sigma}$
is not monotonic, and the minimum MFR is achieved at
![]() $L/{\it\sigma}\approx 2{-}3$
.
$L/{\it\sigma}\approx 2{-}3$
.
When the collisions between the hard discs are inelastic, we found that the MFR increases as the restitution coefficient decreases due to the increase of the velocity slip and the decrease of the effective Knudsen number. We also proposed a simple formula to predict the anomalous velocity slip (which decreases as the Knudsen number increases). This simple formula and numerical solutions of the generalized Enskog equation also showed that the slip velocity could remain constant with varying Knudsen number at appropriate values of
![]() $L/{\it\sigma}$
and the restitution coefficient. Finally, we showed that the normalized MFR reduces as the normalized external acceleration increases. Although we have only considered the diffuse boundary condition, the use of other momentum accommodation coefficients yield qualitatively the same results.
$L/{\it\sigma}$
and the restitution coefficient. Finally, we showed that the normalized MFR reduces as the normalized external acceleration increases. Although we have only considered the diffuse boundary condition, the use of other momentum accommodation coefficients yield qualitatively the same results.
This research sheds new light on the influence of tight confinement on the mass flow rate of dense gases, and indicates that the MFR for Poiseuille flow obtained from the Boltzmann equation is not accurate for dense gases. For practical application to predicting the permeability of ultra-tight shale strata, more work needs to be done; for instance, to include the mean-field term so that a realistic equation of state for the shale gas is recovered, and to properly deal with the gas–wall interactions. Also, the inclusion of a mean-field term will enable us to study the flow dynamics of dense charged grains.
Acknowledgements
This work is financially supported by the UK’s Engineering and Physical Sciences Research Council (EPSRC) under grants EP/M021475/1, EP/L00030X/1, EP/K038621/1, EP/I011927/1 and EP/N016602/1. H.L. gratefully acknowledges the financial support of the ‘Thousand Talents Program’ for Distinguished Young Scholars and the National Natural Science Foundation of China under grant no. 51506168.