The effect of entrained air turbulence on dispersion of droplets (with Stokes number based on the Kolmogorov time scale, 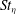 $St_{{\it\eta}}$ , of the order of 1) in a polydispersed spray is experimentally studied through simultaneous and planar measurements of droplet size, velocity and gas flow velocity (Hardalupas et al., Exp. Fluids, vol. 49, 2010, pp. 417–434). The preferential accumulation of droplets at various measurement locations in the spray was examined by two independent methods viz. counting droplets on images by dividing the image in to boxes of different sizes, and by estimating the radial distribution function (RDF). The dimension of droplet clusters (obtained by both approaches) was of the order of Kolmogorov’s length scale of the fluid flow, implying the significant influence of viscous scales of the fluid flow on cluster formation. The RDF of different size classes indicated an increase in cluster dimension for larger droplets (higher
$St_{{\it\eta}}$ , of the order of 1) in a polydispersed spray is experimentally studied through simultaneous and planar measurements of droplet size, velocity and gas flow velocity (Hardalupas et al., Exp. Fluids, vol. 49, 2010, pp. 417–434). The preferential accumulation of droplets at various measurement locations in the spray was examined by two independent methods viz. counting droplets on images by dividing the image in to boxes of different sizes, and by estimating the radial distribution function (RDF). The dimension of droplet clusters (obtained by both approaches) was of the order of Kolmogorov’s length scale of the fluid flow, implying the significant influence of viscous scales of the fluid flow on cluster formation. The RDF of different size classes indicated an increase in cluster dimension for larger droplets (higher  $St_{{\it\eta}}$ ). The length scales of droplet clusters increased towards the outer spray regions, where the gravitational influence on droplets is stronger compared to the central spray locations. The correlation between fluctuations of droplet concentration and droplet and gas velocities were estimated and found to be negative near the spray edge, while it was close to zero at other locations. The probability density function of slip between fluctuating droplet velocity and gas velocity ‘seen’ by the droplets signified presence of considerable instantaneous slip velocity, which is crucial for droplet–gas momentum exchange. In order to investigate different mechanisms of turbulence modulation of the carrier phase, the three correlation terms in the turbulent kinetic energy equation for particle-laden flows (Chen & Wood, Can. J. Chem. Engng, vol. 65, 1985, pp. 349–360) are evaluated conditional on droplet size classes. Based on the comparison of the correlation terms, it is recognized that although the interphase energy transfer due to fluctuations of droplet concentration is low compared to the energy exchange only due to droplet drag (the magnitude of which is controlled by average droplet mass loading), the former cannot be considered negligible, and should be accounted in two phase flow modelling.
$St_{{\it\eta}}$ ). The length scales of droplet clusters increased towards the outer spray regions, where the gravitational influence on droplets is stronger compared to the central spray locations. The correlation between fluctuations of droplet concentration and droplet and gas velocities were estimated and found to be negative near the spray edge, while it was close to zero at other locations. The probability density function of slip between fluctuating droplet velocity and gas velocity ‘seen’ by the droplets signified presence of considerable instantaneous slip velocity, which is crucial for droplet–gas momentum exchange. In order to investigate different mechanisms of turbulence modulation of the carrier phase, the three correlation terms in the turbulent kinetic energy equation for particle-laden flows (Chen & Wood, Can. J. Chem. Engng, vol. 65, 1985, pp. 349–360) are evaluated conditional on droplet size classes. Based on the comparison of the correlation terms, it is recognized that although the interphase energy transfer due to fluctuations of droplet concentration is low compared to the energy exchange only due to droplet drag (the magnitude of which is controlled by average droplet mass loading), the former cannot be considered negligible, and should be accounted in two phase flow modelling.