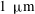1 Introduction
Two-phase displacement flow in a confined geometry is a fundamental problem in fluid mechanics with applications in biomechanics, geophysics and industry. If a viscous fluid (oil) is displaced by an inviscid one (air) and the geometry is sufficiently small that gravitational and inertial effects can be neglected then the dominant dynamic parameter is the capillary number
![]() $Ca={\it\mu}U_{f}^{\ast }/{\it\sigma}$
, which quantifies the ratio of viscous to surface tension forces. Here,
$Ca={\it\mu}U_{f}^{\ast }/{\it\sigma}$
, which quantifies the ratio of viscous to surface tension forces. Here,
![]() ${\it\mu}$
is the viscosity of the oil,
${\it\mu}$
is the viscosity of the oil,
![]() ${\it\sigma}$
the surface tension of the interface and
${\it\sigma}$
the surface tension of the interface and
![]() $U_{f}^{\ast }$
the velocity of the advancing interface. The remaining parameters that influence the behaviour are entirely geometric.
$U_{f}^{\ast }$
the velocity of the advancing interface. The remaining parameters that influence the behaviour are entirely geometric.
Following the classic work of Saffman & Taylor (Reference Saffman and Taylor1958), the tube geometry that has attracted the most attention is the Hele-Shaw channel: an axially uniform tube with rectangular cross-section of large aspect ratio
![]() ${\it\alpha}=W^{\ast }/H^{\ast }\gg 1$
, where
${\it\alpha}=W^{\ast }/H^{\ast }\gg 1$
, where
![]() $W^{\ast }$
is the width and
$W^{\ast }$
is the width and
![]() $H^{\ast }$
the height of the cross-section. Saffman & Taylor (Reference Saffman and Taylor1958) introduced a depth-averaged model of the system that possesses symmetric and asymmetric (Taylor & Saffman Reference Taylor and Saffman1959) families of solutions in the absence of surface tension. The depth-averaged system involves a single modified capillary number
$H^{\ast }$
the height of the cross-section. Saffman & Taylor (Reference Saffman and Taylor1958) introduced a depth-averaged model of the system that possesses symmetric and asymmetric (Taylor & Saffman Reference Taylor and Saffman1959) families of solutions in the absence of surface tension. The depth-averaged system involves a single modified capillary number
![]() $1/B=12\,{\it\alpha}^{2}\,Ca$
combining geometric and dynamic effects. In experiments only a single symmetric family of solutions is ever observed, and the fractional finger width
$1/B=12\,{\it\alpha}^{2}\,Ca$
combining geometric and dynamic effects. In experiments only a single symmetric family of solutions is ever observed, and the fractional finger width
![]() ${\it\lambda}={\it\lambda}^{\ast }/W^{\ast }$
, where
${\it\lambda}={\it\lambda}^{\ast }/W^{\ast }$
, where
![]() ${\it\lambda}^{\ast }$
is the dimensional finger width, does indeed collapse onto a master curve when plotted as a function of
${\it\lambda}^{\ast }$
is the dimensional finger width, does indeed collapse onto a master curve when plotted as a function of
![]() $1/B$
provided
$1/B$
provided
![]() $1/B<7000$
(Tabeling, Zocchi & Libchaber Reference Tabeling, Zocchi and Libchaber1987). The introduction of finite surface tension within the depth-averaged model selects a single family of symmetric solutions with the correct qualitative behaviour as shown by McLean & Saffman (Reference McLean and Saffman1981), who modified the model accordingly, albeit non-rationally in a strict asymptotic sense. A rationally derived, thin-film correction due to Park & Homsy (Reference Park and Homsy1984) is required to give quantitative agreement between this model and experiments (Reinelt & Saffman Reference Reinelt and Saffman1985) at small capillary numbers; capillary numbers of
$1/B<7000$
(Tabeling, Zocchi & Libchaber Reference Tabeling, Zocchi and Libchaber1987). The introduction of finite surface tension within the depth-averaged model selects a single family of symmetric solutions with the correct qualitative behaviour as shown by McLean & Saffman (Reference McLean and Saffman1981), who modified the model accordingly, albeit non-rationally in a strict asymptotic sense. A rationally derived, thin-film correction due to Park & Homsy (Reference Park and Homsy1984) is required to give quantitative agreement between this model and experiments (Reinelt & Saffman Reference Reinelt and Saffman1985) at small capillary numbers; capillary numbers of
![]() $O(10^{-3})$
are required to reduce the relative errors below 10 %. Later, de Lózar, Juel & Hazel (Reference de Lózar, Juel and Hazel2008) showed that the McLean & Saffman (Reference McLean and Saffman1981) depth-averaged model without the thin-film correction is in quantitative agreement with three-dimensional Stokes simulations for
$O(10^{-3})$
are required to reduce the relative errors below 10 %. Later, de Lózar, Juel & Hazel (Reference de Lózar, Juel and Hazel2008) showed that the McLean & Saffman (Reference McLean and Saffman1981) depth-averaged model without the thin-film correction is in quantitative agreement with three-dimensional Stokes simulations for
![]() ${\it\alpha}\geqslant 8$
when
${\it\alpha}\geqslant 8$
when
![]() $Ca\geqslant 10^{-2}$
; the lower bound being a limitation of the Stokes simulations, rather than a failure of the depth-averaged model. In fact, the rational inclusion of surface tension (at large values of
$Ca\geqslant 10^{-2}$
; the lower bound being a limitation of the Stokes simulations, rather than a failure of the depth-averaged model. In fact, the rational inclusion of surface tension (at large values of
![]() $1/B$
) requires a beyond-all-orders asymptotic analysis as reviewed by Tanveer (Reference Tanveer2000) among others. It is also known that the McLean & Saffman (Reference McLean and Saffman1981) model contains alternative families of symmetric solutions (Romero Reference Romero1982; Vanden-Broeck Reference Vanden-Broeck1983), in which the interface forms multiple tips (Gardiner, McCue & Moroney Reference Gardiner, McCue and Moroney2015), but these are all unstable and have remained of academic interest only. It is also possible to find solutions containing multiple distinct fingers in the presence of surface tension (Magdaleno & Casademut Reference Magdaleno and Casademut1999), but these are not the focus of our current study.
$1/B$
) requires a beyond-all-orders asymptotic analysis as reviewed by Tanveer (Reference Tanveer2000) among others. It is also known that the McLean & Saffman (Reference McLean and Saffman1981) model contains alternative families of symmetric solutions (Romero Reference Romero1982; Vanden-Broeck Reference Vanden-Broeck1983), in which the interface forms multiple tips (Gardiner, McCue & Moroney Reference Gardiner, McCue and Moroney2015), but these are all unstable and have remained of academic interest only. It is also possible to find solutions containing multiple distinct fingers in the presence of surface tension (Magdaleno & Casademut Reference Magdaleno and Casademut1999), but these are not the focus of our current study.
Motivated by the finger selection problem, many groups have investigated the effects of geometric perturbations on two-phase flow in a Hele-Shaw channel. The introduction of wires (Zocchi et al.
Reference Zocchi, Shaw, Libchaber and Kadanoff1987; Hong Reference Hong1989), threads or grooves (Rabaud, Couder & Gerard Reference Rabaud, Couder and Gerard1988) parallel to the direction of flow increases the curvature of the finger tip, leading to alternative, narrower, symmetric fingers than in the unperturbed system. Dendrite-like finger shapes have also been observed on introduction of threads (Rabaud et al.
Reference Rabaud, Couder and Gerard1988) or small bubbles in front of the finger tip (Couder et al.
Reference Couder, Cardoso, Dupuy, Tavernier and Thom1986a
; Couder, Gerard & Rabaud Reference Couder, Gerard and Rabaud1986b
); the smooth sides of the finger become unstable and develop oscillatory patterns that grow behind the tip as the finger advances. Tabeling et al. (Reference Tabeling, Zocchi and Libchaber1987) found deviations from the symmetric finger shape with tip splitting occurring for
![]() $1/B>7000$
. A critical value of
$1/B>7000$
. A critical value of
![]() $1/B$
could not be found, but the instability occurred at lower
$1/B$
could not be found, but the instability occurred at lower
![]() $1/B$
when the roughness was adjusted from 0.3 % to 3 % of the channel height, suggesting that small, uncontrollable, geometric non-uniformities were the cause of the instability. Early destabilisation due to controlled perturbations of the interface was demonstrated by Chevalier, Lindner & Clément (Reference Chevalier, Lindner and Clément2007), who studied fingering in a granular suspension in viscous liquid, where the perturbation amplitude was proportional to the grain size. Associated theoretical studies have also explored finger stability (Bensimon Reference Bensimon1986), and the effect of anisotropy on finger selection (Ben Amar & Brener Reference Ben Amar and Brener1996). In addition, a study of viscous fingering in very large aspect ratio channels (
$1/B$
when the roughness was adjusted from 0.3 % to 3 % of the channel height, suggesting that small, uncontrollable, geometric non-uniformities were the cause of the instability. Early destabilisation due to controlled perturbations of the interface was demonstrated by Chevalier, Lindner & Clément (Reference Chevalier, Lindner and Clément2007), who studied fingering in a granular suspension in viscous liquid, where the perturbation amplitude was proportional to the grain size. Associated theoretical studies have also explored finger stability (Bensimon Reference Bensimon1986), and the effect of anisotropy on finger selection (Ben Amar & Brener Reference Ben Amar and Brener1996). In addition, a study of viscous fingering in very large aspect ratio channels (
![]() $158\leqslant {\it\alpha}\leqslant 490$
) revealed unsteady finger propagation in which the finger tip exhibited significant lateral movement (Moore et al.
Reference Moore, Juel, Burgess, McCormick and Swinney2002). Finger width fluctuations were found to scale as
$158\leqslant {\it\alpha}\leqslant 490$
) revealed unsteady finger propagation in which the finger tip exhibited significant lateral movement (Moore et al.
Reference Moore, Juel, Burgess, McCormick and Swinney2002). Finger width fluctuations were found to scale as
![]() $Ca^{-2/3}$
, inversely proportionally to the film thickness deposited on the top and bottom boundaries of the channel (Bretherton Reference Bretherton1961; Park & Homsy Reference Park and Homsy1984). The fluctuations increased as the film thickness decreased and details of the wall roughness began to influence the system. Thus, sensitivity to channel roughness could underlie the meandering of the finger tip.
$Ca^{-2/3}$
, inversely proportionally to the film thickness deposited on the top and bottom boundaries of the channel (Bretherton Reference Bretherton1961; Park & Homsy Reference Park and Homsy1984). The fluctuations increased as the film thickness decreased and details of the wall roughness began to influence the system. Thus, sensitivity to channel roughness could underlie the meandering of the finger tip.
More recently, motivated by the physiological problem of airway reopening, de Lózar et al. (Reference de Lózar, Heap, Box, Hazel and Juel2009), Pailha et al. (Reference Pailha, Hazel, Glendinning and Juel2012) and Hazel et al. (Reference Hazel, Pailha, Cox and Juel2013) investigated two-phase flow through rectangular tubes with aspect ratio
![]() ${\it\alpha}\leqslant 13$
that were partially occluded by axially uniform rectangular blocks occupying 50 % and 33.3 % of the tube height. Multiple stable modes of propagation were found in these geometries including asymmetric and oscillatory modes as well as the expected symmetric mode. These states are connected by a complex bifurcation structure that remains incompletely understood, in part because only stable modes could be identified experimentally. Thompson, Juel & Hazel (Reference Thompson, Juel and Hazel2014) modified the McLean & Saffman (Reference McLean and Saffman1981) depth-averaged model to include a prescribed depth profile and performed numerical simulations for a channel aspect ratio
${\it\alpha}\leqslant 13$
that were partially occluded by axially uniform rectangular blocks occupying 50 % and 33.3 % of the tube height. Multiple stable modes of propagation were found in these geometries including asymmetric and oscillatory modes as well as the expected symmetric mode. These states are connected by a complex bifurcation structure that remains incompletely understood, in part because only stable modes could be identified experimentally. Thompson, Juel & Hazel (Reference Thompson, Juel and Hazel2014) modified the McLean & Saffman (Reference McLean and Saffman1981) depth-averaged model to include a prescribed depth profile and performed numerical simulations for a channel aspect ratio
![]() ${\it\alpha}=10$
and relative obstacle width
${\it\alpha}=10$
and relative obstacle width
![]() ${\it\alpha}_{w}=0.25$
, but with variable values of the relative occlusion height
${\it\alpha}_{w}=0.25$
, but with variable values of the relative occlusion height
![]() ${\it\alpha}_{h}$
. The simulations revealed that all experimentally observed states were predicted by the model. The resulting bifurcation structure was qualitatively consistent with experimental findings, but the nominal aspect ratio
${\it\alpha}_{h}$
. The simulations revealed that all experimentally observed states were predicted by the model. The resulting bifurcation structure was qualitatively consistent with experimental findings, but the nominal aspect ratio
![]() ${\it\alpha}=10$
was conjectured to be too small for the model to yield quantitative agreement. Nonetheless, by continuously reducing the relative height of the occlusion from
${\it\alpha}=10$
was conjectured to be too small for the model to yield quantitative agreement. Nonetheless, by continuously reducing the relative height of the occlusion from
![]() ${\it\alpha}_{h}=0.2$
to 0.01, Thompson et al. (Reference Thompson, Juel and Hazel2014) predicted that multiple states should occur at much lower occlusion heights than used in the previous experiments.
${\it\alpha}_{h}=0.2$
to 0.01, Thompson et al. (Reference Thompson, Juel and Hazel2014) predicted that multiple states should occur at much lower occlusion heights than used in the previous experiments.
In this paper, we exploit the channel geometry introduced by de Lózar et al. (Reference de Lózar, Heap, Box, Hazel and Juel2009) to probe the sensitivity of viscous fingering to a step change in channel depth as a function of channel aspect ratio
![]() ${\it\alpha}$
. The system is simple, robust and enables transitions between multiple states to be clearly identified when the geometric variations are on a larger scale than the wall roughness. We begin by assessing experimentally the predictive capability of Thompson et al.’s model, presented for completeness in § 2. Thus, we conduct new sets of experiments in Hele-Shaw channels of
${\it\alpha}$
. The system is simple, robust and enables transitions between multiple states to be clearly identified when the geometric variations are on a larger scale than the wall roughness. We begin by assessing experimentally the predictive capability of Thompson et al.’s model, presented for completeness in § 2. Thus, we conduct new sets of experiments in Hele-Shaw channels of
![]() ${\it\alpha}\geqslant 20$
containing thin, centred, rectangular occlusions that range from 0.6 % to 12 % of the channel height, which are described in § 3. In §§ 4.1 and 4.2, we demonstrate that the depth-averaged model is in quantitative agreement with the experimental results for
${\it\alpha}\geqslant 20$
containing thin, centred, rectangular occlusions that range from 0.6 % to 12 % of the channel height, which are described in § 3. In §§ 4.1 and 4.2, we demonstrate that the depth-averaged model is in quantitative agreement with the experimental results for
![]() ${\it\alpha}\geqslant 40$
, provided that
${\it\alpha}\geqslant 40$
, provided that
![]() $Ca\leqslant 0.012$
. Moreover, we find that the height of occlusion required to observe bifurcations to asymmetric and oscillatory modes of propagation within the experimental range of
$Ca\leqslant 0.012$
. Moreover, we find that the height of occlusion required to observe bifurcations to asymmetric and oscillatory modes of propagation within the experimental range of
![]() $Ca$
decreases with increasing aspect ratio.
$Ca$
decreases with increasing aspect ratio.
The quantitative agreement between experiments and the model allows us to explore numerically, in §§ 4.3 and 4.4, the links between the multiple modes of finger propagation that arise in the presence of a centred prescribed depth variation, and the classical works in Hele-Shaw channels described above. In fact, we can demonstrate for the first time that the asymmetric and multiple-tipped solutions observed in smaller aspect ratio channels are the unstable asymmetric Saffman–Taylor solutions and symmetric Romero–Vanden-Broeck solutions having been stabilised by the presence of the occlusion. In § 4.5, we find that the decreasing occlusion height required to stabilise the asymmetric solutions with increasing aspect ratio becomes comparable with the typical roughness scale for
![]() ${\it\alpha}>155$
. We conclude with a summary of our results in § 5, in which we conjecture that the sensitivity of Saffman–Taylor flow in large aspect ratio Hele-Shaw channels is an inevitable consequence of the roughness-induced stabilisation of unstable solution branches already present in the perfect system.
${\it\alpha}>155$
. We conclude with a summary of our results in § 5, in which we conjecture that the sensitivity of Saffman–Taylor flow in large aspect ratio Hele-Shaw channels is an inevitable consequence of the roughness-induced stabilisation of unstable solution branches already present in the perfect system.
2 Depth-averaged model
We use the two-dimensional model for finger propagation in a Hele-Shaw channel with spatially varying height profile, previously developed by Thompson et al. (Reference Thompson, Juel and Hazel2014). The channel has dimensional width
![]() $W^{\ast }$
and maximum height
$W^{\ast }$
and maximum height
![]() $H^{\ast }$
. We work in a Cartesian coordinate system
$H^{\ast }$
. We work in a Cartesian coordinate system
![]() $(x^{\ast },y^{\ast },z^{\ast })$
, aligned with the channel such that
$(x^{\ast },y^{\ast },z^{\ast })$
, aligned with the channel such that
![]() $x^{\ast }$
is the axial coordinate and
$x^{\ast }$
is the axial coordinate and
![]() $y^{\ast }$
and
$y^{\ast }$
and
![]() $z^{\ast }$
span the cross-section. Hereinafter, asterisks are used to distinguish dimensional quantities from the dimensionless equivalents. The coordinates
$z^{\ast }$
span the cross-section. Hereinafter, asterisks are used to distinguish dimensional quantities from the dimensionless equivalents. The coordinates
![]() $x^{\ast }$
and
$x^{\ast }$
and
![]() $y^{\ast }$
are non-dimensionalised on the scale
$y^{\ast }$
are non-dimensionalised on the scale
![]() $W^{\ast }/2$
and the depth profile
$W^{\ast }/2$
and the depth profile
![]() $b^{\ast }(y^{\ast })$
on the scale
$b^{\ast }(y^{\ast })$
on the scale
![]() $H^{\ast }$
. Therefore, in dimensionless coordinates
$H^{\ast }$
. Therefore, in dimensionless coordinates
![]() $(x,y,z)$
, the fluid domain is
$(x,y,z)$
, the fluid domain is
![]() $X_{0}\leqslant x\leqslant X_{1}$
,
$X_{0}\leqslant x\leqslant X_{1}$
,
![]() $-1\leqslant y\leqslant 1$
and
$-1\leqslant y\leqslant 1$
and
![]() $0\leqslant z\leqslant b(y)$
where
$0\leqslant z\leqslant b(y)$
where
![]() $X_{0}$
and
$X_{0}$
and
![]() $X_{1}$
are the truncation coordinates behind and ahead of the finger tip. The non-dimensional depth profile does not vary with the axial coordinate
$X_{1}$
are the truncation coordinates behind and ahead of the finger tip. The non-dimensional depth profile does not vary with the axial coordinate
![]() $x$
and the channel cross-section is shown in figure 1. The profile is a smoothed step-like occlusion given by
$x$
and the channel cross-section is shown in figure 1. The profile is a smoothed step-like occlusion given by
where
![]() ${\it\alpha}_{h}$
and
${\it\alpha}_{h}$
and
![]() ${\it\alpha}_{w}$
are the fractional height and the fractional width of the step, respectively. The results have been shown to be independent of the sharpness parameter
${\it\alpha}_{w}$
are the fractional height and the fractional width of the step, respectively. The results have been shown to be independent of the sharpness parameter
![]() $s$
when
$s$
when
![]() $s\geqslant 40$
(Thompson et al.
Reference Thompson, Juel and Hazel2014). In all our calculations the fractional width is
$s\geqslant 40$
(Thompson et al.
Reference Thompson, Juel and Hazel2014). In all our calculations the fractional width is
![]() ${\it\alpha}_{w}=0.25$
and the sharpness parameter
${\it\alpha}_{w}=0.25$
and the sharpness parameter
![]() $s=40$
, while the aspect ratio is varied within
$s=40$
, while the aspect ratio is varied within
![]() $20\leqslant {\it\alpha}\leqslant 160$
and the fractional height
$20\leqslant {\it\alpha}\leqslant 160$
and the fractional height
![]() $0\leqslant {\it\alpha}_{h}\leqslant 0.12$
.
$0\leqslant {\it\alpha}_{h}\leqslant 0.12$
.

Figure 1. Plot of the smoothed non-dimensionalised cross-section for a fractional occlusion width
![]() ${\it\alpha}_{w}=0.25$
and variable fractional occlusion height shown here with
${\it\alpha}_{w}=0.25$
and variable fractional occlusion height shown here with
![]() ${\it\alpha}_{h}=0.12$
, the maximum occlusion fractional height implemented in the numerical model.
${\it\alpha}_{h}=0.12$
, the maximum occlusion fractional height implemented in the numerical model.
A pressure gradient
![]() $-G^{\ast }\boldsymbol{e}_{x}$
is imposed far ahead of the finger tip. The pressure
$-G^{\ast }\boldsymbol{e}_{x}$
is imposed far ahead of the finger tip. The pressure
![]() $p^{\ast }$
is non-dimensionalised on the scale
$p^{\ast }$
is non-dimensionalised on the scale
![]() $G^{\ast }W^{\ast }/2$
and the two components of the depth-averaged horizontal velocity
$G^{\ast }W^{\ast }/2$
and the two components of the depth-averaged horizontal velocity
![]() $\boldsymbol{u}^{\ast }$
on the scale
$\boldsymbol{u}^{\ast }$
on the scale
![]() $U_{0}^{\ast }=G^{\ast }H^{\ast 2}/12{\it\mu}$
, where
$U_{0}^{\ast }=G^{\ast }H^{\ast 2}/12{\it\mu}$
, where
![]() ${\it\mu}$
is the dynamic viscosity of the fluid considered a constant. By applying the lubrication approximation (Reynolds Reference Reynolds1886), the governing equation for the fluid pressure in the frame moving with the constant velocity of the finger tip,
${\it\mu}$
is the dynamic viscosity of the fluid considered a constant. By applying the lubrication approximation (Reynolds Reference Reynolds1886), the governing equation for the fluid pressure in the frame moving with the constant velocity of the finger tip,
![]() $\boldsymbol{U}_{f}=(U_{f},0)$
where
$\boldsymbol{U}_{f}=(U_{f},0)$
where
![]() $U_{f}=U_{f}^{\ast }/U_{0}^{\ast }$
, is
$U_{f}=U_{f}^{\ast }/U_{0}^{\ast }$
, is
the symbol
![]() ${\it\Omega}$
denotes the fluid domain. Following McLean & Saffman (Reference McLean and Saffman1981), Thompson et al. (Reference Thompson, Juel and Hazel2014) proposed the following dimensionless boundary conditions for the interface in the transverse plane
${\it\Omega}$
denotes the fluid domain. Following McLean & Saffman (Reference McLean and Saffman1981), Thompson et al. (Reference Thompson, Juel and Hazel2014) proposed the following dimensionless boundary conditions for the interface in the transverse plane
![]() $\boldsymbol{R}=(x,y)$
, and for the channel boundaries:
$\boldsymbol{R}=(x,y)$
, and for the channel boundaries:
where
![]() $\partial {\it\Omega}_{b}$
denotes the finger boundary. Note that the boundary condition at
$\partial {\it\Omega}_{b}$
denotes the finger boundary. Note that the boundary condition at
![]() $x=X_{0}$
is applied only in the fluid domain, which itself must be determined as part of the solution. Equation (2.3) is the result of introducing the velocity in the frame moving with the tip of the finger,
$x=X_{0}$
is applied only in the fluid domain, which itself must be determined as part of the solution. Equation (2.3) is the result of introducing the velocity in the frame moving with the tip of the finger,
![]() $\boldsymbol{u}=-\boldsymbol{U}_{f}-b^{2}\boldsymbol{{\rm\nabla}}p$
, into the kinematic boundary condition
$\boldsymbol{u}=-\boldsymbol{U}_{f}-b^{2}\boldsymbol{{\rm\nabla}}p$
, into the kinematic boundary condition
![]() $\partial \boldsymbol{R}/\partial t\boldsymbol{\cdot }\boldsymbol{n}=\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{n}$
, where
$\partial \boldsymbol{R}/\partial t\boldsymbol{\cdot }\boldsymbol{n}=\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{n}$
, where
![]() $\boldsymbol{n}$
is the outer unit normal to the interface. We are mainly interested in steady solutions, for which we can simply set
$\boldsymbol{n}$
is the outer unit normal to the interface. We are mainly interested in steady solutions, for which we can simply set
![]() $\partial \boldsymbol{R}/\partial t=0$
; this term is the only time derivative in the problem and prescribes the unsteady evolution of the finger which is important for stability analysis of steady states. Additionally, (2.3) assumes that films deposited above and below the finger have zero thickness. The dynamic boundary condition (2.4) is the non-dimensional form of the Young–Laplace equation where
$\partial \boldsymbol{R}/\partial t=0$
; this term is the only time derivative in the problem and prescribes the unsteady evolution of the finger which is important for stability analysis of steady states. Additionally, (2.3) assumes that films deposited above and below the finger have zero thickness. The dynamic boundary condition (2.4) is the non-dimensional form of the Young–Laplace equation where
![]() $p_{in}$
is the constant finger pressure,
$p_{in}$
is the constant finger pressure,
![]() ${\it\kappa}$
is the non-dimensional curvature of the interface in the
${\it\kappa}$
is the non-dimensional curvature of the interface in the
![]() $(x,y)$
plane and
$(x,y)$
plane and
![]() $Q={\it\mu}U_{0}^{\ast }/{\it\sigma}$
is the dimensionless flow rate based on the average velocity in the unoccluded channel. The capillary number defined in § 1 is
$Q={\it\mu}U_{0}^{\ast }/{\it\sigma}$
is the dimensionless flow rate based on the average velocity in the unoccluded channel. The capillary number defined in § 1 is
![]() $Ca=U_{f}Q$
in terms of the model variables.
$Ca=U_{f}Q$
in terms of the model variables.
We note that, as in McLean & Saffman (Reference McLean and Saffman1981), the model is not rational in the asymptotic sense because additional terms of order
![]() ${\it\alpha}^{-1}$
and
${\it\alpha}^{-1}$
and
![]() ${\it\alpha}^{-2}$
should be included. However, we shall demonstrate that the model is both qualitatively and quantitatively correct (for sufficiently large
${\it\alpha}^{-2}$
should be included. However, we shall demonstrate that the model is both qualitatively and quantitatively correct (for sufficiently large
![]() ${\it\alpha}$
) suggesting that the neglected terms are of small enough numerical value to be negligible in our region of interest. The Park & Homsy (Reference Park and Homsy1984) correction corresponds to multiplying the curvature term by
${\it\alpha}$
) suggesting that the neglected terms are of small enough numerical value to be negligible in our region of interest. The Park & Homsy (Reference Park and Homsy1984) correction corresponds to multiplying the curvature term by
![]() ${\rm\pi}/4$
and is required for asymptotic consistency in the limit of large aspect ratio, small
${\rm\pi}/4$
and is required for asymptotic consistency in the limit of large aspect ratio, small
![]() $Ca$
and no obstacle. The inclusion of this correction can be accommodated in our formulation by rescaling
$Ca$
and no obstacle. The inclusion of this correction can be accommodated in our formulation by rescaling
![]() ${\it\alpha}$
to
${\it\alpha}$
to
![]() ${\it\alpha}/({\rm\pi}/4)$
and
${\it\alpha}/({\rm\pi}/4)$
and
![]() $Q$
to
$Q$
to
![]() $Q({\rm\pi}/4)$
. The correction is valid only for symmetric fingers, however, and very small capillary numbers,
$Q({\rm\pi}/4)$
. The correction is valid only for symmetric fingers, however, and very small capillary numbers,
![]() $Ca\sim O(10^{-3})$
. We have found that its inclusion gives worse quantitative agreement with the experimental data presented in § 4.
$Ca\sim O(10^{-3})$
. We have found that its inclusion gives worse quantitative agreement with the experimental data presented in § 4.
The pressure jump in (2.4) is due only to the surface tension so that viscous stresses at the interface are neglected. We note that if the channel height
![]() $b(y)$
is constant, the cross-sectional curvature term
$b(y)$
is constant, the cross-sectional curvature term
![]() $1/b(y)$
in (2.4) can be absorbed into the pressure, and does not affect the dynamics. However, for occluded channels, this term is dynamically significant, and appears in (2.4) on the order of
$1/b(y)$
in (2.4) can be absorbed into the pressure, and does not affect the dynamics. However, for occluded channels, this term is dynamically significant, and appears in (2.4) on the order of
![]() ${\it\alpha}_{h}{\it\alpha}^{-1}Q^{-1}$
, whereas the effect of the lateral curvature
${\it\alpha}_{h}{\it\alpha}^{-1}Q^{-1}$
, whereas the effect of the lateral curvature
![]() ${\it\kappa}$
is on the order of
${\it\kappa}$
is on the order of
![]() ${\it\alpha}^{-2}Q^{-1}$
. This means that if the aspect ratio
${\it\alpha}^{-2}Q^{-1}$
. This means that if the aspect ratio
![]() ${\it\alpha}$
increases with
${\it\alpha}$
increases with
![]() ${\it\alpha}_{h}$
fixed, the effect of the variable cross-sectional curvature
${\it\alpha}_{h}$
fixed, the effect of the variable cross-sectional curvature
![]() $1/b(y)$
becomes more significant and the two components of curvature will become of a comparable size at smaller values of the relative occlusion height
$1/b(y)$
becomes more significant and the two components of curvature will become of a comparable size at smaller values of the relative occlusion height
![]() ${\it\alpha}_{h}$
. The other effect of the occlusion height on finger propagation occurs through (2.2), which leads to
${\it\alpha}_{h}$
. The other effect of the occlusion height on finger propagation occurs through (2.2), which leads to
![]() $O({\it\alpha}_{h})$
variations in the pressure within the fluid, which also contributes to the pressure jump equation (2.4). The results presented in § 4.5 will confirm this effect quantitatively.
$O({\it\alpha}_{h})$
variations in the pressure within the fluid, which also contributes to the pressure jump equation (2.4). The results presented in § 4.5 will confirm this effect quantitatively.
The equations are discretised using a finite element method and the discrete residuals are assembled and solved using the finite element library oomph-lib (Heil & Hazel Reference Heil, Hazel, Schäfer and Bungartz2006). The numerical methods are unchanged from those described in detail and carefully validated in Thompson et al. (Reference Thompson, Juel and Hazel2014). Briefly, we use a boundary-fitted moving mesh method in which the mesh is updated in response to changes in the fluid interface position. These methods typically have better mass conservation properties than immersed interface methods. We use an isoparametric Galerkin method to solve the weak form of (2.2):
where
![]() ${\it\psi}$
represents piecewise quadratic test functions that are also used to interpolate the fluid pressure and unknown nodal positions. The boundary conditions (2.3) and (2.5a–c
) give conditions for
${\it\psi}$
represents piecewise quadratic test functions that are also used to interpolate the fluid pressure and unknown nodal positions. The boundary conditions (2.3) and (2.5a–c
) give conditions for
![]() $\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p$
on each boundary of the fluid domain and are used on the right-hand side of (2.6).
$\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p$
on each boundary of the fluid domain and are used on the right-hand side of (2.6).
The fluid domain is decomposed into triangular elements and updated in response to changes in the interface position by treating the mesh as a pseudo-elastic body. The required interface deformation is enforced by applying a normal stress to the mesh equations at the free surface, determined by the weak form of the dynamic boundary condition (2.4). The curvature term is not smooth for a piecewise quadratic representation of the interface, so we project a weak derivative of the boundary tangent vector onto a piecewise quadratic space in order to yield a continuous curvature term.
Steady solutions are computed using Newton’s method combined with arc-length continuation steps. The implicit second order BDF2 method is used for unsteady calculations and the eigenproblem associated with a linear stability analysis formulated by Thompson et al. (Reference Thompson, Juel and Hazel2014) is solved using a Block Krylov–Schur iterative algorithm. As the system parameters change, elements within the bulk mesh can become distorted. We perform a complete remesh when selected tolerances are exceeded by either a ‘Z2’ estimate of the error based on continuity of
![]() $-b^{2}\boldsymbol{{\rm\nabla}}p$
between bulk elements or the curvature of the interface. The fluid domain was typically discretised with approximately 1000 triangular elements and we confirmed that further refinement of the mesh to 8000 elements did not change the results to graphical accuracy, e.g. see figure 7.
$-b^{2}\boldsymbol{{\rm\nabla}}p$
between bulk elements or the curvature of the interface. The fluid domain was typically discretised with approximately 1000 triangular elements and we confirmed that further refinement of the mesh to 8000 elements did not change the results to graphical accuracy, e.g. see figure 7.
3 Experimental methods
Experiments on finger propagation were performed in Hele-Shaw channels partially obstructed with thin, centred rectangular occlusions positioned along the bottom boundary. A schematic diagram of the experimental channel is shown in figure 2. It was made of two glass plates of
![]() $60~\text{cm}\times 10~\text{cm}\times 2~\text{cm}$
separated by precision machined brass sheets which fixed the height of the channel to
$60~\text{cm}\times 10~\text{cm}\times 2~\text{cm}$
separated by precision machined brass sheets which fixed the height of the channel to
![]() $H^{\ast }=1$
mm with an accuracy of 0.1 %. Each separator plate was connected to a translation stage so that their positions could be adjusted with micrometric screws, resulting in a channel of length
$H^{\ast }=1$
mm with an accuracy of 0.1 %. Each separator plate was connected to a translation stage so that their positions could be adjusted with micrometric screws, resulting in a channel of length
![]() $L^{\ast }=600$
mm and variable width
$L^{\ast }=600$
mm and variable width
![]() $9\leqslant W^{\ast }\leqslant 60$
mm. We performed experiments for three aspect ratios
$9\leqslant W^{\ast }\leqslant 60$
mm. We performed experiments for three aspect ratios
![]() ${\it\alpha}=W^{\ast }/H^{\ast }=20$
, 40 and 60. The rectangular occlusions were made of thin adhesive films of width
${\it\alpha}=W^{\ast }/H^{\ast }=20$
, 40 and 60. The rectangular occlusions were made of thin adhesive films of width
![]() $w^{\ast }$
and thickness
$w^{\ast }$
and thickness
![]() $h^{\ast }$
, and positioned centrally along the bottom plate. Different adhesive film thicknesses gave occlusions with
$h^{\ast }$
, and positioned centrally along the bottom plate. Different adhesive film thicknesses gave occlusions with
![]() $h^{\ast }=15\pm 1$
,
$h^{\ast }=15\pm 1$
,
![]() $33\pm 1$
,
$33\pm 1$
,
![]() $42\pm 1$
,
$42\pm 1$
,
![]() $60\pm 1$
and
$60\pm 1$
and
![]() $120\pm 1~{\rm\mu}\text{m}$
. These were chosen to yield a series of fractional heights of the occlusion of
$120\pm 1~{\rm\mu}\text{m}$
. These were chosen to yield a series of fractional heights of the occlusion of
![]() ${\it\alpha}_{h}=h^{\ast }/H^{\ast }=0.015$
, 0.033, 0.042, 0.06 and 0.12, respectively. Owing to the technical challenge of implementing adhesive films thinner than
${\it\alpha}_{h}=h^{\ast }/H^{\ast }=0.015$
, 0.033, 0.042, 0.06 and 0.12, respectively. Owing to the technical challenge of implementing adhesive films thinner than
![]() $h^{\ast }<15~{\rm\mu}\text{m}$
, an occlusion with
$h^{\ast }<15~{\rm\mu}\text{m}$
, an occlusion with
![]() ${\it\alpha}_{h}=0.006$
(
${\it\alpha}_{h}=0.006$
(
![]() $h^{\ast }=6\pm 2~{\rm\mu}\text{m}$
) was manufactured by spraying uniformly a strip of acrylic paint over the glass. We measured its height at 5 uniformly distributed locations by recording the difference in height between the glass and the acrylic film using a micrometer with precision
$h^{\ast }=6\pm 2~{\rm\mu}\text{m}$
) was manufactured by spraying uniformly a strip of acrylic paint over the glass. We measured its height at 5 uniformly distributed locations by recording the difference in height between the glass and the acrylic film using a micrometer with precision
![]() $\pm 2~{\rm\mu}\text{m}$
. This occlusion was used in the channel with
$\pm 2~{\rm\mu}\text{m}$
. This occlusion was used in the channel with
![]() ${\it\alpha}=60$
(see § 4.2). The fractional width of the occlusion was kept constant at
${\it\alpha}=60$
(see § 4.2). The fractional width of the occlusion was kept constant at
![]() ${\it\alpha}_{w}=w^{\ast }/W^{\ast }=0.25$
for all experiments. Hence, for the chosen aspect ratios
${\it\alpha}_{w}=w^{\ast }/W^{\ast }=0.25$
for all experiments. Hence, for the chosen aspect ratios
![]() ${\it\alpha}=20$
, 40 and 60, the width of the occlusion was
${\it\alpha}=20$
, 40 and 60, the width of the occlusion was
![]() $w^{\ast }=5\pm 0.1$
mm,
$w^{\ast }=5\pm 0.1$
mm,
![]() $10\pm 0.1~\text{mm}$
and
$10\pm 0.1~\text{mm}$
and
![]() $15\pm 0.1~\text{mm}$
, respectively.
$15\pm 0.1~\text{mm}$
, respectively.

Figure 2. (a) End view and side view schematic diagrams of the channel with a centred rectangular occlusion. The height of the channel was fixed to
![]() $H^{\ast }=1$
mm and its width,
$H^{\ast }=1$
mm and its width,
![]() $W^{\ast }$
, was adjusted to yield channel aspect ratios
$W^{\ast }$
, was adjusted to yield channel aspect ratios
![]() ${\it\alpha}=W^{\ast }/H^{\ast }=20$
, 40 and 60. Different thin film occlusions were selected with fractional heights
${\it\alpha}=W^{\ast }/H^{\ast }=20$
, 40 and 60. Different thin film occlusions were selected with fractional heights
![]() ${\it\alpha}_{h}$
of 0.015 (1.5 %), 0.033 (3.3 %), 0.042 (4.2 %), 0.06 (6.0 %) and 0.12 (12.0 %). The fractional width of the occlusion was fixed to
${\it\alpha}_{h}$
of 0.015 (1.5 %), 0.033 (3.3 %), 0.042 (4.2 %), 0.06 (6.0 %) and 0.12 (12.0 %). The fractional width of the occlusion was fixed to
![]() ${\it\alpha}_{w}=w^{\ast }/W^{\ast }=0.25$
. (b) Sketch of a finger propagating inside the Hele-Shaw channel where a thin occlusion is centred along the bottom boundary.
${\it\alpha}_{w}=w^{\ast }/W^{\ast }=0.25$
. (b) Sketch of a finger propagating inside the Hele-Shaw channel where a thin occlusion is centred along the bottom boundary.
The channel was set-up by first positioning the occlusion half-way across the bottom glass-plate with an accuracy of 1 % and then adjusting the width of the channel by moving the separators and iteratively measuring the distance between the edge of occlusion and the nearest wall along the channel to ensure that the channel had a uniform width and that its walls were parallel to the occlusion. Therefore, the error in the axial uniformity of the channel width was better than 3 %. Fluid reservoirs were sealed to both ends of the channel using a rubber gasket. One of the reservoirs was left open to the atmosphere and the other was connected to a syringe pump (KDS210), which allowed infusion or withdrawal of liquid from the channel.
The channel was filled with silicone oil (Basildon Chemicals Ltd.) with density
![]() ${\it\rho}=961~\text{kg m}^{-3}$
, viscosity
${\it\rho}=961~\text{kg m}^{-3}$
, viscosity
![]() ${\it\mu}=5.5\times 10^{-3}$
Pa s and surface tension
${\it\mu}=5.5\times 10^{-3}$
Pa s and surface tension
![]() ${\it\sigma}=2.1\times 10^{-2}~\text{N m}^{-1}$
, which completely wets the channel. The viscosity was measured at the laboratory temperature of
${\it\sigma}=2.1\times 10^{-2}~\text{N m}^{-1}$
, which completely wets the channel. The viscosity was measured at the laboratory temperature of
![]() $21\pm 1\,^{\circ }\text{C}$
using a suspended level shortened form viscometer (Poulten & Selfe). A free surface displacement flow was induced by withdrawing oil at a fixed flow rate at one end of the channel while leaving the other end open to the atmosphere; the withdrawal of oil circumvents compression effects in the air. This procedure resulted in the steady propagation of a long air finger after the decay of initial transients. The small value of the ratio of gravitational to surface tension forces or Bond number,
$21\pm 1\,^{\circ }\text{C}$
using a suspended level shortened form viscometer (Poulten & Selfe). A free surface displacement flow was induced by withdrawing oil at a fixed flow rate at one end of the channel while leaving the other end open to the atmosphere; the withdrawal of oil circumvents compression effects in the air. This procedure resulted in the steady propagation of a long air finger after the decay of initial transients. The small value of the ratio of gravitational to surface tension forces or Bond number,
![]() $Bo=({\it\rho}gH^{\ast 2})/4{\it\sigma}=0.11$
, suggests that buoyancy effects are negligible because Jensen et al. (Reference Jensen, Libchaber, Pelcé and Zocchi1987) showed that for
$Bo=({\it\rho}gH^{\ast 2})/4{\it\sigma}=0.11$
, suggests that buoyancy effects are negligible because Jensen et al. (Reference Jensen, Libchaber, Pelcé and Zocchi1987) showed that for
![]() $Bo<1$
, there is no change to the pressure jump across the fluid interface in the small-
$Bo<1$
, there is no change to the pressure jump across the fluid interface in the small-
![]() $Ca$
asymptotic limit of the Saffman–Taylor model. Indeed, in § 4.2 we show that the experimental results are in excellent agreement with the model, in which gravity is neglected, as presented in § 2.
$Ca$
asymptotic limit of the Saffman–Taylor model. Indeed, in § 4.2 we show that the experimental results are in excellent agreement with the model, in which gravity is neglected, as presented in § 2.
A Dalsa Genie camera (
![]() $1024\times 1400$
pixels) with a 50 mm
$1024\times 1400$
pixels) with a 50 mm
![]() $f/1.4$
lens was mounted above the experiment at a height of 0.8 m, in order to yield a field of view along the channel of 39.2 cm. Rectangular images of
$f/1.4$
lens was mounted above the experiment at a height of 0.8 m, in order to yield a field of view along the channel of 39.2 cm. Rectangular images of
![]() $1400\times 150\pm 50$
pixels were selected for capture. The field of view was positioned so that it reached the end of the channel where the finger was usually found in a steady state, except near the critical capillary numbers where the transient could extend beyond the channel length. The experiment was back lit with a custom made LED closed light box of inner dimensions
$1400\times 150\pm 50$
pixels were selected for capture. The field of view was positioned so that it reached the end of the channel where the finger was usually found in a steady state, except near the critical capillary numbers where the transient could extend beyond the channel length. The experiment was back lit with a custom made LED closed light box of inner dimensions
![]() $50~\text{cm}\times 11~\text{cm}\times 2.7~\text{cm}$
which was constructed from translucent Perspex sheets (opal 070), and filled with uniformly spaced 12 V LEDs in order to emit white light of uniform intensity. The camera and syringe pump were interfaced to a computer, and controlled with a Labview program which initiated withdrawal by the syringe pump of a given volume of oil at constant flow rate
$50~\text{cm}\times 11~\text{cm}\times 2.7~\text{cm}$
which was constructed from translucent Perspex sheets (opal 070), and filled with uniformly spaced 12 V LEDs in order to emit white light of uniform intensity. The camera and syringe pump were interfaced to a computer, and controlled with a Labview program which initiated withdrawal by the syringe pump of a given volume of oil at constant flow rate
![]() $Q^{\ast }$
and sequentially controlled the capture by the camera of a sequence of images of finger propagation at frame rates of
$Q^{\ast }$
and sequentially controlled the capture by the camera of a sequence of images of finger propagation at frame rates of
![]() $1\leqslant f\leqslant 25$
fps. After the end of the experiment, the channel was refilled by infusing oil back into it so that the set-up was ready for a second experiment, where the flow rate was incremented by a fixed value. This experimental protocol enabled the recording of finger propagation for a prefixed range of flow rates or
$1\leqslant f\leqslant 25$
fps. After the end of the experiment, the channel was refilled by infusing oil back into it so that the set-up was ready for a second experiment, where the flow rate was incremented by a fixed value. This experimental protocol enabled the recording of finger propagation for a prefixed range of flow rates or
![]() $Ca$
numbers.
$Ca$
numbers.

Figure 3. Analysis of a finger profile extracted from an experimental image for
![]() ${\it\alpha}=40$
,
${\it\alpha}=40$
,
![]() ${\it\alpha}_{h}=0.06$
and
${\it\alpha}_{h}=0.06$
and
![]() $Q^{\ast }=45~\text{ml min}^{-1}$
. (a) Original experimental image. (b) The finger offset
$Q^{\ast }=45~\text{ml min}^{-1}$
. (a) Original experimental image. (b) The finger offset
![]() ${\it\delta}=(y_{1}^{\ast }+y_{2}^{\ast })/2W^{\ast }$
is measured from binary profiles, which are extracted from the corresponding original images by subtracting the background, applying contrast enhancement and filtering the outcomes into a black/white colour scale. (c) Binary profile overlapped with the experimental image validating the image processing method. (d) Close-up image of the finger tip shown in (c).
${\it\delta}=(y_{1}^{\ast }+y_{2}^{\ast })/2W^{\ast }$
is measured from binary profiles, which are extracted from the corresponding original images by subtracting the background, applying contrast enhancement and filtering the outcomes into a black/white colour scale. (c) Binary profile overlapped with the experimental image validating the image processing method. (d) Close-up image of the finger tip shown in (c).
An image processing algorithm was developed to extract the outline of the propagating fingers. This algorithm first subtracts the background from the original images, and then the grey scale colours are filtered so that for a given threshold they are replaced by a white colour below it and black otherwise. An original image, the corresponding binary profile and their superposition shown in figure 3 indicate that the outline of the fingers was obtained to within 3 pixels (0.84 mm). A time sequence of finger outlines recorded at a constant flow rate was used to measure the finger-tip speed,
![]() $U_{f}^{\ast }$
, averaged over the visualisation window, from which the capillary number
$U_{f}^{\ast }$
, averaged over the visualisation window, from which the capillary number
![]() $Ca$
was calculated. The position of the finger tip was identified in each profile to yield the distance
$Ca$
was calculated. The position of the finger tip was identified in each profile to yield the distance
![]() $L^{\ast }$
travelled during
$L^{\ast }$
travelled during
![]() $N$
frames,
$N$
frames,
![]() $U_{f}^{\ast }=L^{\ast }f/N$
, where
$U_{f}^{\ast }=L^{\ast }f/N$
, where
![]() $1\leqslant f\leqslant 25$
fps, depending on the imposed flow rate,
$1\leqslant f\leqslant 25$
fps, depending on the imposed flow rate,
![]() $Q^{\ast }$
. Typically, the frame rate was chosen in order to obtain a sequence of approximately
$Q^{\ast }$
. Typically, the frame rate was chosen in order to obtain a sequence of approximately
![]() $N=400$
images.
$N=400$
images.
A local measure of the finger asymmetry was chosen to quantify the mode of finger propagation, and measured from the extracted finger outlines:
where
![]() $y_{1}^{\ast }$
and
$y_{1}^{\ast }$
and
![]() $y_{2}^{\ast }$
are the distances from the centre of the channel to the adjacent points on the finger interface, respectively, see figure 3(b). By definition,
$y_{2}^{\ast }$
are the distances from the centre of the channel to the adjacent points on the finger interface, respectively, see figure 3(b). By definition,
![]() ${\it\delta}=0$
for symmetric fingers, while
${\it\delta}=0$
for symmetric fingers, while
![]() $-0.5<{\it\delta}<0.5$
with
$-0.5<{\it\delta}<0.5$
with
![]() ${\it\delta}\neq 0$
for asymmetric fingers. The finger offset
${\it\delta}\neq 0$
for asymmetric fingers. The finger offset
![]() ${\it\delta}$
was measured at a fixed distance behind the finger tip, typically 50 mm for any finger state. For symmetric and asymmetric states the finger width remains constant beyond this distance (see figure 8). In the case of oscillatory states, as shown in figure 3(b), the selected distance coincides with the point where the interface first meets the edge of the occlusion. The finger offset does not differentiate between asymmetric and oscillatory fingers. We used an additional criterion to identify oscillatory fingers based on the standard deviation of the finger width measured in the region behind the tip, which had to exceed 5 %.
${\it\delta}$
was measured at a fixed distance behind the finger tip, typically 50 mm for any finger state. For symmetric and asymmetric states the finger width remains constant beyond this distance (see figure 8). In the case of oscillatory states, as shown in figure 3(b), the selected distance coincides with the point where the interface first meets the edge of the occlusion. The finger offset does not differentiate between asymmetric and oscillatory fingers. We used an additional criterion to identify oscillatory fingers based on the standard deviation of the finger width measured in the region behind the tip, which had to exceed 5 %.
4 Results
4.1 Generic behaviour of the system
Figure 4 shows the simplified evolution of the bifurcation structure with occlusion height, assuming that occlusion width remains fixed. The same general structure is found to occur at all tube aspect ratios. In the absence of an occlusion there is a single, stable, symmetric solution, which becomes the classic Saffman–Taylor half-width finger (
![]() ${\it\lambda}=1/2$
) as the capillary number increases. As the occlusion height increases a supercritical symmetry-breaking bifurcation is observed, as first reported by de Lózar et al. (Reference de Lózar, Heap, Box, Hazel and Juel2009). The bifurcation moves towards lower capillary numbers and eventually becomes subcritical as the occlusion height increases further. For yet higher occlusions, the asymmetric solution smoothly evolves into a localised asymmetric solution upon decrease of
${\it\lambda}=1/2$
) as the capillary number increases. As the occlusion height increases a supercritical symmetry-breaking bifurcation is observed, as first reported by de Lózar et al. (Reference de Lózar, Heap, Box, Hazel and Juel2009). The bifurcation moves towards lower capillary numbers and eventually becomes subcritical as the occlusion height increases further. For yet higher occlusions, the asymmetric solution smoothly evolves into a localised asymmetric solution upon decrease of
![]() $Ca$
, which can persist even at
$Ca$
, which can persist even at
![]() $Ca=0$
, the capillary static limit (Hazel et al.
Reference Hazel, Pailha, Cox and Juel2013).
$Ca=0$
, the capillary static limit (Hazel et al.
Reference Hazel, Pailha, Cox and Juel2013).

Figure 4. Schematic bifurcation diagram for increasing
![]() ${\it\alpha}_{h}$
within the experimental range of
${\it\alpha}_{h}$
within the experimental range of
![]() $Ca$
. For low values of
$Ca$
. For low values of
![]() ${\it\alpha}_{h}$
, we observe a supercritical symmetry-breaking bifurcation at a critical capillary number
${\it\alpha}_{h}$
, we observe a supercritical symmetry-breaking bifurcation at a critical capillary number
![]() $Ca_{c1}$
; as the value of
$Ca_{c1}$
; as the value of
![]() ${\it\alpha}_{h}$
increases, the symmetry breaking becomes subcritical and is associated with a critical capillary number
${\it\alpha}_{h}$
increases, the symmetry breaking becomes subcritical and is associated with a critical capillary number
![]() $Ca_{c2}$
, and a limit point at
$Ca_{c2}$
, and a limit point at
![]() $Ca_{LP}$
; larger values of
$Ca_{LP}$
; larger values of
![]() ${\it\alpha}_{h}$
lead to a subcritical symmetry breaking with Hopf bifurcations on the asymmetric branch at
${\it\alpha}_{h}$
lead to a subcritical symmetry breaking with Hopf bifurcations on the asymmetric branch at
![]() $Ca_{H1}$
and
$Ca_{H1}$
and
![]() $Ca_{H2}$
; the largest values of
$Ca_{H2}$
; the largest values of
![]() ${\it\alpha}_{h}$
promote an asymmetric solution without oscillations, which is disconnected from the symmetric branch, and continues to a localised state as
${\it\alpha}_{h}$
promote an asymmetric solution without oscillations, which is disconnected from the symmetric branch, and continues to a localised state as
![]() $Ca$
is decreased (see Pailha et al. (Reference Pailha, Hazel, Glendinning and Juel2012) for a similar bifurcation structure in a small aspect ratio occluded tube).
$Ca$
is decreased (see Pailha et al. (Reference Pailha, Hazel, Glendinning and Juel2012) for a similar bifurcation structure in a small aspect ratio occluded tube).
The subcritical symmetry-breaking bifurcation is also associated with oscillatory solutions, identified by Pailha et al. (Reference Pailha, Hazel, Glendinning and Juel2012), who proposed a surface tension-based mechanism to explain their genesis. A fast local decrease in the cross-sectional curvature occurs when the interface of a finger passes over the edge of the occlusion to the less occluded region. Consequently, the fluid pressure just outside the interface increases locally which drives the fluid out of that region, amplifying any growing perturbation. Thus, numerical predictions of oscillatory states can also be made with steady state simulations, by identifying the advancing fingers whose flat interface behind the tip coincides with the edge of the occlusion (see Appendix). This method was validated by Thompson et al. (Reference Thompson, Juel and Hazel2014) using linear stability analysis. Hence, in the present work, we did not compute the time-dependent oscillatory modes, but instead used this accurate estimator for the occurrence of oscillatory modes, which is computationally much more efficient than performing time-dependent runs.
In summary, the qualitative stages in evolution of the system with increasing occlusion height are: steady symmetric propagation; supercritical symmetry breaking; subcritical symmetry breaking; subcritical symmetry breaking with oscillations; appearance of localised asymmetric solutions; disappearance of oscillations. This evolution, or a subset of it, is shown in all experimental data for small capillary numbers, see figures 5–7. At higher capillary numbers, the evolution of the system remains an open problem that cannot be analysed within the current model framework because of the need to include three-dimensional effects.

Figure 5. Finger offset
![]() ${\it\delta}$
as a function of the capillary number
${\it\delta}$
as a function of the capillary number
![]() $Ca$
in a channel of aspect ratio
$Ca$
in a channel of aspect ratio
![]() ${\it\alpha}=20$
. Experimental measurements (open and closed symbols) and numerical calculations (solid lines for asymmetric or symmetric states and circled-solid lines for oscillatory states) are shown for a fractional occlusion width of
${\it\alpha}=20$
. Experimental measurements (open and closed symbols) and numerical calculations (solid lines for asymmetric or symmetric states and circled-solid lines for oscillatory states) are shown for a fractional occlusion width of
![]() ${\it\alpha}_{w}=0.25$
, and different fractional occlusion heights: (
${\it\alpha}_{w}=0.25$
, and different fractional occlusion heights: (
![]() $+$
) no occlusion
$+$
) no occlusion
![]() ${\it\alpha}_{h}=0$
; (○)
${\it\alpha}_{h}=0$
; (○)
![]() ${\it\alpha}_{h}=0.015$
(1.5 %); (▫)
${\it\alpha}_{h}=0.015$
(1.5 %); (▫)
![]() ${\it\alpha}_{h}=0.042$
(4.2 %); (▵)
${\it\alpha}_{h}=0.042$
(4.2 %); (▵)
![]() ${\it\alpha}_{h}=0.06$
(6.0 %); (▾) symmetric states and (▿) oscillatory states
${\it\alpha}_{h}=0.06$
(6.0 %); (▾) symmetric states and (▿) oscillatory states
![]() ${\it\alpha}_{h}=0.12$
(12.0 %). Inset images of experimental finger shapes illustrate the modes of propagation observed, from bottom to top: symmetric, asymmetric, oscillatory.
${\it\alpha}_{h}=0.12$
(12.0 %). Inset images of experimental finger shapes illustrate the modes of propagation observed, from bottom to top: symmetric, asymmetric, oscillatory.

Figure 6. Finger offset
![]() ${\it\delta}$
as a function of the capillary number
${\it\delta}$
as a function of the capillary number
![]() $Ca$
in a channel of aspect ratio
$Ca$
in a channel of aspect ratio
![]() ${\it\alpha}=40$
. Experimental measurements (open and closed symbols) and numerical calculations (solid lines for asymmetric or symmetric states and circled-solid lines for oscillatory states) are shown for a fractional occlusion width of
${\it\alpha}=40$
. Experimental measurements (open and closed symbols) and numerical calculations (solid lines for asymmetric or symmetric states and circled-solid lines for oscillatory states) are shown for a fractional occlusion width of
![]() ${\it\alpha}_{w}=0.25$
and different fractional occlusion heights: supercritical symmetry breaking (○)
${\it\alpha}_{w}=0.25$
and different fractional occlusion heights: supercritical symmetry breaking (○)
![]() ${\it\alpha}_{h}=0.015$
(1.5 %), (▫)
${\it\alpha}_{h}=0.015$
(1.5 %), (▫)
![]() ${\it\alpha}_{h}=0.033$
(3.3 %); limit supercritical–subcritical bifurcations (✩)
${\it\alpha}_{h}=0.033$
(3.3 %); limit supercritical–subcritical bifurcations (✩)
![]() ${\it\alpha}_{h}=0.042$
(4.2 %); subcritical symmetry breaking (▴) symmetric states, (▵) oscillatory states, (
${\it\alpha}_{h}=0.042$
(4.2 %); subcritical symmetry breaking (▴) symmetric states, (▵) oscillatory states, (
![]() $+$
) starting with a high flow rate that then is reduced, (*) starting with the inlet of the channel partially blocked
$+$
) starting with a high flow rate that then is reduced, (*) starting with the inlet of the channel partially blocked
![]() ${\it\alpha}_{h}=0.06$
(6.0 %); localised states (▿)
${\it\alpha}_{h}=0.06$
(6.0 %); localised states (▿)
![]() ${\it\alpha}_{h}=0.12$
(12.0 %). Inset images of experimental finger shapes illustrate the modes of propagation observed, from bottom to top: symmetric, asymmetric, oscillatory, asymmetric, localised.
${\it\alpha}_{h}=0.12$
(12.0 %). Inset images of experimental finger shapes illustrate the modes of propagation observed, from bottom to top: symmetric, asymmetric, oscillatory, asymmetric, localised.

Figure 7. Finger offset
![]() ${\it\delta}$
as a function of the capillary number
${\it\delta}$
as a function of the capillary number
![]() $Ca$
in a channel of aspect ratio
$Ca$
in a channel of aspect ratio
![]() ${\it\alpha}=60$
. Experimental measurements (open and closed symbols) and numerical calculations (solid lines or star-solid symbols for asymmetric or symmetric states and circled-solid lines for oscillatory states) for a fractional occlusion width of
${\it\alpha}=60$
. Experimental measurements (open and closed symbols) and numerical calculations (solid lines or star-solid symbols for asymmetric or symmetric states and circled-solid lines for oscillatory states) for a fractional occlusion width of
![]() ${\it\alpha}_{w}=0.25$
, and different fractional occlusion heights: no occlusion (
${\it\alpha}_{w}=0.25$
, and different fractional occlusion heights: no occlusion (
![]() $+$
)
$+$
)
![]() ${\it\alpha}_{h}=0$
; supercritical symmetry breaking (▫)
${\it\alpha}_{h}=0$
; supercritical symmetry breaking (▫)
![]() ${\it\alpha}_{h}=0.006$
(0.6 %), (○)
${\it\alpha}_{h}=0.006$
(0.6 %), (○)
![]() ${\it\alpha}_{h}=0.015$
(1.5 %); subcritical symmetry breaking (▴) symmetric states, (▵) oscillatory states, (
${\it\alpha}_{h}=0.015$
(1.5 %); subcritical symmetry breaking (▴) symmetric states, (▵) oscillatory states, (
![]() $+$
) starting with a high flow rate that then is reduced, (*) inlet of the channel partially blocked
$+$
) starting with a high flow rate that then is reduced, (*) inlet of the channel partially blocked
![]() ${\it\alpha}_{h}=0.042$
(4.2 %). The convergence of the numerical solutions is tested by recomputing the solutions when
${\it\alpha}_{h}=0.042$
(4.2 %). The convergence of the numerical solutions is tested by recomputing the solutions when
![]() ${\it\alpha}_{h}=0.006$
on a finer (eight times as many elements) mesh (
${\it\alpha}_{h}=0.006$
on a finer (eight times as many elements) mesh (
![]() $\star$
). Inset images of experimental finger shapes illustrate the modes of propagation observed, from bottom to top: symmetric, asymmetric, oscillatory.
$\star$
). Inset images of experimental finger shapes illustrate the modes of propagation observed, from bottom to top: symmetric, asymmetric, oscillatory.
4.2 Comparison between experimental and numerical modes of finger propagation
Experimental results are shown in figures 5–7, for the aspect ratios
![]() ${\it\alpha}=20$
, 40, 60, respectively. In each case, the finger offset defined in (3.1) is shown as a function of both the capillary number
${\it\alpha}=20$
, 40, 60, respectively. In each case, the finger offset defined in (3.1) is shown as a function of both the capillary number
![]() $Ca$
and the Saffman–Taylor parameter
$Ca$
and the Saffman–Taylor parameter
![]() $1/B=12{\it\alpha}^{2}Ca$
for different thin-film occlusions of fractional heights in the range
$1/B=12{\it\alpha}^{2}Ca$
for different thin-film occlusions of fractional heights in the range
![]() $0.006\leqslant {\it\alpha}_{h}\leqslant 0.12$
. The fractional width of the occlusions was always
$0.006\leqslant {\it\alpha}_{h}\leqslant 0.12$
. The fractional width of the occlusions was always
![]() ${\it\alpha}_{w}=0.25$
. The ranges of occlusion heights (
${\it\alpha}_{w}=0.25$
. The ranges of occlusion heights (
![]() ${\it\alpha}_{h}$
) and injection flow rates (non-dimensionalised as
${\it\alpha}_{h}$
) and injection flow rates (non-dimensionalised as
![]() $Ca$
or
$Ca$
or
![]() $1/B$
) were chosen so that all the modes of finger propagation – symmetric, asymmetric and oscillatory fingers – were observed for each value of the aspect ratio. Localised fingers, which arise for higher occlusions or very low
$1/B$
) were chosen so that all the modes of finger propagation – symmetric, asymmetric and oscillatory fingers – were observed for each value of the aspect ratio. Localised fingers, which arise for higher occlusions or very low
![]() $Ca$
, were not investigated in detail. Investigations of the dynamics of localised states can be found in Hazel et al. (Reference Hazel, Pailha, Cox and Juel2013) and Thompson et al. (Reference Thompson, Juel and Hazel2014). In each figure, the different modes of propagation encountered as
$Ca$
, were not investigated in detail. Investigations of the dynamics of localised states can be found in Hazel et al. (Reference Hazel, Pailha, Cox and Juel2013) and Thompson et al. (Reference Thompson, Juel and Hazel2014). In each figure, the different modes of propagation encountered as
![]() ${\it\alpha}_{h}$
is increased are illustrated with inset experimental images. Although the finger offset
${\it\alpha}_{h}$
is increased are illustrated with inset experimental images. Although the finger offset
![]() ${\it\delta}$
captures symmetry-breaking bifurcations about the vertical mid-plane of the channel, it does not distinguish between steady and oscillatory modes. Oscillatory modes are found both numerically and experimentally for all values of
${\it\delta}$
captures symmetry-breaking bifurcations about the vertical mid-plane of the channel, it does not distinguish between steady and oscillatory modes. Oscillatory modes are found both numerically and experimentally for all values of
![]() $Ca$
investigated at
$Ca$
investigated at
![]() ${\it\alpha}_{h}=0.12$
,
${\it\alpha}_{h}=0.12$
,
![]() ${\it\alpha}_{h}=0.06$
and
${\it\alpha}_{h}=0.06$
and
![]() ${\it\alpha}_{h}=0.042$
when
${\it\alpha}_{h}=0.042$
when
![]() ${\it\alpha}=20$
, 40 and 60, respectively. The corresponding numerical solutions, computed by continuing the solution branch from the highest value of
${\it\alpha}=20$
, 40 and 60, respectively. The corresponding numerical solutions, computed by continuing the solution branch from the highest value of
![]() $Ca$
, are also presented in the figures and are in excellent quantitative agreement with the experimental data for
$Ca$
, are also presented in the figures and are in excellent quantitative agreement with the experimental data for
![]() ${\it\alpha}\geqslant 40$
, see figures 6, 7.
${\it\alpha}\geqslant 40$
, see figures 6, 7.
In the experiment, small but unavoidable imperfections mean that fingers are weakly asymmetric even for low
![]() $Ca$
. Hence, they undergo a continuous transition to the selected asymmetric finger and the apparent bifurcation will appear at lower
$Ca$
. Hence, they undergo a continuous transition to the selected asymmetric finger and the apparent bifurcation will appear at lower
![]() $Ca$
in the experimental data when compared to the numerical simulations. Note that the computations are performed on a non-symmetric triangular mesh which also leads to slight imperfections in the bifurcations, but the numerical imperfections are smaller than the experimental ones. For
$Ca$
in the experimental data when compared to the numerical simulations. Note that the computations are performed on a non-symmetric triangular mesh which also leads to slight imperfections in the bifurcations, but the numerical imperfections are smaller than the experimental ones. For
![]() ${\it\alpha}=40$
, the critical
${\it\alpha}=40$
, the critical
![]() $Ca$
at
$Ca$
at
![]() ${\it\alpha}_{h}=0.015$
differs by less than 5 % (figure 6), confirming that the imperfections in the experimental system are generally very small. The only exception is for the very smallest occlusion height (
${\it\alpha}_{h}=0.015$
differs by less than 5 % (figure 6), confirming that the imperfections in the experimental system are generally very small. The only exception is for the very smallest occlusion height (
![]() ${\it\alpha}_{h}=0.006$
, figure 7) corresponding to a
${\it\alpha}_{h}=0.006$
, figure 7) corresponding to a
![]() $6\pm 2~{\rm\mu}\text{m}$
thin film, whose thickness is comparable to the roughness of the top and bottom boundaries (
$6\pm 2~{\rm\mu}\text{m}$
thin film, whose thickness is comparable to the roughness of the top and bottom boundaries (
![]() ${\sim}1~{\rm\mu}\text{m}$
). At this scale, the film thickness was technically challenging to control accurately, as discussed in § 3. This resulted in an imperfect transition to asymmetric fingers for capillary numbers smaller by approximately a factor of 4 compared to the numerical prediction of a perfect supercritical pitchfork bifurcation (
${\sim}1~{\rm\mu}\text{m}$
). At this scale, the film thickness was technically challenging to control accurately, as discussed in § 3. This resulted in an imperfect transition to asymmetric fingers for capillary numbers smaller by approximately a factor of 4 compared to the numerical prediction of a perfect supercritical pitchfork bifurcation (
![]() ${\it\alpha}_{h}=0.006$
, figure 7), although the offset values far beyond the bifurcation point are in excellent agreement. These results point to an uncontrolled bias incurred during the fabrication of the occlusion, such as a small systematic depth variation across the width of the occlusion.
${\it\alpha}_{h}=0.006$
, figure 7), although the offset values far beyond the bifurcation point are in excellent agreement. These results point to an uncontrolled bias incurred during the fabrication of the occlusion, such as a small systematic depth variation across the width of the occlusion.
For all three values of
![]() ${\it\alpha}=20$
, 40 and 60, experimental and numerical finger offset values are in good agreement away from symmetry-breaking bifurcation points, which indicates that the model predicts the finger shapes observed experimentally. The most significant deviation between experimental and numerical values of
${\it\alpha}=20$
, 40 and 60, experimental and numerical finger offset values are in good agreement away from symmetry-breaking bifurcation points, which indicates that the model predicts the finger shapes observed experimentally. The most significant deviation between experimental and numerical values of
![]() ${\it\delta}$
is for
${\it\delta}$
is for
![]() ${\it\alpha}=20$
, where the average discrepancy is of 8 %. However, for
${\it\alpha}=20$
, where the average discrepancy is of 8 %. However, for
![]() ${\it\alpha}=20$
, the critical capillary number
${\it\alpha}=20$
, the critical capillary number
![]() $Ca_{c}$
at which the symmetric finger loses stability to an asymmetric one is overestimated in the numerical calculations by 45 % for
$Ca_{c}$
at which the symmetric finger loses stability to an asymmetric one is overestimated in the numerical calculations by 45 % for
![]() ${\it\alpha}_{h}=0.042$
, and 67 % for
${\it\alpha}_{h}=0.042$
, and 67 % for
![]() ${\it\alpha}_{h}=0.06$
, compared to the experiment. These findings contrast with the channels of aspect ratio
${\it\alpha}_{h}=0.06$
, compared to the experiment. These findings contrast with the channels of aspect ratio
![]() ${\it\alpha}=40$
and
${\it\alpha}=40$
and
![]() ${\it\alpha}=60$
, where the values of
${\it\alpha}=60$
, where the values of
![]() $Ca_{c}$
and
$Ca_{c}$
and
![]() ${\it\delta}$
are mostly in good quantitative agreement with the theoretical model, with average errors of 5 % and 4 %, respectively. The only exception is the thinnest occlusion (
${\it\delta}$
are mostly in good quantitative agreement with the theoretical model, with average errors of 5 % and 4 %, respectively. The only exception is the thinnest occlusion (
![]() ${\it\alpha}_{h}=0.006$
) discussed above.
${\it\alpha}_{h}=0.006$
) discussed above.
Comparing figures 5–7, it is apparent that the symmetry-breaking bifurcations are displaced towards lower capillary numbers as
![]() ${\it\alpha}$
is increased. For example, for
${\it\alpha}$
is increased. For example, for
![]() ${\it\alpha}_{h}=0.015$
, the symmetric finger loses stability through a supercritical pitchfork bifurcation at
${\it\alpha}_{h}=0.015$
, the symmetric finger loses stability through a supercritical pitchfork bifurcation at
![]() $Ca_{c}\approx 4.42\times 10^{-3}$
(
$Ca_{c}\approx 4.42\times 10^{-3}$
(
![]() $1/B\approx 84.86$
) for
$1/B\approx 84.86$
) for
![]() ${\it\alpha}=40$
, while for
${\it\alpha}=40$
, while for
![]() ${\it\alpha}=60$
the bifurcation is still supercritical but
${\it\alpha}=60$
the bifurcation is still supercritical but
![]() $Ca_{c}\approx 1.25\times 10^{-3}$
(
$Ca_{c}\approx 1.25\times 10^{-3}$
(
![]() $1/B\approx 54.0$
); a reduction in critical capillary number of a factor of 3.54. In terms of the Saffman–Taylor parameter the reduction factor is only 1.57 due to the dependence of this parameter on both
$1/B\approx 54.0$
); a reduction in critical capillary number of a factor of 3.54. In terms of the Saffman–Taylor parameter the reduction factor is only 1.57 due to the dependence of this parameter on both
![]() $Ca$
and
$Ca$
and
![]() ${\it\alpha}$
. As will be discussed in § 4.5, we have reason to expect that in the large aspect ratio limit, the occlusion height
${\it\alpha}$
. As will be discussed in § 4.5, we have reason to expect that in the large aspect ratio limit, the occlusion height
![]() ${\it\alpha}_{h}$
at which the pitchfork bifurcation occurs will scale as
${\it\alpha}_{h}$
at which the pitchfork bifurcation occurs will scale as
![]() $B$
; the observed variation of
$B$
; the observed variation of
![]() $1/B$
by a factor of 1.57 at
$1/B$
by a factor of 1.57 at
![]() $Ca_{c}$
for fixed
$Ca_{c}$
for fixed
![]() ${\it\alpha}_{h}$
is likely to arise from transverse curvature effects or changes in the flow field due to variation in the shape, speed and width of the finger tip. In any case, the changes in modes of finger propagation occur at lower occlusion heights for larger channel aspect ratios. In order to obtain qualitatively similar oscillatory modes for
${\it\alpha}_{h}$
is likely to arise from transverse curvature effects or changes in the flow field due to variation in the shape, speed and width of the finger tip. In any case, the changes in modes of finger propagation occur at lower occlusion heights for larger channel aspect ratios. In order to obtain qualitatively similar oscillatory modes for
![]() ${\it\alpha}=20$
and
${\it\alpha}=20$
and
![]() ${\it\alpha}=60$
the occlusion height was reduced from
${\it\alpha}=60$
the occlusion height was reduced from
![]() ${\it\alpha}_{h}=0.12$
to 0.042, respectively. Similar reductions in occlusion heights were required to observe both supercritical and subcritical pitchfork bifurcations. These observations regarding the sensitivity of propagation modes for decreasing values of occlusion heights as the aspect ratio is increased are investigated numerically in § 4.5 for both symmetry breaking and oscillatory onsets.
${\it\alpha}_{h}=0.12$
to 0.042, respectively. Similar reductions in occlusion heights were required to observe both supercritical and subcritical pitchfork bifurcations. These observations regarding the sensitivity of propagation modes for decreasing values of occlusion heights as the aspect ratio is increased are investigated numerically in § 4.5 for both symmetry breaking and oscillatory onsets.
In figure 8, both asymmetric and symmetric finger shapes from experiments and simulations are compared for
![]() ${\it\alpha}=40$
and
${\it\alpha}=40$
and
![]() ${\it\alpha}=60$
, respectively. The finger profiles appear to superpose almost perfectly, but the numerical finger widths (
${\it\alpha}=60$
, respectively. The finger profiles appear to superpose almost perfectly, but the numerical finger widths (
![]() ${\it\lambda}$
) are
${\it\lambda}$
) are
![]() ${<}7\,\%$
smaller than the experimental ones for symmetric states, and
${<}7\,\%$
smaller than the experimental ones for symmetric states, and
![]() ${<}6\,\%$
smaller for asymmetric states. These small differences have previously been shown to be due to the presence of thin films of liquid left on the boundaries of the channel after the passage of the finger, which are not accounted for in the lubrication model developed by Thompson et al. (Reference Thompson, Juel and Hazel2014). Park & Homsy (Reference Park and Homsy1984), Reinelt & Saffman (Reference Reinelt and Saffman1985) and, more recently, Peng et al. (Reference Peng, Pihler-Puzović, Juel, Heil and Lister2015) included thin-film effects by modifying the kinematic and dynamic boundary conditions. Consequently, the interface velocity decreases and the cross-sectional curvature increases by a small factor. Hence, the implementation of both corrections results in wider fingers by the required factor (
${<}6\,\%$
smaller for asymmetric states. These small differences have previously been shown to be due to the presence of thin films of liquid left on the boundaries of the channel after the passage of the finger, which are not accounted for in the lubrication model developed by Thompson et al. (Reference Thompson, Juel and Hazel2014). Park & Homsy (Reference Park and Homsy1984), Reinelt & Saffman (Reference Reinelt and Saffman1985) and, more recently, Peng et al. (Reference Peng, Pihler-Puzović, Juel, Heil and Lister2015) included thin-film effects by modifying the kinematic and dynamic boundary conditions. Consequently, the interface velocity decreases and the cross-sectional curvature increases by a small factor. Hence, the implementation of both corrections results in wider fingers by the required factor (
![]() ${\sim}7\,\%$
). The parameter
${\sim}7\,\%$
). The parameter
![]() ${\it\delta}$
is less sensitive to this discrepancy because the same error occurs in both
${\it\delta}$
is less sensitive to this discrepancy because the same error occurs in both
![]() $y_{1}$
and
$y_{1}$
and
![]() $y_{2}$
, which cancels out when computing
$y_{2}$
, which cancels out when computing
![]() ${\it\delta}$
. Overall, the excellent agreement between experiments and numerical simulations indicates that the averaged lubrication model developed by Thompson et al. (Reference Thompson, Juel and Hazel2014) quantitatively predicts all features of finger propagation in channels of aspect ratio
${\it\delta}$
. Overall, the excellent agreement between experiments and numerical simulations indicates that the averaged lubrication model developed by Thompson et al. (Reference Thompson, Juel and Hazel2014) quantitatively predicts all features of finger propagation in channels of aspect ratio
![]() ${\it\alpha}\geqslant 40$
, with a prescribed depth profile (
${\it\alpha}\geqslant 40$
, with a prescribed depth profile (
![]() ${\it\alpha}_{w}=0.25$
and
${\it\alpha}_{w}=0.25$
and
![]() ${\it\alpha}_{h}\leqslant 0.12$
), for capillary numbers
${\it\alpha}_{h}\leqslant 0.12$
), for capillary numbers
![]() $Ca\leqslant 1.2\times 10^{-2}$
.
$Ca\leqslant 1.2\times 10^{-2}$
.

Figure 8. Experimental (solid line) and numerical (black dots) finger shape comparison for
![]() ${\it\alpha}_{w}=0.25$
. (i)
${\it\alpha}_{w}=0.25$
. (i)
![]() ${\it\alpha}=40$
,
${\it\alpha}=40$
,
![]() ${\it\alpha}_{h}=0.033$
: (a) symmetric finger with
${\it\alpha}_{h}=0.033$
: (a) symmetric finger with
![]() $Ca=7.26\times 10^{-4}$
(
$Ca=7.26\times 10^{-4}$
(
![]() $1/B=13.95$
), (b) asymmetric finger with
$1/B=13.95$
), (b) asymmetric finger with
![]() $Ca=0.0105$
(
$Ca=0.0105$
(
![]() $1/B=195.8$
). (ii)
$1/B=195.8$
). (ii)
![]() ${\it\alpha}=60$
,
${\it\alpha}=60$
,
![]() ${\it\alpha}_{h}=0.015$
: (c) symmetric finger with
${\it\alpha}_{h}=0.015$
: (c) symmetric finger with
![]() $Ca=5.07\times 10^{-4}$
(
$Ca=5.07\times 10^{-4}$
(
![]() $1/B=21.92$
), (d) asymmetric finger with
$1/B=21.92$
), (d) asymmetric finger with
![]() $Ca=3.6\times 10^{-3}$
(
$Ca=3.6\times 10^{-3}$
(
![]() $1/B=155.5$
). The non-uniformity in finger width on the far left indicates the transient evolution of the symmetric initial finger to a steady asymmetric one. The dashed line at the top right of (a) and (c) corresponds to 20 mm.
$1/B=155.5$
). The non-uniformity in finger width on the far left indicates the transient evolution of the symmetric initial finger to a steady asymmetric one. The dashed line at the top right of (a) and (c) corresponds to 20 mm.
4.3 Alternative symmetric states: double-tipped and triple-tipped fingers
Finger propagation in channels of aspect ratio
![]() ${\it\alpha}>60$
was investigated using the numerical simulations only, because of the experimental challenges associated with the manufacture of the very thin occlusions required in channels of large aspect ratios. For
${\it\alpha}>60$
was investigated using the numerical simulations only, because of the experimental challenges associated with the manufacture of the very thin occlusions required in channels of large aspect ratios. For
![]() ${\it\alpha}=80$
and very thin occlusions, less than 0.5 % of the height of the channel (
${\it\alpha}=80$
and very thin occlusions, less than 0.5 % of the height of the channel (
![]() ${\it\alpha}_{h}\leqslant 0.005$
), alternative families of double-tipped and triple-tipped symmetric states were found for the lowest values of capillary number investigated (
${\it\alpha}_{h}\leqslant 0.005$
), alternative families of double-tipped and triple-tipped symmetric states were found for the lowest values of capillary number investigated (
![]() $Ca\sim 1.0\times 10^{-3}$
), see figure 9.
$Ca\sim 1.0\times 10^{-3}$
), see figure 9.

Figure 9. Numerically predicted double-tipped and triple-tipped finger shapes in terms of the pressure colour scale using parameters
![]() ${\it\alpha}=80$
,
${\it\alpha}=80$
,
![]() ${\it\alpha}_{w}=0.25$
and
${\it\alpha}_{w}=0.25$
and
![]() ${\it\alpha}_{h}=0.003$
(
${\it\alpha}_{h}=0.003$
(
![]() $h=0.3\,\%$
) (a)
$h=0.3\,\%$
) (a)
![]() $Ca=1.45\times 10^{-3}$
(
$Ca=1.45\times 10^{-3}$
(
![]() $1/B=111.5$
) (b)
$1/B=111.5$
) (b)
![]() $Ca=3.6\times 10^{-3}$
(
$Ca=3.6\times 10^{-3}$
(
![]() $1/B=277.7$
).
$1/B=277.7$
).
For
![]() ${\it\alpha}_{h}=0$
, these multiple-tipped fingers belong to the countable, infinite family of solutions uncovered by Romero (Reference Romero1982) and Vanden-Broeck (Reference Vanden-Broeck1983) whose finger shapes were recently computed by Gardiner et al. (Reference Gardiner, McCue and Moroney2015). These solutions were calculated using the same model developed by McLean & Saffman (Reference McLean and Saffman1981) to obtain the classical Saffman–Taylor solutions and then relaxing the boundary condition at the finger interface to perturb the system. Once the solutions had been found, the usual boundary conditions were restored. Comparisons between our computed solutions (lines) with the averaged lubrication model by Thompson et al. (Reference Thompson, Juel and Hazel2014), experimental measurements (open circles) and selected data points (filled red symbols) corresponding to the different solutions predicted by McLean & Saffman (Reference McLean and Saffman1981) and Vanden-Broeck (Reference Vanden-Broeck1983) are shown in figure 10, where the finger width
${\it\alpha}_{h}=0$
, these multiple-tipped fingers belong to the countable, infinite family of solutions uncovered by Romero (Reference Romero1982) and Vanden-Broeck (Reference Vanden-Broeck1983) whose finger shapes were recently computed by Gardiner et al. (Reference Gardiner, McCue and Moroney2015). These solutions were calculated using the same model developed by McLean & Saffman (Reference McLean and Saffman1981) to obtain the classical Saffman–Taylor solutions and then relaxing the boundary condition at the finger interface to perturb the system. Once the solutions had been found, the usual boundary conditions were restored. Comparisons between our computed solutions (lines) with the averaged lubrication model by Thompson et al. (Reference Thompson, Juel and Hazel2014), experimental measurements (open circles) and selected data points (filled red symbols) corresponding to the different solutions predicted by McLean & Saffman (Reference McLean and Saffman1981) and Vanden-Broeck (Reference Vanden-Broeck1983) are shown in figure 10, where the finger width
![]() ${\it\lambda}$
is shown as a function of the parameter
${\it\lambda}$
is shown as a function of the parameter
![]() $k=4{\rm\pi}^{2}/((1/B)(1-{\it\lambda})^{2})$
introduced by McLean & Saffman (Reference McLean and Saffman1981). The double-tipped and triple-tipped states correspond to the first (▾) and second (●) Romero–Vanden-Broeck solutions, respectively. The stability of the different numerical solutions was determined by computing the eigenvalues of the system. The multiple-tipped fingers (dashed lines) are unstable, while the Saffman–Taylor fingers (solid line) are stable and hence observed experimentally (open circles). Experimental finger widths are consistently wider than numerical predictions by less than 7 % (reached for
$k=4{\rm\pi}^{2}/((1/B)(1-{\it\lambda})^{2})$
introduced by McLean & Saffman (Reference McLean and Saffman1981). The double-tipped and triple-tipped states correspond to the first (▾) and second (●) Romero–Vanden-Broeck solutions, respectively. The stability of the different numerical solutions was determined by computing the eigenvalues of the system. The multiple-tipped fingers (dashed lines) are unstable, while the Saffman–Taylor fingers (solid line) are stable and hence observed experimentally (open circles). Experimental finger widths are consistently wider than numerical predictions by less than 7 % (reached for
![]() $k=1.05$
) due to the presence of thin films of liquid left on the top and bottom boundaries behind the finger tip, as discussed above. In figure 10 our calculations reveal that the solution branches corresponding to double- and triple-tipped fingers are connected through a bifurcation point (▪) at
$k=1.05$
) due to the presence of thin films of liquid left on the top and bottom boundaries behind the finger tip, as discussed above. In figure 10 our calculations reveal that the solution branches corresponding to double- and triple-tipped fingers are connected through a bifurcation point (▪) at
![]() $k=0.09$
leading to a region of asymmetric states at lower values of
$k=0.09$
leading to a region of asymmetric states at lower values of
![]() $k$
.
$k$
.

Figure 10. Finger width
![]() ${\it\lambda}$
against McLean–Saffman parameter
${\it\lambda}$
against McLean–Saffman parameter
![]() $k=4{\rm\pi}^{2}/((1/B)(1-{\it\lambda})^{2})$
for a channel without occlusion (
$k=4{\rm\pi}^{2}/((1/B)(1-{\it\lambda})^{2})$
for a channel without occlusion (
![]() ${\it\alpha}_{h}=0$
). Smaller values of the parameter
${\it\alpha}_{h}=0$
). Smaller values of the parameter
![]() $k$
correspond to greater values of
$k$
correspond to greater values of
![]() $Ca$
. The single-tipped branch (solid line) corresponds to the classical McLean & Saffman (Reference McLean and Saffman1981) solution (▪). Experimental finger widths (○) are consistently wider by less than 7 %, due to the presence of thin liquid films left on the top and bottom boundaries after the passage of the finger tip. The double-tipped branch (dashed line) corresponds to the first Romero–Vanden-Broeck solution (▾) and the triple-tipped state (red dashed-dotted line) to the second Romero–Vanden-Broeck solution (●). These multiple-tip solutions develop in a range of
$Ca$
. The single-tipped branch (solid line) corresponds to the classical McLean & Saffman (Reference McLean and Saffman1981) solution (▪). Experimental finger widths (○) are consistently wider by less than 7 %, due to the presence of thin liquid films left on the top and bottom boundaries after the passage of the finger tip. The double-tipped branch (dashed line) corresponds to the first Romero–Vanden-Broeck solution (▾) and the triple-tipped state (red dashed-dotted line) to the second Romero–Vanden-Broeck solution (●). These multiple-tip solutions develop in a range of
![]() $1.5<k<9.0$
. For values of
$1.5<k<9.0$
. For values of
![]() $k<1.5$
the Romero–Vanden-Broeck solutions are symmetric single tipped. A connection between the double-tipped and triple-tipped branches occurs at
$k<1.5$
the Romero–Vanden-Broeck solutions are symmetric single tipped. A connection between the double-tipped and triple-tipped branches occurs at
![]() $k=0.09$
(▪) leading to asymmetric states (blue dashed-dotted line).
$k=0.09$
(▪) leading to asymmetric states (blue dashed-dotted line).

Figure 11. Numerical simulation for the finger width
![]() ${\it\lambda}$
(dimensionless finger-tip speed
${\it\lambda}$
(dimensionless finger-tip speed
![]() $U_{f}$
on right) as a function of the capillary number
$U_{f}$
on right) as a function of the capillary number
![]() $Ca={\it\mu}U_{f}^{\ast }/{\it\sigma}$
showing a complex interaction as the occlusion height
$Ca={\it\mu}U_{f}^{\ast }/{\it\sigma}$
showing a complex interaction as the occlusion height
![]() ${\it\alpha}_{h}$
is increased. The parameters are
${\it\alpha}_{h}$
is increased. The parameters are
![]() ${\it\alpha}=80$
,
${\it\alpha}=80$
,
![]() ${\it\alpha}_{w}=0.25$
and different small occlusion fractional heights: (a)
${\it\alpha}_{w}=0.25$
and different small occlusion fractional heights: (a)
![]() ${\it\alpha}_{h}=0.001$
(
${\it\alpha}_{h}=0.001$
(
![]() $h=0.1\,\%$
), (b)
$h=0.1\,\%$
), (b)
![]() ${\it\alpha}_{h}=0.003$
(
${\it\alpha}_{h}=0.003$
(
![]() $h=0.3\,\%$
), (c)
$h=0.3\,\%$
), (c)
![]() ${\it\alpha}_{h}=0.004$
(
${\it\alpha}_{h}=0.004$
(
![]() $h=0.4\,\%$
), (d)
$h=0.4\,\%$
), (d)
![]() ${\it\alpha}_{h}=0.005$
(
${\it\alpha}_{h}=0.005$
(
![]() $h=0.5\,\%$
) and (e)
$h=0.5\,\%$
) and (e)
![]() ${\it\alpha}_{h}=0.01$
(
${\it\alpha}_{h}=0.01$
(
![]() $h=1.0\,\%$
). Solid lines corresponds to stable states, dashed lines to unstable states and dash-dotted lines to a small region of unstable symmetric states, thin lines to symmetric states and thick lines to asymmetric states. The structure evolves from the Saffman–Taylor system in (a), including the unstable Romero–Vanden-Broeck solution branches (double- and triple-tipped symmetric fingers), to the bifurcation structure found by Thompson et al. (Reference Thompson, Juel and Hazel2014) in (e).
$h=1.0\,\%$
). Solid lines corresponds to stable states, dashed lines to unstable states and dash-dotted lines to a small region of unstable symmetric states, thin lines to symmetric states and thick lines to asymmetric states. The structure evolves from the Saffman–Taylor system in (a), including the unstable Romero–Vanden-Broeck solution branches (double- and triple-tipped symmetric fingers), to the bifurcation structure found by Thompson et al. (Reference Thompson, Juel and Hazel2014) in (e).
4.4 Evolution of the bifurcation diagram with occlusion height
 $({\it\alpha}=80)$
$({\it\alpha}=80)$
Bifurcation diagrams for
![]() ${\it\alpha}=80$
are presented in figure 11, in which the finger width and finger-tip speed are plotted as functions of the capillary number
${\it\alpha}=80$
are presented in figure 11, in which the finger width and finger-tip speed are plotted as functions of the capillary number
![]() $Ca$
for
$Ca$
for
![]() ${\it\alpha}_{h}$
in the range
${\it\alpha}_{h}$
in the range
![]() $0.001\leqslant {\it\alpha}_{h}\leqslant 0.01$
. The figure shows the evolution of the system from the classic Saffman–Taylor scenario, figure 11(a), to a bifurcation diagram qualitatively similar to that presented in Thompson et al. (Reference Thompson, Juel and Hazel2014), figure 11(e). Initially, figure 11(a), the Romero–Vanden-Broeck solutions (dashed lines) are disconnected from the symmetric Saffman–Taylor solution (solid line) at
$0.001\leqslant {\it\alpha}_{h}\leqslant 0.01$
. The figure shows the evolution of the system from the classic Saffman–Taylor scenario, figure 11(a), to a bifurcation diagram qualitatively similar to that presented in Thompson et al. (Reference Thompson, Juel and Hazel2014), figure 11(e). Initially, figure 11(a), the Romero–Vanden-Broeck solutions (dashed lines) are disconnected from the symmetric Saffman–Taylor solution (solid line) at
![]() ${\it\alpha}_{h}=0.001$
, but connect to an unstable asymmetric solution branch that was first reported by Taylor & Saffman (Reference Taylor and Saffman1959) (see also figure 10 for
${\it\alpha}_{h}=0.001$
, but connect to an unstable asymmetric solution branch that was first reported by Taylor & Saffman (Reference Taylor and Saffman1959) (see also figure 10 for
![]() ${\it\alpha}_{h}=0$
). As
${\it\alpha}_{h}=0$
). As
![]() ${\it\alpha}_{h}$
increases, the stable and unstable sets of solution branches interact. For
${\it\alpha}_{h}$
increases, the stable and unstable sets of solution branches interact. For
![]() ${\it\alpha}_{h}=0.003$
, figure 11(b), the asymmetric branch emanating from the Romero–Vanden-Broeck solution has developed two limit points, while the stable symmetric branch has developed a pair of supercritical pitchfork bifurcation points (● and ▴) resulting in a small region of unstable symmetric fingers (dashed-dotted lines). The unstable asymmetric branch and the stable symmetric branch do not interact in figure 11(b), despite the position of the upper limit point from the asymmetric branch appearing to coincide with the symmetric branch in this projection.
${\it\alpha}_{h}=0.003$
, figure 11(b), the asymmetric branch emanating from the Romero–Vanden-Broeck solution has developed two limit points, while the stable symmetric branch has developed a pair of supercritical pitchfork bifurcation points (● and ▴) resulting in a small region of unstable symmetric fingers (dashed-dotted lines). The unstable asymmetric branch and the stable symmetric branch do not interact in figure 11(b), despite the position of the upper limit point from the asymmetric branch appearing to coincide with the symmetric branch in this projection.
By
![]() ${\it\alpha}_{h}=0.004$
, figure 11(c), a complex interaction between the previously independent stable and unstable solution structures has taken place, resulting in an altered bifurcation diagram. The upper limit point previously formed on the unstable asymmetric branch has interacted with the second pitchfork point (▴) that previously bounded the region of stable asymmetric fingers on the stable solution branch emanating at low values of
${\it\alpha}_{h}=0.004$
, figure 11(c), a complex interaction between the previously independent stable and unstable solution structures has taken place, resulting in an altered bifurcation diagram. The upper limit point previously formed on the unstable asymmetric branch has interacted with the second pitchfork point (▴) that previously bounded the region of stable asymmetric fingers on the stable solution branch emanating at low values of
![]() $Ca$
. The lower part of the unstable asymmetric branch has connected at this bifurcation point while its upper part has connected with the stable asymmetric branch and restabilised. Hence, symmetric fingers are stable for very small values of
$Ca$
. The lower part of the unstable asymmetric branch has connected at this bifurcation point while its upper part has connected with the stable asymmetric branch and restabilised. Hence, symmetric fingers are stable for very small values of
![]() $Ca$
as they lose stability to a pair of asymmetric fingers for decreasing values of
$Ca$
as they lose stability to a pair of asymmetric fingers for decreasing values of
![]() $Ca$
as
$Ca$
as
![]() ${\it\alpha}_{h}$
increases (●). The unstable symmetric branch connects to a stable symmetric branch at the second pitchfork bifurcation point (▴). In fact, starting on this symmetric stable branch at high values of
${\it\alpha}_{h}$
increases (●). The unstable symmetric branch connects to a stable symmetric branch at the second pitchfork bifurcation point (▴). In fact, starting on this symmetric stable branch at high values of
![]() $Ca$
and decreasing
$Ca$
and decreasing
![]() $Ca$
, the branch’s loss of stability can be seen to arise through a subcritical pitchfork bifurcation to a pair of asymmetric states that connect the single-tipped symmetric finger to the wide multiple-tipped fingers linked to the first and second Romero–Vanden-Broeck solutions. This new bifurcation scenario is confirmed for
$Ca$
, the branch’s loss of stability can be seen to arise through a subcritical pitchfork bifurcation to a pair of asymmetric states that connect the single-tipped symmetric finger to the wide multiple-tipped fingers linked to the first and second Romero–Vanden-Broeck solutions. This new bifurcation scenario is confirmed for
![]() ${\it\alpha}_{h}=0.005$
, figure 11(d).
${\it\alpha}_{h}=0.005$
, figure 11(d).
Finally, increasing
![]() ${\it\alpha}_{h}$
further to 0.01, figure 11(e), the unstable asymmetric region between the second pitchfork bifurcation point on the symmetric Saffman–Taylor branch (▴) and the pitchfork bifurcation point previously highlighted in figure 10 (▪), disappears and the solutions disconnect. Thus, we recover (qualitatively) the bifurcation diagram for low occlusions presented by Thompson et al. (Reference Thompson, Juel and Hazel2014) at
${\it\alpha}_{h}$
further to 0.01, figure 11(e), the unstable asymmetric region between the second pitchfork bifurcation point on the symmetric Saffman–Taylor branch (▴) and the pitchfork bifurcation point previously highlighted in figure 10 (▪), disappears and the solutions disconnect. Thus, we recover (qualitatively) the bifurcation diagram for low occlusions presented by Thompson et al. (Reference Thompson, Juel and Hazel2014) at
![]() ${\it\alpha}=10$
, see their figure 8, with the addition of an isolated symmetric branch that was not found in their investigation. The subsequent changes in bifurcation structure for further increases in
${\it\alpha}=10$
, see their figure 8, with the addition of an isolated symmetric branch that was not found in their investigation. The subsequent changes in bifurcation structure for further increases in
![]() ${\it\alpha}_{h}$
are presented in detail in Thompson et al. (Reference Thompson, Juel and Hazel2014).
${\it\alpha}_{h}$
are presented in detail in Thompson et al. (Reference Thompson, Juel and Hazel2014).
The main features of the interaction between the Saffman–Taylor and Romero–Vanden-Broeck solutions are shown in figure 12, where the symmetry-breaking bifurcation points discussed above are plotted in the
![]() $Ca$
–
$Ca$
–
![]() ${\it\alpha}_{h}$
parameter plane. The pair of pitchfork bifurcation points on the symmetric Saffman–Taylor branch (● and ▴) emerges for a finite value of
${\it\alpha}_{h}$
parameter plane. The pair of pitchfork bifurcation points on the symmetric Saffman–Taylor branch (● and ▴) emerges for a finite value of
![]() ${\it\alpha}_{h}\simeq 0.0022$
, and separate as
${\it\alpha}_{h}\simeq 0.0022$
, and separate as
![]() ${\it\alpha}_{h}$
increases. The second pitchfork bifurcation point (▴) then merges with the Romero–Vanden-Broeck pitchfork point (▪). This interaction results in the separation of solution branches (figure 11
e), which leaves a saddle-node bifurcation point (
${\it\alpha}_{h}$
increases. The second pitchfork bifurcation point (▴) then merges with the Romero–Vanden-Broeck pitchfork point (▪). This interaction results in the separation of solution branches (figure 11
e), which leaves a saddle-node bifurcation point (
![]() $\star$
).
$\star$
).

Figure 12. Location in the
![]() $Ca$
–
$Ca$
–
![]() ${\it\alpha}_{h}$
parameter plane of the symmetry-breaking bifurcation points shown in figure 11 for
${\it\alpha}_{h}$
parameter plane of the symmetry-breaking bifurcation points shown in figure 11 for
![]() ${\it\alpha}=80$
. (▪) Pitchfork bifurcation connecting the unstable first and second Romero–Vanden-Broeck solutions to the unstable Taylor–Saffman asymmetric solutions. (●), (▴) Pair of pitchfork bifurcations which first appear on the stable Saffman–Taylor solution branch at finite
${\it\alpha}=80$
. (▪) Pitchfork bifurcation connecting the unstable first and second Romero–Vanden-Broeck solutions to the unstable Taylor–Saffman asymmetric solutions. (●), (▴) Pair of pitchfork bifurcations which first appear on the stable Saffman–Taylor solution branch at finite
![]() ${\it\alpha}_{h}\simeq 0.0022$
. (
${\it\alpha}_{h}\simeq 0.0022$
. (
![]() $\star$
) Saddle-node bifurcation point emerging from the coalescence of the Romero–Vanden-Broeck pitchfork (▪) with the second pitchfork bifurcation on the symmetric Saffman–Taylor branch (▴).
$\star$
) Saddle-node bifurcation point emerging from the coalescence of the Romero–Vanden-Broeck pitchfork (▪) with the second pitchfork bifurcation on the symmetric Saffman–Taylor branch (▴).
4.5 Reduction of the occlusion height required for symmetry breaking and Hopf bifurcation onset with increasing channel aspect ratio
The results reported in § 4.2 indicate that lower occlusions are required to achieve a similar solution structure as the channel aspect ratio increases. In order to quantify this observation, we focused on the first supercritical pitchfork bifurcation from a stable symmetric finger to a pair of stable asymmetric fingers described in §§ 4.2 and 4.3. We determined the occlusion height
![]() ${\it\alpha}_{h}$
required in order for the critical value of
${\it\alpha}_{h}$
required in order for the critical value of
![]() $Ca$
to remain constant (
$Ca$
to remain constant (
![]() $Ca_{c}=1.8\times 10^{-3}$
) for increasing values of
$Ca_{c}=1.8\times 10^{-3}$
) for increasing values of
![]() ${\it\alpha}$
. The parameter values were selected in order to maximise the finger offset at
${\it\alpha}$
. The parameter values were selected in order to maximise the finger offset at
![]() ${\it\alpha}=40$
while retaining a supercritical bifurcation, so that asymmetric solutions could be resolved numerically over a wide range of
${\it\alpha}=40$
while retaining a supercritical bifurcation, so that asymmetric solutions could be resolved numerically over a wide range of
![]() ${\it\alpha}$
(up to
${\it\alpha}$
(up to
![]() ${\it\alpha}=120$
). The inverse of the occlusion fractional height relative to
${\it\alpha}=120$
). The inverse of the occlusion fractional height relative to
![]() ${\it\alpha}_{h40}=0.031$
is shown as a function of channel aspect ratio relative to
${\it\alpha}_{h40}=0.031$
is shown as a function of channel aspect ratio relative to
![]() ${\it\alpha}=40$
in figure 13. The data closely follows a parabolic curve, which indicates the rapidly increasing sensitivity of finger propagation to decreasing depth perturbations as the aspect ratio is increased. The small discrepancy of the data (♦) with respect to the parabolic fit is due to the difficulty in tracking the critical capillary number to the required value as the occlusion height is varied. The parabolic relationship between
${\it\alpha}=40$
in figure 13. The data closely follows a parabolic curve, which indicates the rapidly increasing sensitivity of finger propagation to decreasing depth perturbations as the aspect ratio is increased. The small discrepancy of the data (♦) with respect to the parabolic fit is due to the difficulty in tracking the critical capillary number to the required value as the occlusion height is varied. The parabolic relationship between
![]() $1/{\it\alpha}_{h}$
and
$1/{\it\alpha}_{h}$
and
![]() ${\it\alpha}$
required to maintain the bifurcation at a fixed value of
${\it\alpha}$
required to maintain the bifurcation at a fixed value of
![]() $Ca$
shown in figure 13 can be predicted from the hypothesis that symmetry breaking occurs due to a balance between surface tension acting through lateral curvature, which favours a centred finger, and variable viscous resistance, which enables the finger to propagate more rapidly in the deeper parts of the channel.
$Ca$
shown in figure 13 can be predicted from the hypothesis that symmetry breaking occurs due to a balance between surface tension acting through lateral curvature, which favours a centred finger, and variable viscous resistance, which enables the finger to propagate more rapidly in the deeper parts of the channel.

Figure 13. The inverse occlusion height
![]() $({\it\alpha}_{h}/{\it\alpha}_{h40})^{-1}$
required to scale a critical capillary number
$({\it\alpha}_{h}/{\it\alpha}_{h40})^{-1}$
required to scale a critical capillary number
![]() $Ca_{c}$
as a function of the normalised aspect ratio
$Ca_{c}$
as a function of the normalised aspect ratio
![]() ${\it\alpha}/{\it\alpha}_{40}$
, where
${\it\alpha}/{\it\alpha}_{40}$
, where
![]() ${\it\alpha}_{40}=40$
and
${\it\alpha}_{40}=40$
and
![]() ${\it\alpha}_{h40}=0.031$
. The data (♦) is obtained by computing supercritical pitchfork bifurcations of finger offset
${\it\alpha}_{h40}=0.031$
. The data (♦) is obtained by computing supercritical pitchfork bifurcations of finger offset
![]() ${\it\delta}$
against capillary number
${\it\delta}$
against capillary number
![]() $Ca$
where the critical capillary number is set to
$Ca$
where the critical capillary number is set to
![]() $Ca_{c}=1.8\times 10^{-3}$
(shown in the inset). The fit (– – – –) follows a parabolic behaviour revealing significant effects on the finger propagation by decreasing the occlusion thickness while the aspect ratio increases.
$Ca_{c}=1.8\times 10^{-3}$
(shown in the inset). The fit (– – – –) follows a parabolic behaviour revealing significant effects on the finger propagation by decreasing the occlusion thickness while the aspect ratio increases.
In order to formalise this argument, we note that lateral curvature of the finger tip and the typical pressure variations within the fluid are both
![]() $O(1)$
, and recall that the
$O(1)$
, and recall that the
![]() $Ca=U_{f}Q$
, where
$Ca=U_{f}Q$
, where
![]() $U_{f}$
is the
$U_{f}$
is the
![]() $O(1)$
steady propagation speed. This means that due to (2.3), the variation in pressure induced by small occlusions are of the order
$O(1)$
steady propagation speed. This means that due to (2.3), the variation in pressure induced by small occlusions are of the order
![]() ${\it\alpha}_{h}$
in (2.4), while the lateral curvature term in (2.4) scales as order
${\it\alpha}_{h}$
in (2.4), while the lateral curvature term in (2.4) scales as order
![]() $({\it\alpha}^{2}\,Ca)^{-1}$
. Balancing these effects in the limit of large aspect ratio implies that
$({\it\alpha}^{2}\,Ca)^{-1}$
. Balancing these effects in the limit of large aspect ratio implies that
![]() ${\it\alpha}_{h}\sim 1/({\it\alpha}^{2}Ca)$
for the symmetry-breaking bifurcation. The effect of the transverse curvature term in (2.4) is of order
${\it\alpha}_{h}\sim 1/({\it\alpha}^{2}Ca)$
for the symmetry-breaking bifurcation. The effect of the transverse curvature term in (2.4) is of order
![]() ${\it\alpha}_{h}/({\it\alpha}Ca)$
, which is unimportant in this scaling compared to the other terms in (2.4) when the aspect ratio
${\it\alpha}_{h}/({\it\alpha}Ca)$
, which is unimportant in this scaling compared to the other terms in (2.4) when the aspect ratio
![]() ${\it\alpha}$
is large.
${\it\alpha}$
is large.
The inset of figure 13 shows the finger offset
![]() ${\it\delta}$
as a function of the capillary number
${\it\delta}$
as a function of the capillary number
![]() $Ca$
for increasing values of
$Ca$
for increasing values of
![]() ${\it\alpha}$
and decreasing values of
${\it\alpha}$
and decreasing values of
![]() ${\it\alpha}_{h}$
. Particularly, when the occlusion height is decreased from
${\it\alpha}_{h}$
. Particularly, when the occlusion height is decreased from
![]() ${\it\alpha}_{h}=0.0031$
to
${\it\alpha}_{h}=0.0031$
to
![]() ${\it\alpha}_{h}=0.0018$
while the aspect ratio is increased from
${\it\alpha}_{h}=0.0018$
while the aspect ratio is increased from
![]() ${\it\alpha}=100$
to
${\it\alpha}=100$
to
![]() ${\it\alpha}=120$
, finger states larger than
${\it\alpha}=120$
, finger states larger than
![]() $Ca>4\times 10^{-3}$
resymmetrise resulting in the existence of a localised region of stable asymmetric states. In other words, in order to retain the bifurcation at the given capillary number, as the aspect ratio increases, the bifurcation structure changes from that shown in figure 11(e) (
$Ca>4\times 10^{-3}$
resymmetrise resulting in the existence of a localised region of stable asymmetric states. In other words, in order to retain the bifurcation at the given capillary number, as the aspect ratio increases, the bifurcation structure changes from that shown in figure 11(e) (
![]() ${\it\alpha}_{h}=0.01$
,
${\it\alpha}_{h}=0.01$
,
![]() ${\it\alpha}=80$
) to that in 11(b) (
${\it\alpha}=80$
) to that in 11(b) (
![]() ${\it\alpha}_{h}=0.003$
,
${\it\alpha}_{h}=0.003$
,
![]() ${\it\alpha}=80$
) where it has been observed that the localised region is enclosed between two supercritical bifurcation points.
${\it\alpha}=80$
) where it has been observed that the localised region is enclosed between two supercritical bifurcation points.
We expect that the inverse occlusion height,
![]() $({\it\alpha}_{h}/{\it\alpha}_{h40})^{-1}$
, on the parabolic fit shown in figure 13 would grow to infinity (i.e.
$({\it\alpha}_{h}/{\it\alpha}_{h40})^{-1}$
, on the parabolic fit shown in figure 13 would grow to infinity (i.e.
![]() ${\it\alpha}_{h}\rightarrow 0$
) as the aspect ratio tends to infinity (
${\it\alpha}_{h}\rightarrow 0$
) as the aspect ratio tends to infinity (
![]() ${\it\alpha}\rightarrow \infty$
). Therefore, an extrapolation of the parabolic behaviour allow us to predict that a step change in channel height of
${\it\alpha}\rightarrow \infty$
). Therefore, an extrapolation of the parabolic behaviour allow us to predict that a step change in channel height of
![]() ${\it\alpha}_{h}=0.001$
, which is equivalent to the typical roughness of the experimental system (
${\it\alpha}_{h}=0.001$
, which is equivalent to the typical roughness of the experimental system (
![]() $1~{\rm\mu}\text{m}$
), would be sufficient to lead to symmetry breaking of the centred finger in channels with aspect ratios
$1~{\rm\mu}\text{m}$
), would be sufficient to lead to symmetry breaking of the centred finger in channels with aspect ratios
![]() ${\it\alpha}>155$
. This is shown to be consistent with the experimental results of Moore et al. (Reference Moore, Juel, Burgess, McCormick and Swinney2002) who observed meandering fingers of variable width in Hele-Shaw channels of
${\it\alpha}>155$
. This is shown to be consistent with the experimental results of Moore et al. (Reference Moore, Juel, Burgess, McCormick and Swinney2002) who observed meandering fingers of variable width in Hele-Shaw channels of
![]() ${\it\alpha}>150$
.
${\it\alpha}>150$
.

Figure 14. The inverse occlusion height
![]() $({\it\alpha}_{h}/{\it\alpha}_{h40})^{-1}$
as a function of the normalised aspect ratio
$({\it\alpha}_{h}/{\it\alpha}_{h40})^{-1}$
as a function of the normalised aspect ratio
![]() ${\it\alpha}/{\it\alpha}_{40}$
(▾, ♦) where the value of occlusion height
${\it\alpha}/{\it\alpha}_{40}$
(▾, ♦) where the value of occlusion height
![]() ${\it\alpha}_{h}$
is the maximum where the Hopf bifurcation is predicted. In contrast with the parabolic behaviour for symmetry breaking, the reduction of the occlusion height in order to follow the oscillatory limit agrees with a linear behaviour (– – – –). The inset presents the finger offset as a function of capillary number (see figure 4) for aspect ratio
${\it\alpha}_{h}$
is the maximum where the Hopf bifurcation is predicted. In contrast with the parabolic behaviour for symmetry breaking, the reduction of the occlusion height in order to follow the oscillatory limit agrees with a linear behaviour (– – – –). The inset presents the finger offset as a function of capillary number (see figure 4) for aspect ratio
![]() ${\it\alpha}=40$
. The occlusion height is increased from
${\it\alpha}=40$
. The occlusion height is increased from
![]() ${\it\alpha}_{h}=0.033$
to
${\it\alpha}_{h}=0.033$
to
![]() ${\it\alpha}_{h}=0.075$
, and the disappearance of the oscillatory fingers is first found at
${\it\alpha}_{h}=0.075$
, and the disappearance of the oscillatory fingers is first found at
![]() ${\it\alpha}_{h}=0.072$
(–*–*–*–) by using a validated geometric criterion (Appendix). The limit is validated by performing the stability analysis along the path shown as a red solid line in the inset where a change of sign of the real part of the eigenvalues is found at
${\it\alpha}_{h}=0.072$
(–*–*–*–) by using a validated geometric criterion (Appendix). The limit is validated by performing the stability analysis along the path shown as a red solid line in the inset where a change of sign of the real part of the eigenvalues is found at
![]() ${\it\alpha}_{h}=0.0718$
(▾).
${\it\alpha}_{h}=0.0718$
(▾).
We also consider the behaviour of the region of oscillatory solutions with increasing aspect ratio. The inset of figure 14 presents the finger offset as a function of capillary number where oscillatory states are predicted with the geometric criterion discussed in the Appendix as the occlusion height is varied. Here we select the maximum occlusion height
![]() ${\it\alpha}_{h}$
at which an oscillatory regime (via Hopf bifurcation) is predicted as our indicator of the regime. The geometric criterion is calibrated at
${\it\alpha}_{h}$
at which an oscillatory regime (via Hopf bifurcation) is predicted as our indicator of the regime. The geometric criterion is calibrated at
![]() ${\it\alpha}=40$
using linear stability calculations: the critical eigenvalues are found at
${\it\alpha}=40$
using linear stability calculations: the critical eigenvalues are found at
![]() ${\it\alpha}_{h}=0.0718$
; and the width of the prediction region used in the geometric criterion (see Appendix) is adjusted so that the oscillatory modes disappear at
${\it\alpha}_{h}=0.0718$
; and the width of the prediction region used in the geometric criterion (see Appendix) is adjusted so that the oscillatory modes disappear at
![]() ${\it\alpha}_{h}=0.072$
. Hence, the width of the prediction region corresponds to 15.2 % of the width of the occlusion. The geometrical criterion is additionally verified for
${\it\alpha}_{h}=0.072$
. Hence, the width of the prediction region corresponds to 15.2 % of the width of the occlusion. The geometrical criterion is additionally verified for
![]() ${\it\alpha}=160$
giving a maximum occlusion height for the Hopf limit of
${\it\alpha}=160$
giving a maximum occlusion height for the Hopf limit of
![]() ${\it\alpha}_{h}=0.0203$
, whereas the stability analysis provides
${\it\alpha}_{h}=0.0203$
, whereas the stability analysis provides
![]() ${\it\alpha}_{h}=0.0198$
resulting in a maximum deviation of 2.5 %. Figure 14 plots this Hopf limit of inverse occlusion height relative to
${\it\alpha}_{h}=0.0198$
resulting in a maximum deviation of 2.5 %. Figure 14 plots this Hopf limit of inverse occlusion height relative to
![]() ${\it\alpha}_{h}=0.072$
as a function of the channel aspect ratio relative to
${\it\alpha}_{h}=0.072$
as a function of the channel aspect ratio relative to
![]() ${\it\alpha}=40$
for aspect ratios up to
${\it\alpha}=40$
for aspect ratios up to
![]() ${\it\alpha}=160$
. The value of capillary number associated with the Hopf limit is always found for
${\it\alpha}=160$
. The value of capillary number associated with the Hopf limit is always found for
![]() $Ca<0.012$
, which indicates that the result presented in figure 14 satisfies the parameter regime in
$Ca<0.012$
, which indicates that the result presented in figure 14 satisfies the parameter regime in
![]() $Ca$
where the quantitative agreement between experiments and numerical computations has been reported. In contrast with the parabolic behaviour for symmetry breaking, the oscillatory onset follows a linear behaviour, possibly due the direct dependence of the oscillatory mechanism on the change of the transverse curvature of the finger interface (Thompson et al.
Reference Thompson, Juel and Hazel2014), which scales with the first power of the aspect ratio as shown in (2.2). This second balance in (2.4) is between the lateral component of curvature, which features at order
$Ca$
where the quantitative agreement between experiments and numerical computations has been reported. In contrast with the parabolic behaviour for symmetry breaking, the oscillatory onset follows a linear behaviour, possibly due the direct dependence of the oscillatory mechanism on the change of the transverse curvature of the finger interface (Thompson et al.
Reference Thompson, Juel and Hazel2014), which scales with the first power of the aspect ratio as shown in (2.2). This second balance in (2.4) is between the lateral component of curvature, which features at order
![]() $({\it\alpha}^{2}Ca)^{-1}$
, and the transverse curvature component, which is of order
$({\it\alpha}^{2}Ca)^{-1}$
, and the transverse curvature component, which is of order
![]() ${\it\alpha}_{h}/({\it\alpha}Ca)$
, yielding a balance when
${\it\alpha}_{h}/({\it\alpha}Ca)$
, yielding a balance when
![]() ${\it\alpha}_{h}\sim {\it\alpha}^{-1}$
. At the tip of the finger, the normal propagation speed is
${\it\alpha}_{h}\sim {\it\alpha}^{-1}$
. At the tip of the finger, the normal propagation speed is
![]() $O(1)$
, and so the effect of the occlusion on the pressure term in (2.4) is
$O(1)$
, and so the effect of the occlusion on the pressure term in (2.4) is
![]() $O({\it\alpha}_{h})$
. However, oscillations usually arise along the side of the finger where the underlying pressure gradients are much smaller.
$O({\it\alpha}_{h})$
. However, oscillations usually arise along the side of the finger where the underlying pressure gradients are much smaller.
5 Discussion
The sensitivity of Saffman–Taylor fingers in large aspect ratio Hele-Shaw channels has been of interest since the original work of Saffman & Taylor (Reference Saffman and Taylor1958), who found symmetric and later asymmetric (Taylor & Saffman Reference Taylor and Saffman1959) continuous families of solutions to their depth-averaged model, but no mechanism to select the experimentally observed symmetric half-width finger occurring at high propagation speeds. The selection mechanism was found to be a consequence of finite surface tension, which enters as a singular perturbation (Park & Homsy Reference Park and Homsy1984). Although the common wisdom is that the singular perturbation problem explains the subsequent sensitivity of the Hele-Shaw to geometric perturbations, this does not necessarily follow because the singular limit is never reached in experiments. Once finite surface tension is present, the selection problem is resolved. Thus, although Tabeling et al. (Reference Tabeling, Zocchi and Libchaber1987) convincingly demonstrated experimentally that roughness affects the tip splitting of viscous fingers, a theoretical explanation was never found. In the present work, we demonstrate that the sensitivity is, in fact, due to the presence of additional unstable solutions at finite surface tension.
Recently, a wide variety of finger propagation modes have been found in Hele-Shaw channels of more modest aspect ratio, partially occluded by occlusions up to 50 % of the channel height (de Lózar et al. Reference de Lózar, Heap, Box, Hazel and Juel2009; Pailha et al. Reference Pailha, Hazel, Glendinning and Juel2012; Hazel et al. Reference Hazel, Pailha, Cox and Juel2013). Thompson et al. (Reference Thompson, Juel and Hazel2014) found that all finger propagation modes in partially occluded Hele-Shaw channels were qualitatively reproduced in an adapted version of the depth-averaged model used by McLean & Saffman (Reference McLean and Saffman1981) to show that finite surface tension selects the half-width finger in unoccluded Hele-Shaw channels. In addition, the depth-averaged model is known to have multiple solutions even in the absence of occlusions (Romero Reference Romero1982; Vanden-Broeck Reference Vanden-Broeck1983). Hence, the aim of the present work was to use this well-understood system with controllable geometric variations to re-examine the question of sensitivity of Saffman–Taylor fingers.
We find that the model is in quantitative agreement with experiments for
![]() ${\it\alpha}\geqslant 40$
and provided that
${\it\alpha}\geqslant 40$
and provided that
![]() $Ca\leqslant 0.012$
. The model is based on the lubrication approximation, which is expected to be valid for sufficiently high aspect ratio channels and small occlusion heights, in the limit of small
$Ca\leqslant 0.012$
. The model is based on the lubrication approximation, which is expected to be valid for sufficiently high aspect ratio channels and small occlusion heights, in the limit of small
![]() $Ca$
where the effect of liquid films on the top and bottom boundaries of the channel is negligible. Hence, this quantitative agreement means that in large aspect ratio channels we are able to use the model to follow the evolution of the solution structure for increasing obstacle heights with a high level of confidence that this represents the situation in the experiments. We believe that this evolution is the same for all aspect ratios which have been investigated, although we cannot confirm this without resorting to three-dimensional Stokes calculations. Thus we can demonstrate that the asymmetric and the double-tipped solutions observed in smaller aspect ratio channels by de Lózar et al. (Reference de Lózar, Heap, Box, Hazel and Juel2009) and others are the unstable asymmetric Saffman–Taylor solutions and the first symmetric Romero–Vanden-Broeck solution having been stabilised by the presence of the occlusion. The occlusion height required to stabilise the asymmetric Saffman–Taylor solutions decreases with increasing aspect ratio, with the critical height for provoking pitchfork bifurcations being proportional to
$Ca$
where the effect of liquid films on the top and bottom boundaries of the channel is negligible. Hence, this quantitative agreement means that in large aspect ratio channels we are able to use the model to follow the evolution of the solution structure for increasing obstacle heights with a high level of confidence that this represents the situation in the experiments. We believe that this evolution is the same for all aspect ratios which have been investigated, although we cannot confirm this without resorting to three-dimensional Stokes calculations. Thus we can demonstrate that the asymmetric and the double-tipped solutions observed in smaller aspect ratio channels by de Lózar et al. (Reference de Lózar, Heap, Box, Hazel and Juel2009) and others are the unstable asymmetric Saffman–Taylor solutions and the first symmetric Romero–Vanden-Broeck solution having been stabilised by the presence of the occlusion. The occlusion height required to stabilise the asymmetric Saffman–Taylor solutions decreases with increasing aspect ratio, with the critical height for provoking pitchfork bifurcations being proportional to
![]() ${\it\alpha}^{-2}$
and that for Hopf bifurcations being proportional to
${\it\alpha}^{-2}$
and that for Hopf bifurcations being proportional to
![]() ${\it\alpha}^{-1}$
. These scalings are consistent with the mechanisms underlying bifurcations described by Thompson et al. (Reference Thompson, Juel and Hazel2014). The pitchfork is principally associated with changes in viscous resistance, whereas the Hopf bifurcation is associated with coincidence of finger and occlusion edges.
${\it\alpha}^{-1}$
. These scalings are consistent with the mechanisms underlying bifurcations described by Thompson et al. (Reference Thompson, Juel and Hazel2014). The pitchfork is principally associated with changes in viscous resistance, whereas the Hopf bifurcation is associated with coincidence of finger and occlusion edges.
If subject to the same driving pressure gradient, both fluid and interface will propagate faster in the deeper parts of the channel. This effect is of order
![]() ${\it\alpha}_{h}$
for small occlusions, and in the absence of surface tension would lead to air fingers preferentially propagating along the deeper sides of the channel. The tip splitting and symmetry-breaking behaviour that would arise from this speed differential is resisted by surface tension acting through the lateral curvature. A simple balance between
${\it\alpha}_{h}$
for small occlusions, and in the absence of surface tension would lead to air fingers preferentially propagating along the deeper sides of the channel. The tip splitting and symmetry-breaking behaviour that would arise from this speed differential is resisted by surface tension acting through the lateral curvature. A simple balance between
![]() $O({\it\alpha}_{h})$
speed differentials and the lateral curvature term leads us to predict that the occlusion height
$O({\it\alpha}_{h})$
speed differentials and the lateral curvature term leads us to predict that the occlusion height
![]() ${\it\alpha}_{h}$
for the onset of symmetry breaking should scale as
${\it\alpha}_{h}$
for the onset of symmetry breaking should scale as
![]() $1/{\it\alpha}^{2}$
at fixed
$1/{\it\alpha}^{2}$
at fixed
![]() $Ca$
, or as
$Ca$
, or as
![]() $1/B$
more generally. The effect of transverse curvature variation on the system is negligible in this limit. This scaling relationship is generally followed by our results, but there is some variation, possibly due to transverse curvature effects, and subtle dependencies of the flow field on the width, shape and speed of the finger tip. However, the scaling relationship does suggest that in the limit of large aspect ratio
$1/B$
more generally. The effect of transverse curvature variation on the system is negligible in this limit. This scaling relationship is generally followed by our results, but there is some variation, possibly due to transverse curvature effects, and subtle dependencies of the flow field on the width, shape and speed of the finger tip. However, the scaling relationship does suggest that in the limit of large aspect ratio
![]() ${\it\alpha}$
or large
${\it\alpha}$
or large
![]() $1/B$
, bifurcations due to changes in viscous resistance can be triggered by vanishingly small perturbations to the channel thickness, which again relates to the experimentally observed sensitivity of finger propagation in channels of large aspect ratio.
$1/B$
, bifurcations due to changes in viscous resistance can be triggered by vanishingly small perturbations to the channel thickness, which again relates to the experimentally observed sensitivity of finger propagation in channels of large aspect ratio.
We further conjecture that the mechanism underlying the oscillatory fingers first discovered by Pailha et al. (Reference Pailha, Hazel, Glendinning and Juel2012), which relies on step changes in channel depth, may also be implicated in the growth of dendrite-like patterns seen in Hele-Shaw channels. The mechanism relies on a balance between both components of the curvature, which leads to the observed scaling of
![]() ${\it\alpha}_{h}$
with
${\it\alpha}_{h}$
with
![]() ${\it\alpha}^{-1}$
for the onset of the Hopf bifurcations. In contrast to the Saffman–Taylor fingering mechanism which can operate in the absence of geometric perturbation and amplifies axial perturbations to the interface, Pailha et al.’s oscillatory mechanism requires geometric perturbations and amplifies lateral perturbations. In general, the advancing interface will be susceptible to both lateral and axial perturbations, meaning that both mechanisms can operate. However, depth perturbations in Hele-Shaw channels are typically uncontrolled, on the scale of the roughness of the top and bottom boundaries. In order to connect the results presented in this paper to previous observations of anomalous fingering (Tabeling et al.
Reference Tabeling, Zocchi and Libchaber1987; Rabaud et al.
Reference Rabaud, Couder and Gerard1988; Moore et al.
Reference Moore, Juel, Burgess, McCormick and Swinney2002), further work is currently underway to investigate the effect of spatially distributed step changes in channel depth, with either regular or random distributions.
${\it\alpha}^{-1}$
for the onset of the Hopf bifurcations. In contrast to the Saffman–Taylor fingering mechanism which can operate in the absence of geometric perturbation and amplifies axial perturbations to the interface, Pailha et al.’s oscillatory mechanism requires geometric perturbations and amplifies lateral perturbations. In general, the advancing interface will be susceptible to both lateral and axial perturbations, meaning that both mechanisms can operate. However, depth perturbations in Hele-Shaw channels are typically uncontrolled, on the scale of the roughness of the top and bottom boundaries. In order to connect the results presented in this paper to previous observations of anomalous fingering (Tabeling et al.
Reference Tabeling, Zocchi and Libchaber1987; Rabaud et al.
Reference Rabaud, Couder and Gerard1988; Moore et al.
Reference Moore, Juel, Burgess, McCormick and Swinney2002), further work is currently underway to investigate the effect of spatially distributed step changes in channel depth, with either regular or random distributions.
Acknowledgements
The support of EPSRC through grant EP/J007927/1 is gratefully acknowledged. A.F.G. was funded by CONICYT and A.B.T. by EPSRC grant EP/K041134/1. All research data supporting this publication are directly available within this publication.

Figure 15. Top view of an experimental oscillatory state (black line) compared to a time-dependent calculation of an oscillatory state (red dots) for
![]() ${\it\alpha}=40$
,
${\it\alpha}=40$
,
![]() ${\it\alpha}_{h}=0.06$
and capillary number
${\it\alpha}_{h}=0.06$
and capillary number
![]() $Ca=3.4\times 10^{-3}$
. The edges of the occlusion are presented as solid blue lines.
$Ca=3.4\times 10^{-3}$
. The edges of the occlusion are presented as solid blue lines.
Appendix. Estimating the occurrence of oscillatory modes
Time-dependent simulations are required in order to predict the dynamics of oscillatory states as discussed by Thompson et al. (Reference Thompson, Juel and Hazel2014). In figure 15, we show a direct comparison between an experimental and a numerical oscillatory finger, which exhibit good agreement in morphology despite some discrepancies in wavelength. The lateral displacements that form the spatially periodic pattern typically occur with speeds larger than the finger-tip speed. Hence, the inclusion of thin-film corrections of normal displacements
![]() $Ca_{n}$
as suggested by Reinelt (Reference Reinelt1987) may be required in order to achieve quantitative agreement between experiment and computations. However, the onset of oscillatory modes can still be predicted using steady calculations. The asymmetric states whose interface behind the finger tip is located in a narrow region around the centre line of the edge of the occlusion are characterised as oscillatory states as illustrated in figure 16. The exact choice of the width of the prediction region is arbitrary, as a consequence, a quantitative prediction of the Hopf bifurcation as discussed by Pailha et al. (Reference Pailha, Hazel, Glendinning and Juel2012) is in principle unknown. Nonetheless, the geometrical criterion, convenient due to its numerical expediency (§ 4.5), is validated using the stability analysis implemented by Thompson et al. (Reference Thompson, Juel and Hazel2014). Therefore, using (2.1), we find that oscillatory states are predicted when
$Ca_{n}$
as suggested by Reinelt (Reference Reinelt1987) may be required in order to achieve quantitative agreement between experiment and computations. However, the onset of oscillatory modes can still be predicted using steady calculations. The asymmetric states whose interface behind the finger tip is located in a narrow region around the centre line of the edge of the occlusion are characterised as oscillatory states as illustrated in figure 16. The exact choice of the width of the prediction region is arbitrary, as a consequence, a quantitative prediction of the Hopf bifurcation as discussed by Pailha et al. (Reference Pailha, Hazel, Glendinning and Juel2012) is in principle unknown. Nonetheless, the geometrical criterion, convenient due to its numerical expediency (§ 4.5), is validated using the stability analysis implemented by Thompson et al. (Reference Thompson, Juel and Hazel2014). Therefore, using (2.1), we find that oscillatory states are predicted when
![]() $|\!\tanh s(y_{crit}-{\it\alpha}_{w})|<0.91$
where
$|\!\tanh s(y_{crit}-{\it\alpha}_{w})|<0.91$
where
![]() $s=40$
and
$s=40$
and
![]() ${\it\alpha}_{w}=0.25$
. Hence,
${\it\alpha}_{w}=0.25$
. Hence,
![]() $0.2119<y_{crit}<0.2882$
and the width of the prediction region is 15.2 % of the width of the occlusion.
$0.2119<y_{crit}<0.2882$
and the width of the prediction region is 15.2 % of the width of the occlusion.

Figure 16. Oscillatory states are predicted by computing asymmetric finger shapes (
![]() $+$
) when their interface behind the finger tip is located inside a prediction gap (red solid line) around the centre line of the edge of the occlusion (blue solid line). In this example for
$+$
) when their interface behind the finger tip is located inside a prediction gap (red solid line) around the centre line of the edge of the occlusion (blue solid line). In this example for
![]() ${\it\alpha}=40$
and
${\it\alpha}=40$
and
![]() ${\it\alpha}_{h}=0.060$
: (a) oscillations are predicted at
${\it\alpha}_{h}=0.060$
: (a) oscillations are predicted at
![]() $Ca=0.01$
(b) no oscillations predicted at
$Ca=0.01$
(b) no oscillations predicted at
![]() $Ca=0.02$
.
$Ca=0.02$
.

Figure 17. Experimental oscillatory states compared to numerical calculations of asymmetric states for
![]() ${\it\alpha}=40$
,
${\it\alpha}=40$
,
![]() ${\it\alpha}_{h}=0.065$
and capillary numbers (a)
${\it\alpha}_{h}=0.065$
and capillary numbers (a)
![]() $Ca=0.0103$
, (b)
$Ca=0.0103$
, (b)
![]() $Ca=0.0252$
and (c)
$Ca=0.0252$
and (c)
![]() $Ca=0.0425$
. A large deviation of the numerical values of finger width and finger offset is observed for capillary numbers larger than
$Ca=0.0425$
. A large deviation of the numerical values of finger width and finger offset is observed for capillary numbers larger than
![]() $Ca>0.012$
. The dashed line on top right corresponds to 20 mm.
$Ca>0.012$
. The dashed line on top right corresponds to 20 mm.
An experimental investigation for larger capillary numbers using
![]() ${\it\alpha}=40$
,
${\it\alpha}=40$
,
![]() ${\it\alpha}_{h}=0.065$
where oscillatory states occurs is shown in figure 17. Here, the Hopf bifurcation is found at
${\it\alpha}_{h}=0.065$
where oscillatory states occurs is shown in figure 17. Here, the Hopf bifurcation is found at
![]() $Ca\approx 0.04$
. Asymmetric states computed with the same parameters are compared to the experiment showing a deviation from the values of finger width
$Ca\approx 0.04$
. Asymmetric states computed with the same parameters are compared to the experiment showing a deviation from the values of finger width
![]() ${\it\lambda}$
and finger offset
${\it\lambda}$
and finger offset
![]() ${\it\delta}$
of 18 % and 14 %, respectively, as the capillary number is increased up to
${\it\delta}$
of 18 % and 14 %, respectively, as the capillary number is increased up to
![]() $Ca=0.0425$
, which then prevents a quantitative prediction of the Hopf bifurcation possibly due to the absence of thin-film correction in the theoretical model. However, our results shown in figures 6 and 7 for
$Ca=0.0425$
, which then prevents a quantitative prediction of the Hopf bifurcation possibly due to the absence of thin-film correction in the theoretical model. However, our results shown in figures 6 and 7 for
![]() ${\it\alpha}_{h}=0.6$
and
${\it\alpha}_{h}=0.6$
and
![]() ${\it\alpha}_{h}=0.42$
, respectively, confirm the quantitative agreement of the region where oscillatory states occur for values of
${\it\alpha}_{h}=0.42$
, respectively, confirm the quantitative agreement of the region where oscillatory states occur for values of
![]() $Ca<0.012$
by using the geometric criterion as the occlusion height
$Ca<0.012$
by using the geometric criterion as the occlusion height
![]() ${\it\alpha}_{h}$
is varied.
${\it\alpha}_{h}$
is varied.