Volume 1026 - 10 January 2026
Latest volume of Journal of Fluid Mechanics
Contents
JFM Papers
Strongly nonlinear waves in an axisymmetric jet of ferrofluid surrounded by a non-magnetisable fluid
-
- Published online by Cambridge University Press:
- 29 December 2025, A10
-
- Article
- Export citation
Theoretical analysis of Stokes flow through a sharp-cornered cross-slot
-
- Published online by Cambridge University Press:
- 26 December 2025, A9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounds on dissipation in three-dimensional planar shear flows: reduction to two-dimensional problems
-
- Published online by Cambridge University Press:
- 29 December 2025, A8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On wedge aerated water entry: experiment and theory
-
- Published online by Cambridge University Press:
- 26 December 2025, A7
-
- Article
- Export citation
The dynamics of Lagrangian mean flow induced by three-dimensional internal waves under viscous conditions
-
- Published online by Cambridge University Press:
- 26 December 2025, A4
-
- Article
- Export citation
Negative differential flow resistance in reverse osmosis
-
- Published online by Cambridge University Press:
- 26 December 2025, A5
-
- Article
- Export citation
Marangoni-driven freezing dynamics of supercooled binary droplets
-
- Published online by Cambridge University Press:
- 26 December 2025, A11
-
- Article
- Export citation
Scale-resolved turbulent Prandtl number for Rayleigh–Bénard convection at
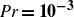 ${{\textit{Pr}}\boldsymbol{=}\boldsymbol{10}^{\boldsymbol{-3}}}$
${{\textit{Pr}}\boldsymbol{=}\boldsymbol{10}^{\boldsymbol{-3}}}$
-
- Published online by Cambridge University Press:
- 26 December 2025, A6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Impact of staggered roughness on transition, momentum and scalar transport at low Reynolds numbers
-
- Published online by Cambridge University Press:
- 26 December 2025, A3
-
- Article
- Export citation
A point vortex model for spike-type instability leading to rotating stall
-
- Published online by Cambridge University Press:
- 26 December 2025, A1
-
- Article
- Export citation
Focus on Fluids
The slippy nature of wetting flows
-
- Published online by Cambridge University Press:
- 26 December 2025, F1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Papers
Fluctuation–dissipation theorems in porous media two-phase flow: statistical characterisation of saturation fluctuations and measurement of Onsager coefficients
-
- Published online by Cambridge University Press:
- 26 December 2025, A2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Rapids
Harnessing cilium oscillations for enhanced transport in chaotic flow
-
- Published online by Cambridge University Press:
- 26 December 2025, R1
-
- Article
- Export citation