1 Introduction
Flow past a stationary circular cylinder is a classical problem in fluid mechanics. Although the geometric configuration is relatively simple, the physics associated with the flow around the cylinder exhibits a range of important phenomena, such as flow separation with attached eddies and the formation of the well-known vortex street. Consequently, the problem has attracted much attention involving theoretical, experimental and computational investigations. Early theoretical work was concerned with uniform flow past a circular cylinder and focused on the steady, low-speed viscous flow of an incompressible fluid where the flow characteristics depend solely on the Reynolds number,
$Re$
. These theoretical studies, which were focused on low-Reynolds-number or ‘creeping flow’ solutions, where
$Re\ll 1$
, can be traced back to the pioneering work of Stokes (Reference Stokes1851). In his work, Stokes neglected the inertia terms and reformulated the Stokes equation in the form
$\unicode[STIX]{x1D6FB}^{4}\unicode[STIX]{x1D713}=0$
to derive a solution, where
$\unicode[STIX]{x1D713}$
is the streamfunction (Basset Reference Basset1888; Lamb Reference Lamb1911; Bairstow, Cave & Lang Reference Bairstow, Cave and Lang1922; Apelt Reference Apelt1961; Happel & Brenner Reference Happel and Brenner1983). Although this approach works for a sphere, if the steady motion of a cylinder is considered, not all conditions can be satisfied and this led to the famous Stokes paradox, where a steady solution to the problem is not possible (Basset Reference Basset1888). Oseen (Reference Oseen1910) resolved the paradox by noting that the inertial terms need to be taken into account and proposed a linearised set of equations that partially accounted for the inertial terms. Lamb (Reference Lamb1911) subsequently developed a solution to Oseen’s equations that was valid for small
$Re$
. Following the work of Oseen and Lamb, a series of asymptotic analyses of different orders were developed (Kaplun Reference Kaplun1957; Proudman & Pearson Reference Proudman and Pearson1957; Underwood Reference Underwood1969; Skinner Reference Skinner1975; Keller & Ward Reference Keller and Ward1996). Despite significant progress in developing theoretical solutions to the Navier–Stokes equations, it has proved extremely challenging and results are generally limited to low-Reynolds-number flows.
As noted by Tritton (Reference Tritton1988), when
$Re\ll 1$
the flow around the cylinder is symmetric, both upstream and downstream. However, as the Reynolds number increases beyond unity and exceeds some critical value,
$Re_{onset}$
, which is around 3–7 (Sen, Mittal & Biswas Reference Sen, Mittal and Biswas2009), the fluid undergoes a steady separation and forms an attached pair of symmetric contra-rotating vortices at the base of the cylinder. The fluid in these vortices circulates continuously, not moving downstream. The length of these eddies will grow approximately linearly with increasing
$Re$
until they reach a second critical value,
$Re_{c}$
, around 40–50 (Kumar & Mittal Reference Kumar and Mittal2006), where the wake downstream of the cylinder becomes unsteady (Zdravkovich Reference Zdravkovich1997). Experiments have naturally played a crucial part in identifying and understanding the various flow regimes that exist, particularly in trying to establish values for
$Re_{onset}$
and
$Re_{c}$
, and especially for unsteady flows at higher Reynolds numbers. Strouhal (Reference Strouhal1878) completed some of the earliest observations showing that the frequency of oscillation is linked to the fluid velocity. Another important quantity for flow past a circular cylinder is the drag coefficient,
$C_{D}$
. It has been experimentally investigated extensively, along with the wake geometry, for incompressible flow in the continuum regime (Taneda Reference Taneda1956; Tritton Reference Tritton1959; Acrivos et al.
Reference Acrivos, Leal, Snowden and Pan1968; Coutanceau & Bouard Reference Coutanceau and Bouard1977; Huner & Hussey Reference Huner and Hussey1977; Wu et al.
Reference Wu, Wen, Yen, Weng and Wang2004). With the advance of computers in the 1960s, the numerical solution of the Navier–Stokes equations for flow past a cylinder became possible, allowing researchers to study the details of the flow physics (Son & Hanratty Reference Son and Hanratty1969; Dennis & Chang Reference Dennis and Chang1970; Fornberg Reference Fornberg1980; Sen et al.
Reference Sen, Mittal and Biswas2009). By analysing the numerical solution of the incompressible Navier–Stokes equations with direct time integration and linear stability analysis methods, Kumar & Mittal (Reference Kumar and Mittal2006) obtained a value for the second critical Reynolds number,
$Re_{c}$
, that is just above 47.
The vast majority of research studying flow past a circular cylinder has been for conventional fluid mechanics where the velocity at the cylinder surface is zero, i.e. the classic no-slip boundary condition. However, when the gas is in a non-equilibrium or rarefied state, the no-slip assumption is no longer valid and both the Reynolds number and the Knudsen number are required to determine the flow physics. The Knudsen number,
$Kn$
, relates the ratio of the molecular mean free path of the gas,
$\unicode[STIX]{x1D706}$
, to a characteristic length of the geometry, e.g. the diameter of a cylinder,
$D$
, and provides a convenient way to determine the extent of the non-equilibrium or rarefaction of the gas. Conventionally, when
$Kn\lesssim 0.001$
, the traditional Navier–Stokes equations are valid and the no-slip boundary condition can be used. When
$0.001\lesssim Kn\lesssim 0.1$
, the flow is in the slip regime and the Navier–Stokes–Fourier (NSF) equations, coupled with appropriate velocity-slip and temperature-jump wall boundary conditions, are able to predict certain main features of the flow for simple problems, but care is needed when thermal effects are present (Sone Reference Sone2000; John, Gu & Emerson Reference John, Gu and Emerson2010). If the Knudsen number lies in the range
$0.1\lesssim Kn\lesssim 10$
, the flow is in the transition regime and the NSF equations are no longer valid. For
$Kn\gtrsim 10$
, the gas is in the free-molecular or collisionless flow regime and kinetic theory is required to study the flow physics. Solutions of the Boltzmann equation (Cercignani Reference Cercignani1975, Reference Cercignani2000) are required and the de facto standard for simulating gas flow in the transition regime and beyond is the direct simulation Monte Carlo (DSMC) method (Bird Reference Bird1994). It is important to note that the Knudsen number is proportional to the product of the Mach number and Reynolds number and is discussed further in § 4.
Despite the numerous studies of flow past a circular cylinder in the continuum regime, for both compressible and incompressible flows, studies involving rarefied flows remain relatively scarce in the literature. In contrast to the difficulty in deriving an analytical solution to flow past a cylinder for the Navier–Stokes equations, exact solutions for drag in the free-molecular regime, as well as other aerodynamic forces, have been derived for many objects. These include a flat plate at an angle of attack (Tsien Reference Tsien1946; Schaaf & Chambre Reference Schaaf and Chambre1961; Sentman Reference Sentman1961), flow past a stationary sphere (Epstein Reference Epstein1924) and the circular cylinder (Heineman Reference Heineman1948; Ashley Reference Ashley1949; Stalder, Goodwin & Creager Reference Stalder, Goodwin and Creager1951; Schaaf & Chambre Reference Schaaf and Chambre1961). There have been several attempts to extend continuum-based analytical expressions for drag; for example, if an analytical solution is available for the Navier–Stokes equations, then it is possible to include the effects of velocity slip, provided geometrical effects like curvature are properly accounted for (Barber et al.
Reference Barber, Sun, Gu and Emerson2004; Lockerby et al.
Reference Lockerby, Reese, Emerson and Barber2004). In the case of a sphere, Basset (Reference Basset1888) extended the solution developed by Stokes to include velocity slip. For the cylinder, Pich (Reference Pich1969) derived an expression for
$C_{D}$
from the early transition to the free-molecular regime by defining a ‘molecular layer’ around the cylinder and considering Lamb’s classical hydrodynamic approximation away from the cylinder. Yamamoto & Sera (Reference Yamamoto and Sera1985) studied low-Reynolds-number flow past a cylinder using the linearised Bhatnagar–Gross–Krook (BGK) kinetic equation. Westerkamp & Torrilhon (Reference Westerkamp and Torrilhon2012) derived an analytic solution for creeping flow past a cylinder based on a linearised version of the regularised 13 moment equations. Although beyond the scope of the current paper, there has been interest in understanding high-speed rarefied gas flow past a cylinder. Experimental investigations have ranged from the continuum to free-molecular flow (Maslach & Schaaf Reference Maslach and Schaaf1963; Ponomarev & Filippova Reference Ponomarev and Filippova1969), whereas simulations based on kinetic approaches have recently been used (Li et al.
Reference Li, Peng, Zhang and Deng2011; John et al.
Reference John, Gu, Barber and Emerson2016; Volkov & Sharipov Reference Volkov and Sharipov2017).
It is clear that there is little data available when
$1<Re<Re_{c}$
and the gas is in the slip and early transition regime. Indeed, little is known about low-Reynolds-number compressible flow, although interest is steadily growing due to the possibility of flight on Mars to survey the terrain (Munday et al.
Reference Munday, Taira, Suwa, Numata and Asai2015). In contrast to the Earth, the atmosphere on Mars is quite rarefied. Recently, Canuto & Taira (Reference Canuto and Taira2015) performed direct numerical simulation of flow past a cylinder with moderate Reynolds and Mach numbers using the compressible Navier–Stokes equations. Their flow conditions lay in the range
$0<Kn\leqslant 0.037$
but rarefaction effects were not considered, which could result in an overprediction of both
$C_{D}$
and the vortex size. Hu, Sun & Fan (Reference Hu, Sun and Fan2009) computed the drag coefficient in the non-equilibrium flow regime with a hybrid kinetic/continuum approach and found that there is a complex interplay between rarefaction and compressibility effects. Currently, there is a lack of fundamental studies in low-Reynolds-number compressible flows and particularly for problems where non-equilibrium effects are important.
Extending hydrothermodynamics into the slip and transition regimes is one of the most promising approaches for accurately capturing the physics associated with non-equilibrium gas flows (Muller & Ruggeri Reference Muller and Ruggeri1993; Struchtrup Reference Struchtrup2005). The method of moments, originally proposed by Grad (Reference Grad1949), provides an approximate solution procedure to the Boltzmann equation and is under active development to bridge the gap between hydrothermodynamics and kinetic theory. In this approach, the Boltzmann equation is satisfied in a certain average sense rather than at the molecular distribution function level. How many moments are required largely depends on the flow regime. It was found (Gu, Emerson & Tang Reference Gu, Emerson and Tang2010; Young Reference Young2011; Gu & Emerson Reference Gu and Emerson2014) that the regularised 13 moment equations (R13) are not adequate enough to capture the Knudsen layer in Kramers’ problem and the regularised 26 moment equations (R26) are required to accurately reproduce the velocity defect found with kinetic data. However, both the R13 and R26 equations are able to capture many of the non-equilibrium phenomena observed using kinetic theory. These include effects such as the tangential heat flux in planar Couette flow and the bimodal temperature profile in planar force-driven Poiseuille flow (Gu & Emerson Reference Gu and Emerson2007, Reference Gu and Emerson2009; Taheri & Struchtrup Reference Taheri and Struchtrup2009; Taheri, Torrilhon & Struchtrup Reference Taheri, Torrilhon and Struchtrup2009). With several extra macroscopic governing equations, the moment method is slightly more expensive than the NSF equations to solve numerically. However, it is much more computationally efficient than the kinetic approaches and capable of capturing the non-equilibrium effects with a high degree of accuracy in the slip and early transition regime.
In the present study, we investigate the impact of rarefaction on steady subsonic compressible flow past a circular cylinder in the Reynolds-number range
$0.1\leqslant Re<45$
, i.e. before the onset of classic unsteady vortex shedding. To capture the non-equilibrium effects, we use the method of moments, as described in § 2, and compare our results with kinetic theory using DSMC, which is outlined in § 3. The problem formulation is described in § 4 and the computed results for drag, the onset of flow separation, the location of the separation point and the size of the attached eddies will be examined in detail in § 5 in terms of Reynolds number, Knudsen number as well as Mach number. Our findings are discussed in § 6.
2 An overview of the method of moments
The traditional hydrodynamic quantities of density
$\unicode[STIX]{x1D70C}$
, velocity
$u_{i}$
and temperature
$T$
correspond to the first five lowest-order moments of the molecular distribution function,
$f$
. The governing equations of these hydrodynamic quantities for a dilute gas can be obtained from the Boltzmann equation and represent mass, momentum and energy conservation laws, respectively (Struchtrup Reference Struchtrup2005):
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}u_{i}}{\unicode[STIX]{x2202}x_{i}}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}u_{i}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}u_{i}u_{j}}{\unicode[STIX]{x2202}x_{j}}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70E}_{ij}}{\unicode[STIX]{x2202}x_{j}}=-\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}x_{i}} & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}T}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}u_{i}T}{\unicode[STIX]{x2202}x_{i}}+\frac{2}{3R}\frac{\unicode[STIX]{x2202}q_{i}}{\unicode[STIX]{x2202}x_{i}}=-\frac{2}{3R}\left(p\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{i}}+\unicode[STIX]{x1D70E}_{ij}\frac{\unicode[STIX]{x2202}u_{j}}{\unicode[STIX]{x2202}x_{i}}\right).\end{eqnarray}$$
Here
$t$
and
$x_{i}$
are temporal and spatial coordinates, respectively, and any suffix
$i$
,
$j$
or
$k$
represents the usual summation convention. The pressure
$p$
is related to the temperature and density by the ideal gas law,
$p=\unicode[STIX]{x1D70C}RT$
, where
$R$
is the specific gas constant. However, the stress term,
$\unicode[STIX]{x1D70E}_{ij}$
, and heat flux term,
$q_{i}$
, given in (2.2) and (2.3) are unknown. The classical way to close this set of equations is through a Chapman–Enskog expansion (see Chapman & Cowling Reference Chapman and Cowling1970) of the molecular distribution function,
$f$
. When
$f$
is truncated at the first order of
$Kn$
, the gradient transport mechanism is obtained as
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{ij}=\unicode[STIX]{x1D70E}_{ij}^{NSF}=-\frac{2\unicode[STIX]{x1D707}}{A_{\unicode[STIX]{x1D70E}}}\frac{\unicode[STIX]{x2202}u_{\langle \!i}}{\unicode[STIX]{x2202}x_{j\!\rangle }}\quad \text{and}\quad q_{i}=q_{i}^{NSF}=-\frac{5\unicode[STIX]{x1D707}R}{2A_{q}}\frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}x_{i}},\end{eqnarray}$$
and equations (2.1)–(2.3) become the NSF equations. The angular brackets are used to denote the traceless part of a symmetric tensor. Alternatively, the governing equations of
$\unicode[STIX]{x1D70E}_{ij}$
and
$q_{i}$
can be derived from the Boltzmann equation, as proposed by Grad (Reference Grad1949):
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70E}_{ij}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}u_{k}\unicode[STIX]{x1D70E}_{ij}}{\unicode[STIX]{x2202}x_{k}}+\frac{\unicode[STIX]{x2202}m_{ijk}}{\unicode[STIX]{x2202}x_{k}}=\text{}\underline{-A_{\unicode[STIX]{x1D70E}}\frac{p}{\unicode[STIX]{x1D707}}\unicode[STIX]{x1D70E}_{ij}-2p\frac{\unicode[STIX]{x2202}u_{\langle \!i}}{\unicode[STIX]{x2202}x_{j\!\rangle }}}-\frac{4}{5}\frac{\unicode[STIX]{x2202}q_{\langle \!i}}{\unicode[STIX]{x2202}x_{j\!\rangle }}-2\unicode[STIX]{x1D70E}_{k\!\langle \!i}\frac{\unicode[STIX]{x2202}u_{j\!\rangle }}{\unicode[STIX]{x2202}x_{k}}\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}q_{i}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}u_{j}q_{i}}{\unicode[STIX]{x2202}x_{j}}+\frac{1}{2}\frac{\unicode[STIX]{x2202}R_{ij}}{\unicode[STIX]{x2202}x_{j}} & = & \displaystyle \text{}\underline{-A_{q}\frac{p}{\unicode[STIX]{x1D707}}q_{i}-\frac{5}{2}pR\frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}x_{i}}}-\frac{7\unicode[STIX]{x1D70E}_{ik}R}{2}\frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}x_{k}}\nonumber\\ \displaystyle & & \displaystyle -\,RT\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70E}_{ik}}{\unicode[STIX]{x2202}x_{k}}+\frac{\unicode[STIX]{x1D70E}_{ij}}{\unicode[STIX]{x1D70C}}\left(\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}x_{j}}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70E}_{jk}}{\unicode[STIX]{x2202}x_{k}}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{2}{5}\left(\frac{7}{2}q_{k}\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{k}}+q_{k}\frac{\unicode[STIX]{x2202}u_{k}}{\unicode[STIX]{x2202}x_{i}}+q_{i}\frac{\unicode[STIX]{x2202}u_{k}}{\unicode[STIX]{x2202}x_{k}}\right)-\frac{1}{6}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}}{\unicode[STIX]{x2202}x_{i}}-m_{ijk}\frac{\unicode[STIX]{x2202}u_{j}}{\unicode[STIX]{x2202}x_{k}}.\qquad\end{eqnarray}$$
By applying a first-order Chapman–Enskog expansion to equations (2.5) and (2.6), only the underlined terms are retained. Therefore, they reduce to equation (2.4) and the NSF equations are recovered. The higher moments
$m_{ijk},R_{ij}$
and
$\unicode[STIX]{x1D6E5}$
need to be known to obtain a solution of equations (2.1)–(2.3), (2.5) and (2.6). Their algebraic expressions, in terms of the derivatives of lower moments, can be used to close this set of equations, as in the R13 equation approach (Struchtrup & Torrilhon Reference Struchtrup and Torrilhon2003). Alternatively, the governing equations of
$m_{ijk},R_{ij}$
and
$\unicode[STIX]{x1D6E5}$
derived from the Boltzmann equation can be used to provide information required in equations (2.5) and (2.6). They are (Gu & Emerson Reference Gu and Emerson2009):
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}m_{ijk}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}u_{l}m_{ijk}}{\unicode[STIX]{x2202}x_{l}}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}_{ijkl}}{\unicode[STIX]{x2202}x_{l}}=-A_{m}\frac{p}{\unicode[STIX]{x1D707}}m_{ijk}-3RT\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70E}_{\langle \!ij}}{\unicode[STIX]{x2202}x_{k\!\rangle }}-\frac{3}{7}\frac{\unicode[STIX]{x2202}R_{\langle \!ij}}{\unicode[STIX]{x2202}x_{k\!\rangle }}+\mathfrak{M}_{ijk}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}R_{ij}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}u_{k}R_{ij}}{\unicode[STIX]{x2202}x_{k}}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{ijk}}{\unicode[STIX]{x2202}x_{k}}=-A_{R1}\frac{p}{\unicode[STIX]{x1D707}}R_{ij}-\frac{28}{5}RT\frac{\unicode[STIX]{x2202}q_{\langle \!i}}{\unicode[STIX]{x2202}x_{j\!\rangle }}-2RT\frac{\unicode[STIX]{x2202}m_{ijk}}{\unicode[STIX]{x2202}x_{k}}-\frac{2}{5}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}_{\langle \!i}}{\unicode[STIX]{x2202}x_{j\!\rangle }}+\Re _{ij}\qquad & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x0394}u_{i}}{\unicode[STIX]{x2202}x_{i}}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}_{i}}{\unicode[STIX]{x2202}x_{i}}=-A_{\unicode[STIX]{x1D6E5}1}\frac{p}{\unicode[STIX]{x1D707}}\unicode[STIX]{x1D6E5}-8RT\frac{\unicode[STIX]{x2202}q_{k}}{\unicode[STIX]{x2202}x_{k}}+\aleph ,\end{eqnarray}$$
in which
$\mathfrak{M}_{ijk},\Re _{ij}$
and
$\aleph$
are the nonlinear source terms listed in appendix A. In equations (2.7)–(2.9), higher-order unknown moments
$\unicode[STIX]{x1D719}_{ijkl},~\unicode[STIX]{x1D713}_{ijk}$
and
$\unicode[STIX]{x1D6FA}_{i}$
are introduced into the system of governing equations, which can be obtained from the Boltzmann equation. However, even higher-order moments will appear in their equations. This is the closure problem in the moment method. Alternatively, they can be approximated by algebraic expressions in terms of the derivatives of lower moments. In the R26 equations (Gu & Emerson Reference Gu and Emerson2009), they were obtained by a Chapman–Enskog expansion. For convenience, they can be expressed as gradient transport terms and high-order nonlinear terms, respectively, by
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D719}_{ijkl}=-\frac{4\unicode[STIX]{x1D707}}{A_{\unicode[STIX]{x1D719}}\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}m_{\langle \!ijk}}{\unicode[STIX]{x2202}x_{l\!\rangle }}+\unicode[STIX]{x1D719}_{ijkl}^{NL}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D713}_{ijk}=-\frac{27\unicode[STIX]{x1D707}}{7A_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}R_{\langle \!ij}}{\unicode[STIX]{x2202}x_{k\!\rangle }}+\unicode[STIX]{x1D713}_{ijk}^{NL} & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\unicode[STIX]{x1D6FA}_{i}=-\frac{7}{3}\frac{\unicode[STIX]{x1D707}}{A_{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}}{\unicode[STIX]{x2202}x_{i}}-4\frac{\unicode[STIX]{x1D707}}{A_{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}R_{ik}}{\unicode[STIX]{x2202}x_{k}}+\unicode[STIX]{x1D6FA}_{i}^{NL}.\end{eqnarray}$$
The full expressions of the nonlinear terms
$\unicode[STIX]{x1D719}_{ijkl}^{NL},~\unicode[STIX]{x1D713}_{ijk}^{NL}$
and
$\unicode[STIX]{x1D6FA}_{i}^{NL}$
are provided by Gu & Emerson (Reference Gu and Emerson2009). The values of the collision constants,
$A_{\unicode[STIX]{x1D70E}}$
,
$A_{q}$
,
$A_{m}$
,
$A_{R1}$
,
$A_{R2}$
,
$A_{\unicode[STIX]{x1D6E5}1}$
,
$A_{\unicode[STIX]{x1D6E5}2}$
,
$A_{\unicode[STIX]{x1D719}}$
,
$A_{\unicode[STIX]{x1D713}}$
and
$A_{\unicode[STIX]{x1D6FA}}$
, depend on the molecular collision model adopted and represent the relaxation time scale for each moment. They are given in table 1 for the case of Maxwell molecules (Truesdell & Muncaster Reference Truesdell and Muncaster1980; Struchtrup Reference Struchtrup2005), as employed in the present study. Although a dilute monatomic gas is employed, all the findings in the present study have relevance to realistic gases, such as air.
Table 1. Collision constants in the moment equations for Maxwell molecules.
To apply any of the foregoing models to flows in confined geometries, appropriate wall boundary conditions are required to determine a unique solution. Gu & Emerson (Reference Gu and Emerson2009) obtained a set of wall boundary conditions for the R26 equations based on Maxwell’s kinetic wall boundary condition (Maxwell Reference Maxwell1879) and a fifth-order approximation of the molecular distribution function in Hermite polynomials. In a frame where the coordinates are attached to the wall, with
$n_{i}$
the normal vector out of the wall pointing towards the gas and
$\unicode[STIX]{x1D70F}_{i}$
the tangential vector of the wall, the slip velocity parallel to the wall,
$u_{\unicode[STIX]{x1D70F}}$
, and temperature-jump conditions are
$$\begin{eqnarray}u_{\unicode[STIX]{x1D70F}}=-\frac{2-\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6FC}}\sqrt{\frac{\unicode[STIX]{x03C0}RT}{2}}\frac{\unicode[STIX]{x1D70E}_{n\unicode[STIX]{x1D70F}}}{p_{\unicode[STIX]{x1D6FC}}}-\frac{q_{\unicode[STIX]{x1D70F}}}{5p_{\unicode[STIX]{x1D6FC}}}\text{}\underline{-\frac{m_{nn\unicode[STIX]{x1D70F}}}{2p_{\unicode[STIX]{x1D6FC}}}+\frac{9\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D70F}}+70\unicode[STIX]{x1D713}_{nn\unicode[STIX]{x1D70F}}}{2520p_{\unicode[STIX]{x1D6FC}}RT}}\end{eqnarray}$$
and
$$\begin{eqnarray}RT-RT_{w}=-\frac{2-\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6FC}}\sqrt{\frac{\unicode[STIX]{x03C0}RT}{2}}\frac{q_{n}}{2p_{\unicode[STIX]{x1D6FC}}}-\frac{RT\unicode[STIX]{x1D70E}_{nn}}{4p_{\unicode[STIX]{x1D6FC}}}+\frac{u_{\unicode[STIX]{x1D70F}}^{2}}{4}\text{}\underline{-\frac{75R_{nn}+28\unicode[STIX]{x1D6E5}}{840p_{\unicode[STIX]{x1D6FC}}}+\frac{\unicode[STIX]{x1D719}_{nnnn}}{24p_{\unicode[STIX]{x1D6FC}}}},\end{eqnarray}$$
where
$$\begin{eqnarray}p_{\unicode[STIX]{x1D6FC}}=p+\frac{\unicode[STIX]{x1D70E}_{nn}}{2}\text{}\underline{-\frac{30R_{nn}+7\unicode[STIX]{x1D6E5}}{840RT}-\frac{\unicode[STIX]{x1D719}_{nnnn}}{24RT}}.\end{eqnarray}$$
Here
$\unicode[STIX]{x1D70E}_{nn}$
,
$\unicode[STIX]{x1D70E}_{n\unicode[STIX]{x1D70F}}$
,
$q_{\unicode[STIX]{x1D70F}}$
,
$m_{nn\unicode[STIX]{x1D70F}}$
,
$m_{nnn}$
,
$R_{nn}$
,
$\unicode[STIX]{x1D713}_{nn\unicode[STIX]{x1D70F}}$
,
$\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D70F}}$
and
$\unicode[STIX]{x1D719}_{nnnn}$
are the tangential and normal components of
$\unicode[STIX]{x1D70E}_{ij}$
,
$q_{i}$
,
$m_{ijk}$
,
$R_{ij}$
,
$\unicode[STIX]{x1D713}_{ijk}$
,
$\unicode[STIX]{x1D6FA}_{i}$
and
$\unicode[STIX]{x1D719}_{ijkl}$
relative to the wall, respectively. It should be noted that the normal velocity at the wall
$u_{n}=0$
, since there is no gas flow through the wall. The accommodation coefficient,
$\unicode[STIX]{x1D6FC}$
, represents the fraction of gas molecules that will be diffusively reflected with a Maxwellian distribution at the temperature of the wall,
$T_{w}$
. The remaining fraction
$(1-\unicode[STIX]{x1D6FC})$
of gas molecules will undergo specular reflection. The rest of the wall boundary conditions are listed in appendix C of Gu & Emerson (Reference Gu and Emerson2009). Equations (2.13) and (2.14) are similar to the velocity-slip and temperature-jump conditions for the NSF equations (Cercignani Reference Cercignani1975; Gad-el-Hak Reference Gad-el-Hak1999) with the additional underlined terms on the right-hand side providing the higher-order moment contributions which are not available in the NSF model. However, these higher-order moment terms can be used to derive a second-order slip boundary condition for the NSF equations (Taheri & Struchtrup Reference Taheri and Struchtrup2010). The solution of the NSF equations in the present study is associated with the wall boundary conditions (2.13) and (2.14) without the underlined terms.
A pressure-based numerical algorithm was introduced by Gu & Emerson (Reference Gu and Emerson2007, Reference Gu and Emerson2009) to solve the moment equations for weakly compressible and low-speed flows. It has been successfully applied in the study of pressure-driven Poiseuille flow (Tang et al. Reference Tang, Zhai, Tao, Gu and Emerson2013), thermal transpiration flow (Sheng et al. Reference Sheng, Tang, Gu, Emerson and Zhang2014) and gas flows in porous media (Lu et al. Reference Lu, Tang, Sheng, Gu, Emerson and Zhang2017; Wu et al. Reference Wu, Ho, Germanou, Gu, Liu, Xu and Zhang2017). To accommodate the compressibility of the gas flow in the present study, the pressure-based method (Ferziger & Perić Reference Ferziger and Perić2002) for arbitrary Mach number has been employed. In addition to the pressure correction, a density correction is integrated into the derivation of the pressure correction equation. The resultant pressure correction equation is no longer a discretised Poisson equation. It contains both convective and unsteady terms. When the Mach number is not negligibly small, the convective term dominates. The pressure correction method automatically adjusts to the local nature of the flow and is ideal for the purpose of the present study.
3 Description of the direct simulation Monte Carlo method
The DSMC method is based on the discrete molecular nature of a gas and essentially captures the physics of a dilute gas governed by the Boltzmann equation. The DSMC method was first introduced by Bird in the early 1960s (Bird Reference Bird1963) as a technique to analyse high-Knudsen-number flows, primarily targeted towards aerospace applications. Since then, the DSMC method has evolved into a powerful numerical approach and is considered one of the most reliable methods for simulating non-equilibrium gaseous flows. However, it is very computationally expensive, particularly for low-Reynolds-number flows in the early transition regime. Despite significant efforts to overcome the numerical difficulties and computing costs, solutions using the Boltzmann equation or DSMC are still too difficult to be widely used in practical engineering applications. Variants of DSMC, like the LVDSMC method (Baker & Hadjiconstantinou Reference Baker and Hadjiconstantinou2005), employ variance reduction techniques to reduce the statistical noise. However, they are more suited for problems involving extremely low flow speeds or very small thermal gradients. This has led to alternative approaches being developed, as exemplified by the method of moments, which aim to alleviate the computational difficulties associated with kinetic theory but are accurate enough for engineering design.
As the most reliable method for non-equilibrium gaseous flow simulations, the DSMC method is employed to complement the computational solution of the macroscopic equations. A detailed explanation of the steps involved in the DSMC method can be found in Bird (Reference Bird1963). In contrast to the molecular dynamics (MD) method (Allen & Tildesley Reference Allen and Tildesley1987), which is deterministic, the exact trajectory of each particle is not calculated in DSMC. Instead, a stochastic algorithm is used to evaluate the collision probabilities and scattering distributions based on kinetic theory. Although the actual nature of the molecular interactions is complex, they can be treated in a DSMC simulation through the use of phenomenological collision models.
The DSMC simulations in this work have been carried out using SPARTA (Gallis et al.
Reference Gallis, Torczynski, Plimpton, Rader, Koehler, Fan and Sun2014). The software is a highly scalable parallel open-source DSMC code recently developed by Sandia National Laboratory (Plimpton & Gallis Reference Plimpton and Gallis2017). The code has been validated on several benchmark test cases (Gallis et al.
Reference Gallis, Koehler, Torczynski and Plimpton2016, Reference Gallis, Bitter, Koehler, Torczynski, Plimpton and Papadakis2017) and is widely used by the DSMC community. For all DSMC simulations in this study, the gas was assumed to be argon and the variable hard sphere (VHS) model was employed. Previous theoretical and numerical studies (Gu & Emerson Reference Gu and Emerson2009, Reference Gu and Emerson2011, Reference Gu and Emerson2014; Gu et al.
Reference Gu, Emerson and Tang2010; Gu, Zhang & Emerson Reference Gu, Zhang and Emerson2016) have indicated that the results from the R26 equations using Maxwell molecules and the DSMC simulations using a VHS model are in close agreement with each other. Bird’s no-time-counter (NTC) scheme (Bird Reference Bird1994) has been employed for calculating the collision probabilities in a cell. Particle–wall interactions were assumed to be fully diffuse. Additionally, the well-known guidelines have been followed with respect to the cell size, time step and particle numbers that are needed for accurate DSMC calculations. The cell sizes in our study are defined to be smaller than one-third of the mean free path. Accordingly, the total number of cells in our simulations ranges from a few hundred thousand to several hundred million, depending on the Knudsen number and operating pressure under consideration. The time step for the DSMC simulations is taken to be five times smaller than
$\unicode[STIX]{x0394}x_{min}/(V_{mp}+U_{\infty })$
, where
$\unicode[STIX]{x0394}x_{min}$
is the smallest cell dimension,
$V_{mp}$
is the most probable molecular velocity given by
$V_{mp}=\sqrt{2RT_{\infty }}$
, and
$U_{\infty }$
is the free-stream velocity. To minimise statistical noise, an average of at least a hundred particles per cell has been considered and the sampling phase has been carried out over a period of several hundred thousand time steps.
The DSMC computational domain is a square shape, with the cylinder centrally placed. The inflow and outflow boundary conditions in our DSMC simulations are implemented by injecting particles based on the Maxwellian distribution and corresponding to the flow conditions at the boundary. For the inflow boundary case, particles are injected based on the free-stream velocity and density conditions. At the subsonic outflow, particles can enter the domain from outside, the properties of which are predominantly determined by the interior solution. We have followed the characteristic boundary conditions (Hirsch Reference Hirsch1991; Sun & Boyd Reference Sun and Boyd2004; John et al.
Reference John, Gu, Barber and Emerson2016) for the subsonic outflow, based on which the exit pressure is specified while other properties like velocity and density are derived from values extrapolated from the adjacent cell in the interior domain. The spatial extent of the DSMC computational domain required for an accurate simulation depends on the Reynolds number and Knudsen number under consideration. In general, a larger computational domain size is required for cases with low Reynolds numbers when compared to cases with high flow velocities (high Reynolds numbers). Accordingly, the largest computational domain size considered is
$60D\times 60D$
, corresponding to the case with
$Re=0.5$
and
$Kn_{\infty }=0.2$
, whereas the smallest computational domain size is
$15D\times 15D$
, corresponding to the case with
$Re=26$
and
$Kn_{\infty }=0.07$
.
A major limitation of the DSMC method is that, although it is valid for all flow regimes, the technique becomes computationally prohibitive in the near-continuum regime. Additionally, statistical noise becomes increasingly significant for very low-speed flows, requiring excessively large sampling periods to improve the signal-to-noise ratio. Therefore, we have carried out DSMC computations of only a few selected combinations of Reynolds number and Knudsen number, for which the simulations were relatively computationally affordable. The simulation time for the DSMC cases that we considered in the present study varies depending on the operating flow conditions. However, in general, DSMC requires 30–50 times more CPU time than for solving the macroscopic equations.
4 Problem formulation
Gaseous flow past a circular cylinder with a uniform wall temperature,
$T_{w}$
, is computationally studied using the moment equations and the DSMC method. The computational domain for the macroscopic equations is illustrated in figure 1 with a circular cylinder of diameter
$D$
. A gas with a free-stream velocity
$u_{\infty }$
, temperature
$T_{\infty }$
and pressure
$p_{\infty }$
(or density
$\unicode[STIX]{x1D70C}_{\infty }$
) flows towards the cylinder. The origin of the Cartesian coordinates
$(x,y)$
and the polar coordinates
$(r,\unicode[STIX]{x1D703})$
sits at the centre of the circular cylinder. The ratio of the computational domain length,
$L$
, to the width,
$H$
, is fixed at 10, while the aspect ratio
$H/D$
varies for different Reynolds numbers. The diameter of the cylinder,
$D$
, is chosen as the characteristic length, so that the Reynolds number,
$Re$
, is calculated from
$$\begin{eqnarray}Re=\frac{\unicode[STIX]{x1D70C}_{\infty }u_{\infty }D}{\unicode[STIX]{x1D707}_{\infty }},\end{eqnarray}$$
where
$\unicode[STIX]{x1D707}_{\infty }$
is the gas viscosity at temperature
$T_{\infty }$
. The Knudsen number,
$Kn_{\infty }$
, is based on the state of the free stream and is obtained from
$$\begin{eqnarray}Kn_{\infty }=\frac{\unicode[STIX]{x1D706}_{\infty }}{D},\end{eqnarray}$$
in which
$\unicode[STIX]{x1D706}_{\infty }$
is the mean free path of the gaseous free stream defined by
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{\infty }=\frac{\unicode[STIX]{x1D707}_{\infty }}{p_{\infty }}\sqrt{\frac{\unicode[STIX]{x03C0}RT_{\infty }}{2}},\end{eqnarray}$$
which indicates that, when the pressure of a gas is lower, the mean free path of the gas becomes larger and vice versa.
Figure 1. Schematic of the macroscopic equation computational domain for the gas flow past a circular cylinder.
For ideal gases, the Mach number of the incoming stream,
$Ma_{\infty }$
, is estimated from
$$\begin{eqnarray}Ma_{\infty }=\frac{u_{\infty }}{\sqrt{\unicode[STIX]{x1D6FE}RT_{\infty }}},\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FE}$
is the ratio of specific heat capacities. For the monatomic gas in the present study,
$\unicode[STIX]{x1D6FE}=5/3$
. The relationship between
$Re$
,
$Kn_{\infty }$
and
$Ma_{\infty }$
is readily obtained as
$$\begin{eqnarray}Ma_{\infty }=\sqrt{\frac{2}{\unicode[STIX]{x1D6FE}\unicode[STIX]{x03C0}}}Re\,Kn_{\infty }.\end{eqnarray}$$
It can be seen from (4.5) that
$Ma_{\infty }$
is proportional to the product of
$Re$
and
$Kn_{\infty }$
. When the gas departs from the continuum state, i.e.
$Kn\gg 0$
, the Reynolds-number effect on the compressibility of the gas increases significantly. In the present study, the investigations are limited to subsonic
$(Ma_{\infty }<1)$
, creeping and steady separation
$(Re<45)$
flows in the slip and early transition regime
$(Kn_{\infty }<1)$
.
5 Results and discussion
Macroscopic sets of the NSF, R13 and R26 equations are solved numerically for flows past a stationary cylinder with a wide range of Reynolds and Knudsen numbers determined by the free-stream parameters,
$u_{\infty },~T_{\infty }$
and
$p_{\infty }$
. The Dirichlet boundary condition is used for the side boundaries and the Neumann boundary condition for the downstream boundary, as illustrated in figure 1. For convenience, the cylinder wall temperature,
$T_{w}$
, is set to the free-stream temperature,
$T_{\infty }$
. A fully diffusive cylinder surface is assumed, i.e. the accommodation coefficient,
$\unicode[STIX]{x1D6FC}=1$
, and a body-fitted mesh is employed around the cylinder. The viscosity was obtained from Sutherland’s law (White Reference White1991). The computed results are analysed in terms of the drag coefficient,
$C_{D}$
, the onset of the twin vortices downstream of the cylinder characterised in terms of the vortex length
$l$
, defined as the distance between the rear base point and the wake stagnation point, and the separation angle
$\unicode[STIX]{x1D703}_{s}$
, as indicated in figure 2.
Figure 2. Schematics of the circular cylinder and the twin vortices.
The non-dimensional pressure and stresses are expressed as the pressure coefficient,
$c_{p}$
, the skin friction coefficient,
$c_{f}$
, and the normal stress coefficient,
$c_{n}$
, respectively, by
$$\begin{eqnarray}c_{p}=\frac{p-p_{\infty }}{\unicode[STIX]{x1D70C}_{\infty }u_{\infty }^{2}/2},\quad c_{f}=\frac{\unicode[STIX]{x1D70E}_{r\unicode[STIX]{x1D703}}}{\unicode[STIX]{x1D70C}_{\infty }u_{\infty }^{2}/2}\quad \text{and}\quad c_{n}=\frac{\unicode[STIX]{x1D70E}_{rr}}{\unicode[STIX]{x1D70C}_{\infty }u_{\infty }^{2}/2},\end{eqnarray}$$
in which
$\unicode[STIX]{x1D70E}_{r\unicode[STIX]{x1D703}}$
and
$\unicode[STIX]{x1D70E}_{rr}$
are the shear and normal stress components, respectively, in the cylindrical coordinate system
$(r,\unicode[STIX]{x1D703})$
illustrated in figure 1. The drag on the circular cylinder is composed of three separate components, namely pressure drag
$F^{p}$
, skin friction drag
$F^{f}$
, and normal stress drag
$F^{n}$
. The corresponding components of the drag coefficient,
$C_{D}^{p}$
,
$C_{D}^{f}$
and
$C_{D}^{n}$
, can be estimated from the computational solution, respectively, by
$$\begin{eqnarray}\displaystyle & \displaystyle C_{D}^{p}=\frac{F^{p}}{\unicode[STIX]{x1D70C}_{\infty }u_{\infty }^{2}D/2}=-\frac{1}{\unicode[STIX]{x1D70C}_{\infty }u_{\infty }^{2}}\int _{0}^{2\unicode[STIX]{x03C0}}(p-p_{\infty })\cos \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle C_{D}^{f}=\frac{F^{f}}{\unicode[STIX]{x1D70C}_{\infty }u_{\infty }^{2}D/2}=\frac{1}{\unicode[STIX]{x1D70C}_{\infty }u_{\infty }^{2}}\int _{0}^{2\unicode[STIX]{x03C0}}\unicode[STIX]{x1D70E}_{r\unicode[STIX]{x1D703}}\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703} & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}C_{D}^{n}=\frac{F^{n}}{\unicode[STIX]{x1D70C}_{\infty }u_{\infty }^{2}D/2}=-\frac{1}{\unicode[STIX]{x1D70C}_{\infty }u_{\infty }^{2}}\int _{0}^{2\unicode[STIX]{x03C0}}\unicode[STIX]{x1D70E}_{rr}\cos \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}.\end{eqnarray}$$
The total drag coefficient,
$C_{D}$
, is the sum of each component, i.e.
$$\begin{eqnarray}C_{D}=C_{D}^{p}+C_{D}^{f}+C_{D}^{n}.\end{eqnarray}$$
For the convenience of discussion in the following subsections, the drag coefficient in the incompressible continuum limit is denoted as
$C_{D,cont}$
.
5.1 Drag coefficient in the continuum limit
In the continuum limit, there are well-documented experimental, theoretical and numerical studies of the drag coefficient, the onset of flow separation, and the geometry of the wake. They are used in the present study to verify the accuracy of the numerical implementation and serve as the baseline to reflect rarefaction and compressibility effects on the flow characteristics as the state of the gas departs from the continuum limit. Incompressible flows in the continuum limit are computed by the Navier–Stokes equations with no-slip boundary conditions for
$0.1\leqslant Re\leqslant 45$
. When a fluid flows past a stationary cylinder, the flow is disturbed not only downstream, but also upstream and sideways. An appropriate computational domain size is required to minimise any boundary effects. The ratio of the domain length,
$L$
, to the width,
$H$
, is fixed at 10, while the aspect ratio of
$H/D$
varies for different Reynolds numbers. Shown in figure 3(a) is the drag coefficient calculated from computational solutions for
$Re=0.1$
, 0.2, 0.5 and 1.0, respectively, for different sizes of computational domain. At
$Re=0.1$
, the aspect ratio,
$H/D$
, must be greater than 2000 to obtain a grid-independent value of
$C_{D,cont}$
, whereas at
$Re=1$
, the value of
$C_{D,cont}$
requires the computational domain to be
$H/D=200$
. To reach a converged value of the drag coefficient,
$C_{D,cont}$
, a large computational domain is required for low-Reynolds-number flow. In the present study, all computations have been obtained using a sufficiently large domain for the specific Reynolds number under investigation.
Figure 3. (a) Effect of the domain size on the computed values of the drag coefficient at different Reynolds numbers. (b) Comparison of the drag coefficient at different Reynolds number for incompressible continuum flow by different approaches.
The computed values of
$C_{D,cont}$
for incompressible continuum flows are plotted against the Reynolds number in figure 3(b), in comparison with theoretical and experimental data. In the creeping flow regime,
$Re<1$
, our computed value for
$C_{D,cont}$
is slightly lower than the solution of Lamb (Reference Lamb1911), which is
$$\begin{eqnarray}C_{D,cont}=\frac{8\unicode[STIX]{x03C0}}{Re}\unicode[STIX]{x1D700},\end{eqnarray}$$
in which
$$\begin{eqnarray}\unicode[STIX]{x1D700}=\left[\frac{1}{2}-\unicode[STIX]{x1D6FE}_{e}-\ln \left(\frac{Re}{8}\right)\right]^{-1},\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FE}_{e}=0.577215$
is Euler’s constant. The present results are in good agreement with the asymptotic solution of Kaplun (Reference Kaplun1957):
$$\begin{eqnarray}C_{D,cont}=\frac{8\unicode[STIX]{x03C0}}{Re}\unicode[STIX]{x1D700}(1-0.87\unicode[STIX]{x1D700}^{2}),\end{eqnarray}$$
which is a higher-order approximation than Lamb’s solution. Skinner (Reference Skinner1975) achieved an even higher-order expansion than Kaplun’s approximation, but the difference between them is negligible. The computational solutions of Rajani, Kandasamy & Majumdar (Reference Rajani, Kandasamy and Majumdar2009) overpredict the value of
$C_{D,cont}$
significantly, particularly at small values of Reynolds number, as indicated in figure 3(b), as their study used a small computational domain. In the region
$Re>1$
, our computed values of
$C_{D,cont}$
agree well with the experimental data (Tritton Reference Tritton1959) and the computational results of Dennis & Shimshoni (Reference Dennis and Shimshoni1965), Takami & Keller (Reference Takami and Keller1969) and Dennis & Chang (Reference Dennis and Chang1970).
5.2 Drag coefficient in the slip and early transition regime
When the state of the gas is no longer in equilibrium, the characteristics of the flow are determined not only by the Reynolds number, but also by the Knudsen number. Yamamoto & Sera (Reference Yamamoto and Sera1985) obtained an approximation of the drag coefficient for
$Re<1$
based on the linearised BGK equation. Following the notation used in the present paper, their drag coefficient can be written as
$$\begin{eqnarray}C_{D}=\frac{8\unicode[STIX]{x03C0}}{Re}\unicode[STIX]{x1D709},\end{eqnarray}$$
where
$$\begin{eqnarray}\unicode[STIX]{x1D709}=\left[\frac{1}{2}-\unicode[STIX]{x1D6FE}_{e}-\ln \left(\frac{Re}{8}\right)+\frac{4Kn_{\infty }}{\sqrt{\unicode[STIX]{x03C0}}}\unicode[STIX]{x1D6EC}\right]^{-1},\end{eqnarray}$$
and
$\unicode[STIX]{x1D6EC}$
is a parameter close to unity in the slip and early transition regime and gradually increases to 1.5 towards the free-molecular regime. The values of
$\unicode[STIX]{x1D6EC}$
are given in table I of Yamamoto & Sera (Reference Yamamoto and Sera1985). As
$Kn_{\infty }\rightarrow 0$
, equations (5.9) and (5.10) reduce to Lamb’s solution. As a close analogy to Kaplun’s higher-order correction to Lamb’s solution, an empirical modification to (5.9) is proposed in the present study as
$$\begin{eqnarray}C_{D}=\frac{8\unicode[STIX]{x03C0}}{Re}\unicode[STIX]{x1D709}(1-0.87\unicode[STIX]{x1D709}^{2}),\end{eqnarray}$$
so that, as
$Kn_{\infty }\rightarrow 0$
, equation (5.11) reduces to Kaplun’s solution in the continuum limit. Figure 4(a) shows the predictions from Yamamoto & Sera’s approximation (5.9) and its modification (5.11) at
$Re=0.5$
. The gap between the two predictions is the difference between Lamb and Kaplun’s solutions as
$Kn_{\infty }\rightarrow 0$
. However, when
$Kn_{\infty }>1$
, the difference between (5.9) and (5.11) diminishes. With the combination of the concept of a ‘molecular layer’ around the cylinder and Oseen’s approximation by Lamb away from the cylinder, Pich (Reference Pich1969) obtained an expression for
$C_{D}$
in the transition regime:
$$\begin{eqnarray}C_{D}=\frac{8\unicode[STIX]{x03C0}}{Re}\left[\frac{1}{2}-\unicode[STIX]{x1D6FE}_{e}-\ln \left(\frac{Re}{8}\right)+1.747Kn_{\infty }-\ln (1+0.749Kn_{\infty })\right]^{-1}.\end{eqnarray}$$
Naturally, when
$Kn_{\infty }\rightarrow 0$
, equation (5.12) recovers Lamb’s solution and is close to the solution of Yamamoto & Sera (Reference Yamamoto and Sera1985) in the slip and transition regime, as shown in figure 4(a).
Figure 4. (a) Predicted drag coefficient from the BGK kinetic equations. (b) Predicted values of
$C_{D}$
from macroscopic models against
$Kn_{\infty }$
in comparison with DSMC data at
$Re=0.5$
.
Figure 4(b) presents the values of
$C_{D}$
calculated for
$Re=0.5$
from the numerical solution of the NSF equations with velocity-slip and temperature-jump boundary conditions, the R13 and R26 equations in the slip and early transition regime along with (5.11) and the DSMC data. The numerical solutions from all three macroscopic models converge to Kaplun’s theoretical value as
$Kn_{\infty }\rightarrow 0$
. As expected, the value of
$C_{D}$
decreases as
$Kn_{\infty }$
increases at a constant
$Re$
. When
$Kn_{\infty }<0.07$
, all three numerical solutions are in close agreement with the modified Yamamoto & Sera approximation, equation (5.11). As
$Kn_{\infty }$
increases above 0.07, the NSF equations with slip boundary conditions start to deviate from the other solutions and overpredict the value of
$C_{D}$
significantly beyond the slip regime. The R13 equations follow the R26 results and (5.11) up to
$Kn_{\infty }=0.3$
. Above this value, the R13 model underpredicts the value of
$C_{D}$
while the R26 equations are in good agreement with (5.11) up to a Knudsen number of approximately unity. This is due to the fact that the R26 model is able to capture the Knudsen layer much more accurately than the R13 model (Gu, Emerson & Tang Reference Gu, Emerson and Tang2009; Gu et al.
Reference Gu, Emerson and Tang2010; Young Reference Young2011; Gu & Emerson Reference Gu and Emerson2014). It is computationally expensive for DSMC to simulate flows with such low Reynolds and Knudsen numbers. Consequently, only limited simulations at moderate Knudsen numbers are shown in figure 4. The values of
$C_{D}$
from the DSMC simulations are close to (5.11) but are slightly higher.
Figure 5. Predicted components of
$C_{D}$
from macroscopic models at
$Re=0.5$
against
$Kn_{\infty }$
.
Using the R26 equation solutions, we can now examine the effect of the Knudsen number on the contribution from the pressure and stress terms (tangential and normal) of the drag coefficient,
$C_{D}$
. At
$Kn_{\infty }=0.01$
, as shown in figure 5 for
$Re=0.5$
, 50 % of the drag coefficient is generated by the pressure component,
$C_{D}^{p}$
, while 48 % of the value of
$C_{D}$
is from the tangential shear stress component,
$C_{D}^{f}$
. The normal stress component,
$C_{D}^{n}$
, only contributes 2 % of drag. Indeed, at the continuum limit, there is no contribution from the normal stress towards
$C_{D}$
. As
$Kn_{\infty }$
increases, the value of
$C_{D}^{n}$
increases and the friction drag decreases, respectively. The value of
$C_{D}^{p}$
remains constant until just beyond the slip regime
$(Kn_{\infty }\sim 0.2)$
and it then reduces as
$Kn_{\infty }$
continues to increase. At
$Kn_{\infty }\approx 0.9$
, the proportions of
$C_{D}^{p}$
,
$C_{D}^{n}$
and
$C_{D}^{f}$
contributing to
$C_{D}$
are 49.5 %, 28 % and 22.5 %, respectively. Although both
$C_{D}^{p}$
and
$C_{D}$
reduce as
$Kn_{\infty }$
increases beyond the slip flow regime, their ratio changes due to the increasing contribution of the normal stress component, which begins to asymptote at
$Kn\sim 1$
. The contribution of
$C_{D}^{f}$
decreases as
$Kn_{\infty }$
increases. The solution of the NSF equations with the velocity-slip boundary condition (represented by the dashed lines in figure 5) follows that of the R26 equations (represented by the solid lines) up to
$Kn_{\infty }\sim 0.07$
. Beyond this value, the NSF equations overpredict
$C_{D}^{n}$
and
$C_{D}^{p}$
in comparison with the R26 equations, which results in an overprediction of the total drag.
Figure 6. Predicted values of the drag coefficient by the R26 equations for different Reynolds numbers plotted against (a)
$Kn_{\infty }$
and (b)
$Ma_{\infty }$
.
The non-equilibrium effects on the value of the drag coefficient for the range of Reynolds number considered are quite distinct. For small Reynolds numbers,
$Re<10$
, the drag coefficient decreases below its corresponding value at the continuum limit as
$Kn_{\infty }$
increases, as shown in figure 6(a). When
$Re\geqslant 10$
, the ratio of rarefied to continuum drag,
$C_{D}/C_{D,cont}$
, shows a slight initial drop close to the continuum regime. However, as
$Kn_{\infty }$
increases, the drag ratio is seen to increase above unity. The larger the Reynolds number, the more obvious the trend is. As indicated by (4.5), both rarefaction and compressibility are related. Although rarefaction increases the velocity slip around the cylinder and tends to reduce the drag coefficient, the effects of compressibility increase the pressure drop across the cylinder and increase the drag coefficient. This will be discussed further in § 5.4. The values of
$C_{D}/C_{D,cont}$
plotted against
$Ma_{\infty }$
are presented in figure 6(b) for the same range of Reynolds number as in figure 6(a). For flows with
$Re>10$
, the drag coefficient will be above its corresponding continuum value as the Mach number increases. Although it is difficult to separate the effects of rarefaction and compressibility, figure 6 implies that compressible effects begin to dominate when
$Re>10$
, whereas rarefied gas effects are stronger when
$Re<10$
(Hu et al.
Reference Hu, Sun and Fan2009).
5.3 Non-equilibrium effects on vortex formation and size
In the continuum limit, a pair of steady twin vortices is formed downstream of the cylinder when the Reynolds number,
$Re$
, is above a critical value, denoted by
$Re_{onset}$
. The onset of flow separation can be detected by gradually increasing the Reynolds number. Above a critical value,
$Re_{onset}$
, the streamlines of the flow start to detach from the cylinder and a pair of symmetric vortices begin to form. The length of the twin vortices behind the cylinder, denoted by
$l$
, and the separation angle,
$\unicode[STIX]{x1D703}_{s}$
, as illustrated in figure 2, are measured against the Reynolds number. The critical Reynolds number can be found by extrapolating
$l$
to zero. Our simulations predict a value of 6.5, which is close to the value of 6.2 obtained by Dennis & Chang (Reference Dennis and Chang1970). The size of these vortices grows as
$Re$
increases until the Reynolds number reaches a second critical value,
$Re_{c}$
; beyond this value, the vortices become unstable. Kumar & Mittal (Reference Kumar and Mittal2006) reviewed the values of the second critical Reynolds number obtained from numerical simulations and experimental observations, and found that it varied from 40 to 50. In their work, they obtained a value of
$Re_{c}$
just above 47 by both direct time integration and linear stability analysis methods. However, as the focus of the present study is on steady-state flows, we only consider Reynolds numbers below this critical value,
$Re_{c}$
.
Figure 7. Predicted vortex size from the R26 equations against
$Re$
for a range of
$Kn_{\infty }$
in comparison with the continuum limit: (a) wake length and (b) separation angle.
Figure 8. The streamlines behind the cylinder calculated from the R26 equation solution and the DSMC data at
$Kn_{\infty }=0.05$
for eight different Reynolds numbers.
The relationship between the Reynolds number and the normalised vortex length,
$l/D$
, has been studied, experimentally and numerically, for continuum incompressible flows by many researchers. Experimental data measured by Taneda (Reference Taneda1956) and Acrivos et al. (Reference Acrivos, Leal, Snowden and Pan1968) for liquid flow past a circular cylinder are indicated by the solid symbols in figure 7(a) along with data from numerical solutions of the incompressible Navier–Stokes equations by Kawaguti & Jain (Reference Kawaguti and Jain1966), Takami & Keller (Reference Takami and Keller1969) and Dennis & Chang (Reference Dennis and Chang1970), indicated by the hollow symbols. They are all in good agreement with the values of
$l/D$
from the present numerical solution of the incompressible Navier–Stokes equations represented by the solid line for the continuum limit. The present values of the corresponding separation angle,
$\unicode[STIX]{x1D703}_{s}$
, plotted in figure 7(b) by the uppermost solid line, are slightly lower than the experimental measurements of Wu et al. (Reference Wu, Wen, Yen, Weng and Wang2004) when
$Re$
is small but agree well with the computational results of Takami & Keller (Reference Takami and Keller1969) and Dennis & Chang (Reference Dennis and Chang1970).
The lines second from the top in figure 7(a,b) are the values of
$l/D$
and
$\unicode[STIX]{x1D703}_{s}$
predicted by the R26 moment equations for gas flow at
$Kn_{\infty }=0.01$
. The vortex length is slightly reduced and the separation point moves in the downstream direction, in comparison to continuum flow, due to non-equilibrium effects at the wall, particularly at larger Reynolds numbers. Within the computed range of Reynolds number,
$Re\leqslant 45$
, the values of
$l/D$
and
$\unicode[STIX]{x1D703}_{s}$
increase as
$Re$
increases for this particular Knudsen number. However, when
$Kn_{\infty }>0.028$
, as shown in figure 7, an interesting phenomenon occurs, which has not been observed in continuum flow. Figure 8 shows the streamlines behind the cylinder calculated from the computational results of the R26 equations and the DSMC data at
$Kn_{\infty }=0.05$
as the Reynolds number increases from 10 to 28.75. The vortex length initially increases as
$Re$
increases and the separation point moves upstream, as illustrated by (a–d) in figure 8. However, when the Reynolds number is above a critical value,
$Re_{cl}$
, the twin vortices gradually diminish in size as
$Re$
increases until they eventually disappear, as demonstrated by figure 8(e–g). The agreement between the R26 equations and the DSMC data is excellent, apart from the stagnation point region where the gas velocity is close to zero and the statistical noise in the DSMC data is high.
Figure 9. Predicted vortex size from the macroscopic models in comparison with the DSMC data: (a) wake length and (b) separation angle. Lines: R26. Symbols: DSMC,
$Kn_{\infty }=0.05$
(○) and
$Kn_{\infty }=0.07$
(▫).
All three macroscopic models, the NSF, R13 and R26 equations, can capture the general phenomenon but differ considerably in capturing the physical detail, as demonstrated in figure 9. In the vortex-growing region, for
$Kn_{\infty }=0.05$
, the vortex lengths predicted by the three models lie close to each other before they reach their respective maximum length. The R26 and NSF equations predict the longest and shortest maximum length, respectively, with the R13 equations close to the R26. The vortex length predicted by DSMC for
$Kn_{\infty }=0.05$
, shown in figure 9(a) by the open symbols, is generally closer to the R26 model than the other two macroscopic models. However, the separation point predicted by the NSF equations with the velocity-slip boundary condition is significantly different from the moment equations and the DSMC data, as illustrated in figure 9(b). At
$Kn_{\infty }=0.07$
, within the traditional slip regime, the discrepancy between the NSF and moment equations is quite substantial. The NSF equations underpredict the vortex size significantly, in terms of both wake length and separation angle.
Figure 10. Vortex existence
$Re{-}Kn_{\infty }$
diagram of non-equilibrium gas behind a circular cylinder.
The Reynolds numbers relating to the onset and end of the symmetric vortices behind the cylinder,
$Re_{onset}$
and
$Re_{end}$
, can be obtained by extrapolating the curves in figures 7 and 9 to
$l/D=0$
and are plotted against Knudsen number in figure 10(a) for the three macroscopic models. The values of
$Re_{onset}$
obtained from both the R13 and R26 equations are almost identical and increase gradually as
$Kn_{\infty }$
increases. Conversely, the values of
$Re_{end}$
from the R13 are close to but slightly lower than those from the R26 equations. From figure 10, we see that the NSF equations predict a much narrower region where the twin vortices can exist in comparison to the moment equations, as indicated by the broken lines in figure 10(a), despite the fact that this is clearly in the traditional slip regime. This significant discrepancy shows that care is needed when using the NSF equations with velocity slip, even when operating in the traditional slip flow regime. Plotted in figure 10(b) is the critical Reynolds number,
$Re_{cl}$
, which divides the twin vortex region into a zone in which the vortices are growing and one where the vortices are diminishing.
Empirical expressions for
$Re_{onset}$
,
$Re_{end}$
and
$Re_{cl}$
are obtained, respectively, by curve fitting the data from the R26 equations, as
$$\begin{eqnarray}\displaystyle & \displaystyle Re_{onset}=6.5+2.169\times (10Kn_{\infty })+1.275\times (10Kn_{\infty })^{2}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle Re_{end}=\frac{1}{Kn_{\infty }}\sqrt{\frac{\unicode[STIX]{x1D6FE}\unicode[STIX]{x03C0}}{2}}-5.886+8.862\times (10Kn_{\infty })-7.190\times (10Kn_{\infty })^{2} & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}Re_{cl}=\frac{0.685}{Kn_{\infty }}\sqrt{\frac{\unicode[STIX]{x1D6FE}\unicode[STIX]{x03C0}}{2}}+5.598-9.927\times (10Kn_{\infty })+4.435\times (10Kn_{\infty })^{2}.\end{eqnarray}$$
The steady twin vortices occur behind the cylinder only in the range
$Re_{onset}<Re<Re_{end}$
. By extrapolating equations (5.13) and (5.14) in figure 10(b), they meet roughly at
$Kn_{\infty }=0.108$
. In other words, no vortices will exist downstream of the cylinder, for any Reynolds number, when
$Kn_{\infty }>0.108$
.
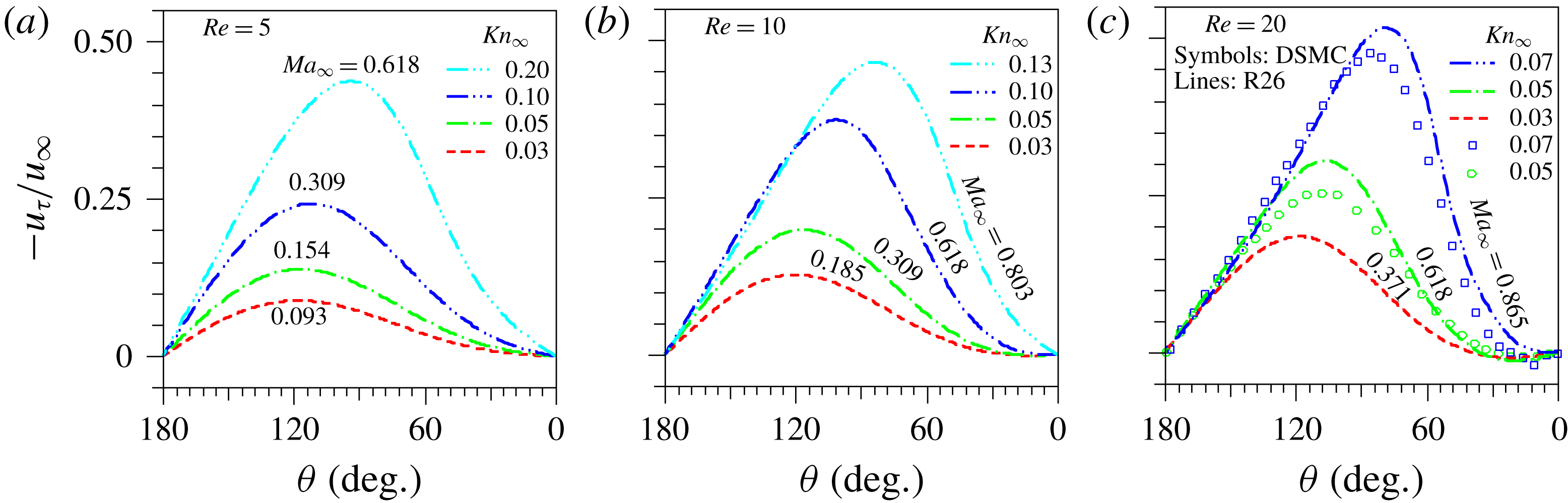
Figure 11. Velocity slip around the cylinder for different
$Re$
and
$Kn_{\infty }$
. Lines: R26. Symbols: DSMC,
$Kn_{\infty }=0.05$
(○) and
$Kn_{\infty }=0.07$
(▫).
5.4 Flow physics around the cylinder
One of the main non-equilibrium phenomena associated with a rarefied gas is the velocity slip at the solid surface. The slip velocity,
$u_{\unicode[STIX]{x1D70F}}$
, is determined by the wall shear stress, tangential heat flux along the surface, and other higher-order moments, as expressed through the boundary condition, equation (2.13). Since the flow configuration under consideration is symmetric and the polar coordinates
$(r,\unicode[STIX]{x1D703})$
are anticlockwise, it is intuitive to plot
$-u_{\unicode[STIX]{x1D70F}}/u_{\infty }$
around the cylinder from the front stagnation point, at
$\unicode[STIX]{x1D703}=180^{\circ }$
, to the cylinder base, at
$\unicode[STIX]{x1D703}=0^{\circ }$
. Figure 11 shows the velocity slip for three different Reynolds numbers and various Knudsen numbers from solutions obtained from the R26 equations and DSMC. For fixed values of
$Re$
and
$Kn_{\infty }$
, the velocity slip along the cylinder increases from the front stagnation point and reaches a maximum value before it drops to zero at
$\unicode[STIX]{x1D703}=0^{\circ }$
. The location of the maximum slip depends on the value of
$Re$
and
$Kn_{\infty }$
. For example, when
$Re=5$
and
$Kn_{\infty }=0.03$
, the maximum velocity slip occurs at
$\unicode[STIX]{x1D703}=120^{\circ }$
in figure 10(a), while it occurs at
$\unicode[STIX]{x1D703}=80^{\circ }$
for
$Re=20$
and
$Kn_{\infty }=0.07$
, as shown in figure 11(c). As anticipated, the velocity slip increases with
$Kn_{\infty }$
for a fixed value of
$Re$
. Comparing figure 11(a) and (c), the velocity slip clearly increases with Reynolds number for a fixed value of
$Kn_{\infty }$
. However, this does not imply that it is purely a Reynolds-number effect. In comparison to the DSMC data in figure 11(c), the R26 equations provide a reliable prediction of the velocity slip around the front half of the cylinder but tend to overpredict the maximum slip velocity in the leeward region.
Figure 12. The local Knudsen number around the cylinder.
Equation (4.5) indicates that
$Ma_{\infty }$
increases with the product of
$Re$
and
$Kn_{\infty }$
. As the values of
$Ma_{\infty }$
, which are illustrated in figure 11, are above 0.3, there will be compressibility effects in the solution. Consequently, the local non-equilibrium state of the gas will differ from its undisturbed free-stream value. The local Knudsen number,
$Kn$
, determined from the local temperature and pressure, is no longer the same as
$Kn_{\infty }$
. In figure 12, we have plotted the ratio,
$Kn/Kn_{\infty }$
, for three Reynolds numbers and different values of
$Kn_{\infty }$
or
$Ma_{\infty }$
around the cylinder. When
$Ma_{\infty }<0.3$
, the value of
$Kn/Kn_{\infty }$
around the cylinder is approximately equal to unity, i.e. the local non-equilibrium state is the same as the nominal one defined by the free stream. The value of
$Kn/Kn_{\infty }$
is less than unity at the front of the cylinder when
$Ma_{\infty }>0.3$
, and when
$\unicode[STIX]{x1D703}<120^{\circ }$
it increases beyond one, as shown in figure 12(a). The larger the value of
$Ma_{\infty }$
, the more obvious the phenomenon, as indicated in figure 12. In the case of
$Re=20$
and
$Kn_{\infty }=0.07$
, the local Knudsen number,
$Kn$
, is only half of its nominal value at the front, while figure 12(c) shows that it exceeds
$3Kn_{\infty }$
at the rear of the cylinder. Although it is in the slip regime in terms of the free-stream Knudsen number,
$Kn_{\infty }$
, the flow around the cylinder experiences a significant shift from the slip regime well into the transition regime. The high value of velocity slip around the rear section of the cylinder moves the separation point further downstream with an increase of
$Re$
and is able to overcome the adverse pressure gradient to reduce the vortex size until it eventually disappears, as shown in figures 8 and 9. The strong variation in local Knudsen number could also explain the discrepancy between DSMC and the R26 equations in predicting velocity slip, as highlighted in figure 11(c).
Figure 13. Viscous and rarefaction effects on (a–c)
$c_{p}$
, (d–f)
$c_{f}$
and (g–i)
$c_{n}$
around the cylinder wall. Lines: R26. Symbols: DSMC,
$Kn_{\infty }=0.05$
(○) and
$Kn_{\infty }=0.07$
(▫).
The high value of local Knudsen number results in the pressure coefficient,
$c_{p}$
, the skin friction coefficient,
$c_{f}$
, and the normal stress coefficient,
$c_{n}$
, deviating significantly from their continuum limits. Figure 13 illustrates the variation in surface value of the coefficients around the cylinder for three Reynolds numbers and various Knudsen numbers. At
$Re=5$
, the value of
$c_{p}$
is below its continuum limit at the front and rear of the cylinder for all
$Kn_{\infty }$
or
$Ma_{\infty }$
considered. It then rises above the continuum limit for
$145^{\circ }>\unicode[STIX]{x1D703}>45^{\circ }$
, approximately, as shown in figure 13(a). At
$Re=10$
, the value of
$c_{p}$
lies close to its continuum value at the front stagnation point for
$Kn_{\infty }\leqslant 0.1$
. However, the value of
$c_{p}$
clearly rises above the continuum limit until
$\unicode[STIX]{x1D703}\simeq 60^{\circ }$
. In contrast, at
$Re=20$
, shown in figure 13(c), the value of
$c_{p}$
is generally above the continuum value at
$\unicode[STIX]{x1D703}=180^{\circ }$
. For all Reynolds numbers considered, the value of
$c_{p}$
for the rarefied gas is always lower than the continuum limit at the rear of the cylinder, i.e.
$\unicode[STIX]{x1D703}=0^{\circ }$
. Moreover, figure 13(a–c) clearly illustrates the separation point moving towards the rear of the cylinder. The flow undergoes compression around the front half of the cylinder, so that
$Kn/Kn_{\infty }<1$
, while the gas expands around the rear half of the cylinder, where
$Kn/Kn_{\infty }>1$
, as indicated in figure 12(c). The variation of
$c_{p}$
predicted by the R26 equations is validated by the DSMC data, as shown in figure 13(c).
The skin friction coefficient,
$c_{f}$
, is zero at the front stagnation point and the cylinder base and reaches a maximum value at
$\unicode[STIX]{x1D703}\approx 110^{\circ }$
for all the Reynolds numbers considered, as shown in figure 13(d–f). The maximum value of
$c_{f}$
is clearly shown to decrease as
$Re$
increases. It can also be seen that the skin friction decreases as
$Kn_{\infty }$
increases for a fixed Reynolds number. The slightly negative value of
$c_{f}$
at the rear of the cylinder is due to the recirculating flow. Our simulations show that the R26 equations and the DSMC data agree well for
$c_{f}$
at both
$Kn_{\infty }=0.05$
and 0.07, as illustrated in figure 13(f). For completeness, the normal stress coefficient,
$c_{n}$
, is plotted along the cylinder wall and is zero in the continuum limit. The magnitude of
$c_{n}$
is much smaller than that of
$c_{p}$
and
$c_{f}$
, but can be seen to increase as
$Kn_{\infty }$
increases, particularly at low Reynolds number, as shown in figure 13(g).
Figure 14. Viscous and rarefaction effects on predicted components of
$C_{D}$
from the R26 equations.
Non-equilibrium effects from the contributions of
$c_{p}$
,
$c_{f}$
and
$c_{n}$
towards the total drag coefficient are presented in figure 14 for the range of Reynolds numbers considered. The contribution of
$c_{n}$
to
$C_{D}$
increases as
$Kn_{\infty }$
increases, but it is small compared to the contributions from
$c_{p}$
and
$c_{f}$
and does not affect the general trend of
$C_{D}$
. The pressure component,
$C_{D}^{p}$
, can be seen to contribute more than 50 % of the total drag and this rises as
$Re$
or
$Kn_{\infty }$
increases. As the Knudsen number increases, the skin friction drag,
$C_{D}^{f}$
, always decreases for a given Reynolds number due to the velocity slip. The resultant trend of
$C_{D}$
against
$Kn_{\infty }$
for a fixed Reynolds number depends on the competition between
$C_{D}^{p}$
and
$C_{D}^{f}$
. At
$Re=5$
, the decrease of
$C_{D}^{f}$
is faster than the corresponding increase in
$C_{D}^{p}$
with increasing
$Kn_{\infty }$
. As a result,
$C_{D}$
is lower than its continuum value, i.e.
$C_{D}/C_{D,cont}<1$
, as the gas departs from its equilibrium state, as shown in figure 14(a). When
$Re=10$
, the rates of change of
$C_{D}^{p}+C_{D}^{n}$
and
$C_{D}^{f}$
are roughly the same but in opposing directions and the value of
$C_{D}/C_{D,cont}$
remains consistently around unity. However, as
$Re$
increases to 20, shown in figure 14(c),
$C_{D}^{p}$
increases much more rapidly with an increase in
$Kn_{\infty }$
due to the compression and expansion of the gas around the cylinder. As a result, the total drag coefficient,
$C_{D}$
, rises above its corresponding continuum limit, i.e.
$C_{D}/C_{D,cont}>1$
, even though the gas is inside the accepted slip flow limit.
Figure 15. Compressibility effect on (a)
$C_{D}$
and (b)
$l/D$
, with and without non-equilibrium effects at
$Re=20$
.
The flow characteristics around the cylinder are determined by a combination of viscous, rarefaction and compressibility effects and the overall behaviour of the flow depends on the complex interplay between these competing effects. Canuto & Taira (Reference Canuto and Taira2015) recently studied how compressibility affects the flow without taking into consideration any non-equilibrium effects. They used the compressible NSF equations with the traditional no-slip boundary condition to compute the flow past a cylinder. In their work, the maximum Knudsen number based on the state of the free stream was 0.037, which occurred for
$Re=20$
at
$Ma_{\infty }=0.5$
. By neglecting velocity slip, they overpredict the drag coefficient against
$Ma_{\infty }$
, as shown in figure 15(a) for
$Re=20$
, particularly for
$Ma_{\infty }>0.3$
. Although the Knudsen number for this case is relatively small, it indicates a clear error in the drag prediction and shows that rarefaction effects need to be considered. Hu et al. (Reference Hu, Sun and Fan2009) studied the same flow conditions with a hybrid strategy of coupling a kinetic approach around the cylinder and a continuum method away from the cylinder. Both rarefaction and compressibility effects were taken into account and their predicted drag coefficient is in good agreement with our results using the R26 equations. The role of the vortex pair is also strongly affected by non-equilibrium effects. Figure 15(b) shows that the vortex length predicted by Canuto & Taira (Reference Canuto and Taira2015) increases with
$Ma_{\infty }$
, which is opposite to the prediction by the R26 equations. This illustrates the importance of velocity slip in the determination of the vortex structure.
6 Conclusions
The method of moments has been used to investigate rarefaction effects on low-speed compressible flow past a circular cylinder. In particular, we employ the R26 equations to study flow in the slip and early transition regime to understand the impact of non-equilibrium effects on drag. Our results are compared with the Navier–Stokes–Fourier equations and data obtained from the direct simulation Monte Carlo method. At the Reynolds numbers considered in this paper, where
$0.1\leqslant Re<45$
, solutions are generally obtained under the assumption that the fluid is incompressible with the classic no-slip boundary condition. This approach provides the baseline results for examining how non-equilibrium effects influence the flow physics. For creeping flow, with
$Re<1$
, a revised expression for the total drag is proposed which approaches Kaplun’s rather than Lamb’s solution when
$Kn_{\infty }$
tends to zero. The drag coefficient predicted from the higher moment equations agrees well with kinetic theory when the Knudsen number is less than unity, while the NSF equations consistently overpredict the drag coefficient, even in the slip regime. In the steady flow regime, it has been shown that velocity slip delays flow separation and acts to reduce the size of the vortices downstream of the cylinder. When
$Kn_{\infty }\geqslant 0.028$
, the vortex length increases initially with the increase of
$Re$
, as observed in the continuum regime. However, once
$Re$
is above a critical value,
$Re_{cl}$
, the lengths of the vortices reduce in size as
$Re$
increases until they eventually disappear. An existence criterion for the vortices was shown in a
$Re{-}Kn_{\infty }$
diagram. The flow physics around the cylinder was analysed in terms of the velocity slip, pressure and skin friction coefficients. We observed that rarefaction reduces the drag coefficient and the combination of viscous, rarefaction and compressibility effects is intimately linked in determining the flow features, as expressed by the relationship of
$Re$
,
$Kn_{\infty }$
and
$Ma_{\infty }$
. An important factor that has a dramatic effect on the flow is that the local state of the gas around the cylinder, as exemplified by the local Knudsen number, can be significantly different from the free-stream value. It is therefore essential to include all of these effects in the computational studies of subsonic gas flow in the slip and early transition regime even with a moderate or low Reynolds number.
Acknowledgements
This work was supported by the United Kingdom Engineering and Physical Sciences Research Council (EPSRC) under grants EP/N016602/1 and EP/K038427/1. We extend our gratitude to the Hartree Centre for access to the Blue Wonder computer facility. The DSMC simulations used the UK’s National Supercomputing Service, ARCHER; resources were awarded through an ARCHER Resource Allocation Panel award.
Appendix A. Source terms in the moment equations (2.7)–(2.9)
$$\begin{eqnarray}\mathfrak{M}_{ijk}=-3\unicode[STIX]{x1D70E}_{\langle \!ij}\frac{\unicode[STIX]{x2202}RT}{\unicode[STIX]{x2202}x_{k\!\rangle }}+\frac{3\unicode[STIX]{x1D70E}_{\langle \!ij}}{\unicode[STIX]{x1D70C}}\left(\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}x_{k\!\rangle }}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70E}_{k\!\rangle \!m}}{\unicode[STIX]{x2202}x_{m}}\right)-\frac{12}{5}q_{\langle \!i}\frac{\unicode[STIX]{x2202}u_{j}}{\unicode[STIX]{x2202}x_{k\!\rangle }}-3m_{m\!\langle \!ij}\frac{\unicode[STIX]{x2202}u_{k\!\rangle }}{\unicode[STIX]{x2202}x_{m}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Re _{ij} & = & \displaystyle -A_{R2}\frac{p}{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x1D70E}_{k\!\langle \!i}\unicode[STIX]{x1D70E}_{j\!\rangle \!k}}{\unicode[STIX]{x1D70C}}+\left(\frac{8}{3}RT\unicode[STIX]{x1D70E}_{ij}-\frac{2}{7}R_{ij}\right)\frac{\unicode[STIX]{x2202}u_{k}}{\unicode[STIX]{x2202}x_{k}}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{4}{7}(7RT\unicode[STIX]{x1D70E}_{k\!\langle \!i}+R_{k\!\langle \!i})\left(\frac{\unicode[STIX]{x2202}u_{j\!\rangle }}{\unicode[STIX]{x2202}x_{k}}+\frac{\unicode[STIX]{x2202}u_{k}}{\unicode[STIX]{x2202}x_{j\!\rangle }}\right)\nonumber\\ \displaystyle & & \displaystyle -\,2R_{k\!\langle \!i}\frac{\unicode[STIX]{x2202}u_{j\!\rangle }}{\unicode[STIX]{x2202}x_{k}}+\frac{28}{5}\frac{q_{\langle \!i}}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70E}_{j\!\rangle \!k}}{\unicode[STIX]{x2202}x_{k}}+\frac{28}{5}RTq_{\langle \!i}\left(\frac{\unicode[STIX]{x2202}p}{p\unicode[STIX]{x2202}x_{j\!\rangle }}-2\frac{\unicode[STIX]{x2202}T}{T\unicode[STIX]{x2202}x_{j\!\rangle }}\right)+2\frac{m_{ijk}}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70E}_{kl}}{\unicode[STIX]{x2202}x_{l}}\nonumber\\ \displaystyle & & \displaystyle +\,m_{ijk}\left(\frac{2}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}x_{k}}-9\frac{\unicode[STIX]{x2202}RT}{\unicode[STIX]{x2202}x_{k}}\right)+\frac{14}{3}\frac{\unicode[STIX]{x1D70E}_{ij}}{\unicode[STIX]{x1D70C}}\left(\frac{\unicode[STIX]{x2202}q_{m}}{\unicode[STIX]{x2202}x_{m}}+\unicode[STIX]{x1D70E}_{ml}\frac{\unicode[STIX]{x2202}u_{m}}{\unicode[STIX]{x2202}x_{l}}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{14}{15}\unicode[STIX]{x1D6E5}\frac{\unicode[STIX]{x2202}u_{\langle \!i}}{\unicode[STIX]{x2202}x_{j\!\rangle }}-2\unicode[STIX]{x1D719}_{ijkl}\frac{\unicode[STIX]{x2202}u_{k}}{\unicode[STIX]{x2202}x_{l}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \aleph & = & \displaystyle -A_{\unicode[STIX]{x0394}2}\frac{p}{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x1D70E}_{kj}\unicode[STIX]{x1D70E}_{jk}}{\unicode[STIX]{x1D70C}}-\frac{4}{3}\unicode[STIX]{x1D6E5}\frac{\unicode[STIX]{x2202}u_{k}}{\unicode[STIX]{x2202}x_{k}}-4(2RT\unicode[STIX]{x1D70E}_{kl}+R_{kl})\frac{\unicode[STIX]{x2202}u_{k}}{\unicode[STIX]{x2202}x_{l}}+8\frac{q_{k}}{\unicode[STIX]{x1D70C}}\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70E}_{kl}}{\unicode[STIX]{x2202}x_{l}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,RTq_{k}\left(8\frac{\unicode[STIX]{x2202}p}{p\unicode[STIX]{x2202}x_{k}}-28\frac{\unicode[STIX]{x2202}T}{T\unicode[STIX]{x2202}x_{k}}\right).\end{eqnarray}$$
Open access
