Article contents
Optimal Taylor–Couette turbulence
Published online by Cambridge University Press: 03 July 2012
Abstract
Strongly turbulent Taylor–Couette flow with independently rotating inner and outer cylinders with a radius ratio of 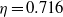 is experimentally studied. From global torque measurements, we analyse the dimensionless angular velocity flux
is experimentally studied. From global torque measurements, we analyse the dimensionless angular velocity flux 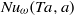 as a function of the Taylor number
as a function of the Taylor number 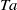 and the angular velocity ratio
and the angular velocity ratio 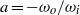 in the large-Taylor-number regime
in the large-Taylor-number regime 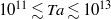 and well off the inviscid stability borders (Rayleigh lines)
and well off the inviscid stability borders (Rayleigh lines) 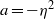 for co-rotation and
for co-rotation and 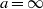 for counter-rotation. We analyse the data with the common power-law ansatz for the dimensionless angular velocity transport flux
for counter-rotation. We analyse the data with the common power-law ansatz for the dimensionless angular velocity transport flux 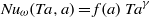 , with an amplitude
, with an amplitude 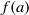 and an exponent
and an exponent 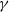 . The data are consistent with one effective exponent
. The data are consistent with one effective exponent 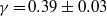 for all
for all  , but we discuss a possible
, but we discuss a possible  dependence in the co- and weakly counter-rotating regimes. The amplitude of the angular velocity flux
dependence in the co- and weakly counter-rotating regimes. The amplitude of the angular velocity flux 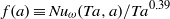 is measured to be maximal at slight counter-rotation, namely at an angular velocity ratio of
is measured to be maximal at slight counter-rotation, namely at an angular velocity ratio of 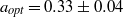 , i.e. along the line
, i.e. along the line 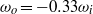 . This value is theoretically interpreted as the result of a competition between the destabilizing inner cylinder rotation and the stabilizing but shear-enhancing outer cylinder counter-rotation. With the help of laser Doppler anemometry, we provide angular velocity profiles and in particular identify the radial position
. This value is theoretically interpreted as the result of a competition between the destabilizing inner cylinder rotation and the stabilizing but shear-enhancing outer cylinder counter-rotation. With the help of laser Doppler anemometry, we provide angular velocity profiles and in particular identify the radial position  of the neutral line, defined by
of the neutral line, defined by 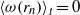 for fixed height
for fixed height  . For these large
. For these large 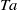 values, the ratio
values, the ratio 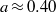 , which is close to
, which is close to 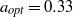 , is distinguished by a zero angular velocity gradient
, is distinguished by a zero angular velocity gradient  in the bulk. While for moderate counter-rotation
in the bulk. While for moderate counter-rotation 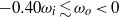 , the neutral line still remains close to the outer cylinder and the probability distribution function of the bulk angular velocity is observed to be monomodal. For stronger counter-rotation the neutral line is pushed inwards towards the inner cylinder; in this regime the probability distribution function of the bulk angular velocity becomes bimodal, reflecting intermittent bursts of turbulent structures beyond the neutral line into the outer flow domain, which otherwise is stabilized by the counter-rotating outer cylinder. Finally, a hypothesis is offered allowing a unifying view and consistent interpretation for all these various results.
, the neutral line still remains close to the outer cylinder and the probability distribution function of the bulk angular velocity is observed to be monomodal. For stronger counter-rotation the neutral line is pushed inwards towards the inner cylinder; in this regime the probability distribution function of the bulk angular velocity becomes bimodal, reflecting intermittent bursts of turbulent structures beyond the neutral line into the outer flow domain, which otherwise is stabilized by the counter-rotating outer cylinder. Finally, a hypothesis is offered allowing a unifying view and consistent interpretation for all these various results.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 76
- Cited by

