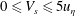1 Introduction
The dynamics and transport of swimming particles in a background flow are important for topics as wide ranging as aquatic ecology (Kiørboe Reference Kiørboe2008; Dusenbery Reference Dusenbery2009; Guasto, Rusconi & Stocker Reference Guasto, Rusconi and Stocker2012; Koehl & Cooper Reference Koehl and Cooper2015; Fuchs & Gerbi Reference Fuchs and Gerbi2016), active matter systems (Underhill, Hernandez-Ortiz & Graham Reference Underhill, Hernandez-Ortiz and Graham2008; Takatori, Yan & Brady Reference Takatori, Yan and Brady2014) and bio-inspired design (Dreyfus et al. Reference Dreyfus, Baudry, Roper, Fermigier, Stone and Bibette2005; ten Hagen et al. Reference ten Hagen, Kümmel, Wittkowski, Takagi, Löwen and Bechinger2014). Small swimming particles can represent planktonic micro-organisms as well as artificial microswimmers.
In this study we consider small, anisotropic, non-interacting, swimming particles in a background turbulent flow. Previous work on swimming particles in a background flow has found that particles can exhibit small-scale clustering, vortical trapping and enhanced or suppressed transport relative to passive particles. In a two-dimensional laminar flow, Torney & Neufeld (Reference Torney and Neufeld2007) found that there was a minimum swimming velocity, dependent on particle aspect ratio, for which there were no barriers to particle transport. In a similar flow field, Khurana, Blawzdziewicz & Ouellette (Reference Khurana, Blawzdziewicz and Ouellette2011) and Khurana & Ouellette (Reference Khurana and Ouellette2012) showed that the diffusion of swimming particles can be lower relative to passive particles, but that this effect is sensitive to the swimming velocity, particle shape and whether the particle motion includes stochastic terms. The case of gyrotactic microswimmers, where there is non-uniform distribution of material density that orients particle swimming upward, has received significant attention given its importance to phytoplankton populations. It has been found that the particle rotations caused by velocity gradients and a non-uniform density distribution combine to produce hydrodynamic focusing of such micro-organisms (Kessler Reference Kessler1985), which may explain the existence of thin layers of phytoplankton found in the ocean (Durham, Kessler & Stocker Reference Durham, Kessler and Stocker2009), small-scale clustering (Durham et al. Reference Durham, Climent, Barry, De Lillo, Boffetta, Cencini and Stocker2013; De Lillo et al. Reference De Lillo, Cencini, Durham, Barry, Stocker, Climent and Boffetta2014; Fouxon & Leshansky Reference Fouxon and Leshansky2015) and enhanced encounter rates (Gustavsson et al. Reference Gustavsson, Berglund, Jonsson and Mehlig2016). The results of gyrotactic and non-gyrotactic particles have been found to depend on whether the particle is spherical or a prolate spheroid.
Fluid turbulence is likely to play a dominant role in the dynamics of swimming anisotropic particles in a vast range of applications. The study of passive anisotropic particles in turbulent flows has led to new insights about the Lagrangian dynamics of small-scale turbulent flow structures from the preferential alignments between the particles’ axes and the directions of the velocity gradient tensor (Chevillard & Meneveau Reference Chevillard and Meneveau2013; Ni, Ouellette & Voth Reference Ni, Ouellette and Voth2014; Pujara & Variano Reference Pujara and Variano2017). However, the coupling between the particle shape and the velocity gradient tensor is likely to be altered in surprising ways when particles deviate from fluid trajectories due to swimming.
Zhan et al. (Reference Zhan, Sardina, Lushi and Brandt2013) investigated how swimming velocity and aspect ratio of rod-shaped microswimmers in isotropic turbulence affected particle clustering. They found that the clustering was strongest for the most elongated rod shapes swimming at the highest velocities. The effect of aspect ratio was monotonic and reached saturation for aspect ratios of three or larger, similar to results for the rotation rate of passive axisymmetric particles (Parsa et al. Reference Parsa, Calzavarini, Toschi and Voth2012; Byron et al. Reference Byron, Einarsson, Gustavsson, Voth, Mehlig and Variano2015). Additionally, the clustering was much weaker in turbulence compared to the two-dimensional steady and unsteady laminar flows discussed above. By investigating particles in a time-frozen snapshot of a turbulent velocity field, Zhan et al. (Reference Zhan, Sardina, Lushi and Brandt2013) concluded that this was due to the complex flow topology of turbulent flows.
In this study, we aim to further understand how the coupling between particle shape and swimming velocity affects the rotational kinematics of particles in homogenous, isotropic turbulence. We extend the study of particle shape to disc-shaped and triaxial-shaped ellipsoids. Given that the effect of aspect ratio has been found to be monotonic for both passive and swimming particles in turbulence (see above), we choose to only study high-aspect-ratio anisotropic particles. We focus on the particle enstrophy, defined as the variance of the particle angular velocity, and its components aligned with the particles’ principal axes. This allows us to investigate whether certain modes of rotation (e.g. roll, pitch, or yaw) are preferred over others. We also examine the sources of particle enstrophy, namely fluid vorticity and fluid strain. These indicate the flow properties of the regions in which particles accumulate. Understanding the biased sampling of the flow would indicate how even a weak amount of clustering might influence particle navigation or the nature of particle encounters.
The remainder of this paper is organized as follows. In § 2, we introduce the ellipsoidal particles and the equations of motion. In the appendix, we also discuss the simplifications made in computing particle dynamics. In § 3, we present the results, which concern particle accumulation and particle enstrophy. Section 4 contains a summary of the main results and how they may lead to an improved understanding of how micro-organisms and microswimmers navigate through turbulent flows.
2 Particle motion
2.1 Ellipsoidal particles
The most general ellipsoid has three distinct principal axes with diameters along these axes denoted by
$d_{1},d_{2},d_{3}$
, where we label the axes such that
$d_{3}\geqslant d_{2}\geqslant d_{1}$
. Therefore, its shape is fully described by the ratios
$d_{3}/d_{2}$
and
$d_{2}/d_{1}$
. An elongated shape has a large value of
$d_{3}/d_{2}$
and a flattened shape has a large value of
$d_{2}/d_{1}$
. We examine particles of four different distinct shapes (see figure 1): sphere
$(d_{3}/d_{2}=d_{2}/d_{1}=1)$
, rod
$(d_{3}/d_{2}=10,d_{2}/d_{1}=1)$
, disc
$(d_{3}/d_{2}=1,d_{2}/d_{1}=10)$
and triaxial
$(d_{3}/d_{2}=d_{2}/d_{1}=10)$
. Note, the shapes in figure 1 are shown at lower aspect ratios than those used for computations.
Figure 1. Four different ellipsoids. The unit vectors
$(\boldsymbol{p}_{1},\boldsymbol{p}_{2},\boldsymbol{p}_{3})$
show the directions of the principal axes with corresponding diameters,
$d_{1},d_{2},d_{3}$
. Repeated equal diameters are not labelled. The swimming direction is
$\boldsymbol{p}_{3}$
, as indicated by the dashed arrows.
2.2 Equations of particle motion
We are interested in the case where neutrally buoyant particles swim in the direction of their longest axis by generating a constant thrust. In a quiescent fluid, this causes particles to translate at their intrinsic swimming velocity,
$V_{s}$
. In a turbulent flow, the coupling between the background turbulent flow and the particle swimming can be simplified by neglecting the effects of fluid inertia and particle inertia in the equations for particle motion. This is possible under the following conditions:
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{d}{\unicode[STIX]{x1D702}}\ll 1, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{d}{\unicode[STIX]{x1D702}}\frac{V_{s}}{u_{\unicode[STIX]{x1D702}}}\ll 1, & \displaystyle\end{eqnarray}$$
$d$
is a characteristic particle length scale,
$V_{s}$
is the particle’s intrinsic swimming velocity and
$\unicode[STIX]{x1D702},u_{\unicode[STIX]{x1D702}}$
are the Kolmogorov length and velocity scales, respectively. Under these limits, the particle velocity is given by the vector sum of the background fluid velocity and the particle’s intrinsic swimming velocity: 
$$\begin{eqnarray}\boldsymbol{v}=\boldsymbol{u}+V_{s}\,\boldsymbol{p}_{3},\end{eqnarray}$$
where
$\boldsymbol{v}$
is particle velocity,
$\boldsymbol{u}$
is the background fluid velocity at the particle’s location and
$V_{s}$
is the particle’s swimming velocity. In the appendix, we show how a general equation of particle motion simplifies to (2.2) under the conditions in (2.1). Equation (2.1b
) shows that the dimensionless swimming velocity
$V_{s}^{\prime }=V_{s}/u_{\unicode[STIX]{x1D702}}$
can be
$O(1)$
or larger as long as
$d/\unicode[STIX]{x1D702}$
is small enough.
If the background flow is non-uniform, velocity gradients cause the particle to rotate. The rotational motion of an ellipsoidal particle in the limit of small inertia is given by (Jeffery Reference Jeffery1922):
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D74E}_{p}\boldsymbol{\cdot }\boldsymbol{p}_{1}=(1/2)\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\boldsymbol{p}_{1}+\unicode[STIX]{x1D706}_{1}\left(\boldsymbol{p}_{2}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{3}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D74E}_{p}\boldsymbol{\cdot }\boldsymbol{p}_{2}=(1/2)\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\boldsymbol{p}_{2}+\unicode[STIX]{x1D706}_{2}\left(\boldsymbol{p}_{3}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{1}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D74E}_{p}\boldsymbol{\cdot }\boldsymbol{p}_{3}=(1/2)\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\boldsymbol{p}_{3}+\unicode[STIX]{x1D706}_{3}\left(\boldsymbol{p}_{1}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{2}\right), & \displaystyle\end{eqnarray}$$
$\unicode[STIX]{x1D74E}_{p}$
is the angular velocity of the particle,
$\unicode[STIX]{x1D74E}$
is the fluid vorticity and
$\unicode[STIX]{x1D64E}=(1/2)[\unicode[STIX]{x1D735}\boldsymbol{u}+(\unicode[STIX]{x1D735}\boldsymbol{u})^{\text{T}}]$
is the fluid strain-rate tensor.
$\unicode[STIX]{x1D706}_{i}$
for
$i=1,2,3$
are the shape parameters given by 
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{1}=\frac{(d_{2}/d_{3})^{2}-1}{(d_{2}/d_{3})^{2}+1};\quad \unicode[STIX]{x1D706}_{2}=\frac{(d_{3}/d_{1})^{2}-1}{(d_{3}/d_{1})^{2}+1};\quad \unicode[STIX]{x1D706}_{3}=\frac{(d_{1}/d_{2})^{2}-1}{(d_{1}/d_{2})^{2}+1}.\end{eqnarray}$$
The left-hand sides of equations (2.3a–c ) represent rotations of the particle about different particle axes, also referred to as yaw, pitch and roll, respectively. The rates-of-change of orientation of the particle axes can be derived from (2.3a–c ) (e.g. see Pujara & Variano Reference Pujara and Variano2017) to give:
$$\begin{eqnarray}\displaystyle & \displaystyle \dot{\boldsymbol{p}}_{1}=\unicode[STIX]{x1D734}\boldsymbol{p}_{1}-\unicode[STIX]{x1D706}_{2}\boldsymbol{p}_{3}\left(\boldsymbol{p}_{3}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{1}\right)+\unicode[STIX]{x1D706}_{3}\boldsymbol{p}_{2}\left(\boldsymbol{p}_{1}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{2}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \dot{\boldsymbol{p}}_{2}=\unicode[STIX]{x1D734}\boldsymbol{p}_{2}+\unicode[STIX]{x1D706}_{1}\boldsymbol{p}_{3}\left(\boldsymbol{p}_{2}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{3}\right)-\unicode[STIX]{x1D706}_{3}\boldsymbol{p}_{1}\left(\boldsymbol{p}_{1}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{2}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \dot{\boldsymbol{p}}_{3}=\unicode[STIX]{x1D734}\boldsymbol{p}_{3}-\unicode[STIX]{x1D706}_{1}\boldsymbol{p}_{2}\left(\boldsymbol{p}_{2}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{3}\right)+\unicode[STIX]{x1D706}_{2}\boldsymbol{p}_{1}\left(\boldsymbol{p}_{3}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{1}\right), & \displaystyle\end{eqnarray}$$
$\unicode[STIX]{x1D734}=(1/2)[\unicode[STIX]{x1D735}\boldsymbol{u}-(\unicode[STIX]{x1D735}\boldsymbol{u})^{\text{T}}]$
is the fluid rotation rate tensor.
2.3 Particle trajectories and orientations in turbulence
The background turbulent fluid velocity is taken from the Johns Hopkins University turbulence database, which contains a dataset of forced homogeneous isotropic turbulence in a triply period box (Perlman et al.
Reference Perlman, Burns, Li and Meneveau2007). The Taylor micro-scale Reynolds number is
$\mathit{Re}_{\unicode[STIX]{x1D706}}\approx 433$
and the ratio of large-eddy turnover time,
$T$
, to the Kolmogorov time scale,
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
, is given by
$T\approx 45\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
. The ratio of the root-mean-square velocity,
$\sqrt{\langle \boldsymbol{u}^{2}\rangle }$
, to the Kolmogorov time scale
$u_{\unicode[STIX]{x1D702}}$
, is given by
$\sqrt{\langle \boldsymbol{u}^{2}\rangle }/u_{\unicode[STIX]{x1D702}}\approx 10$
.
The coupled equations, equations (2.2) and (2.5), are solved using a staggered second-order Runge–Kutta scheme with a time step of
$0.009\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
and particle data are recorded every five integration steps. Where particle locations do not coincide with the simulation grid and time steps, data of velocity and velocity gradients are spatially and temporally interpolated using sixth-order Lagrange polynomials and cubic Hermite interpolation, respectively (Perlman et al.
Reference Perlman, Burns, Li and Meneveau2007).
For each particle shape, five different swimming velocities are tested:
$V_{s}^{\prime }=V_{s}/u_{\unicode[STIX]{x1D702}}=[0,0.5,1,3,5]$
. Analysis of passive particles (
$V_{s}=0$
) has been previously presented in Pujara & Variano (Reference Pujara and Variano2017) for more particle aspect ratios. For each case, 7500 particles are initialized at random initial positions and random orientations and tracked for approximately one large-eddy turnover time. Results are presented from data after the particles have reached a statistically steady equilibrium with the flow, which takes approximately
$5\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
. Thus, the averages are taken over different particles and over time for
$6\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}\leqslant t\leqslant 45\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
.
Figure 2. Probability density functions of the square of the fluid vorticity as sampled by anisotropic swimming particles: (a) rod; (b) disc; (c) triaxial.
3 Results
3.1 Particle accumulation
As swimming particles travel through the flow, they sample the fluid vorticity in a biased manner. The probability density function (PDF) of the square of the fluid vorticity as sampled by anisotropic swimmers is plotted in figure 2. The mean of the PDF, i.e. the mean square fluid vorticity, is shown in figure 3. The PDF for passive particles is independent of their shape and shows the squared fluid vorticity sampled by fluid tracers. In a statistically stationary flow, spatially random sampling of fluid vorticity would give an identical PDF to that of fluid tracers. Instead, we observe a biased sampling of fluid vorticity, which indicates a non-random spatial distribution. The data in figures 2 and 3 show that swimming particles sample regions of high vorticity with a lower probability than passive particles do. In other words, swimming causes particles to accumulate in regions of lower vorticity. Clustering of rod-shaped swimming particles in turbulence has previously been reported by Zhan et al. (Reference Zhan, Sardina, Lushi and Brandt2013), but we find that this occurs for discs and triaxial ellipsoids as well. We also find that this clustering occurs specifically in regions of relatively low fluid vorticity. In turbulence, it is known that high magnitudes of fluid vorticity and dissipation are correlated (Zeff et al. Reference Zeff, Lanterman, McAllister, Roy, Kostelich and Lathrop2003), which means that swimming particles avoid the most dynamically active regions of the flow, where fluid vorticity and dissipation are much higher than their average values.
In the phase space spanned by material line stretching and square of the fluid vorticity, the mean trajectories of fluid tracers have been shown to be cycles in which high magnitude of vorticity is followed by high magnitude of stretching (Kramel et al. Reference Kramel, Voth, Tympel and Toschi2016). This suggests one possible mechanism for swimming particles accumulating in regions of lower vorticity: as particles undergo stretching, their longest axis tend towards the stretching direction and allows them to swim out of the patch of fluid before it experiences high vorticity.
Figure 3. Sampled fluid enstrophy (mean square fluid vorticity) for anisotropic swimming particles as a function of dimensionless swimming velocity: rods (red diamonds); discs (blue squares); triaxials (green triangles).
3.2 Particle enstrophy
Particle accumulation is a monotonic function of swimming velocity, but as we show in this section, the particle enstrophy variation is non-monotonic. Fluid enstrophy is typically defined as the square of the fluid vorticity,
$\unicode[STIX]{x1D714}^{2}$
(e.g. Pope Reference Pope2000). We define the particle enstrophy as the variance of the particle angular velocity. Since the flow is isotropic,
$\langle \unicode[STIX]{x1D714}_{p}\rangle =0$
and the particle enstrophy is given by
$\left\langle \unicode[STIX]{x1D74E}_{p}^{2}\right\rangle$
. The particle enstrophy is the variance of the particle angular velocity (or equivalently, the mean square particle angular velocity). The particle enstrophy can be expressed as the sum of the mean square angular velocities about each particle axis:
$$\begin{eqnarray}\left\langle \unicode[STIX]{x1D714}_{p}^{2}\right\rangle =\left\langle \left(\unicode[STIX]{x1D74E}_{p}\boldsymbol{\cdot }\boldsymbol{p}_{1}\right)^{2}\right\rangle +\left\langle \left(\unicode[STIX]{x1D74E}_{p}\boldsymbol{\cdot }\boldsymbol{p}_{2}\right)^{2}\right\rangle +\left\langle \left(\unicode[STIX]{x1D74E}_{p}\boldsymbol{\cdot }\boldsymbol{p}_{3}\right)^{2}\right\rangle .\end{eqnarray}$$
The mean square angular velocity about each axis can be decomposed into three dynamically relevant components by taking the square of (2.3):
$$\begin{eqnarray}\displaystyle & \displaystyle \left\langle \left(\unicode[STIX]{x1D74E}_{p}\boldsymbol{\cdot }\boldsymbol{p}_{1}\right)^{2}\right\rangle ={\textstyle \frac{1}{4}}\left\langle \left(\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\boldsymbol{p}_{1}\right)^{2}\right\rangle +\left\langle \unicode[STIX]{x1D706}_{1}^{2}\left(\boldsymbol{p}_{2}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{3}\right)^{2}\right\rangle +\left\langle \unicode[STIX]{x1D706}_{1}\left(\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\boldsymbol{p}_{1}\right)\left(\boldsymbol{p}_{2}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{3}\right)\right\rangle , & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left\langle \left(\unicode[STIX]{x1D74E}_{p}\boldsymbol{\cdot }\boldsymbol{p}_{2}\right)^{2}\right\rangle ={\textstyle \frac{1}{4}}\left\langle \left(\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\boldsymbol{p}_{2}\right)^{2}\right\rangle +\left\langle \unicode[STIX]{x1D706}_{2}^{2}\left(\boldsymbol{p}_{3}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{1}\right)^{2}\right\rangle +\left\langle \unicode[STIX]{x1D706}_{2}\left(\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\boldsymbol{p}_{2}\right)\left(\boldsymbol{p}_{3}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{1}\right)\right\rangle , & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left\langle \left(\unicode[STIX]{x1D74E}_{p}\boldsymbol{\cdot }\boldsymbol{p}_{3}\right)^{2}\right\rangle ={\textstyle \frac{1}{4}}\left\langle \left(\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\boldsymbol{p}_{3}\right)^{2}\right\rangle +\left\langle \unicode[STIX]{x1D706}_{3}^{2}\left(\boldsymbol{p}_{1}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{2}\right)^{2}\right\rangle +\left\langle \unicode[STIX]{x1D706}_{3}\left(\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\boldsymbol{p}_{3}\right)\left(\boldsymbol{p}_{1}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{2}\right)\right\rangle . & \displaystyle\end{eqnarray}$$
Pujara & Variano (Reference Pujara and Variano2017) showed that for passive particles, strain-induced rotations were cancelled almost exactly by the cross-correlation of vorticity and strain for all shapes. Hence, the overall particle enstrophy was found to be a very weak function of shape. In figure 4, we see this is not true if particles start swimming. The reason for this can be seen in figure 5, which plots the separate contributions from vorticity-induced rotations, strain-induced rotations and the cross-correlation of rotations due to vorticity and strain. For anisotropic swimming particles, the cross-correlation of vorticity and strain is negligibly small. This allows strain contributions to have a significant influence on the overall particle enstrophy. Of the different shapes, triaxial particles have the largest enstrophy for a given swimming velocity because fluid strain can drive rotations about all three particle axes. The accumulation of anisotropic swimming particles in regions of relatively low fluid vorticity can also be seen in the contributions from vorticity-induced rotations in figure 5.
Figure 4. Particle enstrophy (variance of the particle angular velocity) for anisotropic swimming particles: rods (red diamonds); discs (blue squares); triaxials (green triangles)
Figure 5. Summary of particle enstrophy (variance of the particle angular velocity) and its components. Each of the four groups is a single particle shape. Within each group, the five columns represent the five swimming velocities as shown under the bars for spherical particles. The vertically stacked bars comprising each column are the contributions to particle enstrophy from vorticity-induced rotations (blue), strain-induced rotations (cyan) and the cross-correlation between vorticity and strain (yellow) as in (3.2). The overall particle enstrophy is given by the sum of vertically stacked bars.
Figure 6. Average alignment of particles with directions of the velocity gradient tensor: rods (red diamonds); discs (blue squares); triaxials (green triangles). (a) Longest particle axis and vorticity; (b) longest particle axis and the most extensional strain direction; (c) shortest particle axis and most compressional strain direction. A value of
$1/3$
indicates random alignment. The typical 95 % uncertainty level is
$\pm 0.003$
.
The influence of swimming speed on anisotropic particle enstrophy is non-monotonic because of two competing effects. The strain contributions act to increase the particle enstrophy as
$V_{s}^{\prime }$
increases from zero, but as particles start to swim faster, they cluster in regions of low fluid vorticity. For
$V_{s}^{\prime }>1$
, this biased sampling outweighs the strain contribution and the total particle enstrophy starts decreasing (figure 4). The maximum particle enstrophy occurs near
$V_{s}^{\prime }=0.5$
. A swimming speed of
$V_{s}^{\prime }=1$
indicates that particles move out of the smallest turbulent motions at the same rate at which those motions themselves evolve. The maximum particle enstrophy seems to occur when particles swim rapidly enough so that the negative cross-correlation between vorticity-induced rotations and strain-induced rotations becomes negligible, but slowly enough to sample almost the full lifetime of the smallest turbulent motions.
3.3 Particle alignment and rotations about particle axes
The average alignment of particles with the directions of the velocity gradient tensor determine how the particle enstrophy is partitioned along the particles’ axes (see (3.2)). The directions of the velocity gradient tensor are denoted by
$\boldsymbol{e}_{\unicode[STIX]{x1D714}}$
, the unit vector in the vorticity direction, and
$\boldsymbol{e}_{i}$
for
$i=1,2,3$
, where
$\boldsymbol{e}_{1}$
corresponds to the eigenvector for the most extensional eigenvalue of the strain-rate tensor and
$\boldsymbol{e}_{3}$
corresponds to the eigenvector for the most compressional eigenvalue of the strain-rate tensor.
For passive particles, it is known that the longest particle axis tends to be strongly aligned with
$\boldsymbol{e}_{\unicode[STIX]{x1D714}}$
and
$\boldsymbol{e}_{2}$
, and weakly aligned with
$\boldsymbol{e}_{1}$
, whereas the shortest particle axis tends to be strongly aligned with
$\boldsymbol{e}_{3}$
(Chevillard & Meneveau Reference Chevillard and Meneveau2013; Pujara & Variano Reference Pujara and Variano2017). Figure 6 shows that these results are altered by swimming. The average alignment is shown in figure 6 by plotting the expectation of the square of the inner product between different unit vectors. Values close to 1 signify a strong tendency to the be aligned whereas values close to 0 signify a strong tendency to be orthogonal. A value of
$1/3$
is indicative of a flat probability density of the inner product, i.e. random alignment. Strikingly, figure 6 shows that particle alignment changes for small swimming velocities relative to the case of passive particles. The alignment between fluid vorticity and the longest particle axis is weakened (figure 6
a) and the longest particle axis aligns more strongly with the most extensional strain direction (figure 6
b). Comparing figures 6(a,b), we see that for small swimming velocities,
$\boldsymbol{p}_{3}$
aligns more strongly with
$\boldsymbol{e}_{1}$
than with
$\boldsymbol{e}_{\unicode[STIX]{x1D714}}$
. This effect is most pronounced for elongated particles (rod, triaxial). At small swimming velocities, the alignment of the shortest particle axis with the most compressional strain direction (figure 6
c) also becomes stronger, particularly for flattened particles (disc, triaxial).
The changes in particle alignment with swimming velocity are non-monotonic. Like the peak of the particle enstrophy, the strongest alignment of particles with the strain-rate directions occurs near
$V_{s}^{\prime }=0.5$
. In this range of swimming velocity, swimming particles align in an intuitive way with the strain rate with the longest axis aligned with the most stretching direction and the shortest axis aligned with the most compressional direction.
Particle alignment also affects how particle enstrophy is split into components about different particle axes. The mean square particle angular velocity about each particle axis is shown in figure 7. At moderate swimming velocities, the particle enstrophy is almost equal for all three particle axes for rods. For example, while passive rods rotate most commonly about their axis of symmetry (commonly referred to as spinning or rolling), swimming rods rotate most commonly in reorientations of their axis of symmetry (commonly referred to as tumbling). Discs, on the other hand, rotate most commonly by reorientations of their axis of symmetry (tumbling) regardless of their swimming velocity. The triaxial particle exhibits features of both discs and rods with the notable result that the triaxial particle swimming at small velocities is equally likely to rotate about its longest and middle axes (roll and pitch, respectively) but unlikely to rotate about its shortest axis (yaw). At high swimming velocities, particles of all shapes seem to move towards equipartition of enstrophy amongst the particle axes.
Figure 7. Partitioning of particle enstrophy amongst the particle’s axes for different shapes and swimming velocities: (a) disc; (b) triaxial; (c) sphere; (d) rod. The total particle enstrophy is the sum of bars of different colours in each subgroup.
4 Summary discussion
By using a kinematic model for computing the motion of ellipsoidal swimming particles in a turbulent flow, valid if
$d/\unicode[STIX]{x1D702}\ll 1$
and
$(V_{s}d)/(u_{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D702})\ll 1$
, we show how body shape and swimming velocity affect the rotational statistics of particles and their accumulation. We find that, compared to passive particles, anisotropic swimming particles accumulate in regions of relatively lower fluid vorticity and avoid the most dynamically active regions of the flow where velocity gradients have large magnitudes. We also find that the variance of particle angular velocity increases with swimming velocity for
$V_{s}<u_{\unicode[STIX]{x1D702}}$
and decreases for larger swimming velocities. The increase seen for moderate velocities is due to the contribution of strain-induced particle rotations. The decrease seen at larger swimming velocities is due to particle clustering in regions of lower fluid vorticity. The average alignment of particle axes with the directions of the fluid velocity gradient tensor changes significantly from passive particles to particles swimming at moderate swimming velocities: the longest particle axis (and direction of swimming) changes from being most strongly aligned with the fluid vorticity to being most strongly aligned with the most stretching direction of the strain-rate tensor. This suggests that the swimming particles will, on average, experience greater stretching along their longest axis and greater compression along their shortest axis, compared to passive particles. The altered alignment also results in more even partitioning of enstrophy amongst rotations about all three particle axes. For example, while passive rods preferentially rotate about their axis of symmetry (spinning over tumbling, Byron et al.
Reference Byron, Einarsson, Gustavsson, Voth, Mehlig and Variano2015), swimming rod-shaped particles primarily tumble.
Acknowledgements
N.P. and E.A.V. would like to acknowledge support from the Army Research Office Biomathematics Program (Grant no. W911NF-16-1-0284) and M.A.R.K. would like to acknowledge support from National Science Foundation (Grant no. IOS-1655318). This research benefited from the use of the Savio computational cluster resource provided by the Berkeley Research Computing program at the University of California, Berkeley. The authors also acknowledge the comments of three anonymous referees, which helped to improve the manuscript.
Appendix A
In this appendix, we show that the validity of (2.2) in a turbulent flow rests on the following conditions:
$$\begin{eqnarray}\displaystyle \frac{d}{\unicode[STIX]{x1D702}}\ll 1, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{d}{\unicode[STIX]{x1D702}}\frac{V_{s}}{u_{\unicode[STIX]{x1D702}}}\ll 1, & & \displaystyle\end{eqnarray}$$
$d$
is a characteristic particle length scale and
$\unicode[STIX]{x1D702},u_{\unicode[STIX]{x1D702}}$
are the Kolmogorov length scale and velocity scale, respectively. We assume the particle generates a constant thrust, which, in the absence of a background flow, balances the drag and leads to the particle translating with a constant velocity. We denote this velocity as the particle’s intrinsic velocity,
$V_{s}$
. By re-expressing (A 1b
) as
$V_{s}d/\unicode[STIX]{x1D708}\ll 1$
using the identity
$\unicode[STIX]{x1D702}u_{\unicode[STIX]{x1D702}}/\unicode[STIX]{x1D708}\equiv 1$
, we note that particle swimming is characterized by a low Reynolds number.
We start with the following formulation of particle motion (similar to (26) in Maxey & Riley Reference Maxey and Riley1983):
$$\begin{eqnarray}m\frac{\text{d}\boldsymbol{v}}{\text{d}t}=m\frac{\text{D}\boldsymbol{u}}{\text{D}t}+T_{s}\,\boldsymbol{p}_{3}+\boldsymbol{f},\end{eqnarray}$$
where
$m$
is the mass of the neutrally buoyant particle. The time rate of change following the particle is denoted as
$\text{d}/\text{d}t$
and the time rate of change following the fluid is denoted as
$\text{D}/\text{D}t$
. The terms on the right-hand side represent force due to undisturbed flow (including pressure gradient and viscous stresses), the swimming thrust (aligned with the particle’s swimming direction) and force due to the disturbance flow created by the presence of the particle, respectively.
The separation of the fluid force on the particle into the force due to the undisturbed flow and the force due to the disturbance flow rests on the following assumptions (similar to equation (17) in Maxey & Riley Reference Maxey and Riley1983):
$$\begin{eqnarray}\displaystyle \frac{d^{2}u_{\unicode[STIX]{x1D702}}}{\unicode[STIX]{x1D702}\unicode[STIX]{x1D708}}\ll 1, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\left|\boldsymbol{v}-\boldsymbol{u}\right|d}{\unicode[STIX]{x1D708}}\ll 1. & & \displaystyle\end{eqnarray}$$
$d\ll \unicode[STIX]{x1D702}$
(A 1a
).
To calculate
$\boldsymbol{f}$
, we need to solve the disturbance flow created by the particle swimming, which is subject to a no-slip boundary condition on the particle surface and to the condition that the disturbance flow vanishes far from the particle. The disturbance flow is evaluated in the particle frame and we assume it to be a steady Stokes flow (A 1b
). Without the time-derivate term in the Stokes equation, the added mass and Basset history forces do not arise and the only force due to the disturbance flow is the Stokes drag, which is proportional to the characteristic particle length scale and its slip velocity, i.e.
$\boldsymbol{f}\sim O(\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}d\left|\boldsymbol{v}-\boldsymbol{u}\right|)$
.
The intrinsic swimming velocity can be expressed in terms of the swimming thrust and the drag when the particle swims in a quiescent fluid. This relationship can be inverted to express thrust in terms of the intrinsic swimming velocity. In the low Reynolds number regime required by (A 1b
), this gives
$T_{s}=D_{p3}V_{s}$
, where
$D_{p3}$
is the coefficient of proportionality for the Stokes drag for the particle in the
$\boldsymbol{p}_{3}$
direction. The coefficient of proportionality is
$D_{p3}\sim O(\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}d)$
.
We can now evaluate the relative importance of the inertia terms and the Stokes drag term in (A 2). The particle mass is
$m\sim O(\unicode[STIX]{x1D70C}d^{3})$
. The acceleration of the particle and fluid parcels in a turbulent flow are dominated by the smallest scales of motion:
$\text{d}\boldsymbol{v}/\text{d}t\sim \text{D}\boldsymbol{u}/\text{D}t\sim u_{\unicode[STIX]{x1D702}}/\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
. This shows that the inertia terms are
${\sim}O(\unicode[STIX]{x1D70C}d^{3}u_{\unicode[STIX]{x1D702}}/\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}})$
, whereas the Stokes drag term is
${\sim}O(\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}d\left|\boldsymbol{v}-\boldsymbol{u}\right|)$
. The ratio of the inertia to the Stokes drag is small under the conditions in (A 3a
). Thus, the inertia terms can be neglected and (A 2) simplifies to the balance of the swimming thrust and the Stokes drag. In this case, it is now evident that the Stokes drag must act in the opposite direction to the swimming giving
$\boldsymbol{f}=-D_{p3}(\boldsymbol{v}-\boldsymbol{u})$
. Substituting
$\boldsymbol{f}$
and
$T_{s}$
into (A 2) after neglecting the inertia terms gives
$$\begin{eqnarray}0=D_{p3}V_{s}\,\boldsymbol{p}_{3}-D_{p3}(\boldsymbol{v}-\boldsymbol{u}),\end{eqnarray}$$
which simplifies to (2.2):
$\boldsymbol{v}=\boldsymbol{u}+V_{s}\,\boldsymbol{p}_{3}$
.
