1 Introduction
Jeffery (Reference Jeffery1922) derived the leading-order equations of motion in the limit of low Reynolds number for a triaxial ellipsoid that is of the same density as the surrounding fluid. Under these assumptions, the inertia of the surrounding fluid as well as the inertia of the particle motion are both neglected. In the resulting equations of motion, the particle translates with the same velocity as the fluid that it displaces, but its rotation differs from that of the displaced fluid if the particle has an anisotropic shape. This is because anisotropic particles respond to the strain-rate part of the local velocity gradients as well as the vortical part, whereas spheres respond only to the vortical part (thus rotating at the same rate as the fluid they displace, with angular velocity equal to half the vorticity). The applicability of these equations has been verified experimentally (e.g. Taylor Reference Taylor1923; Trevelyan & Mason Reference Trevelyan and Mason1951; Goldsmith & Mason Reference Goldsmith and Mason1962; Anczurowski & Mason Reference Anczurowski and Mason1968; Parsa et al. Reference Parsa, Guasto, Kishore, Ouellette, Gollub and Voth2011, Reference Parsa, Calzavarini, Toschi and Voth2012; Einarsson et al. Reference Einarsson, Johansson, Mahato, Mishra, Angilella, Hanstorp and Mehlig2013; Ni et al. Reference Ni, Kramel, Ouellette and Voth2015) and many studies have employed them to study the behaviour of anisotropic particles in laminar and turbulent flows (Shin & Koch Reference Shin and Koch2005; Parsa et al. Reference Parsa, Guasto, Kishore, Ouellette, Gollub and Voth2011; Chevillard & Meneveau Reference Chevillard and Meneveau2013; Gustavsson, Einarsson & Mehlig Reference Gustavsson, Einarsson and Mehlig2014; Byron et al. Reference Byron, Einarsson, Gustavsson, Voth, Mehlig and Variano2015; Challabotla, Zhao & Andersson Reference Challabotla, Zhao and Andersson2015; Zhao et al. Reference Zhao, Challabotla, Andersson and Variano2015) with applications such as paper manufacturing (Lundell, Söderberg & Alfredsson Reference Lundell, Söderberg and Alfredsson2011), microbial and plankton ecology (Pedley & Kessler Reference Pedley and Kessler1992; Kaya & Koser Reference Kaya and Koser2009; Guasto, Rusconi & Stocker Reference Guasto, Rusconi and Stocker2012) and sediment transport (Davis Reference Davis1991; Mallier & Maxey Reference Mallier and Maxey1991).
Further analytical progress on the problem of inertialess ellipsoidal particles in laminar shear flows was made by Bretherton (Reference Bretherton1962), who expanded Jeffery’s analysis to more general shapes. Hinch & Leal (Reference Hinch and Leal1979) explicitly considered rotations of ellipsoids that are not axisymmetric and Yarin, Gottlieb & Roisman (Reference Yarin, Gottlieb and Roisman1997) explored the chaotic rotations that can occur for non-axisymmetric ellipsoids. These results were experimentally confirmed by Einarsson et al. (Reference Einarsson, Mihiretie, Laas, Ankardal, Angilella, Hanstorp and Mehlig2016), who also provide a summary of previous experimental investigations. The effects of fluid inertia and particle inertia on particle rotation has also been the subject of many investigations; see, for example, Leal (Reference Leal1980), Ding & Aidun (Reference Ding and Aidun2000), Lundell & Carlsson (Reference Lundell and Carlsson2010), Lundell (Reference Lundell2011), Rosén, Lundell & Aidun (Reference Rosén, Lundell and Aidun2014), Einarsson et al. (Reference Einarsson, Candelier, Lundell, Angilella and Mehlig2015), Candelier, Einarsson & Mehlig (Reference Candelier, Einarsson and Mehlig2016).
In turbulent flows, anisotropic particles are an additional complexity apart from the already complex interaction of spherical particles and turbulence (see review by Voth & Soldati Reference Voth and Soldati2017). Our motivation to study the motion of triaxial ellipsoids in turbulent flows stems from the desire to understand the interaction of planktonic organisms with their turbulent flow environment. Plankton size spans roughly three orders of magnitude from
$10^{-6}\rightarrow 10^{-3}~\text{m}$
, which is typically smaller than the smallest scales of turbulent motion in the natural marine environment (Guasto et al.
Reference Guasto, Rusconi and Stocker2012). Hence their rotation is dominated by approximately uniform velocity gradients, i.e. velocity variations are linear over their body and Jeffery’s model is an appropriate one. Where plankton are larger than the local Kolmogorov length scale, the results given here provide a useful bound to compare with results for larger particles (e.g. Zimmermann et al.
Reference Zimmermann, Gasteuil, Bourgoin, Volk, Pumir and Pinton2011; Byron et al.
Reference Byron, Einarsson, Gustavsson, Voth, Mehlig and Variano2015; Bordoloi & Variano Reference Bordoloi and Variano2017). We study rotation since a variety of life functions depend on organismal rotation (reviewed by Kiørboe Reference Kiørboe2008; Guasto et al.
Reference Guasto, Rusconi and Stocker2012); for example, sensing environmental cues such as gravity, light, chemical gradients and seascape (Wells Reference Wells1968; Pedley & Kessler Reference Pedley and Kessler1992; Jumars et al.
Reference Jumars, Trowbridge, Boss and Karp-Boss2009; Fuchs & Gerbi Reference Fuchs and Gerbi2016) and diffusion-driven mass exchange with the surrounding fluid (Batchelor Reference Batchelor1979; Karp-Boss, Boss & Jumars Reference Karp-Boss, Boss and Jumars1996) are mediated by particle rotation. Plankton are typically triaxial in shape and have behavioural responses to specific components of body motion, which makes it important to consider the particle angular velocity and its partitioning into spin about the particle’s principal axes. Byron et al. (Reference Byron, Einarsson, Gustavsson, Voth, Mehlig and Variano2015) presented such results for axisymmetric particles. Chevillard & Meneveau (Reference Chevillard and Meneveau2013) showed results for triaxial ellipsoids, but they focused on the rate of change of the particle’s orientation vectors to evaluate stochastic models of the Lagrangian velocity gradient tensor and did not show how the particle angular velocity and its partitioning change with particle-shape. We present these results herein. We also show the correlation time scales for rotations about different particle axes and examine the likelihood and causes of extremely fast rotations about different particle axes.
We start in § 2 by introducing the particle-shape parameter space, reviewing the equations for particle rotational motion and providing methods to solve these equations in turbulent flow. Section 3 presents the statistics of rotational motion of triaxial ellipsoids in homogenous isotropic turbulence and discusses the trends of their variation with particle-shape. Finally, § 4 provides the conclusions and directions for future work.
2 Methods
2.1 Triaxial ellipsoids
A diagram of triaxial ellipsoid shape parameters is shown in figure 1. We label the three particle axes such that
$d_{3}>d_{2}>d_{1}$
and use the ratios
$d_{3}/d_{2}$
and
$d_{2}/d_{1}$
to describe particle-shape. The degree to which a particle is elongated is indicated by
$d_{3}/d_{2}$
and the degree to which a particle is flattened is indicated by
$d_{2}/d_{1}$
. Axisymmetric particles occupy positions along the lines given by
$\log (d_{2}/d_{1})=0$
(prolate spheroids, or rod-like particles) and
$\log (d_{3}/d_{2})=0$
(oblate spheroids, or disc-like particles); see sketch in figure 1(b). Other definitions of the parameter space are also possible (e.g. Dusenbery Reference Dusenbery2009; Chevillard & Meneveau Reference Chevillard and Meneveau2013), but in our definition, a particle of a given shape holds a unique position in the particle-shape parameter space.
Figure 1. (a) Nomenclature for triaxial ellipsoids:
$d_{i}$
are diameters corresponding to particle orientation vectors
$\boldsymbol{p}_{\boldsymbol{i}}$
for
$i=1,2,3$
labelled such that
$d_{3}>d_{2}>d_{1}$
. (b) Triaxial ellipsoids showing part of the parameter space to be explored.
We explore the particle shapes in the space spanned by
$[\log (d_{3}/d_{2}),\log (d_{2}/d_{1})]\in (0\rightarrow 1,0\rightarrow 1)$
. Particles whose shapes are beyond the boundaries of our parameter space are not expected to show qualitatively different dynamics than those at the boundaries, as suggested by previous results. Specifically, work on spheroid rotations has shown that the majority of variation in the statistics of spheroid rotation in turbulent flows due to a change of shape occurs over a range of aspect ratio
$10^{-1}\rightarrow 10^{1}$
(Parsa et al.
Reference Parsa, Calzavarini, Toschi and Voth2012; Byron et al.
Reference Byron, Einarsson, Gustavsson, Voth, Mehlig and Variano2015).
To see if the influence of particle-shape on the statistics particle rotation can be described by a single shape parameter, we show the Wadell sphericity parameter,
$\unicode[STIX]{x1D6F9}$
(Wadell Reference Wadell1932), and the Corey shape factor,
$\unicode[STIX]{x1D6F7}$
(e.g. Dietrich Reference Dietrich1982), as functions of
$d_{3}/d_{2}$
and
$d_{2}/d_{1}$
in figure 2.
$\unicode[STIX]{x1D6F9}$
is defined as the ratio of the surface area of a volume-matched sphere to the surface area of a particle and
$\unicode[STIX]{x1D6F7}$
is defined as the ratio of the maximum cross-sectional area of a volume-matched sphere to the maximum cross-sectional area of a particle. Using the expression for the surface area of a triaxial ellipsoid, the inverse of Wadell’s sphericity parameter is given by
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}^{-1}=\frac{1}{2}\left(\frac{d_{3}/d_{2}}{d_{2}/d_{1}}\right)^{1/3}\left\{\left(\frac{d_{3}}{d_{1}}\right)^{-1}+\left(\frac{d_{2}}{d_{1}}\right)\frac{[E(\unicode[STIX]{x1D719},k)\sin ^{2}\unicode[STIX]{x1D719}+F(\unicode[STIX]{x1D719},k)\cos ^{2}\unicode[STIX]{x1D719}]}{\sin \unicode[STIX]{x1D719}}\right\},\end{eqnarray}$$
where
$$\begin{eqnarray}\cos \unicode[STIX]{x1D719}=\frac{d_{1}}{d_{3}};\quad k^{2}=\left(\frac{d_{3}}{d_{2}}\right)^{2}\frac{(d_{2}/d_{1})^{2}-1}{(d_{3}/d_{1})^{2}-1},\end{eqnarray}$$
and
$F(\unicode[STIX]{x1D719},k)$
and
$E(\unicode[STIX]{x1D719},k)$
are the incomplete elliptical integrals of the first kind and second kind, respectively. The Corey shape factor for triaxial ellipsoids is given by
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}=\left(\frac{d_{3}}{d_{2}}\right)^{-1/2}\left(\frac{d_{2}}{d_{1}}\right)^{-1}.\end{eqnarray}$$
Figure 2. Single-parameter shape descriptions shown within the two-parameter shape space defined in figure 1. (a) Wadell sphericity parameter,
$\unicode[STIX]{x1D6F9}$
; (b) Corey shape factor,
$\unicode[STIX]{x1D6F7}$
.
2.2 Evolution of particle orientation
We track the evolution of a particle’s orientation vectors,
$(\boldsymbol{p}_{\mathbf{1}},\boldsymbol{p}_{\mathbf{2}},\boldsymbol{p}_{\mathbf{3}})$
, in a fixed (unmoving) laboratory reference frame. The time rate of change of the orientation vectors, (
$\dot{\boldsymbol{p}_{\mathbf{1}}},\dot{\boldsymbol{p}_{\mathbf{2}}},\dot{\boldsymbol{p}_{\mathbf{3}}}$
), is related to the angular velocity of the particle,
$\unicode[STIX]{x1D74E}_{\boldsymbol{p}}$
, by the following kinematic relations:
$$\begin{eqnarray}\displaystyle & \dot{\boldsymbol{p}_{\mathbf{1}}}=\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\times \boldsymbol{p}_{\mathbf{1}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \dot{\boldsymbol{p}_{\mathbf{2}}}=\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\times \boldsymbol{p}_{\mathbf{2}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \dot{\boldsymbol{p}_{\mathbf{3}}}=\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\times \boldsymbol{p}_{\mathbf{3}}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{1}}={\textstyle \frac{1}{2}}\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{1}}+\unicode[STIX]{x1D706}_{1}({\boldsymbol{p}_{\mathbf{2}}}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{\boldsymbol{ 3}}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{2}}={\textstyle \frac{1}{2}}\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{2}}+\unicode[STIX]{x1D706}_{2}({\boldsymbol{p}_{\mathbf{3}}}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{\boldsymbol{ 1}}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{3}}={\textstyle \frac{1}{2}}\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{3}}+\unicode[STIX]{x1D706}_{3}({\boldsymbol{p}_{\mathbf{1}}}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{\boldsymbol{ 2}}). & \displaystyle\end{eqnarray}$$
$\unicode[STIX]{x1D74E}=\unicode[STIX]{x1D735}\times \boldsymbol{u}$
is the fluid vorticity, and
$\unicode[STIX]{x1D64E}=(1/2)[\unicode[STIX]{x1D735}\boldsymbol{u}+(\unicode[STIX]{x1D735}\boldsymbol{u})^{\text{T}}]$
is the strain-rate tensor. These quantities can also be expressed as symmetric and anti-symmetric parts of the velocity gradient tensor,
$\unicode[STIX]{x1D735}\boldsymbol{u}=\unicode[STIX]{x1D64E}+\unicode[STIX]{x1D734}$
, where the strain rate,
$\unicode[STIX]{x1D64E}$
, is the symmetric part and the rotation-rate tensor,
$\unicode[STIX]{x1D734}$
, is the anti-symmetric part. The shape parameters
$\unicode[STIX]{x1D706}_{i}$
are given by: 
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{1}=\frac{(d_{2}/d_{3})^{2}-1}{(d_{2}/d_{3})^{2}+1};\quad \unicode[STIX]{x1D706}_{2}=\frac{(d_{3}/d_{1})^{2}-1}{(d_{3}/d_{1})^{2}+1};\quad \unicode[STIX]{x1D706}_{3}=\frac{(d_{1}/d_{2})^{2}-1}{(d_{1}/d_{2})^{2}+1}.\end{eqnarray}$$
Jeffery’s (Reference Jeffery1922) equations, as presented in (2.5), are in a fixed (unmoving) laboratory reference frame. Combining the rotation of the particle about all three of its axes, the total angular velocity of the particle in the fixed reference frame is given by
$$\begin{eqnarray}\unicode[STIX]{x1D74E}_{\boldsymbol{p}}={\textstyle \frac{1}{2}}\unicode[STIX]{x1D74E}+\unicode[STIX]{x1D706}_{1}\boldsymbol{p}_{\mathbf{1}}({\boldsymbol{p}_{\mathbf{2}}}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{\boldsymbol{ 3}})+\unicode[STIX]{x1D706}_{2}\boldsymbol{p}_{\mathbf{2}}({\boldsymbol{p}_{\mathbf{3}}}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{\boldsymbol{ 1}})+\unicode[STIX]{x1D706}_{3}\boldsymbol{p}_{\mathbf{3}}({\boldsymbol{p}_{\mathbf{1}}}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{\boldsymbol{ 2}}).\end{eqnarray}$$
Inserting (2.7) into (2.4), and employing the identity
$(\unicode[STIX]{x1D74E}\times \boldsymbol{p})/2\equiv \unicode[STIX]{x1D734}\boldsymbol{p}$
, the rate of change of orientation vectors can be written as
$$\begin{eqnarray}\displaystyle & \dot{\boldsymbol{p}_{\mathbf{1}}}=\unicode[STIX]{x1D734}\boldsymbol{p}_{\mathbf{1}}-\unicode[STIX]{x1D706}_{2}\boldsymbol{p}_{\mathbf{3}}({\boldsymbol{p}_{\mathbf{3}}}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{\mathbf{1}})+\unicode[STIX]{x1D706}_{3}\boldsymbol{p}_{\mathbf{2}}({\boldsymbol{p}_{\mathbf{1}}}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{\mathbf{2}}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \dot{\boldsymbol{p}_{\mathbf{2}}}=\unicode[STIX]{x1D734}\boldsymbol{p}_{\mathbf{2}}+\unicode[STIX]{x1D706}_{1}\boldsymbol{p}_{\mathbf{3}}({\boldsymbol{p}_{\mathbf{2}}}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{\mathbf{3}})-\unicode[STIX]{x1D706}_{3}\boldsymbol{p}_{\mathbf{1}}({\boldsymbol{p}_{\mathbf{1}}}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{\mathbf{2}}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \dot{\boldsymbol{p}_{\mathbf{3}}}=\unicode[STIX]{x1D734}\boldsymbol{p}_{\mathbf{3}}-\unicode[STIX]{x1D706}_{1}\boldsymbol{p}_{\mathbf{2}}({\boldsymbol{p}_{\mathbf{2}}}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{\mathbf{3}})+\unicode[STIX]{x1D706}_{2}\boldsymbol{p}_{\mathbf{1}}({\boldsymbol{p}_{\mathbf{3}}}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{\mathbf{1}}). & \displaystyle\end{eqnarray}$$
2.3 Direct numerical simulations
Data from direct numerical simulations (DNS) of homogeneous isotropic turbulence available from the Johns Hopkins University turbulence database (Perlman et al.
Reference Perlman, Burns, Li and Meneveau2007; Li et al.
Reference Li, Perlman, Wan, Yang, Meneveau, Burns, Chen, Szalay and Eyink2008) are used to calculate the evolution of particle orientation along particle trajectories. The dataset consists of forced isotropic turbulence on a triply periodic cube of
$1024^{3}$
points where the Taylor microscale Reynolds number is
$Re_{\unicode[STIX]{x1D706}}\approx 433$
and the ratio of large-eddy turnover time (integral time scale),
$T$
, to the Kolmogorov time scale,
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
, is given by
$T\approx 45\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
.
Time series of the velocity gradient tensor along 7500 Lagrangian trajectories are extracted and used to integrate the equations for particle orientation, equation (2.8). The duration of each trajectory is approximately one large-eddy turnover time. The Lagrangian tracking is done using a second-order Runge–Kutta scheme with a time step given by
$\unicode[STIX]{x0394}t_{p}/\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}=0.009$
, which is a factor of five smaller than the time step stored on the dataset. Spatial interpolation is done using sixth-order Lagrange polynomials and interpolation in time is done using cubic Hermite interpolation. Further details of the Lagrangian tracking algorithm can be found in Yu et al. (Reference Yu, Kanov, Perlman, Graham, Frederix, Burns, Szalay, Eyink and Meneveau2012). Using the Lagrangian velocity gradient tensor time series, equations (2.8) are numerically integrated using a fourth-order Runge–Kutta scheme. Particles are initialized with random orientations and random positions.
3 Results and discussion
3.1 Initial transient period for particle orientation
The angular velocity of a particle is the vector sum of the components along the particle’s axes. Taking the expectation of this relationship gives the following equation that relates the particle enstrophy,
$\langle {\unicode[STIX]{x1D74E}_{\boldsymbol{p}}}^{2}\rangle$
, to the enstrophy about each particle axes:
$$\begin{eqnarray}\langle {\unicode[STIX]{x1D74E}_{\boldsymbol{p}}}^{2}\rangle =\langle (\unicode[STIX]{x1D74E}_{\boldsymbol{ p}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{1}})^{2}\rangle +\langle (\unicode[STIX]{x1D74E}_{\boldsymbol{ p}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{2}})^{2}\rangle +\langle (\unicode[STIX]{x1D74E}_{\boldsymbol{ p}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{3}})^{2}\rangle .\end{eqnarray}$$
We refer to the total dimensionless particle enstrophy and its components along the particle’s axes as
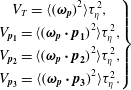$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}V_{T}=\langle (\unicode[STIX]{x1D74E}_{\boldsymbol{p}})^{2}\rangle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}^{2},\\ V_{\boldsymbol{p}_{\mathbf{1}}}=\langle (\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{1}})^{2}\rangle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}^{2},\\ V_{\boldsymbol{p}_{\mathbf{2}}}=\langle (\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{2}})^{2}\rangle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}^{2},\\ V_{\boldsymbol{p}_{\mathbf{3}}}=\langle (\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{3}})^{2}\rangle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}^{2}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
At
$t=0$
, particles are oriented randomly and there is no correlation between the particle orientation vectors,
$(\boldsymbol{p}_{\mathbf{1}},\boldsymbol{p}_{\mathbf{2}},\boldsymbol{p}_{\mathbf{3}})$
, and the local velocity gradient tensor,
$\unicode[STIX]{x1D735}\boldsymbol{u}=\unicode[STIX]{x1D64E}+\unicode[STIX]{x1D734}$
. Thus, the statistics of particle rotation at
$t=0$
can be predicted in terms of the Kolmogorov time scale for isotropic turbulence (Shin & Koch Reference Shin and Koch2005; Chevillard & Meneveau Reference Chevillard and Meneveau2013; Parsa Reference Parsa2013). Extending the calculation in Chevillard & Meneveau (Reference Chevillard and Meneveau2013), the dimensionless particle enstrophy and its components along the particle’s axes for randomly oriented particles are given by
$$\begin{eqnarray}\displaystyle V_{\boldsymbol{p}_{\mathbf{1}}}={\textstyle \frac{1}{12}}+\unicode[STIX]{x1D706}_{1}^{2}{\textstyle \frac{1}{20}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle V_{\boldsymbol{p}_{\mathbf{2}}}={\textstyle \frac{1}{12}}+\unicode[STIX]{x1D706}_{2}^{2}{\textstyle \frac{1}{20}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle V_{\boldsymbol{p}_{\mathbf{3}}}={\textstyle \frac{1}{12}}+\unicode[STIX]{x1D706}_{3}^{2}{\textstyle \frac{1}{20}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle V_{T}={\textstyle \frac{1}{4}}+{\textstyle \frac{1}{20}}(\unicode[STIX]{x1D706}_{1}^{2}+\unicode[STIX]{x1D706}_{2}^{2}+\unicode[STIX]{x1D706}_{3}^{2}). & & \displaystyle\end{eqnarray}$$
$d_{3}/d_{2}$
and
$d_{2}/d_{1}$
. The increase in particle enstrophy is fastest along the line
$d_{3}/d_{2}=d_{2}/d_{1}$
, i.e. for shapes where strain-rate-induced rotations are maximized about all three particle axes.
Figure 3. Variance of particle angular velocities made dimensionless by the Kolmogorov time scale,
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
, shown across the particle-shape parameter space for randomly oriented particles: (a)
$V_{T}$
; (b)
$V_{\boldsymbol{p}_{\mathbf{1}}}$
; (c)
$V_{\boldsymbol{p}_{\mathbf{2}}}$
; (d)
$V_{\boldsymbol{p}_{\mathbf{3}}}$
.
With increasing time, anisotropic particles start to align with the local velocity gradient tensor and the statistics of particle rotation evolve. Figure 4 shows the time evolution of the dimensionless variance of particle angular velocity for two different shapes that occupy two corners of the particle-shape parameter space: the sphere and a high-aspect-ratio triaxial ellipsoid. The initial variance of particle angular velocity is higher than its steady-state value, which is reached by
$t\approx 5\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
. All subsequent results in this paper are calculated from an ensemble average over all particles and over all time steps for
$6\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}\leqslant t\leqslant 45\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
. Neglecting data from the initial transient period removes the influence of the initial conditions on the statistics of particle rotation despite the fact that the equations of motion are derived in the limit of small Reynolds number and small Stokes number (Jeffery Reference Jeffery1922).
Figure 4. Variance of particle angular velocity computed at each time step from the ensemble of 7500 particles for two particle shapes: ○, sphere (
$d_{3}/d_{2}=d_{2}/d_{1}=1$
); ▵, triaxial (
$d_{3}/d_{2}=d_{2}/d_{1}=10$
). The example error bar in red at
$t/\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}\approx 12.5$
shows the 95 % confidence intervals calculated using data only at that time step for the triaxial case.
3.2 Variance and kurtosis of particle angular velocities
In figure 5, we plot the results of particle enstrophy and its components along the particle’s axes. The most striking result is that the total enstrophy of particles is only very weakly shape dependent (figure 5
a), but the enstrophy for rotation about different axes show strong shape dependency (figure 5
b–d). The shape dependency shown here replicates results shown by Parsa et al. (Reference Parsa, Calzavarini, Toschi and Voth2012) and Byron et al. (Reference Byron, Einarsson, Gustavsson, Voth, Mehlig and Variano2015), who only considered axisymmetric particles, and extends the results of Chevillard & Meneveau (Reference Chevillard and Meneveau2013), who only considered the tumbling of the particle orientation vectors. We see that particle enstrophy increases slightly as particles become elongated (increasing
$d_{3}/d_{2}$
), but not as they become flattened (increasing
$d_{2}/d_{1}$
). In this respect, results for triaxial ellipsoids are similar to those of prolate spheroids which are elongated to the same degree. This result is explained in § 3.3, where the contributions to particle enstrophy due to vorticity and strain rate are examined separately.
Figure 5. Variance of particle angular velocities made dimensionless by the Kolmogorov time scale,
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
, shown across the particle-shape parameter space: (a)
$V_{T}$
; (b)
$V_{\boldsymbol{p}_{\mathbf{1}}}$
; (c)
$V_{\boldsymbol{p}_{\mathbf{2}}}$
; (d)
$V_{\boldsymbol{p}_{\mathbf{3}}}$
.
Figure 5(b–d) shows that
$V_{\boldsymbol{p}_{\mathbf{3}}}\geqslant V_{\boldsymbol{p}_{\mathbf{2}}}\geqslant V_{\boldsymbol{p}_{\mathbf{1}}}$
for all shapes. Since the total enstrophy is almost shape independent, it can be concluded that particles of all shapes are most likely to rotate about
$\boldsymbol{p}_{\mathbf{3}}$
, the longest axis, and least likely to rotate about
$\boldsymbol{p}_{\mathbf{1}}$
, the shortest axis.
$V_{\boldsymbol{p}_{\mathbf{1}}}$
varies most strongly with
$d_{2}/d_{1}$
, its value decreasing as
$d_{2}/d_{1}$
increases and particles become more flattened.
$V_{\boldsymbol{p}_{\mathbf{3}}}$
varies most strongly with
$d_{3}/d_{2}$
, its value increasing as
$d_{3}/d_{2}$
increases and particles become more elongated. The bulk of the variation in both cases occurs in the range of aspect ratio
$(d_{3}/d_{2},d_{2}/d_{1})=1\rightarrow 2$
.
While Chevillard & Meneveau (Reference Chevillard and Meneveau2013) show the rotation of the particle axes, we focus on particle rotation about each axis, i.e. spinning about particle axes rather than the tumbling of particle axes. For example, Chevillard & Meneveau (Reference Chevillard and Meneveau2013) show that the tumbling of the intermediate axis,
$\langle (\dot{\boldsymbol{p}_{\mathbf{2}}})^{2}\rangle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}^{2}=V_{\boldsymbol{p}_{\mathbf{1}}}+V_{\boldsymbol{p}_{\mathbf{3}}}$
, is near constant along the line
$d_{3}/d_{2}=d_{2}/d_{1}$
, while the results in figure 5 show that
$V_{\boldsymbol{p}_{\mathbf{2}}}$
is also near constant and that there are systematic variations in
$V_{\boldsymbol{p}_{\mathbf{1}}}$
and
$V_{\boldsymbol{p}_{\mathbf{3}}}$
which cancel each other along this line.
The kurtosis of the particle angular velocity and its components are given by
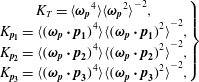$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}K_{T}=\langle {\unicode[STIX]{x1D74E}_{\boldsymbol{p}}}^{4}\rangle \langle {\unicode[STIX]{x1D74E}_{\boldsymbol{p}}}^{2}\rangle ^{-2},\\ K_{\boldsymbol{p}_{\mathbf{1}}}=\langle (\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{1}})^{4}\rangle \langle (\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{1}})^{2}\rangle ^{-2},\\ K_{\boldsymbol{p}_{\mathbf{2}}}=\langle (\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{2}})^{4}\rangle \langle (\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{2}})^{2}\rangle ^{-2},\\ K_{\boldsymbol{p}_{\mathbf{3}}}=\langle (\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{3}})^{4}\rangle \langle (\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{3}})^{2}\rangle ^{-2},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
and are plotted in figure 6. The kurtosis quantifies the likelihood of extreme events. The value of
$K_{T}$
falls within 7 to 10, much higher than the value of 3 for a standard normal distribution.
$K_{T}$
also varies much more strongly than
$V_{T}$
over the shape space, and shows a different dependence on particle-shape. That is, while flattening (increasing
$d_{2}/d_{1}$
) does not affect
$V_{T}$
, it strongly affects
$K_{T}$
. Thus, in terms of the likelihood of extreme angular velocity events, triaxial ellipsoids give results similar to oblate spheroids which are flattened to the same degree. In figure 5, the data contain some noise due to the slow convergence of higher-order moments, but it can be seen that values of
$K_{\boldsymbol{p}_{\boldsymbol{i}}}$
for
$i=1,2,3$
are larger than those of
$K_{T}$
regardless of shape. This is relevant to plankton because their sensory organs (e.g. statocysts) are often aligned so as to sense rotation about a single principal axis (Wells Reference Wells1968; Budelmann Reference Budelmann1989). Sensing in this manner, rather than sensing total angular velocity, gives a more leptokurtic signal, which may be more powerful in guiding behaviour. The bulk of the variation in
$K_{\boldsymbol{p}_{\mathbf{1}}}$
and
$K_{\boldsymbol{p}_{\mathbf{3}}}$
occurs in the range of aspect ratio
$(d_{3}/d_{2},d_{2}/d_{1})=1\rightarrow 2$
, which is a common shape range for planktonic organisms. Interestingly,
$K_{\boldsymbol{p}_{\mathbf{2}}}$
appears to be independent of particle-shape.
Figure 6. Kurtosis of particle angular velocities shown across the particle-shape parameter space: (a)
$K_{T}$
; (b)
$K_{\boldsymbol{p}_{\mathbf{1}}}$
; (c)
$K_{\boldsymbol{p}_{\mathbf{2}}}$
; (d)
$K_{\boldsymbol{p}_{\mathbf{3}}}$
.
Consistent with the results of Chevillard & Meneveau (Reference Chevillard and Meneveau2013), the largest value of kurtosis is observed for
$K_{\boldsymbol{p}_{\mathbf{1}}}$
for particles with
$d_{3}/d_{2}=1,d_{2}/d_{1}\gg 1$
, i.e. discs spinning about their axis of symmetry. Spinning discs have the lowest value of enstrophy (figure 5
b), which means that kurtosis is largest where variance is smallest. This indicates that rotational motion which is less common on average is still subject to large deviations from its mean value.
Kurtosis values show a Reynolds number dependency, seen by comparing our data to results in Parsa et al. (Reference Parsa, Calzavarini, Toschi and Voth2012) and Chevillard & Meneveau (Reference Chevillard and Meneveau2013). We observe a higher value for the kurtosis of the tumbling motion of rod-like particles, i.e.
$\langle (\dot{\boldsymbol{p}_{\mathbf{3}}})^{4}\rangle /\langle (\dot{\boldsymbol{p}_{\mathbf{3}}})^{2}\rangle ^{2}\approx 10.5$
for particles with
$d_{3}/d_{2}\gg 1$
,
$d_{2}/d_{1}=1$
(data not plotted). Chevillard & Meneveau (Reference Chevillard and Meneveau2013) found the same quantity to be approximately 6.3 and Parsa et al. (Reference Parsa, Calzavarini, Toschi and Voth2012) found it to be approximately 7.3. The kurtosis of the tumbling motion of disc-like particles, i.e.
$\langle (\dot{\boldsymbol{p}_{\mathbf{1}}})^{4}\rangle /\langle (\dot{\boldsymbol{p}_{\mathbf{1}}})^{2}\rangle ^{2}$
for particles with
$d_{2}/d_{1}\gg 1$
,
$d_{3}/d_{2}=1$
is almost identical to the kurtosis of the tumbling of rod-like particles in each study. Kurtosis of tumbling motion of axisymmetric particles seems to vary little with particle aspect ratio, as previously noted in Parsa et al. (Reference Parsa, Calzavarini, Toschi and Voth2012). Given that the experimental results of Parsa et al. (Reference Parsa, Calzavarini, Toschi and Voth2012) match their DNS results, and that the values of particle enstrophy match between all three studies, it appears that the kurtosis values are a function of Reynolds number.
$Re_{\unicode[STIX]{x1D706}}\approx 125$
in Chevillard & Meneveau (Reference Chevillard and Meneveau2013),
$Re_{\unicode[STIX]{x1D706}}\approx 180$
in Parsa et al. (Reference Parsa, Calzavarini, Toschi and Voth2012) and
$Re_{\unicode[STIX]{x1D706}}\approx 433$
in this study. The kurtosis value seems to increase with Reynolds number, which is consistent with the fact that it is sensitive to the small-scale intermittency in turbulence (Meneveau Reference Meneveau2011). Using the kurtosis values across the three studies as quoted above, a power law given by
$\langle (\dot{\boldsymbol{p}_{\mathbf{3}}})^{4}\rangle /\langle (\dot{\boldsymbol{p}_{\mathbf{3}}})^{2}\rangle ^{2}\sim Re_{\unicode[STIX]{x1D706}}^{3/8}$
provides a reasonable fit (data not plotted). This Reynolds number dependency is consistent with the Reynolds number dependency observed for the kurtosis of components of the velocity gradient tensor in the same range of Reynolds number (Sreenivasan & Antonia Reference Sreenivasan and Antonia1997; Pope Reference Pope2000). More data are required to be certain of this Reynolds number dependency and to confirm whether it is consistent for kurtosis of particle rotation across the particle-shape parameter space and for rotation about different axes.
To isolate shape effects on the fourth moments from shape effects on the second moments, figure 7 plots the fourth moments made dimensionless by
$\langle {\unicode[STIX]{x1D74E}_{\boldsymbol{p}}}^{2}\rangle ^{2}$
. In this case, it can be seen that
$\langle (\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{3}})^{4}\rangle \geqslant \langle (\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{2}})^{4}\rangle \geqslant \langle (\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{1}})^{4}\rangle$
for all shapes, indicating that extreme angular velocities are most likely to occur about
$\boldsymbol{p}_{\mathbf{3}}$
, the longest axis, and least likely to occur about
$\boldsymbol{p}_{\mathbf{1}}$
, the shortest axis. This is analogous to the trend observed in figure 5 for the variance of angular velocity. However, in the case of the fourth moment,
$\langle (\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{3}})^{4}\rangle$
increases with both
$d_{3}/d_{2}$
and
$d_{2}/d_{1}$
, and the largest value occurs for very elongated and very flattened triaxial particles (
$d_{3}/d_{2}=d_{2}/d_{1}\gg 1$
) rather than being common to all elongated particles (
$d_{3}/d_{2}\gg 1$
).
Figure 7. Fourth moments of particle angular velocities shown across the particle-shape parameter space: (a)
$\langle (\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{1}})^{4}\rangle \langle {\unicode[STIX]{x1D74E}_{\boldsymbol{p}}}^{2}\rangle ^{-2}$
; (b)
$\langle (\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{2}})^{4}\rangle \langle {\unicode[STIX]{x1D74E}_{\boldsymbol{p}}}^{2}\rangle ^{-2}$
; (c)
$\langle (\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{3}})^{4}\rangle \langle {\unicode[STIX]{x1D74E}_{\boldsymbol{p}}}^{2}\rangle ^{-2}$
.
We can conclude from the results of this section that the mean magnitude of the particle angular velocity is approximately
$0.5{\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}}^{-1}$
, and varies weakly with the value of
$d_{3}/d_{2}$
. Of its three axes, a particle of a given shape is most likely to rotate about its longest axis. These results are independent of Reynolds number, or very nearly so, based on comparison with results of Shin & Koch (Reference Shin and Koch2005), Parsa et al. (Reference Parsa, Calzavarini, Toschi and Voth2012) and Chevillard & Meneveau (Reference Chevillard and Meneveau2013). A particle of a given shape is also most likely to experience large angular velocities (
$\gg 0.5{\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}}^{-1}$
) about its longest axis, and this likelihood increases with values of both
$d_{3}/d_{2}$
and
$d_{2}/d_{1}$
so that very elongated and very flattened particles are the most likely to experience large angular velocities. The magnitudes of the large angular velocities will depend on Reynolds number, but the trend with particle-shape will remain the same.
3.3 Particle rotation due to local vorticity and strain rate
The trends discussed in the previous section arise due to non-random particle orientation with respect to the local velocity gradient tensor. In figure 8, the alignment between the particle’s axes,
$(\boldsymbol{p}_{\mathbf{1}},\boldsymbol{p}_{\mathbf{2}},\boldsymbol{p}_{\mathbf{3}})$
, and the direction of the local fluid vorticity,
$\boldsymbol{e}_{\unicode[STIX]{x1D74E}}=\unicode[STIX]{x1D74E}/|\unicode[STIX]{x1D74E}|$
, is shown. Alignment is computed as the median of the distribution of
$|\boldsymbol{e}_{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\boldsymbol{p}_{\boldsymbol{i}}|$
for
$i=1,2,3$
. The probability density functions (PDFs) of
$|\boldsymbol{e}_{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\boldsymbol{p}_{\boldsymbol{i}}|$
have peaks at 1 or 0; otherwise they are flat. Thus, a median value close to 1 demonstrates strong tendency to be aligned, a median value close to 0 demonstrates strong tendency to be orthogonal and a median value close to 0.5 demonstrates random alignment. For all shapes, there is strong alignment between
$\boldsymbol{p}_{\mathbf{3}}$
and vorticity. This tendency becomes even stronger as
$d_{3}/d_{2}$
increases and particles become more elongated. For all shapes, there is also a strong tendency for the vorticity and
$\boldsymbol{p}_{\mathbf{1}}$
to be orthogonal. This tendency becomes stronger as
$d_{2}/d_{1}$
increases and particles become more flattened. The alignment between
$\boldsymbol{p}_{\mathbf{2}}$
and vorticity is almost random for all shapes.
Figure 8. Alignment of particles’ axes with the direction of local fluid vorticity shown across the particle-shape parameter space and quantified by the median value of
$|\boldsymbol{e}_{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\boldsymbol{p}_{\boldsymbol{i}}|$
: (a) median of
$|\boldsymbol{e}_{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{1}}|$
; (b) median of
$|\boldsymbol{e}_{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{2}}|$
; (c) median of
$|\boldsymbol{e}_{\unicode[STIX]{x1D74E}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{3}}|$
.
Particle alignment with vorticity is caused by strain-rate-induced rotations, as can be seen from (2.5) and (2.7). These rotations cause the initially randomly orientated particles to approach a statistically steady state of non-trivial alignment. The alignment between
$\boldsymbol{p}_{\mathbf{3}}$
and vorticity explains the high values of enstrophy for rotations about
$\boldsymbol{p}_{\mathbf{3}}$
for elongated particles seen in figure 5(d). The orthogonality between
$\boldsymbol{p}_{\mathbf{1}}$
and vorticity explains the low values of enstrophy for rotations about
$\boldsymbol{p}_{\mathbf{1}}$
for flattened particles seen in figure 5(b). This tendency of elongated particles to be aligned with the fluid vorticity is well known (Shin & Koch Reference Shin and Koch2005; Pumir & Wilkinson Reference Pumir and Wilkinson2011; Parsa et al.
Reference Parsa, Calzavarini, Toschi and Voth2012; Chevillard & Meneveau Reference Chevillard and Meneveau2013; Byron et al.
Reference Byron, Einarsson, Gustavsson, Voth, Mehlig and Variano2015) and is explained by the similarities between the equations governing evolution of vorticity, material lines and elongated particles (Girimaji & Pope Reference Girimaji and Pope1990; Pumir & Wilkinson Reference Pumir and Wilkinson2011). The results here show that the same effect occurs for all elongated particles (
$d_{3}/d_{2}\gg 1$
) regardless of how flattened they are. The degree to which particles are flattened determines the further subpartitioning of the remaining enstrophy between axes
$\boldsymbol{p}_{\mathbf{1}}$
and
$\boldsymbol{p}_{\mathbf{2}}$
(figure 5
b,c).
Apart from causing particles to align with the vorticity, strain-rate-induced rotations also directly affect particle enstrophy. The separate contributions from vorticity and strain rate can be examined by taking the expectation of the square of (2.5) to give the following equations:
$$\begin{eqnarray}\displaystyle \langle (\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{1}})^{2}\rangle ={\textstyle \frac{1}{4}}\langle (\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{1}})^{2}\rangle +\langle \unicode[STIX]{x1D706}_{1}^{2}({\boldsymbol{p}_{\boldsymbol{ 2}}}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{\boldsymbol{ 3}})^{2}\rangle +\langle \unicode[STIX]{x1D706}_{1}(\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{1}})({\boldsymbol{p}_{\mathbf{2}}}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{\boldsymbol{ 3}})\rangle , & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle (\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{2}})^{2}\rangle ={\textstyle \frac{1}{4}}\langle (\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{2}})^{2}\rangle +\langle \unicode[STIX]{x1D706}_{2}^{2}({\boldsymbol{p}_{\boldsymbol{ 3}}}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{\boldsymbol{ 1}})^{2}\rangle +\langle \unicode[STIX]{x1D706}_{2}(\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{2}})({\boldsymbol{p}_{\mathbf{3}}}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{\boldsymbol{ 1}})\rangle , & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle (\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{3}})^{2}\rangle ={\textstyle \frac{1}{4}}\langle (\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{3}})^{2}\rangle +\langle \unicode[STIX]{x1D706}_{3}^{2}({\boldsymbol{p}_{\boldsymbol{ 1}}}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{\boldsymbol{ 2}})^{2}\rangle +\langle \unicode[STIX]{x1D706}_{3}(\unicode[STIX]{x1D74E}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{3}})({\boldsymbol{p}_{\mathbf{1}}}^{\text{T}}\unicode[STIX]{x1D64E}\boldsymbol{p}_{\boldsymbol{ 2}})\rangle . & & \displaystyle\end{eqnarray}$$
Figure 9 plots the contribution of the second and third terms in (3.5) to the total particle enstrophy. The variation with shape in figure 9 exactly matches that in figure 5(a), which is to be expected since shape effects are only present in the second and third terms in (3.5). This serves to demonstrate that strain-rate-induced rotations are the cause of the weak shape dependency in total particle enstrophy.
Figure 9. Fraction of particle enstrophy due to strain-rate-induced rotations shown across the particle-shape parameter space:
$(\langle {\unicode[STIX]{x1D74E}_{\boldsymbol{p}}}^{2}\rangle -(1/4)\langle \unicode[STIX]{x1D74E}^{2}\rangle )(\langle (\unicode[STIX]{x1D74E}_{\boldsymbol{p}})^{2}\rangle )^{-1}$
.
To explain the pattern seen in figures 5(a) and 9, we examine the effect of each term in (3.5) on the enstrophy about each particle axis. Figure 10 shows the contributions of each term for particles which occupy the four corners of the particle-shape parameter space, whereas figures 11–13 plot the fractional contributions from each term across the particle-shape parameter space. The data show that vorticity-induced rotations and strain-rate-induced rotations are anti-correlated. This can be seen in figures 11(c), 12(c) and 13(c), and by the darkest bars in figure 10. This shows that along Lagrangian trajectories in turbulence, particle angular velocities due to strain rate oppose those due to vorticity, on average. The case of strain rate working against vorticity is familiar from Jeffery’s orbits in simple shear flow, where it causes some phases of the Jeffery’s orbit to be slower than others.
Figure 10. Dimensionless particle enstrophy about each axis due to vorticity, strain rate and cross-correlation between vorticity and strain rate: (a) disc (
$d_{3}/d_{2}=1,d_{2}/d_{1}=10$
); (b) triaxial (
$d_{3}/d_{2}=d_{2}/d_{1}=10$
); (c) sphere (
$d_{3}/d_{2}=d_{2}/d_{1}=1$
); (d) rod (
$d_{3}/d_{2}=10,d_{2}/d_{1}=1$
). As expected, the results show that axisymmetric particles (
$d_{3}/d_{2}=1$
or
$d_{2}/d_{1}=1$
) can only be spun about their axis of symmetry by fluid vorticity and therefore strain-rate-induced rotations only contribute to rotations of the axis of symmetry, i.e. tumbling motions.
Figure 11. Fraction of particle enstrophy for rotations about
$\boldsymbol{p}_{\mathbf{1}}$
shown across the particle-shape parameter space: (a) due to vorticity alone; (b) due to strain rate alone; (c) due to cross-correlation between local vorticity and local strain rate. The superposition of plots (a–c) gives a value of 1.
In examining the relative importance of vorticity-induced rotations and strain-rate-induced rotations to the tumbling motion of rods (
$\langle (\dot{\boldsymbol{p}_{\mathbf{3}}})^{2}\rangle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}^{2}=V_{\boldsymbol{p}_{\mathbf{1}}}+V_{\boldsymbol{p}_{\mathbf{2}}}$
for
$d_{3}/d_{2}\gg 1$
and
$d_{2}/d_{1}=1$
), Ni et al. (Reference Ni, Kramel, Ouellette and Voth2015) observed that the variance of rod tumbling conditioned on local value of fluid enstrophy,
$\unicode[STIX]{x1D74E}^{2}$
, and dissipation,
$2\unicode[STIX]{x1D708}\unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{ij}$
, showed that the tumbling rate monotonically increased with both fluid enstrophy and dissipation. Thus, they concluded that vorticity-induced rotations and strain-rate-induced rotations contribute equally to the tumbling of rods. However, examining the bottom right corners of the plots in figures 11 and 12, we see that vorticity is responsible for approximately 80 % of
$V_{\boldsymbol{p}_{\mathbf{1}}}$
and
$V_{\boldsymbol{p}_{\mathbf{2}}}$
. Ni et al.’s results can be explained by the fact that the fluid enstrophy and dissipation are positively correlated along Lagrangian trajectories (data not plotted, see also Zeff et al. (Reference Zeff, Lanterman, Mcallister, Roy, Kostelich and Lathrop2003), for a discussion on the positive correlation between enstrophy and dissipation).
Having established that the majority of particle enstrophy is due to vorticity-induced rotations for all particle shapes, we can now also comment on its numerical value of
$V_{T}\approx 0.25$
observed in figure 5(a). In isotropic turbulence, the average magnitude of vorticity is given by
$\langle \unicode[STIX]{x1D74E}^{2}\rangle ^{1/2}\approx \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}^{-1}$
. Since the rate of fluid rotation is half the vorticity, the variance of fluid rotation, and thus also the particle enstrophy, is approximately
$0.25\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}^{-2}$
.
Figure 12. Fraction of particle enstrophy for rotations about
$\boldsymbol{p}_{\mathbf{2}}$
shown across the particle-shape parameter space: (a) due to vorticity alone; (b) due to strain rate alone; (c) due to cross-correlation between local vorticity and local strain rate. The superposition of plots (a–c) gives a value of 1.
Figure 13. Fraction of particle enstrophy for rotations about
$\boldsymbol{p}_{\mathbf{3}}$
shown across the particle-shape parameter space: (a) due to vorticity alone; (b) due to strain rate alone; (c) due to cross-correlation between local vorticity and local strain rate. The superposition of plots (a–c) gives a value of 1.
We noted from figures 6 and 7 that extreme angular velocities are most likely to occur about the longest axis,
$\boldsymbol{p}_{\mathbf{3}}$
, and that larger extremes are more likely as
$d_{2}/d_{1}$
increases and particles become flattened. To explore the cause of this trend, we isolate extreme particle angular velocities by only considering those events whose probability of occurring is less than or equal to 0.1 %. The magnitude of these extreme particle angular velocities is
$\langle (\unicode[STIX]{x1D74E}_{\boldsymbol{p}}|P_{i}\geqslant 99.9)^{2}\rangle =48\langle \unicode[STIX]{x1D74E}_{\boldsymbol{p}}^{2}\rangle$
averaged across particles of all shapes. The average value of fluid enstrophy and dissipation during these extreme particle angular velocity events is
$\langle (\unicode[STIX]{x1D74E}|P_{i}\geqslant 99.9)^{2}\rangle =38\langle \unicode[STIX]{x1D74E}^{2}\rangle$
and
$\langle (\unicode[STIX]{x1D716}|P_{i}\geqslant 99.9)\rangle =9\langle \unicode[STIX]{x1D716}\rangle$
, respectively. This confirms that particles experience large angular velocities in regions of the flow where fluid enstrophy and dissipation are both much higher than their average values.
Figure 14. PDF of alignment between the shortest particle axis and the strain-rate eigen-directions during extreme particle angular velocities: (a)
$|\boldsymbol{e}_{\mathbf{1}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{1}}|$
; (b)
$|\boldsymbol{e}_{\mathbf{2}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{1}}|$
; (c)
$|\boldsymbol{e}_{\mathbf{3}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{1}}|$
. ○, sphere (
$d_{3}/d_{2}=d_{2}/d_{1}=1$
); ▫, disc (
$d_{3}/d_{2}=1,d_{2}/d_{1}=10$
); ♢, rod (
$d_{3}/d_{2}=10,d_{2}/d_{1}=1$
); ▵, triaxial (
$d_{3}/d_{2}=d_{2}/d_{1}=10$
).
During extreme particle angular velocity events, the pattern of alignment is different than that shown in figure 8. Figure 14 shows the PDF of the alignment between the shortest particle axis,
$\boldsymbol{p}_{\mathbf{1}}$
, and the eigen-directions of strain rate conditioned on extreme particle angular velocities for particles that occupy the four corners of the particle-shape parameter space. The eigen-directions of strain rate are labelled such that
$\boldsymbol{e}_{\mathbf{1}}$
,
$\boldsymbol{e}_{\mathbf{2}}$
,
$\boldsymbol{e}_{\mathbf{3}}$
correspond to the most extensional, intermediate and most compressional directions, respectively. We choose to show the alignment of the shortest particle axis with the eigen-directions of strain rate because the shortest axis is expected to show the strongest trends as particles become flattened. To explain figure 14, we first note that since extreme angular velocities are most likely to occur about
$\boldsymbol{p}_{\mathbf{3}}$
due to alignment with vorticity and since vorticity tends to be aligned with
$\boldsymbol{e}_{\mathbf{2}}$
(Ashurst et al.
Reference Ashurst, Kerstein, Kerr and Gibson1987; Meneveau Reference Meneveau2011; Ni, Ouellette & Voth Reference Ni, Ouellette and Voth2014), we expect that the shortest particle axis will be orthogonal to
$\boldsymbol{e}_{\mathbf{2}}$
for anisotropic particles. This is indeed observed in figure 14(b). Figure 14(a,c) shows that the most likely orientation of flattened particles (
$d_{2}/d_{1}\gg 1$
) during extreme angular velocities is such that the shortest axis bisects the plane spanned by
$\boldsymbol{e}_{\mathbf{1}}$
and
$\boldsymbol{e}_{\mathbf{3}}$
, forming a 45-degree angle with both. In this orientation,
$|\boldsymbol{e}_{\mathbf{1}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{1}}|=|\boldsymbol{e}_{\mathbf{3}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{1}}|=\cos (\unicode[STIX]{x03C0}/4)\approx 0.7$
. As discussed by Ni et al. (Reference Ni, Kramel, Ouellette and Voth2015) in the context of rotations of rods, the strain-rate-induced rotations are maximized in this orientation. Thus, the alignment of flattened particles with the strain-rate tensor further increases the magnitudes of their extreme angular velocities compared to particles that are axisymmetric about their longest axis.
Figure 15 shows the alignment of the shortest axis with the strain-rate tensor during extreme particle angular velocities across the entire particle-shape parameter space via the median values of
$|\boldsymbol{e}_{\boldsymbol{i}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{1}}|$
for
$i=1,2,3$
. As expected, increasing
$d_{2}/d_{1}$
alters the particle orientation during extreme angular velocities and moves it towards the orientation where
$\boldsymbol{p}_{\mathbf{1}}$
and
$\boldsymbol{p}_{\mathbf{2}}$
both bisect the plane spanned by the most extensional and the most contracting strain-rate directions. Thus, the source of higher values of the fourth moment of flattened particles (
$d_{2}/d_{1}\gg 1$
) seen in figure 6(a) is the addition of strain-rate-induced rotations to the already high values of vorticity-induced rotations about the longest axis in regions of the flow where fluid enstrophy and dissipation are both large.
Computing the alignment of the shortest axis without conditioning on extreme angular velocities shows a different alignment with the strain-rate tensor; the shortest axis is most commonly aligned with
$\boldsymbol{e}_{\mathbf{3}}$
(data not plotted here, but consistent with findings of Chevillard & Meneveau (Reference Chevillard and Meneveau2013)). This also explains why the peak in the PDF of
$|\boldsymbol{e}_{\mathbf{3}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{1}}|$
in figure 14(c) shows a bias towards higher values than the peak in the PDF of
$|\boldsymbol{e}_{\mathbf{1}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{1}}|$
in figure 14(a).
Figure 15. Alignment of particle’s shortest axis with the strain-rate eigen-directions during extreme particle angular velocities shown across the particle-shape parameter space: (a) median of
$|\boldsymbol{e}_{\mathbf{1}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{1}}|$
; (b) median of
$|\boldsymbol{e}_{\mathbf{2}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{1}}|$
; (c) median of
$|\boldsymbol{e}_{\mathbf{3}}\boldsymbol{\cdot }\boldsymbol{p}_{\mathbf{1}}|$
.
We can conclude from the results of this section that the majority of particle enstrophy is due to vorticity-induced rotations, but the weak increase in particle enstrophy with the value of
$d_{3}/d_{2}$
is due to the addition of strain-rate-induced rotations about
$\boldsymbol{p}_{\mathbf{1}}$
and
$\boldsymbol{p}_{\mathbf{2}}$
. The largest share of particle enstrophy is in rotations about the longest axis,
$\boldsymbol{p}_{\mathbf{3}}$
, due to its alignment with vorticity. The increase in the kurtosis of particle angular velocity with the value of
$d_{2}/d_{1}$
is due to contributions of strain-rate-induced rotations about
$\boldsymbol{p}_{\mathbf{3}}$
. The extremely large particle angular velocities occur when fluid enstrophy and dissipation are both large and the particle orientation maximizes strain-rate-induced rotations.
3.4 Persistence of particle rotations
To understand the time scale of particle rotation and how it relates to time scales of turbulent motions at different scales, we examine the two-time autocorrelation function of particles’ angular velocity. This autocorrelation function about axis
$\boldsymbol{p}_{\boldsymbol{i}}$
for
$i=1,2,3$
is given by
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{(\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{p}_{\boldsymbol{i}})}(s)=\frac{\langle (\unicode[STIX]{x1D74E}_{\boldsymbol{p}}(t)\boldsymbol{\cdot }\boldsymbol{p}_{\boldsymbol{i}}(t))(\unicode[STIX]{x1D74E}_{\boldsymbol{p}}(t+s)\boldsymbol{\cdot }\boldsymbol{p}_{\boldsymbol{i}}(t+s))\rangle }{\langle (\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{p}_{\boldsymbol{i}})^{2}\rangle }.\end{eqnarray}$$
The autocorrelation functions do not follow a simple exponential decay. This is consistent with the findings of Chevillard & Meneveau (Reference Chevillard and Meneveau2013), who showed that statistics of particle rotation could not be reproduced with a stochastic model for the velocity gradient tensor that followed a linear Ornstein–Uhlenbeck process, and Shin & Koch (Reference Shin and Koch2005), who showed that autocorrelation functions do not follow an exponential decay for fibre rotations.
The autocorrelation functions can be used to quantify the time scale over which particle angular velocity is persistent about different axes. This is done by computing an integral time scale for particle angular velocity, which is given by the integral of the autocorrelation function (Pope Reference Pope2000):
$$\begin{eqnarray}T_{\boldsymbol{p}_{\boldsymbol{i}}}=\int _{0}^{\infty }\unicode[STIX]{x1D70C}_{(\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{p}_{\boldsymbol{i}})}(s)\,\text{d}s,\end{eqnarray}$$
for particle angular velocity about axis
$\boldsymbol{p}_{\boldsymbol{i}}$
for
$i=1,2,3$
. The integral time scales are shown across the particle-shape parameter space in figure 16. The trends show that for all particle shapes, rotations about
$\boldsymbol{p}_{\mathbf{3}}$
are not only the most likely (figure 5), but also the most persistent, lasting between 5 and 10 multiples of
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
. Conversely, rotations about
$\boldsymbol{p}_{\mathbf{1}}$
are the least likely (figure 5) and are also the least persistent, lasting between 2 and 5 multiples of
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
. Figure 13 shows that only vorticity-induced rotations are responsible for the particle angular velocity about
$\boldsymbol{p}_{\mathbf{3}}$
. Therefore, the longer persistence of rotations about
$\boldsymbol{p}_{\mathbf{3}}$
is consistent with the persistence of vorticity at the smallest scales (Sreenivasan & Antonia Reference Sreenivasan and Antonia1997). Figure 11 showed that strain-rate-induced rotations make significant contribution to rotations about
$\boldsymbol{p}_{\mathbf{1}}$
, especially for shapes that are towards the top right of the particle-shape parameter space. In this case, the shorter persistence of rotations about
$\boldsymbol{p}_{\mathbf{1}}$
(figure 16
a) is consistent with the fact that strain rate is not as persistent as vorticity at the smallest scales (Girimaji & Pope Reference Girimaji and Pope1990; Pope Reference Pope1990).
Figure 16. Dimensionless integral time scale for particle angular velocity shown across the particle-shape parameter space: (a)
$T_{\boldsymbol{p}_{\mathbf{1}}}{\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}}^{-1}$
; (b)
$T_{\boldsymbol{p}_{\mathbf{2}}}{\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}}^{-1}$
; (c)
$T_{\boldsymbol{p}_{\mathbf{3}}}{\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}}^{-1}$
.
Figure 16(a) shows a similar trend to figure 11(a), suggesting that the shape variation of the integral time scale for rotations about the shortest axis is linked to the relative contribution of vorticity-induced rotations about this axis. Similarly, figure 16(b) shows a similar trend to figure 12(a), suggesting that the variation in integral time scale for rotations about the intermediate axis is also linked to the relative contribution of vorticity-induced rotations about the intermediate axis. The shape variation in the integral time scale for rotations about the longest axis in figure 16(c) are due to a more subtle effect of strain-rate-induced rotations. We see that as elongated particles become flattened (
$d_{3}/d_{2}\gg 1$
, increasing
$d_{2}/d_{1}$
), the integral time scale increases. At the same time, from figure 13(a), we see that practically all rotation about the longest axis is due to vorticity and from figure 8(c), we see that there is no difference in the median alignment between
$\boldsymbol{p}_{\mathbf{3}}$
and vorticity for all elongated particles regardless of how flattened they are (
$d_{3}/d_{2}\gg 1$
). This indicates that although the overall alignment of the longest axis with vorticity is the same for all elongated particles, it is more persistent for elongated particles that are axisymmetric. In other words, elongated particles that are axisymmetric (
$d_{3}/d_{2}\gg 1$
and
$d_{2}/d_{1}=1$
) maintain alignment with vorticity over a longer time scale than elongated particles that are also flattened (
$d_{3}/d_{2}\gg 1$
and
$d_{2}/d_{1}\gg 1$
).
The role played by strain-rate-induced rotations is to maintain alignment of the particle’s longest axis with vorticity. But while both the longest particle axis and the vorticity vector tend towards alignment with the most extensional direction of strain rate when viewed in a Lagrangian sense, particle rotations lead rather than lag the tilting of the vorticity vector (Ni et al.
Reference Ni, Ouellette and Voth2014). Further, the response of vorticity to strain-rate-induced tilting and stretching is dampened by viscous effects, whereas anisotropic and inertialess particles respond to strain rate instantaneously and without damping. Additionally, we see from (2.5b
) and the definition of
$\unicode[STIX]{x1D706}_{2}$
that elongated particles that are also flattened are more sensitive to strain-rate-induced rotations about the middle axis,
$\boldsymbol{p}_{\mathbf{2}}$
, than axisymmetric elongated particles for the same value of
$d_{3}/d_{2}$
. It is this extra sensitivity to strain rate that disrupts the alignment of their longest axis with vorticity and leads to lower integral time scales compared to elongated axisymmetric particles.
For plankton, full revolutions about principal axes can be important because they allow for sensing directional environmental cues such as light and gravity (Wells Reference Wells1968), as well as seascape locations (Fuchs & Gerbi Reference Fuchs and Gerbi2016). Herein, however, we see that such motions are rare in turbulence. The number of revolutions that a particle typically completes about each of its axes before the angular velocity decorrelates with itself can be calculated from the product of the integral time scale and the mean angular velocity. The typical number of revolutions is given by
$$\begin{eqnarray}n_{i}=\frac{T_{\boldsymbol{p}_{\boldsymbol{i}}}\sqrt{\langle (\unicode[STIX]{x1D74E}_{\boldsymbol{p}}\boldsymbol{\cdot }\boldsymbol{ p}_{\boldsymbol{i}})^{2}\rangle }}{2\unicode[STIX]{x03C0}}.\end{eqnarray}$$
The results for
$n_{i}$
are plotted in figure 17 across the particle-shape parameter space. They show that, typically, less than one-half of a revolution is completed before the angular velocity becomes decorrelated with itself for any particle axis and for any shape. The variation of
$n_{i}$
is slightly different than the variation seen in the integral time scale (figure 16) because it also incorporates the variation in the mean angular velocity (figure 5).
Figure 17. Number of revolutions completed during an integral time scale for angular velocity across the particle-shape parameter space: (a) about
$\boldsymbol{p}_{\mathbf{1}}$
; (b) about
$\boldsymbol{p}_{\mathbf{2}}$
; (c) about
$\boldsymbol{p}_{\mathbf{3}}$
.
We can conclude from the results of this section that particle rotations persist for 2–10 multiples of
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
with rotations about the longest axis persisting the longest. This persistence is due to alignment with vorticity being maintained over a longer time than for other axes. Full revolutions about any of the particle axes are rare events, but are most common about the longest axis for axisymmetric elongated particles. The integral time scales of angular velocity depend on intermittency and hence are likely to be a function of Reynolds number, but the trends with particle shape are most likely independent of Reynolds number.
4 Conclusions
We have thoroughly examined the rotational dynamics of small, inertialess triaxial ellipsoids in homogenous isotropic turbulence with a focus on describing variations with particle-shape after particles have reached statistically steady alignment with the local velocity gradient tensor. Preferential alignment of particles with the local velocity gradient tensor determines the partitioning of the total particle enstrophy such that the majority of the enstrophy is in rotations about the longest axis. We find the total particle enstrophy to be a very weak function of shape. This is because vorticity–strain correlations cancel almost all of the strain-rate contributions, so that the bulk of the particle enstrophy is due to fluid vorticity, which acts equally on particles of all shapes. There is a weak increase in total particle enstrophy for elongated particles, which is due to the residual contribution of strain-rate-induced rotations about the particle’s shortest and intermediate axes. In the case of axisymmetric ellipsoids, this means that rod-like particles have a slightly higher enstrophy than disc-like particles (as observed in Byron et al. (Reference Byron, Einarsson, Gustavsson, Voth, Mehlig and Variano2015)) due to a residual contribution of strain-rate-induced rotations. The slight increase in enstrophy can then be seen to be in tumbling motions since strain-rate-induced rotations can only cause a tumbling motion for axisymmetric particles.
Particles of all shapes experience angular velocities that are extremely large compared to the mean. These extremely large angular velocities are most likely to occur about the longest axis, and flattened particles are the most likely to experience large extreme angular velocities. These extremes occur when the fluid enstrophy and dissipation are both large.
The integral time scale for particle angular velocities about each axis shows that rotations about the longest axis are the most persistent (linked to the persistence of vorticity at small scales) and rotations about the shortest axis are the least persistent. Events where particles undergo a full revolution about any of their axes are rare, but occur most frequently for axisymmetric rod-like particles for rotations about their axis of symmetry.
We also see that single-parameter descriptions of particle-shape are insufficient to describe statistics of particle rotation. In most of our results, both
$d_{3}/d_{2}$
(how elongated a particle is) and
$d_{2}/d_{1}$
(how flattened a particle is) are required, but for certain quantities, only one of these parameters is important, e.g. the particle enstrophy depends only on
$d_{3}/d_{2}$
and kurtosis of particle angular velocity depends mainly on
$d_{2}/d_{1}$
. The single-parameter shape descriptions that are successful in sedimentation (Waddell sphericity parameter and Corey shape factor) do not parameterize rotation of the neutrally buoyant particles considered herein. This difference between the parameters controlling rotation and settling emphasizes the dynamical differences that appear when gravity is introduced to the problem.
Finally, we note that in the Stokesian regime in which the equations of particle motion have been derived, particle inertia and moments of inertia are negligible (Jeffery Reference Jeffery1922). Thus, there is no resultant force or torque on the particle and the particle instantly reaches equilibrium with the surrounding fluid at all times. If a particle volume is specified, particle angular momentum and particle rotational energy can be computed a posteriori from the particle enstrophy measured herein, but this provides no additional information.
The results of the rotations of small, inertialess anisotropic particles in turbulence presented herein provide a foundation to understanding the behaviour of particles in turbulent flows. For plankton, these results provide a link to understanding how shape may influence complex life functions such as sensing environmental cues and controlling diffusion-driven transport. We have made several simplifying assumptions – parameterizing plankton shape using ellipsoidal geometry, neglecting plankton motility and the effects of particle size greater than the Kolmogorov length scale being the most restrictive ones. How sensitive the results presented herein are to these complexities is left for future work.
Acknowledgements
The authors would like to acknowledge support from the Army Research Office (grant no. W911NF-16-1-0284). This research also benefited from the use of the Savio computational cluster resource provided by the Berkeley Research Computing program supported by the University of California, Berkeley. The authors would like to thank C. Meneveau and L. Chevillard for encouragement at the beginning of this project, G. Voth for illuminating discussions throughout, and three anonymous referees for their comments that helped to improve the manuscript. The colour map used in the majority of the figures was obtained from https://bids.github.io/colormap/.
