Article contents
A spectral model for homogeneous shear-driven anisotropic turbulence in terms of spherically averaged descriptors
Published online by Cambridge University Press: 22 December 2015
Abstract
A nonlinear spectral model in terms of spherically averaged descriptors is derived for the prediction of homogeneous turbulence dynamics in the presence of arbitrary mean-velocity gradients. The governing equations for the tensor 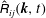 $\hat{\unicode[STIX]{x1D619}}_{ij}(\boldsymbol{k},t)$ , the Fourier transform of the two-point second-order correlation tensor, are first closed by an anisotropic eddy-damped quasinormal Markovian procedure. This closure is restricted to turbulent flows where linear effects induced by mean-flow gradients have no essential qualitative effects on the dynamics of triple correlations compared with the induced production effects in the equations for second-order correlations. Truncation at the first relevant order of spectral angular dependence allows us to derive from these equations in vector
$\hat{\unicode[STIX]{x1D619}}_{ij}(\boldsymbol{k},t)$ , the Fourier transform of the two-point second-order correlation tensor, are first closed by an anisotropic eddy-damped quasinormal Markovian procedure. This closure is restricted to turbulent flows where linear effects induced by mean-flow gradients have no essential qualitative effects on the dynamics of triple correlations compared with the induced production effects in the equations for second-order correlations. Truncation at the first relevant order of spectral angular dependence allows us to derive from these equations in vector 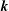 $\boldsymbol{k}$ our final model equations in terms of the wavenumber modulus
$\boldsymbol{k}$ our final model equations in terms of the wavenumber modulus 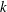 $k$ only. Analytical spherical integration results in a significant decrease in computational cost. Besides, the model remains consistent with the decomposition in terms of directional anisotropy and polarization anisotropy, with a spherically averaged anisotropic spectral tensor for each contribution. Restriction of anisotropy to spherically averaged descriptors, however, entails a loss of information, and realizability conditions are considered to quantify the upper boundary of anisotropy that can be investigated with the proposed model. Several flow configurations are considered to assess the validity of the present model. Satisfactory agreement with experiments on grid-generated turbulence subjected to successive plane strains is observed, which confirms the capability of the model to account for production of anisotropy by mean-flow gradients. The nonlinear transfer terms of the model are further tested by considering the return to isotropy (RTI) of different turbulent flows. Different RTI rates for directional anisotropy and polarization anisotropy allow us to correctly predict the apparent delayed RTI shown after axisymmetric expansion. The last test case deals with homogeneous turbulence subjected to a constant pure plane shear. The interplay between linear and nonlinear effects is reproduced, yielding the eventual exponential growth of the turbulent kinetic energy.
$k$ only. Analytical spherical integration results in a significant decrease in computational cost. Besides, the model remains consistent with the decomposition in terms of directional anisotropy and polarization anisotropy, with a spherically averaged anisotropic spectral tensor for each contribution. Restriction of anisotropy to spherically averaged descriptors, however, entails a loss of information, and realizability conditions are considered to quantify the upper boundary of anisotropy that can be investigated with the proposed model. Several flow configurations are considered to assess the validity of the present model. Satisfactory agreement with experiments on grid-generated turbulence subjected to successive plane strains is observed, which confirms the capability of the model to account for production of anisotropy by mean-flow gradients. The nonlinear transfer terms of the model are further tested by considering the return to isotropy (RTI) of different turbulent flows. Different RTI rates for directional anisotropy and polarization anisotropy allow us to correctly predict the apparent delayed RTI shown after axisymmetric expansion. The last test case deals with homogeneous turbulence subjected to a constant pure plane shear. The interplay between linear and nonlinear effects is reproduced, yielding the eventual exponential growth of the turbulent kinetic energy.
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 36
- Cited by


