Article contents
Transient growth in strongly stratified shear layers
Published online by Cambridge University Press: 07 October 2014
Abstract
We investigate numerically transient linear growth of three-dimensional perturbations in a stratified shear layer to determine which perturbations optimize the growth of the total kinetic and potential energy over a range of finite target time intervals. The stratified shear layer has an initial parallel hyperbolic tangent velocity distribution with Reynolds number 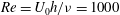 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Re}=U_0 h/\nu =1000$ and Prandtl number
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Re}=U_0 h/\nu =1000$ and Prandtl number 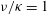 $\nu /\kappa =1$ , where
$\nu /\kappa =1$ , where  $\nu $ is the kinematic viscosity of the fluid and
$\nu $ is the kinematic viscosity of the fluid and  $\kappa $ is the diffusivity of the density. The initial stable buoyancy distribution has constant buoyancy frequency
$\kappa $ is the diffusivity of the density. The initial stable buoyancy distribution has constant buoyancy frequency 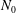 $N_0$ , and we consider a range of flows with different bulk Richardson number
$N_0$ , and we consider a range of flows with different bulk Richardson number 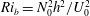 ${\mathit{Ri}}_b=N_0^2h^2/U_0^2$ , which also corresponds to the minimum gradient Richardson number
${\mathit{Ri}}_b=N_0^2h^2/U_0^2$ , which also corresponds to the minimum gradient Richardson number 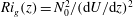 ${\mathit{Ri}}_g(z)=N_0^2/(\mathrm{d}U/\mathrm{d} z)^2$ at the midpoint of the shear layer. For short target times, the optimal perturbations are inherently three-dimensional, while for sufficiently long target times and small
${\mathit{Ri}}_g(z)=N_0^2/(\mathrm{d}U/\mathrm{d} z)^2$ at the midpoint of the shear layer. For short target times, the optimal perturbations are inherently three-dimensional, while for sufficiently long target times and small 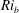 ${\mathit{Ri}}_b$ the optimal perturbations are closely related to the normal-mode ‘Kelvin–Helmholtz’ (KH) instability, consistent with analogous calculations in an unstratified mixing layer recently reported by Arratia et al. (J. Fluid Mech., vol. 717, 2013, pp. 90–133). However, we demonstrate that non-trivial transient growth occurs even when the Richardson number is sufficiently high to stabilize all normal-mode instabilities, with the optimal perturbation exciting internal waves at some distance from the midpoint of the shear layer.
${\mathit{Ri}}_b$ the optimal perturbations are closely related to the normal-mode ‘Kelvin–Helmholtz’ (KH) instability, consistent with analogous calculations in an unstratified mixing layer recently reported by Arratia et al. (J. Fluid Mech., vol. 717, 2013, pp. 90–133). However, we demonstrate that non-trivial transient growth occurs even when the Richardson number is sufficiently high to stabilize all normal-mode instabilities, with the optimal perturbation exciting internal waves at some distance from the midpoint of the shear layer.
Information
- Type
- Rapids
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 34
- Cited by

