Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Pirozzoli, Sergio
Bernardini, Matteo
and
Orlandi, Paolo
2014.
Turbulence statistics in Couette flow at high Reynolds number.
Journal of Fluid Mechanics,
Vol. 758,
Issue. ,
p.
327.
Rawat, Subhandu
Cossu, Carlo
Hwang, Yongyun
and
Rincon, François
2015.
On the self-sustained nature of large-scale motions in turbulent Couette flow.
Journal of Fluid Mechanics,
Vol. 782,
Issue. ,
p.
515.
Gai, Jie
Xia, Zhen-Hua
and
Cai, Qing-Dong
2015.
Effects of the computational domain on the secondary flow in turbulent plane Couette flow.
Chinese Physics B,
Vol. 24,
Issue. 10,
p.
104701.
Ostilla-Mónico, Rodolfo
Lohse, Detlef
and
Verzicco, Roberto
2016.
Effect of roll number on the statistics of turbulent Taylor-Couette flow.
Physical Review Fluids,
Vol. 1,
Issue. 5,
Nikolaidis, M-A
Farrell, B F
Ioannou, P J
Gayme, D F
Lozano-Durán, A
and
Jiménez, J
2016.
A POD-based analysis of turbulence in the reduced nonlinear dynamics system.
Journal of Physics: Conference Series,
Vol. 708,
Issue. ,
p.
012002.
Spandan, Vamsi
Ostilla-Monico, Rodolfo
Lohse, Detlef
and
Verzicco, Roberto
2016.
Identifying coherent structures and vortex clusters in Taylor-Couette turbulence.
Journal of Physics: Conference Series,
Vol. 708,
Issue. ,
p.
012006.
SASAKI, Eiichi
KAWAHARA, Genta
SEKIMOTO, Atsushi
and
JIMÉNEZ, Javier
2016.
Unstable periodic orbits in plane Couette flow with the Smagorinsky model.
Journal of Physics: Conference Series,
Vol. 708,
Issue. ,
p.
012003.
Kawata, Takuya
and
Alfredsson, P. Henrik
2016.
Turbulent rotating plane Couette flow: Reynolds and rotation number dependency of flow structure and momentum transport.
Physical Review Fluids,
Vol. 1,
Issue. 3,
Ostilla-Mónico, R.
Verzicco, R.
and
Lohse, D.
2016.
Turbulent Taylor–Couette flow with stationary inner cylinder.
Journal of Fluid Mechanics,
Vol. 799,
Issue. ,
Ostilla-Mónico, Rodolfo
Verzicco, Roberto
Grossmann, Siegfried
and
Lohse, Detlef
2016.
The near-wall region of highly turbulent Taylor–Couette flow.
Journal of Fluid Mechanics,
Vol. 788,
Issue. ,
p.
95.
Wacławczyk, M
Grebenev, V N
and
Oberlack, M
2017.
Lie symmetry analysis of the Lundgren–Monin–Novikov equations for multi-point probability density functions of turbulent flow.
Journal of Physics A: Mathematical and Theoretical,
Vol. 50,
Issue. 17,
p.
175501.
Miao, Sha
Hendrickson, Kelli
and
Liu, Yuming
2017.
Computation of three-dimensional multiphase flow dynamics by Fully-Coupled Immersed Flow (FCIF) solver.
Journal of Computational Physics,
Vol. 350,
Issue. ,
p.
97.
Wang, Guiquan
Abbas, Micheline
and
Climent, Eric
2017.
Modulation of large-scale structures by neutrally buoyant and inertial finite-size particles in turbulent Couette flow.
Physical Review Fluids,
Vol. 2,
Issue. 8,
Kraheberger, Stefanie
Hoyas, Sergio
and
Oberlack, Martin
2017.
Progress in Turbulence VII.
Vol. 196,
Issue. ,
p.
45.
Yang, Kun
Zhao, Lihao
and
Andersson, Helge I.
2017.
Turbulent Couette–Poiseuille flow with zero wall shear.
International Journal of Heat and Fluid Flow,
Vol. 63,
Issue. ,
p.
14.
Ostilla-Mónico, Rodolfo
and
Lee, Alpha A.
2017.
Controlling turbulent drag across electrolytes using electric fields.
Faraday Discussions,
Vol. 199,
Issue. ,
p.
159.
Shirokov, I. A.
and
Elizarova, T. G.
2017.
Application of Quasi-Gas Dynamic Equations to Numerical Simulation of Near-Wall Turbulent Flows.
Computational Mathematics and Modeling,
Vol. 28,
Issue. 1,
p.
37.
Lee, Myoungkyu
and
Moser, Robert D.
2018.
Extreme-scale motions in turbulent plane Couette flows.
Journal of Fluid Mechanics,
Vol. 842,
Issue. ,
p.
128.
Lluesma-Rodríguez, F.
Hoyas, S.
and
Perez-Quiles, M.J.
2018.
Influence of the computational domain on DNS of turbulent heat transfer up to Reτ=2000 for Pr=0.71.
International Journal of Heat and Mass Transfer,
Vol. 122,
Issue. ,
p.
983.
Owolabi, Bayode E.
and
Lin, Chao-An
2018.
Marginally turbulent Couette flow in a spanwise confined passage of square cross section.
Physics of Fluids,
Vol. 30,
Issue. 7,
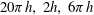 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}20\pi h,\, 2h,\, 6\pi h$) at Reynolds number
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}20\pi h,\, 2h,\, 6\pi h$) at Reynolds number 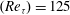 $(\mathit{Re}_{\tau }) =125$, 180, 250 and 550 is described and compared with simulations at lower Reynolds numbers, Poiseuille flows and experiments. The simulations present a logarithmic near-wall layer and are used to verify and revise previously known results. It is confirmed that the fluctuation intensities in the streamwise and spanwise directions do not scale well in wall units. The scaling failure occurs both near to and away from the wall. On the contrary, the wall-normal intensity scales in inner units in the near-wall region and in outer units in the core region. The spectral ridge found by Hoyas & Jiménez (Phys. Fluids, vol. 18, 2003, 011702) for the turbulent Poiseuille flow can also be seen in the present flow. Away from the wall, very large-scale motions are found spanning through all the length of the channel. The statistics of these simulations can be downloaded from the webpage of the Chair of Fluid Dynamics.
$(\mathit{Re}_{\tau }) =125$, 180, 250 and 550 is described and compared with simulations at lower Reynolds numbers, Poiseuille flows and experiments. The simulations present a logarithmic near-wall layer and are used to verify and revise previously known results. It is confirmed that the fluctuation intensities in the streamwise and spanwise directions do not scale well in wall units. The scaling failure occurs both near to and away from the wall. On the contrary, the wall-normal intensity scales in inner units in the near-wall region and in outer units in the core region. The spectral ridge found by Hoyas & Jiménez (Phys. Fluids, vol. 18, 2003, 011702) for the turbulent Poiseuille flow can also be seen in the present flow. Away from the wall, very large-scale motions are found spanning through all the length of the channel. The statistics of these simulations can be downloaded from the webpage of the Chair of Fluid Dynamics.

