Article contents
Wave-activity conservation laws for the three-dimensional anelastic and Boussinesq equations with a horizontally homogeneous background flow
Published online by Cambridge University Press: 14 December 2007
Abstract
Wave-activity conservation laws are key to understanding wave propagation in inhomogeneous environments. Their most general formulation follows from the Hamiltonian structure of geophysical fluid dynamics. For large-scale atmospheric dynamics, the Eliassen–Palm wave activity is a well-known example and is central to theoretical analysis. On the mesoscale, while such conservation laws have been worked out in two dimensions, their application to a horizontally homogeneous background flow in three dimensions fails because of a degeneracy created by the absence of a background potential vorticity gradient. Earlier three-dimensional results based on linear WKB theory considered only Doppler-shifted gravity waves, not waves in a stratified shear flow. Consideration of a background flow depending only on altitude is motivated by the parameterization of subgrid-scales in climate models where there is an imposed separation of horizontal length and time scales, but vertical coupling within each column. Here we show how this degeneracy can be overcome and wave-activity conservation laws derived for three-dimensional disturbances to a horizontally homogeneous background flow. Explicit expressions for pseudoenergy and pseudomomentum in the anelastic and Boussinesq models are derived, and it is shown how the previously derived relations for the two-dimensional problem can be treated as a limiting case of the three-dimensional problem. The results also generalize earlier three-dimensional results in that there is no slowly varying WKB-type requirement on the background flow, and the results are extendable to finite amplitude. The relationship 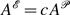 between pseudoenergy
between pseudoenergy 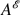 and pseudomomentum
and pseudomomentum 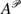 , where c is the horizontal phase speed in the direction of symmetry associated with
, where c is the horizontal phase speed in the direction of symmetry associated with 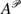 , has important applications to gravity-wave parameterization and provides a generalized statement of the first Eliassen–Palm theorem.
, has important applications to gravity-wave parameterization and provides a generalized statement of the first Eliassen–Palm theorem.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2008
References
REFERENCES
- 11
- Cited by


