Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-24T03:46:31.908Z Has data issue: false hasContentIssue false
  • English
  • Français

Strain-Concentration Factor of Circumferentially V-Notched Cylindrical Bars Under Static Tension

Published online by Cambridge University Press:  05 May 2011

H. M. Tlilan ,
A. S. Al-Shyyab ,
A. M. Jawarneh  and
A. K. Ababneh
H. M. Tlilan*
Affiliation:
Department of Mechanical Engineering, The Hashemite University, Zarqa 13115, Jordan
A. S. Al-Shyyab*
Affiliation:
Department of Mechanical Engineering, The Hashemite University, Zarqa 13115, Jordan
A. M. Jawarneh*
Affiliation:
Department of Mechanical Engineering, The Hashemite University, Zarqa 13115, Jordan
A. K. Ababneh*
Affiliation:
Department of Mechanical Engineering, The Hashemite University, Zarqa 13115, Jordan
*
* Assistant Professor
* Assistant Professor
* Assistant Professor
* Assistant Professor
Get access

Abstract

The FEM is used to study the effects of notch opening angle (β) and notch radius on the new strain-concentration factor (SNCF) for circumferentially V-notched cylindrical bars under static tension. The new SNCF has been defined under the triaxial stress state at the net section. Nevertheless, the conventional SNCF has been defined under uniaxial stress state. The new SNCF (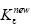) is constant in the elastic deformation. The range where this elastic 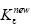value remains constant increases with increasing β and increasing notch radius (ρo). The effect of the notch opening angle on the elastic 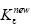decreases with increasing ρo. Particularly, the elastic 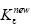of β = 120° is the minimum for all notch radii employed. The new SNCF increases from its elastic value to a peak value and then decreases with plastic deformation for notches with β = 120°. This peak value is the maximum 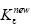. Nevertheless, 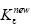for the notches with β < 120° becomes nearly constant or slightly decreasing after the first peak for ρo = 0.5 and 1mm. After that it increases to the maximum SNCF and then slightly decreases for further plastic deformation. The variations in 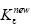with the ratio of tensile load to that at yielding at the notch root (P/PY) are nearly independent of stress-strain curve up to general yielding.

Keywords

StrainBarStrain concentrationFinite element methodNotchStatic tension
Type
Articles
Information
Journal of Mechanics , Volume 24 , Issue 4 , December 2008 , pp. 419 - 427
Copyright
Copyright © The Society of Theoretical and Applied Mechanics, R.O.C. 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Hardrath, H. F. and Ohman, L., “A Study of Elastic and Plastic Stress Concentration Factors Due to Notches and Fillets in Flat Plates,” NACA Report 1117, National Advisory Committee Aeronautics (1953).Google Scholar
2.Nishida, K., Stress Concentration, Morikita Shuppan, Tokyo, Japan (1974) (in Japanese).Google Scholar
3.Noda, N.-A., Sera, M. and Takase, Y., “Stress Concentration Factors for Round and Flat Test Specimens with Notches,” Int. J. Fatigue, 17, pp. 163–178 (1995).CrossRefGoogle Scholar
4.Pilkey, W. D., Peterson's Stress Concentration Factors, Wiley, New York (1997).CrossRefGoogle Scholar
5.Filippi, S., Lazzarin, P. and Tovo, R.,” Developments of Some Explicit Formulas Useful to Describe Elastic Stress Fields Ahead of Notches in Plates,” Int. J. Solids Structures, 39, pp. 4543–4565 (2002).CrossRefGoogle Scholar
6.Noda, N-A. and Takase, Y., “Stress Concentration Factor Formulas Useful for All Notch Shapes in a Flat Test Specimen Under Tension and Bending,” J. Test Eval., 30, pp. 369–381 (2002).CrossRefGoogle Scholar
7.Troyani, N., Hernández, S. I., Villarroel, G. and Pollonais, , Gomes, Y. C., “Theoretical Stress Concentration Factors for Short Flat Bars with Opposite U-Shaped Notches Subjected to In-Plane Bending,” Int. J. Fatigue, 26, pp. 1301–1310(2004).CrossRefGoogle Scholar
8.Smith, E., “The Elastic Stress Distribution Near the Root of an Elliptically Cylindrical Notch Subjected to Mode III Loadings,” Int. J. Engg. Science, 42, pp. 1831–1839(2004).CrossRefGoogle Scholar
9.Neuber, H., “Theory of Stress Concentration Factor for Shear-Strained Prismatical Bodies with Arbitrary Nonlinear Stress-Strain Law,” J. Applied Mechanics, 28, pp. 544–550 (1961).CrossRefGoogle Scholar
10.Theocaris, P. S., “Experimental Solution of Elastic-Plastic Plane Stress Problems,” J. Applied Mechanics, 29, pp. 735–743 (1962).CrossRefGoogle Scholar
11.Theocaris, P. S. and Marketos, E., “Elastic-Plastic Strain and Stress Distribution in Notched Plates Under Plane Stress,” J. Mech. Phys. Solids, 11, pp. 411–428 (1963).CrossRefGoogle Scholar
12.Durelli, A. J. and Sciammarella, C. A., “Elastoplastic Stress and Strain Distribution in a Finite Plate with a Circular Hole Subjected to Unidimensional Load,” J. Applied Mechanics, 30, pp. 115–121 (1963).CrossRefGoogle Scholar
13.Goda, C. V. B. and Topper, T. H., “On the Relation Between Stress and Strain Concentration Factors in Notched Member in Plane Stress,” J. Applied Mechanics, 37, pp. 77–84 (1970).CrossRefGoogle Scholar
14.Majima, T., “Strain-Concentration Factor of Circumferentially Notched Cylindrical Bars under Static Tension,” J. Strain Analysis, 34, pp. 347–360 (1999).CrossRefGoogle Scholar
15.Härkegård, G. and Mann, T., “Neuber Prediction of Elastic-Plastic Strain Concentration in Notched Tensile Specimens Under Large-Scale Yielding,” J. Strain Analysis, 38, pp. 79–94 (2003).CrossRefGoogle Scholar
16.Filippi, S. and Lazzarin, P., “Distributions of the Elastic Principal Stress Due to Notches in Finite Size Plates and Rounded Bars Uniaxially Loaded,” Int. J. Fatigue, 26, pp. 377–391(2004).CrossRefGoogle Scholar
17.Majima, T., Hitsumoto, K., Tanii, Y. and Ito, M., “Plastic Strain Distributions at the Net Section of Circumferentially Notched Cylindrical Bars,” Trans. Japanese Society of Mech. Engrs., 60, pp. 480–486 (1994) (in Japanese).CrossRefGoogle Scholar
18.Majima, T., Tanii, Y., Ando, Y. and Ito, M., “Relation Between Notch Tensile Strength and Stress Triaxiality (A Method of Increasing Notch Tensile Strength),” Trans. Japanese Society of Mech. Engrs., 61, pp. 2280–2287 (1995) (in Japanese).CrossRefGoogle Scholar
19.Majima, T., “A Method of Obtaining Strain Distributions of Circumferentially Notched Cylindrical Bars by Means of Hardness Test,” Japan Soc. Mech. Engrs. Int. J., 134, pp. 477–482(1991).Google Scholar
20.Tlilan, H. M., Sakai, N. and Majima, T., “Strain-Concentration Factor of a Single-Edge Notch under Pure Bending,” Yamanashi District Conference (2004) (in Japanese).CrossRefGoogle Scholar
21.Tlilan, H. M., Yousuke, S. and Majima, T., “Effect of Notch Depth on Strain-Concentration Factor of Notched Cylindrical Bars under Static Tension,” European J. of Mechanics A/Solids, 24, pp. 406–416 (2005).CrossRefGoogle Scholar
22.Tlilan, H. M., Sakai, N. and Majima, T., “Strain-Concentration Factor of Rectangular Bars with a Single-Edge Notch under Pure Bending,” Journal of the Society of Materials Science, 54, pp. 724–729 (2005) (in Japanese).Google Scholar
23.Tlilan, H. M., Sakai, N. and Majima, T., “Effect of Notch Depth on Strain-Concentration Factor of Rectangular Bars with a Single-Edge Notch under Pure Bending,” Int. J. Solids Structures, 43, pp. 459–474 (2006).CrossRefGoogle Scholar