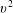1 Introduction
The motion of charged particles in a plasma is due to self-consistent mean electromagnetic field and cumulative effects of fluctuating fields. The latter can be approximated effectively as small-angle collisions. This approximation is in contrast to the case of neutral particles that travel in straight lines between ‘hard-sphere’ collisions. A fully ionized plasma is described by the Vlasov–Maxwell–Fokker–Planck (VM–FP) equation for the phase-space distribution function, ![]() $f(t,\boldsymbol{x},\boldsymbol{v})$, written as
$f(t,\boldsymbol{x},\boldsymbol{v})$, written as
Here, ![]() $\boldsymbol{a}_{s}=(q_{s}/m_{s})(\boldsymbol{E}+\boldsymbol{v}\times \boldsymbol{B})$ is the acceleration due to the Lorentz force, and
$\boldsymbol{a}_{s}=(q_{s}/m_{s})(\boldsymbol{E}+\boldsymbol{v}\times \boldsymbol{B})$ is the acceleration due to the Lorentz force, and ![]() $q_{s}$ and
$q_{s}$ and ![]() $m_{s}$ the charge and mass of species
$m_{s}$ the charge and mass of species ![]() $s$, respectively. The mean electric and magnetic fields,
$s$, respectively. The mean electric and magnetic fields, ![]() $\boldsymbol{E}$ and
$\boldsymbol{E}$ and ![]() $\boldsymbol{B}$ are determined from net charges and currents generated due to the motion of the particles, and are governed by Maxwell’s equations of electromagnetism. The effect of small-angle collisions, written on the right-hand side of the above equation, is described by the nonlinear Fokker–Planck operator (FPO) (Rosenbluth, MacDonald & Judd Reference Rosenbluth, MacDonald and Judd1957) as
$\boldsymbol{B}$ are determined from net charges and currents generated due to the motion of the particles, and are governed by Maxwell’s equations of electromagnetism. The effect of small-angle collisions, written on the right-hand side of the above equation, is described by the nonlinear Fokker–Planck operator (FPO) (Rosenbluth, MacDonald & Judd Reference Rosenbluth, MacDonald and Judd1957) as
Here, ![]() $\langle \unicode[STIX]{x0394}v_{i}\rangle _{s}$ and
$\langle \unicode[STIX]{x0394}v_{i}\rangle _{s}$ and ![]() $\langle \unicode[STIX]{x0394}v_{i}\unicode[STIX]{x0394}v_{j}\rangle _{s}$ are average increments per unit time due to the effect of collisions governed by the inverse-square force between individual particles, and
$\langle \unicode[STIX]{x0394}v_{i}\unicode[STIX]{x0394}v_{j}\rangle _{s}$ are average increments per unit time due to the effect of collisions governed by the inverse-square force between individual particles, and ![]() $i,j$ index the velocity components:
$i,j$ index the velocity components: ![]() $i,j\in \{1,2,3\}$. In general, the increments are determined either from a Landau integral formulation or from the Rosenbluth potentials that themselves are computed by solving elliptic boundary value problems involving the distribution function. This results in a nonlinear integro-differential equation for the effect of collisions on the evolution of the distribution function. See equations (17)–(20) in Rosenbluth et al. (Reference Rosenbluth, MacDonald and Judd1957) or Helander & Sigmar (Reference Helander and Sigmar2005) for details. We refer to this specific system as the Rosenbluth Fokker–Planck operator. An alternative and equivalent formulation of the FPO is the Landau form (Landau Reference Landau1936), often preferred due to its ease of showing conservation and entropy production.
$i,j\in \{1,2,3\}$. In general, the increments are determined either from a Landau integral formulation or from the Rosenbluth potentials that themselves are computed by solving elliptic boundary value problems involving the distribution function. This results in a nonlinear integro-differential equation for the effect of collisions on the evolution of the distribution function. See equations (17)–(20) in Rosenbluth et al. (Reference Rosenbluth, MacDonald and Judd1957) or Helander & Sigmar (Reference Helander and Sigmar2005) for details. We refer to this specific system as the Rosenbluth Fokker–Planck operator. An alternative and equivalent formulation of the FPO is the Landau form (Landau Reference Landau1936), often preferred due to its ease of showing conservation and entropy production.
In this paper we instead approximate the increments, from self-collisions for example, as ![]() $\langle \unicode[STIX]{x0394}v_{i}\rangle _{s}=-\unicode[STIX]{x1D708}_{ss}(v_{i}-u_{i,s})$ and
$\langle \unicode[STIX]{x0394}v_{i}\rangle _{s}=-\unicode[STIX]{x1D708}_{ss}(v_{i}-u_{i,s})$ and ![]() $\langle \unicode[STIX]{x0394}v_{i}\unicode[STIX]{x0394}v_{j}\rangle _{s}=2\unicode[STIX]{x1D708}_{ss}v_{th,s}^{2}\unicode[STIX]{x1D6FF}_{ij}$, where
$\langle \unicode[STIX]{x0394}v_{i}\unicode[STIX]{x0394}v_{j}\rangle _{s}=2\unicode[STIX]{x1D708}_{ss}v_{th,s}^{2}\unicode[STIX]{x1D6FF}_{ij}$, where ![]() $\unicode[STIX]{x1D708}_{ss}$ is the collision frequency, and the primitive moments
$\unicode[STIX]{x1D708}_{ss}$ is the collision frequency, and the primitive moments ![]() $\boldsymbol{u}_{s}$ and
$\boldsymbol{u}_{s}$ and ![]() $v_{th,s}=\sqrt{T_{s}/m_{s}}$ are the mean velocity and thermal speed of the particles, respectively. Clearly this operator, referred to as the D-FPO, involves a significant simplification. However, the essential features of the complete system are still present: the equation is a nonlinear integro-differential equation as the mean velocity
$v_{th,s}=\sqrt{T_{s}/m_{s}}$ are the mean velocity and thermal speed of the particles, respectively. Clearly this operator, referred to as the D-FPO, involves a significant simplification. However, the essential features of the complete system are still present: the equation is a nonlinear integro-differential equation as the mean velocity ![]() $\boldsymbol{u}_{s}$ and the thermal speed
$\boldsymbol{u}_{s}$ and the thermal speed ![]() $v_{th,s}$ are determined by moments of the distribution function; the effect of both drag and diffusion on the particle distribution function is included. The diffusion term means that fine-scale oscillations in velocity space are damped more quickly than long-scale oscillations, as in the full Rosenbluth/Landau Fokker–Planck operator, and unlike the algebraic Krook operator that damps all scales at the same rate. One of the weakness of this simplification is in the use of a mean collision frequency independent of the particle velocity. In the full system the effective collision frequency is smaller for higher speed particles and goes like
$v_{th,s}$ are determined by moments of the distribution function; the effect of both drag and diffusion on the particle distribution function is included. The diffusion term means that fine-scale oscillations in velocity space are damped more quickly than long-scale oscillations, as in the full Rosenbluth/Landau Fokker–Planck operator, and unlike the algebraic Krook operator that damps all scales at the same rate. One of the weakness of this simplification is in the use of a mean collision frequency independent of the particle velocity. In the full system the effective collision frequency is smaller for higher speed particles and goes like ![]() $1/v^{3}$. This deficiency means that in our simplified formulation high energy tails in the distribution function are equally impacted by collisions as the low energy bulk, and this can result in inaccurate physics in some situations. It is possible to improve this model by making the collision frequency a function of velocity, but the definitions of
$1/v^{3}$. This deficiency means that in our simplified formulation high energy tails in the distribution function are equally impacted by collisions as the low energy bulk, and this can result in inaccurate physics in some situations. It is possible to improve this model by making the collision frequency a function of velocity, but the definitions of ![]() $\boldsymbol{u}_{s}$ and
$\boldsymbol{u}_{s}$ and ![]() $v_{th,s}^{2}$ must be modified.
$v_{th,s}^{2}$ must be modified.
The D-FPO already illustrates the challenges in designing a robust, efficient, and production quality numerical method that works well with the discretization of the collisionless terms. Conservation in the presence of both drag and diffusion and finite velocity extents is challenging to maintain. Moments need to be self-consistently determined with the discretization of the collision operator. Diffusion terms need to be handled carefully to ensure momentum and energy conservation. Yet, many features of the D-FPO algorithm designed to handle these challenges remain essentially unchanged for the full FPO, except that in such case the increments are determined from elliptic equations in velocity space.
Our approach to discretize the Vlasov–Maxwell–Fokker–Planck system is to use a version of the discontinuous Galerkin (DG) scheme. High-order DG can be extended to handle complex geometries, offers increased accuracy at reduced cost and maintains favourable data locality. The latter is desirable for high performance computing on modern architectures and allows construction of robust schemes that employ modifications of boundary fluxes (e.g. limiters), similar in concept to the those in finite-volume methods. Previously (Juno et al. Reference Juno, Hakim, TenBarge, Shi and Dorland2018), we presented a nodal DG scheme to solve the collisionless system. This scheme is robust and efficient, and was recently modified to use modal basis functions and computer algebra system (CAS) generated code to further enhance its efficiency. Here, we use the same technique, that is, a modal DG scheme combined with CAS generated code to design a scheme that conserves number density, momentum density and energy. Along with an energy conserving scheme for the collisionless terms, we obtain a robust conservative scheme for the full Vlasov–Maxwell–Fokker–Planck equation.
Although we focus on the DG scheme, previous work on numerical integration of kinetic equations has employed finite difference (Idomura et al. Reference Idomura, Ida, Kano, Aiba and Tokuda2008), finite-volume (Dorf et al. Reference Dorf, Cohen, Compton, Dorr, Rognlien, Angus, Krasheninnikov, Colella, Martin and McCorquodale2012) and spectral methods (Jorge, Ricci & Loureiro Reference Jorge, Ricci and Loureiro2017). Each has advantages for specific applications. In particular Taitano et al. (Reference Taitano, Chacón, Simakov and Molvig2015) presents an exactly conservative implicit method to discretize the multi-species Fokker–Planck operator, using a Jacobian-free Newton–Krylov scheme. In Hirvijoki & Adams (Reference Hirvijoki and Adams2017) the Landau form of the FPO is discretized using a Galerkin formulation and, alternatively in Hirvijoki & Adams (Reference Hirvijoki and Adams2017), Hirvijoki, Burby & Kraus (Reference Hirvijoki, Burby and Kraus2018), a direct discretization of the ‘metriplectic’ structure of the system. There are some advantages of discretizing the Landau form as the proofs of conservation and H-theorem are direct and can be exploited in constructing the scheme. However, the Landau form involves convolutions in six-dimensional velocity space, making the scheme expensive.
In fusion physics there is a long history of methods developed to solve the Rosenbluth/Landau–Fokker–Planck operator. McCoy, Mirin & Killeen (Reference McCoy, Mirin and Killeen1981), Hammett (Reference Hammett1986) and Killeen et al. (Reference Killeen, Kerbel, McCoy and Mirin1986) develop a method to solve the bounce-averaged collision operator using spherical harmonics and finite differences. This early work resulted in a widely used Fokker–Planck code called CQL3D (see https://www.compxco.com/cql3d.html). Note that in these approaches the focus is on the detailed effects of collisions and usually the collisionless terms (streaming and Lorentz forces) are not included, or are treated only approximately. More recently, in Hager et al. (Reference Hager, Yoon, Ku, D’Azevedo, Worley and Chang2016), a conservative finite-volume solver was developed for the Landau form of the operator and incorporated in a particle-in-cell code (these are just some examples, others include Belli & Candy (Reference Belli and Candy2017), Barnes et al. (Reference Barnes, Abel, Dorland, Ernst, Hammett, Ricci, Rogers, Schekochihin and Tatsuno2009), Pan & Ernst (Reference Pan and Ernst2019) and Nakata et al. (Reference Nakata, Nunami, Watanabe and Sugama2015)).
The rest of the paper is organized as follows. We first summarize, in § 2, properties of the continuous Fokker–Planck operator that are important to maintain or control in the discrete system. Section 3 describes the concept of weak equality and its use in computing primitive moments and continuous reconstructions. We then present two D-FPO DG discretizations in § 4 showing why the diffusion operator and velocity-space boundary need to be handled in a particular manner to ensure conservation. Preservation of conservative properties requires special handling of the primitive moments; this is reviewed in § 5. Time-integration stability is briefly commented on in § 6. A series of benchmark problems for both the stand-alone D-FPO as well as the complete Vlasov–Maxwell–Fokker–Planck system illustrate the physics that can be studied with the scheme in § 7. We conclude with some highlights of this work and direction for future research.
The schemes are implemented in Gkeyll, an open-source computational plasma physics package. Gkeyll contains solvers for Vlasov–Maxwell–Fokker–Planck equations, gyrokinetic equations (Shi Reference Shi2017; Shi et al. Reference Shi, Hammett, Stoltzfus-Dueck and Hakim2017) and multi-fluid moment equations (Wang et al. Reference Wang, Hakim, Bhattacharjee and Germaschewski2015). To allow interested readers to reproduce our results, we have made Gkeyll input scripts used in this paper, available in a public source repository. Instructions to obtain Gkeyll and the input files used here are given in appendix A.
2 The continuous collision operator and its properties
The form of the Fokker–Planck operator we will consider here will approximate the coefficients appearing in (1.2), as (Lenard & Bernstein Reference Lenard and Bernstein1958; Dougherty Reference Dougherty1964)
and
Here, ![]() $\unicode[STIX]{x1D708}_{sr}$ is the collision frequency between particles of species
$\unicode[STIX]{x1D708}_{sr}$ is the collision frequency between particles of species ![]() $s$ and
$s$ and ![]() $r$, and
$r$, and ![]() $\boldsymbol{u}_{s}$ and
$\boldsymbol{u}_{s}$ and ![]() $v_{th,s}=\sqrt{T_{s}/m_{s}}$ are the mean (drift) velocity and thermal speed of particles of species
$v_{th,s}=\sqrt{T_{s}/m_{s}}$ are the mean (drift) velocity and thermal speed of particles of species ![]() $s$ respectively and where
$s$ respectively and where ![]() $T_{s}$ for non-Maxwellian species is defined below based on the average energy of the particles. To compute the mean velocity and thermal speed we first define the moments
$T_{s}$ for non-Maxwellian species is defined below based on the average energy of the particles. To compute the mean velocity and thermal speed we first define the moments
In terms of these moments the single-species mean velocities and thermal speeds in three velocity dimensions are ![]() $\boldsymbol{M}_{1}^{s}=n_{s}\boldsymbol{u}_{s}$ and
$\boldsymbol{M}_{1}^{s}=n_{s}\boldsymbol{u}_{s}$ and ![]() $M_{2}^{s}=n_{s}\boldsymbol{u}_{s}^{2}+3n_{s}v_{th,s}^{2}$. For other velocity dimensions, replace the 3 with
$M_{2}^{s}=n_{s}\boldsymbol{u}_{s}^{2}+3n_{s}v_{th,s}^{2}$. For other velocity dimensions, replace the 3 with ![]() $d_{v}$, the dimensionality of velocity space. The multi-species velocities
$d_{v}$, the dimensionality of velocity space. The multi-species velocities ![]() $\boldsymbol{u}_{sr}$ and thermal speeds
$\boldsymbol{u}_{sr}$ and thermal speeds ![]() $v_{th,sr}=\sqrt{T_{sr}/m_{s}}$ are intermediate values that are designed to maintain conservation of total density, momentum and energy; see Greene (Reference Greene1973) for the analogous problem with the Bhatnagar–Gross–Krook operator. These coefficients are chosen to preserve important properties of the FPO, as we discuss below.
$v_{th,sr}=\sqrt{T_{sr}/m_{s}}$ are intermediate values that are designed to maintain conservation of total density, momentum and energy; see Greene (Reference Greene1973) for the analogous problem with the Bhatnagar–Gross–Krook operator. These coefficients are chosen to preserve important properties of the FPO, as we discuss below.
Even though (1.2) has the form of the Fokker–Planck equation, with the specific choice for the increments equation (2.1) and equation (2.2) this operator is sometimes referred to, in plasma physics, by different names. For example, a linear form of the operator, that did not conserve momentum, was presented in Lenard & Bernstein (Reference Lenard and Bernstein1958) to study Landau damping of plasma oscillations in the presence of collisions. The nonlinear and conservative form above was presented first by Dougherty (Reference Dougherty1964). Hence, in the plasma physics literature, this operator is commonly referred to as the Lenard–Bernstein operator or the Dougherty operator. In this paper we refer to the conservative operator as the Dougherty–Fokker–Planck operator (D-FPO). Note that the form of the equation is the same as the generic Fokker–Planck equation. Determining the increments in the operator using Rosenbluth potentials does not change the form of the basic equation and also, as mentioned in the introduction, most of the computational difficulties and solutions developed here carry over to that case.
We next list the properties of the FPO (or other collision operators) that are important to preserve in a good numerical scheme. The most important of these properties are the conservation of number density of each species, and the total, summed over species, momentum and total energy. The corresponding conservation properties of the collisionless Vlasov–Maxwell system were given in Juno et al. (Reference Juno, Hakim, TenBarge, Shi and Dorland2018). The conservation properties are well known and are summarized below. We include these to allow comparison of the identities needed in the continuous proofs which then hint that the corresponding identities also need to be satisfied in the discrete proofs.
As is well known, the collision operator conserves density
and conserves total momentum
In the form we use, for momentum conservation we must ensure that
The FPO conserves total energy
Again, for this to be true we must ensure that
We remark that, for the full VM–FP equation, the integration needs to be performed over the full phase space and not just the velocity space as above, or a local conservation law can be derived with additional terms involving the divergence of spatial fluxes of particle, momentum and energy. The proofs follow from the form of the FPO, equation (1.2), and integrating the drag terms by parts once and the diffusion terms twice. We also need to assume that ![]() $f(t,\boldsymbol{x},\boldsymbol{v})\rightarrow 0$ sufficiently fast as
$f(t,\boldsymbol{x},\boldsymbol{v})\rightarrow 0$ sufficiently fast as ![]() $v_{i}\rightarrow \infty$.
$v_{i}\rightarrow \infty$.
A well-constructed discrete operator should ensure that number density, total momentum and total energy are conserved in the discrete sense. Hence, the scheme must satisfy discrete constraints analogous to momentum and energy conservation in the continuous case. In addition, the proofs for the conservation in the continuous case assumed an infinite velocity domain, but this needs to be truncated in the numerical scheme presented here. Hence, as we will show in § 5, discrete conservation requires accounting for the boundary conditions in velocity space while ensuring constraints on the fluctuations are met. This is unlike the collisionless Vlasov–Maxwell case, see Proposition 8 in Juno et al. (Reference Juno, Hakim, TenBarge, Shi and Dorland2018), in which the velocity boundaries do not appear in the proof of conservation of energy, except implicitly in the assumption of zero flux of particles through the maximum velocity boundary on the grid.
In the remainder of this paper we limit our discussion to the case of a single species for which we can write the Dougherty FPO with our choice of fluctuations as
where the species subscript is now dropped. The generalization to multiple species Dougherty is beyond the scope of this work, but is available in Gkeyll (see the The Gkeyll Team (2020) website). In addition to the conservative properties described above, the D-FPO also has an H theorem and is self-adjoint. These additional features are expanded upon in appendix B.
3 Weak equality, weak operators and recovery scheme for diffusion
Before describing the DG scheme for the D-FPO we discuss the concept of weak equality, weak operators and the recovery of second derivatives. These are essential to the construction of our scheme and to ensuring conservation and high-order accuracy. The ideas of weak equality and weak operators are analogous to weak solutions, long employed in mathematics and finite-element methods (Brenner & Scott Reference Brenner and Scott2008).
Consider some interval ![]() $I$ and some function space
$I$ and some function space ![]() ${\mathcal{P}}$ spanned by basis set
${\mathcal{P}}$ spanned by basis set ![]() $\unicode[STIX]{x1D713}_{k}$,
$\unicode[STIX]{x1D713}_{k}$, ![]() $k=1,\ldots ,N$. We will define two functions
$k=1,\ldots ,N$. We will define two functions ![]() $f$ and
$f$ and ![]() $g$ to be weakly equal if
$g$ to be weakly equal if
We will denote weakly equal functions by ![]() $f\doteq g$. Unlike strong equality, in which functions agree at all points in the interval, weak equality only assures us that the projection of the function on a chosen basis set is the same. However, the functions themselves may be quite different from each other with respect to their behaviour, e.g. the function’s positivity or monotonicity in the interval. The key strength of this concept is that it allows replacing of a function by its weakly equal counterpart in certain terms of the algorithm without changing those terms, e.g. volume integrals in DG, but allows more desirable properties in other terms, e.g. the surface integrals in DG.
$f\doteq g$. Unlike strong equality, in which functions agree at all points in the interval, weak equality only assures us that the projection of the function on a chosen basis set is the same. However, the functions themselves may be quite different from each other with respect to their behaviour, e.g. the function’s positivity or monotonicity in the interval. The key strength of this concept is that it allows replacing of a function by its weakly equal counterpart in certain terms of the algorithm without changing those terms, e.g. volume integrals in DG, but allows more desirable properties in other terms, e.g. the surface integrals in DG.
An application of this concept is to weak operators. These are operators whose solution is only satisfied in the weak sense, but that may have multiple, pointwise different solutions. As an illustration, say we know the density and momentum; see (2.3)–(2.5). To determine the velocity we have the relation ![]() $M_{0}u=M_{1}$. At first sight one may think that it is trivial to compute the velocity from this expression:
$M_{0}u=M_{1}$. At first sight one may think that it is trivial to compute the velocity from this expression: ![]() $u=M_{1}/M_{0}$. However, in a DG scheme we only know the projections of
$u=M_{1}/M_{0}$. However, in a DG scheme we only know the projections of ![]() $M_{0}$ and
$M_{0}$ and ![]() $M_{1}$ on the DG function space and not the function itself. Even in a nodal DG scheme a naive division of nodal values is incorrect and leads to aliasing errors (except for
$M_{1}$ on the DG function space and not the function itself. Even in a nodal DG scheme a naive division of nodal values is incorrect and leads to aliasing errors (except for ![]() $p=1$ polynomials, where one can do division at Gaussian quadrature nodes, though even there, limits need to be applied). Hence, more correctly, to find
$p=1$ polynomials, where one can do division at Gaussian quadrature nodes, though even there, limits need to be applied). Hence, more correctly, to find ![]() $u$ we need to invert the weak division operator
$u$ we need to invert the weak division operator
Using the definition of weak equality above this expression means
This only determines ![]() $u$ to its projection on the function space. Assuming
$u$ to its projection on the function space. Assuming ![]() $u$ belongs to the function space we can write
$u$ belongs to the function space we can write ![]() $u=\sum _{m}u_{m}\unicode[STIX]{x1D713}_{k}$ leading to the linear system of equations
$u=\sum _{m}u_{m}\unicode[STIX]{x1D713}_{k}$ leading to the linear system of equations
for ![]() $k=1,\ldots ,N$. Inverting this determines
$k=1,\ldots ,N$. Inverting this determines ![]() $u_{m}$ and hence the projection of
$u_{m}$ and hence the projection of ![]() $u$ in the function space. We call this process weak division. Note that weak division only determines
$u$ in the function space. We call this process weak division. Note that weak division only determines ![]() $u$ to an equivalence class as we can replace the specific
$u$ to an equivalence class as we can replace the specific ![]() $u$ in the function space with any other function that is weakly equal to it. In addition, note that
$u$ in the function space with any other function that is weakly equal to it. In addition, note that ![]() $M_{0}$ and
$M_{0}$ and ![]() $M_{1}$ themselves have expansions that must be included in this computation.
$M_{1}$ themselves have expansions that must be included in this computation.
One cannot divide by zero in regular division. An analogous situation exists for weak division. To illustrate, consider the interval ![]() $[-1,1]$ and the orthonormal linear basis set
$[-1,1]$ and the orthonormal linear basis set
Let ![]() $M_{1}=1$ and
$M_{1}=1$ and ![]() $M_{0}=n_{0}\unicode[STIX]{x1D713}_{0}+n_{1}\unicode[STIX]{x1D713}_{1}$. For this simple case the result of weak division is
$M_{0}=n_{0}\unicode[STIX]{x1D713}_{0}+n_{1}\unicode[STIX]{x1D713}_{1}$. For this simple case the result of weak division is
Hence, the weak division is not defined for ![]() $n_{1}=\pm n_{0}$ (
$n_{1}=\pm n_{0}$ (![]() $n_{0}>0$ as mean density must be positive). This shows that, even if the mean density is positive, the slope cannot become too steep (see figure 1). When the ‘blow-up’ occurs, i.e.
$n_{0}>0$ as mean density must be positive). This shows that, even if the mean density is positive, the slope cannot become too steep (see figure 1). When the ‘blow-up’ occurs, i.e. ![]() $n_{1}=\pm n_{0}$ case,
$n_{1}=\pm n_{0}$ case, ![]() $M_{0}$ has a zero crossing at either
$M_{0}$ has a zero crossing at either ![]() $x=\pm 1/\sqrt{3}$. Note that there is nothing necessarily unphysical with a piecewise linear reconstruction
$x=\pm 1/\sqrt{3}$. Note that there is nothing necessarily unphysical with a piecewise linear reconstruction ![]() $M_{0}(x)$ having a zero crossing within the domain (and the DG algorithm can result in such solutions), since in principle there is a physically realizable function that is weakly equivalent
$M_{0}(x)$ having a zero crossing within the domain (and the DG algorithm can result in such solutions), since in principle there is a physically realizable function that is weakly equivalent ![]() $\tilde{M}_{0}(x)\doteq M_{0}(x)$ but positive everywhere, as long as
$\tilde{M}_{0}(x)\doteq M_{0}(x)$ but positive everywhere, as long as ![]() $n_{1}<\sqrt{3}n_{0}$). Hence, one must ensure that the density does not become too steep. In practice, we have found that the bound
$n_{1}<\sqrt{3}n_{0}$). Hence, one must ensure that the density does not become too steep. In practice, we have found that the bound ![]() $|n_{1}|<n_{0}$ is not sufficiently restrictive, as it still allows
$|n_{1}|<n_{0}$ is not sufficiently restrictive, as it still allows ![]() $u(x)$ to approach infinity, giving rise to severe CFL (Courant–Friedrich–Levy) limits on the time step. Instead, we restrict
$u(x)$ to approach infinity, giving rise to severe CFL (Courant–Friedrich–Levy) limits on the time step. Instead, we restrict ![]() $|n_{1}|<n_{0}/\sqrt{3}$ in the calculation of
$|n_{1}|<n_{0}/\sqrt{3}$ in the calculation of ![]() $u(x)$. Even if we simply set
$u(x)$. Even if we simply set ![]() $n_{1}=0$ and calculated the mean velocity
$n_{1}=0$ and calculated the mean velocity ![]() $u(x)$ by dividing the momentum
$u(x)$ by dividing the momentum ![]() $M_{1}(x)$ by the mean density, we would still conserve momentum averaged over a cell. There is some numerical diffusion of momentum within a cell caused by changing
$M_{1}(x)$ by the mean density, we would still conserve momentum averaged over a cell. There is some numerical diffusion of momentum within a cell caused by changing ![]() $n_{1}$, but no numerical diffusion across cell boundaries. In smooth regions we use the standard calculations and so retain high-order accuracy there, while introducing limiters where the solution is locally varying too quickly to be accurately resolved, in order to robustly preserve certain properties of the solution.
$n_{1}$, but no numerical diffusion across cell boundaries. In smooth regions we use the standard calculations and so retain high-order accuracy there, while introducing limiters where the solution is locally varying too quickly to be accurately resolved, in order to robustly preserve certain properties of the solution.

Figure 1. Weak division for ![]() $p=1$ basis to compute
$p=1$ basis to compute ![]() $u$ from
$u$ from ![]() $M_{0}u\doteq M_{1}$. In this plot
$M_{0}u\doteq M_{1}$. In this plot ![]() $M_{1}=1$ and the effect of changing
$M_{1}=1$ and the effect of changing ![]() $M_{0}$ (a–c) on speed (d–f) is shown. As the density steepens, the velocity becomes larger and blows up when the density has a zero crossing at
$M_{0}$ (a–c) on speed (d–f) is shown. As the density steepens, the velocity becomes larger and blows up when the density has a zero crossing at ![]() $x=\pm 1/\sqrt{3}$ (magenta crosses). To avoid problems, we set a limit on the slope of
$x=\pm 1/\sqrt{3}$ (magenta crosses). To avoid problems, we set a limit on the slope of ![]() $M_{0}$ used in calculating
$M_{0}$ used in calculating ![]() $u(x)$, which still conserves the cell-averaged momentum.
$u(x)$, which still conserves the cell-averaged momentum.
Another application of weak equality is to recover a continuous function from a discontinuous one. Say we want to construct a continuous representation ![]() $\hat{f}$ on the interval
$\hat{f}$ on the interval ![]() $I=[-1,1]$, from a function,
$I=[-1,1]$, from a function, ![]() $f$, which has a single discontinuity at
$f$, which has a single discontinuity at ![]() $x=0$. We can choose some function spaces
$x=0$. We can choose some function spaces ![]() ${\mathcal{P}}_{L}$ and
${\mathcal{P}}_{L}$ and ![]() ${\mathcal{P}}_{R}$ on the intervals
${\mathcal{P}}_{R}$ on the intervals ![]() $I_{L}=[-1,0]$ and
$I_{L}=[-1,0]$ and ![]() $I_{R}=[0,1]$ respectively. Then, we can reconstruct a continuous function
$I_{R}=[0,1]$ respectively. Then, we can reconstruct a continuous function ![]() $\hat{f}$ such that
$\hat{f}$ such that
where ![]() $f=f_{L}$ for
$f=f_{L}$ for ![]() $x\in I_{L}$ and
$x\in I_{L}$ and ![]() $f=f_{R}$ for
$f=f_{R}$ for ![]() $x\in I_{R}$. Again, this only determines
$x\in I_{R}$. Again, this only determines ![]() $\hat{f}$ to its projections in the left and right intervals. To determine
$\hat{f}$ to its projections in the left and right intervals. To determine ![]() $\hat{f}$ uniquely, we use the fact that, given the
$\hat{f}$ uniquely, we use the fact that, given the ![]() $2N$ pieces of information, where
$2N$ pieces of information, where ![]() $N$ is the number of basis functions in
$N$ is the number of basis functions in ![]() ${\mathcal{P}}_{L,R}$, we can construct a polynomial of maximum order
${\mathcal{P}}_{L,R}$, we can construct a polynomial of maximum order ![]() $2N-1$. We can hence write
$2N-1$. We can hence write
Using this in (3.7) and (3.8) completely determines ![]() $\hat{f}$. In a certain sense the recovery procedure is a special case of a more general method to go from one basis to another under the restriction of weak equality.
$\hat{f}$. In a certain sense the recovery procedure is a special case of a more general method to go from one basis to another under the restriction of weak equality.
Given this procedure to recover a continuous function, we can now compute second derivatives as follows. We wish to compute ![]() $g\doteq f_{xx}$ where we know
$g\doteq f_{xx}$ where we know ![]() $f$ on a mesh with cells
$f$ on a mesh with cells ![]() $I_{j}=[x_{j-1/2},x_{j+1/2}]$. Multiply by some test function
$I_{j}=[x_{j-1/2},x_{j+1/2}]$. Multiply by some test function ![]() $\unicode[STIX]{x1D711}\in {\mathcal{P}}_{j}$, where
$\unicode[STIX]{x1D711}\in {\mathcal{P}}_{j}$, where ![]() ${\mathcal{P}}_{j}$ the function space in cell
${\mathcal{P}}_{j}$ the function space in cell ![]() $I_{j}$ and integrate to get the following weak form,
$I_{j}$ and integrate to get the following weak form,
Where we have replaced ![]() $f$ by the reconstructed function
$f$ by the reconstructed function ![]() $\hat{f}$ in the surface term. Note that we need two reconstructions, one using data in cells
$\hat{f}$ in the surface term. Note that we need two reconstructions, one using data in cells ![]() $I_{j-1},I_{j}$ and the other using data in cells
$I_{j-1},I_{j}$ and the other using data in cells ![]() $I_{j},I_{j+1}$. In the volume term we continue to use
$I_{j},I_{j+1}$. In the volume term we continue to use ![]() $f$ itself and not the left/right reconstructions as the latter are weakly equal to the former and can be replaced without changing the volume term. Once the function space is selected this completely determines
$f$ itself and not the left/right reconstructions as the latter are weakly equal to the former and can be replaced without changing the volume term. Once the function space is selected this completely determines ![]() $g$.
$g$.
Notice that one more integration by parts can be performed in (3.10) to obtain another weak form,
In this form we need to use both the value and first derivative of the reconstructed functions at the cell interfaces. Numerically, each of these weak forms will lead to different update formulas. For example, for piecewise linear basis functions the volume term drops out in (3.11). Also, the properties of each scheme will be different. In fact, as we show in §§ 4 and 5, the second integration by parts is required to ensure momentum and energy conservation.
The procedure outlined above is essentially the recovery discontinuous Galerkin (RDG) scheme first proposed in van Leer & Nomura (Reference van Leer and Nomura2005), van Leer & Lo (Reference van Leer and Lo2007). Extensive study of the properties of the RDG scheme to compute second derivatives is presented in Hakim, Hammett & Shi (Reference Hakim, Hammett and Shi2014) where it is shown that the RDG scheme has some advantages compared to the standard local discontinuous Galerkin schemes (Cockburn & Shu Reference Cockburn and Shu1998) traditionally used to discretize diffusion operators in DG. The formulation in terms of weak equality allows systematic extension to higher dimensions and cross-derivative terms, both of which are needed to discretize the Fokker–Planck operator.
4 The discrete Dougherty Fokker–Planck operator
Although the D-FPO was formulated rather generally in § 2, in order to give a clear explanation of the computational method we will focus, without loss of generality, on the 1V case, that is with one velocity-space dimension and the configuration-space variable effectively appearing as a parameter. The cross-species collision terms are set to zero. This simplified setting is enough to describe the method and the key ideas needed to construct conservative schemes. We have implemented the D-FPO in multiple dimensions, including inter-species collisions, in Gkeyll, and we show multi-dimensional results in § 7.
In the case of a single velocity dimension (![]() $x$ can be thought of as a parameter) the Dougherty FPO is,
$x$ can be thought of as a parameter) the Dougherty FPO is,
where we now refer to ![]() $f_{h}$, the discrete distribution function. This discrete distribution function is the expansion of the distribution function in our corresponding basis set. Here, we are setting
$f_{h}$, the discrete distribution function. This discrete distribution function is the expansion of the distribution function in our corresponding basis set. Here, we are setting ![]() $\unicode[STIX]{x1D708}=1$ (or effectively rescaling the time coordinate by the collision frequency), and note that the drift velocity and thermal speeds are, in general, spatially dependent quantities. We use a DG scheme on a rectangular mesh with cells
$\unicode[STIX]{x1D708}=1$ (or effectively rescaling the time coordinate by the collision frequency), and note that the drift velocity and thermal speeds are, in general, spatially dependent quantities. We use a DG scheme on a rectangular mesh with cells ![]() $\unicode[STIX]{x1D6FA}_{i,j}\equiv [x_{i-1/2},x_{i+1/2}]\times [v_{j-1/2},v_{j+1/2}]$ and select a set of orthonormal basis functions on each cell
$\unicode[STIX]{x1D6FA}_{i,j}\equiv [x_{i-1/2},x_{i+1/2}]\times [v_{j-1/2},v_{j+1/2}]$ and select a set of orthonormal basis functions on each cell ![]() $\unicode[STIX]{x1D713}_{k}(x,v)$, for
$\unicode[STIX]{x1D713}_{k}(x,v)$, for ![]() $k=1,\ldots ,N$:
$k=1,\ldots ,N$:
To construct these basis functions, first a set of monomials is selected and then orthonormalized using the Gram–Schmidt procedure. The monomials are constructed to lie in the serendipity polynomial space (Arnold & Awanou Reference Arnold and Awanou2011) of order ![]() $p$ and dimension
$p$ and dimension ![]() $d$,
$d$, ![]() ${\mathcal{V}}_{d}^{p}$, and are constructed, in two dimensions, as follows
${\mathcal{V}}_{d}^{p}$, and are constructed, in two dimensions, as follows
Where the ![]() $\text{deg}_{2}$ function is defined as the sum of all monomial powers that appear superlinearly. For example,
$\text{deg}_{2}$ function is defined as the sum of all monomial powers that appear superlinearly. For example, ![]() $\text{deg}_{2}(xv^{2})=2$ while
$\text{deg}_{2}(xv^{2})=2$ while ![]() $\text{deg}_{2}(x^{2}v^{2})=4$. This definition works in arbitrary dimensions as shown in Arnold & Awanou (Reference Arnold and Awanou2011). For higher-dimensional systems and for
$\text{deg}_{2}(x^{2}v^{2})=4$. This definition works in arbitrary dimensions as shown in Arnold & Awanou (Reference Arnold and Awanou2011). For higher-dimensional systems and for ![]() $p>1$ the reduction in the number of degrees-of-freedom compared to Lagrange tensor polynomials can be significant. For example, in the five-dimensional
$p>1$ the reduction in the number of degrees-of-freedom compared to Lagrange tensor polynomials can be significant. For example, in the five-dimensional ![]() $p=2$ case there are
$p=2$ case there are ![]() $3^{5}=243$ Lagrange tensor basis functions while there are only
$3^{5}=243$ Lagrange tensor basis functions while there are only ![]() $112$ serendipity basis functions. In general, the cost of the modal DG scheme presented here scales roughly as
$112$ serendipity basis functions. In general, the cost of the modal DG scheme presented here scales roughly as ![]() $N^{2}$ and so the serendipity basis can give
$N^{2}$ and so the serendipity basis can give ![]() $4\times$ cost savings. One could use an even more sparse basis set, for example by using a
$4\times$ cost savings. One could use an even more sparse basis set, for example by using a ![]() $\deg$ function that sums all the monomial powers. In this space,
$\deg$ function that sums all the monomial powers. In this space, ![]() $\text{deg}(xv^{2})=3$. With this, in five dimensions and
$\text{deg}(xv^{2})=3$. With this, in five dimensions and ![]() $p=2$, one would only have 21 basis functions, but we have found that the serendipity basis is a good compromise between efficiency and accuracy. The algorithms presented below do not rely on the specific choice of the basis sets in any case.
$p=2$, one would only have 21 basis functions, but we have found that the serendipity basis is a good compromise between efficiency and accuracy. The algorithms presented below do not rely on the specific choice of the basis sets in any case.
We remark that the configuration space quantities like drift velocity, thermal speed and moments lie in the space ![]() ${\mathcal{V}}_{1}^{p}$ (for the one spatial and one velocity (1X1V) case). The discrete moments are computed using the weak-equality relations
${\mathcal{V}}_{1}^{p}$ (for the one spatial and one velocity (1X1V) case). The discrete moments are computed using the weak-equality relations
on the space ![]() ${\mathcal{V}}_{1}^{p}$. The integrals are taken over all velocity space. The generalization of the function spaces and moment definitions to arbitrary velocity- and configuration-space dimensions is straightforward.
${\mathcal{V}}_{1}^{p}$. The integrals are taken over all velocity space. The generalization of the function spaces and moment definitions to arbitrary velocity- and configuration-space dimensions is straightforward.
A first version of the scheme can be constructed by multiplying the D-FPO by a test function ![]() $w\in {\mathcal{V}}_{2}^{p}$ and, as would be natural for a DG scheme, integrating by parts once. That is we need to find
$w\in {\mathcal{V}}_{2}^{p}$ and, as would be natural for a DG scheme, integrating by parts once. That is we need to find ![]() $f_{h}\in {\mathcal{V}}_{2}^{p}$ such that
$f_{h}\in {\mathcal{V}}_{2}^{p}$ such that
 $$\begin{eqnarray}\displaystyle \int _{\unicode[STIX]{x1D6FA}_{i,j}}w\frac{\unicode[STIX]{x2202}f_{h}}{\unicode[STIX]{x2202}t}\,\text{d}x\,\text{d}v & = & \displaystyle -\int _{x_{i-1/2}}^{x_{i+1/2}}wG(f_{L},f_{R})\,\text{d}x\Bigg|_{v_{j-1/2}}^{v_{j+1/2}}\nonumber\\ \displaystyle & & \displaystyle -\int _{\unicode[STIX]{x1D6FA}_{i,j}}\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}v}\left[(v-u)f_{h}+v_{th}^{2}\frac{\unicode[STIX]{x2202}f_{h}}{\unicode[STIX]{x2202}v}\right]\text{d}x\,\text{d}v.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{\unicode[STIX]{x1D6FA}_{i,j}}w\frac{\unicode[STIX]{x2202}f_{h}}{\unicode[STIX]{x2202}t}\,\text{d}x\,\text{d}v & = & \displaystyle -\int _{x_{i-1/2}}^{x_{i+1/2}}wG(f_{L},f_{R})\,\text{d}x\Bigg|_{v_{j-1/2}}^{v_{j+1/2}}\nonumber\\ \displaystyle & & \displaystyle -\int _{\unicode[STIX]{x1D6FA}_{i,j}}\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}v}\left[(v-u)f_{h}+v_{th}^{2}\frac{\unicode[STIX]{x2202}f_{h}}{\unicode[STIX]{x2202}v}\right]\text{d}x\,\text{d}v.\end{eqnarray}$$ Here, ![]() $G(f_{L},f_{R})$ is the numerical flux written in a penalty form as a function of the solution to the left (
$G(f_{L},f_{R})$ is the numerical flux written in a penalty form as a function of the solution to the left (![]() $f_{L}$) and right (
$f_{L}$) and right (![]() $f_{R}$) of a cell surface
$f_{R}$) of a cell surface
where ![]() $\unicode[STIX]{x1D70F}=\max (|u-v|)$, the maximum computed over the velocity domain at each configuration space cell. The quantity
$\unicode[STIX]{x1D70F}=\max (|u-v|)$, the maximum computed over the velocity domain at each configuration space cell. The quantity ![]() $\hat{f}_{h}$ appearing in the numerical flux is the recovered distribution function and is computed using the weak-equality procedure outlined in § 3. See below for how to determine the discrete drift velocity and thermal speed. The scheme equation (4.7) is called Scheme NC. NC stands for ‘non-conservative’ as is shown below.
$\hat{f}_{h}$ appearing in the numerical flux is the recovered distribution function and is computed using the weak-equality procedure outlined in § 3. See below for how to determine the discrete drift velocity and thermal speed. The scheme equation (4.7) is called Scheme NC. NC stands for ‘non-conservative’ as is shown below.
The velocity space in the FP equation has ![]() $v\in [-\infty ,\infty ]$. In a numerical scheme one must somehow treat this infinite domain in a tractable manner. There are two possible options. First, to assume a form of the distribution function beyond some
$v\in [-\infty ,\infty ]$. In a numerical scheme one must somehow treat this infinite domain in a tractable manner. There are two possible options. First, to assume a form of the distribution function beyond some ![]() $v<v_{\min }$ (
$v<v_{\min }$ (![]() $v>v_{\max }$), and update these ‘half-open’ cells as part of the scheme. The second approach, followed here, is to simply truncate the domain and assume that instead
$v>v_{\max }$), and update these ‘half-open’ cells as part of the scheme. The second approach, followed here, is to simply truncate the domain and assume that instead ![]() $v\in [v_{\min },v_{\max }]$ for some sufficiently small
$v\in [v_{\min },v_{\max }]$ for some sufficiently small ![]() $v_{\min }$ and sufficiently large
$v_{\min }$ and sufficiently large ![]() $v_{\max }$. In this case one must apply boundary conditions by specifying the numerical flux at
$v_{\max }$. In this case one must apply boundary conditions by specifying the numerical flux at ![]() $v_{\min }$ and
$v_{\min }$ and ![]() $v_{\max }$. To ensure that particles are not ‘lost’ to infinity we chose the boundary condition
$v_{\max }$. To ensure that particles are not ‘lost’ to infinity we chose the boundary condition
This ensures that one does not exchange density, momentum or energy with ‘infinity’.
Although Scheme NC seems perfectly reasonable (and would be the natural thing to do based on experience in discretizing hyperbolic equations), in fact, the scheme does not conserve momentum or energy. Density conservation follows on using ![]() $w=1$ as the test function and summing over velocity space and using the boundary conditions, equation (4.9). However, momentum or energy are not conserved. To show the lack of momentum conservation, we choose
$w=1$ as the test function and summing over velocity space and using the boundary conditions, equation (4.9). However, momentum or energy are not conserved. To show the lack of momentum conservation, we choose ![]() $w=v$ in (4.7) and sum over velocity space to obtain,
$w=v$ in (4.7) and sum over velocity space to obtain,
where the continuity of the numerical flux and boundary conditions were used to show the contribution to momentum from surface terms is zero. The first term on the right-hand side vanishes if the discrete moments are computed to satisfy
where ![]() $M_{h,0}$ and
$M_{h,0}$ and ![]() $M_{h,1}$ are the discrete moment operators corresponding to the continuous operators, see (4.4)–(4.5). This condition is discussed in more detail when presenting the conservative scheme in § 5. The second term on the right side of (4.10), on integration by parts, becomes
$M_{h,1}$ are the discrete moment operators corresponding to the continuous operators, see (4.4)–(4.5). This condition is discussed in more detail when presenting the conservative scheme in § 5. The second term on the right side of (4.10), on integration by parts, becomes
where ![]() $f_{h}$ must be evaluated just inside the cell. However, in general,
$f_{h}$ must be evaluated just inside the cell. However, in general, ![]() $f_{h}$ is not continuous so this term will not vanish, and instead pick up the sum of jumps in the distribution function across the velocity direction. Hence, Scheme NC does not conserve momentum. A similar argument with
$f_{h}$ is not continuous so this term will not vanish, and instead pick up the sum of jumps in the distribution function across the velocity direction. Hence, Scheme NC does not conserve momentum. A similar argument with ![]() $w=v^{2}$ shows that Scheme NC does not conserve energy either.
$w=v^{2}$ shows that Scheme NC does not conserve energy either.
The lack of conservation comes about from the gradient in the volume term. This suggests that instead, two integration by parts, as discussed at the end of § 3, should be performed to remove this gradient. That is for ![]() $f_{h}\in {\mathcal{V}}_{2}^{p}$ the weak form describing the second scheme is,
$f_{h}\in {\mathcal{V}}_{2}^{p}$ the weak form describing the second scheme is,
 $$\begin{eqnarray}\displaystyle \int _{\unicode[STIX]{x1D6FA}_{i,j}}w\frac{\unicode[STIX]{x2202}f_{h}}{\unicode[STIX]{x2202}t}\,\text{d}x\,\text{d}v & = & \displaystyle -\int _{x_{i-1/2}}^{x_{i+1/2}}wG(f_{L},f_{R})\,\text{d}x\Bigg|_{v_{j-1/2}}^{v_{j+1/2}}-\int _{x_{i-1/2}}^{x_{i+1/2}}\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}v}v_{th}^{2}\,\hat{f}_{h}\,\text{d}x\Bigg|_{v_{j-1/2}}^{v_{j+1/2}}\nonumber\\ \displaystyle & & \displaystyle -\int _{\unicode[STIX]{x1D6FA}_{i,j}}\left[\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}v}(v-u)f_{h}-\frac{\unicode[STIX]{x2202}^{2}w}{\unicode[STIX]{x2202}v^{2}}v_{th}^{2}\,f_{h}\right]\text{d}x\,\text{d}v,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{\unicode[STIX]{x1D6FA}_{i,j}}w\frac{\unicode[STIX]{x2202}f_{h}}{\unicode[STIX]{x2202}t}\,\text{d}x\,\text{d}v & = & \displaystyle -\int _{x_{i-1/2}}^{x_{i+1/2}}wG(f_{L},f_{R})\,\text{d}x\Bigg|_{v_{j-1/2}}^{v_{j+1/2}}-\int _{x_{i-1/2}}^{x_{i+1/2}}\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}v}v_{th}^{2}\,\hat{f}_{h}\,\text{d}x\Bigg|_{v_{j-1/2}}^{v_{j+1/2}}\nonumber\\ \displaystyle & & \displaystyle -\int _{\unicode[STIX]{x1D6FA}_{i,j}}\left[\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}v}(v-u)f_{h}-\frac{\unicode[STIX]{x2202}^{2}w}{\unicode[STIX]{x2202}v^{2}}v_{th}^{2}\,f_{h}\right]\text{d}x\,\text{d}v,\end{eqnarray}$$ for all ![]() $w\in {\mathcal{V}}_{2}^{p}$. For this scheme, we need to use the recovered distribution function
$w\in {\mathcal{V}}_{2}^{p}$. For this scheme, we need to use the recovered distribution function ![]() $\hat{f}_{h}$ and its derivative at cell boundaries. This scheme is called Scheme C and will be the focus of rest of the paper.
$\hat{f}_{h}$ and its derivative at cell boundaries. This scheme is called Scheme C and will be the focus of rest of the paper.
5 The properties of the discrete Dougherty Fokker–Planck operator. Drift velocity and thermal speed
Having presented the discrete scheme and the motivation for the second integration by parts, we now study its properties. In particular, we examine the scheme’s conservation properties. As we show below the Scheme C described by (4.13) conserves particles as well as momentum and energy. Interestingly, the conditions for conservation also provide recipes to determine the drift velocity and thermal speeds, thus completing the description of the scheme.
Proposition 1 (Discrete Number Density Conservation).
Scheme C conserves number density
Proof. To prove this, use ![]() $w=1$ in (4.13) and sum over all velocity-space cells. Using (4.9) for the boundary conditions at
$w=1$ in (4.13) and sum over all velocity-space cells. Using (4.9) for the boundary conditions at ![]() $v_{\min }$ and
$v_{\min }$ and ![]() $v_{\max }$, and noting that the numerical flux is continuous at cell interfaces in the interior of the domain, makes the surface integrals in the sum over all velocity space a telescopic sum, completing the proof.◻
$v_{\max }$, and noting that the numerical flux is continuous at cell interfaces in the interior of the domain, makes the surface integrals in the sum over all velocity space a telescopic sum, completing the proof.◻
We remark that the sum above, and in all the propositions in this section, is over velocity-space cells as there are no spatial gradients in the FP equation. For the full Vlasov–Maxwell Fokker–Planck equation, however, the sum extends over all of phase space.
Proposition 2 (Discrete Momentum Conservation).
Scheme C conserves momentum
if the following weak-equality relation is satisfied:
Proof. To prove this, use ![]() $w=v$ in (4.13) and sum over all velocity-space cells to get
$w=v$ in (4.13) and sum over all velocity-space cells to get
The contributions from the numerical flux ![]() $G$ drop out due to continuity and boundary conditions. In the first term all interface contributions except the first and last will cancel. Combined with the definition of the discrete moment operators in the second term this leads to the constraint
$G$ drop out due to continuity and boundary conditions. In the first term all interface contributions except the first and last will cancel. Combined with the definition of the discrete moment operators in the second term this leads to the constraint
where ![]() $f_{h}(v_{\max })$ and
$f_{h}(v_{\max })$ and ![]() $f_{h}(v_{\min })$ are the values of the discrete distribution function evaluated at the lower and upper boundaries of velocity space, respectively. Using the definition of weak equality this implies that the momentum will be conserved if (5.3) is satisfied. Notice that the
$f_{h}(v_{\min })$ are the values of the discrete distribution function evaluated at the lower and upper boundaries of velocity space, respectively. Using the definition of weak equality this implies that the momentum will be conserved if (5.3) is satisfied. Notice that the ![]() $\hat{f}_{h}$ was replaced by
$\hat{f}_{h}$ was replaced by ![]() $f_{h}$. At the outer velocity boundaries there is no ‘outside’ cell to allow reconstruction of a distribution function.◻
$f_{h}$. At the outer velocity boundaries there is no ‘outside’ cell to allow reconstruction of a distribution function.◻
The weak-equality constraint, equation (5.3), is stronger than required to satisfy (5.5). However, ensuring that the weak-equality constraint is satisfied automatically ensures that the conditions for momentum conservation are met.
We remark that the first term in (5.3) is generally a small correction for a well-resolved simulation where ![]() $f_{h}$ at the velocity boundaries is small, but it is retained to give exact momentum conservation to within roundoff error. The origin of this term can be understood by looking at momentum conservation with the continuous operator on a finite velocity domain.
$f_{h}$ at the velocity boundaries is small, but it is retained to give exact momentum conservation to within roundoff error. The origin of this term can be understood by looking at momentum conservation with the continuous operator on a finite velocity domain.
Proposition 3 (Discrete Energy Conservation).
Scheme C conserves energy
if the following weak-equality relation is satisfied:
Proof. For this proposition assume that ![]() $p\geqslant 2$ and so
$p\geqslant 2$ and so ![]() $v^{2}\in {\mathcal{V}}_{2}^{p}$. The case of
$v^{2}\in {\mathcal{V}}_{2}^{p}$. The case of ![]() $p=1$ introduces some complexity, dealt with below. To prove the proposition use
$p=1$ introduces some complexity, dealt with below. To prove the proposition use ![]() $w=v^{2}/2$ in (4.13) and sum over all velocity-space cells to obtain,
$w=v^{2}/2$ in (4.13) and sum over all velocity-space cells to obtain,
 $$\begin{eqnarray}\displaystyle \frac{\text{d}}{\text{d}t}\mathop{\sum }_{j}\int _{\unicode[STIX]{x1D6FA}_{i,j}}\frac{1}{2}v^{2}f_{h}\,\text{d}x\,\text{d}v & = & \displaystyle -\mathop{\sum }_{j}\int _{x_{i-1/2}}^{x_{i+1/2}}vv_{th}^{2}\,\hat{f}_{h}\,\text{d}x\Bigg|_{v_{j-1/2}}^{v_{j+1/2}}\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{j}\int _{\unicode[STIX]{x1D6FA}_{i,j}}\left[v(v-u)f_{h}-v_{th}^{2}\,f_{h}\right]\text{d}x\,\text{d}v.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}}{\text{d}t}\mathop{\sum }_{j}\int _{\unicode[STIX]{x1D6FA}_{i,j}}\frac{1}{2}v^{2}f_{h}\,\text{d}x\,\text{d}v & = & \displaystyle -\mathop{\sum }_{j}\int _{x_{i-1/2}}^{x_{i+1/2}}vv_{th}^{2}\,\hat{f}_{h}\,\text{d}x\Bigg|_{v_{j-1/2}}^{v_{j+1/2}}\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{j}\int _{\unicode[STIX]{x1D6FA}_{i,j}}\left[v(v-u)f_{h}-v_{th}^{2}\,f_{h}\right]\text{d}x\,\text{d}v.\end{eqnarray}$$All contributions from interior cell interfaces cancel in the first term. Combined with the definition of the discrete moment operators in the second term leads to the constraint,
Using the definition of weak equality this implies that the energy will be conserved if (5.7) is satisfied.◻
Collecting the constraints needed to satisfy momentum and energy conservation, equations (5.3)–(5.7) can be expressed as a linear system that, on inversion, determines the drift velocity ![]() $u$ and the thermal speed
$u$ and the thermal speed ![]() $v_{th}$ in
$v_{th}$ in ![]() ${\mathcal{V}}_{1}^{p}$, completing the description of the scheme. There are some interesting aspects of this derivation. First, the requirements of discrete momentum and energy conservation lead to unique expressions that determine the drift velocity and thermal speed. This is fundamentally different from other conservative treatments which assume a vanishing distribution function at the boundary (Hirvijoki & Adams Reference Hirvijoki and Adams2017). Second, the boundary conditions in velocity space must be accounted for in the computations. In fact, our first impulse, following experience in discretizing the Vlasov equation, had us expect that energy conservation would follow independent of the boundary conditions. An unexpected result of carefully working through the conservation proofs shows otherwise. Third, in addition to the global conservation of momentum and energy, our discretization of the D-FPO in conservative form via two integrations by parts also guarantees that these quantities are locally conserved.
${\mathcal{V}}_{1}^{p}$, completing the description of the scheme. There are some interesting aspects of this derivation. First, the requirements of discrete momentum and energy conservation lead to unique expressions that determine the drift velocity and thermal speed. This is fundamentally different from other conservative treatments which assume a vanishing distribution function at the boundary (Hirvijoki & Adams Reference Hirvijoki and Adams2017). Second, the boundary conditions in velocity space must be accounted for in the computations. In fact, our first impulse, following experience in discretizing the Vlasov equation, had us expect that energy conservation would follow independent of the boundary conditions. An unexpected result of carefully working through the conservation proofs shows otherwise. Third, in addition to the global conservation of momentum and energy, our discretization of the D-FPO in conservative form via two integrations by parts also guarantees that these quantities are locally conserved.
The energy conservation proof above requires ![]() $p\geqslant 2$. In the the case of
$p\geqslant 2$. In the the case of ![]() $p=1$, instead, a projected energy is conserved. To see this, first observe that the definition of discrete particle energy is
$p=1$, instead, a projected energy is conserved. To see this, first observe that the definition of discrete particle energy is
Using the idea of weak equality, we see that this integral is unchanged if we replace ![]() $v^{2}$ with another function that is weakly equal to it. For use in energy conservation we will choose the projection on the basis set, that is
$v^{2}$ with another function that is weakly equal to it. For use in energy conservation we will choose the projection on the basis set, that is ![]() $\overline{v^{2}}\in {\mathcal{V}}_{2}^{1}$ defined such that
$\overline{v^{2}}\in {\mathcal{V}}_{2}^{1}$ defined such that
A simple calculation shows that the function ![]() $\overline{v^{2}}$ is continuous. With this definition of projected
$\overline{v^{2}}$ is continuous. With this definition of projected ![]() $v^{2}$ we can now state the following proposition that leads to an analogous weak-equality relation as (5.7).
$v^{2}$ we can now state the following proposition that leads to an analogous weak-equality relation as (5.7).
Proposition 4 (Discrete Energy Conservation,  $p=1$ case).
$p=1$ case).
Scheme C conserves energy
if the following weak-equality relation is satisfied:
where ![]() $\check{v}_{j}=(v_{j+1/2}+v_{j-1/2})/2$ is the cell-centre velocity coordinate. The ‘star moments’
$\check{v}_{j}=(v_{j+1/2}+v_{j-1/2})/2$ is the cell-centre velocity coordinate. The ‘star moments’ ![]() $M_{h,k}^{\ast }$ are defined below.
$M_{h,k}^{\ast }$ are defined below.
Proof. As ![]() $v^{2}/2$ does not belong in
$v^{2}/2$ does not belong in ![]() ${\mathcal{V}}_{2}^{1}$ we use its projection to show energy conservation. That is, we use
${\mathcal{V}}_{2}^{1}$ we use its projection to show energy conservation. That is, we use ![]() $w=\overline{v^{2}}/2$, see (5.11). With this choice we can show that
$w=\overline{v^{2}}/2$, see (5.11). With this choice we can show that
Setting ![]() $w=\overline{v^{2}}/2$ in (4.13) and summing over all velocity-space cells we obtain,
$w=\overline{v^{2}}/2$ in (4.13) and summing over all velocity-space cells we obtain,
As before, the contribution from the numerical flux term drops out as ![]() $\overline{v^{2}}/2$ is continuous. However, since
$\overline{v^{2}}/2$ is continuous. However, since ![]() $\check{v}_{j}$ is not continuous the contributions from the first term above cannot be eliminated. This result can be written as,
$\check{v}_{j}$ is not continuous the contributions from the first term above cannot be eliminated. This result can be written as,
where ![]() $\unicode[STIX]{x0394}v_{j}=\check{v}_{j+1}-\check{v}_{j}$ and
$\unicode[STIX]{x0394}v_{j}=\check{v}_{j+1}-\check{v}_{j}$ and ![]() $j\neq \pm j_{\max }$ is taken to mean that the sum excludes the first and last
$j\neq \pm j_{\max }$ is taken to mean that the sum excludes the first and last ![]() $j$ indices. Defining the ‘star moments’ as,
$j$ indices. Defining the ‘star moments’ as,
and using the definition of weak equality, the projected energy will be conserved in the ![]() $p=1$ case if (5.13) is satisfied.◻
$p=1$ case if (5.13) is satisfied.◻
In summary, for the ![]() $p=1$ case the drift velocity and thermal speed must be determined using the simultaneous set of weak-equality relations in (5.3)–(5.13). In this case, one must compute the discrete star moments and the regular moments (except for
$p=1$ case the drift velocity and thermal speed must be determined using the simultaneous set of weak-equality relations in (5.3)–(5.13). In this case, one must compute the discrete star moments and the regular moments (except for ![]() $M_{h,2}$).
$M_{h,2}$).
We remark that we have not managed to analytically show that the discrete operator increases entropy, although, as shown in the benchmarks section, all our simulations increase entropy monotonically. Part of the difficulty is computing ![]() $w\doteq \ln f_{h}$ and its needed gradients. Also, the proof of the self-adjoint property (which we have not yet worked out for the general DG algorithm) requires the definition of a ‘discrete Maxwellian’ for use in the appropriate inner-product norm.
$w\doteq \ln f_{h}$ and its needed gradients. Also, the proof of the self-adjoint property (which we have not yet worked out for the general DG algorithm) requires the definition of a ‘discrete Maxwellian’ for use in the appropriate inner-product norm.
Finally, we remark that the scheme and proofs above are for the 1X1V case but the extension to multiple dimensions is straightforward. The extension of the conservative scheme to cross-species collisions is much more involved and requires carefully computing the intermediate velocities and thermal speeds while taking into account finite boundary effects. In addition, there are some issues in ensuring that the intermediate temperatures remain positive (even in the continuous case) and we will discuss these in a future publication.
6 Time stepping and stability
The focus of this paper is on the spatial discretization of the Fokker–Planck operator and showing that a carefully constructed scheme is conservative. The issue of time stepping is a complex one, especially as the FPO is diffusive and hence for efficient evolutions (when the collision frequency is high) requires some implicit or accelerated time-stepping scheme. As we are focused on the spatial scheme, for the results presented in the benchmark sections we use an explicit three-stage strong-stability preserving Runge–Kutta third-order scheme (Shu Reference Shu2002). Exploring more complex time steppers is left to a future study. The time step is selected such that ![]() $\unicode[STIX]{x1D706}_{\max }\unicode[STIX]{x0394}t$ is small enough that the solutions are stable, where the maximum eigenvalue of the discretized collision operator scales approximately as
$\unicode[STIX]{x1D706}_{\max }\unicode[STIX]{x0394}t$ is small enough that the solutions are stable, where the maximum eigenvalue of the discretized collision operator scales approximately as ![]() $\unicode[STIX]{x1D706}_{\max }\sim \unicode[STIX]{x1D708}((v_{\max }+|u|)/(\unicode[STIX]{x0394}v)+v_{th}^{2}/(\unicode[STIX]{x0394}v)^{2})$. The issue of stability for the full Vlasov–Maxwell Fokker–Planck equation is complex and will be addressed in a paper on discretizing the gyrokinetic version of the operator (Francisquez et al. Reference Francisquez, Bernard, Mandell, Hammett and Hakim2020).
$\unicode[STIX]{x1D706}_{\max }\sim \unicode[STIX]{x1D708}((v_{\max }+|u|)/(\unicode[STIX]{x0394}v)+v_{th}^{2}/(\unicode[STIX]{x0394}v)^{2})$. The issue of stability for the full Vlasov–Maxwell Fokker–Planck equation is complex and will be addressed in a paper on discretizing the gyrokinetic version of the operator (Francisquez et al. Reference Francisquez, Bernard, Mandell, Hammett and Hakim2020).
7 Benchmark problems
The algorithms presented above are being used in production simulations with the Gkeyll code. For example, recent work has employed our collision operator implementation in exploring electrostatic shocks (Sundström et al. Reference Sundström, Juno, TenBarge and Pusztai2019) and six-dimensional kinetic dynamo physics (Pusztai et al. Reference Pusztai, Juno, Brandenburg, TenBarge, Hakim, Francisquez and Sundström2020). An earlier version of the scheme was applied to gyrokinetic equations and was used to study plasma turbulence in straight and helical field-line geometries (Shi Reference Shi2017; Shi et al. Reference Shi, Hammett, Stoltzfus-Dueck and Hakim2017, Reference Shi, Hammett, Stoltzfus-Dueck and Hakim2019), including comparison with experiments (Bernard et al. Reference Bernard, Shi, Gentle, Hakim, Hammett, Stoltzfus-Dueck and Taylor2019). In this section we present benchmark problems that allow testing of the scheme in simpler settings, in particular, paying attention to the conservation properties and the ability of the scheme to reproduce results known analytically or with other schemes. Benchmarks of a similar nature can be found throughout the literature, for example in Pezzi, Valentini & Veltri (Reference Pezzi, Valentini and Veltri2015) for a Dougherty operator and in Belli & Candy (Reference Belli and Candy2017) for advanced operators. Our tests are arranged in increasing order of complexity. First, we benchmark just the collision operator with spatially homogeneous relaxation problems. Next, we introduce streaming terms and study shocks in a neutral gas. We then turn to electrostatic plasma problem and benchmark the scheme with collisional Landau damping. Finally, as an application of the full Vlasov–Maxwell–Fokker–Planck equation we study plasma heating due to ‘magnetic pumping’, a process that converts electromagnetic wave energy into heating via pitch-angle scattering. The numerical treatment of the collisionless terms is discussed in Juno et al. (Reference Juno, Hakim, TenBarge, Shi and Dorland2018) and Hakim & Juno (Reference Hakim and Juno2020). Our algorithm for collisionless terms does not at present conserve momentum. Hence, for the tests that include the collisionless terms only energy conservation is achieved. Developing a fully conservative scheme is difficult and a topic of ongoing research. We also note that in our full-![]() $f$ formulation the energy contributions from the collisionless and collision terms do not interact except via moments and boundaries. However, the moments needed in each operator are computed independently and the boundary conditions are independent also, hence, as each operator by itself conserves energy the full algorithm also conserves energy. Note that although higher than
$f$ formulation the energy contributions from the collisionless and collision terms do not interact except via moments and boundaries. However, the moments needed in each operator are computed independently and the boundary conditions are independent also, hence, as each operator by itself conserves energy the full algorithm also conserves energy. Note that although higher than ![]() $p=2$ order implementations are available in Gkeyll, our benchmarks below focus on
$p=2$ order implementations are available in Gkeyll, our benchmarks below focus on ![]() $p=1,2$ as those are the most practical for the five- and six-dimensional applications we are interested in, as otherwise the number of basis functions in each cell becomes prohibitively large.
$p=1,2$ as those are the most practical for the five- and six-dimensional applications we are interested in, as otherwise the number of basis functions in each cell becomes prohibitively large.
7.1 Relaxation to discrete Maxwellian
In the absence of streaming and body forces, any initial distribution function will quickly relax to a Maxwellian. This is evident as the Fokker–Planck operator increases entropy and the maximum entropy solution is the Maxwellian; see (B 2)–(B 8). A subtle point is that, on a discrete velocity grid, the relaxed distribution function is by definition the discrete Maxwellian. One may at first sight be tempted to define a ‘discrete Maxwellian’ as the projection of (B 9) onto basis functions. However, the derivation that led to (B 9) assumed a continuous and infinite velocity domain. Hence, if the derivation is repeated with the specific form of the discrete scheme, the ‘discrete Maxwellian’ will not be the same as the projection of (B 9), although they will converge towards each other as the grid is refined. In fact, this relaxation process, rather than projection, can be used to define a discrete Maxwellian for use in initializing other simulations.

Figure 2. (a) Relative change in energy for ![]() $p=1$,
$p=1$, ![]() $N=16$ (solid and dashed blue) and
$N=16$ (solid and dashed blue) and ![]() $p=2$,
$p=2$, ![]() $N=8$ (dotted and dash-dot orange) cases for relaxation of a square distribution to a discrete Maxwellian. The energy drop in our conservative scheme is at machine precision. The curves labelled ‘no conservation’ omit the boundary correction terms and use regular moments instead of ‘star moments’ (for
$N=8$ (dotted and dash-dot orange) cases for relaxation of a square distribution to a discrete Maxwellian. The energy drop in our conservative scheme is at machine precision. The curves labelled ‘no conservation’ omit the boundary correction terms and use regular moments instead of ‘star moments’ (for ![]() $p=1$) needed for momentum and energy conservation. (b) Time history of relative change in entropy. When using the conservative scheme the entropy rapidly increases and remains constant once the distribution function becomes a discrete Maxwellian.
$p=1$) needed for momentum and energy conservation. (b) Time history of relative change in entropy. When using the conservative scheme the entropy rapidly increases and remains constant once the distribution function becomes a discrete Maxwellian.
In this test the relaxation of an initial non-Maxwellian distribution function to a discrete Maxwellian, due to collisions, is studied by solving (4.1). The initial distribution function is a step function in velocity space
where ![]() $v_{0}=\sqrt{3}v_{th}$. Piecewise linear and quadratic basis sets on 16 and 8 velocity-space cells, respectively, were used. Velocity extents (
$v_{0}=\sqrt{3}v_{th}$. Piecewise linear and quadratic basis sets on 16 and 8 velocity-space cells, respectively, were used. Velocity extents (![]() $v_{\min },v_{\max }$) were placed at
$v_{\min },v_{\max }$) were placed at ![]() $\pm 6$ and the simulation was run to
$\pm 6$ and the simulation was run to ![]() $\unicode[STIX]{x1D708}t=5$. In each case the relative changes in density and energy are at machine precision, showing excellent conservation properties of the scheme. See figure (2) in which the time history of the error in normalized energy change is plotted. The errors per step of the conservative scheme are machine precision. The small change in energy is due to the damping in the strong-stability preserving Runge–Kutta third order scheme (SSP-RK3). Changing resolution or polynomial has little impact on the magnitude of energy errors, and they always remain close to machine precision. The figure also shows that, as the distribution function relaxes, the entropy rapidly increases and then remains constant once the discrete Maxwellian state is obtained. The change in entropy between the
$\unicode[STIX]{x1D708}t=5$. In each case the relative changes in density and energy are at machine precision, showing excellent conservation properties of the scheme. See figure (2) in which the time history of the error in normalized energy change is plotted. The errors per step of the conservative scheme are machine precision. The small change in energy is due to the damping in the strong-stability preserving Runge–Kutta third order scheme (SSP-RK3). Changing resolution or polynomial has little impact on the magnitude of energy errors, and they always remain close to machine precision. The figure also shows that, as the distribution function relaxes, the entropy rapidly increases and then remains constant once the discrete Maxwellian state is obtained. The change in entropy between the ![]() $p=1$ and
$p=1$ and ![]() $p=2$ is indicative of the fact that different discrete Maxwellians will be obtained depending on grid resolution and polynomial order. The same figure shows that neglecting the boundary corrections and ‘star moments’ (for
$p=2$ is indicative of the fact that different discrete Maxwellians will be obtained depending on grid resolution and polynomial order. The same figure shows that neglecting the boundary corrections and ‘star moments’ (for ![]() $p=1$) needed for conservation degrades energy conservation by many orders of magnitude, and in the case of
$p=1$) needed for conservation degrades energy conservation by many orders of magnitude, and in the case of ![]() $p=1$ can even lead to decreasing entropy. Note that this is not a good test for momentum conservation as the initial momentum is zero.
$p=1$ can even lead to decreasing entropy. Note that this is not a good test for momentum conservation as the initial momentum is zero.

Figure 3. Initial (a) and relaxed (b) distribution function in 1X2V relaxation test. Conservation (c) of energy (orange) and momentum (green, purple) is at machine precision for the Scheme C. Neglecting boundary corrections breaks conservation by more than 8 orders of magnitude. Purple and green curves overlay each other on this scale. (d) Entropy increases rapidly and then remains constant once the discrete Maxwellian is obtained.
Now consider the relaxation in a 1X2V setting. For this the initial condition is selected as a sum of two Maxwellians, the first with drift velocity ![]() $\boldsymbol{u}=(3,0)$ and the second with drift velocity
$\boldsymbol{u}=(3,0)$ and the second with drift velocity ![]() $\boldsymbol{u}=(0,3)$. Both Maxwellians have a thermal speed of
$\boldsymbol{u}=(0,3)$. Both Maxwellians have a thermal speed of ![]() $1/2$. A
$1/2$. A ![]() $16\times 16$ grid with
$16\times 16$ grid with ![]() $p=2$ serendipity basis functions is used. As the particles collide the distribution function will relax to a drifting Maxwellian. The simulation is run to
$p=2$ serendipity basis functions is used. As the particles collide the distribution function will relax to a drifting Maxwellian. The simulation is run to ![]() $\unicode[STIX]{x1D708}t=5$. Figure 3 shows the initial and final distribution functions demonstrating the relaxation to the discrete Maxwellian. The errors in energy and the
$\unicode[STIX]{x1D708}t=5$. Figure 3 shows the initial and final distribution functions demonstrating the relaxation to the discrete Maxwellian. The errors in energy and the ![]() $x$- and
$x$- and ![]() $y$-components of momentum are machine precision when using Scheme C. Neglecting boundary correction terms degrades conservation by many orders of magnitude. Also, the entropy increases monotonically, reaching its steady-state value once the discrete Maxwellian is obtained. These tests demonstrate the high accuracy with which the moments are conserved as well as provide empirical evidence that entropy is a non-decreasing function of time.
$y$-components of momentum are machine precision when using Scheme C. Neglecting boundary correction terms degrades conservation by many orders of magnitude. Also, the entropy increases monotonically, reaching its steady-state value once the discrete Maxwellian is obtained. These tests demonstrate the high accuracy with which the moments are conserved as well as provide empirical evidence that entropy is a non-decreasing function of time.
7.2 Kinetic Sod-shock problems
Consider a neutral gas. The physics is described by the Boltzmann equation, in which the particles stream freely between collisions. Physically accurate solutions require modelling of the collisions as ‘hard-sphere’ or large-angle collisions. However, the Fokker–Planck operator, modelling small-angle collisions, can still be used to test mathematically the convergence of the solution to Euler equations as the mean free path is reduced. (In the collisional limit the transport coefficients computed from the full Boltzmann collision operator will differ somewhat from those computed from the FPO. However, in this test we are not concerned with physically accurate transport coefficients but simply a mathematically interesting test problem). In this benchmark we solve
using the algorithms developed above to study the shock structure in the kinetic regime while at the same time testing the coupling to the collisionless advection term. This additional term is treated with the same algorithm as the drag term of the D-FPO. We select the classic Sod-shock initial conditions
 $$\begin{eqnarray}\left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D70C}_{l}\\ u_{l}\\ p_{l}\end{array}\right]=\left[\begin{array}{@{}c@{}}1\\ 0.0\\ 1.0\end{array}\right],\quad \left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D70C}_{r}\\ u_{r}\\ p_{r}\end{array}\right]=\left[\begin{array}{@{}c@{}}0.125\\ 0.0\\ 0.1\end{array}\right]\end{eqnarray}$$
$$\begin{eqnarray}\left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D70C}_{l}\\ u_{l}\\ p_{l}\end{array}\right]=\left[\begin{array}{@{}c@{}}1\\ 0.0\\ 1.0\end{array}\right],\quad \left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D70C}_{r}\\ u_{r}\\ p_{r}\end{array}\right]=\left[\begin{array}{@{}c@{}}0.125\\ 0.0\\ 0.1\end{array}\right]\end{eqnarray}$$ on a domain ![]() $[0,L]\times [-6v_{th,l},6v_{th,l}]$ with
$[0,L]\times [-6v_{th,l},6v_{th,l}]$ with ![]() $v_{th,l}=p_{l}/\unicode[STIX]{x1D70C}_{l}$ and the initial discontinuity located at
$v_{th,l}=p_{l}/\unicode[STIX]{x1D70C}_{l}$ and the initial discontinuity located at ![]() $x=L/2$. Note that for this 1X1V system, the gas adiabatic constant is
$x=L/2$. Note that for this 1X1V system, the gas adiabatic constant is ![]() $\unicode[STIX]{x1D6FE}=3$. This is because the internal energy is
$\unicode[STIX]{x1D6FE}=3$. This is because the internal energy is ![]() $p/(\unicode[STIX]{x1D6FE}-1)=\unicode[STIX]{x1D70C}v_{th}^{2}/2$, which means
$p/(\unicode[STIX]{x1D6FE}-1)=\unicode[STIX]{x1D70C}v_{th}^{2}/2$, which means ![]() $\unicode[STIX]{x1D6FE}=3$. The simulations were run on a
$\unicode[STIX]{x1D6FE}=3$. The simulations were run on a ![]() $64\times 16$ grid, with piecewise polynomial order-2 elements,
$64\times 16$ grid, with piecewise polynomial order-2 elements, ![]() $L=1$ and
$L=1$ and ![]() $t_{\text{end}}=0.1$. The Knudsen number (
$t_{\text{end}}=0.1$. The Knudsen number (![]() $\mathit{Kn}=\unicode[STIX]{x1D706}_{\text{mfp}}/L$ and
$\mathit{Kn}=\unicode[STIX]{x1D706}_{\text{mfp}}/L$ and ![]() $\unicode[STIX]{x1D708}=v_{th}/\unicode[STIX]{x1D706}_{\text{mfp}}$) is
$\unicode[STIX]{x1D708}=v_{th}/\unicode[STIX]{x1D706}_{\text{mfp}}$) is ![]() $1/10$,
$1/10$, ![]() $1/100$ and
$1/100$ and ![]() $1/500$. In the first case, the gas is collisionless on the time scale of the simulation, and in the last case, the gas is highly collisional. Hence, in the last case the solution should match, approximately, the solution from the Euler equations.
$1/500$. In the first case, the gas is collisionless on the time scale of the simulation, and in the last case, the gas is highly collisional. Hence, in the last case the solution should match, approximately, the solution from the Euler equations.

Figure 4. Density (a), velocity (b), temperature (c) and heat flux (d) from a Sod-shock problem. Plotted are results with Knudsen numbers of ![]() $1/10$ (red),
$1/10$ (red), ![]() $1/100$ (magenta) and
$1/100$ (magenta) and ![]() $1/500$ (blue) with the inviscid Euler results (black dashed) shown for comparison. As the gas becomes more collisional (decreasing Knudsen number) the solutions tend to the Euler result. Note that there is no heat flux in the inviscid limit.
$1/500$ (blue) with the inviscid Euler results (black dashed) shown for comparison. As the gas becomes more collisional (decreasing Knudsen number) the solutions tend to the Euler result. Note that there is no heat flux in the inviscid limit.
Figure 4 shows the density, velocity, temperature and heat flux (![]() $q\equiv \int _{-\infty }^{\infty }(v-u)^{3}\,f_{s}(x,v,t)\,\text{d}v$) obtained from kinetic simulations. For comparison, the exact solution to the corresponding Euler Riemann problem is also shown. It is observed, as expected, that as the gas becomes more collisional the moments tend to the Euler solution. Interesting aspects of the kinetic results, however, are the viscosity, heat conductivity and other transport effects. The impact of these are seen in the smoothing out of the shock structures that are sharp in the Euler solution. In particular, the lower-right plot shows the heat flux, completely absent in the inviscid equations. There is significant heat flux in the low collisionality case, but this reduces as the collisionality increases.
$q\equiv \int _{-\infty }^{\infty }(v-u)^{3}\,f_{s}(x,v,t)\,\text{d}v$) obtained from kinetic simulations. For comparison, the exact solution to the corresponding Euler Riemann problem is also shown. It is observed, as expected, that as the gas becomes more collisional the moments tend to the Euler solution. Interesting aspects of the kinetic results, however, are the viscosity, heat conductivity and other transport effects. The impact of these are seen in the smoothing out of the shock structures that are sharp in the Euler solution. In particular, the lower-right plot shows the heat flux, completely absent in the inviscid equations. There is significant heat flux in the low collisionality case, but this reduces as the collisionality increases.

Figure 5. Density (a), velocity (b) and distribution function (c) for Sod-shock problem with sonic point in rarefaction. Complicated shock structures are formed and are visible both in the moments as well as the distribution function.

Figure 6. Relative change in momentum (a) and energy (b) for ![]() $p=1$ (blue) and
$p=1$ (blue) and ![]() $p=2$ (orange) cases for Sod-shock problem with sonic point in rarefaction. The conservative scheme sees momentum and energy machine precision errors that are nearly independent of polynomial order and only depends on the number of time steps taken in each simulation. Neglecting corrections needed for conservation leads to errors orders of magnitude greater.
$p=2$ (orange) cases for Sod-shock problem with sonic point in rarefaction. The conservative scheme sees momentum and energy machine precision errors that are nearly independent of polynomial order and only depends on the number of time steps taken in each simulation. Neglecting corrections needed for conservation leads to errors orders of magnitude greater.
We next consider a Sod shock with a sonic point in the rarefaction wave. The initial conditions are selected as
 $$\begin{eqnarray}\left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D70C}_{l}\\ u_{l}\\ p_{l}\end{array}\right]=\left[\begin{array}{@{}c@{}}1\\ 0.75\\ 1.0\end{array}\right],\quad \left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D70C}_{r}\\ u_{r}\\ p_{r}\end{array}\right]=\left[\begin{array}{@{}c@{}}0.125\\ 0.0\\ 0.1\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}\left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D70C}_{l}\\ u_{l}\\ p_{l}\end{array}\right]=\left[\begin{array}{@{}c@{}}1\\ 0.75\\ 1.0\end{array}\right],\quad \left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D70C}_{r}\\ u_{r}\\ p_{r}\end{array}\right]=\left[\begin{array}{@{}c@{}}0.125\\ 0.0\\ 0.1\end{array}\right].\end{eqnarray}$$ In contrast to the standard Sod shock, this problem is run on a periodic domain ![]() $[-1,1]$ with the ‘left’ state applied for
$[-1,1]$ with the ‘left’ state applied for ![]() $|x|<0.3$. The Knudsen number is
$|x|<0.3$. The Knudsen number is ![]() $1/200$ and the simulation is run to
$1/200$ and the simulation is run to ![]() $t=0.1$. As the domain is periodic, the total momentum and energy should remain constant, allowing testing conservation properties in more complex setting. Note that the net momentum is not zero in this problem and hence allows testing of momentum conservation in a more complex setting than the relaxation test.
$t=0.1$. As the domain is periodic, the total momentum and energy should remain constant, allowing testing conservation properties in more complex setting. Note that the net momentum is not zero in this problem and hence allows testing of momentum conservation in a more complex setting than the relaxation test.
Figure 5 shows the density, velocity and distribution function at ![]() $t=0.1$. Complex shock structures are visible both in the moments and the distribution function. Figure 6 shows the errors in momentum and energy as a function of time for the
$t=0.1$. Complex shock structures are visible both in the moments and the distribution function. Figure 6 shows the errors in momentum and energy as a function of time for the ![]() $p=1$ and
$p=1$ and ![]() $p=2$ cases. In each the errors are close to machine precision when using our conservative scheme, while neglecting boundary corrections and using regular moments instead of ‘star moments’ (for
$p=2$ cases. In each the errors are close to machine precision when using our conservative scheme, while neglecting boundary corrections and using regular moments instead of ‘star moments’ (for ![]() $p=1$) leads to errors many orders of magnitude greater. Interestingly, the errors seem independent of polynomial order and only depend on the number of time steps taken in the simulations. These tests demonstrate that, even with the streaming terms, the conservation properties of the scheme are excellent. Further, as the collisionality is increased we correctly obtain the inviscid Euler solutions as expected.
$p=1$) leads to errors many orders of magnitude greater. Interestingly, the errors seem independent of polynomial order and only depend on the number of time steps taken in the simulations. These tests demonstrate that, even with the streaming terms, the conservation properties of the scheme are excellent. Further, as the collisionality is increased we correctly obtain the inviscid Euler solutions as expected.
7.3 Collisional Landau damping

Figure 7. Field energy (a) as a function of time for linear collisional Landau damping problem with varying collisionality. The damping rates (b) are computed as the slope of the decaying electric field energy. The black dashed lined in (b) shows an analytical estimate of the damping rate computed from expressions found in Anderson & O’Neil (Reference Anderson and O’Neil2007) and agree well with the results computed here.
Landau damping is the process of damping of electrostatic plasma waves in a collisionless plasma. It is usually studied in the setting of the collisionless Vlasov–Poisson equations. However, collisions can significantly change the damping rate and, in the limit of high collisionality, the damping can be ‘shut off’. This happens when the mean free path becomes shorter than the wavelength, preventing the particles from resonating with the wave and gaining energy before being scattered via collisions.
In this test the ability of the algorithm to capture the phenomena of collisional Landau damping is shown. The Vlasov–Fokker–Planck equation is coupled to Maxwell’s equations to advance the electric field that in turn is used in the Lorentz force to update the distribution function. That is, we solve
where normalized units have been employed, the current density ![]() $J=M_{h,1}$ (see (4.5)) in these units and Ampere’s law (7.6) is solved in a manner consistent with Poisson’s equation so the simulation remains electrostaticFootnote 1. The electrons are initialized with a perturbed Maxwellian given by
$J=M_{h,1}$ (see (4.5)) in these units and Ampere’s law (7.6) is solved in a manner consistent with Poisson’s equation so the simulation remains electrostaticFootnote 1. The electrons are initialized with a perturbed Maxwellian given by
where ![]() $k$ is the wavenumber, with
$k$ is the wavenumber, with ![]() $k\unicode[STIX]{x1D706}_{De}=kv_{te}/\unicode[STIX]{x1D714}_{pe}=0.5$ and where
$k\unicode[STIX]{x1D706}_{De}=kv_{te}/\unicode[STIX]{x1D714}_{pe}=0.5$ and where ![]() $\unicode[STIX]{x1D6FC}$ is the magnitude of the perturbation. Periodic boundary conditions are imposed in configuration space, and the velocity domain is restricted to
$\unicode[STIX]{x1D6FC}$ is the magnitude of the perturbation. Periodic boundary conditions are imposed in configuration space, and the velocity domain is restricted to ![]() $[-6v_{te},6v_{te}]$. The ion density is set to
$[-6v_{te},6v_{te}]$. The ion density is set to ![]() $n_{i}(x)=1$ and is held fixed. To compute the damping rate the decay of the electric field energy is tracked. Figure 7 shows the electric field energy as a function of time for
$n_{i}(x)=1$ and is held fixed. To compute the damping rate the decay of the electric field energy is tracked. Figure 7 shows the electric field energy as a function of time for ![]() $\unicode[STIX]{x1D708}=0,0.25$ and
$\unicode[STIX]{x1D708}=0,0.25$ and ![]() $1.0$. The collisionless damping rates compare well with exact analytical theory. As the collision frequency increases the damping rate decreases rapidly in the moderate collision frequency limit, as seen in panel (b). Although collisionless Landau damping is very well studied, analytical results in the collisional case are harder to come by. Part of the issue is that in this case the linearized Vlasov–Poisson–Fokker–Planck equation becomes a differential equation in velocity space, needing careful treatment. In Anderson & O’Neil (Reference Anderson and O’Neil2007) a collision operator similar to the one presented here is used to derive analytical estimates of the damping rates as a function of collision frequency, although they consider the 1X3V case and here we are doing the 1X1V case so the results are not expected to exactly match. Nevertheless, a fit to the slope in the intermediate collisionality transition regime from the theory in Anderson & O’Neil (Reference Anderson and O’Neil2007) (shown in the black dashed line in figure 7) shows reasonable agreement with the numerical results here.
$1.0$. The collisionless damping rates compare well with exact analytical theory. As the collision frequency increases the damping rate decreases rapidly in the moderate collision frequency limit, as seen in panel (b). Although collisionless Landau damping is very well studied, analytical results in the collisional case are harder to come by. Part of the issue is that in this case the linearized Vlasov–Poisson–Fokker–Planck equation becomes a differential equation in velocity space, needing careful treatment. In Anderson & O’Neil (Reference Anderson and O’Neil2007) a collision operator similar to the one presented here is used to derive analytical estimates of the damping rates as a function of collision frequency, although they consider the 1X3V case and here we are doing the 1X1V case so the results are not expected to exactly match. Nevertheless, a fit to the slope in the intermediate collisionality transition regime from the theory in Anderson & O’Neil (Reference Anderson and O’Neil2007) (shown in the black dashed line in figure 7) shows reasonable agreement with the numerical results here.
7.4 Heating via magnetic pumping
In the final test we combine the D-FPO with the collisionless, electromagnetic Vlasov equation and Maxwell’s equations to study a heating mechanism called magnetic pumping, and an additional viscous mechanism in this parameter regime. In magnetic pumping, oscillations of the magnetic field are converted to particle energy. Magnetic pumping relies on the approximate conservation of magnetic moment, ![]() $\unicode[STIX]{x1D707}=mv_{\bot }^{2}/2B$ in a strong magnetic field. As the magnetic field increases, to maintain magnetic moment conservation,
$\unicode[STIX]{x1D707}=mv_{\bot }^{2}/2B$ in a strong magnetic field. As the magnetic field increases, to maintain magnetic moment conservation, ![]() $v_{\bot }^{2}$ should also increase. In a collisionless system, if the magnetic field is oscillating slowly compared to the gyro-period, then
$v_{\bot }^{2}$ should also increase. In a collisionless system, if the magnetic field is oscillating slowly compared to the gyro-period, then ![]() $v_{\bot }^{2}$ oscillates up and down in a reversible way and there is no net heating of the plasma. However, collisions can provide a route to ‘pitch-angle scatter’ the energy into the parallel direction, leading to an overall irreversible heating of the plasma. This mechanism was originally proposed by Spitzer in the early days of fusion research, and investigated extensively (Berger et al. Reference Berger, Newcomb, Dawson, Frieman, Kulsrud and Lenard1958; Laroussi & Roth Reference Laroussi and Roth1989). Recently, this same mechanism was investigated as a potential source of particle heating in the solar wind (Lichko et al. Reference Lichko, Egedal, Daughton and Kasper2017). We use a similar set-up as Lichko et al. (Reference Lichko, Egedal, Daughton and Kasper2017), with some parameters chosen differently. The study in Lichko et al. (Reference Lichko, Egedal, Daughton and Kasper2017) used a full Coulomb operator evolved with a Monte–Carlo method implemented in a particle-in-cell code. Here, we used the simplified form of the Dougherty FPO. Even though this is simpler than the Coulomb operator it contains enough physics to study the mechanism of magnetic pumping, and demonstrates that our algorithm works robustly in a complex plasma problem.
$v_{\bot }^{2}$ oscillates up and down in a reversible way and there is no net heating of the plasma. However, collisions can provide a route to ‘pitch-angle scatter’ the energy into the parallel direction, leading to an overall irreversible heating of the plasma. This mechanism was originally proposed by Spitzer in the early days of fusion research, and investigated extensively (Berger et al. Reference Berger, Newcomb, Dawson, Frieman, Kulsrud and Lenard1958; Laroussi & Roth Reference Laroussi and Roth1989). Recently, this same mechanism was investigated as a potential source of particle heating in the solar wind (Lichko et al. Reference Lichko, Egedal, Daughton and Kasper2017). We use a similar set-up as Lichko et al. (Reference Lichko, Egedal, Daughton and Kasper2017), with some parameters chosen differently. The study in Lichko et al. (Reference Lichko, Egedal, Daughton and Kasper2017) used a full Coulomb operator evolved with a Monte–Carlo method implemented in a particle-in-cell code. Here, we used the simplified form of the Dougherty FPO. Even though this is simpler than the Coulomb operator it contains enough physics to study the mechanism of magnetic pumping, and demonstrates that our algorithm works robustly in a complex plasma problem.
For this benchmark we thus solved the following normalized system of Vlasov–Fokker–Planck equations for electrons and ions, and Maxwell’s equations:
in a four-dimensional domain with one spatial dimension but three velocity dimensions (1X3V) that has extent ![]() $[0,200\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{e}]\times [-8v_{th,s},8v_{th,s}]^{3}$ on a
$[0,200\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{e}]\times [-8v_{th,s},8v_{th,s}]^{3}$ on a ![]() $256\times 24^{3}$ grid. Here,
$256\times 24^{3}$ grid. Here, ![]() $\unicode[STIX]{x1D70C}_{s}=v_{th,s}/\unicode[STIX]{x1D6FA}_{cs}$ is the gyroradius of species
$\unicode[STIX]{x1D70C}_{s}=v_{th,s}/\unicode[STIX]{x1D6FA}_{cs}$ is the gyroradius of species ![]() $s$. The current in Ampere’s law,
$s$. The current in Ampere’s law, ![]() $\boldsymbol{J}=\sum _{s}q_{s}\boldsymbol{M}_{h,1}^{s}+\tilde{\boldsymbol{J}}$, contains a perturbation which drives an oscillating magnetic field on top of a background magnetic field
$\boldsymbol{J}=\sum _{s}q_{s}\boldsymbol{M}_{h,1}^{s}+\tilde{\boldsymbol{J}}$, contains a perturbation which drives an oscillating magnetic field on top of a background magnetic field ![]() $\boldsymbol{B}=\hat{\boldsymbol{z}}B_{0}$
$\boldsymbol{B}=\hat{\boldsymbol{z}}B_{0}$
(One can think of this antenna as physically realizable as a highly transparent mesh of current carrying wires.) The current is turned on slowly over one pumping period using ![]() $\unicode[STIX]{x1D714}_{\text{ramp}}=\unicode[STIX]{x1D714}_{\text{pump}}$. This ramping phase ensures that the antenna is ‘turned on’ slowly and hence does not excite unwanted waves in the plasma. Further, we need to ensure that the plasma density is low enough that the electromagnetic waves are not ‘trapped’ in the density holes that are created around the antenna.
$\unicode[STIX]{x1D714}_{\text{ramp}}=\unicode[STIX]{x1D714}_{\text{pump}}$. This ramping phase ensures that the antenna is ‘turned on’ slowly and hence does not excite unwanted waves in the plasma. Further, we need to ensure that the plasma density is low enough that the electromagnetic waves are not ‘trapped’ in the density holes that are created around the antenna.
The tests shown here use ![]() $\unicode[STIX]{x1D714}_{\text{pump}}=0.1\unicode[STIX]{x1D6FA}_{ce}$,
$\unicode[STIX]{x1D714}_{\text{pump}}=0.1\unicode[STIX]{x1D6FA}_{ce}$, ![]() $x_{1}=50\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{e}$,
$x_{1}=50\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{e}$, ![]() $x_{2}=150\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{e}$,
$x_{2}=150\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{e}$, ![]() $\unicode[STIX]{x1D70E}_{J}=200\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{e}/256$ and
$\unicode[STIX]{x1D70E}_{J}=200\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{e}/256$ and ![]() $\unicode[STIX]{x1D6FA}_{ce}=2.5\unicode[STIX]{x1D714}_{pe}$. We employ a hydrogen mass ratio
$\unicode[STIX]{x1D6FA}_{ce}=2.5\unicode[STIX]{x1D714}_{pe}$. We employ a hydrogen mass ratio ![]() $m_{i}/m_{e}=1836$ and initialize electron and ion species as Maxwellians with zero mean flow, number density
$m_{i}/m_{e}=1836$ and initialize electron and ion species as Maxwellians with zero mean flow, number density ![]() $n\unicode[STIX]{x1D70C}_{e}^{3}=2.99\times 10^{5}$ and thermal speed
$n\unicode[STIX]{x1D70C}_{e}^{3}=2.99\times 10^{5}$ and thermal speed ![]() $v_{th,e}^{2}/c^{2}=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FA}_{ce}^{2}/[2\unicode[STIX]{x1D714}_{pe}^{2}(1+\unicode[STIX]{x1D70F})]$. The temperature ratio is
$v_{th,e}^{2}/c^{2}=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FA}_{ce}^{2}/[2\unicode[STIX]{x1D714}_{pe}^{2}(1+\unicode[STIX]{x1D70F})]$. The temperature ratio is ![]() $\unicode[STIX]{x1D70F}=T_{i}/T_{e}=1$ and the ratio between plasma and magnetic pressures is
$\unicode[STIX]{x1D70F}=T_{i}/T_{e}=1$ and the ratio between plasma and magnetic pressures is ![]() $\unicode[STIX]{x1D6FD}=2\times 10^{-4}$. With these quantities, the normalized background magnetic field amplitude is
$\unicode[STIX]{x1D6FD}=2\times 10^{-4}$. With these quantities, the normalized background magnetic field amplitude is ![]() $\unicode[STIX]{x1D716}_{0}\unicode[STIX]{x1D714}_{pe}B_{0}/(en)=\unicode[STIX]{x1D6FA}_{ce}/\unicode[STIX]{x1D714}_{pe}$, and we use the normalized driving current density amplitude
$\unicode[STIX]{x1D716}_{0}\unicode[STIX]{x1D714}_{pe}B_{0}/(en)=\unicode[STIX]{x1D6FA}_{ce}/\unicode[STIX]{x1D714}_{pe}$, and we use the normalized driving current density amplitude ![]() $\tilde{J}_{0}/(enc)=\unicode[STIX]{x1D6FA}_{ce}/(2\unicode[STIX]{x1D714}_{pe})$.
$\tilde{J}_{0}/(enc)=\unicode[STIX]{x1D6FA}_{ce}/(2\unicode[STIX]{x1D714}_{pe})$.

Figure 8. Time evolution of the magnetic field (a) from the magnetic pumping problem. As the antenna currents ramp up, an oscillating field is created that then transfers energy, via pitch-angle scattering, to the plasma. Panel (b) shows the time history of the field in the middle of the domain and panel (c) shows the integrated thermal energy history with various collisionalities. As the collision frequency increases, magnetic pumping is more effective in heating the plasma.
Figure 8 shows the evolution of the magnetic field and thermal energy. As the antenna current ramps up an oscillating magnetic field structure is created. The amplitude of oscillations are approximately 15 % of the background. This oscillating energy is then transferred to parallel heating, via pitch-angle scattering. This heating is shown in panel (c) which shows that as the collision frequency increases the plasma heating rate also increases.
Figure 9 shows the heating rate as a function of normalized collision frequency. The heating rate from standard magnetic pumping theory using the Dougherty FPO is ![]() $\unicode[STIX]{x1D6FE}_{\text{mp}}=(\text{d}W/\text{d}t)/W=(2/9)(n_{1}/n_{0})^{2}\unicode[STIX]{x1D714}_{\text{pump}}^{2}\unicode[STIX]{x1D708}/(\unicode[STIX]{x1D714}_{\text{pump}}^{2}+4\unicode[STIX]{x1D708}^{2})$, where the central density
$\unicode[STIX]{x1D6FE}_{\text{mp}}=(\text{d}W/\text{d}t)/W=(2/9)(n_{1}/n_{0})^{2}\unicode[STIX]{x1D714}_{\text{pump}}^{2}\unicode[STIX]{x1D708}/(\unicode[STIX]{x1D714}_{\text{pump}}^{2}+4\unicode[STIX]{x1D708}^{2})$, where the central density ![]() $n(t)=n_{0}+n_{1}\sin (\unicode[STIX]{x1D714}_{\text{pump}}t)$ (after the initial transients). (This heating rate is usually expressed in terms of the relative magnetic field oscillation amplitude,
$n(t)=n_{0}+n_{1}\sin (\unicode[STIX]{x1D714}_{\text{pump}}t)$ (after the initial transients). (This heating rate is usually expressed in terms of the relative magnetic field oscillation amplitude, ![]() $B_{1}/B_{0}$, but that is equal to
$B_{1}/B_{0}$, but that is equal to ![]() $n_{1}/n_{0}$ if the frozen-in condition is perfect. We discuss this further below.)
$n_{1}/n_{0}$ if the frozen-in condition is perfect. We discuss this further below.)

Figure 9. Heating rate via magnetic pumping, and an additional viscous heating mechanism, as a function of normalized collision frequency. The code agrees well with magnetic pumping at lower collision frequency, but shows an additional heating mechanism at higher collisionality due to the viscous damping of out-of-plane flows, which are included in the Braginskii-based theory.
Interestingly, the code agrees with this magnetic pumping theory at small ![]() $\unicode[STIX]{x1D708}/\unicode[STIX]{x1D714}_{\text{pump}}\lessapprox 1$, but indicates an additional heating mechanism for larger collisionality. This trend was also observed, but in a different parameter regime and using Coulomb collisions, in Lichko et al. (Reference Lichko, Egedal, Daughton and Kasper2017). There are several differences between this test case and the classic magnetic pumping test problem. One is that the pump frequency is large compared to the ion gyrofrequency, so the ions are close to stationary as the electrons undergo periodic compressions by the magnetic field. This means that a large electric field is generated in the
$\unicode[STIX]{x1D708}/\unicode[STIX]{x1D714}_{\text{pump}}\lessapprox 1$, but indicates an additional heating mechanism for larger collisionality. This trend was also observed, but in a different parameter regime and using Coulomb collisions, in Lichko et al. (Reference Lichko, Egedal, Daughton and Kasper2017). There are several differences between this test case and the classic magnetic pumping test problem. One is that the pump frequency is large compared to the ion gyrofrequency, so the ions are close to stationary as the electrons undergo periodic compressions by the magnetic field. This means that a large electric field is generated in the ![]() $x$ direction, which in turn drives large
$x$ direction, which in turn drives large ![]() $y$-directed
$y$-directed ![]() $E\times B$ flows in the electrons. We will not go through all of the details of the derivation here, but for
$E\times B$ flows in the electrons. We will not go through all of the details of the derivation here, but for ![]() $\unicode[STIX]{x1D708}\gg \unicode[STIX]{x1D714}_{\text{pump}}$, one can use Braginskii’s stress tensor to calculate the viscous heating of the electrons from these flows, finding that Braginskii’s heating rate is
$\unicode[STIX]{x1D708}\gg \unicode[STIX]{x1D714}_{\text{pump}}$, one can use Braginskii’s stress tensor to calculate the viscous heating of the electrons from these flows, finding that Braginskii’s heating rate is
where ![]() $\unicode[STIX]{x1D702}_{0}=0.96nT\unicode[STIX]{x1D70F}_{i}$ and
$\unicode[STIX]{x1D702}_{0}=0.96nT\unicode[STIX]{x1D70F}_{i}$ and ![]() $\unicode[STIX]{x1D702}_{1}=0.3nT/(\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FA}_{c}^{2})$ are two of Braginskii’s viscosity coefficients. These expressions are for
$\unicode[STIX]{x1D702}_{1}=0.3nT/(\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FA}_{c}^{2})$ are two of Braginskii’s viscosity coefficients. These expressions are for ![]() $\unicode[STIX]{x1D714}_{\text{pump}}\ll \unicode[STIX]{x1D708}\ll \unicode[STIX]{x1D6FA}_{c}$, but are generalized for arbitrary
$\unicode[STIX]{x1D714}_{\text{pump}}\ll \unicode[STIX]{x1D708}\ll \unicode[STIX]{x1D6FA}_{c}$, but are generalized for arbitrary ![]() $\unicode[STIX]{x1D708}/\unicode[STIX]{x1D6FA}_{c}$ in Braginskii’s article (Braginskii Reference Braginskii1965). The
$\unicode[STIX]{x1D708}/\unicode[STIX]{x1D6FA}_{c}$ in Braginskii’s article (Braginskii Reference Braginskii1965). The ![]() $\unicode[STIX]{x1D702}_{0}$ term is well known to be equivalent to magnetic pumping in the collisional limit (Kulsrud Reference Kulsrud2005; Schekochihin et al. Reference Schekochihin, Cowley, Kulsrud, Hammett and Sharma2005), and asymptotic matching can be done to extend the definition of
$\unicode[STIX]{x1D702}_{0}$ term is well known to be equivalent to magnetic pumping in the collisional limit (Kulsrud Reference Kulsrud2005; Schekochihin et al. Reference Schekochihin, Cowley, Kulsrud, Hammett and Sharma2005), and asymptotic matching can be done to extend the definition of ![]() $\unicode[STIX]{x1D702}_{0}$ into the low collisionality regime. This relates Braginskii’s collision time
$\unicode[STIX]{x1D702}_{0}$ into the low collisionality regime. This relates Braginskii’s collision time ![]() $\unicode[STIX]{x1D70F}$ to the Dougherty collision rate by
$\unicode[STIX]{x1D70F}$ to the Dougherty collision rate by ![]() $\unicode[STIX]{x1D70F}=0.52/\unicode[STIX]{x1D708}$. The
$\unicode[STIX]{x1D70F}=0.52/\unicode[STIX]{x1D708}$. The ![]() $\unicode[STIX]{x1D702}_{1}$ term represents additional viscous heating due to classical cross-field momentum transport.
$\unicode[STIX]{x1D702}_{1}$ term represents additional viscous heating due to classical cross-field momentum transport.
One can calculate the time-averaged squared shearing rate given by ![]() $\overline{\left(\unicode[STIX]{x2202}u_{x}/\unicode[STIX]{x2202}x\right)^{2}}=(1/2)\unicode[STIX]{x1D714}_{\text{pump}}^{2}(n_{1}/n_{0})^{2}$, and
$\overline{\left(\unicode[STIX]{x2202}u_{x}/\unicode[STIX]{x2202}x\right)^{2}}=(1/2)\unicode[STIX]{x1D714}_{\text{pump}}^{2}(n_{1}/n_{0})^{2}$, and ![]() $\overline{\left(\unicode[STIX]{x2202}u_{y}/\unicode[STIX]{x2202}x\right)^{2}}=(1/2)$
$\overline{\left(\unicode[STIX]{x2202}u_{y}/\unicode[STIX]{x2202}x\right)^{2}}=(1/2)$![]() $(\unicode[STIX]{x1D714}_{\text{pe}}^{4}/\unicode[STIX]{x1D6FA}_{c}^{2})~(n_{1}/n_{0})^{2}$, to find that the out-of-plane flows are actually larger, with
$(\unicode[STIX]{x1D714}_{\text{pe}}^{4}/\unicode[STIX]{x1D6FA}_{c}^{2})~(n_{1}/n_{0})^{2}$, to find that the out-of-plane flows are actually larger, with ![]() $\overline{u_{y}^{2}}\approx 2.56\,\overline{u_{x}^{2}}$ for our parameters. Viscous heating from damping these flows dominates at high collisionality for these parameters.
$\overline{u_{y}^{2}}\approx 2.56\,\overline{u_{x}^{2}}$ for our parameters. Viscous heating from damping these flows dominates at high collisionality for these parameters.
We have not tried to do a more detailed convergence study for this problem for a few reasons. One is that Braginskii’s transport calculations were based on the full Landau/Rosenbluth FPO, so the ratio of ![]() $\unicode[STIX]{x1D702}_{1}$ to
$\unicode[STIX]{x1D702}_{1}$ to ![]() $\unicode[STIX]{x1D702}_{0}$ will differ some for a transport theory based on the Dougherty operator. Another is that some of the above steps assumed that flows
$\unicode[STIX]{x1D702}_{0}$ will differ some for a transport theory based on the Dougherty operator. Another is that some of the above steps assumed that flows ![]() $u_{x}(x,t)$ and
$u_{x}(x,t)$ and ![]() $u_{y}(x,t)$ had a simple triangle wave shape in
$u_{y}(x,t)$ had a simple triangle wave shape in ![]() $x$ so that the plasma was undergoing uniform compression (or expansion) between the antennae, but in reality the compression is not exactly uniform. The heating rate shown in the figure is measured by computing the slope of the time-averaged temperature near the middle of the simulation domain,
$x$ so that the plasma was undergoing uniform compression (or expansion) between the antennae, but in reality the compression is not exactly uniform. The heating rate shown in the figure is measured by computing the slope of the time-averaged temperature near the middle of the simulation domain, ![]() $x=100\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{e}$, where the amplitude of the density oscillations used in the formulas is also measured. The finite value of
$x=100\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{e}$, where the amplitude of the density oscillations used in the formulas is also measured. The finite value of ![]() $\unicode[STIX]{x1D714}_{\text{pump}}/\unicode[STIX]{x1D6FA}_{c}=0.1$ should also be accounted for in a more detailed theory. While
$\unicode[STIX]{x1D714}_{\text{pump}}/\unicode[STIX]{x1D6FA}_{c}=0.1$ should also be accounted for in a more detailed theory. While ![]() $n_{1}/n_{0}=B_{1}/B_{0}$ in the ideal frozen-in limit, we find
$n_{1}/n_{0}=B_{1}/B_{0}$ in the ideal frozen-in limit, we find ![]() $n_{1}/n_{0}=0.131$ and
$n_{1}/n_{0}=0.131$ and ![]() $B_{1}/B_{0}=0.148$, so using
$B_{1}/B_{0}=0.148$, so using ![]() $n_{1}/n_{0}$ in the formulas gives a slightly smaller heating rate.
$n_{1}/n_{0}$ in the formulas gives a slightly smaller heating rate.
Although more could be done in studying this system, this magnetic pumping problem provides an integrated test of the interactions of the various pieces of the code for the Vlasov–Maxwell–Fokker–Planck system. These types of tests could be repeated in the future when the collision operator is extended to a more complete Rosenbluth form including the velocity dependence of the collision frequency.
8 Conclusion
In this paper we have presented a novel discontinuous Galerkin scheme to solve a class of nonlinear Fokker–Planck equations. Often, this operator is known as the ‘Dougherty’ operator or the ‘Lenard–Bernstein’ operator. These are simplified forms of the full Rosenbluth Fokker–Planck collision operator with specific choices of the mean momentum and energy tensor coefficients. Generalization to the full Rosenbluth collision operator could be considered in future work. Several novel algorithmic innovations are reported here. In particular we highlight:
(i) The use of two integration by parts is required to ensure that momentum and energy, in addition to density, are conserved by the discrete scheme. Without the second integration by parts jumps in the distribution function would be picked up and make the scheme non-conservative. Further, the diffusion term in the FPO requires accounting for finite velocity-space extents. See Scheme C, equation (4.13), and the conservation proofs in § 5. Interestingly, the requirements on momentum and energy conservation, combined with finite velocity extents, also lead to a unique and consistent method to determine the drift velocity and thermal speeds.
(ii) For piecewise linear basis sets energy conservation can be obtained by carefully defining the ‘star’ moments; see Proposition 4. Naively, one may have assumed that
 $\boldsymbol{v}^{2}$ must be included in the basis set. However, with the definition of the star moments we can continue to conserve energy exactly even when using
$\boldsymbol{v}^{2}$ must be included in the basis set. However, with the definition of the star moments we can continue to conserve energy exactly even when using  $p=1$ basis.
$p=1$ basis.
In addition, we have carefully described the conservation properties of the continuous Fokker–Planck operator. Some of this information is found elsewhere, however, it is useful to include it here, both for completeness and to show the analogous steps required to ensure discrete conservation. In particular, the proof of self-adjointness and the H-theorem shows that the inverse of the Maxwellian is the natural weight to define an inner product for the FPO. In the numerical scheme we show empirical evidence that the discrete entropy computed from the scheme is a non-decreasing function.
We have tested the scheme with a series of problems of increasing complexity. Simple relaxation tests with just the collision operator show that a square or bi-Maxwellian distribution quickly relaxes to a discrete Maxwellian. In fact, the steady-state solution obtained from evolving just the collision operator is the discrete Maxwellian, rather than the projection of the continuous Maxwellian on basis functions. Including the streaming term allows one to study neutral gas dynamics in the long-mean-free-path limit. A series of neutral shock problems and the relaxation tests show that momentum and energy are conserved to machine precision. Empirical evidence shows that discrete entropy is non-decreasing. Adding electrostatic terms to the Vlasov equations allowed us to study impact of collisions on Landau damping of Langmuir waves. Finally, the magnetic pumping problem tested the complete Vlasov–Maxwell–Fokker–Planck system, showing that complex collisional kinetic plasma problems can be studied.
The methods presented here are general, and can be extended in a number of ways. First, inter-species collisions are relatively easy to add, although the weak-division calculation of the appropriate intermediate drift velocity and diffusion rates has to be generalized for multi-species energy and momentum conservation. A general formulation is being implemented in Gkeyll and will be used to study both gyrokinetic and full-kinetic problems. The proofs of conservation extend to this general case in a straightforward way. The extension of the scheme to gyrokinetic equations in non-trivial and will be presented in a companion paper. A more challenging task is to extend the scheme to use the Rosenbluth potentials to compute the drag and diffusion coefficients. Rosenbluth potentials are determined by inverting elliptic equations in velocity space. The requirement of momentum and energy conservation will impose constrains on the elliptic solves and their boundary conditions, but these remain to be worked out. Further, to ensure an efficient scheme for the full system, the elliptic solves themselves will require fast methods. This extension forms part of our current algorithm development projects and will be reported on in the future.
Acknowledgements
We are grateful for insights from conversations with P. Cagas, T. Bernard, N. Mandell and other members of the Gkeyll team. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562, resources of the Argonne Leadership Computing Facility, which is a DOE Office of Science User Facility supported under Contract DE-AC02-06CH11357, as well as the Discovery cluster at Dartmouth College, the Eddy cluster at the Princeton Plasma Physics Laboratory, and the MIT-PSFC partition of the Engaging cluster at the MGHPCC facility (funded by DoE grant number DE-FG02-91-ER54109). A.H. and G.H. are supported by the High-Fidelity Boundary Plasma Simulation SciDAC Project, part of the DOE Scientific Discovery Through Advanced Computing (SciDAC) program, through the U.S. Department of Energy contract No. DE-AC02-09CH11466 for the Princeton Plasma Physics Laboratory. A.H. is also supported by Air Force Office of Scientific Research under grant no. FA9550-15-1-0193; M.F. is supported by U.S. Department of Energy grants DOE-SC-0010508 and DE-FC02-08ER54966. J.J. was supported by a NASA Earth and Space Science Fellowship (grant no. 80NSSC17K0428).
Editor William Dorland thanks the referees for their advice in evaluating this article.
Appendix A. Getting Gkeyll and reproducing the results
To allow interested readers to reproduce our results and also use Gkeyll for their applications, the code (in both binary and source format) and input files used here are available online. Full installation instructions for Gkeyll are provided on the The Gkeyll Team (2020) website. The code can be installed on Unix-like operating systems (including Mac OS and Windows using the Windows Subsystem for Linux) either by installing the pre-built binaries using the conda package manager (https://www.anaconda.com) or building the code via sources. The input files used here are under version control and can be obtained from the repository at https://github.com/ammarhakim/gkyl-paper-inp/tree/master/2020_JPP_VmLBO. Except for the magnetic pumping problem, all other tests can be run on a laptop.
Appendix B. H theorem, maximum entropy solution and self-adjointness of the D-FPO
For the single-species D-FPO considered throughout this paper
one can prove that a H-Theorem is satisfied, that is, the total entropy of the system is a non-decreasing function. This property means that that
To prove this, let ![]() $S=-\int _{-\infty }^{\infty }f\ln f\,\text{d}^{3}\boldsymbol{v}$. Then we have
$S=-\int _{-\infty }^{\infty }f\ln f\,\text{d}^{3}\boldsymbol{v}$. Then we have
Write the Fokker–Planck operator as
where ![]() $\boldsymbol{F}=(\boldsymbol{v}-\boldsymbol{u})f+v_{th}^{2}\unicode[STIX]{x1D735}_{\boldsymbol{v}}f$. We have dropped
$\boldsymbol{F}=(\boldsymbol{v}-\boldsymbol{u})f+v_{th}^{2}\unicode[STIX]{x1D735}_{\boldsymbol{v}}f$. We have dropped ![]() $\unicode[STIX]{x1D708}$ without any loss of generality. Substitute to get
$\unicode[STIX]{x1D708}$ without any loss of generality. Substitute to get
after integration by parts and assuming that ![]() $\boldsymbol{F}\rightarrow 0$ as
$\boldsymbol{F}\rightarrow 0$ as ![]() $\boldsymbol{v}\rightarrow \pm \infty$ faster than the logarithmic singularity from
$\boldsymbol{v}\rightarrow \pm \infty$ faster than the logarithmic singularity from ![]() $\ln f$. Substitute
$\ln f$. Substitute ![]() $\unicode[STIX]{x1D735}_{\boldsymbol{v}}f=(\boldsymbol{F}-(\boldsymbol{v}-\boldsymbol{u})f)/v_{th}^{2}$ to get
$\unicode[STIX]{x1D735}_{\boldsymbol{v}}f=(\boldsymbol{F}-(\boldsymbol{v}-\boldsymbol{u})f)/v_{th}^{2}$ to get
Using the definition of ![]() $\boldsymbol{F}$ the second term in this equation becomes
$\boldsymbol{F}$ the second term in this equation becomes
using integration by parts and the definitions of moments. Hence
as long as ![]() $f\geqslant 0$. We remark that for the full Vlasov–Maxwell–Fokker–Planck equation the integration needs to be performed over the complete phase space and not just velocity space, as done above. The definition of entropy and the fact that it increases monotonically can be used to prove the following.
$f\geqslant 0$. We remark that for the full Vlasov–Maxwell–Fokker–Planck equation the integration needs to be performed over the complete phase space and not just velocity space, as done above. The definition of entropy and the fact that it increases monotonically can be used to prove the following.
The maximum entropy solution to the Dougherty (and Rosenbluth–Landau) Fokker–Planck operator is the Maxwellian given by
Hence, in steady state (in the absence of the collisionless terms) the solution must relax to a Maxwellian. To show this we wish to maximize the entropy subject to the constraint that density, momentum and energy do not change during the evolution. Hence we need to find the extremum of
 $$\begin{eqnarray}\displaystyle S & = & \displaystyle -\int _{-\infty }^{\infty }f\ln f\,\text{d}^{3}\boldsymbol{v}+\unicode[STIX]{x1D706}_{0}\left(\int _{-\infty }^{\infty }f\,\text{d}^{3}\boldsymbol{v}-M_{0}\right)+\boldsymbol{\unicode[STIX]{x1D706}}_{1}\boldsymbol{\cdot }\left(\int _{-\infty }^{\infty }\boldsymbol{v}f\,\text{d}^{3}\boldsymbol{v}-\boldsymbol{M}_{1}\right)\nonumber\\ \displaystyle & & \displaystyle +\unicode[STIX]{x1D706}_{2}\left(\int _{-\infty }^{\infty }\boldsymbol{v}^{2}\,f\,\text{d}^{3}\boldsymbol{v}-M_{2}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S & = & \displaystyle -\int _{-\infty }^{\infty }f\ln f\,\text{d}^{3}\boldsymbol{v}+\unicode[STIX]{x1D706}_{0}\left(\int _{-\infty }^{\infty }f\,\text{d}^{3}\boldsymbol{v}-M_{0}\right)+\boldsymbol{\unicode[STIX]{x1D706}}_{1}\boldsymbol{\cdot }\left(\int _{-\infty }^{\infty }\boldsymbol{v}f\,\text{d}^{3}\boldsymbol{v}-\boldsymbol{M}_{1}\right)\nonumber\\ \displaystyle & & \displaystyle +\unicode[STIX]{x1D706}_{2}\left(\int _{-\infty }^{\infty }\boldsymbol{v}^{2}\,f\,\text{d}^{3}\boldsymbol{v}-M_{2}\right),\end{eqnarray}$$ where ![]() $\unicode[STIX]{x1D706}_{0},\boldsymbol{\unicode[STIX]{x1D706}}_{1}$ and
$\unicode[STIX]{x1D706}_{0},\boldsymbol{\unicode[STIX]{x1D706}}_{1}$ and ![]() $\unicode[STIX]{x1D706}_{2}$ are Lagrange multipliers. Varying this Lagrangian and applying the constraints to determine the Lagrange multipliers leads to the Maxwellian. Also, as the entropy is monotonically increasing the Maxwellian maximizes the entropy.
$\unicode[STIX]{x1D706}_{2}$ are Lagrange multipliers. Varying this Lagrangian and applying the constraints to determine the Lagrange multipliers leads to the Maxwellian. Also, as the entropy is monotonically increasing the Maxwellian maximizes the entropy.
Finally, the Dougherty Fokker–Planck operator is self-adjoint: for arbitrary functions ![]() $g(t,\boldsymbol{x},\boldsymbol{v})$,
$g(t,\boldsymbol{x},\boldsymbol{v})$, ![]() $f(t,\boldsymbol{x},\boldsymbol{v})$
$f(t,\boldsymbol{x},\boldsymbol{v})$
with the inner product defined as
where ![]() $f_{M}$ is the Maxwellian that satisfies
$f_{M}$ is the Maxwellian that satisfies ![]() $C[f_{M}]=0$. Integrating equation (B 11) by parts we get
$C[f_{M}]=0$. Integrating equation (B 11) by parts we get
We have the identity
Using this leads to
This is symmetric in ![]() $f$ and
$f$ and ![]() $g$ from which the self-adjoint property follows.
$g$ from which the self-adjoint property follows.
We note that the self-adjointness of the full Rosenbluth–Landau FPO can only be proved for the linearized operator. The self-adjoint property indicates that the eigenvalues of the operator are all real and hence all solutions are damped. One can show that the eigenfunctions of the operator equation (B 1) are simply the multi-dimensional tensor Hermite functions (Grant & Feix Reference Grant and Feix1967; Hammett et al. Reference Hammett, Beer, Dorland, Cowley and Smith1993; Harris Reference Harris2004; Patarroyo Reference Patarroyo2019) and each mode is damped proportional to the mode number.
If we set ![]() $g=f$ in (B 15) we get
$g=f$ in (B 15) we get
 $$\begin{eqnarray}\displaystyle \int _{-\infty }^{\infty }\frac{f}{f_{M}}\frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}t}\,\text{d}^{3}\boldsymbol{v} & = & \displaystyle \frac{\text{d}}{\text{d}t}\int _{-\infty }^{\infty }\frac{f^{2}}{f_{M}}\,\text{d}^{3}\boldsymbol{v}=\langle fC[f]\rangle \nonumber\\ \displaystyle & = & \displaystyle -v_{th}^{2}\int _{-\infty }^{\infty }f_{M}\unicode[STIX]{x1D735}_{\boldsymbol{v}}\left(\frac{f}{f_{M}}\right)\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{v}}\left(\frac{f}{f_{M}}\right)\,\text{d}^{3}\boldsymbol{v}\leqslant 0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{-\infty }^{\infty }\frac{f}{f_{M}}\frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}t}\,\text{d}^{3}\boldsymbol{v} & = & \displaystyle \frac{\text{d}}{\text{d}t}\int _{-\infty }^{\infty }\frac{f^{2}}{f_{M}}\,\text{d}^{3}\boldsymbol{v}=\langle fC[f]\rangle \nonumber\\ \displaystyle & = & \displaystyle -v_{th}^{2}\int _{-\infty }^{\infty }f_{M}\unicode[STIX]{x1D735}_{\boldsymbol{v}}\left(\frac{f}{f_{M}}\right)\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{v}}\left(\frac{f}{f_{M}}\right)\,\text{d}^{3}\boldsymbol{v}\leqslant 0.\end{eqnarray}$$ This shows that the FP operator will decay ![]() $f^{2}/f_{M}$ integrated over velocity space.
$f^{2}/f_{M}$ integrated over velocity space.
The proof of self-adjoint property shows that ![]() $1/f_{M}$ is the natural weight that must be used in defining an inner product for the FP equation. In fact, the
$1/f_{M}$ is the natural weight that must be used in defining an inner product for the FP equation. In fact, the ![]() $L_{2}$ norm (without the weight) of the distribution is not monotonic in general. To see this, use the definition of the Fokker–Planck operator, and integrate by parts
$L_{2}$ norm (without the weight) of the distribution is not monotonic in general. To see this, use the definition of the Fokker–Planck operator, and integrate by parts
Write the first term as
The second term is a total derivative and will vanish on integration. This leaves
Performing integration by parts on the first term
For a Maxwellian the right-hand side vanishes but one can construct perturbations on it that may change the sign. To see this, perform a perturbation around a Maxwellian ![]() $f=f_{M}+\unicode[STIX]{x1D6FF}f$ to get the variation. Without loss of generality, the 1X1V, no-drift case gives,
$f=f_{M}+\unicode[STIX]{x1D6FF}f$ to get the variation. Without loss of generality, the 1X1V, no-drift case gives,
Clearly, ![]() $\unicode[STIX]{x1D6FF}f$ can be of any sign. This result shows that the
$\unicode[STIX]{x1D6FF}f$ can be of any sign. This result shows that the ![]() $L_{2}$ norm is not monotonic and the Maxwellian is not the extremum of the
$L_{2}$ norm is not monotonic and the Maxwellian is not the extremum of the ![]() $L_{2}$ norm. Physically, as the drag velocity
$L_{2}$ norm. Physically, as the drag velocity ![]() $\boldsymbol{v}-\boldsymbol{u}$ is compressible the contribution from the drag term cannot be turned into a total derivative. The compressibility of the drag term is in contrast to the collisionless case, in which the phase-space velocity is incompressible and hence the phase-space integrated
$\boldsymbol{v}-\boldsymbol{u}$ is compressible the contribution from the drag term cannot be turned into a total derivative. The compressibility of the drag term is in contrast to the collisionless case, in which the phase-space velocity is incompressible and hence the phase-space integrated ![]() $f^{2}$ is constant. However, in kinetic theory the essential ingredient is a H-theorem that shows the maximum entropy solution is the Maxwellian, and the Fokker–Planck operator, even with our approximations, possesses one.
$f^{2}$ is constant. However, in kinetic theory the essential ingredient is a H-theorem that shows the maximum entropy solution is the Maxwellian, and the Fokker–Planck operator, even with our approximations, possesses one.
Another way to think about the ![]() $1/f_{M}$ weighting of the inner product is to note that it naturally arises when measuring how much a distribution function deviates away from a Maxwellian in terms of entropy. In other words, writing
$1/f_{M}$ weighting of the inner product is to note that it naturally arises when measuring how much a distribution function deviates away from a Maxwellian in terms of entropy. In other words, writing ![]() $f=f_{M}+\unicode[STIX]{x1D6FF}f$, then the entropy
$f=f_{M}+\unicode[STIX]{x1D6FF}f$, then the entropy ![]() $S[f]=-\int \text{d}v\,f\ln (f)$ as a functional of
$S[f]=-\int \text{d}v\,f\ln (f)$ as a functional of ![]() $f$ can be written as
$f$ can be written as ![]() $S[f_{M}+\unicode[STIX]{x1D6FF}f]=S[f_{M}]-(1/2)\int \text{d}v\,(\unicode[STIX]{x1D6FF}f)^{2}/f_{M}+\cdots$ through second order. This expansion is consistent with the result that any deviation away from a Maxwellian is a state of lower entropy. Note that, to derive this, we have made use of
$S[f_{M}+\unicode[STIX]{x1D6FF}f]=S[f_{M}]-(1/2)\int \text{d}v\,(\unicode[STIX]{x1D6FF}f)^{2}/f_{M}+\cdots$ through second order. This expansion is consistent with the result that any deviation away from a Maxwellian is a state of lower entropy. Note that, to derive this, we have made use of ![]() $\int \text{d}v\,v^{p}\unicode[STIX]{x1D6FF}f=0$ for
$\int \text{d}v\,v^{p}\unicode[STIX]{x1D6FF}f=0$ for ![]() $p=0,1,2$ because the Maxwellian
$p=0,1,2$ because the Maxwellian ![]() $f_{M}$ has the same zeroth through second moments as
$f_{M}$ has the same zeroth through second moments as ![]() $f$. This norm for
$f$. This norm for ![]() $\unicode[STIX]{x1D6FF}f$ is equivalent to a norm on the total
$\unicode[STIX]{x1D6FF}f$ is equivalent to a norm on the total ![]() $f$, plus a constant, since
$f$, plus a constant, since ![]() $\int \text{d}v\,f^{2}/f_{M}=\int \text{d}v\,(f_{M}+\unicode[STIX]{x1D6FF}f)^{2}/f_{M}=n_{0}+\int \text{d}v\,(\unicode[STIX]{x1D6FF}f)^{2}/f_{M}$, where the density
$\int \text{d}v\,f^{2}/f_{M}=\int \text{d}v\,(f_{M}+\unicode[STIX]{x1D6FF}f)^{2}/f_{M}=n_{0}+\int \text{d}v\,(\unicode[STIX]{x1D6FF}f)^{2}/f_{M}$, where the density ![]() $n_{0}=\int \text{d}v\,f$ is conserved by the collision operator. This result that
$n_{0}=\int \text{d}v\,f$ is conserved by the collision operator. This result that ![]() $S[f_{M}+\unicode[STIX]{x1D6FF}f]=\text{ constant}-(1/2)\int \,\text{d}v\,f^{2}/f_{M}+\cdots \,$ shows a relationship between the collision operator causing the entropy to be never decreasing and the
$S[f_{M}+\unicode[STIX]{x1D6FF}f]=\text{ constant}-(1/2)\int \,\text{d}v\,f^{2}/f_{M}+\cdots \,$ shows a relationship between the collision operator causing the entropy to be never decreasing and the ![]() $1/f_{M}$-weighted norm to be never increasing.
$1/f_{M}$-weighted norm to be never increasing.